Evaluation of Multiple Methods for the Production of Continuous Evapotranspiration Estimates from TIR Remote Sensing
Abstract
1. Introduction
- To assess the performances of 8 reference quantities to reconstruct seasonal ET from discontinuous estimates and as a function of the revisit frequency over multiple agricultural ecosystems and climatic areas; an important point within this objective is to test the interest of interpolation reference quantities that introduce information on rain events for resetting the surface water status;
- To estimate the relative importance of the interpolation with respect to the error or uncertainties in the estimates of ET from a remote sensing-based model.
2. Materials and Methods
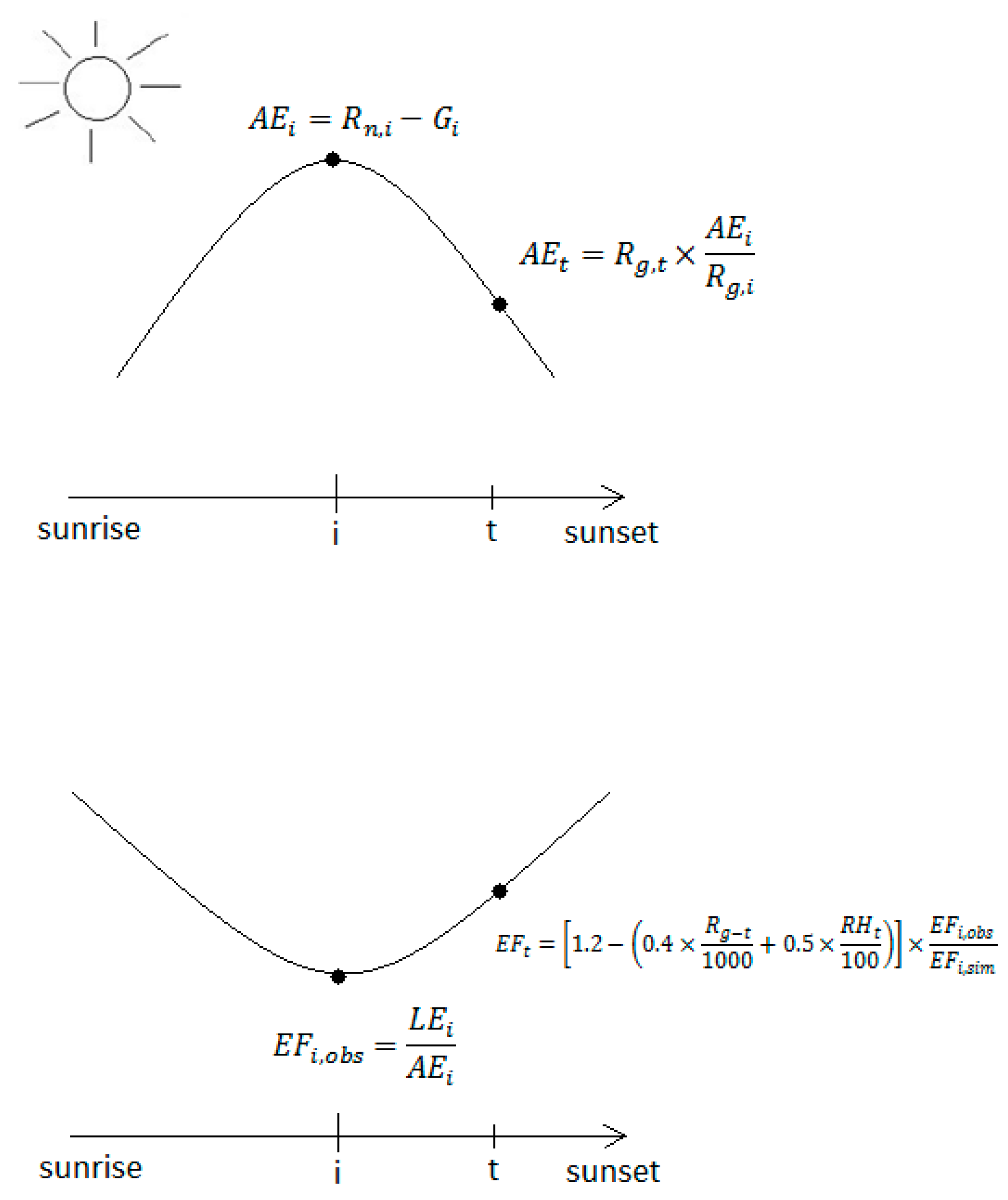
2.1. Rationale and Outlines of the Method
2.2. In Situ Datasets
2.3. Remote Sensing Estimates of ET—SPARSE Model
2.4. Reconstruction of Seasonal ET from Instantaneous Latent Heat Flux on Clear Sky Days—Reference Quantities
2.5. Reconstruction of Daily ET from Instantaneous Latent Heat Flux
2.6. Evaluation of the Results and Statistical Metrics
3. Results
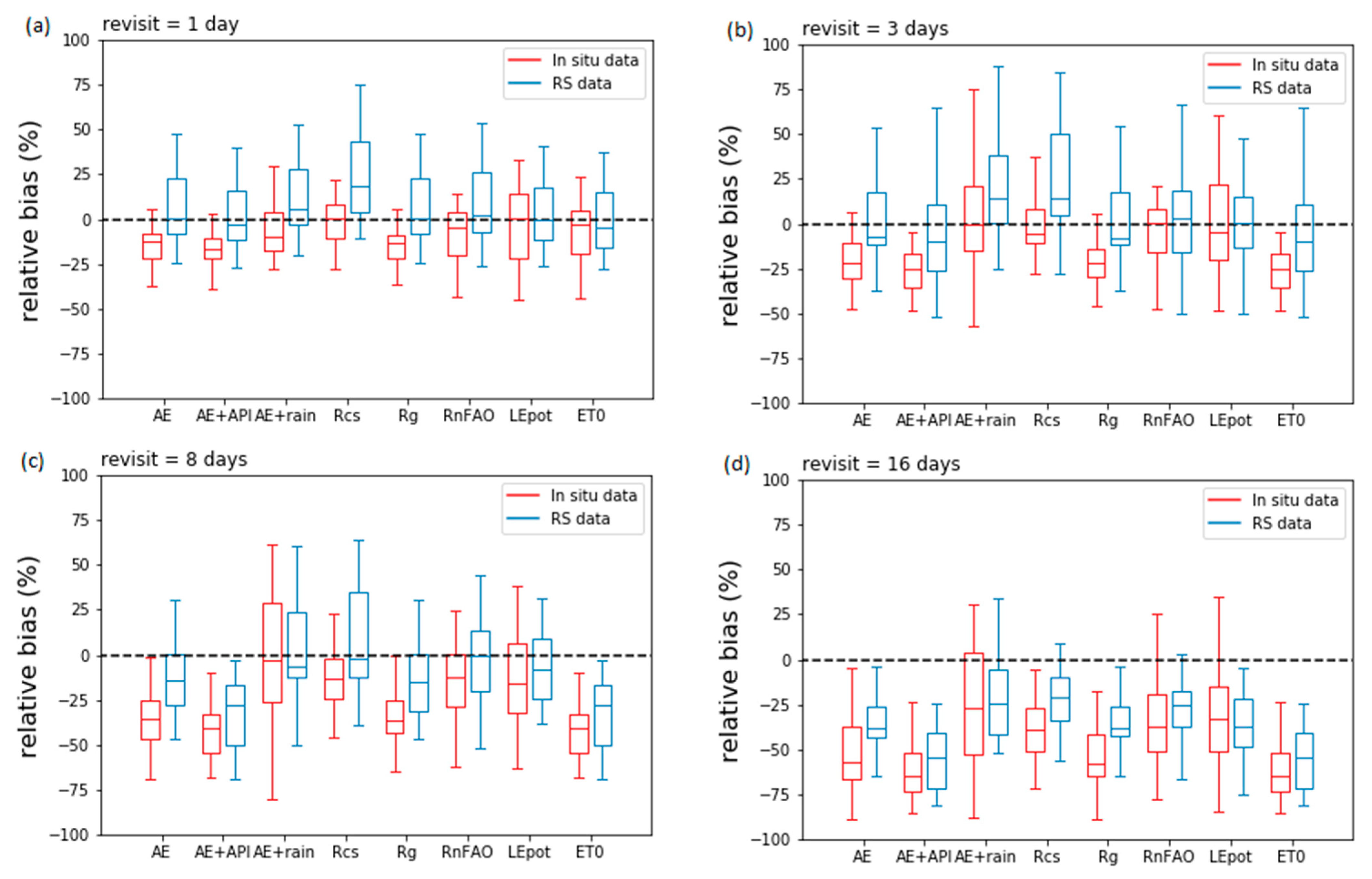
3.1. Reconstruction of Daily ET from Instantaneous Latent Heat Flux on All Clear Sky Days
3.2. Accuracy of the Different Reference Quantities at Seasonal Scale
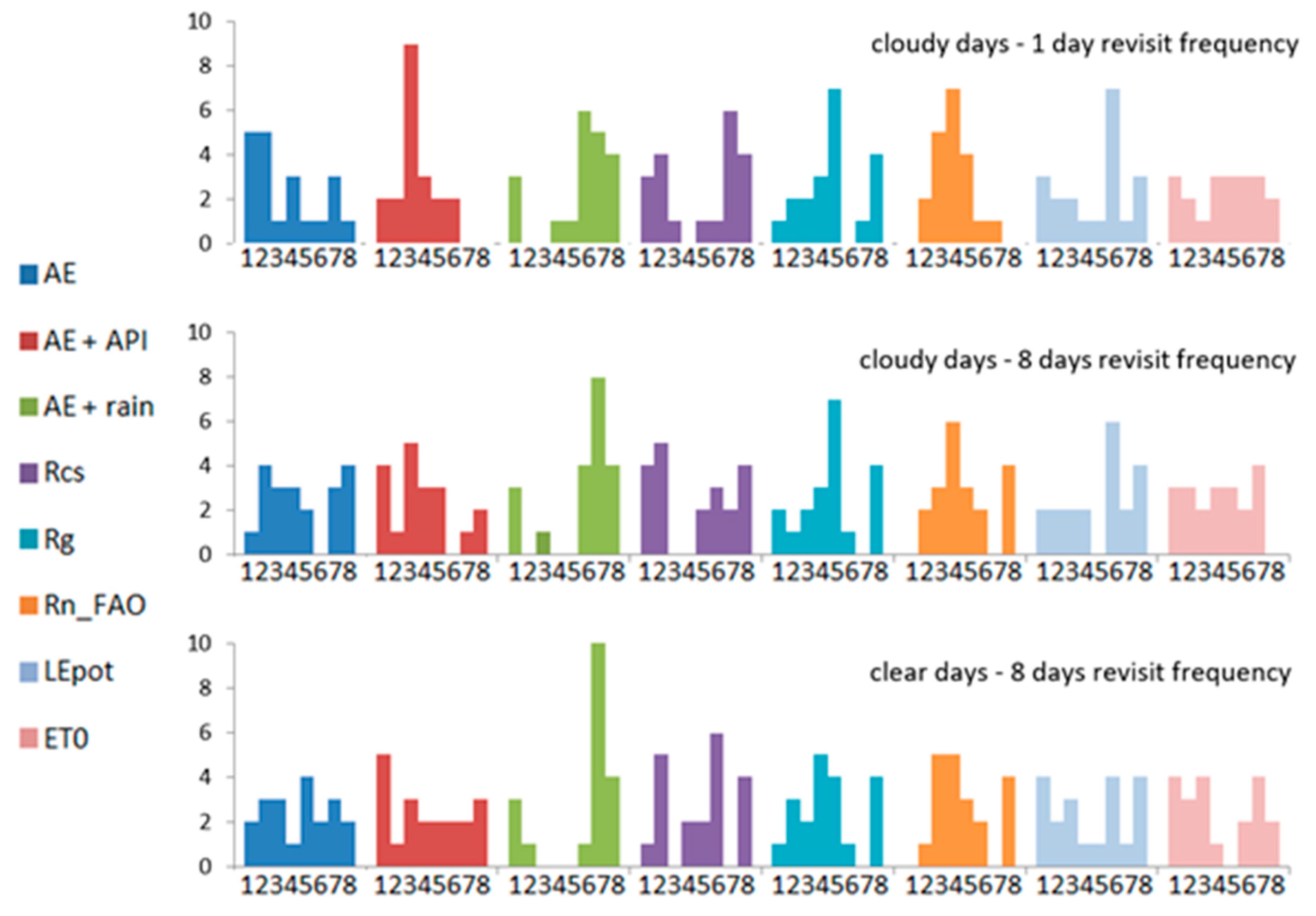
3.3. Clear Sky vs. Cloudy Days
4. Discussion
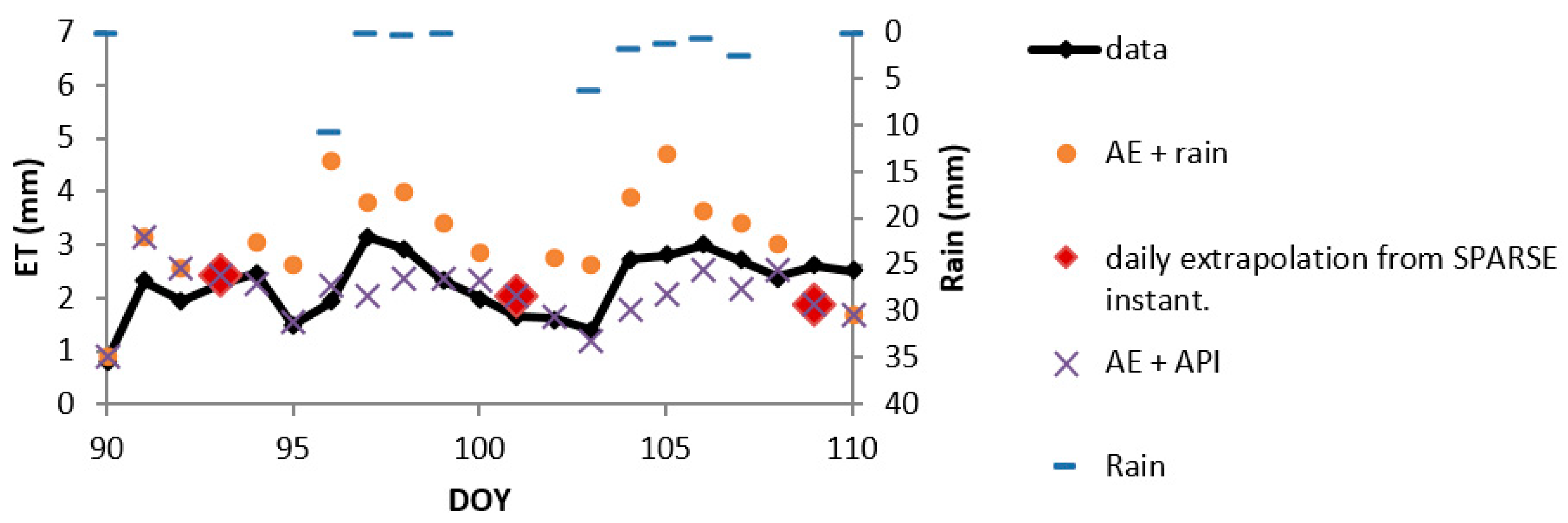
4.1. Extrapolation Errors
4.2. Accuracy of the Temporal Upscaling via Interpolation
4.3. Choice of the Reference Quantity Depends on the Objectives
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
| ETobs | ETAE | ETAE+API | ETAE+rain | ETRcs | ETRg | ETRn_FAO | ETLEpot | ETET0 | |
|---|---|---|---|---|---|---|---|---|---|
| Aur W 2006 | 375 | 344 (−8) | 333 (−11) | 366 (−2) | 401 (+7) | 339 (−10) | 388 (+4) | 498 (+33) | 400 (+7) |
| Aur Su 2007 | 268 | 216 (−19) | 220 (−18) | 274 (+2) | 289 (+8) | 217 (−19) | 273 (+2) | 274 (+2) | 254 (−5) |
| Aur W 2008 | 218 | 258 (+18) | 262 (+20) | 297 (+36) | 319 (+46) | 257 (+18) | 242 (+11) | 283 (+19) | 266 (+22) |
| Lam W 2007 | 340 | 394 (+16) | 382 (+12) | 440 (+29) | 477 (+40) | 390 (+15) | 389 (+14) | 444 (+31) | 413 (+22) |
| Lam C 2008 | 427 | 270 (−37) | 260 (−39) | 309 (−28) | 334 (−22) | 271 (−37) | 270 (−37) | 263 (−39) | 268 (−37) |
| Lam W 2009 | 251 | 220 (−13) | 224 (−11) | 285 (+13) | 306 (+22) | 219 (−13) | 270 (+7) | 300 (+19) | 245 (−3) |
| Lam C 2010 | 361 | 204 (−43) | 209 (−42) | 260 (−28) | 261 (−28) | 204 (−43) | 204 (−43) | 197 (−45) | 200 (−45) |
| Lam C 2012 | 416 | 321 (−23) | 299 (−28) | 357 (−14) | 387 (−7) | 322 (−23) | 303 (−27) | 319 (−23) | 322 (−23) |
| Lam C 2014 | 389 | 308 (−21) | 304 (−22) | 352 (−10) | 344 (−12) | 314 (−19) | 312 (−20) | 286 (−27) | 276 (−29) |
| Lam C 2015 | 531 | 408 (−23) | 415 (−22) | 390 (−27) | 476 (−10) | 408 (−23) | 408 (−23) | 400 (−25) | 656 (+24) |
| Avi P 2005 | 233 | 209 (−10) | 209 (−10) | 209 (−10) | 233 (0) | 209 (−10) | 246 (+6) | 266 (+14) | 225 (−3) |
| Avi W 2006 | 375 | 337 (−10) | 337 (−10) | 337 (−10) | 393 (+5) | 337 (−10) | 366 (−3) | 424 (+13) | 393 (+5) |
| Avi So 2007 | 386 | 338 (−12) | 338 (−12) | 338 (−12) | 372 (−4) | 338 (−12) | 356 (−8) | 352 (−9) | 351 (−9) |
| Avi W 2008 | 424 | 351 (−17) | 351 (−17) | 351 (−17) | 427 (+1) | 352 (−17) | 394 (−7) | 482 (+14) | 402 (−5) |
| Avi W 2012 | 303 | 278 (−8) | 253 (−16) | 311 (+3) | 326 (+8) | 278 (−8) | 277 (−8) | 309 (+2) | 305 (+1) |
| Wan M 2009 | 339 | 257 (−24) | 258 (−24) | 279 (−18) | 278 (−18) | 257 (−24) | 296 (−13) | 265 (−22) | 274 (−19) |
| Wan S 2009 | 335 | 262 (−22) | 260 (−22) | 276 (−18) | 285 (−15) | 263 (−22) | 267 (−20) | 264 (−21) | 270 (−19) |
| Kai W 2012 | 265 | 280 (+6) | 274 (+3) | 287 (+9) | 308 (+16) | 280 (+6) | 291 (+10) | 279 (+5) | 277 (+5) |
| Kai Or 2012/15 | 558 | 510 (−9) | 451 (−19) | 568 (+2) | 524 (−6) | 485 (−13) | 579 (+4) | 551 (−1) | 552 (−1) |
| Hao W 2004 | 288 | 279 (−3) | 274 (−5) | 304 (+6) | 318 (+10) | 279 (−3) | 280 (−3) | 284 (−2) | 282 (−2) |
| overall cumul | 7082 | 6044 | 5913 | 6590 | 7058 | 6019 | 6411 | 6740 | 6631 |
| overall relative bias (%) | −15 | −17 | −7 | −0 | −15 | −9 | −5 | −6 |
| ETobs | ETsparse | ETAE | ETAE+API | ETAE+rain | ETRcs | ETRg | ETRn_FAO | ETLEpot | ETET0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Aur W 2006 | 375 | 299 | 349 (−7) | 335 (−11) | 365 (−3) | 425 (+13) | 349 (−7) | 362 (−3) | 338 (−10) | 332 (−11) |
| Aur Su 2007 | 268 | 368 | 329 (+23) | 301 (+12) | 343 (+28) | 451 (+69) | 329 (+23) | 335 (+25) | 318 (+19) | 303 (+13) |
| Aur W 2008 | 218 | 202 | 261 (+19) | 244 (+12) | 283 (+29) | 382 (+75) | 261 (+19) | 274 (+26) | 241 (+10) | 230 (+5) |
| Lam W 2007 | 340 | 533 | 431 (+27) | 409 (+20) | 456 (+34) | 575 (+69) | 431 (+27) | 447 (+32) | 398 (+17) | 393 (+16) |
| Lam C 2008 | 427 | 396 | 424 (−1) | 396 (−7) | 435 (+2) | 518 (+21) | 423 (−1) | 434 (+2) | 420 (−2) | 395 (−8) |
| Lam W 2009 | 251 | 340 | 370 (+47) | 350 (+40) | 384 (+53) | 393 (+56) | 370 (+47) | 385 (+53) | 353 (+41) | 346 (+38) |
| Lam C 2010 | 361 | 401 | 446 (+24) | 430 (+19) | 473 (+31) | 565 (+57) | 447 (+24) | 443 (+23) | 432 (+20) | 425 (+18) |
| Lam C 2012 | 416 | 364 | 407 (−2) | 376 (−10) | 432 (+4) | 483 (+16) | 399 (−4) | 385 (−8) | 326 (−22) | 328 (−22) |
| Lam C 2014 | 389 | 319 | 367 (−6) | 350 (−10) | 404 (+4) | 400 (+3) | 372 (−5) | 363 (−7) | 342 (−12) | 323 (−17) |
| Lam C 2015 | 531 | 371 | 402 (−24) | 388 (−27) | 423 (−20) | 473 (−11) | 402 (−24) | 393 (−26) | 392 (−26) | 384 (−28) |
| Avi P 2005 | 233 | 286 | 286 (+23) | 286 (+23) | 286 (+23) | 319 (+37) | 286 (+23) | 293 (+26) | 278 (+20) | 277 (+19) |
| Avi W 2006 | 375 | 409 | 429 (+14) | 429 (+14) | 429 (+14) | 481 (+28) | 430 (+14) | 455 (+21) | 413 (+10) | 407 (+8) |
| Avi So 2007 | 386 | 404 | 390 (+1) | 390 (+1) | 390 (+1) | 425 (+10) | 391 (+1) | 398 (+3) | 386 (0) | 380 (−1) |
| Avi W 2008 | 424 | 342 | 368 (−13) | 368 (−13) | 368 (−13) | 440 (+4) | 369 (−13) | 391 (−8) | 344 (−19) | 341 (−19) |
| Avi W 2012 | 303 | 357 | 370 (+22) | 343 (+13) | 375 (+24) | 422 (+39) | 370 (+22) | 391 (+29) | 351 (+16) | 349 (+15) |
| Wan M 2009 | 339 | 417 | 428 (+26) | 418 (+23) | 434 (+28) | 458 (+35) | 428 (+26) | 438 (+29) | 429 (+27) | 430 (+27) |
| Wan S 2009 | 335 | 448 | 285 (−15) | 282 (−16) | 294 (−12) | 304 (−9) | 285 (−15) | 291 (−13) | 288 (−14) | 283 (−15) |
| Kai W 2012 | 265 | 297 | 252 (−5) | 239 (−10) | 254 (−4) | 285 (+7) | 252 (−5) | 259 (−2) | 249 (−6) | 243 (−8) |
| Kai Or 2013 | 558 | 484 | 484 (−13) | 448 (−20) | 598 (+7) | 529 (−5) | 484 (−13) | 517 (−7) | 530 (−5) | 482 (−14) |
| Hao W 2004 | 288 | 271 | 252 (−13) | 248 (−14) | 273 (−5) | 284 (−1) | 252 (−13) | 255 (−12) | 257 (−11) | 243 (−16) |
| overall cumul | 7082 | 7308 | 7330 | 7030 | 7699 | 8612 | 7330 | 7509 | 7085 | 6894 |
| overall relative bias vs. measurements (%) | - | 3 | 4 | −1 | 9 | 22 | 4 | 6 | 0 | −3 |
| overall relative bias vs. SPARSE (%) | −3 | - | 0 | −4 | 5 | 18 | 0 | 3 | −3 | −6 |
References
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Boulet, G.; Olioso, A.; Ceschia, E.; Marloie, O.; Coudert, B.; Rivalland, V.; Chirouze, J.; Chehbouni, G. An empirical expression to relate aerodynamic and surface temperatures for use within single-source energy balance models. Agric. For. Meteorol. 2012, 161, 148–155. [Google Scholar] [CrossRef]
- Hain, C.R.; Mecikalski, J.R.; Anderson, M.C. Retrieval of an Available Water-Based Soil Moisture Proxy from Thermal Infrared Remote Sensing. Part I: Methodology and Validation. J. Hydrometeorol. 2009, 10, 665–683. [Google Scholar] [CrossRef]
- Fisher, J.B.; Lee, B.; Purdy, A.J.; Halverson, G.H.; Dohlen, M.B.; Cawse-Nicholson, K.; Wang, A.; Anderson, R.G.; Aragon, B.; Arain, M.A.; et al. ECOSTRESS: NASA’s Next Generation Mission to Measure Evapotranspiration from the International Space Station. Water Resour. Res. 2020, 56, e2019WR026058. [Google Scholar] [CrossRef]
- Hulley, G.; Shivers, S.; Wetherley, E.; Cudd, R. New ECOSTRESS and MODIS Land Surface Temperature Data Reveal Fine-Scale Heat Vulnerability in Cities: A Case Study for Los Angeles County, California. Remote Sens. 2019, 11, 2136. [Google Scholar] [CrossRef]
- Koetz, B.; Bastiaanssen, W.; Berger, M.; Defourny, P. High Spatio-Temporal Resolution Land Surface Temperature Mission—A Copernicus candidate mission in support of agricultural monitoring. In IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium; IEEE: Piscataway, NY, USA, 2018; Available online: https://dial.uclouvain.be/pr/boreal/object/boreal:201985 (accessed on 19 June 2020).
- Lagouarde, J.; Bhattacharya, B.K.; Crébassol, P.; Gamet, P.; Babu, S.S.; Boulet, G.; Briottet, X.; Buddhiraju, K.M.; Cherchali, S.; Dadou, I.; et al. The Indian-French Trishna Mission: Earth Observation in the Thermal Infrared with High Spatio-Temporal Resolution. In IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium; IEEE: Piscataway, NY, USA, 2018; pp. 4078–4081. [Google Scholar]
- Jackson, R.D.; Reginato, R.J.; Idso, S.B. Wheat canopy temperature: A practical tool for evaluating water requirements. Water Resour. Res. 1977, 13, 651–656. [Google Scholar] [CrossRef]
- Jackson, R.D.; Hatfield, J.L.; Reginato, R.J.; Idso, S.B.; Pinter, P.J. Estimation of daily evapotranspiration from one time-of-day measurements. Agric. Water Manag. 1983, 7, 351–362. [Google Scholar] [CrossRef]
- Brutsaert, W.; Sugita, M. Application of self-preservation in the diurnal evolution of the surface energy budget to determine daily evaporation. J. Geophys. Res. Atmos. 1992, 97, 18377–18382. [Google Scholar] [CrossRef]
- Crago, R.D. Conservation and variability of the evaporative fraction during the daytime. J. Hydrol. 1996, 180, 173–194. [Google Scholar] [CrossRef]
- Nichols, W.E.; Cuenca, R.H. Evaluation of the evaporative fraction for parameterization of the surface energy balance. Water Resour. Res. 1993, 29, 3681–3690. [Google Scholar] [CrossRef]
- Zhang, L.; Lemeur, R. Evaluation of daily evapotranspiration estimates from instantaneous measurements. Agric. For. Meteorol. 1995, 74, 139–154. [Google Scholar] [CrossRef]
- Ryu, Y.; Baldocchi, D.D.; Black, T.A.; Detto, M.; Law, B.E.; Leuning, R.; Miyata, A.; Reichstein, M.; Vargas, R.; Ammann, C.; et al. On the temporal upscaling of evapotranspiration from instantaneous remote sensing measurements to 8-day mean daily-sums. Agric. For. Meteorol. 2012, 152, 212–222. [Google Scholar] [CrossRef]
- Van Niel, T.G.; McVicar, T.R.; Roderick, M.L.; van Dijk, A.I.J.M.; Beringer, J.; Hutley, L.B.; van Gorsel, E. Upscaling latent heat flux for thermal remote sensing studies: Comparison of alternative approaches and correction of bias. J. Hydrol. 2012, 468–469, 35–46. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Menenti, M.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Evett, S.R.; Howell, T.A.; Tolk, J.A. Comparison of Five Models to Scale Daily Evapotranspiration from One-Time-of-Day Measurements. Trans. ASABE 2006, 49, 10. [Google Scholar] [CrossRef]
- Crago, R.; Brutsaert, W. Daytime evaporation and the self-preservation of the evaporative fraction and the Bowen ratio. J. Hydrol. 1996, 178, 241–255. [Google Scholar] [CrossRef]
- Delogu, E.; Boulet, G.; Olioso, A.; Coudert, B.; Chirouze, J.; Ceschia, E.; Le Dantec, V.; Marloie, O.; Chehbouni, G.; Lagouarde, J.-P. Reconstruction of temporal variations of evapotranspiration using instantaneous estimates at the time of satellite overpass. Hydrol. Earth Syst. Sci. 2012, 16, 2995–3010. [Google Scholar] [CrossRef]
- Hoedjes, J.C.B.; Chehbouni, G.; Jacob, F.; Ezzahar, J.; Boulet, G. Deriving daily evapotranspiration from remotely sensed instantaneous evaporative fraction over olive orchard in semi-arid Morocco. J. Hydrol. 2008, 254, 53–64. [Google Scholar] [CrossRef]
- Suleiman, A.; Crago, R. Hourly and Daytime Evapotranspiration from Grassland Using Radiometric Surface Temperatures. Agron. J. 2004, 96, 384–390. [Google Scholar] [CrossRef]
- Van Niel, T.G.; McVicar, T.R.; Roderick, M.L.; van Dijk, A.I.J.M.; Renzullo, L.J.; van Gorsel, E. Correcting for systematic error in satellite-derived latent heat flux due to assumptions in temporal scaling: Assessment from flux tower observations. J. Hydrol. 2011, 409, 140–148. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Gao, F.; Hain, C.R.; Kustas, W.P. Mapping daily evapotranspiration at field scales over rainfed and irrigated agricultural areas using remote sensing data fusion. Agric. For. Meteorol. 2014, 186, 1–11. [Google Scholar] [CrossRef]
- Guillevic, P.C.; Olioso, A.; Hook, S.J.; Fisher, J.B.; Lagouarde, J.-P.; Vermote, E.F. Impact of the Revisit of Thermal Infrared Remote Sensing Observations on Evapotranspiration Uncertainty—A Sensitivity Study Using AmeriFlux Data. Remote Sens. 2019, 11, 573. [Google Scholar] [CrossRef]
- Lhomme, J.-P.; Elguero, E. Examination of evaporative fraction diurnal behaviour using a soil-vegetation model coupled with a mixed-layer model. Hydrol. Earth Syst. Sci. 1999, 3, 259–270. [Google Scholar] [CrossRef]
- Peng, S.; Piao, S.; Wang, T.; Sun, J.; Shen, Z. Temperature sensitivity of soil respiration in different ecosystems in China. Soil Biol. Biochem. 2009, 41, 1008–1014. [Google Scholar] [CrossRef]
- Gentine, P.; Entekhabi, D.; Chehbouni, A.; Boulet, G.; Duchemin, B. Analysis of evaporative fraction diurnal behaviour. Agric. For. Meteorol. 2007, 143, 13–29. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Alfieri, J.G.; Anderson, M.C.; Kustas, W.P.; Cammalleri, C. Effect of the revisit interval and temporal upscaling methods on the accuracy of remotely sensed evapotranspiration estimates. Hydrol. Earth Syst. Sci. 2017, 21, 83–98. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guideline for computing crop water requirements. Irrig. Drain. 1998, 56, 300. [Google Scholar]
- McNaughton, S.J. Serengeti Migratory Wildebeest: Facilitation of Energy Flow by Grazing. Science 1976, 191, 92–94. [Google Scholar] [CrossRef]
- Raupach, M.R. Combination theory and equilibrium evaporation. Q. J. R. Meteorol. Soc. 2001, 127, 1149–1181. [Google Scholar] [CrossRef]
- Boulet, G.; Mougenot, B.; Lhomme, J.-P.; Fanise, P.; Lili-Chabaane, Z.; Olioso, A.; Bahir, M.; Rivalland, V.; Jarlan, L.; Merlin, O.; et al. The SPARSE model for the prediction of water stress and evapotranspiration components from thermal infra-red data and its evaluation over irrigated and rainfed wheat. Hydrol. Earth Syst. Sci. Discuss. 2015, 4653–4672. [Google Scholar] [CrossRef]
- Delogu, E.; Boulet, G.; Olioso, A.; Garrigues, S.; Brut, A.; Tallec, T.; Demarty, J.; Soudani, K.; Lagouarde, J.-P. Evaluation of the SPARSE Dual-Source Model for Predicting Water Stress and Evapotranspiration from Thermal Infrared Data over Multiple Crops and Climates. Remote Sens. 2018, 10, 1806. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. AgFM 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 978-0-470-87366-3. [Google Scholar]
- Allen, R.G.; Smith, M.; Perrier, A.; Pereira, L.S. An update for the definition of reference evapotranspiration. ICID Bull. 1994, 43, 1–34. [Google Scholar]
- Allies, A.; Demarty, J.; Olioso, A.; Bouzou Moussa, I.; Issoufou, H.B.-A.; Velluet, C.; Bahir, M.; Maïnassara, I.; Oï, M.; Chazarin, J.-P.; et al. Evapotranspiration Estimation in the Sahel Using a New Ensemble-Contextual Method. Remote Sens. 2020, 12, 380. [Google Scholar] [CrossRef]
- Farah, H.O.; Bastiaanssen, W.G.M.; Feddes, R.A. Evaluation of the temporal variability of the evaporative fraction in a tropical watershed. Int. J. Appl. Earth Obs. Geoinf. 2004, 5, 129–140. [Google Scholar] [CrossRef]
- Lu, J.; Tang, R.; Tang, H.; Li, Z.-L. Derivation of Daily Evaporative Fraction Based on Temporal Variations in Surface Temperature, Air Temperature, and Net Radiation. Remote Sens. 2013, 5, 5369–5396. [Google Scholar] [CrossRef]
- Gallego-Elvira, B.; Olioso, A.; Mira, M.; Castillo, S.R.-; Boulet, G.; Marloie, O.; Garrigues, S.; Courault, D.; Weiss, M.; Chauvelon, P.; et al. EVASPA (EVapotranspiration Assessment from SPAce) Tool: An overview. Procedia Environ. Sci. 2013, 19, 303–310. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Ahmad, M.; Chemin, Y. Satellite surveillance of evaporative depletion across the Indus Basin. Water Resour. Res. 2002, 38, 9-1–9-9. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Gao, F.; Hain, C.R.; Kustas, W.P. A data fusion approach for mapping daily evapotranspiration at field scale. Water Resour. Res. 2013, 49, 4672–4686. [Google Scholar] [CrossRef]
- Béziat, P.; Ceschia, E.; Dedieu, G. Carbon balance of a three crop succession over two cropland sites in South West France. Agric. For. Meteorol. 2009, 149, 1628–1645. [Google Scholar] [CrossRef]
- Garrigues, S.; Olioso, A.; Calvet, J.C.; Martin, E.; Lafont, S.; Moulin, S.; Chanzy, A.; Marloie, O.; Buis, S.; Desfonds, V.; et al. Evaluation of land surface model simulations of evapotranspiration over a 12-year crop succession: Impact of soil hydraulic and vegetation properties. Hydrol. Earth Syst. Sci. 2015, 19, 3109–3131. [Google Scholar] [CrossRef]
- Chebbi, W.; Boulet, G.; Le Dantec, V.; Lili Chabaane, Z.; Fanise, P.; Mougenot, B.; Ayari, H. Analysis of evapotranspiration components of a rainfed olive orchard during three contrasting years in a semi-arid climate. Agric. For. Meteorol. 2018, 256–257, 159–178. [Google Scholar] [CrossRef]
- Velluet, C.; Demarty, J.; Cappelaere, B.; Braud, I.; Issoufou, H.B.A.; Boulain, N.; Ramier, D.; Mainassara, I.; Charvet, G.; Boucher, M.; et al. Building a field- and model-based climatology of surface energy and water cycles for dominant land cover types in the cultivated Sahel. Annual budgets and seasonality. Hydrol. Earth Syst. Sci. 2014, 18, 5001–5024. [Google Scholar] [CrossRef]


| Site Name (Country) | Ecosystem | Studied Year | Name Code | Number of Days Studied | ET0 (mm) | Rain (mm) | Maximal Observed LAI (m2 m−2) | Soil Type (%Clay/%Sand) | Irrigation (mm) | Soil Albedo | Energy Balance Closure |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Temperate climate | |||||||||||
| Auradé (FR) | Wheat | 2006 | Aur W 2006 | 246 | 323 | 369 | 3.1 | 32/21 | 0 | 0.25 | 93% |
| Auradé (FR) | Sunflower | 2007 | Aur Su 2007 | 164 | 394 | 374 | 1.7 | 32/21 | 0 | 0.25 | 88% |
| Auradé (FR) | Wheat | 2008 | Aur W 2008 | 258 | 307 | 507 | 2.4 | 32/21 | 0 | 0.25 | 89% |
| Lamasquère (FR) | Wheat | 2007 | Lam W 2007 | 269 | 656 | 531 | 4.5 | 54/12 | 0 | 0.25 | 94% |
| Lamasquère (FR) | Corn | 2008 | Lam C 2008 | 161 | 416 | 296 | 3.8 | 54/12 | 50 | 0.25 | 83% |
| Lamasquère (FR) | Wheat | 2009 | Lam W 2009 | 237 | 447 | 386 | 1.7 | 54/12 | 0 | 0.25 | 92% |
| Lamasquère (FR) | Corn | 2010 | Lam C 2010 | 180 | 452 | 446 | 4.1 | 54/12 | 130 | 0.25 | 79% |
| Lamasquère (FR) | Corn | 2012 | Lam C 2012 | 119 | 365 | 342 | 5.9 | 54/12 | 144 | 0.25 | 91% |
| Lamasquère (FR) | Corn | 2014 | Lam C 2014 | 126 | 339 | 362 | 5.2 | 54/12 | 175 | 0.25 | 85% |
| Lamasquère (FR) | Corn | 2015 | Lam C 2015 | 127 | 384 | 333 | 6.6 | 54/12 | 140 | 0.25 | 98% |
| Avignon (FR) | Peas | 2005 | Avi P 2005 | 160 | 318 | 203 | 2.8 | 33/14 | 100 | 0.25 | 95% |
| Avignon (FR) | Wheat | 2006 | Avi W 2006 | 246 | 439 | 256 | 5.5 | 33/14 | 20 | 0.25 | 94% |
| Avignon (FR) | Sorghum | 2007 | Avi So 2007 | 161 | 501 | 168 | 3.0 | 33/14 | 80 | 0.25 | 95% |
| Avignon (FR) | Wheat | 2008 | Avi W 2008 | 231 | 415 | 502 | 1.9 | 33/14 | 20 | 0.25 | 95% |
| Avignon (FR) | Wheat | 2012 | Avi W 2012 | 248 | 460 | 437 | 1.1 | 33/14 | 0 | 0.25 | 96% |
| Sahelian climate | |||||||||||
| Wankama-M (NI) | Millet | 2009 | Wan M 2009 | 275 | 867 | 430 | 0.4 | 13/85 | 0 | 0.30 | 91% |
| Wankama-F (NI) | Savannah | 2009 | Wan S 2009 | 262 | 793 | 442 | 0.3 | 13/85 | 0 | 0.30 | 91% |
| Semi-arid climate | |||||||||||
| Kairouan (TU) | Wheat | 2012 | Kai W 2012 | 167 | 381 | 161 | 2.1 | 31/40 | 0 | 0.25 | 60% |
| Kairouan (TU) | Olive | 2012–2015 | Kai Or 2012/15 | 241 365 365 281 | 141 330 225 223 | 640 653 626 502 | 0.2 | 8/88 | 0 | 0.29 | 55% |
| Haouz (MO) | Wheat | 2004 | Hao W 2004 | 148 | 338 | 192 | 4.1 | 34/20 | 170 | 0.20 | 93% |
| Symbol Reference Quantities | Main Inputs | Availability | |
|---|---|---|---|
| AE | Available Energy | Rn, G | clear sky day at the time of satellite overpass |
| Rcs | Clear Sky Radiation | Day, time, lat, lon | 30 min |
| Rg | Global Radiation | - | 30 min |
| Rn_FAO | Net Radiation (FAO) | Relative Humidity, Air Temperature, Rg, Rcs, albedo | 30 min |
| LEpot | Potential latent heat flux | 30 min | |
| ET0 | Reference Evapotranspiration | Relative Humidity, Air Temperature, Rn, G, wind speed | 30 min |
| API | Antecedent Precipitation Index | Day, rain | 30 min |
| Rain | Rain | - | 30 min |
| In Situ Dataset | RS Derived Dataset | |||||
|---|---|---|---|---|---|---|
| RMSE (mm) | Bias (mm) | NI | RMSE (mm) | Bias (mm) | NI | |
| Aur W 2006 | 0.94 | 0.05 | 0.62 | 1.14 | −0.12 | 0.48 |
| Aur Su 2007 | 0.92 | 0.13 | 0.26 | 0.49 | 0.15 | 0.79 |
| Aur W 2008 | 0.76 | −0.19 | 0.49 | 0.43 | −0.29 | 0.92 |
| Lam W 2007 | 0.41 | 0.02 | 0.83 | 1.01 | −0.67 | 0.68 |
| Lam C 2008 | 0.19 | 0.12 | 0.71 | 1.08 | −0.45 | 0.46 |
| Lam W 2009 | 0.53 | 0.05 | 0.79 | 1.42 | −1.08 | 0.44 |
| Lam C 2010 | 0.92 | 0.78 | 0.72 | 0.50 | −0.23 | 0.86 |
| Lam C 2012 | 0.98 | 0.65 | 0.33 | 0.54 | 0.50 | 0.71 |
| Lam C 2014 | 0.88 | 0.61 | 0.41 | 0.64 | 0.51 | 0.69 |
| Lam C 2015 | 0.81 | 0.25 | 0.23 | 0.71 | 0.35 | 0.75 |
| Avi P 2005 | 0.49 | 0.13 | 0.92 | 1.14 | −0.46 | 0.41 |
| Avi W 2006 | 0.75 | 0.13 | 0.79 | 0.67 | 0.01 | 0.83 |
| Avi So 2007 | 0.74 | 0.20 | 0.86 | 0.52 | 0.12 | 0.89 |
| Avi W 2008 | 0.64 | 0.26 | 0.80 | 0.88 | 0.33 | 0.48 |
| Avi W 2012 | 0.40 | 0.12 | 0.88 | 0.93 | −0.35 | 0.42 |
| Wan M 2009 | 0.56 | 0.21 | 0.70 | 0.90 | −0.18 | 0.39 |
| Wan S 2009 | 0.55 | 0.20 | 0.82 | 0.83 | 0.04 | 0.30 |
| Kai W 2012 | 0.64 | −0.26 | 0.38 | 0.66 | 0.04 | 0.60 |
| Kai Or 2012/15 | 0.60 | −0.17 | 0.75 | 0.91 | −0.07 | 0.35 |
| Hao W 2004 | 0.41 | 0.02 | 0.83 | 0.83 | 0.20 | 0.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delogu, E.; Olioso, A.; Alliès, A.; Demarty, J.; Boulet, G. Evaluation of Multiple Methods for the Production of Continuous Evapotranspiration Estimates from TIR Remote Sensing. Remote Sens. 2021, 13, 1086. https://doi.org/10.3390/rs13061086
Delogu E, Olioso A, Alliès A, Demarty J, Boulet G. Evaluation of Multiple Methods for the Production of Continuous Evapotranspiration Estimates from TIR Remote Sensing. Remote Sensing. 2021; 13(6):1086. https://doi.org/10.3390/rs13061086
Chicago/Turabian StyleDelogu, Emilie, Albert Olioso, Aubin Alliès, Jérôme Demarty, and Gilles Boulet. 2021. "Evaluation of Multiple Methods for the Production of Continuous Evapotranspiration Estimates from TIR Remote Sensing" Remote Sensing 13, no. 6: 1086. https://doi.org/10.3390/rs13061086
APA StyleDelogu, E., Olioso, A., Alliès, A., Demarty, J., & Boulet, G. (2021). Evaluation of Multiple Methods for the Production of Continuous Evapotranspiration Estimates from TIR Remote Sensing. Remote Sensing, 13(6), 1086. https://doi.org/10.3390/rs13061086







