Semantically Derived Geometric Constraints for MVS Reconstruction of Textureless Areas
Abstract
1. Introduction
2. Related Work
2.1. Image Segmentation
2.2. Semantic 3D Reconstruction
2.3. PatchMatch
2.4. Prior-Assisted PatchMatch
2.5. 3D Reconstruction Benchmarks
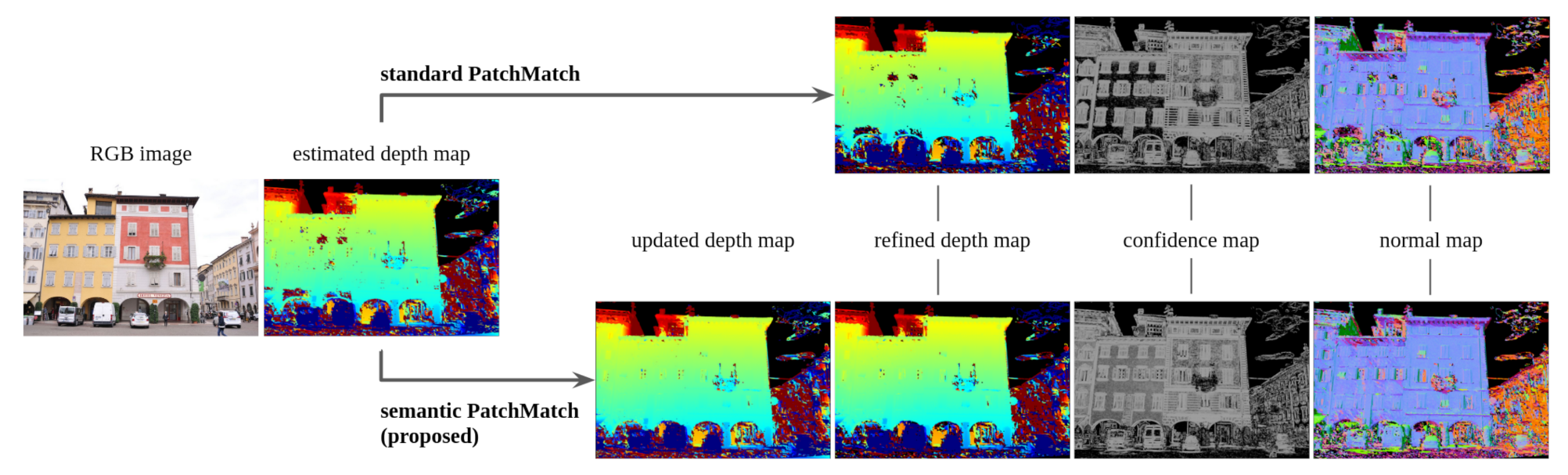
3. PatchMatch in Multi View Stereo
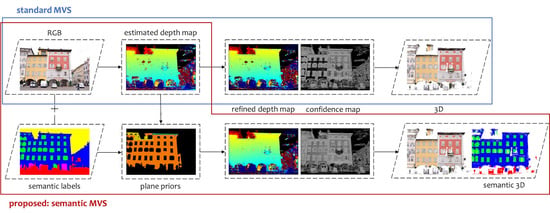
4. Proposed Methodology: Semantic PatchMatch MVS
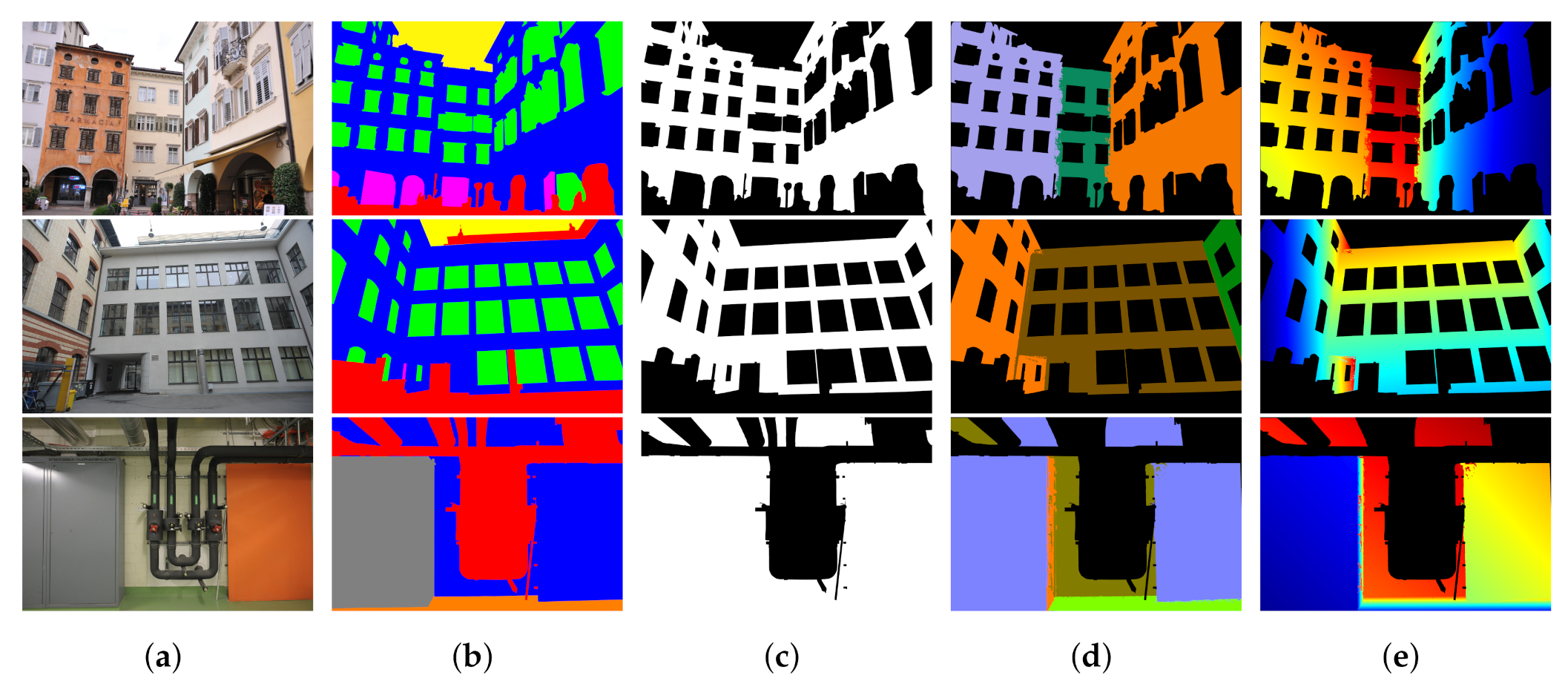
4.1. Plane Fitting for Depth Prior Generation
4.2. Proposed Cost Function
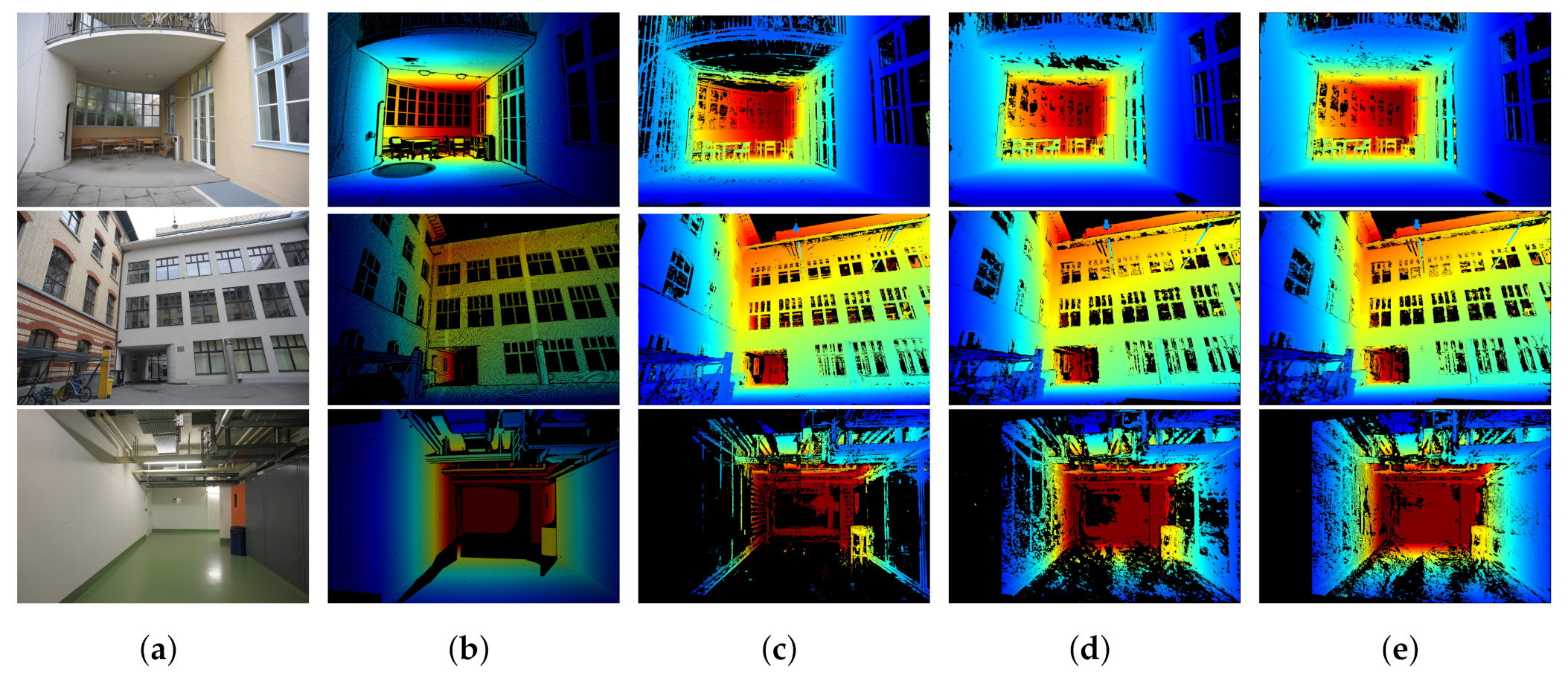
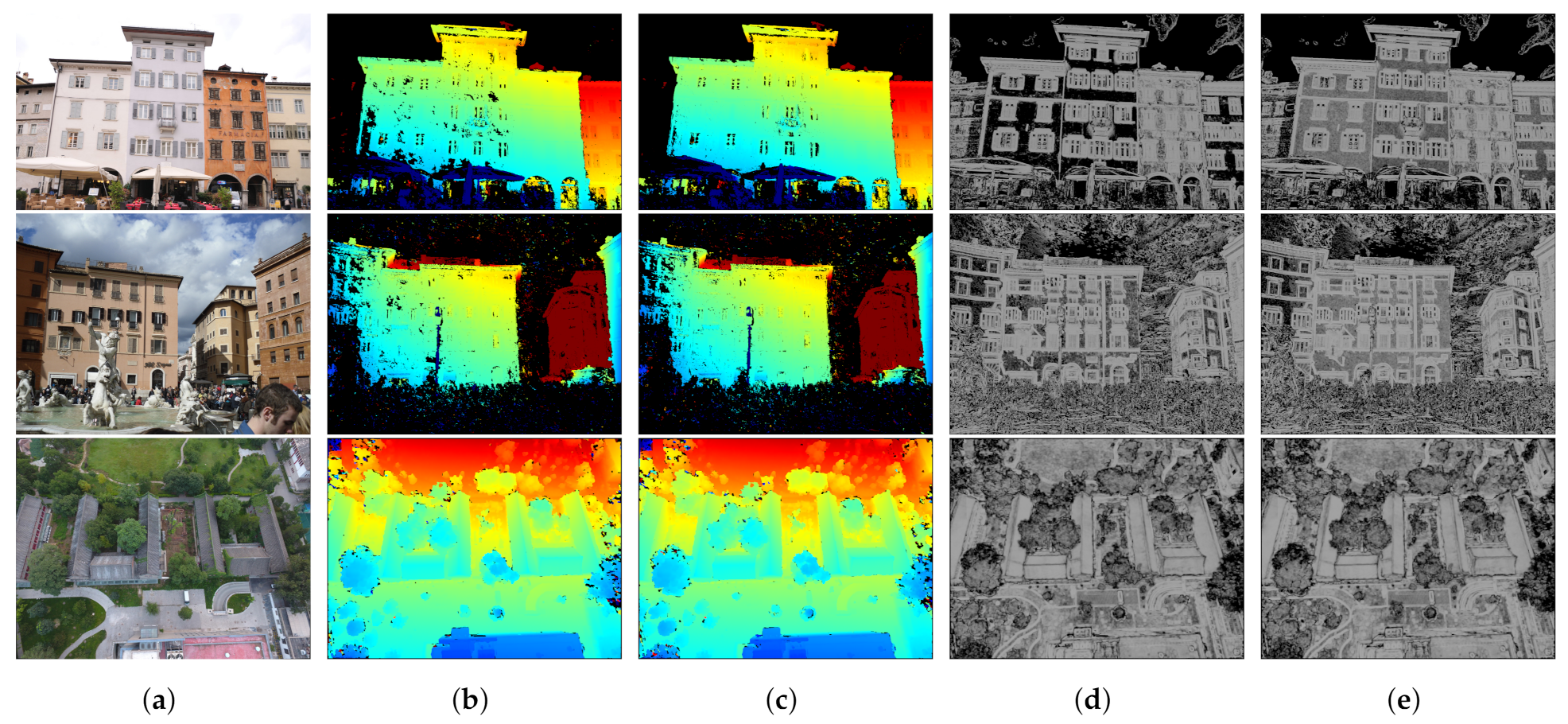
5. Experiments and Results
5.1. Datasets
5.2. Parameter Settings
5.3. Evaluation Metrics
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A comparison and evaluation of multi-view stereo reconstruction algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; Volume 1, pp. 519–528. [Google Scholar]
- Knapitsch, A.; Park, J.; Zhou, Q.Y.; Koltun, V. Tanks and temples: Benchmarking large-scale scene reconstruction. ACM Trans. Graph. (ToG) 2017, 36, 1–13. [Google Scholar] [CrossRef]
- Schops, T.; Schonberger, J.L.; Galliani, S.; Sattler, T.; Schindler, K.; Pollefeys, M.; Geiger, A. A multi-view stereo benchmark with high-resolution images and multi-camera videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3260–3269. [Google Scholar]
- Hirschmuller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 328–341. [Google Scholar] [CrossRef]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. Mvsnet: Depth inference for unstructured multi-view stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 767–783. [Google Scholar]
- Huang, P.H.; Matzen, K.; Kopf, J.; Ahuja, N.; Huang, J.B. Deepmvs: Learning multi-view stereopsis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2821–2830. [Google Scholar]
- Wang, C.; Miguel Buenaposada, J.; Zhu, R.; Lucey, S. Learning depth from monocular videos using direct methods. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2022–2030. [Google Scholar]
- Bleyer, M.; Rhemann, C.; Rother, C. PatchMatch Stereo-Stereo Matching with Slanted Support Windows. In Proceedings of the British Machine Vision Conference, Dundee, UK, 29 August–2 September 2011; Volume 11, pp. 1–11. [Google Scholar]
- Shen, S. Accurate multiple view 3d reconstruction using patch-based stereo for large-scale scenes. IEEE Trans. Image Process. 2013, 22, 1901–1914. [Google Scholar] [CrossRef]
- Schönberger, J.L.; Zheng, E.; Frahm, J.M.; Pollefeys, M. Pixelwise view selection for unstructured multi-view stereo. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 14–16 October 2016; pp. 501–518. [Google Scholar]
- Zheng, E.; Dunn, E.; Jojic, V.; Frahm, J.M. Patchmatch based joint view selection and depthmap estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–24 June 2014; pp. 1510–1517. [Google Scholar]
- Galliani, S.; Lasinger, K.; Schindler, K. Massively parallel multiview stereopsis by surface normal diffusion. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 June 2015; pp. 873–881. [Google Scholar]
- Jancosek, M.; Pajdla, T. Exploiting visibility information in surface reconstruction to preserve weakly supported surfaces. Int. Sch. Res. Not. 2014, 2014, 798595. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Paszke, A.; Chaurasia, A.; Kim, S.; Culurciello, E. Enet: A deep neural network architecture for real-time semantic segmentation. arXiv 2016, arXiv:1606.02147. [Google Scholar]
- Knyaz, V.A.; Kniaz, V.V.; Remondino, F.; Zheltov, S.Y.; Gruen, A. 3D Reconstruction of a Complex Grid Structure Combining UAS Images and Deep Learning. Remote. Sens. 2020, 12, 3128. [Google Scholar] [CrossRef]
- Stathopoulou, E.K.; Remondino, F. Multi-view stereo with semantic priors. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2019, XLII-2/W15, 1135–1140. [Google Scholar] [CrossRef]
- Häne, C.; Zach, C.; Cohen, A.; Angst, R.; Pollefeys, M. Joint 3D scene reconstruction and class segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 97–104. [Google Scholar]
- Romanoni, A.; Ciccone, M.; Visin, F.; Matteucci, M. Multi-view stereo with single-view semantic mesh refinement. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 706–715. [Google Scholar]
- Blaha, M.; Rothermel, M.; Oswald, M.R.; Sattler, T.; Richard, A.; Wegner, J.D.; Pollefeys, M.; Schindler, K. Semantically informed multiview surface refinement. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3819–3827. [Google Scholar]
- Romanoni, A.; Matteucci, M. Tapa-mvs: Textureless-aware patchmatch multi-view stereo. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 10413–10422. [Google Scholar]
- Xu, Q.; Tao, W. Multi-scale geometric consistency guided multi-view stereo. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seoul, Korea, 27 October–2 November 2019; pp. 5483–5492. [Google Scholar]
- Xu, Q.; Tao, W. Planar Prior Assisted PatchMatch Multi-View Stereo. arXiv 2019, arXiv:1912.11744. [Google Scholar]
- Shotton, J.; Winn, J.; Rother, C.; Criminisi, A. Textonboost for image understanding: Multi-class object recognition and segmentation by jointly modeling texture, layout, and context. Int. J. Comput. Vis. 2009, 81, 2–23. [Google Scholar] [CrossRef]
- Shotton, J.; Johnson, M.; Cipolla, R. Semantic texton forests for image categorization and segmentation. In Proceedings of the 2008 IEEE conference on computer vision and pattern recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Fulkerson, B.; Vedaldi, A.; Soatto, S. Class segmentation and object localization with superpixel neighborhoods. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 4 October–29 September 2009; pp. 670–677. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Minaee, S.; Boykov, Y.; Porikli, F.; Plaza, A.; Kehtarnavaz, N.; Terzopoulos, D. Image segmentation using deep learning: A survey. arXiv 2020, arXiv:2001.05566. [Google Scholar]
- Brostow, G.J.; Fauqueur, J.; Cipolla, R. Semantic object classes in video: A high-definition ground truth database. Pattern Recognit. Lett. 2009, 30, 88–97. [Google Scholar] [CrossRef]
- Riemenschneider, H.; Bódis-Szomorú, A.; Weissenberg, J.; Van Gool, L. Learning where to classify in multi-view semantic segmentation. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 516–532. [Google Scholar]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The cityscapes dataset for semantic urban scene understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3213–3223. [Google Scholar]
- Armeni, I.; Sax, S.; Zamir, A.R.; Savarese, S. Joint 2d-3d-semantic data for indoor scene understanding. arXiv 2017, arXiv:1702.01105. [Google Scholar]
- Song, S.; Lichtenberg, S.P.; Xiao, J. Sun rgb-d: A rgb-d scene understanding benchmark suite. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 567–576. [Google Scholar]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor segmentation and support inference from rgbd images. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 746–760. [Google Scholar]
- McCormac, J.; Handa, A.; Leutenegger, S.; Davison, A.J. Scenenet rgb-d: 5m photorealistic images of synthetic indoor trajectories with ground truth. arXiv 2016, arXiv:1612.05079. [Google Scholar]
- Chen, Y.; Wang, Y.; Lu, P.; Chen, Y.; Wang, G. Large-scale structure from motion with semantic constraints of aerial images. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Guangzhou, China, 23–26 November 2018; pp. 347–359. [Google Scholar]
- Lyu, Y.; Vosselman, G.; Xia, G.S.; Yilmaz, A.; Yang, M.Y. UAVid: A semantic segmentation dataset for UAV imagery. ISPRS J. Photogramm. Remote. Sens. 2020, 165, 108–119. [Google Scholar] [CrossRef]
- Rottensteiner, F.; Sohn, G.; Jung, J.; Gerke, M.; Baillard, C.; Benitez, S.; Breitkopf, U. The ISPRS benchmark on urban object classification and 3D building reconstruction. Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. I-3 2012, 1, 293–298. [Google Scholar] [CrossRef]
- Ladickỳ, L.; Sturgess, P.; Russell, C.; Sengupta, S.; Bastanlar, Y.; Clocksin, W.; Torr, P.H. Joint optimization for object class segmentation and dense stereo reconstruction. Int. J. Comput. Vis. 2012, 100, 122–133. [Google Scholar] [CrossRef]
- Schneider, L.; Cordts, M.; Rehfeld, T.; Pfeiffer, D.; Enzweiler, M.; Franke, U.; Pollefeys, M.; Roth, S. Semantic stixels: Depth is not enough. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gotenburg, Sweden, 19–22 June 2016; pp. 110–117. [Google Scholar]
- Kundu, A.; Li, Y.; Dellaert, F.; Li, F.; Rehg, J.M. Joint semantic segmentation and 3d reconstruction from monocular video. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 703–718. [Google Scholar]
- Zhang, C.; Wang, L.; Yang, R. Semantic segmentation of urban scenes using dense depth maps. In Proceedings of the European Conference on Computer Vision, Crete, Greece, 5–11 September 2010; pp. 708–721. [Google Scholar]
- Häne, C.; Zach, C.; Cohen, A.; Pollefeys, M. Dense semantic 3d reconstruction. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1730–1743. [Google Scholar] [CrossRef]
- Savinov, N.; Häne, C.; Ladicky, L.; Pollefeys, M. Semantic 3d reconstruction with continuous regularization and ray potentials using a visibility consistency constraint. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5460–5469. [Google Scholar]
- Blaha, M.; Vogel, C.; Richard, A.; Wegner, J.D.; Pock, T.; Schindler, K. Large-scale semantic 3d reconstruction: An adaptive multi-resolution model for multi-class volumetric labeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3176–3184. [Google Scholar]
- Cherabier, I.; Schonberger, J.L.; Oswald, M.R.; Pollefeys, M.; Geiger, A. Learning priors for semantic 3d reconstruction. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 314–330. [Google Scholar]
- Yingze Bao, S.; Chandraker, M.; Lin, Y.; Savarese, S. Dense object reconstruction with semantic priors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1264–1271. [Google Scholar]
- Ulusoy, A.O.; Black, M.J.; Geiger, A. Semantic multi-view stereo: Jointly estimating objects and voxels. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2017; pp. 4531–4540. [Google Scholar]
- Furukawa, Y.; Curless, B.; Seitz, S.M.; Szeliski, R. Manhattan-world stereo. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1422–1429. [Google Scholar]
- Gallup, D.; Frahm, J.M.; Pollefeys, M. Piecewise planar and non-planar stereo for urban scene reconstruction. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1418–1425. [Google Scholar]
- Chen, W.; Hou, J.; Zhang, M.; Xiong, Z.; Gao, H. Semantic stereo: Integrating piecewise planar stereo with segmentation and classification. In Proceedings of the 2014 4th IEEE International Conference on Information Science and Technology, Shenzhen, China, 26–28 April 2014; pp. 200–204. [Google Scholar]
- Guney, F.; Geiger, A. Displets: Resolving stereo ambiguities using object knowledge. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 4165–4175. [Google Scholar]
- Barnes, C.; Shechtman, E.; Finkelstein, A.; Goldman, D.B. PatchMatch: A randomized correspondence algorithm for structural image editing. ACM Trans. Graph. 2009, 28, 24. [Google Scholar] [CrossRef]
- Besse, F.O. PatchMatch Belief Propagation for Correspondence Field Estimation and Its Applications. Ph.D. Thesis, University College London, London, UK, 2013. [Google Scholar]
- Heise, P.; Klose, S.; Jensen, B.; Knoll, A. Pm-huber: Patchmatch with huber regularization for stereo matching. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2360–2367. [Google Scholar]
- Duggal, S.; Wang, S.; Ma, W.C.; Hu, R.; Urtasun, R. Deeppruner: Learning efficient stereo matching via differentiable patchmatch. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 4384–4393. [Google Scholar]
- Kuhn, A.; Lin, S.; Erdler, O. Plane completion and filtering for multi-view stereo reconstruction. In Proceedings of the German Conference on Pattern Recognition, Dortmund, Germany, 10–13 September 2019; pp. 18–32. [Google Scholar]
- Liu, H.; Tang, X.; Shen, S. Depth-map completion for large indoor scene reconstruction. Pattern Recognit. 2020, 99, 107112. [Google Scholar] [CrossRef]
- Schonberger, J.L.; Frahm, J.M. Structure-from-motion revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Wang, Y.; Guan, T.; Chen, Z.; Luo, Y.; Luo, K.; Ju, L. Mesh-Guided Multi-View Stereo With Pyramid Architecture. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 2039–2048. [Google Scholar]
- Scharstein, D.; Szeliski, R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comput. Vis. 2002, 47, 7–42. [Google Scholar] [CrossRef]
- Scharstein, D.; Hirschmüller, H.; Kitajima, Y.; Krathwohl, G.; Nešić, N.; Wang, X.; Westling, P. High-resolution stereo datasets with subpixel-accurate ground truth. In Proceedings of the German Conference on Pattern Recognition, Münster, Germany, 2–5 September 2014; pp. 31–42. [Google Scholar]
- Strecha, C.; Von Hansen, W.; Van Gool, L.; Fua, P.; Thoennessen, U. On benchmarking camera calibration and multi-view stereo for high resolution imagery. In Proceedings of the 2008 IEEE conference on computer vision and pattern recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Menze, M.; Geiger, A. Object scene flow for autonomous vehicles. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3061–3070. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Jensen, R.; Dahl, A.; Vogiatzis, G.; Tola, E.; Aanæs, H. Large scale multi-view stereopsis evaluation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 406–413. [Google Scholar]
- Aanæs, H.; Jensen, R.R.; Vogiatzis, G.; Tola, E.; Dahl, A.B. Large-Scale Data for Multiple-View Stereopsis. Int. J. Comput. Vis. 2016, 120, 153–168. [Google Scholar] [CrossRef]
- Stathopoulou, E.K.; Remondino, F. Semantic photogrammetry – boosting image-based 3D reconstruction with semantic labelling. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2019, XLII-2/W9, 685–690. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2007; Volume 26, pp. 214–226. [Google Scholar]
- CGAL (Computational Geometry Algorithms Library). Available online: https://www.cgal.org (accessed on 5 February 2021).
- Cernea, D. OpenMVS: Multi-View Stereo Reconstruction Library. Available online: https://github.com/cdcseacave/openMVS (accessed on 5 February 2021).






| = 2 cm | = 10 cm | ||||||
| Method | Accuracy | Completeness | Accuracy | Completeness | |||
| ETH3D-terrace | COLMAP | 96.79 | 75.67 | 84.94 | 99.29 | 93.83 | 96.48 |
| TAPA-MVS | 94.00 | 82.37 | 87.80 | 98.45 | 98.15 | 98.30 | |
| ACMM | 96.19 | 84.13 | 89.76 | 99.13 | 96.16 | 97.62 | |
| ACMP | 96.14 | 84.45 | 89.92 | 99.14 | 96.42 | 97.76 | |
| PCF-MVS | 92.72 | 84.75 | 88.56 | 98.09 | 97.46 | 97.78 | |
| OpenMVS | 88.72 | 87.52 | 88.12 | 98.00 | 98.53 | 98.27 | |
| ours | 89.81 | 88.83 | 89.32 | 98.28 | 98.98 | 98.63 | |
| ours-no labels | 89.77 | 88.65 | 89.21 | 98.26 | 98.94 | 98.60 | |
| ETH3D-courtyard | COLMAP | 88.98 | 73.47 | 80.49 | 99.14 | 92.20 | 95.54 |
| TAPA-MVS | 84.69 | 77.04 | 80.68 | 97.64 | 96.14 | 96.89 | |
| ACMM | 91.35 | 82.85 | 86.89 | 99.51 | 91.90 | 95.56 | |
| ACMP | 90.83 | 80.96 | 85.61 | 99.43 | 90.80 | 94.92 | |
| PCF-MVS | 86.12 | 83.67 | 84.88 | 98.43 | 94.44 | 96.39 | |
| OpenMVS | 80.46 | 90.10 | 85.01 | 97.85 | 97.63 | 97.74 | |
| ours | 79.66 | 90.58 | 84.77 | 97.61 | 97.22 | 97.41 | |
| ours-no labels | 79.69 | 90.43 | 84.72 | 97.60 | 97.04 | 97.32 | |
| ETH3D-pipes | COLMAP | 97.77 | 34.24 | 50.72 | 99.18 | 62.75 | 76.86 |
| TAPA-MVS | 93.71 | 63.80 | 75.91 | 97.90 | 86.70 | 91.96 | |
| ACMM | 96.63 | 53.97 | 69.26 | 98.89 | 66.25 | 79.34 | |
| ACMP | 97.65 | 53.54 | 69.16 | 99.20 | 65.80 | 79.12 | |
| PCF-MVS | 90.40 | 69.18 | 78.38 | 98.48 | 88.47 | 93.21 | |
| OpenMVS | 82.33 | 64.55 | 72.36 | 95.95 | 85.42 | 90.38 | |
| ours | 85.33 | 73.50 | 78.97 | 96.89 | 93.63 | 95.23 | |
| ours-no labels | 84.19 | 69.88 | 76.37 | 97.32 | 91.08 | 94.10 | |
| Method | Acc. | Compl. | ||
| PiazzaDuomo | COLMAP | 88.89 | 38.00 | 52.24 |
| TAPA-MVS | 25.56 | 23.74 | 24.62 | |
| ACMM | 50.87 | 50.51 | 50.69 | |
| ACMP | 40.92 | 25.93 | 31.75 | |
| OpenMVS | 70.53 | 68.55 | 69.52 | |
| ours | 71.08 | 69.38 | 70.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stathopoulou, E.K.; Battisti, R.; Cernea, D.; Remondino, F.; Georgopoulos, A. Semantically Derived Geometric Constraints for MVS Reconstruction of Textureless Areas. Remote Sens. 2021, 13, 1053. https://doi.org/10.3390/rs13061053
Stathopoulou EK, Battisti R, Cernea D, Remondino F, Georgopoulos A. Semantically Derived Geometric Constraints for MVS Reconstruction of Textureless Areas. Remote Sensing. 2021; 13(6):1053. https://doi.org/10.3390/rs13061053
Chicago/Turabian StyleStathopoulou, Elisavet Konstantina, Roberto Battisti, Dan Cernea, Fabio Remondino, and Andreas Georgopoulos. 2021. "Semantically Derived Geometric Constraints for MVS Reconstruction of Textureless Areas" Remote Sensing 13, no. 6: 1053. https://doi.org/10.3390/rs13061053
APA StyleStathopoulou, E. K., Battisti, R., Cernea, D., Remondino, F., & Georgopoulos, A. (2021). Semantically Derived Geometric Constraints for MVS Reconstruction of Textureless Areas. Remote Sensing, 13(6), 1053. https://doi.org/10.3390/rs13061053