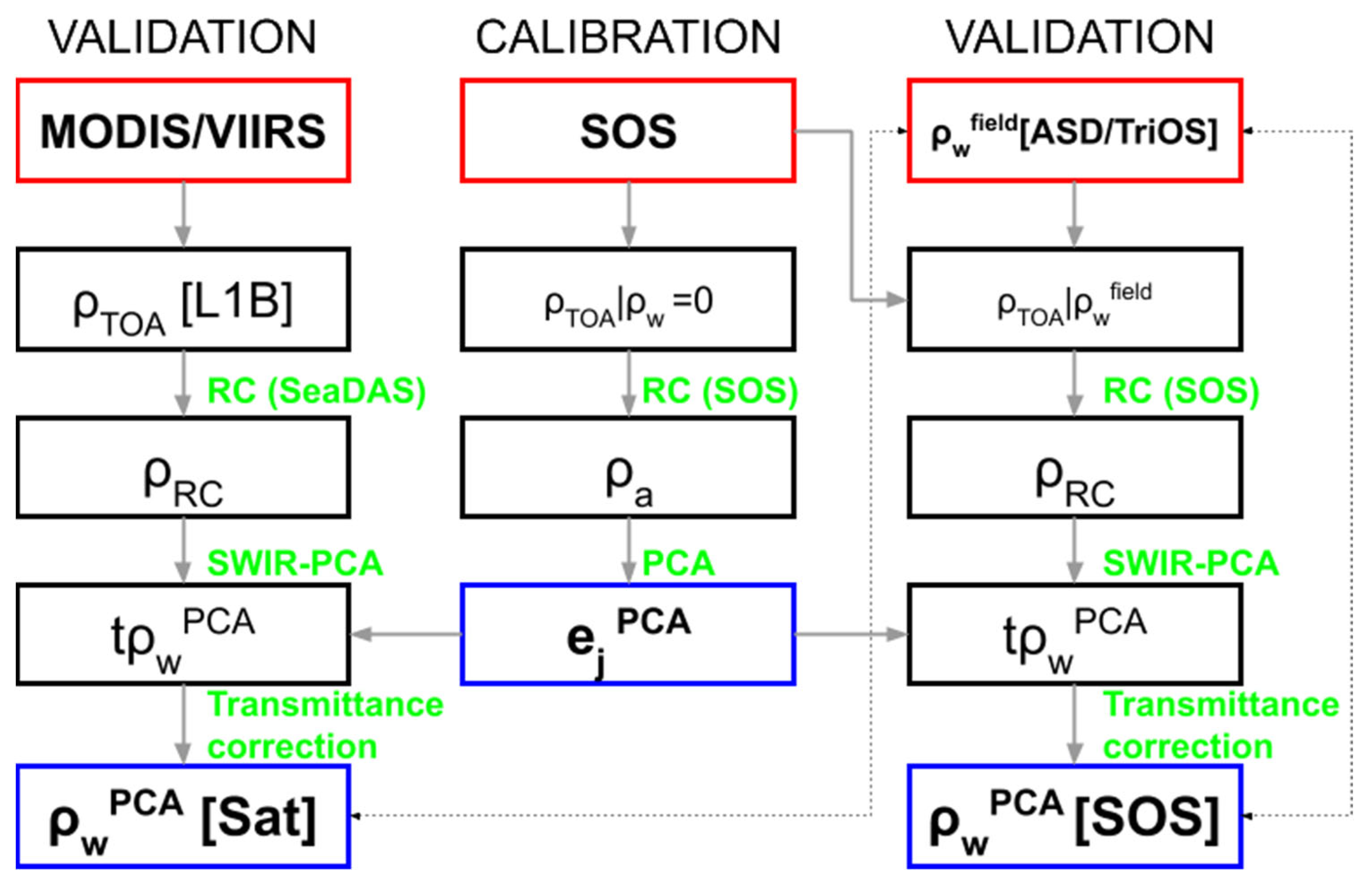
Figure 1.
Global scheme of the methodology developed in this study. In red boxes are the sources/inputs: satellite data (Moderate Resolution Imaging Spectrometer (MODIS)/ Visible Infrared Imaging Radiometer Suite (VIIRS)), simulated data using the successive orders of scattering radiative transfer code (SOS) and field measurements (Analytic Spectral Device (ASD)/”Tri” Optical Sensors (TriOS)). In blue boxes the outputs: the principal component analysis (PCA) eigenvectors and the PCA-shortwave infrared (SWIR)-derived satellite and simulated water reflectance. Gray solid arrows symbolize each of the intermediate steps in each process, and the dashed black arrows show the comparisons that were performed to test the algorithm.
Figure 1.
Global scheme of the methodology developed in this study. In red boxes are the sources/inputs: satellite data (Moderate Resolution Imaging Spectrometer (MODIS)/ Visible Infrared Imaging Radiometer Suite (VIIRS)), simulated data using the successive orders of scattering radiative transfer code (SOS) and field measurements (Analytic Spectral Device (ASD)/”Tri” Optical Sensors (TriOS)). In blue boxes the outputs: the principal component analysis (PCA) eigenvectors and the PCA-shortwave infrared (SWIR)-derived satellite and simulated water reflectance. Gray solid arrows symbolize each of the intermediate steps in each process, and the dashed black arrows show the comparisons that were performed to test the algorithm.
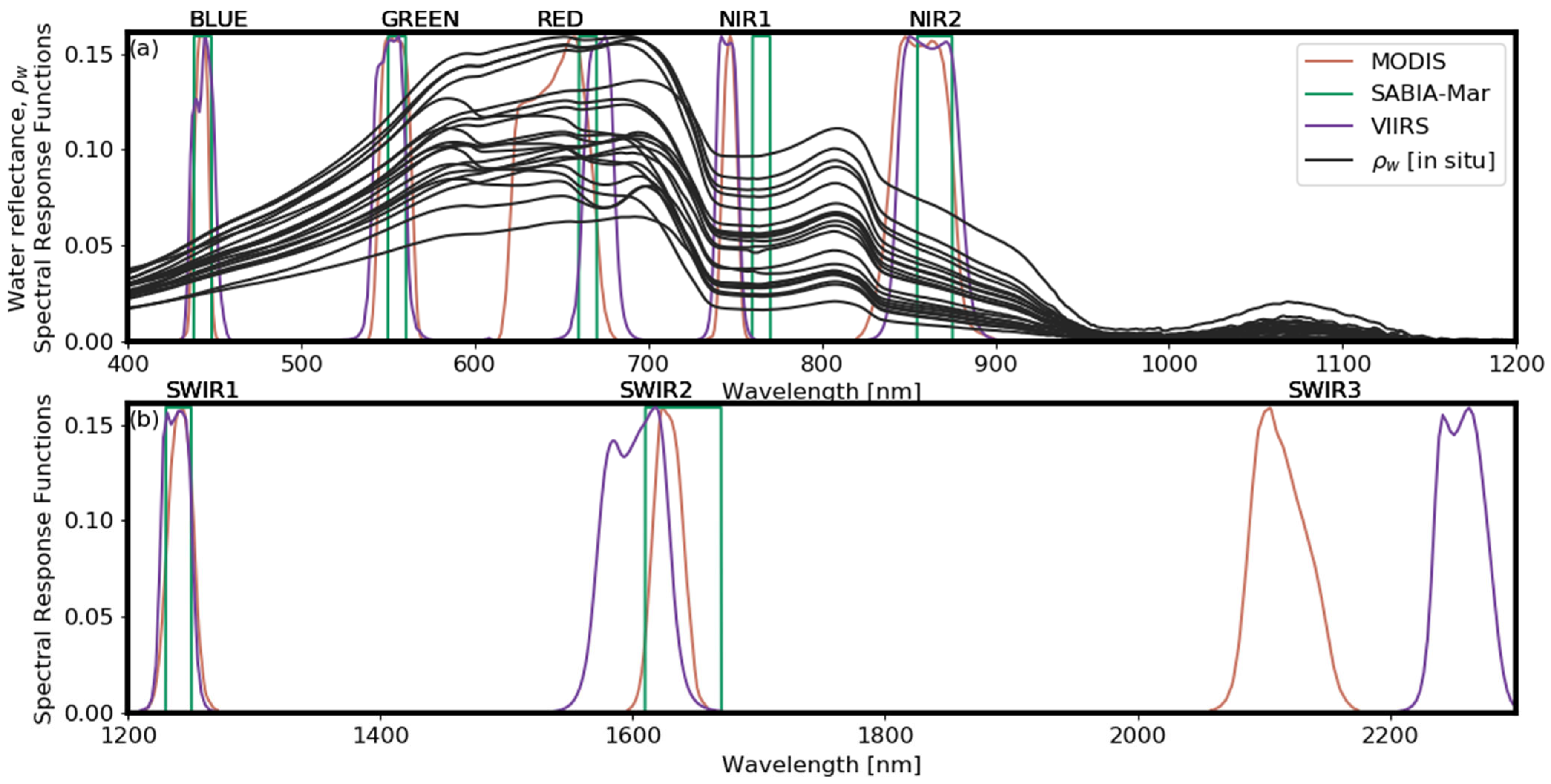
Figure 2.
Water reflectance spectra measured in the Río de la Plata (RdP) with ASD – (
a), solid black lines - and spectral response functions (SRFs) of the ocean color sensors MODIS, VIIRS, and Satélite Argentino-Brasileño para Información Ambiental del Mar (SABIA-Mar) (squared SRFs) at the visible (VIS)/near-infrared (NIR) (
a) and SWIR (
b) bands considered in this study (see
Table 1).
Figure 2.
Water reflectance spectra measured in the Río de la Plata (RdP) with ASD – (
a), solid black lines - and spectral response functions (SRFs) of the ocean color sensors MODIS, VIIRS, and Satélite Argentino-Brasileño para Información Ambiental del Mar (SABIA-Mar) (squared SRFs) at the visible (VIS)/near-infrared (NIR) (
a) and SWIR (
b) bands considered in this study (see
Table 1).
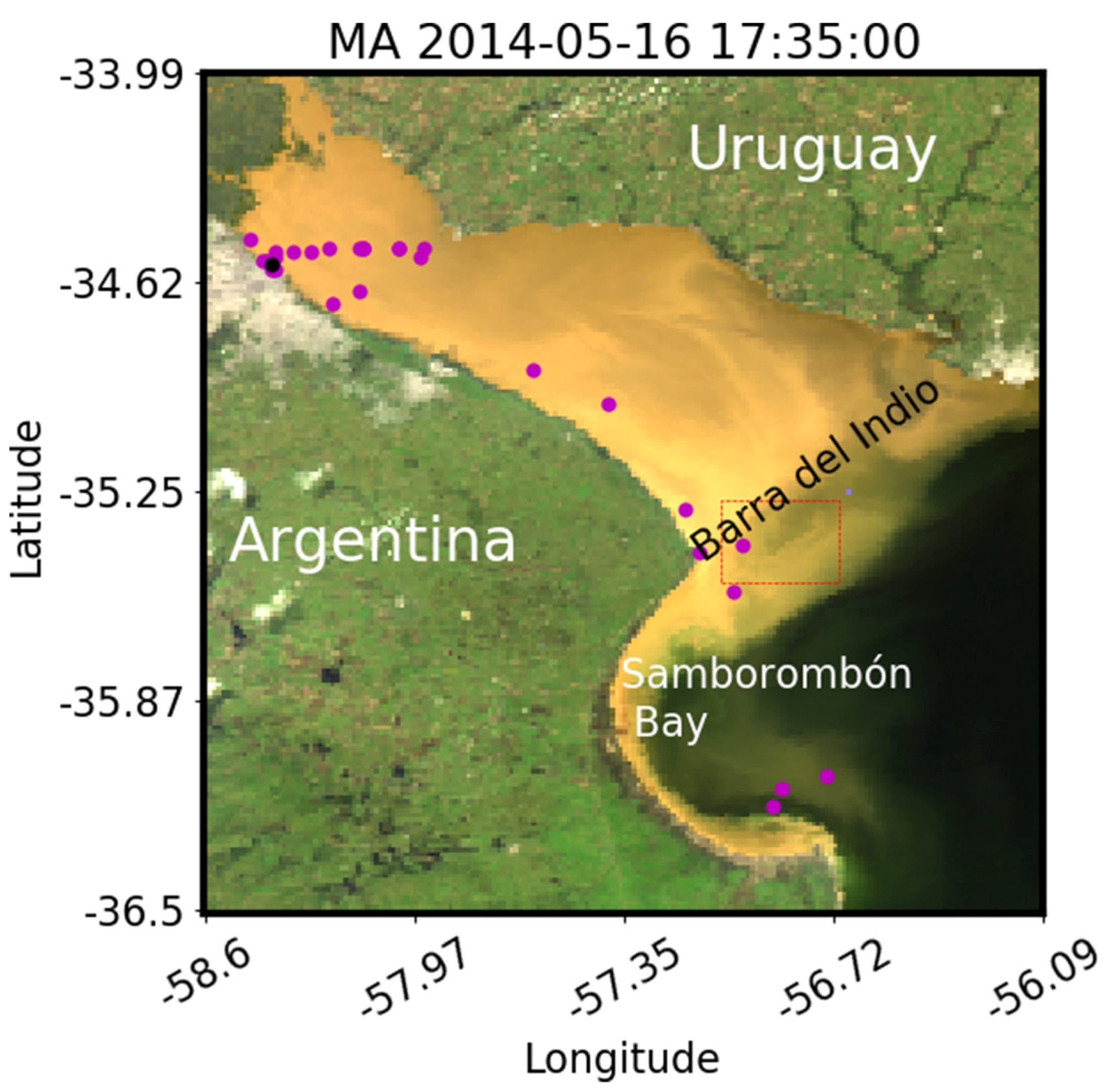
Figure 3.
Red-Green-Blue composite in Plate Carrée projection of the Río de la Plata Estuary as seen by MODIS/Aqua (2014-02-16T17:35:00Z). The location of the sites where the field radiometric measurements were performed are marked in magenta, except for the Fishermen Pier, which has a specific coastal match-up protocol and is marked in black (see
Section 2.3). A red-dashed rectangle indicates the region used to apply the geostatistical approach to estimate the effect of sensor noise over the performance of the PCA-SWIR AC (see
Section 4.1.4).
Figure 3.
Red-Green-Blue composite in Plate Carrée projection of the Río de la Plata Estuary as seen by MODIS/Aqua (2014-02-16T17:35:00Z). The location of the sites where the field radiometric measurements were performed are marked in magenta, except for the Fishermen Pier, which has a specific coastal match-up protocol and is marked in black (see
Section 2.3). A red-dashed rectangle indicates the region used to apply the geostatistical approach to estimate the effect of sensor noise over the performance of the PCA-SWIR AC (see
Section 4.1.4).
Figure 4.
PCA eigenvectors, ejPCA (computed using Set 0), at VIIRS VIS/NIR (a–g) bands plus the SWIR bands at 1241 nm (SWIR1), 1602 nm (SWIR2), and 2257 nm (SWIR3), numbered in decreasing order of explained variance.
Figure 4.
PCA eigenvectors, ejPCA (computed using Set 0), at VIIRS VIS/NIR (a–g) bands plus the SWIR bands at 1241 nm (SWIR1), 1602 nm (SWIR2), and 2257 nm (SWIR3), numbered in decreasing order of explained variance.
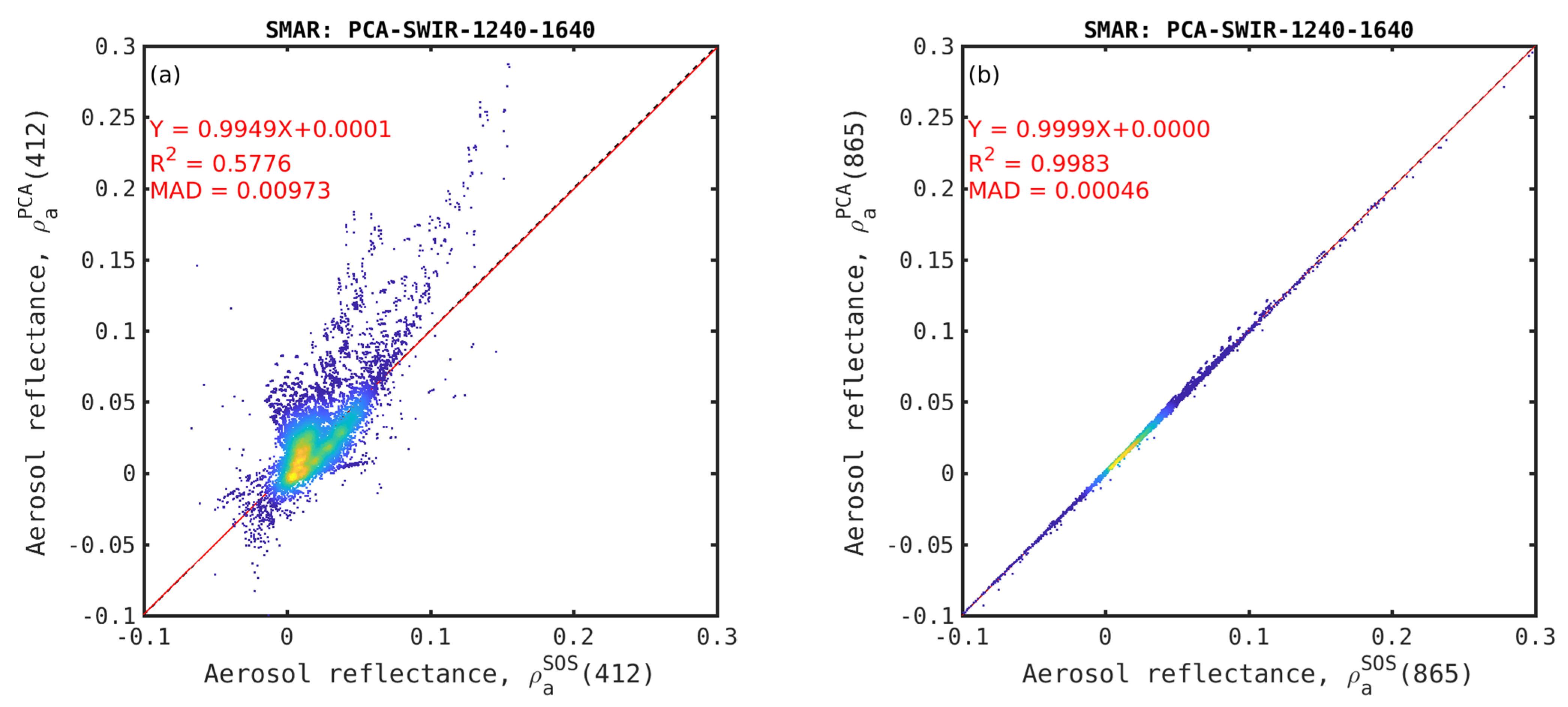
Figure 5.
Retrieved (ρaPCA) vs. true (ρaSOS) aerosol reflectance at 412 nm (a) and 865 nm (b) SABIA-Mar bands.
Figure 5.
Retrieved (ρaPCA) vs. true (ρaSOS) aerosol reflectance at 412 nm (a) and 865 nm (b) SABIA-Mar bands.
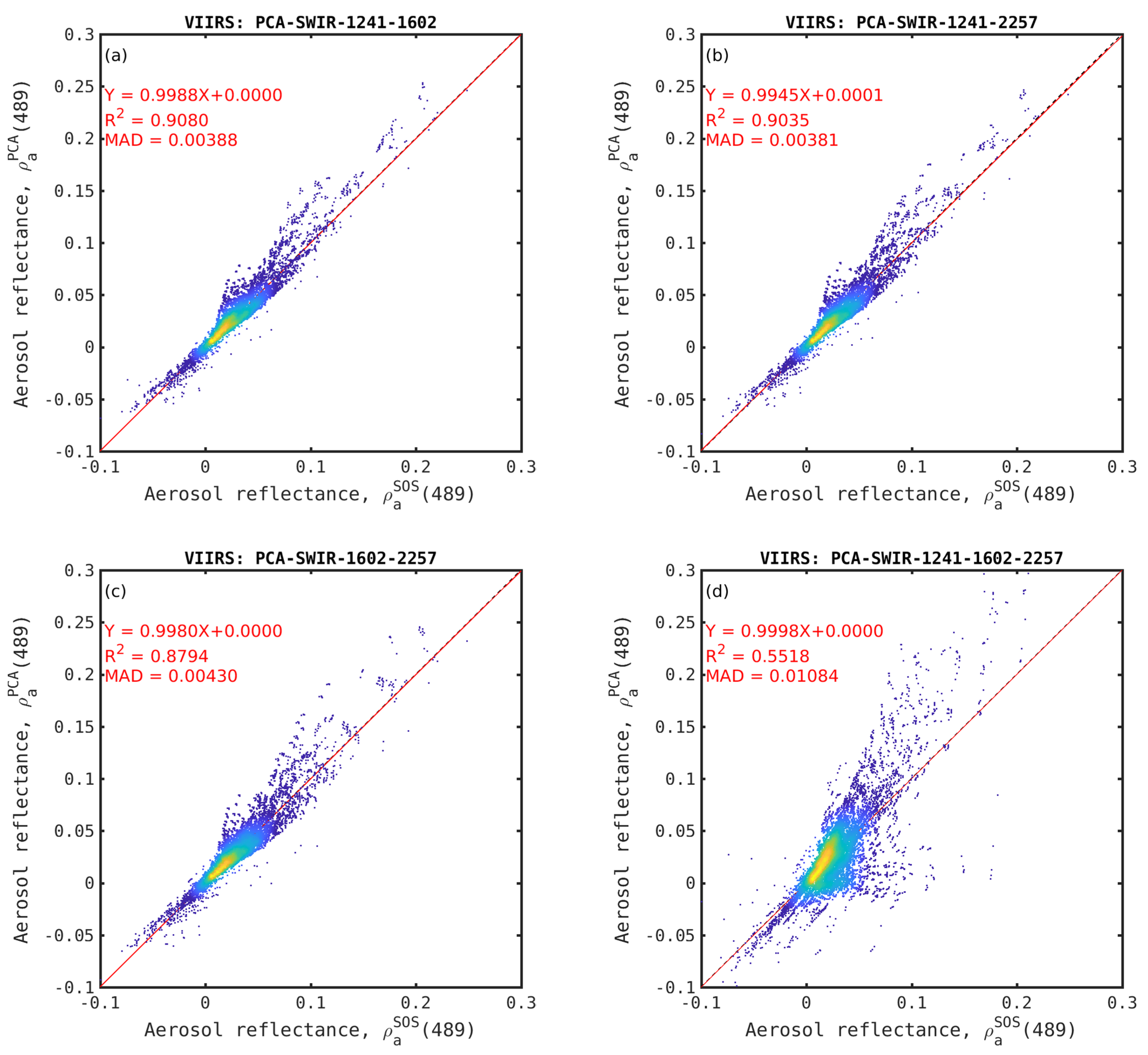
Figure 6.
Same as
Figure 5 but for VIIRS 489 nm band using PCA-SWIR12 (
a), PCA-SWIR13 (
b), PCA-SWIR23 (
c), PCA-SWIR123 (
d) schemes.
Figure 6.
Same as
Figure 5 but for VIIRS 489 nm band using PCA-SWIR12 (
a), PCA-SWIR13 (
b), PCA-SWIR23 (
c), PCA-SWIR123 (
d) schemes.
Figure 7.
Same as
Figure 6 but for 862 nm VIIRS band, (
a), PCA-SWIR13 (
b), PCA-SWIR23 (
c), PCA-SWIR123 (
d) schemes.
Figure 7.
Same as
Figure 6 but for 862 nm VIIRS band, (
a), PCA-SWIR13 (
b), PCA-SWIR23 (
c), PCA-SWIR123 (
d) schemes.
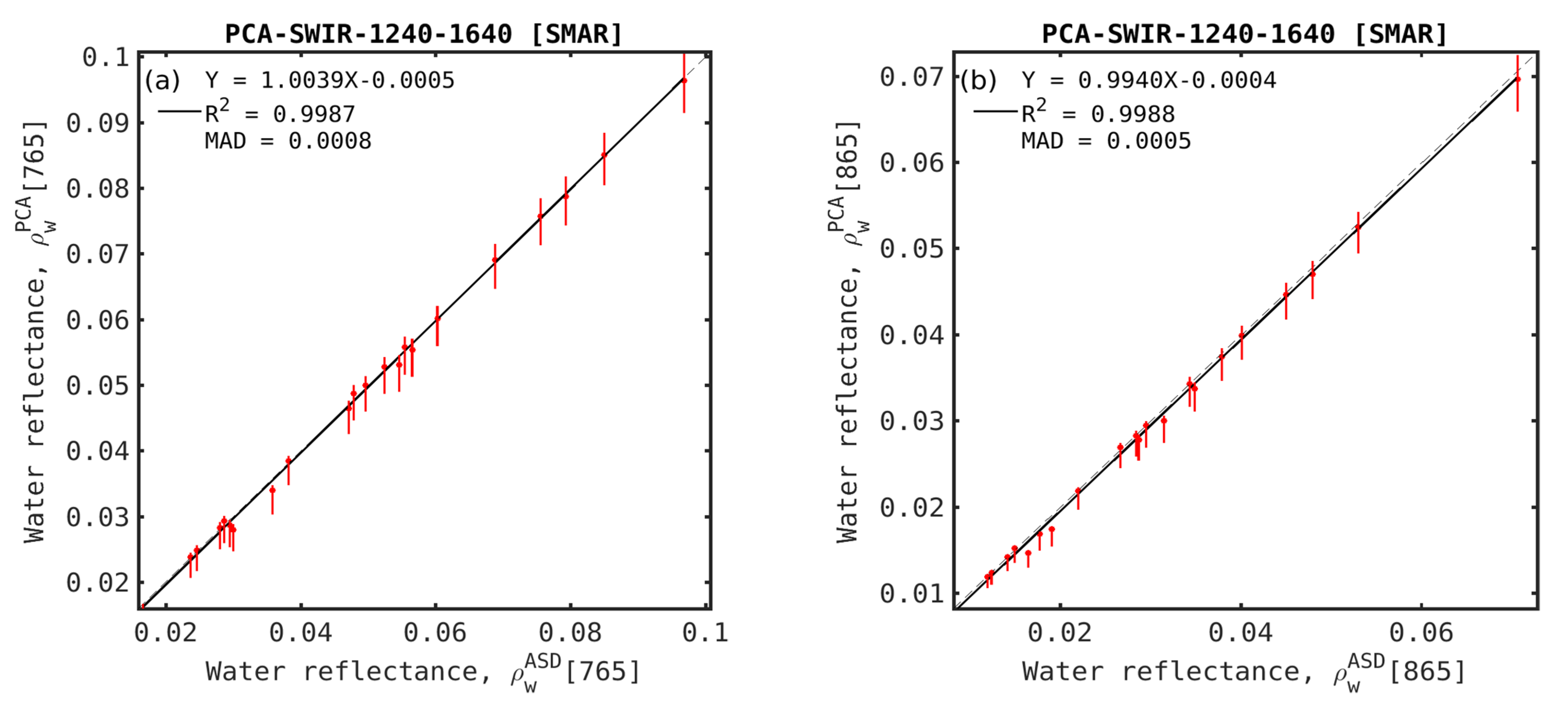
Figure 8.
Retrieved (ρwPCA) vs. field (ρwASD) water reflectance at SABIA-Mar (a) 765 nm (NIR1) and (b) 865 nm (NIR2) bands. Mean values are represented as red dots and vertical red bars correspond to the interquartile range (IQR).
Figure 8.
Retrieved (ρwPCA) vs. field (ρwASD) water reflectance at SABIA-Mar (a) 765 nm (NIR1) and (b) 865 nm (NIR2) bands. Mean values are represented as red dots and vertical red bars correspond to the interquartile range (IQR).
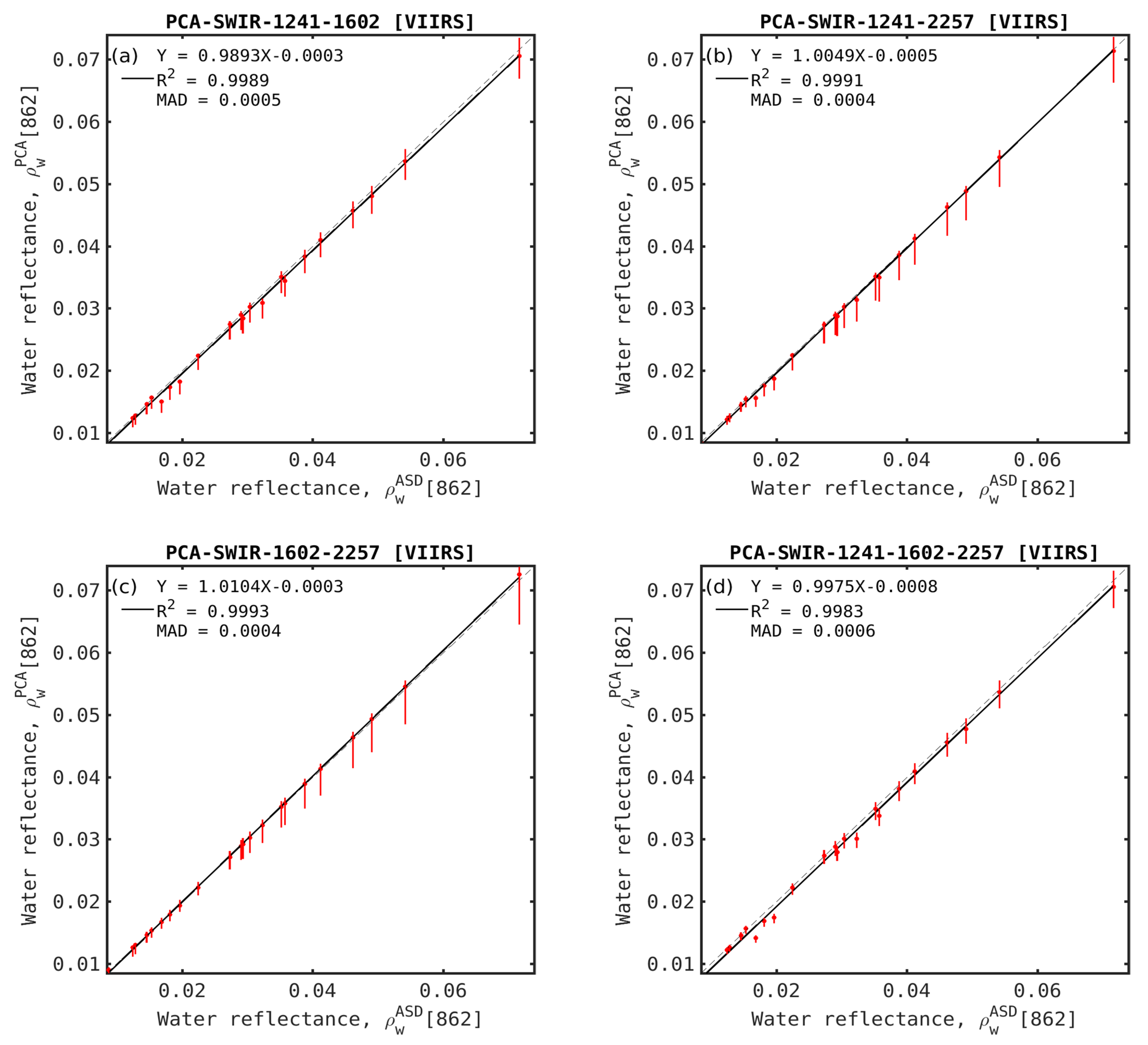
Figure 9.
Retrieved (ρwPCA) vs. field (ρwASD) water reflectance at VIIRS 862 nm (NIR2) band using (a) PCA-SWIR12, (b) PCA-SWIR12, (c) PCA-SWIR12, and (d) PCA-SWIR12 schemes. Dots are mean values and bars are the interquartile range (IQR).
Figure 9.
Retrieved (ρwPCA) vs. field (ρwASD) water reflectance at VIIRS 862 nm (NIR2) band using (a) PCA-SWIR12, (b) PCA-SWIR12, (c) PCA-SWIR12, and (d) PCA-SWIR12 schemes. Dots are mean values and bars are the interquartile range (IQR).
Figure 10.
Satellite-derived water reflectance () vs. field water reflectance () in the BLUE band (~445 nm) for MODIS/Aqua (MA), MODIS/Terra (MT), VIIRS/NOAA20 (VNOAA20), and VIIRS/Suomi-NPP (VSNPP) sensors shown in red, green, blue, and magenta, respectively. Each inset corresponds to a different AC: (a) NIR iterative scheme (ITER-NIR), (b) Rayleigh correction AC, i.e., without aerosol correction (RC), (c) SeaDAS SWIR AC using bands SWIR1 and SWIR3 (GW94-SWIR13), and (d) PCA-SWIR13 AC (PCA-SWIR13).
Figure 10.
Satellite-derived water reflectance () vs. field water reflectance () in the BLUE band (~445 nm) for MODIS/Aqua (MA), MODIS/Terra (MT), VIIRS/NOAA20 (VNOAA20), and VIIRS/Suomi-NPP (VSNPP) sensors shown in red, green, blue, and magenta, respectively. Each inset corresponds to a different AC: (a) NIR iterative scheme (ITER-NIR), (b) Rayleigh correction AC, i.e., without aerosol correction (RC), (c) SeaDAS SWIR AC using bands SWIR1 and SWIR3 (GW94-SWIR13), and (d) PCA-SWIR13 AC (PCA-SWIR13).
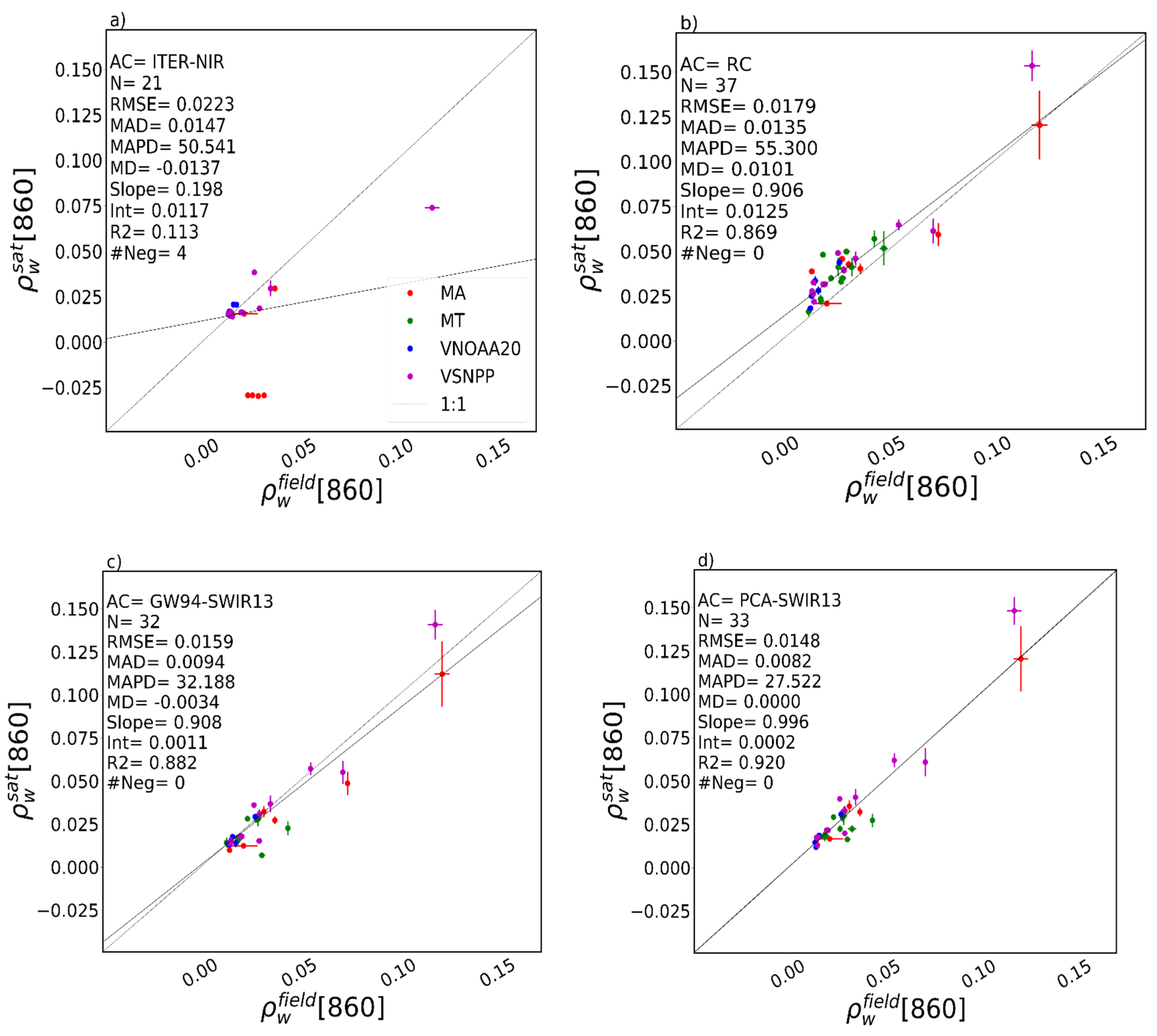
Figure 11.
Same as
Figure 10, but in the NIR2 band (~860 nm): (
a) NIR iterative scheme (ITER-NIR), (
b) Rayleigh correction AC, i.e., without aerosol correction (RC), (
c) SeaDAS SWIR AC using bands SWIR1 and SWIR3 (GW94-SWIR13), and (
d) PCA-SWIR13 AC (PCA-SWIR13).
Figure 11.
Same as
Figure 10, but in the NIR2 band (~860 nm): (
a) NIR iterative scheme (ITER-NIR), (
b) Rayleigh correction AC, i.e., without aerosol correction (RC), (
c) SeaDAS SWIR AC using bands SWIR1 and SWIR3 (GW94-SWIR13), and (
d) PCA-SWIR13 AC (PCA-SWIR13).
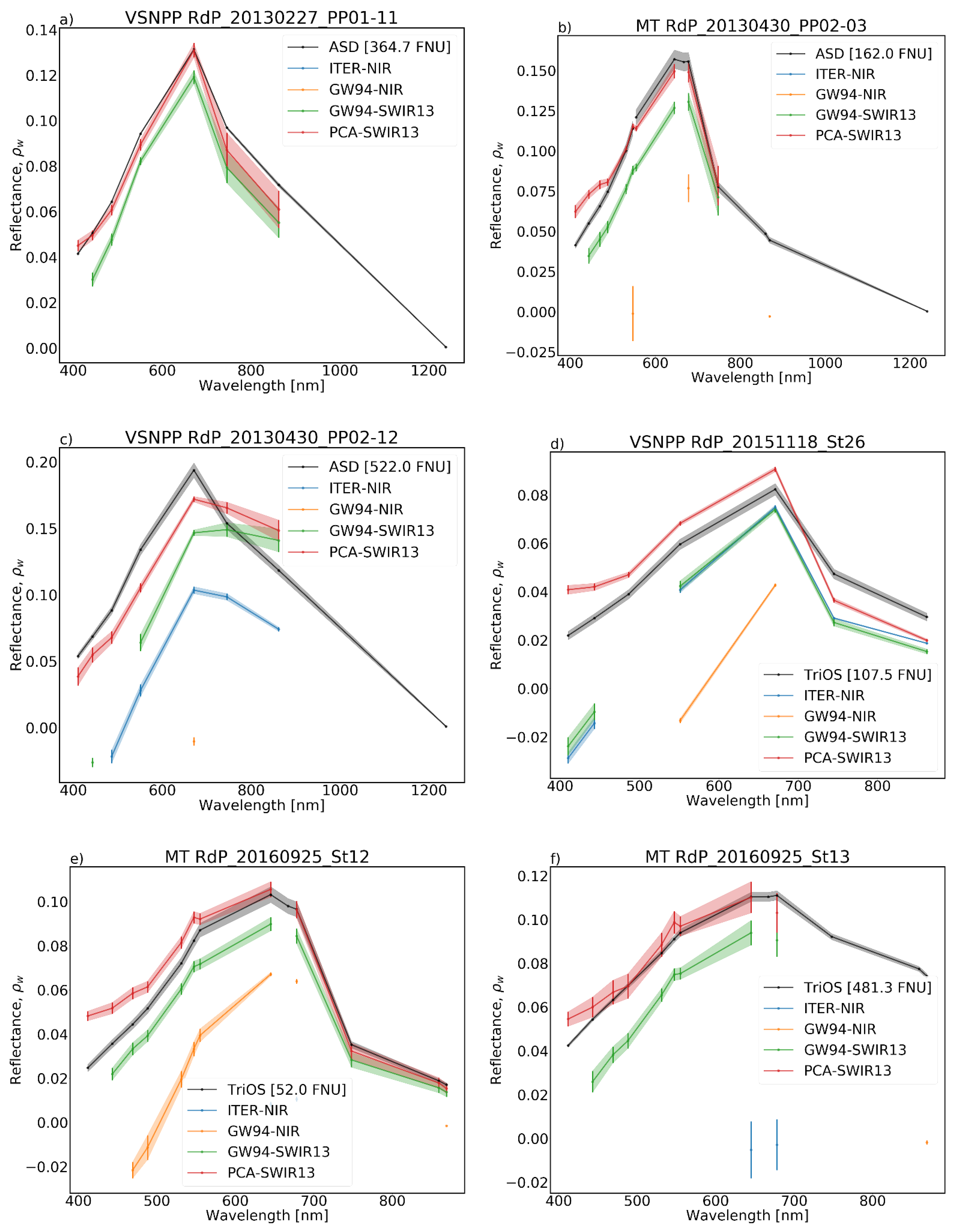
Figure 12.
Satellite-derived vs. field reflectance (TriOS or ASD in black) using several AC schemes: ITER-NIR (blue), GW94-NIR (orange), GW94-SWIR13 (green), and PCA-SWIR13 (red) for different match-ups: (a) RdP_20130227_PP01-11 (VSNPP overpass), (b) RdP_20130430_PP02-03 (MT overpass), (c) RdP_20130430_PP02-12 (VSNPP), (d) RdP_20151118_St26 (VSNPP), (e) RdP_20160925_St12 (MT), and (f) RdP_20160925_St13 (MT). Solid dotted lines show mean values of the 3 × 3 pixel window and uncertainty areas are shaded. Missing values correspond to AC or match-up failures. Simultaneous field measured turbidity (obtained using a portable HACH 2100Qis turbidimeter) is indicated inside each panel.
Figure 12.
Satellite-derived vs. field reflectance (TriOS or ASD in black) using several AC schemes: ITER-NIR (blue), GW94-NIR (orange), GW94-SWIR13 (green), and PCA-SWIR13 (red) for different match-ups: (a) RdP_20130227_PP01-11 (VSNPP overpass), (b) RdP_20130430_PP02-03 (MT overpass), (c) RdP_20130430_PP02-12 (VSNPP), (d) RdP_20151118_St26 (VSNPP), (e) RdP_20160925_St12 (MT), and (f) RdP_20160925_St13 (MT). Solid dotted lines show mean values of the 3 × 3 pixel window and uncertainty areas are shaded. Missing values correspond to AC or match-up failures. Simultaneous field measured turbidity (obtained using a portable HACH 2100Qis turbidimeter) is indicated inside each panel.
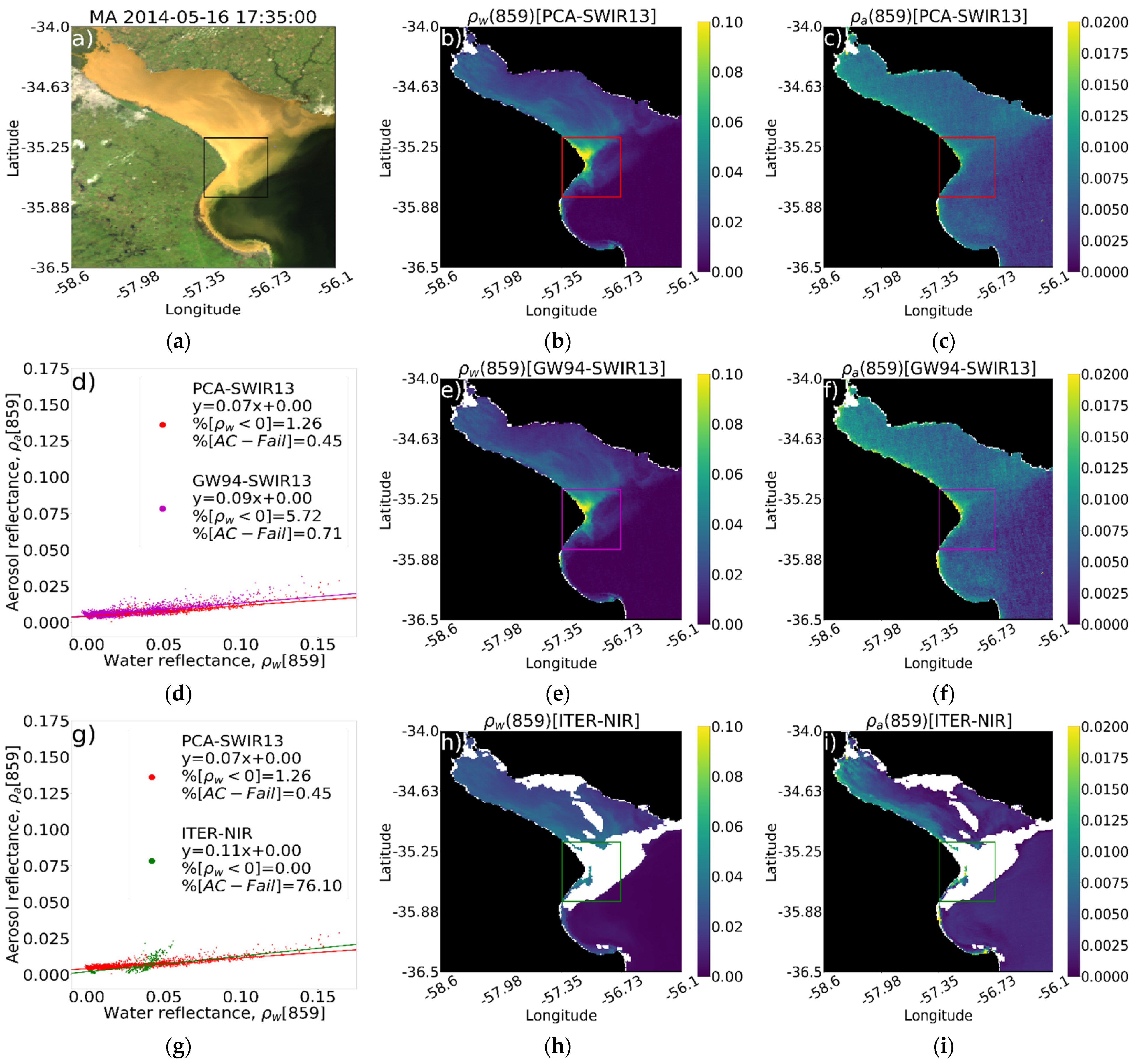
Figure 13.
Comparison of spatial patterns of water and aerosol reflectance retrieved by PCA-SWIR13, GW94-SWIR13, GW94-NIR, and ITER-NIR ACs from MODIS/Aqua image of the Río de la Plata acquired on 2014-05-16T15:35:00Z. RGB composite (a), water (b,e,h,k), and aerosol (c,f,i,l) reflectance at 443 nm, retrieved using PCA-SWIR13 (b,c), GW94-SWIR13 (e,f), GW94-NIR (h,i), and ITER-NIR (k,l) schemes. Plots show aerosol vs. water reflectance in the Río de la Plata’s turbidity front region marked with squares (d,g,j).
Figure 13.
Comparison of spatial patterns of water and aerosol reflectance retrieved by PCA-SWIR13, GW94-SWIR13, GW94-NIR, and ITER-NIR ACs from MODIS/Aqua image of the Río de la Plata acquired on 2014-05-16T15:35:00Z. RGB composite (a), water (b,e,h,k), and aerosol (c,f,i,l) reflectance at 443 nm, retrieved using PCA-SWIR13 (b,c), GW94-SWIR13 (e,f), GW94-NIR (h,i), and ITER-NIR (k,l) schemes. Plots show aerosol vs. water reflectance in the Río de la Plata’s turbidity front region marked with squares (d,g,j).
Figure 14.
Same as
Figure 13 but at 859 nm and not considering the performance of the GW94-NIR scheme, as it retrieves trivially null water reflectance in the NIR bands. RGB composite (
a), water (
b,
e,
h), and aerosol (
c,
f,
i) reflectance at 748 nm, retrieved using PCA-SWIR13 (
b,
c), and GW94-SWIR13 (
e,
f), ITER-NIR (
h,
i). Plots show aerosol vs. water reflectance in the Río de la Plata’s turbidity front region marked with squares (
d,
g).
Figure 14.
Same as
Figure 13 but at 859 nm and not considering the performance of the GW94-NIR scheme, as it retrieves trivially null water reflectance in the NIR bands. RGB composite (
a), water (
b,
e,
h), and aerosol (
c,
f,
i) reflectance at 748 nm, retrieved using PCA-SWIR13 (
b,
c), and GW94-SWIR13 (
e,
f), ITER-NIR (
h,
i). Plots show aerosol vs. water reflectance in the Río de la Plata’s turbidity front region marked with squares (
d,
g).
Table 1.
Spectral bands of the sensors used to theoretically test the SWIR-PCA algorithm. The bands in which the black water assumption is valid are marked in green. In yellow, the bands in which this assumption is affected only with very high sediment concentrations.
Table 1.
Spectral bands of the sensors used to theoretically test the SWIR-PCA algorithm. The bands in which the black water assumption is valid are marked in green. In yellow, the bands in which this assumption is affected only with very high sediment concentrations.
| Band Tag | MODIS | VIIRS | SABIA-Mar |
|---|
| BLUE | 443 nm | 443 nm | 443 nm |
| GREEN | 555 nm | 551 nm | 555 nm |
| RED | 645 nm | 667 nm | 665 nm |
| NIR1 | 748 nm | 745 nm | 750 nm |
| NIR2 | 859 nm | 862 nm | 865 nm |
| SWIR1 | 1240 nm | 1238 nm | 1240 nm |
| SWIR2 | 1640 nm | 1601 nm | 1640 nm |
| SWIR3 | 2130 nm | 2257 nm | |
Table 2.
Atmospheric, surface, geometric, and optical parameters used as input to the sets of simulations using Centre National d’Études Spatiales/Successive Orders of Scattering (CNES-SOS).
Table 2.
Atmospheric, surface, geometric, and optical parameters used as input to the sets of simulations using Centre National d’Études Spatiales/Successive Orders of Scattering (CNES-SOS).
| CNES-SOS Parameter | Input Value/Range |
|---|
| λ (Wavelength) | 400 nm to 2500 nm. step 2 nm (VIS/NIR) and 10 nm (far SWIR). |
| θs (Solar Zenith Angle, SZA) | 15° to 60° (step 15°) |
| θv (Viewing Zenith Angle, VZA) | 0° to 45° (step 15°) |
| ϕ (Relative Azimuth Angle, RAA) | 0° to 180° (step 15°) |
| ρw (Water reflectance) | Set W: ASD in situ (RdP), see Figure 2 |
| w (Wind speed) | 0, 2, 4, 8, 16 m/s |
| nw (Relative air–water interface) | 1.334 |
| τr (Rayleigh optical thickness) | Bodhaine et al., 1999 [22] |
| δr (Depolarization Factor) | Bodhaine et al., 1999 [22] |
| Hr (e-folding height scale for molecules) | 8 km |
| τa (Aerosol optical thickness at 500 nm) | 0:0.1:0.4 |
| dVa/dlnr (Aerosol granulometry) | Continental, Marine, and Urban scenarios [23] |
| na + ima (Refractive index, aerosols) | Continental, Marine, and Urban scenarios [23] |
| Ha (e-folding height scale for aerosols) | 2 km |
| nmax (Maximum scattering order) | 20 |
| Ipol (Polarization index) | 1 (consider polarization) |
Table 3.
Specific inputs (aerosol correction type “aer_opt” and wavelengths of the corrector bands “aer_wave_short” and “aer_wave_long”) of each of the studied L2Gen atmospheric corrections (ACs). The band wavelengths used for aerosol calculations are here represented with the band tags of
Table 1, since they depend on each sensor. General inputs to L2Gen that were not changed among ACs are mentioned in the text. GW94-NIR, NIR multi-scattering extrapolative approach; ITER-NIR, standard NASA’s iterative scheme in the NIR; GW94-SWIR, SWIR multi-scattering extrapolative approach; RC, Rayleigh correction.
Table 3.
Specific inputs (aerosol correction type “aer_opt” and wavelengths of the corrector bands “aer_wave_short” and “aer_wave_long”) of each of the studied L2Gen atmospheric corrections (ACs). The band wavelengths used for aerosol calculations are here represented with the band tags of
Table 1, since they depend on each sensor. General inputs to L2Gen that were not changed among ACs are mentioned in the text. GW94-NIR, NIR multi-scattering extrapolative approach; ITER-NIR, standard NASA’s iterative scheme in the NIR; GW94-SWIR, SWIR multi-scattering extrapolative approach; RC, Rayleigh correction.
| Atmospheric Correction (AC) | Aer_Opt (Description) | Aer_Wave_Short | Aer_Wave_Long |
|---|
| GW94-NIR | −1 (Multi-scattering with 2-band model selection) | NIR1 | NIR2 |
| ITER-NIR | −2 (Multi-scattering with 2-band, RH-based model selection and iterative NIR correction) | NIR1 | NIR2 |
| GW94-SWIR13 | −1 (Multi-scattering with 2-band model selection) | SWIR1 | SWIR3 |
| RC | −99 (No aerosol correction) | – | – |
Table 4.
Cumulative variance explained with one, two, and three principal components of the simulated aerosol reflectance and inversion conditional numbers for the PCA-SWIR123 and PCA-SWIR13 schemes applied to VIIRS bands.
Table 4.
Cumulative variance explained with one, two, and three principal components of the simulated aerosol reflectance and inversion conditional numbers for the PCA-SWIR123 and PCA-SWIR13 schemes applied to VIIRS bands.
| Band (nm) (Band Tag) | PCA-SWIR123 (VIIRS) Explained Variance (%) | Inversion Conditional Number | PCA-SWIR13 (VIIRS) Explained Variance (%) | Inversion Conditional Number |
|---|
| 1 Component | 2 Components | 3 Components (Total Used) | 1 Component | 2 Components (Total used) |
|---|
| 443 (BLUE) | 69.04 | 95.36 | 99.43 | 389.3 | 67.14 | 95.42 | 4.8 |
| 551 (GREEN) | 73.52 | 97.04 | 99.54 | 26.9 | 72.46 | 97.28 | 4.0 |
| 667 (RED) | 77.08 | 97.49 | 99.69 | 14.0 | 76.16 | 97.70 | 3.4 |
| 74 (NIR1) | 79.44 | 97.69 | 99.74 | 10.3 | 78.50 | 97.92 | 2.9 |
| 862 (NIR2) | 82.87 | 98.10 | 99.81 | 6.2 | 81.92 | 98.38 | 2.3 |
Table 5.
(
a). Eigenvector components of the PCA-SWIR13 AC scheme for MODIS/Aqua. Here, λ
tbc stands for the wavelength of the band to be corrected (i.e., either the BLUE, GREEN, RED, NIR1, or NIR2 band). (
b). Same as
Table 5a, but for VIIRS/Suomi-NPP.
Table 5.
(
a). Eigenvector components of the PCA-SWIR13 AC scheme for MODIS/Aqua. Here, λ
tbc stands for the wavelength of the band to be corrected (i.e., either the BLUE, GREEN, RED, NIR1, or NIR2 band). (
b). Same as
Table 5a, but for VIIRS/Suomi-NPP.
| Eigenvector Component | Band to be Corrected |
|---|
| BLUE | GREEN | RED | NIR1 | NIR2 |
|---|
| (a) |
| e1PCA(λtbc) | 0.56754 | 0.64103 | 0.64783 | 0.63771 | 0.62218 |
| e1PCA(SWIR1) | 0.62019 | 0.57974 | 0.57276 | 0.5766 | 0.58281 |
| e1PCA(SWIR3) | 0.54153 | 0.50297 | 0.50226 | 0.51074 | 0.52271 |
| e2PCA(λtbc) | 0.80075 | 0.73023 | 0.70876 | 0.69681 | 0.66258 |
| e2PCA(SWIR1) | −0.26275 | −0.25892 | −0.2115 | −0.14924 | −0.03639 |
| e2PCA(SWIR3) | −0.53829 | −0.63223 | −0.673 | −0.70155 | −0.74811 |
| e3PCA(λtbc) | −0.19155 | −0.2363 | −0.27924 | −0.32829 | −0.41698 |
| e3PCA(SWIR1) | 0.73914 | 0.77257 | 0.79197 | 0.80328 | 0.81179 |
| e3PCA(SWIR3) | −0.64574 | −0.58932 | −0.54297 | −0.49696 | −0.4088 |
| (b) |
| e1PCA(λtbc) | 0.57084 | 0.64113 | 0.64876 | 0.6392 | 0.62309 |
| e1PCA(SWIR1) | 0.62211 | 0.58309 | 0.57521 | 0.57871 | 0.58499 |
| e1PCA(SWIR3) | 0.53583 | 0.49895 | 0.49824 | 0.50648 | 0.51918 |
| e2PCA(λtbc) | 0.79439 | 0.72537 | 0.7005 | 0.68722 | 0.64802 |
| e2PCA(SWIR1) | −0.25348 | −0.24815 | −0.19558 | −0.13422 | −0.01441 |
| e2PCA(SWIR3) | −0.55199 | −0.64208 | −0.68633 | −0.71394 | −0.76149 |
| e3PCA(λtbc) | −0.20758 | −0.25057 | −0.29734 | −0.34518 | −0.43798 |
| e3PCA(SWIR1) | 0.74076 | 0.77358 | 0.79428 | 0.80442 | 0.81091 |
| e3PCA(SWIR3) | −0.6389 | −0.58205 | −0.52981 | −0.48349 | −0.38806 |
Table 6.
Noise-equivalent RC reflectance for each of the MODIS/Aqua sensor bands in the NIR and SWIR, obtained by applying the geostatistical method to the RC reflectance of the mentioned set.
Table 6.
Noise-equivalent RC reflectance for each of the MODIS/Aqua sensor bands in the NIR and SWIR, obtained by applying the geostatistical method to the RC reflectance of the mentioned set.
| Wavelength (nm) (Band Tag) | Noise Equivalent Reflectance, NEρRC |
|---|
| 748 (NIR1) | 0.001845 |
| 859 (NIR2) | 0.003686 |
| 1240 (SWIR1) | 0.000279 |
| 1640 (SWIR2) | 0.000178 |
| 2130 (SWIR3) | 0.000174 |
Table 7.
Comparison between performance metrics of simulated water reflectance ρw (PCA) vs. ρw (field) at MODIS/Aqua 857 nm band (Set W) with and without noise added to simulations. MAD, mean absolute difference; Int, intercept.
Table 7.
Comparison between performance metrics of simulated water reflectance ρw (PCA) vs. ρw (field) at MODIS/Aqua 857 nm band (Set W) with and without noise added to simulations. MAD, mean absolute difference; Int, intercept.
| AC/Sensor | Noise Added | MAD | Slope | Int | R2 |
|---|
| PCA-SWIR13 MODIS/Aqua | No | 0.0005 | 0.984 | −0.0006 | 0.999 |
| Yes | 0.0008 | 1.006 | −0.0008 | 0.998 |
Table 8.
Performance metrics of satellite-derived water reflectance (ρwsat) vs. field water reflectance () in the BLUE, GREEN, RED, NIR1, and NIR2 bands of MODIS/Aqua (MA), MODIS/Terra (MT), VIIRS/NOAA20 (VNOAA20), and VIIRS/Suomi-NPP (VSNPP) sensors. Results are shown for ITER-NIR, GW94-NIR, GW94-SWIR13, and PCA_SWIR13 ACs. RMSE, root mean square error; MAD, mean absolute difference; MAPD, mean absolute percentage difference; MD, mean difference.
Table 8.
Performance metrics of satellite-derived water reflectance (ρwsat) vs. field water reflectance () in the BLUE, GREEN, RED, NIR1, and NIR2 bands of MODIS/Aqua (MA), MODIS/Terra (MT), VIIRS/NOAA20 (VNOAA20), and VIIRS/Suomi-NPP (VSNPP) sensors. Results are shown for ITER-NIR, GW94-NIR, GW94-SWIR13, and PCA_SWIR13 ACs. RMSE, root mean square error; MAD, mean absolute difference; MAPD, mean absolute percentage difference; MD, mean difference.
| Band | AC | N | #Neg | RMSE | MAD | MAPD | MD | Slope | Int | R2 |
|---|
| BLUE | ITER-NIR | 9 | 5 | 0.037 | 0.032 | 93.7 | −0.026 | 0.074 | 0.000 | 0.000 |
| GW94-NIR | 6 | 6 | 0.039 | 0.035 | 104.2 | −0.051 | 1.011 | −0.054 | 0.663 |
| GW94-SWIR13 | 20 | 5 | 0.031 | 0.025 | 70.0 | −0.016 | −0.154 | 0.036 | 0.170 |
| PCA-SWIR13 | 34 | 1 | 0.027 | 0.024 | 74.3 | 0.019 | 0.330 | 0.041 | 0.061 |
| GREEN | ITER-NIR | 16 | 0 | 0.035 | 0.027 | 34.6 | −0.008 | 0.214 | 0.039 | 0.233 |
| GW94-NIR | 17 | 5 | 0.043 | 0.036 | 49.5 | −0.049 | −0.141 | 0.024 | 0.072 |
| GW94-SWIR13 | 36 | 0 | 0.025 | 0.017 | 22.2 | −0.006 | 0.426 | 0.037 | 0.297 |
| PCA-SWIR13 | 40 | 0 | 0.020 | 0.017 | 23.9 | 0.011 | 0.536 | 0.046 | 0.429 |
| RED | ITER-NIR | 27 | 7 | 0.053 | 0.040 | 40.8 | −0.033 | 0.147 | 0.055 | 0.047 |
| GW94-NIR | 34 | 1 | 0.048 | 0.034 | 32.9 | −0.033 | 0.503 | 0.014 | 0.161 |
| GW94-SWIR13 | 40 | 0 | 0.019 | 0.015 | 14.7 | −0.002 | 0.679 | 0.026 | 0.656 |
| PCA-SWIR13 | 40 | 0 | 0.023 | 0.019 | 20.5 | 0.013 | 0.812 | 0.027 | 0.671 |
| NIR1 | ITER-NIR | 17 | 0 | 0.017 | 0.013 | 26.9 | −0.008 | 0.490 | 0.014 | 0.847 |
| GW94-SWIR13 | 34 | 0 | 0.011 | 0.007 | 16.4 | −0.004 | 0.935 | 0.002 | 0.843 |
| PCA-SWIR13 | 37 | 0 | 0.009 | 0.007 | 16.0 | 0.000 | 1.029 | 0.002 | 0.866 |
| NIR2 | ITER-NIR | 21 | 4 | 0.022 | 0.015 | 50.5 | −0.014 | 0.198 | 0.012 | 0.113 |
| GW94-SWIR13 | 32 | 0 | 0.016 | 0.009 | 32.2 | −0.003 | 0.908 | 0.001 | 0.882 |
| PCA-SWIR13 | 33 | 0 | 0.015 | 0.008 | 27.5 | 0.000 | 0.996 | 0.000 | 0.920 |