Twenty-Seven Years of Scatterometer Surface Wind Analysis over Eastern Boundary Upwelling Systems
Abstract
1. Introduction
2. Data
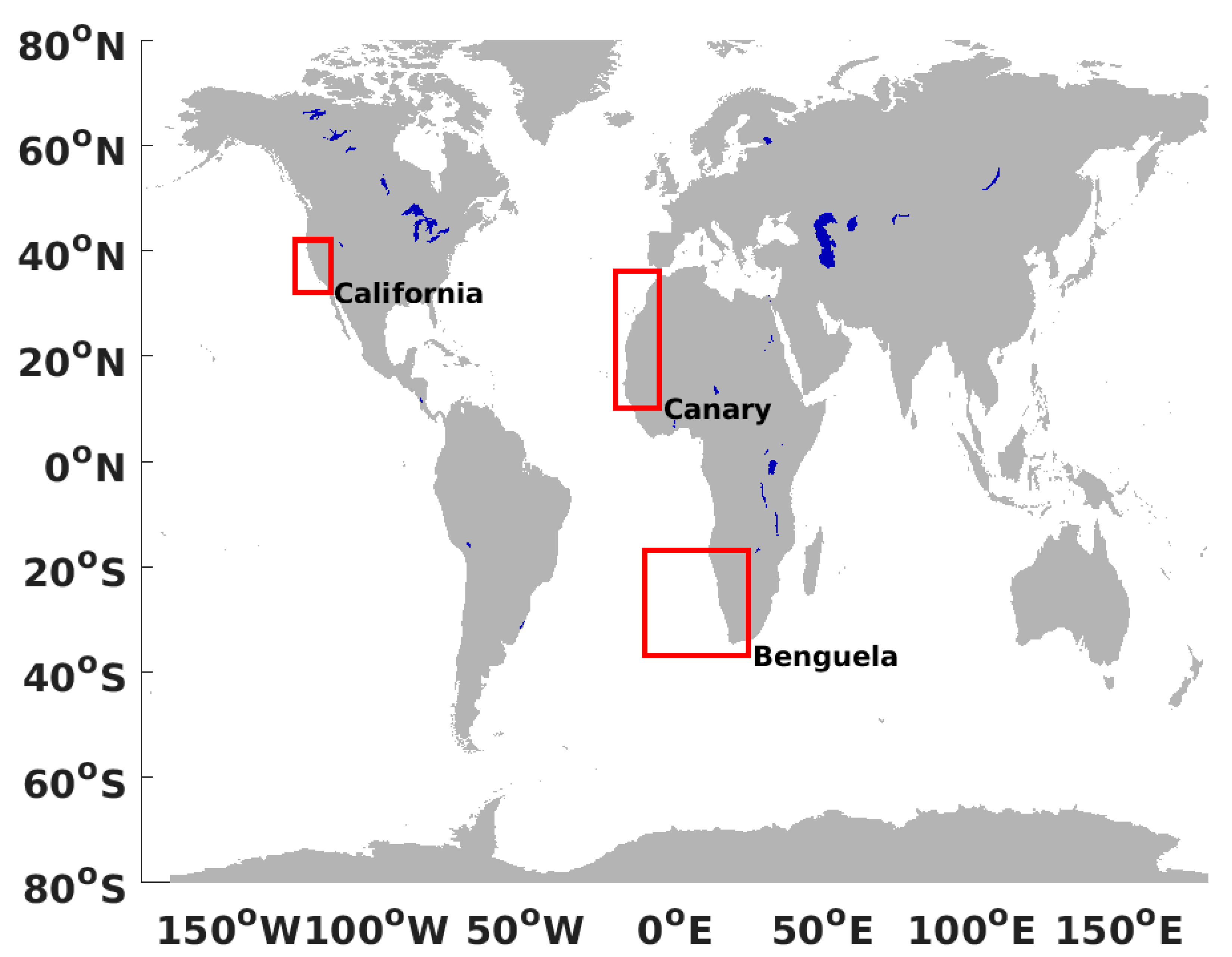
2.1. In Situ Data
2.2. Remote Sensing Data
2.3. Copernicus/Marine Environment Monitoring Service (CMEMS) L4 Wind Analyses
2.4. Cross-Calibrated Multi-Platform (CCMP) Wind Analysis
2.5. Atmospheric Reanalysis
3. Analysis Method
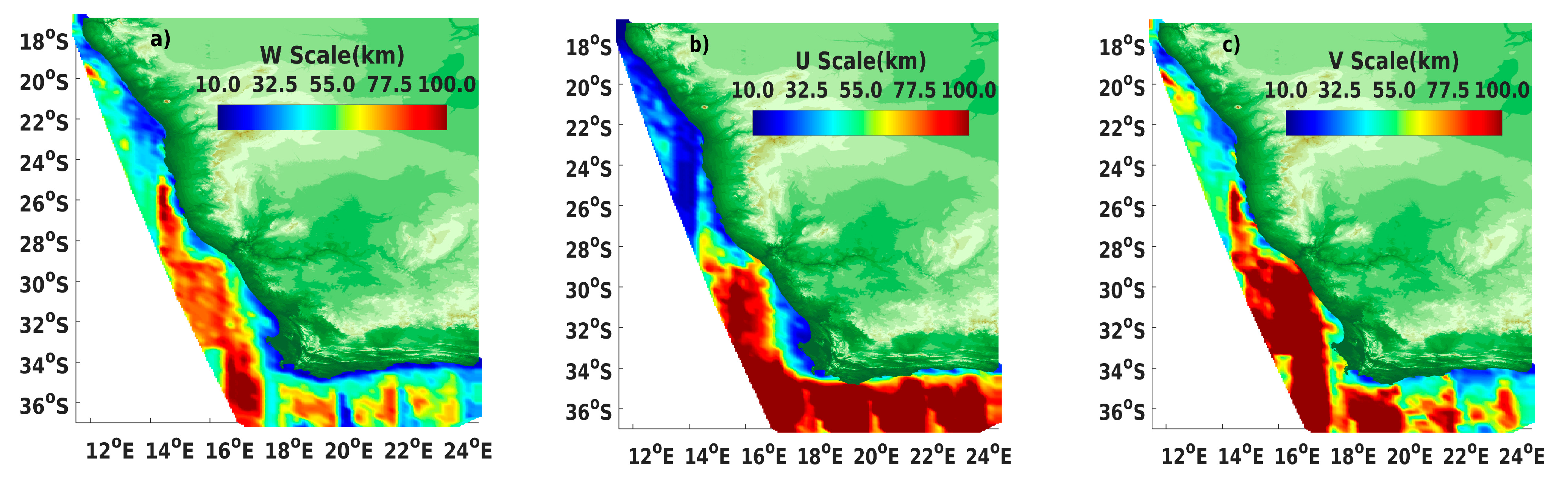
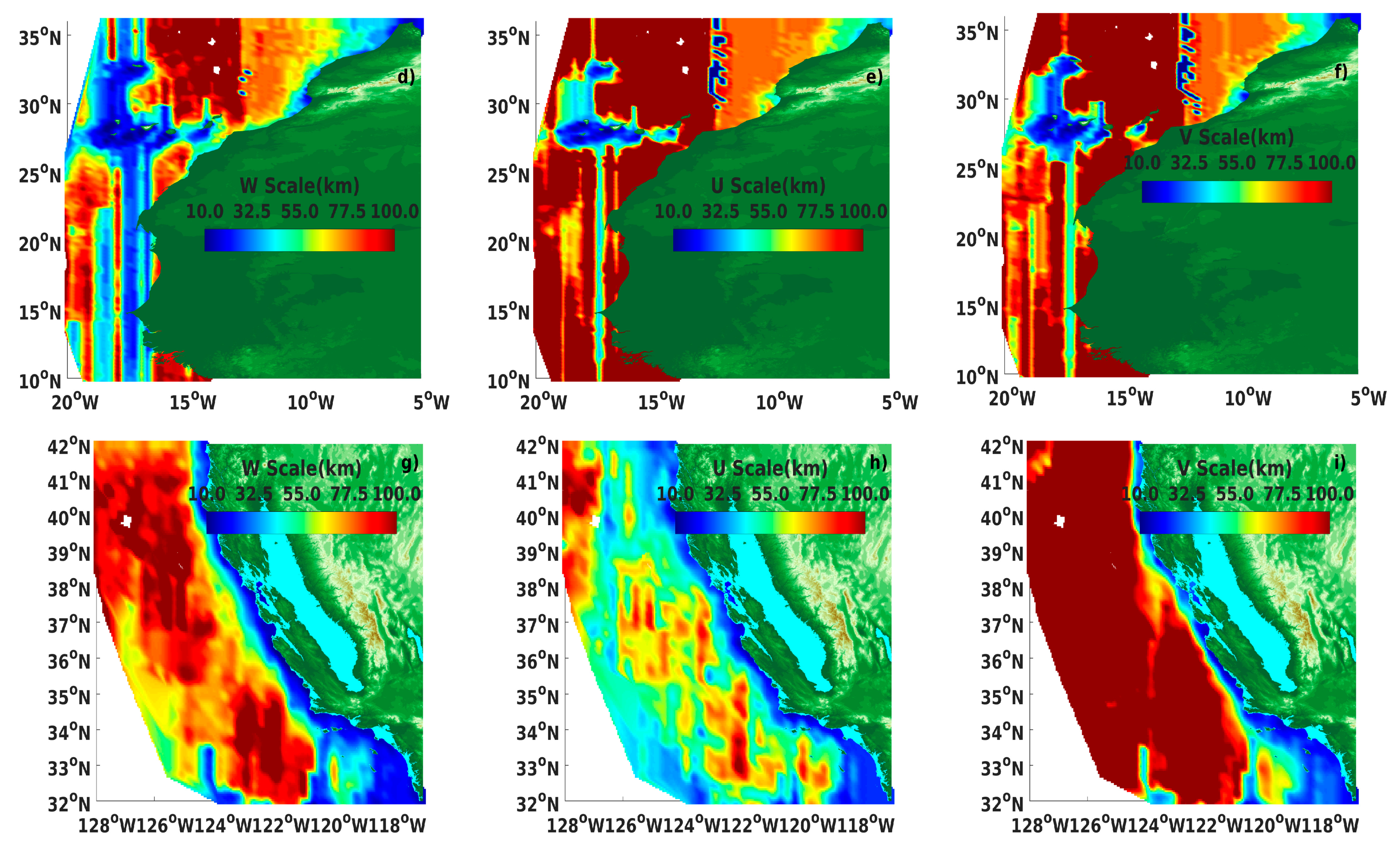
3.1. Spatial Structure Functions
3.2. Temporal Structure Functions
3.3. IFREMER Satellite Wind Analyses
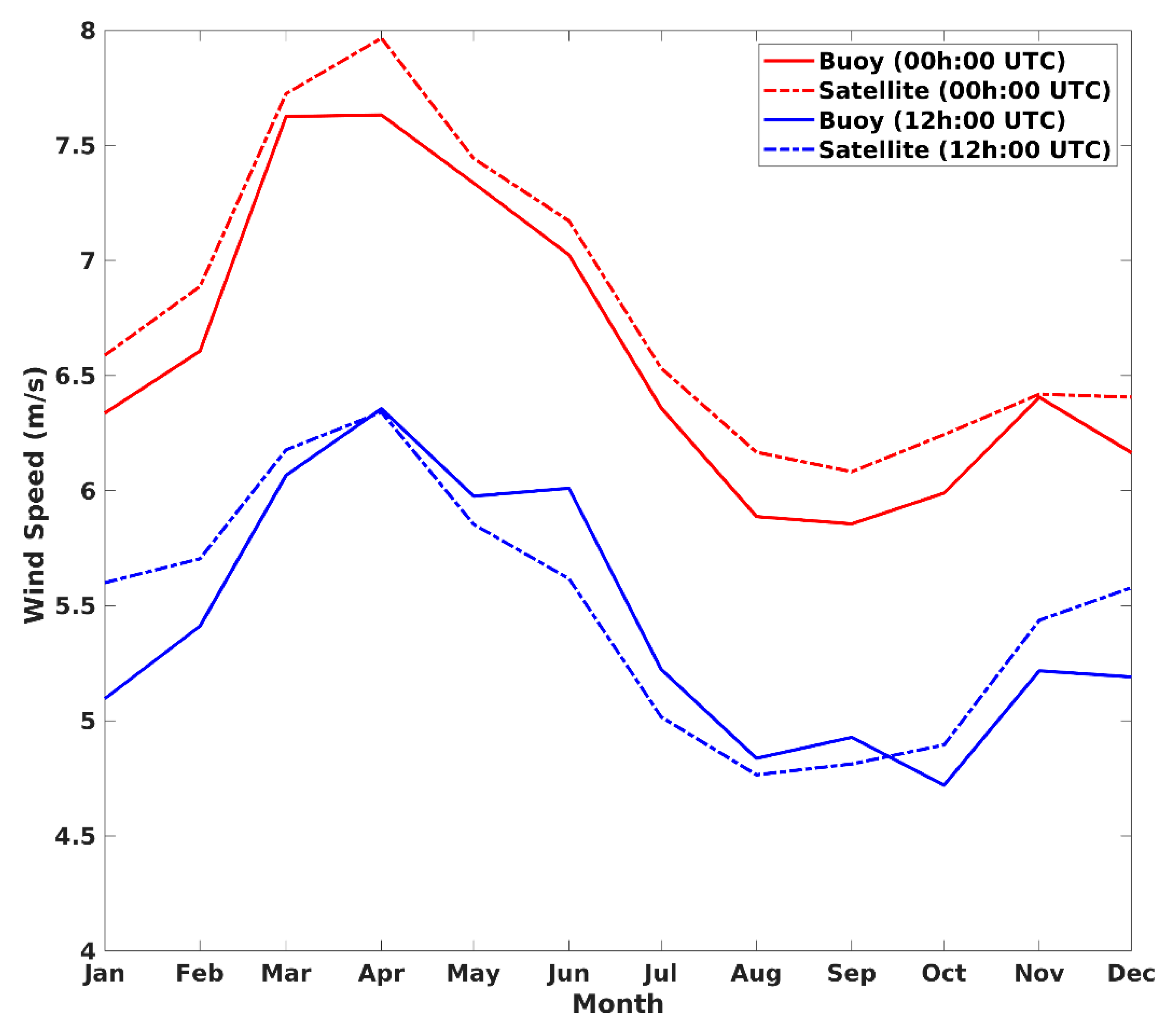
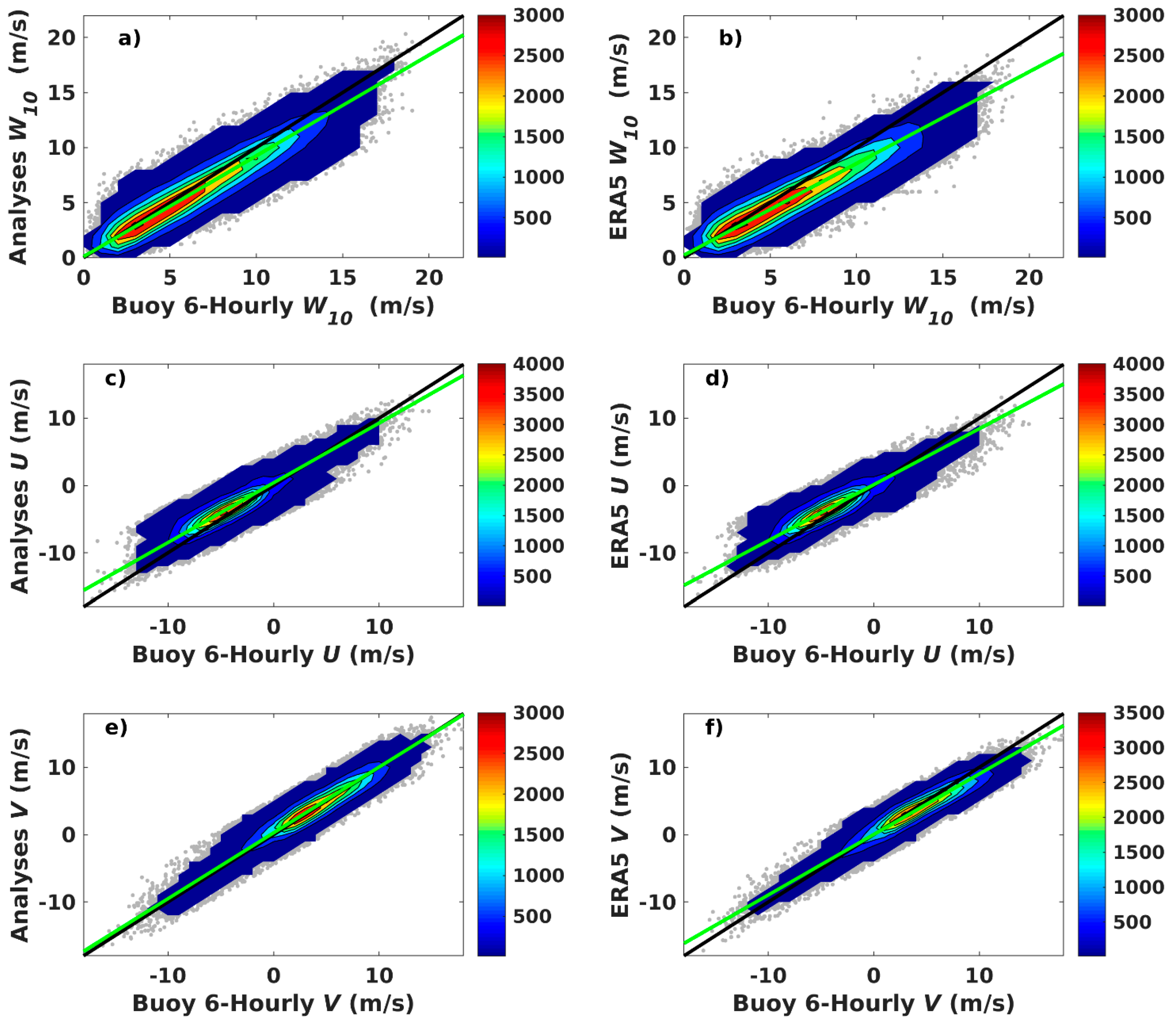
3.4. Accuracy of Satellite Wind Analyses
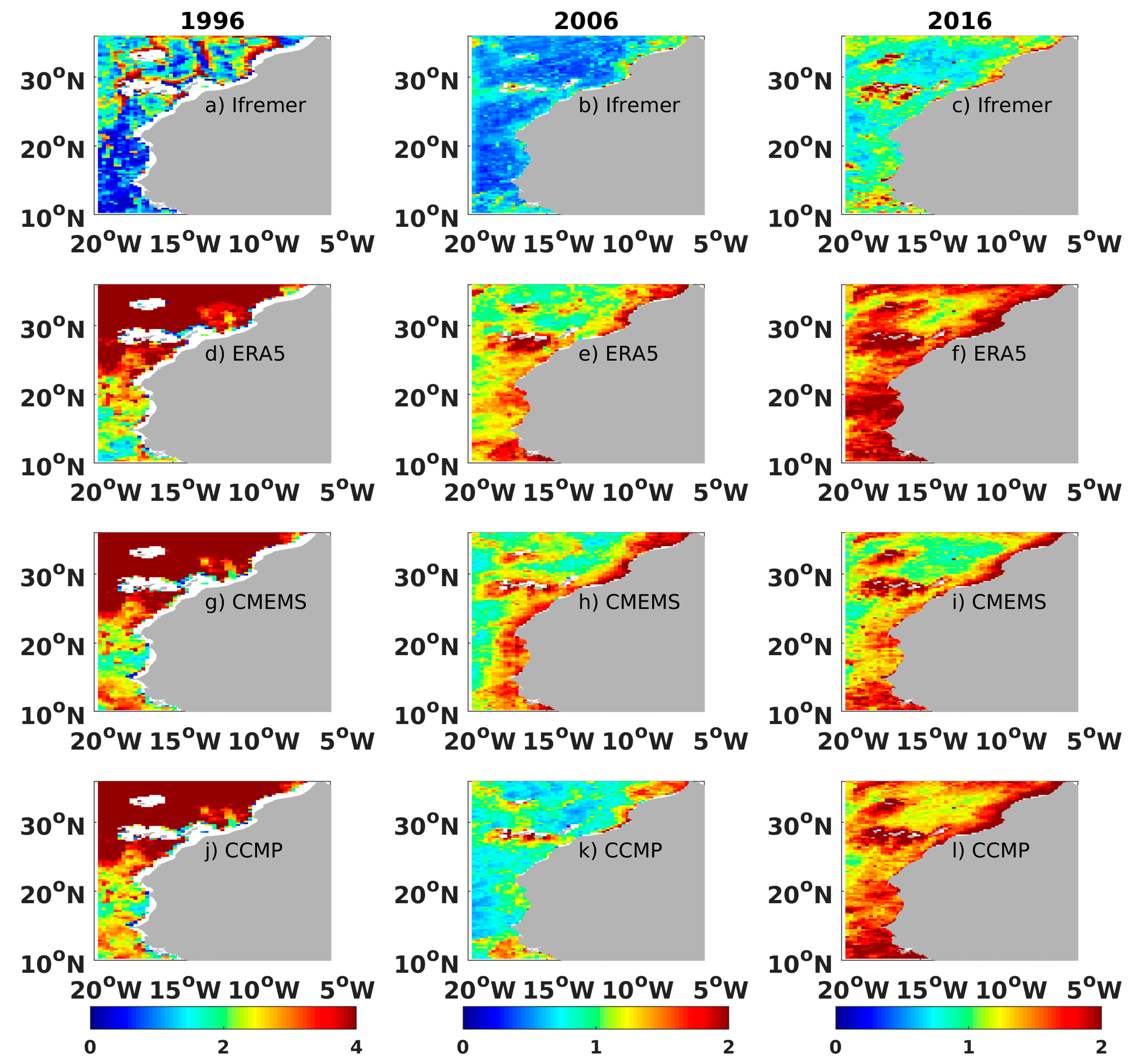
4. Surface Wind Analyses Versus Scatterometer Wind Retrievals
4.1. Wind Vector Issues
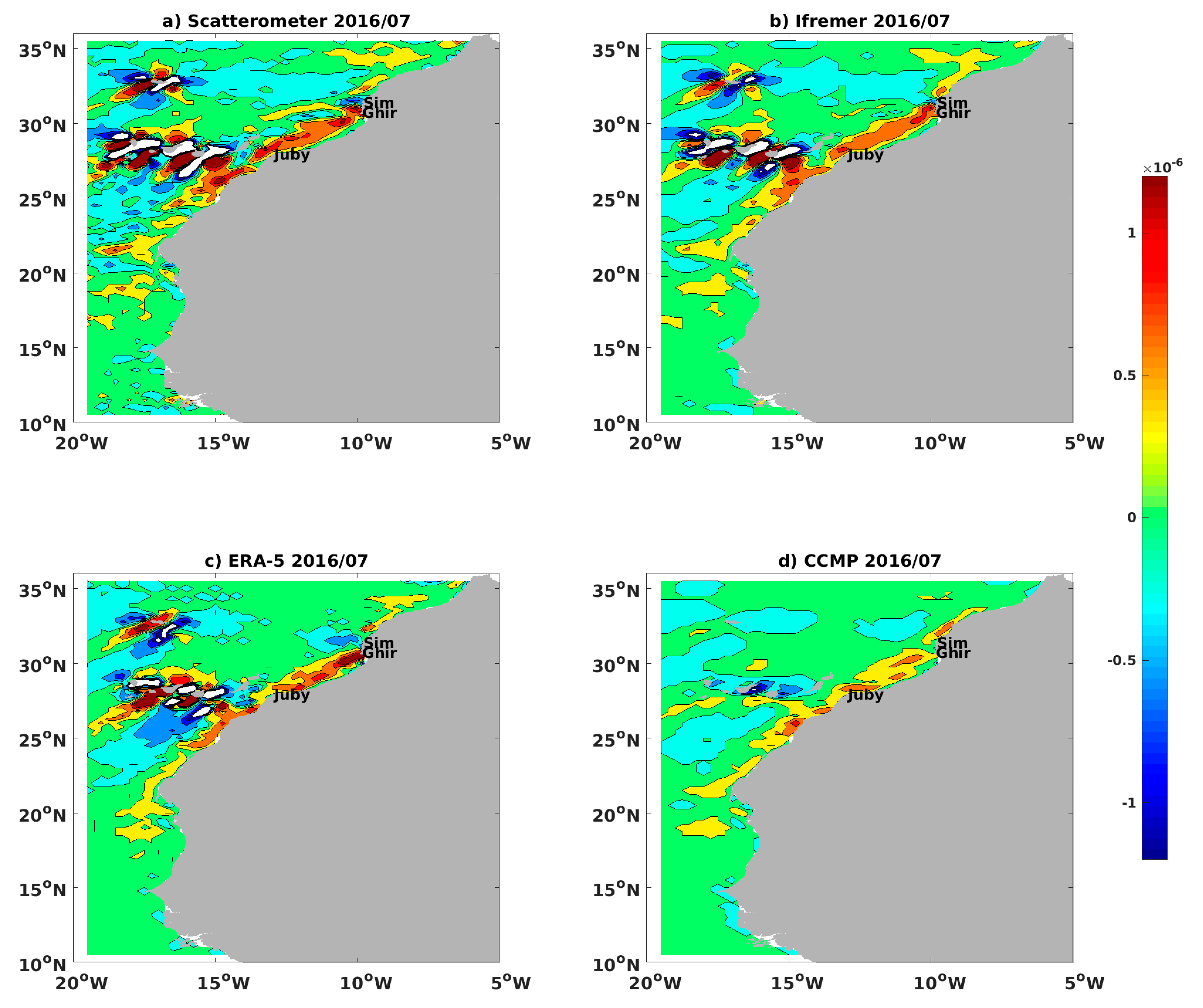
4.2. Wind Stress Issues
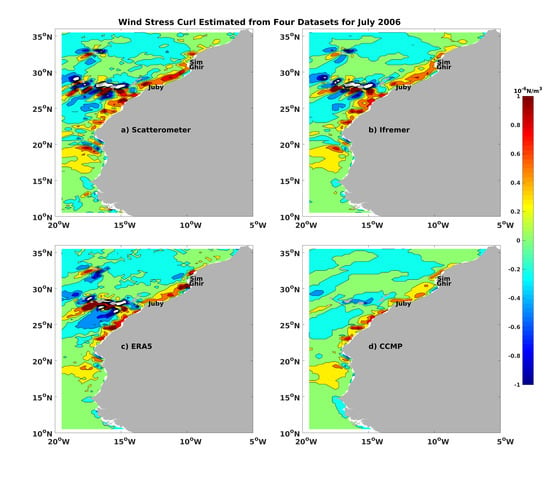
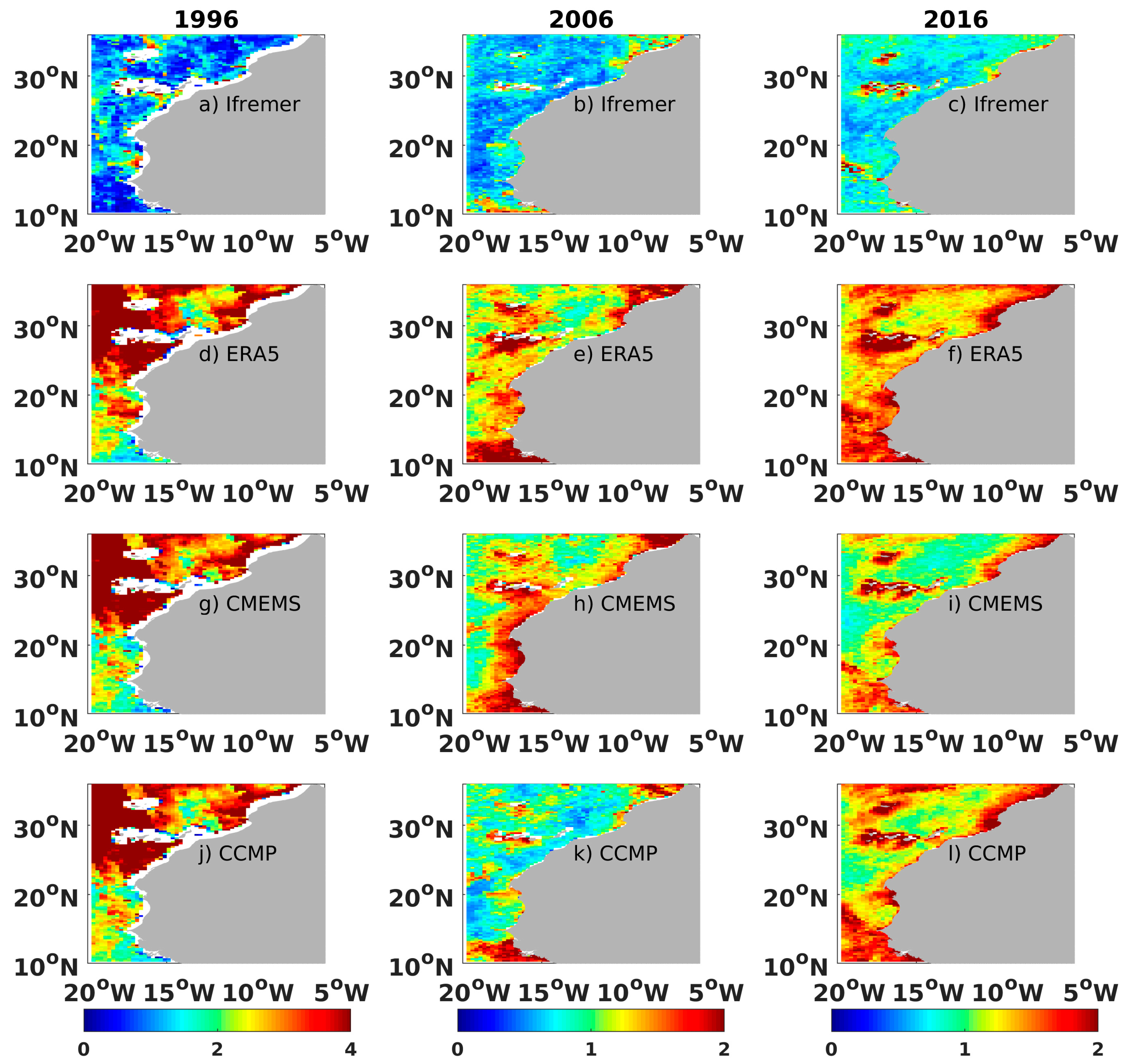
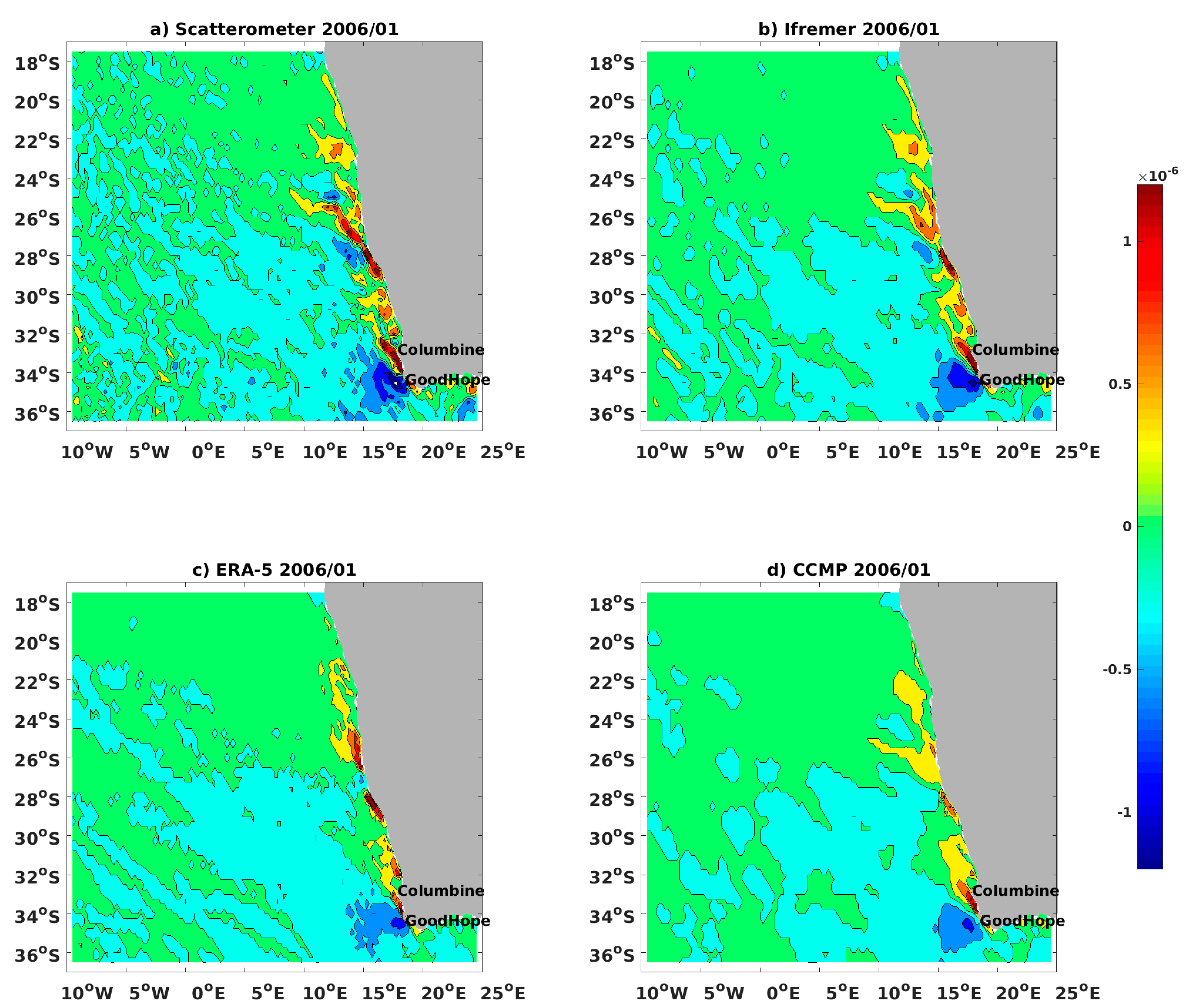
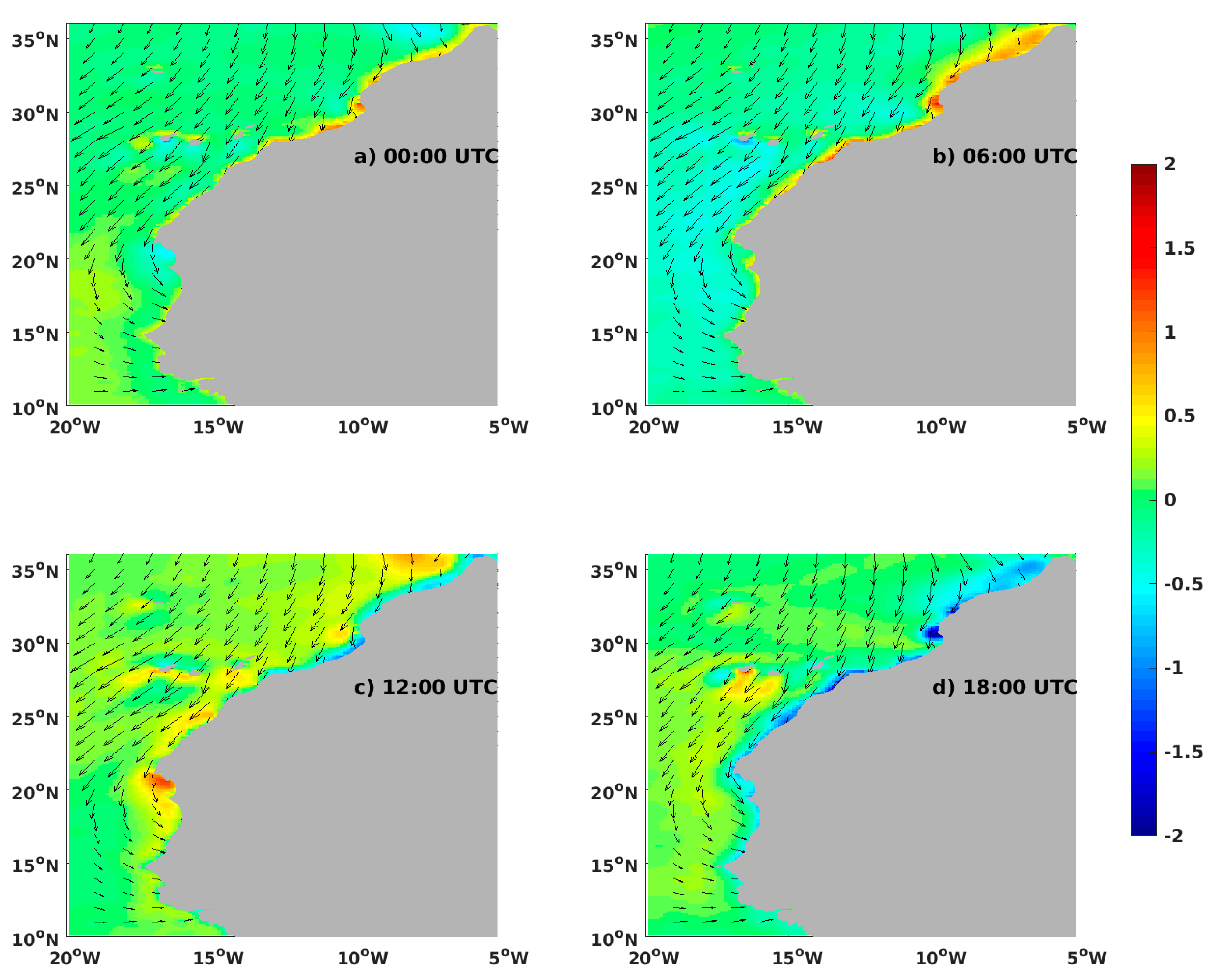
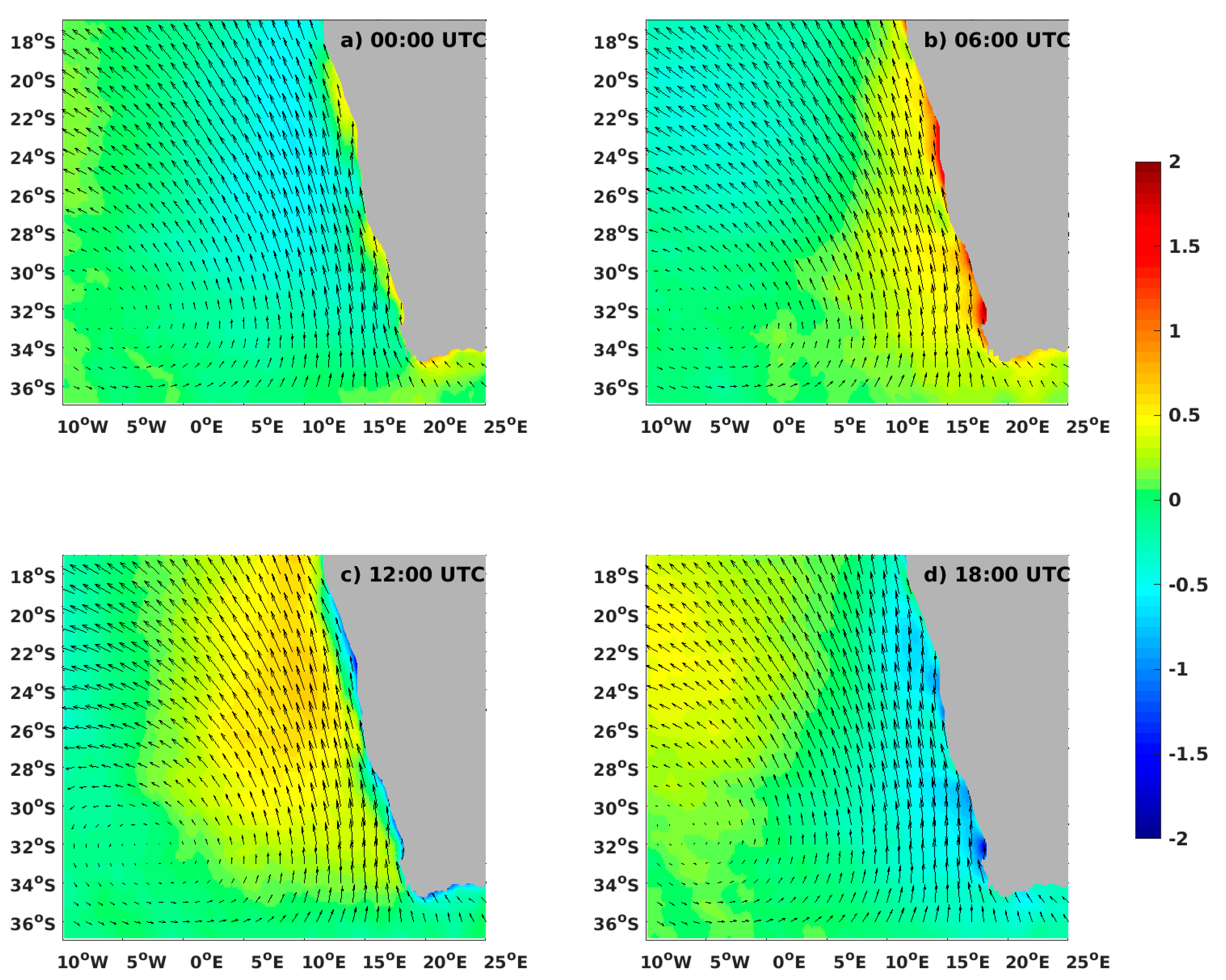
4.3. Assessment of the Local Wind Patterns
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A



References
- Desbiolles, F.; Blanke, B.; Bentamy, A.; Grima, N. Origin of fine-scale wind stress curl structures in the Benguela and Canary upwelling systems. J. Geophys. Res. Oceans 2014, 119, 7931–7948. [Google Scholar] [CrossRef]
- Desbiolles, F.; Blanke, B.; Bentamy, A. Short-term upwelling events at the western African coast related to synoptic atmospheric structures as derived from satellite observations. J. Geophys. Res. Oceans 2014, 119, 461–483. [Google Scholar] [CrossRef]
- Wang, D.; Gouhier, T.C.; Menge, B.A.; Ganguly, A.R. Intensification and spatial homogenization of coastal upwelling under climate change. Nat. Cell Biol. 2015, 518, 390–394. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Santos, I.; Seguel, R.; Schneider, W.; Linford, P.; Donoso, D.; Navarro, E.; Amaya-Cárcamo, C.; Pinilla, E.; Daneri, G. Synoptic-scale variability of surface winds and ocean response to atmospheric forcing in the eastern austral Pacific Ocean. Ocean Sci. 2019, 15, 1247–1266. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B. A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. J. Comput. Phys. 2008, 227, 3465–3485. [Google Scholar] [CrossRef]
- García-Reyes, M.; Largier, J. Observations of increased wind-driven coastal upwelling off central California. J. Geophys. Res. Space Phys. 2010, 115, C04011. [Google Scholar] [CrossRef]
- Freeman, E.; Woodruff, S.D.; Worley, S.J.; Lubker, S.J.; Kent, E.C.; Angel, W.E.; Berry, D.I.; Brohan, P.; Eastman, R.; Gates, L.; et al. ICOADS Release 3.0: A major update to the historical marine climate record. Int. J. Clim. 2017, 37, 2211–2232. [Google Scholar] [CrossRef]
- Bentamy, A.; Grodsky, S.A.; Elyouncha, A.; Chapron, B.; Desbiolles, F. Homogenization of scatterometer wind retrievals. Int. J. Clim. 2017, 37, 870–889. [Google Scholar] [CrossRef]
- Blanke, B.; Speich, S.; Bentamy, A.; Roy, C.; Sow, B. Modeling the structure and variability of the southern Benguela upwelling using QuikSCAT wind forcing. J. Geophys. Res. Space Phys. 2005, 110, C07018. [Google Scholar] [CrossRef]
- Capet, X.; Colas, F.; McWilliams, J.; Penven, P.; Marchesiello., P. Eddies in eastern boundary subtropical upwelling systems. In Ocean. Modeling in an Eddying Regime; Hecht, M.W., Hasumi, H., Eds.; Wiley: Hoboken, NJ, USA, 2008; Volume 177, pp. 131–147. [Google Scholar] [CrossRef]
- Renault, L.; Dewitte, B.; Marchesiello, P.; Illig, S.; Echevin, V.; Cambon, G.; Ramos, M.; Astudillo, O.; Minnis, P.; Ayers, J.K. Upwelling response to atmospheric coastal jets off central Chile: A modeling study of the October 2000 event. J. Geophys. Res. Space Phys. 2012, 117, C02030. [Google Scholar] [CrossRef]
- Grodsky, S.A.; Kudryavtsev, V.N.; Bentamy, A.; Carton, J.A.; Chapron, B. Does direct impact of sst on short wind waves matter for scatterometry ? Geophys. Res. Lett. 2012, 39, L12602. [Google Scholar] [CrossRef]
- Muñoz, E.; Weijer, W.; Grodsky, S.A.; Bates, S.C.; Wainer, I. Mean and Variability of the Tropical Atlantic Ocean in the CCSM4. J. Clim. 2012, 25, 4860–4882. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Freilich, M.H.; Milliff, R.F. Satellite Measurements Reveal Persistent Small-Scale Features in Ocean Winds. Science 2004, 303, 978–983. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, L.W.; Chelton, D.B.; Esbensen, S.K. The effects of sst-induced surface wind speed and direction gradients on midlatitude surface vorticity and divergence. J. Clim. 2010, 23, 255–281. [Google Scholar]
- Desbiolles, F.; Bentamy, A.; Blanke, B.; Roy, C.; Mestas-Nuñez, A.M.; Grodsky, S.A.; Herbette, S.; Cambon, G.; Maes, C. Two decades [1992–2012] of surface wind analyses based on satellite scatterometer observations. J. Mar. Syst. 2017, 168, 38–56. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk Parameterization of Air-Sea Fluxes: Updates and Verification for the COARE3.0 Algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Bentamy, A.; Queffeulou, P.; Quilfen, Y.; Katsaros, K. Ocean surface wind fields estimated from satellite active and passive microwave instruments. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2469–2486. [Google Scholar] [CrossRef]
- Wentz, F.J.; Smith, D.K. A model function for the ocean-normalized radar cross section at 14 GHz derived from NSCAT observations. J. Geophys. Res. Space Phys. 1999, 104, 11499–11514. [Google Scholar] [CrossRef]
- Hersbach, H.; Stoffelen, A.; De Haan, S. An improved C-band scatterometer ocean geophysical model function: CMOD5. J. Geophys. Res. Space Phys. 2007, 112, C03006. [Google Scholar] [CrossRef]
- Bentamy, A.; Grodsky, S.A.; Chapron, B.; Carton, J.A. Compatibility of C-and Ku-band scatterometer winds: ERS-2 and QuikSCAT. J. Mar. Syst. 2013, 117–118, 72–80. [Google Scholar] [CrossRef]
- Grodsky, S.A.; Carton, J.A.; Nigam, S.; Okumura, Y.M. Tropical Atlantic Biases in CCSM4. J. Clim. 2012, 25, 3684–3701. [Google Scholar] [CrossRef]
- Tomita, H.; Kubota, M. An analysis of the accuracy of Japanese Ocean Flux data sets with Use of Remote sensing Observations (J-OFURO) satellite-derived latent heat flux using moored buoy data. J. Geophys. Res. Space Phys. 2006, 111, C07007. [Google Scholar] [CrossRef]
- Atlas, R.; Hoffman, R.N.; Ardizzone, J.; Leidner, S.M.; Jusem, J.C.; Smith, D.K.; Gombos, D. A Cross-calibrated, Multiplatform Ocean Surface Wind Velocity Product for Meteorological and Oceanographic Applications. Bull. Am. Meteorol. Soc. 2011, 92, 157–174. [Google Scholar] [CrossRef]
- Ebuchi, N.; Graber, H.C.; Caruso, M.J. Evaluation of Wind Vectors Observed by QuikSCAT/SeaWinds Using Ocean Buoy Data. J. Atmos. Ocean. Technol. 2002, 19, 2049–2069. [Google Scholar] [CrossRef]
- Bentamy, A.; Croize-Fillon, D.; Perigaud, C. Characterization of ASCAT measurements based on buoy and QuikSCAT wind vector observations. Ocean Sci. 2008, 4, 265–274. [Google Scholar] [CrossRef]
- Verspeek, J.; Stoffelen, A.; Portabella, M.; Bonekamp, H.; Anderson, C.; Saldana, J. Validation and Calibration of ASCAT Using CMOD5.n. IEEE Trans. Geosci. Remote Sens. 2009, 48, 386–395. [Google Scholar] [CrossRef]
- Yamartino, R.J. A Comparison of Several "Single-Pass" Estimators of the Standard Deviation of Wind Direction. J. Clim. Appl. Meteorol. 1984, 23, 1362–1366. [Google Scholar] [CrossRef]
- Freilich, M.H.; Dunbar, R.S. The accuracy of the NSCAT-1 vector winds: Comparison with NDBC buoys. J. Geophys. Res. 1999, 104, 246. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Hersbach, H.; de Rosnay, P.; Bell, B.; Schepers, D.; Simmons, A.; Soci, C.; Abdalla, S.; Alonso-Balmaseda, M.; Balsamo, G.; Bechtold, P.; et al. Operational global reanalysis: Progress, future directions and synergies with NWP. ERA Rep. Ser. 2018. [Google Scholar] [CrossRef]
- Rivas, M.B.; Stoffelen, A. Characterizing ERA-Interim and ERA5 surface wind biases using ASCAT. Ocean Sci. 2019, 15, 831–852. [Google Scholar] [CrossRef]
- Bentamy, A.; Fillon, D.C. Gridded surface wind fields from Metop/ASCAT measurements. Int. J. Remote Sens. 2011, 33, 1729–1754. [Google Scholar] [CrossRef]
- Sangrà, P.; Troupin, C.; Barreiro-González, B.; Barton, E.D.; Orbi, A.; Arístegui, J. The C ape G hir filament system in A ugust 2009 (NW Africa). J. Geophys. Res. Oceans 2015, 120, 4516–4533. [Google Scholar] [CrossRef]




| Instrument (Satellite) | Period | Repeat Cycle (Days) | Swath Width (km) | Provider and Useful Product Link |
|---|---|---|---|---|
| Scatterometers | ||||
| ERS-1 (ERS-1) | 1992–1996 | 3, 35, 168 | 500 | OSI SAF/KNMI http://projects.knmi.nl/scatterometer/ers_prod (accessed on 2 March 2021) |
| ERS-2 (ERS-2) | 1995–2001 | 3, 35 | 500 | OSI SAF/KNMI http://projects.knmi.nl/scatterometer/ers_prod (accessed on 2 March 2021) |
| NSCAT (ADEOS-1) | 1996–1997 | 41 | 2 × 600 | JPL/PODAAC https://podaac.jpl.nasa.gov/dataset/NSCAT_LEVEL_2_V2 (accessed on 2 March 2021) |
| SeaWinds (QuikSCAT) | 1999–2009 | 4 | 1800 | JPL/PODAAC https://podaac.jpl.nasa.gov/dataset/QSCAT_LEVEL_2B_OWV_COMP_12_KUSST_LCRES_4.0 (accessed on 2 March 2021) |
| SeaWinds (ADEOS-2) | 2002–2003 | 4 | 1800 | JPL/PODAAC https://podaac.jpl.nasa.gov/dataset/RSCAT_LEVEL_2B_OWV_COMP_12_V1.1 (accessed on 2 March 2021) |
| ASCAT-A (METOP-A) | 2007–Present | 29 | 2×550 | OSI SAF/KNMI http://projects.knmi.nl/scatterometer/publications/pdf/ASCAT_Product_Manual.pdf (accessed on 2 March 2021) |
| OSCAT2 (OceanSat-2) | 2009–2014 | 2 | 1400 | OSI SAF/KNMI http://projects.knmi.nl/scatterometer/publications/pdf/osisaf_cdop2_ss3_pum_Oceansat2_L2_winds_datarecord_1.1.pdf (accessed on 2 March 2021) |
| HY-2a (HY-2a) | 2012–Present | 14, 168 | 1600 | OSI SAF/KNMI under cooperation between NSOAS and EUMETSAT http://projects.knmi.nl/scatterometer/publications/pdf/osisaf_cdop2_ss3_pum_scatsat1_winds.pdfhttps://www-cdn-int.eumetsat.int/files/2020-04/pdf_hy-2a_user_guide.pdf (accessed on 2 March 2021) |
| ASCAT-B (METOP-B) | 2012–Present | 29 | 2 × 550 | OSI SAF/KNMI http://projects.knmi.nl/scatterometer/publications/pdf/ASCAT_Product_Manual.pdf (accessed on 2 March 2021) |
| RapidScat (ISSS) | 2014–2016 | 900 | JPL/PODAAC https://podaac.jpl.nasa.gov/dataset/RSCAT_LEVEL_2B_OWV_COMP_12_V1.1 (accessed on 2 March 2021) | |
| ScatSat-1 (ScatSat-1) | 2016–Present | 1400 | OSI SAF/KNMI http://projects.knmi.nl/scatterometer/publications/pdf/osisaf_cdop2_ss3_pum_scatsat1_winds.pdf (accessed on 2 March 2021) | |
| Radiometers | ||||
| SSM/I(F10–F15) | 1992–2009 | 1400 | RSS http://www.remss.com/missions/ssmi/ (accessed on 2 March 2021) | |
| SSMIS(F16–F19) | 2003–Present | 1400 | RSS http://www.remss.com/missions/ssmi/ (accessed on 2 March 2021) | |
| AMSRE(AQUA) | 2002–2011 | 16 days | 1445 | RSS http://www.remss.com/missions/amsr/ (accessed on 2 March 2021) |
| AMSR-2(GCOM) | 2012–Present | 16 days | 1600 | RSS http://data.remss.com/amsr2/ (accessed on 2 March 2021) |
| Wind Speed | Wind Direction | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Length | Bias (m/s) | RMSD (m/s) | ρ | bs | As (m/s) | Bias (deg) | RMSD (deg) | ρ² | |
| ERS1 | 7802 | 0.10 | 3.21 | 0.72 | 1.01 | −0.17 | −6 | 39.00 | 1.07 |
| ERS2 | 11,141 | 0.26 | 3.29 | 0.71 | 1.00 | −0.28 | −7 | 39.05 | 1.04 |
| QSCAT | 159,752 | 0.06 | 0.63 | 0.98 | 0.99 | 0.02 | −3 | 18.56 | 1.89 |
| ASCAT-A | 110,837 | 0.15 | 0.62 | 0.98 | 1.00 | −0.12 | −0 | 17.98 | 1.90 |
| ASCAT-B | 56,170 | 0.08 | 0.58 | 0.99 | 1.00 | −0.11 | −1 | 18.54 | 1.89 |
| RSCAT | 16,408 | 0.00 | 0.67 | 0.98 | 1.00 | 0.03 | −0 | 18.81 | 1.89 |
| HY-2A | 26,600 | 0.08 | 0.75 | 0.98 | 1.01 | −0.14 | −1 | 18.15 | 1.87 |
| SSCAT | 15,321 | 0.00 | 0.76 | 0.99 | 1.01 | −0.04 | −2 | 19.92 | 1.88 |
| WindSat | 69,398 | 0.00 | 0.75 | 0.97 | 0.96 | 0.33 | −0 | 22.01 | 1.81 |
| SAR | 628,922 | 0.18 | 1.45 | 0.92 | 0.97 | −0.01 | −3 | 40.53 | 1.51 |
| SSM/I F10 | 36,914 | 0.03 | 0.98 | 0.96 | 1.03 | −0.24 | |||
| SSM/I F11 | 63,152 | 0.04 | 0.96 | 0.96 | 1.02 | −0.21 | |||
| SSM/I F13 | 164,042 | 0.09 | 0.93 | 0.97 | 1.01 | −0.15 | |||
| SSM/I F14 | 122,351 | 0.12 | 0.92 | 0.97 | 1.01 | −0.19 | |||
| SSM/I F15 | 83,844 | 0.09 | 0.92 | 0.97 | 1.01 | −0.19 | |||
| SSMIS F16 | 142,448 | 0.07 | 0.91 | 0.97 | 1.01 | −0.13 | |||
| SSMIS F17 | 108,457 | 0.04 | 0.87 | 0.97 | 1.01 | −0.11 | |||
| SSMIS F18 | 51,617 | −0.02 | 0.82 | 0.97 | 1.00 | 0.00 | |||
| AMSRE | 140,027 | 0.19 | 0.89 | 0.97 | 1.01 | −0.28 | |||
| AMSR2 | 69,398 | 0.00 | 0.75 | 0.97 | 0.96 | 0.33 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bentamy, A.; Grodsky, S.A.; Cambon, G.; Tandeo, P.; Capet, X.; Roy, C.; Herbette, S.; Grouazel, A. Twenty-Seven Years of Scatterometer Surface Wind Analysis over Eastern Boundary Upwelling Systems. Remote Sens. 2021, 13, 940. https://doi.org/10.3390/rs13050940
Bentamy A, Grodsky SA, Cambon G, Tandeo P, Capet X, Roy C, Herbette S, Grouazel A. Twenty-Seven Years of Scatterometer Surface Wind Analysis over Eastern Boundary Upwelling Systems. Remote Sensing. 2021; 13(5):940. https://doi.org/10.3390/rs13050940
Chicago/Turabian StyleBentamy, Abderrahim, Semyon A. Grodsky, Gildas Cambon, Pierre Tandeo, Xavier Capet, Claude Roy, Steven Herbette, and Antoine Grouazel. 2021. "Twenty-Seven Years of Scatterometer Surface Wind Analysis over Eastern Boundary Upwelling Systems" Remote Sensing 13, no. 5: 940. https://doi.org/10.3390/rs13050940
APA StyleBentamy, A., Grodsky, S. A., Cambon, G., Tandeo, P., Capet, X., Roy, C., Herbette, S., & Grouazel, A. (2021). Twenty-Seven Years of Scatterometer Surface Wind Analysis over Eastern Boundary Upwelling Systems. Remote Sensing, 13(5), 940. https://doi.org/10.3390/rs13050940