Temperature Variations in Multiple Air Layers before the Mw 6.2 2014 Ludian Earthquake, Yunnan, China
Abstract
1. Introduction
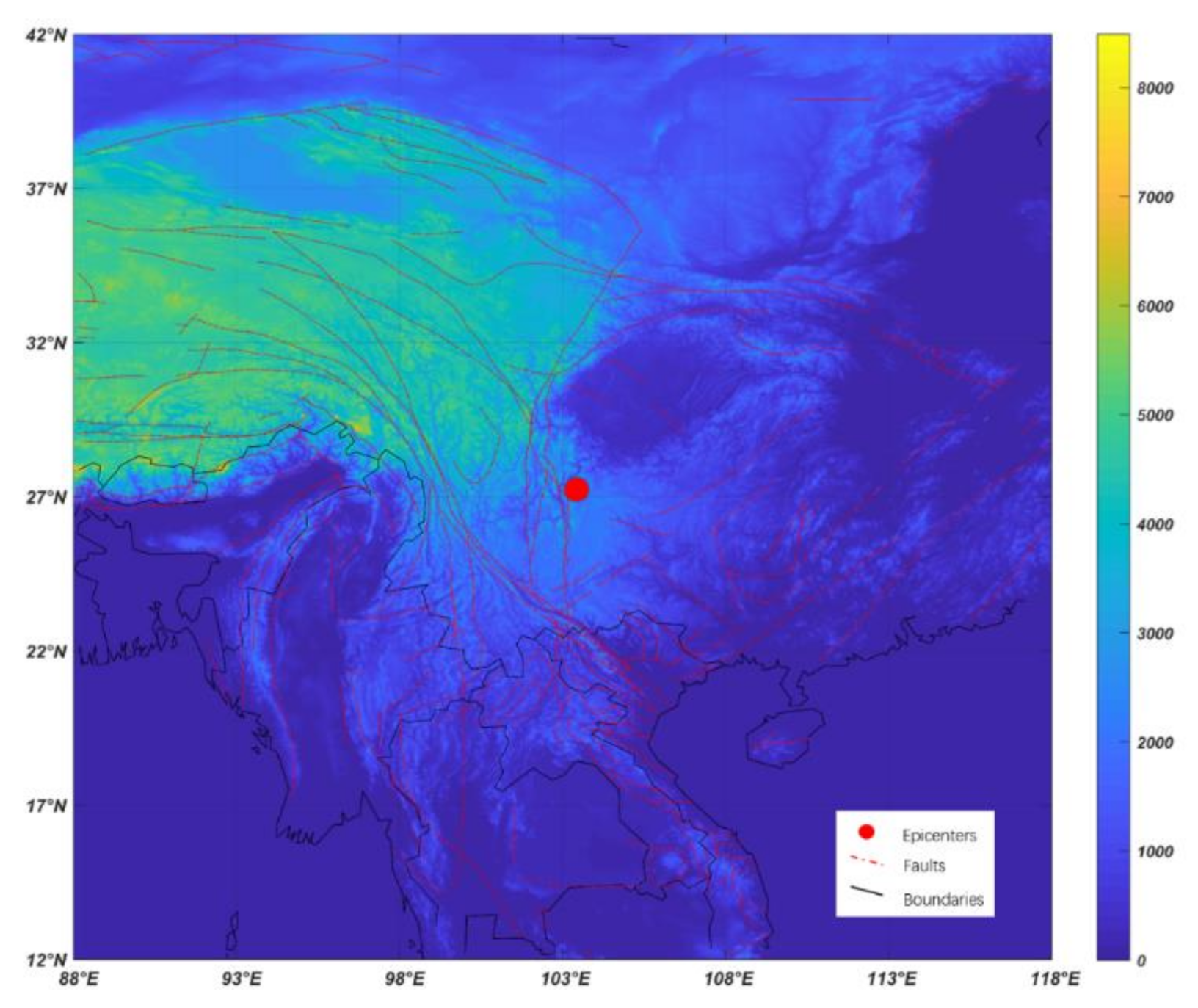
2. Tectonic Environment of Ludian Earthquake
3. Change of Tidal Force and the TFFA Method
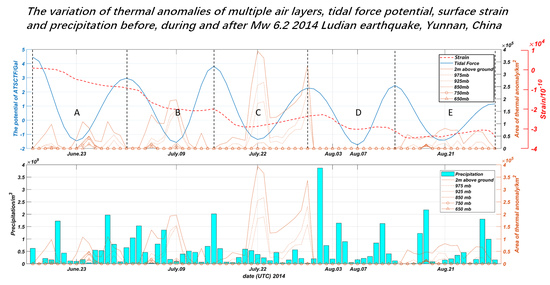
4. Thermal Analysis
4.1. Multiple Layers of Air Temperature Evolution
4.2. Significance Test for Thermal Anomalies
- Relative intensity rule—similar to the thermal anomalies of the Ludian earthquake, we set 11 K as the threshold;
- Temporal persistence rule—unlike some thermal anomalies caused by short-term and instantaneous change of weather, the thermal anomalies of earthquakes should be extended in time, so that the seismic thermal anomalies should appear for at least two consecutive days.
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bi, Y.; Wu, S.; Xiong, P.; Shen, X. A Comparative Analysis for Detecting Seismic Anomalies in Data Sequences of Outgoing Longwave Radiation; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Carreno, E.; Capote, R.; Yague, A.; Tordesillas, J.M.; Lopez, M.M.; Ardizone, J.; Suarez, A.; Lzquierdo, A.; Tsige, M.; Martinez, J.; et al. Observations of Thermal Anomaly Associated to Seismic Activity from Remote Sensing; General Assembly of European Seismology Commission: Lisbon, Portugal, 2001; pp. 10–15. [Google Scholar]
- Saraf, A.K.; Choudhury, S. Cover: Satellite detects surface thermal anomalies associated with the Algerian earthquakes of May 2003. Int. J. Remote Sens. 2005, 26, 2705–2713. [Google Scholar] [CrossRef]
- Jing, F.; Shen, X.H.; Kang, C.L.; Xiong, P. Variations of multi-parameter observations in atmosphere related to earthquake. Nat. Hazards Earth Syst. Sci. 2013, 13, 27–33. [Google Scholar] [CrossRef]
- Lu, X.; Meng, Q.Y.; Gu, X.F.; Zhang, X.D.; Xie, T.; Geng, F. Thermal Infrared Anomalies Associated with Multi-year Earthquakes in the Tibet Region Based on China’s FY-2E Satellite Data. Adv. Space Res. 2016, 58, 989–1001. [Google Scholar] [CrossRef]
- Ouzounov, D.; Freund, F. Mid-infrared emission prior to strong earthquakes analyzed by remote sensing data. Adv. Space Res. 2004, 33, 268–273. [Google Scholar] [CrossRef]
- Ouzounov, D.; Liu, D.; Chunli, K.; Cervone, G.; Kafatos, M.; Taylor, P. Outgoing long wave radiation variability from IR satellite data prior to major earthquakes. Tectonophysics 2007, 431, 211–220. [Google Scholar] [CrossRef]
- Panda, S.K.; Choudhury, S.; Saraf, A.K.; Das, J.D. MODIS land surface temperature data detects thermal anomaly preceding 8 October 2005 Kashmir earthquake. Int. J. Remote Sens. 2007, 28, 4587–4596. [Google Scholar] [CrossRef]
- Qin, K.; Wu, L.; Zheng, S.; Liu, S. A Deviation-Time-Space-Thermal (DTS-T) Method for Global Earth Observation System of Systems (GEOSS)-Based Earthquake Anomaly Recognition: Criterions and Quantify Indices. Remote Sens. 2013, 5, 5143–5151. [Google Scholar] [CrossRef]
- Saraf, A.K.; Choudhury, S. Thermal remote sensing technique in the study of pre-earthquake thermal anomalies. J. Ind. Geophys. Union 2005, 9, 197–207. [Google Scholar]
- Saraf, A.K.; Choudhury, S. Cover: NOAA-AVHRR detects thermal anomaly associated with the 26 January 2001 Bhuj earthquake, Gujarat, India. Int. J. Remote Sens. 2005, 26, 1065–1073. [Google Scholar] [CrossRef]
- Saraf, A.K.; Rawat, V.; Choudhury, S.; Dasgupta, S.; Das, J. Advances in understanding of the mechanism for generation of earthquake thermal precursors detected by satellites. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 373–379. [Google Scholar] [CrossRef]
- Tronin, A.A.; Hayakawa, M.; Molchanov, O.A. Thermal IR satellite data application for earthquake research in Japan and China. J. Geodyn. 2002, 33, 519–534. [Google Scholar] [CrossRef]
- Tronin, A.A. Satellite thermal survey a new tool for the study of seismoactive regions. Int. J. Remote Sens. 1996, 17, 1439–1455. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, X.; Zhong, M.; Shen, W.; Li, W.; He, B. Wenchuan earthquake: Brightness temperature changes from satellite infrared information. Sci. Bull. 2010, 55, 1917–1924. [Google Scholar] [CrossRef]
- Aliano, C.; Corrado, R.; Filizzola, C.; Pergola, N.; Tramutoli, V. Robust Satellite Techniques (RST) for Seismically Active Areas Monitoring: The Case of 21st May, 2003 Boumerdes/Thenia (Algeria) Earthquake. In Proceedings of the 2007 International Workshop on the Analysis of Multi-temporal Remote Sensing Images, Leuven, Belgium, 18–20 July 2007. [Google Scholar]
- Aliano, C.; Corrado, R.; Filizzola, C.; Genzano, N.; Lanorte, V.; Mazzeo, G.; Pergola, N.; Tramutoli, V. Robust Satellite Techniques (RST) for monitoring thermal anomalies in seismically active areas. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Bellaoui, M.; Hassini, A.; Kada, B. Pre-seismic Anomalies in Remotely Sensed Land Surface Temperature measurements: The Case Study of 2003 Boumerdes Earthquake. Adv. Space Res. 2017, 59, 2645–2657. [Google Scholar] [CrossRef]
- Boudin, F.; Bernard, P.; Esnoult, M.F.; Olcay, M.; Tassera, C.; Aissaoui, E.M.; Nercessian, A.; Vilotte, J.P. Evidence for slow slip events preceeding the M8, April 1rst, 2014 Pisagua Earthquake (Chile), from an underground, long base hydrostatic tiltmeter. In AGU Fall Meeting Abstracts; American Geophysical Union: San Francisco, CA, USA, 2014. [Google Scholar]
- Genzano, N.; Aliano, C.; Corrado, R.; Filizzola, C.; Lisi, M.; Mazzeo, G.; Paciello, R.; Pergola, N.; Tramutoli, V. RST analysis of MSG-SEVIRI TIR radiances at the time of the Abruzzo 6 April 2009 earthquake. Nat. Hazards Earth Syst. Sci. Discuss. 2009, 9, 2073–2084. [Google Scholar] [CrossRef]
- Genzano, N.; Corrado, R.; Coviello, I.; Grimaldi, C.S.; Filizzola, C.; Lacava, T.; Lisi, M.; Marchese, F.; Mazzeo, G.; Paciello, R.; et al. A multi-sensors analysis of RST-based thermal anomalies in the case of the Abruzzo earthquake. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Lisi, M.; Filizzola, C.; Genzano, N.; Grimaldi, C.S.; Lacava, T.; Marchese, F.; Mazzeo, G.; Pergola, N.; Tramutoli, V. A study on the Abruzzo 6 April 2009 earthquake by applying the RST approach to 15 years of AVHRR TIR observations. Nat. Hazards Earth System Sci. 2010, 10, 395–406. [Google Scholar] [CrossRef]
- Lisi, M.; Filizzola, C.; Genzano, N.; Paciello, R.; Pergola, N.; Tramutoli, V. Reducing atmospheric noise in RST analysis of TIR satellite radiances for earthquakes prone areas satellite monitoring. Phys. Chem. Earth Parts A/B/C 2015, 85, 87–97. [Google Scholar] [CrossRef]
- Pergola, N.; Aliano, C.; Coviello, I.; Filizzola, C.; Genzano, N.; Lacava, T.; Lisi, M.; Mazzeo, G.; Tramutoli, V. Using RST approach and EOS-MODIS radiances for monitoring seismically active regions: A study on the 6 April 2009 Abruzzo earthquake. Nat. Hazards Earth System Sci. 2010, 10, 239–249. [Google Scholar] [CrossRef]
- Sannazzaro, F.; Filizzola, C.; Marchese, F.; Corrado, R.; Paciello, R.; Mazzeo, G.; Pergola, N.; Tramutoli, V. Identification of dust outbreaks on infrared MSG-SEVIRI data by using a Robust Satellite Technique (RST). Acta Astronaut. 2014, 93, 64–70. [Google Scholar] [CrossRef]
- Weiyu, M.; Xuedong, Z.; Liu, J.; Yao, Q.; Zhou, B.; Yue, C.; Kang, C.; Lu, X. Influences of multiple layers of air temperature differences on tidal forces and tectonic stress before, during and after the Jiujiang earthquake. Remote Sens. Environ. 2018, 210, 159–165. [Google Scholar] [CrossRef]
- Blackett, M.; Wooster, M.J.; Malamud, B.D. Exploring land surface temperature earthquake precursors: A focus on the Gujarat (India) earthquake of 2001. Geophys. Res. Lett. 2011, 38, L15303. [Google Scholar] [CrossRef]
- Zhang, Y.; Qingyan, M. A statistical analysis of TIR anomalies extracted by RSTs in relation to an earthquake in the Sichuan area using MODIS LST data. Nat. Hazards Earth Syst. Sci. 2019, 19, 535–549. [Google Scholar] [CrossRef]
- Cochran, E.S.; Vidale, J.E.; Tanaka, S. Earth Tides Can Trigger Shallow Thrust Fault Earthquakes. Science 2004, 306, 1164–1166. [Google Scholar] [CrossRef]
- Tanaka, S.; Ohtake, M.; Sato, H. Spatio-temporal variation of the tidal triggering effect on earthquake occurrence associated with the 1982 South Tonga earthquake of Mw 7.5. Geophys. Res. Lett. 2002, 29, 3-1–3-4. [Google Scholar] [CrossRef]
- Heaton, T.H. Tidal Triggering of Earthquakes. Geophys. J. R. Astron. Soc. 1975, 43, 307–326. [Google Scholar] [CrossRef]
- Kilston, S.; Knopoff, L. Lunar–solar periodicities of large earthquakes in southern California. Nature 1983, 304, 21–25. [Google Scholar] [CrossRef]
- Mcnutt, S.R.; Beavan, R.J. Volcanic earthquakes at Pavlof Volcano correlated with the solid earth tide. Nature 1981, 294, 615–618. [Google Scholar] [CrossRef]
- Ma, W.Y.; Wang, H.; Li, F.S.; Ma, W.M. Relation between the celestial tide-generating stress and the temperature variations of the Abruzzo M = 6.3 Earthquake in April 2009. Nat. Hazards Earth System Sci. 2012, 12, 819–827. [Google Scholar] [CrossRef]
- Yan, Z.; Chunli, K.; Weiyu, M.; Qi, Y. The Change in Outgoing Long-wave Radiation before the Ludian Ms6.5 Earthquake Based on Tidal Force Niche Cycles. Earthq. Res. China 2017, 3, 422–430. [Google Scholar]
- Zhang, X.; Kang, C.; Ma, W.; Ren, J.; Wang, Y. Study on thermal anomalies of earthquake process by using tidal-force and outgoing-longwave-radiation. Therm. Sci. 2017, 22, 153. [Google Scholar] [CrossRef]
- Ma, W.; Kong, X.; Kang, C.; Zhong, X.; Wu, H.; Zhan, X.; Joshi, M. Research on the changes of the tidal force and the air temperature in the atmosphere of Lushan (China) MS7.0 earthquake. Therm. Sci. 2015, 19, 148. [Google Scholar] [CrossRef]
- Beeler, N.; Lockner, D. Why earthquakes correlate weakly with the solid Earth tides: Effects of periodic stress on the rate and probability of earthquake occurrence. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Kistler, R.; Kalnay, E.; Collins, W.; Saha, S.; White, G.; Woollen, J.; Chelliah, M.; Ebisuzaki, W.; Kanamitsu, M.; Kousky, V.; et al. The NCEP-NCAR 50-Year Reanalysis: Monthly Means CD-ROM and Documentation. Bull. Am. Meteorol. Soc. 2001, 82, 247–268. [Google Scholar] [CrossRef]
- Chen, S.; Liu, L.; Liu, P.; Ma, J.; Chen, G. Theoretical and experimental study on relationship between stress-strain and temperature variation. Sci. China Ser. D Earth Sci. 2009, 39, 1446–1455. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, Y. Discovery of Spatial-temporal Causal Interactions between Thermal and Methane Anomalies Associated with the Wenchuan Earthquake. Eur. Phys. J. Spec. Top. 2021, 230, 247–261. [Google Scholar] [CrossRef]












| Description | |
|---|---|
| 1 | |
| 3.12 | |
| 12.06 | |
| 4 | 12.83 |
| 2.24 | |
| 0.57 |
| Time | Depth (km) | Mag (Mw) | |||
|---|---|---|---|---|---|
| EQ1 | 30-08-2008 | 26.24 | 101.89 | 11 | 6 |
| EQ2 | 31-08-2008 | 26.23 | 101.97 | 10 | 5.6 |
| EQ3 | 09-07-2009 | 25.63 | 101.10 | 7 | 5.7 |
| EQ4 | 07-09-2012 | 27.58 | 103.98 | 10 | 5.5 |
| EQ5 | 03-08-2014 | 27.24 | 103.42 | 12 | 6.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Meng, Q.; Wang, Z.; Lu, X.; Hu, D. Temperature Variations in Multiple Air Layers before the Mw 6.2 2014 Ludian Earthquake, Yunnan, China. Remote Sens. 2021, 13, 884. https://doi.org/10.3390/rs13050884
Zhang Y, Meng Q, Wang Z, Lu X, Hu D. Temperature Variations in Multiple Air Layers before the Mw 6.2 2014 Ludian Earthquake, Yunnan, China. Remote Sensing. 2021; 13(5):884. https://doi.org/10.3390/rs13050884
Chicago/Turabian StyleZhang, Ying, Qingyan Meng, Zian Wang, Xian Lu, and Die Hu. 2021. "Temperature Variations in Multiple Air Layers before the Mw 6.2 2014 Ludian Earthquake, Yunnan, China" Remote Sensing 13, no. 5: 884. https://doi.org/10.3390/rs13050884
APA StyleZhang, Y., Meng, Q., Wang, Z., Lu, X., & Hu, D. (2021). Temperature Variations in Multiple Air Layers before the Mw 6.2 2014 Ludian Earthquake, Yunnan, China. Remote Sensing, 13(5), 884. https://doi.org/10.3390/rs13050884