Uncertainty and Sensitivity Analysis of a Remote-Sensing-Based Penman–Monteith Model to Meteorological and Land Surface Input Variables
Abstract
1. Introduction
2. Materials and Methods
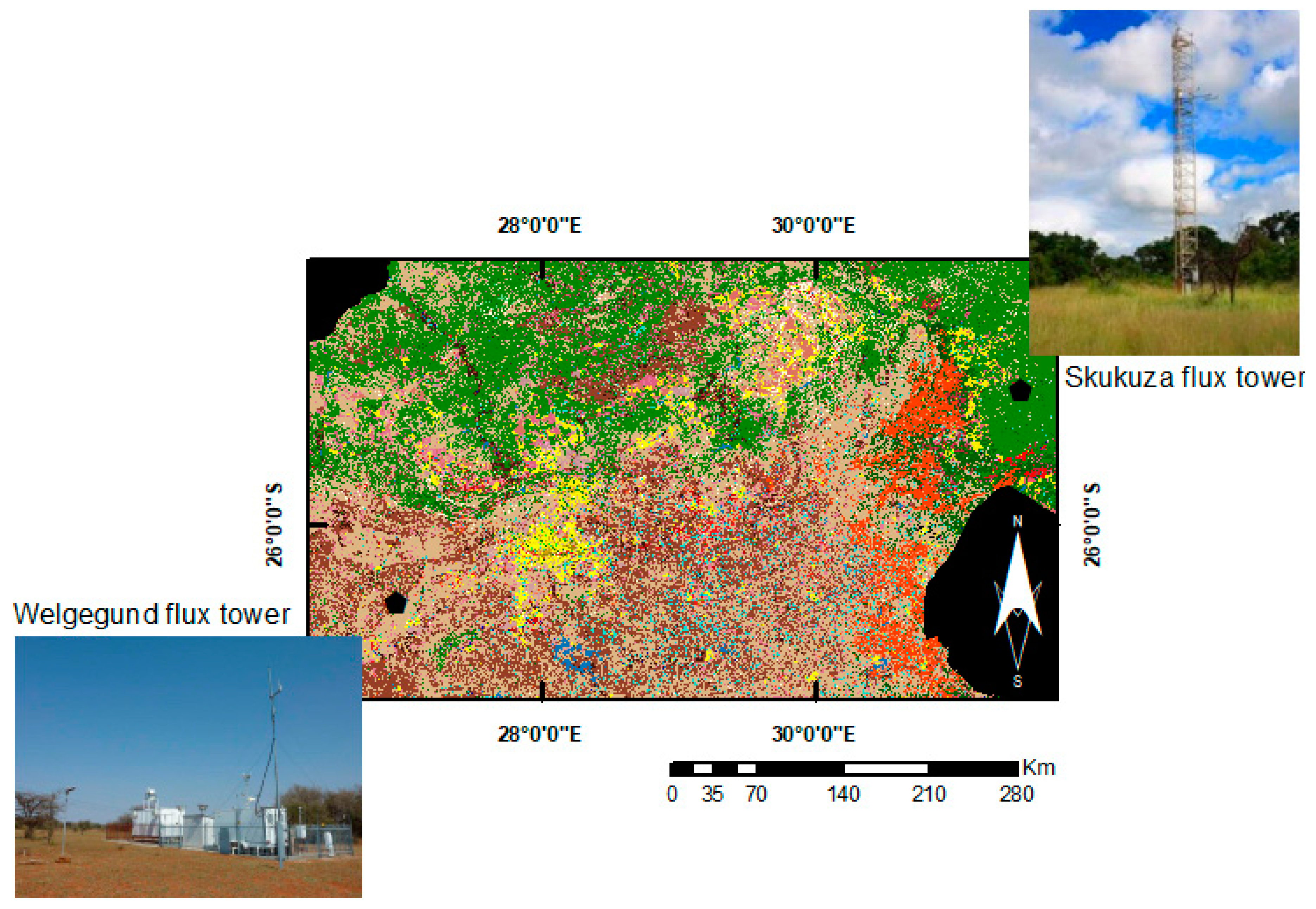
2.1. Site Description
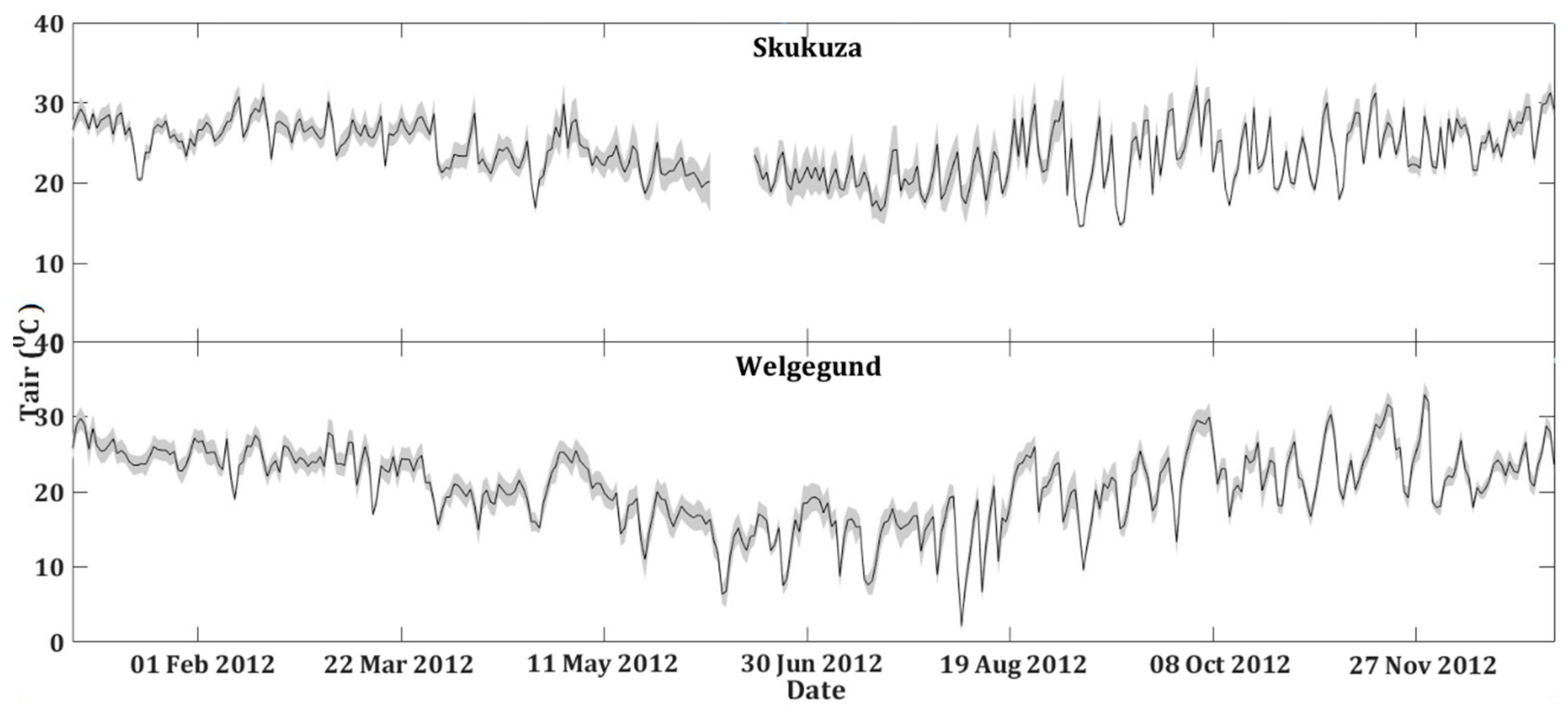
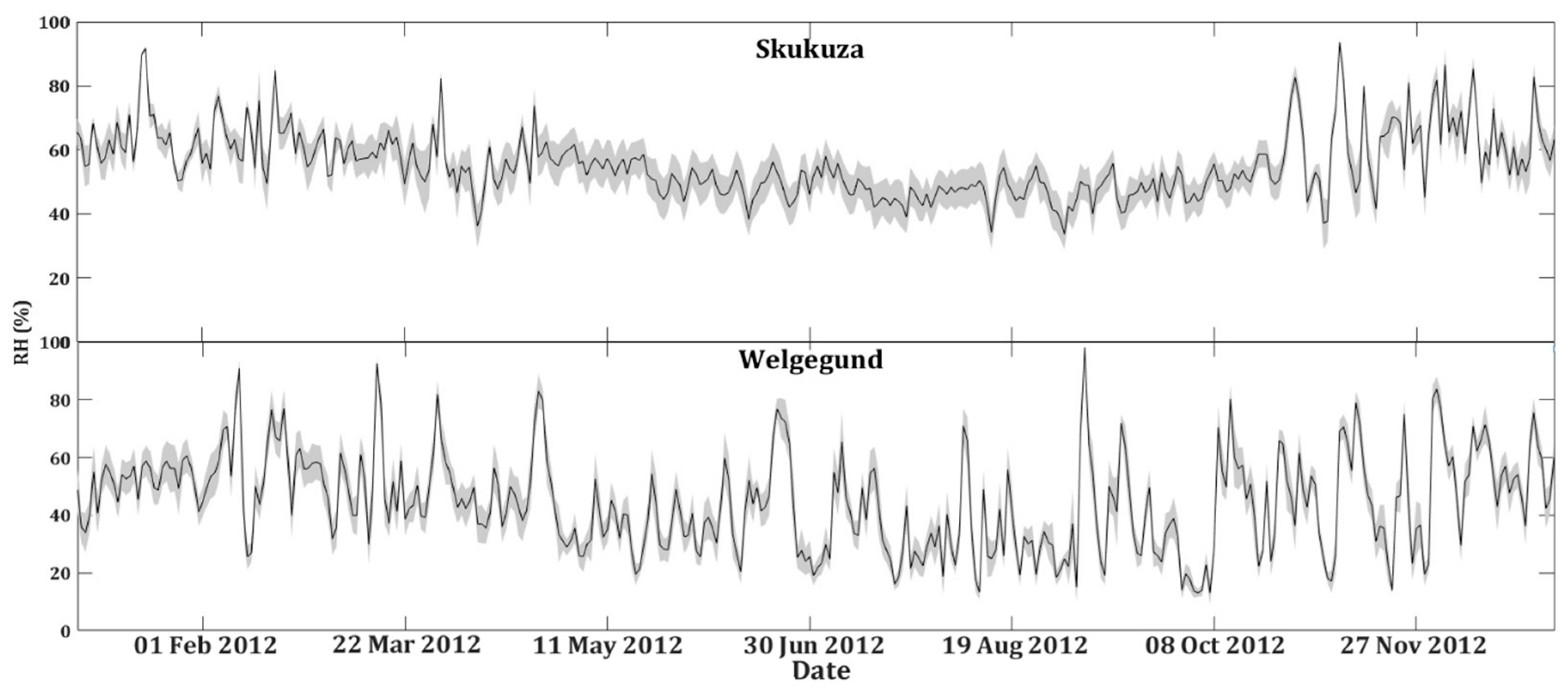
- The Skukuza FLUXNET site, located in a savanna ecosystem in the Kruger National Park, South Africa, sits at 365 m above mean sea level. The site is characterised by low rainfall averaging 550 ± 160 mm per annum between November and April, with notable inter-annual variability, and temperatures ranging between 15.6 and 29.6 °C, with a mean of 22.6 °C. Soils in this part of the park are generally shallow, comprising coarse sandy to sandy-loam texture. The vegetation is mainly open woodland, with approximately 30% tree canopy cover of mixed Acacia and Combretum savanna types. The canopy height is 5–8 m, with occasional trees (mostly Sclerocarya birrea) reaching 10 m. The grassy and herbaceous understorey comprises grasses such as Panicum maximum, Digitaria eriantha, Eragrostis rigidor and Pogonarthria squarrosa. The eddy covariance system, which has been running since 2000, was installed on a vegetation transition characterised by a catenal pattern of soils and vegetation, with broad-leaved Combretum savanna on the crests dominated by Combretum apiculatum, and fine-leaved Acacia savanna in the valleys dominated by Acacia nigrescens [34,35].
- Welgegund flux tower site (26°34′10″S, 26°56′21″E) is located on a semi-arid, subtropical grazed grassland plain. It is situated approximately 100 km west of Johannesburg, in South Africa. The mean annual rainfall is 540 ± 112 mm, spreading between October and April. Temperature ranges between 0 and 30 °C, with an average of 18 °C. The dominant vegetation comprises grasses, geophytes and herbs. The dominant grass species are Hyparrhenia hirta and Sporobolus pyramidalis. Non-grassy forbs include Acacia sieberiana, Rhus rehmanniana, Walafrida densiflora, Spermacoce natalensis, Kohautia cynanchica and Phyllanthus glaucophyllus Räsänen, et al. [36].
2.2. Remote-Sensing-Based Penman–Monteith Model
2.3. Uncertainty and Sensitivity Analysis
- Estimating the uncertainty of model inputs and parameters, i.e., the meteorological and land surface characteristics, representing both point- and remote-sensing-based inputs;
- Propagating input uncertainties through to the ET model and computing output uncertainties;
- Estimating the sensitivity coefficients of the model inputs.
2.3.1. Core Input Variable Uncertainties
2.3.2. Remote-Sensing-Based Input Uncertainties
- Land surface temperature (LST) and surface emissivity (ɛs): these variables are essential in land surface-atmosphere studies, including the estimation of evapotranspiration and atmospheric water vapour. In our study, we used the MODIS-derived MOD11A1 V006 product, which is generated from the thermal infrared channels 31 (10.78 to 11.28 μm) and 32 (11.77 to 12.27 μm) using the physically-based day-night split-window algorithm by [37]. The uncertainties associated with these products are extensively discussed in the MODIS Land-Surface Temperature ATBD [38,39,40]. They indicate an absolute error of 1 K for LST, which can increase up to 5 K in arid regions. For surface emissivity, the absolute accuracy is reported to be 0.02.
- Land surface albedo (α): defined as a dimensionless characteristic of the soil–plant canopy system representing the fraction of total solar energy reflected by the surface, it is expressed as the ratio of the radiant energy scattered upward by a surface in all directions to that received from all directions, integrated over the wavelengths of the solar spectrum. Surface albedo is one of the key geophysical parameters that control the surface energy budget. The MODIS bi-directional reflectance distribution function (BRDF) and albedo product (MCD43A3 version VOO6) was used in this study. This product was derived using a kernel-driven semi-empirical BRDF model using the RossThick-LiSparse kernel functions for characterising isotropic, volume and surface scattering [41,42,43]. Studies have given an absolute accuracy of 0.02 to 0.05 as a requirement for climate modelling [44,45], with other validation studies [46,47] reporting errors falling within the 0.02 accuracy.
- Leaf Area Index (LAI): defined as the total one-sided green leaf area per unit ground surface area, it is also dimensionless. This variable measures the total amount of leaf material in an ecosystem. It is used in the estimation of biogeochemical processes like photosynthesis, evapotranspiration and net primary production. The MOD15A2 V005 product used in this study was derived using the three-dimensional radiative transfer (3D RT) model [48,49]. The product ATBD reports the accuracy of the LAI product at 0.2 [48]. Furthermore, a review by Fang, et al. [50] summarises the uncertainties of MODIS, CYCLOPES and GLOBCARBON LAI products under different biomes, showing a relative uncertainty of 0.26 in the savanna biome for the MODIS product.
2.3.3. Intermediate Input Uncertainty
2.4. Sensitivity Analysis
3. Results
3.1. Core Input Variables Uncertainty
3.2. Intermediate Input Uncertainty
3.2.1. Net Radiation Uncertainty
3.2.2. Aerodynamic and Surface Resistances
3.2.3. Uncertainty in Evapotranspiration
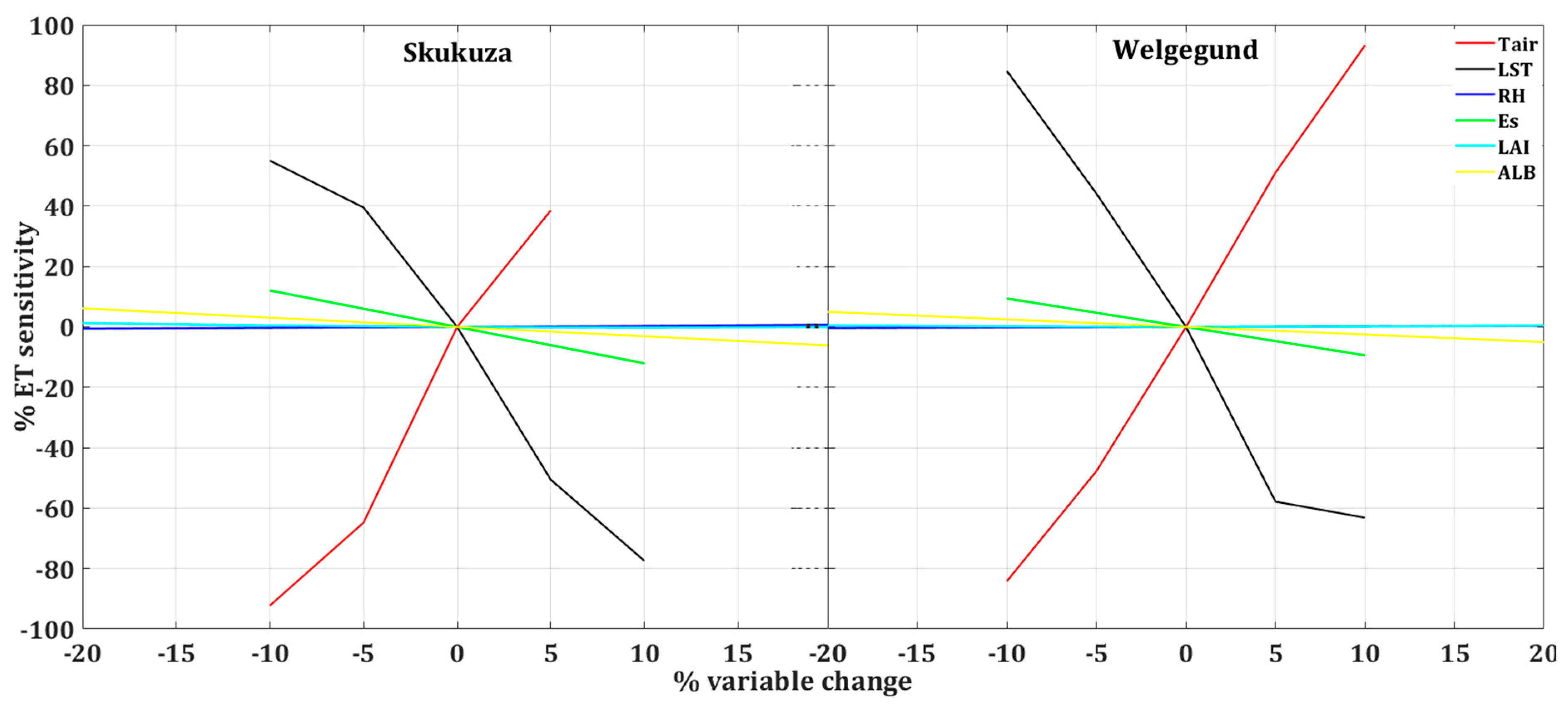
3.3. Sensitivity of PM-Mu Model to Core Input Variables
4. Discussion
4.1. Input Variable and Parameter Uncertainty
4.1.1. Core Inputs
4.1.2. Intermediate Data Components
4.1.3. Uncertainty in PM-Mu Evapotranspiration Estimation
4.2. Sensitivity of PM-Mu ET Estimates to Input Variables
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
- Bowen, I.S. The ratio of heat losses by conduction and by evaporation from any water surface. Phys. Rev. 1926, 27, 779. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and surface temperature. Q. J. R. Meteorol. Soc. 1981, 107, 1–27. [Google Scholar] [CrossRef]
- Nichols, J.; Eichinger, W.; Cooper, D.; Prueger, J.; Hipps, L.; Neale, C.; Bawazir, A. Comparison of Evaporation Estimation Methods for a Riparian Area; College of Engineering, University of Iowa: Iowa City, IA, USA, 2004; p. 50. [Google Scholar]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. Discuss. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Vinukollu, R.K.; Wood, E.F.; Ferguson, C.R.; Fisher, J.B. Global estimates of evapotranspiration for climate studies using multi-sensor remote sensing data: Evaluation of three process-based approaches. Remote Sens. Environ. 2011, 115, 801–823. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Chaney, N.W.; Wood, E.F. Multi-site evaluation of terrestrial evaporation models using FLUXNET data. Agric. For. Meteorol. 2014, 187, 46–61. [Google Scholar] [CrossRef]
- McCabe, M.F.; Ershadi, A.; Jimenez, C.; Miralles, D.G.; Michel, D.; Wood, E.F. The GEWEX LandFlux project: Evaluation of model evaporation using tower-based and globally-gridded forcing data. Geosci. Model Dev. Discuss. 2015, 8, 6809–6866. [Google Scholar]
- Michel, D.; Jiménez, C.; Miralles, D.G.; Jung, M.; Hirschi, M.; Ershadi, A.; Martens, B.; McCabe, M.; Fisher, J.B.; Mu, Q.; et al. The WACMOS-ET project – Part 1: Tower-scale evaluation of four remote-sensing-based evapotranspiration algorithms. Hydrol. Earth Syst. Sci. 2016, 20, 803–822. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; Wiley: Chichester, UK, 2004. [Google Scholar]
- Brugnach, M.; Pahl-Wostl, C.; Lindenschmidt, K.; Janssen, J.; Filatova, T.; Mouton, A.; Holtz, G.; Van der Keur, P.; Gaber, N. Chapter four complexity and uncertainty: Rethinking the modelling activity. Dev. Integr. Environ. Assess. 2008, 3, 49–68. [Google Scholar]
- Bich, W.; Cox, M.G.; Dybkaer, R.; Elster, C.; Estler, W.T.; Hibbert, B.; Imai, H.; Kool, W.; Michotte, C.; Nielsen, L. Revision of the ‘Guide to the Expression of Uncertainty in Measurement’. Metrologia 2012, 49, 702. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Morio, J. Global and local sensitivity analysis methods for a physical system. Eur. J. Phys. 2011, 32, 1577. [Google Scholar] [CrossRef]
- Yang, S.; Tian, W.; Cubi, E.; Meng, Q.; Liu, Y.; Wei, L. Comparison of sensitivity analysis methods in building energy assessment. Procedia Eng. 2016, 146, 174–181. [Google Scholar] [CrossRef]
- Nguyen, A.-T.; Reiter, S. A performance comparison of sensitivity analysis methods for building energy models. Build. Simul. 2015, 8, 651–664. [Google Scholar] [CrossRef]
- Frey, C.H.; Patil, S.R. Identification and review of sensitivity analysis methods. Risk Anal. 2002, 22, 553–578. [Google Scholar] [CrossRef]
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef]
- Hamby, D.M. A comparison of sensitivity analysis techniques. Health Phys. 1995, 68, 195–204. [Google Scholar] [CrossRef]
- Lilburne, L.; Tarantola, S. Sensitivity analysis of spatial models. Int. J. Geogr. Inf. Sci. 2009, 23, 151–168. [Google Scholar] [CrossRef]
- Saint-Geours, N.; Lilburne, L. Comparison of three spatial sensitivity analysis techniques. In Proceedings of the 9th International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences, Leicester, UK, 20–23 July 2010; pp. 421–424. [Google Scholar]
- Talsma, C.J.; Good, S.P.; Miralles, D.G.; Fisher, J.B.; Martens, B.; Jimenez, C.; Purdy, A.J. Sensitivity of evapotranspiration components in remote sensing-based models. Remote Sens. 2018, 10, 1601. [Google Scholar] [CrossRef]
- Pérez, M.; Ángel, J.; García-Galiano, S.G.; Martin-Gorriz, B.; Baille, A. Satellite-based method for estimating the spatial distribution of crop evapotranspiration: Sensitivity to the priestley-taylor coefficient. Remote Sens. 2017, 9, 611. [Google Scholar] [CrossRef]
- Sharifi, A.; Dinpashoh, Y. Sensitivity Analysis of the Penman-Monteith reference Crop Evapotranspiration to Climatic Variables in Iran. Water Resour. Manag. 2014, 28, 5465–5476. [Google Scholar] [CrossRef]
- Guo, D.; Westra, S.; Maier, H.R. Sensitivity of potential evapotranspiration to changes in climate variables for different Australian climatic zones. Hydrol. Earth Syst. Sci. 2017, 21, 2107–2126. [Google Scholar] [CrossRef]
- Westerhoff, R. Using uncertainty of Penman and Penman–Monteith methods in combined satellite and ground-based evapotranspiration estimates. Remote Sens. Environ. 2015, 169, 102–112. [Google Scholar] [CrossRef]
- Hofreiter, M.; Jirka, V. Uncertainty Analysis of Evapotranspiration Estimates in Ecosystems. Asian Rev. Mechnical Eng. 2012, 1, 46. [Google Scholar]
- Chen, L.-H.; Chen, J.; Chen, C. Effect of Environmental Measurement Uncertainty on Prediction of Evapotranspiration. Atmosphere 2018, 9, 400. [Google Scholar] [CrossRef]
- RefGrab-It Install Page. Vol. 2014. Available online: https://www.refworks.com/refgrabit/linkpage.aspx (accessed on 1 January 2021).
- Van der Kwast, J.; Timmermans, W.; Gieske, A.; Su, Z.; Olioso, A.; Jia, L.; Elbers, J.; Karssenberg, D.; De Jong, S.; de Jong, S. Evaluation of the Surface Energy Balance System (SEBS) applied to ASTER imagery with flux-measurements at the SPARC 2004 site (Barrax, Spain). Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 1165–1196. [Google Scholar]
- Wang, J.; Sammis, T.; Gutschick, V.; Gebremichael, M.; Miller, D. Sensitivity analysis of the surface energy balance algorithm for land (SEBAL). Trans. ASABE 2009, 52, 801–811. [Google Scholar] [CrossRef]
- Majozi, N.P.; Mannaerts, C.M.; Ramoelo, A.; Mathieu, R.; Mudau, A.E.; Verhoef, W. An intercomparison of satellite-based daily evapotranspiration estimates under different eco-climatic regions in South Africa. Remote Sens. 2017, 9, 307. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Scholes, R.J.; Bond, W.J.; Eckhardt, H.C. Vegetation Dynamics in the Kruger Ecosystem; The Kruger Experience: Ecology and Management of Savanna Heterogeneity; Island Press: Washington, DC, USA, 2003. [Google Scholar]
- Scholes, R.J.; Gureja, N.; Giannecchinni, M.; Dovie, D.; Wilson, B.; Davidson, N.; Piggott, K.; McLoughlin, C.; Van der Velde, K.; Freeman, A. The environment and vegetation of the flux measurement site near Skukuza, Kruger National Park. Koedoe-Afr. Prot. Area Conserv. Sci. 2001, 44, 73–83. [Google Scholar] [CrossRef]
- Räsänen, M.; Aurela, M.; Vakkari, V.; Beukes, J.P.; Tuovinen, J.-P.; Van Zyl, P.G.; Josipovic, M.; Venter, A.D.; Jaars, K.; Siebert, S.J. Carbon balance of a grazed savanna grassland ecosystem in South Africa. Biogeosciences 2017, 14, 1039. [Google Scholar] [CrossRef]
- Wan, Z. MODIS land-surface temperature algorithm theoretical basis document (LST ATBD). Inst. Comput. Earth Syst. Sci. St. Barbar. 1999, 75. [Google Scholar]
- Hulley, G.; Malakar, N.; Hughes, T.; Islam, T.; Hook, S. Moderate Resolution Imaging Spectroradiometer (MODIS) MOD21 Land Surface Temperature and Emissivity Algorithm Theoretical Basis Document; Jet Propulsion Laboratory, National Aeronautics and Space: Pasadena, CA, USA, 2016; p. 102. [Google Scholar]
- Wanner, W.; Strahler, A.; Hu, B.; Lewis, P.; Muller, J.P.; Li, X.; Schaaf, C.B.; Barnsley, M. Global retrieval of bidirectional reflectance and albedo over land from EOS MODIS and MISR data: Theory and algorithm. J. Geophys. Res. Atmos. 1997, 102, 17143–17161. [Google Scholar] [CrossRef]
- Schaaf, C.; Liu, J.; Gao, F.; Strahler, A.H. MODIS albedo and reflectance anisotropy products from Aqua and Terra. Land Remote Sens. Glob. Environ. Chang. NASA’s Earth Obs. Syst. Sci. ASTER MODIS 2011, 11, 549–561. [Google Scholar]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Nobre, C.A.; Sellers, P.J.; Shukla, J. Amazonian deforestation and regional climate change. J. Clim. 1991, 4, 957–988. [Google Scholar] [CrossRef]
- Sellers, P.; Meeson, B.; Hall, F.; Asrar, G.; Murphy, R.; Schiffer, R.; Bretherton, F.; Dickinson, R.; Ellingson, R.; Field, C. Remote sensing of the land surface for studies of global change: Models—algorithms—experiments. Remote Sens. Environ. 1995, 51, 3–26. [Google Scholar] [CrossRef]
- Jin, Y.; Schaaf, C.B.; Woodcock, C.E.; Gao, F.; Li, X.; Strahler, A.H.; Lucht, W.; Liang, S. Consistency of MODIS surface bidirectional reflectance distribution function and albedo retrievals: 2. Validation. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Wang, K.; Liu, J.; Zhou, X.; Sparrow, M.; Ma, M.; Sun, Z.; Jiang, W. Validation of the MODIS global land surface albedo product using ground measurements in a semidesert region on the Tibetan Plateau. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Glassy, J.; Privette, J.; Tian, Y.; Lotsch, A.; Zhang, Y.; Wang, Y.; Morisette, J.; Votava, P.; Myneni, R. MODIS Leaf Area Index (LAI) and Fraction of Photosynthetically Active Radiation Absorbed by Vegetation (FPAR) Product (MOD15) Algorithm Theoretical Basis Document; Theoretical Basis Document, NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1999; Volume 20771. [Google Scholar]
- Myneni, R.B.; Ramakrishna, R.; Nemani, R.; Running, S.W. Estimation of global leaf area index and absorbed PAR using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar] [CrossRef]
- Fang, H.; Wei, S.; Jiang, C.; Scipal, K. Theoretical uncertainty analysis of global MODIS, CYCLOPES, and GLOBCARBON LAI products using a triple collocation method. Remote Sens. Environ. 2012, 124, 610–621. [Google Scholar] [CrossRef]
- Strahler, A.H.; Muller, J.; Lucht, W.; Schaaf, C.; Tsang, T.; Gao, F.; Li, X.; Lewis, P.; Barnsley, M.J. MODIS BRDF/albedo product: Algorithm theoretical basis document version 5.0. MODIS Doc. 1999, 23, 42–47. [Google Scholar]
- Muniz, P.R.; Kalid, R.D.A.; Cani, S.P.; Magalhães, R.S. Handy method to estimate uncertainty of temperature measurement by infrared thermography. Opt. Eng. 2014, 53, 074101. [Google Scholar] [CrossRef]
- Lin, X.; Hubbard, K. Uncertainties of derived dewpoint temperature and relative humidity. J. Appl. Meteorol. 2004, 43, 821–825. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hughes, C.G.; Hook, S.J. Quantifying uncertainties in land surface temperature and emissivity retrievals from ASTER and MODIS thermal infrared data. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Mira, M.; Olioso, A.; Gallego-Elvira, B.; Courault, D.; Garrigues, S.; Marloie, O.; Hagolle, O.; Guillevic, P.; Boulet, G. Uncertainty assessment of surface net radiation derived from Landsat images. Remote Sens. Environ. 2016, 175, 251–270. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.; Evans, J.; Wood, E. Impact of model structure and parameterization on Penman–Monteith type evaporation models. J. Hydrol. 2015, 525, 521–535. [Google Scholar] [CrossRef]
- Bailey, W.; Davies, J. Evaporation from soybeans. Bound.-Layer Meteorol. 1981, 20, 417–428. [Google Scholar] [CrossRef]
- Irmak, S.; Mutiibwa, D. On the dynamics of stomatal resistance: Relationships between stomatal behavior and micrometeorological variables and performance of Jarvis-type parameterization. Trans. ASABE 2009, 52, 1923–1939. [Google Scholar] [CrossRef]
- Langensiepen, M.; Fuchs, M.; Bergamaschi, H.; Moreshet, S.; Cohen, Y.; Wolff, P.; Jutzi, S.C.; Cohen, S.; Rosa, L.M.G.; Li, Y.; et al. Quantifying the uncertainties of transpiration calculations with the Penman–Monteith equation under different climate and optimum water supply conditions. Agric. For. Meteorol. 2009, 149, 1063–1072. [Google Scholar] [CrossRef]
- Ferguson, C.R.; Sheffield, J.; Wood, E.F.; Gao, H. Quantifying uncertainty in a remote sensing-based estimate of evapotranspiration over continental USA. Int. J. Remote Sens. 2010, 31, 3821–3865. [Google Scholar] [CrossRef]
- Eslamian, S.; Khordadi, M.J.; Abedi-Koupai, J. Effects of variations in climatic parameters on evapotranspiration in the arid and semi-arid regions. Glob. Planet. Chang. 2011, 78, 188–194. [Google Scholar] [CrossRef]
- Debnath, S.; Adamala, S.; Raghuwanshi, N.S. Sensitivity Analysis of FAO-56 Penman-Monteith Method for Different Agro-ecological Regions of India. Environ. Process. 2015, 2, 689–704. [Google Scholar] [CrossRef]
- Tabari, H.; Hosseinzadeh Talaee, P. Sensitivity of evapotranspiration to climatic change in different climates. Glob. Planet. Chang. 2014, 115, 16–23. [Google Scholar] [CrossRef]
- Garcia, M.; Raes, D.; Allen, R.; Herbas, C. Dynamics of reference evapotranspiration in the Bolivian highlands (Altiplano). Agric. For. Meteorol. 2004, 125, 67–82. [Google Scholar] [CrossRef]
- Gong, L.; Xu, C.-Y.; Chen, D.; Halldin, S.; Chen, Y.D. Sensitivity of the Penman–Monteith reference evapotranspiration to key climatic variables in the Changjiang (Yangtze River) basin. J. Hydrol. 2006, 329, 620–629. [Google Scholar] [CrossRef]
| Surface Resistance | Aerodynamic Resistance | ||||||
|---|---|---|---|---|---|---|---|
| Core Input | Rnet | rswc | rst | rstot | rawc | rat | ras |
| Tair | x | x | x | ||||
| LST | x | x | x | x | |||
| Tmin | x | ||||||
| α | x | ||||||
| LAI | x | x | x | ||||
| εs | x | ||||||
| RH | x | x | x | x | x | ||
| Skukuza | Welgegund | |||
|---|---|---|---|---|
| Measurement | Sensor | Quoted accuracy | Sensor | Quoted accuracy |
| Temperature | Campbell Scientific HMP50 | 0.4 °C at 15 °C, | Vaisala WXT510 meteorological station (Helsinki, Finland) | 0.3 °C at 20 °C, |
| 0.5 °C at 40 °C, | 0.4 °C at 40 °C, | |||
| 0.8 °C at 60 °C | 0.7 °C at 60 °C | |||
| Relative humidity | at 20 °C | at 20 °C | ||
| ±3% 0 to 90% RH, | ±3% 0 to 90% RH, | |||
| ±5% 90 to 98% RH | ±5% 90 to 100% RH | |||
| Error Values | Units | Reference | |
|---|---|---|---|
| LST | ±3.5 | K | Hulley, et al. [39] |
| ɛs | ±0.02 | - | Wan [38] |
| LAI | ±0.2 | - | Knyazikhin, et al. [48] |
| α | ±0.02 | - | Strahler, et al. [51] |
| Skukuza | Welgegund | |||
|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | |
| Total uncertainty | 22.12 | 5.58 | 14.73 | 5.16 |
| % Tair | 23.28 | 9.85 | 30.25 | 10.23 |
| % LST | 59.31 | 12.87 | 89.42 | 22.07 |
| % α | 13.13 | 0.42 | 22.06 | 10.31 |
| % ɛs | 25.76 | 5.44 | 38.81 | 9.43 |
| Skukuza | Welgegund | |||||||
|---|---|---|---|---|---|---|---|---|
| Aerodynamic Resistance | Surface Resistance | Aerodynamic Resistance | Surface Resistance | |||||
| Mean | Standard Deviation | Mean | Standard Deviation | Mean | Standard Deviation | Mean | Standard Deviation | |
| Interception Evaporation | 1.1 × 10−3 | 3.5 × 10−4 | 10.34 | 10.07 | 1 × 10−3 | 3 × 10−4 | 18.02 | 18.96 |
| Transpiration | 1.6 × 10−3 | 7 × 10−4 | 21.68 | 19.68 | 1.5 × 10−3 | 4.3 × 10−4 | 30.71 | 26.92 |
| Soil evaporation | 3.8 × 10−3 | 2.4 × 10−4 | 0.53 | 0.04 | 3.8 × 10−3 | 2.5 × 10−4 | 0.51 | 0.06 |
| Transpiration | Interception Loss | Potential Soil Evaporation | Wet Soil Evaporation | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | Mean | Standard Deviation | Mean | Standard Deviation | |
| Total standard uncertainty (mmday−1) | 0.33 | 0.41 | 0.038 | 0.14 | 0.89 | 0.34 | 0.12 | 0.22 |
| % RH (VPD) | 14.63 | 8.71 | 6.37 | 1.45 | (21.49) | (13.37) | (9.71) | (2.66) |
| % Fc (1-Fc) | 1.36 | 1.02 | 0.67 | 0.28 | (0.85) | (0.38) | ||
| % Fwet (1-Fwet) | 9.64 | 3.31 | 0.97 | 0.05 | (2.69) | (5.19) | 12.92 | 4.49 |
| % ras | 1.93 | 0.8 | 2.02 | 0.74 | ||||
| % rstot | 1.29 | 0.49 | 1.25 | 0.45 | ||||
| % rat | 0.89 | 0.08 | ||||||
| % rst | 2.42 | 5.03 | ||||||
| % rawc | 0.97 | 0.05 | ||||||
| % rswc | 21.46 | 5.97 | ||||||
| Transpiration | Potential Soil Evaporation | |||
|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | |
| Total Uncertainty | 0.13 | 0.28 | 1.05 | 0.29 |
| % RH (VPD) | 26.93 | 15.13 | (46.11) | (53.05) |
| % Fc (1-Fc) | 3.85 | 3.10 | (1.27) | (0.81) |
| % Fwet (1-Fwet) | 0 | 0 | 0 | 0 |
| % ras | 1.97 | 0.46 | ||
| % rstot | 1.45 | 0.25 | ||
| % rst | 0.87 | 0.12 | ||
| % rs | 8.98 | 1.67 | ||
| Station | Input Variables | % Change in ET with Respect to % Change in Input Variables | |||||
|---|---|---|---|---|---|---|---|
| −20 | −10 | −5 | 5 | 10 | 20 | ||
| Skukuza | Tair | −92.25 | −64.80 | 38.60 | |||
| LST | 55.08 | 39.56 | −50.56 | −77.45 | |||
| RH | −0.57 | −0.30 | −0.16 | 0.17 | 0.35 | 0.75 | |
| ɛa | 12.06 | 6.03 | −6.03 | −12.06 | |||
| LAI | 1.28 | 0.47 | 0.19 | −0.12 | −0.16 | −0.02 | |
| α | 6.16 | 3.08 | 1.54 | −1.54 | −3.08 | −6.16 | |
| Welgegund | Tair | −84.17 | −47.71 | 51.12 | 93.29 | ||
| LST | 84.75 | 44.15 | −57.83 | −63.15 | |||
| RH | −0.37 | −0.19 | −0.10 | 0.10 | 0.20 | 0.43 | |
| ɛa | 9.42 | 4.69 | −4.69 | −9.38 | |||
| LAI | 0.50 | 0.12 | 0.03 | 0.03 | 0.13 | 0.48 | |
| α | 5.00 | 2.50 | 1.25 | −1.25 | −2.50 | −5.00 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majozi, N.P.; Mannaerts, C.M.; Ramoelo, A.; Mathieu, R.; Verhoef, W. Uncertainty and Sensitivity Analysis of a Remote-Sensing-Based Penman–Monteith Model to Meteorological and Land Surface Input Variables. Remote Sens. 2021, 13, 882. https://doi.org/10.3390/rs13050882
Majozi NP, Mannaerts CM, Ramoelo A, Mathieu R, Verhoef W. Uncertainty and Sensitivity Analysis of a Remote-Sensing-Based Penman–Monteith Model to Meteorological and Land Surface Input Variables. Remote Sensing. 2021; 13(5):882. https://doi.org/10.3390/rs13050882
Chicago/Turabian StyleMajozi, Nobuhle P., Chris M. Mannaerts, Abel Ramoelo, Renaud Mathieu, and Wouter Verhoef. 2021. "Uncertainty and Sensitivity Analysis of a Remote-Sensing-Based Penman–Monteith Model to Meteorological and Land Surface Input Variables" Remote Sensing 13, no. 5: 882. https://doi.org/10.3390/rs13050882
APA StyleMajozi, N. P., Mannaerts, C. M., Ramoelo, A., Mathieu, R., & Verhoef, W. (2021). Uncertainty and Sensitivity Analysis of a Remote-Sensing-Based Penman–Monteith Model to Meteorological and Land Surface Input Variables. Remote Sensing, 13(5), 882. https://doi.org/10.3390/rs13050882






