Landsat 8 OLI Broadband Albedo Validation in Antarctica and Greenland
Abstract
1. Introduction
2. Materials and Methods
2.1. Satellite Data Processing
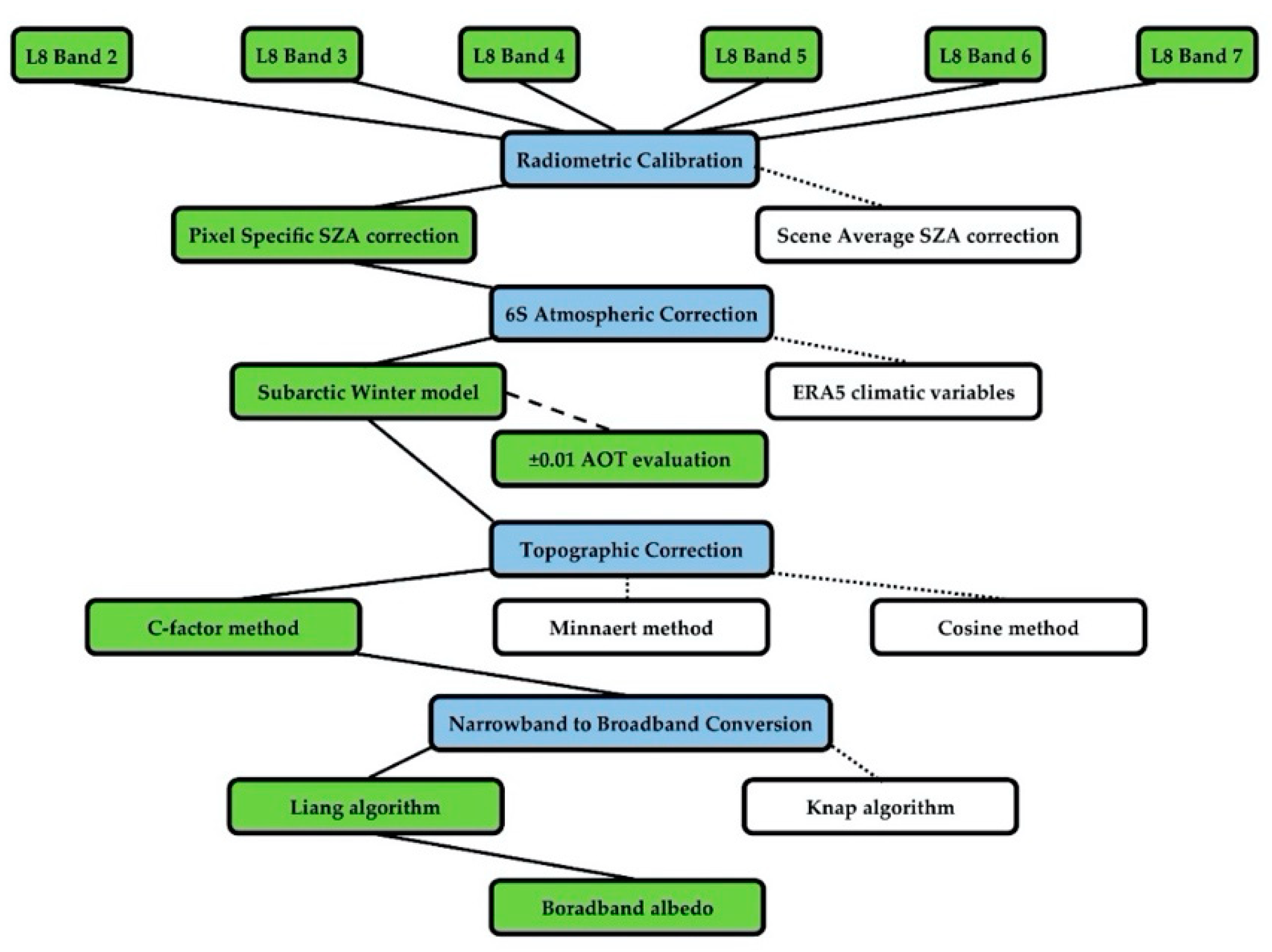
2.1.1. Radiometric Calibration and SZA Correction
2.1.2. Atmospheric Correction
2.1.3. Topographic Correction
2.1.4. Narrowband to Broadband Albedo Conversion
2.2. In Situ Broadband Albedo Data
3. Results and Discussion
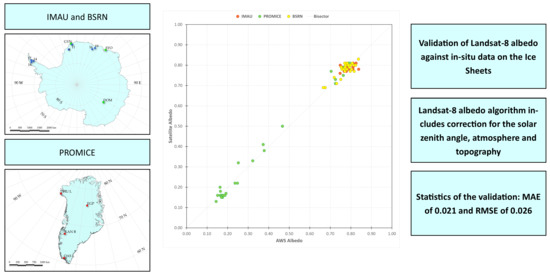
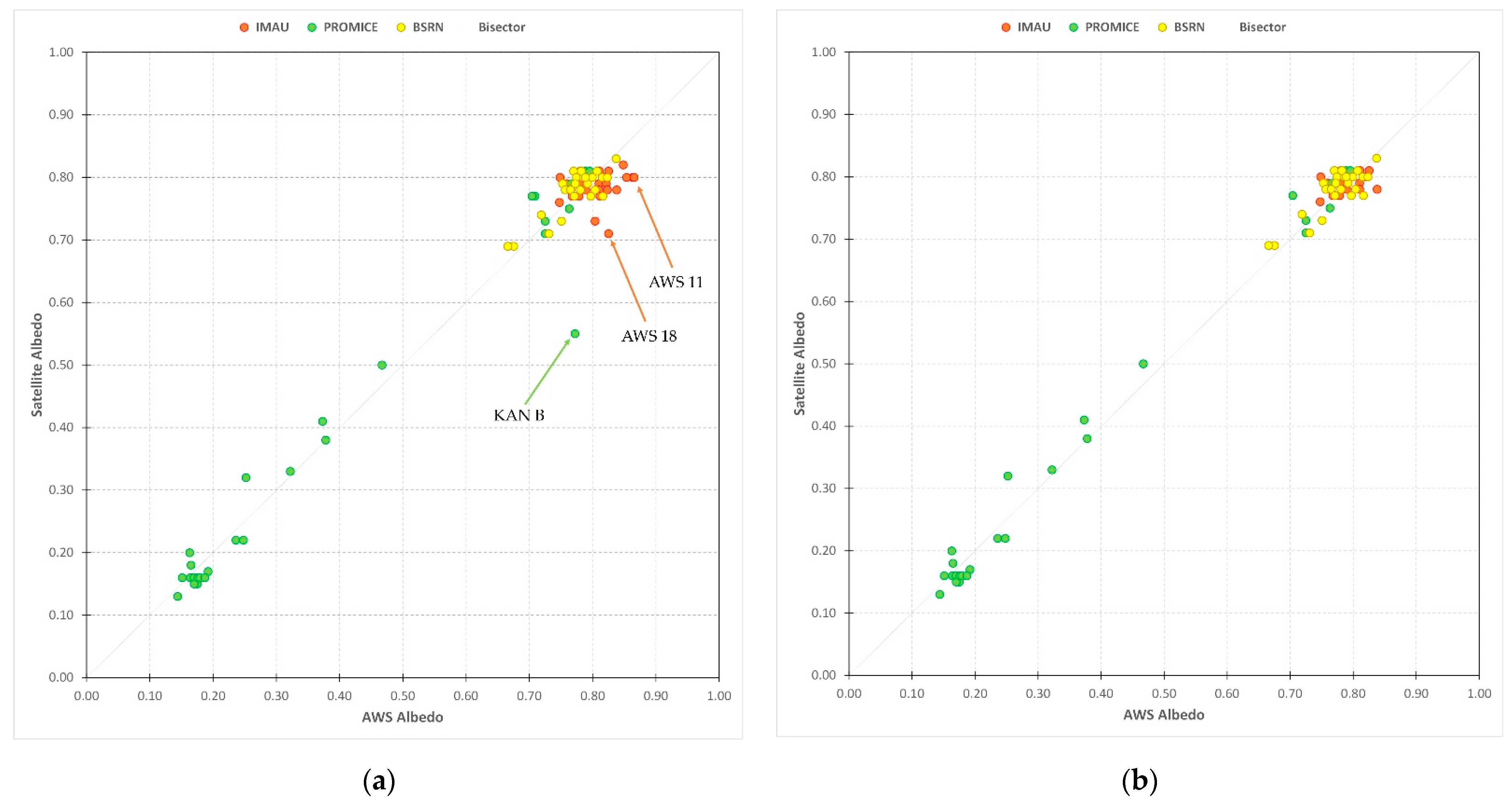
3.1. Method Validation
3.2. IMAU AWSs (Antarctica)
3.3. BSRN AWSs (Antarctica)
3.4. PROMICE AWSs (Greenland)
3.5. Analysis of the Cleaned Dataset
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance Quantities in Optical Remote Sensing—Definitions and Case Studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Grenfell, T.C. Albedo. Encyclopedia of Snow, Ice and Glaciers; Singh, V., Singh, P., Haritahya, U., Eds.; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Grenfell, T.C.; Warren, S.G.; Mullen, P.C. Warren Reflection of Solar Radiation by the Antarctic Snow Surface at Ultraviolet, Visible, and near-Infrared Wavelengths. J. Geophys. Res. 1994, 99, 18669–18684. [Google Scholar] [CrossRef]
- Gay, M.; Fily, M.; Genthon, C.; Frezzotti, M.; Oerter, H.; Winther, J.-G. Snow Grain-Size Measurements in Antarctica. J. Glaciol. 2002, 48, 527–535. [Google Scholar] [CrossRef][Green Version]
- Warren, S.G.; Brandt, R.E.; Grenfell, T.C. Visible and Near-Ultraviolet Absorption Spectrum of Ice from Transmission of Solar Radiation into Snow. Appl. Opt. 2006, 45, 5320–5334. [Google Scholar] [CrossRef] [PubMed]
- Gallet, J.-C.; Domine, F.; Arnaud, L.; Picard, G.; Savarino, J. Vertical Profile of the Specific Surface Area and Density of the Snow at Dome C and on a Transect to Dumont D’Urville, Antarctica—Albedo Calculations and Comparison to Remote Sensing Products. Cryosphere 2011, 5, 631–649. [Google Scholar] [CrossRef]
- Picard, G.; Libois, Q.; Arnaud, L.; Verin, G.; Dumont, M. Development and Calibration of an Automatic Spectral Albedometer to Estimate Near-Surface Snow SSA Time Series. Cryosphere 2016, 10, 1297–1316. [Google Scholar] [CrossRef]
- Frezzotti, M.; Gandolfi, S.; Marca, F.L.; Urbini, S. Snow Dunes and Glazed Surfaces in Antarctica: New Field and Remote-Sensing Data. Ann. Glaciol. 2002, 34, 81–88. [Google Scholar] [CrossRef]
- Scambos, T.A.; Frezzotti, M.; Haran, T.; Bohlander, J.; Lenaerts, J.T.M.; Van Den Broeke, M.R.; Jezek, K.; Long, D.; Urbini, S.; Farness, K.; et al. Extent of Low-Accumulation “wind Glaze” Areas on the East Antarctic Plateau: Implications for Continental Ice Mass Balance. J. Glaciol. 2012, 58, 633–647. [Google Scholar] [CrossRef]
- Das, I.; Bell, R.E.; Scambos, T.A.; Wolovick, M.; Creyts, T.T.; Studinger, M.; Frearson, N.; Nicolas, J.P.; Lenaerts, J.T.M.; van den Broeke, M.R. Influence of Persistent Wind Scour on the Surface Mass Balance of Antarctica. Nat. Geosci. 2013, 6, 367–371. [Google Scholar] [CrossRef]
- Pirazzini, R. Surface Albedo Measurements over Antarctic Sites in Summer. J. Geophys. Res. 2004, 109, D20118. [Google Scholar] [CrossRef]
- Picard, G.; Domine, F.; Krinner, G.; Arnaud, L.; Lefebvre, E. Inhibition of the Positive Snow-Albedo Feedback by Precipitation in Interior Antarctica. Nat. Clim. Chang. 2012, 2, 795–798. [Google Scholar] [CrossRef]
- Lenaerts, J.T.M.; Lhermitte, S.; Drews, R.; Ligtenberg, S.R.M.; Berger, S.; Helm, V.; Smeets, C.; Van Den Broeke, M.R.; Van De Berg, W.J.; Van Meijgaard, E. Meltwater Produced by Wind–Albedo Interaction Stored in an East Antarctic Ice Shelf. Nat. Clim. Chang. 2017, 7, 58–62. [Google Scholar] [CrossRef]
- Rusin, N.P. Meteorological and Radiational Regime of Antarctica. Jerus. Isr. Program Sci. Transl. 1961. [Google Scholar]
- Bintanja, R.; Van Den Broeke, M.R. The Surface Energy Balance of Antarctic Snow and Blue Ice. J. Appl. Meteorol. Climatol. 1995, 34, 902–926. [Google Scholar] [CrossRef]
- van As, D.; Ahlstrøm, A.P.; Andersen, M.L.; Citterio, M.; Edelvang, K.; Gravesen, P.; Machguth, H.; Nick, F.M. Programme for Monitoring of the Greenland Ice Sheet (PROMICE): First Temperature and Ablation Records. Geol. Surv. Den. Greenl. Bull. 2011, 23, 73–76. [Google Scholar]
- Driemel, A.; Augustine, J.; Behrens, K.; Colle, S.; Cox, C.; Cuevas-Agulló, E.; Denn, F.M.; Duprat, T.; Fukuda, M.; Grobe, H.; et al. Baseline Surface Radiation Network (BSRN): Structure and Data Description (1992–2017). Earth Syst. Sci. Data 2018, 10, 1491–1501. [Google Scholar] [CrossRef]
- Jakobs, C.L.; Reijmer, C.H.; Smeets, C.J.P.P.; Trusel, L.D.; van de Berg, W.J.; van den Broeke, M.R.; van Wessem, J.M. A Benchmark Dataset of in Situ Antarctic Surface Melt Rates and Energy Balance. J. Glaciol. 2020, 66, 291–302. [Google Scholar] [CrossRef]
- Fugazza, D.; Senese, A.; Azzoni, R.S.; Maugeri, M.; Diolaiuti, G.A. Spatial Distribution of Surface Albedo at the Forni Glacier (Stelvio National Park, Central Italian Alps). Cold Reg. Sci. Technol. 2016, 125, 128–137. [Google Scholar] [CrossRef]
- Azzoni, R.S.; Senese, A.; Zerboni, A.; Maugeri, M.; Smiraglia, C.; Diolaiuti, G.A. Estimating Ice Albedo from Fine Debris Cover Quantified by a Semi-Automatic Method: The Case Study of Forni Glacier, Italian Alps. Cryosphere 2016, 10, 665–679. [Google Scholar] [CrossRef]
- Brock, B.W.; Willis, I.C.; Sharp, M.J. Measurement and Parameterization of Albedo Variations at Haut Glacier d’Arolla, Switzerland. J. Glaciol. 2000, 46, 675–688. [Google Scholar] [CrossRef]
- Senese, A.; Maugeri, M.; Ferrari, S.; Confortola, G.; Soncini, A.; Bocchiola, D.; Diolaiuti, G. Modelling Shortwave and Longwave Downward Radiation and Air Temperature Driving Ablation at the Forni Glacier (Stelvio National Park, Italy). Geogr. Fis. Dinam. Quat. 2016, 39, 89–100. [Google Scholar]
- Stroeve, J.; Box, J.E.; Wang, Z.; Schaaf, C.; Barrett, A. Re-Evaluation of MODIS MCD43 Greenland Albedo Accuracy and Trends. Remote Sens. Environ. 2013, 138, 199–214. [Google Scholar] [CrossRef]
- Box, J.E.; van As, D.; Steffen, K. Greenland, Canadian and Icelandic Land-Ice Albedo Grids (2000–2016). Geol. Surv. Den. Greenl. Bull. 2017, 4, 53–56. [Google Scholar] [CrossRef][Green Version]
- Liang, S. Mapping Daily Snow/Ice Shortwave Broadband Albedo from Moderate Resolution Imaging Spectroradiometer (MODIS): The Improved Direct Retrieval Algorithm and Validation with Greenland in Situ Measurement. J. Geophys. Res. 2005, 110, D10109. [Google Scholar] [CrossRef]
- Hui, F.; Ci, T.; Cheng, X.; Scambos, T.A.; Liu, Y.; Zhang, Y.; Chi, Z.; Huang, H.; Wang, X.; Wang, F. Mapping Blue-Ice Areas in Antarctica Using ETM+ and MODIS Data. Ann. Glaciol. 2014, 55, 129–137. [Google Scholar] [CrossRef]
- Traversa, G.; Fugazza, D.; Senese, A.; Diolaiuti, G.A. Preliminary Results on Antarctic Albedo from Remote Sensing Observations. Geogr. Fis. Din. Quat. 2019, 42, 245–254. [Google Scholar]
- Reijmer, C.H.; Bintanja, R.; Greuell, W. Surface Albedo Measurements over Snow and Blue Ice in Thematic Mapper Bands 2 and 4 in Dronning Maud Land, Antarctica. J. Geophys. Res. Atmos. 2001, 106, 9661–9672. [Google Scholar] [CrossRef]
- Klok, E.L.; Greuell, W.; Oerlemans, J. Temporal and Spatial Variation of the Surface Albedo of Morteratschgletscher, Switzerland, as Derived from 12 Landsat Images. J. Glaciol. 2003, 49, 491–502. [Google Scholar] [CrossRef]
- Shuai, Y.; Masek, J.G.; Gao, F.; Schaaf, C.B. An Algorithm for the Retrieval of 30-m Snow-Free Albedo from Landsat Surface Reflectance and MODIS BRDF. Remote Sens. Environ. 2011, 115, 2204–2216. [Google Scholar] [CrossRef]
- Wang, J.; Ye, B.; Cui, Y.; He, X.; Yang, G. Spatial and Temporal Variations of Albedo on Nine Glaciers in Western China from 2000 to 2011. Hydrol. Process. 2014, 28, 3454–3465. [Google Scholar] [CrossRef]
- Naegeli, K.; Damm, A.; Huss, M.; Wulf, H.; Schaepman, M.; Hoelzle, M. Cross-Comparison of Albedo Products for Glacier Surfaces Derived from Airborne and Satellite (Sentinel-2 and Landsat 8) Optical Data. Remote Sens. 2017, 9, 110. [Google Scholar] [CrossRef]
- Fugazza, D.; Senese, A.; Azzoni, R.S.; Maugeri, M.; Maragno, D.; Diolaiuti, G.A. New Evidence of Glacier Darkening in the Ortles-Cevedale Group from Landsat Observations. Glob. Planet. Chang. 2019, 178, 35–45. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to Broadband Conversions of Land Surface Albedo I: Algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Knap, W.H.; Reijmer, C.H.; Oerlemans, J. Narrowband to Broadband Conversion of Landsat TM Glacier Albedos. Int. J. Remote Sens. 1999, 20, 2091–2110. [Google Scholar] [CrossRef]
- Foga, S.; Scaramuzza, P.L.; Guo, S.; Zhu, Z.; Dilley, R.D., Jr.; Beckmann, T.; Schmidt, G.L.; Dwyer, J.L.; Hughes, M.J.; Laue, B. Cloud Detection Algorithm Comparison and Validation for Operational Landsat Data Products. Remote Sens. Environ. 2017, 194, 379–390. [Google Scholar] [CrossRef]
- Zanter, K. Landsat 8 (L8) Data Users Handbook. In Landsat Sci. Off. Website. Available online: https://www.usgs.gov/media/files/landsat-8-data-users-handbook (accessed on 19 February 2021).
- Picard, G.; Libois, Q.; Arnaud, L.; Vérin, G.; Dumont, M. Estimation of Superficial Snow Specific Surface Area from Spectral Albedo Time-Series at Dome C, Antarctica. Cryosphere Discuss 2016, 1–39. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanré, D.; Deuze, J.L.; Herman, M.; Morcette, J.-J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An Overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Howat, I.M.; Porter, C.; Smith, B.E.; Noh, M.-J.; Morin, P. The Reference Elevation Model of Antarctica. Cryosphere 2019, 13, 665–674. [Google Scholar] [CrossRef]
- Howat, I.M.; Negrete, A.; Smith, B.E. The Greenland Ice Mapping Project (GIMP) Land Classification and Surface Elevation Data Sets. Cryosphere 2014, 8, 1509–1518. [Google Scholar] [CrossRef]
- Wiscombe, W.J.; Warren, S.G. A Model for the Spectral Albedo of Snow. I: Pure Snow. J. Atmos. Sci. 1980, 37, 2712–2733. [Google Scholar] [CrossRef]
- Lupi, A. Basic and Other Measurements of Radiation at Concordia Station; Institute of Atmospheric Sciences and Climate of the Italian National Research Council: Bologna, Italy, 2020. [Google Scholar]
- Schmithüsen, H. Basic and Other Measurements of Radiation at Neumayer Station; Alfred Wegener Institute, Helmholtz Centre for Polar and Marine Research: Bremerhaven, Germany, 2020. [Google Scholar]
- Ogihara, H. Basic and Other Measurements of Radiation at Station Syowa; National Institute of Polar Research: Tokyo, Japan, 2019. [Google Scholar]
- Briegleb, B.P.; Minnis, P.; Ramanathan, V.; Harrison, E. Comparison of Regional Clear-Sky Albedos Inferred from Satellite Observations and Model Computations. J. Clim. Appl. Meteorol. 1986, 25, 214–226. [Google Scholar] [CrossRef]
- Dickinson, R.E. Land surface processes and climate—Surface albedos and energy balance. In Advances in Geophysics, Proceedings of the A Symposium Commemorating the Two-Hundredth Anniversary of the Academy of Sciences of Lisbon, Lisbon, Portugal, 12–14 October 1981; Academic Press: Cambridge, MI, USA, 1983; Volume 25, pp. 305–353. [Google Scholar]
- Pinker, R.T.; Laszlo, I. Modeling Surface Solar Irradiance for Satellite Applications on a Global Scale. J. Appl. Meteorol. Climatol. 1992, 31, 194–211. [Google Scholar] [CrossRef]
- Wang, Z.; Barlage, M.; Zeng, X.; Dickinson, R.E.; Schaaf, C.B. The Solar Zenith Angle Dependence of Desert Albedo. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Yang, F.; Mitchell, K.; Hou, Y.-T.; Dai, Y.; Zeng, X.; Wang, Z.; Liang, X.-Z. Dependence of Land Surface Albedo on Solar Zenith Angle: Observations and Model Parameterization. J. Appl. Meteor. Climatol. 2008, 47, 2963–2982. [Google Scholar] [CrossRef]
- Citterio, M.; Van As, D.; Ahlstrøm, A.P.; Andersen, M.L.; Andersen, S.B.; Box, J.E.; Charalampidis, C.; Colgan, W.T.; Fausto, R.S.; Nielsen, S.; et al. Automatic Weather Stations for Basic and Applied Glaciological Research. GEUS Bull. 2015, 69–72. [Google Scholar] [CrossRef]
- Arndt, J.E.; Schenke, H.W.; Jakobsson, M.; Nitsche, F.O.; Buys, G.; Goleby, B.; Rebesco, M.; Bohoyo, F.; Hong, J.; Black, J.; et al. The International Bathymetric Chart of the Southern Ocean (IBCSO) Version 1.0—A New Bathymetric Compilation Covering Circum-Antarctic Waters. Geophys. Res. Lett. 2013, 40, 3111–3117. [Google Scholar] [CrossRef]
- Yamanouchi, T. Variations of Incident Solar Flux and Snow Albedo on the Solar Zenith Angle and Cloud Cover, at Mizuho Station, Antarctica. J. Meteorol. Soc. Jpn. Ser. II 1983, 61, 879–893. [Google Scholar] [CrossRef][Green Version]
- Munneke, P.K.; Reijmer, C.H.; Van den Broeke, M.R. Assessing the Retrieval of Cloud Properties from Radiation Measurements over Snow and Ice. Int. J. Climatol. 2011, 31, 756–769. [Google Scholar] [CrossRef]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers; Academic Press: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Bintanja, R. On the Glaciological, Meteorological, and Climatological Significance of Antarctic Blue Ice Areas. Rev. Geophys. 1999, 37, 337–359. [Google Scholar] [CrossRef]
- Rignot, E.; Mouginot, J.; Scheuchl, B. MEaSUREs InSAR-Based Antarctica Ice Velocity Map, Version 2; NASA DAAC at the National Snow and Ice Data Center: Boulder, CO, USA, 2017. [Google Scholar]
- Jakobs, C.L.; Reijmer, C.H.; Kuipers Munneke, P.; König-Langlo, G.; Van Den Broeke, M.R. Quantifying the Snowmelt-Albedo Feedback at Neumayer Station, East Antarctica. Cryosphere 2019, 13, 1473–1485. [Google Scholar] [CrossRef]
- Munneke, P.K.; van den Broeke, M.R.; Lenaerts, J.T.M.; Flanner, M.G.; Gardner, A.S.; van de Berg, W.J. A New Albedo Parameterization for Use in Climate Models over the Antarctic Ice Sheet. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Oerlemans, J. The Microclimate of Valley Glaciers; Igitur, Utrecht Publishing & Archiving Services: Utrecht, The Netherlands, 2010. [Google Scholar]
- Gusain, H.S.; Singh, D.K.; Mishra, V.D.; Arora, M.K. Estimation of Net Radiation Flux of Antarctic Ice Sheet in East Dronning Maud Land, Antarctica, During Clear Sky Days Using Remote Sensing and Meteorological Data. Remote Sens. Earth Syst. Sci. 2018, 1, 89–99. [Google Scholar] [CrossRef]
- Stroeve, J.C.; Box, J.E.; Haran, T. Evaluation of the MODIS (MOD10A1) Daily Snow Albedo Product over the Greenland Ice Sheet. Remote Sens. Environ. 2006, 105, 155–171. [Google Scholar] [CrossRef]
- Li, Z.; Erb, A.; Sun, Q.; Liu, Y.; Shuai, Y.; Wang, Z.; Boucher, P.; Schaaf, C. Preliminary Assessment of 20-m Surface Albedo Retrievals from Sentinel-2A Surface Reflectance and MODIS/VIIRS Surface Anisotropy Measures. Remote Sens. Environ. 2018, 217, 352–365. [Google Scholar] [CrossRef]
- Knap, W.H.; Brock, B.W.; Oerlemans, J.; Willis, I.C. Comparison of Landsat TM-Derived and Ground-Based Albedos of Haut Glacier d’Arolla, Switzerland. Int. J. Remote Sens. 1999, 20, 3293–3310. [Google Scholar] [CrossRef]
- He, T.; Liang, S.; Wang, D.; Cao, Y.; Gao, F.; Yu, Y.; Feng, M. Evaluating Land Surface Albedo Estimation from Landsat MSS, TM, ETM+, and OLI Data Based on the Unified Direct Estimation Approach. Remote Sens. Environ. 2018, 204, 181–196. [Google Scholar] [CrossRef]
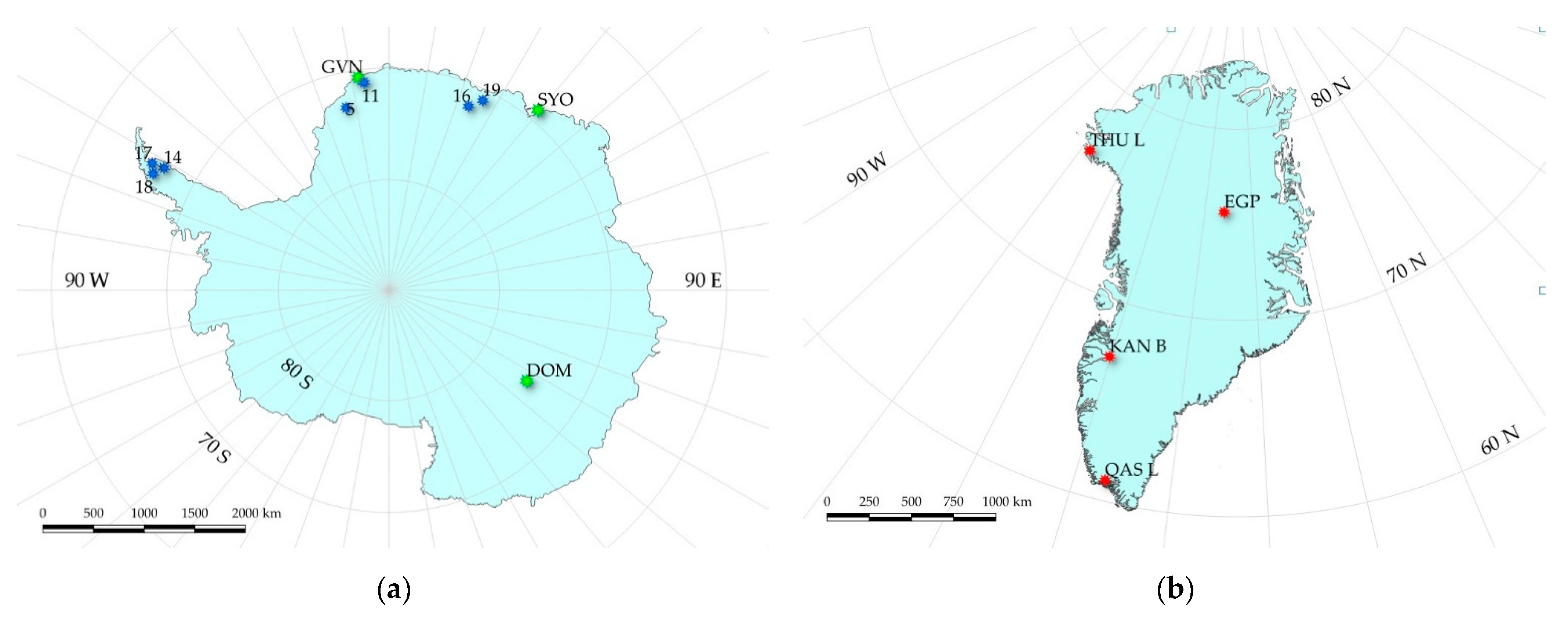
| Dataset | In Situ Stations | Coordinates (Lat°; Long°) | Elevation (m a.s.l.) | Period | Landsat Scene | Landsat Dates | SZA (Deg) | Surface Type |
|---|---|---|---|---|---|---|---|---|
| IMAU | ||||||||
| AWS 05 | −73.10; −13.17 | 360 | 1998–2014 | 178112 | 21/11/2013 | 62 | Snow | |
| 07/12/2013 | 61 | |||||||
| AWS 11 | −71.17; −6.80 | 690 | 2007–2019 | 178110 | 07/12/2013 * | 58 | Snow | |
| 24/01/2014 * | 63 | |||||||
| 27/01/2015 * | 66 | |||||||
| 28/02/2015 * | 76 | |||||||
| 15/02/2016 * | 71 | |||||||
| 12/10/2016 * | 74 | |||||||
| 16/01/2017 * | 63 | |||||||
| AWS 14 | −67.02; −61.50 | 50 | 2009–2015 | 217107 | 13/02/2015 | 68 | Snow | |
| AWS 16 | −71.95; 23.33 | 1300 | 2009–2015 | 156111 | 27/11/2013 | 64 | Snow | |
| 30/01/2014 | 69 | |||||||
| 03/03/2014 | 79 | |||||||
| 13/10/2014 | 76 | |||||||
| 29/10/2014 | 70 | |||||||
| 14/11/2014 | 66 | |||||||
| 16/10/2015 | 74 | |||||||
| 17/11/2015 | 65 | |||||||
| 03/12/2015 | 63 | |||||||
| AWS 17 | −65.93; −61.85 | 50 | 2011–2016 | 217106 | 11/10/2015 | 70 | Snow | |
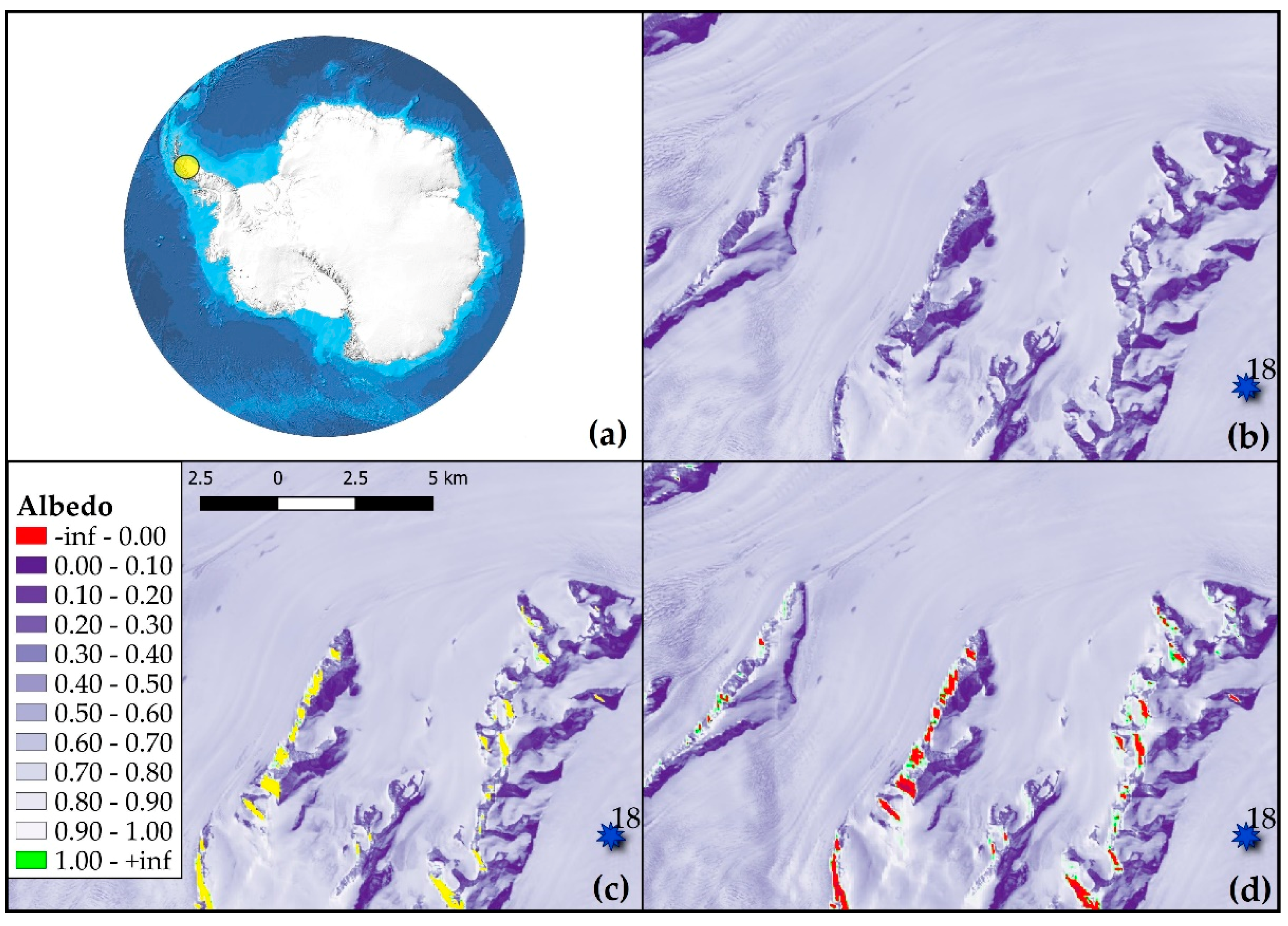
| AWS 18 | −66.40; −63.73 | 70 | 2014–2018 | 217107 | 11/10/2015 * | 71 | Snow | |
| 03/12/2017 * | 58 | |||||||
| 03/10/2018 * | 74 | |||||||
| AWS 19 | −70.95; 26.27 | 50 | 2014–2016 | 156110 | 16/10/2015 | 76 | Snow | |
| 17/11/2015 | 67 | |||||||
| 03/12/2015 | 64 | |||||||
| BSRN | ||||||||
| DOM | −75.10; 123.38 | 3233 | 2006–2020 | 089113 | 24/11/2014 | 61 | Snow | |
| 12/02/2015 | 70 | |||||||
| 29/12/2015 | 60 | |||||||
| 28/10/2016 | 68 | |||||||
| 18/12/2017 | 59 | |||||||
| 20/02/2018 | 73 | |||||||
| 21/10/2019 | 71 | |||||||
| GVN | −70.65; −8.25 | 42 | 1992–2020 | 178110 | 07/12/2013 | 56 | Snow | |
| 29/12/2015 | 56 | |||||||
| 15/02/2016 | 67 | |||||||
| 02/03/2016 | 72 | |||||||
| 12/10/2016 | 70 | |||||||
| 16/01/2017 | 59 | |||||||
| 05/12/2018 | 56 | |||||||
| 09/01/2020 | 57 | |||||||
| SYO | −69.01; 39.59 | 18 | 1994–2019 | 148109 | 12/10/2014 | 69 | Snow | |
| 28/10/2014 | 63 | |||||||
| 13/11/2014 | 59 | |||||||
| 29/11/2014 | 56 | |||||||
| 16/11/2015 | 58 | |||||||
| 03/01/2016 | 55 | |||||||
| 07/03/2016 | 73 | |||||||
| 04/12/206 | 55 | |||||||
| 22/02/2017 | 68 | |||||||
| 20/10/2017 | 66 | |||||||
| 08/01/2018 | 56 | |||||||
| 23/10/2018 | 65 | |||||||
| PROMICE | ||||||||
| EGP | 75.62; −35.97 | 2660 | 2016–2019 | 007006 | 26/07/2016 | 57 | Snow | |
| 26/05/2017 | 55 | |||||||
| 11/06/2017 | 53 | |||||||
| 29/07/2017 | 57 | |||||||
| 29/05/2018 | 54 | |||||||
| KAN B | 67.13; −50.18 | 350 | 2011–2019 | 007013 | 29/04/2013 * | 52 | Rock | |
| 31/05/2013 | 45 | |||||||
| 19/08/2013 | 55 | |||||||
| 06/08/2014 | 51 | |||||||
| 23/05/2016 | 46 | |||||||
| 08/06/2016 | 44 | |||||||
| 10/07/2016 | 45 | |||||||
| 26/07/2016 | 48 | |||||||
| 10/05/2017 | 49 | |||||||
| 27/06/2017 | 44 | |||||||
| 29/07/2017 | 49 | |||||||
| 14/08/2017 | 53 | |||||||
| QAS L | 61.03; −46.85 | 280 | 2007–2019 | 002017 | 02/07/2014 | 39 | Ice | |
| 03/08/2014 | 45 | |||||||
| 03/06/2015 | 40 | |||||||
| 21/06/2016 | 39 | |||||||
| 05/04/2017 | 56 | |||||||
| 07/05/2017 | 45 | |||||||
| 24/06/2017 | 39 | |||||||
| 10/05/2018 | 44 | |||||||
| 13/07/2018 | 41 | |||||||
| 29/07/2018 | 44 | |||||||
| 29/05/2019 | 41 | |||||||
| THU L | 76.40; −68.27 | 570 | 2010–2019 | 032005 | 04/07/2014 | 54 | Ice | |
| 04/05/2015 | 61 | |||||||
| 20/05/2015 | 57 | |||||||
| 23/07/2015 | 57 | |||||||
| 24/08/2015 | 66 |
| Dataset | MAE tot | MAE Antarctica | MAE Greenland | STD | BE | Cc | RMSE | BRRMSE |
|---|---|---|---|---|---|---|---|---|
| Proposed model | 0.027 | 0.026 | 0.029 | 0.029 | 0.005 | 0.987 | 0.040 | 0.039 |
| Ave. SZA c. | 0.030 | 0.028 | 0.033 | 0.029 | 0.003 | 0.986 | 0.042 | 0.041 |
| ERA5 | 0.028 | 0.028 | 0.028 | 0.030 | 0.011 | 0.987 | 0.041 | 0.040 |
| AOT -0.01 | 0.028 | 0.027 | 0.030 | 0.029 | 0.007 | 0.987 | 0.040 | 0.040 |
| AOT +0.01 | 0.028 | 0.026 | 0.031 | 0.028 | 0.002 | 0.987 | 0.040 | 0.040 |
| Cosine c. | 0.026 | 0.026 | 0.027 | 0.025 | 0.009 | 0.990 | 0.036 | 0.035 |
| Minnaert c. | 0.027 | 0.025 | 0.030 | 0.028 | 0.007 | 0.988 | 0.039 | 0.038 |
| Knap a. | 0.047 | 0.043 | 0.053 | 0.039 | 0.040 | 0.984 | 0.061 | 0.046 |
| 1 pixel | 0.028 | 0.027 | 0.030 | 0.030 | 0.004 | 0.986 | 0.041 | 0.041 |
| 4 pixels | 0.028 | 0.026 | 0.031 | 0.031 | 0.005 | 0.986 | 0.042 | 0.041 |
| Dataset | MAE tot | MAE Antarctica | MAE Greenland | STD | BE | Cc | RMSE | BRRMSE |
|---|---|---|---|---|---|---|---|---|
| Proposed model | 0.021 | 0.020 | 0.023 | 0.015 | −0.005 | 0.995 | 0.026 | 0.025 |
| Ave. SZA c. | 0.024 | 0.022 | 0.027 | 0.017 | −0.006 | 0.994 | 0.030 | 0.029 |
| ERA5 | 0.021 | 0.021 | 0.022 | 0.016 | 0.001 | 0.995 | 0.026 | 0.026 |
| AOT -0.01 | 0.022 | 0.020 | 0.024 | 0.015 | −0.002 | 0.995 | 0.026 | 0.026 |
| AOT +0.01 | 0.023 | 0.021 | 0.025 | 0.015 | −0.007 | 0.995 | 0.027 | 0.027 |
| Cosine c. | 0.021 | 0.021 | 0.022 | 0.014 | 0.001 | 0.995 | 0.026 | 0.026 |
| Minnaert c. | 0.021 | 0.019 | 0.025 | 0.015 | −0.002 | 0.995 | 0.026 | 0.026 |
| Knap a. | 0.040 | 0.035 | 0.047 | 0.029 | 0.032 | 0.992 | 0.049 | 0.037 |
| 1 pixel | 0.022 | 0.021 | 0.024 | 0.017 | −0.006 | 0.994 | 0.028 | 0.027 |
| 4 pixels | 0.022 | 0.019 | 0.025 | 0.016 | −0.004 | 0.995 | 0.027 | 0.027 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Traversa, G.; Fugazza, D.; Senese, A.; Frezzotti, M. Landsat 8 OLI Broadband Albedo Validation in Antarctica and Greenland. Remote Sens. 2021, 13, 799. https://doi.org/10.3390/rs13040799
Traversa G, Fugazza D, Senese A, Frezzotti M. Landsat 8 OLI Broadband Albedo Validation in Antarctica and Greenland. Remote Sensing. 2021; 13(4):799. https://doi.org/10.3390/rs13040799
Chicago/Turabian StyleTraversa, Giacomo, Davide Fugazza, Antonella Senese, and Massimo Frezzotti. 2021. "Landsat 8 OLI Broadband Albedo Validation in Antarctica and Greenland" Remote Sensing 13, no. 4: 799. https://doi.org/10.3390/rs13040799
APA StyleTraversa, G., Fugazza, D., Senese, A., & Frezzotti, M. (2021). Landsat 8 OLI Broadband Albedo Validation in Antarctica and Greenland. Remote Sensing, 13(4), 799. https://doi.org/10.3390/rs13040799