Abstract
Radar penetration in brine-wetted snow-covered sea ice is almost nil, yet reports exist of a correlation between snow depth or ice thickness and SAR parameters. This article presents a description of snow depth and first-year sea ice thickness distributions in three fjords of the Hudson Strait and of their tenuous correlation with SAR backscattering in the C- and X-band. Snow depth and ice thickness were directly measured in three fjords of the Hudson Strait from 2015 to 2018 in April or May. Bayesian linear regression analysis was used to investigate their relationship with RADARSAT-2 (C-band) or TerraSAR-X (X-band). Polarimetric ratios and the Cloude–Pottier decomposition parameters were explored along with the HH, HV and VV bands. Linear correlations were generally no higher than 0.3 except for a special case in May 2018. The co-polarization ratio did not perform better than the backscattering coefficients.
1. Introduction
1.1. Context
Seasonal snow and ice covers in Nunavik are affected by the impacts of climate change: Kangiqsujuammiut (people of Kangiqsujuaq, Nunavik, in Canada) have reported later sea ice freeze-up in the fall [1], as well as less snow on the ground, earlier sea ice breakup in spring, changes in travel routes and more variable winds [2]. Inuit lives are embedded in the climate change context, and its impacts on sea ice have practical and immediate consequences on personal safety and access to travel and marine wildlife [3]. With shipping traffic in the Canadian Arctic having markedly increased over the last decade [4] and 2040–2064 climate projections for the region showing shorter snow cover periods [5], sea ice conditions and their impact on land-use and marine transport will continue to evolve. Yet, historically, the scientific community has undertaken monitoring efforts at scales too coarse to account for regional or local variations in ice conditions [3].
In this study, we investigate snow depth and ice thickness distributions in Salluit, Deception Bay, and Kangiqsujuaq, all Nunavik fjords of the Hudson Strait, as well as their correlation with C- and X-band SAR. This work is relevant due to land use and shipping-related operations by communities and industries in the area and for the sea ice remote sensing community. It is part of the Ice Monitoring project, a collaboration between the Kativik Regional Government, Raglan Mine (a Glencore company), the Northern Villages of Salluit and Kangiqsujuaq, and Institut national de la recherche scientifique (INRS). Both communities’ Land Holding Corporations gave their approval for this project. The Avataq Cultural Institute was consulted to ensure the project did not encroach on archaeological sites important to Inuit.
1.2. Local Snow Depth and Sea Ice Thickness Monitoring in Nunavik and Nunavut
Using direct measurements, Iacozza and Barber [6] observed that the distribution of snow depth on smooth first-year sea ice is governed by snowfall and drifting events. In Nunavik, Tremblay et al. [7] have characterized snow depth and ice thicknesses on local trails near Kangiqsujuaq, Umiujaq, Kangiqsualujjuaq and Kawawachikamach, in the context of increased travel risk due to ice instability and weather unpredictability. Their community-based participatory study revealed that some ice trail areas remained dangerous even 5 weeks after freeze-up and when average ice thickness was roughly 50 cm. Similarly, snow depth and ice thickness were monitored as part of a community-based observation network in Barrow, Alaska, Clyde River, Nunavut, and Qaanaaq, Greenland [8]. Their comparison revealed thinner ice in Qannaaq than in the other sites, despite thinner snow which should promote ice growth. This was attributed to warm Atlantic water encroachment in the area progressing farther inland than in the past. More recently, the SmartICE program developed a sled-mounted electromagnetic induction sensor to document ice thickness along travel routes in Nunavut communities [9,10]. They support public safety through near-real-time data generation and dissemination.
1.3. Relationship with C- and X-Band Backscattering
SAR sensors are widely used for sea ice monitoring, both by governments and in scientific communities, due to their ability to operate in the presence of clouds and at night-time [11]. Current applications of this technology include characterizing melt pond fraction [12,13] and community-relevant sea ice features [10,14], as well as estimating ice stability [15]. Recent work by Yackel et al. [16] showed that, prior to melting onset, the daily variance in C- and Ku-band backscattering is correlated with relative snow thickness. While the majority of these sea ice applications rely on the C-band [11], other SAR frequencies like the Ku-, X-, and L-bands have also been investigated [17,18,19,20]. The X-band can adequately discriminate between newly formed ice and its surroundings [17] and is more sensitive to melt onset and surface roughness than the C-band [21], as well as changes in top-layer snow salinity [19].
This article and the references cited hereafter focus on undeformed first-year sea ice in cold conditions with air temperatures below the freezing degree point. We explore the VV, HV and VV polarizations as well as polarimetric ratios and the Cloude–Pottier decomposition parameters [22]. Nandan et al. [23] have recently demonstrated the extent to which SAR penetration in the snow covering first-year sea ice is limited by brine. They reported a maximum penetration of four cm into the brine-wetted snow for the C- and X-bands, near Resolute Bay in Nunavut. How can these results be reconciled with several observations of a correlation between undeformed sea ice thickness or snow depth and SAR parameters? Indeed, linear correlation coefficients of 0.4 to 0.6 were reported between ice thicknesses ranging from 15 to 150 cm and the HH or VV backscattering coefficients in the X-, C- or L-band over undeformed first-year drift ice in the Sea of Okhotsk [24,25]. In these cases, the co-polarization ratio (VV/HH) performed better than the individual polarizations, reaching an r-squared of 0.8 for the C-band [25]. A strong exponential relationship was observed between ice thickness ranging from 0 to 200 cm and the C-band CP ratio for drift and landfast undeformed first-year ice in the Labrador Sea, based on simulated compact polarimetry data [26]. This ice thickness estimation parameter is based on circular right-hand transmission and linear HH and VV detection, i.e., the compact polarimetry mode developped for the RADARSAT Constellation Mission [26].
As for snow covers on smooth landfast first-year ice, Gill et al. [27] noted that a positive correlation between C-band HH backscattering and snow depth is best observed in cold (−7.9 C) than warm conditions (−0.4 C). The associated r-squared values ranged from 0.3 to 0.8 for incidence angles of 27 to 36, with measurements performed in Franklin Bay, Northwest Territories. In contrast, Nandan et al. [19] rather observed that the HH backscattering was greater from a thin snow cover of 4 cm than from snow 8 or 14 cm deep, which they attributed to steeper salinity gradients in thin snow causing enhanced surface scattering. In this study of sea ice near Resolute Bay, Nunavut, they also noted that the HH polarization was more sensitive to snow depth variations than its VV counterpart.
1.4. Objectives
This article combines field measurements and remote sensing data in order to characterize seasonal snow-covered sea ice from 2015 to 2018 in three Nunavik fjords of the Hudson Strait. The objectives of this article are to (1) characterize and explain snow depth and ice thickness distributions in Salluit, Deception Bay, and Kangiqsujuaq over three winters (2015–2018) and (2) investigate the empirical relationship between C- and X-band polarimetric SAR parameters and snow depth and ice thickness.
2. Materials and Methods
2.1. Study Areas
The study sites are three neighbouring fjords located along the coast of Nunavik in the Hudson Strait (Figure 1). Two of them are home to Inuit communities: Salluit and Kangiqsujuaq. The third, Deception Bay, is located between the two communities, 50 km west of Salluit. Two mining companies have the marine infrastructure in Deception Bay, where their icebreakers transit year-round except from the mid-March to 1 June black-out window [28].
Figure 1.
Map of Nunavik in Inuit Nunangat. Inset: Salluit, Deception Bay and Kangiqsujuaq.
Freeze-up occurs in November or December and breakup in June or July [1,29,30,31]; freeze-up generally proceeds through consolidation of young ice types. During the ice season, the study areas are covered in undeformed and smooth landfast first-year sea ice, except along the broken ice track left by ice-breaking transport in Deception Bay and near the shores where the tides lead to deformation. These features were excluded from the study. There is typically some small-scale surface roughness, on the order of the radar wavelength. Some areas may also sometimes feature either radar-smooth ice, or ice pieces sticking out of the ice by up to 15 cm. Monthly total precipitation data from Salluit airport is presented in the supplementary materials (Figure S1). No weather station was operating in Deception Bay during the study and no precipitation data was available from the Kangiqsujuaq airport weather station. The bathymetry maps (Figure S2 in the supplementary) show maximum water depths greater than 100 m in Salluit, 80 m in Deception Bay, and 200 m in Kangiqsujuaq. The difference between high and low tide ranges from 1.5 to 5 m in Salluit, from 2 to 5.5 m in Deception Bay, and from 4 to 8.5 m in Kangiqsujuaq [32]. In Deception Bay, GENIVAR [28] measured water salinity between 29 and 33 ppt. Top-layer ice salinity measured in January 2018 ranged from 5 to 10 psu [29]. Brine-wetted snow salinity near the ice surface ranged from 23 to 33 psu in January 2018 [29] and from 7 to 19 psu in May 2018.
2.2. Snow Depth and Sea Ice Thickness Measurements
Measurements were performed in January–February and April–May of 2016, 2017 and 2018, for each site, except for April 2016 where bad weather prevailed in Salluit (Table 1). Snow depth was measured using a meter-rule and ice thickness using a 2.5 cm diameter Kovacs ice auger and measuring tape. For a given site, sampling was done at 20 to 30 target locations arranged in a grid-like pattern with 1 to 2 km spacing (Figure 2) and within 48 h or less except for Kangiqsujuaq in May 2018. This article focuses on the end-of-winter April–May data.

Table 1.
Fieldwork measurement campaign dates.
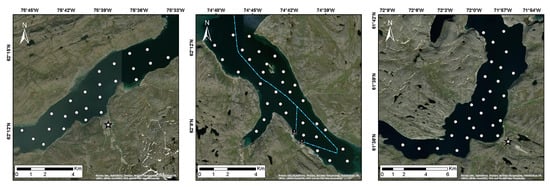
Figure 2.
January 2018 sampling locations for Salluit, Deception Bay, and Kangiqsujuaq. Also shown for Deception Bay: The ship track (blue) and wharves (anchor markers). For Salluit and Kangiqsujuaq, community location is indicated with a white star.
Table 2 and Table 3 show mean snow depth and ice thickness for January–February and April–May measurements, respectively. Kangiqsujuaq always presented the deepest snow and thinnest ice (except in January 2017). Snow was deeper in January 2016 than in 2018 (Table 2), despite earlier measurements by one week (Table 1). Ice thickness at the end of the winter (Table 3) was greater in 2016 than in the other two years for both Deception Bay and Kangiqsujuaq; no data are available for Salluit in April–May 2016. Deception Bay presented its thinnest ice cover in 2017, whereas both 2017 and 2018 were similar for Salluit and Kangiqsujuaq.

Table 2.
Mean January–February snow depth and ice thickness with standard deviations in parentheses.

Table 3.
Mean April–May snow depth and ice thickness with standard deviations in parentheses.
Note that even in 2016 with an average thickness of 1.43 m, the ice in Deception Bay fell short of the historical range. Indeed, the most recent measurements, probably dating back to 1991, gave a thickness of 1.7 to 2 m [33]. In contrast, thicknesses measured from 2015 to 2018 ranged from 1.10 to 1.65 for extreme values and 1.20 to 1.43 on average. The ice in Deception Bay was therefore generally 50 cm thinner during our study than 25 years prior. Although historical data for the other two sites was not available, reports from 2007 by local experts stated that the ice was forming later and growing thicker more slowly than before in Salluit and Deception Bay [33].
2.3. Satellite SAR Data
2.3.1. RADARSAT-2
The Canadian Ice Service secured RADARSAT-2 Wide-Fine Quad-Pol single look complex images for each site from 2015 to 2018 (Table 4). The C-band satellite operates at 5.405 GHz (5.55 cm wavelength), with a repeat period of 24 days. The acquisitions were performed in the descending orbit at roughly 6:30 local time (UTC-5 h). Six images were acquired per winter except in 2016, where a Deception Bay acquisition was cancelled. Scene size was 50 by 25 km before subsetting, with a spatial resolution of 5.2 and 7.6 m (range and azimuth, respectively) [34]. Air temperature at the time of acquisition was always below −10 C except for Kangiqsujuaq in May 2018 where it was −3 C (see Tables S1 and S2 in the supplementary). The noise-equivalent value in the Wide-Fine Quad-Pol mode is −33 ± 6 dB [34].

Table 4.
RADARSAT-2 acquisition parameters. Local time (LT) is UTC-5 hours.
The RADARSAT-2 images were processed with SNAP’s Sentinel-1 Toolbox (version 6.0.0), a European Space Agency (ESA) open-access software. The toolbox was used through java-snap, a Java application made available on Gitlab [35]. After subsetting to the study areas, the data was converted from digital number to backscattering coefficient [36]. Speckle filtering was performed over a 7 × 7 window using the Refined Lee or Polarimetric Refined Lee filter depending on the desired output (backscattering coefficient or covariance matrix). Lee filters preserve image details and contours [37]. This processing follows the ESA Polarimetric Tutorial [38], in which no multilooking is performed.
We computed the Cloude–Pottier decomposition to extract the entropy (H), anisotropy (A) and alpha angle (alpha) [22,39]. Data position in the H-alpha plane provides information on the nature of dominant scattering mechanisms, for instance, surface or volume scattering [39]. The geometric correction was then performed using the Range-Doppler Terrain Correction algorithm using the freely accessible Canadian Digital Elevation Model [40] and nearest neighbour resampling for both the image and the DEM. Pixel spacing after this step was 8 m. The images did not present a large enough homogeneous area to estimate the equivalent number of looks after processing using the procedure outlined by Anfinsen et al. [41]. After geometric correction, linear was converted to decibels. The co-polarization VV/HH and the cross-polarization VH/VV and HV/HH ratios were computed from linear .
2.3.2. TerraSAR-X
The DLR secured TerraSAR-X or TanDEM-X acquisitions of StripMap dual-pol single look complex images over Deception Bay from 2015 to 2018. Acquired in ascending orbit 13 at 17:30 local time (UTC-5 h) with polarizations HH and VV, the images have an incidence angle of 38. A total of 75 images were acquired between 2015-12-23 and 2018-07-26. The X-band satellites operate at 9.65 GHz (3.11 cm wavelength) with a repeat period of 11 days. Images were acquired in a dual-pol orbit with polarizations HH and VV. The scene size before subsetting to the study area was 15 by 50 km, with a spatial resolution of 0.9 and 2.5 m for range and azimuth, respectively [42]. Air temperature at the time of acquisition was always below −10 C (see Table S2 in the supplementary). The noise-equivalent value in the StripMap mode for orbit 13 is −24.5 dB [42].
The DLR data was processed by using their in-house Multi-SAR System [43]. This processing includes converting from digital number to backscattering coefficient, multi-looking to produce square pixels and increase radiometric quality, geometric correction using bilinear interpolation for the DEM and cubic convolution resampling for the image, and image enhancement to reduce speckle [44]. The output images have a pixel spacing of 2.5 m pixels with a radiometric resolution of 1.6 looks. Linear was converted to decibels.
2.3.3. Computing SAR Parameter Seasonal Medians
Seasonal medians were computed from the satellite images acquired in each season. Areas of interest (AOIs) roughly 120 by 100 m and each containing between 600 and 650 pixels were distributed over the homogeneous study areas in a grid-like pattern with 0.7 to 1 km separation, avoiding special features like the shore or a ship’s track. The Salluit, Deception Bay, and Kangiqsujuaq study areas counted 35, 43, and 78 AOIs, respectively. Median backscattering was computed over each AOI and then over all AOIs for a given image, yielding a single median value per image. Only images between January and May were used to avoid the freeze-up and spring transitions. The seasonal medians were computed from the resulting time-series to yield a single value per year, allowing interannual comparisons between sites. This step was performed using Python [45]. For the comparison with the X-band, this step was also performed on the processed TerraSAR-X images as described in Dufour-Beauséjour et al [31]; 32 of the 43 AOIs were covered by the TerraSAR-X images, with a higher spatial resolution.
2.3.4. Extracting SAR Parameter Values Coincident with Thickness Measurements
For every field campaign except those in January 2016, thickness measurements were paired with the image acquired in closest temporal proximity. The relative timing of fieldwork and image acquisitions is presented in the supplementary materials (Tables S1 and S2). We used Python to identify pixels coinciding with sampling locations and to extract the backscattering coefficient value over that location [46]. To mitigate speckle noise, a 3 × 3 pixel window average was used for the RADARSAT-2 images, corresponding to an area size of 576 m. For the comparison between the C-band and the X-band, mean TerraSAR-X values were extracted over a 9 × 9 pixel window, which corresponds to 506 m. The co-polarized SAR backscattering values were well above the noise-equivalent for each sensor. Linear correlation coefficients were computed between thickness variables and all available SAR parameters. Because the Bayesian linear regression is a relatively new method in our field, we chose to apply it to a single parameter. The HH backscattering coefficient was chosen because it is commonly used in sea ice applications, was available for both radar frequencies, and was not systematically outperformed by another parameter in terms of the linear correlation coefficient (see Table S3 in the supplementary).
2.4. Statistical Tools
2.4.1. Bayesian Framework
We used Bayesian linear regression to investigate a potential linear relationship between snow depth or ice thickness and C- or X-band SAR. The advantage of the Bayesian framework, compared to the frenquentist approach (e.g., Pearson’s correlation coefficient) is that it provides a quantitative evaluation of the evidence against the null hypothesis [47]. It also relies on a direct pairwise comparison between hypotheses based on a probability ratio, a quantity which is easy to interpret. Bayesian statistics are susceptible to the same caveats as the frequentist approach in cases of spatial autocorrelation: an illusion of more independent data points than there really are, which may for instance exaggerate the relationship between two variables if their spatial structures are aligned [48]. In a Bayesian analysis, different hypotheses are compared to identify which is most likely, and what values its parameters are most probable to take on. Bayesian linear regression is performed in two steps: model fitting and model comparison.
For a given hypothesis H, Bayes’ theorem states:
where
= the probability H given the data (D), i.e., the posterior probability of the model;
= the probability of the data (D) given H, i.e., the likelihood;
= the probability of H, i.e., the prior probability of the model;
= the probability of the data (D), i.e., the evidence.
2.4.2. Model Fitting: Bayesian Linear Regression
During model fitting, Bayes’ theorem is used to infer the probability distribution of a given model’s parameters based on the observed data (D). This is done for each hypothesis being considered. Equation (2) presents a linear model for a hypothesis H denoted as , where the model parameters are coefficients and standard deviation . It is given here for the ith sample of a dataset. The noise term in Equation (2) comes from a Gaussian probability distribution centered on zero with parameter as a standard deviation, i.e., , as shown in Equation (3). It is assumed to hold all of the measured data’s variability.
where
= the variable being modeled,
= a vector representation of the model variables,
= a vector representation of the coefficients,
= a noise term depending on model parameter ,
and
where
= a model parameter.
Rearranging Equation (2) to express the noise term as the difference between observations and model results , we have:
Assuming measurements are independent, the probability of observing the data given model (i.e., the likelihood for a particular set of parameter values) can be developped as a product of the individual probabilities for each of the N samples in the dataset:
, which is the quantity needed for model comparison, can now be computed by combining Equations (5) and (6):
Equation (7) is computed over a range of discrete values for all model parameters. The resulting probability distribution includes , the maximum probability in the distribution when all coefficients are zero, i.e., the null hypothesis , and , the maximum probability that can be found within the parameter space, i.e., the non trivial hypothesis . Other hypotheses can be constructed from the linear model by setting only some of the coefficients to zero. The parameter space should accomodate the full distribution of each parameter’s marginal probability, i.e., , , etc. Examples for our model are shown in the supplementary (Figure S7). The source code for our analysis is available on GitHub [49].
2.4.3. Model Comparison: Bayes Factor
Models are compared based on their probability given the data, i.e., . Although these probabilities cannot be computed directly, their pairwise ratio can be estimated based on each model’s posterior probability . In the absence of a priori information on which values the model parameters will take, we assume a uniform prior probability for every possible set of parameter values. The therefore cancel out, as well as the evidence which is the same regardless of the hypothesis. This pairwise ratio is called the Bayes factor K; it quantifies the evidence in favor of one of the hypotheses. Considering two hypotheses, e.g., a non trivial hypothesis and the null and using Equation (1), the Bayes factor is therefore:
If , the data offers no evidence against . A value of is deemed sufficient to give substantial evidence against , while and respectively denote strong and decisive evidence [50]. We used the Bayes factor to compare a linear-dependence hypothesis with a null hypothesis , where the parameter associated with the linear dependency is set to zero. We computed the Bayes factor using each hypothesis’ maximum posterior probability:
2.4.4. Application to Snow Depth, Ice Thickness and SAR
We explored the dependence of the C- and X-band SAR HH log-scale backscattering coefficient on snow depth and ice thickness by assuming a linear relationship with either snow depth via parameter (), ice thickness via parameter (), or with both snow depth and ice thickness (). Our approach to investigating the linear correlation between variables under a Bayesian framework is similar to the one proposed by Wetzels and Wagenmakers [47]. From previous studies, we expect and . The dual-linear-dependence hypothesis is therefore a function of an offset parameter , linear terms and , and a noise parameter , as shown in Equation (10). The null hypothesis is Equation (10) with both the and parameters set to zero; the snow-only hypothesis is the same equation with only set to zero; the ice-only hypothesis is Equation (10) with only set to zero. The most likely hypothesis out of the four (, , , ) is the one which surpasses all the others based on the pairwise Bayes factor K. Mean and standard deviations for the marginal probability distributions of each model parameter are presented in the supplementary (Figures S10 to S13).
where
= backscattering coefficient,
= offset,
= snow slope,
= snow depth,
= ice slope,
= ice thickness,
= backscattering coefficient variability.
2.4.5. Geary’s C for Spatial Autocorrelation
We used Geary’s C to investigate the presence of autocorrelation in our snow depth and ice thickness measurements. Real environments are structured by physical processes, such as currents and winds, which create gradients and patches [51]. In a variable such as snow depth or ice thickness, these features manifest as spatial autocorrelation - nearby measurements take values that are most or less similar than expected for a randomly assigned pair. This dependence violates the independence assumption central to many statistical tests such as Pearson’s correlation coefficient. Autocorrelation will generally exaggerate the significance of such a test, for instance lowering its p-value [52]. Geary’s C is a statistic developed to quantify spatial autocorrelation and for which a p-value may be evaluated for significance. Positive autocorrelation translates to a C value between 0 and 1, and negative autocorrelation produces values greater than 1; the no-correlation value is C = 1 [51].
3. Results
Here we present spatial distributions for snow depth and ice thickness measurements and an estimation of their spatial autocorrelation using Geary’s C and seasonal median values for polarimetric parameters H- and the HH backscattering coefficient, for all cases in the study. We then present the linear correlation coefficients between these variables and the results of the Bayesian linear regression analysis.
3.1. Snow Depth and Ice Thickness Spatial Distributions
Figure 3 highlights the spatial distribution of snow depth by showing end-of-winter standardized thickness measurements, color-coded according to their deviation from the mean, and the associated Geary’s C value when its p-value was above 0.05. These results serve to evaluate the reliability of the statistical analyses presented in Section 3.3. In Salluit, snow accumulation is concentrated in the center of the study area in 2017, with a C value of 0.1 indicating strong positive autocorrelation, while being rather heterogeneous in 2018. In Deception Bay, the 2016 distribution is also heterogeneous. In 2017, snow accumulated to the north-west of the study area, around Moosehead Island, as reflected by a C value of 0.2. In 2018, accumulation appears to follow a gradient aligned to the north-east, with the deepest snow along the north-eastern shore and in front of the fjord’s transverse arm. In Kangiqsujuaq, snow depth seems to increase along a south-east gradient for the three years, with higher accumulation in front of the community and along the south-eastern shore. When tested using the Shapiro–Wilk test, snow depth measurements rejected the normality hypothesis for three cases: Salluit in 2017 and Deception Bay in 2017 and 2018 (see Figure S3 in the supplementary materials).
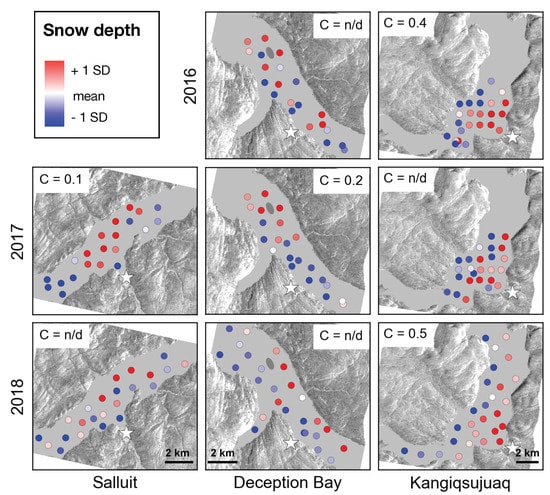
Figure 3.
Standardized end-of-winter snow depth for Salluit (left), Deception Bay (center), and Kangiqsujuaq (right), for 2016 (top), 2017 (middle) and 2018 (bottom). Markers are color-coded according to the measurement’s deviation from their dataset’s mean: thinner than the mean by one standard deviation (SD) or more (blue), equal to the mean depth (white) or greater than the mean by one standard deviation or more (red). Geary’s C is annotated in each case, with either the statistic’s value or n/d if its p-value was above 0.05. In the background for terrain are 2015 RADARSAT-2 HH images from December 19, 26, and 23, respectively, with the sea ice masked out in gray. White stars indicate Salluit, wharves in Deception Bay, and Kangiqsujuaq. Moosehead Island is marked by a gray ellipse.
Figure 4 shows the spatial distribution of ice thickness for the same cases. Geary’s C could not be reliably determined for any of the cases. Notable spatial structures in Salluit include thicker ice to the south-west of the study area both in 2017 and 2018. In Deception Bay, the ice was generally thicker along the south-western shore for all years, and thinner around Moosehead Island in 2017. In Kangiqsujuaq, features vary from year to year: thinner ice along the fjord’s deepest area in 2016, a south-eastern gradient in 2017, and thicker ice in the north of the broader 2018 study area. When tested using the Shapiro–Wilk test, ice thickness measurements rejected the normality hypothesis for two cases, namely Deception Bay in 2017 and 2018 (see Figure S3 in the supplementary materials).
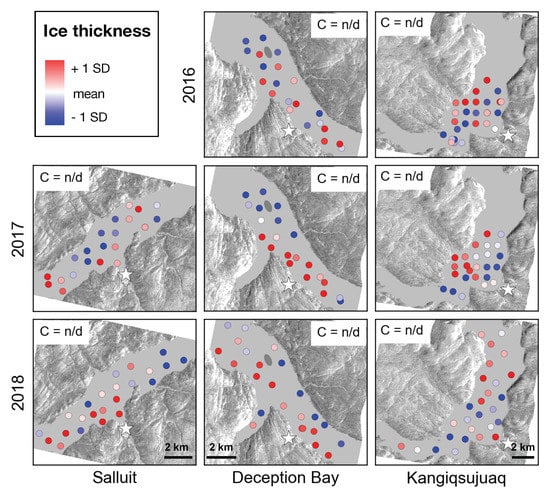
Figure 4.
Same as Figure 3 but for ice thickness.
3.2. C- and X-Band SAR Seasonal Medians
Figure 5 shows seasonal median entropy (H) and alpha angle in the C-band, as well as HH backscattering coefficients in the C-band and the X-band when available, for each site and each season. All cases fall in the region of the H-alpha plane associated with surface scattering, i.e., alpha [39]. For Salluit, 2015–2016 stands out with a higher alpha angle than the other seasons, suggesting a bigger volume contribution, and a lower C-band HH backscattering of −21 dB. Of all the sites and cases put together, Deception Bay 2015–2016 is the closest to the region of volume scattering. Its C-band backscattering is also the lowest with −25 dB compared to −17 dB in the next two years. In the X-band, the backscattering is also lowest that year with −20 dB. The difference in backscattering intensity between the C- and X-band is −5 dB for 2015–2016, zero in 2016–2017, and −1 dB in 2017–2018. For Kangiqsujuaq, the alpha angle was generally higher than for the other sites except in 2015–2016, where it was surpassed by the remarkably high alpha angle for Deception Bay.
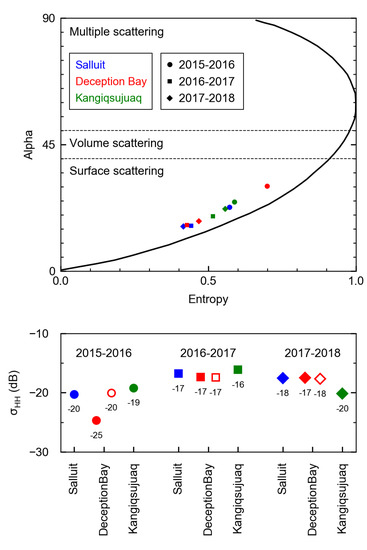
Figure 5.
Seasonal median SAR parameters for Salluit, Deception Bay, and Kangiqsujuaq in 2015–2016, 2016–2017, and 2017–2018. Top: Alpha angle versus entropy in the C-band, plotted in the Cloude–Pottier H-alpha plane [39]. Bottom: HH backscattering coefficients in the C-band (full markers) and X-band (empty markers).
3.3. Relationship between SAR and End-of-Winter Snow Depth or Ice Thickness
The linear correlation coefficient (r-squared) between the C-band HH backscattering coefficient and either snow depth or ice thickness at the end of the winter is between zero and 0.1 for all cases in Salluit. In Deception Bay, it ranged from zero to 0.3 for the C-band and zero to 0.6 for the X-band, and was always zero in Kangiqsujuaq (Figure S4–S6 in the supplementary materials). We also investigated the following parameters: VV and HV backscattering coefficients, the VV/HH co-polarization ratio, the HV/HH and VH/VV cross-polarization ratios, and the entropy, anisotropy and alpha angle. They did not perform systematically better than the HH band as shown in the supplementary materials (Tables S3 and S4), despite the VV band sometimes having an r-squared 0.1 higher than the HH band or the alpha angle have a linear correlation coefficient of 0.5 with both snow depth and ice thickness in Deception Bay 2017.
Figure 6 shows the most likely hypothesis from the Bayesian linear regression analysis of the relationship between the C- or X-band HH backscattering coefficient and either snow depth, ice thickness, or both. The associated pairise Bayes factor K is shown in the supplementary materials (Figures S8 and S9). In the Salluit cases, the most likely hypotheses for 2017 and 2018 were the null and a negative relationship between C-band backscattering and snow depth, respectively. In Deception Bay, the most likely hypothesis for the C-band in 2016 was a negative relationship with ice thickness, while the null was most likely for the X-band. In 2017, it was a negative relationship with snow depth for both the C- and X-band. In 2018, the most likely relationship was a positive one with ice thickness for both bands. In Kangiqsujuaq, no hypothesis was more likely than the null for the three C-band cases.
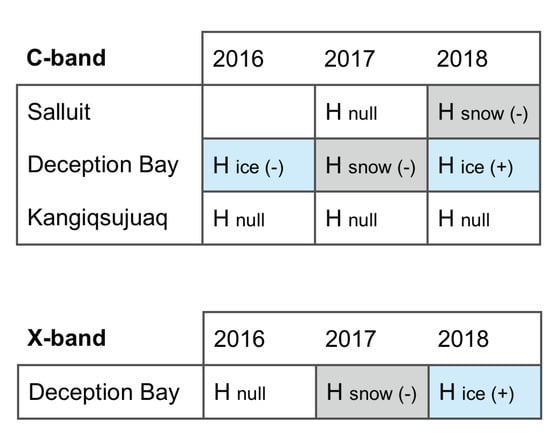
Figure 6.
Most likely hypothesis in the Bayesian linear regression analysis for HH backscattering vs snow depth and ice thickness, out of the null (, in white), snow (, in gray), and ice (, in blue). The sign of the linear relationship is identified with a plus or minus sign.
4. Discussion
In this section, we discuss the spatial distribution of environmental variables ice thickness and snow depth, the relationship between C- or X-band backscattering and either variable, the interpretation of Bayesian linear regression results and perspectives for future work.
4.1. Spatial Structure in Environmental Variables
Here we investigate spatial structure in snow depth and ice thickness, in part because of its possible impact on our correlation analysis. Consider similar spatial structures in two environmental variables A and B (e.g., ice thickness and ice surface roughness), caused either by chance or by a physical process which affects both of them. An observed correlation between variable A and a third variable C (e.g., SAR backscattering) could be the accidental byproduct of a correlation between variables B and C, mirrored onto variable A because of its spatial structure’s alignment with that of variable B.
4.1.1. Snow Depth Distribution
According to Geary’s C, snow depth presented spatial autocorrelation in half of the cases, while the test was inconclusive for the other half (Figure 3). A total of 30 measurement points was sometimes insufficient to get a conclusive statistic. This precluded the use of more advanced spatial structure analysis tools such as correlograms. We therefore conservatively assume all cases presented spatial autocorrelation.
Wind action is known to cause preferential snow accumulation patterns, such as in Van Mijenfjorden, a Norwegian fjord of the Svalbard archipelago [53]. The heterogeneous snow depth distribution observed in Salluit in 2018 (Figure 3) suggests along-fjord winds might have transported snow in and out of the study area. Spatial structure would then be caused by another factor than wind alone, such as ice surface roughness [6]. By contrast, in 2017 the snow accumulated in the middle of the Salluit study area. Because the C-band backscattering was similar in both seasons, suggesting comparable ice roughness, we speculate that dominant winds were oriented parallel to the fjord length during depositional or drifting events in 2017. There are no recent wind data available for Salluit; 2001 data [54] give northern and north-eastern winds as dominant. Since Inuit have reported more variable winds [2], readers should be aware that the situation might have changed in 20 years.
In Deception Bay, we suggest that heterogeneous snow depth in 2016 (Figure 3) might be associated with the remarkable smoothness of the ice that year, as illustrated by a C-band HH backscattering coefficient of −25 dB (Figure 5) and documented in a previous study [31]. Snow accumulation around Moosehead Island in 2017 suggests a predominance of the along-fjord dominant winds, both north-western and south-eastern). In contrast, greater snow depth along the north-eastern shore and at the outset of the fjord’s transverse valley in 2018 is rather consistent with the effect of across-fjord dominant winds. Indeed, transverse winds may be funnelled by valleys leading into the fjord [55]. We do not have up-to-date information on dominant winds in Deception Bay; the most recent observations date back to 1963–1973, more than 40 years ago [28]. In Kangiqsujuaq, snow depth consistently exhibited a south-eastern gradient (Figure 3). This is consistent with across-fjord dominant winds reported by NAV Canada in 2001 [54].
4.1.2. Ice Thickness Distribution
None of the cases included enough data to quantify spatial autocorrelation in ice thickness using Geary’s C. Yet, visual interpretation of the ice thickness distributions (Figure 4) shows that the ice was generally thicker towards the south-western end of the study area in Salluit, where the water is more shallow. The ice was also thicker along the south-western shore in Deception Bay, where the snow is usually thin. In 2017 and 2018, ice thickness patterns in Deception Bay seemed to mirror those in snow depth, with thicker snow leading to thin ice and vice versa, similarly to observations made in Van Mijenfjorden (Svalbard, Norway) [53]. In Kangiqsujuaq, the ice in 2015 was thinner along the middle of the fjord’s length, i.e., in the deepest part. It was thicker in the northern part of the broader study area in 2018, despite deep waters. We speculate that ice formation is more dynamic near the Hudson Strait and potentially included greater ice rafting and other accumulation processes. Near Pangnirtung in Nunavut, fjord outlets are known to present strong currents, even preventing solid ice formation [56].
4.2. Ice Thickness vs. C- or X-Band Backscattering
4.2.1. Case A: Thin Snow Cover
Deception Bay 2018 is one of only two cases where the ice thickness hypothesis was most likely to explain C- or X-band HH backscattering, here through a positive relationship (Figure 6). It also presented the strongest Bayes factor supporting a non trivial hypothesis and a linear correlation coefficient of 0.6 between ice thickness and the X-band (Figures S5, S8 and S9 and in the Supplementary Materials). This case is similar to other Salluit and Deception Bay cases in 2017 and 2018 in that it featured smaller alpha angles and higher backscattering (Figure 5) than the smooth ice 2016 case in Deception Bay. Both indicators suggest surface scattering, which we attribute to slightly rougher ice due to freeze-up from nilas patches in dynamic conditions, as confirmed for one of the sites in a previous study [31]. It stands out from the other slightly rough ice cases with its thinner snow cover of eight cm on average (Table 3).
We speculate that in this case, (i) the brine-wetted snow was not thick enough to prevent the radar from reaching the ice surface, (ii) small-scale surface roughness allowed the surface scattering from the ice to make its way back to the radar, (iii) the dominant backscattering mechanism was surface scattering on saline ice and iv) the top-layer salinity, surface roughness or both were positively correlated with ice thickness which led to a positive correlation between the latter and HH backscattering. The Bayes factor associated with this correlation might also have been inflated by spatial autocorrelation, which we cannot rule out due to an inconclusive Geary’s C (Figure 3 and Figure 4). Note that the Deception Bay 2017 case also presented opposite snow depth and ice thickness gradients (Figure 3 and Figure 4) but with thicker snow of 15 cm on average, and no correlation between backscattering and ice thickness was detected in that case. Our results for this thin snow case are similar to those of Nakamura et al. [24,25] in that we observed a positive correlation.
4.2.2. Case B: Thick Snow Cover
The three end-of-winter cases from Kangiqsujuaq stand out by their total lack of correlation between either snow depth or ice thickness and the HH backscattering coefficient (Figure S6 in the supplementary materials). Similarly, none of the tested hypotheses was more likely than the null in the Bayesian linear regression analysis (Figure 6). We attribute this behavior to the deeper snow found in Kangiqsujuaq compared to the other two sites: 22 to 25 cm on average during the study (Table 3). We speculate that in this case (i) the brine-wetted snow was too thick to allow the radar signal to reach the ice surface, (ii) the dominant backscattering mechanism was surface scattering on the interface between dry snow and brine-wetted snow.
4.2.3. Case C: Very Smooth Ice
Deception Bay 2016 is the second of only two cases where the ice thickness hypothesis was most likely in the Bayesian analysis, and only for the C-band (Figure 6). The relationship is negative, contrary to case A for a thin snow cover. This case stands out due to a lower backscattering coefficient and a higher alpha angle than all others (Figure 5). The ice cover was particularly smooth ice due to a thermal freeze-up [31] and its alpha angle (Figure 5) indicates that volume scattering played a more prominent role that year for the C-band than in the other cases [39]. We made the same conclusion for the X-band data in a previous publication [31]. Our observed difference of 5 dB between the two bands (Figure 5) is identical to reports by Nandan et al. in a similar case where volume scattering was deemed to be important [23].
In the C-band, the hypothesis for a negative linear relationship with ice thickness was most likely (Figure 6). In the X-band, however, the null was most likely and the linear correlation coefficient between snow depth or ice thickness and either frequency’s HH backscattering coefficient was zero (Figure S4 in the supplementary materials). The relationship is therefore almost imperceptible and in the opposite direction than in case A for a thin snow cover over slightly rougher ice. We speculate that (i) the brine-wetted snow was not thick enough to prevent the radar from reaching the ice surface, (ii) small-scale surface roughness was too small for the surface scattering from the ice to make its way back to the radar. Note that what little relationship there is between ice thickness and backscattering is negative in this case, which differs from previous reports [24,25].
4.2.4. Relationship with Other SAR Parameters
The C-band co-polarization and cross-polarization ratios did not perform significantly better than the HH band. The strongest linear correlation coefficient we observed was 0.3 between the cross-polarization ratios and the ice thickness in the Salluit 2017 and 2018 cases (Table S3 in the supplementary materials). This is different from results by Nakamura et al. at a comparable incidence angle of 37 [57]. They reported an improved correlation with ice thicknesses up to 120 cm for the co-polarization ratio (r-squared ) compared to the correlation with the HH and VV backscattering coefficients themselves (r-squared and 0.3). The authors attribute this to ratio sensitivity to the dielectric constant of the top-layer ice [24], i.e., its brine content, and cancelling out of the small-scale surface roughness effect. The fact that the co-polarization ratio hides what little correlation there was between ice thickness and C-band SAR in Deception Bay 2018, with an r-squared of 0.0 compared to 0.3 (Table S3 in the supplementary), suggests that surface roughness was responsible for at least part of the observed correlation.
4.3. Snow Depth vs. C- or X-Band Backscattering
There are only two cases where the snow thickness hypothesis was most likely to explain the HH backscattering, both for the C- and X-band: Deception Bay in 2017 and Salluit in 2018 (Figure 6). However, the associated linear correlation coefficients are very low, either 0.1 or 0.2 depending on the frequency (Figures S4 and S5 in the supplementary materials). These cases are similar to a third, Salluit 2017, in terms of average snow thickness (Table 3), position in the H-alpha plane and median HH C-band backscattering (Figure 5), and near-zero linear correlation coefficient between the two variables (Figure S4 in the supplementary materials). We were therefore unable to reproduce observations by Gill et al. [27] of a moderate positive correlation (r-squared ) between snow depths ranging from 5 to 35 cm and C-band HH backscattering at comparable incidence angles of 32 to 36.
4.4. Interpreting Results from a Bayesian Linear Regression
Despite very low linear correlation coefficients of zero to 0.3 between either thickness variable and the C-band HH backscattering coefficient (Figures S4 to S6 in the supplementary materials), the Bayesian linear regression analysis gave a non trivial hypothesis as more likely than the null for half of the eight cases (Figure 6). While these four cases all presented at least substantial evidence [50] against the null hypothesis (), the evidence in the Deception Bay 2018 case was decisive () both with the C- and X-band (Figures S8 and S9 in the supplementary materials). In that case, the linear correlation coefficients with ice thickness were 0.3 and 0.6 (Figure S4 in the supplementary materials). This illustrates the need to contextualize results from a Bayesian model comparison analysis with a familiar indicator such as Pearson’s linear correlation coefficient. The apparent disparity between the Bayesian and frequentist approaches, for example in case A, can be traced back to the fact that the Bayesian linear regression model evaluates the probability that a linear relationship exists considering the data provided. In contrast, the linear correlation coefficient provides a quantitative assessment of the degree to which the variables are correlated. The Bayesian hypothesis testing allowed us to identify the cases where the null hypothesis was more likely than a linear relationship with either thickness variable. For the other cases, we used it to identify which variable carried the most information about the backscattering coefficient.
4.5. Perspective for Future Work
Further work is needed to elucidate which of small-scale surface roughness or top-layer ice salinity is correlated with ice thickness in such a case. The freeze-up process and resulting small-scale roughness at each measurement location would be useful information for such a study, and processes such as the impact of snow redistribution on snow and ice salinity profiles should be taken into account. Surface desalination from snow redistribution might be different according to ice roughness and sheltering of the study area, and may differ between landfast and drift ice. Additionnaly, ice formed in an open area more than 250 km wide in the southern portion of the Sea of Okhotsk might be difficult to compare with ice formed in sheltered fjords less than 5 km wide, as evidenced by our lower X- and C-band HH backscattering coefficients. This might explain disparities between this study on fjord landfast ice and studies by Nakamura et al. on drift ice in the Sea of Okhotsk [24,25]. Future sampling should be designed to ensure that spatial autocorrelation may be quantified, for instance using Geary’s C. Grid-like sampling may not be the best strategy to capture the spatial variability of snow depth and ice thickness. Local experts can help design a sampling strategy which would cover extremes and may help outline homogenous areas. Careful treatment of spatial autocorrelation is essential because it can inflate our confidence in the detection of a correlation between two variables [48,52]. While none of the polarimetric parameters we explored performed systematically better than the co-polarized backscattering coefficients, we did not examine the compact polarimetry parameter developed by Zhang et al. [26]. Following the launch of the RADARSAT Constellation Mission in 2019, access to RCM data started in 2020 and will continue to improve. Finally, although the incidence angles used in this study were already steep (35 to 38), it would be interesting to see if even higher incidence angles could improve our results. Indeed, Gill et al. [27] saw that the strength of the linear correlation between snow depth and C-band HH backscattering increased with incidence angle between 26–28 to 35–37, and in the Nakamura et al. studies [24,25] reporting a strong correlation between ice thickness and HH backscattering, the incidence angles were 45 and 39 for the C- and X-band, respectively.
5. Conclusions
In this article, we combined field measurements and satellite SAR data in order to characterize seasonal snow-covered sea ice from 2015 to 2018 in three Nunavik fjords of the Hudson Strait.
In cases of landfast and undeformed first-year sea ice, we conclude that the necessary conditions for detecting a correlation between sea ice thicknesses above 30 cm and SAR HH backscattering in the C- or X-band are a snow cover thinner than 10 cm and slightly rough ice formed from dynamic processes. In terms of usability for predictions, the correlations we observed in these conditions were poor at best for the C- or X-band, respectively, with r-squared values of 0.2 and 0.6. In cases with snow thicker than 20 cm on average or with very smooth ice, no correlation could be detected with ice thickness. No correlation above 0.3 was observed between snow depth and backscattering. The Bayesian linear regression analysis proved to be useful in categorizing each case according to their most likely hypothesis out of the ones we tested. Our results differ from previous reports of a correlation either between ice thickness and the co-polarization ratio in the C-band [25] or between snow depth and the HH backscattering coefficient in either frequency [27].
Backscattering in the C- and X-bands was either different or similar depending on the type of ice. Over smooth ice formed from thermal freeze-up, backscattering from both bands has a significant volume scattering contribution and their HH backscattering coefficients present a 5 dB difference. Over slightly rougher ice formed from consolidated nilas patches, surface scattering dominates at both frequencies. Their HH backscattering coefficients differ by 1 dB or less.
Supplementary Materials
The following are available at https://www.mdpi.com/2072-4292/13/4/768/s1, Figure S1: Monthly total precipitation measured at Salluit airport, Figure S2: Bathymetry for Salluit, Deception Bay, and Kangiqsujuaq, Figure S3: Measurement distributions for snow depth and ice thickness measured in April–May of each season, Figure S4: C-band backscattering HH coefficient versus snow depth and ice thickness for available cases in Salluit, Figure S5: Same as S4 for Deception Bay, including X-band data, Figure S6: Same as S4 for Kangiqsujuaq, Figure S7: Marginal probability distributions for the H hypothesis parameters in the Salluit 2018 case, Figure S8: Pair-wise logarithmic Bayes factors for the relationship between the C-band HH backscattering coefficient and either snow depth, ice thickness, or both, Figure S9: Same as S8 for the X-band in Deception Bay, Figure S10: Mean and standard deviation of the parameters’ marginal probability distributions for H applied to C-band data, Figure S11: Same as S10 for H, Figure S12: Same as S10 for H, Figure S13: Same as S10 for H, H, and H, applied to X-band data; Table S1: Fieldwork dates in Salluit and Kangiqsujuaq, RADARSAT-2 acquisition dates, and the difference between the two, Table S2: Fieldwork dates in Deception Bay, RADARSAT-2 and TerraSAR-X acquisition dates, and the difference between the two, Table S3: Linear correlation coefficient (r-squared) between C-band SAR parameter values and April–May snow depth and ice thickness.
Author Contributions
Conceptualization, S.D.-B., M.B., V.G.; Methodology, S.D.-B. and J.S.; Software, S.D.-B., J.S., A.W.; Validation, S.D.-B., M.B., S.H.; Formal Analysis, S.D.-B., J.S., A.W.; Investigation, S.D.-B., M.B., J.S.; Resources, V.G., A.R., J.T.; Data Curation, A.R., V.G., J.T.; Writing—Original Draft Preparation, S.D.-B.; Writing—Review and Editing, S.D.-B., M.B., J.S., S.H., A.W.; Visualization, S.D.-B.; Supervision, M.B., S.H.; Project Administration, M.B., V.G., Y.G.; Funding Acquisition, M.B., V.G., Y.G. All authors have read and agreed to the published version of the manuscript.
Funding
This INRS research was supported by Polar Knowledge Canada (Safe Passage, project number PKC-NST-1617-0003), Raglan Mine, the Kativik Regional Government, the NSERC Discovery Grant and the Northern Research Supplements Program (attributed to Monique Bernier), the Ministère des Transports du Québec, and the Northern Scientific Training Program (attributed to Sophie Dufour-Beauséjour). Ph.D. scholarships were provided to the first author by NSERC (Alexander Graham Bell Canada Graduate Scholarship—Doctoral) and the W. Garfield Weston Foundation (The W. Garfield Weston Awards for Northern Research).
Data Availability Statement
The data presented in this study will be available in the public repository PANGAEA in 2021. They include: (i) SAR parameter statistics at AOIs for every RADARSAT-2 and TerraSAR-X image, (ii) SAR parameter values at snow or ice thickness measurement locations for each case, and (iii) shapefiles of snow depth and ice thickness measurements for each case [58]. The code used to process the RADARSAT-2 images using ESA’s SNAP is available at https://gitlab.com/sdufourbeausejour/java-snap, accessed on 12 February 2021 [35]. The code used to compute SAR parameter median from AOIs is available at https://github.com/sdufourbeausejour/tiffstats, accessed on 12 February 2021 [45]. The code used to extract SAR parameter values at shapefile feature locations is available at https://github.com/sdufourbeausejour/tiff_at_shp, accessed on 12 February 2021 [46].
Acknowledgments
This work was done within the Ice Monitoring project, a research collaboration between the Kativik Regional Government (KRG), Raglan Mine, Institut national de la recherche scientifique (INRS), and the Northern Villages of Salluit and Kangiqsujuaq. The authors would like to thank the Inuit guides who participated in data acquisition: (from Salluit, in alphabetical order) Chris Alaku, Johnny Ashevak, Michael Cameron, Putulik Cameron, Charlie Ikey, Luuku Isaac, Markusi Jaaka, Adamie Raly Kadjulik, Joannasie Kakayuk, Jani Kenuajuak, Pierre Lebreux, Casey Mark, Denis Napartuk, Eyetsiaq Papigatuk, and Kululak Tayara; (from Kangiqsujuaq, in alphabetical order): Charlie Alaku, Dany Alaku, Noah Annahatak, Maasiu Arngak, Peter Arngak, Jamie Jaaka, Elijah Ningiuruvik, Joe Pilurtuut, Elijah Qisiiq, Peter Qisiiq, and Adamie Jr. Sakiagak. Thanks also to INRS students who also participated in data acquisition: Pierre-Olivier Carreau, Étienne Lauzier-Hudon, and Valérie Plante Lévesque. Thanks to Claudie Ratté-Fortin (INRS), Erwan Gloaguen (INRS) and Jean-Gabriel Young (University of Michigan) for their advice on statistical analyses. Thanks also to Jasmin Gill-Fortin (INRS) for his help with additional remote sensing products, and to Andreas Schmitt (DLR) for his insight on SAR processing. Finally, thanks to Amélie Rouleau and Charles Levac (Raglan Mine) for their support. The java-snap algorithm used to process RADARSAT-2 data was developed in part during the Polar High Performance Computing Workshop and Hackathon organized by the Polar Research Coordination Network in 2017. Thank you to Adrienne Tivy (Canadian Ice Service), Derek Mueller (Carleton University) and Normand Bergeron (INRS) for reviewing an earlier version of this manuscript, as well as to our anonymous reviewers. This study was made possible by Raglan Mine, who financed the Ice Monitoring research project (2016–2019) and provided in-kind support through airplane travelling and logistical support and accommodation in Deception Bay. Thanks to the Canadian Ice Service for securing the RADARSAT-2 images. Thanks also to the German Space Agency (DLR) for providing the TerraSAR-X images and data processing with the Multi-SAR-System. The authors acknowledge the use of RADARSAT-2 (©MDA) and TerraSAR-X (©DLR 2017–18). Jérome Simon received scholarships from the FRQNT and the Vanier Canada Graduate Scholarships program.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nickels, S.; Furgal, C.; Buell, M.; Moquin, H. Unikkaaqatigiit—Putting the Human Face on Climate Change: Perspectives from Inuit in Canada, pre-release english only version ed.; Inuit Tapiriit Kanatami, Nasivvik Centre for Inuit Health and Changing Environments at Université Laval and the Ajunnginiq Centre at the National Aboriginal Health Organization: Ottawa, ON, Canada, 2005; Available online: https://www.itk.ca/wp-content/uploads/2016/07/Nunavik.pdf (accessed on 13 February 2021).
- Cuerrier, A.; Brunet, N.D.; Gérin-Lajoie, J.; Downing, A.; Lévesque, E. The Study of Inuit Knowledge of Climate Change in Nunavik, Quebec: A Mixed Methods Approach. Hum. Ecol. 2015, 43, 379–394. [Google Scholar] [CrossRef]
- Laidler, G.J. Inuit and Scientific Perspectives on the Relationship Between Sea Ice and Climate Change: The Ideal Complement? Clim. Chang. 2006, 78, 407–444. [Google Scholar] [CrossRef]
- Dawson, J.; Pizzolato, L.; Howell, S.E.; Copland, L.; Johnston, M.E. Temporal and Spatial Patterns of Ship Traffic in the Canadian Arctic from 1990 to 2015 + Supplementary Appendix 1: Figs. S1–S7 (See Article Tools). ARCTIC 2018, 71, 15. [Google Scholar] [CrossRef]
- Mailhot, A.; Chaumont, D. Élaboration du Portrait Bioclimatique Futur du Nunavik—Tome II. Rapport présenté au Ministère de la forêt, de la Faune et des parcs; Ouranos: Montréal, QC, Canada, 2017; p. 215. [Google Scholar]
- Iacozza, J.; Barber, D.G. An examination of snow redistribution over smooth land-fast sea ice. Hydrol. Processes 2010, 24, 850–865. [Google Scholar] [CrossRef]
- Tremblay, M.; Furgal, C.; Larrivée, C.; Savard, J.P.; Barrett, M.; Annanack, T.; Enish, N.; Etidloie, B. Communities and Ice: Bringing Together Traditional and Scientific Knowledge. In Climate Change: Linking Traditionnal and Scientific Knowledge; Aboriginal Issues Press: Winnipeg, MB, Canada, 2006; p. 289. [Google Scholar]
- Mahoney, A.; Gearheard, S.; Oshima, T.; Qillaq, T. Sea ice thickness measurements from a community-based observing network. Bull. Am. Meteorol. Soc. 2009, 90, 370. [Google Scholar] [CrossRef]
- Tremblay, M.; Ford, J.; Statham, S.; Pearce, T.; Ljubicic, G.J.; Gauthier, Y.; Braithwaite, L. Chapter 11: Access to the Land and Ice: Travel and Hunting in a Changing Environment. In From Science to Policy in the Eastern Canadian Arctic: An Integrated Regional Impact Study (IRIS) of Climate Change and Moderization; Bell, T., Brown, T.M., Eds.; ArcticNet: Québec City, QC, Canada, 2018; pp. 323–342. [Google Scholar]
- Bell, T.; Briggs, R.; Bachmayer, R.; Li, S. Augmenting Inuit knowledge for safe sea-ice travel; The SmartICE information system. In Proceedings of the 2014 Oceans, St. John’s, NL, Canada, 14–19 September 2014; pp. 1–9. [Google Scholar] [CrossRef]
- Zakhvatkina, N.; Smirnov, V.; Bychkova, I. Satellite SAR Data-based Sea Ice Classification: An Overview. Geosciences 2019, 9, 152. [Google Scholar] [CrossRef]
- Ramjan, S.; Geldsetzer, T.; Scharien, R.; Yackel, J. Predicting Melt Pond Fraction on Landfast Snow Covered First Year Sea Ice from Winter C-Band SAR Backscatter Utilizing Linear, Polarimetric and Texture Parameters. Remote Sens. 2018, 10, 1603. [Google Scholar] [CrossRef]
- Scharien, R.K.; Hochheim, K.; Landy, J.; Barber, D.G. First-year sea ice melt pond fraction estimation from dual-polarisation C-band: Part 2: Scaling in situ to Radarsat-2. Cryosphere 2014, 8, 2163–2176. [Google Scholar] [CrossRef]
- Segal, R.A.; Scharien, R.K.; Duerden, F.; Tam, C.L. The Best of Both Worlds: Connecting Remote Sensing and Arctic Communities for Safe Sea Ice Travel. ARCTIC 2021, 73, 461–484. [Google Scholar] [CrossRef]
- Dammann, D.O.; Eriksson, L.E.B.; Mahoney, A.R.; Eicken, H.; Meyer, F.J. Mapping pan-Arctic landfast sea ice stability using Sentinel-1 interferometry. Cryosphere 2019, 13, 557–577. [Google Scholar] [CrossRef]
- Yackel, J.; Geldsetzer, T.; Mahmud, M.; Nandan, V.; Howell, S.; Scharien, R.; Lam, H. Snow Thickness Estimation on First-Year Sea Ice from Late Winter Spaceborne Scatterometer Backscatter Variance. Remote Sens. 2019, 11, 417. [Google Scholar] [CrossRef]
- Johansson, A.M.; Brekke, C.; Spreen, G.; King, J.A. X-, C-, and L-band SAR signatures of newly formed sea ice in Arctic leads during winter and spring. Remote Sens. Environ. 2018, 204, 162–180. [Google Scholar] [CrossRef]
- Singha, S.; Johansson, M.; Hughes, N.; Hvidegaard, S.M.; Skourup, H. Arctic Sea Ice Characterization Using Spaceborne Fully Polarimetric L-, C-, and X-Band SAR With Validation by Airborne Measurements. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3715–3734. [Google Scholar] [CrossRef]
- Nandan, V.; Geldsetzer, T.; Mahmud, M.; Yackel, J.; Ramjan, S. Ku-, X-and C-Band Microwave Backscatter Indices from Saline Snow Covers on Arctic First-Year Sea Ice. Remote Sens. 2017, 9, 757. [Google Scholar] [CrossRef]
- Fors, A.S.; Brekke, C.; Doulgeris, A.P.; Eltoft, T.; Renner, A.H.H.; Gerland, S. Late-summer sea ice segmentation with multi-polarisation SAR features in C and X band. Cryosphere 2016, 10, 401–415. [Google Scholar] [CrossRef]
- Eriksson, L.E.B.; Pemberton, P.; Lindh, H.; Karlson, B. Evaluation of new spaceborne SAR sensors for sea-ice monitoring in the Baltic Sea. Can. J. Remote Sens. 2010, 36, S56–S73. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Nandan, V.; Geldsetzer, T.; Islam, T.; Yackel, J.J.; Gill, J.P.; Fuller, M.C.; Gunn, G.; Duguay, C. Ku-, X- and C-band measured and modeled microwave backscatter from a highly saline snow cover on first-year sea ice. Remote Sens. Environ. 2016, 187, 62–75. [Google Scholar] [CrossRef]
- Nakamura, K.; Wakabayashi, H.; Naoki, K.; Nishio, F.; Moriyama, T.; Uratsuka, S. Observation of sea-ice thickness in the sea of Okhotsk by using dual-frequency and fully polarimetric airborne SAR (pi-SAR) data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2460–2469. [Google Scholar] [CrossRef]
- Nakamura, K.; Wakabayashi, H.; Uto, s.; Naoki, K.; Nishio, F.; Uratsuka, s. Sea-Ice thickness retrieval in the Sea of Okhotsk using dual-polarization SAR data. Ann. Glaciol. 2006, 44, 261–268. [Google Scholar] [CrossRef]
- Zhang, X.; Dierking, W.; Zhang, J.; Meng, J.; Lang, H. Retrieval of the thickness of undeformed sea ice from simulated C-band compact polarimetric SAR images. Cryosphere 2016, 10, 1529–1545. [Google Scholar] [CrossRef]
- Gill, J.P.S.; Yackel, J.J.; Geldsetzer, T.; Fuller, M.C. Sensitivity of C-band synthetic aperture radar polarimetric parameters to snow thickness over landfast smooth first-year sea ice. Remote Sens. Environ. 2015, 166, 34–49. [Google Scholar] [CrossRef]
- GENIVAR. Environmental and Social Impact Assessment of the Deception Bay Wharf and Sediment Management; Report from GENIVAR for Canadian Royalties Inc.; GENIVAR: Montréal, QC, Canada, 2012; p. 281. [Google Scholar]
- Gauthier, Y.; Dufour-Beauséjour, S.; Poulin, J.; Bernier, M. ICE Monitoring in Deception Bay: Progress report 2016–2018; Institut National de la Recherche Scientifique: Quebec City, QC, Canada, 2018; p. 65, Number 1792; Available online: http://espace.inrs.ca/id/eprint/7538/ (accessed on 12 February 2021).
- Greydanus, K.; Provencher, J.; Carter, N.A.; Dawson, J.; Kochanowicz, Z. Arctic Corridors and Northern Voices: Governing marine transportation in the Canadian Arctic (Salluit, Quebec Community Report); University of Ottawa: Ottawa, ON, Canada, 2018; p. 50. Available online: https://ruor.uottawa.ca/handle/10393/38036 (accessed on 12 February 2021).
- Dufour-Beauséjour, S.; Wendleder, A.; Gauthier, Y.; Bernier, M.; Poulin, J.; Gilbert, V.; Tuniq, J.; Rouleau, A.; Roth, A. Combining TerraSAR-X and time-lapse photography for seasonal sea ice monitoring: The case of Deception Bay, Nunavik. Cryosphere 2020, 14, 1595–1609. [Google Scholar] [CrossRef]
- DFO; Canadian Hydrological Service. Tides, Currents, and Water Levels—2019 Tide Tables; Number Volume 4-Arctic and Hudson Bay; Available online: https://www.tides.gc.ca/Eng/data/predictions/2019 (accessed on 14 February 2021).
- GENIVAR. Study on Maritime Navigation in Deception Bay—Impact on Marine Mammals and Traditional Inuit Activity; Report from GENIVAR for Canadian Royalties Inc.; GENIVAR: Montréal, QC, Canada, 2007; p. 71. [Google Scholar]
- MDA. RADARSAT-2 Product Description; Number RN-SP-52-1238; Maxar Technologies Ltd: Richmond, CO, Canada, 2018; p. 91. [Google Scholar]
- Dufour-Beausejour, S. java-snap 2019. Available online: https://zenodo.org/record/3930921#.YCYV3HkRVPY (accessed on 12 February 2021).
- Veci, L. SAR Basics with the Sentinel-1 Toolbox. Tutorials. 2015. Available online: http://step.esa.int/docs/tutorials/S1TBX%20SAR%20Basics%20Tutorial.pdf (accessed on 14 February 2021).
- Foucher, S.; Lopez-Martinez, C. Analysis, Evaluation, and Comparison of Polarimetric SAR Speckle Filtering Techniques. IEEE Trans. Image Process. 2014, 23, 1751–1764. [Google Scholar] [CrossRef] [PubMed]
- Veci, L.; Braun, A. Sentinel-1 Toolbox Polarimetric Tutorial. 2015. Available online: http://step.esa.int/docs/tutorials/S1TBX%20Polarimetry%20with%20Radarsat-2%20Tutorial_v2.pdf (accessed on 14 February 2021).
- Pottier, E. Polarimetry Basics. 2007. Available online: http://earth.esa.int/landtraining07/D1LA3-Pottier.pdf (accessed on 14 February 2021).
- Canada, N.R. Canadian Digital Elevation Model, 1945–2011. 2015. Available online: https://open.canada.ca/data/en/dataset/7f245e4d-76c2-4caa-951a-45d1d2051333 (accessed on 14 February 2021).
- Anfinsen, S.; Doulgeris, A.; Eltoft, T. Estimation of the Equivalent Number of Looks in Polarimetric Synthetic Aperture Radar Imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3795–3809. [Google Scholar] [CrossRef]
- Eineder, M.; Fritz, T.; Mittermayer, J.; Roth, A.; Boerner, E.; Breit, H. TerraSAR-X Ground Segment, Basic Product Specification Document; Number TX-GS-DD-3302; DLR: Oberpfaffenhofen, Germany, 2008; Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a515513.pdf (accessed on 14 February 2021).
- Bertram, A.; Wendleder, A.; Schmitt, A.; Huber, M. Long-Term Monitoring of Water Dynamics in the Sahel Region using the Multi-SAR-System. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Schmitt, A.; Wendleder, A.; Hinz, S. The Kennaugh element framework for multi-scale, multi-polarized, multi-temporal and multi-frequency SAR image preparation. ISPRS J. Photogramm. Remote Sens. 2015, 102, 122–139. [Google Scholar] [CrossRef]
- Dufour-Beauséjour, S. tiffstats 2019. Available online: https://doi.org/10.5281/zenodo.3352367 (accessed on 12 February 2021).
- Dufour-Beauséjour, S. tiff-at-shp 2019. Available online: https://doi.org/10.5281/zenodo.3930953 (accessed on 12 February 2021).
- Wetzels, R.; Wagenmakers, E.J. A default Bayesian hypothesis test for correlations and partial correlations. Psychonomic Bull. Rev. 2012, 19, 1057–1064. [Google Scholar] [CrossRef] [PubMed]
- Donegan, C. Re: Spatial Autocorrelation: Its Consequence on Bayesian Linear Regression. 2020. Available online: https://discourse.mc-stan.org/t/spatial-autocorrelation-its-consequence-on-bayesian-linear-regression/17266/3 (accessed on 14 February 2021).
- Simon, J.; Dufour-Beauséjour, S. RS2_bayesian_linear_regression 2020. Available online: https://doi.org/10.5281/zenodo.3905286 (accessed on 12 February 2021).
- Jeffreys, H. The Theory of Probability, 3rd ed.; OUP Oxford: Oxford, UK, 1998. [Google Scholar]
- Legendre, P.; Legendre, L. Numerical Ecology, Volume 24—3rd Edition, second english edition; Developments in Environmental Modelling, Elsevier: Amsterdam, Netherlands, 2003; Volume 20. [Google Scholar]
- Saas, Y.; Gosselin, F. Comparison of regression methods for spatially-autocorrelated count data on regularly- and irregularly-spaced locations. Ecography 2014, 37, 476–489. [Google Scholar] [CrossRef]
- Høyland, K.V. Ice thickness, growth and salinity in Van Mijenfjorden, Svalbard, Norway. Polar Res. 2009, 28, 339–352. [Google Scholar] [CrossRef]
- Hudson, E.; Aihoshi, D.; Gaines, T.; Simard, G.; Mullock, J. The Weather of Nunavut and the Arctic - Graphic Area Forecast 36 and 37; NAV CANADA: Ottawa, ON, Canada, 2001; p. 245. [Google Scholar]
- Kimble, G.H.T.; Collaborators. Wind in Icelandic Fjords. Bull. Am. Meteorol. Soc. 1946, 27, 216–223. [Google Scholar] [CrossRef][Green Version]
- Laidler, G.J.; Dialla, A.; Joamie, E. Human geographies of sea ice: Freeze/thaw processes around Pangnirtung, Nunavut, Canada. Polar Rec. 2008, 44, 335–361. [Google Scholar] [CrossRef]
- Nakamura, K.; Wakabayashi, H.; Uto, S.; Ushio, S.; Nishio, F. Observation of Sea-Ice Thickness Using ENVISAT Data From LÜtzow-Holm Bay, East Antarctica. IEEE Geosci. Remote Sens. Lett. 2009, 6, 277–281. [Google Scholar] [CrossRef]
- Bernier, M.; Dufour-Beausejour, S.; Gilbert, V.; Rouleau, A.; Tuniq, J.; Gauthier, Y. Ice Monitoring: Ice and Snow Thickness Data from Salluit Fjord, Deception Bay and Kangiqsujuaq (Nunavik, Canada); Canadian Cryospheric Information Network: Toronto, ON, Canada, 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).