Impact of Lightning Data Assimilation on the Short-Term Precipitation Forecast over the Central Mediterranean Sea
Abstract
1. Introduction
2. Datasets and Methodology
2.1. Satellite Precipitation Data
2.2. Model Setup and Lightning Data Assimilation Procedure
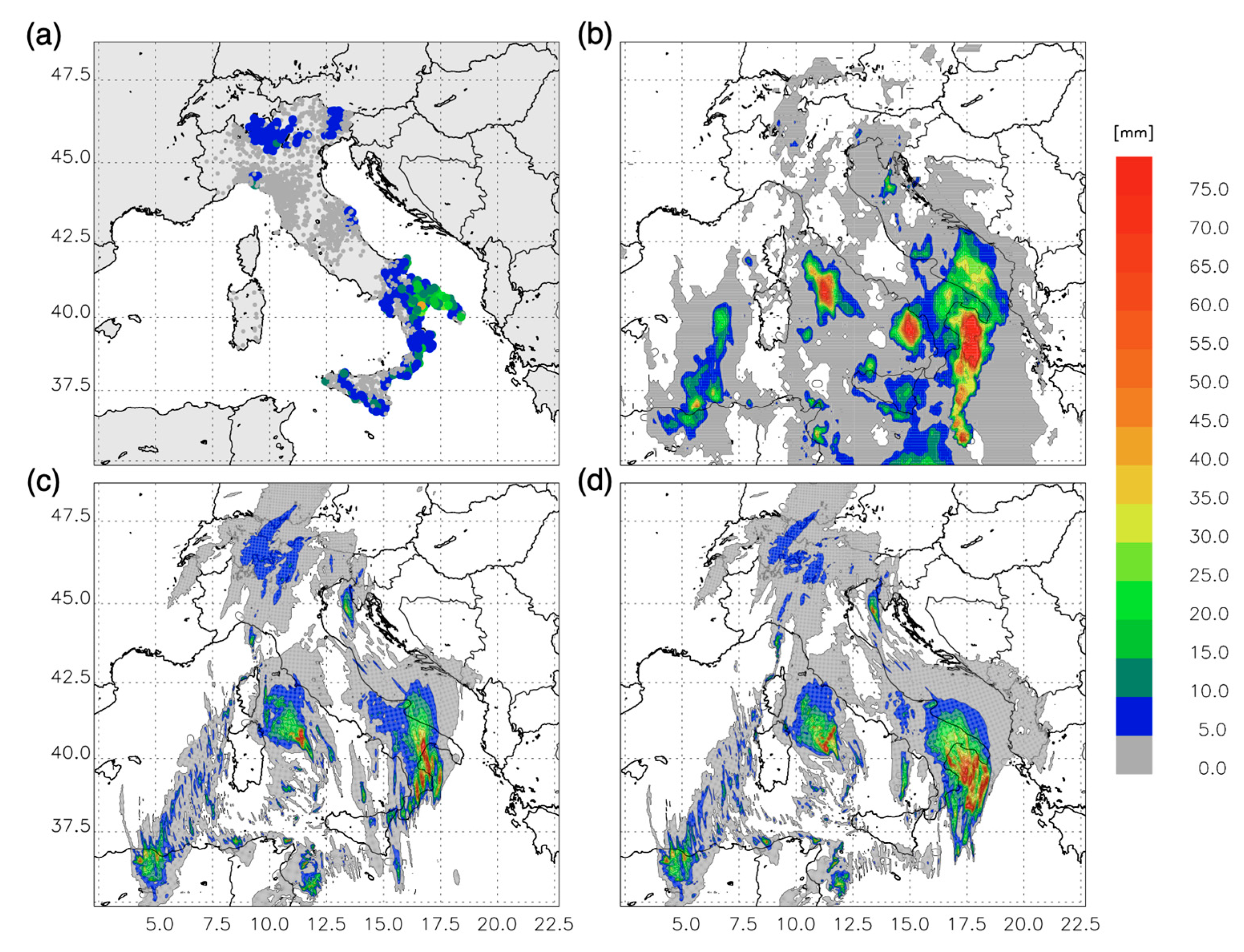
3. Results
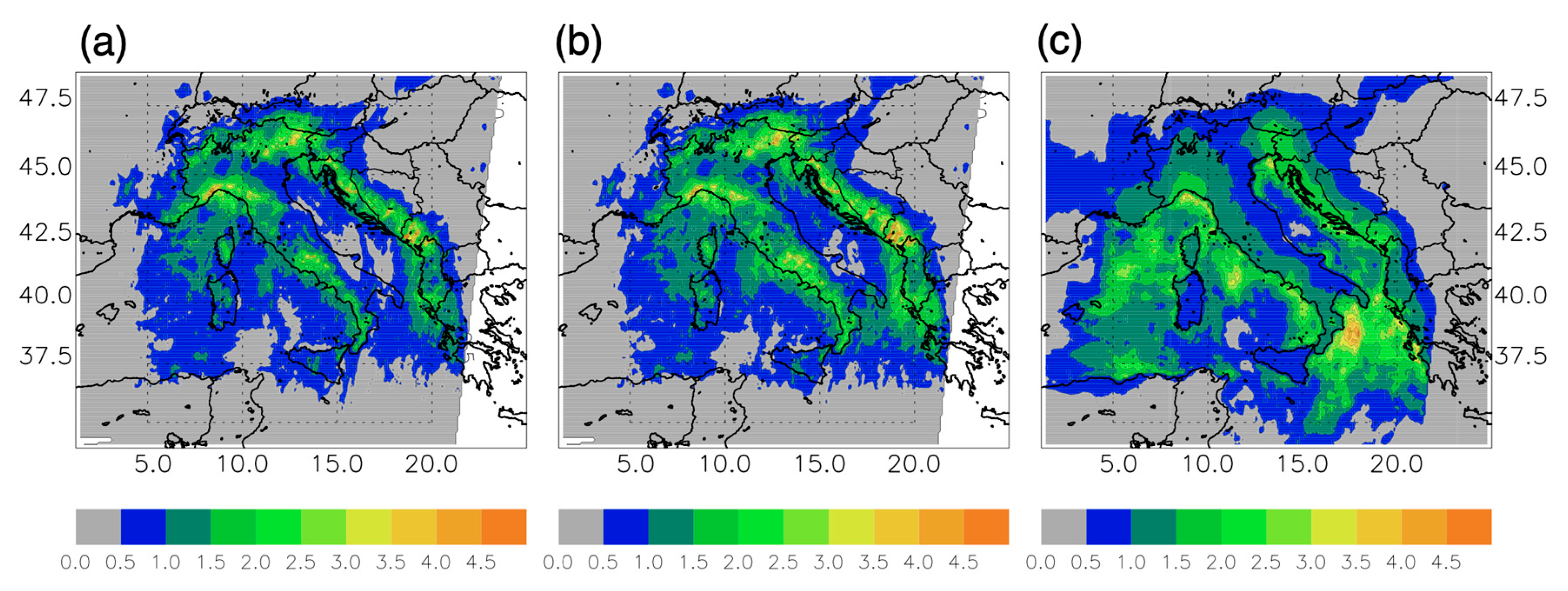
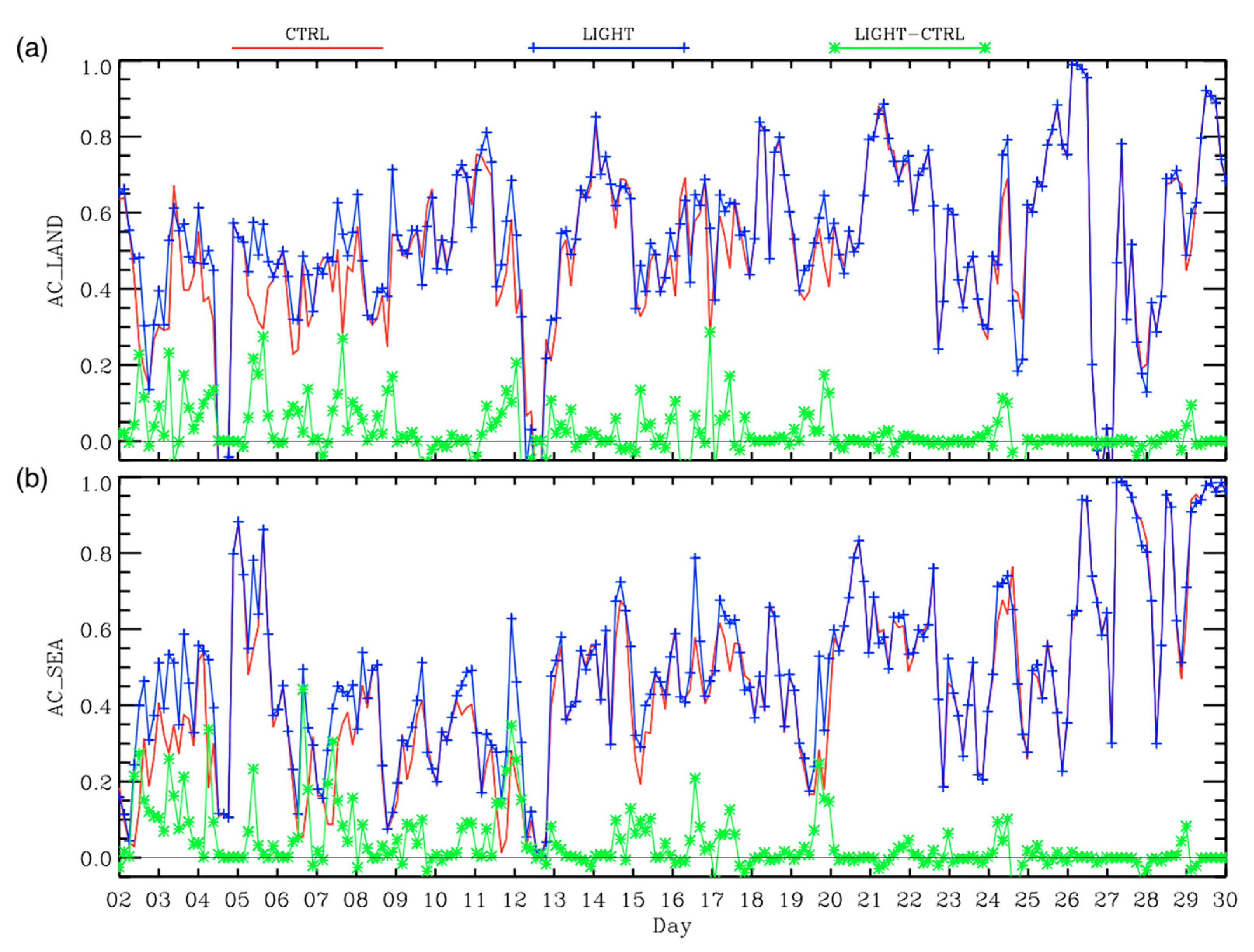
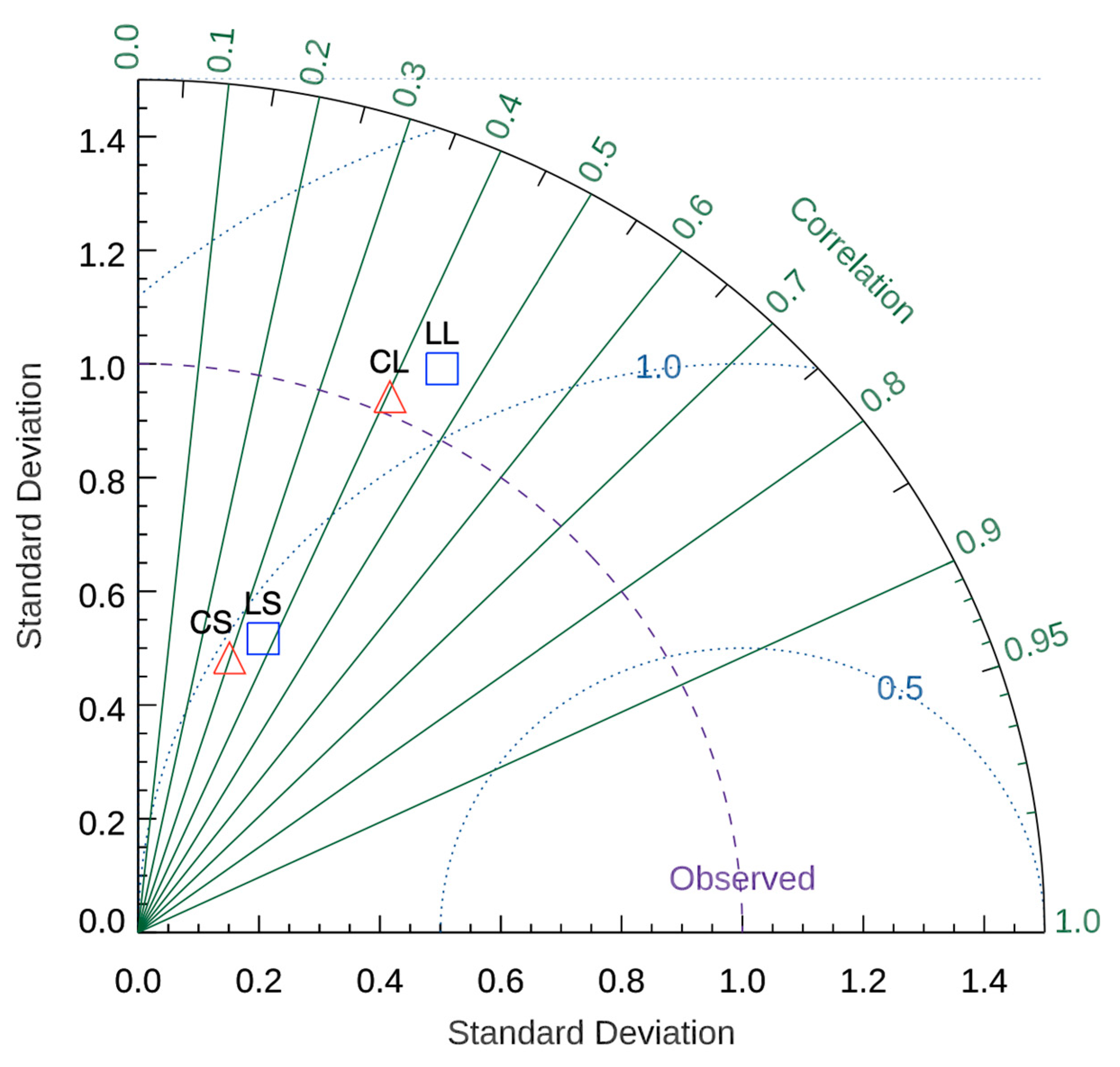
3.1. Pearson Correlation Coefficient, Anomaly Correlation, and Taylor Diagram
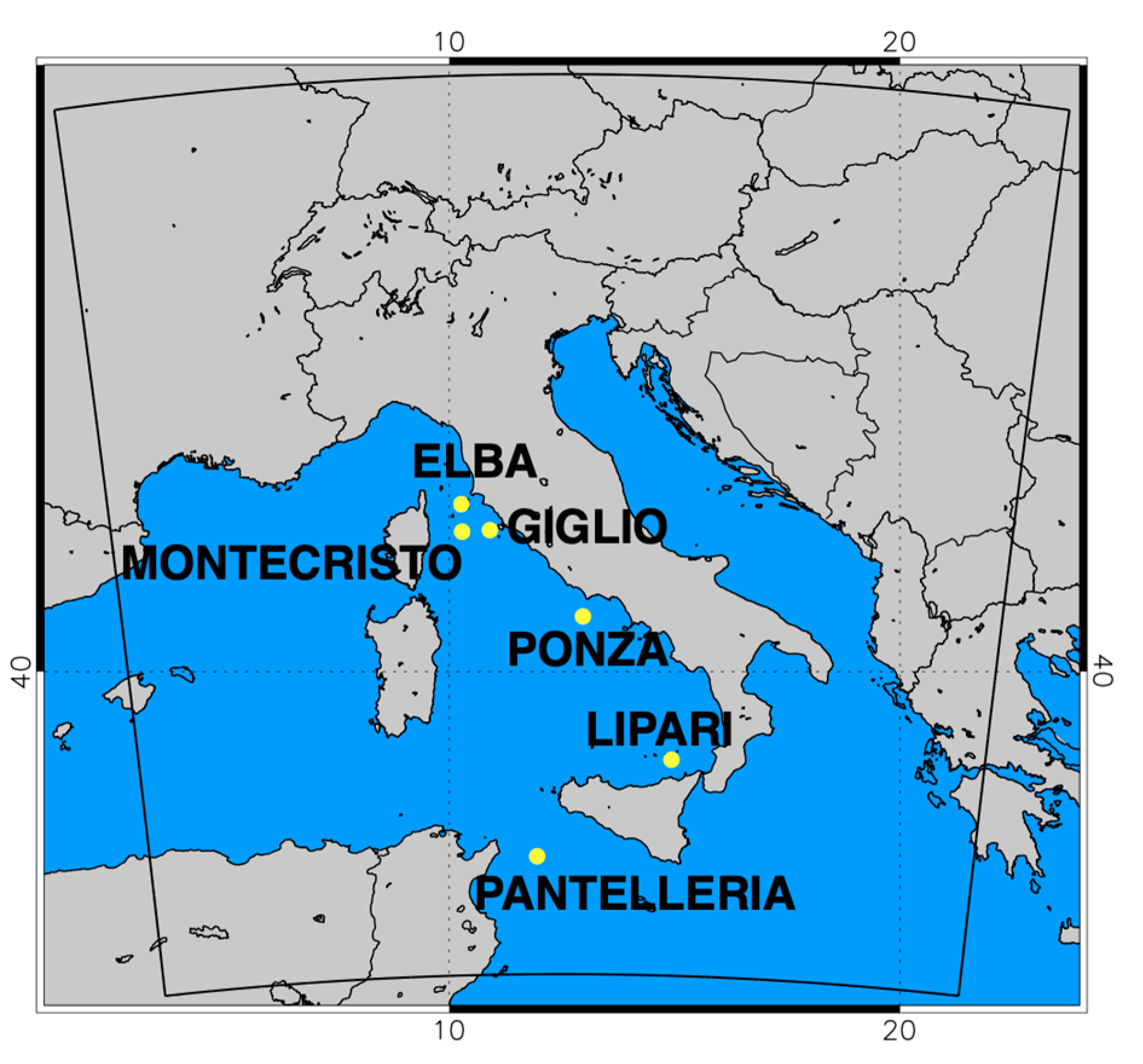
3.2. Impact on Small Islands
3.3. A Case Study: 12 November 2019
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, X.; Yang, T.; Hsu, K.; Liu, C.; Sorooshian, S. Evaluating the streamflow simulation capability of PERSIANN-CDR daily rainfall products in two river basins on the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2017, 21, 169–181. [Google Scholar] [CrossRef]
- Vasiloff, S.V.; Seo, D.-J.; Howard, K.; Zhang, J.; Kitzmiller, D.H.; Mullusky, M.G.; Krajewski, W.F.; Brandes, E.A.; Rabin, R.M.; Berkowitz, D.S.; et al. Improving QPE and Very Short Term QPF: An Initiative for a Community-Wide Integrated Approach. Bull. Am. Meteorol. Soc. 2007, 88, 1899–1911. [Google Scholar] [CrossRef]
- Zhu, Q.; Hsu, K.-L.; Xu, Y.-P.; Yang, T. Evaluation of a new satellite-based precipitation data set for climate studies in the Xiang River basin, southern China. Int. J. Clim. 2017, 37, 4561–4575. [Google Scholar] [CrossRef]
- Lagasio, M.; Parodi, A.; Pulvirenti, L.; Meroni, A.N.; Boni, G.; Pierdicca, N.; Marzano, F.S.; Luini, L.; Venuti, G.; Realini, E.; et al. A Synergistic Use of a High-Resolution Numerical Weather Prediction Model and High-Resolution Earth Observation Products to Improve Precipitation Forecast. Remote Sens. 2019, 11, 2387. [Google Scholar] [CrossRef]
- Nam, D.; Mai, D.T.; Udo, K.; Mano, A. Short-term flood inundation prediction using hydrologic-hydraulic models forced with downscaled rainfall from global NWP. Hydrol. Process. 2013, 28, 5844–5859. [Google Scholar] [CrossRef]
- Robertson, D.E.; Shrestha, D.L.; Wang, Q.J. Post-processing rainfall forecasts from numerical weather prediction models for short-term streamflow forecasting. Hydrol. Earth Syst. Sci. 2013, 17, 3587–3603. [Google Scholar] [CrossRef]
- Zahraei, A.; Hsu, K.-L.; Sorooshian, S.; Yong, B.; Hong, Y.; Behrangi, A. Short-term quantitative precipitation forecasting using an object-based approach. J. Hydrol. 2013, 483, 1–15. [Google Scholar] [CrossRef]
- Federico, S.; Petracca, M.; Panegrossi, G.; Dietrich, S. Improvement of RAMS precipitation forecast at the short-range through lightning data assimilation. Nat. Hazards Earth Syst. Sci. 2017, 17, 61–76. [Google Scholar] [CrossRef]
- Ballard, S.P.; Li, Z.; Simonin, D.; Caron, J.-F. Performance of 4D-Var NWP-based nowcasting of precipitation at the Met Office for summer 2012. Q. J. R. Meteorol. Soc. 2015, 142, 472–487. [Google Scholar] [CrossRef]
- Sun, J.; Xue, M.; Wilson, J.W.; Zawadzki, I.; Ballard, S.P.; Onvlee-Hooimeyer, J.; Joe, P.; Barker, D.M.; Li, P.-W.; Golding, B.; et al. Use of NWP for Nowcasting Convective Precipitation: Recent Progress and Challenges. Bull. Am. Meteorol. Soc. 2014, 95, 409–426. [Google Scholar] [CrossRef]
- Wang, G.; Yang, J.; Wang, D.; Liu, L. A quantitative comparison of precipitation forecasts between the storm-scale numerical weather prediction model and auto-nowcast system in Jiangsu, China. Atmos. Res. 2016, 181, 1–11. [Google Scholar] [CrossRef]
- Stensrud, D.J.; Xue, M.; Wicker, L.J.; Kelleher, K.E.; Foster, M.P.; Schaefer, J.T.; Schneider, R.S.; Benjamin, S.G.; Weygandt, S.S.; Ferree, J.T.; et al. Convective-scale Warn-On-Forecast system: A vision for 2020. Bull. Am. Meteor. Soc. 2009, 90, 1487–1499. [Google Scholar] [CrossRef]
- Fritsch, J.M.; Houze, R.A.; Adler, R.; Bluestein, H.; Bosart, L.; Brown, J.; Carr, F.; Davis, C.; Johnson, R.H.; Junker, N.; et al. Quantitative precipitation forecasting: Report of the eighth prospectus development team, U.S. Weather Research Program. Bull. Am. Meteorol. Soc. 1998, 79, 285–299. [Google Scholar] [CrossRef]
- Foresti, L.; Reyniers, M.; Seed, A.; Delobbe, L. Development and verification of a real-time stochastic precipitation nowcasting system for urban hydrology in Belgium. Hydrol. Earth Syst. Sci. 2016, 20, 505–527. [Google Scholar] [CrossRef]
- Johnson, A.; Wang, X.; Carley, J.R.; Wicker, L.J.; Karstens, C. A Comparison of Multiscale GSI-Based EnKF and 3DVar Data Assimilation Using Radar and Conventional Observations for Midlatitude Convective-Scale Precipitation Forecasts. Mon. Weather Rev. 2015, 143, 3087–3108. [Google Scholar] [CrossRef]
- Park, S.K.; Xu, L. Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications (Vol. III). Assim. Atmos. Ocean. Hydrol. Appl. 2017, 2. [Google Scholar] [CrossRef]
- Mansell, E.R.; Ziegler, C.L.; MacGorman, D.R. A Lightning Data Assimilation Technique for Mesoscale Forecast Models. Mon. Weather Rev. 2007, 135, 1732–1748. [Google Scholar] [CrossRef]
- Fierro, A.O.; Wang, Y.; Gao, J.; Mansell, E.R. Variational Assimilation of Radar Data and GLM Lightning-Derived Water Vapor for the Short-Term Forecasts of High-Impact Convective Events. Mon. Weather Rev. 2019, 147, 4045–4069. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Mitchell, H. Data assimilation using an ensemble Kalman filter technique. Mon. Wea. Rev. 1998, 126, 796–811. [Google Scholar] [CrossRef]
- Godinez, H.C.; Reisner, J.M.; Fierro, A.O.; Guimond, S.R.; Kao, J. Determining Key Model Parameters of Rapidly Intensifying Hurricane Guillermo (1997) Using the Ensemble Kalman Filter. J. Atmos. Sci. 2012, 69, 3147–3171. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Liu, D.; Zhang, D.; Yao, W.; Wang, C. A Case Study of Assimilating Lightning-Proxy Relative Humidity with WRF-3DVAR. Atmosphere 2017, 8, 55. [Google Scholar] [CrossRef]
- Mazzarella, V.; Maiello, I.; Ferretti, R.; Capozzi, V.; Picciotti, E.; Alberoni, P.P.; Marzano, F.S.; Budillon, G. Reflectivity and velocity radar data assimilation for two flash flood events in central Italy: A comparison between 3D and 4D variational methods. Q. J. R. Meteorol. Soc. 2020, 146, 348–366. [Google Scholar] [CrossRef]
- Gao, J.; Stensrud, D.J. Assimilation of reflectivity data in a convective-scale, cycled 3DVAR framework with hydrometeor classification. J. Atmos. Sci. 2012, 69, 1054–1065. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H. Radar Data Assimilation with WRF 4D-Var. Part II: Comparison with 3D-Var for a Squall Line over the U.S. Great Plains. Mon. Weather Rev. 2013, 141, 2245–2264. [Google Scholar] [CrossRef]
- Zhang, Y.; Weng-Sippel, J.A.; Meng, Z.; Bishop, C.H. Cloud- resolving hurricane initialization and prediction through assimilation of Doppler radar observations with an ensemble Kalman filter. Mon. Wea. Rev. 2009, 137, 2105–2125. [Google Scholar] [CrossRef]
- Aksoy, A.; Dowell, D.C.; Snyder, C. A Multicase Comparative Assessment of the Ensemble Kalman Filter for Assimilation of Radar Observations. Part I: Storm-Scale Analyses. Mon. Weather Rev. 2009, 137, 1805–1824. [Google Scholar] [CrossRef]
- Xu, W.; Rutledge, S.A.; Zhang, W. Relationships between total lightning, deep convection, and tropical cyclone intensity change. J. Geophys. Res. Atmos. 2017, 122, 7047–7063. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Y.; Zheng, D.; Wang, F.; Xu, L. Relationship between lightning activity and tropical cyclone intensity over the northwest Pacific. J. Geophys. Res. Atmos. 2015, 120, 4072–4089. [Google Scholar] [CrossRef]
- Fierro, A.O.; Mansell, E.R.; Ziegler, C.L.; MacGorman, D.R. Application of a Lightning Data Assimilation Technique in the WRF-ARW Model at Cloud-Resolving Scales for the Tornado Outbreak of 24 May 2011. Mon. Weather Rev. 2012, 140, 2609–2627. [Google Scholar] [CrossRef]
- Prat, A.C.; Federico, S.; Torcasio, R.C.; Fierro, A.O.; Dietrich, S. Lightning data assimilation in the WRF-ARW model for short-term rainfall forecasts of three severe storm cases in Italy. Atmos. Res. 2021, 247, 105246. [Google Scholar] [CrossRef]
- Alexander, G.D.; Weinman, J.A.; Karyampudi, V.M.; Olson, W.S.; Lee, A.C.L. The Effect of Assimilating Rain Rates Derived from Satellites and Lightning on Forecasts of the 1993 Superstorm. Mon. Weather Rev. 1999, 127, 1433–1457. [Google Scholar] [CrossRef]
- Chang, D.-E.; Weinman, J.A.; Morales, C.A.; Olson, W.S. The Effect of Spaceborne Microwave and Ground-Based Continuous Lightning Measurements on Forecasts of the 1998 Groundhog Day Storm. Mon. Weather Rev. 2001, 129, 1809–1833. [Google Scholar] [CrossRef]
- Jones, C.D.; MacPherson, B. A latent heat nudging scheme for the assimilation of precipitation data into an operational mesoscale model. Meteorol. Appl. 1997, 4, 269–277. [Google Scholar] [CrossRef]
- Pessi, A.T.; Businger, S. Relationships among Lightning, Precipitation, and Hydrometeor Characteristics over the North Pacific Ocean. J. Appl. Meteorol. Clim. 2009, 48, 833–848. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Dévényi, D.; Weygandt, S.S.; Brundage, K.J.; Brown, J.M.; Grell, G.A.; Kim, D.; Schwartz, B.E.; Smirnova, T.G.; Smith, T.L.; et al. An Hourly Assimilation–Forecast Cycle: The RUC. Mon. Weather Rev. 2004, 132, 495–518. [Google Scholar] [CrossRef]
- Papadopoulos, A.; Chronis, T.G.; Anagnostou, E.N. Improving Convective Precipitation Forecasting through Assimilation of Regional Lightning Measurements in a Mesoscale Model. Mon. Weather Rev. 2005, 133, 1961–1977. [Google Scholar] [CrossRef]
- Kain-John, S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Giannaros, T.M.; Kotroni, V.; Lagouvardos, K. WRF-LTNGDA: A lightning data assimilation technique implemented in the WRF model for improving precipitation forecasts. Environ. Model. Softw. 2016, 76, 54–68. [Google Scholar] [CrossRef]
- Fierro, A.O.; Clark, A.J.; Mansell, E.R.; MacGorman, D.R.; Dembek, S.R.; Ziegler, C.L. Impact of Storm-Scale Lightning Data Assimilation on WRF-ARW Precipitation Forecasts during the 2013 Warm Season over the Contiguous United States. Mon. Weather Rev. 2015, 143, 757–777. [Google Scholar] [CrossRef]
- Fierro, A.O.; Gao, J.; Ziegler, C.L.; Mansell, E.R.; MacGorman, D.R.; Dembek, S.R. Evaluation of a Cloud-Scale Lightning Data Assimilation Technique and a 3DVAR Method for the Analysis and Short-Term Forecast of the 29 June 2012 Derecho Event. Mon. Weather Rev. 2014, 142, 183–202. [Google Scholar] [CrossRef]
- Qie, X.; Zhu, R.; Yuan, T.; Wu, X.; Li, W.; Liu, D. Application of total-lightning data assimilation in a mesoscale convective system based on the WRF model. Atmos. Res. 2014, 145–146, 255–266. [Google Scholar] [CrossRef]
- Chen, Z.; Qie, X.; Liu, D.; Xiong, Y. Lightning data assimilation with comprehensively nudging water contents at cloud- re-solving scale using WRF model. Atmos. Res. 2019, 221, 72–87. [Google Scholar] [CrossRef]
- Drobinski, P.; Ducrocq, V.; Alpert, P.; Anagnostou, E.; Béranger, K.; Borga, M.; Braud, I.; Chanzy, A.; Davolio, S.; Delrieu, G.; et al. HyMeX: A 10-Year Multidisciplinary Program on the Mediterranean Water Cycle. Bull. Am. Meteorol. Soc. 2014, 95, 1063–1082. [Google Scholar] [CrossRef]
- Llasat, M.C.; Llasat-Botija, M.; Petrucci, O.; Pasqua, A.A.; Rossello, J.L.; Vinet, F.; Boissier, L. Towards a database on societal impact of Mediterranean floods within the framework of the HYMEX project. Nat. Hazards Earth Syst. Sci. 2013, 13, 1337–1350. [Google Scholar] [CrossRef]
- Ducrocq, V.; Braud, I.; Davolio, S.; Ferretti, R.; Flamant, C.; Jansá, A.; Kalthoff, N.; Richard, E.; Taupier-Letage, I.; Ayral, P.-A.; et al. HyMeX-SOP1: The Field Campaign Dedicated to Heavy Precipitation and Flash Flooding in the Northwestern Mediterranean. Bull. Am. Meteorol. Soc. 2014, 95, 1083–1100. [Google Scholar] [CrossRef]
- Jansa, A.; Alpert, P.; Arbogast, P.; Buzzi, A.; Ivancanpicek, B.; Kotroni, V.; Llasat, M.C.; Ramis, C.; Richard, E.; Romero, R.; et al. MEDEX: A general overview. Nat. Hazards Earth Syst. Sci. 2014, 14, 1965–1984. [Google Scholar] [CrossRef]
- Romero, R.; Ramis, C.; Alonso, S. Numerical simulation of an extreme rainfall event in Catalonia: Role of orography and evaporation from the sea. Q. J. R. Meteorol. Soc. 1997, 123, 537–559. [Google Scholar] [CrossRef]
- Kotroni, V.; Lagouvardos, K.; Kallos, G.; Ziakopoulos, D. Severe flooding over central and southern greece associated with pre-cold frontal orographic lifting. Q. J. R. Meteorol. Soc. 1999, 125, 967–991. [Google Scholar] [CrossRef]
- Jansa, A.; Genoves, A.; Garcia-Moya, J.A. Western Mediterranean cyclones and heavy rain. Part 1: Numerical experiment concerning the Piedmont flood case. Meteorol. Appl. 2000, 7, 323–333. [Google Scholar] [CrossRef]
- Lee, K.-O.; Flamant, C.; Ducrocq, V.; Duffourg, F.; Fourrié, N.; Davolio, S. Convective initiation and maintenance processes of two back-building mesoscale convective systems leading to heavy precipitation events in Southern Italy during HyMeX IOP 13. Q. J. R. Meteorol. Soc. 2016, 142, 2623–2635. [Google Scholar] [CrossRef]
- Cassola, F.; Ferrari, F.; Mazzino, A. Numerical simulations of Mediterranean heavy precipitation events with the WRF model: A verification exercise using different approaches. Atmos. Res. 2015, 164–165, 210–225. [Google Scholar] [CrossRef]
- Dafis, S.; Lagouvardos, K.; Kotroni, V.; Giannaros, T.M.; Bartzokas, A. Observational and modeling study of a mesoscale convective system during the HyMeX—SOP1. Atmos. Res. 2017, 187, 1–15. [Google Scholar] [CrossRef]
- Avolio, E.; Federico, S. WRF simulations for a heavy rainfall event in southern Italy: Verification and sensitivity tests. Atmos. Res. 2018, 209, 14–35. [Google Scholar] [CrossRef]
- Davolio, S.; Della-Fera, S.; Laviola, S.; Miglietta, M.M.; Levizzani, V. Heavy Precipitation over Italy from the Mediterranean Storm “Vaia” in October 2018: Assessing the Role of an Atmospheric River. Mon. Weather Rev. 2020, 148, 3571–3588. [Google Scholar] [CrossRef]
- Torcasio, R.C.; Federico, S.; Puca, S.; Vulpiani, G.; Prat, A.C.; Dietrich, S. Application of Lightning Data Assimilation for the 10 October 2018 Case Study over Sardinia. Atmosphere 2020, 11, 541. [Google Scholar] [CrossRef]
- Federico, S.; Bellecci, C.; Colacino, M. Quantitative precipitation of the Soverato flood: The role of orography and surface fluxes. Nuovo Cimento C 2003, 26, 7–22. [Google Scholar]
- Federico, S.; Avolio, E.; Bellecci, C.; Lavagnini, A.; Colacino, M.; Walko, R.L. Numerical analysis of an intense rainstorm occurred in southern Italy. Nat. Hazards Earth Syst. Sci. 2008, 8, 19–35. [Google Scholar] [CrossRef]
- Senatore, A.; Mendicino, G.; Knoche, H.R.; Kunstmann, H. Sensitivity of Modeled Precipitation to Sea Surface Temperature in Regions with Complex Topography and Coastlines: A Case Study for the Mediterranean. J. Hydrometeorol. 2014, 15, 2370–2396. [Google Scholar] [CrossRef]
- Pastor, F.; Estrela, M.A.J.; Penarrocha, D.A.; Millán, M.M. Torrential Rains on the Spanish Mediterranean Coast: Modeling the Effects of the Sea Surface Temperature. J. Appl. Meteorol. 2001, 40, 1180–1195. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Carnevale, D.; Levizzani, V.; Rotunno, R. Role of moist and dry air advection in the development of Mediterranean tropical-like cyclones (medicanes). Q. J. R. Meteorol. Soc. 2020, 1. [Google Scholar] [CrossRef]
- Moscatello, A.; Miglietta, M.M.; Rotunno, R. Numerical Analysis of a Mediterranean “Hurricane” over Southeastern Italy. Mon. Weather Rev. 2008, 136, 4373–4397. [Google Scholar] [CrossRef]
- Marra, A.; Porcù, F.; Baldini, L.; Petracca, M.; Casella, D.; Dietrich, S.; Mugnai, A.; Sanò, P.; Vulpiani, G.; Panegrossi, G. Observational analysis of an exceptionally intense hailstorm over the Mediterranean area: Role of the GPM Core Observatory. Atmos. Res. 2017, 192, 72–90. [Google Scholar] [CrossRef]
- Dafis, S.; Claud, C.; Kotroni, V.; Lagouvardos, K.; Rysman, J. Insights into the convective evolution of Mediterranean tropical-like cyclones. Q. J. R. Meteorol. Soc. 2020, 146, 4147–4169. [Google Scholar] [CrossRef]
- Marra, A.C.; Federico, S.; Montopoli, M.; Avolio, E.; Baldini, L.; Casella, D.; D’Adderio, L.P.; Dietrich, S.; Sanò, P.; Torcasio, R.C.; et al. The Precipitation Structure of the Mediterranean Tropical-Like Cyclone Numa: Analysis of GPM Observations and Numerical Weather Prediction Model Simulations. Remote Sens. 2019, 11, 1690. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Rotunno, R. Development mechanisms for Mediterranean tropical-like cyclones (medicanes). Q. J. R. Meteorol. Soc. 2019, 145, 1444–1460. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Moscatello, A.; Conte, D.; Mannarini, G.; Lacorata, G.; Rotunno, R. Numerical analysis of a Mediterranean ‘hurricane’ over south-eastern Italy: Sensitivity experiments to sea surface temperature. Atmos. Res. 2011, 101, 412–426. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (GPM) Mission for Science and Society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef]
- Kidd, C.; Shige, S.; Vila, D.; Tarnavsky, E.; Yamamoto, M.K.; Maggioni, V.; Maseko, B. The IPWG Satellite Precipitation Validation Effort. In Advances in Global Change Research; Springer Nature: Cham, Switzerland, 2020; pp. 453–470. [Google Scholar]
- Panegrossi, G.; Casella, D.; Dietrich, S.; Marra, A.C.; Sanò, P.; Mugnai, A.; Baldini, L.; Roberto, N.; Adirosi, E.; Cremonini, R.; et al. Use of the GPM Constellation for Monitoring Heavy Precipitation Events Over the Mediterranean Region. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2733–2753. [Google Scholar] [CrossRef]
- Huffman, G.J.; Stocker, D.T.; Bolvin, E.J.; Nelkin-Jackson, T. GPM IMERG Final Precipitation L3 Half Hourly 0.1 Degree x 0.1 Degree V06; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA. Available online: https://docserver.gesdisc.eosdis.nasa.gov/public/project/GPM/IMERG_ATBD_V06.pdf (accessed on 12 February 2021). [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Version 4; No. NCAR/TN-556+STR, NCAR Technical Note; National Center for Atmospheric Research: Boulder, CO, USA, 2019; 145p. [Google Scholar] [CrossRef]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A Revised Scheme for the WRF Surface Layer Formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the Winter Monsoon Experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Space Phys. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Federico, S.; Petracca, M.; Panegrossi, G.; Transerici, C.; Dietrich, S. Impact of the assimilation of lightning data on the precipitation forecast at different forecast ranges. Adv. Sci. Res. 2017, 14, 187–194. [Google Scholar] [CrossRef]
- Betz, H.D.; Schmidt, K.; Laroche, P.; Blanchet, P.; Oettinger, W.P.; Defer, E.; Dziewit, Z.; Konarski, J. LINET—An international lightning detection network in Europe. Atmos. Res. 2009, 91, 564–573. [Google Scholar] [CrossRef]
- Betz, H.-D.; Schmidt, K.; Oettinger, P.; Wirz, M. Lightning detection with 3-D discrimination of intracloud and cloud-to-ground discharges. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Federico, S.; Avolio, E.; Petracca, M.; Panegrossi, G.; Sanò, P.; Casella, D.; Dietrich, S. Simulating lightning into the RAMS model: Implementation and preliminary results. Nat. Hazards Earth Syst. Sci. 2014, 14, 2933–2950. [Google Scholar] [CrossRef][Green Version]
- Dixon, K.; Mass, C.F.; Hakim, G.J.; Holzworth, R.H. The Impact of Lightning Data Assimilation on Deterministic and Ensemble Forecasts of Convective Events. J. Atmos. Ocean. Technol. 2016, 33, 1801–1823. [Google Scholar] [CrossRef]
- Accadia, C.; Mariani, S.; Casaioli, M.; Lavagnini, A.; Speranza, A. Sensitivity of Precipitation Forecast Skill Scores to Bilinear Interpolation and a Simple Nearest-Neighbor Average Method on High-Resolution Verification Grids. Weather Forecast. 2003, 18, 918–932. [Google Scholar] [CrossRef]
- Mesinger, F. Improvements in Quantitative Precipitation Forecasts with the Eta Regional Model at the National Centers for Environmental Prediction: The 48-km Upgrade. Bull. Am. Meteorol. Soc. 1996, 77, 2637–2649. [Google Scholar] [CrossRef][Green Version]
- Levine, R.A.; Wilks, D.S. Statistical Methods in the Atmospheric Sciences. J. Am. Stat. Assoc. 2000, 95, 344. [Google Scholar] [CrossRef]
- Navarro, A.; García-Ortega, E.; Merino, A.; Sánchez, J.L.; Kummerow, C.; Tapiador, F.J. Assessment of IMERG Precipitation Estimates over Europe. Remote Sens. 2019, 11, 2470. [Google Scholar] [CrossRef]
- Fierro, A.O.; Gao, J.; Ziegler, C.L.; Calhoun, K.M.; Mansell, E.R.; MacGorman, D.R. Assimilation of Flash Extent Data in the Variational Framework at Convection-Allowing Scales: Proof-of-Concept and Evaluation for the Short-Term Forecast of the 24 May 2011 Tornado Outbreak. Mon. Weather Rev. 2016, 144, 4373–4393. [Google Scholar] [CrossRef]
- Pessi, A.T.; Businger, S. The Impact of Lightning Data Assimilation on a Winter Storm Simulation over the North Pacific Ocean. Mon. Weather Rev. 2009, 137, 3177–3195. [Google Scholar] [CrossRef]


| Correlation Coefficient Threshold | ||||
|---|---|---|---|---|
| R | 0.1 | 0.3 | 0.5 | 0.7 |
| CTRL | 24,783 | 16,237 | 5476 | 731 |
| LIGHT | 24,908 | 18,327 | 8067 | 1242 |
| AC | CTRL | LIGHT | Variation (%) |
|---|---|---|---|
| LAND_3 h | 0.50 | 0.53 | 5% |
| SEA_3 h | 0.44 | 0.49 | 8% |
| Elba | Giglio | Lipari | Montecristo | Pantelleria | Ponza | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | L | C | L | C | L | C | L | C | L | C | L | |
| RMSE (mm) | 1.76 | 1.36 | 4.36 | 4.22 | 2.34 | 1.50 | 2.26 | 2.15 | 1.39 | 1.32 | 2.46 | 2.60 |
| r | 0.70 | 0.83 | 0.45 | 0.49 | 0.58 | 0.78 | 0.40 | 0.47 | 0.49 | 0.54 | 0.66 | 0.60 |
| Elba | Giglio | Lipari | Montecristo | Pantelleria | Ponza | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | L | C | L | C | L | C | L | C | L | C | L | |
| RMSE (mm) | 7.09 | 5.28 | 13.33 | 11.64 | 6.19 | 4.65 | 8.20 | 8.19 | 4.45 | 3.78 | 9.93 | 11.61 |
| r | 0.71 | 0.85 | 0.50 | 0.60 | 0.85 | 0.92 | 0.48 | 0.48 | 0.81 | 0.91 | 0.62 | 0.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torcasio, R.C.; Federico, S.; Comellas Prat, A.; Panegrossi, G.; D'Adderio, L.P.; Dietrich, S. Impact of Lightning Data Assimilation on the Short-Term Precipitation Forecast over the Central Mediterranean Sea. Remote Sens. 2021, 13, 682. https://doi.org/10.3390/rs13040682
Torcasio RC, Federico S, Comellas Prat A, Panegrossi G, D'Adderio LP, Dietrich S. Impact of Lightning Data Assimilation on the Short-Term Precipitation Forecast over the Central Mediterranean Sea. Remote Sensing. 2021; 13(4):682. https://doi.org/10.3390/rs13040682
Chicago/Turabian StyleTorcasio, Rosa Claudia, Stefano Federico, Albert Comellas Prat, Giulia Panegrossi, Leo Pio D'Adderio, and Stefano Dietrich. 2021. "Impact of Lightning Data Assimilation on the Short-Term Precipitation Forecast over the Central Mediterranean Sea" Remote Sensing 13, no. 4: 682. https://doi.org/10.3390/rs13040682
APA StyleTorcasio, R. C., Federico, S., Comellas Prat, A., Panegrossi, G., D'Adderio, L. P., & Dietrich, S. (2021). Impact of Lightning Data Assimilation on the Short-Term Precipitation Forecast over the Central Mediterranean Sea. Remote Sensing, 13(4), 682. https://doi.org/10.3390/rs13040682









