A Modeling Approach for Predicting the Resolution Capability in Terrestrial Laser Scanning
Abstract
1. Introduction
2. Phase-Based LiDAR
3. Mixed Pixel and Resolution Capability Models
3.1. Mixed Pixel Bias
3.2. Resolution Capability
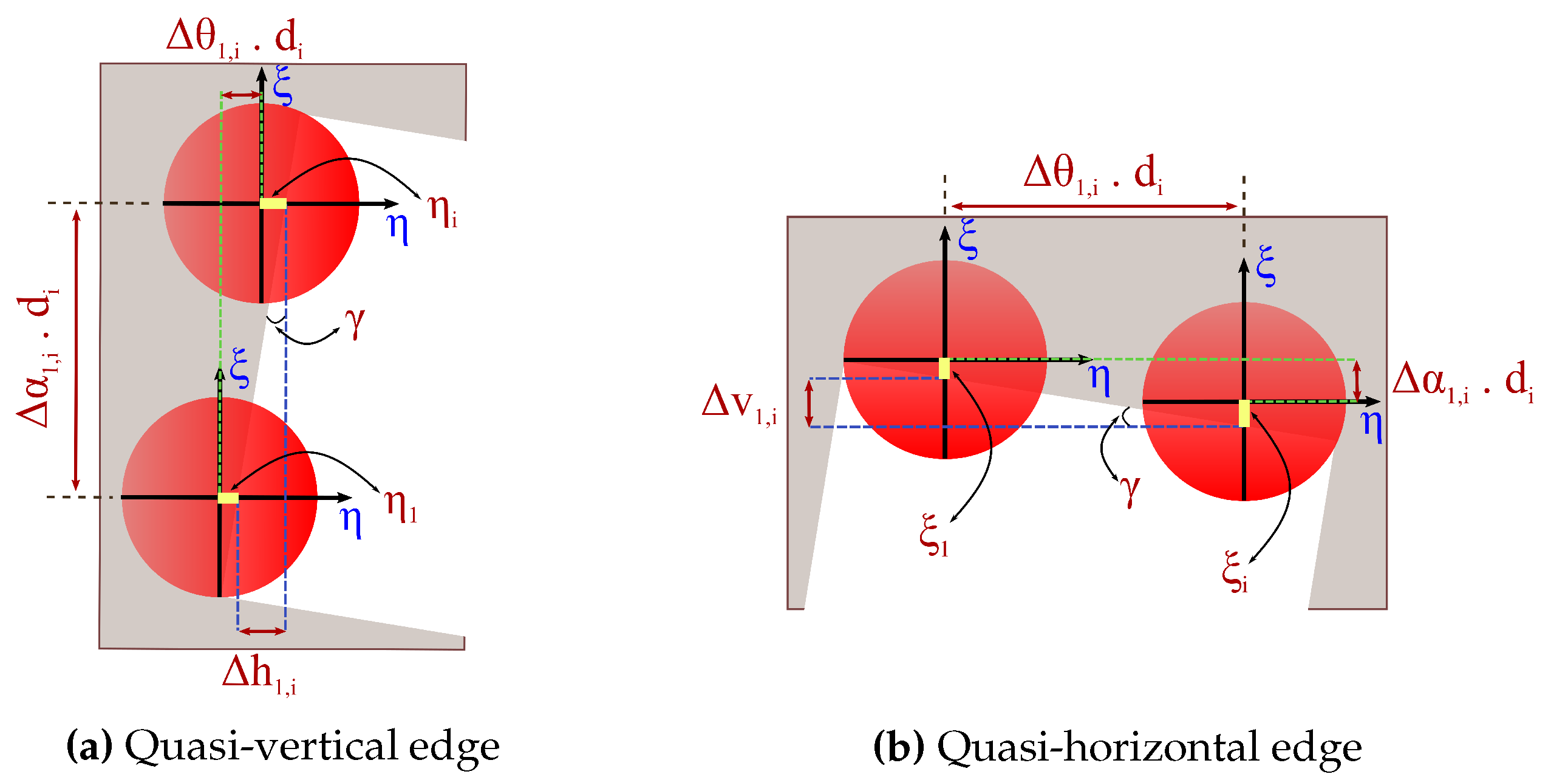
4. Practical Approach for Mixed Pixel Analysis
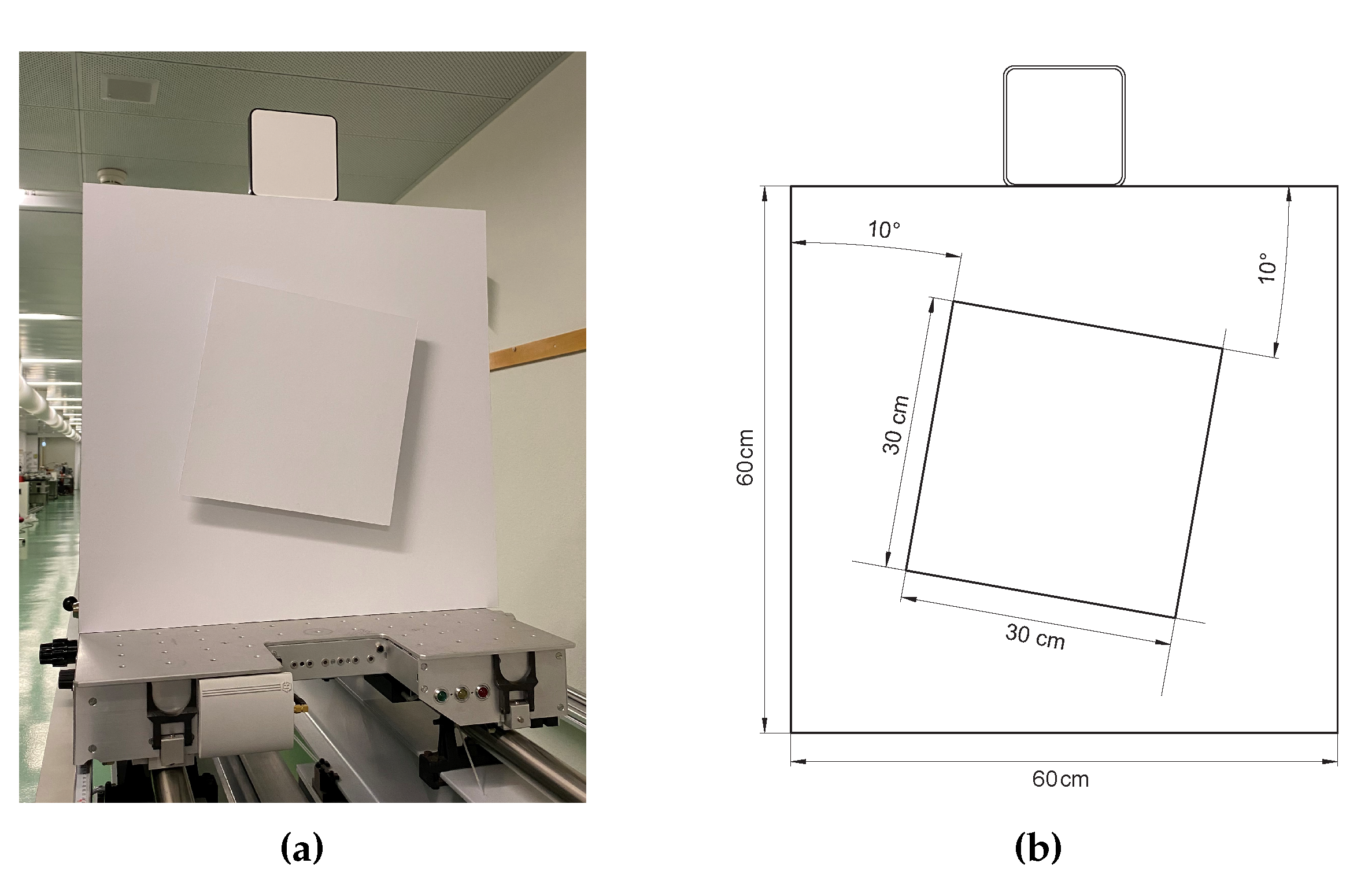
4.1. Experimental Investigation
4.2. Numerical Simulation
5. Experimental Results
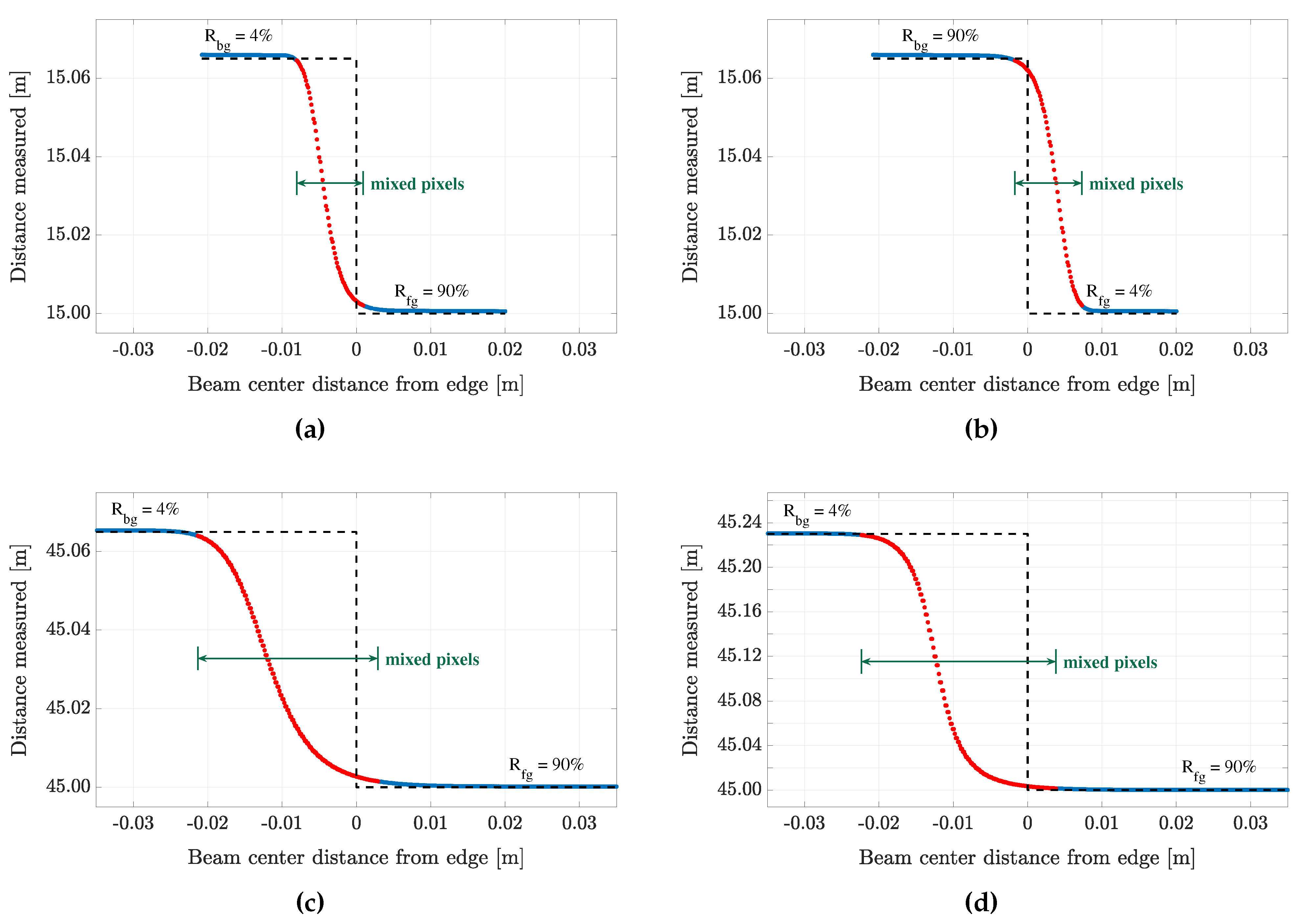
5.1. Mixed Pixels
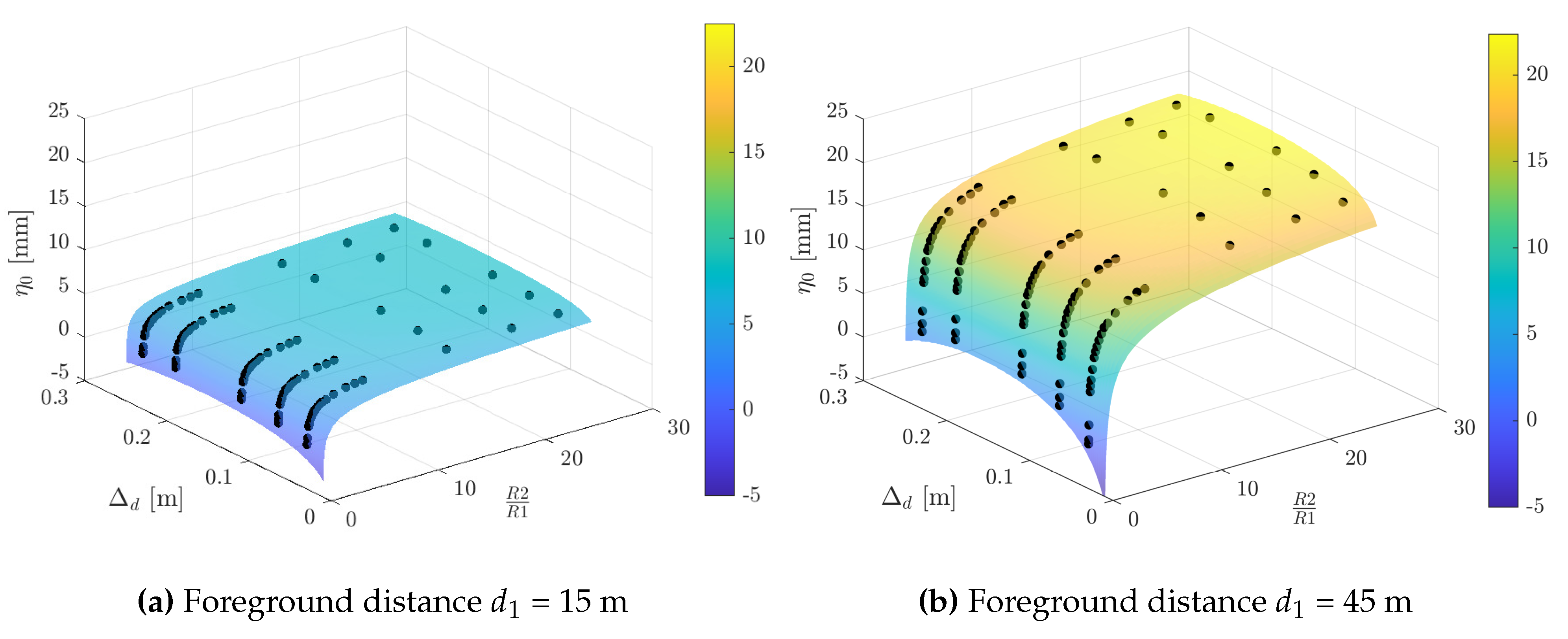
5.2. Beam Parameter Estimation
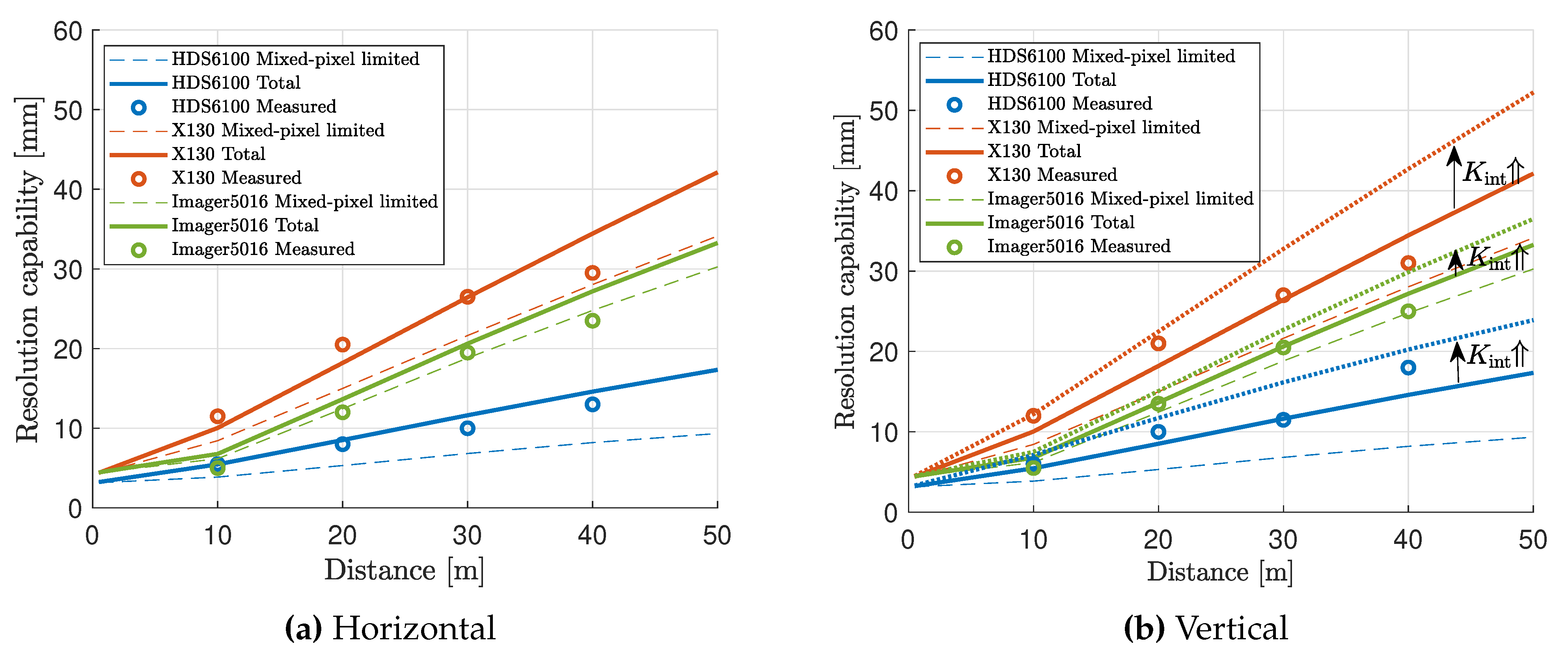
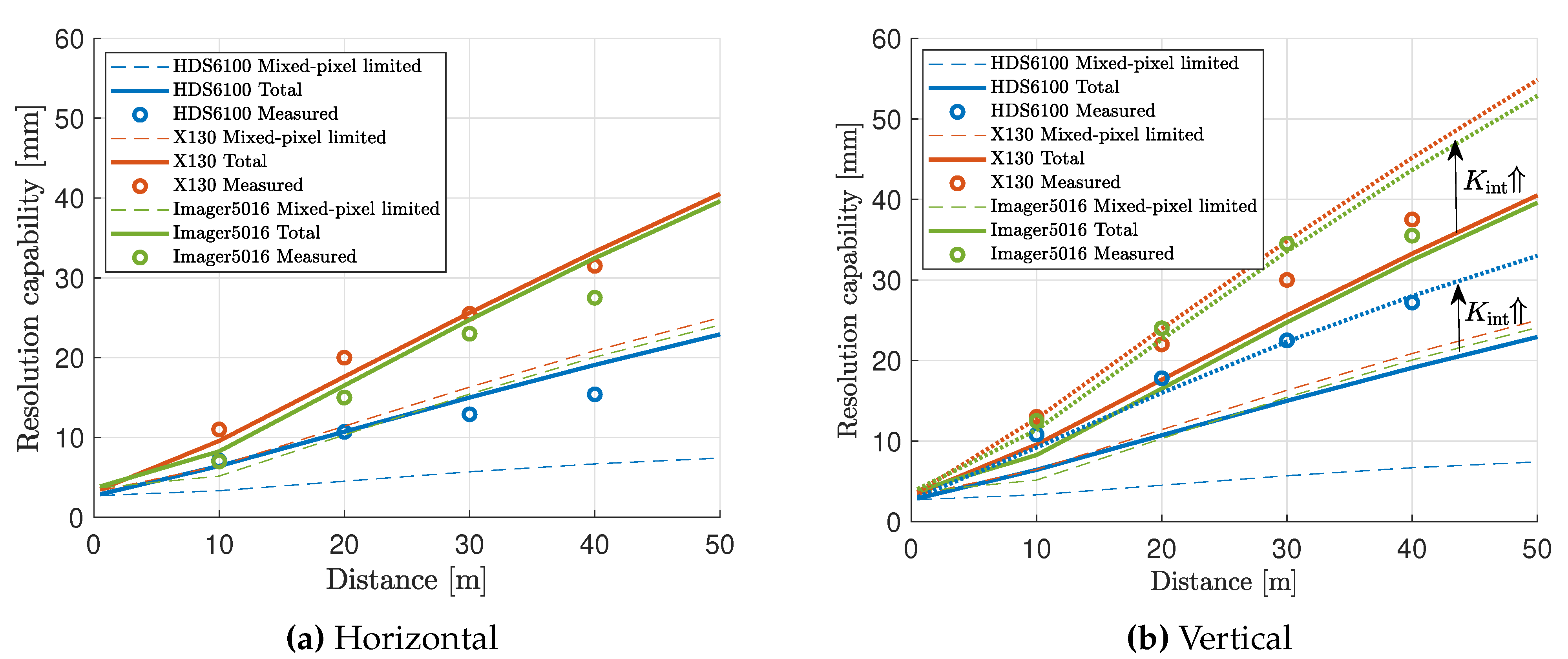
6. Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lichti, D.D.; Gordon, S.J.; Tipdecho, T. Error Models and Propagation in Directly Georeferenced Terrestrial Laser Scanner Networks. J. Surv. Eng. 2005, 131, 135–142. [Google Scholar] [CrossRef]
- Kim, M.K.; Sohn, H.; Chang, C.C. Automated dimensional quality assessment of precast concrete panels using terrestrial laser scanning. Autom. Constr. 2014, 45, 163–177. [Google Scholar] [CrossRef]
- Wang, Q.; Kim, M.K.; Cheng, J.C.P.; Sohn, H. Automated quality assessment of precast concrete elements with geometry irregularities using terrestrial laser scanning. Autom. Constr. 2016, 68, 170–182. [Google Scholar] [CrossRef]
- Tang, P.; Akinci, B.; Huber, D. Quantification of edge loss of laser scanned data at spatial discontinuities. Autom. Constr. 2009, 18, 1070–1083. [Google Scholar] [CrossRef]
- Godbaz, J.P.; Dorrington, A.A.; Cree, M.J. Understanding and Ameliorating Mixed Pixels and Multipath Interference in AMCW Lidar. In TOF Range-Imaging Cameras; Springer: Berlin/Heidelberg, Germany, 2013; pp. 91–116. ISBN 978-3-642-27523-4. [Google Scholar]
- Hodge, R.A. Using simulated Terrestrial Laser Scanning to analyse errors in high-resolution scan data of irregular surfaces. ISPRS J. Photogramm. Remote Sens. 2010, 65, 227–240. [Google Scholar] [CrossRef]
- Olsen, M.J.; Kuester, F.; Chang, B.J.; Hutchinson, T.C. Terrestrial laser scanning-based structural damage assessment. J. Comput. Civ. Eng. 2010, 24, 264–272. [Google Scholar] [CrossRef]
- Hebert, M.; Krotkov, E. 3D measurements from imaging laser radars: How good are they? Image Vis. Comput. 1992, 10, 170–178. [Google Scholar] [CrossRef]
- Adams, M.D.; Probert, P.J. The Interpretation of Phase and Intensity Data from AMCW Light Detection Sensors for Reliable Ranging. Int. J. Robot. Res. 1996, 15, 441–458. [Google Scholar] [CrossRef]
- Tuley, J.; Vandapel, N.; Hebert, M. Analysis and Removal of Artifacts in 3-D LADAR Data. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; Volume 15, pp. 2203–2210. [Google Scholar]
- Tang, P.; Huber, D.; Akinci, B. A comparative analysis of depth-discontinuity and mixed-pixel detection algorithms. In Proceedings of the Sixth International Conference on 3-D Digital Imaging and Modeling (3DIM 2007), Montreal, QC, Canada, 21–23 August 2007; pp. 29–38. [Google Scholar]
- Wang, Q.; Sohn, H.; Cheng, J.C.P. Development of a mixed pixel filter for improved dimension estimation using AMCW laser scanner. ISPRS J. Photogramm. Remote Sens. 2016, 119, 246–258. [Google Scholar] [CrossRef]
- Wang, Q.; Sohn, H.; Cheng, J.C.P. Development of high-accuracy edge line estimation algorithms using terrestrial laser scanning. Autom. Constr. 2019, 101, 59–71. [Google Scholar] [CrossRef]
- Wang, Q.; Tan, Y.; Mei, Z. Computational methods of acquisition and processing of 3D point cloud data for construction applications. Arch. Comput. Methods Eng. 2020, 27, 479–499. [Google Scholar] [CrossRef]
- Schmitz, B.; Kuhlmann, H.; Holst, C. Investigating the resolution capability of terrestrial laser scanners and its impact on the effective number of measurements. ISPRS J. Photogramm. Remote Sens. 2020, 159, 41–52. [Google Scholar] [CrossRef]
- Lichti, D.D.; Jamtsho, S. Angular resolution of terrestrial laser scanners. Photogramm. Rec. 2006, 21, 141–160. [Google Scholar] [CrossRef]
- Boehler, W.; Vicent, M.B.; Marbs, A. Investigating laser scanner accuracy. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2003, 34, 696–701. [Google Scholar]
- Lichti, D.D. A resolution measure for terrestrial laser scanners. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 34, B5. [Google Scholar]
- Pesci, A.; Teza, G.; Bonali, E. Terrestrial Laser Scanner Resolution: Numerical Simulations and Experiments on Spatial Sampling Optimization. Remote Sens. 2011, 3, 167–184. [Google Scholar] [CrossRef]
- Huxhagen, U.; Kern, F.; Siegrist, B. Untersuchung zum Auflösungsvermögen terrestrischer Laserscanner mittels Böhler-Stern. DGPF Tagungsband 2011, 20, 409–418. [Google Scholar]
- Schmitz, B.; Coopmann, D.; Kuhlmann, H.; Holst, C. Using the Resolution Capability and the Effective Num-ber of Measurements to Select the “Right” Terrestrial Laser Scanner. In Proceedings of the Contributions to International Conferences on Engineering Surveying, Dubrovnik, Croatia, 1–4 April 2020; pp. 92–104. [Google Scholar]
- Marshall, G.F. Gaussian laser beam diameters. In Laser Beam Scanning: Opto-Mechanical Devices, Systems, and Data Storage Optics; Marcel Dekker, Inc.: New York, NY, USA, 1985; pp. 289–301. [Google Scholar]
- Milonni, P.W.; Eberly, J.H. Laser Physics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Saleh, B.; Teich, M. Fundamentals of Photonics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2019; ISBN 9781119506874. [Google Scholar]
- Rüeger, J.M. Electronic Distance Measurement: An Introduction; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Proakis, J.G.; Salehi, M. Digital Communications, 5th ed.; McGraw Hill: New York, NY, USA, 2007. [Google Scholar]
- Chaudhry, S.; Salido-Monzú, D.; Wieser, A. Simulation of 3D laser scanning with phase-based EDM for the prediction of systematic deviations. In Proceedings of the International Society for Optics and Photonics (SPIE), Munich, Germany, 24–27 June 2019; Volume 11057, pp. 92–104. [Google Scholar]
- Braasch, M.S.; Van Dierendonck, A.J. GPS Receiver Architectures and Measurements. Proc. IEEE 1999, 87, 48–64. [Google Scholar] [CrossRef]
- Self, S.A. Focusing of spherical Gaussian beams. Appl. Opt. 1983, 22, 658–661. [Google Scholar] [CrossRef] [PubMed]
- Siegman, A.E.; Sasnett, M.W.; Johnston, T.F. Choice of clip levels for beam width measurements using knife-edge techniques. IEEE J. Quantum Electron. 1991, 27, 1098–1104. [Google Scholar] [CrossRef]
- Siegman, A.E. How to (maybe) measure laser beam quality. In Diode Pumped Solid State Lasers: Applications and Issues; DPSS: Washington, DC, USA, 1998; Volume 27, p. MQ1. [Google Scholar]
- Soudarissanane, S.S. The Geometry of Terrestrial Laser Scanning; Identification of Errors, Modeling and Mitigation of Scanning Geometry. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 2016. [Google Scholar]
- Rees, W.G. Physical Principles of Remote Sensing; Scott Polar Research Institute: Cambridge, UK, 2001. [Google Scholar]
- Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-Range Photogrammetry and 3D Imaging; De Gruyter: Berlin, Germany, 2020; ISBN 9783110607246. [Google Scholar]





| Foreground Distance [m] | Beam Radius w [mm] | |||
|---|---|---|---|---|
| 6.0 | 1.8 | 2.0 | 1.9 | 2.1 |
| 21.4 | 7.0 | 7.0 | 7.7 | 7.7 |
| 25.0 | 8.2 | 8.2 | 9.0 | 9.2 |
| 40.0 | 13.3 | 13.7 | 15.4 | 14.9 |
| 51.8 | 17.3 | 17.3 | 20.1 | 19.8 |
| Dimension | Estimated Beam Waist | Estimated Beam Divergence | ||||
|---|---|---|---|---|---|---|
| Position | Radius | Half Angle | ||||
| [m] | [m] | [mm] | [mm] | [mrad] | [mrad] | |
| hz | 2.15 | 0.1 | 1.35 | 0.01 | 0.35 | 0.003 |
| vt | 1.93 | 0.1 | 1.22 | 0.02 | 0.39 | 0.006 |
| [mm @ 10 m] | Quality Setting | Beam Radius w [mm] | |||
|---|---|---|---|---|---|
| 0.8 | premium | 7.0 | 7.0 | 7.7 | 7.7 |
| 1.6 | premium | 7.1 | 7.0 | 9.3 | 9.3 |
| 3.2 | premium | 7.3 | 7.2 | 13.9 | 14.1 |
| 0.8 | high | 7.1 | 7.0 | 7.7 | 7.6 |
| 1.6 | high | 7.1 | 6.9 | 9.3 | 9.2 |
| 3.2 | high | 7.5 | 7.4 | 14.1 | 14.0 |
| 1.6 | normal | 7.1 | 7.0 | 9.3 | 9.3 |
| 3.2 | low | 7.1 | 7.3 | 13.9 | 13.8 |
| Scanner | Beam Waist Radius [mm] | Beam Waist Position [m] | Divergence Half-Angle [mrad] | Range Noise Standard Deviation [mm] | |
|---|---|---|---|---|---|
| High-Quality | Low-Quality | ||||
| Leica HDS6100 | 1.5 | 0 | 0.11 | 0.72 @ 10 m 2.00 @ 50 m | 1.44 @ 10 m 4.00 @ 50 m |
| Faro Focus X130 | 1.6 | 0 | 0.27 | 0.26 @ 10 m 0.44 @ 50 m | 1.47 @ 10 m 2.51 @ 50 m |
| Z&F Imager 5016 | 1.6 | 3.43 | 0.3 | 0.14 @ 10 m 0.30 @ 50 m | 0.42 @ 10 m 0.85 @ 50 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaudhry, S.; Salido-Monzú, D.; Wieser, A. A Modeling Approach for Predicting the Resolution Capability in Terrestrial Laser Scanning. Remote Sens. 2021, 13, 615. https://doi.org/10.3390/rs13040615
Chaudhry S, Salido-Monzú D, Wieser A. A Modeling Approach for Predicting the Resolution Capability in Terrestrial Laser Scanning. Remote Sensing. 2021; 13(4):615. https://doi.org/10.3390/rs13040615
Chicago/Turabian StyleChaudhry, Sukant, David Salido-Monzú, and Andreas Wieser. 2021. "A Modeling Approach for Predicting the Resolution Capability in Terrestrial Laser Scanning" Remote Sensing 13, no. 4: 615. https://doi.org/10.3390/rs13040615
APA StyleChaudhry, S., Salido-Monzú, D., & Wieser, A. (2021). A Modeling Approach for Predicting the Resolution Capability in Terrestrial Laser Scanning. Remote Sensing, 13(4), 615. https://doi.org/10.3390/rs13040615







