Estimating Coastal Chlorophyll-A Concentration from Time-Series OLCI Data Based on Machine Learning
Abstract
1. Introduction
2. Study Area and Data
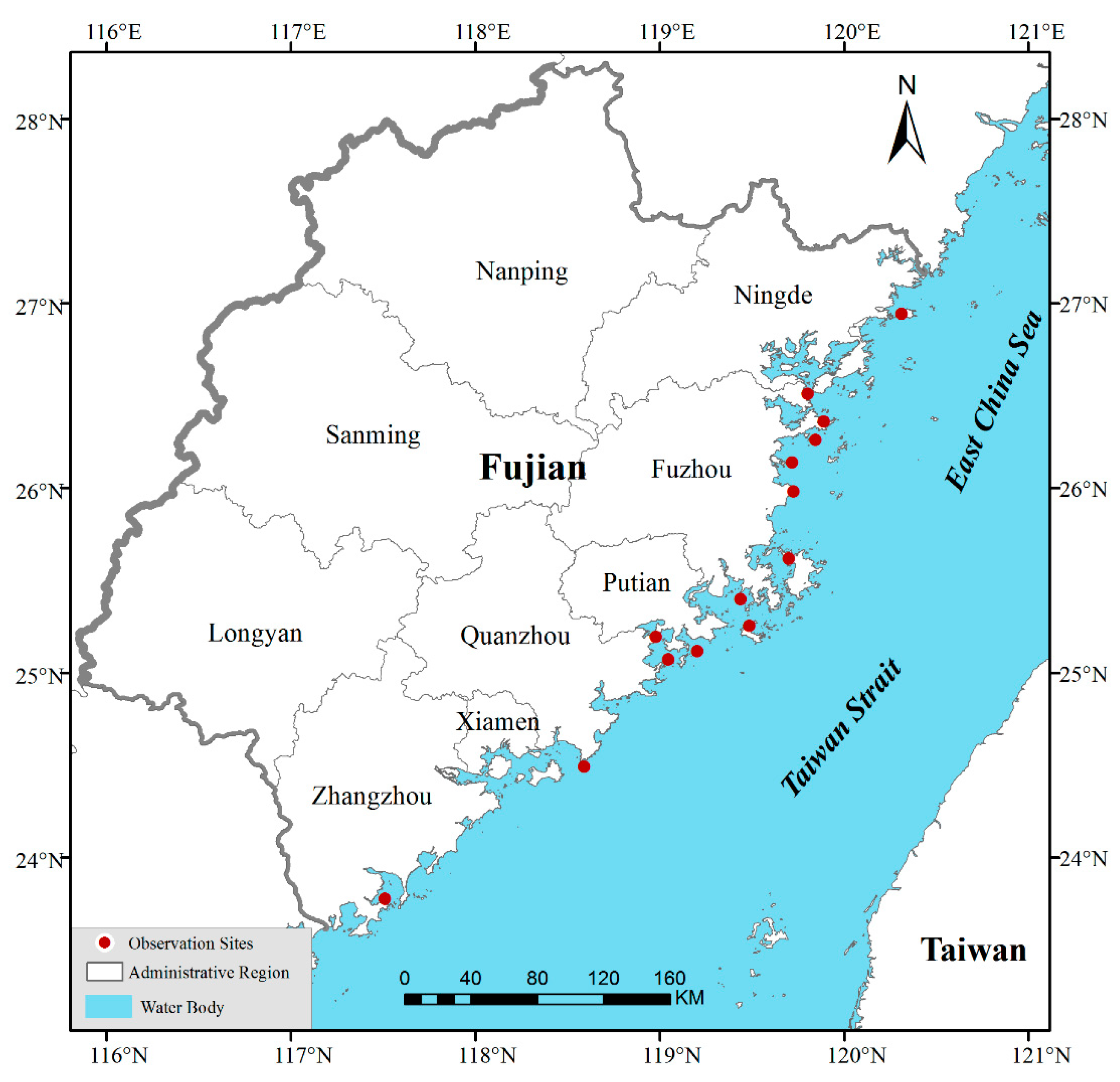
2.1. Study Area and In Situ Data
2.2. Satellite Data and Preprocessing
3. Methods
3.1. LightGBM
3.2. Input Variables
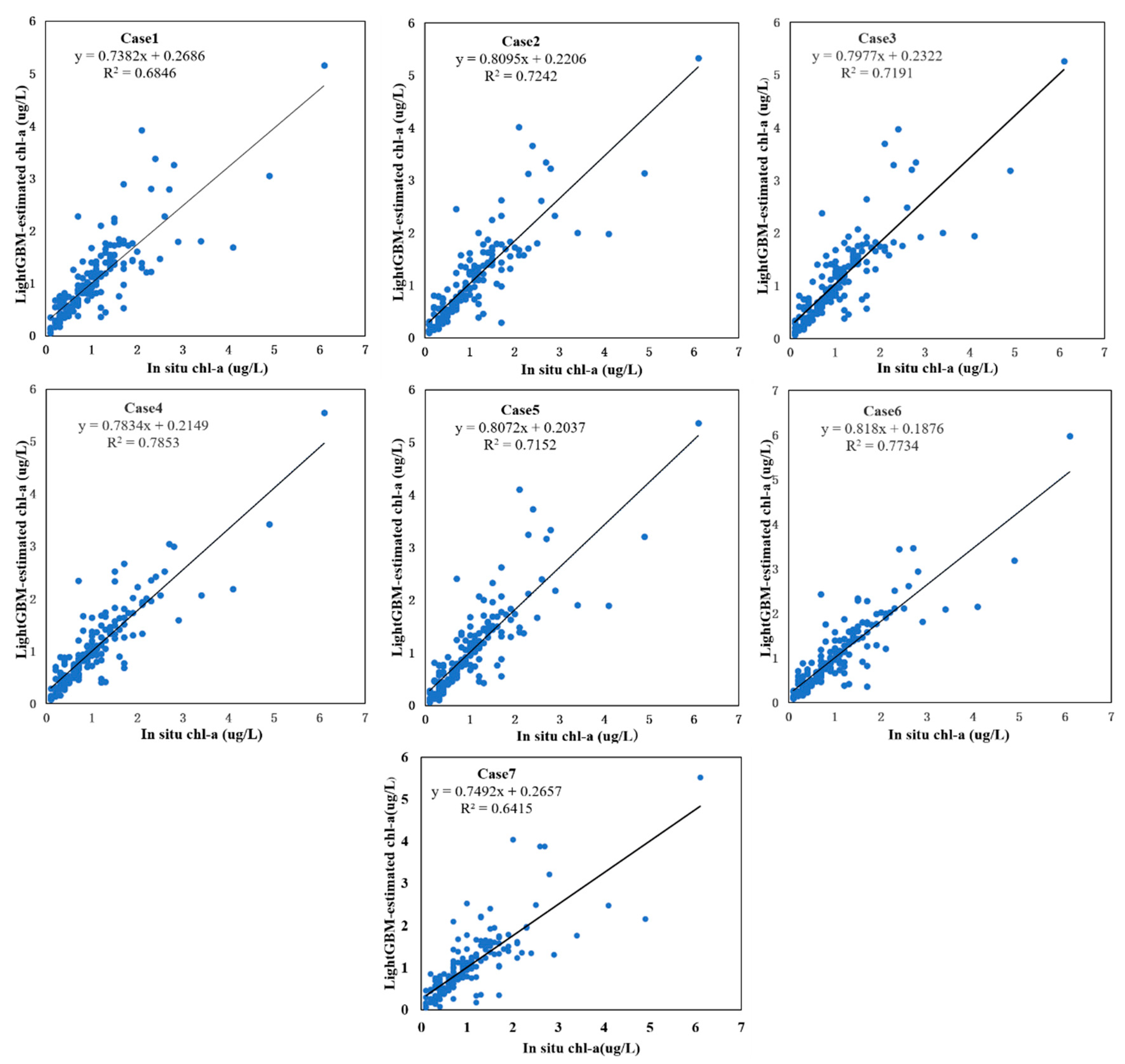
3.3. Experimental Design
4. Results
4.1. Optimal Input Feature Variables
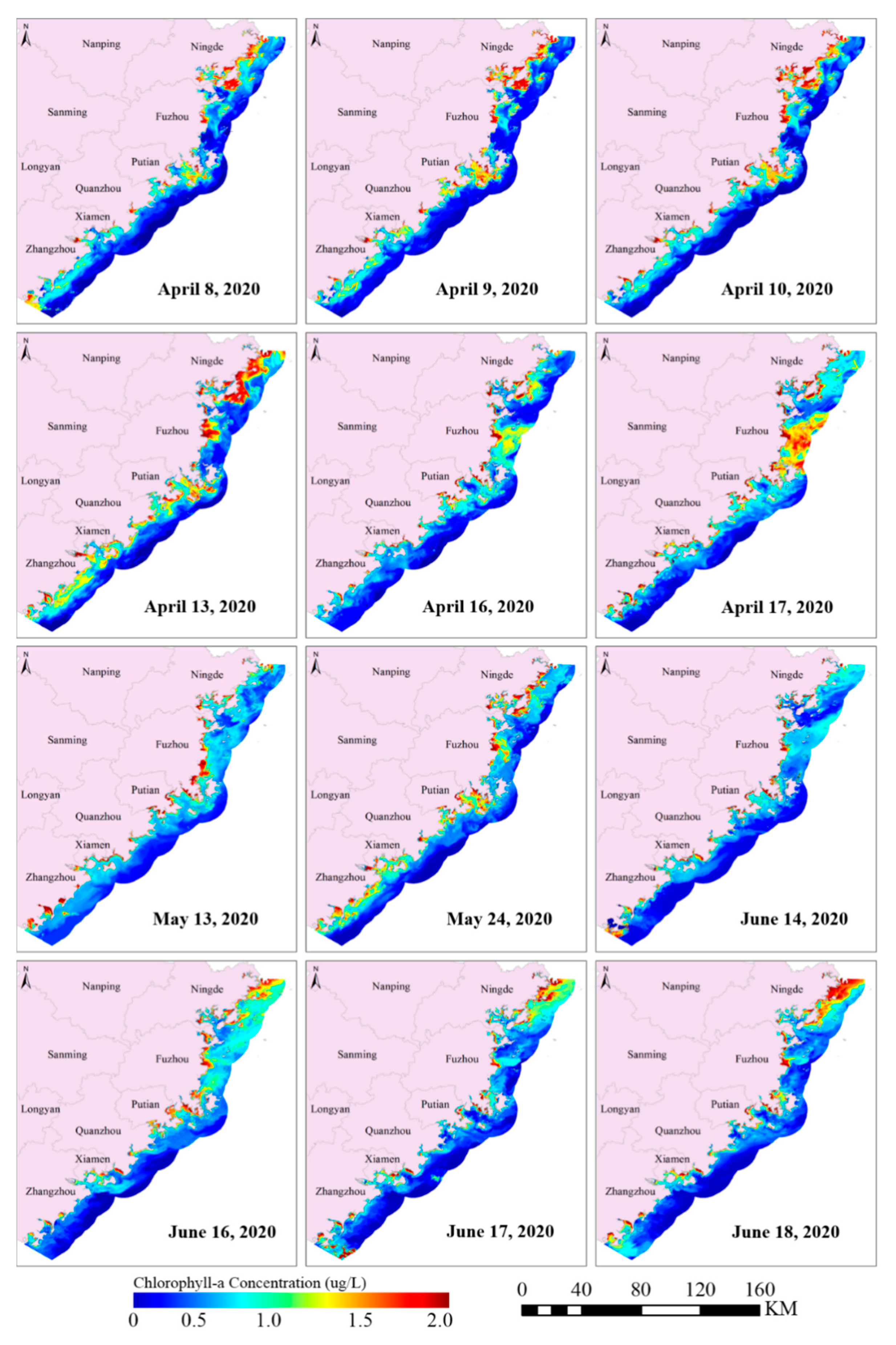
4.2. Mapping Chl-a Concentration from the OLCI Images
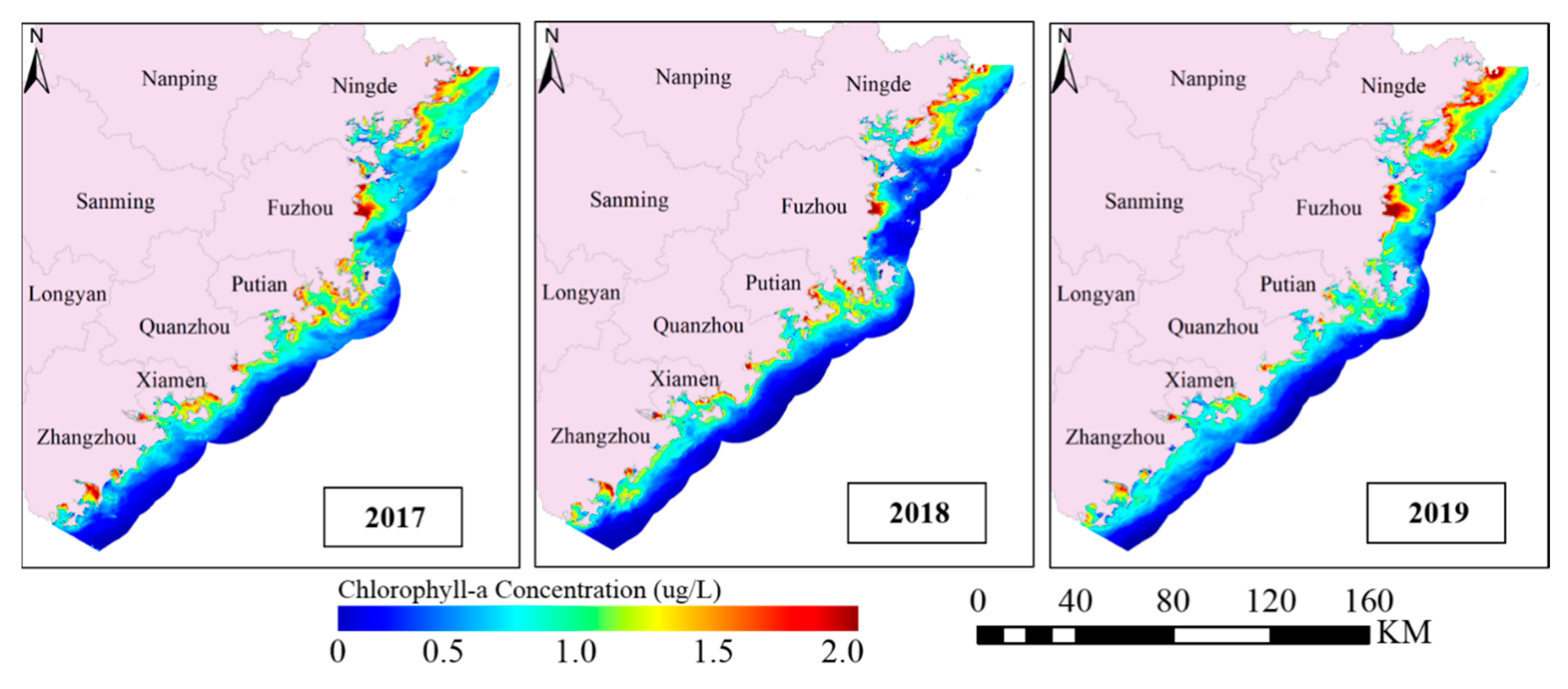
4.3. Spatiotemporal Distribution Analysis
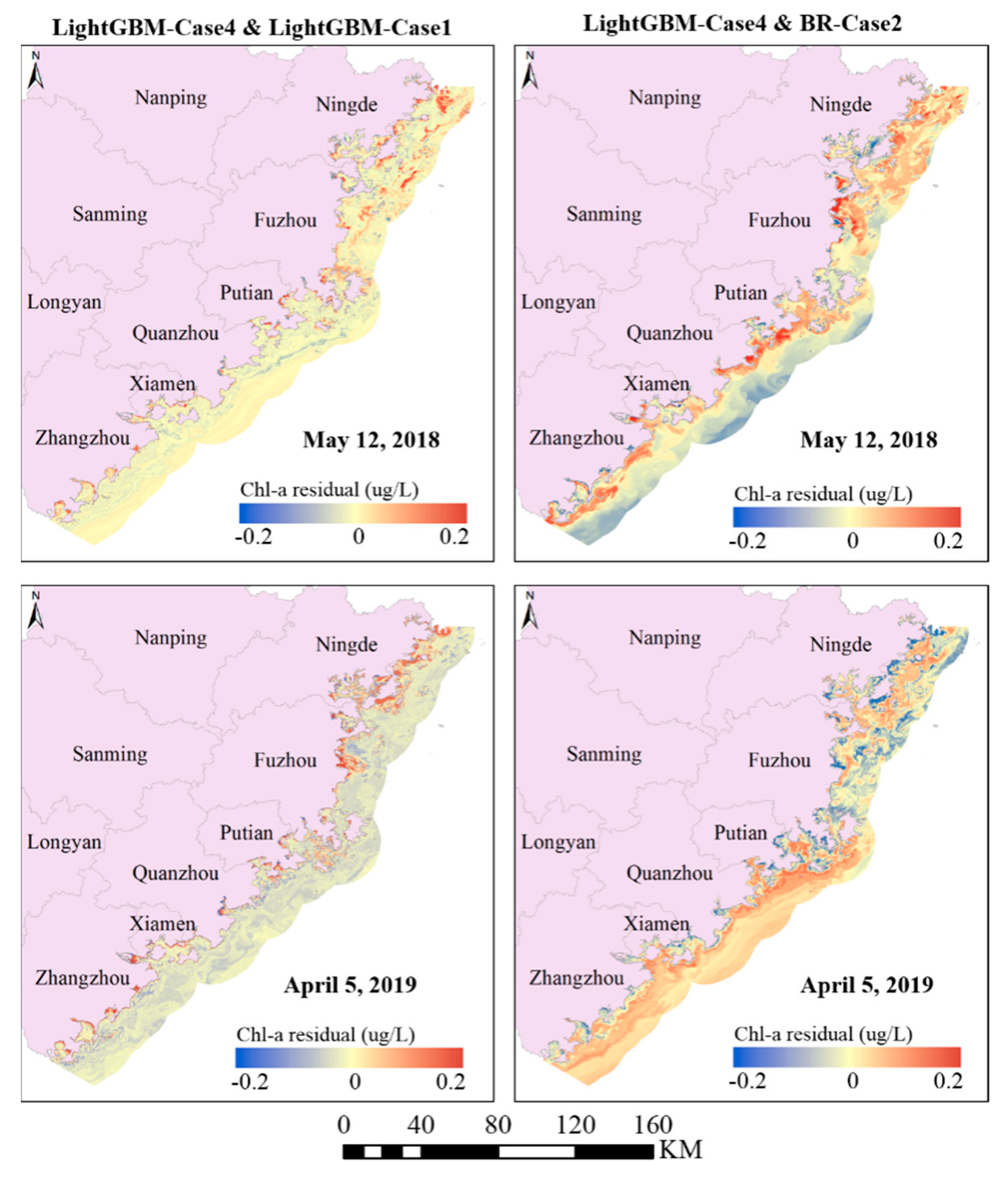
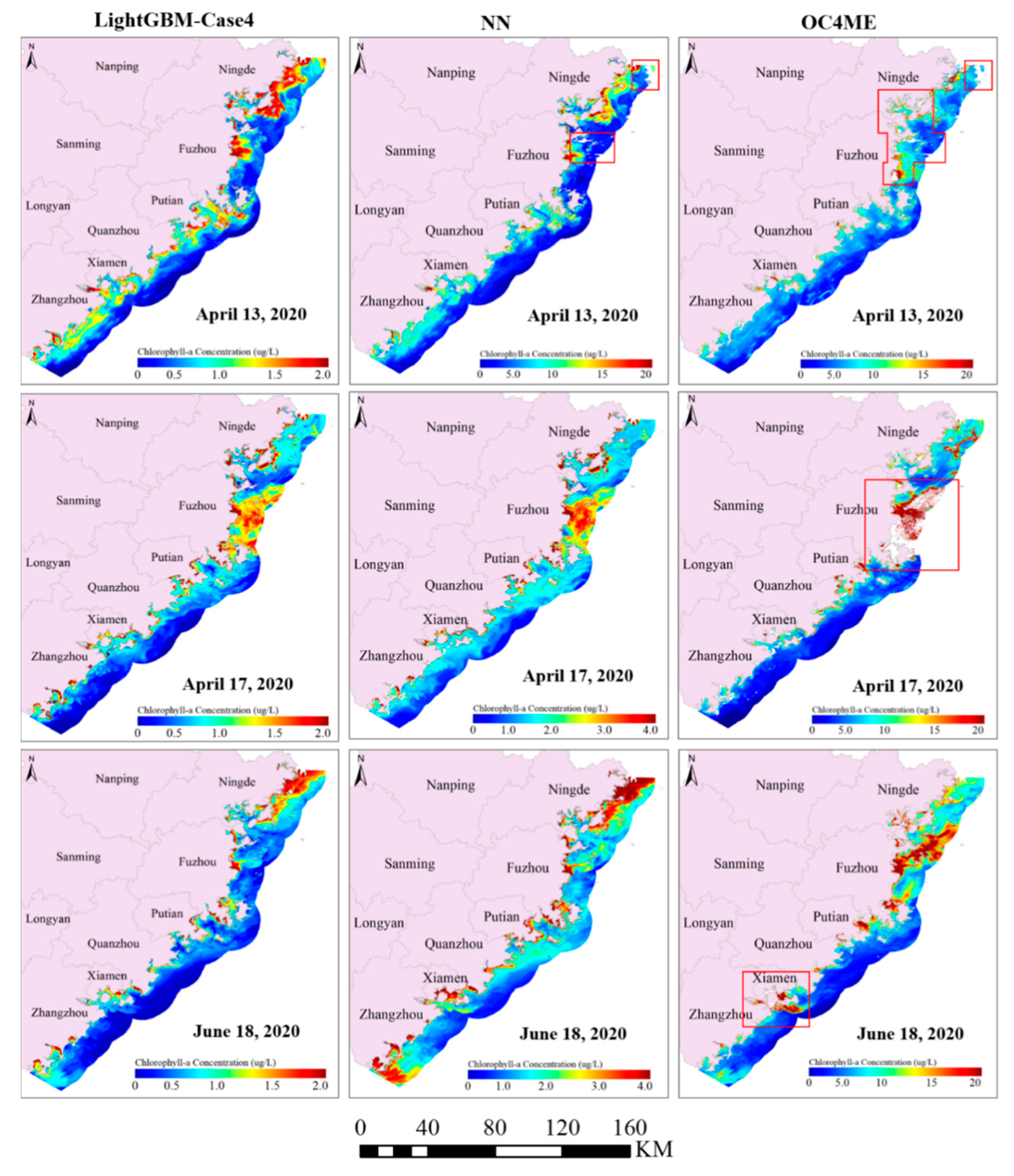
4.4. Comparison with Other Previous Algorithms and OLCI L2 Products
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harvey, E.T.; Kratzer, S.; Philipson, P. Satellite-based water quality monitoring for improved spatial and temporal retrieval of chlorophyll-a in coastal waters. Remote Sens. Environ. 2015, 158, 417–430. [Google Scholar] [CrossRef]
- Blix, K.; Li, J.; Massicotte, P.; Matsuoka, A. Developing a New Machine-Learning Algorithm for Estimating Chlorophyll-a Concentration in Optically Complex Waters: A Case Study for High Northern Latitude Waters by Using Sentinel 3 OLCI. Remote Sens. 2019, 11, 2076. [Google Scholar] [CrossRef]
- Harding, L.W., Jr.; Mallonee, M.E.; Perry, E.S. Toward a Predictive Understanding of Primary Productivity in a Temperate, Partially Stratified Estuary. Estuar. Coast. Shelf Sci. 2002, 55, 437–463. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Povazhnyy, V. Estimation of chlorophyll- a concentration in case II waters using MODIS and MERIS data—successes and challenges. Environ. Res. Lett. 2009, 4, 045005. [Google Scholar] [CrossRef]
- Hafeez, S.; Wong, M.S.; Ho, H.C.; Nazeer, M.; Nichol, J.E.; Abbas, S.; Tang, D.; Lee, K.-H.; Pun, L. Comparison of Machine Learning Algorithms for Retrieval of Water Quality Indicators in Case-II Waters: A Case Study of Hong Kong. Remote Sens. 2019, 11, 617. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Werdell, P.J. Chlorophyll algorithms for ocean color sensors—OC4, OC5 & OC6. Remote Sens. Environ. 2019, 229, 32–47. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R.; Clark, D.K.; Brown, J.W.; Brown, O.B.; Evans, R.H.; Broenkow, W.W. Phytoplankton pigment concentrations in the Middle Atlantic Bight: Comparison of ship determinations and CZCS estimates. Appl. Opt. 1983, 22, 20–36. [Google Scholar] [CrossRef]
- George, D.G.; Malthus, T.J. Using a compact airborne spectrographic imager to monitor phytoplankton biomass in a series of lakes in north Wales. Sci. Total Environ. 2001, 268, 215–226. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Shen, Q.; Zhang, B.; Tian, L.; Ye, H.; Wang, S.; Lu, Z. A soft-classification-based chlorophyll-a estimation method using MERIS data in the highly turbid and eutrophic Taihu Lake. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 138–149. [Google Scholar] [CrossRef]
- Yang, Z.; Reiter, M.; Munyei, N. Estimation of chlorophyll-a concentrations in diverse water bodies using ratio-based NIR/Red indices. Remote Sens. Appl. Soc. Environ. 2017, 6, 52–58. [Google Scholar] [CrossRef]
- Tao, B.; Mao, Z.; Pan, D.; Shen, Y.; Zhu, Q.; Chen, J. Influence of bio-optical parameter variability on the reflectance peak position in the red band of algal bloom waters. Ecol. Inform. 2013, 16, 17–24. [Google Scholar] [CrossRef]
- Watanabe, F.S.Y.; Alcântara, E.; Stech, J.L. High performance of chlorophyll- a prediction algorithms based on simulated OLCI Sentinel-3A bands in cyanobacteria-dominated inland waters. Adv. Space Res. 2018, 62, 265–273. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Gower, J.F.R.; Doerffer, R.; Borstad, G.A. Interpretation of the 685nm peak in water-leaving radiance spectra in terms of fluorescence, absorption and scattering, and its observation by MERIS. Int. J. Remote Sens. 2010, 20, 1771–1786. [Google Scholar] [CrossRef]
- El-Habashi, A.; Ioannou, I.; Tomlinson, M.C.; Stumpf, R.P.; Ahmed, S. Satellite Retrievals of Karenia brevis Harmful Algal Blooms in the West Florida Shelf Using Neural Networks and Comparisons with Other Techniques. Remote Sens. 2016, 8, 377. [Google Scholar] [CrossRef]
- Molkov, А.А.; Fedorov, S.V.; Pelevin, V.V.; Korchemkina, E.N. Regional Models for High-Resolution Retrieval of Chlorophyll a and TSM Concentrations in the Gorky Reservoir by Sentinel-2 Imagery. Remote Sens. 2019, 11, 1215. [Google Scholar] [CrossRef]
- Binding, C.E.; Greenberg, T.A.; Bukata, R.P. Time series analysis of algal blooms in Lake of the Woods using the MERIS maximum chlorophyll index. J. Plankton Res. 2011, 33, 1847–1852. [Google Scholar] [CrossRef]
- Hu, C. A novel ocean color index to detect floating algae in the global oceans. Remote Sens. Environ. 2009, 113, 2118–2129. [Google Scholar] [CrossRef]
- Chen, X.; Shang, S.; Lee, Z.; Qi, L.; Yan, J.; Li, Y. High-frequency observation of floating algae from AHI on Himawari-8. Remote Sens. Environ. 2019, 227, 151–161. [Google Scholar] [CrossRef]
- Garcia, R.A.; Fearns, P.; Keesing, J.K.; Liu, D. Quantification of floating macroalgae blooms using the scaled algae index. J. Geophys. Res. Oceans 2013, 118, 26–42. [Google Scholar] [CrossRef]
- Odermatt, D.; Gitelson, A.; Brando, E. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Dall’Olmo, G.; Moses, W.; Rundquist, D.; Barrow, T.; Fisher, T.R.; Gurlin, D.; Holz, J. A simple semi-analytical model for remote estimation of chlorophyll-a in turbid waters: Validation. Remote Sens. Environ. 2008, 112, 3582–3593. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Bryan, F. Chlorophyll-a Algorithms for Oligotrophic Oceans: A Novel Approach Based on Three-Band Reflectance Difference. J. Geophys. Res. Atmos. 2012, 117, 92–99. [Google Scholar] [CrossRef]
- Huang, C.; Zou, J.; Li, Y.; Yang, H.; Shi, K.; Li, J.; Wang, Y.; Chena, X.; Zheng, F. Assessment of NIR-red algorithms for observation of chlorophyll-a in highly turbid inland waters in China. ISPRS J. Photogramm. Remote Sens. 2014, 93, 29–39. [Google Scholar] [CrossRef]
- Sun, D.; Hu, C.; Qiu, Z.; Cannizzaro, J.P.; Barnes, B.B. Influence of a red band-based water classification approach on chlorophyll algorithms for optically complex estuaries. Remote Sens. Environ. 2004, 155, 289–302. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Lu, H. A four-band semi-analytical model for estimating chlorophyll a in highly turbid lakes: The case of Taihu Lake, China. Remote Sens. Environ. 2009, 113, 1175–1182. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Hà, N.; et al. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Charantonis, A.; Badran, F.; Thiria, S. Retrieving the evolution of vertical profiles of Chlorophyll-a from satellite observations using Hidden Markov Models and Self-Organizing Topological Maps. Remote Sens. Environ. 2015, 163, 229–239. [Google Scholar] [CrossRef]
- Ruescas, A.; Hieronymi, M.; Mateo-Garcia, G.; Koponen, S.; Kallio, K.; Camps-Valls, G. Machine Learning Regression Approaches for Colored Dissolved Organic Matter (CDOM) Retrieval with S2-MSI and S3-OLCI Simulated Data. Remote Sens. 2018, 10, 786. [Google Scholar] [CrossRef]
- Blix, K.; Pálffy, K.; Tóth, V.R.; Eltoft, T. Remote Sensing of Water Quality Parameters over Lake Balaton by Using Sentinel-3 OLCI. Water 2018, 10, 1428. [Google Scholar] [CrossRef]
- Lei, S.; Xu, J.; Li, Y.; Du, C.; Liu, G.; Zheng, Z.; Xu, Y.; Lyu, H.; Mu, M.; Miao, S.; et al. An approach for retrieval of horizontal and vertical distribution of total suspended matter concentration from GOCI data over Lake Hongze. Sci. Total Environ. 2020, 700, 134524. [Google Scholar] [CrossRef]
- Zhang, Y.; Pulliainen, J.; Koponen, S.; Hallikainen, M. Application of an empirical neural network to surface water quality estimation in the Gulf of Finland using combined optical data and microwave data. Remote Sens. Environ. 2002, 81, 327–336. [Google Scholar] [CrossRef]
- Kim, Y.-H.; Im, J.; Ha, H.K.; Choi, J.-K.; Ha, S. Machine learning approaches to coastal water quality monitoring using GOCI satellite data. GIScience Remote Sens. 2014, 51, 158–174. [Google Scholar] [CrossRef]
- Kong, X.; Sun, Y.; Su, R.; Shi, X. Real-time eutrophication status evaluation of coastal waters using support vector machine with grid search algorithm. Mar. Pollut. Bull. 2017, 119, 307–319. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Wu, L.; Ma, X.; Zhang, W.; Fan, J.; Yu, X.; Zeng, W.; Zhou, H. Evaluation of CatBoost method for prediction of reference evapotranspiration in humid regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
- Su, H.; Yang, X.; Lu, W.; Yan, X.-H. Estimating Subsurface Thermohaline Structure of the Global Ocean Using Surface Remote Sensing Observations. Remote Sens. 2019, 11, 1598. [Google Scholar] [CrossRef]
- Mouw, B.; Greb, S.; Aurin, D. Aquatic color radiometry remote sensing of coastal and inland waters: Challenges and recom-mendations for future satellite missions. Remote Sens. Environ. 2015, 160, 15–30. [Google Scholar] [CrossRef]
- Nazeer, M.; Nichol, J.E. Development and application of a remote sensing-based Chlorophyll-a concentration prediction model for complex coastal waters of Hong Kong. J. Hydrol. 2016, 532, 80–89. [Google Scholar] [CrossRef]
- Bernardo, N.; Watanabe, F.; Rodrigues, T.; Alcântara, E. Evaluation of the suitability of MODIS, OLCI and OLI for mapping the distribution of total suspended matter in the Barra Bonita Reservoir (Tietê River, Brazil). Remote Sens. Appl. Soc. Environ. 2016, 4, 68–82. [Google Scholar] [CrossRef]
- Fu, Y.; Xu, S.; Zhang, C.; Sun, Y. Spatial downscaling of MODIS Chlorophyll-a using Landsat 8 images for complex coastal water monitoring. Estuar. Coast. Shelf Sci. 2018, 209, 149–159. [Google Scholar] [CrossRef]
- Brockmann, C.; Doerffer, R.; Peters, M.; Kerstin, S.; Embacher, S.; Ruescas, A. Evolution of the C2RCC neural network for sentinel 2 and 3 for the retrieval of ocean colour products in normal and extreme optically complex waters. ESASP 2016, 740, 54. [Google Scholar]
- Toming, K.; Kutser, T.; Uiboupin, R.; Arikas, A.; Vahter, K.; Paavel, B. Mapping Water Quality Parameters with Sentinel-3 Ocean and Land Colour Instrument imagery in the Baltic Sea. Remote Sens. 2017, 9, 1070. [Google Scholar] [CrossRef]
- Kyryliuk, D.; Kratzer, S. Evaluation of Sentinel-3A OLCI Products Derived Using the Case-2 Regional CoastColour Processor over the Baltic Sea. Sensors 2019, 19, 3609. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]




| Band Number | Central Wavelength (nm) | Bandwidth (nm) | Signal-to-Noise Ratio |
|---|---|---|---|
| Band 3 | 442.5 | 10 | 1811 |
| Band 4 | 490 | 10 | 1541 |
| Band 5 | 510 | 10 | 1488 |
| Band 6 | 560 | 10 | 1280 |
| Band 7 | 620 | 10 | 997 |
| Band 8 | 665 | 10 | 883 |
| Band 9 | 673.75 | 7.5 | 707 |
| Band 10 | 681.25 | 7.5 | 745 |
| Band 11 | 708.75 | 10 | 785 |
| Band 12 | 753.75 | 7.5 | 605 |
| Feature Variables | The Full Name | Expression Forms | Reference |
|---|---|---|---|
| Spectral bands | Spectral bands | B3, B4, B5, B6, B7, B8, B9, B10, B11, B12 | [27] |
| BRI | Band ratio index | B11/B8 | [10] |
| B11/B9 | |||
| NDCI | Normalized difference chlorophyll index | (B11 − B8)/(B11 + B8) | [13] |
| (B11 − B9)/(B11 + B9) | |||
| NFHI | Normalized fluorescence height index | B10/B6 | [15] |
| B10/B9 | |||
| TBI | Three-band index | (1/B8 − 1/B11) × B12 | [22] |
| (1/B9 − 1/B11) × B12 |
| Experiment | Input Features |
|---|---|
| Case 1 | Spectral bands |
| Case 2 | Spectral bands + BRI |
| Case 3 | Spectral bands + NDCI |
| Case 4 | Spectral bands + NFHI |
| Case 5 | Spectral bands + TBI |
| Case 6 | All variables |
| Case 7 | Spectral indices |
| Parameters | Meaning (Default Values) | Ranges | Optimal Values |
|---|---|---|---|
| learning_rate | Shrinkage rate (0.1) | [0, 1] | 0.05 |
| n_estimators | The number of trees (100) | [1, ∝] | 400 |
| num_leaves | Max number of leaves in one tree (31) | [1, 131072] | 40 |
| lambda_L1 | L2 regularization (0) | [0, ∝] | 1 |
| lambda_L2 | L1 regularization (0) | [0, ∝] | 3 |
| boosting_type | Boosting type (gbdt) | gbdt, rf, dart, goss | gbdt |
| Experimental Cases | RMSE | MAE | MAPE (%) | R2 |
|---|---|---|---|---|
| Case 1 | 0.469 | 0.274 | 31.42 | 0.685 |
| Case 2 | 0.445 | 0.260 | 31.73 | 0.724 |
| Case 3 | 0.447 | 0.262 | 31.64 | 0.719 |
| Case 4 | 0.388 | 0.225 | 28.33 | 0.785 |
| Case 5 | 0.452 | 0.262 | 31.52 | 0.715 |
| Case 6 | 0.397 | 0.225 | 28.49 | 0.772 |
| Case 7 | 0.509 | 0.304 | 36.92 | 0.641 |
| Model | Expression | x-Variable | RMSE | R2 |
|---|---|---|---|---|
| BR-Case 1 | y = 4.2969x − 1.8276 | Rrs (708.75)/Rrs (665) | 0.635 | 0.586 |
| BR-Case 2 | y = 3.6923x − 1.6779 | Rrs (708.75)/Rrs (673.75) | 0.634 | 0.588 |
| TB-Case 1 | y = 15.416x + 2.426 | (Rrs (665) −1 − Rrs (681.25) −1) × Rrs (753.75) | 0.719 | 0.586 |
| TB-Case 2 | y = 12.952x + 1.956 | (Rrs (673.75) −1 − Rrs (681.25) −1) × Rrs (753.75) | 0.636 | 0.587 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, H.; Lu, X.; Chen, Z.; Zhang, H.; Lu, W.; Wu, W. Estimating Coastal Chlorophyll-A Concentration from Time-Series OLCI Data Based on Machine Learning. Remote Sens. 2021, 13, 576. https://doi.org/10.3390/rs13040576
Su H, Lu X, Chen Z, Zhang H, Lu W, Wu W. Estimating Coastal Chlorophyll-A Concentration from Time-Series OLCI Data Based on Machine Learning. Remote Sensing. 2021; 13(4):576. https://doi.org/10.3390/rs13040576
Chicago/Turabian StyleSu, Hua, Xuemei Lu, Zuoqi Chen, Hongsheng Zhang, Wenfang Lu, and Wenting Wu. 2021. "Estimating Coastal Chlorophyll-A Concentration from Time-Series OLCI Data Based on Machine Learning" Remote Sensing 13, no. 4: 576. https://doi.org/10.3390/rs13040576
APA StyleSu, H., Lu, X., Chen, Z., Zhang, H., Lu, W., & Wu, W. (2021). Estimating Coastal Chlorophyll-A Concentration from Time-Series OLCI Data Based on Machine Learning. Remote Sensing, 13(4), 576. https://doi.org/10.3390/rs13040576











