Abstract
Deep convolutional neural networks (DCNNs) have shown significant improvements in remote sensing image scene classification for powerful feature representations. However, because of the high variance and volume limitations of the available remote sensing datasets, DCNNs are prone to overfit the data used for their training. To address this problem, this paper proposes a novel scene classification framework based on a deep Siamese convolutional network with rotation invariance regularization. Specifically, we design a data augmentation strategy for the Siamese model to learn a rotation invariance DCNN model that is achieved by directly enforcing the labels of the training samples before and after rotating to be mapped close to each other. In addition to the cross-entropy cost function for the traditional CNN models, we impose a rotation invariance regularization constraint on the objective function of our proposed model. The experimental results obtained using three publicly-available scene classification datasets show that the proposed method can generally improve the classification performance by 2~3% and achieves satisfactory classification performance compared with some state-of-the-art methods.
1. Introduction
Remote sensing image scene classification [1] has been widely used in many practical applications such as urban planning, environment monitoring, and natural hazard detection [2,3,4,5,6]. The goal of scene classification is to assign a unique label (e.g., airport or playground) to a query remote sensing image. However, scene classification is a challenging problem due to the complex spatial structure and land cover categories diversity in remote sensing scene images. Thus, many scene classification methods have been proposed over the past years [7,8,9,10,11,12].
Recently, many deep convolutional neural network (DCNN)-based models have been proposed [13,14,15,16], replacing scene classification based on handcrafted-features such as color histograms [17], scale-invariant feature transform (SIFT) [18], histogram of oriented gradients (HOG) [19], and global image descriptor (GIST) [20]. These models can achieve better classification performance due to the powerful feature representation and generalization ability of pre-trained DCNN models (e.g., AlexNet [21], VGG-VD16 [22], GoogLeNet [23], and ResNet [24]) on the ImageNet [25]. However, although these methods have significantly improved the classification performance, two challenging problems still remain in remote sensing scene classification: the small scale of labeled training data has limited the potential of DCNN-based methods for scene classification due to the overfitting problem; the orientations of geospatial objects are diverse because remote sensing images are taken from the upper airspace, but objects in the nature scene images generally show small orientation variations due to the gravity of Earth [26].
To address this problem, we propose an effective and robust approach to learn a rotation-invariant DCNN model for remote sensing scene classification that is achieved by adopting a Siamese DCNN [27,28] architecture and introducing a new rotation invariance regularization (RIR) on the basis of the existing successful DCNN architectures (e.g., VGG-VD16 [22]). Our architecture has two identical DCNN layers that combine the identification and contrastive modules. The identification module is the traditional DCNN model that accepts an input image and predicts its label by optimizing the cross-entropy objective. The contrastive module compares the outputs of the final softmax layer of original and rotated images and minimizes the Jensen–Shannon divergence [29] in the probability distribution space. As shown in Figure 1, the scene images with different rotation angles contain the same information, and thus it should produce the same outputs including the similarity of the other categories. However, because the probability distributions has the correct class at a very high probability, with all other class probabilities very close to 0, the Kullback–Leibler (KL) divergence of images with the same category will be very small. Therefore, we take the soft labels obtained by the “softmax temperature” [30] to provide more information as to which classes of the original image are more similar to the rotated image. Comprehensive evaluations on three scene datasets and comparisons with state-of-the-art methods, including traditional DCNN architectures without RIR, demonstrate the effectiveness of the proposed method.

Figure 1.
Examples of remote sensing imagery with different rotation.
The remainder of this paper is organized as follows. We briefly review related works on DCNN-based scene classification and rotation invariance features in Section 2. In Section 3, we describe the proposed method in detail. The experimental datasets and setup are shown in Section 4. Section 5 reports comprehensive results with exhaustive comparison and discussions. Finally, conclusions are drawn in Section 6.
2. Related Work
Remote sensing scene classification has been investigated by a wide variety of methods in recent years. In this section, we briefly review the existing DCNN-based scene classification algorithms and rotation invariance in DCNN.
2.1. DCNN-Based Scene Classification
The goal of remote sensing classification is to categorize scene images into a discrete set of meaningful land use classes according to the image contents. In recent years, various deep learning methods, particularly DCNNs [21,22,31,32,33,34], have shown powerful feature representation and attracted increasing research attention. However, the small scale of remote sensing scene datasets makes training a DCNN model from scratch unrealistic. Fortunately, DCNNs pre-trained on large natural image datasets (e.g., ImageNet [25]) show a powerful generalization ability in different domains [6,7,8,9,11,12].
Despite their effectiveness, it is problematic to directly use DCNN features for remote sensing scene classification because the method is sensitive to the object orientation. This can can lead to misclassification of scene images that are of the same category with different orientations and therefore influences the classification performance.
2.2. Rotation Invariance Features
During recent decades, most of the works for scene classification were based on handcrafted features such as color histograms [17,35], gray level co-occurrence matrix (GLCM) [36], Gabor feature [37], local binary patterns (LBPs) [38], SIFT [18], GIST [20], and HOG [19]. The global features (e.g., color histogram, GLCM, Gabor feature, LBPs, and GIST) that describe the overall image as a whole to generalize the entire object or scene are generally rotation-invariant. Thus, they can be directly used for scene classification. By contrast, the local features (e.g., SIFT and HOG) that describe the image patches (key points in the image) are usually applied to construct global representation such as the bag-of-visual-words (BoVW) models [2,39,40,41]. These middle-level BoVW methods represent each image as a frequency histogram features, so that these features are rotation-invariant for scene classification.
These human-engineered features that require domain expertise greatly limit the representation capability for the complex scene images. Inspired by the recent success achieved by DCNNs in the computer vision community, many CNN models have been extended for various applications including remote sensing scene classification and have shown impressive feature representation capability [11,15,42,43,44]. However, these DCNNs are not actually invariant to large rotations of the input data [45] and this inevitably influences the performance of DCNN features for scene classification.
To overcome this limitation, many investigations of invariant features have been carried out based on DCNNs [14,26,46,47,48,49,50,51]. For examples, TI-Pooling [47] utilizes the tiny rotation invariance of max-pooling that considers a set of rotation angles to find the optimal canonical instance. The concentric circle pooling method [14] introduces the concentric circle-based partition strategy [50,52] in the context of DCNN-based models for scene classification. The spatial transformer network (STN) [53] includes an additional network module that can rotate or scale an input image or feature map to remove rotation variance, but the problem of the complex transformation of parameters using a CNN has not been solved well to date [54]. In addition to these architecture design methods, data augmentation-based methods can more directly learn rotation invariance information by rotating the image at random orientation [49,51,55,56]. Furthermore, this approach can alleviate the overfitting problem that arises from the inadequate available samples. Zhou et al. [51] propose a novel data augmentation strategy based on siamese DCNN to learn rotation-invariant features. The rotation-invariant convolutional neural networks (RICNN) [49] present a rotation-invariant layer on the basis of the existing CNN architecture to address this problem. These two methods introduce additional middle layers and impose regularization constraints to enforce the input and its rotated images with similar features.
Different from the previous methods, we propose a novel rotation invariance regularization network that we call RIR-net by using Siamese DCNNs [27] and soft label [30] for DCNN-based remote sensing scene classification methods. Specifically, we utilize Siamese DCNNs to combine identification and constrastive models that can learn in parallel to recognize the same images with different rotation orientations. The soft label is proposed in knowledge distillation to decrease the gap between the probabilities of different classes that can measure the similarity among the classes for the input and its rotated images. Soft labels contain more information than binary hard labels. We can further reduce the amount of overfitting by forcing the model to contain co-label effects during training. Unlike the previous DCNN-based scene classification methods, our proposed methods can be directly applied to existing DCNNs and effectively handle the problems of rotation variations in remote sensing scene classification.
3. Proposed Method
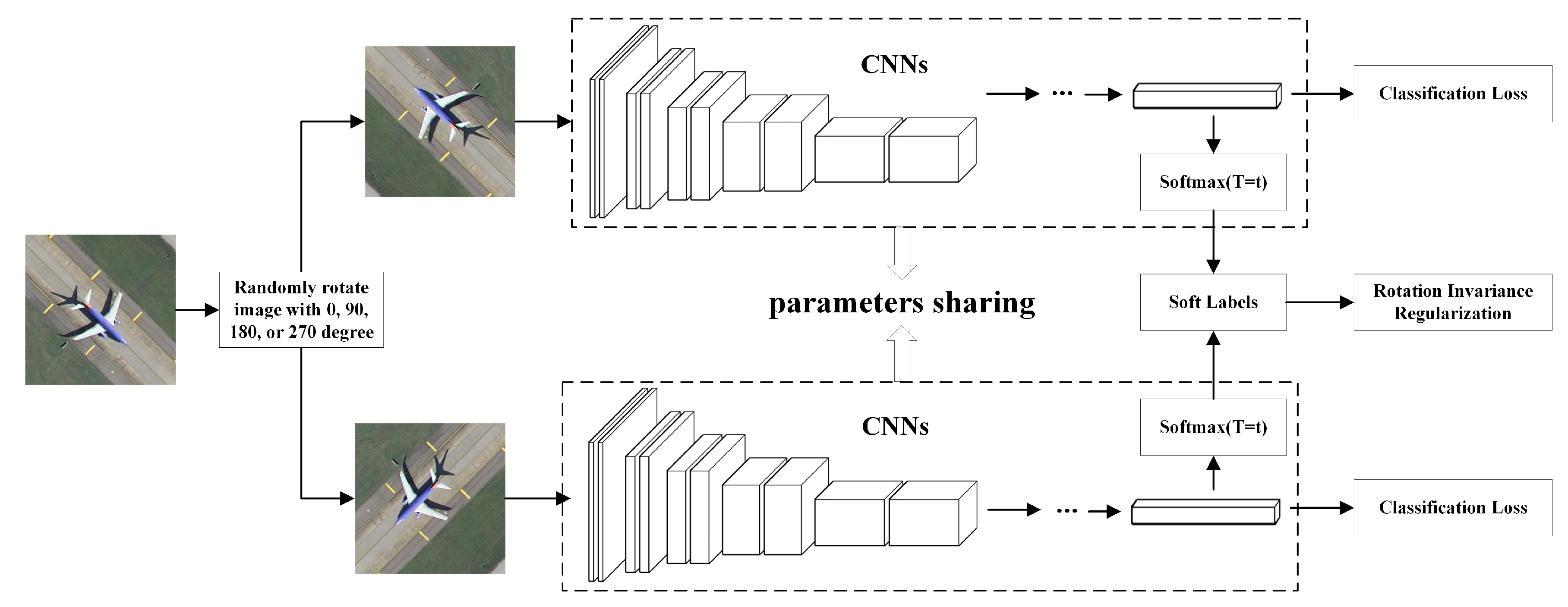
We utilize Siamese CNNs to learn rotation invariance for remote sensing scene classification. Figure 2 presents the overall architecture. The network consists of two identical pre-trained CNN models that share weights and predict the categories of the input image pair simultaneously. The CNN models can either be the popular CNN architectures such as AlexNet [21], VGG-VD16 [22], GoogLeNet [23], and ResNet [24], or other network architectures. The loss of the whole network includes two parts: identification and regularization losses. For the identification loss, we use the cross-entropy loss to measure the distance between the probability outputs and labels for the input and its rotated images. For the regularization loss, we propose the RIR method to alleviate the rotation variation problem on the basis of data augmentation. The overall framework of our proposed method consists of two modules: data augmentation and rotation invariance regularization. We next describe these two modules in detail.
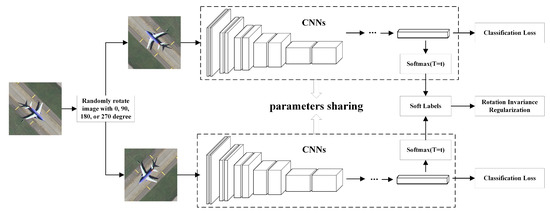
Figure 2.
Architecture of the proposed network model. This network is composed of two identical convolutional neural network (CNN) models. The input image is randomly rotated by 0, 90, 180, or 270 degrees. These two CNN models takes a pair of rotated images with different rotation angles as input. The rotation invariance regularization term is imposed on the features learned through these two CNN models.
3.1. Data Augmentation
For the limited size of the available samples for remote sensing scene classification, data augmentation is an effective approach to increase the number of training sets and assist DCNNs to avoid overfitting. Rather than using a range of transform operations such as shifts, flips, and zooms, we only adapt rotation and color jitter augmentations to verify the effectiveness of our proposed methods. For simplicity and consistency, we randomly rotate the input images to generate input image pairs. The color channels of the input images are randomly jittered to avoid shortcuts due to chromatic aberration [57]. The horizontal and vertical flipping augmentations certainly can be used with rotation and color jitter augmentations.
Specifically, we denote a rotation transformed image , where is the operator that applies the rotation transformation with angle to a scene image x. The images at the two rotated angles of each image pair should be different. The CNN models are pre-trained on large natural image datasets, ImageNet [25], to avoid overfitting given the small scale of the remote sensing data sets.
3.2. Rotation Invariance Regularization
Based on the pre-trained DCNN models, we apply Siamese CNNs to realize our RIR method. For these DCNN models, we replace the final 1000-way softmax classification layer with an C-way softmax classification layer, where C denotes the number of categories. The whole architecture takes a pair of images as the input that are the same image with different rotation angles. Different from these baseline DCNNs, the whole network is trained by optimizing a new objective function that consists of two cross-entropy losses and one RIR term. The proposed regularization constraint term is imposed to enforce the training samples rotated at different angles to produce identical probability distribution over classes.
However, in these baseline DCNNs, the correct answers with very high confidence are always generated during the training phase. While we seek to directly minimize the distance of the probability distribution of the image pair, it will be very small since the probabilities are so close to one or zero. In addition, much of the information that resides in the ratios of very small probabilities fails to be used for the learned function. For example, a category of forest may be given a probability of of being an agricultural category and of being a golf course category. This indicates that the characteristic of the forest category, at least for some images in this category, are similar to those of the agricultural and golf course categories. This is valuable information but it does not influence the cross-entropy loss function because the target labels are hardly 0 or 1. Inspired by the “distillation” in [30], we produce soft labels by raising the temperature of the final softmax in the RIR term.
In the proposed RIR methods, the parameters of all of the layers except for the final softmax layer are transferred from the baseline DCNNs to avoid overfitting in scene classification. Then, we fine-tune the pre-trained layers with a smaller learning rate and a higher learning rate for the last randomly initialized softmax layer. For a pair of input images (), let and denote the outputs of the final layer for each class. Thus, the probabilities for each class, and , can be computed by
where T is the temperature, and C is the number of categories. will be the normal “softmax” with the temperature T of 1 and will produce a softer probability distribution over classes with a high value for T. This is often used in knowledge distillation to transfer knowledge to the distilled model. We introduce it to mine the rotation invariance of DCNNs for scene classification.
We define the training samples , their corresponding rotation transformed samples , and labels , where denotes the target possibilities of sample with one-hot encoding and N denotes the number of training samples. To achieve rotation invariance for any set of the training sample pairs (), we propose a new objective function with RIR by the following formula:
where and R are the losses of the identification and contrastive terms, and denotes the tradeoff parameter that tunes the weighted average between the two components of the loss. The first component forces the optimization toward approximating the ground truth labels for the training samples, whereas the second component forces the optimization toward a similarly softened softmax distribution between the pair of the training samples before and after the rotation. This model will degenerate to the traditional DCNN with rotation augmentation operation while .
We use the cross-entropy loss for the identification term and RIR for the contrastive term. The identification term adopts softmax as the predicted classification probabilities. For C categories, we can compute by
where is the cross-entropy loss for the sample , and is the normal softmax score that can be viewed as a special case of the temperature .
The contrastive term is a RIR constraint. We enforce the output classification probabilities of the original and rotated training samples (X and ) to be as identical as possible. We use the Jensen–Shannon divergence [29] to measure the similarity between the predicted probability distribution of the input image pairs. The regularization constraint term is defined as
where denotes the Kullback–Leibler divergence [58] that is a measure the differences between the probability distributions, denotes the Jensen–Shannon divergence, are the average probabilities of and , and are computed by
Due to the cross-entropy loss in identification term, the regularization constraint term requires a large T to become effective. However, noise may be introduced by a large T and this will enlarge the probabilities of too many categories in the output classification vector. Thus, we multiple by , to obtain
To prevent division by 0 in , we add a small constant , e.g., , to the probabilities and . By incorporating Equations (3) and (6), the loss function is given by
The loss function defined in Equation (7) imposes a regularization constraint to achieve rotation invariance on basis of the existing DCNN architectures. The gradient for each output unit of the input image , , can be computed by
We can minimize this loss function by using the stochastic gradient descent (SGD) [59] or adaptive moment estimation (Adam) [60] methods.
The RIR model can be expanded from two input images to multiple input images with different rotation transformations. Then, the regularization constraint term becomes
where K is the total number of rotation transformations for each , and is the soft probability of the image , which is the version of the input image rotated by angle . The average probability can be computed by
Then, we can compute the loss function by
For the input image , the gradient of each output unit is same as Equation (8) besides the value of average probability . Due to the stability of mean value, a larger value of K gives better performance, but requires greater computational capability and iterations.
The proper value of T is important for network performance. If T is too high, it disturbs the identification term to affect classification accuracy. However, if T is too small, we cannot benefit from the regularization term. Inspired by the deterministic annealing process [61], we can slowly increase the value of by the step s to benefit from the RIR without impacting the classification performance.
where s is the current step, and are the steps at which the increase in the temperature is started and stopped, respectively, for the optimizer in this paper. We evaluate together with the tuning parameter .
4. Experiments
4.1. Data Sets
We evaluate the performance of our proposed method on three challenging remote sensing scene image datasets. These are the UC Merced land use (UC) dataset [39], the Aerial Image dataset (AID) [62], and the NWPU-RESISC45 (NWPU) dataset [1].
The UC (http://vision.ucmerced.edu/datasets/landuse.html) [39] dataset contains 21 typical remote sensing scene categories. There are 100 images with a size of pixels for each class in the red–green–blue color space. The pixel resolution of images is approximately one foot. Two examples of ground truth images from each class are shown in Figure 3. The high interclass similarity among the categories (e.g., medium and dense residential areas) results in some challenges for the classification of the UC dataset. The AID (http://www.lmars.whu.edu.cn/xia/AID-project.html) [62] dataset contains 10,000 images with a size of pixels within 30 scene classes. The number of images for different categories varies from 220 to 420. The spatial resolution changes from approximately 8 m to 0.5 m per pixel. Figure 4 shows examples of the AID dataset. The NWPU (http://www.escience.cn/people/JunweiHan/NWPU-RESISC45.html) [1] dataset contains 31,500 images with a size of pixels. There are 45 scene classes, and each class consists of 700 images. The spatial resolution changes from approximately 30 m to 0.2 m per pixel for most of the scene categories. The classification of the NWPU dataset is more challenging because of the rich image variations, large within-class diversity, and high between-class similarity.

Figure 3.
Two examples of ground truth images of each scene category in the UC data set.

Figure 4.
Examples of ground truth images of each scene category in the AID data set.
4.2. Experimental Setup
We consider three kinds of widely used DCNNs, including AlexNet [21], VGG-VD16 [22], and ResNet50 [24] as baselines to evaluate the performance improvement for the RIR. We utilize these models pre-trained on ImageNet dataset and then fine-tune them to adopt them to the remote sensing scene images. We replace the flatten layer in the AlexNet [21] and VGG-VD16 [22] with an adaptive average pooling layer for arbitrary input image size. Thus, the original image sizes are used for these data sets.
We randomly select proportional samples of each class for training, and the remaining samples are used for testing 10 times. These 10-time random splits are prepared prior to the experiments. For the UC dataset [39], we randomly select 10%, 20%, 50%, 80% of samples for training, and the remaining samples are used for testing. For the AID dataset [62], the training ratios are set to 20% and 50%, and the remaining 80% and 50%, respectively, are used for testing. For the NWPU dataset [1], we set the training ratios to 10% and 20%, and the remaining 90% and 80%, respectively, are used for testing.
To quantitatively evaluate the performance of the proposed method, we adopt the average accuracy (AA), overall accuracy (OA), and confusion matrix as the evaluation metrics in this paper. The OA is recorded as the number of correctly classified samples divided by the total number of samples. The AA is defined as the average classification accuracy of each class. The confusion matrix is a summary of prediction results that analyze the errors and confusions between different scene classes. It can be computed by the number of correct and incorrect predictions for each class and organized into a table.
We implement these networks by means of an open-source neural network library named Pytorch [63]. Experiments in this work are implemented using VSCode 1.31.1/Ubuntu 18.04 and conducted on a workstation equipped with a single NVIDIA GeForce RTX 2080 8 GB GPU.
4.3. Implementation
To transfer features from the aforementioned DCNNs to the scene classification, we fine-tune these DCNNs on each scene dataset individually. The final classification layer trained on the ImageNet dataset is substituted by a randomly initialized C-way softmax layer, where C is the number of classes in the scene dataset. We use the original input image dimension for all data sets.
We set the rotation angles as 0, 90, 180, or 270 degrees to decrease the impact of discrepancy from random rotation. For the proposed network, we set a higher learning rate for the final layer (randomly initialized) to achieve fast convergence of the model and a lower learning rate for the other fine-tuning layer in order to avoid too rapid and too high distortion of the pre-trained weights. Based on the pre-trained DCNN architectures, we train the models via Adam with a momentum of (0.9, 0.99).
5. Results and Discussion
5.1. Tradeoff of Temperature and Tuning Parameters
In the proposed method, there are two main parameters, the temperature parameter and tuning parameter , that can affect the performance of scene classification. The temperature affects the quality of the RIR and the setting of also affects the overall classification accuracy of the proposed method. These parameters are determined in a heuristic way for the scene classification. We set temperature from and the tuning parameter in , respectively. Using a higher value for or a lower value for strengthens the regularization effect on the scene classification task.
Table 1 summarizes the detailed parameters used for the models with different baseline DCNNs on the UC dataset. The learning rate is set to for the last fully connected layer and for the other layers. These models are trained for 5000 iterations and the learning rate is dynamically divided by a factor of 0.1 every 4000 iterations. To facilitate evaluation, the step parameters and are set to 0. We also list the training times of the no-RIR and RIR DCNNs by hours. Because the gradient of the regularization term has a low computational complexity, the training times of these two DCNNs are almost equal.

Table 1.
Parameters utilized for models with different baseline deep convolutional neural networks (DCNNs) on the UC data set.
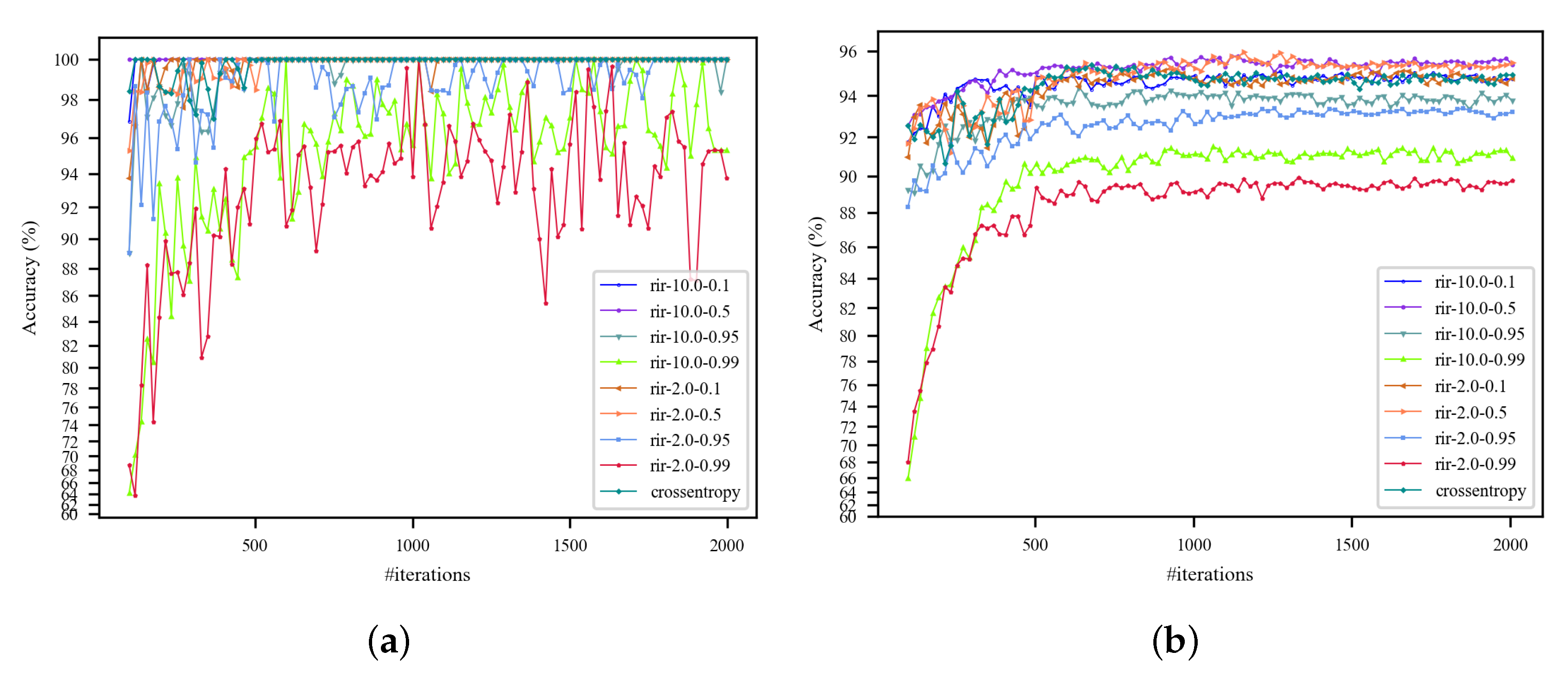
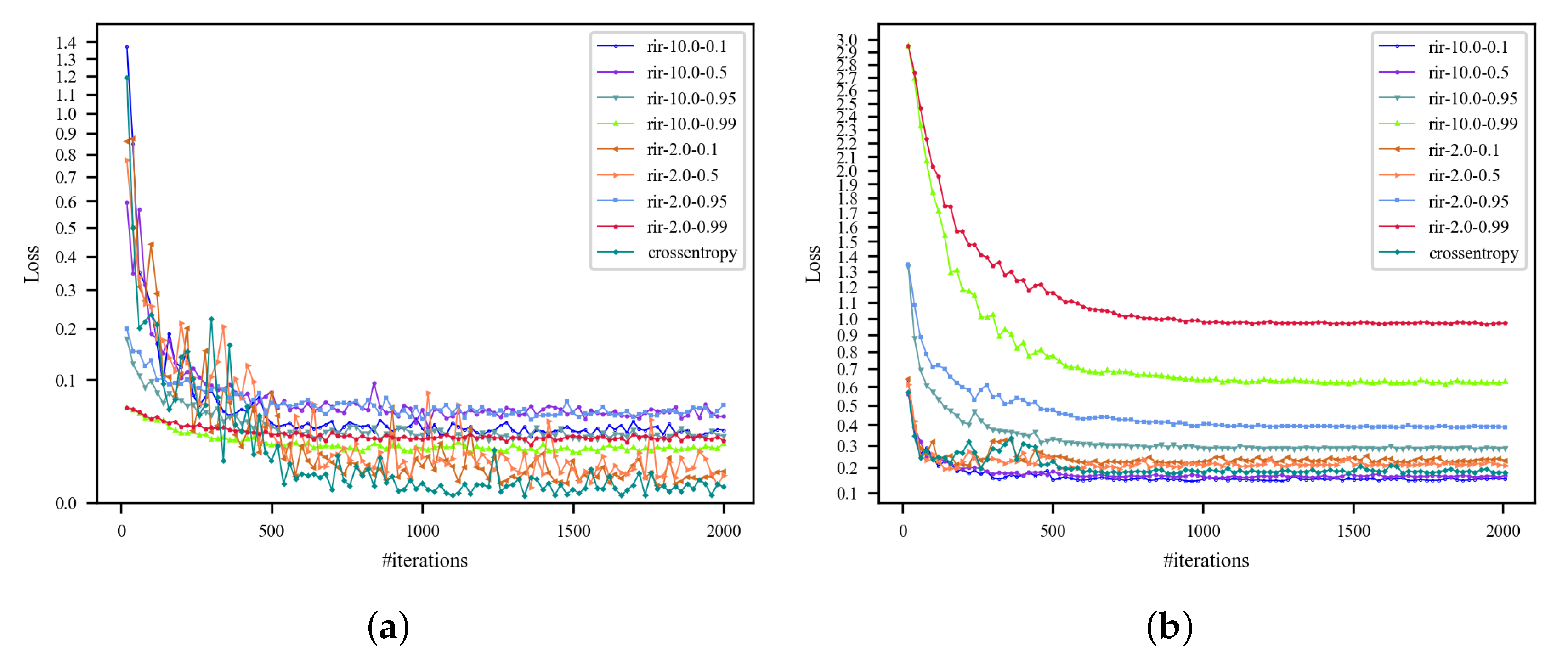
Figure 5 and Figure 6 summarize the training and testing results with the AlexNet-based RIR-net on the UC dataset. We evaluate this method with different parameter settings. The classification is measuring in terms of OA for all categories. It is found that the RIR with a softer label does indeed help the baseline DCNNs to generalize better, but requires more iterations for convergence. As shown in Figure 5a, these methods show fast convergence except for the RIR-nets with excessively high parameter of 0.99. This is because underfitting occurs when the model is regularized too much for high . In addition, the models with high (e.g., 0.95) show divergence for low temperature T (e.g., 2.0), but convergence for high T (e.g., 10.0). The curves in Figure 6 indicate that the losses of the RIR-nets are higher for the regularization term. As shown in Figure 6b, larger T and can lead to a more stable convergence of the loss.
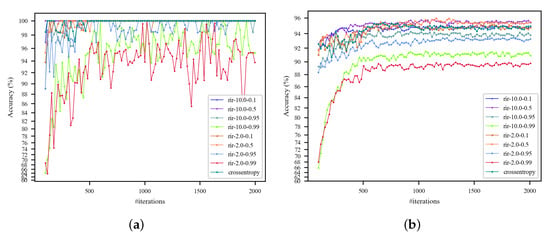
Figure 5.
Training and testing accuracy curves with pre-trained AlexNet on the UC dataset (training ratio = 50%). The rotation invariance regularization (RIR)-nets in the legend with different parameter settings are denoted as rir-T-. (a) Training accuracy curves; (b) testing accuracy curves.
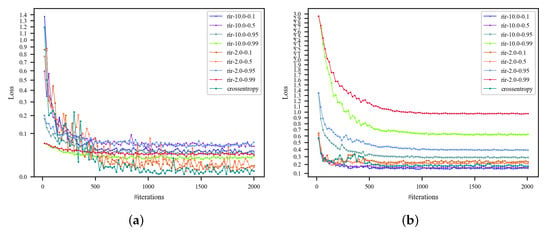
Figure 6.
Training and testing loss curves with pre-trained AlexNet on the UC dataset (training ratio = 50%). (a) Training loss curves; (b) testing loss curves.
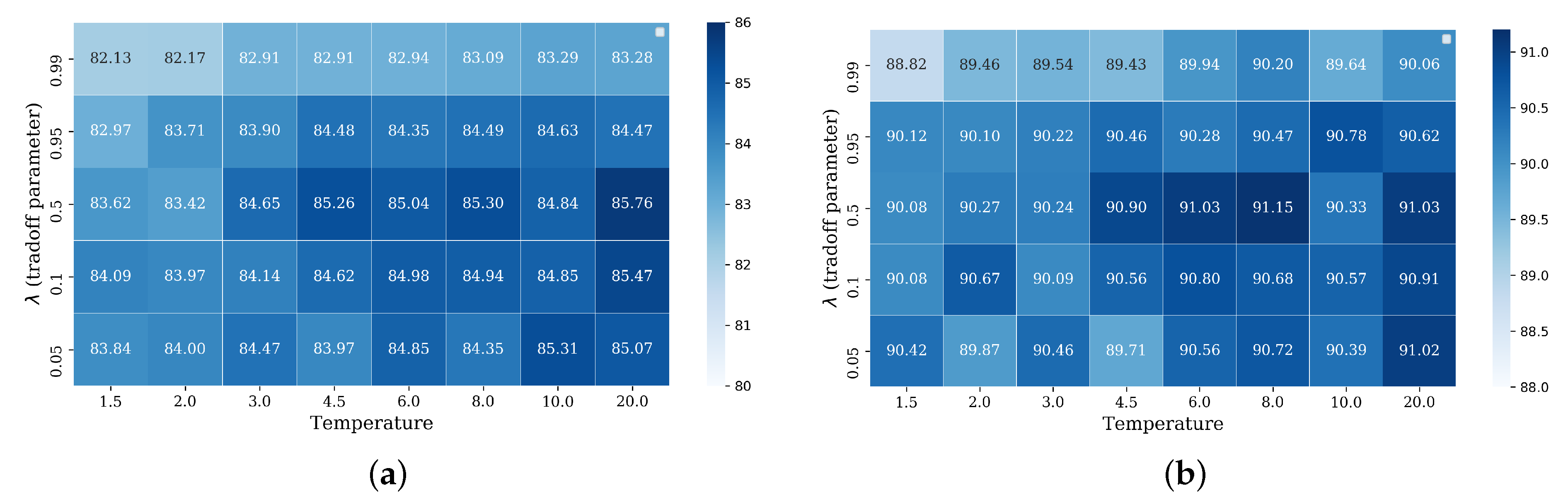
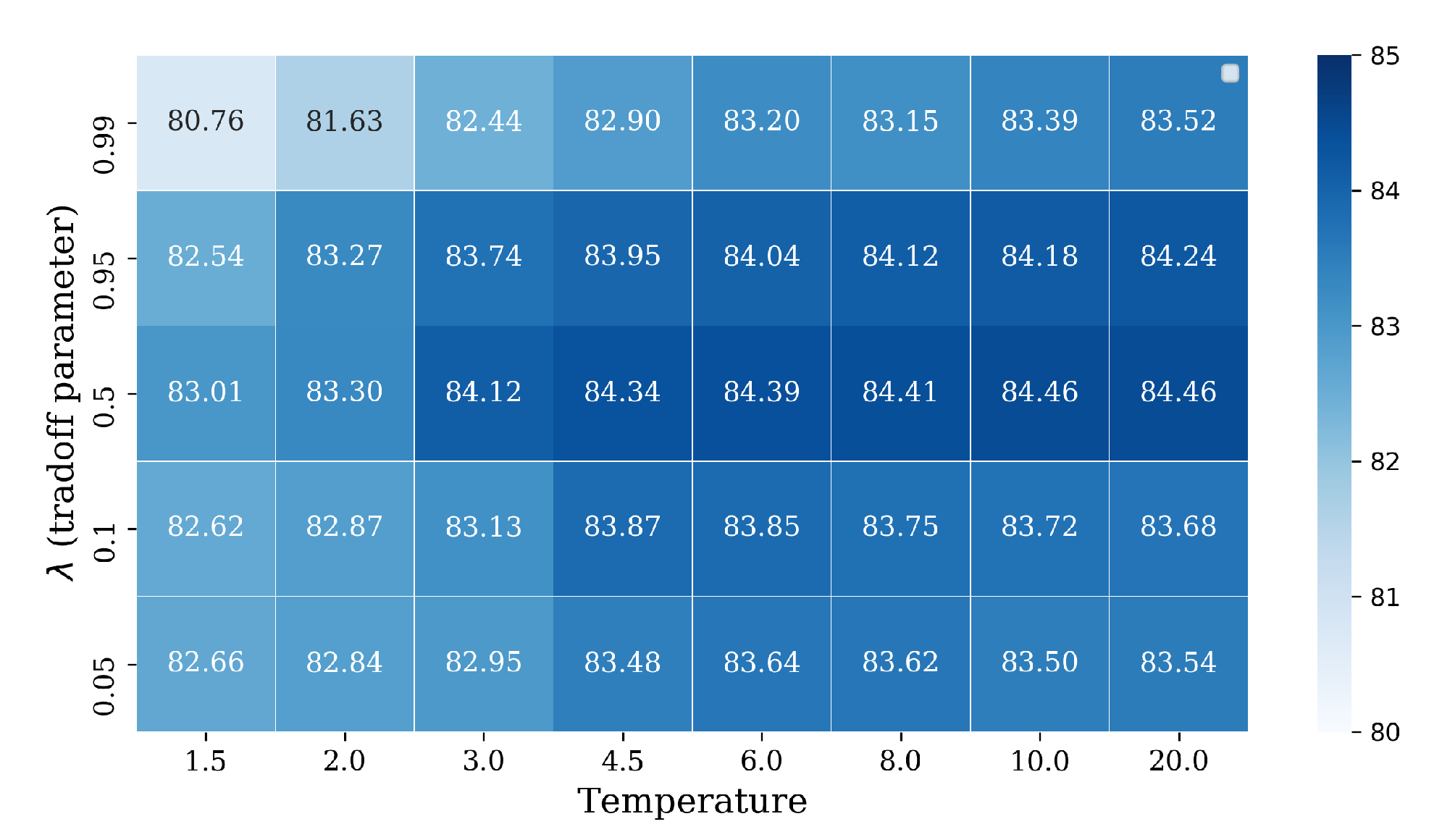
We evaluate the hyper-parameters of temperature T and tuning parameter for the AlexNet-based RIR-net and baseline in Figure 7. As observed from Figure 7, the optimal value of the tuning parameter is generally 0.5 under most temperatures T. For too large or too small T, the RIR-nets obtain poor results that are even worse than the model that only uses cross-entropy criteria (84.01% and 89.81%, respectively). The performance of the RIR-nets with other settings are clearly better than the baseline model. Thus, higher temperatures T are better for scene classification accuracies.
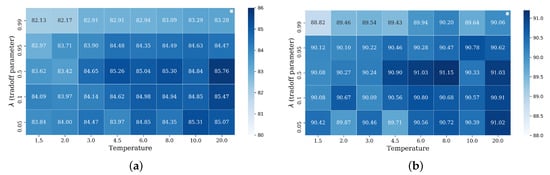
Figure 7.
Evaluation of the temperature T and tuning parameter as hyper-parameters for the AlexNet-based RIR-net on the UC dataset. The testing classification results are measuring in terms of overall accuracy (%). The testing accuracy of the model only with cross-entropy criteria is 84.01% and 89.81% for the training ratios of 10% and 20%, respectively. (a) training ratio = 10%; (b) training ratio = 20%.
Table 2 summarizes the results for different baseline network architectures under different training ratios. Our results show considerable improvement over the no-RIR baseline DCNNs, which have same architecture with RIR-net except for the regularization term. The larger performance gain of RIR-net over no-RIR are due to the smaller training samples. For each baseline DCNN, the RIR method can improve the classification accuracies by almost 2% on the UC dataset with the training ratio of 10%. With respect to the variance, these baseline DCNNs with RIR are mostly lower than the corresponding baseline DCNNs. This result indicates that the RIR method can not only reduce the prediction error, but also boosts the generalization of DCNNs.

Table 2.
Classification accuracies (%) on the UC data set.
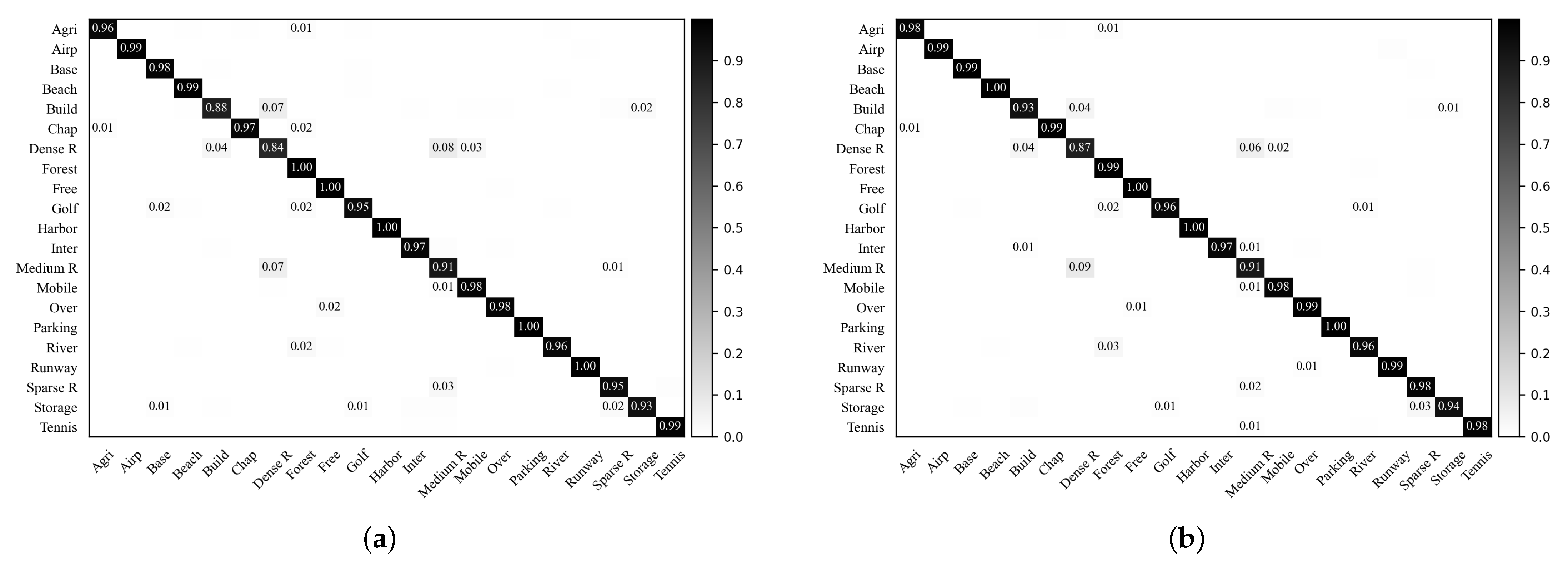
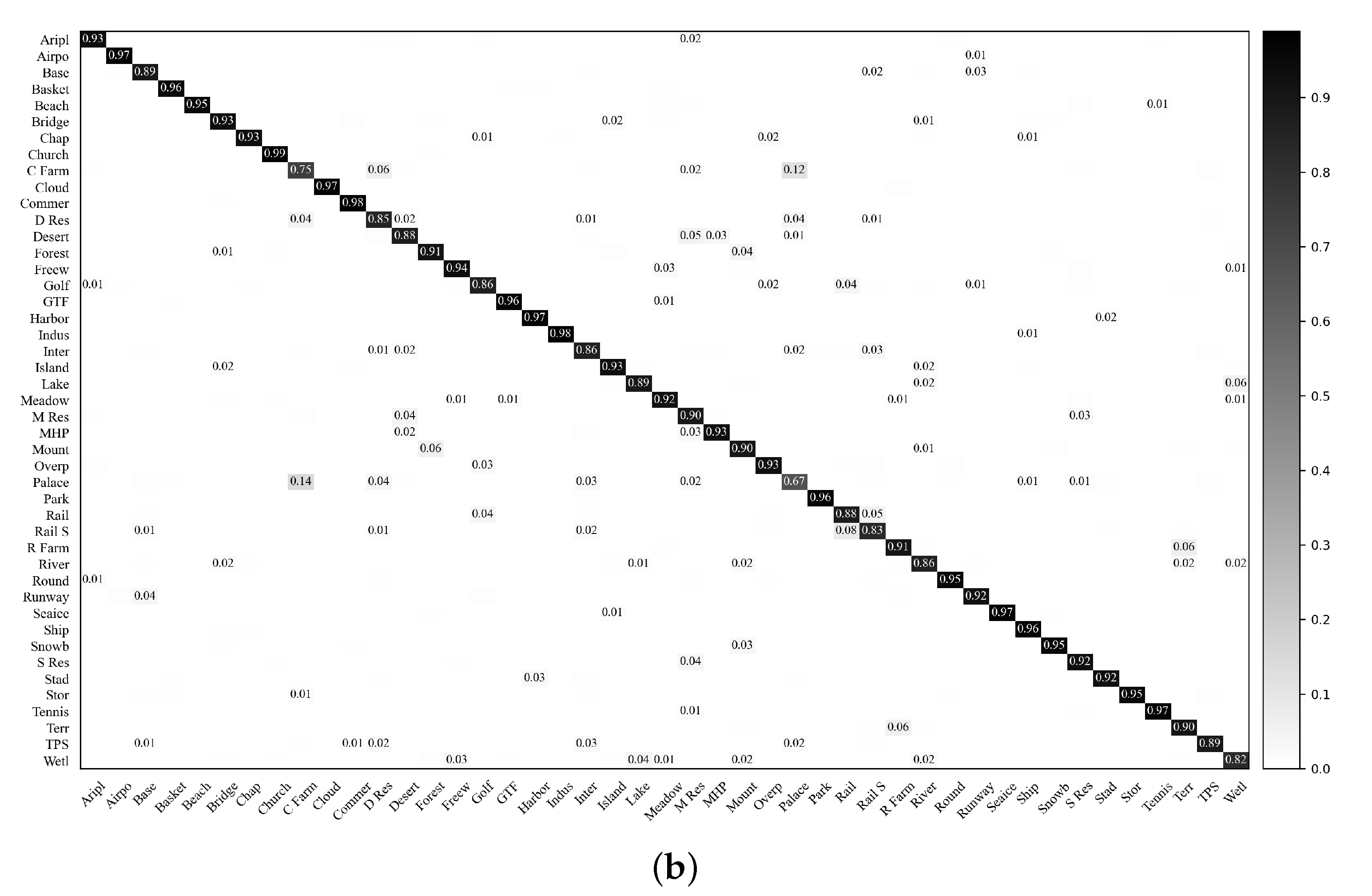
For the VGG-VD16-based RIR-net and baseline DCNN, the confusion matrices on the UCM dataset with a training ratio of 50% are provided in Figure 8. It is observed that the performances for each class are improved except classes (forest) and (tennis court) categories that decrease to lower than 1%. The classification accuracies of most scene categories achieve a satisfactory level, and some categories are close to 100%. The category (building) that is easily confused with category (dense residential), is the most improved category. In addition, the performances of classes (dense residential) and (sparse residential) are boosted, but that of their commonly confused category (medium residential) is unchanged, possibly due to the limitations of the representation capability of the VGG-VD16 architectures for the remote sensing scene classification.
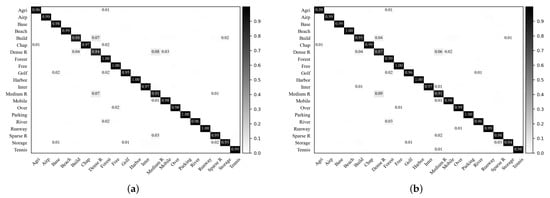
Figure 8.
Confusion matrices of the VGG-VD16-based baseline DCNN and RIR-net for the UCM dataset (training ratio = 80%). (a) VGG-VD16-based baseline DCNN; (b) VGG-VD16-based RIR-net.
In Table 3, we compare our method with the previously reported state-of-the-art methods. Deep-learning-based methods exhibit superior performance compared to the handcrafted-feature method. The RIR-net obtains higher classification accuracies than the other pre-trained DCNN-based methods with the AlexNet or VGG-VD16. AN examination of the data presented in Table 3 shows that RIR-net achieves more desirable classification accuracies for a smaller number of training samples. Our best network with pre-trained ResNet50 achieves 98.28% and 99.15% on the testing set with the training ratios of 50% and 80%, respectively. Compare with the Siamese CNN in [28], the RIR-net achieves significantly better performance, especially for the training ratio of 50%. In addition, the RIR-net is generally independent of the architecture, so that we expect that it will further improve the deeper and larger DCNN architectures, e.g., VGG-VD19 [22] and ResNet101 [24].

Table 3.
Comparison of overall accuracies (OA) (%) on the UC dataset (training ratio = 80%).
5.2. Effect of Increasing Temperature Strategy
In this section, we compare the results of the proposed RIR-net with fixed and increasing temperature T on the NWPU dataset. The detailed parameters on the NWPU dataset are shown in Table 4 for different baseline DCNNs. The hyper-parameters of temperature T and tuning parameter for the AlexNet-based RIR-net with the training ratio = 10% are evaluated in Figure 9. For each tuning parameter , the classification accuracies gradually increase with increasing temperature T. For the NWPU dataset, the gap between RIR-net with and is smaller than that of the UCM dataset. This may be caused by the use of more training samples and steps. Except for the , all of the RIR-nets are superior to the baseline DCNN models. Because more training steps are required for higher temperature, we select the optimal temperature and tuning parameter for the NWPU data set.

Table 4.
Parameters utilized for models with different baseline DCNNs on the NWPU data set.
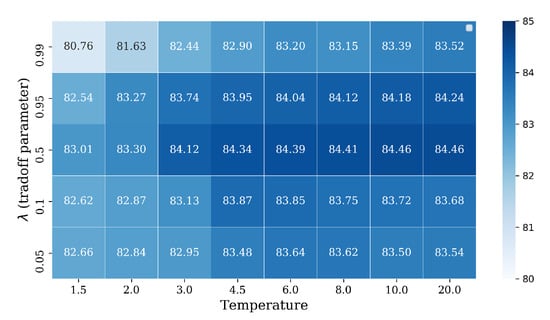
Figure 9.
Evaluation of the temperature T and tradoff as the hyper-parameters for the AlexNet-based RIR-net on the NWPU dataset (training ratio = 10%). The testing classification results are measuring in terms of overall accuracy (%). The testing accuracy of the model with the cross-entropy criteria only is 82.37%.
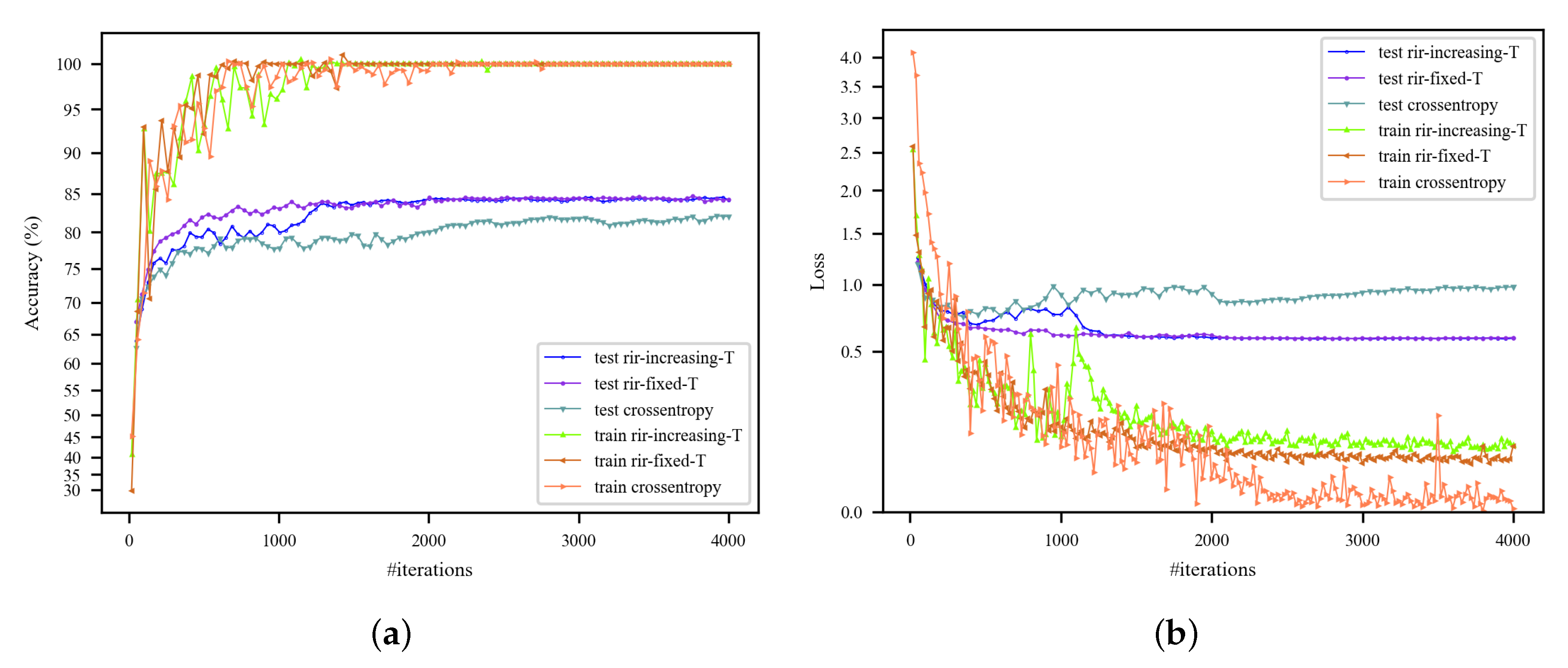
In addition, we evaluate the strategy of slowly increasing T as described in Equation (12). To demonstrate the effectiveness of this strategy, we take larger and on the NWPU dataset with a training ratio of 10%. The AlexNet architecture is employed with the parameters and . As shown in Figure 10, the RIR-nets with increasing or fixed T finally achieve the same testing accuracies and losses. With increasing T, the accuracy increases sharply from #iteration 1000 at which the temperature starts to rise. It is interesting that the no-RIR baselines have a growth point at #iteration 2000, that the learning rate starts to decay. However, the performance of RIR-nets was not improved further after the learning rate decay. It can be concluded that the temperature increasing strategy resembles the learning rate decay method. For fair comparison, we still adopt the learning decay method in the rest of the experiments.
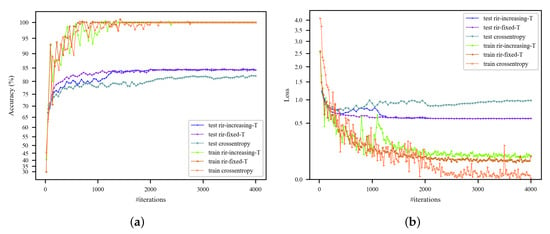
Figure 10.
Training accuracy and loss curves with AlexNet-based architectures on the NWPU dataset (training ratio = 10%). (a) Training and testing accuracy curves; (b) training and testing loss curves.
The results in the Table 5 show considerable improvement over the no-RIR baselines on the NWPU dataset. An examination of the data presented in Table 5 shows that the performance of AlexNet and VGG-VD16 based architectures is boosted more significantly than that of the ResNet50 based architecture.

Table 5.
Classification accuracies (%) on the NWPU data set.
As described in Equation (9), we evaluate our RIR-net for where all rotated samples are used in the regularization term. With same hyper-parameters and , the AlexNet-based RIR-net with obtain classification accuracy of when using the training ratio of 10%. The larger K is conducive to the performance improvement. However, due to the greater GPU memory and iteration requirements, we use in the experiments reported in this paper.
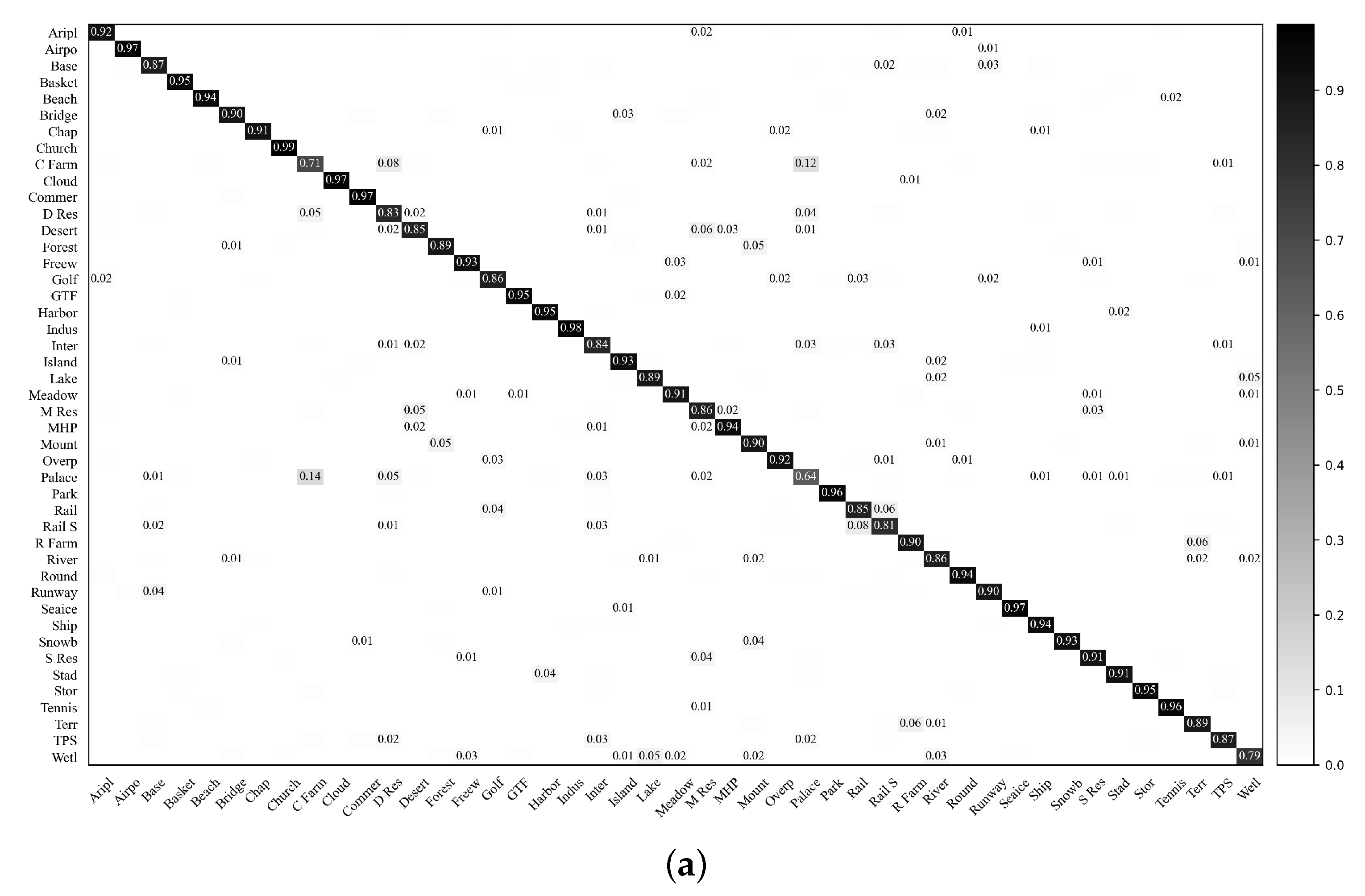
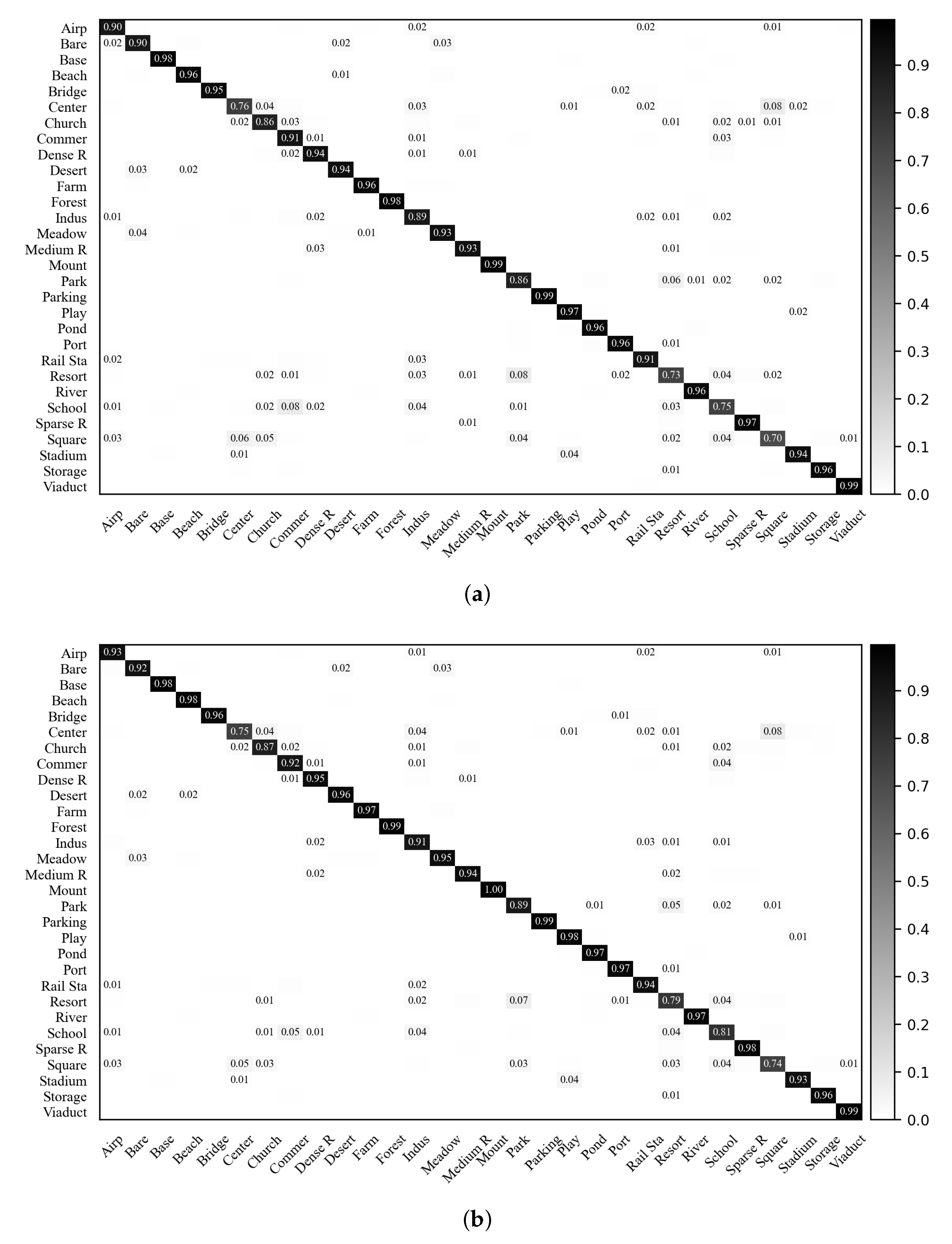
Figure 11 shows the confusion matrices conducted with the VGG-VD16-based RIR-net and baseline DCNN on the NWPU dataset with training ratio of 20%. It is observed that our proposed RIR-net can improve the classification accuracies on nearly all classes, particularly for categories (bridge), (circular farmland), (intersection), (medium residential), (palace), and (wetland) categories. As shown in Figure 11, RIR-net reduces the confusion between the classes (circular farmland) and (dense residential), (medium residential) and (mobile home park), and (wet land) and (lake). These results indicate that our method extracts a more discriminative description for the remote sensing scene images.
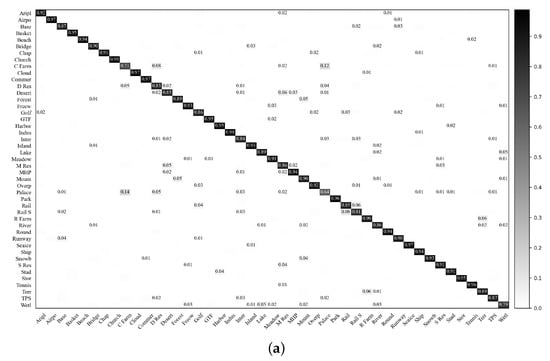
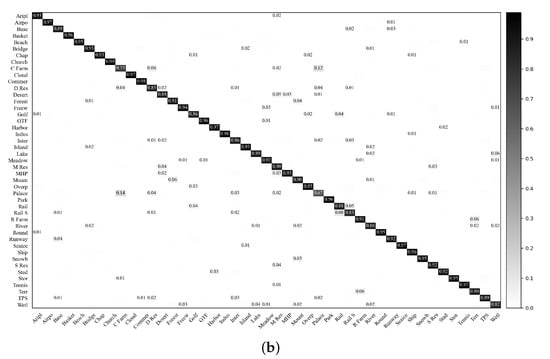
Figure 11.
Confusion matrices of the VGG-VD16-based baseline DCNN and RIR-net for the NWPU dataset (training ratio = 20%). (a) VGG-VD16-based baseline DCNN; (b) VGG-VD16-based RIR-net.
We compare our proposed RIR-net with some other pre-trained CNN-based classification methods. As shown in Table 6, the RIR-nets achieve higher accuracy than the baseline DCNNs. It is important to note that the gain in the performance is not only due to the data augmentation for the comparison in Table 5. The RIR-net performs better than all of the other methods based on the same DCNN architectures, but shows slightly worse performance than the latest D-CNN model [11] under the training ratio of 10%. Compared to the MSCP [43] and SAFF [44] methods, the AlexNet-based RIR-net obtains comparable performance to that of other VGG-VD16-based architectures. The highest classification accuracies are obtained by the ResNet50-based RIR-net that achieves 92.05% and 94.06% for the training ratios of 10% and 20%, respectively.

Table 6.
Comparison of the classification results (%) on the NWPU dataset (training ratio = 10% and 20%).
5.3. Validation on the AID Data Set
With optimal temperature and tuning parameters based on the UC and NWPU datasets, we evaluate the proposed RIR-net on the AID dataset. As shown in Table 7, we set the parameters with different input sizes due to the greater GPU memory required by the larger image size in the AID dataset. We transform the size of input images into and for AlexNet and the other two baseline DCNNs, respectively. Table 8 shows the results for different baseline DCNNs with temperature and .

Table 7.
Parameters utilized for the models with different baseline DCNNs on the AID data set.

Table 8.
Classification accuracies (%) on the AID data set.
As shown in Figure 8, our RIR-net can also improve the classification accuracy for the large size of input images. It is observed that the RIR-nets are better than the no-RIR DCNNs for the results on the AID datasets with optimal temperature and tuning parameters based on the UC and NWPU datasets. For the VGG-VD16 and ResNet50 architecture, the performance boost on the input image of large size and is not much reduced by shrinking the image size.
Figure 12 shows the confusion matrix of the VGG-VD16-based RIR-net under the training ratio of 20%. The classification accuracies of most of the categories are increased. For the classes (center) and (stadium), the performances are decreased by less than 1%. The classes (school) and (resort) achieve a greater than 5% enhancement in performance due to the discrimination improvement between the classes (school) and (church), (resort) and (church), and (resort) and (sparse residential). These classes usually share building objects, thereby making these categories similar and their classification challenging.
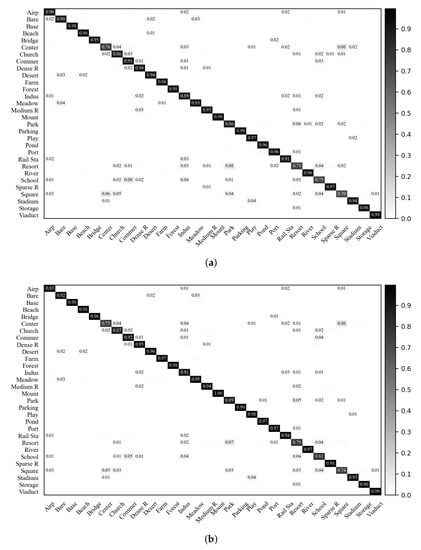
Figure 12.
Confusion matrices of the VGG-VD16-based baseline DCNN and RIR-net for the AID dataset (training ratio = 20%). (a) VGG-VD16-based baseline DCNN; (b) VGG-VD16-based RIR-net.
Table 9 summarizes the comparison of our results with the state-of-the-art methods on the AID dataset. Our results with the AlexNet are superior to the results obtained using the previous AlexNet-based methods, and even surpass the previous VGG-VD16-based methods. The best performances (94.45% and 96.48%) are achieved by the ResNet50-based RIR-net with the training ratios of 20% and 50%.

Table 9.
Comparison of the OAs (%) on the AID dataset (training ratio = 20% and 50%).
5.4. Visualization of the Softmax Outputs
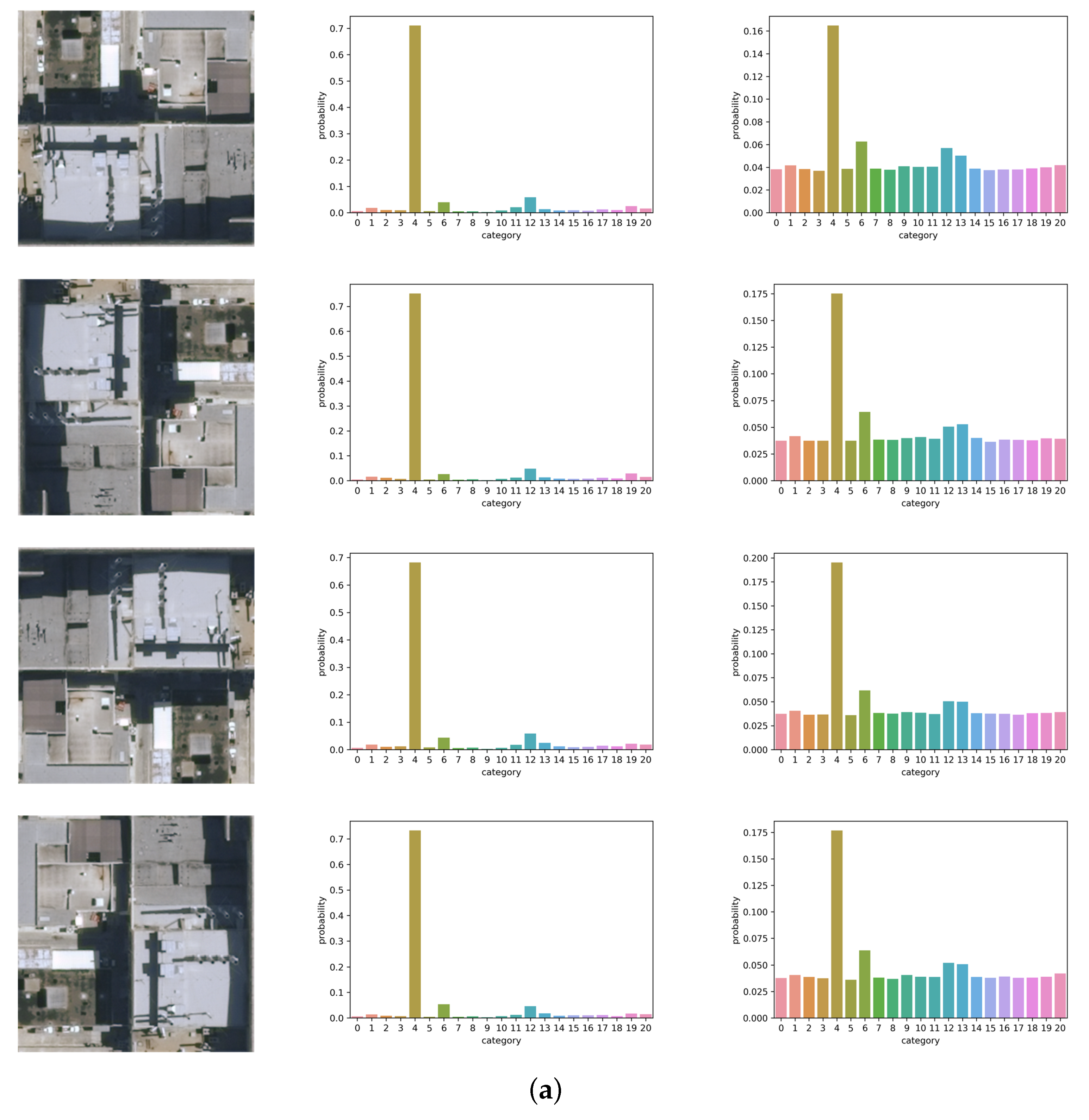
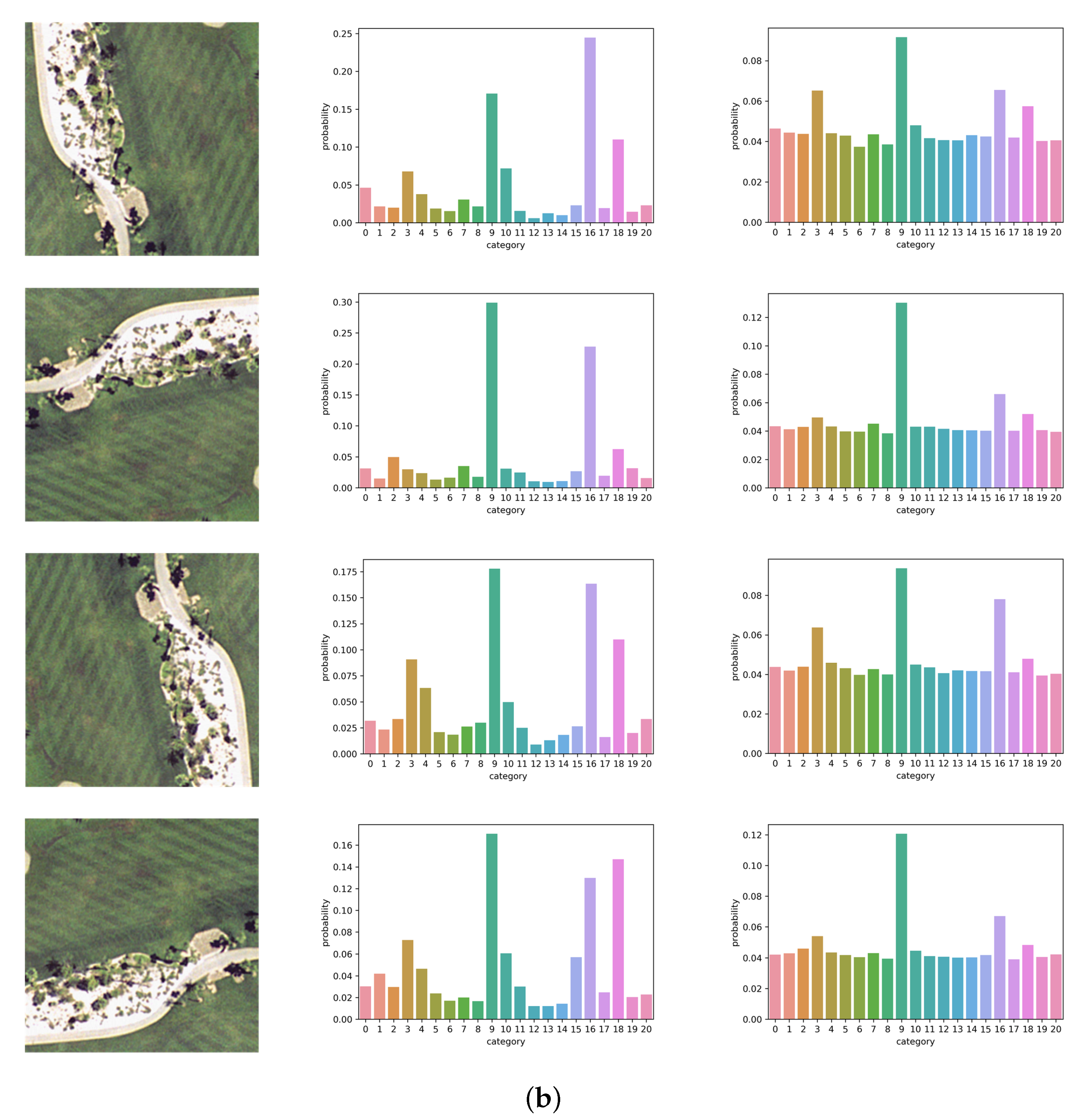
In this section, we visualize the outputs of the last layer of baseline CNN and RIR-net. Figure 13 shows two test examples of different scene classes (building and golf course) and their corresponding probabilities of categories for the baseline DCNN and RIR-net. These test examples are rotated by 0, 90, 180, 270 degrees, respectively. We use softmax with temperature to facilitate visualization. The softmax outputs of AlexNet-based RIR-net and baseline are shown in Figure 13. As shown in Figure 13, the output of CNN of different test examples of the same category are not rotation-invariant. For the scene image of #4 (building category), the most similar categories are #6 (dense residential), #12 (medium residential), and #13 (mobile home park). For the CNN model, the major differences between the outputs of the images with different orientations are found for the categories #6 (dense residential), #13, and #19 (storage tank). For the scene image of #9 (golf course), it appears similar to the categories of #3 (beach), #16 (river), and #18 (sparse residential). Particularly for the #16, some of this scene image is misclassified because the baseline CNN cannot capture the invariance information between the images with different orientations. In contrast, the output of RIR-net of these examples of the same object class are clearly more similar. These results demonstrate the effectiveness of the proposed RIR method.
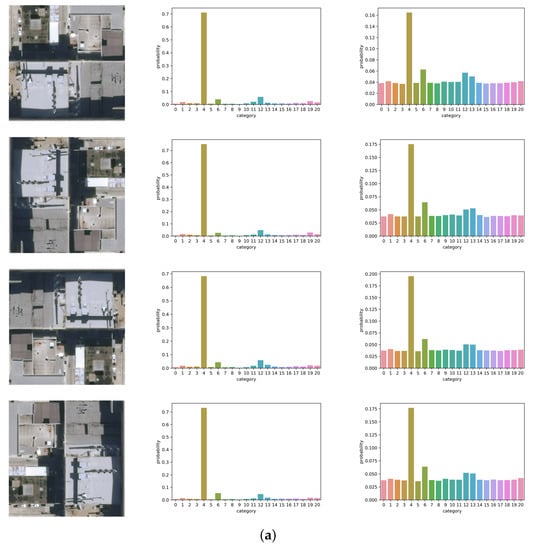
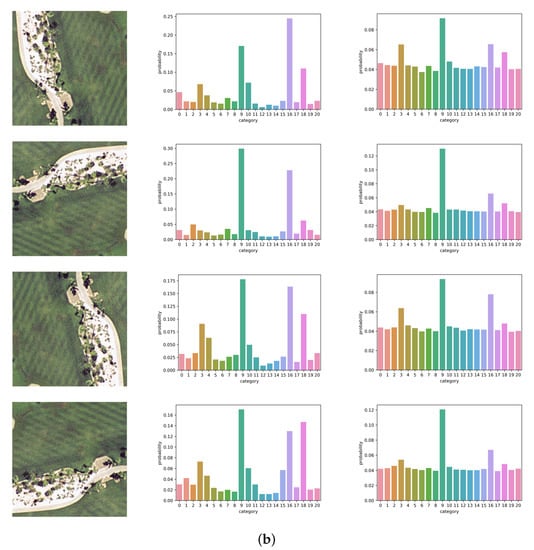
Figure 13.
Softmax outputs with temperature T = 5.0 of examples with different orientations. The first column shows test examples and their corresponding rotated versions. The second column shows the softmax output of baseline CNN with T = 5. The last column shows the softmax output of RIR-net with T = 5. (a) Example #4 (building category), which appears similar to the categories of #6 (dense residential), #12 (medium residential), and #13 (mobile home park); (b) Example of #9 (golf course), which appears similar to the categories of #3 (beach), #16 (river), and #18 (sparse residential).
6. Conclusions
In this study, we propose a novel and effective method based on the Siamese convolutional neural networks that aim to increase the robustness and reduce the overfitting for the remote sensing scene classification. We enforce the output classification probabilities of the training samples before and after the rotation to be similar by optimizing a new objective function with the RIR. To compare the probability distributions, we introduce the soft labels proposed in the “softmax temperature”. By raising the temperature of the final softmax, we enlarge the diversity of the output distribution to be characteristic of the similarities between different categories. The quantitative comparison results on the publicly available remote sensing scene classification datasets demonstrate the performance gain of the proposed method compares with state-of-the-art approaches. In the future, we plan to investigate the effectiveness of this regularization for the semi-supervised methods and the metric learning-based DCNN architectures.
Author Contributions
Conceptualization, K.Q.; methodology, K.Q. and C.Y.; software, C.H.; validation, S.S.; formal analysis, K.Q.; investigation, C.Y.; resources, K.Q., Y.S., and S.S.; data curation, C.Y. and C.H.; writing—original draft preparation, K.Q.; writing—review and editing, Y.S., C.Y., and H.W.; visualization, C.Y. and C.H.; supervision, K.Q.; project administration, K.Q.; funding acquisition, K.Q. and C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Key Research and Development Program of China under Grant No. 2019YFB2102903, the National Natural Science Foundation of China under Grant Nos. 41701410, 41601298 and 41701511, and the Fundamental Research Funds for the Central Universities, China University of Geosciences (Wuhan) under Grant No. CUG190624.
Institutional Review Board Statement
The study did not involve humans or animals.
Informed Consent Statement
The study did not involve humans.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank the editors and reviewers for their detailed comments and efforts toward improving our study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cheng, G.; Han, J.; Lu, X. Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Geographic image retrieval using local invariant features. IEEE Trans. Geosci. Remote Sens. 2013, 51, 818–832. [Google Scholar] [CrossRef]
- Martha, T.R.; Kerle, N.; van Westen, C.J.; Jetten, V.; Kumar, K.V. Segment optimization and data-driven thresholding for knowledge-based landslide detection by object-based image analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4928–4943. [Google Scholar] [CrossRef]
- Qi, K.; Wu, H.; Shen, C.; Gong, J. Land-use scene classification in high-resolution remote sensing images using improved correlatons. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2403–2407. [Google Scholar]
- Du, Z.; Li, X.; Lu, X. Local structure learning in high resolution remote sensing image retrieval. Neurocomputing 2016, 207, 813–822. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, T.; Ouyang, C. End-to-end airplane detection using transfer learning in remote sensing images. Remote Sens. 2018, 10, 139. [Google Scholar] [CrossRef]
- Oquab, M.; Bottou, L.; Laptev, I.; Sivic, J. Learning and transferring mid-level image representations using convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1717–1724. [Google Scholar]
- Penatti, O.A.; Nogueira, K.; Dos Santos, J.A. Do deep features generalize from everyday objects to remote sensing and aerial scenes domains? In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 44–51. [Google Scholar]
- Hu, F.; Xia, G.S.; Hu, J.; Zhang, L. Transferring deep convolutional neural networks for the scene classification of high-resolution remote sensing imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Romero, A.; Gatta, C.; Camps-Valls, G. Unsupervised deep feature extraction for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1349–1362. [Google Scholar] [CrossRef]
- Cheng, G.; Yang, C.; Yao, X.; Guo, L.; Han, J. When deep learning meets metric learning: Remote sensing image scene classification via learning discriminative CNNs. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2811–2821. [Google Scholar] [CrossRef]
- Pires de Lima, R.; Marfurt, K. Convolutional neural network for remote-sensing scene classification: Transfer learning analysis. Remote Sens. 2020, 12, 86. [Google Scholar] [CrossRef]
- Li, E.; Xia, J.; Du, P.; Lin, C.; Samat, A. Integrating multilayer features of convolutional neural networks for remote sensing scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5653–5665. [Google Scholar] [CrossRef]
- Qi, K.; Guan, Q.; Yang, C.; Peng, F.; Shen, S.; Wu, H. Concentric Circle Pooling in Deep Convolutional Networks for Remote Sensing Scene Classification. Remote Sens. 2018, 10, 934. [Google Scholar] [CrossRef]
- Xie, J.; He, N.; Fang, L.; Plaza, A. Scale-free convolutional neural network for remote sensing scene classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6916–6928. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J.; Pan, B.; Shi, Z. Domain Adaptation Based on Correlation Subspace Dynamic Distribution Alignment for Remote Sensing Image Scene Classification. IEEE Trans. Geosci. Remote. Sens. 2020, 58, 7920–7930. [Google Scholar] [CrossRef]
- Swain, M.J.; Ballard, D.H. Color indexing. Int. J. Comput. Vis. 1991, 7, 11–32. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; IEEE Computer Society: Washington, DC, USA, 2005; Volume 1, pp. 886–893. [Google Scholar]
- Oliva, A.; Torralba, A. Modeling the shape of the scene: A holistic representation of the spatial envelope. Int. J. Comput. Vis. 2001, 42, 145–175. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.-F. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Li, K.; Cheng, G.; Bu, S.; You, X. Rotation-insensitive and context-augmented object detection in remote sensing images. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2337–2348. [Google Scholar] [CrossRef]
- Bromley, J.; Guyon, I.; LeCun, Y.; Säckinger, E.; Shah, R. Signature verification using a “siamese” time delay neural network. In Proceedings of the 7th International Conference on Neural Information Processing Systems, Denver, Colorado, USA, 28 November–1 December 1994; pp. 737–744. [Google Scholar]
- Liu, X.; Zhou, Y.; Zhao, J.; Yao, R.; Liu, B.; Zheng, Y. Siamese convolutional neural networks for remote sensing scene classification. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1200–1204. [Google Scholar] [CrossRef]
- Endres, D.M.; Schindelin, J.E. A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Hariharan, B.; Arbeláez, P.; Girshick, R.; Malik, J. Simultaneous detection and segmentation. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Cham, Switzerland, 2014; pp. 297–312. [Google Scholar]
- Li, Z.; Song, Y.; Mcloughlin, I.; Dai, L. Compact convolutional neural network transfer learning for small-scale image classification. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 2737–2741. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Li, H.; Gu, H.; Han, Y.; Yang, J. Object-oriented classification of high-resolution remote sensing imagery based on an improved colour structure code and a support vector machine. Int. J. Remote Sens. 2010, 31, 1453–1470. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Jain, A.K.; Ratha, N.K.; Lakshmanan, S. Object detection using Gabor filters. Pattern Recognit. 1997, 30, 295–309. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 270–279. [Google Scholar]
- Zhao, L.J.; Tang, P.; Huo, L.Z. Land-use scene classification using a concentric circle-structured multiscale bag-of-visual-words model. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 4620–4631. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhong, Y.; Zhao, B.; Xia, G.S.; Zhang, L. Bag-of-visual-words scene classifier with local and global features for high spatial resolution remote sensing imagery. IEEE Geosci. Remote Sens. Lett. 2016, 13, 747–751. [Google Scholar] [CrossRef]
- Cheng, G.; Li, Z.; Yao, X.; Guo, L.; Wei, Z. Remote sensing image scene classification using bag of convolutional features. IEEE Trans. Geosci. Remote Sens. 2017, 14, 1735–1739. [Google Scholar] [CrossRef]
- He, N.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Remote sensing scene classification using multilayer stacked covariance pooling. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6899–6910. [Google Scholar] [CrossRef]
- Cao, R.; Fang, L.; Lu, T.; He, N. Self-Attention-Based Deep Feature Fusion for Remote Sensing Scene Classification. IEEE Geosci. Remote. Sens. Lett. 2021, 18, 43–47. [Google Scholar] [CrossRef]
- Lenc, K.; Vedaldi, A. Understanding image representations by measuring their equivariance and equivalence. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 991–999. [Google Scholar]
- Marcos, D.; Volpi, M.; Tuia, D. Learning rotation invariant convolutional filters for texture classification. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 2012–2017. [Google Scholar]
- Laptev, D.; Savinov, N.; Buhmann, J.M.; Pollefeys, M. TI-POOLING: Transformation-invariant pooling for feature learning in convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 289–297. [Google Scholar]
- Kohli, D.; Das, B.C.; Gopalakrishnan, V.; Iyer, K.N. Learning rotation invariance in deep hierarchies using circular symmetric filters. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 2846–2850. [Google Scholar]
- Cheng, G.; Zhou, P.; Han, J. Learning rotation-invariant convolutional neural networks for object detection in VHR optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7405–7415. [Google Scholar] [CrossRef]
- Wang, G.; Wang, X.; Fan, B.; Pan, C. Feature extraction by rotation-invariant matrix representation for object detection in aerial image. IEEE Geosci. Remote Sens. Lett. 2017, 14, 851–855. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, X.; Zhao, J.; Ma, D.; Yao, R.; Liu, B.; Zheng, Y. Remote sensing scene classification based on rotation-invariant feature learning and joint decision making. EURASIP J. Image Video Process. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Lazebnik, S.; Schmid, C.; Ponce, J. A sparse texture representation using local affine regions. IEEE Trans. Pattern Anal. 2005, 27, 1265–1278. [Google Scholar] [CrossRef]
- Jaderberg, M.; Simonyan, K.; Zisserman, A.; Kavukcuoglu, K. Spatial transformer networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–10 December 2015; pp. 2017–2025. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Perez, L.; Wang, J. The effectiveness of data augmentation in image classification using deep learning. arXiv 2017, arXiv:1712.04621. [Google Scholar]
- Yu, X.; Wu, X.; Luo, C.; Ren, P. Deep learning in remote sensing scene classification: A data augmentation enhanced convolutional neural network framework. GISci. Remote Sens. 2017, 54, 741–758. [Google Scholar] [CrossRef]
- Noroozi, M.; Favaro, P. Unsupervised learning of visual representations by solving jigsaw puzzles. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Cham, Switzerland, 2016; pp. 69–84. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Lee, D.H. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. In Proceedings of the ICML 2013 Workshop on Challenges in Representation Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 3. [Google Scholar]
- Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A benchmark data set for performance evaluation of aerial scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the 32th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 8024–8035. [Google Scholar]
- Sivic, J.; Zisserman, A. Video Google: A text retrieval approach to object matching in videos. In Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; p. 1470. [Google Scholar]
- Han, X.; Zhong, Y.; Cao, L.; Zhang, L. Pre-trained alexnet architecture with pyramid pooling and supervision for high spatial resolution remote sensing image scene classification. Remote Sens. 2017, 9, 848. [Google Scholar] [CrossRef]
- Anwer, R.M.; Khan, F.S.; van de Weijer, J.; Molinier, M.; Laaksonen, J. Binary patterns encoded convolutional neural networks for texture recognition and remote sensing scene classification. ISPRS J. Photogramm. Remote Sens. 2018, 138, 74–85. [Google Scholar] [CrossRef]
- Bi, Q.; Qin, K.; Zhang, H.; Li, Z.; Xu, K. RADC-Net: A residual attention based convolution network for aerial scene classification. Neurocomputing 2020, 377, 345–359. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).