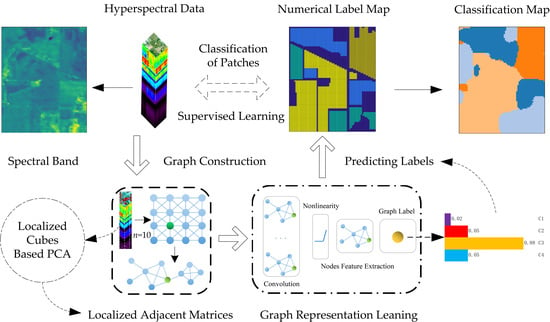
Hyperspectral Image Classification with Localized Graph Convolutional Filtering
Abstract
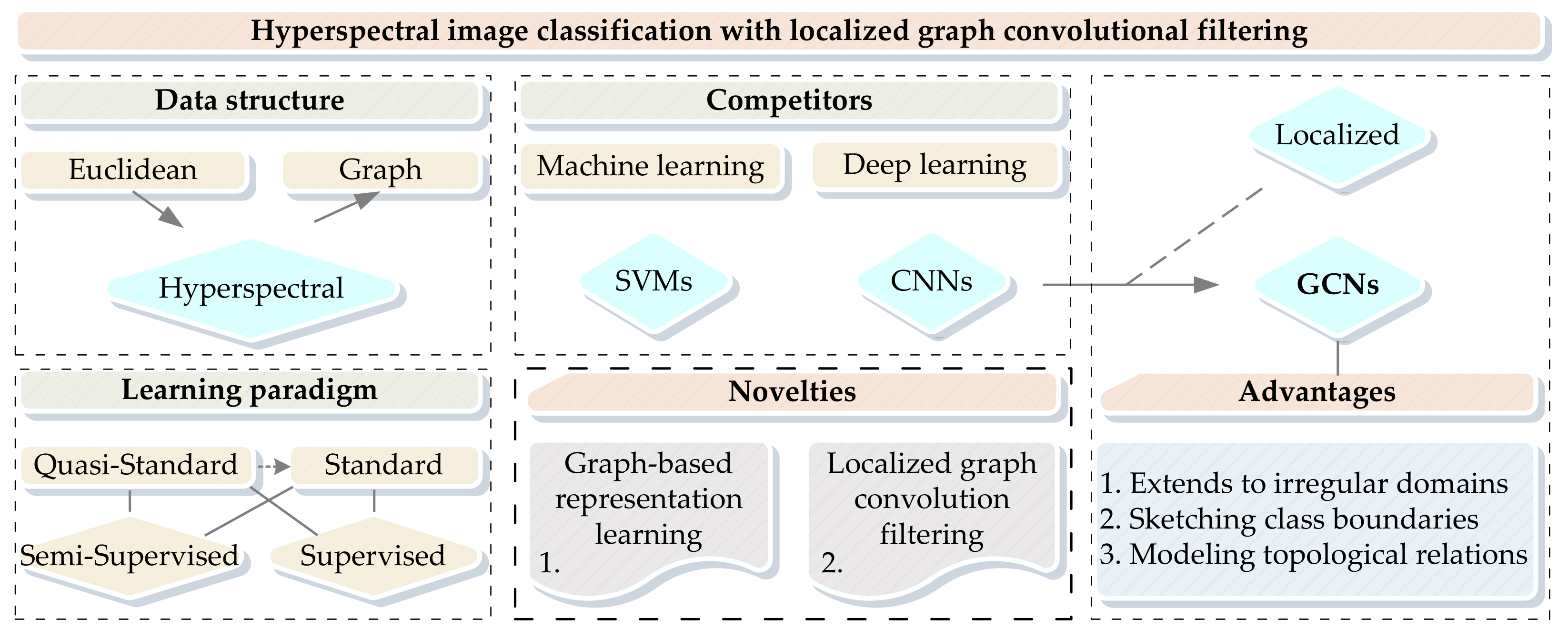
1. Introduction
- (1)
- The usual supervised setting regarding fitting the graph-based learning models is designed through collecting the patch-based feature cubes and localized graph adjacent matrices.
- (2)
- The graph convolution layer is used to learn the spatially local graph representation and to represent the localized topological patterns of the graph nodes.
- (3)
- The experiments demonstrate that the presented study could achieve promising classification performance based on the localized graph convolutional filter.
2. Related Work
3. Preliminaries
3.1. Graph Structure
3.2. Adjacency Matrix
- (1)
- (2)
- the distance function is defined between two samples and , where is an optional parameter, and is the dimension of the feature vector. When is 1 or 2, it becomes Manhattan distance or Euclidean distance (i.e., used in this study), respectively. The distance metric of all sample pairs can form a symmetric distance matrix . For example, at row and column in the matrix denotes the distance between the pixel and the pixel [20].
3.3. Graph Laplacian
3.4. Graph Fourier Transform
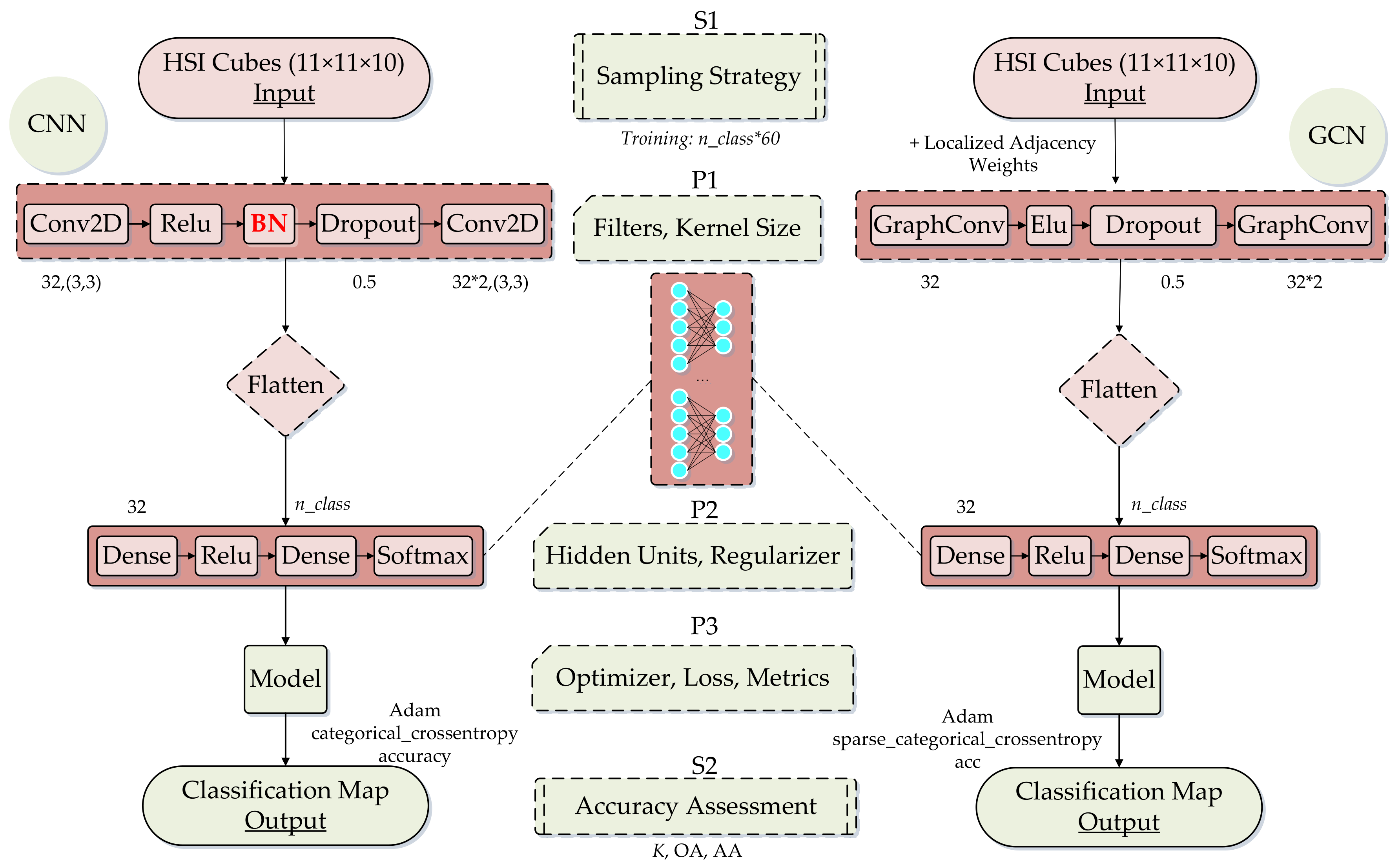
4. Proposed Method
4.1. Graph Construction
4.2. Graph Convolution Filter
4.3. Localized Graph Convolution
4.4. Graph-Based CNN
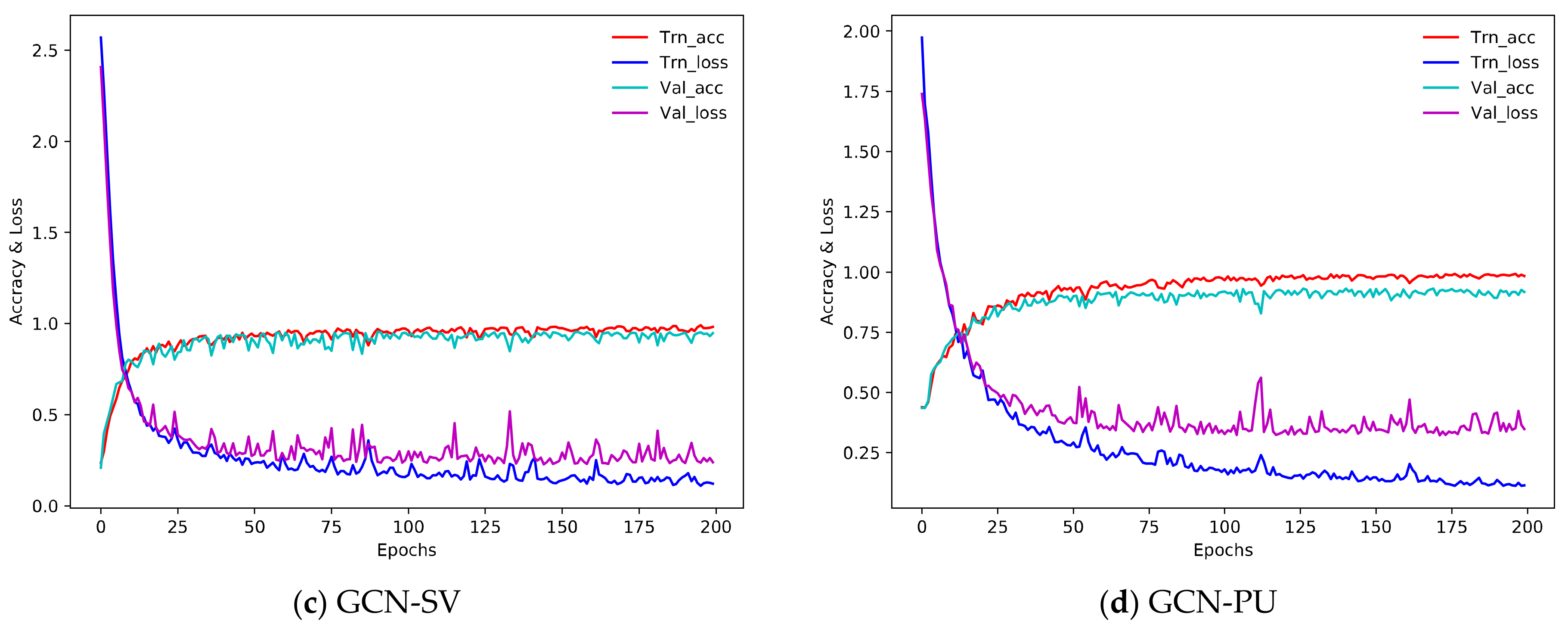
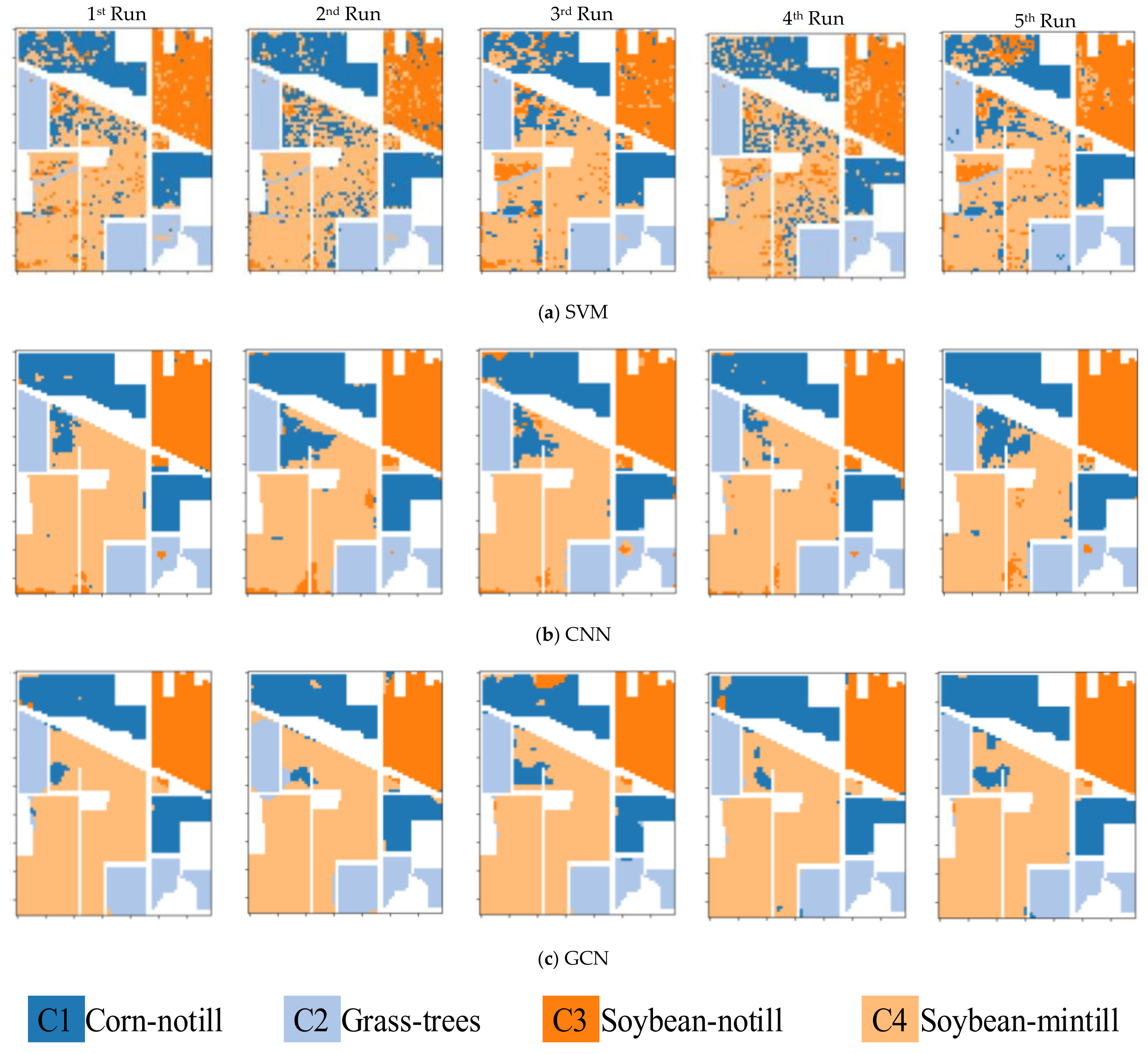
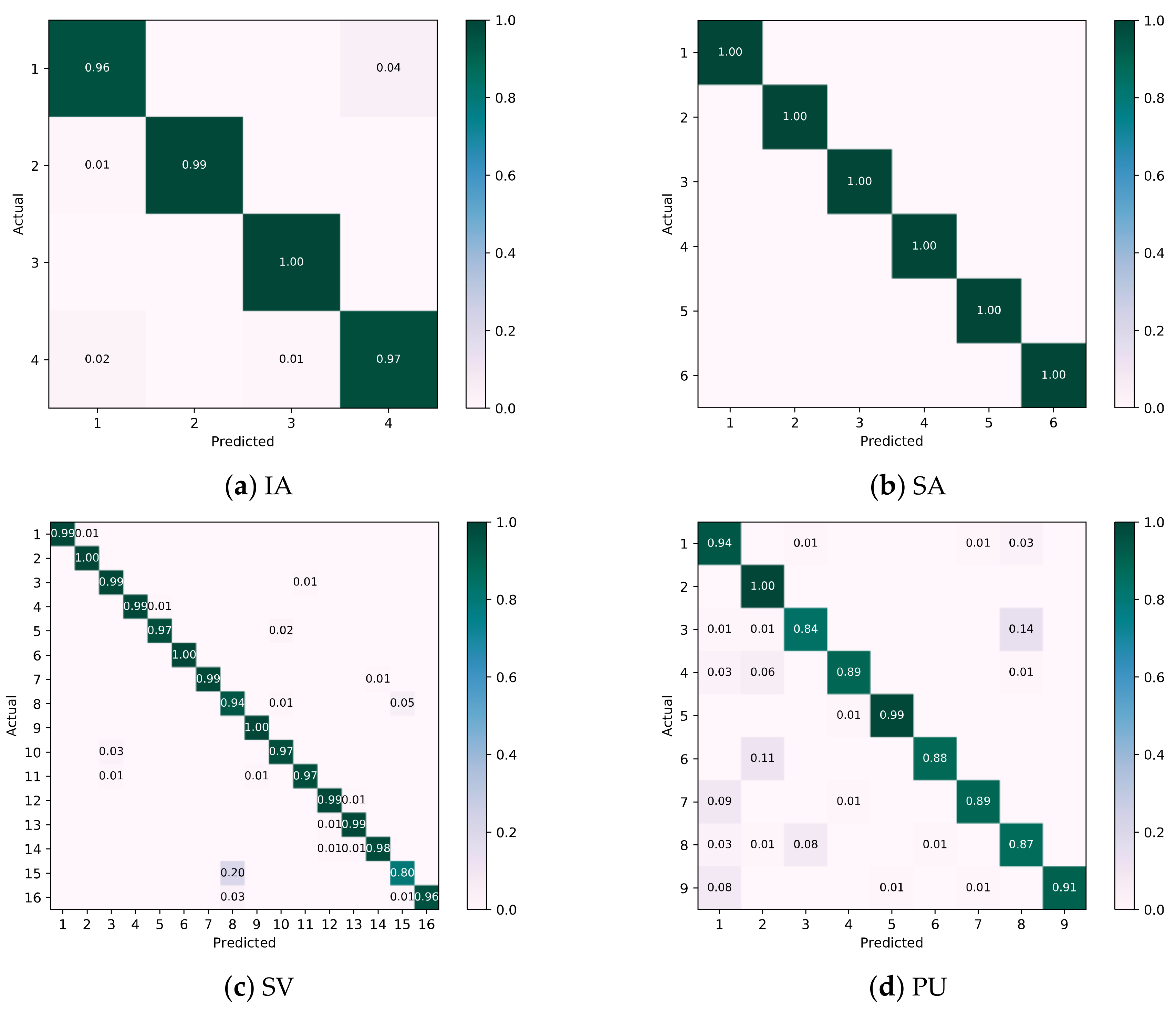
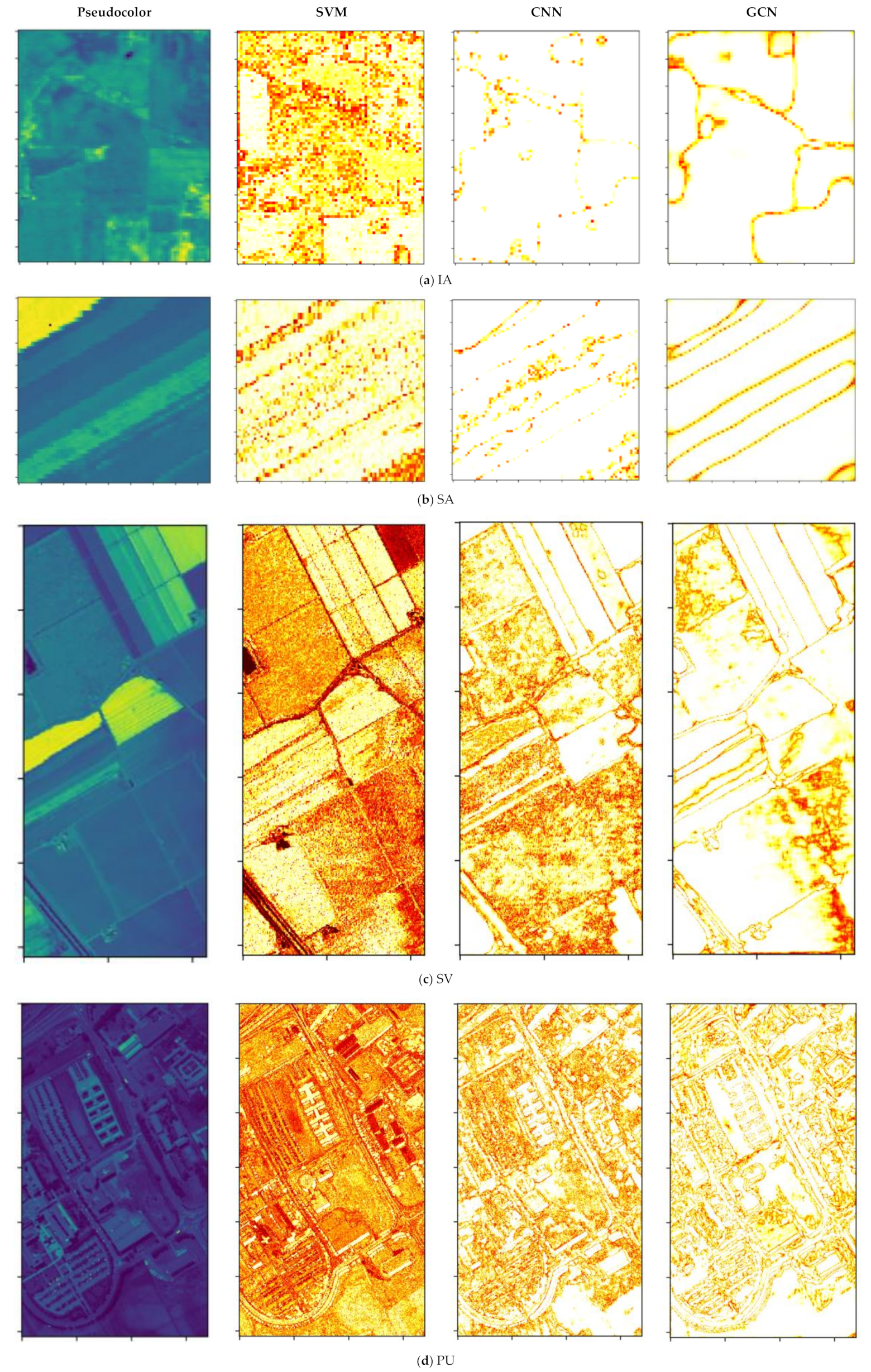
5. Experiments and Analysis
5.1. Datasets and Settings
5.2. Classification Maps
5.3. Classification Accuracies
5.4. Probability Maps
5.5. Time Consumption
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rasti, B.; Hong, D.; Hang, R.; Ghamisi, P.; Kang, X.; Chanussot, J.; Benediktsson, J.A. Feature extraction for hyperspectral imagery: The evolution from shallow to deep (overview and toolbox). IEEE Geosci. Remote Sens. Mag. 2020, 8, 60–88. [Google Scholar] [CrossRef]
- Hong, D.; Yokoya, N.; Chanussot, J.; Zhu, X.X. An augmented linear mixing model to address spectral variability for hyperspectral unmixing. IEEE Trans. Image Process. 2019, 28, 1923–1938. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Du, Q.; Zhang, B.; Yang, W.; Wu, Y. A comparative study on linear regression-based noise estimation for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 488–498. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, X.; Gao, L.; Yang, L. Endmember extraction of hyperspectral remote sensing images based on the ant colony optimization (ACO) algorithm. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2635–2646. [Google Scholar] [CrossRef]
- Zhang, B.; Li, S.; Jia, X.; Gao, L.; Peng, M. Adaptive Markov random field approach for classification of hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2011, 8, 973–977. [Google Scholar] [CrossRef]
- Zhang, B.; Yang, W.; Gao, L.; Chen, D. Real-Time target detection in hyperspectral images based on spatial-spectral information extraction. EURASIP J. Adv. Signal Process. 2012, 142. [Google Scholar] [CrossRef]
- Qin, A.; Shang, Z.; Tian, J.; Wang, Y.; Zhang, T.; Tang, Y.Y. Spectral-Spatial graph convolutional networks for semisupervised hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2018, 16, 241–245. [Google Scholar] [CrossRef]
- Hong, D.; Yokoya, N.; Chanussot, J.; Zhu, X.X. Cospace: Common subspace learning from hyperspectral-multispectral correspondences. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4349–4359. [Google Scholar] [CrossRef]
- Richards, J.A.; Jia, X. Remote Sensing Digital Image Analysis: An Introduction; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph convolutional networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Wan, S.; Gong, C.; Zhong, P.; Du, B.; Zhang, L.; Yang, J. Multiscale dynamic graph convolutional network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3162–3177. [Google Scholar] [CrossRef]
- Cao, J.; Chen, Z.; Wang, B. Graph-Based deep convolutional networks for hyperspectral image classification. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3270–3273. [Google Scholar]
- Hong, D.; Wu, X.; Ghamisi, P.; Chanussot, J.; Yokoya, N.; Zhu, X.X. Invariant attribute profiles: A spatial-frequency joint feature extractor for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3791–3808. [Google Scholar] [CrossRef]
- Gao, L.; Li, J.; Khodadadzadeh, M.; Plaza, A.; Zhang, B.; He, Z.; Yan, H. Subspace-Based support vector machines for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2014, 12, 349–353. [Google Scholar]
- Yu, H.; Gao, L.; Li, J.; Li, S.S.; Zhang, B.; Benediktsson, J.A. Spectral-Spatial hyperspectral image classification using subspace-based support vector machines and adaptive Markov random fields. Remote Sens. 2016, 8, 355. [Google Scholar] [CrossRef]
- Gao, L.; Yu, H.; Zhang, B.; Li, Q. Locality-Preserving sparse representation-based classification in hyperspectral imagery. J. Appl. Remote Sens. 2016, 10, 042004. [Google Scholar] [CrossRef]
- Yu, H.; Gao, L.; Li, W.; Du, Q.; Zhang, B. Locality sensitive discriminant analysis for group sparse representation-based hyperspectral imagery classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1358–1362. [Google Scholar] [CrossRef]
- Gao, L.; Zhao, B.; Jia, X.; Liao, W.; Zhang, B. Optimized kernel minimum noise fraction transformation for hyperspectral image classification. Remote Sens. 2017, 9, 548. [Google Scholar] [CrossRef]
- Yu, H.; Gao, L.; Liao, W.; Zhang, B.; Pižurica, A.; Philips, W. Multiscale superpixel-level subspace-based support vector machines for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2142–2146. [Google Scholar] [CrossRef]
- Liu, B.; Gao, K.; Yu, A.; Guo, W.; Wang, R.; Zuo, X. Semisupervised graph convolutional network for hyperspectral image classification. J. Appl. Remote Sens. 2020, 14, 026516. [Google Scholar] [CrossRef]
- Zhang, F.; Du, B.; Zhang, L. Saliency-Guided unsupervised feature learning for scene classification. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2175–2184. [Google Scholar] [CrossRef]
- Zhong, P.; Gong, Z.; Li, S.; Schonlieb, C.-B. Learning to diversify deep belief networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3516–3530. [Google Scholar] [CrossRef]
- Hang, R.; Liu, Q.; Hong, D.; Ghamisi, P. Cascaded recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5384–5394. [Google Scholar] [CrossRef]
- Cui, X.; Zheng, K.; Gao, L.; Zhang, B.; Yang, D.; Ren, J. Multiscale spatial-spectral convolutional network with image-based framework for hyperspectral imagery classification. Remote Sens. 2019, 11, 2220. [Google Scholar] [CrossRef]
- Gao, L.; Gu, D.; Zhuang, L.; Ren, J.; Yang, D.; Zhang, B. Combining t-Distributed Stochastic Neighbor Embedding with Convolutional Neural Networks for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1368–1372. [Google Scholar] [CrossRef]
- Yu, H.; Gao, L.; Liao, W.; Zhang, B.; Zhuang, L.; Song, M.; Chanussot, J. Global spatial and local spectral similarity-based manifold learning group sparse representation for hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3043–3056. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, L.; Xiao, C.; Qu, Y.; Zheng, K.; Marinoni, A. Hyperspectral Image Classification Based on a Shuffled Group Convolutional Neural Network with Transfer Learning. Remote Sens. 2020, 12, 1780. [Google Scholar] [CrossRef]
- Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R.; et al. Relational inductive biases, deep learning, and graph networks. arXiv 2018, arXiv:1806.01261. [Google Scholar]
- Yang, X.; Ye, Y.; Li, X.; Lau, R.Y.K.; Zhang, X.; Huang, X. Hyperspectral image classification with deep learning models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5408–5423. [Google Scholar] [CrossRef]
- Wan, S.; Gong, C.; Zhong, P.; Pan, S.; Li, G.; Yang, J. Hyperspectral Image Classification with Context-Aware Dynamic Graph Convolutional Network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 597–612. [Google Scholar] [CrossRef]
- Defferrard, M.I.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neural Inf. Process. Syst. 2016, 29, 3844–3852. [Google Scholar]
- Chung, F.R.K.; Graham, F.C. Spectral Graph Theory; American Mathematical Society: Providence, RI, USA, 1997. [Google Scholar]
- Hong, D.; Yokoya, N.; Ge, N.; Chanussot, J.; Zhu, X.X. Learnable manifold alignment (LeMA): A semi-supervised cross-modality learning framework for land cover and land use classification. ISPRS J. Photogramm. Remote Sens. 2019, 147, 193–205. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.M.; Yang, X.; Guo, Y. Local-Manifold-Learning-Based graph construction for semisupervised hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2832–2844. [Google Scholar] [CrossRef]
- Gao, L.; Hong, D.; Yao, J.; Zhang, B.; Gamba, P.; Chanussot, J. Spectral superresolution of multispectral imagery with joint sparse and low-rank learning. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Tan, K.; Zhou, S.; Du, Q. Semisupervised discriminant analysis for hyperspectral imagery with block-sparse graph. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1765–1769. [Google Scholar] [CrossRef]
- Luo, F.; Huang, H.; Ma, Z.; Liu, J. Semisupervised sparse manifold discriminative analysis for feature extraction of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6197–6211. [Google Scholar] [CrossRef]
- De Morsier, F.; Borgeaud, M.; Gass, V.; Thiran, J.P.; Tuia, D. Kernel low-rank and sparse graph for unsupervised and semi-supervised classification of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3410–3420. [Google Scholar] [CrossRef]
- Shao, Y.; Sang, N.; Gao, C.; Ma, L. Probabilistic class structure regularized sparse representation graph for semi-supervised hyperspectral image classification. Pattern Recognit. 2017, 63, 102–114. [Google Scholar] [CrossRef]
- Hong, D.; Yokoya, N.; Chanussot, J.; Xu, J.; Zhu, X.X. Learning to propagate labels on graphs: An iterative multitask regression framework for semi-supervised hyperspectral dimensionality reduction. ISPRS J. Photogramm. Remote Sens. 2019, 158, 35–49. [Google Scholar] [CrossRef]
- Yang, L.; Yang, S.; Jin, P.; Zhang, R. Semi-Supervised hyperspectral image classification using spatio-spectral Laplacian support vector machine. IEEE Geosci. Remote Sens. Lett. 2013, 11, 651–655. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Marsheva, T.V.B.; Zhou, D. Semi-Supervised graph-based hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3044–3054. [Google Scholar] [CrossRef]
- Gao, Y.; Ji, R.; Cui, P.; Dai, Q.; Hua, G. Hyperspectral image classification through bilayer graph-based learning. IEEE Trans. Image Process. 2014, 23, 2769–2778. [Google Scholar] [CrossRef]
- Martínez-Usó, A.; Pla, F.; Sotoca, J.M. Modelling contextual constraints in probabilistic relaxation for multi-class semi-supervised learning. Knowl. Based Syst. 2014, 66, 82–91. [Google Scholar] [CrossRef]
- Wang, L.; Hao, S.; Wang, Q.; Wang, Y. Semi-Supervised classification for hyperspectral imagery based on spatial-spectral label propagation. ISPRS J. Photogramm. Remote Sens. 2014, 97, 123–137. [Google Scholar] [CrossRef]
- Luo, R.; Liao, W.; Huang, X.; Pi, Y.; Philips, W. Feature extraction of hyperspectral images with semisupervised graph learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4389–4399. [Google Scholar] [CrossRef]
- Kruse, F.A.; Boardman, J.W.; Huntington, J.F. Comparison of airborne hyperspectral data and EO-1 Hyperion for mineral mapping. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1388–1400. [Google Scholar] [CrossRef]
- Chen, P.; Jiao, L.; Liu, F.; Zhao, J.; Zhao, Z.; Liu, S. Semi-Supervised double sparse graphs based discriminant analysis for dimensionality reduction. Pattern Recognit. 2017, 61, 361–378. [Google Scholar] [CrossRef]
- Xue, Z.; Du, P.; Li, J.; Su, H. Sparse graph regularization for hyperspectral remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2351–2366. [Google Scholar] [CrossRef]
- Aydemir, M.S.; Bilgin, G. Semisupervised hyperspectral image classification using small sample sizes. IEEE Geosci. Remote Sens. Lett. 2017, 14, 621–625. [Google Scholar] [CrossRef]
- Ma, L.; Ma, A.; Ju, C.; Li, X. Graph-Based semi-supervised learning for spectral-spatial hyperspectral image classification. Pattern Recognit. Lett. 2016, 83, 133–142. [Google Scholar] [CrossRef]
- Shahraki, F.F.; Prasad, S. Graph convolutional neural networks for hyperspectral data classification. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–28 November 2018; pp. 968–972. [Google Scholar]
- Hong, D.; Gao, L.; Yokoya, N.; Yao, J.; Chanussot, J.; Du, Q.; Zhang, B. More diverse means better: Multimodal deep learning meets remote-sensing imagery classification. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Hong, D.; Yokoya, N.; Xia, G.S.; Chanussot, J.; Zhu, X.X. X-ModalNet: A semi-supervised deep cross-modal network for classification of remote sensing data. ISPRS J. Photogramm. Remote Sens. 2020, 167, 12–23. [Google Scholar] [CrossRef]
- Hamilton, W.L. Graph representation learning. Synth. Lect. Artif. Intell. Mach. Learn. 2020, 14, 1–159. [Google Scholar] [CrossRef]
- Shuman, D.I.; Narang, S.K.; Frossard, P.; Ortega, A.; Vandergheynst, P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- McGillem, C.D.; Cooper, G.R. Continuous and Discrete Signal and System Analysis; Oxford University Press: New York, NY, USA, 1991. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Hammond, D.K.; Vandergheynst, P.; Gribonval, R. Wavelets on graphs via spectral graph theory. Appl. Comput. Harmon. Anal. 2011, 30, 129–150. [Google Scholar] [CrossRef]
- Susnjara, A.; Perraudin, N.; Kressner, D.; Vandergheynst, P. Accelerated filtering on graphs using Lanczos method. arXiv 2015, arXiv:1509.04537. [Google Scholar]
- Rhee, S.; Seo, S.; Kim, S. Hybrid approach of relation network and localized graph convolutional filtering for breast cancer subtype classification. arXiv 2017, arXiv:1711.05859. [Google Scholar]
- Deng, F.; Pu, S.; Chen, X.; Shi, Y.; Yuan, T.; Pu, S. Hyperspectral image classification with capsule network using limited training samples. Sensors 2018, 18, 3153. [Google Scholar] [CrossRef]

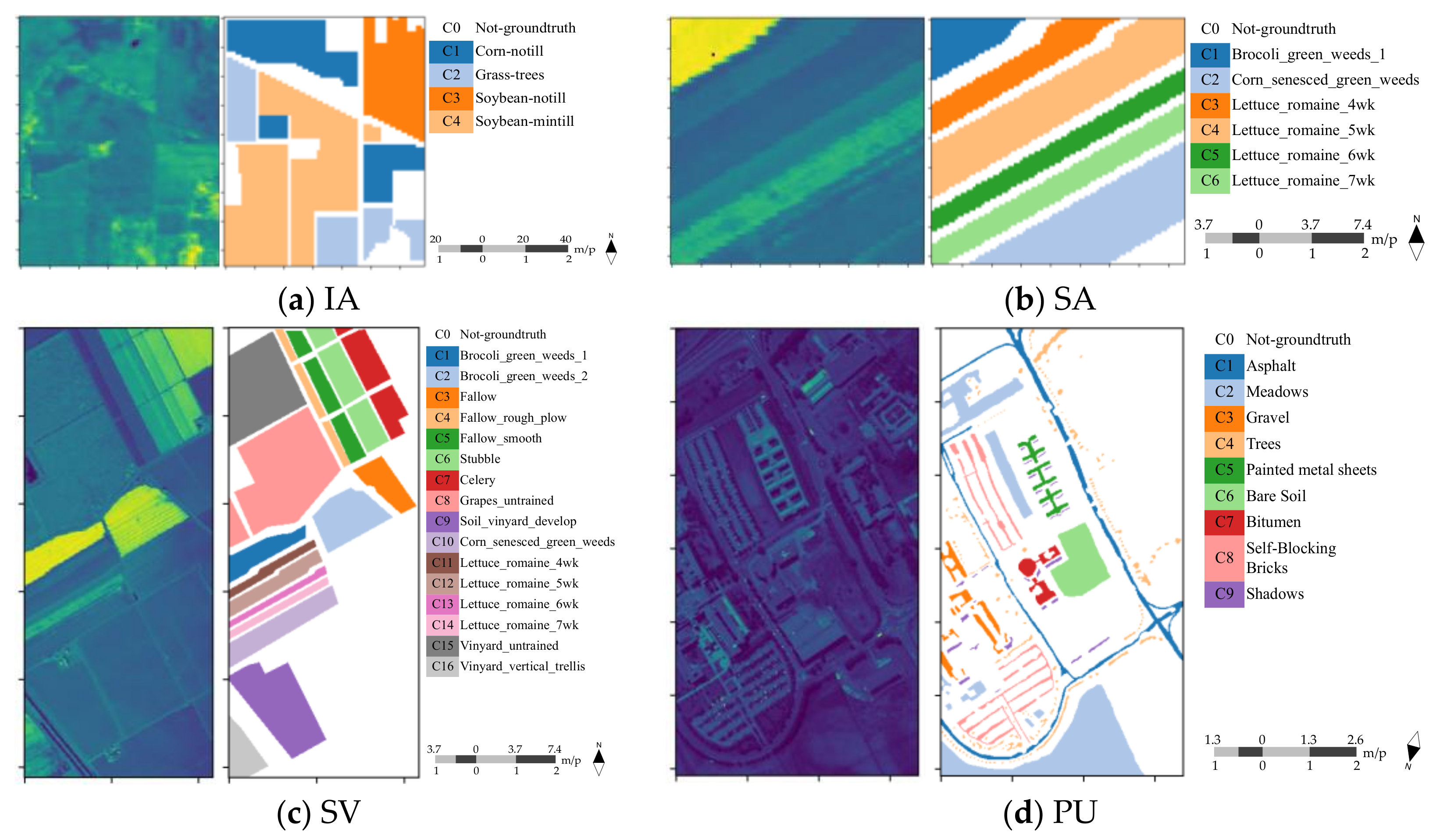


| Datasets | Codes | Classes | Total | Training | Test | Validation |
|---|---|---|---|---|---|---|
| IA | C0 | Not-ground truth | 1534 | 0 | 0 | 0 |
| C1 | Corn-notill | 1005 | 60 | 885 | 60 | |
| C2 | Grass-trees | 730 | 60 | 610 | 60 | |
| C3 | Soybean-notill | 741 | 60 | 621 | 60 | |
| C4 | Soybean-mintill | 1924 | 60 | 1804 | 60 | |
| SA | C0 | Not-ground truth | 1790 | 0 | 0 | 0 |
| C1 | Brocoli_green_weeds_1 | 391 | 60 | 271 | 60 | |
| C2 | Corn_senesced_green_weeds | 1343 | 60 | 1223 | 60 | |
| C3 | Lettuce_romaine_4wk | 616 | 60 | 496 | 60 | |
| C4 | Lettuce_romaine_5wk | 1525 | 60 | 1405 | 60 | |
| C5 | Lettuce_romaine_6wk | 674 | 60 | 554 | 60 | |
| C6 | Lettuce_romaine_7wk | 799 | 60 | 679 | 60 | |
| SV | C0 | Not-ground truth | 56,975 | 0 | 0 | 0 |
| C1 | Brocoli_green_weeds_1 | 2009 | 60 | 1889 | 60 | |
| C2 | Brocoli_green_weeds_2 | 3726 | 60 | 3606 | 60 | |
| C3 | Fallow | 1976 | 60 | 1856 | 60 | |
| C4 | Fallow_rough_plow | 1394 | 60 | 1274 | 60 | |
| C5 | Fallow_smooth | 2678 | 60 | 2558 | 60 | |
| C6 | Stubble | 3959 | 60 | 3839 | 60 | |
| C7 | Celery | 3579 | 60 | 3459 | 60 | |
| C8 | Grapes_untrained | 11,271 | 60 | 11,151 | 60 | |
| C9 | Soil_vinyard_develop | 6203 | 60 | 6083 | 60 | |
| C10 | Corn_senesced_green_weeds | 3278 | 60 | 3158 | 60 | |
| C11 | Lettuce_romaine_4wk | 1068 | 60 | 948 | 60 | |
| C12 | Lettuce_romaine_5wk | 1927 | 60 | 1807 | 60 | |
| C13 | Lettuce_romaine_6wk | 916 | 60 | 796 | 60 | |
| C14 | Lettuce_romaine_7wk | 1070 | 60 | 950 | 60 | |
| C15 | Vinyard_untrained | 7268 | 60 | 7148 | 60 | |
| C16 | Vinyard_vertical_trellis | 1807 | 60 | 1687 | 60 | |
| PU | C0 | Not-ground truth | 164,624 | 0 | 0 | 0 |
| C1 | Asphalt | 6631 | 60 | 6511 | 60 | |
| C2 | Meadows | 18,649 | 60 | 18,529 | 60 | |
| C3 | Gravel | 2099 | 60 | 1979 | 60 | |
| C4 | Trees | 3064 | 60 | 2944 | 60 | |
| C5 | Painted metal sheets | 1345 | 60 | 1225 | 60 | |
| C6 | Bare Soil | 5029 | 60 | 4909 | 60 | |
| C7 | Bitumen | 1330 | 60 | 1210 | 60 | |
| C8 | Self-Blocking Bricks | 3682 | 60 | 3562 | 60 | |
| C9 | Shadows | 947 | 60 | 827 | 60 |
| Alg. | SVM | CNN | GCN | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Dat./Acc. | K | OA | AA | K | OA | AA | K | OA | AA |
| IA5 | 0.7646 ± 0.0174 | 0.8343 ± 0.0120 | 0.8574 ± 0.0136 | 0.8990 ± 0.0103 | 0.9294 ± 0.0076 | 0.9506 ± 0.0043 | 0.9550 ± 0.0064 | 0.9685 ± 0.0045 | 0.9692 ± 0.0062 |
| SA5 | 0.9793 ± 0.0054 | 0.9836 ± 0.0043 | 0.9818 ± 0.0065 | 0.9477 ± 0.0153 | 0.9586 ± 0.0122 | 0.9701 ± 0.0079 | 0.9983 ± 0.0010 | 0.9987 ± 0.0008 | 0.9982 ± 0.0011 |
| SV5 | 0.8370 ± 0.0076 | 0.8533 ± 0.0070 | 0.9229 ± 0.0027 | 0.7895 ± 0.0126 | 0.8101 ± 0.0115 | 0.8244 ± 0.0057 | 0.9360 ± 0.0099 | 0.9426 ± 0.0088 | 0.9614 ± 0.0090 |
| PU5 | 0.7015 ± 0.0065 | 0.7651 ± 0.0051 | 0.8270 ± 0.0090 | 0.7238 ± 0.0235 | 0.7856 ± 0.0204 | 0.8423 ± 0.0121 | 0.9113 ± 0.0080 | 0.9336 ± 0.0059 | 0.8927 ± 0.0128 |
| IA10 | 0.7671 ± 0.0156 | 0.8355 ± 0.0114 | 0.8613 ± 0.0106 | 0.8930 ± 0.0249 | 0.9250 ± 0.0182 | 0.9475 ± 0.0094 | 0.9579 ± 0.0104 | 0.9706 ± 0.0072 | 0.9702 ± 0.0075 |
| SA10 | 0.9795 ± 0.0046 | 0.9837 ± 0.0036 | 0.9823 ± 0.0055 | 0.9637 ± 0.0074 | 0.9713 ± 0.0058 | 0.9783 ± 0.0038 | 0.9978 ± 0.0020 | 0.9982 ± 0.0016 | 0.9977 ± 0.0021 |
| SV10 | 0.8389 ± 0.0080 | 0.8551 ± 0.0073 | 0.9224 ± 0.0037 | 0.7896 ± 0.0069 | 0.8105 ± 0.0064 | 0.8234 ± 0.0098 | 0.9405 ± 0.0136 | 0.9465 ± 0.0123 | 0.9663 ± 0.0063 |
| PU10 | 0.7038 ± 0.0168 | 0.7674 ± 0.0148 | 0.8274 ± 0.0088 | 0.7218 ± 0.0314 | 0.7836 ± 0.0267 | 0.8424 ± 0.0152 | 0.9079 ± 0.0153 | 0.9309 ± 0.0117 | 0.8916 ± 0.0185 |
| Alg. (Para.)/Dat. (Num.)/Time (s) | IA (86 × 69 × 200) | SA (83 × 86 × 204) | SV (512 × 217 × 204) | PU (610 × 340 × 103) | ||||
|---|---|---|---|---|---|---|---|---|
| Training (240) | Test (3920) | Training (360) | Test (4628) | Training (960) | Test (52209) | Training (540) | Test (41696) | |
| SVM5 | 1.00 ± 0.04 | 0.01 ± 0.01 | 2.22 ± 0.01 | 0.02 ± 0.01 | 17.35 ± 0.25 | 1.29 ± 0.05 | 5.77 ± 0.01 | 0.55 ± 0.04 |
| CNN5 (1.22 × 105) | 14.65 ± 4.47 | 0.31 ± 0.01 | 17.07 ± 3.33 | 0.39 ± 0.02 | 18.49 ± 0.27 | 5.00 ± 0.14 | 15.03 ± 0.94 | 3.21 ± 0.05 |
| GCN5 (2.50 × 105) | 13.22 ± 1.22 | 0.24 ± 0.00 | 20.41 ± 0.72 | 0.31 ± 0.00 | 43.39± 0.48 | 3.61 ± 0.07 | 28.10 ± 0.59 | 3.03 ± 0.06 |
| SVM10 | 1.05 ± 0.06 | 0.01 ± 0.00 | 2.24 ± 0.03 | 0.02 ± 0.01 | 17.47 ± 0.20 | 1.27 ± 0.03 | 5.80 ± 0.10 | 0.56 ± 0.04 |
| CNN10 (1.22 × 105) | 12.69 ± 2.98 | 0.33 ± 0.03 | 14.79 ± 2.34 | 0.37 ± 0.01 | 18.06 ± 1.16 | 4.79 ± 0.31 | 13.72 ± 0.85 | 3.04 ± 0.04 |
| GCN10 (2.50 × 105) | 13.50 ± 4.12 | 0.24 ± 0.01 | 21.52 ± 1.31 | 0.32 ± 0.01 | 50.04 ± 2.85 | 4.08 ± 0.13 | 35.08 ± 2.69 | 3.62 ± 0.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, S.; Wu, Y.; Sun, X.; Sun, X. Hyperspectral Image Classification with Localized Graph Convolutional Filtering. Remote Sens. 2021, 13, 526. https://doi.org/10.3390/rs13030526
Pu S, Wu Y, Sun X, Sun X. Hyperspectral Image Classification with Localized Graph Convolutional Filtering. Remote Sensing. 2021; 13(3):526. https://doi.org/10.3390/rs13030526
Chicago/Turabian StylePu, Shengliang, Yuanfeng Wu, Xu Sun, and Xiaotong Sun. 2021. "Hyperspectral Image Classification with Localized Graph Convolutional Filtering" Remote Sensing 13, no. 3: 526. https://doi.org/10.3390/rs13030526
APA StylePu, S., Wu, Y., Sun, X., & Sun, X. (2021). Hyperspectral Image Classification with Localized Graph Convolutional Filtering. Remote Sensing, 13(3), 526. https://doi.org/10.3390/rs13030526