Abstract
Understanding swash zone dynamics is of crucial importance for coastal management as the swash motion, consisting of the uprush of the wave on the beach face and the subsequent downrush, is responsible for driving changes in the beach morphology through sediment exchanges between the sub-aerial and sub-aqueous beach. Improved understanding of the probabilistic characteristics of these motions has the potential to allow coastal engineers to develop improved sediment transport models which, in turn, can be further developed into coastal management tools. In this paper, novel descriptors of swash motions are obtained by combining field data and statistical modelling. Our results indicate that the probability distribution function (PDF) of shoreline height timeseries () and trough-to-peak swash heights () measured at a high energy, sandy beach were both inherently multimodal. Based on the observed multimodality of these PDFs, Gaussian mixtures are shown to be the best method to statistically model them. Further, our results show that both offshore and surf zone dynamics are responsible for driving swash zone dynamics, which indicates unsaturated swash. The novel methods and results developed in this paper, both data collection and analysis, could aid coastal managers to develop improved swash zone models in the future.
1. Introduction
The swash zone encompasses the transition region between the sub-aqueous and the sub-aerial beach [1]. It is a highly dynamic environment with alternating wet and dry conditions. Over the past five decades, this region has attracted increased research interest due to the significant role it plays in sediment dynamics and beach erosion [2]. The cross-shore shoreline oscillation, globally referred to as swash, can be divided into two main components: the uprush of the wave on the beach face and the subsequent downrush. Each of these two divisions can be described by their horizontal and vertical (height) components (Figure 1). A large proportion of swash zone research has focused on obtaining empirical parametric formulae to describe extreme runup heights (see Atkinson et al. [3] and Power et al. [4] for recent reviews)[CES],; however, as highlighted by Hughes et al. [5], this approach may not be fully satisfactory to provide information to coastal managers to develop operational tools other than inundation models.
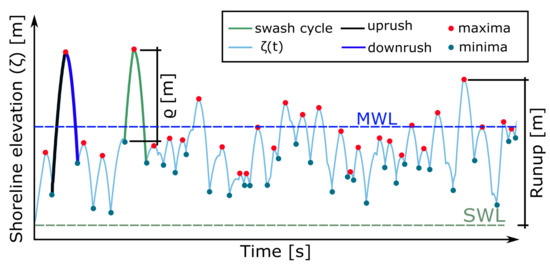
Figure 1.
Swash zone definitions. Note that runup is defined relative to the still water level (SWL), the shoreline height (or elevation, ) is defined centred on the mean water level (MWL), and the trough-to-peak swash height () is defined for each swash cycle. Here, each swash cycle was defined by a local minima analysis.Swash zone definitions.
The natural variability of the probability distribution functions (PDFs) of swash motions has received little research attention to date. To the authors’ knowledge, only two studies have attempted to describe the variability of these PDFs in detail [5,6], both of which [CES]focused on comparingcompared measured [CES]shoreline elevation heightswash maxima PDFs [CES]) to Cartwright and Longuet-Higgins’ [7] theoretical PDF [CES]for the maxima of a random variable. This theoretical PDF is a direct function of the spectral width () of the analysed timeseries and reduces to the Rayleigh PDF for narrow bandwidth processes ( = 0) or to the Gaussian PDF for wide bandwidth processes ( = 1). Holland and Holman [6] found that their measured [CES]shoreline heightswash maxima PDFs matched Cartwright and Longuet-Higgins’ [7] PDF for some values of , but they could not [CES]directly correlate the variability in their PDFs to environmental parameters. [CES]It has been observed [8], however, that the spectral width parameter does not correlate with wave height PDFs in the surf zone and, by induction, should not correlate with swash heights either. More recently, Hughes et al. [5][CES]showed that both their shoreline height PDFs () and trough-to-peak swash height PDFs () resembled, but were not statistically similar to, Cartwright and Longuet-Higgins’ [7] theoretical PDFs.investigated the PDFs of the shoreline height timeseries () and trough-to-peak runup heights (), in addition to swash maxima PDFs. [CES]Hughes et al. [5]They observed that, on average, [CES]observed PDFs were consistently right skewed when compared to the [CES]theoryGaussian PDF predicted by Longuet-Higgins [9], possibly due to the broad-band wave spectrum observed on natural beaches. [CES]It has been observed [8], however, that the spectral width parameter does not correlate with wave height PDFs in the surf zone and, by induction, should not correlate with swash heights either.Further, these authors compared with both the Rayleigh and Gaussian PDFs but neither of these PDFs seemed to satisfactorily describe their observations (see Figure 6 in Hughes et al. [5], for example).
In this paper, we provide novel field observations of swash motion PDFs obtained from a high-resolution LiDAR system deployed at a high-energy sandy beach [CES]and test the hypothesis that well defined, uni-variate and uni-modal PDFs (for example, the Gaussian PDF) are able to describe observed swash zone data. Specifically, the statistical properties of shoreline height [CES]timeseries () and trough-to-peak swash height () [CES]PDFs are investigated in detail. In addition, detailed surf zone and offshore data are used to the assess the patterns observed in the swash zone. The results obtained here deviate significantly from the theoretical predictions from Longuet-Higgins [9][CES]for the analysis of and do not support the concept of swash saturation [10]. The present data indicate that a combination of surf zone and offshore forcing control swash zone dynamics. Finally, an approach that [CES]does not require prior knowledge of is investigated to predict the characteristics of swash motion PDFsallows offshore and surf zone parameters be linked to the variability of is investigated. This paper is organised as follows. Section 2 describes the data collection methods and pre-processing, Section 3 presents the results of the field data collection with a focus on probabilistic descriptors for swash, Section 4 discusses the results, and Section 5 concludes.
2. Materials and Methods
2.1. Data Collection
Data were collected at [CES]at Seven Mile Beach, Gerroa, New South Wales, Australia, hereafter SMB. This beach is classed as modally dissipative in the Australian morphodynamic beach model [11,12] and for the duration of the present experiment, was characterised by a gently sloping profile (with slope ) with no significant barred morphology, beach cusps, or alongshore variability. Video imagery, pressure transducer (PT), offshore spectral wave, Light imaging Detection And Ranging (LiDAR), acoustic Doppler velocimeter (ADV), and topographic data were collected during a field data collection experiment over six days in June 2018. In this paper, the focus will be on the LiDAR [CES], surf zone (PT) and offshore data. The experimental design is shown in Figure 2 and is summarised below. See Stringari et al. [13] and Stringari and Power [14] for further details.
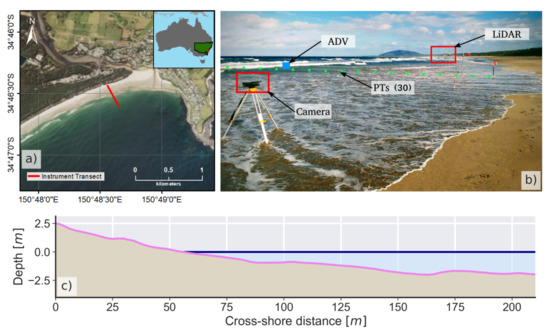
Figure 2.
(a) Experiment location. The red line shows the instrumentation transect. (b) Photo of the experimental setup (19/06/2018). (c) Representative beach profile (16/08/2018).Experiment location, deployed instruments, and representative beach profile.
The PT data collection consisted of 30 PTs (RBR Solo and INW P2X ) deployed on the seabed in a cross-shore orientation. The LiDAR (SiCK LMS511) was mounted on a scaffold frame and recorded in the same cross-shore orientation as the PT transect (see Figure 2a,b). [CES]The ADV (Sontek Hydra) was deployed approximately 50 m seaward of the LiDAR. [CES]AThe Datawell waverider buoy was deployed offshore of the transect line at the 10 m isobath. [CES]Two video cameras were used: a Sony camera (HDR-CX240)
mounted at Gerroa headland and a Raspberry-Pi-based system [15] mounted directly facing the LiDAR (shown in Figure 2b). The beach was surveyed several times each day using a Trimble S5 total station and a Trimble R4 RTK GPS, and the representative beach profile is shown in Figure 2c. Figure 3 shows the offshore conditions for the duration of the field campaign. This dataset was ultimately chosen for the analyses presented in this paper because it overcomes the limitations of classical remote-sensing datasets (e.g., pixel misregistration; see Vousdoukas et al.’s [16] Figure 7), it has precise and unique offshore conditions, and it has a high degree of offshore wave variability for comparable tidal water levels and beach slopes.
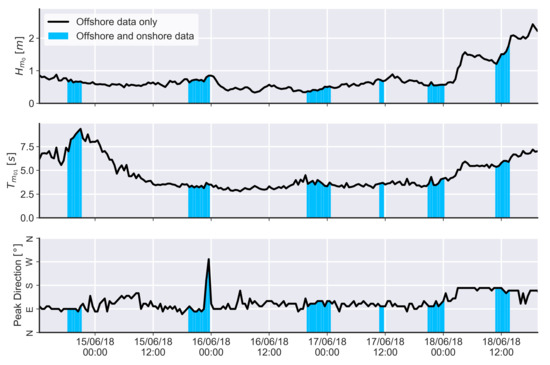
Figure 3.
Offshore data (spectral significant wave heights, , and periods, ), for the duration of the field campaign. The filled blue regions indicate periods of simultaneous offshore, Light imaging Detection And Ranging (LiDAR), and pressure transducer (PT) data collection.Offshore data (, and peak wave direction) for the duration of the field campaign.
2.2. Data Processing
From the raw LiDAR data (Figure 4a), timeseries of the cross-shore evolution of the water surface elevation were extracted at 10 Hz and stacked in time, resulting [CES]in a dataset similar to a video-derived timestack [17] (Figure 4b, color scale). Incoming waves were tracked using a modified version of the method from Stringari, Harris, and Power [13]. For each LIDAR timestack, the vertical Sobel [18] edge detector was applied to the timestack, and pixel intensity peaks in the resulting image were extracted and then clustered using the DBSCAN algorithm [19]. Unlike the original method, no colour-based machine learning was applied to the dataset. The absence of the colour-learning step resulted in a significant increase in the number of false-positive cases of wave crests being detected. These erroneous wave crests were manually corrected in QGIS [CES](version 10.4) to ensure that no errors were propagated into subsequent analyses. Optimal wave paths were then obtained as per the original tracking algorithm [13]. The tracking algorithm was set to stop tracking waves if the water elevation above the bed was less than 0.015 m, which is significantly lower than other recent works [20,21]. [CES]Note that in this paper, we have not quantified uncertainties related to the raw LiDAR data; future research should, however, focus on developing methods to quantify and correct for such uncertainties.
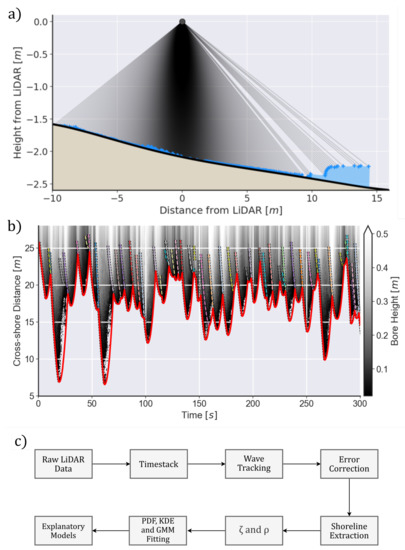
Figure 4.
(a) Raw LiDAR data showing a bore running up the beach profile. (b) Example of LiDAR timestack showing the tracked wave paths (coloured dashed lines) and the resulting time-varying shoreline position (thick red line). The grey scale indicates the bore height (that is, water depth) in relation to the measured profile in (a). [CES](c) Flowchart indicating the methodological steps used in this paper.Examples of raw LiDAR data and a timestack derived from LiDAR data.
The temporal evolution of the shoreline position was obtained in three steps: (1) the uprush was obtained from the tracked wave paths as described above, (2) the downrush was obtained via edge detection using the horizontal Sobel [18] operator, and (3) the continuous shoreline timeseries was obtained by combining the results of steps (1) and (2) and interpolating the data to a regular time vector with a sample frequency of 5 Hz using a Gaussian radial basis function (RBF) interpolation. Finally, horizontal shoreline excursion timeseries were converted to shoreline height () timeseries and to trough-to-peak swash heights () using the measured beach profiles and a local minima analysis (see Figure 1 for definitions). The Australian Height Datum (AHD, [22]) was used as the vertical reference.
3. Results
3.1. Surf Zone Dynamics
The cross-shore variation of surf zone significant wave heights () and the fraction of broken waves () were used to assess the surf zone dynamics (Figure 5). In this paper, was calculated as follows: for each data run in which there were unique offshore, surf zone, and swash zone data available, 10 min of PT data were extracted from the raw records and, from these records, individual waves were extracted using a local minima analysis as per Power et al. [23] and classified as broken or unbroken using the neural network from Stringari and Power [14]. The neural network was updated with field data from Seven Mile Beach to increase the classification performance for the present dataset. The updated neural network accuracy score reached 95% when classifying waves in a test dataset (that is, data that the neural network had never seen) and correlation scores () were >0.95 for predictions (not shown).
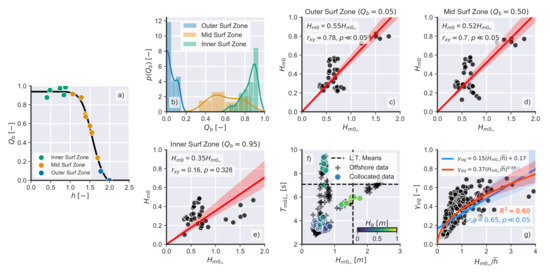
Figure 5.
(a) Example of curve segmentation using k-means for one 10 min data run. (b) Algorithm clustered probability distribution functions (PDFs). The number of bins for these histograms was calculated using the Freedman and Diaconis [27] rule. Correlations between offshore () and surf zone () wave heights in (c) the outer surf zone, (d) the mid surf zone, and (e) the inner surf zone. The red swath shows the 95% confidence interval for the linear regression. (f) Comparison between offshore conditions ( and ) and break point wave height (). The crosses show all the measured offshore data, and the dashed lines show the long-term and averages for the nearest offshore wave buoy (Port Kembla) [28]. (g) Analysis of against / (analogous to Figure 11 in Power et al. [23]). The coloured swaths show the 95% confidence interval for the regressions.Surf zone dynamics analyses.
Data from each curve were segmented into three clusters using the k-means algorithm (Figure 5a): one cluster that was representative of the outer surf zone, one cluster representative of the mid surf zone, and one cluster representative of the inner surf zone. The probability distribution of () was then calculated for each class (Figure 5b)[CES], which showed that in the outer surf zone, most of the waves were unbroken (); in the mid surf zone, about half of the waves were broken (); and in the inner surf zone, most waves were broken (). This result is consistent with the conceptual hydro-kinematic model for gently sloping beaches [24]. Interestingly, values close to the surf–swash boundary were never , which indicates that small unbroken waves reach the swash zone, even on a dissipative beach such as SMB (average Iribarren Number [25], where is the wave length calculated as , and averaged , where is the sediment fall velocity). Based on the observed distributions of , three locations in the surf zone were chosen to assess wave heights: (inner surf zone), (mid surf zone), and (outer surf zone).
The analysis of the correlation between offshore () and surf zone () wave heights showed that there was a direct correlation between and across the full width of the surf zone (Figure 5c–f). Following the definition of surf zone saturation from Power et al. [26], the observed correlations strongly suggest that the surf zone was unsaturated during [CES]the experiment, despite the dissipative nature of the beach. Finally, the wave-height-to-water-depth ratio () was compared to the offshore wave height normalised by averaged water depth for each 10 min data run (/) (Figure 5g). The results from this analysis are analogous to Figure 11 in Power et al. [23] and indicate that (1) the surf zone was unsaturated and (2) there was a terminal bore height reaching the surf–swash boundary. Following from the analysis in Figure 5a that , this terminal bore height could represent either broken or unbroken waves. These results are significant because if the surf zone is unsaturated, it is probable that the swash zone is also unsaturated. This is discussed further in Section 4.
3.2. Shoreline Height Timeseries PDFs
For each data run in which there were unique offshore and LiDAR data, 10 min timeseries were extracted from the raw LiDAR record and the time-varying shoreline was obtained using the method described in Section 2.2. The PDFs of normalised () and non-normalised () shoreline height [CES]timeseries were then obtained via histograms and kernel density estimations (KDEs). The use of KDEs to obtain PDFs is advantageous over more traditional histogram methods because (1) they are a fully non-parametric approach, and (2) they are able to identify fluctuations in the data’s distribution that are usually not seen when using histograms with potentially non-ideal bin sizes.
Analysis of individual normalised shoreline height PDFs indicated a high degree of variability between runs and that the majority of PDFs were multimodal (97.5%). The Shapiro and Wilk [29] test at the 95% confidence interval confirmed that none of the analysed timeseries were normally distributed. The observed PDFs were then grouped into three clusters based on the observed offshore conditions (Figure 6a). Cluster A represents average wave height conditions with short periods, Cluster B represents calm conditions (low wave heights and short wave periods), and cluster C represents calm conditions with long wave periods. Figure 6b shows the PDFs for cluster A, Figure 6c shows the PDFs for cluster B, and Figure 6d shows the PDFs for cluster C. By averaging the PDFs in each cluster, a right-skewed PDF similar to Hughes et al.’s [5] ensemble PDF was observed (see their Figure 2). To assess the effect of the normalisation strategy and offshore conditions on the shape of the shoreline height PDFs, each PDF was compared to every other PDF in the same cluster, and then to every PDF in each of the other two clusters using the Kullback and Leibler [30] divergence as the similarity measurement. The results from this analysis indicated that (1) non-normalised PDFs () are dissimilar within and between clusters (Figure 6h), except PDFs in cluster C[CES], which are strongly similar to each other, and (2) normalised PDFs () are strongly similar within and between clusters (Figure 6i). For further discussion see Section 4.
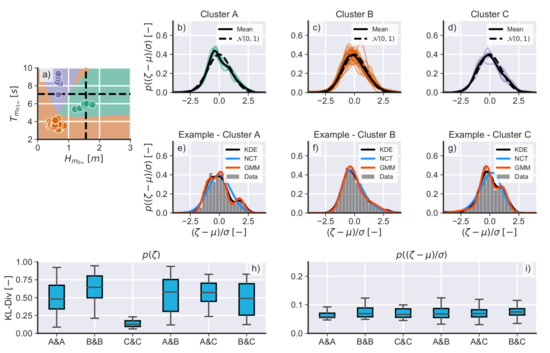
Figure 6.
(a) Clustering analysis of offshore wave conditions (, ). The dashed lines show the long-term and averages for Port Kembla wave buoy [28]. Kernel density estimation (KDE) approximations, mean KDEs, and standard Gaussian PDF () for (b) cluster A , (c) cluster B, and (d) cluster C. Representative examples of PDFs for (e) cluster A, (f) cluster B, and (g) cluster C showing the KDE approximations (black), non-central Student’s T (NCT) fits (blue), and Gaussian mixture model (GMM) approximations (red). The number of bins for these histograms was calculated using the Freedman–Diaconis rule [27]. Analysis was performed using the Kullback and Leibler [30] divergence (KL-Div) for (h) non-normalised PDFs ((), and (i) normalised () to assess PDF similarity within each cluster and between pairs of clusters. In (h,i) lower values indicate more similar PDFs. Note that the KL-Div has no upper-bound value.Shoreline height PDF analyses
Two other methods were assessed for obtaining a function (or combination of functions) to describe the observed PDFs. This was done because KDE is a non-parametric method that requires prior knowledge of the input timeseries, thus preventing an assessment of correlations between descriptors of the analysed PDFs and environmental parameters. Note that the results presented below were invariant regardless of which PDF ( or ) was being modelled. The first method consisted of fitting all PDFs available in the SciPy library [31] to the observed data (96 PDFs were available as of December 2020) and using three metrics to evaluate the fitted PDFs: the sum of squared errors, the Akaike information criterion [32], and the Kullback–Leibler divergence [30]. The results from these analyses indicated that none of the best-fit PDFs were able to statistically satisfactorily describe the majority (>50%) of the observed PDFs, regardless of the metric adopted to rank them. The analytical PDF that best fitted the greatest number of observed PDFs (≈35%) was the non-central Student’s T (NCT) PDF, which is a complicated four-parameter function [33] and thus is impractical. Examples of the NCT fit to the data are shown in Figure 6e–g (blue lines). Given the poor overall performance of the NCT and given that this PDF cannot describe the multimodal characteristics of the data, this strategy was not pursued further.
To account for the multimodality observed in the data, a second approach to obtain analytical descriptions of and was used. In this method, the analysed PDFs were approximated by the sum of a number of Gaussian PDFs, each described individually by their mean (), standard deviation (), and mixing weight (), that is, a Gaussian mixture model (GMM) [34]. This approach was able to precisely reproduce the observed multimodality in all the shoreline height PDFs (see Figure 5e–g, for example) and the Kolmogorov–Smirnov test confirmed that the PDFs predicted by the GMMs were statistically similar to the observed PDFs at the 95% confidence level (which is expected, given the characteristics of the method). A Gaussian mixture model is, however, a parametric method that requires prior knowledge of the number of mixtures to be used. By using the Akaike Information Criterion [32] as an evaluation metric, a mixture with three components was found to be the optimal value to statistically satisfactorily represent the majority of the observed data (≥90%) whilst maintaining model simplicity. As GMMs provide the parameters , , , and the optimal number of mixtures (), it becomes possible to correlate these parameters to known variables in a predictive way, thus overcoming the major limitation of KDEs.[CES] and methods such as Cartwright and Longuet-Higgins’ [7]. A model using surf zone and offshore parameters to assess the variability observed in , assuming that such variability is directly correlated to the optimal number of Gaussian mixtures () for each PDF, is discussed in Section 4.
3.3. Trough-To-Peak Swash Height PDFs
In the previous section, was observed to be multimodally distributed and, consequently, to deviate from the expected [CES]theoreticalGaussian PDF. Based on this, it is therefore reasonable to assume that PDFs derived from a swash-by-swash analysis would follow a similar [CES]multimodal pattern. In this section, the trough-to-peak swash height () was used as a proxy variable for such analysis (see Figure 1 for definitions). By applying the wavelet decomposition method detailed in Stringari and Power [35] (see their Appendix A) it was possible to classify each swash event as occurring under infragravity or sea-swell wave dominant forcing. For each timestack, was calculated for each individual swash cycle and compared to the time-varying infragravity and sea-swell energy levels obtained using data from the PT in the surf zone that was closest to the surf–swash boundary in each data run. If energy in the infragravity band was greater than energy in the sea-swell band (that is, ) during the time of swash excursion, the swash event was considered to be dominated by an infragravity wave, otherwise, the swash event was considered to be dominated by a sea-swell wave. Due to the characteristic long-period of infragravity motions, there was no need to account for time offsets between the shoreline and nearest surf zone PT timeseries. Finally, it is worth noting that the approach used here is equivalent to Guza and Thornton’s [10] classical approach, only more robust, as it considers both time and frequency domains whereas the classical approach only works in the frequency domain.
As with the analyses shown in Section 3.1, both and () in both [CES]sea-swell and infragravity frequency bands presented great variability, were mostly multimodal (>95%), and were[CES], consequently, significantly statistically different ( using the Kolmogorov–Smirnov test) from [CES]the theoretical PDFs predicted by Cartwright and Longuet-Higgins [7]. To be in accordance with the theory, the observed PDFs should have collapsed to a Rayleigh PDF for non-normalised PDFs (, Figure 7a to c), or to a Gaussian PDF for normalised PDFs (, Figure 7d to f), but this was not observed.both the Rayleigh and Gaussian PDFs previously tested by Hughes et al. [36]. The mean PDF for each frequency band in each cluster was also obtained (black lines in Figure 7a–f) and these mean PDFs also deviated from [CES]the PDFs predicted by the theorythe two theoretical PDFs tested by Hughes et al. [36]. It is worth noting, however, that non-normalised PDFs () in cluster C closely approached but were not statistically similar to a Rayleigh PDF as assessed by the Kolmogorov–Smirnov test (). Further, when all the data in each frequency band were aggregated (Figure 7g,f), the observed PDFs [CES]did not collapse into the expected Gaussian PDF either, with the observed aggregated PDFs in both the sea-swell and infragravity bands [CES]beingwere right-skewed and statistically similar to the Beta PDF, [CES]which is partially consistent with Hughes et al.’s [5] results (their Figure 7). Similar results to Figure 7g,f were observed when aggregating the data in each frequency band based on the offshore clusters (not shown). See Section 4 for further discussion on the correlation between offshore parameters and the observed swash height PDFs.
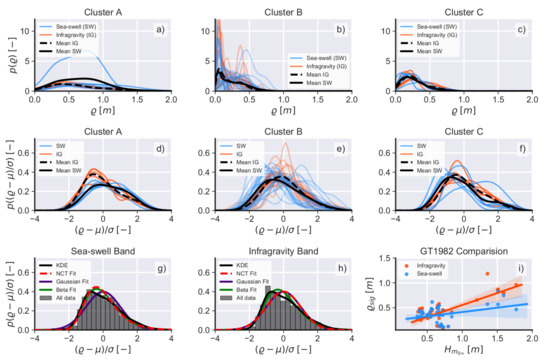
Figure 7.
Non-normalised trough-to-peak swash height PDFs () at infragravity (red) and sea-swell (blue) frequency bands for offshore (a) cluster A, (b) cluster B, and (c) cluster C. Normalised trough-to-peak swash height PDFs () at infragravity (red) and sea-swell (blue) frequency bands for offshore (d) cluster A, (e) cluster B, and (f) cluster C. The black lines in (a–f) show the mean PDF for each frequency band. (g) Normalised trough-to-peak swash height PDF for all data from panels (a–c) in the sea-swell frequency band. (e) Normalised trough-to-peak swash height PDF for all data from panels (a–c) in the infragravity frequency band. In (g,h), the black lines show the KDE approximation to the data, the red dashed lines show the NCT PDF fit to the data, the blue lines show the Gaussian PDF fit to the data, and the green lines show the Beta PDF fit to the data. The number of bins in the histograms was calculated according to the Freedman–Diaconis rule [27]. (i) Correlation between offshore wave height and significant trough-to-peak swash height () for infragravity and sea-swell frequency bands. The coloured swaths in e) show the 95% confidence intervals. The regression lines are (, ) in the infragravity band and (, ) in the sea-swell band. Note that at .Trough-to-peak swash height PDFs analyses
Finally, Figure 7i shows an analysis similar to that of Guza and Thornton’s [10] (their Figure 7), which has been widely used in the literature to support the concept of swash saturation in the sea-swell frequency band. For each data run, the trough-to-peak significant swash height () in each frequency band was calculated and compared to the observed offshore wave height. In contrast to Guza and Thornton’s [10] data, the data analysed here showed a correlation between increases in the offshore wave height and increases in the significant trough-to-peak swash height in both the sea-swell and infragravity frequency bands. These results do not, therefore, support the assumption of swash saturation in the sea-swell band. For further discussion on swash saturation, see Section 4.
4. Discussion
In this paper we have presented a novel, data-driven approach for analysing the probability distribution functions of swash motions. Both shoreline height [CES]timeseries () and trough-to-peak swash height () PDFs were observed to be strongly multimodal, highly variable, and systematically statistically different from expected theoretical PDFs. Previous [CES]previous research [5,6] has shown that [CES]PDFs of different swash motions can deviate from [CES]Cartwright and Longuet-Higgins’the expected Gaussian PDF [9][CES]theory but, to the authors’ knowledge, multimodal and have not been [CES]previously reported.[CES] before. Given the observed multimodality of shoreline height [CES]timeseries PDFs, Gaussian Mixture Models (GMMs) were shown to be the best method to approximate (e.g., Figure 6), [CES]which areand have the benefit of being easily transferable to model , , and . Interestingly, when the data were normalised, the shoreline height PDFs () collapsed into very similar PDFs, indicating that environmental forcing directly correlates with the shape of the non-normalised PDFs, further supporting the clustering approach based on offshore conditions. The influence of offshore wave conditions on swash motion PDFs is further supported by three other observations: (1) that shoreline height [CES]timeseries PDFs in cluster C, which had a narrow offshore wave height band, were very similar to each other regardless of data normalisation (see Figure 6h); (2) that the width of directly increased with increasing offshore height in both frequency bands; and (3) that the mean PDFs in cluster C were only marginally statistically different [CES]tofrom the [CES]predictedexpected Rayleigh PDF (see Figure 7c)[CES], which is consistent with the narrow offshore wave height band of this cluster. Ultimately, these results suggest that the swash zone was unsaturated in both infragravity and sea-swell frequency bands for the data analysed here.
The multimodality observed in both shoreline height and trough-to-peak swash height PDFs can theoretically be linked to the observation by Guza and Thornton [10] that energy in different frequency bands will result in distinct density peaks at different swash height elevations. This assumption is consistent with the analysis presented in Section 3.3, in which clear density peaks in are observed at different frequency bands (e.g., note the separation between the mean PDFs in Figure 7d–f). Therefore, the fact that GMMs were the only method that satisfactorily reproduced the observed PDFs may be a direct consequence of this (physical) phenomenon and not necessarily a result of pure statistical inference. In contrast to the observations of Guza and Thornton [10], however, the data analysed here do not support swash saturation in the sea-swell frequency band (see Figure 7f). It is worth noting, however, that Guza and Thornton’s (1982) data were from a beach more dissipative than SMB and, therefore, the present results may not be directly comparable to theirs. The results in this paper showed, nonetheless, that as a consequence of the surf zone being unsaturated, the swash zone was also unsaturated, which is supported by the correlations between the offshore clusters and swash motion PDFs. This result is consistent with recent results from Hughes et al. [37][CES], who also showed that swash saturation is not always the case on natural beaches. [CES]Future swash zone research should focus on better linking surf and swash zone dynamics with particular emphasis on swash-by-swash approaches that have the potential to elucidate surf–swash interactions (for example, bore–bore capture) and their impact on runup and beach morphodynamics, which are currently poorly understood.
Finally, an investigation into which environmental parameters best explained the variability seen in was conducted. Assuming that the optimal number of mixtures () is a direct proxy for the degree of variability and, consequently, the complexity of , a model that ranks which environmental parameters best explained was constructed. This analysis provides an initial insight into which variables are most important for describing the trends seen in the data and aims to further support our observations that the observed surf zone dynamics were directly controlling the swash zone. A random forest model was chosen to accomplish this task (see Appendix A for details). Note that, in contrast to Section 3.2, the maximum number of mixtures was not restricted to three and was, therefore, chosen based on the lowest AIC for each 10 min data run (although the is unbounded here, the highest number of optimal mixtures observed was six because models with too large a number of mixtures get heavily penalised by AIC). As inputs for the model, wave heights and periods at four cross-shore locations were used (offshore, = 0.05, = 0.50, and = 0.95). The model was trained one hundred times to account for statistical variability and the feature importance for each variable was obtained. The same approach can be used to predict which parameters best explain , , and but this was not attempted here due to the small size of the dataset (see Section 6.4 in Stringari [38] for an attempt at using these model data). The results shown in Figure 8 indicate that a combination of several parameters was responsible for best explaining , with the wave height at the seaward end of the surf zone () consistently being the most important parameter for the model. In general, this result [CES]agressagrees with the results from Section 3.1 as directly correlates with surf zone wave heights[CES], which implies that, as a consequence of the surf zone being unsaturated, the swash zone is unsaturated and, therefore, driven by incoming bores with non-negative terminal heights, as previously shown by two recent studies [21,23]. As more data become available in the future, models based on the present approach could provide a robust predictor for shoreline statistical properties based solely on known parameters, which will be valuable tools for coastal managers.
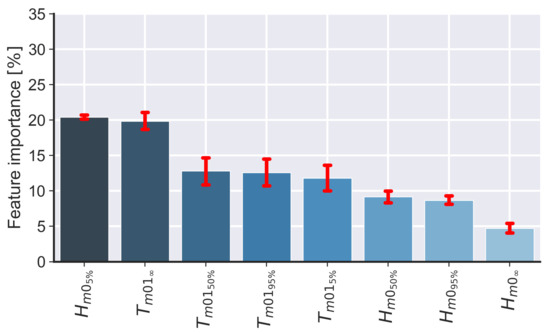
Figure 8.
Feature importance of the random forest model. In this plot, and are the significant wave height and significant wave period offshore of the surf zone; , , , , , and are the significant wave height and significant wave period at the value indicated by indexes where is representative of the outer surf zone, is representative of the mid surf zone, and is representative of the inner surf zone.Feature importance.
5. Conclusions
In this paper, analysis of swash motions from a gently sloping sandy beach under varying offshore forcing showed that the majority of observed PDFs (both [CES]the shoreline height timeseries PDF () and [CES]the trough-to-crest swash height PDF ()) were multimodal, [CES]and were statistically different from the PDFs predicted by the theorywhich, to our knowledge, has not previously been reported. Hence, Gaussian mixtures were shown to be the best approach to model , which could easily be extended to other swash processes. The parameters of the Gaussian mixtures that described these swash motions were closely correlated to wave conditions in the surf zone and further offshore, which [CES]had also not previously been directly shown and is indicative of unsaturated swash. Analysis of the correlation between significant trough-to-peak swash heights () and offshore wave heights further confirmed unsaturated swash in both short- and long-wave frequency bands. The field data collection and statistical methods used in this paper were shown to overcome the limitations of more traditional methods and allowed for [CES]a novel statistical descriptions of swash motions. [CES]Future research on swash zone dynamics should leverage the recent developments on LiDAR technology to further explore wave-swash interactions and the impact that these phenomena have on shoreline dynamics and beach morphology. [CES]TheseThe approaches [CES]used in this paper, although preliminary [CES](for example, LiDAR uncertainties were not quantified here) and limited by a small dataset, should provide a robust basis for coastal managers when developing improved swash zone models in the future.
Author Contributions
Conceptualization, C.E.S. and H.E.P.; methodology, C.E.S. and H.E.P.; software, C.E.S.; validation, C.E.S. and H.E.P., ; formal analysis, C.E.S. and H.E.P.; investigation, C.E.S.; data curation, C.E.S.; writing—original draft preparation, C.E.S. and H.E.P.; writing—review and editing, C.E.S. and H.E.P.; visualization, C.E.S.; supervision, H.E.P. All authors have read and agreed to the published version of the manuscript.
Funding
C.E.S. was funded by a University of Newcastle Research Degree Scholarship and a Central and Faculty Scholarship (5050UNRS).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Code and data are available at https://github.com/caiostringari/BeachLiDAR.
Acknowledgments
The authors are grateful to Tom Doyle, Kaya Wilson, Madeleine Broadfoot, Murray Kendall, Kendall Mollison, and David Schmidt, who assisted with the field data collection. We kindly thank Tom Baldock from University of Queensland who lent some of the pressure transducers used for data collection. We are particularly thankful to David Hanslow and Mike Kinsela from New South Wales Department of Planning Industry, and Environment (DPIE) who conducted the offshore data collection. The authors are also thankful to the Academic Research Computing Support Team, particularly Aaron Scott, at the University of Newcastle for support with the I.T. infrastructure and to Michael Hughes, Robert Holman, and Evan Goldstein, whose helpful comments shaped the final version of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
This appendix describes the predictor for the optimal number of Gaussian Mixtures for a given sea-state. The eXtreme Gradient Boost (XGB) model [39] was chosen as the classifier. The goal was to obtain a non-linear function that maps input features into the predicted number of Gaussian Mixtures. Mathematically, this relationship can be written as:
in which and are the significant wave height and significant wave period offshore of the surf zone respectively and, , , , , , and are the significant wave heights and significant wave periods at the value indicated by the subscripts. These features were chosen based on the results results from Section 3.1–Section 3.3.
The model is then defined as:
where is the predicted number of mixtures, is a function (in this case, a decision tree) that takes input training samples (), and is the space of functions containing all decision trees. The objective () of the model is to learn the best function(s) that minimises a loss function (l) while, at the same time, keeping the model ensemble as simple as possible. This is done by considering a regularisation parameter ():
The model is then trained using the greedy algorithm know as adaptive training [40]. The loss function for the model was the mean absolute error (MAE):
where is the predicted number of mixtures and is the observed number of mixtures. For the training step, the data were randomly split into training (70%) and testing (30%) datasets and the model was run 100 hundred times for each combination to account for statistical variability. The for all models always reached values greater than 95%. References
References
- Komar, P.D. Beach Processes and Sedimentation; Prentice-Hall: Upper Saddle River, NJ, USA, 1976. [Google Scholar]
- Masselink, G.; Puleo, J.A. Swash-zone morphodynamics. Cont. Shelf Res. 2006, 26, 661–680. [Google Scholar] [CrossRef]
- Atkinson, A.L.; Power, H.E.; Moura, T.; Hammond, T.; Callaghan, D.P.; Baldock, T.E. Assessment of runup predictions by empirical models on non-truncated beaches on the south-east Australian coast. Coast. Eng. 2017, 119, 15–31. [Google Scholar] [CrossRef]
- Power, H.E.; Gharabaghi, B.; Bonakdari, H.; Robertson, B.; Atkinson, A.L.; Baldock, T.E. Prediction of wave runup on beaches using Gene-Expression Programming and empirical relationships. Coast. Eng. 2019, 144, 47–61. [Google Scholar] [CrossRef]
- Hughes, M.G.; Moseley, A.S.; Baldock, T.E. Probability distributions for wave runup on beaches. Coast. Eng. 2010, 57, 575–584. [Google Scholar] [CrossRef]
- Holland, K.T.; Holman, R.A. The Statistical Distribution of Swash Maxima on Natural Beache. J. Geophys. Res. 1993, 98, 271–278. [Google Scholar] [CrossRef]
- Cartwright, D.E.; Longuet-Higgins, M.S. The Statistical Distribution of the Maxima of a Random Function. Proc. R. Soc. A Math. Phys. Eng. Sci. 1956, 283, 212–232. [Google Scholar]
- Goda, Y. Reanalysis of Regular and Random Breaking Wave Statistics. Coast. Eng. J. 2010, 52, 71–106. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. On the Statistical Distribution of the Heights of Sea Waves. JMR 1952, 11, 245–266. [Google Scholar]
- Guza, R.T.; Thornton, E.B. Swash Oscillations on a Natural Beach. J. Geophys. Res. 1982, 87, 483–491. [Google Scholar] [CrossRef]
- Wright, L.D.; Guza, R.T.; Short, A.D. Dynamics of a high-energy dissipative surf zone. Mar. Geol. 1982, 45, 41–62. [Google Scholar] [CrossRef]
- Wright, L.D.; Short, A.D. Morphodynamic variability of surf zones and beaches: A synthesis. Mar. Geol. 1984, 56, 93–118. [Google Scholar] [CrossRef]
- Stringari, C.E.; Harris, D.L.; Power, H.E. A Novel Machine Learning Algorithm for Tracking Remotely Sensed Waves in the Surf Zone. Coast. Eng. 2019, 147, 149–158. [Google Scholar] [CrossRef]
- Stringari, C.E.; Power, H.E. The Fraction of Broken Waves in Natural Surf Zones. J. Geophys. Res. Ocean. 2019, 124, 1–27. [Google Scholar] [CrossRef]
- Power, H.E.; Kinsela, M.A.; Stringari, C.E.; Kendall, M.J.; Morris, B.D.; Hanslow, D.J. Automated sensing of wave inundation across a rocky shore platform using a low-cost camera system. Remote Sens. 2018, 10, 11. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Kirupakaramoorthy, T.; Oumeraci, H.; de la Torre, M.; Wübbold, F.; Wagner, B.; Schimmels, S. The role of combined laser scanning and video techniques in monitoring wave-by-wave swash zone processes. Coast. Eng. 2014, 83, 150–165. [Google Scholar] [CrossRef]
- Aagaard, T.; Holm, J. Digitization of Wave Run-up Using Video Records. J. Coast. Res. 1989, 5, 547–551. [Google Scholar]
- Sobel, I. An Isotropic 3 × 3 Image Gradient Operator. Comput. Sci. 1968. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. Density-Based Clustering Methods. Compr. Chemom. 1996, 2, 635–654. [Google Scholar] [CrossRef]
- Fiedler, J.W.; Brodie, K.L.; McNinch, J.E.; Guza, R.T. Observations of runup and energy flux on a low-slope beach with high-energy, long-period ocean swell. Geophys. Res. Lett. 2015, 42, 9933–9941. [Google Scholar] [CrossRef]
- Bergsma, E.W.J.; Blenkinsopp, C.E.; MArtins, K.; Almar, R.; de Almeida, L.P.M. Bore collapse and wave run-up on a sandy beach. Cont. Shelf Res. 2019, 174, 132–139. [Google Scholar] [CrossRef]
- Roelse, A.; Granger, H.W.; Graham, J.W. Technical Report 12: The Adjustment of the Australian Levelling Survey 1970–1971; Division of National Mapping: Canberra, Australia, 1975. [Google Scholar]
- Power, H.E.; Hughes, M.G.; Aagaard, T.; Baldock, T.E. Nearshore wave height variation in unsaturated surf. J. Geophys. Res. Ocean. 2010, 115, 1–15. [Google Scholar] [CrossRef]
- Svendsen, I.A.; Madsen, P.A.; Hansen, J.B. Wave Characteristics in the Surf Zone. In Proceedings of the 16th International Conference on Coastal Engineering, Hamburg, Germany, 27 August–3 September 1978; pp. 520–539. [Google Scholar]
- Iribarren, C.R.; Nogales, C.M. Protection des Ports. In Proceedings of the XVIIth International Naval Congress, Lisbon, Portugal, 19–22 September 1949. [Google Scholar]
- Power, H.E.; Holman, R.A.; Baldock, T.E. Swash zone boundary conditions derived from optical remote sensing of swash zone flow patterns. J. Geophys. Res. Ocean. 2011, 116, 1–13. [Google Scholar] [CrossRef]
- Freedman, D.; Diaconis, P. On the histogram as a density estimator:L 2 theory. Z. Wahrscheinlichkeitstheorie Verwandte Geb. 1981, 57, 453–476. [Google Scholar] [CrossRef]
- New South Wales Department of Planning Industry, and Environment. Ocean Wave Data Collection Program. Available online: https://www.mhl.nsw.gov.au/Station-PTKMOW (accessed on 11 December 2020).
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 311–319. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On infromation and sufficiency. Ann. Math. Statist. 1951, 37, 688–697. [Google Scholar] [CrossRef]
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open Source Scientific Tools for Python. 2001. Available online: https://www.scipy.org/ (accessed on 25 January 2021).
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Hogben, D.; Pinkham, R.S.; Wilk, M.B. The Moments of the Non-Central t-Distribution. Biometrika 1961, 48, 465–468. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001. [Google Scholar]
- Stringari, C.E.; Power, H.E. Quantifying Bore-bore Capture on Natural Beaches. J. Geophys. Res. Ocean. 2020, 125, 1–16. [Google Scholar] [CrossRef]
- Hughes, M.G.; Aagaard, T.; Baldock, T.E.; Power, H.E. Spectral signatures for swash on reflective, intermediate and dissipative beaches. Mar. Geol. 2014, 355, 88–97. [Google Scholar] [CrossRef]
- Hughes, M.G.; Baldock, T.E.; Aagaard, T. Swash saturation: An assessment of available models. Ocean Dyn. 2018, 68, 911–922. [Google Scholar] [CrossRef]
- Stringari, C.E. Data-Driven Investigations of Broken Wave Behaviour in the Surf And Swash Zones. Ph.D. Thesis, University of Newcastle, Callaghan, Australia, 2020. Available online: http://hdl.handle.net/1959.13/1411217 (accessed on 25 January 2021).
- Chen, T.; Guestrin, C. XGBoost: Reliable Large-scale Tree Boosting System. In Proceedings of the Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1–6. [Google Scholar]
- Friedman, J. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).