Monitoring Key Forest Structure Attributes across the Conterminous United States by Integrating GEDI LiDAR Measurements and VIIRS Data
Abstract
1. Introduction
2. Materials and Methods
2.1. VIIRS Multitemporal Metrics
2.2. The GEDI Data
2.3. GEDI Data Processing
2.4. Calibration and Validation of the Random Forest Regression Models
2.5. Derivation and Assessment of Vegetation Structure Attributes for CONUS
3. Results
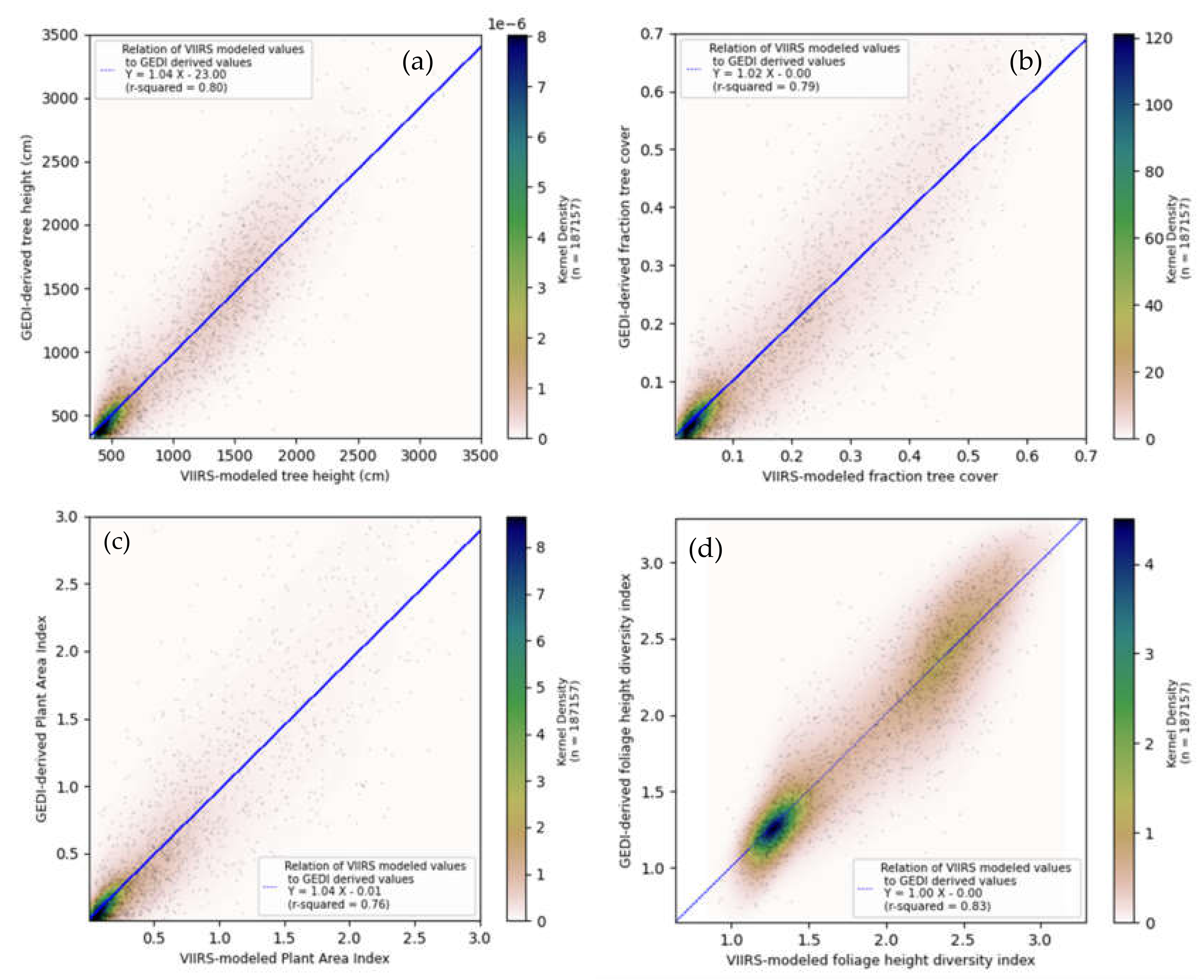
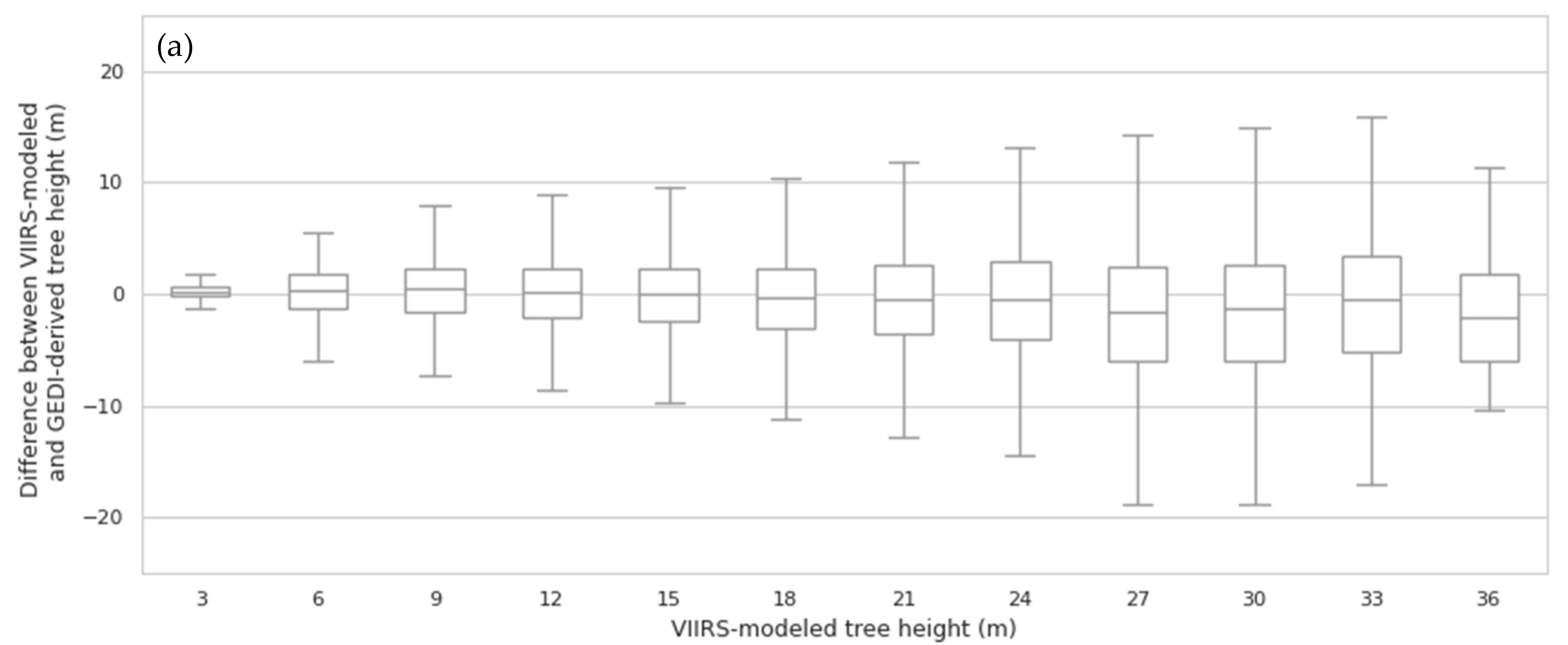
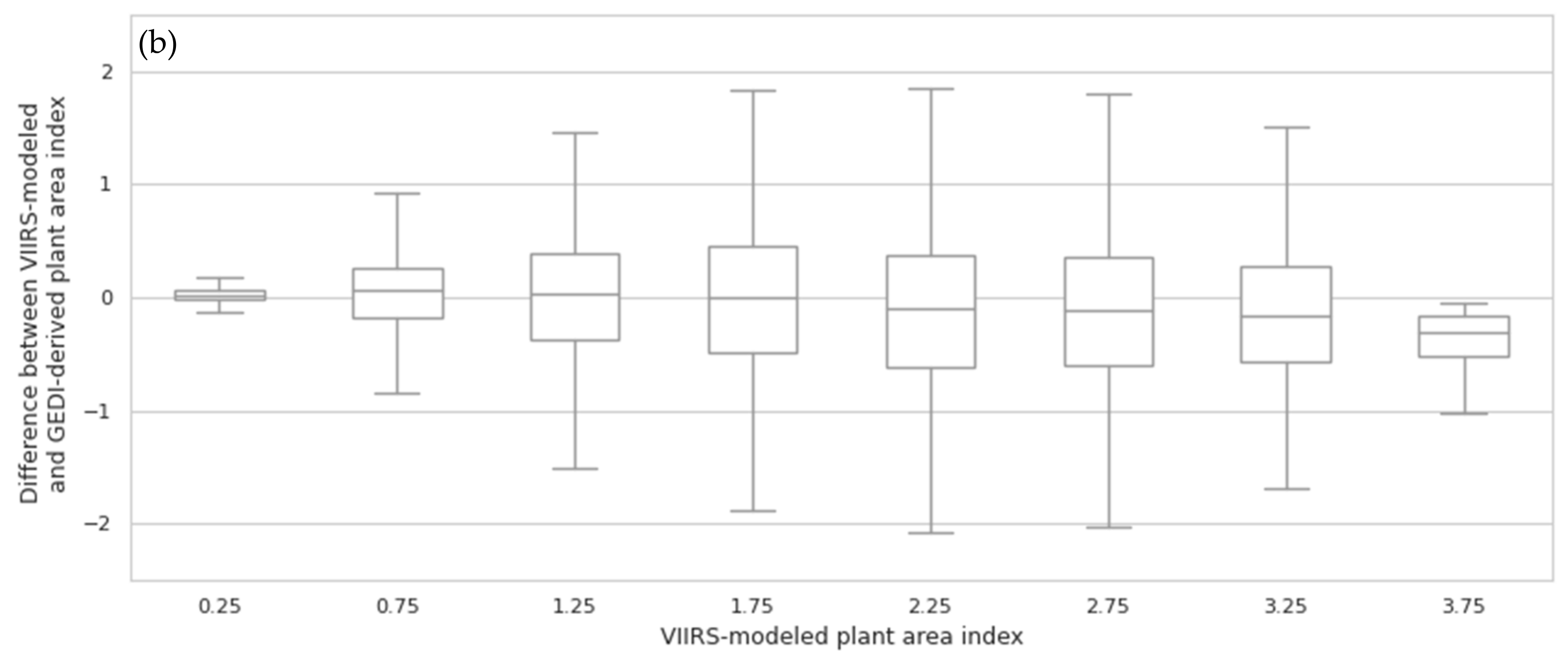
3.1. Random Forest Model Validation
3.2. Wall-to-Wall Maps of Canopy Structure for the Conterminous US
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hall, F.G.; Bergen, K.; Blair, J.B.; Dubayah, R.; Houghton, R.; Hurtt, G.; Kellndorfer, J.; Lefsky, M.; Ranson, J.; Saatchi, S.; et al. Characterizing 3D Vegetation Structure from Space: Mission Requirements. Remote Sens. Environ. 2011, 115, 2753–2775. [Google Scholar] [CrossRef]
- Houghton, R.A. Aboveground Forest Biomass and the Global Carbon Balance. Glob. Chang. Biol. 2005, 11, 945–958. [Google Scholar] [CrossRef]
- Pereira, H.M.; Ferrier, S.; Walters, M.; Geller, G.N.; Jongman, R.H.G.; Scholes, R.J.; Bruford, M.W.; Brummitt, N.; Butchart, S.H.M.; Cardoso, A.C.; et al. Essential Biodiversity Variables. Science 2013, 339, 277–278. [Google Scholar] [CrossRef] [PubMed]
- Mitchard, E.T.; Saatchi, S.S.; Baccini, A.; Asner, G.P.; Goetz, S.J.; Harris, N.L.; Brown, S. Uncertainty in the Spatial Distribution of Tropical Forest Biomass: A Comparison of Pan-Tropical Maps. Carbon Balance Manag. 2013, 8, 10. [Google Scholar] [CrossRef] [PubMed]
- Goetz, S.; Dubayah, R. Advances in Remote Sensing Technology and Implications for Measuring and Monitoring Forest Carbon Stocks and Change. Carbon Manag. 2011, 2, 231–244. [Google Scholar] [CrossRef]
- Forsell, N.; Turkovska, O.; Gusti, M.; Obersteiner, M.; den Elzen, M.; Havlik, P. Assessing the INDCs’ Land Use, Land Use Change, and Forest Emission Projections. Carbon Balance Manag. 2016, 11, 26. [Google Scholar] [CrossRef]
- Griscom, B.W.; Adams, J.; Ellis, P.W.; Houghton, R.A.; Lomax, G.; Miteva, D.A.; Schlesinger, W.H.; Shoch, D.; Siikamäki, J.V.; Smith, P.; et al. Natural Climate Solutions. Proc. Natl. Acad. Sci. USA 2017, 114, 11645–11650. [Google Scholar] [CrossRef]
- Fargione, J.E.; Bassett, S.; Boucher, T.; Bridgham, S.D.; Conant, R.T.; Cook-Patton, S.C.; Ellis, P.W.; Falcucci, A.; Fourqurean, J.W.; Gopalakrishna, T.; et al. Natural Climate Solutions for the United States. Sci. Adv. 2018, 4, eaat1869. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping Global Forest Canopy Height Through Integration of GEDI and Landsat Data. Remote Sens. Environ. 2020, 112165. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-Resolution Laser Ranging of the Earth’s Forests and Topography. Sci. Remote Sens. 2020, 1. [Google Scholar] [CrossRef]
- Knapp, N.; Fischer, R.; Huth, A. Linking Lidar and Forest Modeling to Assess Biomass Estimation across Scales and Disturbance States. Remote Sens. Environ. 2018, 205, 199–209. [Google Scholar] [CrossRef]
- Knapp, N.; Fischer, R.; Cazcarra-Bes, V.; Huth, A. Structure Metrics to Generalize Biomass Estimation from Lidar across Forest Types from Different Continents. Remote Sens. Environ. 2020, 237, 111597. [Google Scholar] [CrossRef]
- Köhler, P.; Huth, A. The Effects of Tree Species Grouping in Tropical Rainforest Modelling: Simulations with the Individual-Based Model Formind. Ecol. Model. 1998, 109, 301–321. [Google Scholar] [CrossRef]
- Hurtt, G.C.; Dubayah, R.; Drake, J.; Moorcroft, P.R.; Pacala, S.W.; Blair, J.B.; Fearon, M.G. Beyond Potential Vegetation: Combining Lidar Data and a Height-Structured Model for Carbon Studies. Ecol. Appl. 2004, 14, 873–883. [Google Scholar] [CrossRef]
- Hurtt, G.C.; Thomas, R.Q.; Fisk, J.P.; Dubayah, R.O.; Sheldon, S.L. The Impact of Fine-Scale Disturbances on the Predictability of Vegetation Dynamics and Carbon Flux. PLoS ONE 2016, 11. [Google Scholar] [CrossRef] [PubMed]
- Hurtt, G.; Zhao, M.; Sahajpal, R.; Armstrong, A.; Birdsey, R.; Campbell, E.; Dolan, K.; Dubayah, R.; Fisk, J.P.; Flanagan, S.; et al. Beyond MRV: High-Resolution Forest Carbon Modeling for Climate Mitigation Planning over Maryland, USA. Environ. Res. Lett. 2019, 14, 045013. [Google Scholar] [CrossRef]
- Schneider, F.D.; Ferraz, A.; Hancock, S.; Duncanson, L.I.; Dubayah, R.O.; Pavlick, R.P.; Schimel, D.S. Towards Mapping the Diversity of Canopy Structure from Space with GEDI. Environ. Res. Lett. 2020, 15, 115006. [Google Scholar] [CrossRef]
- Friedl, M.A.; McIver, D.K.; Hodges, J.C.F.; Zhang, X.Y.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A.; et al. Global Land Cover Mapping from MODIS: Algorithms and Early Results. Remote Sens. Environ. 2002, 83, 287–302. [Google Scholar] [CrossRef]
- Hansen, M.C.; Defries, R.S.; Townshend, J.R.G.; Sohlberg, R. Global Land Cover Classification at 1 km Spatial Resolution Using a Classification Tree Approach. Int. J. Remote Sens. 2000, 21, 1331–1364. [Google Scholar] [CrossRef]
- Hansen, M.C.; Stehman, S.V.; Potapov, P.V. Quantification of Global Gross Forest Cover Loss. Proc. Natl. Acad. Sci. USA 2010, 107, 8650–8655. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, R.; Zhan, X.; Csiszar, I. Derivation of Global Surface Type Products from VIIRS. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5992–5995. [Google Scholar]
- Zhang, X.; Liu, L.; Liu, Y.; Jayavelu, S.; Wang, J.; Moon, M.; Henebry, G.M.; Friedl, M.A.; Schaaf, C.B. Generation and Evaluation of the VIIRS Land Surface Phenology Product. Remote Sens. Environ. 2018, 216, 212–229. [Google Scholar] [CrossRef]
- Hansen, M.C.; DeFries, R.S.; Townshend, J.R.G.; Sohlberg, R.; Dimiceli, C.; Carroll, M. Towards an Operational MODIS Continuous Field of Percent Tree Cover Algorithm: Examples Using AVHRR and MODIS Data. Remote Sens. Environ. 2002, 83, 303–319. [Google Scholar] [CrossRef]
- Sexton, J.O.; Song, X.-P.; Feng, M.; Noojipady, P.; Anand, A.; Huang, C.; Kim, D.-H.; Collins, K.M.; Channan, S.; DiMiceli, C.; et al. Global, 30-m Resolution Continuous Fields of Tree Cover: Landsat-Based Rescaling of MODIS Vegetation Continuous Fields with Lidar-Based Estimates of Error. Int. J. Digit. Earth 2013, 6, 427–448. [Google Scholar] [CrossRef]
- Price, J.C. Estimating Leaf Area Index from Satellite Data. IEEE Trans. Geosci. Remote Sens. 1993, 31, 727–734. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Martonchik, J.V.; Diner, D.J.; Myneni, R.B.; Verstraete, M.; Pinty, B.; Gobron, N. Estimation of Vegetation Canopy Leaf Area Index and Fraction of Absorbed Photosynthetically Active Radiation from Atmosphere-Corrected MISR Data. J. Geophys. Res. Atmos. 1998, 103, 32239–32256. [Google Scholar] [CrossRef]
- Zhao, F.; Huang, C.; Goward, S.N.; Schleeweis, K.; Rishmawi, K.; Lindsey, M.A.; Denning, E.; Keddell, L.; Cohen, W.B.; Yang, Z.; et al. Development of Landsat-Based Annual US Forest Disturbance History Maps (1986–2010) in Support of the North American Carbon Program (NACP). Remote Sens. Environ. 2018, 209, 312–326. [Google Scholar] [CrossRef]
- Hofton, M.; Blair, J.B.; Dubayah, R. Algorithm Theoretical Basis Document (ATBD) for GEDI Transmit and Receive Waveform Processing for L1 and L2 Products; University of Maryland: College Park, MD, USA, 2019; p. 44. [Google Scholar]
- Tang, H.; Armston, J.; Dubayah, R. Algorithm Theoretical Basis Document (ATBD) for GEDI L2B Footprint Canopy Cover and Vertical Profile Metrics; University of Maryland: College Park, MD, USA, 2019; p. 39. [Google Scholar]
- Qi, W.; Saarela, S.; Armston, J.; Ståhl, G.; Dubayah, R. Forest Biomass Estimation over Three Distinct Forest Types Using TanDEM-X InSAR Data and Simulated GEDI Lidar Data. Remote Sens. Environ. 2019, 232, 111283. [Google Scholar] [CrossRef]
- Duncanson, L.; Neuenschwander, A.; Hancock, S.; Thomas, N.; Fatoyinbo, T.; Simard, M.; Silva, C.A.; Armston, J.; Luthcke, S.B.; Hofton, M.; et al. Biomass Estimation from Simulated GEDI, ICESat-2 and NISAR across Environmental Gradients in Sonoma County, California. Remote Sens. Environ. 2020, 242, 111779. [Google Scholar] [CrossRef]
- Hancock, S.; Armston, J.; Hofton, M.; Sun, X.; Tang, H.; Duncanson, L.I.; Kellner, J.R.; Dubayah, R. The GEDI Simulator: A Large-Footprint Waveform Lidar Simulator for Calibration and Validation of Spaceborne Missions. Earth Space Sci. 2019, 6, 294–310. [Google Scholar] [CrossRef]
- Patterson, P.L.; Healey, S.P.; Stahl, G.; Saarela, S.; Holm, S.; Andersen, H.-E.; Dubayah, R.O.; Duncanson, L.; Hancock, S.; Armston, J.; et al. Statistical Properties of Hybrid Estimators Proposed for GEDI—NASA’s Global Ecosystem Dynamics Investigation. Environ. Res. Lett. 2019, 14, 065007. [Google Scholar] [CrossRef]
- Adam, M.; Urbazaev, M.; Dubois, C.; Schmullius, C. Accuracy Assessment of GEDI Terrain Elevation and Canopy Height Estimates in European Temperate Forests: Influence of Environmental and Acquisition Parameters. Remote Sens. 2020, 12, 3948. [Google Scholar] [CrossRef]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Bolton, D.K.; Tompalski, P.; Bater, C.W. Three Decades of Forest Structural Dynamics over Canada’s Forested Ecosystems Using Landsat Time-Series and Lidar Plots. Remote Sens. Environ. 2018, 216. [Google Scholar] [CrossRef]
- Potapov, P.; Tyukavina, A.; Turubanova, S.; Talero, Y.; Hernandez-Serna, A.; Hansen, M.C.; Saah, D.; Tenneson, K.; Poortinga, A.; Aekakkararungroj, A.; et al. Annual Continuous Fields of Woody Vegetation Structure in the Lower Mekong Region from 2000–2017 Landsat Time-Series. Remote Sens. Environ. 2019, 232, 111278. [Google Scholar] [CrossRef]
- Zhang, R.; Huang, C.; Zhan, X.; Dai, Q.; Song, K. Development and Validation of the Global Surface Type Data Product from S-NPP VIIRS. Remote Sens. Lett. 2016, 7, 51–60. [Google Scholar] [CrossRef]
- Zhang, R.; Huang, C.; Zhan, X.; Jin, H.; Song, X.-P. Development of S-NPP VIIRS Global Surface Type Classification Map Using Support Vector Machines. Int. J. Digit. Earth 2017, 11, 212–232. [Google Scholar] [CrossRef]
- MacArthur, R.H.; Horn, H.S. Foliage Profile by Vertical Measurements. Ecology 1969, 50, 802–804. [Google Scholar] [CrossRef]
- Visible Infrared Imaging Radiometer Suite (VIIRS)—LAADS DAAC. Available online: https://ladsweb.modaps.eosdis.nasa.gov/missions-and-measurements/viirs/ (accessed on 13 November 2020).
- Strahler, A.; Muchoney, D.; Borak, J.; Gopal, S.; Lambin, E.; Friedl, M.; Moody, A. MODIS Land Cover and Land-Cover Change; Boston Univesity: Boston, MA, USA, 1999; p. 72. [Google Scholar]
- Friedl, M.A.; Brodley, C.E.; Strahler, A.H. Maximizing Land Cover Classification Accuracies Produced by Decision Trees at Continental to Global Scales. IEEE Trans. Geosci. Remote Sens. 1999, 37, 969–977. [Google Scholar] [CrossRef]
- Bian, J.; Li, A.; Huang, C.; Zhang, R.; Zhan, X. A Self-Adaptive Approach for Producing Clear-Sky Composites from VIIRS Surface Reflectance Datasets. ISPRS J. Photogramm. Remote Sens. 2018, 144, 189–201. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of Maximum-Value Composite Images from Temporal AVHRR Data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a Two-Band Enhanced Vegetation Index without a Blue Band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Jennings, S.B.; Brown, N.D.; Sheil, D. Assessing Forest Canopies and Understorey Illumination: Canopy Closure, Canopy Cover and Other Measures. Forestry (Lond) 1999, 72, 59–74. [Google Scholar] [CrossRef]
- Bergen, K.M.; Goetz, S.J.; Dubayah, R.O.; Henebry, G.M.; Hunsaker, C.T.; Imhoff, M.L.; Nelson, R.F.; Parker, G.G.; Radeloff, V.C. Remote Sensing of Vegetation 3-D Structure for Biodiversity and Habitat: Review and Implications for Lidar and Radar Spaceborne Missions. J. Geophys. Res. Biogeosci. 2009, 114. [Google Scholar] [CrossRef]
- Dubayah, R.; Tang, H.; Armston, J.; Luthcke, S.; Hofton, M.; Blair, J.B. GEDI L2B Canopy Cover and Vertical Profile Metrics Data Global Footprint Level V001 2019; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2019. [Google Scholar]
- Boucher, P.B.; Hancock, S.; Orwig, D.A.; Duncanson, L.; Armston, J.; Tang, H.; Krause, K.; Cook, B.; Paynter, I.; Li, Z.; et al. Detecting Change in Forest Structure with Simulated GEDI Lidar Waveforms: A Case Study of the Hemlock Woolly Adelgid (HWA; Adelges tsugae) Infestation. Remote Sens. 2020, 12, 1304. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar Sampling for Large-Area Forest Characterization: A Review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Carroll, M.L.; Townshend, J.R.; DiMiceli, C.M.; Noojipady, P.; Sohlberg, R.A. A New Global Raster Water Mask at 250 m Resolution. Int. J. Digit. Earth 2009, 2, 291–308. [Google Scholar] [CrossRef]
- Omernik, J.M. Ecoregions of the Conterminous United States. Ann. Assoc. Am. Geogr. 1987, 77, 118–125. [Google Scholar] [CrossRef]
- Omernik, J.M. Perspectives on the Nature and Definition of Ecological Regions. Environ. Manag. 2004, 34, S27–S38. [Google Scholar] [CrossRef]
- Omernik, J.M.; Griffith, G.E. Ecoregions of the Conterminous United States: Evolution of a Hierarchical Spatial Framework. Environ. Manag. 2014, 54, 1249–1266. [Google Scholar] [CrossRef] [PubMed]
- Qi, W.; Lee, S.-K.; Hancock, S.; Luthcke, S.; Tang, H.; Armston, J.; Dubayah, R. Improved Forest Height Estimation by Fusion of Simulated GEDI Lidar Data and TanDEM-X InSAR Data. Remote Sens. Environ. 2019, 221, 621–634. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A Meta-Analysis of Terrestrial Aboveground Biomass Estimation Using Lidar Remote Sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Keller, M.; Pang, Y.; de Camargo, P.B.; Hunter, M.O. Revised Method for Forest Canopy Height Estimation from Geoscience Laser Altimeter System Waveforms. J. Appl. Remote Sens. 2007, 1, 013537. [Google Scholar] [CrossRef]
- Neigh, C.S.R.; Masek, J.G.; Bourget, P.; Cook, B.; Huang, C.; Rishmawi, K.; Zhao, F. Deciphering the Precision of Stereo IKONOS Canopy Height Models for US Forests with G-LiHT Airborne LiDAR. Remote Sens. 2014, 6, 1762–1782. [Google Scholar] [CrossRef]
- Dubayah, R.; Hofton, M.A.; Blair, J.B.; Armston, J.; Tang, H.; Luthcke, S. GEDI L2A Elevation and Height Metrics Data Global Footprint Level V001 2020; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2020. [Google Scholar]
- Asner, G.P.; Powell, G.V.N.; Mascaro, J.; Knapp, D.E.; Clark, J.K.; Jacobson, J.; Kennedy-Bowdoin, T.; Balaji, A.; Paez-Acosta, G.; Victoria, E.; et al. High-Resolution Forest Carbon Stocks and Emissions in the Amazon. Proc. Natl. Acad. Sci. USA 2010, 107, 16738–16742. [Google Scholar] [CrossRef]
- Mascaro, J.; Detto, M.; Asner, G.P.; Muller-Landau, H.C. Evaluating Uncertainty in Mapping Forest Carbon with Airborne LiDAR. Remote Sens. Environ. 2011, 115, 3770–3774. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated Impact of Sample Plot Size and Co-Registration Error on the Accuracy and Uncertainty of LiDAR-Derived Estimates of Forest Stand Biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Gobakken, T.G.; Næsset, E.N. Assessing Effects of Positioning Errors and Sample Plot Size on Biophysical Stand Properties Derived from Airborne Laser Scanner Data. Can. J. For. Res. 2009. [Google Scholar] [CrossRef]
- Huang, C. Improved Land Cover Characterization from Satellite Remote Sensing. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 1999. [Google Scholar]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-Resolution Mapping of Forest Canopy Height Using Machine Learning by Coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 Data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global Products of Vegetation Leaf Area and Fraction Absorbed PAR from Year One of MODIS Data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Healey, S.P.; Yang, Z.; Gorelick, N.; Ilyushchenko, S. Highly Local Model Calibration with a New GEDI LiDAR Asset on Google Earth Engine Reduces Landsat Forest Height Signal Saturation. Remote Sens. 2020, 12, 2840. [Google Scholar] [CrossRef]
- Rodriguez, A.C.; Wegner, J.D. Counting the Uncountable: Deep Semantic Density Estimation from Space. In Proceedings of the GCPR 2018: Pattern Recognition, Sttutgart, Germany, 9–12 October 2018; Brox, T., Bruhn, A., Fritz, M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 351–362. [Google Scholar]
- Lang, N.; Schindler, K.; Wegner, J.D. Country-Wide High-Resolution Vegetation Height Mapping with Sentinel-2. Remote Sens. Environ. 2019, 233, 111347. [Google Scholar] [CrossRef]
- Qi, W.; Dubayah, R.O. Combining Tandem-X InSAR and Simulated GEDI Lidar Observations for Forest Structure Mapping. Remote Sens. Environ. 2016, 187, 253–266. [Google Scholar] [CrossRef]
- Choi, C.; Pardini, M.; Papathanassiou, K. A Structure-Based Framework for the Combination of GEDI and Tandem-X Measurements over Forest Scenarios. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 4488–4490. [Google Scholar]
- Lee, S.; Fatoyinbo, T.; Qi, W.; Hancock, S.; Armston, J.; Dubayah, R. Gedi and Tandem-X Fusion for 3D Forest Structure Parameter Retrieval. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 380–382. [Google Scholar]
- Huang, C.; Townshend, J.R.G.; Liang, S.; Kalluri, S.N.V.; DeFries, R.S. Impact of Sensor’s Point Spread Function on Land Cover Characterization: Assessment and Deconvolution. Remote Sens. Environ. 2002, 80, 203–212. [Google Scholar] [CrossRef]
 Marine West Coast Forests,
Marine West Coast Forests,  the Cascades,
the Cascades,  Klamath Mountains,
Klamath Mountains,  Sierra Nevada,
Sierra Nevada,  Eastern Cascades,
Eastern Cascades,  North Cascades,
North Cascades,  Northern Rockies,
Northern Rockies,  Northern Hardwood Forests,
Northern Hardwood Forests,  Central Appalachians,
Central Appalachians,  Blue Ridge Mountains,
Blue Ridge Mountains,  Piedmont Plateau,
Piedmont Plateau,  Southern Plains, and
Southern Plains, and  Coastal Plains.
Coastal Plains.
 Marine West Coast Forests,
Marine West Coast Forests,  the Cascades,
the Cascades,  Klamath Mountains,
Klamath Mountains,  Sierra Nevada,
Sierra Nevada,  Eastern Cascades,
Eastern Cascades,  North Cascades,
North Cascades,  Northern Rockies,
Northern Rockies,  Northern Hardwood Forests,
Northern Hardwood Forests,  Central Appalachians,
Central Appalachians,  Blue Ridge Mountains,
Blue Ridge Mountains,  Piedmont Plateau,
Piedmont Plateau,  Southern Plains, and
Southern Plains, and  Coastal Plains.
Coastal Plains.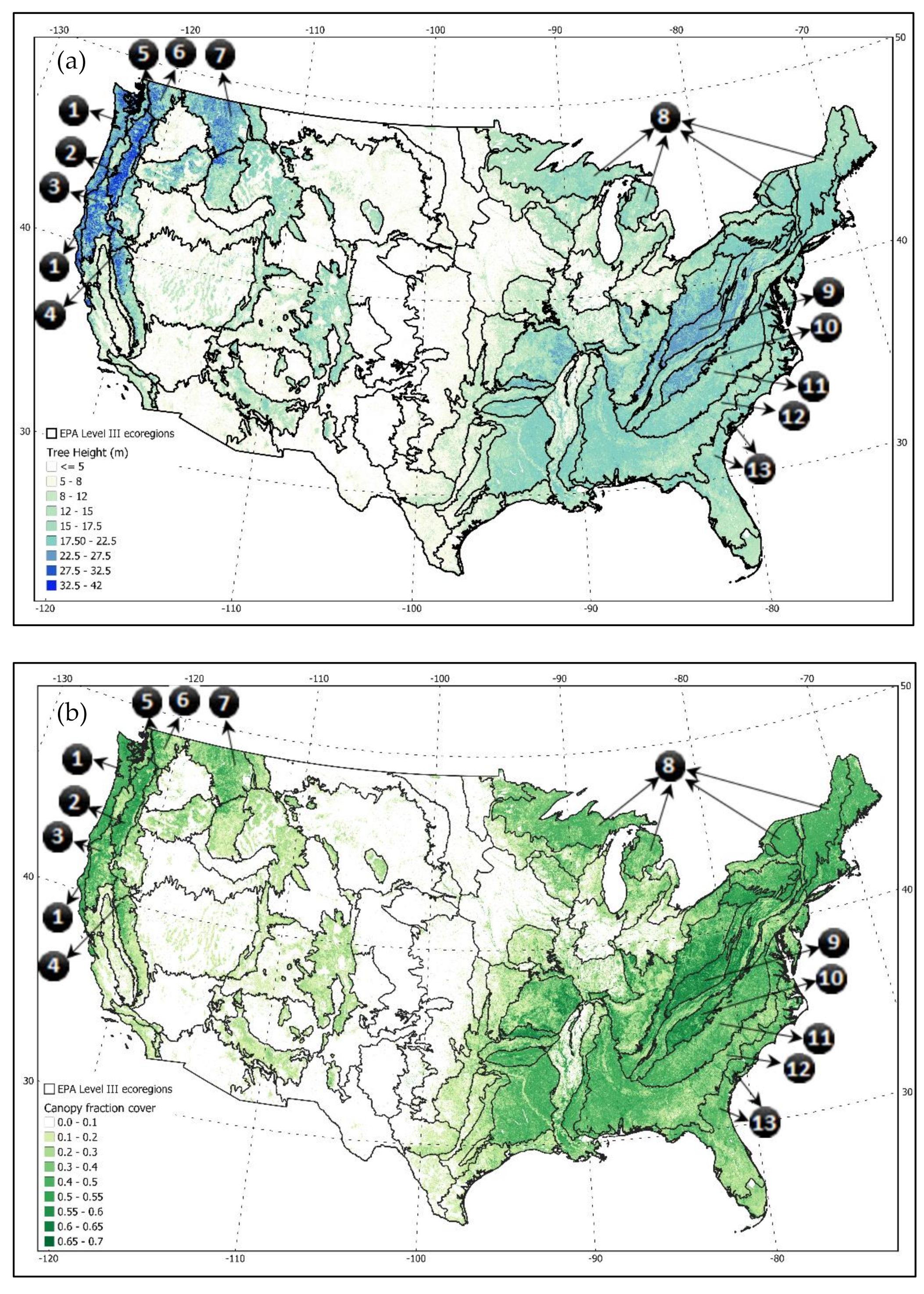
 North Central Appalachians,
North Central Appalachians,  Western Allegheny Platea,
Western Allegheny Platea,  Central Appalachians,
Central Appalachians,  Blue Ridge,
Blue Ridge,  Ouachita/Boston Mountains,
Ouachita/Boston Mountains,  Sierra Nevada Range,
Sierra Nevada Range,  Marine Coast Range,
Marine Coast Range,  Klamath,
Klamath,  Cascades,
Cascades,  Middle Rockies,
Middle Rockies,  Southern Rockies, and
Southern Rockies, and  Interior Plateau.
Interior Plateau.
 North Central Appalachians,
North Central Appalachians,  Western Allegheny Platea,
Western Allegheny Platea,  Central Appalachians,
Central Appalachians,  Blue Ridge,
Blue Ridge,  Ouachita/Boston Mountains,
Ouachita/Boston Mountains,  Sierra Nevada Range,
Sierra Nevada Range,  Marine Coast Range,
Marine Coast Range,  Klamath,
Klamath,  Cascades,
Cascades,  Middle Rockies,
Middle Rockies,  Southern Rockies, and
Southern Rockies, and  Interior Plateau.
Interior Plateau. 
| Band Number | Wavelength (μm) |
|---|---|
| M1 | 0.412 |
| M2 | 0.445 |
| M3 | 0.488 |
| M4 | 0.555 |
| M5 | 0.672 |
| M7 | 0.865 |
| M8 | 1.24 |
| M10 | 1.61 |
| M11 | 2.25 |
| Metric Name | Description |
|---|---|
| Annual Metrics (69 variables) | Maximum NDVI value |
| Minimum NDVI value of 8 greenest months | |
| Mean NDVI value of 8 greenest months | |
| Amplitude of NDVI over 8 greenest months | |
| Mean NDVI value of 4 warmest months | |
| NDVI value of warmest month | |
| Maximum band x value of 8 greenest months. | |
| Minimum band x value of 8 greenest months. | |
| Mean band x value of 8 greenest months. | |
| Amplitude of band x value over 8 greenest months. | |
| Band x value from month of maximum NDVI. | |
| Mean band x value of 4 warmest months. | |
| Band x value of warmest month. | |
| Monthly Composites (72 variables) | Band X-32 days composite value for every month in the year |
| 5-Days composites (only for bands 4,5,7,8, 10, and 11) | Band X 5-days composite value for the compositing period bounding the GEDI observation date |
| Solar Zenith Angle of the selected value in the compositing procedure | |
| VIIRS Global Land Surface Phenology product | Greenup onset (start of growth season) |
| maturity onset (start of the peak of the growth season) | |
| senescence onset (end of the peak of the growth season) | |
| dormancy onset (end of the growth season) | |
| Length of the growth season (dormancy-Greenup) | |
| growth season integrated EVI2 | |
| Average rate of EVI increase for period Greenup to maturity | |
| Average rate of EVI decrease for period Greenup to maturity | |
| Annual Surface type | Surface type IGBP class value |
| Pixel geographic coordinates | Longitude value of VIIRS pixel in decimal degree |
| Latitude value of VIIRS pixel in decimal degree |
| Hyper-Parameter | Minimum Value | Maximum Value | Interval Value |
|---|---|---|---|
| Number of Trees | 100 | 2000 | 211 |
| Maximum Tree Depth | 10 | 110 | 10 |
| Minimum Number of samples to split a node | 10 | 410 | 100 |
| Minimum number of samples in a leaf | 5 | 205 | 50 |
| Size of input features subset | 12 | 159 | 85 |
| Model Output | Number of Trees | Maximum Tree Depth | Minimum Number of Samples to Split a Node | Minimum Number of Samples in a Leaf | Size of Input Features Subset | Node Split Criterion |
|---|---|---|---|---|---|---|
| Canopy Height (CH) | 733 | 90 | 5 | 10 | 53 | MAE¥ |
| Plant Area Index (PAI) | 522 | 60 | 5 | 10 | 53 | MAE |
| Canopy Fraction cover (CFC) | 733 | 90 | 5 | 10 | 53 | MAE |
| Foliage Height Diversity (FHD) Index | 733 | 90 | 5 | 10 | 53 | MAE |
| Model Output | Median Absolute Error | R Squared | Mean Absolute Error | RMSE |
|---|---|---|---|---|
| Canopy Height (CH) (m) | 1.22 | 0.80 | 2.09 | 3.35 |
| Plant Area Index (PAI) | 0.12 | 0.76 | 0.24 | 0.41 |
| Canopy Fraction Cover (CFC) | 0.03 | 0.79 | 0.06 | 0.09 |
| Foliage Height Diversity (FHD) | 0.14 | 0.83 | 0.18 | 0.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rishmawi, K.; Huang, C.; Zhan, X. Monitoring Key Forest Structure Attributes across the Conterminous United States by Integrating GEDI LiDAR Measurements and VIIRS Data. Remote Sens. 2021, 13, 442. https://doi.org/10.3390/rs13030442
Rishmawi K, Huang C, Zhan X. Monitoring Key Forest Structure Attributes across the Conterminous United States by Integrating GEDI LiDAR Measurements and VIIRS Data. Remote Sensing. 2021; 13(3):442. https://doi.org/10.3390/rs13030442
Chicago/Turabian StyleRishmawi, Khaldoun, Chengquan Huang, and Xiwu Zhan. 2021. "Monitoring Key Forest Structure Attributes across the Conterminous United States by Integrating GEDI LiDAR Measurements and VIIRS Data" Remote Sensing 13, no. 3: 442. https://doi.org/10.3390/rs13030442
APA StyleRishmawi, K., Huang, C., & Zhan, X. (2021). Monitoring Key Forest Structure Attributes across the Conterminous United States by Integrating GEDI LiDAR Measurements and VIIRS Data. Remote Sensing, 13(3), 442. https://doi.org/10.3390/rs13030442






