You are currently on the new version of our website. Access the old version .
MDPIMDPI
Search all articles
Remote SensingRemote Sensing
Download PDF
  • Article
  • Open Access

21 January 2021

A Regional Maize Yield Hierarchical Linear Model Combining Landsat 8 Vegetative Indices and Meteorological Data: Case Study in Jilin Province

,
,
,
,
and
College of Geo-Exploration Science and Technology, Jilin University, Changchun 130026, China
*
Author to whom correspondence should be addressed.
Remote Sens.2021, 13(3), 356;https://doi.org/10.3390/rs13030356
This article belongs to the Special Issue Application of Remote Sensing in Agroforestry
Version Notes
Order Reprints

Abstract

The use of satellite remote sensing could effectively predict maize yield. However, many statistical prediction models using remote sensing data cannot extend to the regional scale without considering the regional climate. This paper first introduced the hierarchical linear modeling (HLM) method to solve maize-yield prediction problems over years and regions. The normalized difference vegetation index (NDVI), calculated by the spectrum of the Landsat 8 operational land imager (OLI), and meteorological data were introduced as input parameters in the maize-yield prediction model proposed in this paper. We built models using 100 samples from 10 areas, and used 101 other samples from 34 areas to evaluate the model’s performance in Jilin province. HLM provided higher accuracy with an adjusted determination coefficient equal to 0.75, root mean square error (RMSEV) equal to 0.94 t/ha, and normalized RMSEV equal to 9.79%. Results showed that the HLM approach outperformed linear regression (LR) and multiple LR (MLR) methods. The HLM method based on the Landsat 8 OLI NDVI and meteorological data could flexibly adjust in different regional climatic conditions. They had higher spatiotemporal expansibility than that of widely used yield estimation models (e.g., LR and MLR). This is helpful for the accurate management of maize fields.

1. Introduction

As one of the world’s most productive food crops, maize plays a vital role in agriculture. Maize-yield prediction before harvest is closely linked to individual farmers, private enterprises, and national strategic planning [1,2,3,4]. Accurate yield predictions can help individual farmers to improve field management, achieve higher yield in time [5,6,7,8,9], and provide relevant and valuable information to private companies (e.g., crop insurers or commodity traders) [10]. It is also a strong guarantee for national governments and international institutions (especially in developing countries) to strengthen supply chain management, food safety, and quality assessment. Therefore, increasing attention is being paid to prediction methods of maize yield [11,12].
Traditional agricultural yield data are obtained by routine sampling methods that take considerable time and fail to guarantee regional-scale timeliness. With the rapid development of sensors, satellite remote sensing has become an essential tool for obtaining maize yield information from the field to large regional areas [13]. Previous studies used remote sensing mechanistic and empirical methods to establish the quantitative relationship between obtaining satellite remote sensing data and crop yield [13,14]. Physical methods integrate satellite remote sensing data into physiological plant crop growth models [15,16,17]. Such methods often use crop growth variables (leaf area index, biomass, soil water content, etc.) observed by remote sensing to adjust crop models to obtain more accurate predictions. This has the advantage of clear mechanisms accounting for complex interactions between climate change, environmental conditions, field management practices, and yields [18]. However, the difficulty in obtaining accurate input variables (e.g., meteorological, soil, and crop variety) in time, the complexity of the model operation, and the long computation time prevent the method from being popularized in a large area [18,19].
Empirical approaches aim at finding mathematical relationships between crop yield and indices calculated by remote sensing data (e.g., normalized difference vegetation index (NDVI), visible and shortwave infrared drought index (VSDI), and enhanced vegetation index (EVI)) [1,13,20]. These approaches include linear regression (LR), multiple LR (MLR), and machine learning regression (e.g., random forest [21] and neural networks [22]), which usually take meteorological factors and indices as input variables. Some empirical multivariable models considering meteorological variables obtained good forecast accuracy [23,24]. Such methods describe more complex relationships between more variables, such as critical meteorological data and remote sensing information [24,25,26,27]. They were considered as the simplest methods to predict yields with high computational efficiency. However, the neglected fact in these models is that remote sensing data record the instantaneous state of crops, and the same data may have different explanations under various environmental conditions. Piedallu et al. proved that remote sensing data could represent crops at a particular time, containing joint climatic and environmental information [28]. Therefore, empirical approaches without considering meteorological conditions may only apply to local regions, with low spatial and temporal portability [12,20]. A remote sensing prediction model that can account for the integrated utility of remote sensing and meteorological data may be more suitable for forecasting maize yields [29].
Hierarchical linear modeling (HLM) is a potentially suitable method for improving empirical yield models. It is a multilevel and upgraded expression of LR, which accounts for interactions between different data levels [30]. With the development of statistics, HLM has been widely used in social work [31,32] and spatial science [33] to solve the hierarchical problem of grouped data. The HLM method can simultaneously investigate the relationship between and within hierarchical levels of grouped data, and it is more effective than existing analyses in calculating differences between variables at different levels. However, it is rarely present in agricultural research. In HLM, there are usually two or three levels to coordinate the expression of multiple independent variables. Studies showed that meteorological data can explain yield differences between years and regions [34,35,36]. The correlation between yield and remote sensing information varies in different areas and years, which forms another level to explain unexplained yield changes in weather models [35,36]. This possibility assumes that HLM can be an effective method for predicting crop yields under different climatic conditions.
Therefore, in this study, Landsat 8 images, meteorological and measured yield data were acquired to determine the optimal vegetation index (VI) for maize-yield prediction using the LR method, and to build regional maize-yield prediction models using HLM and assess its accuracy.

2. Methods

HLM is a hierarchical hybrid model, which is an upgraded model of LR regression. The HLM used in this study consisted of two levels. The first level is similar to the ordinary LR model, which contains independent remote sensing data variables and yield. The independent variables in the second layer were environmental factors. The dependent variable corresponds to slope and intercept in the first layer model. Details are as follows.
The HLM prediction model used in this study is a two-level, completely random coefficient model. Level-1yield is an LR model about VI and yield, as shown in Equation (1):
L e v e l- 1 :   Y i e l d i j = β 0 j   + β 1 j × V I i   + e i j
where β0j is the intercept of the model, β1j is the slope of the model, and eij is the random error.
In the second level of the model, β0j, β1j, and meteorological factors constitute the equation. Average meteorological data (hours of sunshine (RAD), rainfall (PRE), maximal temperature (Tmax), and minimal temperature (Tmin)) before the filling stage were independent variables, as shown in Equation (2):
L e v e l- 2 :   β m j = γ m 0 + γ m 1 × R A D + γ m 2 × T max + γ m 3 × T min + γ m 4 × P R E + u m j ,
where βmj represents the intercept β0j and slope β1j of the Level-1 model, γm0 is the intercept of the Level-2 model, γm1–γm4 stand for the slopes of meteorological parameters, and umj represents the random error of this level function.

3. Materials

3.1. Study Area

The research area is located in Jilin province, northeastern China (40°52′–46°18′N, 121°38′–130°19′E), covering an area of 187,400 km2 (Figure 1). It has the highest elevation in the southeast at about 2000 m and drops gently to the northwest. Average temperature varies from 4.9 to 5.5 °C. The maximal temperature is up to 39.5 °C in July, while the lowest temperature can be at –39.8 °C in January. Total hours of sunlight per year vary from 2630 to 2930 h, and annual average precipitation ranges from 350 to >1500 mm in the southeast [37,38]. This region is part of the subhumid continental monsoon, where rain-fed spring maize is annually grown, sown at the end of April, and maturing at the beginning of October [38].
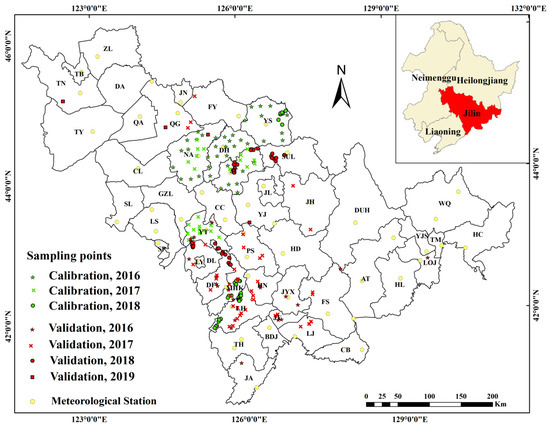
Figure 1. Location of Jilin Province, sampling site, and weather station.

3.2. Remote Sensing Data

We chose 18 Landsat 8 operational land imager (OLI) atmospherically corrected surface reflectance data images to obtain sampling points for filling-stage spectrum information. Image acquisition time was within 1 week after the crops had entered the filling stage. The study only chooses the images with no rainfall events before acquisition for at least 5 days to avoid the infrared band’s rainfall influence. Unreliable pixels identified as cloud and shadow were removed with information from the quality attribute (QA) layer provided in Landsat 8 OLI. Landsat 8 OLI pixel-quality attributes were generated from the CFMASK algorithm [39]; bit 3 and bit 5 represent cloud shadow and cloud pixel, respectively. We excluded any pixel with its bits values equal to 1. Table 1 gives detailed information about Landsat 8 OLI images, sampling areas, and the corresponding filling date.
Table 1. Information about selected Landsat 8 OLI images.
The 11 VIs considered as potential predictors of crop yield were calculated by Landsat 8 reflectance data. Table 2 shows equations and references for the 11 VIs. The correlation coefficients between the yield and VIs of calibration samples were calculated (Table 2) to find the best VI to build yield estimation HLM.
Table 2. Selected spectral indices for establishing prediction models and correlation coefficients between each spectral index and yield. Note: GI, greenness index; MSR, modified simple ratio; NDVI, normalized difference vegetation index; SPVI, spectral polygon vegetation index; RVI, ratio vegetation index; CInir, chlorophyll index; SAVI, soil-adjusted vegetation index; TVI, triangular vegetation index; EVI, enhanced vegetation index; WDRVI, wide dynamic range vegetation index.

3.3. Climatic Data

Daily minimal temperature (Tmin, °C), maximal temperature (Tmax, °C), hours of sunshine (RAD), rainfall (PRE, mm), and the date of the critical reproductive period of the meteorological station during 2016–2019 were downloaded from the National Information Center of the China Meteorological Administration (http://data.cma.cn/) (Figure 1). The average value of meteorological data of 1 month before the grain-filling stage was calculated as the climatic factor variable of the HLM.

3.4. Yield Measurement

Maize in the study area reaches full maturity in late September/early October. We measured the yield at the maize maturity stage, and used GPS to mark the latitude and longitude of the sampling points. Maize grain for the determination of yield was taken from a 3 m2 area with three replicates from each plot in a central 15 × 15 m field. Maize yield was measured in dry conditions, uniformly converted into a weight with 14% water moisture [50], and maize yield was then calculated with t/ha. Table 3 summarizes the statistics of grain yield during 2016–2019: sample size, maximal yield (Max), mean yield (Mean), minimal yield (Min), standard deviation (SD), and coefficient of variation (CV).
Table 3. Summary statistics of maize grain yield (t/ha) during 2016–2019 in Jilin province. Note: Min, minimal yield; Mean, mean yield; Max, maximal yield; SD, standard deviation; CV, coefficient of variation.

3.5. Statistical Analysis

Field data, including yield data, spectral VI data, and meteorological factors, collected from 10 areas (n = 100, calibration group), were used to calculate Pearson’s correlation coefficient between yield and VIs. Then, VIs were used to establish the LR model, and VI and meteorological variables were used to establish MLR and HLM for predicting yield. Other field data obtained from 34 regions (n = 101, validation group) were used to compare the models’ yield estimation accuracy. The ratio of calibration sets and validation sets was 1:1. In the calibration set, only a few area samples were selected for model establishment. In the validation set, on the other hand, sampling points from more areas were included to verify the model’s applicability in unknown areas. Model evaluation parameters included determination coefficient (R2; Equation (3)), adjusted R2 (Equation (4)), root mean square error (RMSEV; Equation (5)), and normalized RMSEV (nRMSE; Equation (6)),
R 2 =   1 − ∑ i = 1 n ( P i − M i ) ∑ i = 1 n ( M ¯ − M i ) ,
a d j u s t e d   R 2 = 1 − ( 1 − R 2 ) ( n − 1 ) n − p − 1 ,
R M S E V = ∑ i = 1 n ( P i − M i ) 2 / n ,
n R M S E = R M S E V / M ¯ ,
where n, p, Pi, Mi, and M ¯ represent numbers of sampling points, numbers of input variables, predicted values, measured values, and the mean value of the measured datasets.
The Akaike information criterion (AIC) is a standard for assessing the complexity of statistical models. In general, the model with a smaller AIC value is more acceptable. We used the AIC value to evaluate the performance of HLM and MLR when more factors than LR were considered. The AIC value was calculated as Equation (7) [50]:
A I C = ( − 2 l n ( L )   + 2 k ) / n ,
where L is the maximum likelihood function, k represents the numbers of input parameters, and n is the numbers of samples.
All statistical indicators and charts were calculated and drawn using the lmerTest [51] and gglot2 [52] packages of the R language (R Studio Inc., Boston, MA, USA).

4. Result

4.1. Correlations between Yield and Spectral Vegetation Indices

Correlations between VIs and maize yield, calculated using calibration samples, were different (Table 2). All selected VIs presented highly significant correlation with maize yield (p < 0.01), with NDVI having the best correlation (r = 0.677), followed by wide dynamic range vegetation index (WDRVI) (r = 0.676) and modified simple ratio (MSR) (r = 0.665) (Table 2).
The LR models of grain yield were established using NDVI, which had the best correlation with maize yield (Figure 2 and Table 4). When all calibration samples were used to build the LR model with NDVI regardless of year and region, the R2, RMSEV, and nRMSE of the NDVI LR model were 0.46, 2.08 t/ha, and 21.72%, respectively (Table 4). This model was similar to the LR model build for 2018JT, but overestimated yield for 2017NA, 2018LH, and 2018MHK, and underestimated yield for 2016DH, 2016JT, 2016NA, and 2016YS. The difference showed that the LR yield model built by VI exhibited some spatial instability in prediction.
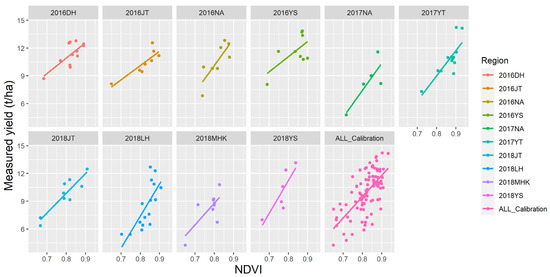
Figure 2. Linear relationship between yield and normalized difference vegetation index (NDVI) observed in different regions.
Table 4. Relationship between yield and vegetation indices (VIs) of different region datasets and calibrated experimental dataset. Note: LR, linear regression; RMSE, root mean square error.

4.2. Yield-Predicting Model Combining Landsat 8 Vegetative Indices and Meteorological Data

4.2.1. HLM

VIs and meteorological data were used in the yield-predicting model established by HLM. Three vegetation indices—NDVI, WDRVI, and MSR—closely associated with yield in the calibrated dataset are involved in developing prediction models (Table 5 and Figure 3). Among these three indices, the HLM constructed by NDVI had the highest precision with R2 = 0.75, RMSEV = 0.94 t/ha, and nRMSE = 9.79%). Compared with the LR and MLR models, HLM accuracy was significantly improved. Predicted yield error rates were reduced in HLM (Figure 2, Figure 3 and Figure 4), and data were well-distributed along a 1:1 line (Figure 3).
Table 5. Coefficient value of each variable in hierarchical linear modeling (HLM) for yield prediction.
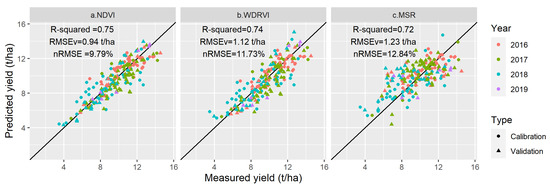
Figure 3. Relationships between measured and predicted yield under hierarchical linear modeling (HLM) using (a) NDVI, (b) wide dynamic range vegetation index (WDRVI), and (c) modified simple ratio (MSR).
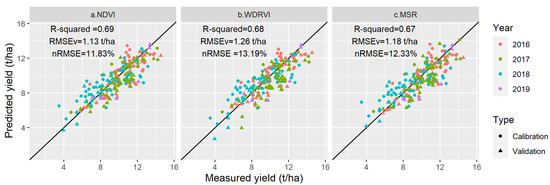
Figure 4. Relationships between measured and predicted yield under the MLR model using (a) NDVI, (b) WDRVI, and (c) MSR.

4.2.2. MLR Model

The MLR method, combining VI information and metrological data, was used for building a model for yield prediction. The three spectral indices having the best relationship with yield, i.e., NDVI, WDRVI, and MSR, participated in model building and validation (Table 6 and Figure 4). Significant differences in predictive ability between MLR and LR were observed. There was relatively better consistency between predicted and measured yields in the MLR model. The best MLR model was with NDVI, which obtained R2, RMSEV, and nRMSE with 0.69, 1.13 t/ha, and 11.83%.
Table 6. Coefficient value of each variable in yield model by multiple linear regression (MLR). Note: PRE, rainfall; RAD, hours of sunshine.

4.3. Evaluation of HLM Method for Yield Prediction

4.3.1. Accuracy Comparison between LR, MLR, and HLM

The HLM method was more effective in predicting yield than LR and MLR were. Comparing the three models in which NDVI participated in modeling (Table 7), NDVI HLM demonstrated the most significant degree of variation, with R2 equaling 0.75 and adjusted R2 equaling 0.74, followed by the MLR and the LR models. The nRMSE of the NDVI HLM method was only 45.1% of the LR and 82.8% of the MLR. AIC results also showed that the NDVI HLM method was lower than the LR and MLR methods, equal to 3.35, which further proves the ability of HLM to predict yield across years and regions.
Table 7. Comparison of model precision of using LR, MLR, and HLM to predict maize yield.

4.3.2. Accuracy Comparison of HLM and MLR Methods in Different Regions

The MLR and the HLM methods showed higher prediction accuracy than that of LR. Meteorological factors are helpful in modeling. The prediction difference between HLM and MLR in all regions was further compared. The nRMSE of MLR was evenly distributed in the range of 0–26%, and most of the nRMSE of HLM was below 15% (Figure 5a). The nRMSE values of MLR and HLM models were consistent with each other in 22 regions, distributed diagonally as shown in Figure 5a. HLM showed a significantly smaller nRMSE in 12 areas, of which the scattered points were located on the diagonal’s upper left side. The better MLR region corresponded to the other five points at the bottom right of the diagonal. Although MLR showed better accuracy, the difference was less than 5% (Figure 5a).
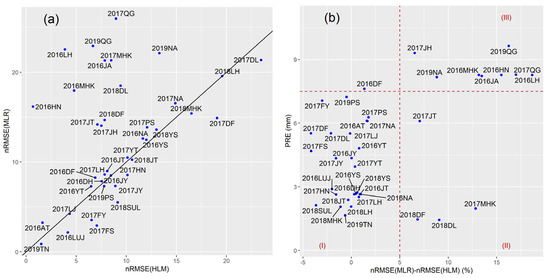
Figure 5. Relationship between the normalized root mean square error (nRMSE) of MLR and HLM, and precipitation. (a) The scatter diagram of nRMSE(MLR) and nRMSE(HLM) in different regions; (b) Relationship between PRE and difference between nRMSE(MLR)–nRMSE(HLM).
Further analysis of the results showed that precipitation in different regions affected the two models’ prediction accuracy (Figure 5b). The scatter plot with the nRMSE difference between the MLR and HLM models as the horizontal axis and the rainfall as the vertical axis was divided into three parts. In Part I, average daily precipitation was less than 7.5 mm, the nRMSE difference between the MLR and HLM models was controlled within 5%, and nRMSE distribution was random with time and region. Parts II and III showed that HLM had a better prediction region. In Part II, average daily precipitation was below 7.5 mm, and the nRMSE difference between the two prediction models was more than 5%. In Part III, average daily rainfall was more than 7.5 mm, nRMSE difference was increased, and the instability of MLR was more prominent. Each region’s prediction accuracy showed a trend of large difference of nRMSE(MLR)–nRMSE(HLM) with the increase in daily precipitation. In areas with low or high average daily rainfall, MLR performance was more unstable.

5. Discussion

5.1. Predicting Yield Model

Research results showed that the LR model had rational accuracy from R2 results, some even up to 0.82 (Figure 2 and Table 4). In this study, spectral indices such as NDVI and WDRVI [53] at crucial growth stages could evaluate maize yield due to the direct correlation between grain yield, and plant growth and biomass. However, large model differences between regions were not easily accepted (Figure 2 and Table 4). Satellite remote sensing data are one of the most useful tools for yield, but the usage of VIs to forecast crop yield is not sufficient alone. Different background conditions among years and regions lead to a similar but inconsistent relationship between vegetation index and maize yield. Prediction accuracy declines when indiscriminately placing all samples into the same model (Table 4). Background conditions are composed of many factors, such as phenology, soil type, and climatic conditions. Researchers demonstrated the effects of meteorological conditions on grain yield, especially during the silking and filling stages [34,53]. Therefore, the critical growth period’s meteorological data should act as background factors in constructing yield prediction models.
Our research area, Jilin province, mainly has a distribution of black soil, chernozem, and luvisols. These soils are rich in nutrients and have a humus layer on top. With similar soil surface sampling properties, we built yield models using LR, MLR, and HLM, combining Landsat 8 OLI VI and meteorological data (Table 7). In comparison with the LR method, MLR and HLM performed better for yield prediction over several regions and years with noticeably reduced AIC and nRMSE values. Butts-Wilmsmeyer et al. showed significant correlation between maize quality and climate at crucial growth stages [34]. Lee et al. used precipitation, temperature, and solar radiation to forecast wheat yield [36]. Similar to the conclusions of Piedallu et al. [28], VI differences between areas and years were due to both predictive variables and environmental differences. Therefore, a VI is not suitable as the sole measure of yield.
In this study, both HLM and MLR methods make reasonable use of meteorological factors. In the MLR method, meteorological factors are used as crop growth influence variables to predict yield with vegetation index. In the HLM method, meteorological factors are used as environmental regulators to adjust the relationship between yield and vegetation index according to region. According to a further comparison between these two methods, HLM had excellent predicting precision in more areas. HLM also showed better stability, as average daily precipitation was higher than 7.5 nm or lower than 2 mm (Figure 5). The HLM structure ensures that it can construct a more detailed regional yield equation according to climate. When meteorological conditions in the verification set data did not appear in the calibration set, the prediction result was also good. However, the MLR model could only ensure that the sampling points had acceptable prediction accuracy under climatic conditions corresponding to the calibration set. Once out of range, there was a large error. The MLR method takes meteorological data as independent variables that exist independently of a vegetation index. Meteorological changes in the models do not affect the slope coefficient of vegetation index variables. The relationship between VIs and yield becomes unstable in some areas where climatic conditions deviate from the average level. HLM further adjusts this problem by assuming that the relationship between spectral indices and yields varies from region to region (Figure 5). The nested structure of variables ensures that the slope and intercept of VI and yield regression model are simultaneously adjusted by climatic conditions. Results showed that the idea of determining the slope and intercept of the first-layer vegetation index by using the meteorological factors in the HLM method could synthesize the influence of environmental factors and prediction variables on the signal, thus improving the prediction ability of the MLR method.
We further analyzed the relationship between meteorological factors and equation parameters (slope and intercept). Results showed that the slope and intercept of the yield regression equation had obvious correlation with meteorological factors, especially rainfall (PRE), which proved the initial hypothesis that the environment influences NDVI variations. Table 8 shows significant and positive correlations that were observed between PRE and function slope (r = 0.87), and substantial and negative correlations observed between PRE and intercept (r = -0.91) (Table 8). In other words, when average precipitation was higher, the NDVI in the same range may have corresponded to a broader production distribution. Of course, PRE is not the only influential factor. Tmax, Tmin, and RAD also had a regulating effect on slope and intercept with correlations like Tmax and intercept (r = 0.37), Tmax and slope (r = –0.49), and RAD and slope (r = –0.29) (Table 8). Meteorological data are associated with regional equations and play an essential role in HLM yield-predicting models.
Table 8. Pearson’s correlation coefficients among weather data, slope, and intercept of regional equations in HLM.

5.2. Potential and Limitations for Yield Prediction

HLM provides a good direction for yield prediction, but its accuracy still has much room for improvement (Figure 5). This study used four meteorological parameters as regional and annual variability to calibrate yield prediction models with spectral indices during specific growth periods, thus improving yield accuracy. It was verified that meteorological indicators such as temperature and rainfall are valuable sources of information for crop estimation and prediction [54]. The month’s meteorological factors before the filling stage are obviously helpful for predicting yield [34]. The selection of sample points in this study considered the acquisition time of satellite images and the consistency of soil types in the sampling points. Therefore, further study of the influence of other satellite data, soil types, or other meteorological parameters on predicted yields may expand the model’s scope of application. However, considering more input parameters may increase the complexity of the HLM production prediction model. Therefore, when applied to regional scales or commercial systems, the best choice of significant input parameters should be one of the following. One possible way to improve the model’s accuracy is to increase the precision of crop phenological prediction. Araya et al. [55] used remote sensing imagery to determine the phenological phases of crops. Nissanka et al. [56] used crop growth models to simulate crop phenological periods on the basis of meteorological data. Better methods for estimating crop growth periods are expected to improve large-scale yield prediction. Adding image data with more bands and higher spatial resolution is another method that can improve the accuracy of model predictions. Sentinel-2 [57], a red-edge sensor that is more sensitive to vegetation, and RapidEye [58], with a spatial resolution of 5 m may bring new precision levels to model prediction.

6. Conclusions

In comparing the LR, MLR, and HLM methods, the LR prediction model presented unstable performance in verification in terms of overall accuracy. The best result was by the model with NDVI (R2 = 0.46, RMSEV = 2.08 t/ha, nRMSE = 21.72%). MLR combined with NDVI and meteorological data significantly improved prediction accuracy (R2 = 0.69, RMSEV =1.13 t/ha, nRMSE = 11.93%). HLM with NDVI had the best prediction results (R2 = 0.75, RMSEV = 0.94 t/ha, nRMSE = 9.79%). In further comparison between HLM and MLR, HLM produced more sensitive adjustments to the region’s environmental changes to achieve better prediction accuracy in more regions, and obtained acceptable accuracy in a broader range of areas. These results showed that the HLM method has great potential in predicting interannual and regional maize yield. It allows for provinces or even countries with extensive planting areas to build models with only small regional historical data, and complete wider yield forecast.

Author Contributions

Conceptualization, B.Z. and S.C.; Methodology, B.Z.; Software, B.Z.; Validation, B.Z. and S.C.; Formal Analysis, B.Z.; Investigation, B.Z., Y.C., Z.X., Y.Y., and C.H.; Resources, B.Z., Y.C. and S.C.; Data Curation, B.Z., Y.C., Z.X., Y.Y., and C.H.; Writing-Original Draft Preparation, B.Z.; Writing—Review and Editing, B.Z.; Visualization, B.Z., Y.C., and S.C.; Supervision, S.C.; Project Administration, S.C.; Funding Acquisition, S.C. All authors have read and agreed to the published version of the manuscript.

Funding

This paper was supported by the three-year action plan for nurturing and developing new industries in the northeastern region of the National Development and Reform Commission ([2016]512) funded by central government budget, Special construction plan for provincial and University, the program for JLU Science and Technology Innovative Research Team (JLUSTIRT, 2017TD-26) which is funded by the Fundamental Research Funds for the Central Universities, China, and the Changbai Mountain Scholars Program, Jilin Province, China.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
  2. Kantanantha, N.; Serban, N.; Griffin, P. Yield and price forecasting for stochastic crop decision planning. J. Agric. Biol. Environ. Stat. 2010, 15, 362–380. [Google Scholar] [CrossRef]
  3. Stone, R.C.; Meinke, H. Operational seasonal forecasting of crop performance. Philos. Trans. R. Soc. B Biol. Sci. 2005, 360, 2109–2124. [Google Scholar] [CrossRef]
  4. Córdoba, M.A.; Bruno, C.I.; Costa, J.L.; Peralta, N.R.; Balzarini, M.G. Protocol for multivariate homogeneous zone delineation in precision agriculture. Biosyst. Eng. 2016, 143, 95–107. [Google Scholar] [CrossRef]
  5. Cui, B.; Zhao, Q.; Huang, W.; Song, X.; Ye, H.; Zhou, X. A new integrated vegetation index for the estimation of winter wheat leaf chlorophyll content. Remote Sens. 2019, 11, 974. [Google Scholar] [CrossRef]
  6. Ciampitti, I.A.; Vyn, T.J. Grain nitrogen source changes over time in maize: A review. Crop Sci. 2013, 53, 366–377. [Google Scholar] [CrossRef]
  7. Meng, Q.; Cui, Z.; Yang, H.; Zhang, F.; Chen, X. Establishing High-Yielding Maize System for Sustainable Intensification in China, 1st ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2018; Volume 148, ISBN 9780128151792. [Google Scholar]
  8. Silva, P.R.F.D.; Strieder, M.L.; Coser, R.P.D.S.; Rambo, L.; Sangoi, L.; Argenta, G.; Forsthofer, E.L.; Silva, A.A.D. Grain yield and kernel crude protein content increases of maize hybrids with late nitrogen side-dressing. Sci. Agric. 2005, 62, 487–492. [Google Scholar] [CrossRef]
  9. Filippi, P.; Jones, E.J.; Wimalathunge, N.S.; Somarathna, P.D.S.N.; Pozza, L.E.; Ugbaje, S.U.; Jephcott, T.G.; Paterson, S.E.; Whelan, B.M.; Bishop, T.F.A. An approach to forecast grain crop yield using multi-layered, multi-farm data sets and machine learning. Precis. Agric. 2019, 20, 1015–1029. [Google Scholar] [CrossRef]
  10. Kogan, F.; Guo, W.; Yang, W. Drought and food security prediction from NOAA new generation of operational satellites. Geomat. Nat. Hazards Risk 2019, 10, 651–666. [Google Scholar] [CrossRef]
  11. Battude, M.; Al Bitar, A.; Morin, D.; Cros, J.; Huc, M.; Marais Sicre, C.; Le Dantec, V.; Demarez, V. Estimating maize biomass and yield over large areas using high spatial and temporal resolution Sentinel-2 like remote sensing data. Remote Sens. Environ. 2016, 184, 668–681. [Google Scholar] [CrossRef]
  12. Lobell, D.B.; Asner, G.P.; Ortiz-Monasterio, J.I.; Benning, T.L. Remote sensing of regional crop production in the Yaqui Valley, Mexico: Estimates and uncertainties. Agric. Ecosyst. Environ. 2003, 94, 205–220. [Google Scholar] [CrossRef]
  13. Karthikeyan, L.; Chawla, I.; Mishra, A.K. A review of remote sensing applications in agriculture for food security: Crop growth and yield, irrigation, and crop losses. J. Hydrol. 2020, 586, 124905. [Google Scholar] [CrossRef]
  14. Corti, M.; Cavalli, D.; Cabassi, G.; Marino Gallina, P.; Bechini, L. Does remote and proximal optical sensing successfully estimate maize variables? A review. Eur. J. Agron. 2018, 99, 37–50. [Google Scholar] [CrossRef]
  15. Li, Z.; Wang, J.; Xu, X.; Zhao, C.; Jin, X.; Yang, G.; Feng, H. Assimilation of two variables derived from hyperspectral data into the DSSAT-CERES model for grain yield and quality estimation. Remote Sens. 2015, 7, 12400–12418. [Google Scholar] [CrossRef]
  16. Ban, H.Y.; Ahn, J.B.; Lee, B.W. Assimilating MODIS data-derived minimum input data set and water stress factors into CERES-Maize model improves regional corn yield predictions. PLoS ONE 2019, 14, 1–21. [Google Scholar] [CrossRef]
  17. Jin, X.; Li, Z.; Feng, H.; Ren, Z.; Li, S. Estimation of maize yield by assimilating biomass and canopy cover derived from hyperspectral data into the AquaCrop model. Agric. Water Manag. 2020, 227, 105846. [Google Scholar] [CrossRef]
  18. Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
  19. Dorigo, W.A.; Zurita-Milla, R.; de Wit, A.J.W.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 165–193. [Google Scholar] [CrossRef]
  20. Zhou, X.; Zheng, H.B.; Xu, X.Q.; He, J.Y.; Ge, X.K.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.X.; Tian, Y.C. Predicting grain yield in rice using multi-temporal vegetation indices from UAV-based multispectral and digital imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 246–255. [Google Scholar] [CrossRef]
  21. Ramos, A.P.M.; Osco, L.P.; Furuya, D.E.G.; Gonçalves, W.N.; Santana, D.C.; Teodoro, L.P.R.; da Silva Junior, C.A.; Capristo-Silva, G.F.; Li, J.; Baio, F.H.R.; et al. A random forest ranking approach to predict yield in maize with uav-based vegetation spectral indices. Comput. Electron. Agric. 2020, 178, 105791. [Google Scholar] [CrossRef]
  22. Johnson, M.D.; Hsieh, W.W.; Cannon, A.J.; Davidson, A.; Bédard, F. Crop yield forecasting on the Canadian Prairies by remotely sensed vegetation indices and machine learning methods. Agric. For. Meteorol. 2016, 218–219, 74–84. [Google Scholar] [CrossRef]
  23. Alganci, U.; Ozdogan, M.; Sertel, E.; Ormeci, C. Estimating maize and cotton yield in southeastern Turkey with integrated use of satellite images, meteorological data and digital photographs. F. Crop. Res. 2014, 157, 8–19. [Google Scholar] [CrossRef]
  24. Balaghi, R.; Tychon, B.; Eerens, H.; Jlibene, M. Empirical regression models using NDVI, rainfall and temperature data for the early prediction of wheat grain yields in Morocco. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 438–452. [Google Scholar] [CrossRef]
  25. Aghighi, H.; Azadbakht, M.; Ashourloo, D.; Shahrabi, H.S.; Radiom, S. Machine Learning Regression Techniques for the Silage Maize Yield Prediction Using Time-Series Images of Landsat 8 OLI. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4563–4577. [Google Scholar] [CrossRef]
  26. Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
  27. Singh, R.P.; Roy, S.; Kogan, F. Vegetation and temperature condition indices from NOAA AVHRR data for drought monitoring over India. Int. J. Remote Sens. 2003, 24, 4393–4402. [Google Scholar] [CrossRef]
  28. Piedallu, C.; Chéret, V.; Denux, J.P.; Perez, V.; Azcona, J.S.; Seynave, I.; Gégout, J.C. Soil and climate differently impact NDVI patterns according to the season and the stand type. Sci. Total Environ. 2019, 651, 2874–2885. [Google Scholar] [CrossRef]
  29. Li, Z.; Taylor, J.; Yang, H.; Casa, R.; Jin, X.; Li, Z.; Song, X.; Yang, G. A hierarchical interannual wheat yield and grain protein prediction model using spectral vegetative indices and meteorological data. Field Crop. Res. 2020, 248, 107711. [Google Scholar] [CrossRef]
  30. Osborne, J.; Osborne, J.W. A Brief Introduction to Hierarchical Linear Modeling. Best Pract. Quant. Methods 2011, 8, 444–450. [Google Scholar]
  31. Gavin, M.B.; Hofmann, D.A. Using hierarchical linear modeling to investigate the moderating influence of leardership climate. Leadersh. Q. 2002, 13, 15–33. [Google Scholar] [CrossRef]
  32. Bock, R.D. Multilevel Analysis of Educational Data; Academic Press, Inc.: London, UK, 1989. [Google Scholar]
  33. Banerjee, S.; Carlin, B.P.; Gelfand, A.E. Hierarchical Modeling and Analysis for Spatial Data, 2nd ed.; Taylor & Francis: Abingdon, UK, 2015. [Google Scholar]
  34. Butts-Wilmsmeyer, C.J.; Seebauer, J.R.; Singleton, L.; Below, F.E. Weather during key growth stages explains grain quality and yield of maize. Agronomy 2019, 9, 16. [Google Scholar] [CrossRef]
  35. Vollmer, E.; Mußhoff, O. Average protein content and its variability in winter wheat: A forecast model based on weather parameters. Earth Interact. 2018, 22, 1–24. [Google Scholar] [CrossRef]
  36. Lee, B.H.; Kenkel, P.; Brorsen, B.W. Pre-harvest forecasting of county wheat yield and wheat quality using weather information. Agric. For. Meteorol. 2013, 168, 26–35. [Google Scholar] [CrossRef]
  37. Guo, E.; Zhang, J.; Wang, Y.; Si, H.; Zhang, F. Dynamic risk assessment of waterlogging disaster for maize based on CERES-Maize model in Midwest of Jilin Province, China. Nat. Hazards 2016, 83, 1747–1761. [Google Scholar] [CrossRef]
  38. Wang, M.; Li, Y.; Ye, W.; Bornman, J.F.; Yan, X. Effects of climate change on maize production, and potential adaptation measures: A case study in Jilin province, China. Clim. Res. 2011, 46, 223–242. [Google Scholar] [CrossRef]
  39. Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4-7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
  40. Zarco-Tejada, P.J.; Berjón, A.; López-Lozano, R.; Miller, J.R.; Martín, P.; Cachorro, V.; González, M.R.; De Frutos, A. Assessing vineyard condition with hyperspectral indices: Leaf and canopy reflectance simulation in a row-structured discontinuous canopy. Remote Sens. Environ. 2005, 99, 271–287. [Google Scholar] [CrossRef]
  41. Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
  42. Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS- MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
  43. Vincini, M.; Frazzi, E. Angular dependence of maize and sugar beet VIs from directional CHRIS/Proba data. In Proceedings of the 4th ESA CHRIS PROBA Workshop, Frascati, Italy, 19–21 September 2006; Volume 2006, pp. 19–21. [Google Scholar]
  44. Jordan, C.F. Derivation of leaf-area index from qualityof light on the forest floor. Ecol. Soc. Am. 1969, 50, 663–666. [Google Scholar]
  45. Sripada, R.P.; Heiniger, R.W.; White, J.G.; Weisz, R. Aerial color infrared photography for determining late-season nitrogen requirements in corn. Agron. J. 2005, 97, 1443–1451. [Google Scholar] [CrossRef]
  46. Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
  47. Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
  48. Wu, C.; Wang, L.; Niu, Z.; Gao, S.; Wu, M. Nondestructive estimation of canopy chlorophyll content using Hyperion and Landsat/TM images. Int. J. Remote Sens. 2010, 31, 2159–2167. [Google Scholar] [CrossRef]
  49. Gitelson, A.A. Wide Dynamic Range Vegetation Index for Remote Quantification of Biophysical Characteristics of Vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef]
  50. Bozdogan, H. Model selection and Akaike’s Information Criterion (AIC): The general theory and its analytical extensions. Psychometrika 1987, 52, 345–370. [Google Scholar] [CrossRef]
  51. Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. lmerTest Package: Tests in Linear Mixed Effects Models. J. Stat. Softw. 2017, 82, 1–26. [Google Scholar] [CrossRef]
  52. Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer-Verlag: New York, NY, USA, 2016; ISBN 978-3-319-24277-4. [Google Scholar]
  53. Cociu, A.I.; Alionte, E. Effect of Different Tillage Systems on Grain Yield and Its Quality of Winter Wheat, Maize and Soybean under Different Weather Conditions. Rom. Agric. Res. 2017, 34, 59–67. [Google Scholar]
  54. Prasad, A.K.; Chai, L.; Singh, R.P.; Kafatos, M. Crop yield estimation model for Iowa using remote sensing and surface parameters. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 26–33. [Google Scholar] [CrossRef]
  55. Araya, S.; Ostendorf, B.; Lyle, G.; Lewis, M. CropPhenology: An R package for extracting crop phenology from time series remotely sensed vegetation index imagery. Ecol. Inform. 2018, 46, 45–56. [Google Scholar] [CrossRef]
  56. Nissanka, S.P.; Karunaratne, A.S.; Perera, R.; Weerakoon, W.M.W.; Thorburn, P.J.; Wallach, D. Calibration of the phenology sub-model of APSIM-Oryza: Going beyond goodness of fit. Environ. Model. Softw. 2015, 70, 128–137. [Google Scholar] [CrossRef]
  57. Ramoelo, A.; Cho, M.; Mathieu, R.; Skidmore, A.K. The potential of Sentinel-2 spectral configuration to assess rangeland quality. Remote Sens. Agric. Ecosyst. Hydrol. XVI 2014, 9239, 92390C. [Google Scholar] [CrossRef]
  58. Magney, T.S.; Eitel, J.U.H.; Vierling, L.A. Mapping wheat nitrogen uptake from RapidEye vegetation indices. Precis. Agric. 2017, 18, 429–451. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Automatic Building Detection from High-Resolution Remote Sensing Images Based on Joint Optimization and Decision Fusion of Morphological Attribute Profiles
Previous
Scrutinizing Relationships between Submarine Groundwater Discharge and Upstream Areas Using Thermal Remote Sensing: A Case Study in the Northern Persian Gulf
Next