Fusion of SAR Interferometry and Polarimetry Methods for Landslide Reactivation Study, the Bureya River (Russia) Event Case Study
Abstract
:1. Introduction
2. Materials and Methods
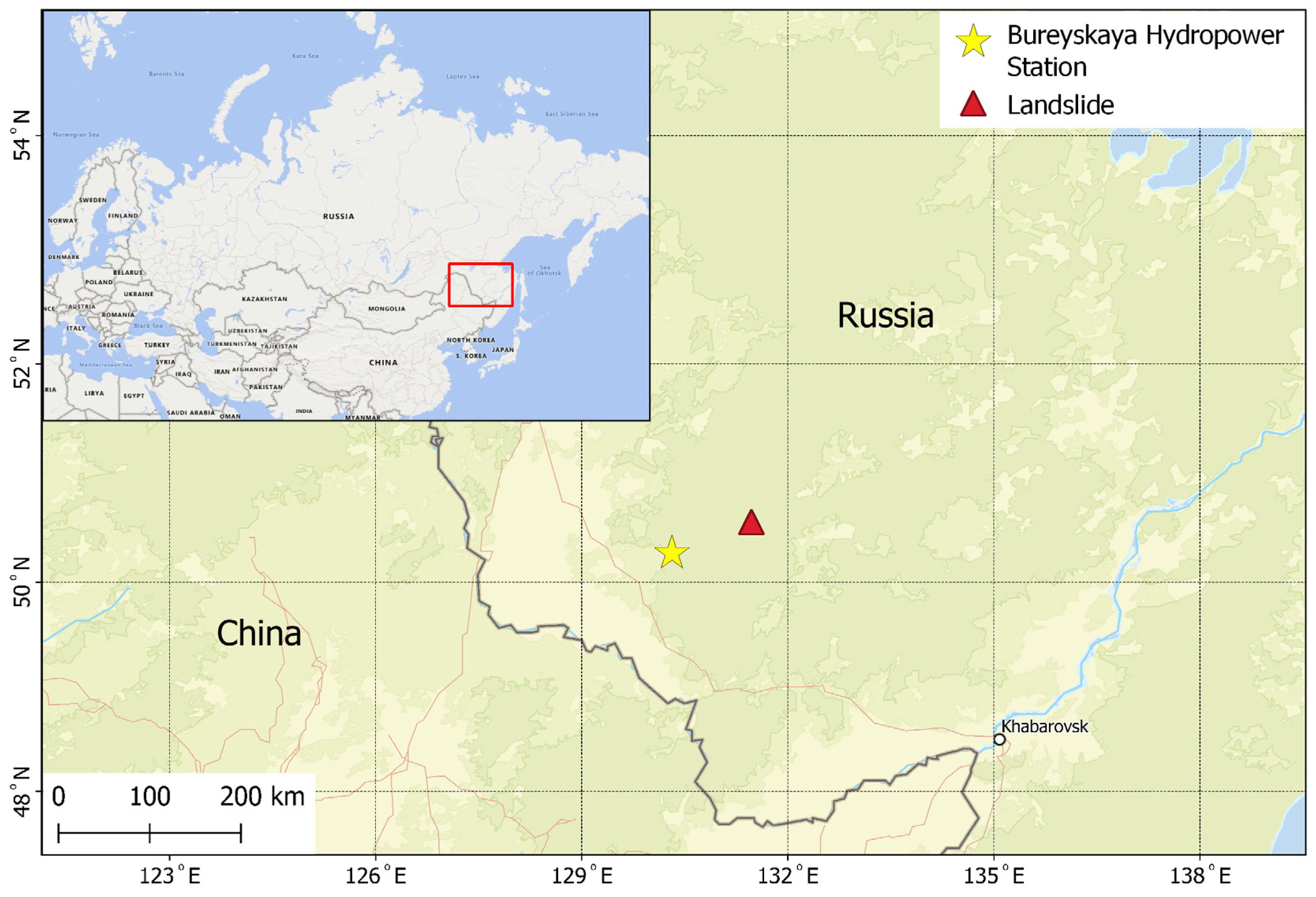
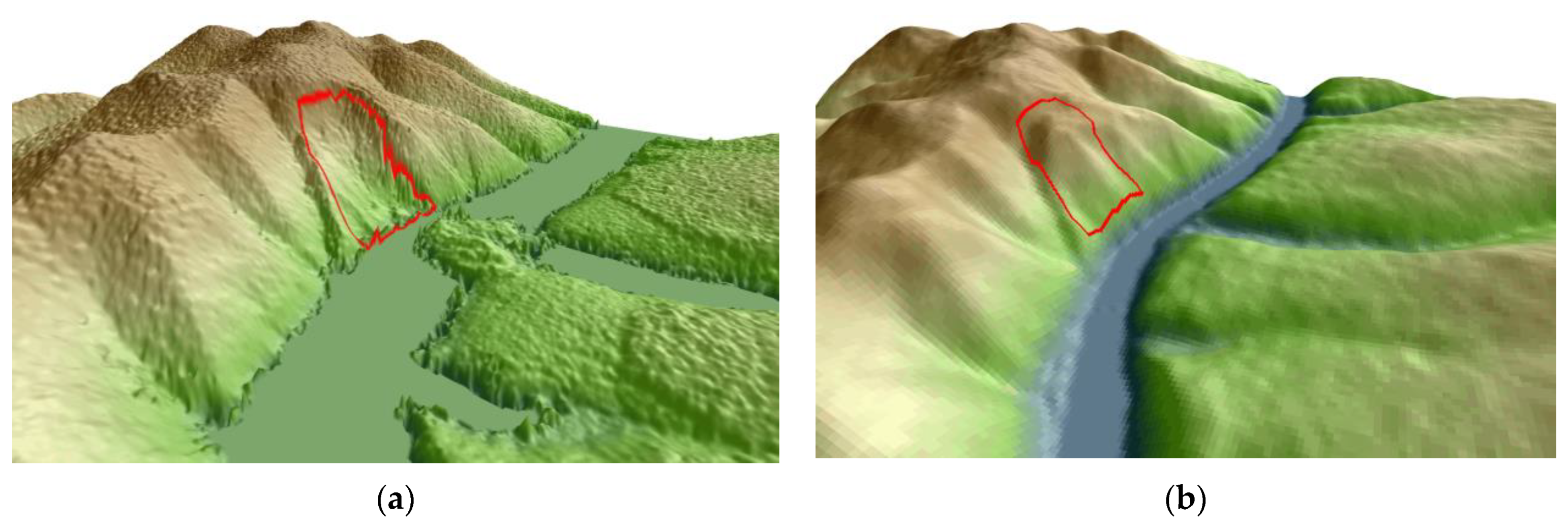
2.1. Study Area
2.2. Data and Methods
- Analyzing the results of cloud computing of backscattering time series allowing for sensing geometry and relief features;
- Cloude–Pottier decomposition of Sentinel-1 dual polarimetry data;
- PSI and SBAS-InSAR with Sentinel-1 data.
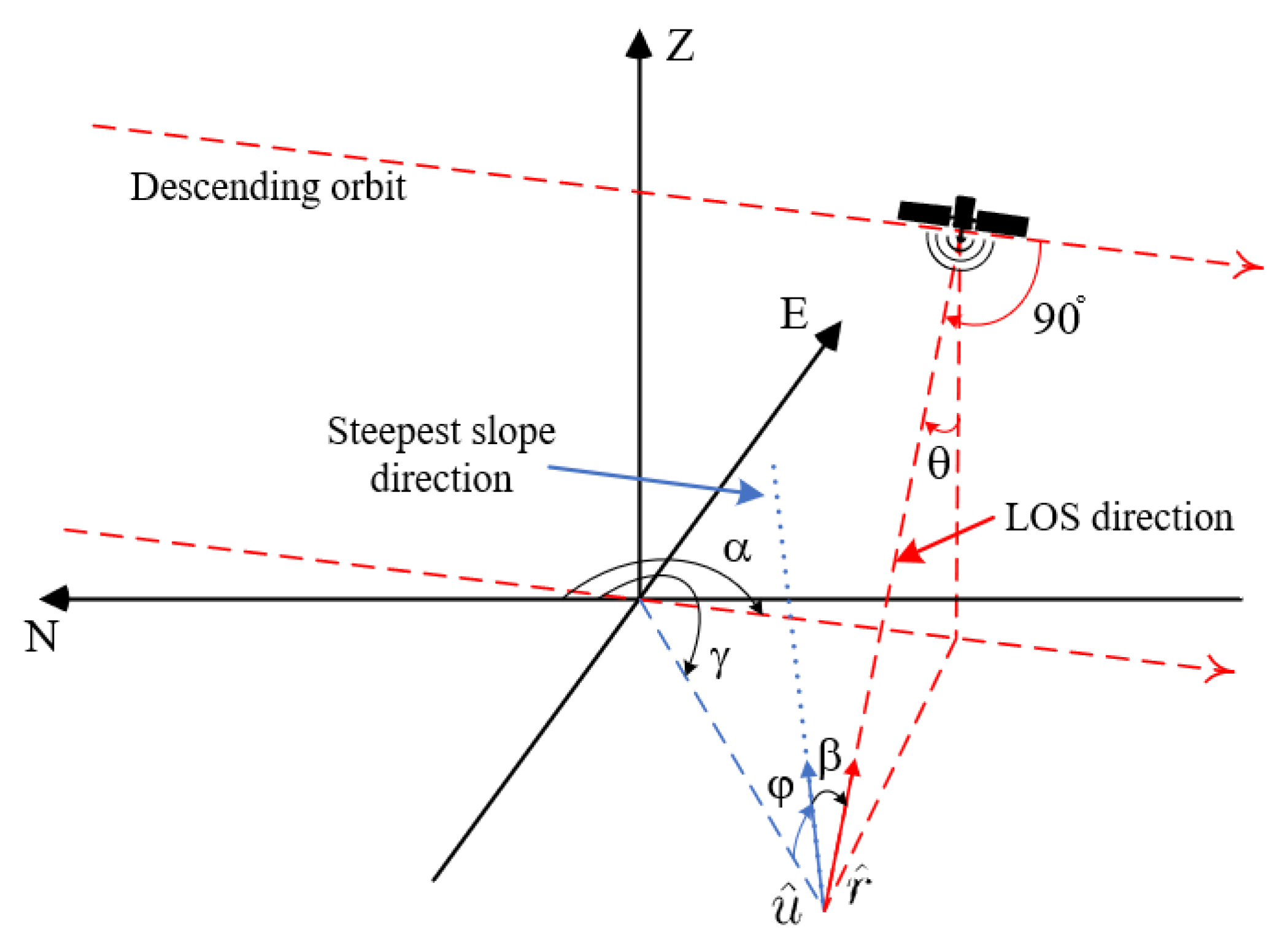
Geometric Parameters
3. Results and Discussion
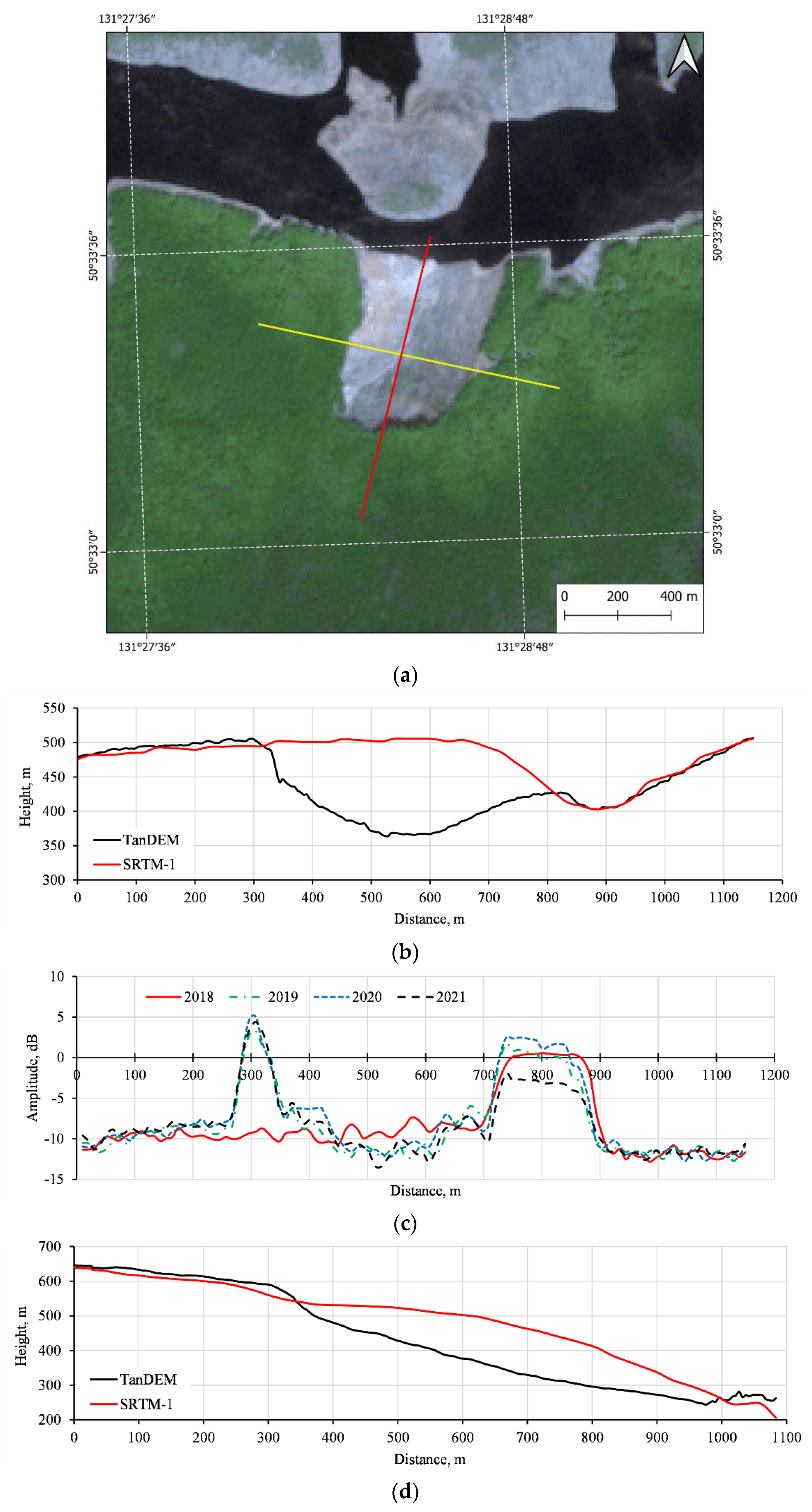
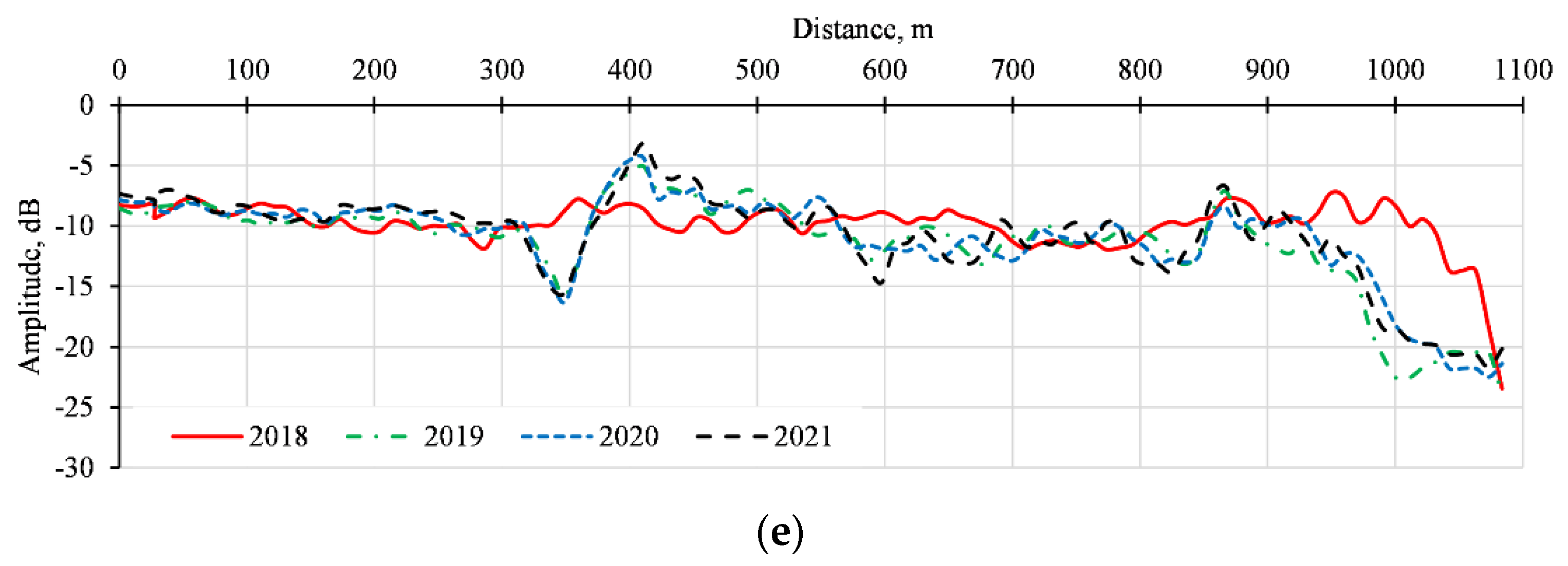
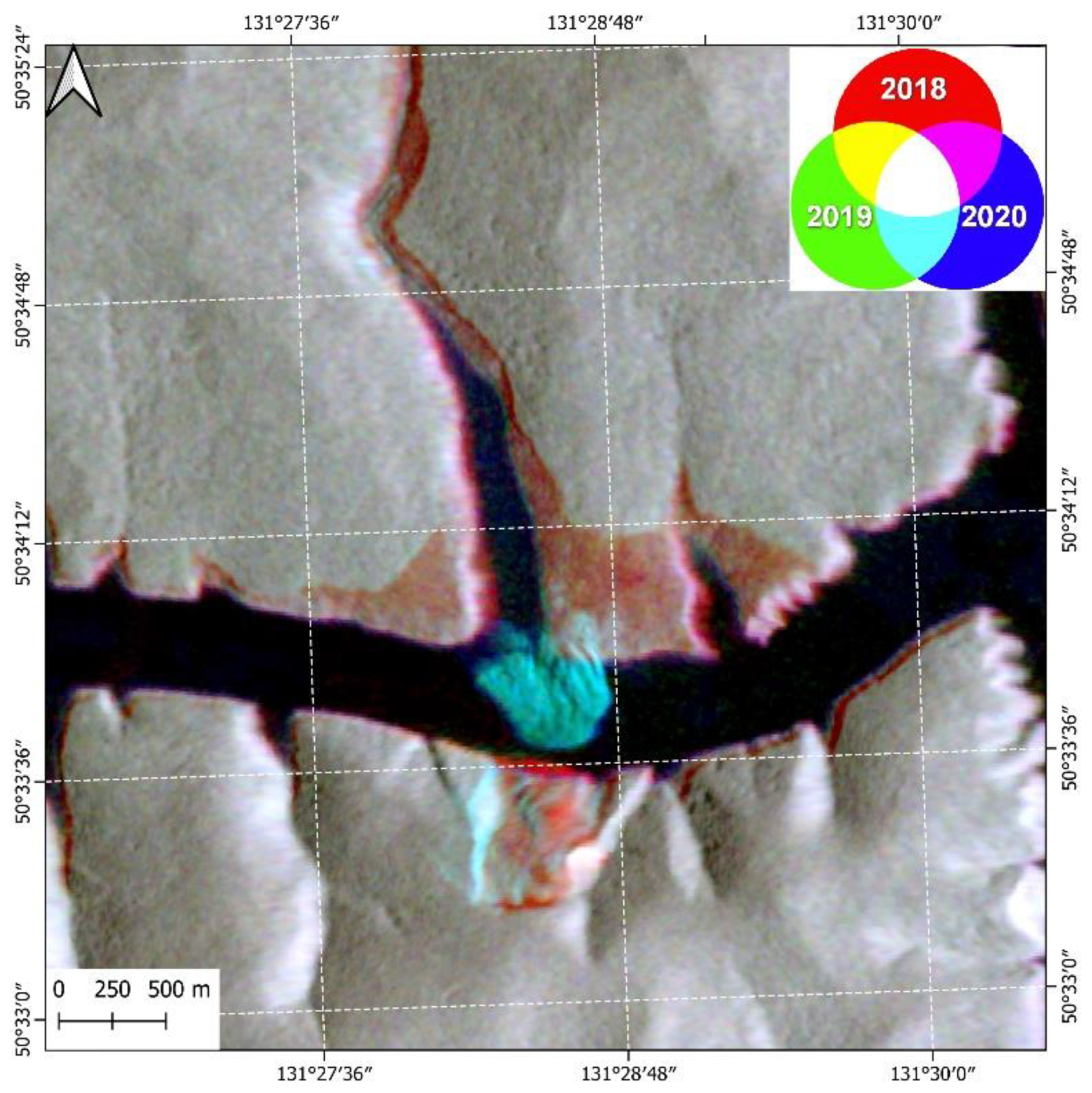
3.1. Backscattering
3.2. Polarimetric Decomposition
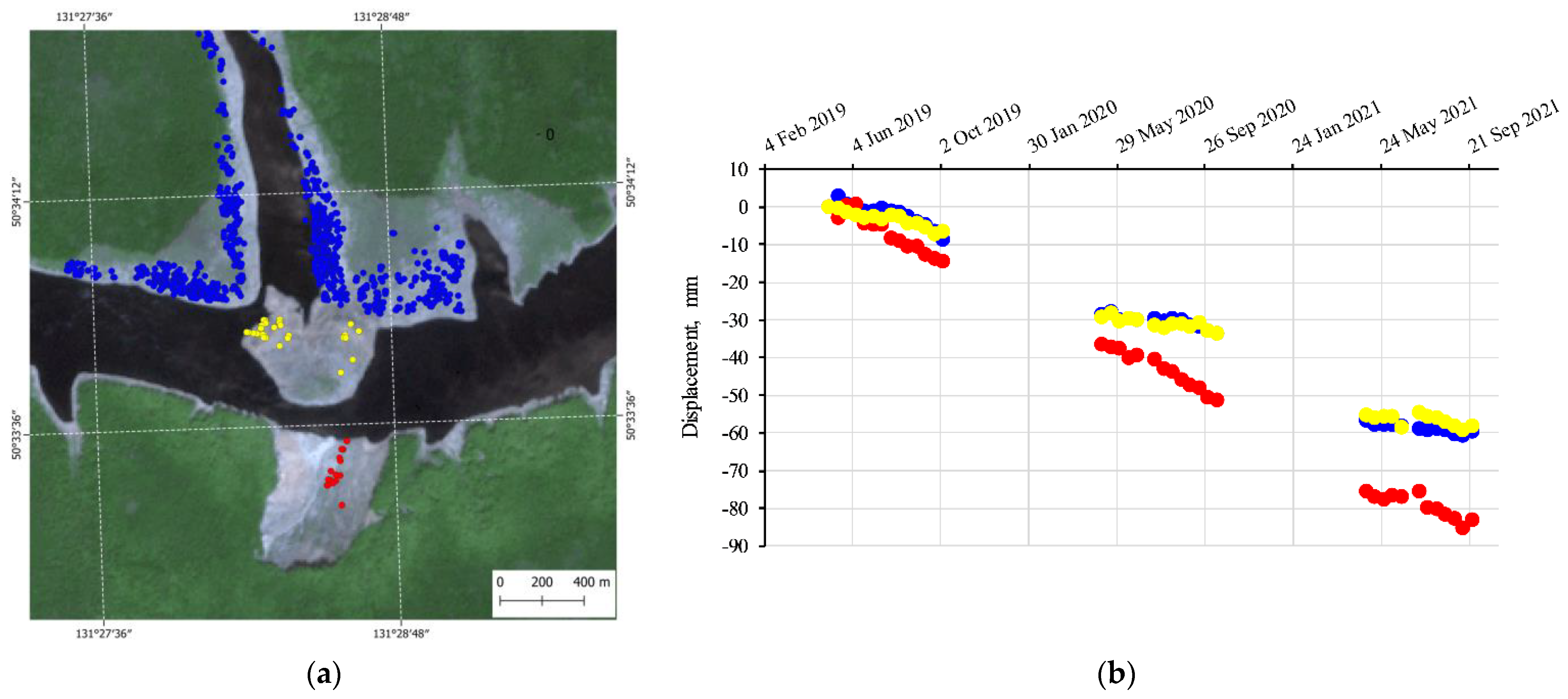
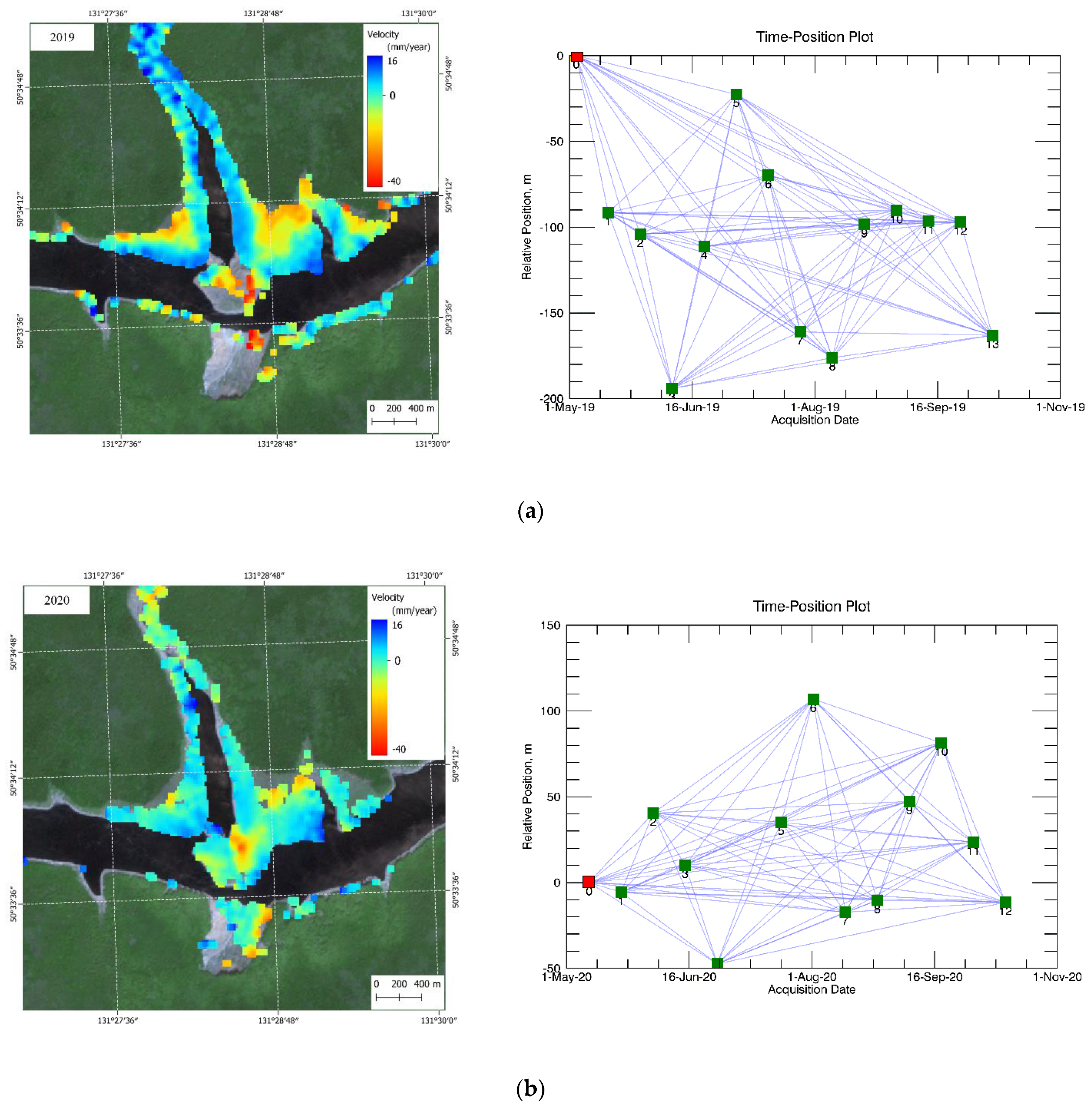
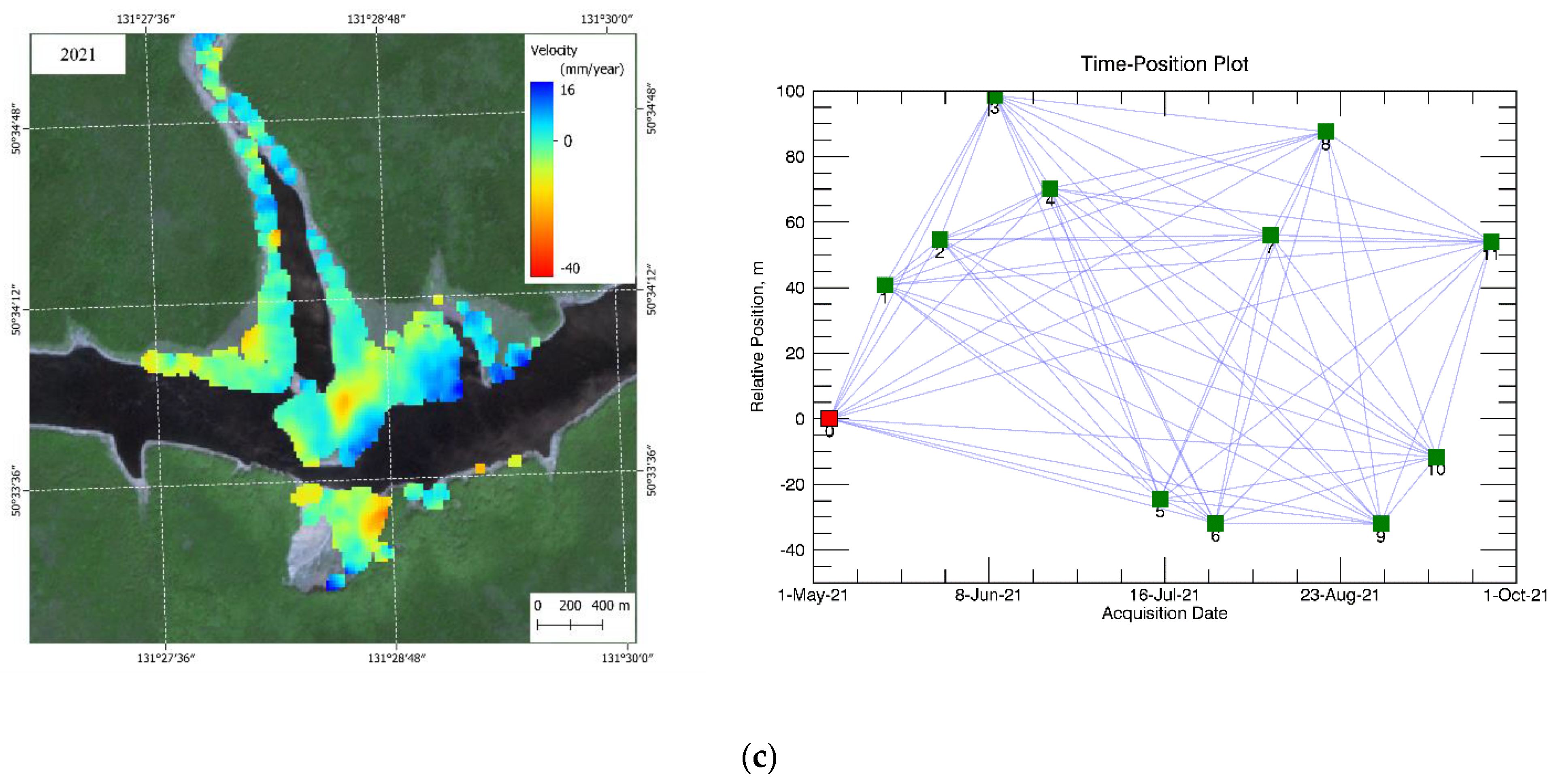
3.3. PSI and SBAS-InSAR
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Simoes, R.; Camara, G.; Queiroz, G.; Souza, F.; Andrade, P.R.; Santos, L.; Carvalho, A.; Ferreira, K. Satellite Image Time Series Analysis for Big Earth Observation Data. Remote Sens. 2021, 13, 2428. [Google Scholar] [CrossRef]
- Yao, X.; Li, G.; Xia, J.; Ben, J.; Cao, Q.; Zhao, L.; Ma, Y.; Zhang, L.; Zhu, D. Enabling the Big Earth Observation Data via Cloud Computing and DGGS: Opportunities and Challenges. Remote Sens. 2020, 12, 62. [Google Scholar] [CrossRef] [Green Version]
- Pulinets, S.; Davidenko, D. Ionospheric Precursors of Earthquakes and Global Electric Circuit. Adv. Space Res. 2014, 53, 709–723. [Google Scholar] [CrossRef]
- Bondur, V.G.; Smirnov, V.M. Method for Monitoring Seismically Hazardous Territories by Ionospheric Variations Recorded by Satellite Navigation Systems. Dokl. Earth Sci. 2005, 403, 736–740. [Google Scholar]
- Bondur, V.G.; Garagash, I.A.; Gokhberg, M.B.; Lapshin, V.M.; Nechaev, Y.V.; Steblov, G.M.; Shalimov, S.L. Geomechanical Models and Ionospheric Variations Related to Strongest Earthquakes and Weak Influence of Atmospheric Pressure Gradients. Dokl. Earth Sci. 2007, 414, 666–669. [Google Scholar] [CrossRef]
- Bondur, V.G.; Zverev, A.T. A Method of Earthquake Forecast Based on the Lineament Analysis of Satellite Images. Dokl. Earth Sci. 2005, 402, 561–567. [Google Scholar]
- Pulinets, S.A.; Ouzounov, D.; Karelin, A.V.; Boyarchuk, K.A.; Pokhmelnykh, L.A. The Physical Nature of Thermal Anomalies Observed before Strong Earthquakes. Phys. Chem. Earth Parts A/B/C 2006, 31, 143–153. [Google Scholar] [CrossRef]
- Bondur, V.G.; Garagash, I.A.; Gokhberg, M.B.; Lapshin, V.M.; Nechaev, Y.V. Connection between Variations of the Stress-Strain State of the Earth’s Crust and Seismic Activity: The Example of Southern California. Dokl. Earth Sci. 2010, 430, 147–150. [Google Scholar] [CrossRef]
- Bondur, V.G.; Garagash, I.A.; Gokhberg, M.B.; Rodkin, M.V. The Evolution of the Stress State in Southern California Based on the Geomechanical Model and Current Seismicity. Izv. Phys. Solid Earth 2016, 52, 117–128. [Google Scholar] [CrossRef]
- Akopian, S.T.; Bondur, V.G.; Rogozhin, E.A. Technology for Monitoring and Forecasting Strong Earthquakes in Russia with the Use of the Seismic Entropy Method. Izv. Phys. Solid Earth 2017, 53, 32–51. [Google Scholar] [CrossRef]
- Bondur, V.G.; Gordo, K.A. Satellite Monitoring of Burnt-out Areas and Emissions of Harmful Contaminants Due to Forest and Other Wildfires in Russia. Izv. Atmos. Ocean. Phys. 2018, 54, 955–965. [Google Scholar] [CrossRef]
- Bondur, V.G.; Gordo, K.A.; Kladov, V.L. Spacetime Distributions of Wildfire Areas and Emissions of Carbon-Containing Gases and Aerosols in Northern Eurasia According to Satellite-Monitoring Data. Izv. Atmos. Ocean. Phys. 2017, 53, 859–874. [Google Scholar] [CrossRef]
- Bondur, V.G. Satellite Monitoring of Trace Gas and Aerosol Emissions during Wildfires in Russia. Izv. Atmos. Ocean. Phys. 2016, 52, 1078–1091. [Google Scholar] [CrossRef]
- Bondur, V.G.; Pulinets, S.A.; Kim, G.A. Role of Variations in Galactic Cosmic Rays in Tropical Cyclogenesis: Evidence of Hurricane Katrina. Dokl. Earth Sci. 2008, 422, 1124. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic Aperture Radar Interferometry. Inverse Probl. 1998, 14, R1–R54. [Google Scholar] [CrossRef]
- Chimitdorzhiev, T.N.; Dagurov, P.N.; Bykov, M.E.; Dmitriev, A.V.; Kirbizhekova, I.I. Comparison of ALOS PALSAR Interferometry and Field Geodetic Leveling for Marshy Soil Thaw/Freeze Monitoring, Case Study from the Baikal Lake Region, Russia. J. Appl. Remote. Sens. 2016, 10, 016006. [Google Scholar] [CrossRef]
- Strozzi, T.; Wegmuller, U.; Werner, C.L.; Wiesmann, A.; Spreckels, V. JERS SAR Interferometry for Land Subsidence Monitoring. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1702–1708. [Google Scholar] [CrossRef]
- Zakharov, A.I.; Epov, M.I.; Mironov, V.L.; Chymitdorzhiev, T.N.; Seleznev, V.S.; Emanov, A.F.; Bykov, M.E.; Cherepenin, V.A. Earth Surface Subsidence in the Kuznetsk Coal Basin Caused by Manmade and Natural Seismic Activity According to ALOS PALSAR Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1578–1583. [Google Scholar] [CrossRef]
- Cigna, F.; Bianchini, S.; Casagli, N. How to Assess Landslide Activity and Intensity with Persistent Scatterer Interferometry (PSI): The PSI-Based Matrix Approach. Landslides 2013, 10, 267–283. [Google Scholar] [CrossRef] [Green Version]
- Raspini, F.; Moretti, S.; Casagli, N. Landslide Mapping Using SqueeSAR Data: Giampilieri (Italy) Case Study. In Landslide Science and Practice: Volume 1: Landslide Inventory and Susceptibility and Hazard Zoning; Margottini, C., Canuti, P., Sassa, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 147–154. ISBN 978-3-642-31325-7. [Google Scholar]
- Bardi, F.; Raspini, F.; Ciampalini, A.; Kristensen, L.; Rouyet, L.; Lauknes, T.R.; Frauenfelder, R.; Casagli, N. Space-Borne and Ground-Based InSAR Data Integration: The Åknes Test Site. Remote Sens. 2016, 8, 237. [Google Scholar] [CrossRef] [Green Version]
- Mondini, A.C.; Guzzetti, F.; Chang, K.-T.; Monserrat, O.; Martha, T.R.; Manconi, A. Landslide Failures Detection and Mapping Using Synthetic Aperture Radar: Past, Present and Future. Earth Sci. Rev. 2021, 216, 103574. [Google Scholar] [CrossRef]
- Berardino, P.; Costantini, M.; Franceschetti, G.; Iodice, A.; Pietranera, L.; Rizzo, V. Use of Differential SAR Interferometry in Monitoring and Modelling Large Slope Instability at Maratea (Basilicata, Italy). Eng. Geol. 2003, 68, 31–51. [Google Scholar] [CrossRef]
- Hilley, G.E.; Bürgmann, R.; Ferretti, A.; Novali, F.; Rocca, F. Dynamics of Slow-Moving Landslides from Permanent Scatterer Analysis. Science 2004, 304, 1952–1955. [Google Scholar] [CrossRef] [Green Version]
- Tofani, V.; Raspini, F.; Catani, F.; Casagli, N. Persistent Scatterer Interferometry (PSI) Technique for Landslide Characterization and Monitoring. Remote Sens. 2013, 5, 1045–1065. [Google Scholar] [CrossRef] [Green Version]
- Komac, M.; Holley, R.; Mahapatra, P.; van der Marel, H.; Bavec, M. Coupling of GPS/GNSS and Radar Interferometric Data for a 3D Surface Displacement Monitoring of Landslides. Landslides 2015, 12, 241–257. [Google Scholar] [CrossRef]
- Carlà, T.; Raspini, F.; Intrieri, E.; Casagli, N. A Simple Method to Help Determine Landslide Susceptibility from Spaceborne InSAR Data: The Montescaglioso Case Study. Environ. Earth Sci. 2016, 75, 1492. [Google Scholar] [CrossRef] [Green Version]
- Lu, P.; Catani, F.; Tofani, V.; Casagli, N. Quantitative Hazard and Risk Assessment for Slow-Moving Landslides from Persistent Scatterer Interferometry. Landslides 2014, 11, 685–696. [Google Scholar] [CrossRef]
- Frodella, W.; Ciampalini, A.; Gigli, G.; Lombardi, L.; Raspini, F.; Nocentini, M.; Scardigli, C.; Casagli, N. Synergic Use of Satellite and Ground Based Remote Sensing Methods for Monitoring the San Leo Rock Cliff (Northern Italy). Geomorphology 2016, 264, 80–94. [Google Scholar] [CrossRef]
- Tomás, R.; Li, Z.; Lopez-Sanchez, J.M.; Liu, P.; Singleton, A. Using Wavelet Tools to Analyse Seasonal Variations from InSAR Time-Series Data: A Case Study of the Huangtupo Landslide. Landslides 2016, 13, 437–450. [Google Scholar] [CrossRef] [Green Version]
- Intrieri, E.; Gigli, G.; Casagli, N.; Nadim, F. Brief Communication “Landslide Early Warning System: Toolbox and General Concepts”. Nat. Hazards Earth Syst. Sci. 2013, 13, 85–90. [Google Scholar] [CrossRef] [Green Version]
- Gigli, G.; Intrieri, E.; Lombardi, L.; Nocentini, M.; Frodella, W.; Balducci, M.; Venanti, L.D.; Casagli, N. Event Scenario Analysis for the Design of Rockslide Countermeasures. J. Mt. Sci. 2014, 11, 1521–1530. [Google Scholar] [CrossRef]
- Raspini, F.; Bianchini, S.; Ciampalini, A.; Del Soldato, M.; Solari, L.; Novali, F.; Del Conte, S.; Rucci, A.; Ferretti, A.; Casagli, N. Continuous, Semi-Automatic Monitoring of Ground Deformation Using Sentinel-1 Satellites. Sci. Rep. 2018, 8, 7253. [Google Scholar] [CrossRef] [Green Version]
- Carlà, T.; Intrieri, E.; Raspini, F.; Bardi, F.; Farina, P.; Ferretti, A.; Colombo, D.; Novali, F.; Casagli, N. Perspectives on the Prediction of Catastrophic Slope Failures from Satellite InSAR. Sci. Rep. 2019, 9, 14137. [Google Scholar] [CrossRef] [Green Version]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping Small Elevation Changes over Large Areas: Differential Radar Interferometry. J. Geophys. Res. Space Phys. 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar Interferometry and Its Application to Changes in the Earth’s Surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef] [Green Version]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; ISBN 978-0-7923-6945-5. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Osmanoğlu, B.; Sunar, F.; Wdowinski, S.; Cabral-Cano, E. Time Series Analysis of InSAR Data: Methods and Trends. ISPRS J. Photogramm. Remote Sens. 2016, 115, 90–102. [Google Scholar] [CrossRef]
- Xue, F.; Lv, X.; Dou, F.; Yun, Y. A Review of Time-Series Interferometric SAR Techniques: A Tutorial for Surface Deformation Analysis. IEEE Geosci. Remote Sens. Mag. 2020, 8, 22–42. [Google Scholar] [CrossRef]
- Czuchlewski, K.R.; Weissel, J.K.; Kim, Y. Polarimetric Synthetic Aperture Radar Study of the Tsaoling Landslide Generated by the 1999 Chi-Chi Earthquake, Taiwan. J. Geophys. Res. Earth Surf. 2003, 108, 6006. [Google Scholar] [CrossRef]
- Yonezawa, C.; Watanabe, M.; Saito, G. Polarimetric Decomposition Analysis of ALOS PALSAR Observation Data before and after a Landslide Event. Remote Sens. 2012, 4, 2314–2328. [Google Scholar] [CrossRef] [Green Version]
- Li, N.; Wang, R.; Deng, Y.; Liu, Y.; Wang, C.; Balz, T.; Li, B. Polarimetric Response of Landslides at X-Band Following the Wenchuan Earthquake. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1722–1726. [Google Scholar] [CrossRef]
- Shibayama, T.; Yamaguchi, Y.; Yamada, H. Polarimetric Scattering Properties of Landslides in Forested Areas and the Dependence on the Local Incidence Angle. Remote Sens. 2015, 7, 15424–15442. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, M.; Thapa, R.B.; Shimada, M. Pi-SAR-L2 Observation of the Landslide Caused by Typhoon Wipha on Izu Oshima Island. Remote Sens. 2016, 8, 282. [Google Scholar] [CrossRef] [Green Version]
- Freeman, A.; Durden, S.L. A Three-Component Scattering Model for Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef] [Green Version]
- Cloude, S. Polarisation: Applications in Remote Sensing; OUP: Oxford, UK, 2009; ISBN 978-0-19-158038-3. [Google Scholar]
- Lee, J.-S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; Optical science and engineering; CRC Press: Boca Raton, FL, USA, 2009; ISBN 978-1-4200-5497-2. [Google Scholar]
- Zakharova, L.N.; Zakharov, A.I.; Zakharov, A.I. Interferometric Observation of Landslide Area Dynamics on the Bureya River by Means of Sentinel-1 Radar Data in 2017–2018. Sovr. Probl. DZZ Kosm. 2019, 16, 273–277. [Google Scholar] [CrossRef]
- Bondur, V.G.; Zakharova, L.N.; Zakharov, A.I. Monitoring the State of the Landslide Zone on the Bureya River in 2018–2019 with Radar and Optical Satellite Images. Izv. Atmos. Ocean. Phys. 2020, 56, 1520–1527. [Google Scholar] [CrossRef]
- Bondur, V.G.; Zakharova, L.N.; Zakharov, A.I.; Chimitdorzhiev, T.N.; Dmitriev, A.V.; Dagurov, P.N. Monitoring Landslide Processes by Means of L-Band Radar Interferometric Observations: Using the Example of the Bureya River Bank Caving. Izv. Atmos. Ocean. Phys. 2020, 56, 1053–1061. [Google Scholar] [CrossRef]
- Bondur, V.G.; Chimitdorzhiev, T.N.; Dmitriev, A.V.; Dagurov, P.N.; Zakharov, A.I.; Zakharova, L.N. Application of Radar Polarimetry to Monitor Changes in Backscattering Mechanisms in Landslide Zones Using the Example of the Collapse of the Bureya River Bank. Izv. Atmos. Ocean. Phys. 2020, 56, 11. [Google Scholar] [CrossRef]
- Mikhailov, V.O.; Kiseleva, E.A.; Smol’yaninova, E.I.; Dmitriev, P.N.; Golubev, V.I.; Isaev, Y.S.; Dorokhin, K.A.; Timoshkina, E.P.; Khairetdinov, S.A. Some Problems of Landslide Monitoring Using Satellite Radar Imagery with Different Wavelengths: Case Study of Two Landslides in the Region of Greater Sochi. Izv. Phys. Solid Earth 2014, 50, 576–587. [Google Scholar] [CrossRef]
- Zakharov, A.I.; Zakharova, L.N.; Krasnogorskii, M.G. Monitoring Landslide Activity by Radar Interferometry Using Trihedral Corner Reflectors. Izv. Atmos. Ocean. Phys. 2018, 54, 1110–1120. [Google Scholar] [CrossRef]
- Makhinov, A.N. Large tsunami-generated landslide in the Bureysky Reservoir. Geomorfologiya 2020, 3, 31–43. [Google Scholar] [CrossRef]
- Zerkal, O.V.; Makhinov, A.N.; Strom, A.; Kim, V.I.; Kharitonov, M.E.; Fomenko, I.K. Formation of the 2018 Bureya Landslide, Far East of Russia. In Understanding and Reducing Landslide Disaster Risk: Volume 5 Catastrophic Landslides and Frontiers of Landslide Science; Vilímek, V., Wang, F., Strom, A., Sassa, K., Bobrowsky, P.T., Takara, K., Eds.; ICL Contribution to Landslide Disaster Risk Reduction; Springer International Publishing: Cham, Switzerland, 2021; pp. 111–116. ISBN 978-3-030-60319-9. [Google Scholar]
- Ostroukhov, A.V.; Kim, V.I.; Makhinov, A.N.; Makhinov, A.N. Estimation of the Morphometric Parameters of the Landslide on the Bureyskoe Reservoir and Its Consequences on the Basis of Remote Sensing Data and Field Measurements. Sovr. Probl. DZZ Kosm. 2019, 16, 254–258. [Google Scholar] [CrossRef]
- Cruden, D.M.; Varnes, D.J. Landslide types and processes. In Landslides Investigation and Mitigation; Special Report 247; Transportation Research Board, US National Research Council: Washington, DC, USA, 1996; Chapter 3; pp. 36–75. [Google Scholar]
- Temme, A.; Guzzetti, F.; Samia, J.; Mirus, B.B. The Future of Landslides’ Past—a Framework for Assessing Consecutive Landsliding Systems. Landslides 2020, 17, 1519–1528. [Google Scholar] [CrossRef]
- RGS Expedition to the Bureysky Landslide. Available online: https://www.rgo.ru/ru/article/ekspediciya-rgo-k-bureyskomu-opolznyu (accessed on 2 November 2021).
- Expedition “Bureya” 2019. Available online: http://tsun.sscc.ru/hiwg/Bureya2019_photos_eng.htm (accessed on 2 November 2021).
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Enviorn. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Solari, L.; Del Soldato, M.; Raspini, F.; Barra, A.; Bianchini, S.; Confuorto, P.; Casagli, N.; Crosetto, M. Review of Satellite Interferometry for Landslide Detection in Italy. Remote Sens. 2020, 12, 1351. [Google Scholar] [CrossRef]
- Mantovani, M.; Bossi, G.; Marcato, G.; Schenato, L.; Tedesco, G.; Titti, G.; Pasuto, A. New Perspectives in Landslide Displacement Detection Using Sentinel-1 Datasets. Remote Sens. 2019, 11, 2135. [Google Scholar] [CrossRef] [Green Version]
- Liang, H.; Li, X.; Zhang, L.; Chen, R.-F.; Ding, X.; Chen, K.-L.; Wang, C.-S.; Chang, C.-S.; Chi, C.-Y. Investigation of Slow-Moving Artificial Slope Failure with Multi-Temporal InSAR by Combining Persistent and Distributed Scatterers: A Case Study in Northern Taiwan. Remote Sens. 2020, 12, 2403. [Google Scholar] [CrossRef]
- Reyes-Carmona, C.; Barra, A.; Galve, J.P.; Monserrat, O.; Pérez-Peña, J.V.; Mateos, R.M.; Notti, D.; Ruano, P.; Millares, A.; López-Vinielles, J.; et al. Sentinel-1 DInSAR for Monitoring Active Landslides in Critical Infrastructures: The Case of the Rules Reservoir (Southern Spain). Remote Sens. 2020, 12, 809. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Liu, D.; Dong, J.; Zhang, L.; Guo, J.; Liao, M.; Gong, J. On the Applicability of Satellite SAR Interferometry to Landslide Hazards Detection in Hilly Areas: A Case Study of Shuicheng, Guizhou in Southwest China. Landslides 2021, 18, 2609–2619. [Google Scholar] [CrossRef]
- Copernicus Open Access Hub. Available online: https://scihub.copernicus.eu/dhus/#/home (accessed on 2 November 2021).
- Cascini, L.; Fornaro, G.; Peduto, D. Advanced Low- and Full-Resolution DInSAR Map Generation for Slow-Moving Landslide Analysis at Different Scales. Eng. Geol. 2010, 112, 29–42. [Google Scholar] [CrossRef]
- Shuttle Radar Topography Mission (SRTM) 1 Arc-Second Global. 2017. Available online: https://www.usgs.gov/centers/eros/science/usgs-eros-archive-digital-elevation-shuttle-radar-topography-mission-srtm-1 (accessed on 2 November 2021).
- Ji, K.; Wu, Y. Scattering Mechanism Extraction by a Modified Cloude-Pottier Decomposition for Dual Polarization SAR. Remote Sens. 2015, 7, 7447–7470. [Google Scholar] [CrossRef] [Green Version]
- Dagurov, P.N.; Chimitdorzhiev, T.N.; Dmitriev, A.V.; Dobrynin, S.I. Estimation of Snow Water Equivalent from L-Band Radar Interferometry: Simulation and Experiment. Int. J. Remote Sens. 2020, 41, 9328–9359. [Google Scholar] [CrossRef]
- Mastro, P.; Serio, C.; Masiello, G.; Pepe, A. The Multiple Aperture SAR Interferometry (MAI) Technique for the Detection of Large Ground Displacement Dynamics: An Overview. Remote Sens. 2020, 12, 1189. [Google Scholar] [CrossRef] [Green Version]
- Herrera, G.; Gutiérrez, F.; García-Davalillo, J.C.; Guerrero, J.; Notti, D.; Galve, J.P.; Fernández-Merodo, J.A.; Cooksley, G. Multi-Sensor Advanced DInSAR Monitoring of Very Slow Landslides: The Tena Valley Case Study (Central Spanish Pyrenees). Remote Sens. Environ. 2013, 128, 31–43. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bondur, V.; Chimitdorzhiev, T.; Dmitriev, A.; Dagurov, P. Fusion of SAR Interferometry and Polarimetry Methods for Landslide Reactivation Study, the Bureya River (Russia) Event Case Study. Remote Sens. 2021, 13, 5136. https://doi.org/10.3390/rs13245136
Bondur V, Chimitdorzhiev T, Dmitriev A, Dagurov P. Fusion of SAR Interferometry and Polarimetry Methods for Landslide Reactivation Study, the Bureya River (Russia) Event Case Study. Remote Sensing. 2021; 13(24):5136. https://doi.org/10.3390/rs13245136
Chicago/Turabian StyleBondur, Valery, Tumen Chimitdorzhiev, Aleksey Dmitriev, and Pavel Dagurov. 2021. "Fusion of SAR Interferometry and Polarimetry Methods for Landslide Reactivation Study, the Bureya River (Russia) Event Case Study" Remote Sensing 13, no. 24: 5136. https://doi.org/10.3390/rs13245136
APA StyleBondur, V., Chimitdorzhiev, T., Dmitriev, A., & Dagurov, P. (2021). Fusion of SAR Interferometry and Polarimetry Methods for Landslide Reactivation Study, the Bureya River (Russia) Event Case Study. Remote Sensing, 13(24), 5136. https://doi.org/10.3390/rs13245136







