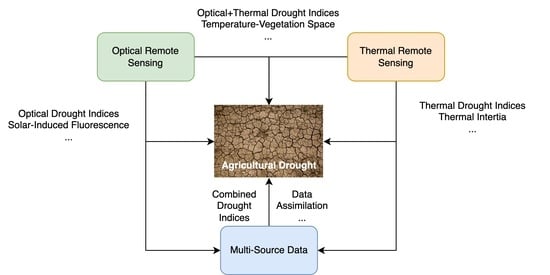
Optical and Thermal Remote Sensing for Monitoring Agricultural Drought

Abstract

By effectively observing the land surface and obtaining farmland conditions, satellite remote sensing has played an essential role in agricultural drought monitoring over past decades. Among all remote sensing techniques, optical and thermal remote sensing have the most extended history of being utilized in drought monitoring. The primary goal of this paper is to illustrate how optical and thermal remote sensing have been and will be applied in the monitoring, assessment, and prediction of agricultural drought. We group the methods into four categories: optical, thermal, optical and thermal, and multi-source. For each category, a concise explanation is given to show the inherent mechanisms. We pay special attention to solar-induced chlorophyll fluorescence, which has great potential in early drought detection. Finally, we look at the future directions of agricultural drought monitoring, including (1) early detection; (2) spatio-temporal resolution; (3) organic combination of multi-source data; and (4) smart prediction and assessment based on deep learning and cloud computing.

1. Introduction

Drought is a state in which the water supply does not meet the demand. As a natural hazard, it is considered to have the most remarkable impacts on human beings among all types of hazards [1,2]. Drought differs from other natural hazards in that it is an accumulating process or a “creeping phenomenon” as defined by Tannehill [3]. Although Tannehill’s book was written more than 70 years ago, the exact definition of drought has been a continuing controversy until now [1,4]. That notwithstanding, a four-category classification is widely recognized, namely, meteorological, agricultural, hydrological, and socioeconomic drought [5]. As the name suggests, agricultural drought is the result of a water deficit in farmland and is immediately related to insufficient soil moisture and consequent crop failure [6]. For this reason, agricultural drought is also called soil moisture drought [7,8].

Since the 1950s, with accelerated industrialization and urbanization, global warming has become undoubtedly prominent. The frequency and intensity of extreme climate events caused by global warming have increased significantly, as has the drought vulnerability in many regions all over the world [9,10]. As a sector most constrained by climate and weather [10], agriculture is greatly impacted by weather-induced disasters, especially drought. When a long-lasting drought is not handled properly, a food crisis usually follows closely, thus causing famine and mortality. Based on the Emergency Events Database (EM-DAT) (https://www.emdat.be, accessed on 20 August 2018), we have compiled the most severe drought events (considering total economic damage and human deaths) that happened after 1960 into Figure 1. We can see the great impact of drought on agriculture from the coincidence of drought events and major agricultural areas.

During the growth period, crop water use mainly involves transpiration and metabolic consumption. When agricultural drought occurs, the soil water deficit leads to reduced soil evaporation and capillary edge water. Crops become unable to take in enough water via their roots to keep their water balance. As a result, leaf transpiration decreases [11]. Since soil evaporation and crop transpiration are two main contributors to farmland evapotranspiration, the decline of both causes the total evapotranspiration to drop; consequently, both soil and canopy temperature rise, which aggravates the drought condition. When the drought is severe enough, crop leaves and stalks begin to show notable physiological or morphological changes, i.e., wilting, yellowing, and shedding [12]. If the drastic water shortage cannot be controlled or reverted, dehydration will start to collapse leaf and stem cells and ultimately cause plant deaths and yield loss [13].

Crop yield is the lifeline of not only farmers but also humankind. Farmers have been concerned about agricultural drought ever since early farming society. In the 20th century, Kincer [14] was among the first to assess agricultural drought using precipitation data collected by meteorological stations. The major problem is that drought occurrence at different growth stages has different effects on crop growth and the final grain yield [12]. Moreover, there are differences in drought vulnerability and tolerance even among crops within the same field block, depending on species and genotypes. Therefore, there is a high demand for temporal and spatial resolutions of agricultural drought monitoring [15], which cannot be satisfied by traditional meteorological stations or the re-analysis of data based on station observations, especially on large scales.

The rising of satellite remote sensing has provided a new solution to this issue. In past decades, remote sensing datasets on precipitation, snow, soil moisture, land surface temperature, evapotranspiration, vegetation, and land cover have become increasingly abundant with the development of satellite remote sensing [16,17], thereby creating a solid foundation for the timely and effective implementation of agricultural drought monitoring. According to the sensor type, remote sensing can be further divided into optical remote sensing, thermal remote sensing, microwave remote sensing (including active and passive), and other categories such as LiDAR or gravity remote sensing. They each offer unique and complementary information for drought detection.

1

Optical and thermal data are the most widely used in identifying vegetation conditions, soil water status, and evapotranspiration [17];

2

Microwave remote sensing has a direct and solid link to soil moisture, which is a crucial indicator of agricultural drought [18];

3

LiDAR is the best approach to obtaining structural information of vegetation, and it can also be used to retrieve various biochemical variables such as leaf water content [19];

4

Gravity measurement is essential for monitoring groundwater; thus, it can be utilized to monitor those regions where groundwater is massively used for irrigation, especially when drought occurs [20].

We will not cover all these aspects in this review; instead, we will focus on optical and thermal remote sensing, considering their data abundance, availability and applicability. It should be noted that microwave remote sensing, especially passive microwave remote sensing, is the most direct and reliable way to estimate soil moisture from space [18], and it has a significant advantage over optical and thermal remote sensing in that it is less affected by clouds and weather conditions [21,22]. However, there are several issues when microwave remote sensing is applied to agricultural drought monitoring: (1) the variability in penetration depth due to soil types, temperature and soil moisture makes it hard to compare the soil moisture estimations of microwave remote sensing with field measurements, especially in the case of drought monitoring [23]; (2) the effects of vegetation on microwave signals are not easy to handle [24,25,26,27], whereas cropland is the primary concern in the monitoring of agricultural drought; (3) the coarse spatial resolution of passive microwaves (active microwaves generally have much better spatial resolution than passive microwaves) cannot meet the requirements of agriculture. For further information about microwave remote sensing of soil moisture, one can refer to Karthikeyan et al. [28,29] for both algorithms and products, and Sabaghy et al. [15] for downscaling techniques used to enhance the spatial resolution of passive microwave-derived soil moisture. For the usage of gravity data in groundwater storage monitoring, one can turn to Frappart and Ramillien [20]. Moreover, for LiDAR, research articles such as Zhu et al. [19] can be a good reference.

Based on the understanding of existing reviews (e.g., [6,17,30,31]), as well as an extensive collection of the latest research results, this paper is aimed at reviewing and summarizing developments in optical and thermal remote sensing-based drought monitoring in the context of agriculture and food security. Section 2 discusses optical remote sensing, highlighting the promising utilization of solar-induced fluorescence as an early indicator, while Section 3 is about thermal remote sensing, and Section 4 is on the combination of optical and thermal remote sensing, with a detailed analysis of the temperature-vegetation space. Section 5 illustrates methods and techniques that utilize multi-source data or data assimilation. Finally, in Section 6, we discuss future development directions and give perspectives on the more effective monitoring of agricultural drought.

2. Optical Remote Sensing

2.1. The Effect of Water Content on Soil and Crop Reflectance in the Solar Region (400–2500 nm)

Optical sensors can measure the surface reflectance in visible (VIS), near-infrared (NIR), and short-wave infrared (SWIR) bands, within which solar radiation is the driving force. In this range, water has two major absorption peaks centered at 1470 nm and 1900 nm, and two minor ones centered at 970 nm and 1200 nm, while even smaller peaks and shoulders can be found at 514 nm, 606 nm, 739 nm and 836 nm [32,33,34]. These characteristics lay the foundation of soil moisture monitoring within the solar range. Many researchers observed that wetted natural soils showed lower reflectance [35]. This rule generally holds; however, we can see from Figure 2 that when soil moisture is high, the change in soil reflectance becomes subtler. There can even be an inversion at higher moisture levels, as pointed out by Patel [36] and Neema et al. [37]. That is to say, after the soil moisture exceeds a threshold, the reflectance of soil begins to increase with soil moisture. This critical point generally appears within the 0.15–0.40 $\mathrm{g}/{\mathrm{cm}}^3$ soil moisture range, which depends on soil types [38]. Since the critical point is below the saturation point, the reversion phenomenon cannot be neglected in soil moisture retrieval. Nevertheless, within the field of drought monitoring, we can safely assume that the soil moisture level is below this turning point. Thus, soil reflectance is considered to decrease monotonically with increasing soil moisture. The exact relationship between soil reflectance and soil moisture can be very complex and is affected by many other factors, such as mineralogy, salinity, texture, organic matter content, or roughness. Several empirical or physical models have been proposed [34,39,40,41,42], which we will not discuss in detail here.

Water content also affects the reflectance of crops, mainly in NIR and SWIR bands [43]. To identify the sensitive spectral bands of vegetation water content, Thomas et al. [44] obtained the spectra of leaves with different water content by gradually drying saturated leaves at room temperature. The results showed that the spectral reflectance of leaf samples increased with decreasing leaf water content, and the reflectance at 1450 and 1930 nm are significantly correlated with the relative water content of leaf blades. Sims and Gamon [45] pointed out that the reflectance at 950–970, 1150–1260, and 1520–1540 nm are well correlated with canopy water content. Here, simple simulations using the leaf radiative transfer model PROSPECT-D [46] and the canopy radiative transfer model 4SAIL [47] are carried out to illustrate the effects of water content on crop reflectance (see Figure 3 and Figure 4). It can be seen from the simulations that leaf water content has a remarkable impact on crop reflectance at both the leaf and canopy level, indicating that remotely sensed reflectance can be a measure of crop water content and water stress. However, sensitivity analysis shows that the other factors, such as leaf area index (LAI), average leaf angle (ALA), and leaf chlorophyll concentration, make it difficult to accurately retrieve leaf water content directly from reflectance data, especially at the canopy level [48].

Besides the direct influences on crop reflectance, the water content can also affect crop reflectance via its effects on crop physiology. The water needed for growth, development, and reproduction is mainly absorbed from the soil during crop growth. When soil moisture falls below a certain threshold and cannot meet the water demand, crop cells start to lose water, causing decreases in swelling pressure and changes in morphological structure and canopy cover (e.g., the leaf area). Water stress can also cause changes in biochemical (such as chlorophyll, carotenoids) concentrations, resulting in further changes in crop spectral reflectance [12].

2.2. Spectral Indices as Drought Indicators

Optical remote sensing is used to identify soil and vegetation water status based on the spectral reflectance of soil and vegetation in the VIS-NIR-SWIR regions. Due to the complicated relationship between soil moisture, crop water content, and remotely sensed reflectance, this representation is usually implemented by proxy of a spectral index, a mathematical formulation of two or more bands. In particular, spectral indices that reflect the growth of vegetation are called vegetation indices (VIs).

The simplest form is a ratio of two bands (e.g., the Moisture Stress Index (MSI) [49], the Simple Ratio Water Index (SRWI) [50]), or a linear mixture of several bands (e.g., the Visible and Shortwave Infrared Drought Index (VSDI) [51]). However, the most prominent form is without doubt [52] that of the Normalized Difference Vegetation Index (NDVI) proposed by Rouse et al. [53]. Through an equation as simple as

$$\mathrm{NDVI}=\frac{{\rho }_{\mathrm{NIR}}-{\rho }_{\mathrm{Red}}}{{\rho }_{\mathrm{NIR}}+{\rho }_{\mathrm{Red}}}$$

(1)

NDVI can effectively assess the status of vegetation, thus reflecting environmental changes [54], including water stress and drought [55,56]. Beyond its own use, in the following decades, forms of NDVI have been adopted by numerous spectral indices (e.g., the Normalized Difference Water Index (NDWI) [57], the Photochemical Reflectance Index (PRI) [58], the Normalized Difference Infrared Index (NDII) [59] and the Normalized Multiband Drought Index (NDMI) [60]).

Since NDVI is directly related to the fractional vegetation cover (FVC), a common practice is to measure the severity of water stress based on NDVI anomalies instead of NDVI itself. Based on historical data of NDVI, Kogan [61] established the vegetation condition index (VCI):

$$\mathrm{VCI}=\frac{100(\mathrm{NDVI}-{\mathrm{NDVI}}_{min})}{{\mathrm{NDVI}}_{max}-{\mathrm{NDVI}}_{min}}$$

(2)

where ${\mathrm{NDVI}}_{min}$ is the historical minimum NDVI value for a specific location, while ${\mathrm{NDVI}}_{max}$ is the historical maximum NDVI value for the same location. Since VCI is normalized by historical values, it allows one to compare the impact of drought in neighboring areas, even when they have different ecological and economic resources. Similarly, Chen et al. [62] defined the Anomaly Vegetation Index (AVI):

$$\mathrm{AVI}=\mathrm{NDVI}-\overline{\mathrm{NDVI}}$$

(3)

where $\overline{\mathrm{NDVI}}$ is the multi-year averaged NDVI value for a given location in a specific month, thus reflecting the average soil moisture. Based on the deviation from this average, AVI can indicate drought severity. Additionally, Peters et al. [63] proposed the Standardized Vegetation Index (SVI):

$$\begin{array}{cc}\hfill & z=\frac{\mathrm{NDVI}-\overline{\mathrm{NDVI}}}{\sigma }\hfill \\ \hfill & \mathrm{SVI}=\mathrm{P}(Z<z)\hfill \end{array}$$

(4)

Of all these methods, VCI is the most acknowledged and has been used to monitor or evaluate droughts in many countries and regions after being proposed [64,65,66,67].

Due to the saturation of NDVI in the case of dense vegetation and its sensitivity to the soil background, a series of new vegetation indices have been proposed, such as the Soil Adjusted VI (SAVI) [68], the Atmospherically Resistant VI (ARVI) [69], the Enhanced VI (EVI) [70,71], and the Inverted Difference VI (IDVI) [72], but none of these indices have taken the place of NDVI in agricultural drought monitoring.

An alternative way to combine the information from multiple bands is the reflectance space, i.e., building a linear space with the spectral reflectance of each band. Figure 5 gives a sketch of the NIR-Red reflectance space. When enough vegetation and soil pixels are gathered in the plot, the outline of the points corresponding to the pixels will form a triangle. The points of bare soil pixels tend to form a line in this plot called the soil line. Based on the NIR-Red reflectance space, Richardson and Wiegand [73] first established the Perpendicular Vegetation Index (PVI), which is the vertical distance from an observed point to the soil line. Zhan et al. [74] further found that the two-dimensional NIR–Red space is related to the characteristics of land cover and soil/vegetation water: the lower-left edge of the triangle represents the water-saturated status and the upper-right edge represents the extremely dry status, while the parallel lines of the soil line correspond to different vegetation covers. Based on this finding, Ghulam et al. [75] proposed the Perpendicular Drought Index (PDI):

$$\mathrm{PDI}={\displaystyle \frac{1}{\sqrt{M^2+1}}}({\rho }_{\mathrm{Red}}+M{\rho }_{\mathrm{NIR}})$$

(5)

where M is the slope of the soil line. As is shown in Figure 5, PDI is the vertical distance from an observed point to the perpendicular line of the soil line which crosses the origin. PDI proves to be highly effective in soil moisture estimation over bare soil. To compensate for the effect of vegetation cover, Ghulam et al. [76] further introduced the concept of vegetation coverage and proposed the Modified PDI (MPDI) to resolve this limitation:

$$\mathrm{MPDI}={\displaystyle \frac{1}{1-\mathrm{FVC}}}(\mathrm{PDI}-\mathrm{FVC}·{\mathrm{PDI}}_{\mathrm{v}})$$

(6)

where $\mathrm{FVC}$ is the fractional vegetation cover, and ${\mathrm{PDI}}_{\mathrm{v}}$ is the PDI value for fully covered vegetation, which is often taken as an empirical value. In this way, mixed pixels in the NIR-Red space are decomposed to obtain pure soil information. The MPDI can be applied to various land cover types and hydrothermal conditions and has a clear biophysical meaning. Moreover, it does not require complex calculations and can be easily interpreted. Rao et al. [77] analyzed Landsat-derived MPDI and long-term Climatic Water Deficit (CWD) data for the year 2014 to evaluate the impacts of the 2014 California drought on forest and agriculture ecosystems in California, U.S. The results demonstrated that MPDI is an effective and direct method to monitor vegetation stress and forest declines at the landscape scale and provide land managers and stakeholders with forest management and planning guidance. To avoid the determination of ${\mathrm{PDI}}_{\mathrm{v}}$, Li and Tan [78] proposed the second Modified Perpendicular Drought Index (MPDI1):

$$\mathrm{MPDI}1=\sqrt{{\mathrm{PDI}}^2+{\mathrm{PVI}}^2}$$

(7)

which equals segment DF in Figure 5. Zhang et al. [79] proposed the Ratio Dryness Monitoring Index (RDMI), which is defined as the ratio of the segment PE to the segment PQ in Figure 5. These two new indices can be directly obtained from the NIR-Red reflectance space, but more evaluations are required to compare their feasibilities with MPDI.

Attempts have also been made to develop indices that utilize SWIR bands, which are more sensitive to water content [80,81]. Gao [57] established the Normalized Difference Water Index (NDWI) based on a NIR band (860 nm) and a SWIR band (1240 nm). The NDWI can sensitively reflect canopy water levels because water absorption is enhanced by canopy decentralization. The influence of the atmosphere on NDWI is weaker than on NDVI because there is less atmospheric aerosol scattering within 860–1240 nm. Similar to NDVI, NDWI also fails to remove the effect of the soil background completely. To reduce this effect, Zhang et al. [51] proposed the Visible and Shortwave infrared Drought Index (VSDI), which made use of the Blue, Red, and SWIR bands to monitor agricultural drought over different land-cover types during plant growing seasons.

Since the NIR-SWIR reflectance space has similar features to the NIR-Red space, Ghulam et al. [82] analyzed the potential of the NIR-SWIR space in drought monitoring. The established Shortwave infrared Perpendicular Water Stress Index (SPSI) has the same form of PDI, but unlike PDI, SPSI fits well in various vegetation conditions, from bare soil to full coverage. Ghulam et al. [83] further developed the Vegetation Water Stress Index (VWSI) to quantify the vegetation water stress at the canopy level. The relationship between the VWSI and fuel moisture content was examined through leaf- (i.e., PROSPECT [46,84,85]) and canopy-level radiative transfer simulations [47,86] incorporating field measurements. Based on the fuel moisture content under different water stress conditions and corresponding VWSI values, the authors established threshold values for VWSI to help precision irrigation. Several follow-up studies have utilized the NIR-SWIR space for estimating vegetation water stress, aboveground dry biomass, and yield [87] and understanding drought impacts on forest ecosystems [88]. Later, Feng et al. [89] proposed the Modified Shortwave Infrared Perpendicular Water Stress Index (MSPSI), which keeps the form of SPSI but uses the $R_{\mathrm{s}}$-$R_{\mathrm{d}}$ ($R_{\mathrm{s}}={\rho }_{\mathrm{SWIR}}+{\rho }_{\mathrm{Red}}$; $R_{\mathrm{d}}={\rho }_{\mathrm{SWIR}}-{\rho }_{\mathrm{Red}}$) space instead.

When hyperspectral data are available, the Photochemical Reflectance Index (PRI) should not be neglected. PRI is often used as an early indicator of plant health [90,91,92,93]. It can reflect the epoxidation state of the xanthophyll cycle pigments and photosynthetic efficiency [58], thus providing scale-invariant signatures of early water stress for various vegetation types [94]. PRI is usually calculated using 531 nm and 570 nm as the reference bands [58]:

$$\mathrm{PRI}=\frac{{\rho }_{531}-{\rho }_{570}}{{\rho }_{531}+{\rho }_{570}}$$

(8)

However, there are a number of candidates, e.g., 512 nm [95], 515 nm [90], 519 nm [96] and 586 nm [91].

The aforementioned spectral indices are elementary to calculate and use. Compared with traditional long-time drought indices, the indices and their anomalies can be a near-real-time indicator of the onset, extent, intensity, and duration of agricultural water stress and droughts. However, it should be noted that it is hard to exclude the effects of other environmental stress and adversities, e.g., diseases and pests [63], since the indices are merely mathematical results and do not have a definite physical or biophysical meaning. Another caveat is that their relationships with soil moisture or crop water content are often restricted to a particular area and cannot be represented by a unified formula. Therefore, these indices are only capable of rough estimations of drought conditions, while their model parameters must be recalibrated when applied in regions with different soil and crop types or different climatic characteristics.

For the convenience of our readers,

Table 1. Summary of spectral indices suitable for agricultural drought monitoring.

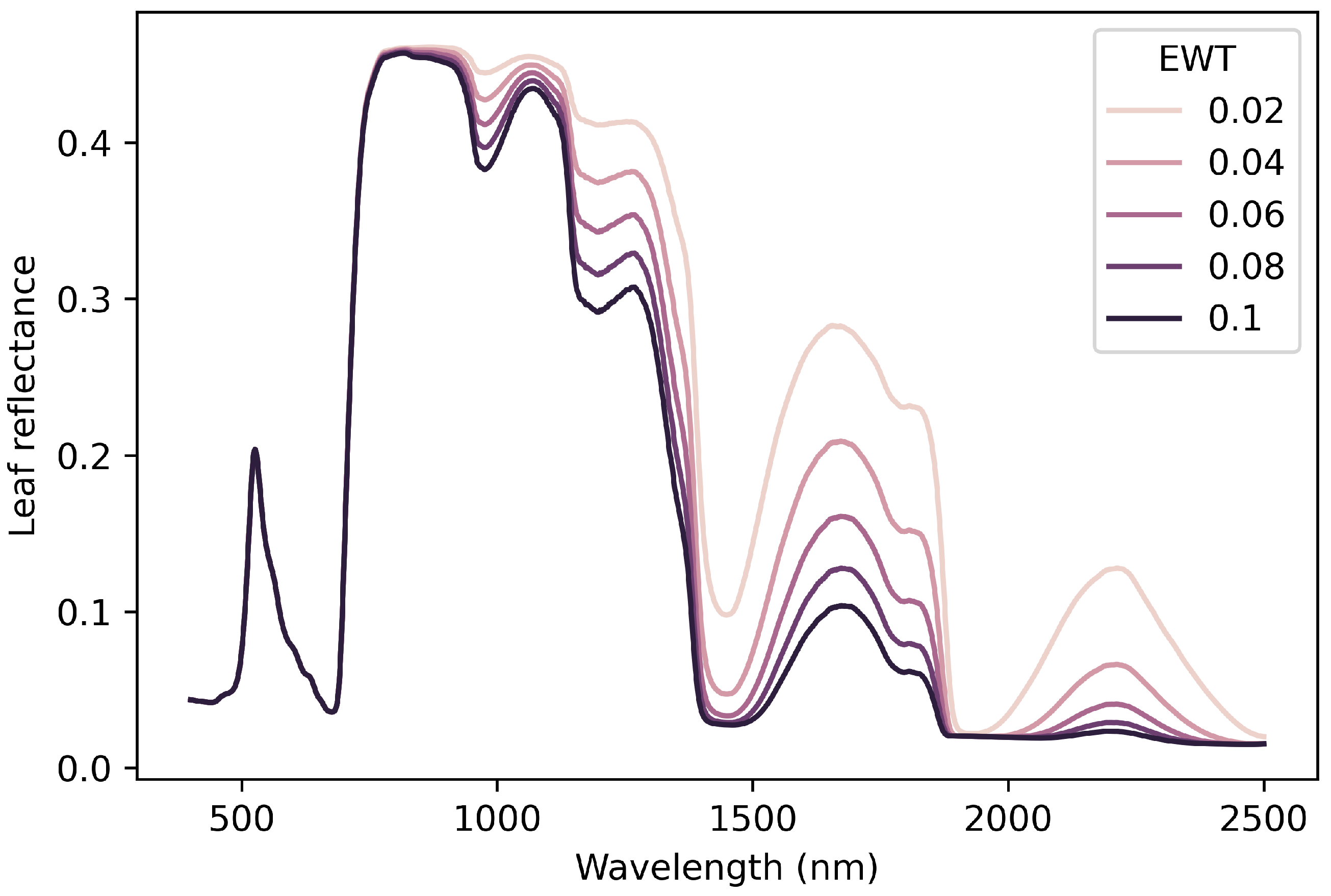
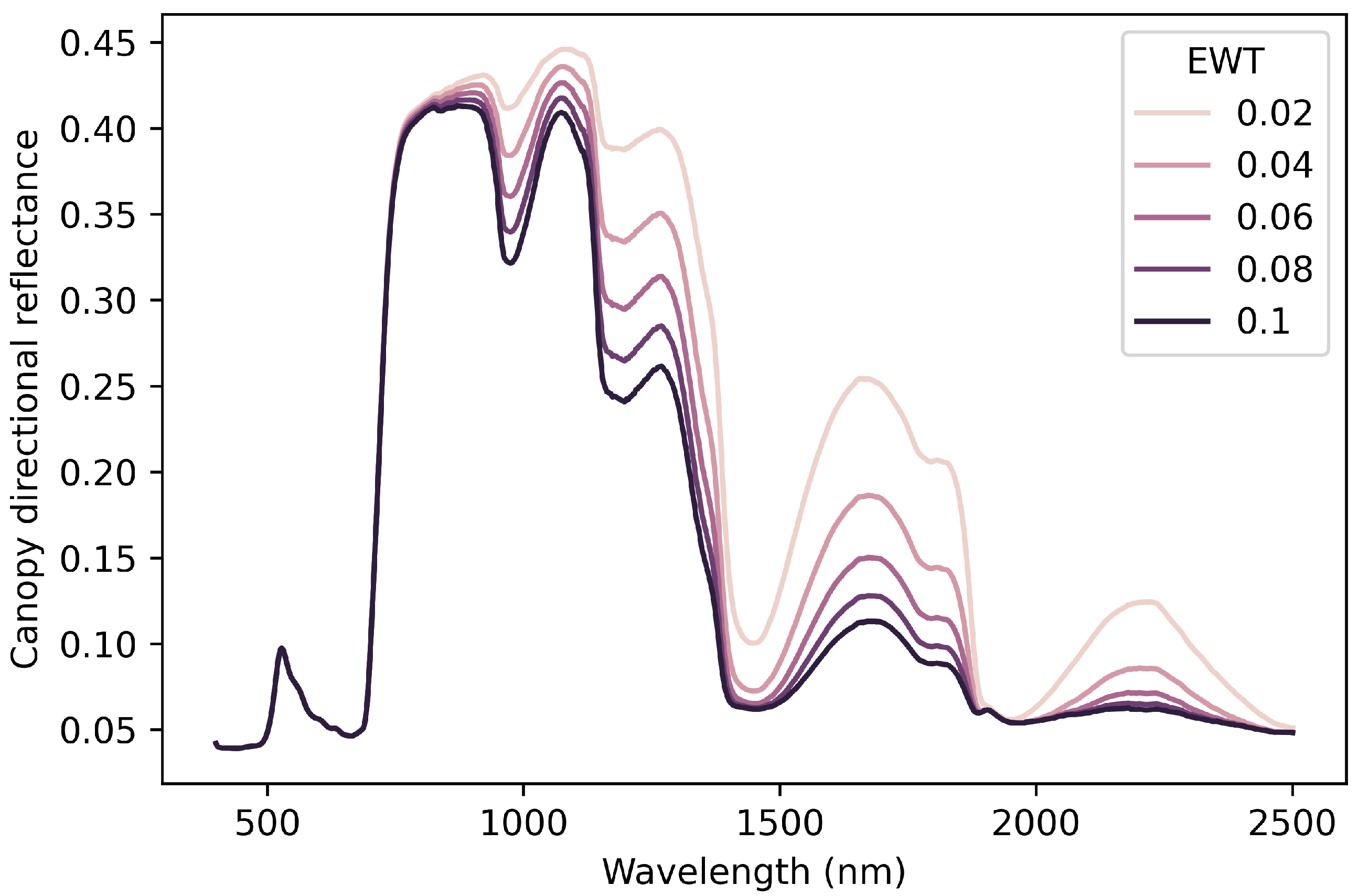
Index	Expression	Notes	Year Introduced	Applications
Normalized Difference Vegetation Index (NDVI)	${\displaystyle \frac{{\rho }_{\mathrm{NIR}}-{\rho }_{\mathrm{Red}}}{{\rho }_{\mathrm{NIR}}+{\rho }_{\mathrm{Red}}}}$		1974 [53]	U.S. [97], Poland [98]
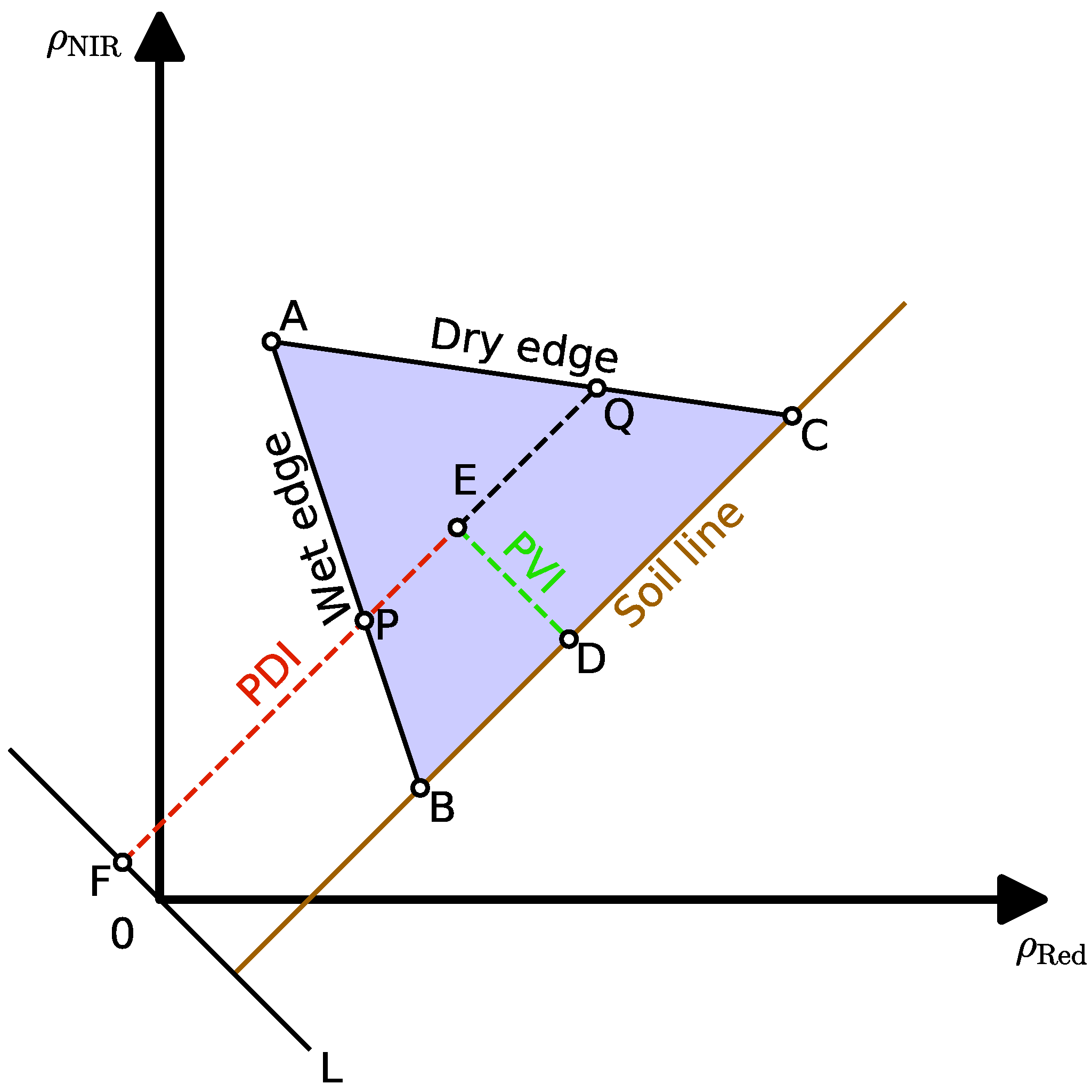
Perpendicular Vegetation Index (PVI)	${\displaystyle \frac{1}{\sqrt{M^2+1}}}({\rho }_{\mathrm{NIR}}-M{\rho }_{\mathrm{Red}}-I)$	M and I are the slope and interception of the soil line in the NIR-Red reflectance space	1977 [73]
Soil Adjusted Vegetation Index (SAVI)	$(1+L){\displaystyle \frac{{\rho }_{\mathrm{NIR}}-{\rho }_{\mathrm{Red}}}{{\rho }_{\mathrm{NIR}}+{\rho }_{\mathrm{Red}}+L}}$	L is an empirical coefficient	1988 [68]	Kenya [99]
Moisture Stress Index (MSI)	${\displaystyle \frac{{\rho }_{1600}}{{\rho }_{820}}}$		1989 [49]	Morocco [100], India [101]
Vegetation Condition Index (VCI)	${\displaystyle \frac{100(\mathrm{NDVI}-{\mathrm{NDVI}}_{min})}{{\mathrm{NDVI}}_{max}-{\mathrm{NDVI}}_{min}}}$	${\mathrm{NDVI}}_{min}$ is the historical minimum NDVI value for a specific location, while ${\mathrm{NDVI}}_{max}$ is the historical maximum NDVI value for the same location	1990 [61]	U.S. [65,102], China [64,66,67], South Korea [103]
Atmospherically Resistant Vegetation Index (ARVI)	${\displaystyle \frac{{\rho }_{\mathrm{NIR}}-(1+\gamma ){\rho }_{\mathrm{Red}}+\gamma {\rho }_{\mathrm{Blue}}}{{\rho }_{\mathrm{NIR}}+(1+\gamma ){\rho }_{\mathrm{Red}}-\gamma {\rho }_{\mathrm{Blue}}}}$	$\gamma$ is an empirical coefficient	1992 [69]	Poland [98]
Anomaly Vegetation Index (AVI)	$\mathrm{NDVI}-\overline{\mathrm{NDVI}}$	$\overline{\mathrm{NDVI}}$ is the multi-year average of NDVI for a given location in a specific month	1994 [62]	China [104]
Enhanced Vegetation Index (EVI)	$G{\displaystyle \frac{{\rho }_{\mathrm{NIR}}-{\rho }_{\mathrm{Red}}}{{\rho }_{\mathrm{NIR}}+C_1{\rho }_{\mathrm{Red}}-C_2{\rho }_{\mathrm{Blue}}+L}}$	G, $C_1$, $C_2$ and L are empirical coeifficents	1995 [70]	East Asia [105]
Normalized Difference Water Index (NDWI)	${\displaystyle \frac{{\rho }_{860}-{\rho }_{1240}}{{\rho }_{860}+{\rho }_{1240}}}$		1996 [57]	India [106], Morocco [100]
Photochemical Reflectance Index (PRI)	${\displaystyle \frac{{\rho }_{531}-{\rho }_{570}}{{\rho }_{531}+{\rho }_{570}}}$	There are other wavelength selections	1997 [58]	Bolivia [107], Spain [108], China [109,110]
Simple Ratio Water Index (SRWI)	${\displaystyle \frac{{\rho }_{860}}{{\rho }_{1240}}}$		2001 [50]	Brazil [111]
Standardized Vegetation Index (SVI)	$\begin{array}{cc}& z={\displaystyle \frac{\mathrm{NDVI}-\overline{\mathrm{NDVI}}}{\sigma }}\hfill \\ & \mathrm{SVI}=\mathrm{P}(Z<z)\hfill \end{array}$	$\sigma$ is the standard deviation of multi-year NDVI for a given location at a specific time of year.	2002 [63]	U.S. [63], South Korea [103]
Shortwave Infrared Water Stress Index (SIWSI), also known as the Normalized Difference Infrared Index (NDII)	$\begin{array}{c}\hfill {\displaystyle \frac{{\rho }_{\mathrm{SWIR}}-{\rho }_{\mathrm{NIR}}}{{\rho }_{\mathrm{SWIR}}+{\rho }_{\mathrm{NIR}}}}\end{array}$	The SWIR band can be MODIS band 5 or 6	2003 [59]	China [112]
Normalized Multiband Drought Index (NMDI)	${\displaystyle \frac{{\rho }_{860}-({\rho }_{1640}-{\rho }_{2130})}{{\rho }_{860}+({\rho }_{1640}-{\rho }_{2130})}}$		2007 [60]	Jordan [113]
Perpendicular Drought Index (PDI)	${\displaystyle \frac{1}{\sqrt{M^2+1}}}({\rho }_{\mathrm{Red}}+M{\rho }_{\mathrm{NIR}})$	M is the slope of the soil line in the NIR-Red reflectance space	2007 [75]	Iran [114,115], China [116]
Modified Perpendicular Drought Index (MPDI)	${\displaystyle \frac{1}{1-\mathrm{FVC}}}(\mathrm{PDI}-\mathrm{FVC}·{\mathrm{PDI}}_{\mathrm{v}})$	FVC is the fractional vegetation cover, and ${\mathrm{PDI}}_{\mathrm{v}}$ is the PDI value calculated for fully covered vegetation.	2007 [76]	Iran [114,115], China [116,117]
Shortwave Infrared Perpendicular Water Stress Index (SPSI)	${\displaystyle \frac{1}{\sqrt{M^2+1}}}({\rho }_{\mathrm{SWIR}}+M{\rho }_{\mathrm{NIR}})$	M is the slope of the soil line in the NIR-SWIR reflectance space	2007 [82]	China [112]
Two-band Enhanced Vegetation Index (EVI2)	$G{\displaystyle \frac{{\rho }_{\mathrm{NIR}}-{\rho }_{\mathrm{Red}}}{{\rho }_{\mathrm{NIR}}+C{\rho }_{\mathrm{Red}}+1}}$	G and C are empirical coefficients	2008 [71]	China [118]
Vegetation Water Stress Index (VWSI)	${\displaystyle \frac{\mathrm{EG}}{\mathrm{EF}}}$	G is the point of the pixel in the NIR-SWIR space, and EF is the parallel line of the base soil line that crosses G, which intersects the wet edge at E and the dry edge at F (see Figure 4 in [83]).	2008 [83]	India [119]
Visible and Shortwave Infrared Drought Index (VSDI)	$1-({\rho }_{\mathrm{SWIR}}+{\rho }_{\mathrm{Red}}-2{\rho }_{\mathrm{Blue}})$		2013 [51]	Jordan [113], Iraq [120], China [104]
Modified Shortwave Infrared Perpendicular Water Stress Index (MSPSI)	${\displaystyle \frac{1}{\sqrt{M^2+1}}}(R_{\mathrm{s}}+M{R}_{\mathrm{d}})$	$R_{\mathrm{s}}={\rho }_{\mathrm{SWIR}}+{\rho }_{\mathrm{Red}}$; $R_{\mathrm{d}}={\rho }_{\mathrm{SWIR}}-{\rho }_{\mathrm{Red}}$; M is the slope of the soil line in the $R_{\mathrm{s}}$-$R_{\mathrm{d}}$ space	2013 [89]	China [89]
Second Modified Perpendicular Drought Index (MPDI1)	$\sqrt{{\mathrm{PDI}}^2+{\mathrm{PVI}}^2}$		2013 [78]	China [78]
Inverted Difference Vegetation Index (IDVI)	${\displaystyle \frac{1+({\rho }_{\mathrm{NIR}}-{\rho }_{\mathrm{Red}})}{1-({\rho }_{\mathrm{NIR}}-{\rho }_{\mathrm{Red}})}}$		2018 [72]
Ratio Dryness Monitoring Index (RDMI)	${\displaystyle \frac{\mathrm{DP}}{\mathrm{DE}}}$	P is the point of the pixel in the NIR-Red space, and DE is the parallel line of the base soil line that crosses P, which intersects the wet edge at D and the dry edge at E (see Figure 8 in [79]).	2019 [79]	China [79]

gives an overview of the indices mentioned above, along with references for typical applications of these indices in agricultural drought monitoring.

2.3. Solar-Induced Chlorophyll Fluorescence as an Early Drought Indicator

An obvious shortcoming of spectral indices is that they lack explicit physical meanings. To deal with this, several vegetation physiological or biochemical parameters (which can be estimated via optical remote sensing) have been considered as drought indicators, e.g., the Leaf Area Index (LAI) [121], the Fraction of Absorbed Photosynthetically Active Radiation (FAPAR) [122,123,124,125], and the leaf chlorophyll concentration [126]. However, most of these parameters still cannot overcome the problem of time latency. When precipitation shortages and soil moisture deficits take place, they show no significant change within a temporal range of ten days to two months [127,128,129,130] because they are reflections of accumulated vegetation growth rather than instant indicators.

Solar-induced chlorophyll fluorescence (SIF) is a stimulated emission which occurs after the chlorophyll absorbs light [131]. The spectral emission spans approximately 650–800 nm, normally having two local maxima—one located in the red region around 685–690 nm (called ${\mathrm{F}}_{685}$), and the other located in the far-red region around 730–740 nm (called ${\mathrm{F}}_{740}$) [132]. A conceptual illustration of the distribution of absorbed radiation in plant leaves is given as Figure 6. There are four possible fates for an absorbed exciton: (i) it can be consumed during photochemical reactions via Photosystem I (PSI) or Photosystem II (PSII); (ii) it can undergo radiationless decay without emitting electromagnetic energy; (iii) it can be quenched by a non-photochemical trapping center, in which case the process is called non-photochemical quenching (NPQ); and (iv) it can be re-emitted as a fluorescence emission [132,133].

A detailed introduction to the physiological and biochemical processes related to the emission of SIF can be referred to in Jonard et al. [134]. SIF has a notable potential in agricultural drought monitoring, and is beneficial for drought early warning due to its response to early water stress, which can be a precursor to impending agricultural drought, large scale vegetation dieback and community shifts. At the early stage, crop water stress is not readily apparent, causing a failure to recognize impending vegetation dieback before the process has advanced beyond recovery. In contrast, early stress can be reflected via SIF since SIF is an immediate signal of plant photosynthetic status [132,135,136,137]. Studies based on leaf- and canopy-level experiments have demonstrated the possibility of using SIF to track diurnal changes caused by heat and water stress [138,139].

To calculate solar-induced chlorophyll fluorescence, the Fraunhofer Line Depthmethod [131], leaf and canopy fluorescence simulations using Fluorescence Model (FluorMOD) [140] and Soil-Canopy Observation Photosynthesis and Energy fluxes (SCOPE) are used [141]. The amount of chlorophyll fluorescence emitted by a leaf under natural sunlight only makes up to 1–3% of the absorbed light in the visible part of the spectrum, making it hard to quantify [131]. At Fraunhofer lines, however, fluorescence can be quantified because there is no reflected light at those wavelengths. In recent decades, several space missions have been utilized for global SIF measurements, and a space mission targeted at SIF, the FLuorescence EXplorer (FLEX), is planned to be launched in 2024, which will offer a much higher spatial resolution. A summary of related missions can be seen in

Table 2. Summary of satellite missions capable of solar-induced chlorophyll fluorescence measurements.

Mission	Sensor	Time Range	References
Greenhouse gases Observing SATellite (GOSAT)	Thermal And Near-infrared Sensor for carbon Observation Fourier Transform Spectrometer (TANSO-FTS)	2009–Now	[142,143]
GOSAT-2	TANSO-FTS/2	2018–Now	[144]
Meteorological Operational satellite (MetOp)	Global Ozone Monitoring Experiment-2 (GOME-2)	2006–Now (MetOp-A); 2012–Now (MetOp-B); 2018–Now (MetOp-C)	[145,146,147]
Environmental Satellite (EnviSat)	SCanning Imaging Absorption spectroMeter for Atmospheric CHartographY (SCIAMACHY)	2002–2012	[146,147]
	MEdium Resolution Imaging Spectrometer (MERIS)
Orbiting Carbon Observatory (OCO-2)	Orbiting Carbon Observatory (OCO)	2014–Now	[148]
Sentinel-5 Precursor (S-5P)	TROPOspheric Monitoring Instrument (TROPOMI)	2017–Now	[149]
Carbon Dioxide Observation Satellite (TanSat)	Atmospheric Carbon dioxide Grating Spectrometer (ACGS)	2016–Now	[150,151,152]
FLuorescence EXplorer (FLEX)	FLuORescence Imaging Spectrometer (FLORIS)	2024 (Planned)	[153,154]

.

3. Thermal Remote Sensing

3.1. Thermal Properties of Crops and Soil

Thermal infrared sensors mainly receive the thermal radiation emitted by the Earth itself, and its amplitude is related to the land surface temperature (LST) and land surface emissivity (LSE):

$$L(\lambda ,T)={\int }_{{\lambda }_1}^{{\lambda }_2}{\epsilon }_{\mathrm{s}}\left(\lambda \right)\mu (\lambda ,T)h\left(\lambda \right)\mathrm{d}\lambda$$

(9)

where T is the LST, $\lambda$ is the wavelength, $L(\lambda ,T)$ is the spectral radiance received by a thermal sensor, ${\epsilon }_{\mathrm{s}}\left(\lambda \right)$ is the LSE, which is a function of $\lambda$, $\mu (\lambda ,T)$ is the Planck function, and $h\left(\lambda \right)$ represents the spectral response function. The integral of $\mathrm{d}\lambda$ is done within the sensitive range $[{\lambda }_1,{\lambda }_2]$ of the sensor. Thus, parameters, such as surface temperature and surface emissivity, can be retrieved after radiation calibration and atmospheric correction of the thermal radiation signal received by the spaceborne thermal infrared sensor. It should be noted that LST is a skin temperature, reflecting the temperature of the top 1–2 mm of the soil for bare surfaces [155,156].

Under severe water stress, the evaporation of soil remarkably declines [157]. Meanwhile, the decrease of the stomatal conductance of crop leaves leads to the inhibition of transpiration [158,159]. The decline of evapotranspiration thus contributes to the rise in the observed LST. Moreover, the difference between the leaf/canopy temperature and the air temperature also increases [160].

LSE is also affected by soil moisture. Experiments [161,162] show that the LSE of soil can increase up to 16–17% after wetting; the change varies for different soil types. Mira et al. [163] further shows that it is possible to retrieve soil moisture from LSE with a standard estimation error of about $\pm 0.08{\mathrm{m}}^3·{\mathrm{m}}^{-3}$, but this method depends on known organic matter content and thus is not feasible for remote sensing use.

Another important thermal property of the land surface is the thermal inertia, which is defined as follows:

$$P=\sqrt{K\rho c_{\mathrm{p}}}$$

(10)

where P is the thermal inertia, K is the thermal conductivity, $\rho$ is the density, and $c_{\mathrm{p}}$ is the specific heat at a constant pressure [164,165]. Because K, $\rho$ and $c_{\mathrm{p}}$ all increase with increasing soil moisture [166], soil with higher moisture content has higher thermal inertia and a smaller diurnal temperature difference, and vice versa. In contrast to LST, thermal inertia is a bulk property and can reflect the change of root-zone soil moisture [165].

3.2. Thermal Inertia as a Drought Indicator

Watson [167] constructed a simple forward model to simulate the temperature of terrestrial objects. In this model, the attributes of terrestrial objects (thermal inertia, albedo, and emissivity), meteorological factors (transmission, effective air temperature), location (latitude), and season (solar declination) are set as input parameters. Subsequently, Pohn et al. [164] proposed an empirical formula based on simulated data to invert the thermal inertia of terrestrial objects based on albedo and diurnal temperature difference. It was found that inversion results are closely related to soil density and interstitial water content and have considerable potential for application in near-surface moisture monitoring. Price [168] constructed a thermal inertia inversion model using thermal infrared observations from the Synchronous Meteorological Satellite-2 (SMS-2). This model is more universal than the empirical formula developed by Pohn et al. [164]. Price [169] further developed the theoretical model of Price [168] and successfully applied it to data of the Heat Capacity Mapping Mission (HCMM). By analyzing the relationship of the inversion results with the soil moisture and the evaporation rate, it was revealed that the 24-h mean surface temperature is sensitive to the mean evaporation rate, whereas the diurnal temperature difference is sensitive to the near-surface soil moisture. This finding indicates that space-borne thermal infrared data has potential applications in assessing the surface water budget.

Nevertheless, most thermal inertia inversion models require meteorological parameters as inputs, which are difficult to acquire through remote sensing [170]. This requirement complicates thermal inertia inversion but can be addressed by apparent thermal inertia (ATI), a simpler alternative to thermal inertia, defined as

$$\mathrm{ATI}=\frac{C(1-\alpha )}{T_{\mathrm{day}}-T_{\mathrm{night}}}$$

(11)

where C is a constant coefficient, $\alpha$ is the surface albedo, and $T_{\mathrm{day}}$ and $T_{\mathrm{night}}$ are day/night LST [171].

ATI products have been used to characterize the diurnal temperature change of the land surface. The algorithmic method of ATI is simpler than that of thermal inertia because it does not require input parameters that satellites are unable to offer. Watson [172] and Kahle and Alley [173] initially verified the feasibility of ATI products for soil moisture monitoring, and many researchers have followed their footsteps [165,174,175,176]. However, the ATI method assumes that the effect of soil evaporation on temperature changes is negligible. This assumption is invalid in areas experiencing considerable soil evaporation [171].

The thermal inertia and ATI methods are mainly applied to soil moisture inversion under bare soil or sparse vegetation conditions [168,177]. Therefore, the thermal inertia and ATI need to be modified under dense vegetation conditions [170,178,179].

3.3. Temperature-Based Drought Indices

To retrieve parameters such as thermal inertia or ATI, diurnal surface temperature changes have to be determined. However, many widely used thermal sensors do not provide nighttime data products, e.g., Landsat-8 [180], limiting the application of thermal inertia to sensors that offer day-night observations, e.g., MODIS [181].

To monitor drought severity from a single thermal observation, additional information is needed. Kogan [102] used the maximum and minimum changes in surface temperature to monitor agricultural drought and constructed the TCI by using a long time-series of daytime LST:

$$\mathrm{TCI}=100\frac{T_{max}-T}{T_{max}-T_{min}}$$

(12)

where T is the smoothed weekly temperature, and $T_{max}$ and $T_{min}$ are the multi-year maximum and minimum. Originally, the brightness temperature is used as T forsimplicity [102,182], while LST is used instead in the most recent literature to exclude the influence of the atmosphere [183,184,185]. Similar to VCI, TCI weakens the impact of the uncertainty of the relationship between drought and LST on drought assessment by integrating historical data as a reference [186]. The advantage of TCI is that its calculation is simple and requires lower temporal resolution than thermal inertia or ATI. Nevertheless, the calculation of TCI requires accumulating a long time series of surface temperature data that must include extremely dry and wet conditions to ensure representativeness. In addition, seasonal variation in surface temperature influences TCI. In different seasons, the same drought conditions can lead to different TCI values, which adds to the uncertainty of TCI [187].

McVicar et al. [188] and Jupp et al. [189] constructed the Normalized Difference Temperature Index (NDTI) by applying daytime surface temperatures obtained from the Advanced Very High Resolution Radiometer (AVHRR) to eliminate the influence of seasonal changes. The NDTI is defined as:

$$\mathrm{NDTI}=\frac{T_{\infty }-T_{\mathrm{s}}}{T_{\infty }-T_0}$$

(13)

where $T_{\infty }$ is the LST when the composite surface resistance $r_{\mathrm{s}}$ is infinity and the evapotranspiration (ET) is zero, $T_{\mathrm{s}}$ is actual LST, $T_0$ is the LST when $r_{\mathrm{s}}$ is zero and the ET is equal to the potential ET. The actual LST can be obtained through thermal remote sensing, and the LST under boundary conditions can be obtained by inverting a resistance energy balance model (REBM) [190]. In contrast to TCI, NDTI does not need a long time series: only a single observation phase is required for calculation. NDTI does not suffer from seasonal changes and is a close approximation to soil moisture availability. Given the latter characteristic, NDTI can be used as an easily calculable surrogate for moisture availability in drought monitoring [187]. The simulation of LST under boundary conditions, however, relies on high-resolution meteorological parameters. Thus, the application of the NDTI is limited because meteorological data associated with satellite observation times are often difficult to obtain.

When the temporal resolution of surface temperature data is no longer an issue, as in the case of geostationary satellites, Hu et al. [191] proposed a new index called the Temperature Rise Index (TRI), defined as:

$$\mathrm{TRI}=\frac{{(\mathrm{d}T/\mathrm{d}t)}_{max}-{(\mathrm{d}T/\mathrm{d}t)}_i}{{(\mathrm{d}T/\mathrm{d}t)}_{max}-{(\mathrm{d}T/\mathrm{d}t)}_{min}}$$

(14)

in which $\mathrm{d}T/\mathrm{d}t$ is the slope of the LST-time fitting line for the observations within the time span of 1.5–3.5 h after the sunrise. Furthermore, ${(\mathrm{d}T/\mathrm{d}t)}_i$ is the average value for a compositing period, and ${(\mathrm{d}T/\mathrm{d}t)}_{max}$ and ${(\mathrm{d}T/\mathrm{d}t)}_{min}$ are the maximum and minimum for the same period among multiple years. When evaluated over the Australian wheatbelt using the Multifunction Transport Satellite-2 (MTSAT-2) data, the TRI showed a strong correlation with precipitation and soil moisture anomalies, and its correlations with wheat yields peaked higher and earlier by almost one month in comparison to other indices [191], implying the great potential of geostationary satellite observations for agricultural drought monitoring.

Table 3. Summary of thermal indices suitable for agricultural drought monitoring.

Index	Expression	Notes	Year Introduced	Applications
Apparent Thermal Inertia (ATI)	${\displaystyle \frac{C(1-\alpha )}{T_{\mathrm{day}}-T_{\mathrm{night}}}}$	C is a constant coefficient, $\alpha$ is the surface albedo, and $T_{\mathrm{day}}$ and $T_{\mathrm{night}}$ are day/night LST	1985 [171]	China [192], Thailand [165]
Normalized Difference Temperature Index (NDTI)	${\displaystyle \frac{T_{\infty }-T_{\mathrm{s}}}{T_{\infty }-T_0}}$	$T_{\infty }$ is the LST when the composite surface resistance $r_{\mathrm{s}}$ is infinity and the evapotranspiration (ET) is zero, $T_{\mathrm{s}}$ is actual LST, and $T_0$ is the LST when $r_{\mathrm{s}}$ is zero and the ET is equal to the potential ET	1992 [188]	Australia [187]
Temperature Condition Index (TCI)	$100{\displaystyle \frac{T_{max}-T}{T_{max}-T_{min}}}$	T is the smoothed weekly temperature, and $T_{max}$ and $T_{min}$ are the multi-year maximum and minimum	1995 [102]	U.S. [102]
Temperature Rise Index (TRI)	${\displaystyle \frac{{(\mathrm{d}T/\mathrm{d}t)}_{max}-{(\mathrm{d}T/\mathrm{d}t)}_i}{{(\mathrm{d}T/\mathrm{d}t)}_{max}-{(\mathrm{d}T/\mathrm{d}t)}_{min}}}$	${(\mathrm{d}T/\mathrm{d}t)}_i$ is the average value for a compositing period, and ${(\mathrm{d}T/\mathrm{d}t)}_{max}$ and ${(\mathrm{d}T/\mathrm{d}t)}_{min}$ are the maximum and minimum for the same period among multiple years	2020 [191]	Australia [191]

gives an overview of the indices mentioned in this section.

4. Combination of Optical and Thermal Remote Sensing

As has been stated in the previous sections, both the vegetation indices (VI) from optical remote sensing and the land surface temperature (LST) from thermal remote sensing are closely related to vegetation growth conditions and soil moisture. VI can reflect vegetation growth status and leaf water content underwater stress through the various combinations of VIS, NIR, or SWIR reflectance spectra of green plants [193], while LST can be used to indirectly reflect soil moisture conditions under the same vegetation cover conditions [194]. On the other hand, despite the difference in internal mechanisms (optical remote sensing relies on the reflectance of solar radiation, while thermal remote sensing measures the emission of the land surface itself), optical and thermal remote sensing often share similar spatiotemporal resolutions and data availability, for many satellite sensors have optical and thermal detecting capabilities at the same time, e.g., AVHRR [182,195], MODIS [196,197], and the Visible/Infrared Imager Radiometer Suite (VIIRS) [198,199]. These two respects form the mechanical and practical foundations for the combination of optical and thermal remote sensing in agricultural drought monitoring [200,201].

4.1. Simple Integrations

The most straightforward approach is to construct a drought index using VI and LST at the same time. Carlson et al. [202,203] first used the ratio of LST to NDVI as an indicator of surface soil moisture, which was later named the Vegetation Supply Water Index (VSWI) and has been widely applied as a drought index [204,205,206].

Based on VCI and TCI, the Vegetation Health Index (VHI) was proposed by Kogan [102,186,207,208]. It was originally named V/TCI in Kogan [102], VCI/T4 in Kogan [186], and VTI in Kogan [207]. VHI is a linear mixture of VCI and TCI:

$$\mathrm{VHI}=\alpha \mathrm{VCI}+(1-\alpha )\mathrm{TCI}$$

(15)

In Kogan [102], $\alpha =0.7$ was suggested, while in most later works, $\alpha =0.5$ was used as a default value [184,186].

Kogan [102] mentioned that the weighting coefficient $\alpha$ could be calibrated via correlation analysis on the validation dataset but did not provide a practical scheme. Bento et al. [183,185] proposed a reference-based method, in which the StandardizedPrecipitation-Evapotranspiration Index (SPEI) was used as a reference to estimate the value of $\alpha$. From their findings, VCI could dominate as high as 80% for dry land pixels, which suggests that a larger $\alpha$ should be chosen for drought monitoring.

4.2. The Concept of Temperature-Vegetation Space

Simple integrations like VSWI or VHI are easy to apply while lacking a solid physical foundation, and thus cannot be theoretically interpreted. Emerging for the first time in the 1990s, the Temperature-Vegetation space (also called LST-FVC or LST-VI space in other literature; here, LST is short for Land Surface Temperature, and FVC is short for Fractional Vegetation Cover) is considered to be a vital tool for estimations of surface energy fluxes and soil moisture [209]. As the name suggests, the space leverages both LST from thermal observation and vegetation conditions, usually from optical remote sensing. The basic idea is that LST, and, by association, the surface turbulent energy fluxes, are sensitively dependent on soil moisture and water fluxes Carlson [200], and this dependence can be modulated by vegetation through the process of transpiration Jasechko et al. [210]. Practically, the space appears when drawing LST-FVC or LST-VI pairs obtained from a remotely sensed image as a scatter plot. Since the outline of the scatter plot is usually a triangle or a trapezoid, the Temperature-Vegetation space is also called the triangle or trapezoid space. Simulations using several soil/vegetation/atmosphere transfer (SVAT) models also strongly support the existence of such a triangular or trapezoidal outline [200,211].

Figure 7 conceptually illustrates the evolution of the understanding of the Temperature-Vegetation space. The most significant properties of the Temperature-Vegetation space are the wet edge and the dry edge, which are the lower and the upper boundary of the triangle or trapezoid, respectively. In some literature, e.g., Carlson [200], the wet edge is also called the cold edge, while the dry edge is also called the warm edge.

The difference between the triangle and the trapezoid lies in the temperature variation under full vegetation coverage. In the triangle (Figure 7a), vegetation transpiration is considered to occur at near potential regardless of the surface soil moisture, so there is no temperature variation when a pixel is fully covered by vegetation ($T_{\mathrm{v}}$ is a constant). This assumption precludes any analysis of the water stress on vegetation [200]. In the trapezoid (Figure 7b), however, vegetation is no longer considered to be unaffected by soil moisture variation. Thus, there is temperature variation from $T_{\mathrm{v}}^{min}$ to $T_{\mathrm{v}}^{max}$ even under full vegetation coverage.

Recently, a two-stage explanation of the Temperature-Vegetation trapezoid has attracted much attention. Conventionally, the sloping straight lines connecting quantile points on the left and the right border of the trapezoid (dashed lines in Figure 7b) are considered to be soil moisture availability isopleths, based on the assumption that soil evaporation and vegetation transpiration change synchronously. Nevertheless, due to the difference in their direct source (surface soil moisture for soil evaporation and root-zone soil moisture for vegetation transpiration), this assumption can hardly hold [211]. In the two-stage trapezoid(Figure 7c), however, it is assumed that soil evaporation varies first, while vegetation transpiration does not start to change until the surface soil moisture availability drops to 0 (“Dry Edge I” in Figure 7c). Thus, points which fall below the Dry Edge I have near-potential vegetation transpiration, while points above Dry Edge I have minimum soil evaporation. In this way, both surface and root-zone soil moisture availability can be obtained. According to Sun [211]’s simulations (Figure 4 in the same paper), although there are still some mismatches, the two-stage explanation better reflects the variation of surface and root-zone soil moisture.

No matter which hypothesis is chosen (triangle, trapezoid, or two-stage trapezoid), once the outline is determined, the soil moisture availability of a given $(\mathrm{FVC},T)$ pair can be easily calculated. Therefore, the primary issue is to determine the outline. There are generally three ways to solve this issue: visual recognition, automatic fitting, and theoretical calculation [212]. Visual recognition relies on human experience and judgment and has great subjectivity and uncertainties. Automatic fitting is usually based on a set of rules to find representative pixels for the dry edge and the wet edge or exclude outliners (usually water and cloud pixels). The chosen (if representative pixels are picked) or remaining (if outliners are excluded) pixels are used in the regression of a linear or nonlinear expression of the dry/wet edges. Tang et al. [213] is a good example of such methods. However, these methods still have some empirical parameters which require fine-tuning for different regions and datasets, and they also lack physical interpretability. Moreover, if the study area does not have extremely dry and wet pixels as well as bare and fully vegetation-covered pixels at the same time, these methods may yield biased outputs. In contrast, the theoretical calculation is directly based on the energy balance equation, facilitating the understanding and interpretation of the dry/wet edges’ physical meanings. They can be applied to any area, or even a single pixel [214], regardless of its coverage of the Temperature-Vegetation space [212,215,216]. A major drawback of theoretical methods is their dependence on meteorological data such as surface air temperature, wind speed, or roughness length, which are difficult to obtain from remote sensing.

The capability of detecting both surface and root-zone soil moisture status ensures the value of the Temperature-Vegetation space in drought monitoring. Nevertheless, one should take caution that the Temperature-Vegetation space is not suitable for certain subarctic or arctic regions where temperature, instead of water, is the primary limit of vegetation growth [217].

4.3. Applications of the Temperature-Vegetation Space in Drought Monitoring

First utilized in evapotranspiration estimation in the 1990s [209], the Temperature-Vegetation space began to be used in drought monitoring soon after. Based on the triangular Temperature-Vegetation space, Wang et al. [194] developed the Vegetation Temperature Condition Index (VTCI):

$$\mathrm{VTCI}=\frac{{\mathrm{LST}}_{{\mathrm{NDVI}}_i}^{max}-{\mathrm{LST}}_{{\mathrm{NDVI}}_i}}{{\mathrm{LST}}_{{\mathrm{NDVI}}_i}^{max}-{\mathrm{LST}}_{{\mathrm{NDVI}}_i}^{min}}$$

(16)

$${\mathrm{LST}}_{{\mathrm{NDVI}}_i}^{max}=a_1+b_1{\mathrm{NDVI}}_i$$

(17)

$${\mathrm{LST}}_{{\mathrm{NDVI}}_i}^{min}=a_2+b_2{\mathrm{NDVI}}_i$$

(18)

where ${\mathrm{LST}}_{{\mathrm{NDVI}}_i}^{max}$ and ${\mathrm{LST}}_{{\mathrm{NDVI}}_i}^{min}$ represent the maximum and minimum LST of pixels with the same ${\mathrm{NDVI}}_i$ value in the study area, respectively. $a_1$, $a_2$, $b_1$, and $b_2$ are the coefficients of the fitting equation for the LST and NDVI of the dry and wet edges. From the discussion above, it can be seen that VTCI is equivalent to the soil moisture availability defined in the conventional trapezoid. Patel et al. [197] verified the feasibility of applying VTCI in monitoring drought threats in India by using MODIS/Terra NDVI and LST 8-day composition products.

Similarly, Sandholt et al. [218] established the Temperature Vegetation Dryness Index (TVDI):

$$\mathrm{TVDI}=\frac{\mathrm{LST}-{\mathrm{LST}}_{min}}{a+b·\mathrm{NDVI}-{\mathrm{LST}}_{min}}$$

(19)

TVDI is almost equivalent to VTCI (ideally, $\mathrm{VTCI}=1-\mathrm{TVDI}$); however, the wet edge is assumed to have a constant temperature ${\mathrm{LST}}_{min}$ instead of a linear function of $\mathrm{NDVI}$. Due to its simplicity and clarity, TVDI is one of the most widely used remote-sensing-based drought indices [219].

Besides LST and FVC (or by proxy NDVI), other physical variables have also been exploited in constructing the Temperature-Vegetation space. Petropoulos et al. [220] made a comprehensive review of different variable combinations. LST has been substituted with surface-air temperature difference [221] and day-night temperature difference [222], while FVC/NDVI has been substituted with surface albedo [223]. The improved TVDI (iTVDI) proposed by Rahimzadeh-Bajgiran et al. [224] used the surface-air temperature difference $\Delta T=T_{\mathrm{s}}-T_{\mathrm{a}}$ for the temperature axis and was found to have stronger relationships with precipitation and soil moisture than the traditional TVDI; thus, it was considered to be a better indicator of water stress.

Such attempts have continued in recent decades. For instance, Liu et al. [225] assessed a long-term drought across China using the Microwave TVDI (MTVDI), which has the same form as TVDI but uses the microwave brightness temperature instead of thermal infrared LST, and Microwave NDVI (MNDVI), which is based on the Microwave Polarization Difference Index (MPDI) instead of optical NDVI. Zhang et al. [226] proposed the Temperature Fluorescence Drought Index (TFDI), which replaces NDVI with SIF. Applications in Henan Province, China, showed that this new drought index could effectively reflect the severity of the agricultural drought. It should be noted here that such replacements still need to be evaluated and validated by physical models (e.g., the SVAT models) to be better calibrated and illustrated.

A potential improvement lies in the usage of the two-stage trapezoid in drought monitoring. Currently, the two-stage trapezoid is mainly used for evapotranspiration estimation [227], while the drought monitoring community has not widely adopted this concept.

Table 4. Summary of optical-thermal combined indices suitable for agricultural drought monitoring.

Index	Expression	Notes	Year Introduced	Applications
Vegetation Supply Water Index (VSWI)	${\displaystyle \frac{\mathrm{LST}}{\mathrm{NDVI}}}$		1990 [202]	China [204], Brazil [205,206]
Vegetation Health Index (VHI)	$\alpha \mathrm{VCI}+(1-\alpha )\mathrm{TCI}$	$\alpha$ is an empirical coefficient	1995 [102]	U.S. [102,186,207], Indonesia [228], Euro-Mediterranean [183], Ethiopia [229]
Vegetation Temperature Condition Index (VTCI)	${\displaystyle \frac{{\mathrm{LST}}_{{\mathrm{NDVI}}_i}^{max}-{\mathrm{LST}}_{{\mathrm{NDVI}}_i}}{{\mathrm{LST}}_{{\mathrm{NDVI}}_i}^{max}-{\mathrm{LST}}_{{\mathrm{NDVI}}_i}^{min}}}$	${\mathrm{LST}}_{{\mathrm{NDVI}}_i}^{max}$ and ${\mathrm{LST}}_{{\mathrm{NDVI}}_i}^{min}$ represent the maximum and minimum LST of pixels with the same NDVI value	2001 [194]	China [194,230], India [197]
Temperature Vegetation Drought Index (TVDI)	${\displaystyle \frac{\mathrm{LST}-{\mathrm{LST}}_{min}}{a+b·\mathrm{NDVI}-{\mathrm{LST}}_{min}}}$	a and b are fitting coefficients of ${\mathrm{LST}}_{max}$ and NDVI	2002 [218]	Senegal [218], China [231], Turkmenistan [232]
Improved TVDI (iTVDI)	${\displaystyle \frac{\Delta T-\Delta T_{min}}{\Delta T_{max}-\Delta T_{min}}}$	$\Delta T=T_{\mathrm{s}}-T_{\mathrm{a}}$ is the difference between LST and the surface air temperature	2012 [224]	Iran [224]
Microwave TVDI (MTVDI)	${\displaystyle \frac{\mathrm{LST}-(a_2+b_2·\mathrm{MNDVI})}{a_1+b_1·\mathrm{MNDVI}-(a_2+b_2·\mathrm{MNDVI})}}$	MNDVI is the Microwave NDVI calculated from the Microwave Polarization Difference Index (MPDI), $a_1$ and $b_1$ are fitting coefficients of LST${}_{max}$ and MNDVI, and $a_2$ and $b_2$ are fitting coefficients of LST${}_{min}$ and MNDVI; there is also iMTVDI which is similar to iTVDI	2017 [225]	China [225]
Temperature Fluorescence Drought Index (TFDI)	${\displaystyle \frac{\mathrm{LST}-(a_2+b_2·\mathrm{SIF})}{a_1+b_1·\mathrm{SIF}-(a_2+b_2·\mathrm{SIF})}}$	$a_1$ and $b_1$ are fitting coefficients of LST${}_{max}$ and SIF, and $a_2$ and $b_2$ are fitting coefficients of LST${}_{min}$ and SIF	2020 [226]	China [226]

gives an overview of the drought indices in this section.

5. Multi-Source Data and Data Assimilation

5.1. Combination of Remote Sensing and Other Data Sources

Meteorological indicators can reflect the cause and development of agricultural drought, while remote sensing indicators can directly describe the state and influence of agricultural drought. The combination of existing remote sensing and meteorological indicators has already proven to be beneficial for the comprehensive monitoring of agricultural drought [233,234,235]. Except for comprehensive utilization of existing indicators, a series of agricultural drought monitoring models and methods that combine remote sensing and meteorological data have been constructed.

Soil moisture budgets affect vegetation transpiration directly, which in turn changes vegetation canopy temperature [236,237]. Idso et al. [238] found that the difference between the foliage temperature and the air temperature of the crop under potential evaporation conditions is linearly correlated with the vapor pressure deficits of the air. The crop water stress index (CWSI) is proposed as:

$$\mathrm{CWSI}=\frac{\Delta T-\Delta T_{\mathrm{PE}}}{\Delta T_{\mathrm{NE}}-\Delta T_{\mathrm{PE}}}$$

(20)

where $\Delta T=T_f-T_a$ refers to the difference between crop foliage temperature and the air temperature [238]. $\Delta T_{\mathrm{PE}}$ is the difference between the foliage temperature and the air temperature in the potential evaporation state of the crop and is the lower limit of the temperature difference, while $\Delta T_{\mathrm{NE}}$ is the difference between the foliage temperature and the air temperature of a crop in the absence of transpiration and is the upper limit of the temperature difference.

Since foliage temperature cannot be obtained from the space, Jackson et al. [239] replaced the foliage temperature in CWSI with the canopy temperature. With CWSI, thermal infrared (canopy temperature) and meteorological data (air temperature) are combined to invert soil moisture under crop cover conditions indirectly. This method is based on the principle of energy balance and has a clear physical meaning and high precision. The soil moisture inversion accuracy of the CWSI in vegetated areas is better than that of the thermal inertia method. However, CWSI also has its limitations. CWSI has a poor effect when the canopy is sparse, which is the actuality during the early stage of crop growth. Moreover, massive input data are required for model calculation, and the calculation is complicated. The errors introduced by the surface meteorological data in scale expansion also affect the accuracy of CWSI.

CWSI can only be applied under the condition of full vegetation coverage. Moran et al. [221] combined VI and LST to expand the application of the CWSI theory to partially-vegetated conditions and established the water deficit index (WDI). The WDI can be used to estimate the relative soil moisture based on the trapezoidal feature space characterized by the VI and the surface-air temperature difference. The WDI replaces $\Delta T$ in the CWSI with $\Delta T^{\prime }=T_s-T_a$, in which $T_s$ is the surface composite temperature, which can be seen as a weighted average of crop leaf temperature and soil surface temperature. In contrast to CWSI, WDI is applicable in agricultural drought monitoring under various vegetation cover conditions. Like CWSI, WDI requires air temperature as its input; it cannot be calculated only using remote sensing data.

Anderson et al. [240] proposed the atmosphere–land exchange (ALEXI) model, which uses thermal infrared data from the Geostationary Operational Environmental Satellite (GOES) and LAI products from MODIS to simulate daily ET at a 10-km spatial resolution. Besides the remote sensing data, the ALEXI model also requires shelter-level wind speed and air temperature data. Based on the ALEXI model, Anderson et al. [241] constructed the Evaporative Stress Index (ESI) as a water stress indicator for drought monitoring:

$$\mathrm{ESI}=1-f_{\mathrm{PET}}=1-\frac{\mathrm{E}}{\mathrm{PET}}$$

(21)

where E is the actual ET fluxes from the system (canopy and soil), and PET is the potential ET rate. ESI shows strong correlations with Palmer’s Drought Severity Index (PDSI) and monthly precipitation anomalies. ESI is constructed based on surface energy balance and accounts for the effects of available energy and atmospheric conditions on LST. This makes it applicable in both water-limited and energy-limited situations [241,242].

5.2. Data Assimilation

Data assimilation can improve the accuracy of inversed parameters (e.g., LAI and soil moisture) by assimilating observation information into dynamic models (here, a dynamic model is a discrete stochastic-dynamical system whose parameters may include the external forcings or the boundary conditions [243]) and minimizing the differences between observed and simulated values [243,244,245,246]. The temporal resolutions of dynamic models are usually higher than those of remote sensing data, thus addressing the discontinuity of remotely sensed data. As for drought monitoring, data assimilation can improve the accuracy and temporal resolution of soil moisture inversion. Moreover, the root-zone soil moisture could be acquired through assimilating remote sensing data into hydrological models, which is critical for evaluating agricultural drought [247]. However, most remote sensing detection methods can only obtain surface soil moisture [248,249]. When drought occurs, surface soil moisture is decoupled from root-zone soil moisture, and the vertical gradient of soil moisture cannot be directly retrieved [250,251]. In recent years, it has become a notable trend to assimilate remote sensing soil moisture products and related meteorological factors into dynamic models [251,252,253,254,255,256,257,258,259].

The ensemble Kalman filter (EnKF) is currently the mainstream method for data assimilation [260,261,262,263]. Margulis et al. [260] and Reichle et al. [261] demonstrated that the inversion accuracy and efficiency of soil moisture could be improved by assimilating microwave data into the land surface and radiative transfer models with EnKF. Zhu et al. [262] proved that the precision of simulated soil moisture of the Boreal Ecosystem Production Simulator (BEPS) in arid and semi-arid areas was higher after assimilating inversed soil moisture of remote sensing. Crow and Yilmaz [263] constructed the Auto-Tuned Land Data Assimilation System (ATLAS) to analyze soil moisture anomalies and monitor drought by assimilating the rainfall data and soil moisture inversed with remote sensing. Apart from soil moisture, Silvestro et al. [264] also used EnKF to assimilate other parameters (e.g., LAI, FVC, fraction of absorbed photosynthetically active radiation (FAPAR) and chlorophyll content, which are inversed mainly with optical remote sensing) into the AcquaCrop model and estimated the loss of wheat grain yield caused by drought.

Root-zone soil moisture can be obtained from surface moisture conditions with the utilization of dynamic models, especially in the context of microwave remote sensing. It has been demonstrated that the assimilation of the Advanced Microwave Scanning Radiometer for Earth Observing System (AMSR-E) as well as the Scanning Multichannel Microwave Radiometer (SMMR) soil moisture to NASA’s Catchment land surface model can achieve higher accuracies in both surface and root-zone soil moisture estimation [265,266]. Subsequent studies have made use of more data sources, e.g., the Advanced SCATterometer (ASCAT, active microwave), the Soil Moisture and Ocean Salinity (SMOS, passive microwave), the Soil Moisture Active Passive (SMAP, activate/passive microwave) and GRACE (gravity), and further enhanced the retrieval of root-zone soil moisture [267,268,269,270,271,272].

The correlation between surface and root-zone soil moisture is often nonlinear or non-significant [273]. For hydrological models with nonlinear expressions, it is inappropriate to assume that errors in EnKF follow a Gaussian distribution. Moreover, linear updating rules might violate the conservation of mass [274]. To solve this problem, Moradkhani et al. [275] noticed that the particle filter (PF) method could relax the Gaussian hypothesis while conforming to the conservation of mass. Additionally, PF does not rely on the cross-covariance between the surface and root-zone soil moisture. Therefore, PF is considered more suitable than EnKF for estimating soil moisture in the root zone [276]. Subsequently, the PF-MCMC method combining PF with Markov Chain Monte Carlo (MCMC) was proposed [275], which can effectively improve the accuracy of soil moisture estimation in the root zone. This method was later validated by Yan and Moradkhani [277], and utilized in drought monitoring of spring and winter wheat over the entire continental United States (CONUS) [278].

The above data assimilation methods can estimate soil moisture more accurately and obtain the root-zone soil moisture vital to agriculture. Thus, better decisions and management become possible when we are faced with agricultural droughts.

6. Perspectives

Thanks to the rapid development of satellite sensors and the outstanding contributions of many researchers, the use of remote sensing in the monitoring of agricultural drought has been dramatically expanded ever since the 1960s. This paper introduced the physical mechanisms behind agricultural drought monitoring via optical and thermal remote sensing, summarized classical and state-of-the-art models and methods, and explained how sensor advancement has contributed to better monitoring of agricultural drought. Reviewing the past and looking to the future, we suggest that in future research onthe remote sensing of agricultural drought, the following aspects should be prioritized.

6.1. Early Detection of Drought

In contrast to many other natural hazards, drought does not happen immediately. Instead, it is the accumulated consequence of continuous water scarcity. It then becomes crucial whether we could detect agricultural drought at an early stage so that quick actions can be taken to prevent crops from being damaged. Traditional VIs such as NDVI can reflect crop water deficit, but only after it has lasted long enough to cause greenness changes. Solar-induced fluorescence is a very promising early indicator of agricultural drought [132], and as has been introduced in Section 3, much research has been carried out to investigate how to monitor agricultural drought with SIF [226,279]. However, more work still needs to be done to elaborate on the physiological bond between water stress and SIF, especially at the spatial scale of satellite remote sensing [132,134].

6.2. Improvements in Spatiotemporal Resolution

Most satellite remote sensing data are not available at high spatial and temporal resolutions simultaneously, meaning that they cannot fully meet the requirements of precision agriculture. Due to the characteristics of different crop growth stages and spatial heterogeneity of soil conditions (e.g., micro-typography, texture, moisture, nutrient status), frequent observations at a high spatial resolution are needed during the entire crop growth period to determine the precise timing and location of irrigation or fertilization [280]. Concerning drought monitoring, precision agriculture has exerted higher technical demands [281,282]. Faced with the challenge, researchers have experimentally applied the unified system of satellites, unmanned aerial vehicles (UAVs) [283,284], and ground-based sensor networks [285] to the monitoring of agricultural drought [286]. Well-designed space-air-ground coordination can provide more accurate information on spatially heterogeneous farmland conditions. We can thus perform precision irrigation to stem water deficits before damage and losses are caused. With regards to continuous observation, geostationary satellites and virtual satellite constellations are also going to play more significant roles [287].

6.3. Organic Combination with Other Data Sources

This paper focuses on optical and thermal remote sensing, whereas many other data sources have also been utilized in agricultural drought monitoring [288]. These include microwave remote sensing, LiDAR, gravity remote sensing (e.g., GRACE), and other non-remote-sensing data sources. The most significant obstacle lies in that the mechanisms behind each data source can be dramatically different. For example, optical and thermal remote sensing mainly captures the information of the “skin” of the land surface [155,156], while microwaves can have a penetrating depth ranging from several centimeters to several decimeters. The gap is even more prominent when comparing remote sensing data with station-based or reanalyzed meteorological or hydrological data. It is acceptable to combine different data sources through some machine learning processes [289,290,291], but it would be better to have a better depiction of the underlying physical mechanisms and find out how to coalesce their information while minimizing obfuscation errors. That is why models with better comprehensibility and interpretability are preferred.

6.4. Smart Prediction and Assessment

At present, massive remote sensing and meteorological data pose new challenges to existing empirical and theoretical methods. These methods need to be corrected or adjusted according to specific regions and crop species, thereby limiting the accuracy of monitoring agricultural drought on a large scale. In this context, the deep learning method and cloud computing on Google Earth Engine (GEE) [292] or Amazon Web Services (AWS) [293] is increasing in popularity because of its ability to process, analyze, and effectively mine information in a large area promptly. Some researchers have applied deep learning methods to agricultural drought prediction and assessment successfully [294,295,296,297]. However, deep learning has its limitations. At present, the mainstream models require a huge amount of labeled training data, and the workload of marking remote sensing images is very heavy [298]. A possible way to make up for this efficiency is to integrate knowledge-driven drought expert systems [299], which can structurize expert knowledge and experience flexibly with the support of a cloud computing ecosystem. The combination of deep learning and expert systems within cloud computing can make the intelligence of agricultural drought prediction and assessment more adaptive and promising from field to global scales.