Abstract
The cadastral detail data is used for overlap analysis with digitized graphic cadastral maps to solve the problem of inconsistencies between cadastral maps and the current land situation. This study investigated the feasibility of a handheld LiDAR scanner to collect 3D point clouds in an efficient way for a detail survey in urban environments with narrow and winding streets. Then, urban detail point clouds were collected by the handheld LiDAR scanner. After point cloud filtering and the ranging systematic error correction that was determined by a plane-based calibration method, the collected point clouds were transformed to the TWD97 cadastral coordinate system using control points. The land detail line data were artificially digitized and the results showed that about 97% error of the digitized detail positions was less than 15 cm compared to the check points surveyed by a total station. The results demonstrated the feasibility of using a handheld LiDAR scanner to perform an urban cadastral detail survey in digitized graphic areas. Therefore, the handheld LiDAR scanner could be used for the production of the detail lines for urban cadastral detail surveying for digitized cadastral areas in Taiwan.
1. Introduction
Depending on the surveying method and the way the cadastral maps are stored in Taiwan, the areas corresponding to the cadastral maps can be categorized into digital cadastral areas, graphic cadastral areas, and digitized graphic cadastral areas. Although graphic cadastral maps have been digitized as digitized graphic cadastral maps, they still preserve differential shrinkage, wrinkles, folds, and damage from the original maps, and give rise to problems such as the difference between maps and land details in the real world, map joins, and changes to the area subsequent to a map’s registration [1]. In that case, the possible parcel points along the parcel boundaries must be surveyed for overlap analysis and map registration between the digitized cadastral maps and land detail data (possible parcel points) to eliminate inconsistencies between cadastral maps and the actual land details. The surveying of possible parcel points along the parcel boundaries or possible lines is called a cadastral detail survey. Therefore, an urban cadastral detail survey in the digitized cadastral area of Taiwan’s urban city is to eliminate inconsistencies between cadastral maps and the actual land details in urban areas. However, most studies examining this issue focused on ground survey methods in a local area using ground instruments such as the GNSS (Global Navigation Satellite System) systems or total stations, and it is time-consuming. For an urban cadastral detail survey by GNSS, it is still necessary to consider the environmental sky view, multipath effects, and other errors, which are easily restricted by the urban construction environment. With this technological development, a terrestrial LiDAR scanner, a vehicle-based LiDAR system, and UAV aerial images were studied for an urban cadastral detail survey. For example, Chio and Chiang [2] investigated the feasibility of UAV aerial photogrammetry for a boundary verification survey of a digitized cadastral area in an urban city of Taiwan, the study demonstrated its feasibility in the accuracy of the urban cadastral detail data by UAV aerial photogrammetry.
The GeoSLAM Zeb-Horizon LiDAR scanner is a form of handheld mobile mapping system (HMMS) and the HMMS has been applied on many occasions due to its compact size, cost effectiveness, and high performance [3]. Because the HMMS uses a simultaneous localization and mapping (SLAM) algorithm [3,4,5] with IMU (inertial measurement unit) data for positioning without using GNSS data [6], it can avoid the environmental limits and be used in narrow and winding alleys, indoors and other areas where GNSS signals cannot be received. Compared to a total station and a terrestrial LiDAR scanner, it also shows high performance in collecting terrain data in general areas, such as in non-narrow alleys. Therefore, it has been employed in different fields, for example, cultural asset preservation in ancient cities [7], forest investigations [6,8,9,10], mine monitoring [3,11], disaster site reconstruction [12], tunnel surveying [13], topographic surveying [14], and the mapping of the building interior structures [7,15].
This study investigated the feasibility of GeoSLAM Zeb-Horizon LiDAR scanner for a detail survey in urban environments with narrow and winding streets. Such an application for a cadastral detail survey needs to consider the accuracy problem. To date, only two studies concerning the accuracy evaluation focused on forest investigations. Park and Um [9] employed GeoSLAM Zeb-Horizon to measure the diameter at breast height (DBH), and showed a deviation of less than 4 cm compared to the caliper measurement. Hunčaga et al. [10] used GeoSLAM Zeb-Horizon for diameter at DBH estimation by a circle-fitting method from point clouds, and a 1.62 cm root mean squared error (RMSE) was reached. The average RMSE of all cross sections was 1.26 cm. There is no relevant research on the application of HMMS to the cadastral survey. As the maximum scale of the cadastral map of the graphic digitized area in Taiwan’s urban area is 1/500, and the maximum mapping accuracy is 0.3 mm, this corresponds to a 15 cm error in situ. Based on the accuracy demand, this study investigated the feasibility of a handheld LiDAR scanner, GeoSLAM Zeb-Horizon, which uses the SLAM algorithm for positioning without GNSS data, to collect 3D point cloud with as an efficient way to conduct a detail survey in urban environments with narrow and winding streets. First, a plane-based calibration method proposed in our previous study [16] was used to calibrate the handheld LiDAR scanner to improve the accuracy of the handheld LiDAR point cloud. The rough result was presented in [16] due to the paper page limit, therefore, the detailed derivation and result improvement were described in this study. Then, the urban detail point cloud in the test area was collected by the handheld LiDAR scanner. After point cloud filtering and ranging systematic error correction, the handheld LiDAR point cloud was transformed to the TWD97 cadastral coordinate system using ground control points. The land detail line data was artificially digitized from the handheld LiDAR point cloud. The accuracy was evaluated to investigate the feasibility of a handheld LiDAR scanner for the urban cadastral detail line survey in a digitized cadastral area of Taiwan’s urban city. The following section will introduce the methodology used in this study.
2. Methodology
Figure 1 shows the study flowchart. This study was mainly divided into two parts: (1) the handheld LiDAR scanner calibration, as seen in the left part of Figure 1; and (2) the urban cadastral detail survey, as seen in the right part of Figure 1. A detailed description of a handheld LiDAR scanner calibration was explained in Section 2.1. Section 2.2 described how to apply a handheld LiDAR scanner on collecting the point data and correcting the system error to perform an urban cadastral detail survey with more details. Both results were verified by the check data.
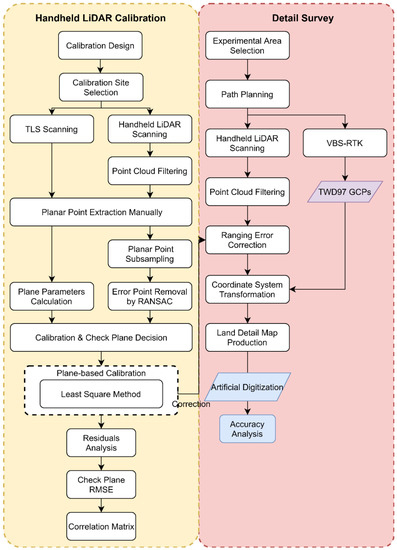
Figure 1.
Study flowchart.
2.1. Handheld LiDAR Scanner Calibration
The calibration steps for the handheld LiDAR scanner were described as follows, and the description was more detailed than those presented by us in [16]. First, an indoor calibration field was selected. Then, the points of this calibration field were collected by a ground-based LiDAR scanner and the plane features in the calibration field were classified into the calibration planes and check planes. Subsequently, the points on the corresponding calibration planes were dynamically collected by a handheld LiDAR scanner, GeoSLAM Zeb-Horizon. The points corresponding to the calibration planes and check planes were selected manually and the blunder points were removed by a RANSC algorithm. The plane-based dynamic calibration method for GeoSLAM Zeb-Horizon proposed in our previous study [16] was used to calculate the ranging systematic errors, including the range scale factor (S) and the rangefinder offset (C), by the least-squares adjustment method. The calibration results were investigated. Details for each step were described in the following subsections.
2.1.1. Selection of the Calibration Field
The calibration field had to be filled with plane features and be large enough to collect point clouds with various ranging measurements to extract planes as calibration reference data for calibration.
2.1.2. Acquisition and Extraction of Calibration Reference Data
Ground-Based LiDAR Point Cloud Acquisition
In this study, a Faro ground-based LiDAR scanner was used to capture the point cloud of the calibration site in one station instead of multiple stations to avoid the registration errors of point clouds and affecting the accuracy of calibration reference data. The specification of FARO Focus S350 ground-based LiDAR scanner was tabulated in Table 1. FARO Focus S350 is a phase-based 3D laser scanner and has better accuracy than a 3D laser scanner based on time of flight (TOF) scanning technique for the collection points in short distances under indoor conditions without interference.

Table 1.
Technical information of FARO Focus S350. (https://echosurveying.com/3d-laser-scanner/faro-focus-s350-laser-scanner, accessed on 2 December 2021).
Extraction of Calibration Planes and Check Planes
This study used the plane features that were abundant in building interior environments as the calibration reference data, eliminating the need for a large number of construction procedures for the calibration targets. The plane equation of the plane feature k is shown in the following Equation (1).
where is a unit normal vector of plane feature k.
The plane parameters () were regarded as a priori parameters in the calibration process and served as the calibration reference data. As mentioned in Section 2.1.2, in order to improve the precision and efficiency of data acquisition, a FARO Focus S350 ground-based LiDAR scanner was operated to acquire point clouds of the calibration field, and the points located on the used plane features were manually extracted. The extracted plane points were used to determine the plane parameters by the least-squares method. Moreover, the extracted plane features were classified into the calibration planes and check planes. The calibration planes were used for the determination of the planar parameters for calibration, and the check planes were used for the verification of the calibration result.
2.1.3. Acquisition of Handheld LiDAR Pnt Cloud for Calibration Data
The GeoSLAM Zeb-Horizon handheld LiDAR scanner with the technical specification shown in Table 2 was used to collect the point cloud data of the calibration field in a mobile manner to obtain as many point clouds on various plane features as possible for calibration data. To compare with static calibration, dynamic calibration can obtain richer points with various ranging measurements, and there is no need to place the handheld LiDAR scanner in multiple stations to capture data separately, thus saving a lot of time [17]. According to the manual of GeoSLAM Zeb-Horizon, the scanned path must be closed to the starting point of the trajectory in order to employ the SLAM algorithm [3,4,5] together with IMU data to calculate the better scanning trajectory. The Velodyne multibeam LiDAR sensor was installed on the GeoSLAM Zeb-Horizon.

Table 2.
Technical specification of GeoSLAM Zeb-Horizon. (https://microsolresources.com/wp-content/uploads/2019/06/GeoSLAM-Family-Brochure.pdf, accessed on 2 December 2021).
Filtering and Subsampling of Point Clouds
According to the studies of Glennie and Lichti [18] and Glennie [17], if the Velodyne multibeam LiDAR sensor has an excessively large incident angle to the object surface during scanning, it is likely to cause a significant increase in point cloud noise due to the decrease in reflection intensity. Although GeoSLAM Zeb-Horizon scans the data with VLP-16 in a rotating manner, it might also decrease the accuracy of the point cloud due to the large incident angle. In order to reduce the influence of errors caused by factors other than the ranging measurement of the handheld LiDAR scanner, the GeoSLAM Hub software was used to output the normal information of each point and the SLAM calculation quality (SLAM condition) to calculate the incident angle λ of each point and obtain the quality index of trajectory calculation for filtering point clouds. Points with a large incident and bad SLAM condition were filtered out.
After the point cloud was filtered, the point cloud located on the calibration planes and check planes were manually extracted for calibration data. In order to avoid a large difference in the point number on different planes and the excessive concentration in certain ranging measurements to affect the determination of the ranging system error parameters, including the range scale factor (S) and the rangefinder offset (C), the same number of point clouds was randomly subsampled on each plane so that the calibration point data could be evenly collected in various ranging measurements.
Blunder Point Filtering Using the RANSAC Algorithm
In order to avoid the error or noisy points being included in the determination of the range scale factor (S) and the rangefinder offset (C), the blunder points of the subsampled points were removed using the RANSAC algorithm [19]. RANSAC is an algorithm for estimating a specific mathematical model from a sample containing gross errors. A fixed amount of data is randomly sampled from the sample to calculate a mathematical model that matches the sampled data. The remaining data after sampling is substituted into this mathematical model and the residual is calculated. If the residual error is less than the threshold, the data are regarded as the inner group conforming to the mathematical model. If the residual error is greater than the threshold, the data is regarded as gross error or blunder. The above steps are repeated and the largest number of inner groups conforming to the mathematical model is regarded as the best model parameter to classify and locate gross error data.
2.1.4. Mathematical Model for Calibration
Based on our preliminary study [16], the ranging system error ∆r described only by the range scale factor (S) and the rangefinder offset (C). They were regarded as the additional parameters (APs) of the adjustment system and solved in the least-squares adjustment. Due to paper page limits, the rough description was presented in [16], and the sequent subsections describe the plane-based dynamic calibration with more detail.
Scanning Center Determination of Each Point
GeoSLAM Zeb-Horizon cannot output the original ranging measurements. In order to obtain each ranging measurement of , called pseudo-ranging measurement, the laser scanning center coordinates corresponding to each point should be obtained from the trajectory data. The trajectory data could be output by the GeoSLAM Hub software. The recording frequency in the trajectory data was 0.01 s. Therefore, the corresponding laser scanning center coordinates () for point i were determined by the linear interpolation formula as follows:
where
is the scanning time of point i
is the trajectory coordinates that the scanning time of point i is less than but is closest to .
is the trajectory coordinates that the scanning time of point i is larger than but is closest to .
is the time of the calculated trajectory that is less than the scanning time for point i and is closest to .
is the time of the calculated trajectory that is larger than the scanning time . for point i and is closest to .
By using the laser center coordinates of point i, the space vector () of point i was calculated by the following Equation (3).
The calculated pseudo-ranging measurement , the horizontal angle and vertical angle should be calculated according to the following Equations (4)–(6) for subsequent derivation.
Through the pseudo-ranging measurement corrected by ranging error APs (S for the ranging scale factor and C for the rangefinder offset), the horizontal angle , the vertical angle , and the corresponding laser center coordinates (), the coordinates of point i could be reconstructed by Equation (7):
Mathematical Model for Calibration
The data obtained by the ground-based LiDAR scanner and the handheld LiDAR scanner were respectively located in the ground-based LiDAR coordinate system and the handheld LiDAR coordinate system. Only when the LiDAR point cloud was converted to the ground-based LiDAR coordinate system, could the plane parameters obtained by the ground-based LiDAR scanner be used as the calibration reference data to solve the ranging APs. Therefore, the six rigid body conversion parameters (three translation parameters and three rotation parameters) were regarded as the unknowns and added to the adjustment equation for simultaneous determination. The following Equation (8) describes the conversion of the handheld LiDAR point () after the correction of the ranging system error to the ground-based LiDAR coordinate system through the rigid body six conversion parameters.
where R: rotational transformation matrix; (, , ): translation vector
Equation (8) is the main equation of the plane-based dynamic calibration method that was originally developed by us [16]. Equation (8) also means the point i after correction by range scale factor and rangefinder offset and conversion should be located on the corresponding calibration plane fitted by the point cloud from the ground-based LiDAR scanner. Due to the random error, the converted point could be not located on the calibration plane. Thus, to minimize the sum of distance squares from the converted points to their corresponding calibration plane, the mathematical model of adjustment was developed to determine the ranging APs. The mathematical model included the functional model and the stochastic model. If the observation equations were regarded as the identical weight. Equation (9) shows the functional model for the least-squares adjustment. The calibration plane parameters () used in this study were unit vectors, so the above-mentioned sum of distance squares from the converted points to their corresponding calibration plane could be regarded as the square sums of correction (i.e., residuals), and the pseudo-observation equation was shown in Equation (9). Each handheld LiDAR point could establish a pseudo-observation equation, and simultaneously solve the ranging APs and the rigid body six conversion parameters according to the least-squares principle.
where are plane parameters of plane k. () are the coordinates of point i on the ground-based LiDAR system after rigid body conversion.
The unknowns of this adjustment were two ranging APs (S and C) and six coordinate transformation parameters. Since Equation (9) is a non-linear equation, it should be linearized by Taylor expansion to establish the indirect observation adjustment matrix form, see Equation (10) required by the least-squares method. The pseudo-observation equations were regarded as equal weights, the corrections to the initial values of the unknowns were determined by Equation (11), and then the corrections were added to the initial value before iterations to reorganize the indirect observation adjustment matrix, also see Equation (10). During iterations, the termination condition was set as the ratio of the posterior variance change less than 0.000001; the ranging APs and the rigid body six conversion parameters could be solved until the posterior variance change ratio converges.
where: J is Jacobian matrix.
X is the correction vector to the initial value of the unknowns.
K is the difference vector between 0 and the value of substituting the initial value into pseudo observation equations.
V is the residual vector of the pseudo observation equations.
N is the number of pseudo observation equations.
2.1.5. Result Analysis
This subsection described the analysis of the calibration results.
Residuals Analysis
The influences on the residual distribution, the average value of the residuals, and the posterior unit weight standard deviation before and after the ranging system error correction were used to verify whether the residual error distribution has the trend of implicit system error or not; whether the average value of the residual error and the standard deviation have decreased or not in order to evaluate if the calibrated ranging system error parameters could correct the system error and improve the accuracy of the handheld LiDAR points.
Verification by the RMSE of Check Planes
The RMSE of the calibration data from corrected and uncorrected handheld point clouds to each corresponding check plane before and after the adjustment was calculated for evaluation of calibration results. The improvement ratio for each check plane was calculated by the following Equation (12) to verify the efficiency of the system error correction.
where
is the RMSE calculated by adding the ranging additional parameters (APs) to the adjustment
is the RMSE calculated by not adding the ranging additional parameters (APs) to the adjustment.
Analysis of Correlation Matrix of the Unknowns
Through the correlation coefficient matrix, the quality and robustness of the calibration results [20] can be verified, and check if there is a high correlation between the parameters of the ranging system or the parameters of the ranging system and the conversion parameters. High correlation means that the calibration method or calibration data is not enough to solve the calibration parameters well. The correlation coefficients after the adjustment were shown as discussed in this study.
Analysis of Ranging Systematic Error Parameters
In this study, two systematic errors were estimated, S for the range scale factor and C for the rangefinder offset. The influence of certain ranging measurements, for example, 20 m, 30 m, and 40 m, was investigated.
2.2. Urban Cadastral Detail Survey
2.2.1. Ground Control Survey
The ground control survey collected the 3D coordinates for converting the handheld LiDAR points to the cadastral coordinate system. In Taiwan, the TWD97 coordinate system was adopted for the cadastral coordinate system which is a horizontal coordinate system. However, the elevation for each control point was also surveyed for 3D coordinate conversion of the handheld LiDAR points. The TWVD2001 system was used for elevation systems in Taiwan.
The control points might be of the announced TWD97 coordinates and for the selected supplementary control points. Therefore, considering accuracy, cost, and ease of operation, VBS-RTK Technology was employed for the control survey to determine the 3D coordinates, which were in the GNSS coordinate system. The ground control points were surveyed twice for averaging. For each survey, the standard deviation in the horizontal coordinate component and the elevation component should not exceed 2 cm and 5 cm, respectively. At the same time, the differences in horizontal position and elevation between the two surveys should be less than 3 cm and 5cm, respectively. However, the TWD97 coordinate system was used for horizontal coordinates, and the TWVD2001 system was used for the elevation system in Taiwan. Therefore, surveyed elevation was converted to the ortho-height system according to the geoid model announced by the Ministry of the Interior (Taiwan).
Subsequently, coordinate conversion had to be performed to estimate and eliminate the systematic errors between the TWD97 cadastral coordinate system and GNSS coordinate system, as well as to verify the correctness of coordinate conversion. The systematic error might be caused by the tension between the VBS-RTK coordinate system and the TWD97 cadastral coordinate system due to the control network tension, crustal changes, and projection deformation. Least-squares collocation is a combination of least-squares adjustment, estimation, and filtering. Compared with the traditional adjustment method that can only deal with random errors in observation [21], therefore, the least-squares collocation method was implemented in this study to estimate the systematic error between two kinds of coordinates, namely the TWD97 cadastral coordinate system and VBS-RTK coordinate system, where the observation was not made [22] to determine the cadastral coordinates for those control points without announced cadastral coordinates.
2.2.2. Path Planning for Data Collection
According to the manual of the GeoSLAM Zeb-Horizon, the scanned path must be closed to the starting point of the scanning in order to employ the SLAM algorithm [3,4,5] together with IMU data to calculate a better scanning trajectory. The start and end points of the scanned path should be the same point to create a closed route and reduce the deviation caused by error propagation in the trajectory [6,8].
If the scanned path passes through control points, the alignment device provided, as shown in Figure 2, could be used to align the control point with the hole in the front of the alignment device and stop for ten seconds. The GeoSLAM Zeb-Horizon scanner could record the coordinates of this control point in the handheld LiDAR coordinate system for subsequent coordinate conversion.

Figure 2.
GeoSLAM control point alignment device.
Since the GeoSLAM Zeb-Horizon scanner uses the SLAM algorithm [3,4,5] together with IMU data to calculate a better scanning trajectory, the scanning environment will have a significant impact on the quality of its trajectory calculation. It is necessary to investigate the application environment and plan an appropriate path before scanning to understand the scan area and its situations, which might cause incorrect estimation of the SLAM algorithm, such as the lack of features, and good path planning could ensure the stability of the SLAM trajectory calculation. In this study, the test area was in the urban area. According to the user manual and past literature, the following guidelines organized the following items:
- Avoid scanning moving objects, the SLAM algorithm may recognize them as static features and cause calculation errors [23].
- The start and end points of the scanned path should be the same point to create a closed route and reduce the offset caused by error propagation in the trajectory [7,9].
- The moving speed should not be too fast which is not more than normal walking speed (1.1~1.5 m/s), and normal walking speed should be maintained to ensure a good point cloud density. When passing the building corner, because the scanning angle of view changes greatly, the speed and travel should be slowed down to obtain sufficient features to establish a trajectory [15,24].
- The scanning distance is recommended to be kept within 50 m to maintain good point cloud accuracy and point cloud density.
- The time of a single scanning task should be less than 30 min. When scanning a large field, the scanning task should be divided into several portions and the point cloud should be registered to reduce the probability of trajectory deviation [23].
- Avoid areas containing a lot of glass and windows. Glass and windows are prone to refraction of the laser beam and cause false point clouds [25].
- When scanning narrow passages, the scanned path should be in the middle of the passage so that the scanner can obtain the features of the walls on both sides. If it is too close to the wall, the scanning angle is too small and it will lack feature acquisition [23].
2.2.3. Point Cloud Processing
Filtering of Point Clouds
As mentioned in Section 2.1.3, after the point cloud data collection, the point cloud normal vector and the SLAM calculation quality were exported from GeoSLAM Hub software, and the point cloud was filtered to remove the point cloud with poor quality or poor observation conditions.
In addition to the above-mentioned filtering conditions, namely the angle of incidence and the SLAM calculation quality, the point cloud with a longer ranging measurement would be affected by the ranging measurement capability of the LiDAR scanner, and a point cloud with an abnormal distance usually has a larger error and is also more likely to be erroneous data in an outdoor environment. For mobile surveying and mapping of a LiDAR system, the ranging measurement data of a short distance could be retained to retain the point cloud with higher accuracy. According to the manual, the scanning distance is recommended to be kept within 50 m. In order to maintain a good point cloud accuracy, the scanning distance threshold was added to the filtering condition of the points to eliminate points of possible poor quality.
Ranging System Error Correction of Point Clouds
The corresponding laser center coordinates of each point by linear interpolation was determined, and the space vector () of each point was calculated, then the pseudo-ranging measurement r, horizontal and vertical angle were calculated for each point according to Equations (4)–(6).
The ranging APs (S and C) of the ranging system obtained by the calibration method described in Section 2.1 were employed to correct the ranging system error, and the pseudo-ranging measurement r of each point was corrected and Equation (7) is used to reconstruct the point coordinates to complete the system error correction.
Coordinate Conversion
After the point cloud filtering and the ranging system errors were corrected, the control point coordinates in the handheld LiDAR coordinate system and their corresponding horizontal coordinates in the TWD97 coordinate system and the elevation in the TWVD2001 system were used to calculate the conversion parameters, and the corrected point cloud was converted from the handheld LiDAR coordinate system to the TWD97 cadastral coordinate system through the rigid body six conversion parameters.
2.2.4. Urban Cadastral Detail Line Data Production
The urban cadastral detail lines mean possible parcel points on parcel boundaries. The production of the urban cadastral detail line data is difficult to extract automatically because it contains some subjective factors to be identified and digitized with reference to actual building conditions, cadastral reconnaissance, existing cadastral maps, and land use zoning maps. Therefore, this study used PointCab software to digitize the detail line data manually. While digitizing manually, the following principles should be followed:
- (1)
- For urban buildings along roads, most of them are bounded by the building line designated by the road centerline stake of the urban planning road or the boundary of the existing road boundary. Road boundaries are the detail lines for manual digitization.
- (2)
- The detail lines of townhouses are mostly bounded by the center of the wall, but they still need to be judged by considering the difference in their structure or the decorative form of the exterior. The centerline of a wall on a building façade with the same building style except for the wall on the outer most boundary of a building.
- (3)
- Where there are exposed steel bars on the walls of side houses or independent houses, the center of the wall shall be the boundary, otherwise, the outer edge of the wall shall be the boundary.
- (4)
- The outer edge of a wall on the most outside boundary of a building with the same building style, and the outer edge of a wall of a single building except the wall attached with exposed steel reinforcing;
- (5)
- The eaves of the building belong to the building itself.
Results Analysis
- (1)
- Analysis of digitized detail lines.
The results analysis of the error of the urban cadastral detail survey using the handheld LiDAR points was divided into planar position error analysis (Figure 3a) and vertical distance error analysis (Figure 3b). If the points surveyed by a total station can be analyzed definitely by the junction points of the digitized lines, the planar position errors of those points could be calculated, as shown in Figure 3a. Otherwise, the vertical distances of the remaining points surveyed by a total station to the closest digitized detail line segment were calculated for analysis, as shown in Figure 3b.
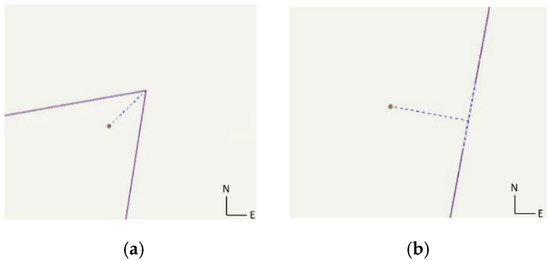
Figure 3.
The demonstration of error calculation for an urban cadastral detail survey using the handheld LiDAR points where points mean the survey points measured by a total station and lines were digitized manually from the handheld LiDAR points. (a) Planar position error analysis. (b) Vertical distance error analysis.
- (2)
- Analysis on the effect of ranging system error correction.
The effect analysis of error correction of the ranging system was represented by the difference, as expressed in Equation (13), of digitized detail lines using the handheld LiDAR point clouds after and before ranging system error correction, compared with the detail points surveyed by a total station.
where,
is the digitized error using uncorrected point cloud for digitization compared with the detail points surveyed by a total station.
is the digitized error using corrected point cloud for digitization compared with the detail points surveyed by a total station.
3. Results and Discussion
3.1. Handheld LiDAR Scanner Calibration
3.1.1. Selection of the Calibration Field
The size of the calibration site was about 35 m by 27 m by 3 m, located in the underground parking lot of Research and Innovation-Incubation Center at National Chengchi University in Taiwan. The calibration site provided a large variety of planar features with different ranges for calibration, as shown in Figure 4.

Figure 4.
Calibration site.
3.1.2. Acquisition and Extraction of Calibration Reference Data
As mentioned in Section 2.1.2, a Faro ground-based LiDAR scanner was used to capture the point cloud of the calibration site in one station instead of multiple stations to avoid the point cloud registration errors. The collected point cloud data are shown in Figure 5.

Figure 5.
Top and side views of the collected points by a FARO Focus S350 in a single station. (a) Top view. (b) Side view.
Seventeen plane locations, labeled A to Q, were manually extracted for calibration reference data, and the location of each plane is shown in Figure 6. The size of each plane was about 0.7 m by 1.2 m and its planar parameters were determined by the least-squares method. The parameters and fitting RMSEs are shown in Table 3. All plane fitting RMSEs were not greater than 0.001 m, indicating that the point cloud data of the FARO Focus S350 was of a certain accuracy and reliability as the calibration planes and the check planes.
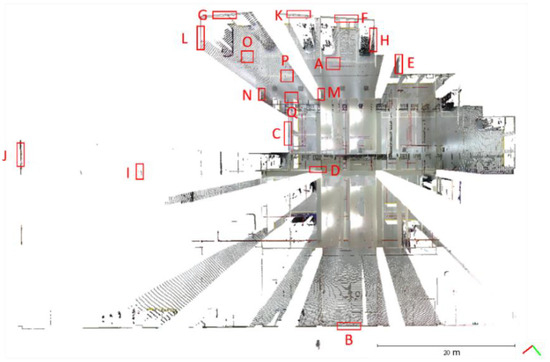
Figure 6.
Locations of the selected 17 planes (labeled A to Q) for calibration reference data.

Table 3.
Fitting plane information.
In order to solve simultaneously the ranging APs together with the six-parameter rigid body conversion parameters. three planes with orthogonal normal were included in the plane selection [20]. The horizontal and vertical planes were identified from the DIP in Table 3. Table 3 shows the planes including 4 horizontal (DIP 0°) and 13 vertical (DIP 89°) planes. The triple pair (a, b, c) indicated the unit normal vector in Table 3.
3.2. Acquisition of Handheld LiDAR Point Cloud for Calibration Data
A plane-based dynamic calibration developed in our previous study [11] and mentioned in Section 2.1.4 was employed to investigate the calibration results. The dynamic or kinematic calibration means to capture the point cloud data for calibration in a mobile way. The calibration data was collected on 26 January 2021 at 9:30 a.m., the scanning time took about 87 s, the number of point clouds was about 160,000,000 points. Figure 7 shows the collected calibration data and the scanning trajectory, the colors of points in Figure 7a were determined based on the SLAM quality (SLAM condition), the best quality was blue (R = 0; G = 0; B = 255), the closer to red, the worse was the quality. In an indoor environment with rich features, the SLAM quality was noticeably stable, and the majority of the point clouds were dark blue indicating no significant problem of SLAM solution or failure of the SLAM solution. The color of the point clouds in Figure 7b was given according to the scanning time of the scanning trajectory, and the color of the point clouds gradually changed from red to blue according to the scanning time, where red was the scanning time at the beginning, and blue was the scanning time at the end. The scanned path was planned to walk around the center of the parking lot and close to the starting point at a normal walking speed to ensure that the complete calibration field was scanned. It could be found that the starting point represented by red and the scanning end point represented by blue were closed, which met the scanning requirements.
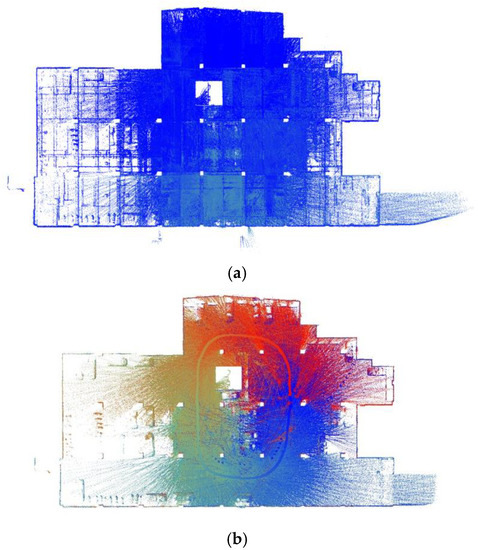
Figure 7.
Point cloud and scanning trajectory of calibration data. (a) Colored by SLAM condition. (b) Colored by scanning time.
3.2.1. Filtering and Subsampling of Point Clouds
In this study, the filtering conditions of the handheld LiDAR point cloud were performed by the SLAM quality and the incident angle of the point. In order to remove the influence caused by the poor SLAM quality, the threshold value was set to R = 0, G = 0, and B = 255, namely the blue points colored by the best SLAM solution were used for the calibration data. Based on the study of Glennie and Lichti [18] and Glennie [17], the thresholds of the incidence angle for the effectiveness of filtering with the incident angle were 60° and 70°, respectively. However, the point cloud filtered at 60°, the plane features in the horizontal direction were relatively insufficient. Considering that a certain number of planes in the horizontal direction must be extracted, this study used 70° as the filter threshold for the incident angle.
In order to evaluate the effectiveness in filtering point clouds with poor quality by the thresholds, a point cloud on one plane was taken for analysis to discuss whether the RMSE of the plane fitting after filtering was reduced or not. The analysis results are shown in Table 4. After filtering using the SLAM quality or incident angle separately, the plane fitting RMSE was reduced from 0.0110 m to 0.0108 m. If both the SLAM quality and incident angle were used for filtering, the plane fitting RMSE was further reduced to 0.0106 m. The results showed that the plane fitting RMSE of the point cloud by the three filtering conditions were all better than the original point cloud used for plane fitting. It could say that the used conditions and thresholds could retain the point cloud with better observation conditions, therefore this study used these combined conditions for filtering. Figure 8 shows the point cloud data after filtering. After the point cloud filtering, the number of point clouds was 1,401,803, and the filtering ratio was about 91%. The remaining good quality point cloud data was employed as calibration data for calibration adjustment.

Table 4.
Analysis results of filtering conditions using a planar point cloud.

Figure 8.
Handheld LiDAR point cloud after point cloud filtering.
The handheld LiDAR point cloud corresponding to each plane, see Figure 6, was selected manually, and the point number contained on each plane and the ranging measurement between each point relative to their corresponding laser center was calculated. The coordinates of each laser center could be seen in Equation (2). In order to increase the calculation efficiency and allow the calibration calculation to include uniform and various ranging measurements, the points on each plane were randomly subsampled to select the same number of point clouds as the calibration data, except for planes B, E, I, and J, which were of a lower number of points, the least number of points on the other planes was plane D, and the point number was 613. Therefore, this study randomly subsampled 600 points for the remaining planes, and evaluated whether there was a significant difference in the calculated pseudo-ranging measurements or not before and after subsampling and blunder removing by the RANSAC algorithm.
The statistical results of calculated pseudo-ranging measurements for each plane of calibration data before and after subsampling and blunder removing by the RANSAC algorithm are shown in Table 5. The statistics for pseudo-ranging measurements were divided into minimum, maximum, median, and average to evaluate the distance measurements provided by the points in each plane for calibration adjustment calculation. As seen in Table 5, planes B, I, and J were of relatively fewer points due to the longer scanning distances. Plane E was blocked by a wall, the point number was also relatively insufficient. The box diagram of the calculated pseudo-ranging measurements before and after subsampling and blunder removing by the RANSAC algorithm is shown in Figure 9. According to Table 5 and Figure 9, there was no significant difference between the minimum, maximum, median, and average values of the calculated pseudo-ranging measurements in each plane before and after subsampling and blunder removing by the RANSAC algorithm. The difference of statics of the calculated pseudo-ranging measurements in each plane before and after subsampling and blunder removing by the RANSAC algorithm was less than 1 m, indicating that the same rich calculated pseudo-ranging measurements could be retained after subsampling and blunder removing by the RANSAC algorithm could be used for calibration. Therefore, 600 points could be used as the number of subsampling points, taking into account the richness of the calibration data and improving the calculation efficiency.

Table 5.
The statistics of pseudo-ranging measurements in each plane for calibration data before and after subsampling and blunder removing by the RANSAC algorithm for calibration data.
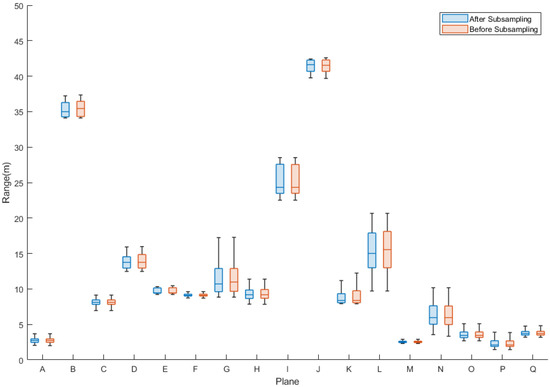
Figure 9.
Box diagram of the calculated pseudo-ranging measurements of each plane before and after subsampling and blunder removing by the RANSAC algorithm.
3.2.2. Blunder Point Filtering Using the RANSAC Algorithm
The RANSAC algorithm was used to remove the gross errors of the subsampled points in each plane for the calibration data. According to the point cloud precision announced by the GeoSLAM Zeb-Horizon manufacturer, the allowable error threshold is set to 0.03 m. The results are shown in Table 6, where the red points were evaluated as a gross error by the RANSAC algorithm.

Table 6.
RANSAC result for calibration data.
3.2.3. Results Analysis
A plane-based dynamic calibration proposed in our previous study [16] was performed. The location distribution of the calibration planes in this study is shown in Figure 10. The selection of the calibration planes should enclose the entire calibration field as much as possible and be evenly distributed. In order to solve the rigid body conversion parameters at the same time during the calibration adjustment calculation, in addition to the vertical planes, the calibration planes must also include the horizontal planes (such as planes A, O, Q) [20]. In particular, although plane E seems to be closer to the periphery of the calibration field than plane H, plane H was of a richer scanning distance than plane E from the maximum and minimum values in Table 6, plane H instead of plane E was selected as a calibration plane. The following subsections investigate the calibration results.
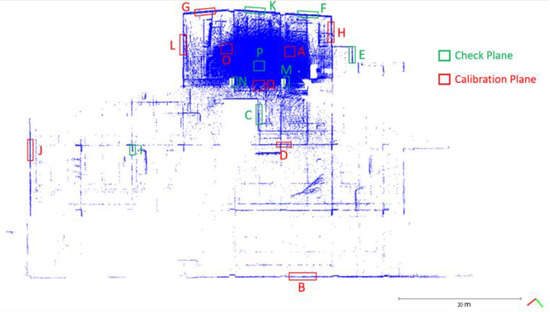
Figure 10.
The locations of calibration planes (labeled A, B, D, G, H, J, L, O, Q) and check planes (labeled C, E, F, I, K, M, N, P).
Residuals Analysis
Figure 11 shows the residual distribution plots and Figure 12 shows the residual scatter plots after adjustment with or without determination of the ranging system error, respectively, where Figure 11a and Figure 12a are the residual distribution plots and the residual scatter plots of the adjustment results by incorporating the ranging system error into the adjustment system as an additional parameter (referred to with APs) for determining together with the rigid body six conversion parameters, Figure 11b and Figure 12b are the residual distribution plots and the residual scatter plots of the adjustment results without adding the ranging system error as the additional parameter (referred to without APs)) and only the rigid body six conversion parameters retained as the unknowns for determination.
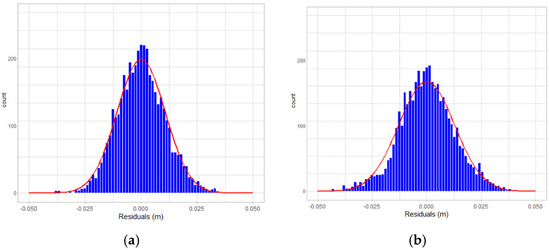
Figure 11.
The residual distribution plots of calibration data. (a) With APs. (b) Without APs.
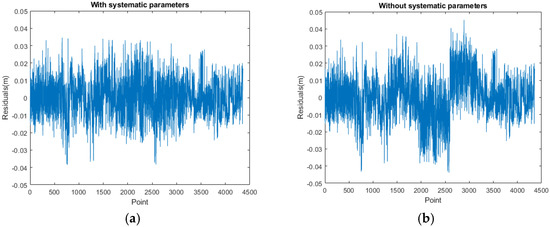
Figure 12.
The residual scatter diagram of calibration data. (a) With APs. (b) Without APs.
Comparing Figure 11a,b, the residual value distribution was much more concentrated at 0 and was more in line with the normal distribution curve. Regarding further analysis by the residual scatter diagram, as shown in Figure 12, the residuals in Figure 12a were stably and evenly dispersed within ±0.03 m, which conformed to the 3 cm precision of point cloud announced by the manufacturer. The residuals in Figure 12b were affected by more significant systematic errors, which caused the residual dispersion to present an unstable undulation. After adding the ranging APs, the average residual was closer to 0 (from −0.000045195 m to −0.000014845 m), and the posterior unit weight standard deviation became smaller (from ±0.01278 m to ±0.01077 m), both of which were improved compared to those without adding the ranging APs into the adjustment. There might be no significant statistical difference in the figures. However, it could be clearly understood from the change of the relevant figures that adding the ranging APs in this study could eliminate most of the ranging system errors.
Verification by the RMSE of Check Planes
By evaluating the calibration results, the RMSE of each check plane was calculated for calibration data using least-squares adjustment with and without ranging APs. Table 7 shows the RMSE results of each check plane for three datasets. Among them, the RMSE of all check planes were all improved after the correction of the ranging system error, also see the RMSE bar chart of each check plane in Figure 13. Among them, the RMSE of the check planes E, F, K, M, and N were significantly improved. Up to 72.12% in plane F, an increase of about 2.4 cm and an improvement of 1.6 cm in plane E were reached. The overall average improvement was 32.61%, which demonstrated that the proposed calibration approach could effectively improve the overall point cloud accuracy.

Table 7.
RMSE of each check plane.
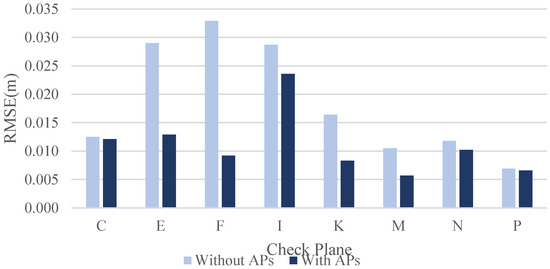
Figure 13.
The bar chart of RMSE for check planes.
Analysis of Correlation Matrix of the Unknowns
Table 8 shows part of the matrix of correlation coefficients of the unknowns of the least-squares calibration solution. The correlation coefficients between the ranging APs and the coordinate conversion parameters were maintained at a low correlation, and the absolute values of the correlation coefficients were mostly not larger than 0.7. This result is consistent with Glennie and Lichti [18], that the calibration reference and calibration data collected in different coordinate systems did not significantly affect the calculation of the system error parameters; however, there was a high negative correlation between the ranging APs (S and C), −0.82. The lower negative correlation between the ranging APs made the solution results of the ranging APs more reliable. The result was more reliable than the test in our previous study [16], the correlation between the ranging APs (S and C) was −0.985. However, in the calibration data of this test, only points in the planes B and J were with long pseudo-ranging measurements for calibration, as shown in Figure 10, and the calculated pseudo-ranging measurements from the points on these two planes ranged from about 35.3 m to 41.8 m, as shown in Table 5. In the future, if a larger calibration site or suitable plan for scanning could be found to collect the handheld LiDAR points to obtain more calculated pseudo-ranging measurements for calibration, the negative correlation between the ranging APs could be reduced and the solutions of S and C could be more reliable.

Table 8.
The matrix of correlation coefficients of the unknowns for calibration data.
Analysis of Ranging Systematic Error Parameters
The estimated ranging systematic parameters S and C were 0.9996 and −0.0088, the corresponding standard deviations were 0.0000397 m and 0.00055 m. Table 9 indicates the correction for different distances. If the ranging measurement was 10 m, the correction was 1 cm; the ranging measurement was 30 m, the correction is 2 cm; the ranging measurement was 40 m, the correction is 2 cm. Even it was 2 m, the correction would be 1 cm. When using a handheld LiDAR scanner for precise surveying, for example, cadastral surveying, this ranging system error should be corrected to obtain a more accurate result.

Table 9.
The different distance values after correction (unit: m).
3.3. Urab Cadastral Detail Survey
The test area of an urban cadastral detail survey was located near National Cheng-Chi University in Taiwan, as shown in the red box in Figure 14. The aerial photographs illustrate that the area was densely built and filled with narrow lanes that were difficult to use GNSS for a detail survey and was time-consuming to use total stations for a detail survey.
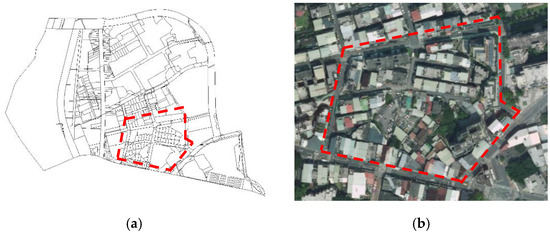
Figure 14.
The test area of an urban cadastral detail survey. (a) Cadastral map. (b) Aerial image.
3.3.1. Ground Control Survey
The locations of four cadastral control points (red points) used in this study and two supplementary control points (blue points) are shown in Figure 15. Four cadastral control points were of the known announced control points in the TWD97 cadastral coordinate system, including point nos. 100005, NA0591, NA0657, and GA0477; and two supplementary control points, including point no. 1 and no. 2 were not. The cadastral coordinates of these two points were obtained by the process of least-squares collocation adjustment, as described in Section 2.2.3.
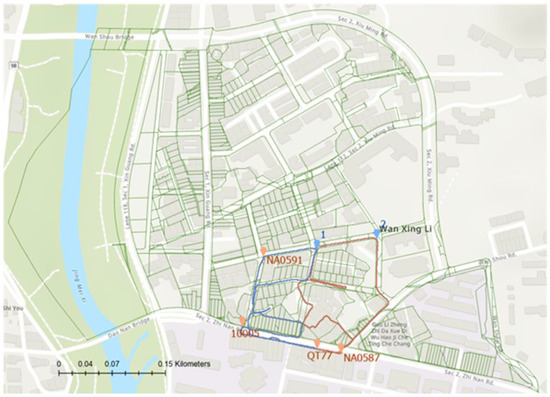
Figure 15.
Two independent scanning operation areas and scanned paths.
Thee cadastral control point nos. QT77 and NA0587 were under the building eave, the ortho-height could not be surveyed by VBS-RTK after conversion. The ortho-height of these two points was surveyed by levelling from the known height point 10005, and their N, E coordinates were adopted by the announced TWD97 cadastral coordinates. After the other six points were surveyed by VBS-RTK, the TWD97 cadastral control coordinates of point nos. 1 and 2 were obtained using least-squares collocation, as shown in Table 10. The ortho-height was converted by the geoid undulation. The final cadastral (N, E) coordinates and ortho-height of all control points are organized in Table 10.

Table 10.
The cadastral TWD97 coordinates and ortho-height of used control points.
3.3.2. Path Planning for Data Collection
After evaluating the area and scanning time of the test area, it was divided into two independent scanned paths. The area of these two scanned paths and the distribution of control points are shown in Figure 15. The scanned path 1 in red started from the control point no. QT77, passed through control point no. NA0587, 1, 2, and NA0587, then it closed at the starting point; the scanned path 2 in blue started from the control point no. QT77, passed through control point no. 100005, 1, NA0591, and closed at the starting point.
3.3.3. Point Cloud Filtering, System Error Correction, and Coordinate Conversion
In order to retain more point clouds for an urban cadastral detail survey to digitize the detail line data, the SLAM quality threshold value was changed to R ≤ 50 and G ≤ 50 and B ≥ 250, and the point cloud data that was closer to the blue (good SLAM solution) was retained. The incident angle threshold was consistent with the calibration operation, set to 70°. In addition, according to the manual, the scanning distance is recommended to be kept within 50 m. The calibration results in the previous section indicate that the point cloud larger than the calibration calculation range would tend to increase the error. Therefore, this study set the scanning distance threshold to 50 m. The conditions and thresholds of point cloud filtering for a land detail survey are summarized in Table 11.

Table 11.
Conditions and thresholds of point cloud filtering for a cadastral detail survey.
By using the calculated ranging system error parameters, the pseudo-ranging measurement between the coordinates of each point and the corresponding laser center coordinates were corrected, see Equation (14), and the point coordinates after the correction of the ranging system error were recalculated based on Equation (7).
The recalculated point cloud data of scanned paths 1 and 2 after filtering, merge, and conversion are shown in Figure 16. The control points used in scanned path 1 included four control point nos. QT77, NA0587, 1, and 2. The RMSE of the coordinate conversion was 0.0354 m, and the number of point clouds after point cloud filtering was 68118612 points, and the filtering ratio was about 40%. The control points used in the scanned path 2 included four control point nos. QT77, 100005, NA0591, and 1, the RMSE of coordinate conversion was 0.0309 m, the number of point clouds after point cloud filtering was 93961336 points, and the filtering ratio was about 31%. The points after filtering were used for an urban cadastral detail survey. The result will be demonstrated in the next subsection.
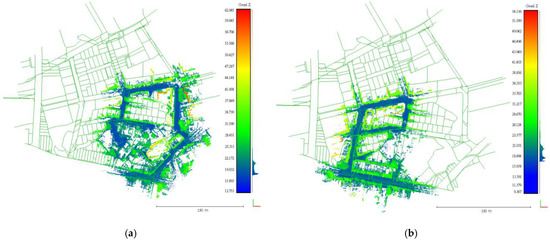
Figure 16.
Point cloud after filtering. (a) Point cloud after filtering for scanned path 1. (b) Point cloud after filtering for scanned path 2.
3.3.4. Urban Cadastral Detail Data Production
Detail Line Data by Manual Digitization
According to the principles described in Section 2.2.4 to digitize the cadastral detail lines, the types of possible cadastral detail lines in the test area of this study could be roughly divided into the boundary between townhouses and the existing road boundaries. The two types of possible cadastral detail lines are shown in Figure 17 and Figure 18 after manual digitization.
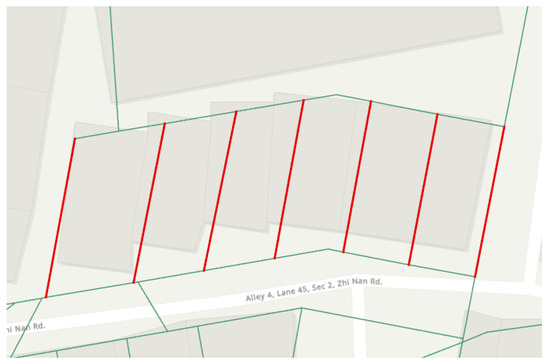
Figure 17.
Possible cadastral detail line on the boundary between townhouses.
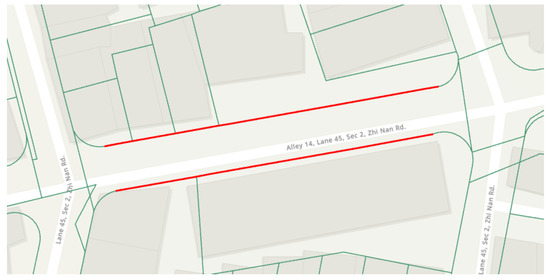
Figure 18.
Possible cadastral detail line on an existing road boundary.
- Possible cadastral detail line on the boundary between townhouses
The possible cadastral detail line of the townhouses was mostly located at the center of the wall or the center of the stairwells. Taking the selected possible cadastral detail line in Figure 19a as an example, Figure 19b shows the overlapping results of the point cloud data and the cadastral map. As seen, the cadastral line was located at the center line of the stairwell of the townhouses and was roughly parallel to the plane on both sides of the stairwell. The point cloud data and the image of the townhouse are shown in Figure 20.
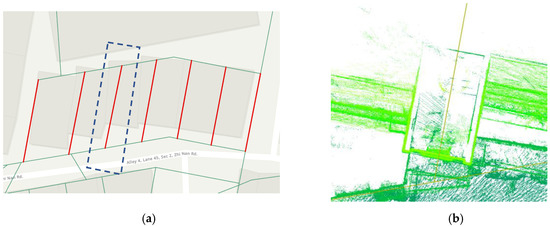
Figure 19.
An example of the possible cadastral detail line between townhouses. (a) The digitized possible cadastral detail lines. (b) Overlap of point cloud and the cadastral map.

Figure 20.
The image of a stairwell and its corresponding point cloud. (a) Image of a stairwell. (b) Point cloud of a stairwell.
The digitized process of the possible cadastral detail line between townhouses is shown in Figure 21. The blue structure in the figure is the stairwell front façade. First, line AB was digitized according to the width of the stairwell, and a line CD from one of the two wall sides of the stairwell was also digitized. The line CD was translated to the midpoint of line AB to become the line C’D’ parallel to the line CD, the line C’D’ is the position of the possible cadastral detail line.
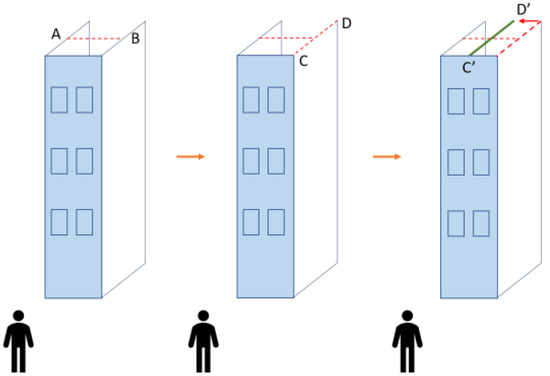
Figure 21.
The digitized process of the possible cadastral detail line between townhouse.
If there were a gap between different townhouses, as shown in Figure 22, the midpoint of the gap space was digitized as the possible cadastral detail line. The digitization process was similar to the above, the line digitized at one side of the gap was translated to the midpoint of the gap width, and the translated line was regarded as a possible cadastral detail line.

Figure 22.
The image of two different townhouses with a gap.
- Possible cadastral line on an existing road boundary
The possible cadastral detail line on an existing road boundary is as shown as the red line in Figure 23a. Figure 23b shows the overlapping results of the point cloud data and the cadastral map. The possible cadastral detail line was located at the junction of the outermost wall of the building area and the road, namely the boundary of an existing road boundary. The point cloud data and image of the wall are shown in Figure 24.
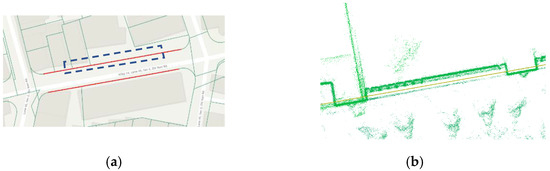
Figure 23.
Possible cadastral detail line on an existing road boundary. (a) The digitized possible cadastral lines. (b) Overlap of point cloud and the cadastral map.

Figure 24.
The image of a road boundary and the corresponding point cloud. (a) Image of a road boundary. (b) Point cloud of a road boundary.
The digitization of a possible cadastral detail line on an existing road boundary is illustrated in Figure 25 where blue lines indicated the outermost boundary of the building top view. The outer boundary of the wall located on the road boundary was digitized, and then those line segments were connected as the possible cadastral detail line, as the line EF shown in Figure 25.

Figure 25.
The digitized process of the possible cadastral line close to the road boundary.
According to the obtained hand-held LiDAR point cloud, the possible cadastral boundaries between the townhouses and on the existing roads were digitized manually and joined in AutoCAD software to produce the results of the urban cadastral detail lines of the test area. The final results are shown in Figure 26.
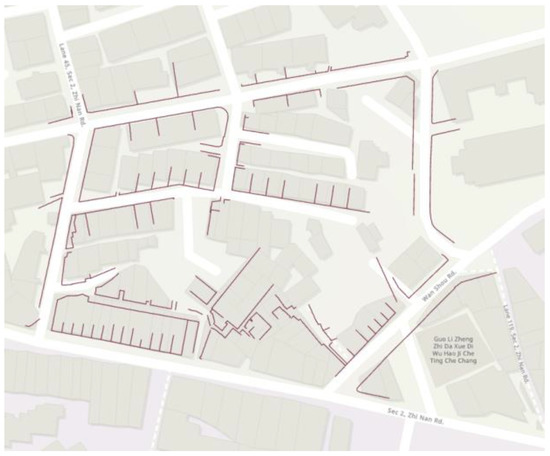
Figure 26.
The result of digitized detail lines from the corrected handheld LiDAR point cloud.
3.3.5. Results Analysis
- (1)
- Analysis of detail line data
The digitized data of the corrected hand-held LiDAR point cloud and the results survey by a total station are shown in Figure 27. The orange points were the detail points surveyed by a total station. By visual inspection, there was no significant difference between the digitized detail lines and detail points.
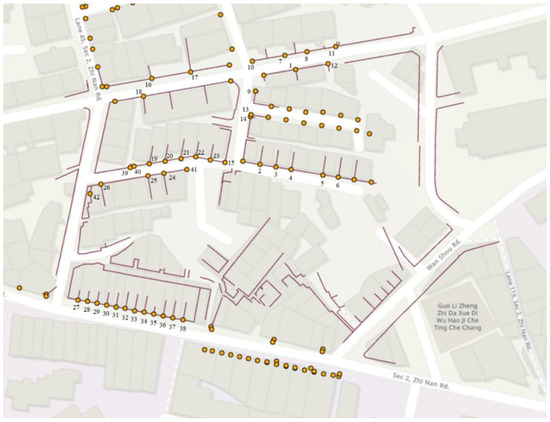
Figure 27.
The digitized results of the corrected handheld LiDAR points and detail points surveyed by a total station.
This test area contained 10 detail points surveyed by a total station which could be used for planar position analyses (see Figure 3a) and 32 detail points surveyed by a total station which were used for vertical distance analyses (see Figure 3b). The calculated error value is shown in Figure 28. The maximum plane position error of the current point is about 8.3 cm, most of which is between 2 to 4 cm; the maximum error of the vertical distance between the digitized detail lines and the detail points was about 16.5 cm, and most of them were below 5 cm. In Taiwan, the maximum map scale in graphic digitized areas is 1/500, the accuracy is 15 cm on-site. Therefore, 5 cm was used for the first level for the analysis, then 5 cm to 10 cm was the second level, 10 cm to 15 cm was the third level, the other level was greater than 15 cm. Figure 29 shows the error statistics of the integration of the two error analyses based on the four levels.
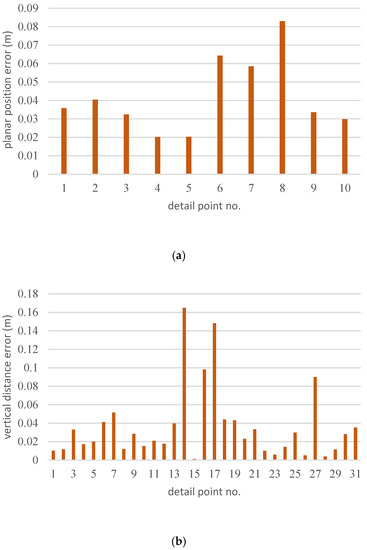
Figure 28.
The error analysis of digitized detail line data. (a) Planar position analysis. (b) Vertical distance error analysis.
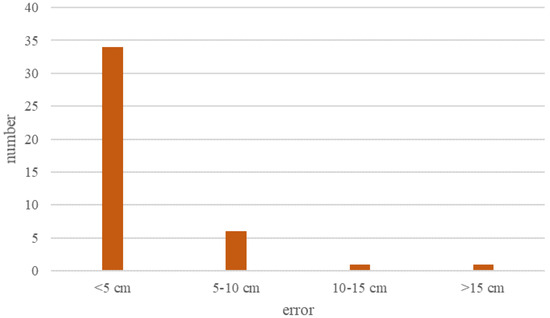
Figure 29.
The statistics of two error analyses of the digitized line data.
The error of the digitized detail data using the point cloud after the error correction of the ranging system verified by the detail points surveyed by a total station, the average error was 3.44 cm. About 97.62% of the digitized detail line data was less than 15 cm. There was still one digitized detail error greater than 15 cm, but the selection of the detail point location obtained by a total station implied the subjective judgment of the surveyor.
In areas with more complex building types, the selection of the detail point location by the surveyor might be slightly different from the digitized location. The digitized detail line data was the centerline of the stairwell in the townhouses. The surveyor could only visually observe the approximate centerline position when surveying by a total station instrument. Compared with the corner points of the townhouses, the detail point surveyed by a total station was more susceptible to the influence of subjective judgment of the surveyor. Therefore, these test results verified that digitized detail line data using the corrected hand-held LiDAR point cloud was sufficient for the detail line data production in the cadastral graphic digitized area. With the advantages of its fast scanning speed and mobile mapping, it could scan a larger amount of detail point cloud on the ground in a short time, and the required detail line data could be digitized for subsequent cadastral overlap analysis.
- (2)
- Analysis of the effect of ranging system error correction.
Based on the description in Section 2.2.4, the error difference of digitized detail lines using the handheld LiDAR point clouds after and before ranging system error correction is shown in Figure 30. Among 42 detail points, the error of 25 detail points, compared with the digitized line data using uncorrected point clouds, was greater than the digitized line data using the corrected point cloud. The positive values shown in Figure 30 indicate that the accuracy was improved. The error was reduced by a maximum of 2.7 cm. The error of 17 detail points compared with the digitized line data using uncorrected point clouds was less than the digitized line data using corrected point cloud. The negative values shown in Figure 30 indicate that the accuracy was not improved.
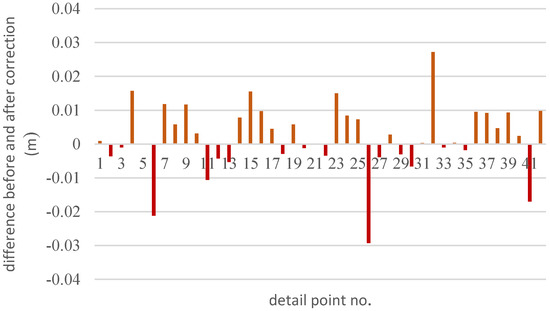
Figure 30.
Error difference of digitized detail line data using the corrected and uncorrected handheld LiDAR point clouds.
Regardless of the error difference within 5 mm, about 73% error of the digitized detail line data was reduced from the detail line data digitized using the uncorrected collected handheld LiDAR points. Although 27% error of the digitized detail line data was still higher than the digitized detail line data using the uncorrected collected handheld LiDAR points, only less than 5% of the digitized detail data was of an error difference greater than 2 cm. This suggests that the correction of the ranging system error could improve the accuracy of most of the digitized detail data. An error difference greater than 2 cm was not only affected by the quality of the trajectory solution of the handheld LiDAR but also affected by the detail points from the subjective judgment of the surveyor.
4. Conclusions
In this study, the feasibility of using a hand-held LiDAR scanner for the urban cadastral detail survey was studied. Before performing the urban cadastral detail survey by the handheld LiDAR scanner, named the GeoSLAM Zeb-Horizon scanner, the scanner calibration was conducted by using the ground LiDAR scanner to collect the planar point cloud in the selected indoor calibration field for calibration planes to calculate the planar parameters for calibration. The ranging system error parameters, including the range scale factor (S) and the rangefinder offset (C), of the VLP-16 multi-beam sensor carried by the GeoSLAM Zeb-Horizon handheld LiDAR scanner were determined by the plane-based calibration method proposed in our previous study [16].
After calibration, the distribution of residuals was more concentrated at 0 and the residual distribution was more in line with the normal distribution curve. The average residual was much closer to 0, and the posterior unit weight standard deviation became smaller, both of which were improved compared to those without adding the ranging system error parameter into the adjustment. Therefore, the plane-based dynamic calibration method proposed in our previous study [16] used in this study could eliminate most of the ranging system errors of the GeoSLAM Zeb-Horizon handheld LiDAR scanner.
From the analysis of the RMSE results of the check planes, the RMSE of all the check planes was improved after the correction of the ranging system error for calibration data. Up to 72.12% in one plane, an increase of about 2.4 cm was reached. The overall average improvement was 32.61%. From the improvement of the RMSE of the check planes, it demonstrated again that the proposed calibration approach could effectively improve the overall point cloud accuracy of the GeoSLAM Zeb-Horizon handheld scanner.
From the investigation of the correlation between the additional ranging parameters S and C, the negative correlation between the ranging additional parameters S and C was −0.82. The lower negative correlation between the ranging additional parameters makes the solution results of the ranging additional parameters S and C more reliable. Meanwhile, the calibration data with about 40 ~45 m longer pseudo-calculated ranging measurements for calibration, the calibration data used in our previous study [16] with about only 20 m calculated pseudo-ranging measurements for calibration. Therefore, the negative correction in [16] was extremely high to −0.985. However, −0.82 was also high, so if a larger calibration site or a suitable scanning could be planned to collect the handheld LiDAR points with longer calculated pseudo-ranging measurements for calibration in the future, the negative correlation would expect to be reduced.
For the analysis of ranging systematic error parameters S and C, this study concluded that scanning by a handheld LiDAR scanner, even if it was 2 m, the correction would be 1 cm for the ranging measurement. When using a handheld LiDAR scanner for precise surveying, for example, cadastral surveying, the errors of this ranging system should be corrected to obtain more accurate results.
For the urban cadastral detail survey test, two independent scannings were performed in the test area. Each scanning task took about 15 min and each scanned path was all closed paths to ensure the accuracy of the trajectory calculations. Those scanning points were corrected by the calibration ranging system error and they were used to manually digitize the urban detail line data. According to the test results, the use of a handheld LiDAR scanner could collect the 3D detail point clouds more globally and is easy to use in narrow lanes where it is not easy for GNSS to receive the satellite signals and a total station or a ground LiDAR scanner is difficult to set up.
Using the detail points surveyed by a total station to verify the detail line data digitized from the corrected handheld LiDAR point cloud, 97% error of the digitized detail data was less than 15 cm. It demonstrated the digitized detail data was sufficient for the urban cadastral detail survey in the cadastral graphic digitization area in Taiwan.
Compared with the digitized detail data from uncorrected handheld LiDAR points, regardless of the 5 mm difference between the digitized detail line data before and after the system error correction, about 73% error of the digitized detail line data were reduced against the detail line data digitized using the uncorrected collected handheld LiDAR points. Although 27% error of the digitized detail line data was still higher than the digitized detail line data using the uncorrected collected handheld LiDAR points, only less than 5% of the digitized detail data was of a difference greater than 2 cm, indicating that the correction of the ranging system error could improve the accuracy of most of the digitized detail data.
The results demonstrated the feasibility of using a handheld LiDAR scanner to perform an urban cadastral detail survey in digitized graphic areas. Therefore, the handheld LiDAR scanner could be used for the production of the detail lines for an urban cadastral detail survey for digitized cadastral areas in Taiwan. In the future, it is possible that it could also be used as a handheld scanner to create a 3D cadaster for land management.
Author Contributions
S.-H.C. conceived, designed the experiments; S.-H.C. and K.-W.H. K.-W.H. simultaneously performed the test, analyzed the data, and wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This study was financially supported under the project number of the Ministry of Science and Technology, Taiwan: MOST 109-2221-E-004-001. A special thanks to the Ministry of Science and Technology, Taiwan.
Conflicts of Interest
The founding sponsors had no role in the design of the study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
References
- Wu, T.P.; Kao, S.P.; Ning, F.S. Study on Computer Registering for Land Revision of Digitalized Graphic Maps. J. Cadastr. Surv. 2003, 22, 1–23. (In Chinese) [Google Scholar]
- Chio, S.-H.; Chiang, C.-C. Feasibility Study Using UAV Aerial Photogrammetry for a Boundary Verification Survey of a Digitalized Cadastral Area in an Urban City of Taiwan. Remote Sens. 2020, 12, 1682. [Google Scholar] [CrossRef]
- Park, J.; Lee, K.-W. Analysis of the Status of Mine and Methods of Mine Geospatial Information Construction Technology for Systematic Mine Management. J. Korea Acad.-Ind. Coop. Soc. 2018, 19, 355–361. [Google Scholar]
- Bosse, M.; Zlot, R. Continuous 3D scan-matching with a spinning 2D laser. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4312–4319. [Google Scholar] [CrossRef]
- Bosse, M.; Zlot, R.; Flick, P. Zebedee: Design of a spring-mounted 3-D range sensor with application to mobile mapping. IEEE Trans. Robot. 2012, 28, 1104–1119. [Google Scholar] [CrossRef]
- Chen, S.; Liu, H.; Feng, Z.; Shen, C.; Chen, P. Applicability of personal laser scanning in forestry inventory. PLoS ONE 2019, 14, e0211392. [Google Scholar] [CrossRef] [PubMed]
- Mudicka, S.; Matolak, M.; Kapica, R.P. Application of handheld scanner in documentation of historical buildings. Sofia Surv. Geol. Min. Ecol. Manag. (SGEM) 2019, 10, 39–46. [Google Scholar]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest Inventory with Terrestrial LiDAR: A Comparison of Static and Hand-Held Mobile Laser Scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef] [Green Version]
- Park, J.K.; Um, D.Y. Application of Handheld Scanner to Investigate Diameter at Breast Height and Tree Height. Int. J. Mob. Device Eng. 2019, 3, 1. [Google Scholar] [CrossRef]
- Hunčaga, M.; Chudá, J.; Tomaštík, J.; Slámová, M.; Koreň, M.; Chudý, F. The Comparison of Stem Curve Accuracy Determined from Point Clouds Acquired by Different Terrestrial Remote Sensing Methods. Remote Sens. 2020, 12, 2739. [Google Scholar] [CrossRef]
- Dewez, T.; Plat, E.; Degas, M.; Richard, T.; Pannet, P.; Thuon, Y.; Meire, B.; Watelet, J.-M.; Cauvin, L.; Lucas, J. Handheld Mobile Laser Scanners Zeb-1 and Zeb-Revo to map an underground quarry and its above-ground surroundings. In Proceedings of the 2nd Virtual Geosciences Conference: VGC, Bergen, Norway, 21–23 September 2016. [Google Scholar]
- Chiabrando, F.; Sammartano, G.; Spanò, A. A Comparison among Different Optimization Levels in 3D Multi-Sensor Models: A Test Case in Emergency Context: 2016. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W3, 155–162. [Google Scholar] [CrossRef] [Green Version]
- Makkonen, T.; Heikkilä, R.; Kaaranka, A.; Naatsaari, M. The Applicability of the Rapid Handheld Laser Scanner to Underground Tunnel Surveying. In Proceedings of the 32nd International Symposium on Automation and Robotics in Construction, Oulu, Finland, 15–18 June 2015. [Google Scholar]
- James, M.R.; Quinton, J.N. Ultra-rapid topographic surveying for complex environments: The hand-held mobile laser scanner (HMLS). Earth Surf. Process. Landf. 2014, 39, 138–142. [Google Scholar] [CrossRef] [Green Version]
- Sršan, A. Mogućnosti Primjene GeoSLAM Tehnologije za Izmjeru Zatvorenih Prostora. Undergraduate Thesis, Polytechnic of Međimurje in Čakovec, Čakovec, Croatia, 2019. Available online: https://urn.nsk.hr/urn:nbn:hr:110:324934 (accessed on 2 December 2021).
- Hou, K.-W.; Chio, S.-H. Plane-based range calibration method for geoslam zeb-horizon handheld lidar instrument. In Proceedings of the International Symposium on Remote Sensing (ISRS) (ISRS 2021), Virtual Conference, 26–28 May 2021. [Google Scholar]
- Glennie, C.; Lichti, D.D. Static Calibration and Analysis of the Velodyne HDL-64E S2 for High Accuracy Mobile Scanning. Remote Sens. 2010, 2, 1610–1624. [Google Scholar] [CrossRef] [Green Version]
- Glennie, C. Calibration and Kinematic Analysis of the Velodyne HDL-64E S2 Lidar Sensor. Photogramm. Eng. Remote Sens. 2012, 78, 339–347. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with application to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Chan, T.; Lichti, D.D.; Roesler, G.; Cosandier, D.; Durgham, K. Range scale-factor calibration of the velodyne vlp-16 lidar system for position tracking applications. In Proceedings of the 11th International Conference on Mobile Mapping, Shenzhen, China, 6–8 May 2019; Volume 70–77, pp. 350–355. [Google Scholar]
- Moritz, H. Advanced Least-Squares Methods; Reports of the Department of Geodetic Science, Report No. 175; Ohio State University Research Foundation: Columbus, OH, USA, 1972. [Google Scholar]
- Ruffhead, A. An introduction to least-squares collocation. Surv. Rev. 1987, 29, 85–94. [Google Scholar] [CrossRef]
- Jana, Š. Testování Přístroje GeoSLAM ZEB-REVO RT. Master’s Thesis, Czech Technical University in Prague, Prague, Czech Republic, 2020. [Google Scholar]
- Maboudi, M.; Bánhidi, D.; Gerke, M. Evaluation of indoor mobile mapping systems. In Proceedings of the GFaI Workshop 3D North East, Berlin, Germany, 7–8 December 2017. [Google Scholar]
- Russhakim, N.; Mohd Ariff, M.F.; Darwin, N.; Majid, Z.M.; Idris, K.; Abbas, M.; Zainuddin, K.; Yusoff, A. The suitability of terrestrial laser scanning for strata building. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 67–76. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).


















