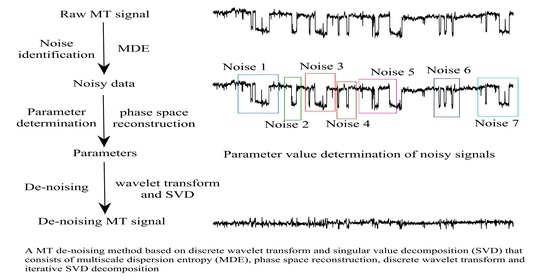
De-Noising of Magnetotelluric Signals by Discrete Wavelet Transform and SVD Decomposition
Abstract
:1. Introduction
2. Methods
2.1. Multiscale Dispersion Entropy
- (1)
- Time series uj (j = 1, 2, …, N) are taken via a coarse graining preprocessing for non-overlapping segments xb and are obtained as follows:where τ is the scale factor, L = [N/τ] represents the length of the data segment, N is the length of time series, and [•] is the integral function.
- (2)
- xb is mapped to c classes from 1 to c. First, the normal cumulative distribution function (NCDF) is employed to map the segment to yb from 0 to 1:where rms represents the root mean square and σ is the standard deviation (SD) of the segment, t is the length of observation time in each data segment. A linear algorithm zbc = round(c• yb + 0.5) is used for yb to zbc from 1 to c. Then, the embedding dimension m and time delay d are introduced to reconstruct zim,c as follows:where i = 1, 2…L(m1)d. The number of possible dispersion patterns that can be assigned to each time-series zim,c is equal to cm, since the signal has m members and each member can be an integer from 1 to c.Finally, for each cm potential dispersion pattern, the relative frequency is defined as follows:where represents the number of dispersion patterns that are assigned to zim,c divided by the total number of embedding signals with embedding dimension m. , …, .
- (3)
- The MDE is obtained as follows:where represents the dispersion entropy based on Shannon’s entropy.
2.2. Phase Space Reconstruction
2.2.1. Mutual Information Function
2.2.2. False Nearest Neighbors
2.3. Discrete Wavelet Transform
2.4. SVD Decomposition
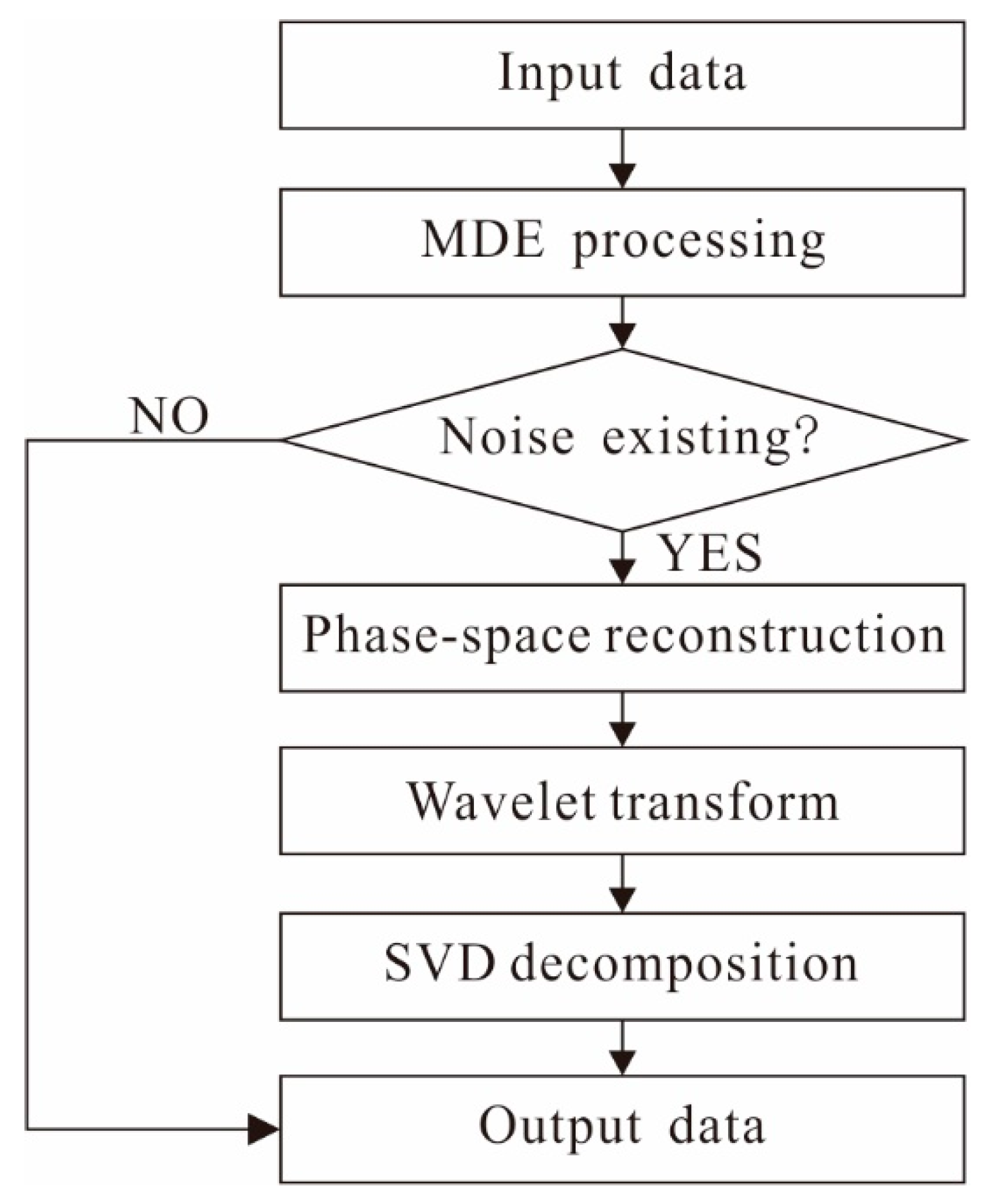
- Overlap data to segments to ensure the continuity of the data;
- Calculate the MDE for each data segment, for which the value below the threshold is the noisy data segment;
- Apply phase space reconstruction to calculate the number of wavelet decomposition level in noisy data segments;
- Perform discrete wavelet transform and discrete wavelet inverse transform for multiple components;
- Decompose the components using iterative SVD to obtain the de-noised section;
- Reconstruct the MT de-noising signal with the useful data segments given in Step 1 and the de-noising data segments given in Step 5, where the average value of the two segments is adopted for the overlapping data.
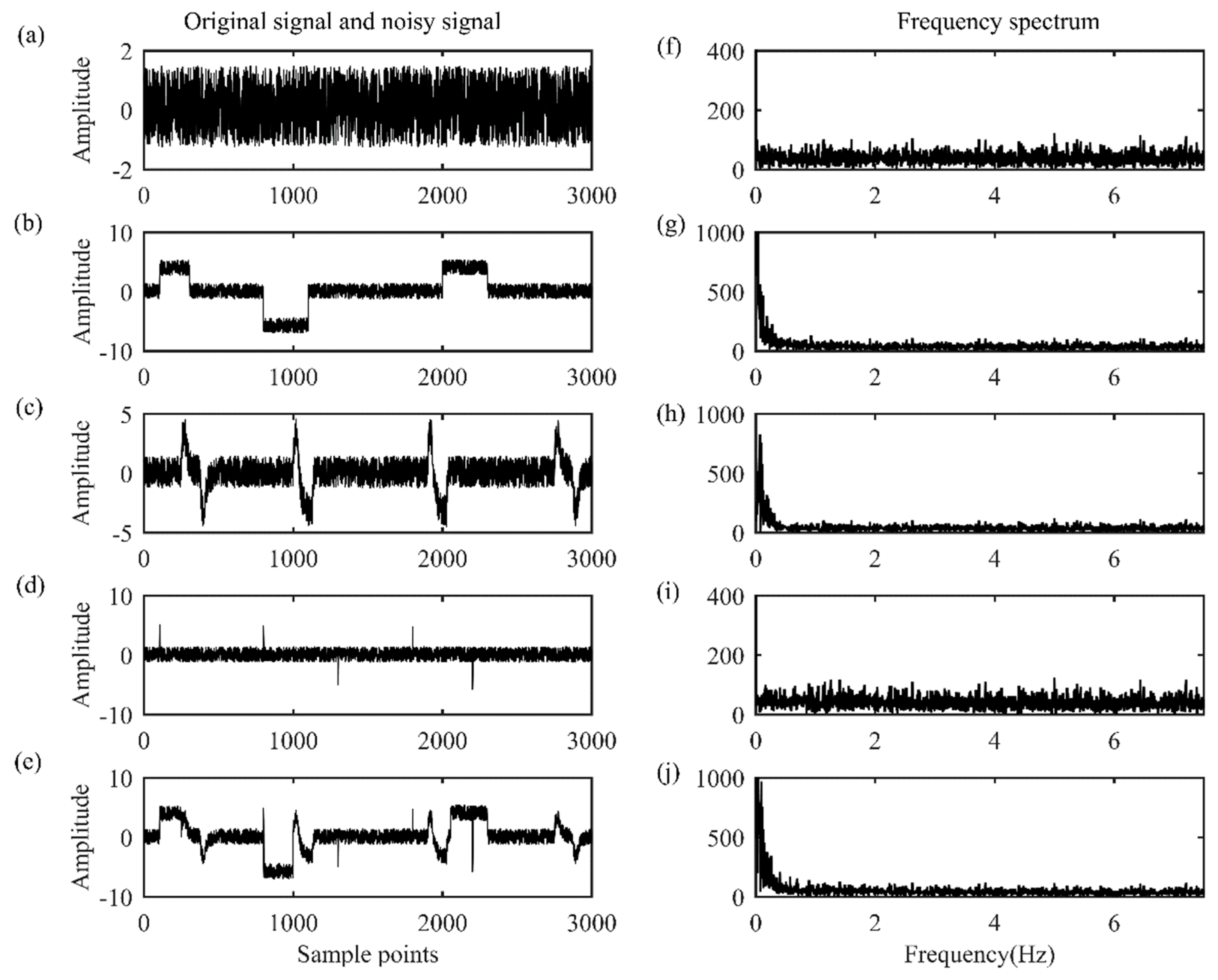
3. Synthetic Cases
3.1. Entropy Analysis
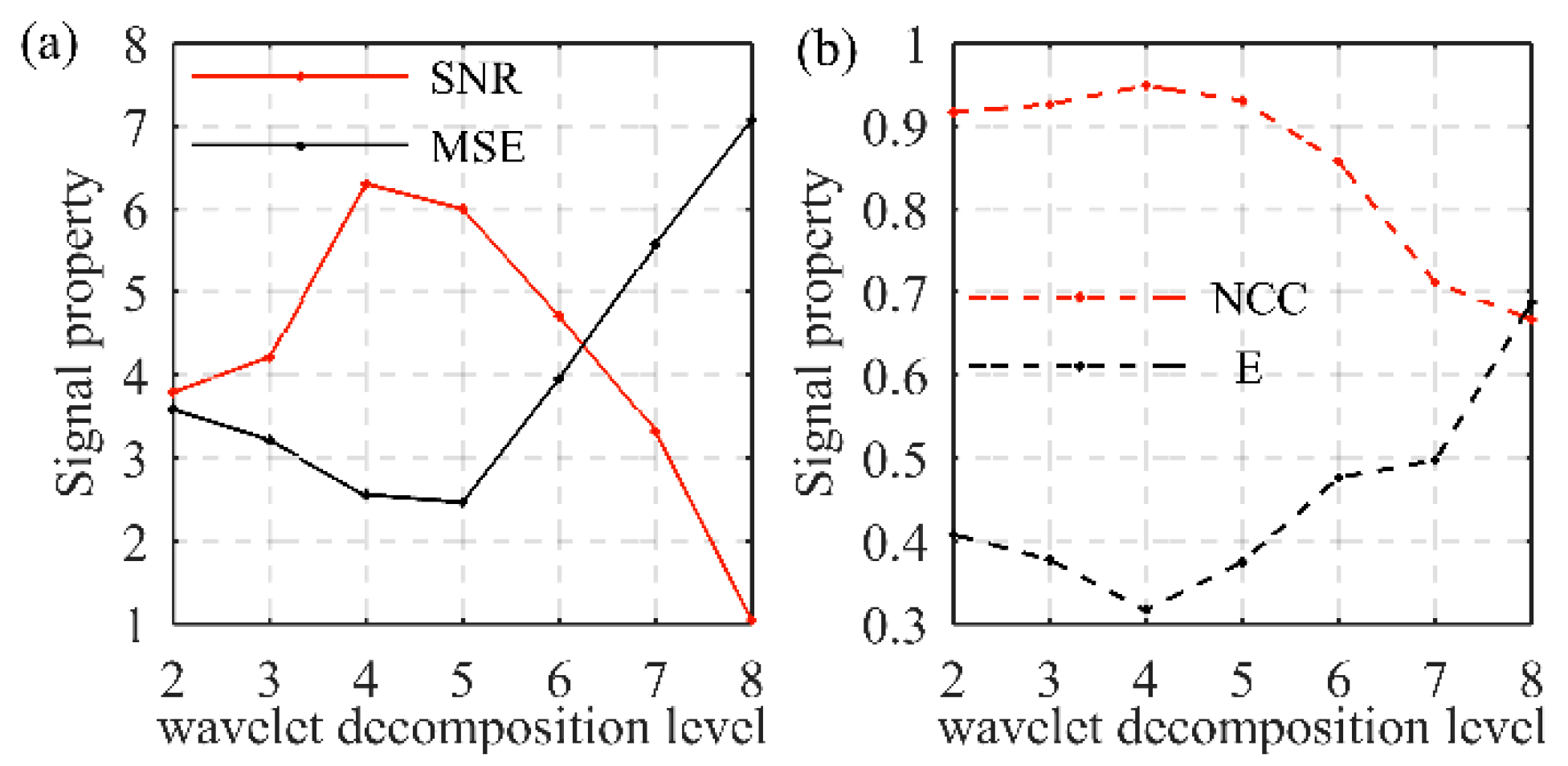
3.2. Parameter Calculation
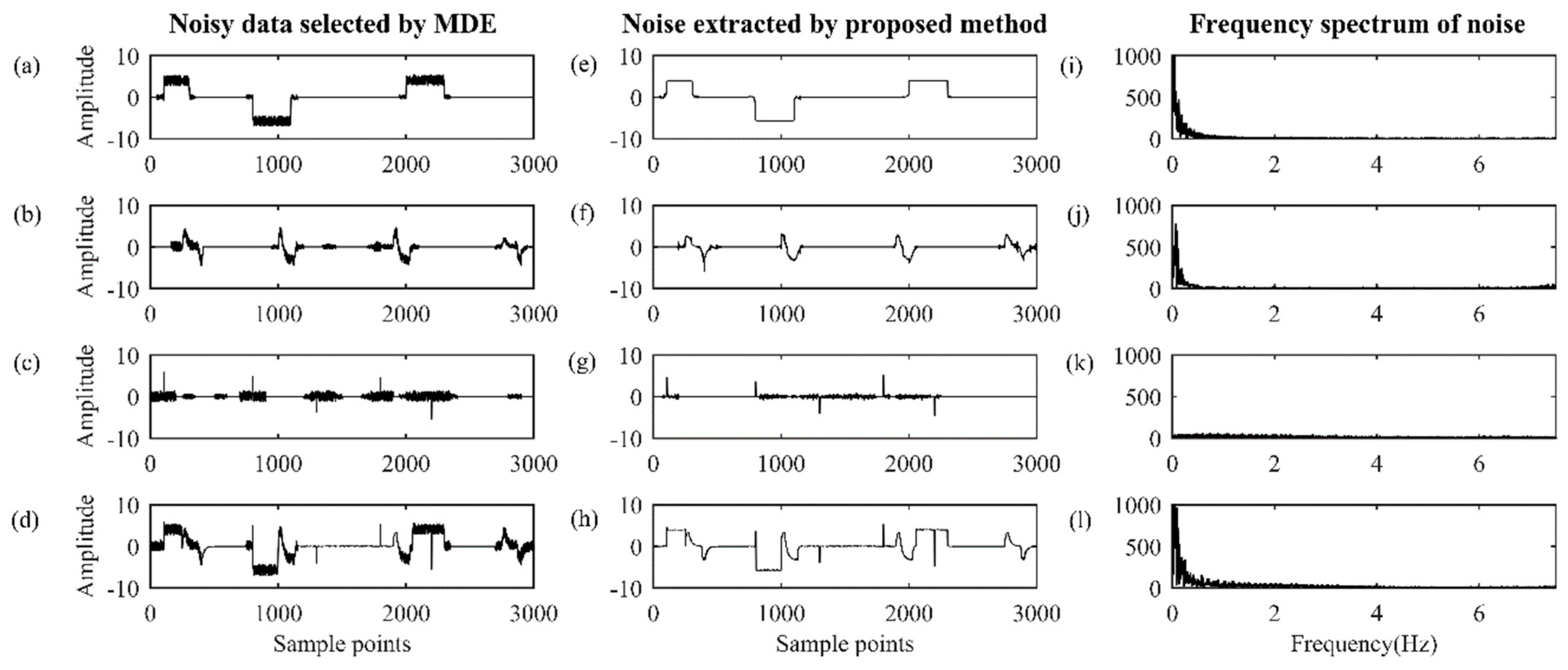
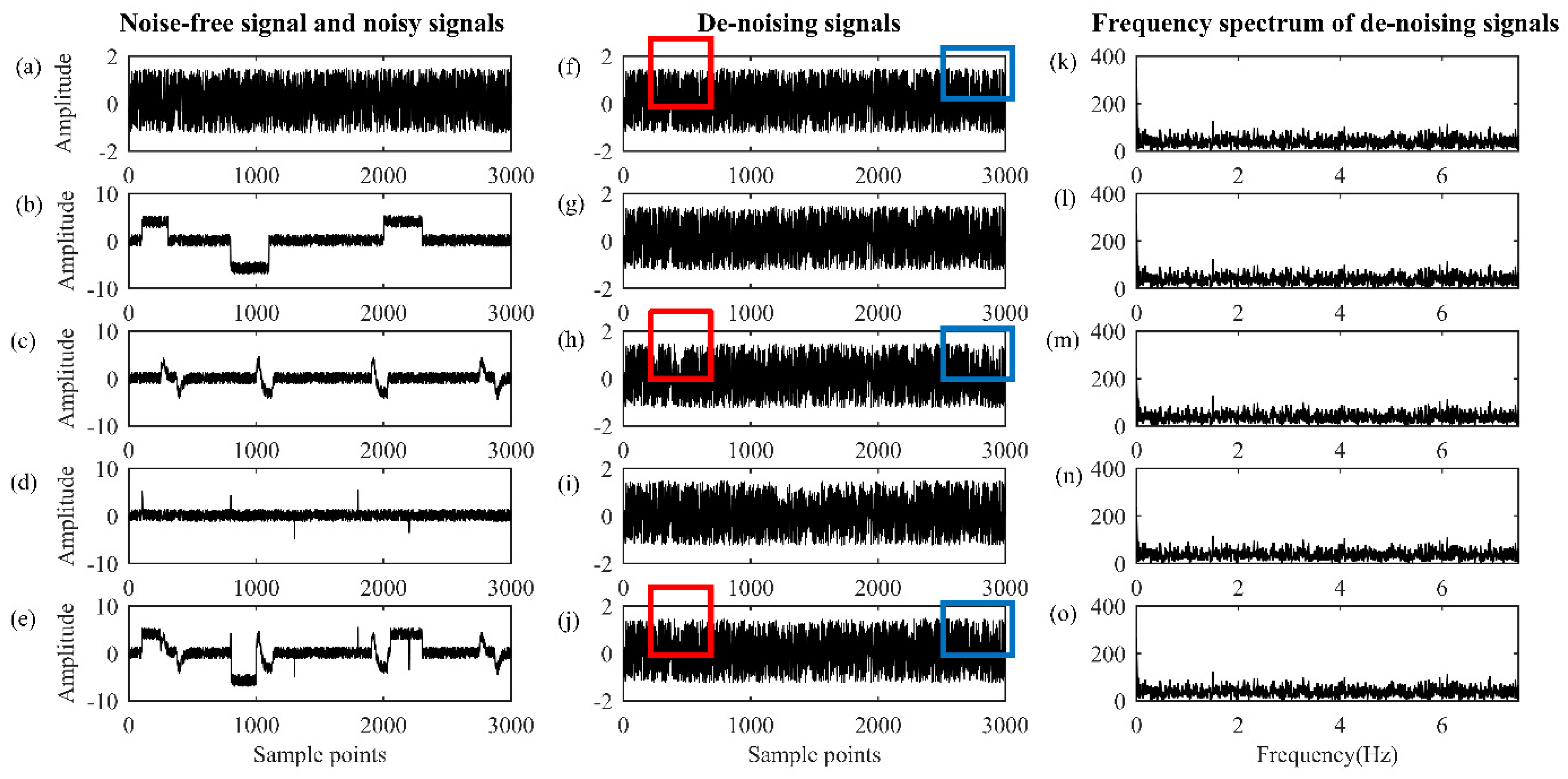
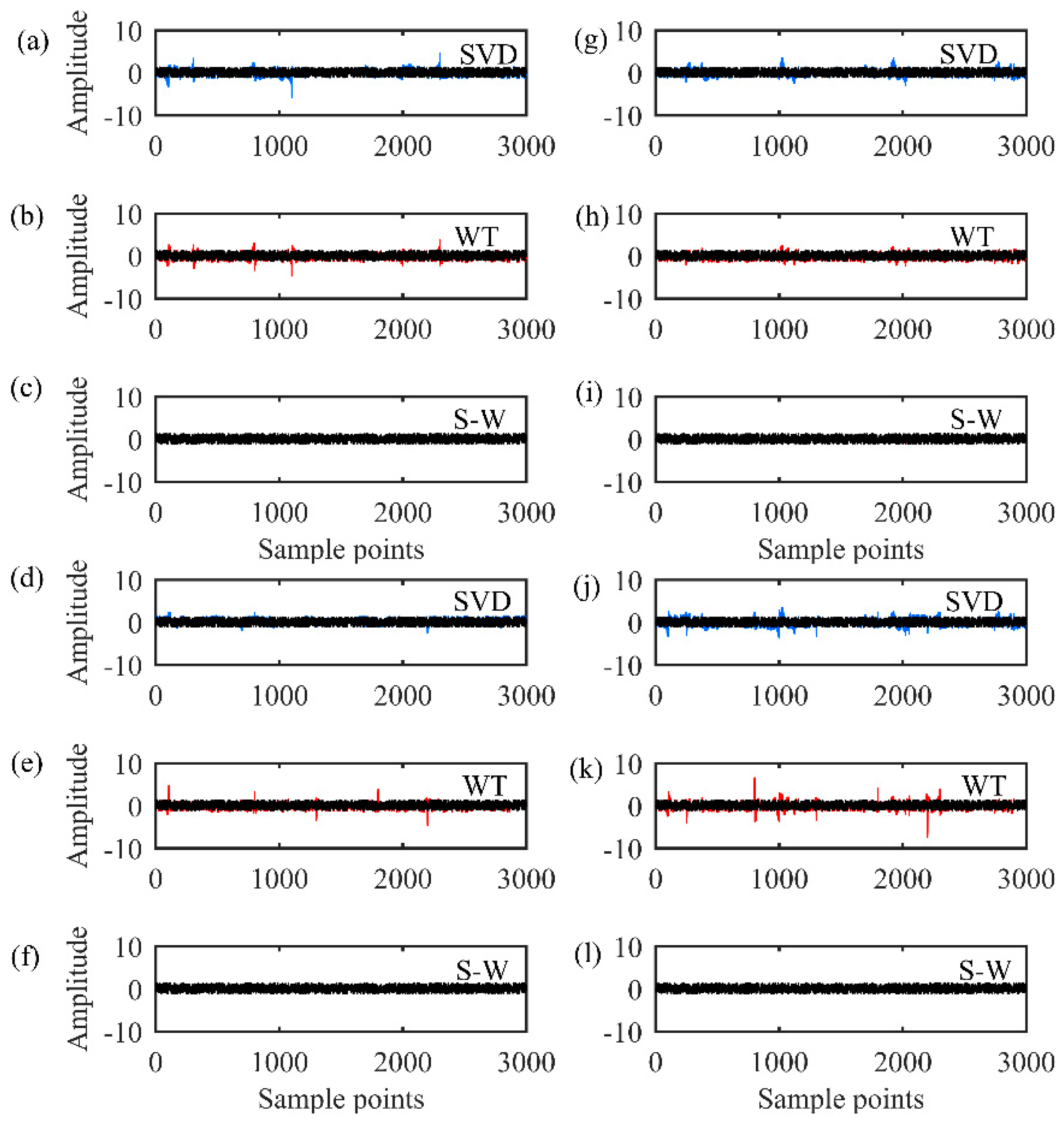
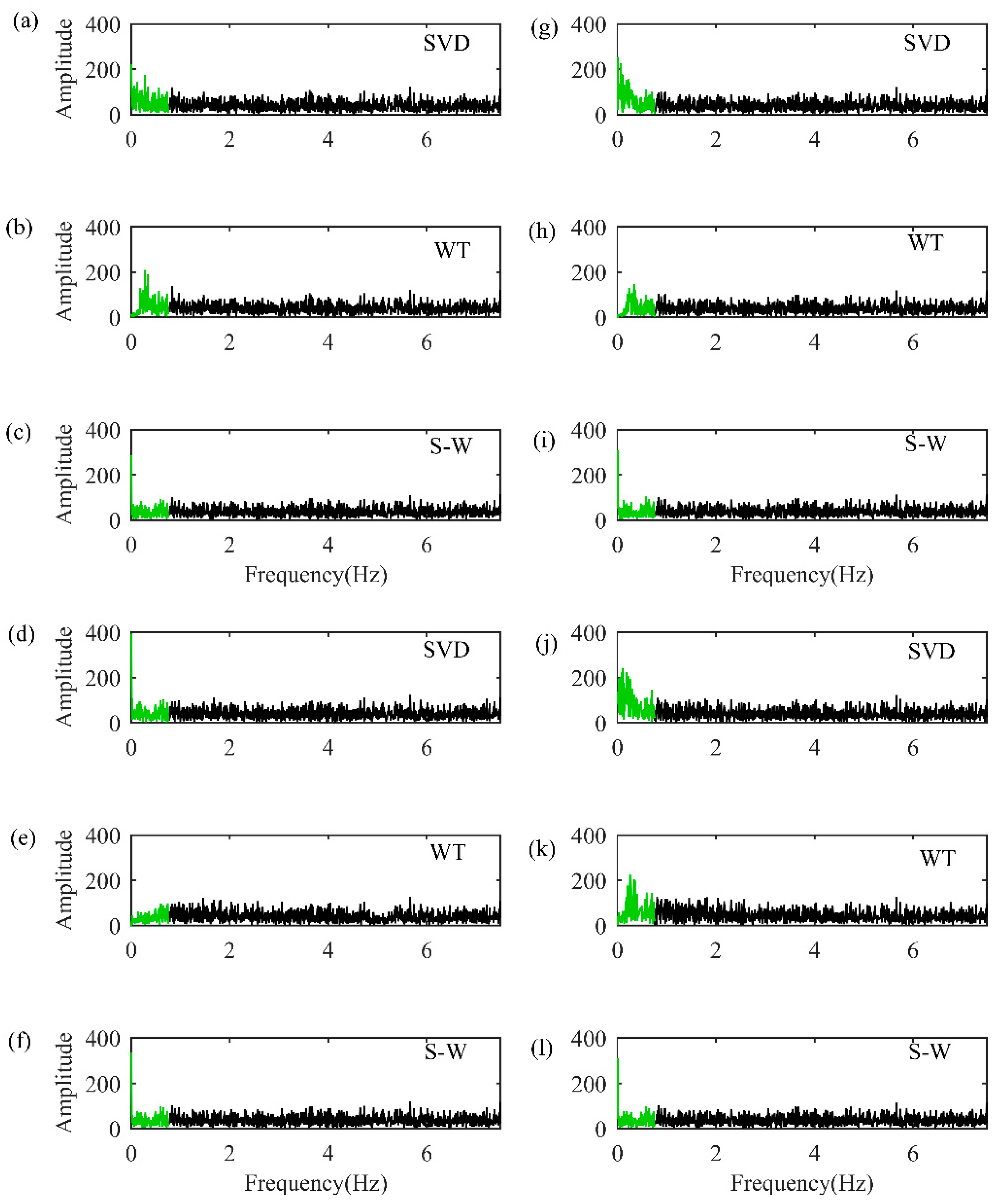
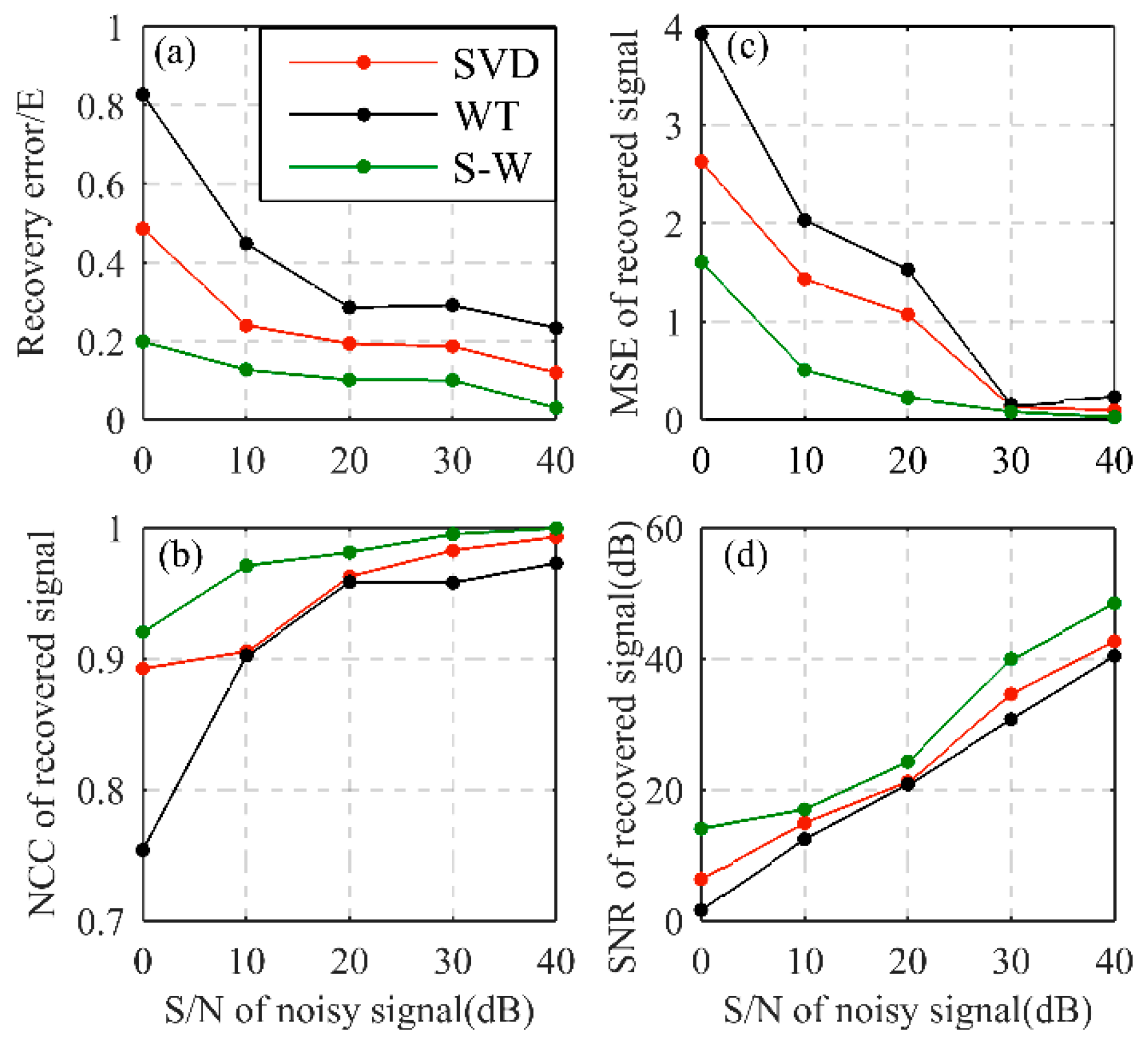
3.3. Performance Evaluation
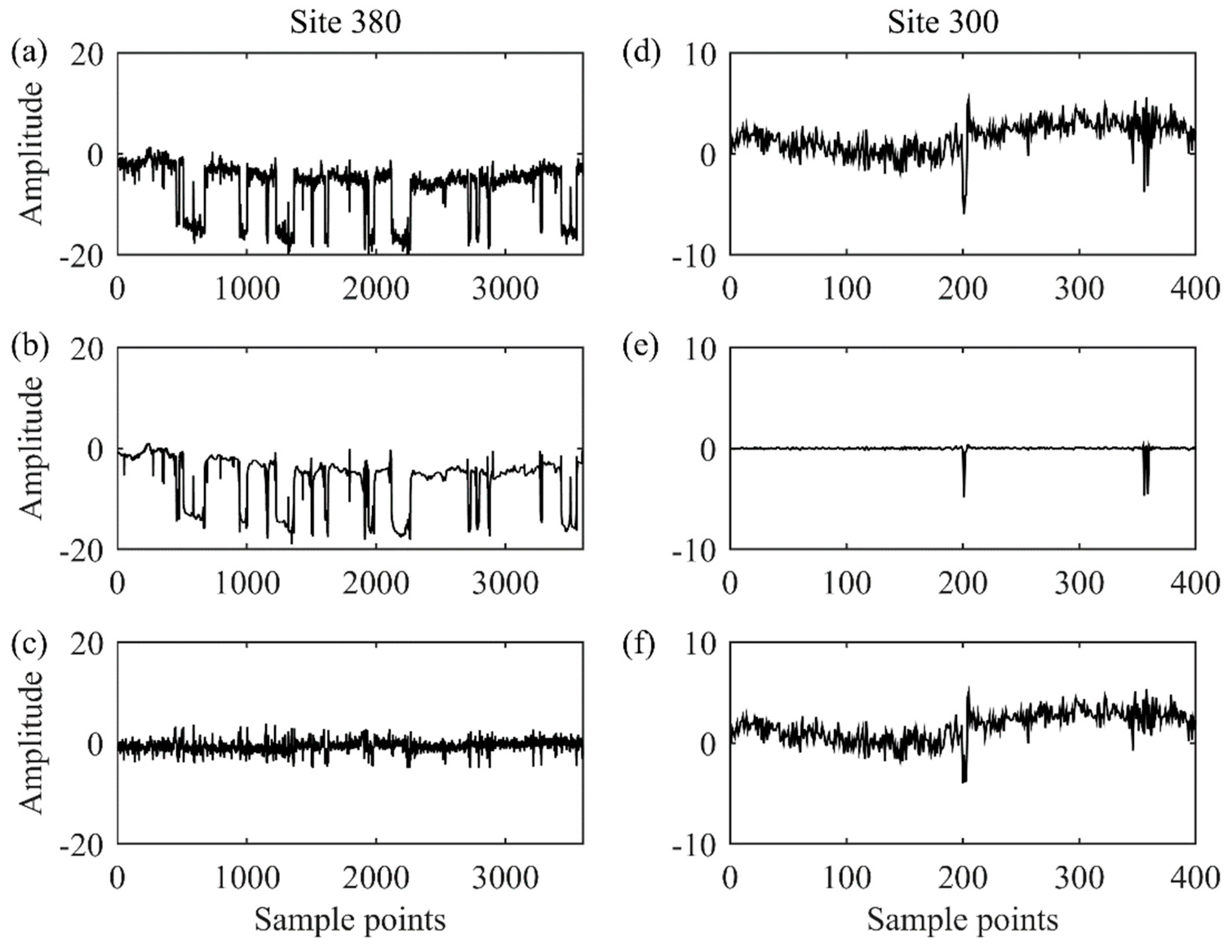
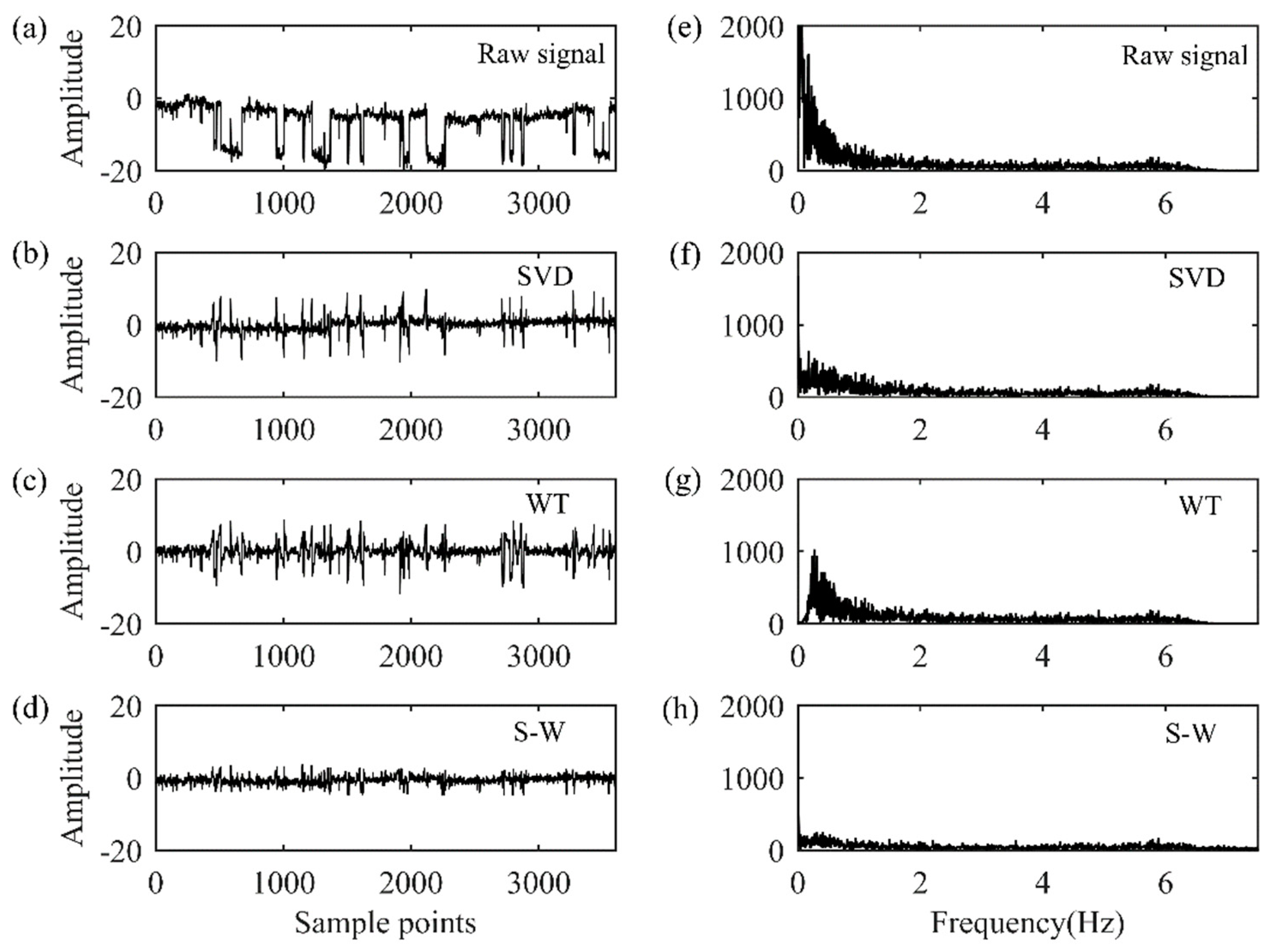
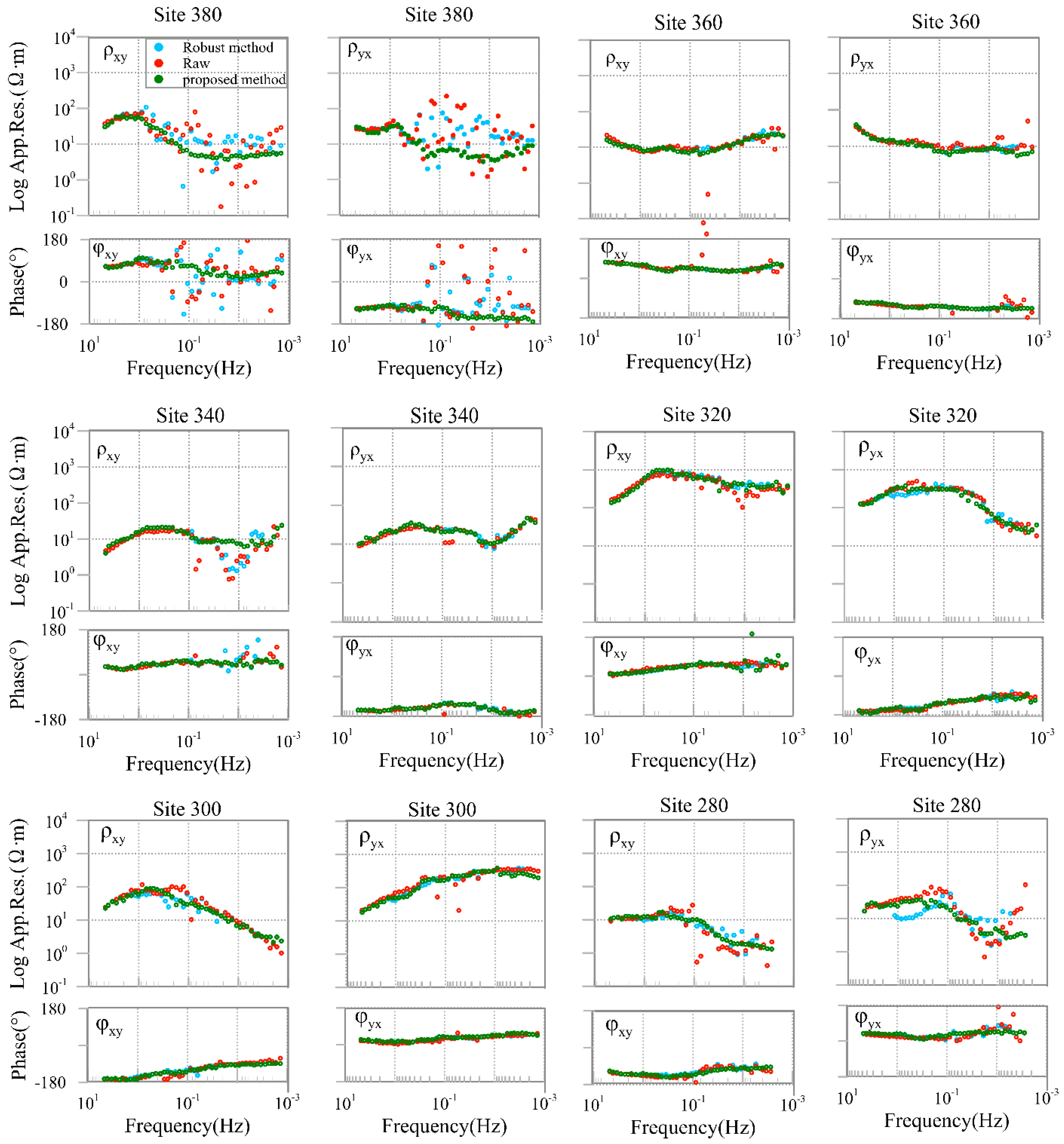
4. Implementation for MT Field Data
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Oliver-Ocaño, F.M.; Gallardo, L.A.; Romo-Jones, J.M.; Perez-Flores, M.A. Structure of the Cerro Prieto Pull-apart basin from joint inversion of gravity, magnetic and magne-totelluric data. J. Appl. Geophys. 2019, 170, 103835. [Google Scholar] [CrossRef]
- Xin, Z.; Han, J.; Liu, C.; Liu, L.; Tian, Y.; Yang, B.; Li, Z.; Mu, Q. Lithospheric structure and transformation of the Songnen and Jiamusi blocks in the eastern segment of the Central Asian Orogenic Belt revealed by 3D magnetotelluric inversion. Tectonophysics 2021, 816, 229015. [Google Scholar] [CrossRef]
- Wu, Y.; Han, J.; Liu, Y.; Ma, G.; Han, F.; Yang, Y.; Liu, L.; Guo, L.; Guan, Y.; Zhang, Y.; et al. Metallogenic model of the Shuangjianzishan Ag-Pb-Zn district, Northeast China: Revealed from integrated geophysical investigation. Geosci. Front. 2021, 10132, (prepubilsh). [Google Scholar] [CrossRef]
- Sims, W.E.; Bostick, F.X., Jr.; Smith, H.W. The estimation of magnetotelluric impedance tensor elements from measured data. Geophysics 1971, 36, 938–942. [Google Scholar] [CrossRef] [Green Version]
- Gamble, T.D.; Goubau, W.M.; Clarke, J. Error analysis for remote reference magnetotellurics. Geophysics 1979, 44, 959–968. [Google Scholar] [CrossRef]
- Jones, A.; Jödicke, H. Magnetotelluric transfer function estimation improvement by a coherence-based rejection technique. In SEG Technical Program Expanded Abstracts 1984; Society of Exploration Geophysicists: Houston, TX, USA, 1984; Volume 50, pp. 51–55. [Google Scholar]
- Egbert, G.D.; Booker, J.R. The robust estimation of geomagnetic transfer functions. Geophys. J. Int. 1986, 87, 173–194. [Google Scholar] [CrossRef] [Green Version]
- Chave, A.D.; Thomson, D.J. Bounded influence magnetotelluric response function estimation. Geophys. J. Int. 2004, 157, 988–1006. [Google Scholar] [CrossRef]
- Sutarno, D.; Vozoff, K. Robust M-estimation of magnetotelluric impedance tensors. Explor. Geophys. 1989, 20, 383–398. [Google Scholar] [CrossRef]
- Streich, R.; Becken, M.; Ritter, O. Robust processing of noisy land-based controlled-source electromagnetic data. Geophysics 2013, 78, E237–E247. [Google Scholar] [CrossRef]
- Smirnov, M.Y. Magnetotelluric data processing with a robust statistical procedure having a high breakdown point. Geophys. J. Int. 2003, 152, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Chave, A.D. Magnetotelluric data, stable distributions and impropriety: An existential combination. Geophys. Geophys. J. Int. 2014, 198, 622–636. [Google Scholar] [CrossRef] [Green Version]
- Weckmann, U.; Magunia, A.; Ritter, O. Effective noise separation for magnetotelluric single site data processing using a frequency domain selection scheme. Geophys. J. Int. 2005, 161, 635–652. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition method and the Hilbert spectrum for non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Clarke, J.; Gamble, T.D.; Goubau, W.M.; Koch, R.H.; Miracky, R.F. Remote-reference magnetotellurics: Equipment and procedures. Geophys. Prospect. 1983, 31, 149–170. [Google Scholar] [CrossRef] [Green Version]
- Egbert, G.D. The robust multiple station magnetotelluric data processing. Geophys. J. Int. 1997, 130, 475–496. [Google Scholar] [CrossRef] [Green Version]
- Ritter, O.; Junge, A.; Dawes, G.J. New equipment and processing for magnetotelluric remote reference observations. Geophys. J. Int. 1998, 132, 535–548. [Google Scholar] [CrossRef] [Green Version]
- Oettinger, G.; Haak, V.; Larsen, J.C. Noise reduction in magnetotelluric time-series with a new signal-noise separation method and its application to a field experiment in the Saxonian Granulite Massif. Geophys. J. Int. 2001, 146, 659–669. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.T.; Hua, X.R.; Cao, Z.M.; Ren, Z.Y.; Duan, S.L. Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data. Chin. J. Geophys. 2008, 51, 603–610. (In Chinese) [Google Scholar]
- Wang, Y.; Zhu, Y.; Wang, Q.; Yuan, S.; Tang, S.; Zheng, Z. Effective component extraction for hydraulic pump pressure signal based on fast empirical mode decomposition and relative entropy. AIP Adv. 2020, 10, 075103. [Google Scholar] [CrossRef]
- Li, Y.; Gao, S.; Zhang, S.; He, H.; Xian, P.; Yuan, C. The baseline wander correction based on the improved ensemble empirical mode decomposition (EEMD) algorithm for grounded electrical source airborne transient electromagnetic signals. Geosci. Instrum. Methods Data Syst. 2020, 9, 443–450. [Google Scholar] [CrossRef]
- Li, J.; Cai, J.; Tang, J.-T.; Li, G.; Zhang, X.; Xu, Z.-M. Magnetotelluric signal-noise separation method based on SVM–CEEMDWT. Appl. Geophys. 2019, 16, 160–170. [Google Scholar] [CrossRef]
- Li, G.; Liu, X.; Tang, J.; Li, J.; Ren, Z.; Chen, C. De-noising low-frequency magnetotelluric data using mathematical morphology filtering and sparse representation. J. Appl. Geophys. 2020, 172, 103919. [Google Scholar] [CrossRef]
- Li, J.; Liu, X.; Li, G.; Tang, J. Magnetotelluric noise suppression based on impulsive atoms and NPSO-OMP algorithm. Pure Appl. Geophys. 2020, 177, 5275–5297. [Google Scholar] [CrossRef]
- Morlet, J.; Arens, G.; Fourgeau, E.; Giard, D. Wave propogation and sampling theory, 1, Complex signal and scattering in multi-layered media. Geophysics 1982, 47, 203–236. [Google Scholar] [CrossRef] [Green Version]
- Daubechies, I. Orthonormal bases of compactly supported wavelets. Commun. Pure Appl. Math. 1988, 41, 901–996. [Google Scholar] [CrossRef] [Green Version]
- Mallat, S.G. Multiresolution approximations and wavelet orthonormal bases of L2(R). Trans. Am. Math. Soc. 1989, 315, 69–87. [Google Scholar]
- Meyer, Y. Wavelets and Operators; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Chui, C.K. An Introduction to Wavelets; Academic Press: Cambridge, MA, USA, 1995; Volume 2, pp. 50–61. [Google Scholar]
- Kumar, P.; Foufoula-Georgiou, E. Wavelet analysis for geophysical applications. Rev. Geophys. 1997, 35, 385–412. [Google Scholar] [CrossRef] [Green Version]
- Trad, D.O.; Travassos, M.J. Wavelet filtering of magnetotelluric data. Geophysics 2000, 65, 482–491. [Google Scholar] [CrossRef]
- Escalas, M.; Queralt, P.; Ledo, J.; Marcuello, A. Polarisation analysis of magnetotelluric time series using a wavelet-based scheme: A method for detection and characterisation of cultural noise sources. Phys. Earth Planet. Inter. 2013, 218, 31–50. [Google Scholar] [CrossRef]
- Liu, H.W. A Study on Feature Selection Algorithms Using Information Entropy. Ph.D. Thesis, Jilin University, Changchun, China, 2010. [Google Scholar]
- Zhang, X.; Li, J.; Li, D.; Li, Y.; Liu, B.; Hu, Y. Separation of magnetotelluric signals based on refined composite multiscale dispersion entropy and orthogonal matching pursuit. Earth Planets Space 2021, 73, 1–18. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Mammone, N.; Morabito, F.C.; Adeli, H. A new dispersion entropy and fuzzy logic system methodology for automated classification of dementia stages using electroencephalograms. Clin. Neurol. Neurosurg. 2021, 201, 106446. [Google Scholar] [CrossRef]
- Chen, K.; Han, B.T. A survey of state space reconstruction of chaotic time series analysis. Comput. Sci. 2005, 32, 67–70. (In Chinese) [Google Scholar]
- Yoo, M.W.; Rontani, D.; Létang, J.; Petit-Watelot, S.; Devolder, T.; Sciamanna, M.; Bouzehouane, K.; Cros, V.; Kim, J.V. Pattern generation and symbolic dynamics in a nanocontact vortex oscillator. Nat. Commun. 2020, 11, 601. [Google Scholar] [CrossRef] [Green Version]
- de Paula Viveiros, A.M. Non-orbital characterizations of strange attractors: Effective intervals and multifractality measures. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 033139. [Google Scholar] [CrossRef] [PubMed]
- Jiayu, L.; Yueke, W.; Zhiping, H.; Zhenkang, S. Selection of proper time-delay in phase space reconstruction of speech signals. Signal. Process. 1999, 15, 220–225. (In Chinese) [Google Scholar]
- Broomhead, D.S.; King, G.P. Extracting qualitative dynamics from experimental data. Phys. Sect. D Nonlinear Phenom. 1986, 20, 217–236. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134. [Google Scholar] [CrossRef] [PubMed]
- Kennel, M.B.; Brown, R.; Abarbanel, H. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [Green Version]
- Takens, F. Detecting strange attractors in turbulence, dynamical systems and turbulence. Lect. Notes Math. 1981, 898, 366–381. [Google Scholar]
- Grossmann, A.; Morlet, J. Decomposition of hardy functions into square integrable wavelets of constant shape. SIAM J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Wei, D. Coiflet-Type Wavelets: Theory, Design and Applications. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 1998. [Google Scholar]
- Carbonari, R.; D’Auria, L.; Di Maio, R.; Petrillo, Z. De-noising of magnetotelluric signals by polarization analysis in the discrete wavelet domain. Comput. Geosci. 2017, 100, 135–141. [Google Scholar] [CrossRef]
- Kousika, N.; Premalatha, K. An improved privacy-preserving data mining technique using singular value decomposition with three-dimensional rotation data perturbation. J. Supercomput. 2021, 77, 10003–10011. [Google Scholar] [CrossRef]
- Shao-Qing, Y.; Chuan-Ying, J. Two practical methods of phase space reconstruction. Acta Phys. Sin. 2002, 51, 2452–2459. (In Chinese) [Google Scholar]
- Candès, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal. Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Li, G.; He, Z.; Tang, J.; Deng, J.; Liu, X.; Zhu, H. Dictionary learning and shift-invariant sparse coding de-noising for CSEM data combined with CEEMD. Geophysics 2021, 86, 1–52. [Google Scholar] [CrossRef]
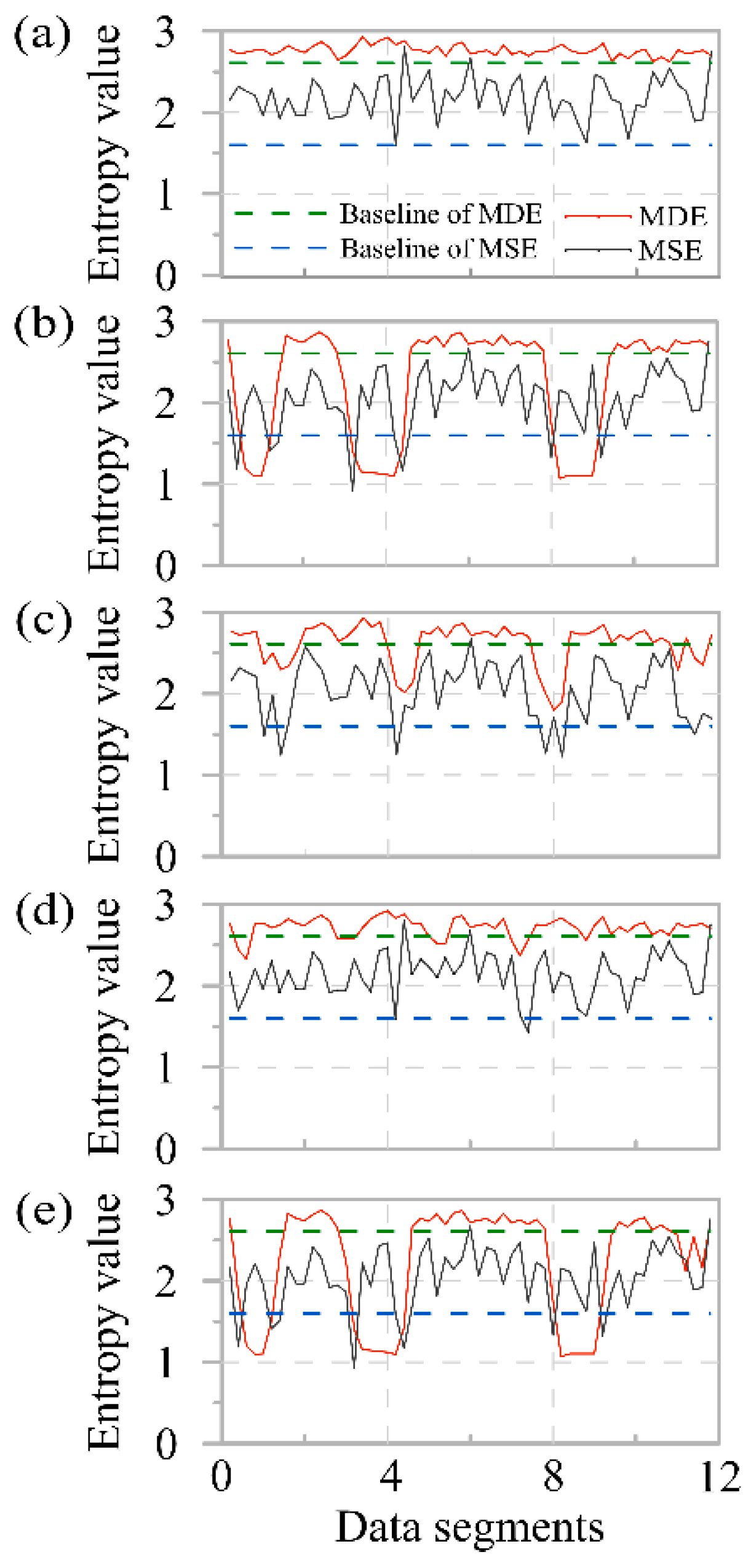
| Different Signals | MAE | MSE | MFE | MDE |
|---|---|---|---|---|
| Noise-free signal | 0.2531 | 1.6493 | 0.1582 | 2.7568 |
| With square wave | 0.4519 | 0.9279 | 0.1369 | 1.1521 |
| With triangle wave | 0.3458 | 1.3142 | 0.1174 | 2.0091 |
| With impulse noise | 0.3379 | 1.5034 | 0.1041 | 2.3361 |
| With various noise | 0.4323 | 0.9013 | 0.1124 | 1.1055 |
| Signals with Different Noise | Noisy Segment1 | Noisy Segment2 | Noisy Segment3 | Noisy Segment4 | Noisy Segment5 | Noisy Segment6 | Noisy Segment7 | Noisy Segment8 |
|---|---|---|---|---|---|---|---|---|
| Square wave | 4 | 5 | 4 | 5 | 4 | 5 | - | - |
| Triangle wave | 5 | 5 | 4 | 5 | 4 | 4 | 4 | 4 |
| Impulse noise | 4 | 5 | 4 | 4 | 4 | 5 | 4 | 4 |
| Various noise | 4 | 5 | 4 | 4 | 4 | 4 | 4 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, R.; Han, J.; Guo, Z.; Li, T. De-Noising of Magnetotelluric Signals by Discrete Wavelet Transform and SVD Decomposition. Remote Sens. 2021, 13, 4932. https://doi.org/10.3390/rs13234932
Zhou R, Han J, Guo Z, Li T. De-Noising of Magnetotelluric Signals by Discrete Wavelet Transform and SVD Decomposition. Remote Sensing. 2021; 13(23):4932. https://doi.org/10.3390/rs13234932
Chicago/Turabian StyleZhou, Rui, Jiangtao Han, Zhenyu Guo, and Tonglin Li. 2021. "De-Noising of Magnetotelluric Signals by Discrete Wavelet Transform and SVD Decomposition" Remote Sensing 13, no. 23: 4932. https://doi.org/10.3390/rs13234932
APA StyleZhou, R., Han, J., Guo, Z., & Li, T. (2021). De-Noising of Magnetotelluric Signals by Discrete Wavelet Transform and SVD Decomposition. Remote Sensing, 13(23), 4932. https://doi.org/10.3390/rs13234932