On the Potential of 3D Transdimensional Surface Wave Tomography for Geothermal Prospecting of the Reykjanes Peninsula
Abstract
1. Introduction
2. Transdimensional Surface Wave Tomography
2.1. Model Parameterization
2.2. The Likelihood
2.3. Forward Modeling
2.4. The Prior
2.5. Reversible Jump McMC
3. Experiment Setup and Computational Performance Tests
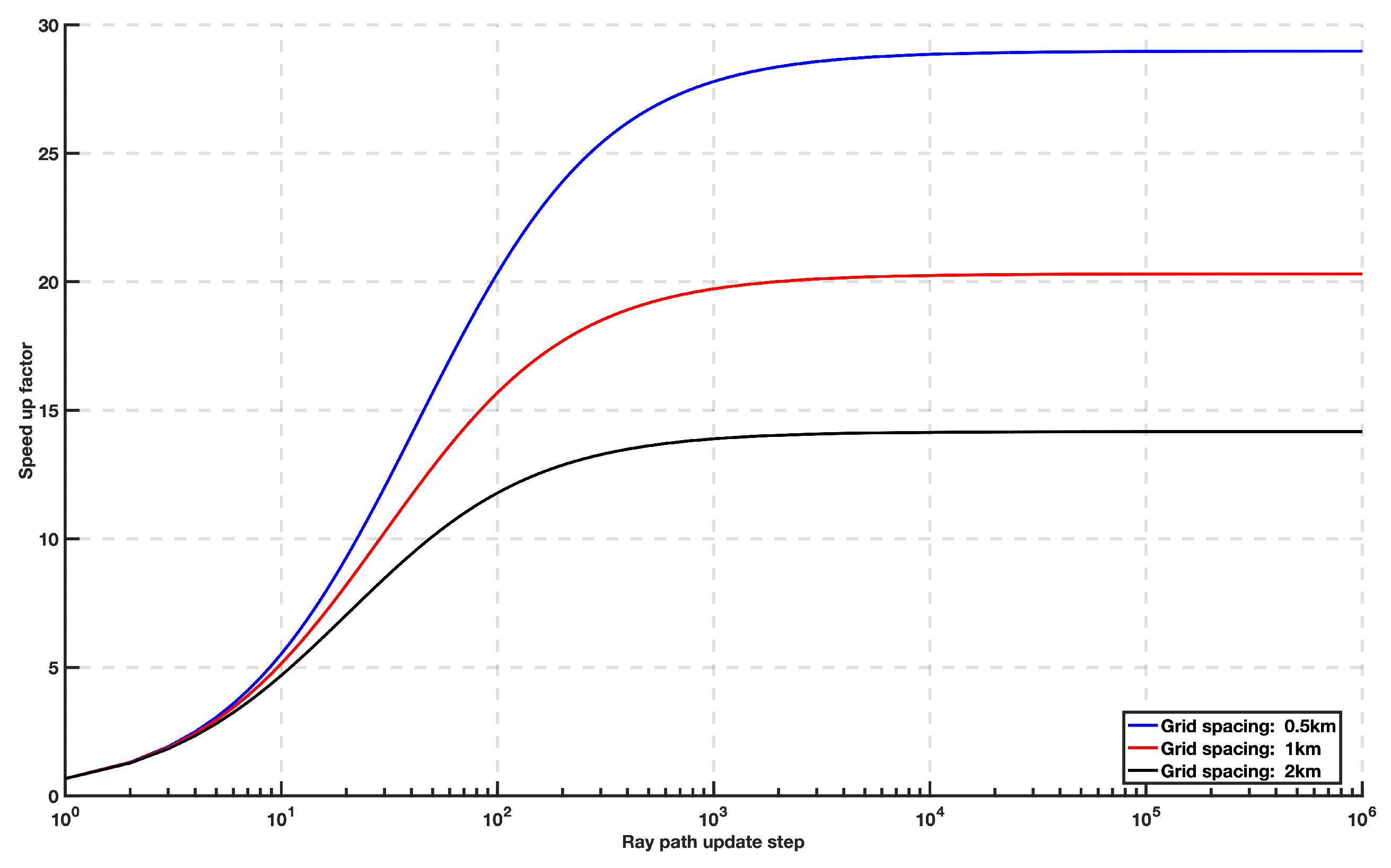
3.1. Ray Path Update and Computational Cost
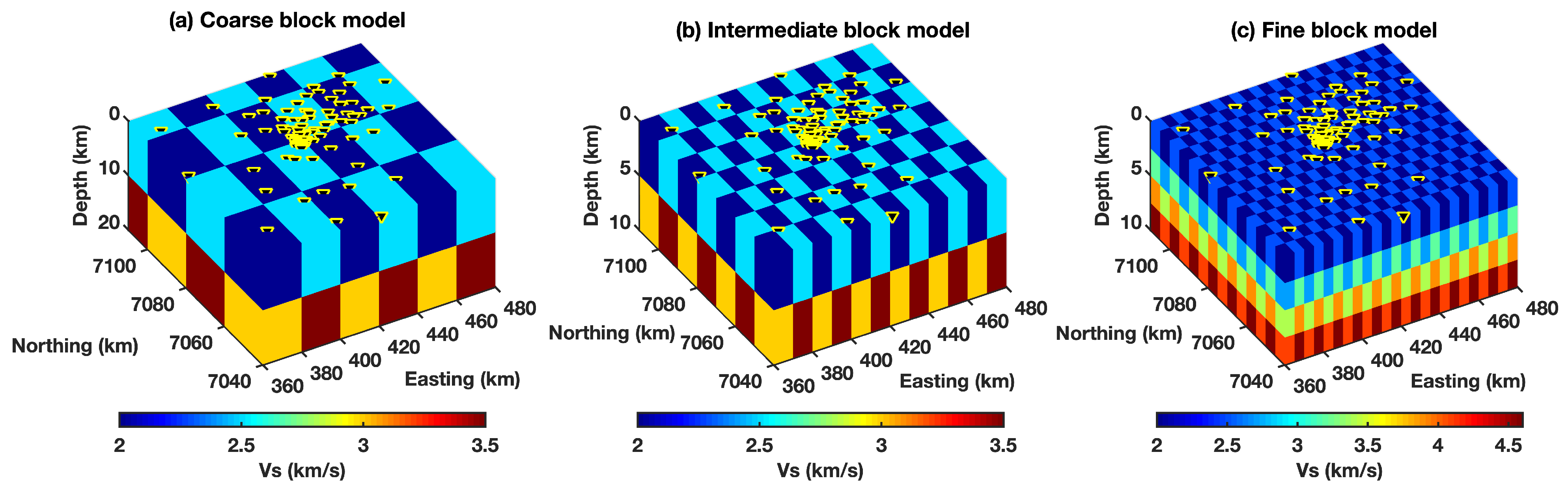
3.2. Block Models
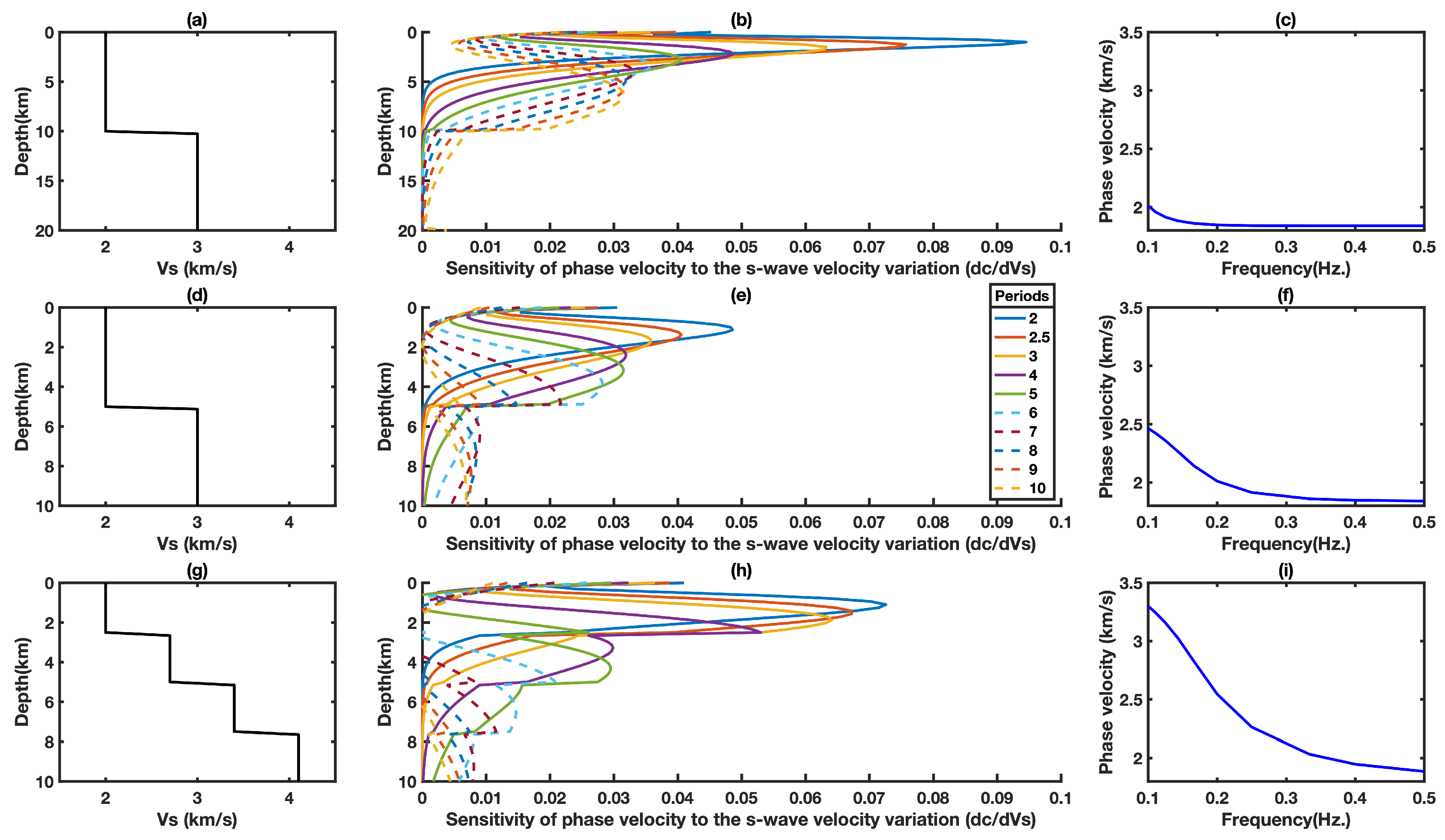
3.3. Sensitivity Kernels
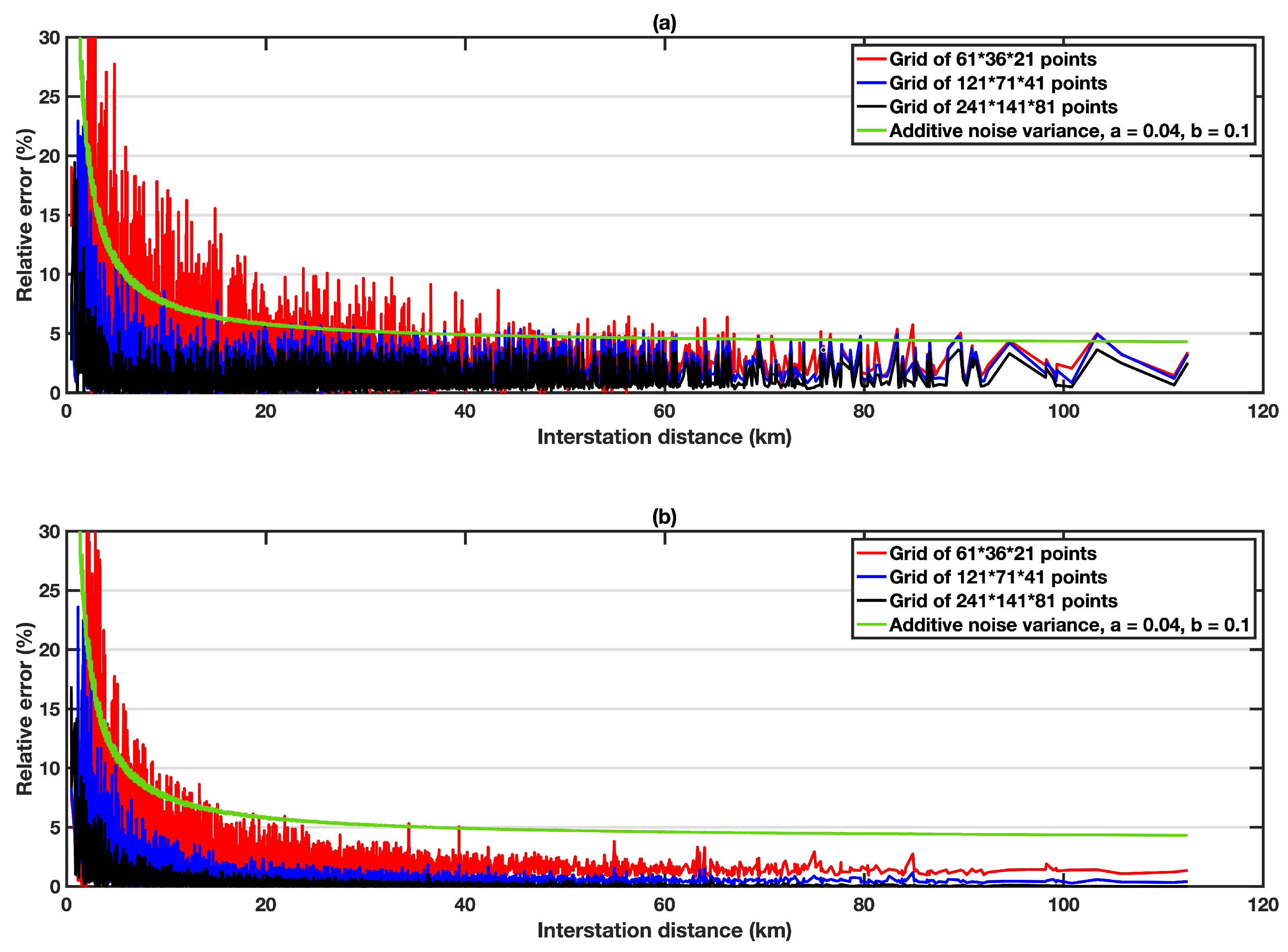
3.4. Additive Noise and Modeling Errors
3.5. Modeling and Inversion Parameters
4. Results and Discussion
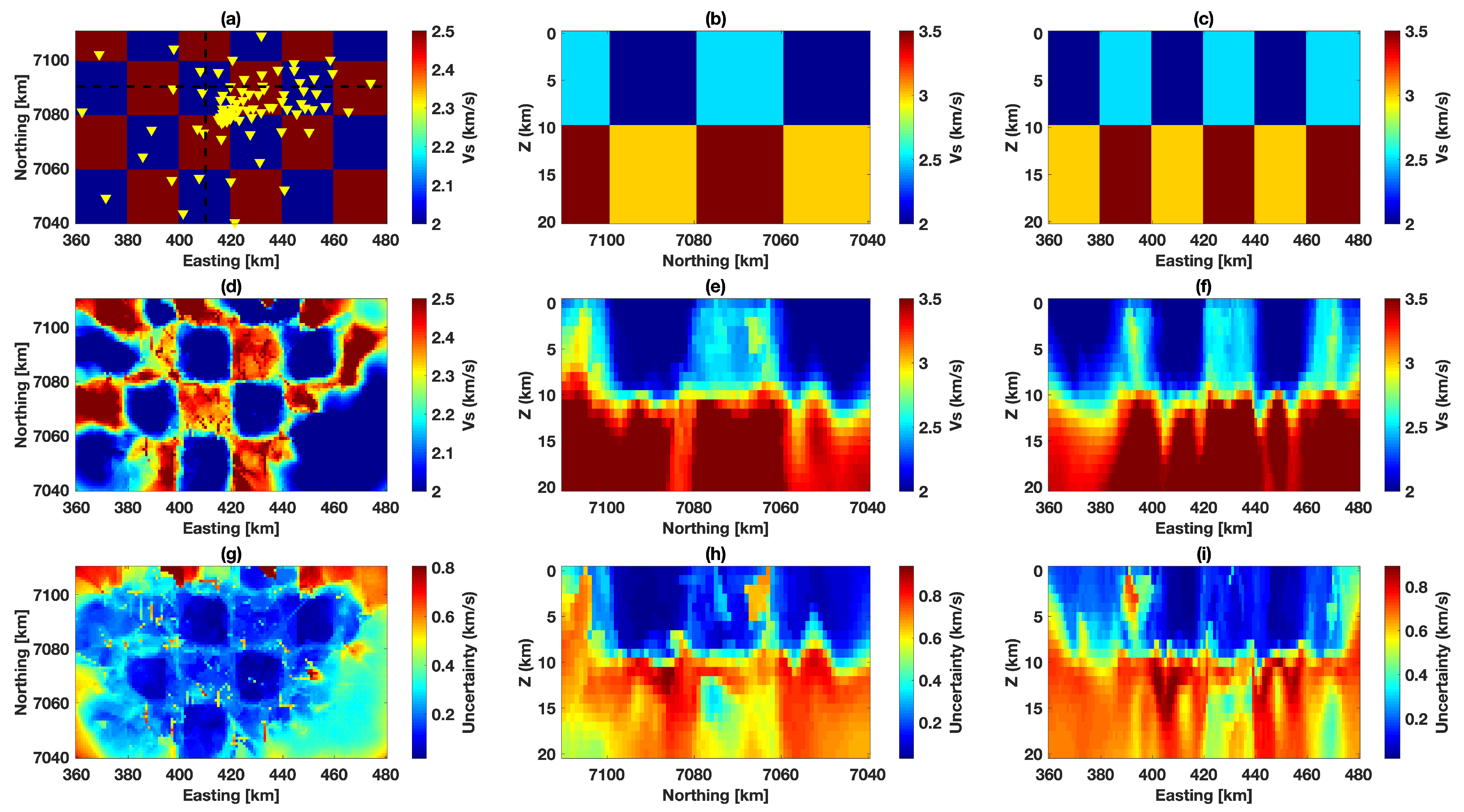
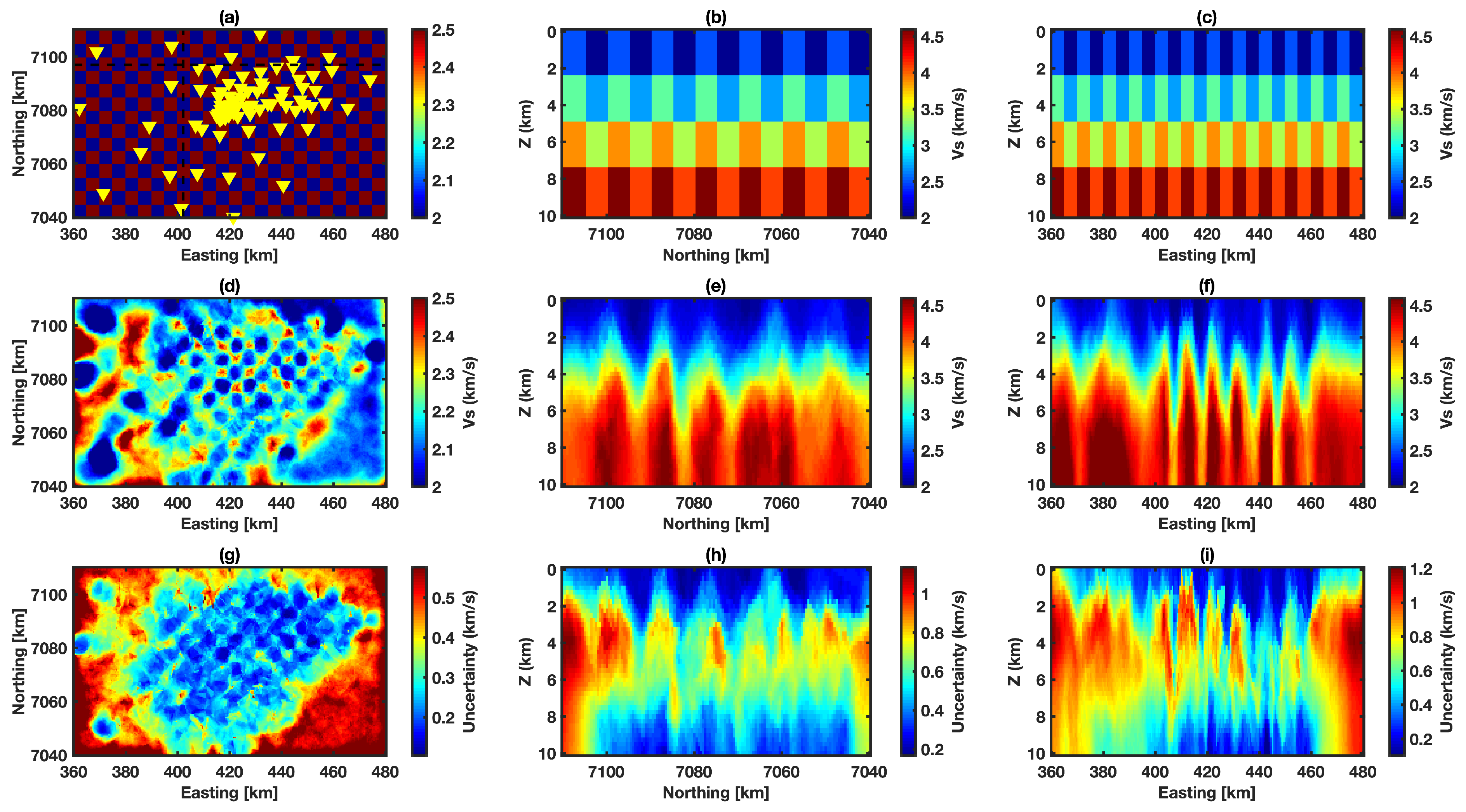
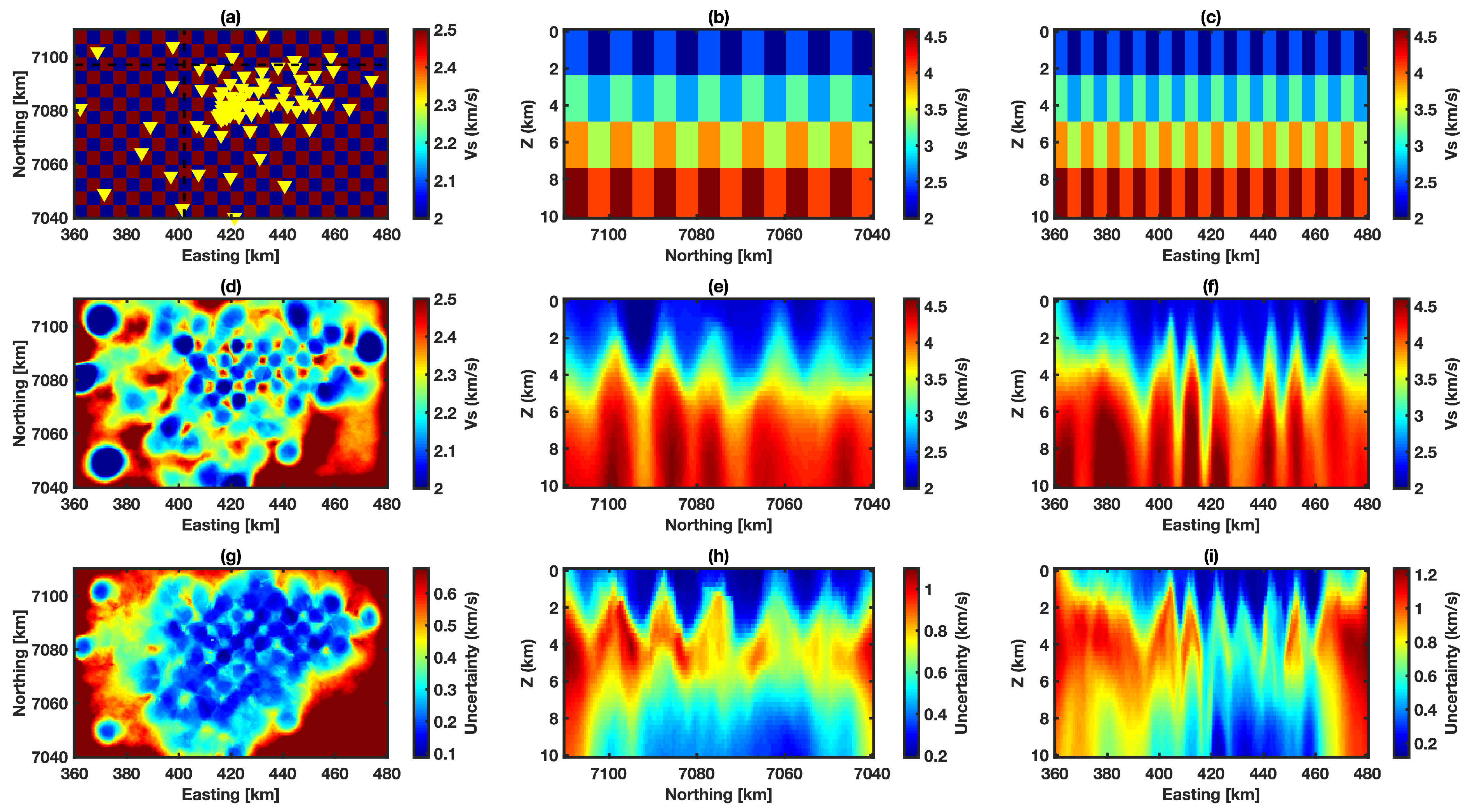
4.1. Coarse Block Model
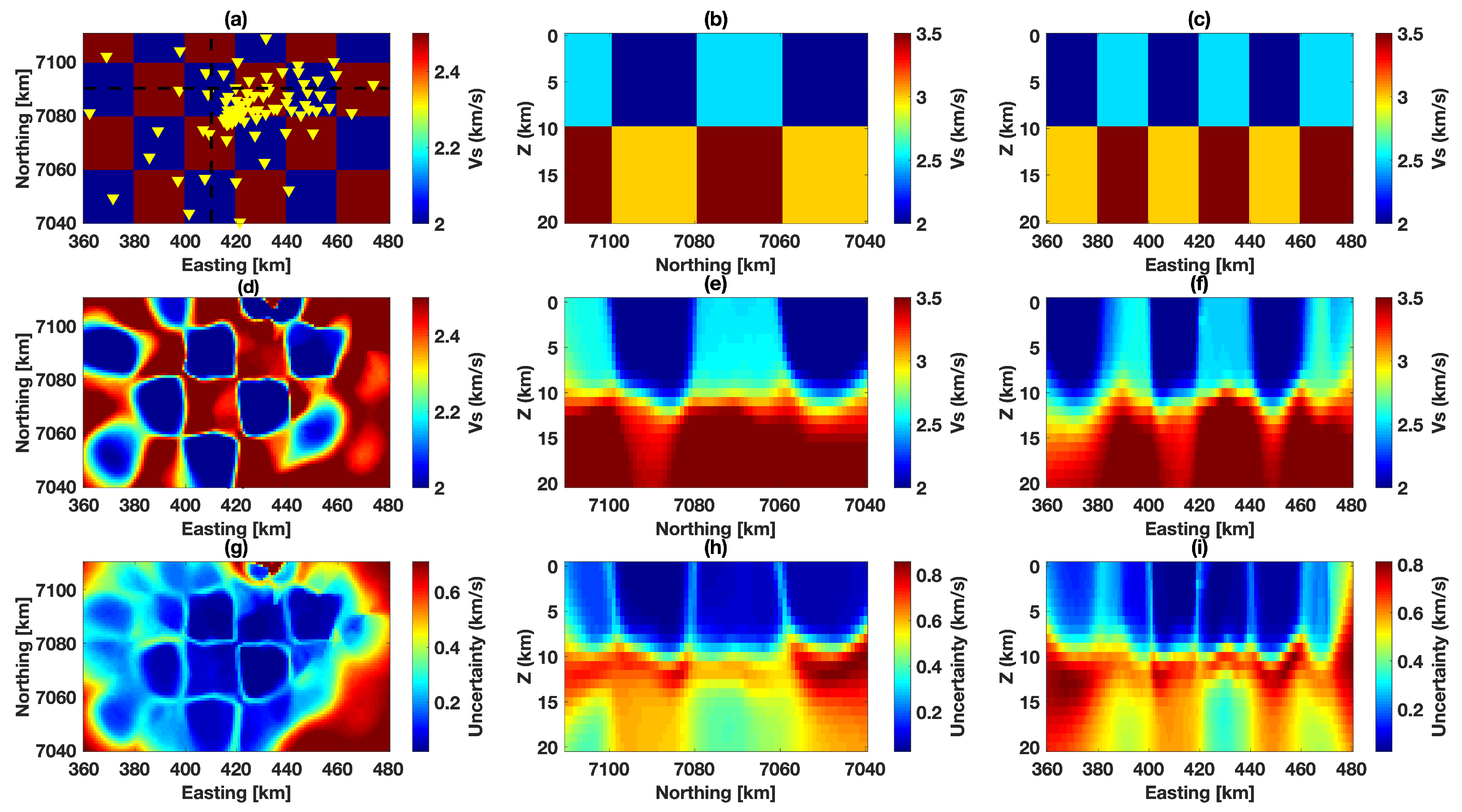
4.2. Intermediate Block Model
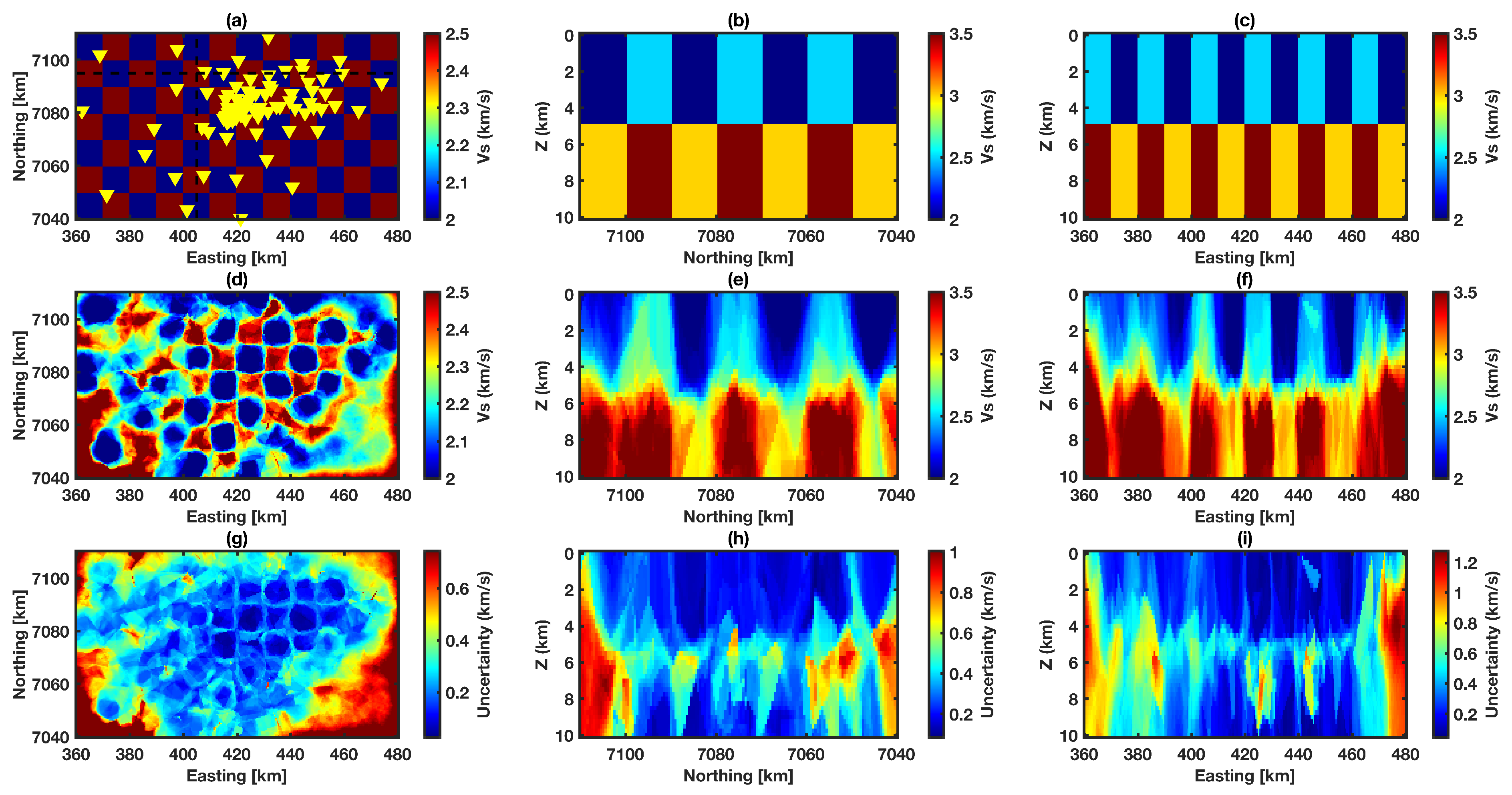
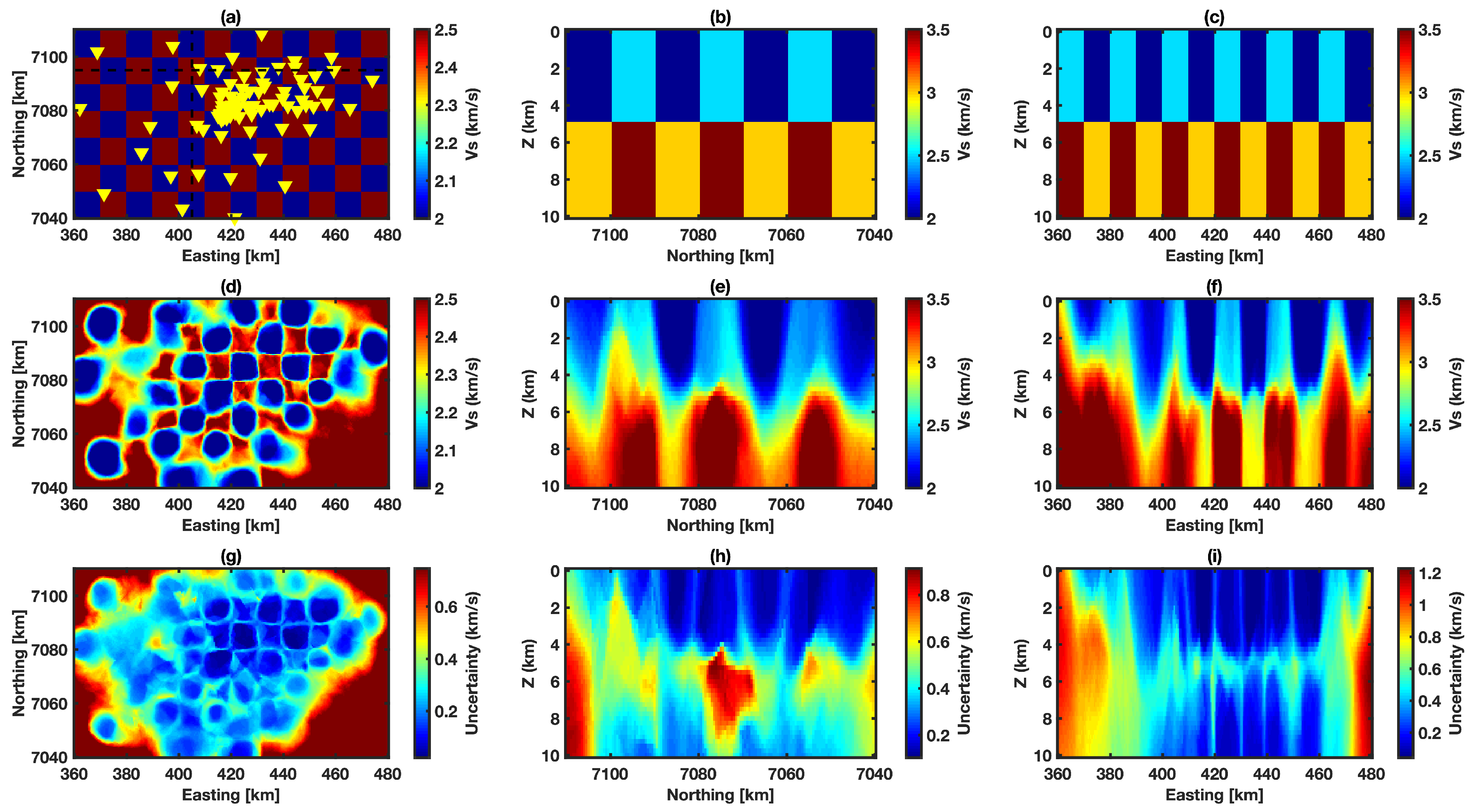
4.3. Fine Block Model
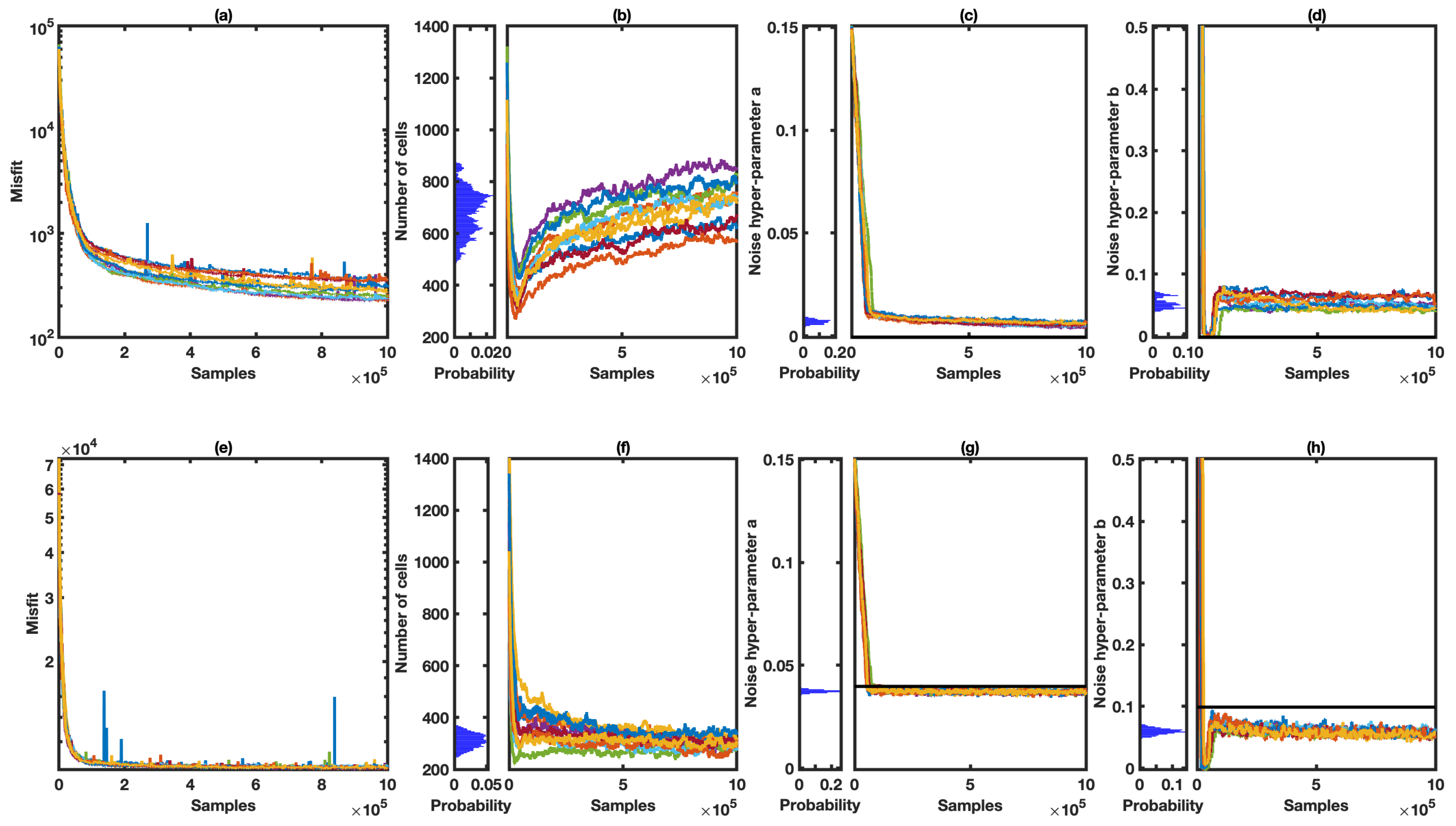
4.4. Chain Statistics and Convergence
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Friðleifsson, G.; Albertsson, A.; Elders, W.; Sigurdsson, Ó.; Karlsdottir, R.; Pálsson, B. The Iceland Deep Drilling Project (IDDP): Planning for the second deep well at Reykjanes. Geotherm. Resour. Counc. Trans 2011, 35, 347–354. [Google Scholar]
- Friðleifsson, G.Ó.; Elders, W.A.; Zierenberg, R.A.; Fowler, A.P.; Weisenberger, T.B.; Mesfin, K.G.; Sigurðsson, Ó.; Níelsson, S.; Einarsson, G.; Óskarsson, F.; et al. The Iceland Deep Drilling Project at Reykjanes: Drilling into the root zone of a black smoker analog. J. Volcanol. Geotherm. Res. 2020, 391, 106435. [Google Scholar] [CrossRef]
- Martins, J.E.; Weemstra, C.; Ruigrok, E.; Verdel, A.; Jousset, P.; Hersir, G. 3D S-wave velocity imaging of Reykjanes Peninsula high-enthalpy geothermal fields with ambient-noise tomography. J. Volcanol. Geotherm. Res. 2020, 391, 106685. [Google Scholar] [CrossRef]
- Darnet, M.; Wawrzyniak, P.; Coppo, N.; Nielsson, S.; Schill, E.; Fridleifsson, G. Monitoring geothermal reservoir developments with the Controlled-Source Electro-Magnetic method—A calibration study on the Reykjanes geothermal field. J. Volcanol. Geotherm. Res. 2020, 391, 106437. [Google Scholar] [CrossRef]
- Weemstra, C.; Boschi, L.; Goertz, A.; Artman, B. Seismic attenuation from recordings of ambient noise. Geophysics 2013, 78, Q1–Q14. [Google Scholar] [CrossRef]
- Wapenaar, K.; Fokkema, J. Green’s function representations for seismic interferometry. Geophysics 2006, 71, SI33–SI46. [Google Scholar] [CrossRef]
- Kästle, E.D.; Soomro, R.; Weemstra, C.; Boschi, L.; Meier, T. Two-receiver measurements of phase velocity: Cross-validation of ambient-noise and earthquake-based observations. Geophys. J. Int. 2016, 207, 1493–1512. [Google Scholar] [CrossRef]
- Sánchez-Pastor, P.; Obermann, A.; Schimmel, M.; Weemstra, C.; Verdel, A.; Jousset, P. Short- and Long-Term Variations in the Reykjanes Geothermal Reservoir From Seismic Noise Interferometry. Geophys. Res. Lett. 2019, 46, 5788–5798. [Google Scholar] [CrossRef]
- Zhou, Y.; Dahlen, F.; Nolet, G. Three-dimensional sensitivity kernels for surface wave observables. Geophys. J. Int. 2004, 158, 142–168. [Google Scholar] [CrossRef]
- Herrmann, R.B. Computer programs in seismology: An evolving tool for instruction and research. Seismol. Res. Lett. 2013, 84, 1081–1088. [Google Scholar] [CrossRef]
- Bodin, T.; Sambridge, M. Seismic tomography with the reversible jump algorithm. Geophys. J. Int. 2009, 178, 1411–1436. [Google Scholar] [CrossRef]
- Korostelev, F.; Weemstra, C.; Leroy, S.; Boschi, L.; Keir, D.; Ren, Y.; Molinari, I.; Ahmed, A.; Stuart, G.W.; Rolandone, F.; et al. Magmatism on rift flanks: Insights from ambient noise phase velocity in Afar region. Geophys. Res. Lett. 2015, 42, 2179–2188. [Google Scholar] [CrossRef]
- Rawlinson, N.; Sambridge, M. Seismic traveltime tomography of the crust and lithosphere. Adv. Geophys. 2003, 46, 81–199. [Google Scholar]
- Nolet, G. A Breviary of Seismic Tomography; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Rawlinson, N.; Pozgay, S.; Fishwick, S. Seismic tomography: A window into deep Earth. Phys. Earth Planet. Inter. 2010, 178, 101–135. [Google Scholar] [CrossRef]
- Bensen, G.; Ritzwoller, M.; Yang, Y. A 3-D shear velocity model of the crust and uppermost mantle beneath the United States from ambient seismic noise. Geophys. J. Int. 2009, 177, 1177–1196. [Google Scholar] [CrossRef]
- Martins, J.E.; Ruigrok, E.; Draganov, D.; Hooper, A.; Hanssen, R.; White, R.; Soosalu, H. Imaging Torfajökull’s magmatic plumbing system with seismic interferometry and phase velocity surface wave tomography. J. Geophys. Res. Solid Earth 2019, 124, 2920–2940. [Google Scholar] [CrossRef]
- Young, M.K.; Rawlinson, N.; Bodin, T. Transdimensional inversion of ambient seismic noise for 3D shear velocity structure of the Tasmanian crustTransdimensional shear velocity inversion. Geophysics 2013, 78, WB49–WB62. [Google Scholar] [CrossRef]
- Tikhonov, A.N. On the solution of ill-posed problems and the method of regularization. In Doklady Akademii Nauk; Russian Academy of Sciences: Jerusalem, Russia, 1963; Volume 151, pp. 501–504. [Google Scholar]
- Bodin, T.; Sambridge, M.; Rawlinson, N.; Arroucau, P. Transdimensional tomography with unknown data noise. Geophys. J. Int. 2012, 189, 1536–1556. [Google Scholar] [CrossRef]
- Green, P.J.; Hastie, D.I. Reversible jump MCMC. Genetics 2009, 155, 1391–1403. [Google Scholar]
- Galetti, E.; Curtis, A.; Meles, G.A.; Baptie, B. Uncertainty loops in travel-time tomography from nonlinear wave physics. Phys. Rev. Lett. 2015, 114, 148501. [Google Scholar] [CrossRef] [PubMed]
- Galetti, E.; Curtis, A.; Baptie, B.; Jenkins, D.; Nicolson, H. Transdimensional Love-wave tomography of the British Isles and shear-velocity structure of the East Irish Sea Basin from ambient-noise interferometry. Geophys. J. Int. 2017, 208, 36–58. [Google Scholar] [CrossRef]
- Zhang, X.; Curtis, A.; Galetti, E.; De Ridder, S. 3-D Monte Carlo surface wave tomography. Geophys. J. Int. 2018, 215, 1644–1658. [Google Scholar] [CrossRef]
- Zhang, X.; Hansteen, F.; Curtis, A.; de Ridder, S. 1-D, 2-D, and 3-D Monte Carlo Ambient Noise Tomography Using a Dense Passive Seismic Array Installed on the North Sea Seabed. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018552. [Google Scholar] [CrossRef]
- Weemstra, C.; De Laat, J.I.; Verdel, A.; Smets, P. Systematic recovery of instrumental timing and phase errors using interferometric surface-waves retrieved from large-N seismic arrays. Geophys. J. Int. 2021, 224, 1028–1055. [Google Scholar] [CrossRef]
- Weemstra, C.; Obermann, A.; Verdel, A.; Paap, B.; Blanck, H.; Guðnason, E.Á.; Hersir, G.; Jousset, P.; Sigurðsson, A. Time-lapse seismic imaging of the Reykjanes geothermal reservoir. In Proceedings of the European Geothermal Congress, Strasbourg, France, 19–24 September 2016. [Google Scholar]
- Bayes, T. Essay towards solving a problem in the doctrine of chances. Biometrika 1958, 45, 293–315. [Google Scholar] [CrossRef]
- Sambridge, M.; Rawlinson, N.; Levander, A.; Nolet, G. Seismic tomography with irregular meshes. Geophys.-Monogr.-Am. Geophys. Union 2005, 157, 49. [Google Scholar]
- Bodin, T.; Sambridge, M.; Gallagher, K. A self-parametrizing partition model approach to tomographic inverse problems. Inverse Probl. 2009, 25, 055009. [Google Scholar] [CrossRef]
- Belhadj, J.; Romary, T.; Gesret, A.; Noble, M.; Figliuzzi, B. New parameterizations for Bayesian seismic tomography. Inverse Probl. 2018, 34, 065007. [Google Scholar] [CrossRef]
- Hawkins, R.; Bodin, T.; Sambridge, M.; Choblet, G.; Husson, L. Trans-dimensional surface reconstruction with different classes of parameterization. Geochem. Geophys. Geosyst. 2019, 20, 505–529. [Google Scholar] [CrossRef]
- Ryberg, T.; Haberland, C. Bayesian inversion of refraction seismic traveltime data. Geophys. J. Int. 2017, 212, 1645–1656. [Google Scholar] [CrossRef]
- Kurita, T. Regional variations in the structure of the crust in the central United States from P-wave spectra. Bull. Seismol. Soc. Am. 1973, 63, 1663–1687. [Google Scholar] [CrossRef]
- Vidale, J.E. Finite-difference calculation of traveltimes in three dimensions. Geophysics 1990, 55, 521–526. [Google Scholar] [CrossRef]
- Qin, F.; Luo, Y.; Olsen, K.B.; Cai, W.; Schuster, G.T. Finite-difference solution of the eikonal equation along expanding wavefronts. Geophysics 1992, 57, 478–487. [Google Scholar] [CrossRef]
- Sethian, J.A. A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. USA 1996, 93, 1591–1595. [Google Scholar] [CrossRef] [PubMed]
- Rawlinson, N.; Sambridge, M. Wave front evolution in strongly heterogeneous layered media using the fast marching method. Geophys. J. Int. 2004, 156, 631–647. [Google Scholar] [CrossRef]
- Gorbatov, A.; Fukao, Y.; Widiyantoro, S.; Gordeev, E. Seismic evidence for a mantle plume oceanwards of the Kamchatka—Aleutian trench junction. Geophys. J. Int. 2001, 146, 282–288. [Google Scholar] [CrossRef]
- Andrieu, C.; de Freitas, N.; Doucet, A. Robust Full Bayesian Learning for Neural Networks. Citeseer. 1999. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.36.5243 (accessed on 6 October 2021).
- Gelman, A.; Roberts, G.O.; Gilks, W.R. Efficient Metropolis jumping rules. Bayesian Stat. 1996, 5, 42. [Google Scholar]
| Modeling and Inversion Parameters | Coarse Block Model | Intermediate Block Model | Fine Block Model |
|---|---|---|---|
| Model dimension (km) | 120 × 70 × 20 | 120 × 70 × 10 | 120 × 70 × 10 |
| Number of grid points in generating synthetic data | 241 × 141 × 81 | 241 × 141 × 81 | 241 × 141 × 81 |
| Number of grid points in McMC sampling | 121 × 71 × 41 | 121 × 71 × 41 | 121 × 71 × 41 |
| Number of grid points for calculating post-burn-in pointwise average | 241 × 141 × 41 | 241 × 141 × 41 | 241 × 141 × 41 |
| Valid range of shear wave velocity (km/s) | 1.5–6 | 1.5–6 | 1.5–6 |
| Valid range of noise hyper parameter a | –1 | –1 | –1 |
| Valid range of noise hyper parameter b | 0–2 | 0–2 | 0–2 |
| Proposal width for a move step. is the model dimension. | |||
| Velocity proposal width (km/s) | 0.4 | 0.4 | 0.3 |
| Proposal width for a | |||
| Proposal width for b | |||
| Thinning level | 200 | 200 | 200 |
| Ray path update step | 200 | 200 | 200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahimi Dalkhani, A.; Zhang, X.; Weemstra, C. On the Potential of 3D Transdimensional Surface Wave Tomography for Geothermal Prospecting of the Reykjanes Peninsula. Remote Sens. 2021, 13, 4929. https://doi.org/10.3390/rs13234929
Rahimi Dalkhani A, Zhang X, Weemstra C. On the Potential of 3D Transdimensional Surface Wave Tomography for Geothermal Prospecting of the Reykjanes Peninsula. Remote Sensing. 2021; 13(23):4929. https://doi.org/10.3390/rs13234929
Chicago/Turabian StyleRahimi Dalkhani, Amin, Xin Zhang, and Cornelis Weemstra. 2021. "On the Potential of 3D Transdimensional Surface Wave Tomography for Geothermal Prospecting of the Reykjanes Peninsula" Remote Sensing 13, no. 23: 4929. https://doi.org/10.3390/rs13234929
APA StyleRahimi Dalkhani, A., Zhang, X., & Weemstra, C. (2021). On the Potential of 3D Transdimensional Surface Wave Tomography for Geothermal Prospecting of the Reykjanes Peninsula. Remote Sensing, 13(23), 4929. https://doi.org/10.3390/rs13234929








