Rosetta CONSERT Data as a Testbed for In Situ Navigation of Space Probes and Radiosciences in Orbit/Escort Phases for Small Bodies of the Solar System
Abstract
1. Introduction: Rosetta Science and the CONSERT Experiment
2. Autonomous Navigation of Deep Space Probes
3. Data
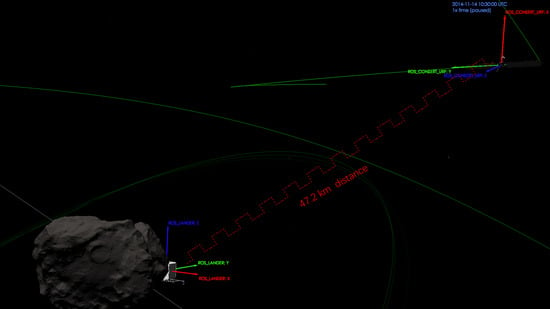
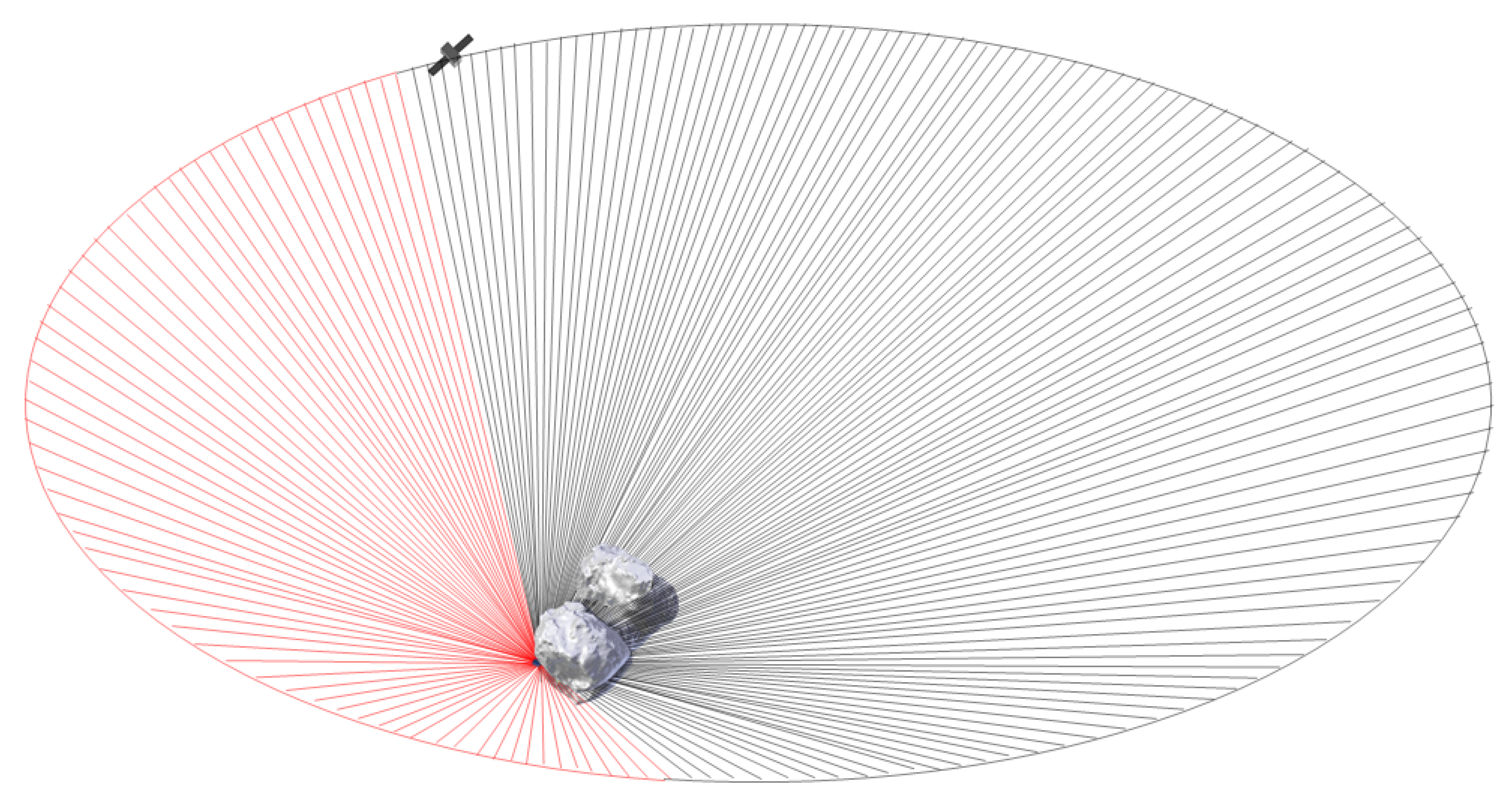
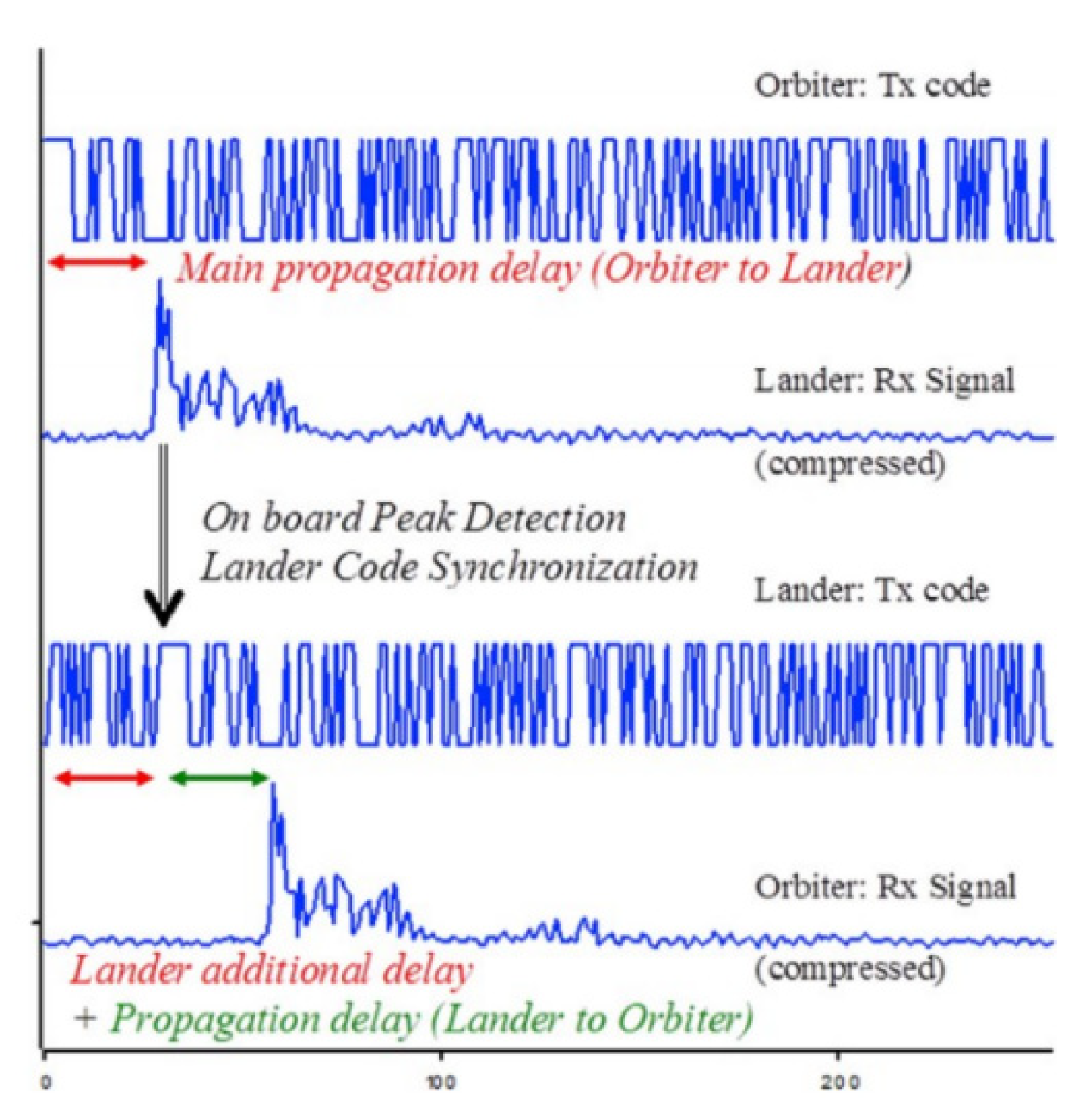
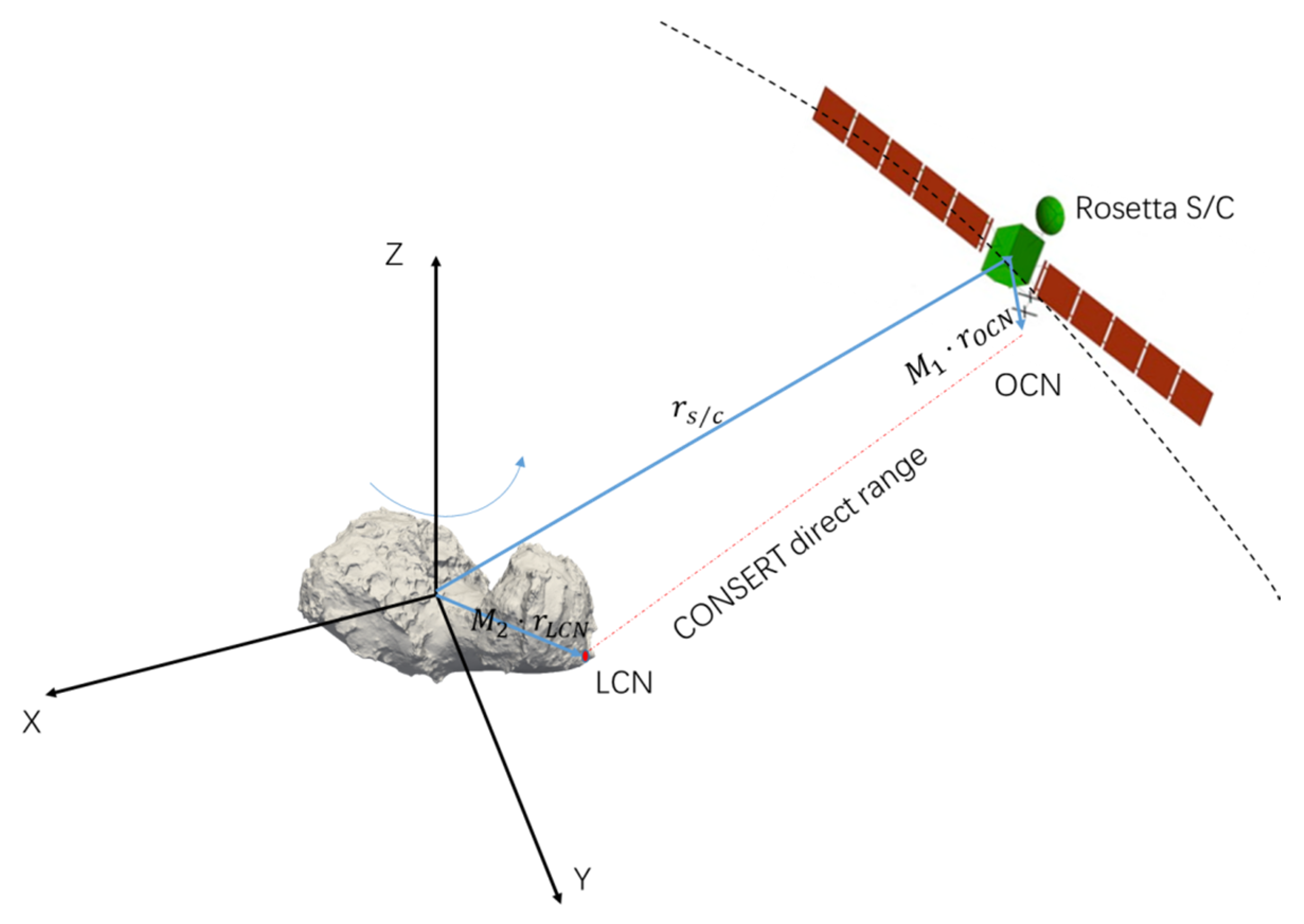
3.1. CONSERT Direct Visibility Ranging Data
3.2. Philae Lander Rest Position
4. 67P/C-G GM and Philae Lander Positions Solutions
4.1. Lander-Orbiter “One-Way” Range Model and Solution Method and Solve-for Method
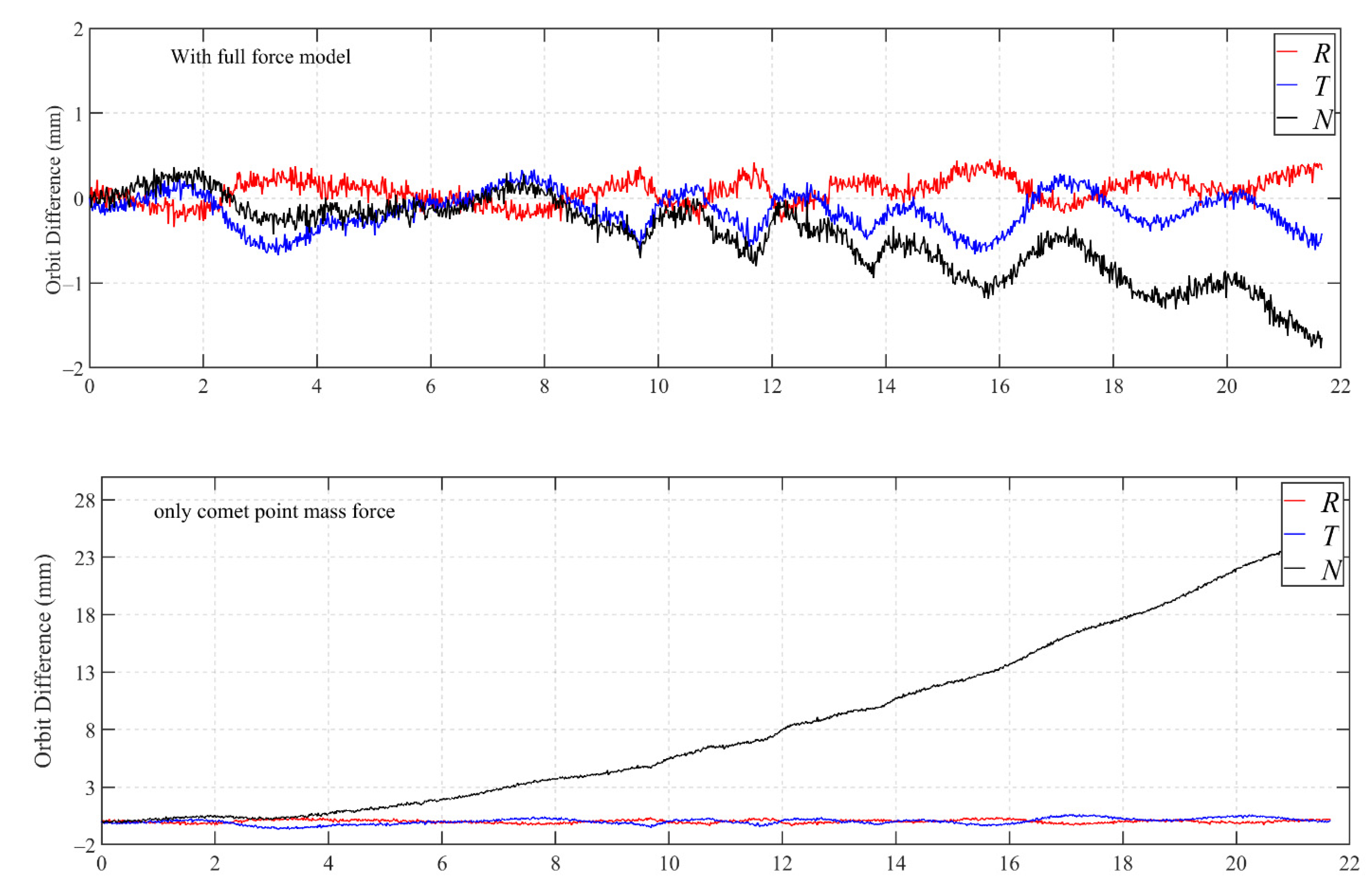
4.2. Rosetta Orbit Dynamics and Error Source Analysis
4.3. Compatibility of CONSERT Measurements with the Tracking Nominal Parameters
4.4. In-Situ Navigation Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. The CONSERT Instrument
References
- Bibring, J.-P.; Rosenbauer, H.; Boehnhardt, H.; Ulamec, S.; Biele, J.; Espinasse, S.; Feuerbacher, B.; Gaudon, P.; Hemmerich, P.; Kletzkine, P.; et al. The Rosetta Lander (“Philae”) Investigations. Space Sci. Rev. 2007, 128, 205–220. [Google Scholar] [CrossRef]
- Glassmeier, K.-H.; Boehnhardt, H.; Koschny, D.; Kührt, E.; Richter, I. The Rosetta Mission: Flying Towards the Origin of the Solar System. Space Sci. Rev. 2007, 128, 1–21. [Google Scholar] [CrossRef]
- Ulamec, S.; Biele, J.; Blazquez, A.; Cozzoni, B.; Delmas, C.; Fantinati, C.; Gaudon, P.; Geurts, K.; Jurado, E.; Küchemann, O.; et al. Rosetta Lander—Philae: Landing preparations. Acta Astronaut. 2015, 107, 79–86. [Google Scholar] [CrossRef][Green Version]
- Jurado, E.; Martin, T.; Canalias, E.; Blazquez, A.; Garmier, R.; Ceolin, T.; Gaudon, P.; Delmas, C.; Biele, J.; Ulamec, S.; et al. Rosetta lander Philae: Flight Dynamics analyses for landing site selection and post-landing operations. Acta Astronaut. 2016, 125, 65–79. [Google Scholar] [CrossRef]
- Moussi, A.; Fronton, J.-F.; Gaudon, P.; Delmas, C.; Lafaille, V.; Jurado, E.; Durand, J.; Hallouard, D.; Mangeret, M.; Charpentier, A.; et al. The Philae Lander: Science planning and operations. Acta Astronaut. 2016, 125, 92–104. [Google Scholar] [CrossRef]
- Kofman, W.; Herique, A.; Barbin, Y.; Barriot, J.P.; Ciarletti, V.; Clifford, S.; Edenhofer, P.; Elachi, C.; Eyraud, C.; Goutail, J.P.; et al. Properties of the 67P/Churyumov-Gerasimenko interior revealed by CONSERT radar. Science 2015, 349, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Herique, A.; Kofman, W.; Beck, P.; Bonal, L.; Buttarazzi, I.; Heggy, E.; Lasue, J.; Levasseur-Regourd, A.C.; Quirico, E.; Zine, S. Cosmochemical implications of CONSERT permittivity characterization of 67P/CG. Mon. Not. R. Astron. Soc. 2016, 462, S516–S532. [Google Scholar] [CrossRef]
- Herique, A.; Kofman, W.; Zine, S.; Blum, J.; Vincent, J.-B.; Ciarletti, V. Homogeneity of 67P/Churyumov-Gerasimenko as seen by CONSERT: Implication on composition and formation. Astron. Astrophys. 2019, 630, A6. [Google Scholar] [CrossRef]
- Massironi, M.; Simioni, E.; Marzari, F.; Cremonese, G.; Giacomini, L.; Pajola, M.; Jorda, L.; Naletto, G.; Lowry, S.; El-Maarry, M.R.; et al. Two independent and primitive envelopes of the bilobate nucleus of comet 67P. Nature 2015, 526, 402–405. [Google Scholar] [CrossRef]
- Bibring, J.-P.; Taylor, M.G.G.T.; Alexander, C.; Auster, U.; Biele, J.; Finzi, A.E.; Goesmann, F.; Klingelhoefer, G.; Kofman, W.; Mottola, S.; et al. Philae’s First Days on the Comet. Science 2015, 349, 493. [Google Scholar] [CrossRef][Green Version]
- Sierks, H.; Barbieri, C.; Lamy, P.L.; Rodrigo, R.; Koschny, D.; Rickman, H.; Keller, H.U.; Agarwal, J.; A’Hearn, M.F.; Angrilli, F.; et al. On the nucleus structure and activity of comet 67P/Churyumov-Gerasimenko. Science 2015, 347, aaa1044. [Google Scholar] [CrossRef]
- Wright, I.P.; Sheridan, S.; Barber, S.J.; Morgan, G.H.; Andrews, D.J.; Morse, A.D. CHO-bearing organic compounds at the surface of 67P/Churyumov-Gerasimenko revealed by Ptolemy. Science 2015, 349, 3–5. [Google Scholar] [CrossRef] [PubMed]
- Thomas, N.; Sierks, H.; Barbieri, C.; Lamy, P.L.; Rodrigo, R.; Rickman, H.; Koschny, D.; Keller, H.U.; Agarwal, J.; A’Hearn, M.F.; et al. The morphological diversity of comet 67P/Churyumov-Gerasimenko. Science 2015, 347, aaa0440. [Google Scholar] [CrossRef] [PubMed]
- Schulz, R.; Hilchenbach, M.; Langevin, Y.; Kissel, J.; Silen, J.; Briois, C.; Engrand, C.; Hornung, K.; Baklouti, D.; Bardyn, A.; et al. Comet 67P/Churyumov-Gerasimenko sheds dust coat accumulated over the past four years. Nature 2015, 518, 216–218. [Google Scholar] [CrossRef] [PubMed]
- Pätzold, M.; Andert, T.; Hahn, M.; Asmar, S.W.; Barriot, J.P.; Bird, M.K.; Hausler, B.; Peter, K.; Tellmann, S.; Grun, E.; et al. A homogeneous nucleus for comet 67P/Churyumov-Gerasimenko from its gravity field. Nature 2016, 530, 63–65. [Google Scholar] [CrossRef] [PubMed]
- El-Maarry, M.R.; Groussin, O.; Thomas, N.; Pajola, M.; Auger, A.T.; Davidsson, B.; Hu, X.; Hviid, S.F.; Knollenberg, J.; Gttler, C.; et al. Surface changes on comet 67P/Churyumov-Gerasimenko suggest a more active past. Science 2017, 355, 1392–1395. [Google Scholar] [CrossRef] [PubMed]
- Kofman, W.; Zine, S.; Herique, A.; Rogez, Y.; Jorda, L.; Levasseur-Regourd, A.-C. The interior of Comet 67P/C–G; revisiting CONSERT results with the exact position of the Philae lander. Mon. Not. R. Astron. Soc. 2020, 497, 2616–2622. [Google Scholar] [CrossRef]
- Ulamec, S.; Fantinati, C.; Maibaum, M.; Geurts, K.; Biele, J.; Jansen, S.; Kchemann, O.; Cozzoni, B.; Finke, F.; Lommatsch, V.; et al. Rosetta Lander—Landing and operations on comet 67P/Churyumov–Gerasimenko. Acta Astronaut. 2016, 125, 80–91. [Google Scholar] [CrossRef]
- Biele, J.; Ulamec, S.; Maibaum, M.; Roll, R.; Witte, L.; Jurado, E.; Muoz, P.; Arnold, W.; Auster, H.-U.; Casas, C.; et al. The landing(s) of Philae and inferences about comet surface mechanical properties. Science 2015, 349, aaa9816. [Google Scholar] [CrossRef]
- Ulamec, S.; O’Rourke, L.; Biele, J.; Grieger, B.; Andrés, R.; Lodiot, S.; Muñoz, P.; Charpentier, A.; Mottola, S.; Knollenberg, J.; et al. Rosetta Lander—Philae: Operations on comet 67P/Churyumov-Gerasimenko, analysis of wake-up activities and final state. Acta Astronaut. 2017, 137, 38–43. [Google Scholar] [CrossRef]
- Pablo, M.; Frank, B.; Vicente, C.; Bernard, G.; Carlos, M.C.; Trevor, M.; Vishnu, J. Rosetta navigation during lander delivery phase and reconstruction of Philae descent trajectory and rebound. In Proceedings of the 25th International Symposium on Space Flight Dynamics—25th ISSFD, Munich, Germany, 19–23 October 2015. [Google Scholar]
- Schulz, R. Rosetta—One comet rendezvous and two asteroid fly-bys. Sol. Syst. Res. 2009, 43, 343–352. [Google Scholar] [CrossRef]
- Boehnhardt, H.; Bibring, J.P.; Apathy, I.; Auster, H.U.; Ercoli Finzi, A.; Goesmann, F.; Klingelhofer, G.; Knapmeyer, M.; Kofman, W.; Kruger, H.; et al. The Philae lander mission and science overview. Philos. Trans. A Math. Phys. Eng. Sci. 2017, 375, 20160248. [Google Scholar] [CrossRef]
- Kofman, W.; Barbin, Y.; Klinger, J.; Levasseur-Regourd, A.C.; Barriot, J.P.; Herique, A.; Hagfors, T.; Nielsen, E.; Grün, E.; Edenhofer, P.; et al. Comet nucleus sounding experiment by radiowave transmission. Adv. Space Res. 1998, 21, 1589–1598. [Google Scholar] [CrossRef]
- Kofman, W.; Herique, A.; Goutail, J.P.; Hagfors, T.; Williams, I.P.; Nielsen, E.; Barriot, J.P.; Barbin, Y.; Elachi, C.; Edenhofer, P.; et al. The Comet Nucleus Sounding Experiment by Radiowave Transmission (CONSERT): A Short Description of the Instrument and of the Commissioning Stages. Space Sci. Rev. 2007, 128, 413–432. [Google Scholar] [CrossRef]
- O’Rourke, L.; Tubiana, C.; Güttler, C.; Lodiot, S.; Muñoz, P.; Herique, A.; Rogez, Y.; Durand, J.; Charpentier, A.; Sierks, H.; et al. The search campaign to identify and image the Philae Lander on the surface of comet 67P/Churyumov-Gerasimenko. Acta Astronaut. 2019, 157, 199–214. [Google Scholar] [CrossRef]
- Herique, A.; Rogez, Y.; Pasquero, O.P.; Zine, S.; Puget, P.; Kofman, W. Philae localization from CONSERT/Rosetta measurement. Planet. Space Sci. 2015, 117, 475–484. [Google Scholar] [CrossRef]
- Herique, A.; Plettemeier, D.; Lange, C.; Grundmann, J.T.; Ciarletti, V.; Ho, T.-M.; Kofman, W.; Agnus, B.; Du, J.; Fa, W.; et al. A radar package for asteroid subsurface investigations: Implications of implementing and integration into the MASCOT nanoscale landing platform from science requirements to baseline design. Acta Astronaut. 2019, 156, 317–329. [Google Scholar] [CrossRef]
- Lange, C.; Biele, J.; Ulamec, S.; Krause, C.; Cozzoni, B.; Küchemann, O.; Tardivel, S.; Ho, T.-M.; Grimm, C.; Grundmann, J.T.; et al. MASCOT2—A small body lander to investigate the interior of 65803 Didymos’ moon in the frame of the AIDA/AIM mission. Acta Astronaut. 2018, 149, 25–34. [Google Scholar] [CrossRef]
- Michel, P.; Cheng, A.; Küppers, M.; Pravec, P.; Blum, J.; Delbo, M.; Green, S.F.; Rosenblatt, P.; Tsiganis, K.; Vincent, J.B.; et al. Science case for the Asteroid Impact Mission (AIM): A component of the Asteroid Impact & Deflection Assessment (AIDA) mission. Adv. Space Res. 2016, 57, 2529–2547. [Google Scholar] [CrossRef]
- Iess, L.; Di Benedetto, M.; James, N.; Mercolino, M.; Simone, L.; Tortora, P. Astra: Interdisciplinary study on enhancement of the end-to-end accuracy for spacecraft tracking techniques. Acta Astronaut. 2014, 94, 699–707. [Google Scholar] [CrossRef]
- Thornton, C.L.; Border, J.S. Radiometric Tracking Techniques for Deep-Space Navigation; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Ely, T.A.; Burt, E.A.; Prestage, J.D.; Seubert, J.M.; Tjoelker, R.L. Using the Deep Space Atomic Clock for Navigation and Science. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 950–961. [Google Scholar] [CrossRef]
- Ely, T.A.; Seubert, J.; Prestage, J.; Tjoelker, R.; Burt, E. Deep space atomic clock mission overview. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Portland, ME, USA, , 11–13 August 2019. [Google Scholar]
- Li, S.; Cui, P.; Cui, H. Autonomous navigation and guidance for landing on asteroids. Aerosp. Sci. Technol. 2006, 10, 239–247. [Google Scholar] [CrossRef]
- Scheeres, D.J.; Marzari, F.; Tomasella, L.; Vanzani, V. ROSETTA mission: Satellite orbits around a cometary nucleus. Planet. Space Sci. 1998, 46, 649–671. [Google Scholar] [CrossRef]
- Bhaskaran, S.; Riedel, J.; Synnott, S.; Wang, T. The Deep Space 1 autonomous navigation system—A post-flight analysis. In Proceedings of the Astrodynamics Specialist Conference, Denver, CO, USA, 14–17 August 2000; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012. [Google Scholar] [CrossRef]
- Mastrodemos, N.; Kubitschek, D.G.; Synnott, S.P. Autonomous Navigation for the Deep Impact Mission Encounter with Comet Tempel 1. Space Sci. Rev. 2005, 117, 95–121. [Google Scholar] [CrossRef]
- Lages, J.; Shevchenko, I.I.; Rollin, G. Chaotic dynamics around cometary nuclei. Icarus 2018, 307, 391–399. [Google Scholar] [CrossRef]
- Wei, E.; Jin, S.; Zhang, Q.; Liu, J.; Li, X.; Yan, W. Autonomous navigation of Mars probe using X-ray pulsars: Modeling and results. Adv. Space Res. 2013, 51, 849–857. [Google Scholar] [CrossRef]
- Stastny, N.B.; Geller, D.K. Autonomous Optical Navigation at Jupiter: A Linear Covariance Analysis. J. Spacecr. Rocket. 2008, 45, 290–298. [Google Scholar] [CrossRef]
- Graven, P.; Collins, J.; Sheikh, S.; Hanson, J.; Ray, P.; Wood, K. XNAV for Deep Space Navigation. In Proceedings of the 31st, Rocky Mountain Guidance and Control Conference, Breckenridge, CO, USA, 1–6 February 2008; pp. 349–364. [Google Scholar]
- Paolo, T.; Marco, Z.; Edoardo, G.; Riccardo, L.M.; Sebastien, L.M.; Ryan, S.P.; Giacomo, T.; Ozgur, K.; Hannah, G.; Paolo, M.; et al. Didymos Gravity Science Investigations through Ground-based and Inter-Satellite Links Doppler Tracking. In Proceedings of the EGU General Assembly 2021, online. 19–30 April 2021. [Google Scholar]
- Scheeres, D.J.; French, A.S.; Tricarico, P.; Chesley, S.R.; Takahashi, Y.; Farnocchia, D.; McMahon, J.W.; Brack, D.N.; Davis, A.B.; Ballouz, R.L.; et al. Heterogeneous mass distribution of the rubble-pile asteroid (101955) Bennu. Sci. Adv. 2020, 6, eabc3350. [Google Scholar] [CrossRef]
- Pätzold, M.; Andert, T.; Hahn, M.; Barriot, J.-P.; Asmar, S.W.; Häusler, B.; Bird, M.K.; Tellmann, S.; Oschlisniok, J.; Peter, K. The Nucleus of comet 67P/Churyumov–Gerasimenko—Part I: The global view—Nucleus mass, mass-loss, porosity, and implications. Mon. Not. R. Astron. Soc. 2019, 483, 2337–2346. [Google Scholar] [CrossRef]
- Rogez, Y.; Puget, P.; Zine, S.; Hérique, A.; Kofman, W.; Altobelli, N.; Ashman, M.; Barthélémy, M.; Biele, J.; Blazquez, A.; et al. The CONSERT operations planning process for the Rosetta mission. Acta Astronaut. 2016, 125, 212–233. [Google Scholar] [CrossRef]
- Preusker, F.; Scholten, F.; Matz, K.D.; Roatsch, T.; Willner, K.; Hviid, S.F.; Knollenberg, J.; Jorda, L.; Gutirrez, P.J.; Khrt, E.; et al. Shape model, reference system definition, and cartographic mapping standards for comet 67P/Churyumov-Gerasimenko—Stereo-photogrammetric analysis of Rosetta/OSIRIS image data. Astron. Astrophys. 2015, 583, A33. [Google Scholar] [CrossRef]
- Jorda, L.; Gaskell, R.; Capanna, C.; Hviid, S.; Lamy, P.; Ďurech, J.; Faury, G.; Groussin, O.; Gutirrez, P.; Jackman, C.; et al. The global shape, density and rotation of Comet 67P/Churyumov-Gerasimenko from preperihelion Rosetta/OSIRIS observations. Icarus 2016, 277, 257–278. [Google Scholar] [CrossRef]
- Preusker, F.; Scholten, F.; Matz, K.D.; Roatsch, T.; Hviid, S.F.; Mottola, S.; Knollenberg, J.; Khrt, E.; Pajola, M.; Oklay, N.; et al. The global meter-level shape model of comet 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2017, 607, L1. [Google Scholar] [CrossRef]
- Berry, M.M.; Coppola, V.T. Correct Modeling of the Indirect Term for Third Body Perturbations. Adv. Astronaut. Sci. 2008, 129, 2625. [Google Scholar]
- Tapley, B.D.; Schutz, B.E.; Born, G.H. Statistical Orbit Determination; Academic Press: Burlington, MA, USA; San Diego, CA, USA; London, UK, 2004; p. 547. [Google Scholar] [CrossRef]
- Scholten, F.; Preusker, F.; Jorda, L.; Hviid, S. Reference Frames and Mapping Schemes of Comet 67P/C-G, v2 (24 September 2015), RO-C-MULTI-5-67P-SHAPE-V1.0:CHEOPS_REF_FRAME_V1, NASA Planetary Data System and ESA Planetary Science Archive. 2015. Available online: https://pdssbn.astro.umd.edu/holdings/ro-c-multi-5-67p-shape-v1.0/document/cheops_ref_frame_v1.pdf (accessed on 26 November 2017).
- Takahashi, S.; Scheeres, D.J. Autonomous navigation and exploration of a small near-earth asteroid. In Proceedings of the 2020 AAS/AIAA Astrodynamics Specialist Conference, Lake Tahoe, CA, USA, 9–13 August 2020. [Google Scholar]
- Pasquero, O.P.; Hérique, A.; Kofman, W. Oversampled Pulse Compression Based on Signal Modeling: Application to CONSERT/Rosetta Radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2225–2238. [Google Scholar] [CrossRef]

| Instrument | Frequency | Ranging Accuracy |
|---|---|---|
| CONSERT | 90 Mhz | ~6 m |
| S-Band | 1.5–2.2 Ghz | ~2 m |
| X-Band | 7.2–8.4 GHz | ~0.6 m |
| Sequence Number | Numbers of Set | Start Time UTC | End Time UTC | Distance between LCN and OCN (km) | Numbers of Direct Measurements |
|---|---|---|---|---|---|
| 1 | 3 | 2014-11-13T22:04:26.79 | 2014-11-13T22:08:29.12 | 36.79~36.95 | 12 |
| 2 | 12 | 2014-11-14T10:20:50.49 | 2014-11-14T10:42:22.92 | 47.19~47.35 | 51 |
| 3 | 3 | 2014-11-14T23:42:00.24 | 2014-11-14T23:46:00.12 | 45.38~45.43 | 11 |
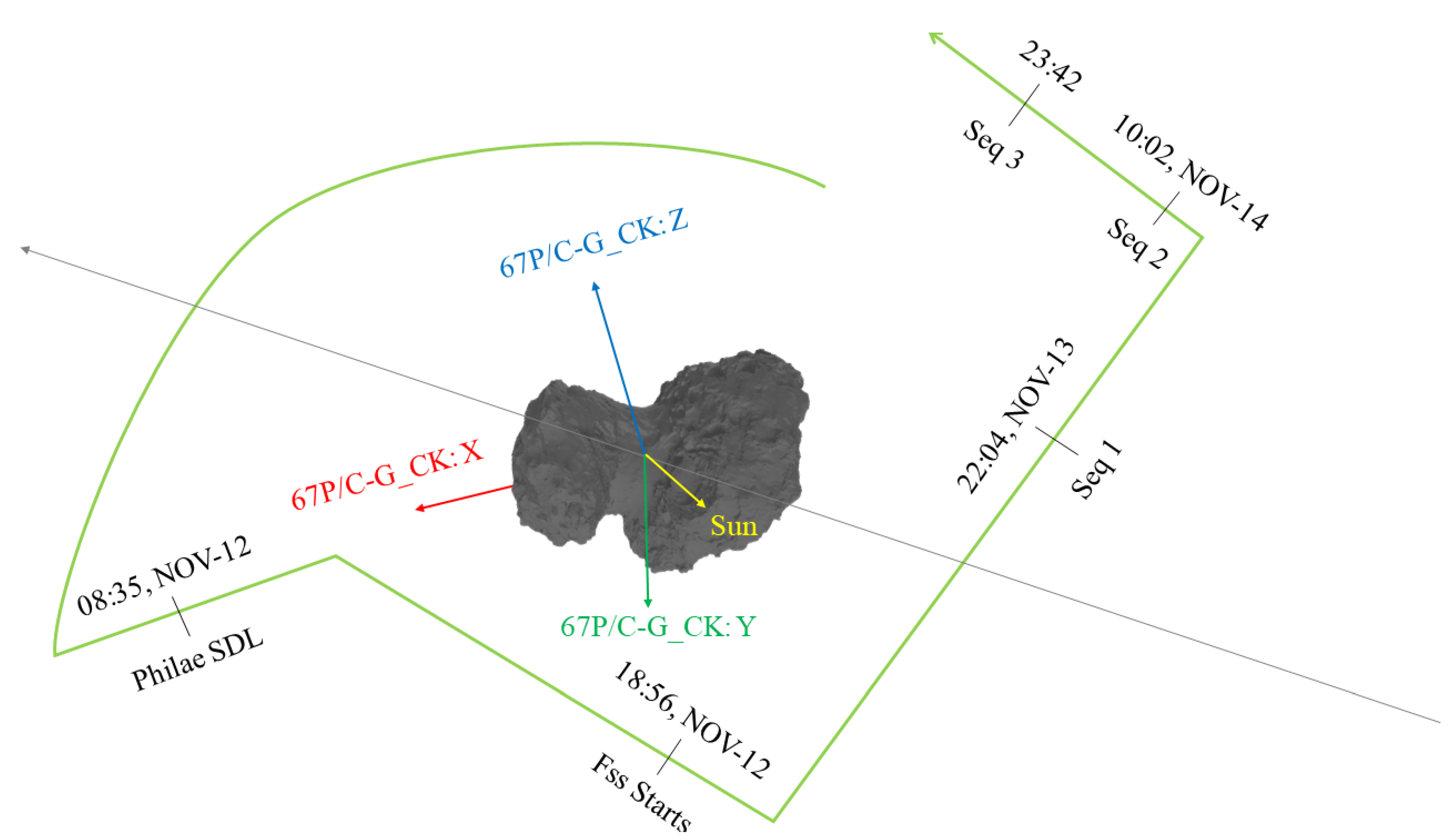
| Cartesian Coordinates in the Comet-Fixed 67P/C-G_CK Frame (Meters) | Data Source | ||
|---|---|---|---|
| X | Y | Z | |
| 2443.22366 | −62.6126 | −348.0192 | CRM_4_V9-Shape4S-DLR-SPG-v1.0-June 2015 [47] |
| 2447.064555 | −62.711025 | −348.566278 | DTM_Abydos_V2-LAM-SPC-v3.0-October 2016 [48] |
| 2445.568314 | −62.67267 | −348.352951 | LAM (SPC) + DLR (SPG) [cg-dlr_spg-shap7-v1.0] [49] |
| 2416.40500 | −101.27740 | −393.88200 | From CONSERT team, first estimate of the lander position using only the data corresponding to signal that propagated through the comet. SPICE_PHILAE_CFF_CN_V1_1.BSP (SPICE SPK) |
| 2447.3 | −62.7 | −348.6 | From SONC team, SPICE_PHILAE_CFF_SONC_V2_0.BSP (SPICE SPK) |
| 2449.18 | −67.611 | −342.469 | (Kofman, private communication) from SPC shap8 v2.1 [17] |
| Kernel Type | Kernel Name |
|---|---|
| Rosetta frame kernel (FK) | ROS_V32.TF |
| Rosetta S/C orbit kernel (SPK) | RORB_DV_257_03___T19_00345.BSP |
| 67P/C-G ephemeris kernel (SPK) | CORB_DV_257_03___T19_00345.BSP |
| Rosetta S/C attitude kernel (CK) | RATT_DV_145_01_01_T6_00216.BC |
| 67P/C-G attitude kernel (CK) | CATT_DV_145_02_______00216.BC |
| Rosetta S/C clock kernel (SCLK) | ROS_160929_STEP.TSC |
| Acceleration | Magnitude |
|---|---|
| Comet point mass | 2.7 × 10−7 |
| Solar radiation pressure (SRP) | 3.1 × 10−8 |
| Comet out-gassing | 2.9 × 10−10 |
| Non-spherical gravitational | 2.8 × 10−10 |
| Three-body perturbations | 9.1 × 10−11 |
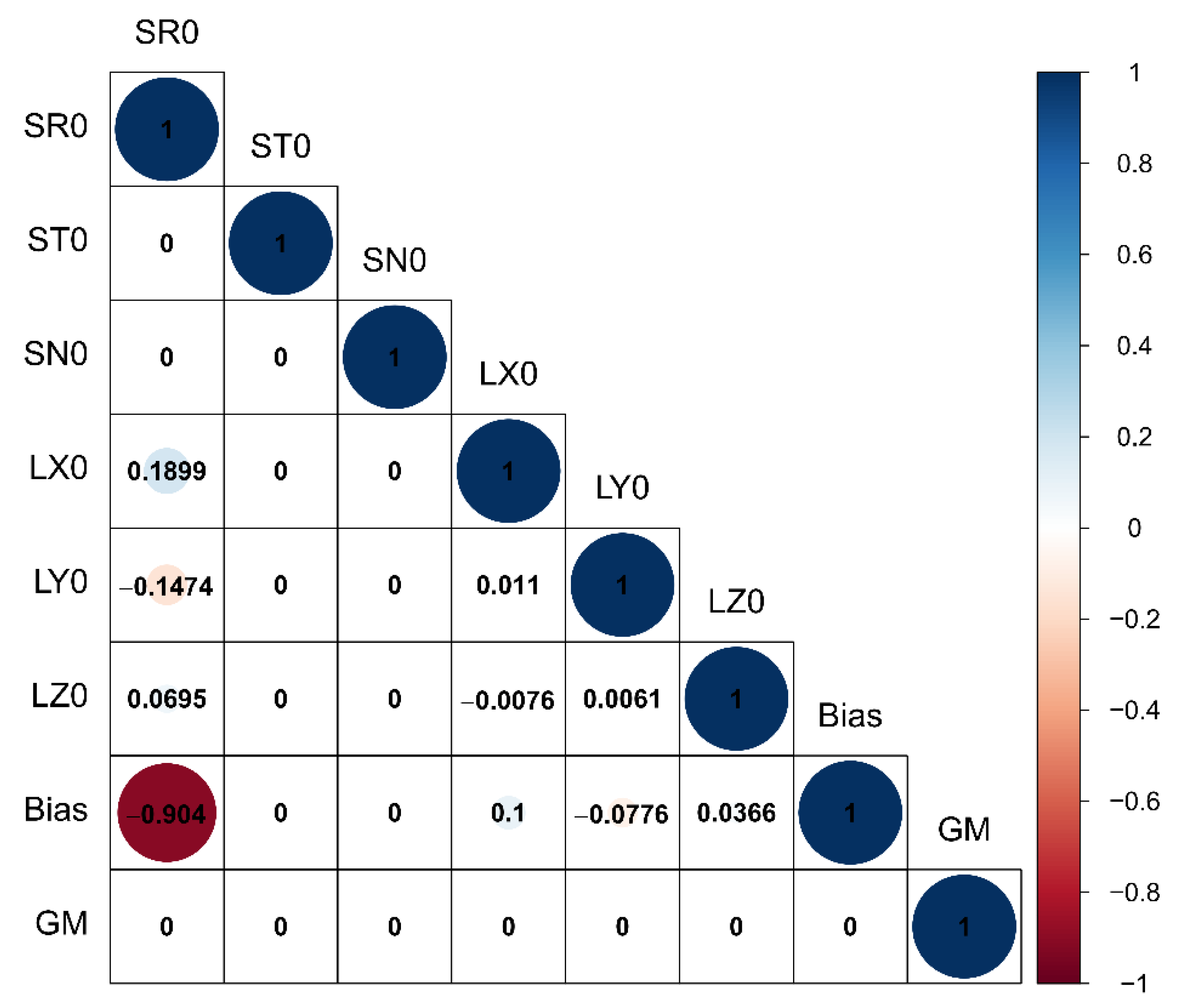
| Parameter Name | A Priori Values | Errors (1σ) | Reference | |
|---|---|---|---|---|
| Comet 67P/C-G GM (m3/s2) | 666.2 | 0.2 | [15] | |
| Rosetta S/C position at epoch 10:20:50.49 UTC (m) in the J2000 comet-centered frame | SX0 | −16,816.785 | 8.4 | [27] |
| SY0 | −33,068.614 | 2.1 | ||
| SZ0 | 32,219.679 | 20.6 | ||
| Philae lander position in the comet-fixed 67P/C-G_CK frame (m) | LX0 | 2449.18 | 2.0 | [17] |
| LY0 | −67.611 | 2.0 | ||
| LZ0 | −342.469 | 2.0 | ||
| 67P/C-G rotation model | RA | 69.54° | 0.05 | [47,52] |
| DEC | 64.11° | 0.03 | ||
| Period | 12.4041 h | 0.0004 | ||
| Electronic bias(m) | Bias | 0.0 | 6 | [27] |
| Estimated Parameter | Corrections (m) | Deviations (mm) | |
|---|---|---|---|
| Rosetta S/C position corrections in the J2000 comet-centered frame | SX0 (m) | 0.522 | 8.238 |
| SY0 (m) | 0.022 | 2.092 | |
| SZ0 (m) | −5.019 | 9.554 | |
| Philae lander position corrections in the comet-fixed frame 67P/C-G_CK frame | LX0 (m) | −0.393 | 1.986 |
| LY0 (m) | −0.585 | 1.987 | |
| LZ0 (m) | 0.029 | 1.999 | |
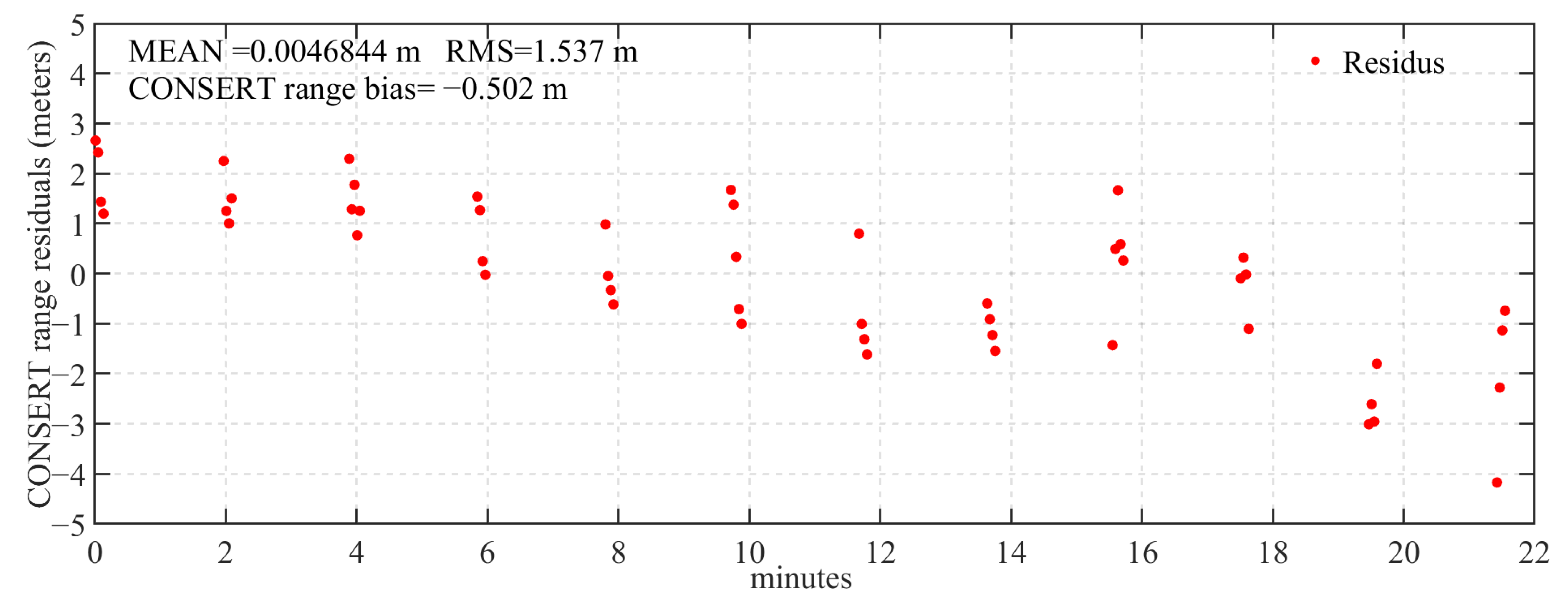
| Ranging Bias | Bias (m) | −0.502 | 5.536 |
| 67P Gravity Constant | GM (m3/s2) | 1.380 × 10−5 | 0.199 |
| Estimated Parameter | Perturbed A Priori Values | A Priori Sigma | Corrections | A Posteriori Values | A Posteriori Sigma | |
|---|---|---|---|---|---|---|
| Rosetta S/C Initial Position in J2000 | SX0 (m) | −16,732.785 (10-sigma error) | 8.4 | 13.181 | −16,719.604 | 8.209 |
| SY0 (m) | −33,047.614 (10-sigma error) | 2.1 | 4.424 | −33,043.190 | 2.090 | |
| SZ0 (m) | 32,425.679 (10-sigma error) | 20.6 | −144.133 | 32,281.547 | 4.944 | |
| Ranging Bias | Bias (m) | 0 | 6.0 | - | - | - |
| 67P Gravity Constant | GM (m3/s2) | 666.8 (3-sigma error) | 0.2 | - | - | - |
| Orbit Error | Case A, Table 8 | Case B, Table 10 | Case C, Table 11 | Case D |
|---|---|---|---|---|
| R (m) | −9.76 | −9.75 | −9.54 | −3.80 |
| T (m) | 116.21 | 116.21 | 121.98 | 34.55 |
| N (m) | −11.92 | −11.91 | −17.63 | −3.73 |
| Estimated Parameter | A Priori Values | A Priori Sigma | Total Corrections | A Posteriori Sigma | |
|---|---|---|---|---|---|
| Rosetta S/C Initial Position in J2000 | SX0 (m) | −16,732.785 (10-sigma error) | 8.4 | 13.179 | 8.208 |
| SY0 (m) | −33,047.614 (10-sigma error) | 2.1 | 4.425 | 2.090 | |
| SZ0 (m) | 32,425.679 (10-sigma error) | 20.6 | −144.122 | 4.942 | |
| 67P Gravity Constants | GM (m3/s2) | 732.82 (10% relative GM error) | 0.2 | - | - |
| Estimated Parameter | A Priori Values | A Priori Sigma | Corrections | A Posteriori Sigma | |
|---|---|---|---|---|---|
| Rosetta S/C Initial Position in J2000 | SX0 (m) | −16,732.785 (10-sigma error) | 8.4 | 24.395 | 8.203 |
| SY0 (m) | −33,047.614 (10-sigma error) | 2.1 | 0.128 | 2.087 | |
| SZ0 (m) | 32,425.679 (10-sigma error) | 20.6 | −142.214 | 4.801 | |
| 67P Gravity Constants | GM (m3/s2) | 999.3 (50% relative GM error) | 0.2 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, M.; Li, F.; Yan, J.; Hérique, A.; Kofman, W.; Rogez, Y.; Andert, T.P.; Guo, X.; Barriot, J.-P. Rosetta CONSERT Data as a Testbed for In Situ Navigation of Space Probes and Radiosciences in Orbit/Escort Phases for Small Bodies of the Solar System. Remote Sens. 2021, 13, 3747. https://doi.org/10.3390/rs13183747
Ye M, Li F, Yan J, Hérique A, Kofman W, Rogez Y, Andert TP, Guo X, Barriot J-P. Rosetta CONSERT Data as a Testbed for In Situ Navigation of Space Probes and Radiosciences in Orbit/Escort Phases for Small Bodies of the Solar System. Remote Sensing. 2021; 13(18):3747. https://doi.org/10.3390/rs13183747
Chicago/Turabian StyleYe, Mao, Fei Li, Jianguo Yan, Alain Hérique, Wlodek Kofman, Yves Rogez, Thomas P. Andert, Xi Guo, and Jean-Pierre Barriot. 2021. "Rosetta CONSERT Data as a Testbed for In Situ Navigation of Space Probes and Radiosciences in Orbit/Escort Phases for Small Bodies of the Solar System" Remote Sensing 13, no. 18: 3747. https://doi.org/10.3390/rs13183747
APA StyleYe, M., Li, F., Yan, J., Hérique, A., Kofman, W., Rogez, Y., Andert, T. P., Guo, X., & Barriot, J.-P. (2021). Rosetta CONSERT Data as a Testbed for In Situ Navigation of Space Probes and Radiosciences in Orbit/Escort Phases for Small Bodies of the Solar System. Remote Sensing, 13(18), 3747. https://doi.org/10.3390/rs13183747