PM2.5 Concentration Forecasting over the Central Area of the Yangtze River Delta Based on Deep Learning Considering the Spatial Diffusion Process
Abstract
:1. Introduction
2. Study Area and Materials
2.1. Study Area
2.2. Data Source
2.2.1. Air Quality Data
2.2.2. Meteorological Data
3. Methodology
3.1. Establishing the Dataset
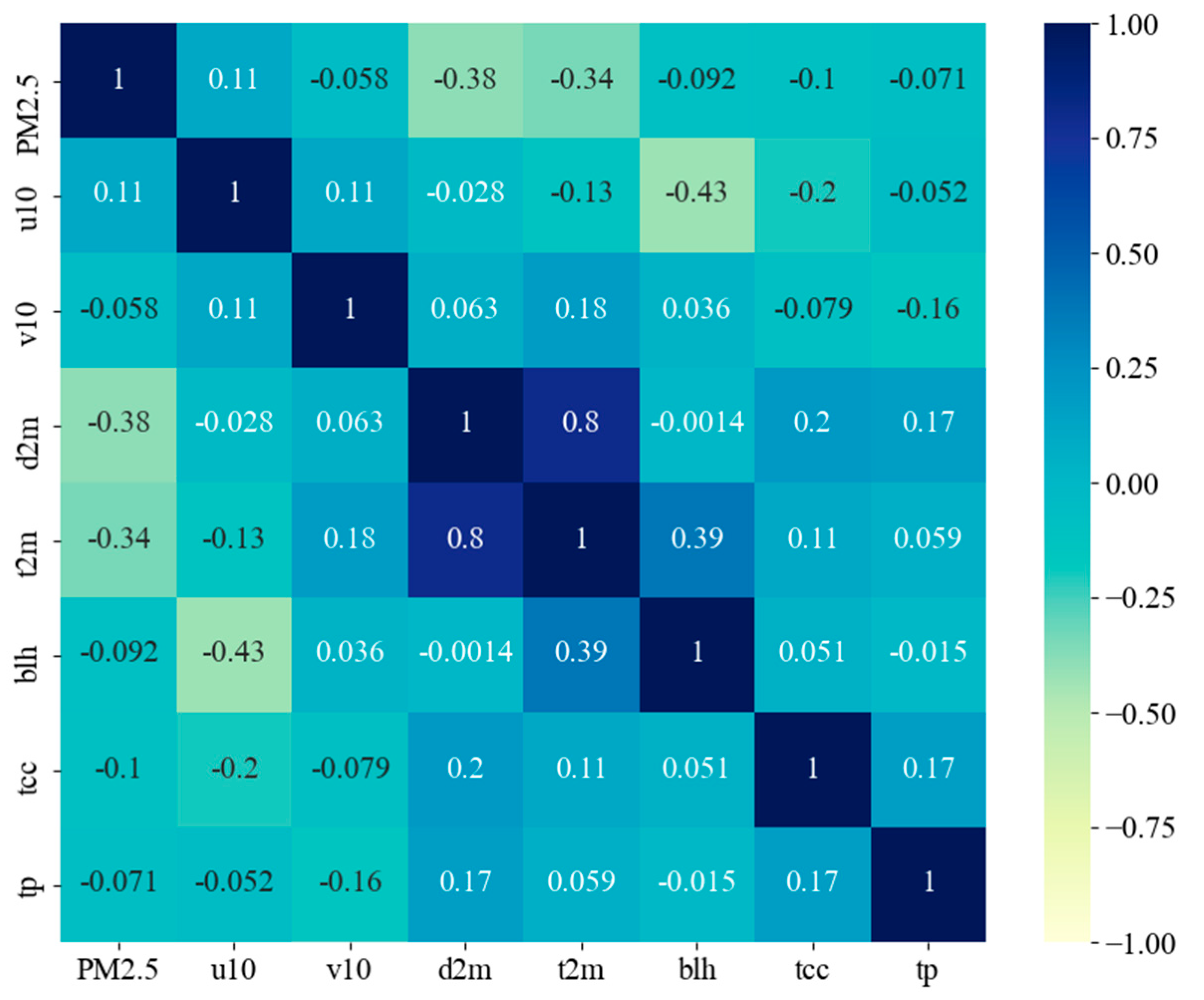
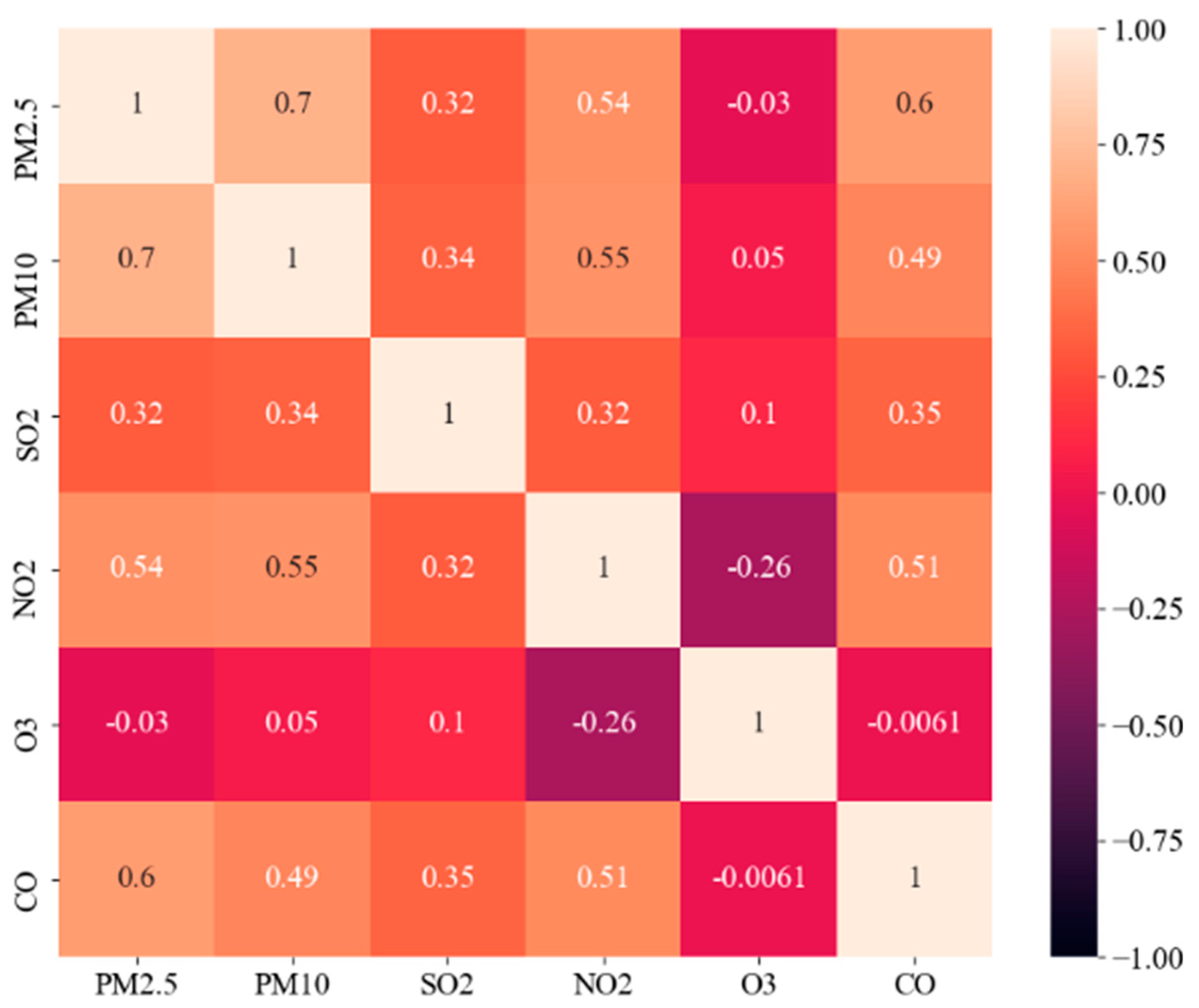
3.1.1. Influence on the PM2.5 Concentration Feature Selection
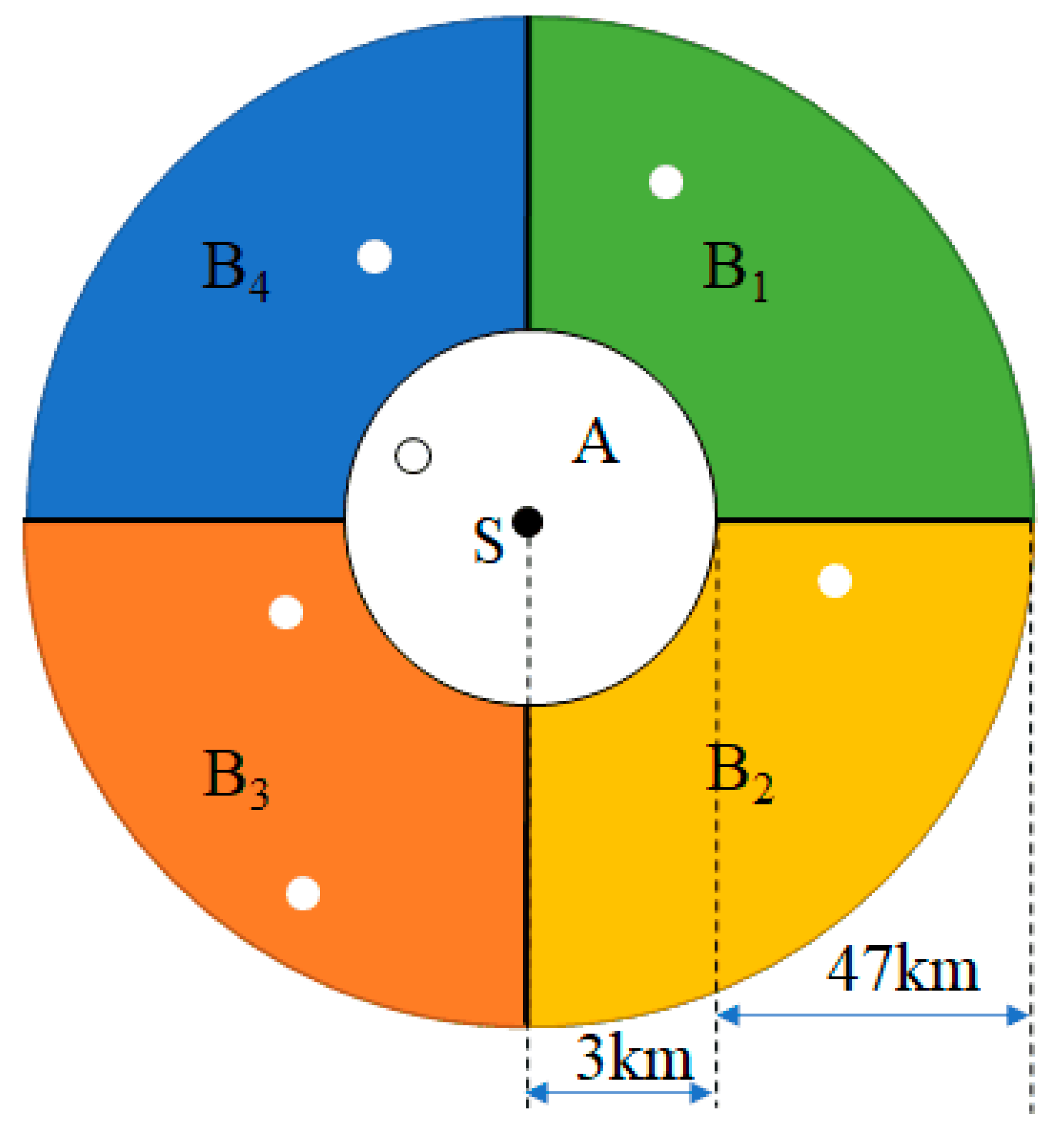
3.1.2. Spatial Diffusion Process Expression
3.1.3. Establishing the Dataset
3.2. Forecasts Method
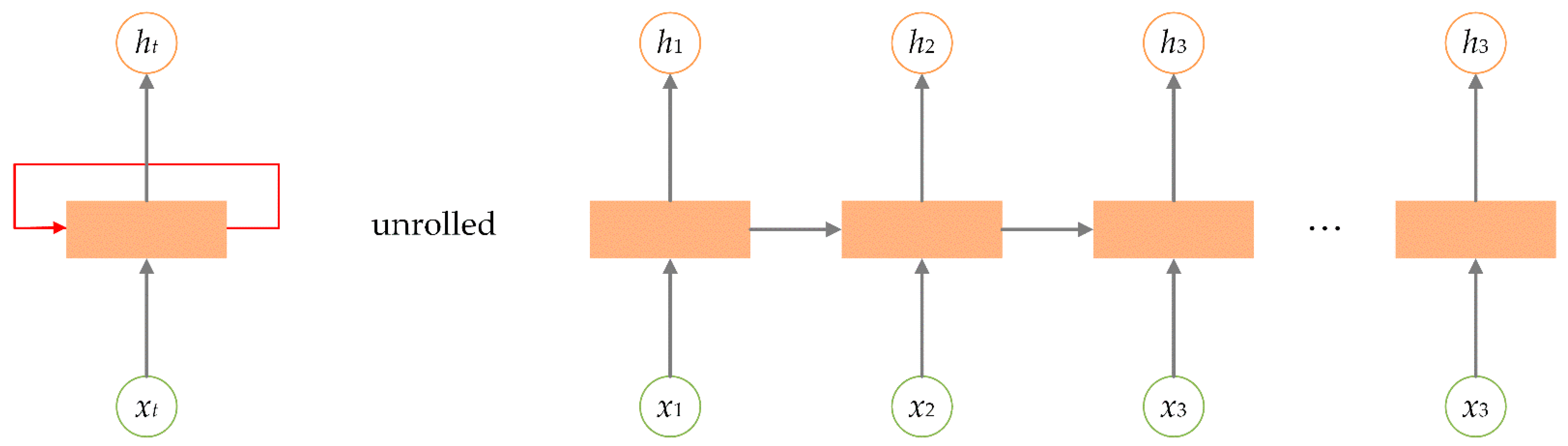
3.2.1. RNN Models
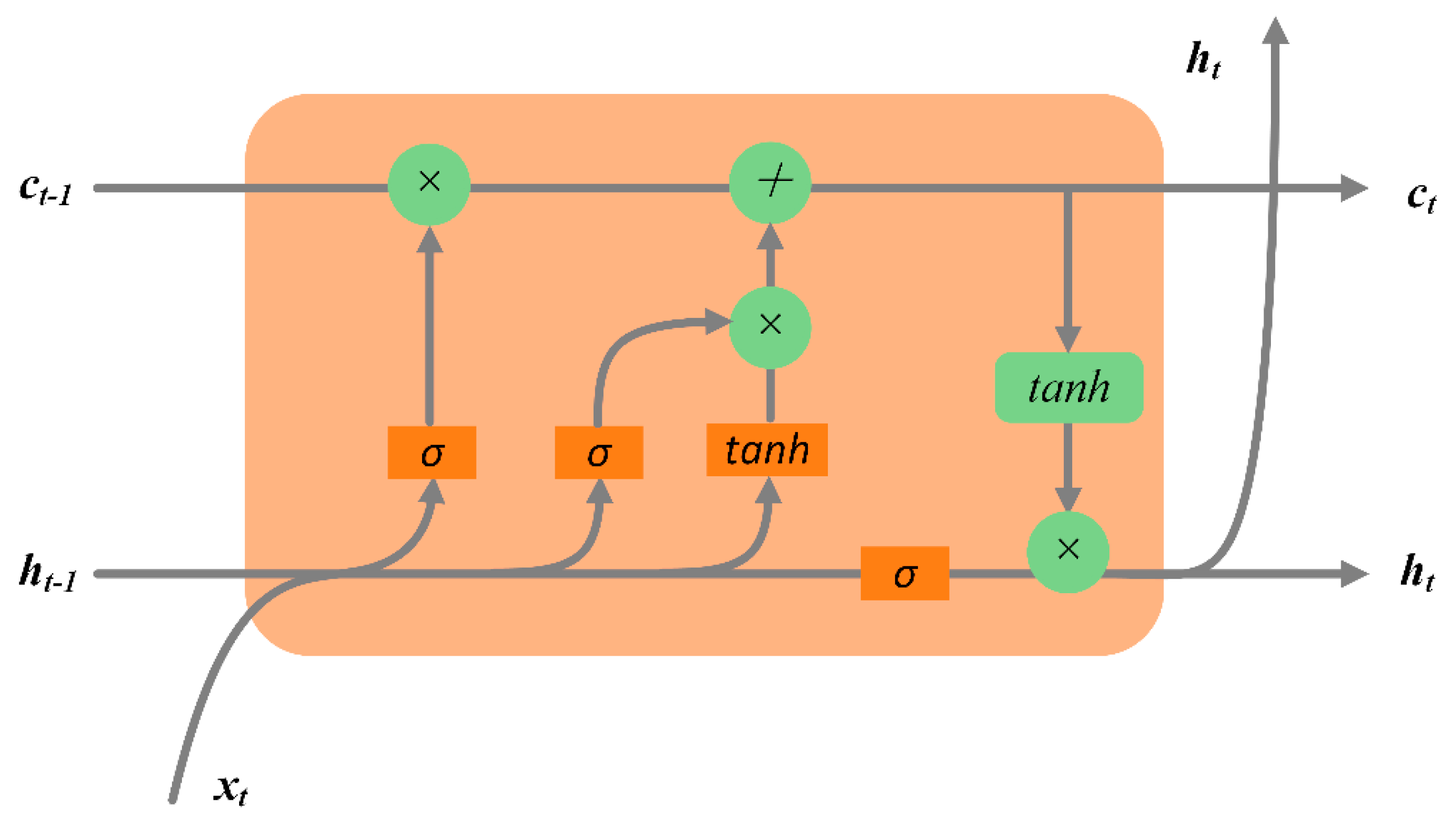
3.2.2. LSTM Models
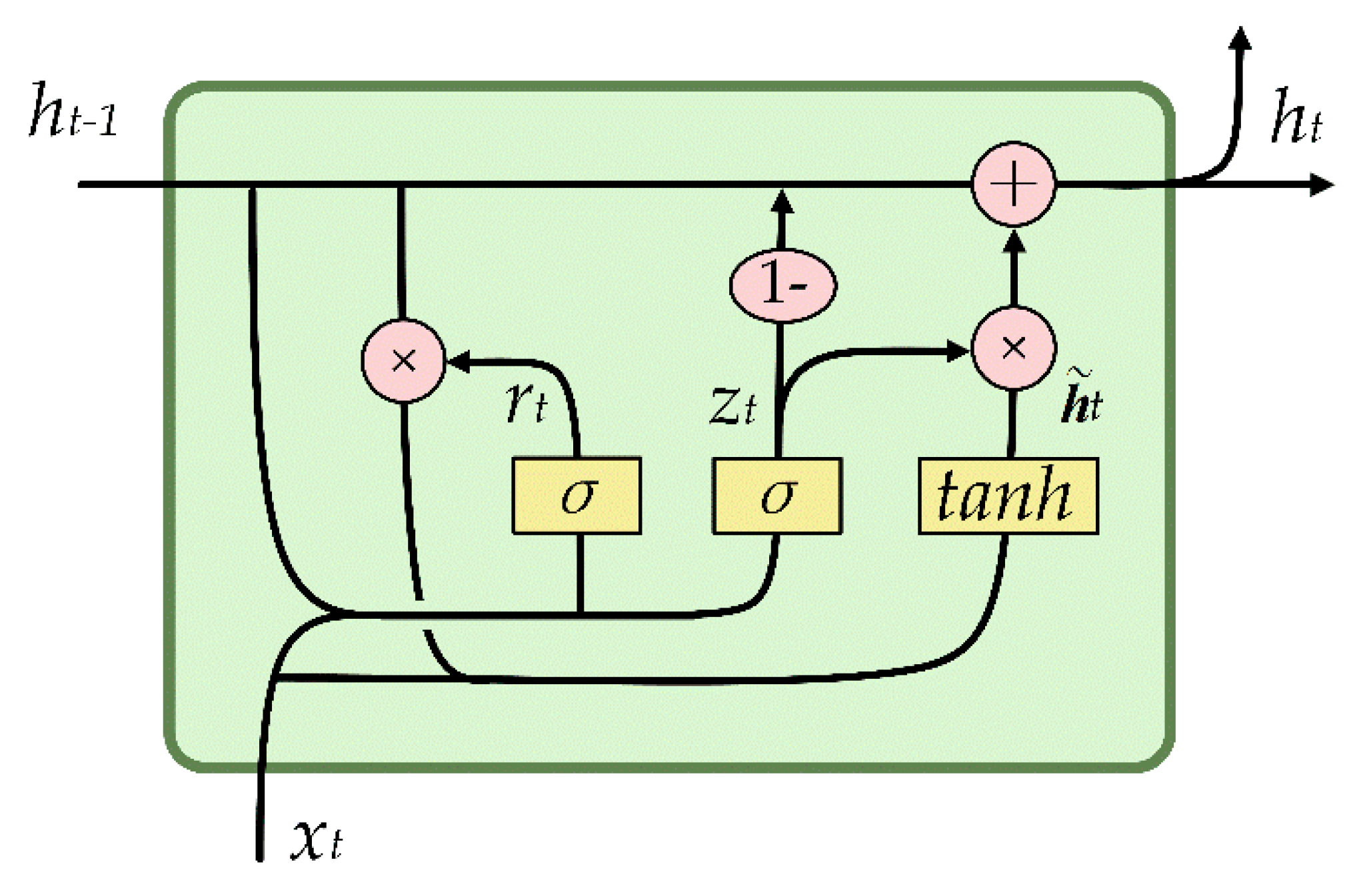
3.2.3. GRU Models
3.3. Accuracy Evaluation Measure
4. Experimental Results and Analysis
4.1. Experimental Setup
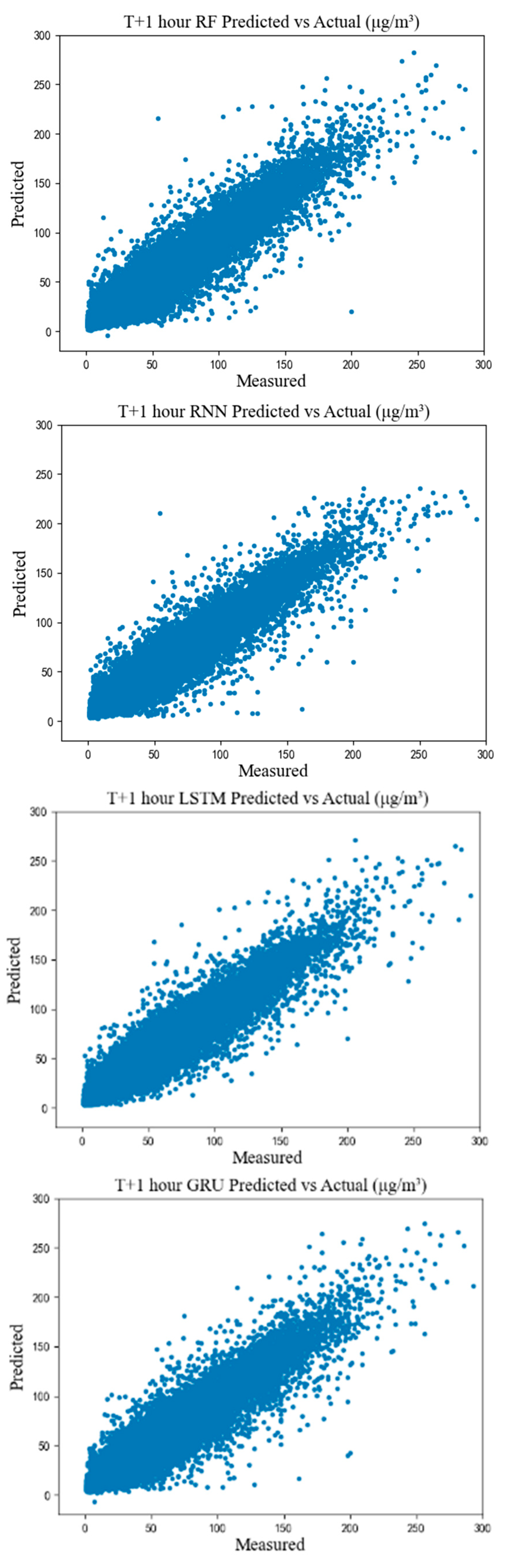
4.2. Results and Analysis
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, D.; Ma, J.; Cheng, T.; van Genderen, J.L.; Shao, Z. Challenges and opportunities for the development of MEGACITIES. Int. J. Digit. Earth 2018, 12, 1382–1395. [Google Scholar] [CrossRef]
- Shao, Z.; Fu, H.; Li, D.; Altan, O.; Cheng, T. Remote sensing monitoring of multi-scale watersheds impermeability for urban hydrological evaluation. Remote Sens. Environ. 2019, 232, 111338. [Google Scholar] [CrossRef]
- Xu, X.; Tong, T.; Zhang, W.; Meng, L. Fine-grained prediction of PM2.5 concentration based on multisource data and deep learning. Atmos. Pollut. Res. 2020, 11, 1728–1737. [Google Scholar] [CrossRef]
- Spatial Variation of Multiple Air Pollutants and Their Potential Contributions to All-Cause, Respiratory, and Cardiovascular Mortality across China in 2015–2016. Available online: https://www.researchgate.net/publication/319575435_Spatial_variation_of_multiple_air_pollutants_and_their_potential_contributions_to_all-cause_respiratory_and_cardiovascular_mortality_across_China_in_2015-2016 (accessed on 17 October 2021).
- Adipose Mesenchymal Stem Cell-Derived Antioxidative Extracellular Vesicles Exhibit Anti-Oxidative Stress and Immunomodulatory Effects under PM2.5 Exposure. Available online: https://www.researchgate.net/publication/347911247_Adipose_mesenchymal_stem_cell-derived_antioxidative_extracellular_vesicles_exhibit_anti-oxidative_stress_and_immunomodulatory_effects_under_PM25_exposure (accessed on 17 October 2021).
- Ma, J.; Ding, Y.; Cheng, J.C.P.; Jiang, F.; Gan, V.J.L.; Xu, Z. A Lag-FLSTM deep learning network based on Bayesian Optimization for multi-sequential-variant PM2.5 prediction. Sustain. Cities Soc. 2020, 60, 102237. [Google Scholar] [CrossRef]
- Zhang, Y.; Bocquet, M.; Mallet, V.; Seigneur, C.; Baklanov, A. Real-time air quality forecasting, part I: History, techniques, and current status. Atmos. Environ. 2012, 60, 632–655. [Google Scholar] [CrossRef]
- Parrish, D.; Trainer, M.; Trivikrama Rao, S.; Solomon, P.A. Regional photochemical measurement and modeling studies conference San Diego, California 8–12 November 1993. Atmos. Environ. 1995, 29, 2885–2886. [Google Scholar] [CrossRef]
- Wen, W.; Shen, S.; Liu, L.; Ma, X.; Wei, Y.; Wang, J.; Xing, Y.; Su, W. Comparative Analysis of PM2.5 and O3 Source in Beijing Using a Chemical Transport Model. Remote Sens. 2021, 13, 3457. [Google Scholar] [CrossRef]
- Dou, C.; Ji, Z.; Xiao, Y.; Hu, Z.; Zhu, X.; Dong, W. Projection of Air Pollution in Northern China in the Two RCPs Scenarios. Remote Sens. 2021, 13, 3064. [Google Scholar] [CrossRef]
- Vautard, R.; Builtjes, P.H.J.; Thunis, P.; Cuvelier, C.; Bedogni, M.; Bessagnet, B.; Honoré, C.; Moussiopoulos, N.; Pirovano, G.; Schaap, M.; et al. Evaluation and intercomparison of Ozone and PM10 simulations by several chemistry transport models over four European cities within the CityDelta project. Atmos. Environ. 2007, 41, 173–188. [Google Scholar] [CrossRef]
- Jian, L.; Zhao, Y.; Zhu, Y.P.; Zhang, M.B.; Bertolatti, D. An application of ARIMA model to predict submicron particle concentrations from meteorological factors at a busy roadside in Hangzhou, China. Sci. Total Environ. 2012, 426, 336–345. [Google Scholar] [CrossRef]
- Particulate Matter Air Quality Assessment Using Integrated Surface, Satellite, and Meteorological Products. Available online: https://www.researchgate.net/publication/252788692_Particulate_Matter_Air_Quality_Assessment_using_Integrated_Surface_Satellite_and_Meteorological_Products (accessed on 2 October 2021).
- Davis, J.M.; Speckman, P. A model for predicting maximum and 8 h average ozone in Houston. Atmos. Environ. 1999, 33, 2487–2500. [Google Scholar] [CrossRef]
- Hu, X.; Waller, L.A.; Al-Hamdan, M.Z.; Crosson, W.L.; Estes, M.G.; Estes, S.M.; Quattrochi, D.A.; Sarnat, J.A.; Liu, Y. Estimating ground-level PM2.5 concentrations in the southeastern U.S. using geographically weighted regression. Environ. Res. 2013, 121, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Zhang, H.; Palazoglu, A.; Singh, A.; Zhang, W.; Liu, S. Prediction of 24-hour-average PM2.5 concentrations using a hidden Markov model with different emission distributions in Northern California. Sci. Total Environ. 2013, 443, 93–103. [Google Scholar] [CrossRef] [PubMed]
- García Nieto, P.J.; Combarro, E.F.; Del Coz Díaz, J.J.; Montañés, E. A SVM-based regression model to study the air quality at local scale in Oviedo urban area (Northern Spain): A case study. Appl. Math. Comput. 2013, 219, 8923–8937. [Google Scholar] [CrossRef]
- Chang-Hoi, H.; Park, I.; Oh, H.R.; Gim, H.J.; Hur, S.K.; Kim, J.; Choi, D.R. Development of a PM2.5 prediction model using a recurrent neural network algorithm for the Seoul metropolitan area, Republic of Korea. Atmos. Environ. 2021, 245, 118021. [Google Scholar] [CrossRef]
- Laña, I.; Del Ser, J.; Padró, A.; Vélez, M.; Casanova-Mateo, C. The role of local urban traffic and meteorological conditions in air pollution: A data-based case study in Madrid, Spain. Atmos. Environ. 2016, 145, 424–438. [Google Scholar] [CrossRef]
- Hooyberghs, J.; Mensink, C.; Dumont, G.; Fierens, F.; Brasseur, O. A neural network forecast for daily average PM10 concentrations in Belgium. Atmos. Environ. 2005, 39, 3279–3289. [Google Scholar] [CrossRef]
- Kamińska, J.A. A random forest partition model for predicting NO2 concentrations from traffic flow and meteorological conditions. Sci. Total Environ. 2019, 651, 475–483. [Google Scholar] [CrossRef]
- Shang, Z.; Deng, T.; He, J.; Duan, X. A novel model for hourly PM2.5 concentration prediction based on CART and EELM. Sci. Total Environ. 2019, 651, 3043–3052. [Google Scholar] [CrossRef]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Li, X.; Peng, L.; Hu, Y.; Shao, J.; Chi, T. Deep learning architecture for air quality predictions. Environ. Sci. Pollut. Res. 2016, 23, 22408–22417. [Google Scholar] [CrossRef] [PubMed]
- Tian, H.; Zhao, Y.; Luo, M.; He, Q.; Han, Y.; Zeng, Z. Estimating PM2.5 from multisource data: A comparison of different machine learning models in the Pearl River Delta of China. Urban Clim. 2021, 35, 100740. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Computation, 9, 1735–1780.—References—Scientific Research Publishing. Available online: https://www.scirp.org/reference/referencespapers.aspx?referenceid=2693822 (accessed on 2 October 2021).
- Li, X.; Peng, L.; Yao, X.; Cui, S.; Hu, Y.; You, C.; Chi, T. Long short-term memory neural network for air pollutant concentration predictions: Method development and evaluation. Environ. Pollut. 2017, 231, 997–1004. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, H.; Zhao, G.; Lian, J. Constructing a PM2.5 concentration prediction model by combining auto-encoder with Bi-LSTM neural networks. Environ. Model. Softw. 2020, 124, 104600. [Google Scholar] [CrossRef]
- Chang, Y.S.; Chiao, H.T.; Abimannan, S.; Huang, Y.P.; Tsai, Y.T.; Lin, K.M. An LSTM-based aggregated model for air pollution forecasting. Atmos. Pollut. Res. 2020, 11, 1451–1463. [Google Scholar] [CrossRef]
- Abirami, S.; Chitra, P. Regional air quality forecasting using spatiotemporal deep learning. J. Clean. Prod. 2021, 283, 125341. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Tao, Q.; Liu, F.; Li, Y.; Sidorov, D. Air Pollution Forecasting Using a Deep Learning Model Based on 1D Convnets and Bidirectional GRU. IEEE Access 2019, 7, 76690–76698. [Google Scholar] [CrossRef]
- Huang, G.; Li, X.; Zhang, B.; Ren, J. PM2.5 concentration forecasting at surface monitoring sites using GRU neural network based on empirical mode decomposition. Sci. Total Environ. 2021, 768, 144516. [Google Scholar] [CrossRef]
- Pasquill, F.; Smith, F. Atmospheric Diffusion; E. Horwood: New York, NY, USA, 1983. [Google Scholar]
- Chen, X.; Shao, S.; Tian, Z.; Xie, Z.; Yin, P. Impacts of air pollution and its spatial spillover effect on public health based on China’s big data sample. J. Clean. Prod. 2017, 142, 915–925. [Google Scholar] [CrossRef]
- Li, X.; Wu, C.; Meadows, M.E.; Zhang, Z.; Lin, X.; Zhang, Z.; Chi, Y.; Feng, M.; Li, E.; Hu, Y. Factors Underlying Spatiotemporal Variations in Atmospheric PM2.5 Concentrations in Zhejiang Province, China. Remote Sens. 2021, 13, 3011. [Google Scholar] [CrossRef]
- Pan, S.; Du, S.; Wang, X.; Zhang, X.; Xia, L.; Liu, J.; Pei, F.; Wei, Y. Analysis and interpretation of the particulate matter (PM10 and PM2.5) concentrations at the subway stations in Beijing, China. Sustain. Cities Soc. 2019, 45, 366–377. [Google Scholar] [CrossRef]
- Pearson, K., VII. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar] [CrossRef]
- Huang, L.; Sun, J.; Jin, L.; Brown, N.J.; Hu, J. Strategies to reduce PM2.5 and O3 together during late summer and early fall in San Joaquin Valley, California. Atmos. Res. 2021, 258, 105633. [Google Scholar] [CrossRef]
- Air Quality Designations for the 2012 PM-2.5 National Ambient Air Quality Standards Established. Available online: https://www.zhangqiaokeyan.com/academic-journal-foreign_air-pollution-consultant_thesis/0204110280407.html (accessed on 5 October 2021).
- Sak, H.; Senior, A.; Beaufays, F. Long Short-Term Memory Based Recurrent Neural Network Architectures for Large Vocabulary Speech Recognition. arXiv 2014, arXiv:1402.1128. [Google Scholar]
- Gao, S.; Huang, Y.; Zhang, S.; Han, J.; Wang, G.; Zhang, M.; Lin, Q. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation. J. Hydrol. 2020, 589, 125188. [Google Scholar] [CrossRef]


| Parameters | Unit | Range | Average | St. Dev. |
|---|---|---|---|---|
| PM2.5 | μg/m3 | (1, 690] | 35.88 | 30.25 |
| PM10 | μg/m3 | [1, 1017] | 55.52 | 46.02 |
| SO2 | μg/m3 | [1, 777] | 7.75 | 7.41 |
| NO2 | μg/m3 | [1, 545] | 32.89 | 24.93 |
| CO | mg/m3 | [1, 700] | 59.64 | 48.95 |
| O3 | μg/m3 | [1, 300] | 58.37 | 43.82 |
| Parameter | Value |
|---|---|
| Loss | MSE |
| Optimizer | Adam |
| Epochs | 1000 |
| Learning rate | 0.001 |
| Hidden size | 40 |
| Num layers | 4 |
| Input size | 16 |
| Model | RNN | LSTM | GRU | RF | ||||
|---|---|---|---|---|---|---|---|---|
| Spatial RNN | Original RNN | Spatial LSTM | Original LSTM | Spatial GRU | Original GRU | Spatial RF | Original RF | |
| MAE | 5.521 | 6.478 | 4.881 | 5.523 | 5.210 | 5.834 | 5.106 | 7.041 |
| RMSE | 8.663 | 9.921 | 7.770 | 8.604 | 8.309 | 9.135 | 8.176 | 10.288 |
| 0.914 | 0.887 | 0.931 | 0.915 | 0.921 | 0.904 | 0.923 | 0.879 | |
| MAPE | 0.226 | 0.289 | 0.176 | 0.223 | 0.199 | 0.240 | 0.192 | 0.316 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, M.; Lao, T.; Yu, M.; Zhang, Y.; Zheng, J.; Li, Y. PM2.5 Concentration Forecasting over the Central Area of the Yangtze River Delta Based on Deep Learning Considering the Spatial Diffusion Process. Remote Sens. 2021, 13, 4834. https://doi.org/10.3390/rs13234834
Lu M, Lao T, Yu M, Zhang Y, Zheng J, Li Y. PM2.5 Concentration Forecasting over the Central Area of the Yangtze River Delta Based on Deep Learning Considering the Spatial Diffusion Process. Remote Sensing. 2021; 13(23):4834. https://doi.org/10.3390/rs13234834
Chicago/Turabian StyleLu, Mingyue, Tengfei Lao, Manzhu Yu, Yadong Zhang, Jianqin Zheng, and Yuchen Li. 2021. "PM2.5 Concentration Forecasting over the Central Area of the Yangtze River Delta Based on Deep Learning Considering the Spatial Diffusion Process" Remote Sensing 13, no. 23: 4834. https://doi.org/10.3390/rs13234834
APA StyleLu, M., Lao, T., Yu, M., Zhang, Y., Zheng, J., & Li, Y. (2021). PM2.5 Concentration Forecasting over the Central Area of the Yangtze River Delta Based on Deep Learning Considering the Spatial Diffusion Process. Remote Sensing, 13(23), 4834. https://doi.org/10.3390/rs13234834








