Using Airborne Laser Scanning to Characterize Land-Use Systems in a Tropical Landscape Based on Vegetation Structural Metrics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
- Tropical rainforest—areas dominated by trees (mainly including secondary rainforests as well as primary degraded rainforests), containing a minimum of 50% tree canopy closure above the lowest vegetation layer (to exclude tall, closed canopy transitional lands);
- Jungle rubber—rubber trees (Hevea brasiliensis) scattered in the jungle, with as little as 10% rubber tree stems out of the total stem number in a 2500 m2 area;
- Rubber plantation—regular plantation monocultures of rubber trees;
- Oil palm plantation—any oil palm (Elaeis guineensis) monoculture, including intercropped and uneven-aged stands;
- Transitional land (shrubland)—unused fallow land, including grasslands, which are in transition to secondary forest or cleared for plantation, containing up to 50% tree canopy closure above the lowest vegetation layer.
2.2. ALS Data Acquisition and Pre-Processing
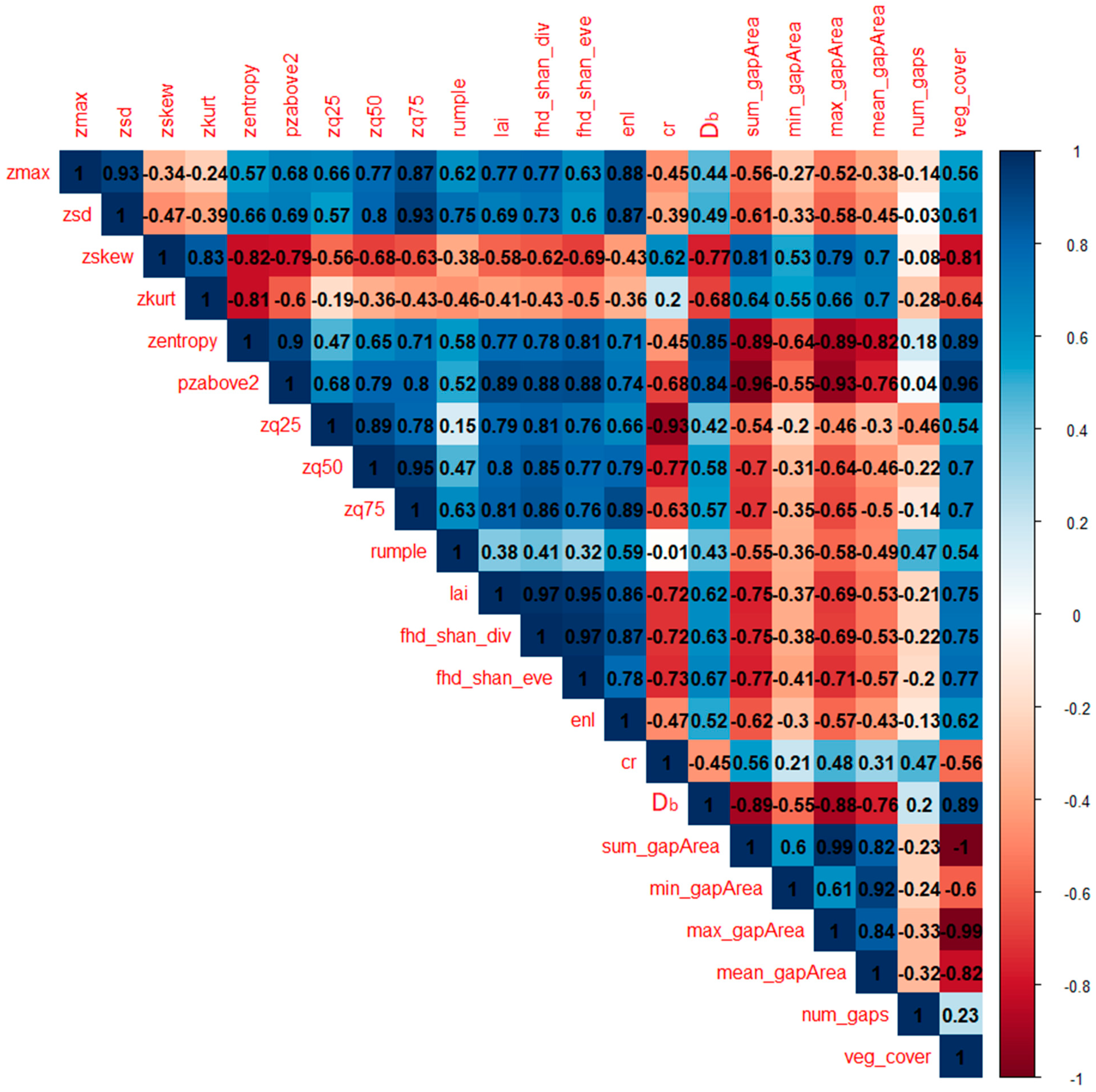
2.3. Metrics Extraction and Calculation
2.4. Statistical Analysis
2.4.1. Principal Component Analysis (PCA)
2.4.2. Analysis of Variance (ANOVA) and Post-Hoc Pairwise Comparison
2.4.3. Random Forest Land-Use Characterization
3. Results
3.1. Principal Component Analysis (PCA)
3.2. Analysis of Variance (ANOVA) and Post-Hoc Pairwise Comparison
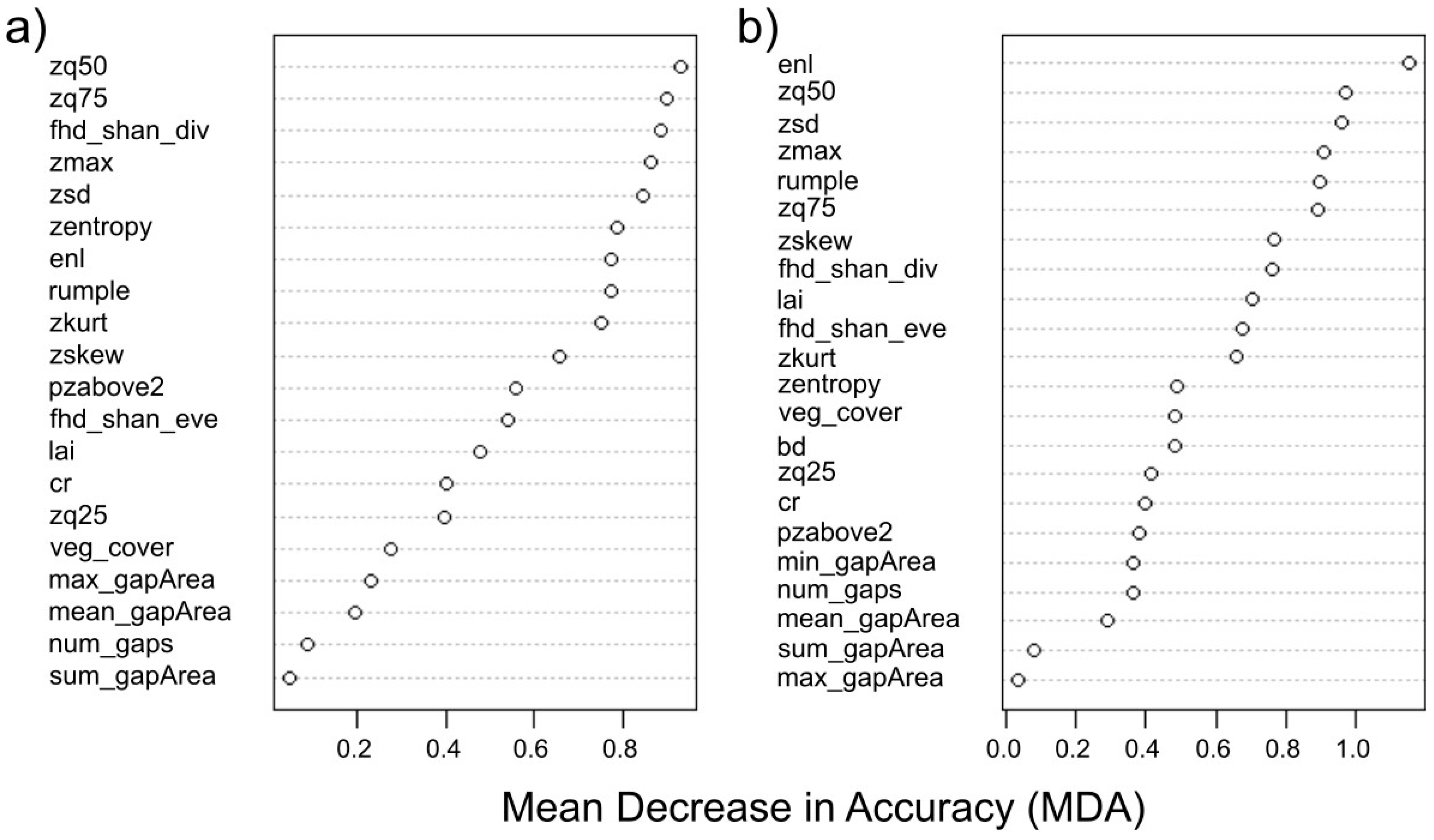
3.3. Random Forest Land-Use Characterizations
4. Discussions
- -
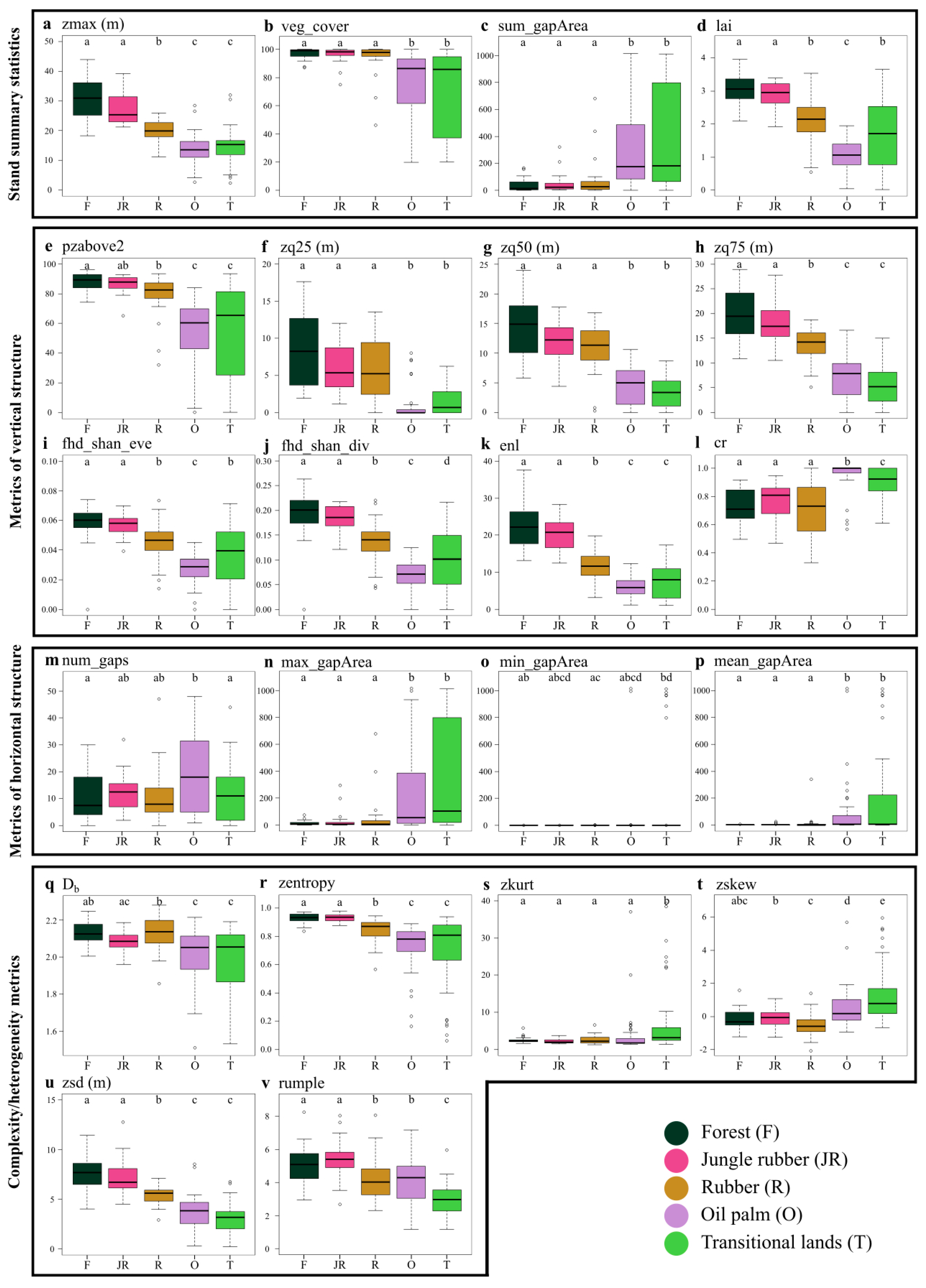
- Secondary rainforest and jungle rubber plots share the same structural properties. These properties consist of a high (≈100%) vegetation cover, with a top of the canopy layer reaching heights of 20–40 m, lai values ranging between 2 and 4, a relatively low number of gaps in the canopy (<30 per plot), high values of box dimension, enl, canopy surface roughness (i.e., rumple), entropy and standard deviation of height points and the lowest values in height kurtosis and skewness. Indeed, these characteristics could indicate the presence of higher vegetation structural complexity (compared to the other land uses), which translates to a greater volume of potential available habitat for different species to occupy, likely leading to higher levels of species richness [21,46].
- -
- Rubber plantation plots in many cases share similar trait values with rainforest and jungle rubber, with a high vegetation cover, low number and size of canopy gaps and low values of height kurtosis and skewness, while displaying intermediate values between forests and oil palm plantations in terms of canopy height (i.e., 10–20 m), lai (i.e., 1–3.5), enl (i.e., 5–20), box dimension and entropy of height points. These characteristics result in an intermediate vegetation structural complexity between forest plots and oil palm and transitional land plots, thus providing reduced habitat availability for the local native species [48].
- -
- Plots of oil palm plantation and transitional land are very similar to each other in most traits considered, with a lower extent and higher variation in vegetation cover and canopy height (i.e., 5–20 m), higher number of gaps (and their size) and lower values of structural complexity (box dimension) and entropy of height points compared to the other land uses. Between the two land uses, oil palm plots had lower lai values and higher values of rumple, cr and number of gaps. This is likely connected with the emblematic shape of the oil palm fronds and with their regular plantation design. Again, the lower values of ALS-derived vegetation metrics identified for oil palm plantations are indicative of this extremely simplified land-use system, which is connected to low habitat availability and reduced ecosystem functioning [94]. Additionally, the higher canopy gap area found in oil palm plots could explain the higher within-canopy temperature observed in a previous study on a subset of the same plots [18]. Although the results obtained for the transitional land class might be due to the highly variable (and in some cases degraded) nature of this land use, rather than to intensive management, its overall structural complexity remains quite low, potentially also resulting in low habitat provision.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Singh, S.; Jaiswal, D.K.; Krishna, R.; Mukherjee, A.; Verma, J.P. Restoration of degraded lands through bioenergy plantations. Restor. Ecol. 2020, 28, 263–266. [Google Scholar] [CrossRef]
- Aini, F.K.; Hergoualc’h, K.; Smith, J.U.; Verchot, L.; Martius, C. How does replacing natural forests with rubber and oil palm plantations affect soil respiration and methane fluxes? Ecosphere 2020, 11, e03284. [Google Scholar] [CrossRef]
- Margono, B.A.; Potapov, P.V.; Turubanova, S.; Stolle, F.; Hansen, M.C. Primary forest cover loss in indonesia over 2000–2012. Nat. Clim. Chang. 2014, 4, 730–735. [Google Scholar] [CrossRef]
- Haines-Young, R. Land use and biodiversity relationships. Land Use Policy 2009, 26, S178–S186. [Google Scholar] [CrossRef]
- Davis, K.F.; Koo, H.I.; Dell’Angelo, J.; D’Odorico, P.; Estes, L.; Kehoe, L.J.; Kharratzadeh, M.; Kuemmerle, T.; Machava, D.; de Jesus Rodrigues Pais, A.; et al. Tropical forest loss enhanced by large-scale land acquisitions. Nat. Geosci. 2020, 13, 482–488. [Google Scholar] [CrossRef]
- Purnomo, H.; Shantiko, B.; Sitorus, S.; Gunawan, H.; Achdiawan, R.; Kartodihardjo, H.; Dewayani, A.A. Fire economy and actor network of forest and land fires in Indonesia. For. Policy Econ. 2017, 78, 21–31. [Google Scholar] [CrossRef]
- Chen, B.; Kennedy, C.M.; Xu, B. Effective moratoria on land acquisitions reduce tropical deforestation: Evidence from Indonesia. Environ. Res. Lett. 2019, 14, 044009. [Google Scholar] [CrossRef]
- McElhinny, C.; Gibbons, P.; Brack, C.; Bauhus, J. Forest and woodland stand structural complexity: Its definition and measurement. For. Ecol. Manag. 2005, 218, 1–24. [Google Scholar] [CrossRef]
- Seidel, D. A holistic approach to determine tree structural complexity based on laser scanning data and fractal analysis. Ecol. Evol. 2018, 8, 128–134. [Google Scholar] [CrossRef]
- MacArthur, R.H.; MacArthur, J.W. On bird species diversity. Ecology 1961, 42, 594–598. [Google Scholar] [CrossRef]
- Lindenmayer, D.B.; Margules, C.R.; Botkin, D.B. Indicators of Biodiversity for Ecologically Sustainable Forest Management. Conserv. Biol. 2000, 14, 941–950. [Google Scholar] [CrossRef]
- Schmeller, D.S.; Weatherdon, L.V.; Loyau, A.; Bondeau, A.; Brotons, L.; Brummitt, N.; Geijzendorffer, I.R.; Haase, P.; Kuemmerlen, M.; Martin, C.S.; et al. A suite of essential biodiversity variables for detecting critical biodiversity change. Biol. Rev. 2018, 93, 55–71. [Google Scholar] [CrossRef]
- Seidel, D.; Annighöfer, P.; Ehbrecht, M.; Magdon, P.; Wöllauer, S.; Ammer, C. Deriving stand structural complexity from airborne laser scanning data-what does it tell us about a forest? Remote Sens. 2020, 12, 1854. [Google Scholar] [CrossRef]
- Ehbrecht, M.; Seidel, D.; Annighöfer, P.; Kreft, H.; Köhler, M.; Zemp, D.C.; Puettmann, K.; Nilus, R.; Babweteera, F.; Willim, K.; et al. Global patterns and climatic controls of forest structural complexity. Nat. Commun. 2021, 12, 519. [Google Scholar] [CrossRef]
- Noss, R.F. Indicators for monitoring biodiversity: A hierarchical approach. Conserv. Biol. 1990, 4, 355–364. [Google Scholar] [CrossRef]
- Ehbrecht, M.; Schall, P.; Ammer, C.; Seidel, D. Quantifying stand structural complexity and its relationship with forest management, tree species diversity and microclimate. Agric. For. Meteorol. 2017, 242, 1–9. [Google Scholar] [CrossRef]
- Kovács, B.; Tinya, F.; Ódor, P. Stand structural drivers of microclimate in mature temperate mixed forests. Agric. For. Meteorol. 2017, 234–235, 11–21. [Google Scholar] [CrossRef] [Green Version]
- Meijide, A.; Badu, C.S.; Moyano, F.; Tiralla, N.; Gunawan, D.; Knohl, A. Impact of forest conversion to oil palm and rubber plantations on microclimate and the role of the 2015 ENSO event. Agric. For. Meteorol. 2018, 252, 208–219. [Google Scholar] [CrossRef]
- Garden, J.G.; Mcalpine, C.A.; Possingham, H.P.; Jones, D.N. Habitat structure is more important than vegetation composition for local-level management of native terrestrial reptile and small mammal species living in urban remnants: A case study from Brisbane, Australia. Austral Ecol. 2007, 32, 669–685. [Google Scholar] [CrossRef]
- Sukma, H.T.; Di Stefano, J.; Swan, M.; Sitters, H. Mammal functional diversity increases with vegetation structural complexity in two forest types. For. Ecol. Manag. 2019, 433, 85–92. [Google Scholar] [CrossRef]
- Davies, A.B.; Ancrenaz, M.; Oram, F.; Asner, G.P. Canopy structure drives orangutan habitat selection in disturbed Bornean forests. Proc. Natl. Acad. Sci. USA 2017, 114, 8307–8312. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bain, G.C.; MacDonald, M.A.; Hamer, R.; Gardiner, R.; Johnson, C.N.; Jones, M.E. Changing bird communities of an agricultural landscape: Declines in arboreal foragers, increases in large species. R. Soc. Open Sci. 2020, 7, 200076. [Google Scholar] [CrossRef] [Green Version]
- Martinsen, G.D.; Whitham, T.G. More birds nest in hybrid cottonwood trees. Wilson Bull. 1994, 106, 474–481. [Google Scholar]
- Jucker, T.; Bongalov, B.; Burslem, D.F.R.P.; Nilus, R.; Dalponte, M.; Lewis, S.L.; Phillips, O.L.; Qie, L.; Coomes, D.A. Topography shapes the structure, composition and function of tropical forest landscapes. Ecol. Lett. 2018, 21, 989–1000. [Google Scholar] [CrossRef]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Givnish, T.J. On the causes of gradients in tropical tree diversity. J. Ecol. 1999, 87, 193–210. [Google Scholar] [CrossRef]
- John, R.; Dalling, J.W.; Harms, K.E.; Yavitt, J.B.; Stallard, R.F.; Mirabello, M.; Hubbell, S.P.; Valencia, R.; Navarrete, H.; Vallejo, M.; et al. Soil nutrients influence spatial distributions of tropical tree species. Proc. Natl. Acad. Sci. USA 2007, 104, 864–869. [Google Scholar] [CrossRef] [Green Version]
- Werner, F.A.; Homeier, J. Is tropical montane forest heterogeneity promoted by a resource-driven feedback cycle? Evidence from nutrient relations, herbivory and litter decomposition along a topographical gradient. Funct. Ecol. 2015, 29, 430–440. [Google Scholar] [CrossRef]
- Struebig, M.J.; Turner, A.; Giles, E.; Lasmana, F.; Tollington, S.; Bernard, H.; Bell, D. Quantifying the Biodiversity Value of Repeatedly Logged Rainforests. In Advances in Ecological Research; Elsevier Ltd.: Amsterdam, The Netherlands, 2013; Volume 48, pp. 183–224. ISBN 9780124171992. [Google Scholar]
- Camarretta, N.; Harrison, P.A.; Bailey, T.; Potts, B.; Lucieer, A.; Davidson, N.; Hunt, M. Monitoring forest structure to guide adaptive management of forest restoration: A review of remote sensing approaches. New For. 2020, 51, 573–596. [Google Scholar] [CrossRef]
- Dash, J.P.; Watt, M.S.; Pearse, G.D.; Heaphy, M.; Dungey, H.S. Assessing very high resolution UAV imagery for monitoring forest health during a simulated disease outbreak. ISPRS J. Photogramm. Remote Sens. 2017, 131, 1–14. [Google Scholar] [CrossRef]
- Thomson, E.R.; Malhi, Y.; Bartholomeus, H.; Oliveras, I.; Gvozdevaite, A.; Peprah, T.; Suomalainen, J.; Quansah, J.; Seidu, J.; Adonteng, C.; et al. Mapping the leaf economic spectrum across West African tropical forests using UAV-Acquired hyperspectral imagery. Remote Sens. 2018, 10, 1532. [Google Scholar] [CrossRef] [Green Version]
- Camarretta, N.; Harrison, P.A.; Lucieer, A.; Potts, B.M.; Davidson, N.; Hunt, M. Handheld Laser Scanning Detects Spatiotemporal Differences in the Development of Structural Traits among Species in Restoration Plantings. Remote Sens. 2021, 13, 1706. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J.; Anderson, C.; Knapp, D.E.; Martin, R.E.; Kennedy-bowdoin, T.; Van Breugel, M.; Davies, S.; Hall, J.S.; Muller-landau, H.C.; et al. High-fidelity national carbon mapping for resource management and REDD+. Carbon Balance Manag. 2013, 8, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonnet, S.; Gaulton, R.; Lehaire, F.; Lejeune, P. Canopy Gap Mapping from Airborne Laser Scanning: An Assessment of the Positional and Geometrical Accuracy. Remote Sens. 2015, 7, 11267–11294. [Google Scholar] [CrossRef] [Green Version]
- Asner, G.P.; Kellner, J.R.; Kennedy-Bowdoin, T.; Knapp, D.E.; Anderson, C.; Martin, R.E. Forest Canopy Gap Distributions in the Southern Peruvian Amazon. PLoS ONE 2013, 8, e60875. [Google Scholar] [CrossRef] [Green Version]
- Detto, M.; Asner, G.P.; Muller-Landau, H.C.; Sonnentag, O. Spatial variability in tropical forest leaf area density from multireturn lidar and modeling. J. Geophys. Res. Biogeosci. 2015, 120, 294–309. [Google Scholar] [CrossRef]
- Getzin, S.; Fischer, R.; Knapp, N.; Huth, A. Using airborne LiDAR to assess spatial heterogeneity in forest structure on Mount Kilimanjaro. Landsc. Ecol. 2017, 32, 1881–1894. [Google Scholar] [CrossRef]
- Guo, X.; Coops, N.C.; Tompalski, P.; Nielsen, S.E.; Bater, C.W.; John Stadt, J. Regional mapping of vegetation structure for biodiversity monitoring using airborne lidar data. Ecol. Inform. 2017, 38, 50–61. [Google Scholar] [CrossRef]
- Camarretta, N.; Harrison, P.A.; Lucieer, A.; Potts, B.M.; Davidson, N.; Hunt, M. From Drones to Phenotype: Using UAV-LiDAR to Detect Species and Provenance Variation in Tree Productivity and Structure. Remote Sens. 2020, 12, 3184. [Google Scholar] [CrossRef]
- Coss, S.; Durand, M.; Yi, Y.; Jia, Y.; Guo, Q.; Tuozzolo, S.; Shum, C.K.; Allen, G.H.; Calmant, S.; Pavelsky, T. Global River Radar Altimetry Time Series (GRRATS): New river elevation earth science data records for the hydrologic community. Earth Syst. Sci. Data 2020, 12, 137–150. [Google Scholar] [CrossRef] [Green Version]
- Marselis, S.M.; Tang, H.; Armston, J.D.; Calders, K.; Labrière, N.; Dubayah, R. Distinguishing vegetation types with airborne waveform lidar data in a tropical forest-savanna mosaic: A case study in Lopé National Park, Gabon. Remote Sens. Environ. 2018, 216, 626–634. [Google Scholar] [CrossRef]
- Deere, N.J.; Guillera-Arroita, G.; Swinfield, T.; Milodowski, D.T.; Coomes, D.A.; Bernard, H.; Reynolds, G.; Davies, Z.G.; Struebig, M.J. Maximizing the value of forest restoration for tropical mammals by detecting three-dimensional habitat associations. Proc. Natl. Acad. Sci. USA 2020, 117, 26254–26262. [Google Scholar] [CrossRef]
- Wayo, K.; Sritongchuay, T.; Chuttong, B.; Attasopa, K.; Bumrungsri, S. Local and landscape compositions influence stingless bee communities and pollination networks in tropical mixed fruit orchards, Thailand. Diversity 2020, 12, 482. [Google Scholar] [CrossRef]
- Barnes, A.D.; Allen, K.; Kreft, H.; Corre, M.D.; Jochum, M.; Veldkamp, E.; Clough, Y.; Daniel, R.; Darras, K.; Denmead, L.H.; et al. Direct and cascading impacts of tropical land-use change on multi-trophic biodiversity. Nat. Ecol. Evol. 2017, 1, 1511–1519. [Google Scholar] [CrossRef] [PubMed]
- Ishii, H.T.; Tanabe, S.I.; Hiura, T. Exploring the relationships among canopy structure, stand productivity, and biodiversity of temperate forest ecosystems. For. Sci. 2004, 50, 342–355. [Google Scholar] [CrossRef]
- Beukema, H.; Danielsen, F.; Vincent, G.; Hardiwinoto, S.; van Andel, J. Plant and bird diversity in rubber agroforests in the lowlands of Sumatra, Indonesia. Agrofor. Syst. 2007, 70, 217–242. [Google Scholar] [CrossRef] [Green Version]
- Drescher, J.; Rembold, K.; Allen, K.; Beckschäfer, P.; Buchori, D.; Clough, Y.; Faust, H.; Fauzi, A.M.; Gunawan, D.; Hertel, D.; et al. Ecological and socio-economic functions across tropical land use systems after rainforest conversion. Philos. Trans. R. Soc. B Biol. Sci. 2016, 371, 20150275. [Google Scholar] [CrossRef] [PubMed]
- Andaya, B.W. To Live as Brothers: Southeast Sumatra in the Seventeenth and Eighteenth Centuries; University of Hawaii Press: Honolulu, HI, USA, 1993; ISBN 0824814894. [Google Scholar]
- Kathirithamby-Wells, J. Hulu-hilir Unity and Conflict: Malay Statecraft in East Sumatra before the Mid-Nineteenth Century. Archipel 1993, 45, 77–96. [Google Scholar] [CrossRef]
- Gouyon, A.; de Foresta, H.; Levang, P. Does “jungle rubber” deserve its name? An analysis of rubber agroforestry systems in southeast Sumatra. Agrofor. Syst. 1993, 22, 181–206. [Google Scholar] [CrossRef] [Green Version]
- Gatto, M.; Wollni, M.; Qaim, M. Oil palm boom and land-use dynamics in Indonesia: The role of policies and socioeconomic factors. Land Use Policy 2015, 46, 292–303. [Google Scholar] [CrossRef] [Green Version]
- Elmhirst, R. Migrant pathways to resource access in Lampung’s political forest: Gender, citizenship and creative conjugality. Geoforum 2011, 42, 173–183. [Google Scholar] [CrossRef]
- Badan Pusat Statistik. Jambi Dalam Angka 2014; Badan Pusat Statistik: Jambi, Indonesia, 2014.
- R Core Team R: A Language and Environment for Statistical Computing. Available online: https://www.r-project.org (accessed on 9 January 2017).
- Roussel, J.-R.; Auty, D.; De Boissieu, F.; Meador, A.S. lidR; R Package Version 1.4.1; 2018. [Google Scholar]
- de Almeida, D.R.A.; Stark, S.C.; Silva, C.A.; Hamamura, C.; Valbuena, R. leafR; R Package Version 0.3; 2019. [Google Scholar]
- Arseniou, G.; MacFarlane, D.W.; Seidel, D. Measuring the Contribution of Leaves to the Structural Complexity of Urban Tree Crowns with Terrestrial Laser Scanning. Remote Sens. 2021, 13, 2773. [Google Scholar] [CrossRef]
- Ehbrecht, M.; Schall, P.; Juchheim, J.; Ammer, C.; Seidel, D. Effective number of layers: A new measure for quantifying three-dimensional stand structure based on sampling with terrestrial LiDAR. For. Ecol. Manag. 2016, 380, 212–223. [Google Scholar] [CrossRef]
- Silva, C.A.; Valbuena, R.; Pinagé, E.R.; Mohan, M.; de Almeida, D.R.A.; North Broadbent, E.; Jaafar, W.S.W.M.; de Almeida Papa, D.; Cardil, A.; Klauberg, C. ForestGapR: An r Package for forest gap analysis from canopy height models. Methods Ecol. Evol. 2019, 10, 1347–1356. [Google Scholar] [CrossRef] [Green Version]
- Runkle, J.R. Guidelines and Sample Protocol for Sampling Forest Gaps; U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 1992; Volume PNW-GTR-28.
- Latifi, H.; Fassnacht, F.E.; Müller, J.; Tharani, A.; Dech, S.; Heurich, M. Forest inventories by LiDAR data: A comparison of single tree segmentation and metric-based methods for inventories of a heterogeneous temperate forest. Int. J. Appl. Earth Obs. Geoinf. 2015, 42, 162–174. [Google Scholar] [CrossRef]
- Puliti, S.; Ørka, H.; Gobakken, T.; Næsset, E. Inventory of Small Forest Areas Using an Unmanned Aerial System. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef] [Green Version]
- Ene, L.T.; Næsset, E.; Gobakken, T.; Mauya, E.W.; Bollandsås, O.M.; Gregoire, T.G.; Ståhl, G.; Zahabu, E. Large-scale estimation of aboveground biomass in miombo woodlands using airborne laser scanning and national forest inventory data. Remote Sens. Environ. 2016, 186, 626–636. [Google Scholar] [CrossRef]
- Melin, M.; Hinsley, S.A.; Broughton, R.K.; Bellamy, P.; Hill, R.A. Living on the edge: Utilising lidar data to assess the importance of vegetation structure for avian diversity in fragmented woodlands and their edges. Landsc. Ecol. 2018, 33, 895–910. [Google Scholar] [CrossRef] [Green Version]
- Vepakomma, U.; Kneeshaw, D.D.; De Grandpré, L. Influence of natural and anthropogenic linear canopy openings on forest structural patterns investigated using LiDAR. Forests 2018, 9, 540. [Google Scholar] [CrossRef] [Green Version]
- Kane, V.R.; McGaughey, R.J.; Bakker, J.D.; Gersonde, R.F.; Lutz, J.A.; Franklin, J.F. Comparisons between field- and LiDAR-based measures of stand structural complexity. Can. J. For. Res. 2010, 40, 761–773. [Google Scholar] [CrossRef]
- Schneider, F.D.; Ferraz, A.; Hancock, S.; Duncanson, L.I.; Dubayah, R.O.; Pavlick, R.P.; Schimel, D.S. Towards mapping the diversity of canopy structure from space with GEDI. Environ. Res. Lett. 2020, 15, 115006. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer Series in Statistics; Springer: New York, NY, USA, 2002; ISBN 0-387-95442-2. [Google Scholar]
- Josse, J.; Husson, F. FactoMineR, R Package version 2.3; 2008. [Google Scholar]
- Kassambara, A.; Mundt, F. Factoextra, R Package version 1.0.7; 2020. [Google Scholar]
- Heiberger, R.M.; Neuwirth, E. One-Way ANOVA. In R Through Excel; Springer: New York, NY, USA, 2009; pp. 165–191. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591. [Google Scholar] [CrossRef]
- Levene, H. Robust tests for equality of variances. In Contribution to Probablity and Statistics: Essays in Honor of Harold Hotelling; Olkin, I., Hotelling, H., Al., E., Eds.; Stanford University Press: Stanford, CA, USA, 1960; pp. 278–292. [Google Scholar]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Shingala, M.C.; Rajyaguru, A. Comparison of post hoc tests for unequal variance. Int. J. New Technol. Sci. Eng. 2015, 2, 22–33. [Google Scholar]
- Signorell, A. DescTools, R Package version 0.99.41; 2021. [Google Scholar]
- Games, P.A.; Howell, J.F. Pairwise Multiple Comparison Procedures with Unequal N’s and/or Variances: A Monte Carlo Study. J. Educ. Stat. 1976, 1, 113–125. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Ellis, N.; Smith, S.J.; Pitcher, C.R. Gradient Forests: Calculating importance gradients on physical predictors. Ecology 2012, 93, 156–168. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirami, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [Green Version]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Costa e Silva, J.; Potts, B.; Harrison, P.A.; Bailey, T. Temperature and rainfall are separate agents of selection shaping population differentiation in a forest tree. Forests 2019, 10, 1145. [Google Scholar] [CrossRef] [Green Version]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Nakazawa, M. fmsb, R Package version 0.7.1; 2021. [Google Scholar]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- White, L.; Abernethy, K. A Guide to the Vegetation of the Lopé Reserve; New York Wildlife Conservation Society: New York, NY, USA, 1997; ISBN 963206427. [Google Scholar]
- Guillaume, T.; Kotowska, M.M.; Hertel, D.; Knohl, A.; Krashevska, V.; Murtilaksono, K.; Scheu, S.; Kuzyakov, Y. Carbon costs and benefits of Indonesian rainforest conversion to plantations. Nat. Commun. 2018, 9, 2388. [Google Scholar] [CrossRef]
- FAO. FAO Economic and Social Development Series 3: The Oil Palm; FAO: Rome, Italy, 1977. [Google Scholar]
- Gérard, A.; Wollni, M.; Hölscher, D.; Irawan, B.; Sundawati, L.; Teuscher, M.; Kreft, H. Oil-palm yields in diversified plantations: Initial results from a biodiversity enrichment experiment in Sumatra, Indonesia. Agric. Ecosyst. Environ. 2017, 240, 253–260. [Google Scholar] [CrossRef]
- Seidel, D.; Stiers, M.; Ehbrecht, M.; Werning, M.; Annighöfer, P. On the structural complexity of central European agroforestry systems: A quantitative assessment using terrestrial laser scanning in single-scan mode. Agrofor. Syst. 2021, 95, 669–685. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Evans, J.S.; Martinuzzi, S.; Gessler, P.E.; Hudak, A.T. Characterizing forest succession with lidar data: An evaluation for the Inland Northwest, USA. Remote Sens. Environ. 2009, 113, 946–956. [Google Scholar] [CrossRef] [Green Version]
- Fedrigo, M.; Newnham, G.J.; Coops, N.C.; Culvenor, D.S.; Bolton, D.K.; Nitschke, C.R. Predicting temperate forest stand types using only structural profiles from discrete return airborne lidar. ISPRS J. Photogramm. Remote Sens. 2018, 136, 106–119. [Google Scholar] [CrossRef]
- Zemp, D.C.; Ehbrecht, M.; Seidel, D.; Ammer, C.; Craven, D.; Erkelenz, J.; Irawan, B.; Sundawati, L.; Hölscher, D.; Kreft, H. Mixed-species tree plantings enhance structural complexity in oil palm plantations. Agric. Ecosyst. Environ. 2019, 283, 106564. [Google Scholar] [CrossRef]
- Ekadinata, A.; Vincent, G. Rubber agroforests in a changing landscape: Analysis of land use/cover trajectories in Bungo district, Indonesia. For. Trees Livelihoods 2011, 20, 3–14. [Google Scholar] [CrossRef]
- ITTO. Status of Tropical Forest Management 2005: Indonesia; ITTO: Yokohama, Japan, 2005. [Google Scholar]



| Stand Summary Measures | |
| Metrics | Description |
| zmax (m) | Maximum height within the point cloud. Calculated using the “stdmetrics()” function from the lidR package [56] |
| veg_cover (%) | Vegetation cover above 2.5 m. Calculated as the inverse of sum_gapArea. |
| sum_gapArea | Total extent of gaps > 2.5 m, calculated on a CHM raster with a pixel size of 0.5 m (m2). Obtained using the “GapStats()” function from the ForestGapR package [63] |
| lai | Leaf area index, derived from the vertical distribution of points using the “lai()” function from leafR package [64] |
| Complexity/Heterogeneity Measures | |
| Metrics | Description |
| Db | Box dimension, a holistic index of vegetation structural complexity. This metric was the only one calculated using the Mathematica software version 12 (Wolfram Research, Champaign, USA) calculated following Seidel [9] and Arseniou et al. [65] but adapted to the lower resolution of ALS point clouds by using a lower cut off of 1 m |
| zentropy | Entropy of height points. Calculated using the “stdmetrics()” function from the lidR package [56] |
| zkurt | Kurtosis of height points. Calculated using the “stdmetrics()” function from the lidR package [56] |
| zskew | Skewness of height points. Calculated using the “stdmetrics()” function from the lidR package [56] |
| zsd (m) | Standard deviation of height points. Calculated using the “stdmetrics()” function from the lidR package [56] |
| rumple | Rumple index, a measure of top canopy surface roughness [66]. Calculated using the “rumple_index()” function from lidR [56] |
| Measures of Vertical Structure | |
| Metrics | Description |
| pzabove2 | Number of points above a 2 m height threshold. Calculated using the “stdmetrics()” function from the lidR package [56] |
| zqNN (m) | Percentiles of height returns (NN = 25, 50, 75). Calculated using the “stdmetrics()” function from the lidR package [56] |
| fhd_shan_eve | Foliage Height Diversity, calculated as Shannon evenness, computed using the “FHD” function of the leafR package [64] |
| fhd_shan_div | Foliage Height Diversity, calculated as Shannon diversity, computed using the “FHD” function of the leafR package [64] |
| enl | Effective Number of Layers, a structural complexity index, calculated following Ehbrecht et al. [67] |
| cr | Canopy ratio, calculated as (zmax—zq25)/zmax [68] |
| Measures of Horizontal Structure | |
| Metrics | Description |
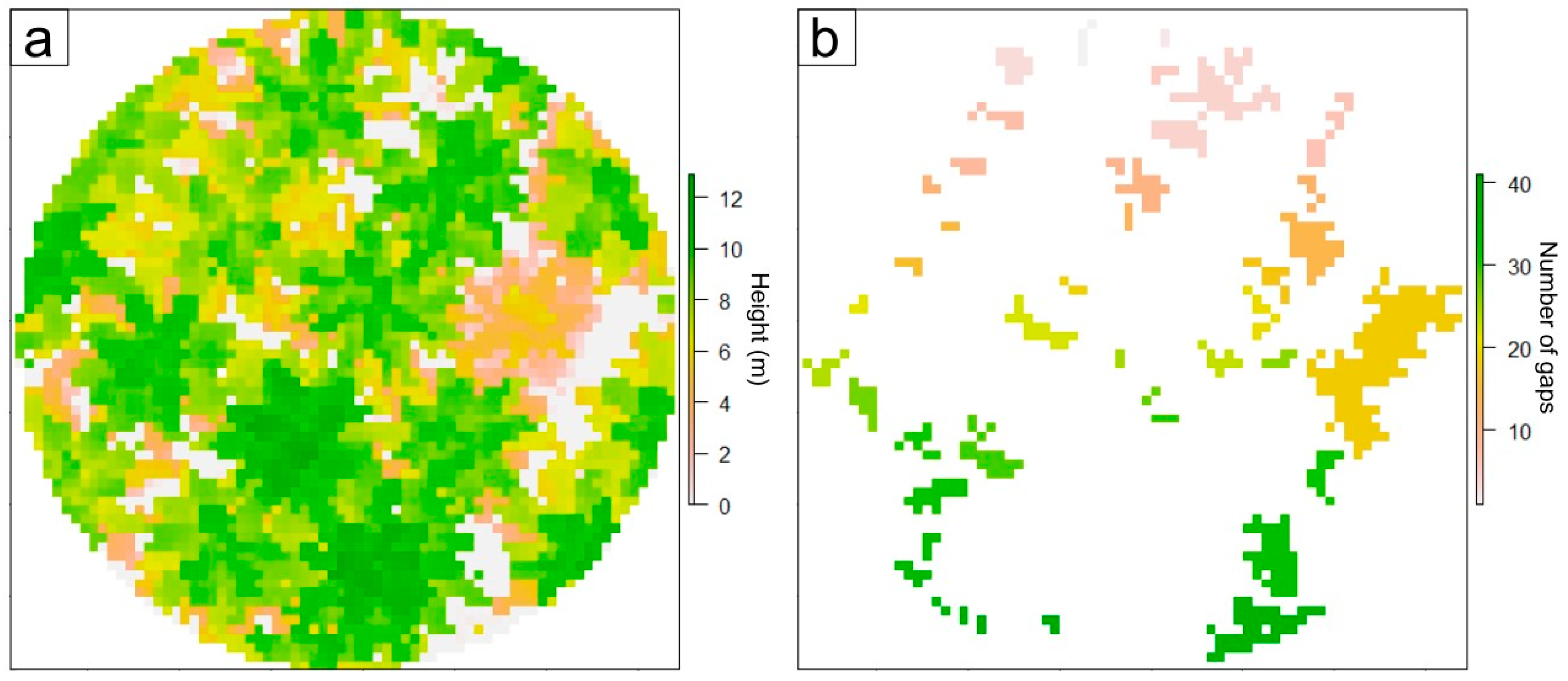
| num_gaps | Total number of gaps in the canopy > 2.5 m, calculated on a CHM raster with a pixel size of 0.5 m. Obtained using the “GapStats()” function from the ForestGapR package [63] |
| max_gapArea | maximum gap size > 2.5 m, calculated on a CHM raster with a pixel size of 0.5 m (m2). Obtained using the “GapStats()” function from the ForestGapR package [63] |
| min_gapArea | minimum gap size > 2.5 m, calculated on a CHM raster with a pixel size of 0.5 m (m2). Obtained using the “GapStats()” function from the ForestGapR package [63] |
| mean_gapArea | mean gap size > 2.5 m, calculated on a CHM raster with a pixel size of 0.5 m (m2). Obtained using the “GapStats()” function from the ForestGapR package [63] |
| PC 1 | PC 2 | ||||
| Metric | Eigenvalue | p-Value | Metric | Eigenvalue | p-Value |
| pzabove2 | 0.97 | *** | zq25 | 0.57 | *** |
| veg_cover | 0.92 | *** | mean_gapArea | 0.51 | *** |
| zentropy | 0.92 | *** | zkurt | 0.50 | *** |
| fhd_shan_div | 0.91 | *** | min_gapArea | 0.48 | *** |
| Lai | 0.89 | *** | zq50 | 0.36 | *** |
| fhd_shan_eve | 0.89 | *** | max_gapArea | 0.36 | *** |
| zq75 | 0.89 | *** | zmax | 0.35 | *** |
| zq50 | 0.87 | *** | fhd_shan_div | 0.31 | *** |
| Enl | 0.82 | *** | enl | 0.31 | *** |
| Db | 0.82 | *** | lai | 0.30 | *** |
| Zsd | 0.79 | *** | zq75 | 0.29 | *** |
| Zmax | 0.76 | *** | sum_gapArea | 0.26 | *** |
| zq25 | 0.73 | *** | zskew | 0.23 | ** |
| rumple | 0.59 | *** | fhd_shan_eve | 0.21 | ** |
| min_gapArea | −0.58 | *** | zsd | 0.20 | ** |
| Zkurt | −0.64 | *** | veg_cover | −0.26 | *** |
| Cr | −0.67 | *** | zentropy | −0.27 | *** |
| mean_gapArea | −0.76 | *** | rumple | −0.28 | *** |
| Zskew | −0.81 | *** | Db | −0.33 | *** |
| max_gapArea | −0.89 | *** | cr | −0.48 | *** |
| sum_gapArea | −0.92 | *** | num_gaps | −0.80 | *** |
| PC 3 | PC 4 | ||||
| Metric | Eigenvalue | p-value | Metric | Eigenvalue | p-value |
| rumple | 0.67 | *** | min_gapArea | 0.62 | *** |
| Zsd | 0.52 | *** | mean_gapArea | 0.35 | *** |
| Cr | 0.47 | *** | num_gaps | 0.24 | *** |
| Zmax | 0.46 | *** | zskew | −0.18 | * |
| Enl | 0.36 | *** | |||
| num_gaps | 0.34 | *** | |||
| Zskew | 0.33 | *** | |||
| zq75 | 0.26 | *** | |||
| Db | −0.18 | * | |||
| fhd_shan_eve | −0.19 | ** | |||
| zq25 | −0.22 | ** | |||
| Predicted | ||||||
|---|---|---|---|---|---|---|
| Observed | Forest | Jungle Rubber | Rubber | Oil Palm | Transitional Land | PA (%) |
| Forest | 4 | 3 | 1 | 0 | 0 | 44.4 |
| Jungle rubber | 4 | 4 | 1 | 0 | 0 | 44.4 |
| Rubber | 0 | 0 | 4 | 2 | 3 | 44.4 |
| Oil palm | 0 | 0 | 1 | 3 | 5 | 33.3 |
| Transitional land | 0 | 0 | 0 | 1 | 8 | 88.9 |
| UA (%) | 50.0 | 57.1 | 57.1 | 50.0 | 47.1 | |
| OA (%) | 51.1 | Kappa | 0.39 |
| Predicted | |||||
|---|---|---|---|---|---|
| Observed | Forest | Rubber | Oil Palm | Transitional Land | PA (%) |
| Forest | 9 | 0 | 0 | 0 | 100.0 |
| Rubber | 0 | 4 | 2 | 3 | 44.4 |
| Oil palm | 0 | 1 | 7 | 1 | 77.8 |
| Transitional land | 0 | 0 | 3 | 6 | 66.7 |
| UA (%) | 100.0 | 80.0 | 80.0 | 60.0 | |
| OA (%) | 72.2 | Kappa | 0.63 |
| Forest | Jungle Rubber | Rubber | Oil Palm | Transitional Land | |||||
|---|---|---|---|---|---|---|---|---|---|
| Metrics | MDA | Metrics | MDA | Metrics | MDA | Metrics | MDA | Metrics | MDA |
| zmax | 2.1 | fhd_shan_div | 1.6 | zq50 | 1.5 | fhd_shan_div | 1.9 | rumple | 1.9 |
| zq75 | 1.7 | Enl | 1.4 | fhd_shan_div | 1.2 | lai | 1.7 | zsd | 1.9 |
| zsd | 1.6 | zmax | 1.1 | zskew | 1.1 | zsd | 1.6 | zq75 | 1.7 |
| zentropy | 1.5 | pzabove2 | 0.9 | veg_cover | 1.0 | zmax | 1.5 | zq50 | 1.7 |
| enl | 1.5 | fhd_shan_eve | 0.9 | zsd | 0.9 | zq75 | 1.5 | zskew | 1.2 |
| fhd_shan_div | 1.3 | zentropy | 0.8 | pzabove2 | 0.8 | enl | 1.4 | zkurt | 1.1 |
| fhd_shan_eve | 1.2 | Lai | 0.8 | cr | 0.7 | zkurt | 1.1 | zmax | 0.9 |
| zq50 | 1.1 | zkurt | 0.7 | sum_gapArea | 0.7 | zq25 | 0.9 | veg_cover | 0.8 |
| zq25 | 0.8 | zq75 | 0.7 | zmax | 0.6 | zentropy | 0.9 | max_gapArea | 0.8 |
| cr | 0.8 | num_gaps | 0.5 | zq75 | 0.6 | fhd_shan_eve | 0.9 | enl | 0.6 |
| zkurt | 0.7 | zq50 | 0.5 | zentropy | 0.5 | num_gaps | 0.8 | pzabove2 | 0.6 |
| rumple | 0.5 | zq25 | 0.4 | rumple | 0.3 | cr | 0.8 | zentropy | 0.5 |
| lai | 0.4 | rumple | 0.4 | lai | 0.3 | zskew | 0.8 | mean_gapArea | 0.3 |
| pzabove2 | 0.4 | Zsd | 0.2 | mean_gapArea | 0.2 | zq50 | 0.7 | zq25 | 0.1 |
| num_gaps | 0.1 | Cr | 0.2 | zkurt | 0.1 | rumple | 0.5 | sum_gapArea | 0.1 |
| zskew | 0.1 | max_gapArea | 0.1 | zq25 | 0.1 | max_gapArea | 0.5 | fhd_shan_eve | −0.1 |
| max_gapArea | 0.0 | mean_gapArea | 0.1 | max_gapArea | −0.1 | pzabove2 | 0.3 | cr | −0.2 |
| mean_gapArea | −0.1 | veg_cover | 0.0 | enl | −0.1 | mean_gapArea | 0.0 | lai | −0.3 |
| veg_cover | −0.1 | sum_gapArea | −0.2 | fhd_shan_eve | −0.2 | veg_cover | −0.1 | fhd_shan_div | −0.4 |
| sum_gapArea | −0.2 | zskew | −0.3 | num_gaps | −0.2 | sum_gapArea | −0.5 | num_gaps | −0.7 |
| Forest | Rubber | Oil Palm | Transitional Land | ||||
|---|---|---|---|---|---|---|---|
| Metrics | MDA | Metrics | MDA | Metrics | MDA | Metrics | MDA |
| enl | 2.2 | enl | 1.5 | fhd_shan_eve | 1.4 | zq75 | 1.7 |
| zsd | 1.9 | zq50 | 1.4 | zsd | 1.4 | rumple | 1.6 |
| lai | 1.6 | zskew | 1.4 | zq75 | 1.3 | zsd | 1.5 |
| zmax | 1.6 | zmax | 1.3 | enl | 1.3 | zq50 | 1.5 |
| zentropy | 1.5 | zsd | 1.2 | zq25 | 1.2 | zkurt | 1.3 |
| fhd_shan_div | 1.4 | veg_cover | 1.1 | lai | 1.2 | enl | 1.0 |
| zq75 | 1.3 | cr | 1.1 | zmax | 1.1 | max_gapArea | 1.0 |
| zq50 | 1.0 | lai | 0.9 | rumple | 0.9 | min_gapArea | 0.8 |
| rumple | 1.0 | zkurt | 0.8 | zkurt | 0.7 | zmax | 0.8 |
| fhd_shan_eve | 0.9 | fhd_shan_div | 0.8 | num_gaps | 0.7 | mean_gapArea | 0.7 |
| zq25 | 0.9 | Db | 0.7 | cr | 0.7 | zskew | 0.7 |
| Db | 0.9 | zq75 | 0.6 | zskew | 0.6 | pzabove2 | 0.6 |
| pzabove2 | 0.8 | zq25 | 0.5 | fhd_shan_div | 0.6 | veg_cover | 0.4 |
| mean_gapArea | 0.7 | sum_gapArea | 0.5 | pzabove2 | 0.6 | fhd_shan_div | 0.4 |
| veg_cover | 0.6 | rumple | 0.4 | Db | 0.5 | sum_gapArea | 0.3 |
| num_gaps | 0.4 | fhd_shan_eve | 0.4 | zq50 | 0.5 | zentropy | 0.2 |
| zkurt | 0.3 | num_gaps | 0.3 | zentropy | 0.1 | fhd_shan_eve | 0.1 |
| cr | 0.2 | mean_gapArea | 0.2 | sum_gapArea | 0.1 | Db | 0.0 |
| min_gapArea | 0.0 | min_gapArea | 0.0 | veg_cover | 0.0 | num_gaps | −0.1 |
| zskew | −0.2 | max_gapArea | −0.3 | mean_gapArea | −0.3 | lai | −0.3 |
| max_gapArea | −0.4 | pzabove2 | −0.4 | min_gapArea | −0.3 | zq25 | −0.5 |
| sum_gapArea | −0.9 | zentropy | −0.4 | max_gapArea | −0.4 | cr | −0.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camarretta, N.; Ehbrecht, M.; Seidel, D.; Wenzel, A.; Zuhdi, M.; Merk, M.S.; Schlund, M.; Erasmi, S.; Knohl, A. Using Airborne Laser Scanning to Characterize Land-Use Systems in a Tropical Landscape Based on Vegetation Structural Metrics. Remote Sens. 2021, 13, 4794. https://doi.org/10.3390/rs13234794
Camarretta N, Ehbrecht M, Seidel D, Wenzel A, Zuhdi M, Merk MS, Schlund M, Erasmi S, Knohl A. Using Airborne Laser Scanning to Characterize Land-Use Systems in a Tropical Landscape Based on Vegetation Structural Metrics. Remote Sensing. 2021; 13(23):4794. https://doi.org/10.3390/rs13234794
Chicago/Turabian StyleCamarretta, Nicolò, Martin Ehbrecht, Dominik Seidel, Arne Wenzel, Mohd. Zuhdi, Miryam Sarah Merk, Michael Schlund, Stefan Erasmi, and Alexander Knohl. 2021. "Using Airborne Laser Scanning to Characterize Land-Use Systems in a Tropical Landscape Based on Vegetation Structural Metrics" Remote Sensing 13, no. 23: 4794. https://doi.org/10.3390/rs13234794
APA StyleCamarretta, N., Ehbrecht, M., Seidel, D., Wenzel, A., Zuhdi, M., Merk, M. S., Schlund, M., Erasmi, S., & Knohl, A. (2021). Using Airborne Laser Scanning to Characterize Land-Use Systems in a Tropical Landscape Based on Vegetation Structural Metrics. Remote Sensing, 13(23), 4794. https://doi.org/10.3390/rs13234794









