Abstract
The mapping function is crucial for the conversion of slant total electron content (TEC) to vertical TEC for low Earth orbit (LEO) satellite-based observations. Instead of collapsing the ionosphere into one single shell in commonly used mapping models, we defined a new mapping function assuming the vertical ionospheric distribution as an exponential profiler with one simple parameter: the plasmaspheric scale height in the zenith direction of LEO satellites. The scale height obtained by an empirical model introduces spatial and temporal variances into the mapping function. The performance of the new method is compared with the mapping function F&K by simulating experiments based on the global core plasma model (GCPM), and it is discussed along with the latitude, seasons, local time, as well as solar activity conditions and varying LEO orbit altitudes. The assessment indicates that the new mapping function has a comparable or better performance than the F&K mapping model, especially on the TEC conversion of low elevation angles.
1. Introduction
Benefitting from the accomplishment of the global navigation satellite system (GNSS) and many low Earth orbit (LEO) satellite missions, ionospheric exploration is greatly facilitated by various spaceborne measurements. Several successful LEO missions, such as Constellation Observing System for Meteorology, Ionosphere, and Climate (COSMIC), contribute greatly to the ionospheric modeling and data assimilation system [1,2,3,4,5]. One significant product provided by these satellites is the sounding measurements that contain the total electron density content (TEC) along the signal paths. To obtain the absolute TEC from the raw GNSS/LEO observations, data analysis centers and scientific researchers have devoted great efforts into the main procedures, including the cycle slip detection and correction, carrier-phase to pseudorange leveling, multipath effect correction, and the differential code bias (DCB) estimation [6,7,8,9,10]. The conversion between the slant TEC (STEC) along the ray path and the vertical TEC (VTEC) in the zenith is an essential procedure during the data processing. An obliquity factor called mapping function (MF) is commonly used to do the conversion. MF is a crucial parameter in the estimation of receiver DCB by assuming the simultaneous VTECs transformed from two GNSS slant observations of one LEO antenna are equal [8]. Furthermore, the mapping function plays a significant role in ionospheric and plasmaspheric TEC modeling due to the fact that the accuracy of the MF is highly correlated with the estimated VTEC and DCB [11].
Several mapping functions are widely used in the TEC conversion, such as the thin layer model (TLM) [12], the simple “geometric” model proposed by Foelsche and Kichengast (called F&K hereafter) [13], and some extended investigations [14,15,16,17,18]. The vertical structure of the ionosphere is usually assumed concentrating on one single thin layer. The height of the layer is called the ionospheric effective height (IEH) or shell height, which is calculated by the centroid method or integral median method or simplified as a constant value. The performance of mapping functions differs when receivers are located at different orbit heights or applying different IEH selections. How to choose the optimized IEH for the LEO-based TEC conversion needs systematical investigation. According to Zhong et al. [19] and Huang & Yuan [20], the IEH selection becomes more significant for the mapping function with an increasing zenith angle. Xiang & Gao [16] reviewed several mapping functions and proposed a mapping function that utilizes the ionospheric varying height assisted by the International Reference Ionosphere (IRI) model [21]. The study by Gulyaeva et al. [22] explored the center-of-mass of the ionosphere as the effective varying shell height produced by the ionospheric equivalent slab thickness. Zhong et al. [19] examined the applicability of three mapping functions for LEO-based GNSS observations: the thin layer model, the F&K model, and the Lear model, and found that the F&K geometric mapping function together with the IEH from the centroid method is more suitable to convert the LEO-based TEC measurements. The optimized IEH for the F&K can be approximately expressed as km under medium solar activity (MSA) conditions. As a consequence, the COSMIC-based TEC conversion (with satellites running at ~800 km) will get minimum mapping errors when the IEH is set to be around 2,100 km during MSA years. The current data processing in the COSMIC data analysis and archive center (CDAAC) applied the F&K mapping model, and the IEH is fixed at several hundreds or thousands of kilometers to simplify the uses [3,23]. However, one common drawback of these thin-layer mapping functions is that they ignore the vertical structure of the ionosphere and plasmasphere, and the IEH without spatial and temporal variations will affect the accuracy of the TEC conversion. One option to improve the TEC mapping is to estimate the 3D ionospheric electron density distribution by tomography or data assimilation based on the dense measuring network of sufficient spatial and temporal resolution and deduce realistic and persistent estimates of the ionospheric effective height [24]. Another approach is to assume multiple layers in the ionosphere implemented with specific mapping functions [17,20]. To further consider the vertical distribution of the ionosphere, Hoque & Jakowski [15] proposed a multi-layer mapping function according to the typical structure described by the Chapman layer. Nevertheless, the above methods are dependent on either extensive data coverage or accurate ionospheric models and parameters that are difficult to obtain in the global scope. Therefore, more advanced ionospheric mapping functions with simple free parameters deserve continuous attention and potential development.
The scale height in the plasmasphere () is an important factor to present the dynamic nature and variations of the plasmasphere [25]. In Wu et al. [26], we have developed a scale height model depending on parameters, including the month of the year, local time, geographic latitude, and the solar radio flux index F10.7. This study is aimed to propose a new mapping function taking advantage of the former scale height model (named as the scale-height-based mapping function) to give an accurate obliquity factor to convert LEO-based slant TEC to vertical TEC and vice versa. The ionosphere is no longer collapsed into any shell but assumes an exponential vertical structure. The scale height introduces realistic spatial and temporal variations in the ionospheric and plasmaspheric electron density into the TEC conversion. With the proposed method, we expect to solve the problem of optimized IEH specification and neglect of ionospheric physical variations in the current single layer mapping models and, finally, facilitate the TEC and DCB estimations of LEO satellites. Section 2 introduces the mathematical solutions of the new mapping function, and Section 3 gives the distribution of plasmaspheric scale height and the associated mapping function values; in Section 4, global assessments of the scale-height-based mapping function and the F&K model are performed according to different seasons, locations, solar activity levels, and orbit altitudes, and the conclusion is drawn in Section 5.
2. Materials and Methods
The scale height is one of the most important characteristics in the ionosphere–plasmasphere system due to the role in shaping the electron density profile [25,27,28,29]. There are various definitions of scale heights in published literature, including the theoretical plasma scale height, the vertical scale height, and the effective scale height. Alessio Pignalberi et al. [25] discussed the possible relationships among the different definitions of scale height. In this study, the plasmaspheric scale height adopts the definition of effective scale height, in which the analytical formulation of fitting the electron profile is chosen as exponential function. The new scale-height-based mapping function is not associated with specific IEH or thin-layer assumption but relates to the plasmaspheric scale height deduced from the exponential layer ionospheric model proposed by Stankov et al. [30]; i.e., the vertical electron density profile can be represented as:
where is the base electron density of plasmasphere (here set to be the electron density at the receiver height ), and is the plasmaspheric scale height. Thus, the mapping function can be written as the ratio of slant and vertical integral of electron density along the slant ray and the vertical path:
where and represent the locations of LEO and GNSS satellites from the Earth center, respectively; and are the corresponding satellite heights above Earth’s surface; is the zenith angle of the ray at the LEO receiver. Figure 1 shows the geometric schematic of the mapping function. If the ionospheric spherical symmetry assumption is adopted, together with Equation (1), the numerical expression of the scale-height-based mapping function is
where ; represents the radius of LEO satellite orbit from the Earth center; is the zenith angle of the ray at the LEO receiver. can be obtained by numerical integral if is known. Since the plasmaspheric scale height varies with the solar activity, season, local time, and location [26], this mapping function is embedded with temporal and spatial variations. It should be mentioned that the scale-height-based mapping function implicitly assumes the exponential distribution of the ionosphere and plasmasphere. Considering the general orbit range of spaceborne satellites, the assumption is reasonable when dealing with LEO-based TEC conversion.
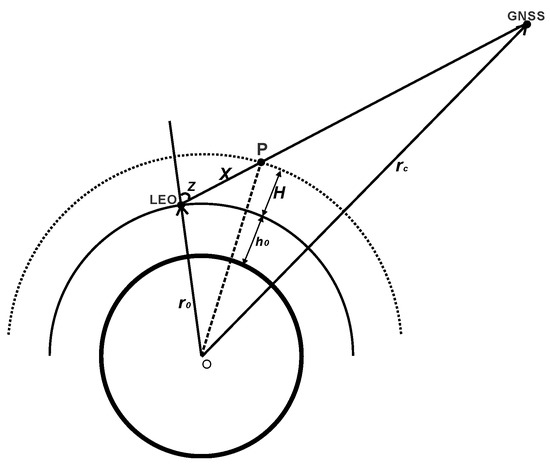
Figure 1.
Geometric schematic of LEO-based GNSS TEC mapping model; LEO—Low Earth orbit.
Besides the numerical expression, an analytical solution for the mapping function can be written as:
where and is the complementary error function. The process to obtain Equation (4) is shown in Appendix A. There are differences between the numerical and analytical expression of because the analytical solution adopts some approximations. We noticed that Hoque & Jakowski [15,31] presented a multi-layer mapping function approach for potential space-based augmentation system (SBAS) service under the assumption of Chapman layer distribution of the vertical electron density depending on the peak ionization height and atmospheric scale height. Here, we adopt the hypothesis of an exponential scale height to deal with the LEO-based slant to vertical TEC conversion.
The scale-height-based mapping function is compared with the F&K method in this study. The F&K mapping function was originally proposed to describe the dependence of the hydrostatic path delay with only one free parameter: “effective height”. When applied to the LEO-based TEC conversion, the IEH is assumed at the height of a thick spherical layer above the receiver, hypothetically concentrating the whole impact of the ionosphere. The F&K mapping function is written as
where and are the radii of the assumed layer and LEO satellite, respectively; is the zenith angle. The mapping factor may differ a lot with diverse IEH specifications.
3. Results
We calculate a mapping factor grid of zenith angle varying between and with resolution, and varying in (100, 6000) km with a 50 km step according to Equations (3) and (4). The obliquity factor of arbitrary TEC conversion can be obtained by interpolation with specified and . The grid map along with zenith angle and retrieved from the numerical and analytical solutions are demonstrated in Figure 2 (panel (a) and (c)). As an example, the spaceborne receiver is assumed at 800 km and the transmitter is assumed at 20,000 km. Moreover, the F&K model with the shell height varying from 100 km to 6000 km is displayed in panel (b). The blank in panel (b) is caused by the unreasonable result of the F&K model when the IEH is lower than the assumed LEO satellite height at high zenith angles. Similarly, the analytical resolution is not available when the ray path is approaching the zenith direction. We see the mapping factor increases when the zenith angle gets greater, and the difference brought by varying the value or shell height selection becomes significant when the zenith angle is larger than . The mapping factor has similar variations along with the scale height or IEH. The numerical and analytical results differ more with a large zenith angle and higher values (shown in panel (d)).
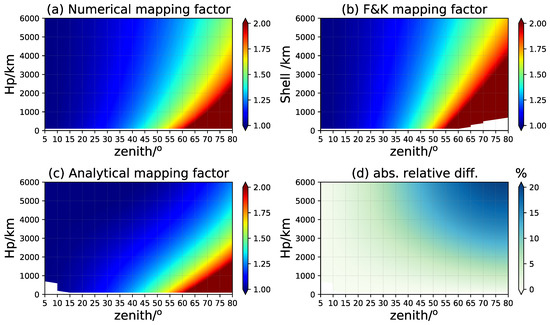
Figure 2.
The mapping factor grid of zenith angle and the plasmaspheric scale height ; panel (a,c) are the numerical and analytical results of scale-height-based mapping function, respectively; (b) is those for F&K model; (d) is the absolute relative difference between (a,c).
The only free parameter in the scale-height-based mapping function is the plasmaspheric scale height. In Wu et al. [26], we have calculated the plasmaspheric scale height from the COSMIC measurements from 2007 to 2014 and proposed an empirical monthly climate model that has reasonable accuracy validated by the scale height retrieved from the International Satellites for Ionospheric Studies (ISIS) observations during its mission period. This model is suitable to provide the essential parameter in the scale-height-based mapping function. Besides the COSMIC-derived , the scale height obtained by the global core plasma model (GCPM) provides an alternative option [32]. The GCPM provides empirically derived core plasma density and ion composition (, , and ) as a function of the geomagnetic and solar conditions throughout the inner magnetosphere. The model merges with the IRI model at low altitudes and is composed of separate models for the plasmasphere, plasmapause, trough, and polar cap. The is calculated from the overhead vertical TEC simulated with the GCPM electron density field and the base electron density at the assumed receiver altitude since the integral in Equation (1) could be approximately written as . The retrieved from the observations and empirical model (represented by and , respectively) are shown according to four seasons, local time, and dipole geomagnetic latitude in the low solar activity (LSA) year 2008 (Figure 3) and high solar activity (HSA) year 2013 (Figure 4), respectively. The four seasons are represented by March equinox (March, April, May), June solstice (June, July, August), September equinox (September, October, November), and December solstice (January, February, December) in this work. The is generally greater than the GCPM simulations, but they have generally similar variations along with the latitude, local time, season, and solar activity. The nighttime scale height is larger than that in the daytime and usually achieves the maximum before the sunrise, which is consistent with the conclusion drawn in Wu et al. [26]. The seasonal variations are more predominant for COSMIC scale heights, with higher values in the winter hemisphere and lower at the summer half. Under high solar activity conditions, the scale height decreases for both the observational and empirical models. The obliquity factor will differ a bit when applying and in the mapping function. At the high latitudes (~), the electron density is quite small and rarely changed, so the scale height value can be regarded as a constant. The derived from satellite observations is assumed more reliable when dealing with the realistic mapping issues, but, in the following study, the is discussed because we are aiming at the comprehensive validation of the scale-height-based mapping function in a simulation way.
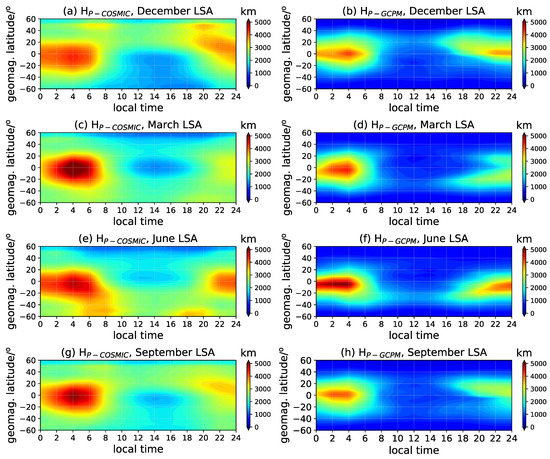
Figure 3.
The distribution of the COSMIC and GCPM retrieved (represented by ‘’ and ‘’) along with the local time, geomagnetic latitude, and season in the LSA year; panels (a,c,e,g) are for , panels (b,d,f,h) are for .
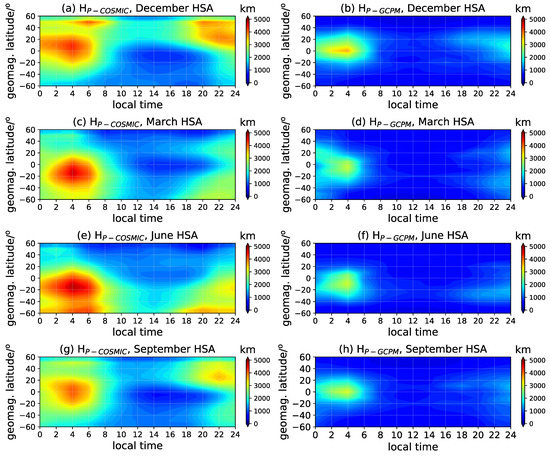
Figure 4.
Same as Figure 3 but for the HSA year.
4. Discussion
4.1. Assessment by Global Statistics
To assess the performance of the new mapping function, the GCPM is used to generate simulating LEO-based TEC observations and examine the retrieved errors of both mapping models. The LEO satellite orbit is chosen at 800 km, which is the typical orbit altitude of the COSMIC-1 constellation that made a great contribution to the ionosphere and plasmasphere exploration. The signal transmitter is at 20,000 km, referring to the GNSS satellites. It should be noted that both the scale-height-based and the F&K mapping function assume the spherical symmetric distribution of the ionosphere, which means the electron density on the same sphere is identical everywhere. Thus, the simulated STEC of a different zenith angle is actually equal to the integral of vertical electron density along the slant ray path with a 50 km step. The VTEC retrieved from the slant TEC and mapping function is compared to the VTEC ‘truth’ integrated directly from the GCPM background (regarded as ). The relative root mean square (RMS) of each zenith angle is calculated as the assessment criteria:
where is the TEC observation number of global grids at the zenith angle . Given the difference between the numerical and analytical representation of mapping function, we checked the performance of the scale-height-based mapping function of both solutions, denoted as ‘’ and ‘’, respectively, hereafter. To introduce independent reference into the validation, the F&K mapping function is also considered with adjustable IEH represented as a function of the LEO orbit height and solar flux proxy F10.7 () according to Zhong et al. [19]:
Thus, the IEH specifications take different satellite altitudes and solar activity levels into consideration, and the F&K mapping model is optimized by choosing a constant IEH. The zenith angle of the simulated slant ray path varies from to in steps of , and the geophysical location of the receiver changes with horizontal resolution of latitudinal from to and longitudinal from to . The simulating experiments are executed on one day in four seasons with a temporal resolution of 2 h under both the low and high solar activity conditions. The mean retrieved RMS errors for each season are calculated according to the zenith angles and shown in Figure 5. The F&K mapping function depends on the fixed IEH globally; thus, the retrieved errors are closely associated with the ionospheric variations of the GCPM background. According to Figure 5, the behavior of the numerical and analytical mapping functions differs from each other while indicating better retrieved results than the F&K model, especially with increasing zenith angles greater than . In the LSA years, the retrieved errors of the numerical mapping function are slightly less than those of the analytical solution at lower zeniths. When the solar activity is more active, the mapping errors of all the methods decrease to some extent, and the analytical mapping function achieves the best performance throughout the year. The difference between the two scale-height-based models is associated with the variation in the value under different solar activity conditions and the zenith angles. From the statistics, we conclude that, with the LEO satellite located at the 800 km, the -based mapping function is a competitive approach in comparison with the F&K model, especially at low elevation angles; i.e., at high zenith angles.
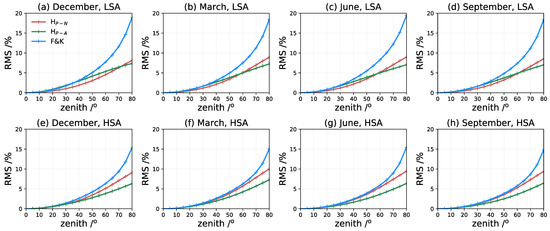
Figure 5.
The relative RMS statistics of the scale-height-based mapping function with numerical and analytical solutions (denoted as ‘’ and ‘’, respectively), and the F&K model (‘F&K’) in four seasons under low and high solar activity conditions (represented by ‘LSA’ and ‘HSA’); panels (a–d) are for the LSA year, and (e–h) are for HSA year.
4.2. Global Variations of Mapping Errors
To further analyze the time and spatial dependence of the mapping functions, the global maps of mean retrieved error with the zenith angle fixed at are displayed in Figure 6 and Figure 7 of the LSA and HSA years, respectively. The scale-height-based mapping function of the numerical or analytical solutions and the F&K model exhibit quite different characteristics with the local time, geographical latitude, and seasons. Corresponding to the predominant seasonal asymmetric features of , the VTEC retrieved by the new method is overestimated in the nighttime winter hemisphere, especially when using the analytical mapping factor. Both the scale-height-based models underestimate the VTEC during the daytime at low and equatorial latitudes. Consistent with the statistics in Figure 5, the general performance of the numerical mapping function is fairly good, with the mapping error varying between −5% and 5%. The latitudinal and temporal variations of the mapping errors reflect the reliability of the exponential assumption in the GCPM model. It proves that the variations in the ionosphere and plasmasphere are more complicated and nonuniform at low latitudes. For the F&K model, the relative error maps indicate the inhomogeneous variations of the ionospheric effective height of the background. The VTEC is significantly underestimated during the whole day at low latitudinal areas, while it is overestimated at higher latitudes. The performance of all the methods is remarkably improved under higher solar activity, as shown in Figure 7. Generally, the scale-height-based mapping function achieves better conversion results than the F&K method, especially in the equatorial anomaly regions between and .
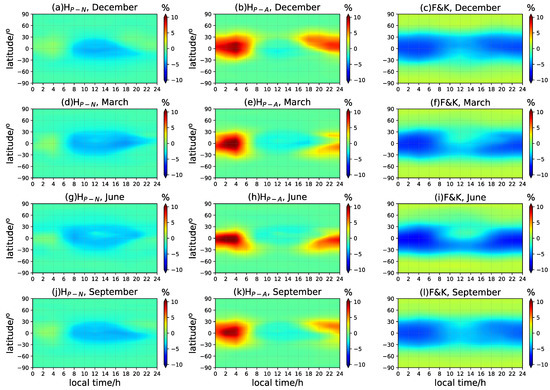
Figure 6.
The local time and latitude-dependent variations of the retrieved VTEC mean deviation for the mapping experiments in different seasons in LSA years. The zenith angle is fixed at . The ‘’, ‘’, and ‘F&K’ represent the numerical and analytical mapping functions and the F&K model, respectively; panels (a,d,g,j) are -based mapping errors; (b,e,h,k) are -based mapping errors; (c,f,i,l) are F&K mapping errors.
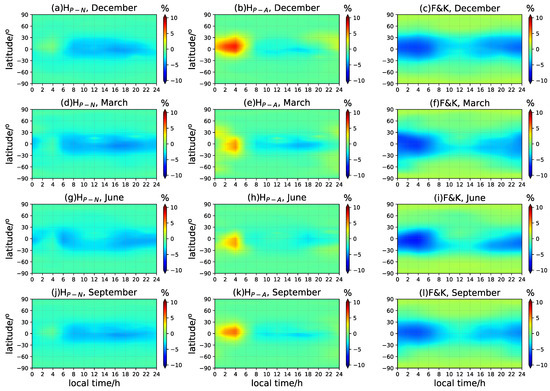
Figure 7.
Same as Figure 6 but for HSA year.
Figure 8 and Figure 9 demonstrate the mean deviation of the VTEC along with the latitude and longitude of three chosen zenith angles, , , and , in the December solstice. The VTEC at low latitudinal areas beside the geomagnetic equator rather underestimated when applying the numerical mapping function and the F&K model. At higher elevation angles, the TEC conversion errors brought by various mapping functions are negligible with minor differences. However, the residuals increase pronouncedly when the elevation angle is lower, especially for the F&K model. The performance of the analytical solution is generally the best at mid- and high latitudes, especially in a high solar activity year. The winter hemispheric overestimation along the geomagnetic equator is associated with the seasonal variation in scale height. As mentioned earlier, the geographical error distribution of the F&K model actually reflects the inhomogeneity of the IEH and the ionospheric background model. The results depend greatly on the IEH selection and the ionospheric model used to specify the IEH. The scale-height-based mapping model considers the vertical structure and variations in the ionosphere by involving the plasmaspheric scale height, and it is more convenient and reliable to provide realistic TEC conversion results. Moreover, the degradation in the performance is minor for scale-height-based mapping along with an increasing zenith, so it is especially suitable to be used on observations of low elevation angles.
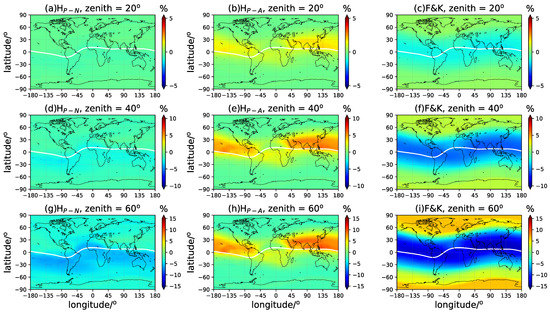
Figure 8.
The longitude- and latitude-dependent variations of the retrieved VTEC mean deviation in the December solstice in LSA years. The zenith angle is chosen at (panels (a–c)), (panels (d–f)), and (panels (g–i)), respectively. The ‘’, ‘’, and ‘F&K’ represent the numerical and analytical mapping functions and the F&K model, respectively.
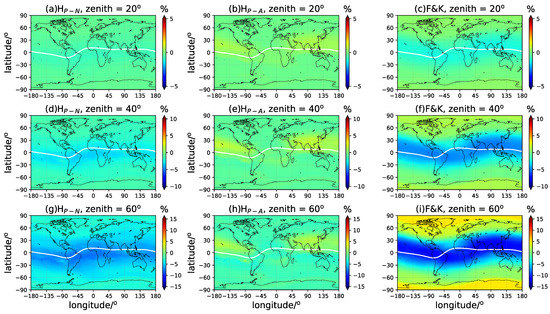
Figure 9.
Same as Figure 8 but for HSA year.
4.3. Influence of LEO Orbit Altitudes
Given the diversity of the orbit altitudes of different LEO satellites, we set up another two scenarios for more detailed discussion: the receiver being located at 500 km and 1400 km, respectively. The performances of the scale-height-based mapping function and the F&K model with the IEH specified according to Equation (7) are investigated in the same way as in Section 4.1. In Figure 10, when the LEO orbit altitude is 500 km, the mapping errors increase. The reason is that, at 500 km of altitude, the reliability of considering an exponential vertical profile for the electron density (with the associated scale height) is quite low [33,34,35]. This hypothesis adopted in the scale-height-based mapping will produce higher errors than at 1400 km of altitude. In an LSA year, both the numerical and analytical mapping function achieve fewer RMS errors than the F&K model, and the analytical solution is slightly better than the numerical one. Under an HSA condition, the numerical mapping factor results in similar or even a bit worse results than the F&K model below a zenith angle of , while the analytical mapping function is promising to obtain the least mapping errors. The situation is quite different with the LEO satellite higher at 1400 km. According to Figure 11, the numerical mapping function remarkablely improves the mapping errors in both LSA and HSA years. The analytical solution has a relatively poor peformance at high elevation compared to the F&K method but still functions well with greater zenith angles.
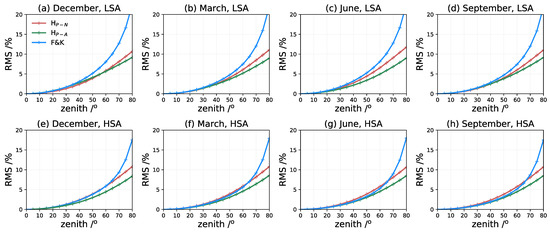
Figure 10.
Same as Figure 5 but for LEO satellite at 500 km.
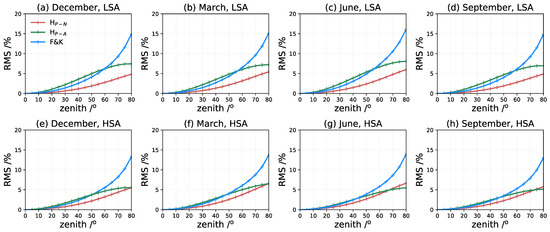
Figure 11.
Same as Figure 5 but for LEO satellite at 1400 km.
To understand the distinctive performance of the scale-height-based mapping function refering to different LEO orbit height, it should be noted that the obtained in this work is basically the averaged scale height under the assumption that the ionosphere and plasmasphere are varying roughly in an exponential trend above the satellite orbit. In fact, the actual scale height is varying with the altitude gradually below the - transition height, which peaks at 700 km and achieves an average value of 862 km [36], and approaching constant when the dominant ion becomes or in the plasmasphere [26]. Therefore, the averaged has a larger deviation with the varying scale height, especially when the satellite is locating below the transition height, such as in the 500-km-scenario. The retrieved VTEC is generally less than the truth since the mapping factor is overestimated because of the averaged . It agrees with the underestimation of the VTEC of the numerical solution in Figure 6, Figure 7, Figure 8 and Figure 9. Along with the increase in the orbit height, the averaged is closer to the realistic scale height and leads to fewer conversion errors. That accounts for the improvement in the performance of the numerical solution with the orbit varying from 500 km to 1400 km. Due to the assumption and approximation adopted in the analytical mapping function, a higher value leads to a smaller mapping factor (Figure 2). Therefore, the analytical solution basically compensates the overestimation of , sometimes presenting a better performance than the numerical one in an HSA year. Given the overall performances of the three methods, the scale-height-based mapping function with the numerical solution is the most stable approach under varying solar activity conditions and in changing LEO orbits, and it improves the F&K model significantly, especially at lower elevation angles.
5. Conclusions
This paper proposed a new model of an LEO-based TEC mapping function based on a prior model of the plasmaspheric scale height. The numerical and analytical forms of the mapping function are illustrated, and the mapping factor grid is obtained as a function of the scale height and zenith angle. The scale height and mapping factor are accessible to the public at the database: https://www.researchgate.net/publication/353703384_mapping_factor_grid (accessed on 1 August 2021) and https://www.researchgate.net/publication/353704297_plasmapsheric_scale_height (accessed on 1 August 2021).
The new mapping model is driven by the only free parameter, , obtained either from realistic observations or the empirical model. The performance of this mapping function is assessed by the simulated TEC conversion experiments based on the GCPM electron density field. This method is promising to be applied to LEO-based TEC conversion as a comparable or better alternative to the F&K model according to the assessments under various spatial and temporal specifications. Instead of collapsing the ionosphere into a thin shell, the new formulation considers the exponential layer assumption of the electron density distribution and applies the plasmaspheric scale height to introduce seasonal, local time, and geolocation-dependent variations into the mapping model. The performance of the F&K model is highly correlated with the IEH specification at different latitudes during varying solar activity periods, as well as the orbit altitudes of LEO satellites. The scale-height-based mapping model has advantages in dealing with the spaceborne TEC conversion, especially with low-elevation-angle observations of higher orbit height.
We recognize that the major errors remaining in the TEC conversion are associated with the horizontal inhomogeneous distribution of the ionosphere. Therefore, a comprehensive mapping model involving the azimuth angle variation of the signal ray paths is now under development based on this investigation.
Author Contributions
Conceptualization, M.W. and J.X.; methodology, W.Z.; software, M.W. and J.X.; validation, X.H.(Xingyuan Han), Y.M.; formal analysis, P.G. and M.W. ; investigation, M.W.; resources, X.H.(Xiaogong Hu); data curation, X.H.(Xiaogong Hu); writing—original draft preparation, M.W.; writing—review and editing, P.G., W.Z. and X.H.(Xingyuan Han); supervision, P.G.; project administration, X.H.(Xiaogong Hu); funding acquisition, M.W. and Y.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China, grant number 2020YFA0713501; the National Natural Science Foundation of China, grant number 11903064, U1831116; the stability support fund project of national key laboratory, 2020SSFNKLSMT-06; the stability support fund project of Science and Industry Bureau, grant number HTKJ2020KL504006; the opening project of Shanghai Key Laboratory of Space Navigation and Positioning Techniques, NO. KFKT201906.
Data Availability Statement
The data presented in this study are openly available in ResearchGate at https://www.researchgate.net/publication/353703384_mapping_factor_grid (accessed on 1 August 2021) and https://www.researchgate.net/publication/353704297_plasmapsheric_scale_height (accessed on 1 August 2021).
Acknowledgments
The authors are very thankful for the open access provided by CDAAC for all the COSMIC data involved and the national aeronautics and space administration for GCPM sources codes. The processed data and figure datasets used for this paper are available at the site: https://doi.org/10.5281/zenodo.5205255 (accessed on 1 August 2021).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviation List
| TEC | total electron content |
| STEC | slant TEC |
| VTEC | vertical TEC |
| LEO | low Earth orbit |
| GCPM | global core plasma model |
| GNSS | global navigation satellite system |
| COSMIC | Constellation Observing System for Meteorology, Ionosphere, and Climate |
| DCB | differential code bias |
| MF | mapping function |
| TLM | thin layer model |
| IEH | ionospheric effective height |
| IRI | International Reference Ionosphere |
| MSA | medium solar activity |
| LSA | low solar activity |
| HAS | high solar activity |
| CDAAC | COSMIC data analysis and archive center |
| SBAS | space-based augmentation system |
| ISIS | International Satellites for Ionospheric Studies |
| RMS | root mean square |
Appendix A
Assuming an arbitrary point P on the ray path in Figure 1, the relationship between the slant ray and the vertical projection to the receiver is approximately written as
where represents the radius of LEO satellite orbit from the Earth center; is the zenith angle of the ray path. Under the assumption of ionospheric spherical symmetry, the slant TEC is obtained by integrating the electron density along the ray path,
If and , then
is the electron density at the receiver. The vertical TEC is easy to obtain with integration as ; therefore, the analytic solution of relates to the scale height , zenith angle , and the complementary error function ():
where .
References
- Schreiner, W.; Rocken, C.; Sokolovskiy, S.; Syndergaard, S.; Hunt, D. Estimates of the precision of GPS radio occultations from the COSMIC/FORMOSAT-3 mission. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Yue, X.; Schreiner, W.S.; Kuo, Y.H.; Hunt, D.C.; Wang, W.; Solomon, S.C.; Burns, A.G.; Bilitza, D.; Liu, J.Y.; Wan, W.; et al. Global 3-D ionospheric electron density reanalysis based on multisource data assimilation. J. Geophys. Res. Space Phys. 2012, 117, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; Yue, X.; Zhao, S. Estimation and analysis of GPS satellite DCB based on LEO observations. GPS Solut. 2016, 20, 251–258. [Google Scholar] [CrossRef]
- Wu, M.J.; Guo, P.; Fu, N.F.; Hu, X.G.; Hong, Z.J. Improvement of the IRI Model Using F2 Layer Parameters Derived From GPS/COSMIC Radio Occultation Observations. J. Geophys. Res. Space Phys. 2018, 123, 9815–9835. [Google Scholar] [CrossRef]
- Fu, N.; Guo, P.; Wu, M.; Huang, Y.; Hu, X.; Hong, Z. The two-parts step-by-step ionospheric assimilation based on ground-based/spaceborne observations and its verification. Remote Sens. 2019, 11, 1172. [Google Scholar] [CrossRef] [Green Version]
- Mannucci, A.J.; Wilson, B.D.; Yuan, D.N.; Ho, C.H.; Lindqwister, U.J.; Runge, T.F. A global mapping technique for GPS-derived ionospheric total electron content measurements. Radio Sci. 1998, 33, 565–582. [Google Scholar] [CrossRef]
- Syndergaard, S. A new algorithm for retrieving GPS radio occultation total electron content. Geophys. Res. Lett. 2002, 29, 55-1–55-4. [Google Scholar] [CrossRef] [Green Version]
- Yue, X.; Schreiner, W.S.; Hunt, D.C.; Rocken, C.; Kuo, Y.H. Quantitative evaluation of the low Earth orbit satellite based slant total electron content determination. Space Weather 2011, 9. [Google Scholar] [CrossRef] [Green Version]
- Yuan, L.; Jin, S.; Hoque, M. Estimation of LEO-GPS receiver differential code bias based on inequality constrained least square and multi-layer mapping function. GPS Solut. 2020, 24, 57. [Google Scholar] [CrossRef]
- Noja, M.; Stolle, C.; Park, J.; Lühr, H. Long-term analysis of ionospheric polar patches based on CHAMP TEC data. Radio Sci. 2013, 48, 289–301. [Google Scholar] [CrossRef]
- Yuan, L.; Hoque, M.; Jin, S. A new method to estimate GPS satellite and receiver differential code biases using a network of LEO satellites. GPS Solut. 2021, 25, 71. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Foelsche, U.; Kirchengast, G. A simple “geometric” mapping function for the hydrostatic delay at radio frequencies and assessment of its performance. Geophys. Res. Lett. 2002, 29, 1473. [Google Scholar] [CrossRef] [Green Version]
- Schaer, S. Mapping and predicting the Earth’s ionosphere using the Global Positioning System. Ph.D. TThesis, University of Bern, Bern, Switzerland, 1999. [Google Scholar]
- Hoque, M.M.; Jakowski, N. Mitigation of ionospheric mapping function error. In Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation, ION GNSS+ 2013, Nashville, Tennessee, 16–20 September 2013; Volume 3, pp. 1848–1855. [Google Scholar]
- Xiang, Y.; Gao, Y. An enhanced mapping function with ionospheric varying height. Remote Sens. 2019, 11, 1497. [Google Scholar] [CrossRef] [Green Version]
- Lyu, H.; Hernández-Pajares, M.; Nohutcu, M.; García-Rigo, A.; Zhang, H.; Liu, J. The Barcelona ionospheric mapping function (BIMF) and its application to northern mid-latitudes. GPS Solut. 2018, 22, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Su, K.; Jin, S.; Jiang, J.; Hoque, M.; Yuan, L. Ionospheric VTEC and satellite DCB estimated from single-frequency BDS observations with multi-layer mapping function. GPS Solut. 2021, 25, 67. [Google Scholar] [CrossRef]
- Zhong, J.; Lei, J.; Dou, X.; Yue, X. Assessment of vertical TEC mapping functions for space-based GNSS observations. GPS Solut. 2016, 20, 353–362. [Google Scholar] [CrossRef]
- Huang, Z.; Yuan, H. Analysis and improvement of ionospheric thin shell model used in SBAS for China region. Adv. Space Res. 2013, 51, 2035–2042. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Gulyaeva, T.L.; Nava, B.; Stanislawska, I. Modeling Center-of-Mass of the Ionosphere From the Slab-Thickness. Radio Sci. 2021, 56, 1–17. [Google Scholar] [CrossRef]
- Pedatella, N.M.; Zakharenkova, I.; Braun, J.J.; Cherniak, I.; Hunt, D.; Schreiner, W.S.; Straus, P.R.; Valant-Weiss, B.L.; Vanhove, T.; Weiss, J.; et al. Processing and Validation of FORMOSAT-7/COSMIC-2 GPS Total Electron Content Observations. Radio Sci. 2021, 56, 1–15. [Google Scholar] [CrossRef]
- Hernàndez-Pajares, M.; Juan, J.M.; Sanz, J.; Garcia-Fernàndez, M. Towards a more realistic ionospheric mapping function. In Proceedings of the XXVIII URSI General Assembly, Delhi, India, 23–29 October 2005. [Google Scholar]
- Pignalberi, A.; Pezzopane, M.; Nava, B.; Coïsson, P. On the link between the topside ionospheric effective scale height and the plasma ambipolar diffusion, theory and preliminary results. Sci. Rep. 2020, 10, 17541. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Xu, X.; Li, F.; Guo, P.; Fu, N. Plasmaspheric scale height modeling based on COSMIC radio occultation data. J. Atmos. Solar-Terr. Phys. 2021, 217, 105555. [Google Scholar] [CrossRef]
- Liu, L.; Le, H.; Wan, W.; Sulzer, M.P.; Lei, J.; Zhang, M.L. An analysis of the scale heights in the lower topside ionosphere based on the Arecibo incoherent scatter radar measurements. J. Geophys. Res. Space Phys. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Wan, W.; Zhang, M.L.; Ning, B.; Zhang, S.R.; Holt, J.M. Variations of topside ionospheric scale heights over Millstone Hill during the 30-day incoherent scatter radar experiment. Ann. Geophys. 2007, 25, 2019–2027. [Google Scholar] [CrossRef] [Green Version]
- Luan, X.; Liu, L.; Wan, W.; Lei, J.; Zhang, S.R.; Holt, J.M.; Sulzer, M.P. A study of the shape of topside electron density profile derived from incoherent scatter radar measurements over Arecibo and Millstone Hill. Radio Sci. 2006, 41, 1–11. [Google Scholar] [CrossRef]
- Stankov, S.M.; Jakowski, N.; Heise, S.; Muhtarov, P.; Kutiev, I.; Warnant, R. A new method for reconstruction of the vertical electron density distribution in the upper ionosphere and plasmasphere. J. Geophys. Res. Space Phys. 2003, 108. [Google Scholar] [CrossRef]
- Hoque, M.M.; Jakowski, N.; Berdermann, J. A new approach for mitigating ionospheric mapping function errors. In Proceedings of the 27th International Technical Meeting of the Satellite Division of the Institute of Navigation, Tampa, FL, USA, 8–12 September 2014. [Google Scholar]
- Gallagher, D.L.; Craven, P.D.; Comfort, R.H. Global core plasma model. J. Geophys. Res. Space Phys. 2000, 105, 18819–18833. [Google Scholar] [CrossRef]
- Fonda, C.; Coïsson, P.; Nava, B.; Radicella, S.M. Comparison of analytical functions used to describe topside electron density profiles with satellite data. Ann. Geophys. 2009, 48. [Google Scholar] [CrossRef]
- Pignalberi, A.; Pezzopane, M.; Rizzi, R. Modeling the Lower Part of the Topside Ionospheric Vertical Electron Density Profile Over the European Region by Means of Swarm Satellites Data and IRI UP Method. Space Weather 2018, 16, 304–320. [Google Scholar] [CrossRef]
- Stankov, T.; Verhulst, S.M. Evaluation of ionospheric profilers using topside sounding data. Radio Sci. 2014, 49, 181–195. [Google Scholar] [CrossRef]
- Kutiev, I.; Marinov, P. Topside sounder model of scale height and transition height characteristics of the ionosphere. Adv. Space Res. 2007, 39, 759–766. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).