Abstract
In multiple-input-multiple-output synthetic aperture radar (MIMO-SAR) systems, sparse arrays are usually applied, resulting in increased sidelobes of the point spread function. In this paper, a phase shift migration (PSM) imaging algorithm based on the explosion reflection model with modified coherent factor was proposed for sidelobe suppression in MIMO-SAR three-dimensional (3D) imaging application. By defining the virtual difference wavenumber, reconstructing the raw echo by data rearrangement in wavenumber domain, the original coherent factor algorithm operating in spatial domain can be achieved by the PSM algorithm frame in the wavenumber domain, which means two orders of magnitude increase in computational efficiency. The correctness of the theory is verified by simulation. Finally, a bistatic prototype imaging system in the 0.3 THz band was designed for the proof-of-principle experiments. The experimental results show that the proposed algorithm has a 0.948 structural similarity value to the original coherent factor back-projection algorithm (CF-BPA) which means comparable image quality with much superior efficiency.
1. Introduction
Terahertz (THz) wave is generally referred to electromagnetic wave with frequency ranging from 0.1 THz to 10.0 THz, which lies between the microwave band and infrared. THz waves can penetrate clothing; compared to X-rays, the photon energy of THz wave is lower and will not produce harmful photoionization effects on biological tissues; compared to the microwave band, it can achieve higher imaging resolution [1,2]. Thus, active THz imaging systems have attracted extensive attention in the fields of security check, non-destructive testing (NDT) [3], biomedical testing [4] and so on.
Considering the system cost, THz 3D imaging systems were often designed based on a wideband transceiver combined with a 2D spatial scanning scheme in the early stage. This scheme suffers from the problem of long data acquisition time [5,6,7,8,9,10]; thus, it is difficult to apply in practice. As the constant growth of various application requirements, lower system cost and higher data acquisition efficiency becomes more and more necessary, especially for real-time security checking scenario, in order to meet the above requirements, multiple-input-multiple-output (MIMO) linear array combined with synthetic aperture scanning is an effective solution to realize 3D imaging in the THz band [11,12,13,14,15]. It takes full advantage of the good penetration, high resolution, and non-ionization of THz waves, while greatly reducing the system cost.
The development of imaging algorithms is closely related to the system scheme. Early imaging algorithms were mostly based on Monostatic SAR. Later, with the emergence of bistatic SAR systems, some Monostatic-based algorithms were also modified and extended to bistatic SAR imaging. For the imaging applications with the complex bistatic data, a conventional Back-projection algorithm (BPA) based on the phase-compensated and coherent summations in time/spatial domain [16] is a common technology which suffers from a huge computational cost. It does not meet real-time imaging requirements; thus, researchers developed several methods to accelerate the BPA. In [17], a bistatic Fast Factorized BPA (BiFFBP) working in an approximative fashion was proposed, then Zhang et al. [18] proposed an accelerated BiBulk FFBP based on an integrated range processing scheme. Such kinds of methods are based on the far-field approximation for sub-aperture decomposition, sub-aperture data extraction and sub-image fusion processes involving interpolation operations. In the airborne bistatic SAR applications, the approximation error and interpolation error may be negligible; while in near-field high-resolution imaging applications, the errors in distance approximation and sub-image interpolation may have a more obvious impact on the final imaging results.
By contrast, the wavenumber domain algorithms based on Fourier Transform are more suitable. In [19], a modified Range Doppler algorithm was proposed for bistatic SAR focusing based on a Taylor series expansion. In [20], a Nonlinear Chirp Scaling algorithm combined with Keystone Transform was proposed to deal with the problem of 2-D variation of both Doppler characteristics and range cell migration. In [21], a Range Migration algorithm (RMA, also known as Omega-k algorithm) for bistatic SAR focusing was proposed based on Generalized Loffeld’s bistatic formula. Since the MIMO system is different from the SAR system in data acquisition, the above methods cannot be directly used in the MIMO imaging process; while it is worth noting that the development of the MIMO imaging algorithm has really benefited from bistatic SAR. Zhuge et al. [22] first proposed an RMA for MIMO 3D imaging based on a 2D array which reduced the computational cost greatly as compared with the BPA. Then, Zhu et al. [13] extended the MIMO-RMA to MIMO-SAR regime based on the spherical wave decomposition. After that, two Modified Kirchhoff based wavenumber domain algorithms were also proposed in [15] which are also based on the Stolt interpolation. The second algorithm decomposes the MIMO imaging problem into several single-input-multiple-output (SIMO) problems, which allows a more flexible distribution of the transmitters, but at the cost of time-consuming problems when the number of transmitting array elements is huge. In the RMA process, the wavenumber-domain interpolation plays a key role in final imaging quality; more accurate interpolation methods usually mean higher computational cost which means that such a kind of Stolt interpolation method is inevitably affected by interpolation kernel. The phase shift migration (PSM) algorithm which originated from reflection seismology applies the phase shift factor and wavenumber integral operation to achieve range compression based on monostatic data. Gao et al. [23] extended it to the MIMO sidelooking 2D imaging scheme. This non-interpolation approach avoids the truncation effect of the interpolation kernel. Although the calculation efficiency of the PSM algorithm is slightly slower than that of RMA using nearest neighbor interpolation, the PSM algorithm can achieve higher imaging quality and is more suitable for short-range high-precision imaging applications [24]. In addition, some virtual monostatic array methods have also been reported in the MIMO-SAR scheme [25], which can avoid the data rearrangement operation to increase the computational efficiency. However, the approximation error should be considered and evaluated according to the imaging scene especially in short-range imaging application. In summary, the MIMO PSM algorithm takes into account both high imaging efficiency and high accuracy. Therefore, it has a wider range of applicable scenarios.
To apply FT techniques conveniently and control the system cost, MIMO linear arrays always apply sparse interval and uniform layout, which means the element interval of the transmitting and receiving arrays are greater than half-wavelength. The sparse array inevitably leads to an increase in the side lobes of the point spread function, which interferes with the imaging quality and dynamic range.
With the growing demand for compact array antennas, the physical footprint of the arrays needs to be smaller and the consequence of this is severe degradation in the performance of the array resulting from strong mutual-coupling and crosstalk effects between adjacent radiating elements. Thus, many researchers have conducted in-depth research on this problem and provided some solutions to the coupling problem in the imaging system such as metamaterial (MTM) [26], metasurface (MTS) [27] and hybrid coupler approaches [28], which promoted the development of the terahertz imaging system.
In radar imaging systems, common methods to improve image quality include sub-array [29,30], coherence factor (CF) [31] and its variants [32,33]. The sub-array approach can suppress the sidelobe but widen the full width at half-maximum (FWHM). CF and its variants can get a sharp FWHM and suppress the sidelobe; but they were developed in the time/spatial domain combined with BPA, which means huge computational load. Other methods based on spectrum estimation [34,35] and regularization [36] are not commonly used in imaging radars or remote sensing systems due to the complex processing and a huge amount of calculation.
To overcome this obstacle, in this work, the concept of coherence factor was reconsidered for real-time imaging implementation. In this paper, we modified the implementation of the incoherent power term of CF, integrating it with the PSM framework. Specifically, to reconstruct the virtual echo, the double integration while calculating incoherent power is equivalent to a single integration based on the rearrange method in defined difference wavenumber. After data reconstruction in the difference wavenumber domain, the incoherent power can be calculated by another independent PSM program. Finally, a MIMO-SAR prototype system was designed for proof-of-principle experiments in the 0.3 THz band. As demonstrated by simulation and practical measurements, the proposed modified CF-PSM (MCF-PSM) algorithm enhances the imaging performance of the PSM algorithm, while retaining the high efficiency of PSM.
The rest of this paper is organized as follows. Detailed theory and application of the imaging algorithms are shown in Section 2. Then, the simulation and experimental results in the 0.3 THz band are given in Section 3 to demonstrate the effectiveness and advantages of the proposed algorithm. Finally, a conclusion is drawn in Section 4.
2. Theory and Formulation
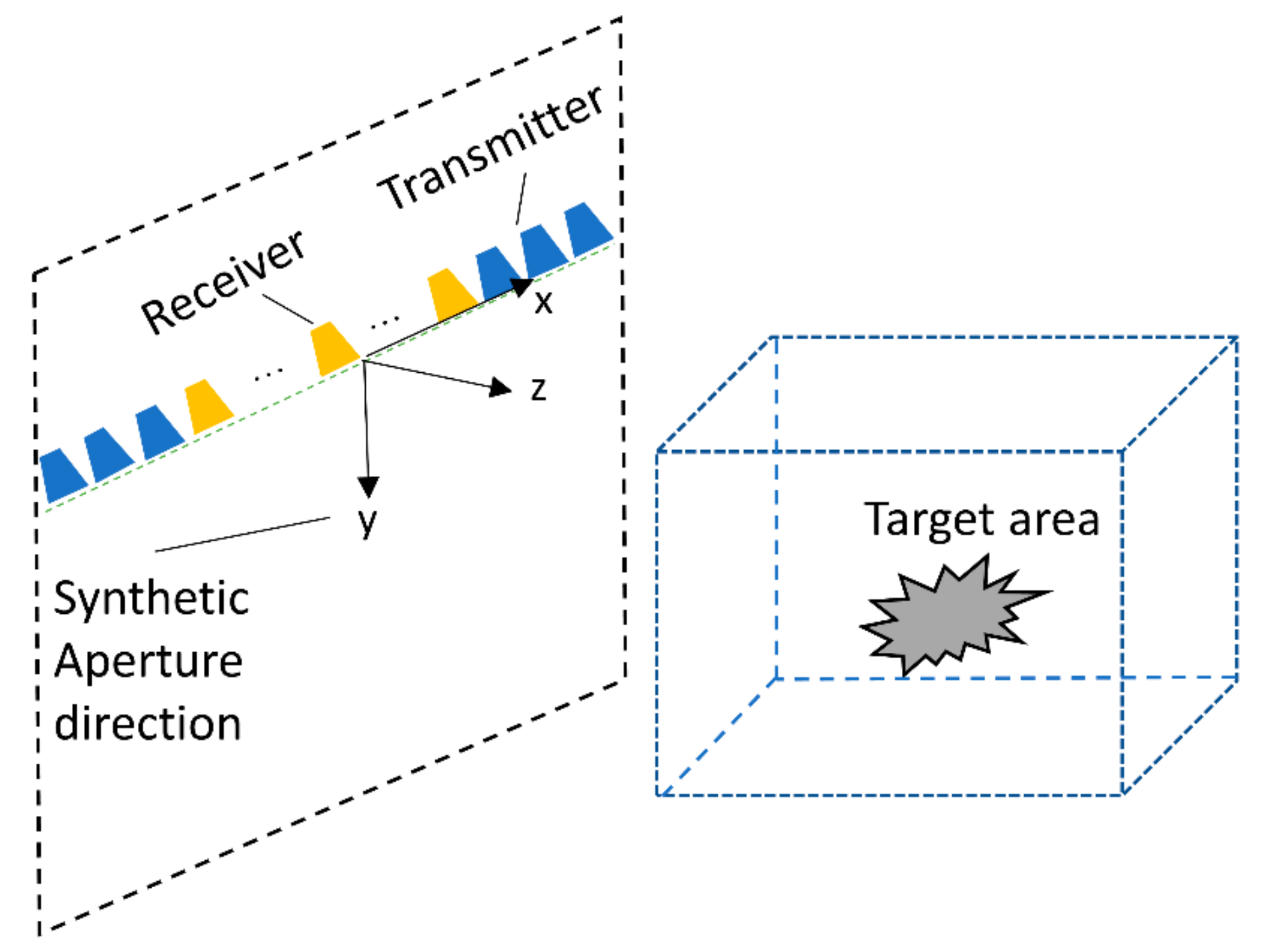
Synthetic aperture scanning in the perpendicular direction of the linear MIMO array is called the MIMO-SAR imaging scheme. Figure 1 shows the MIMO-SAR imaging geometry; the 2D field of view in the x-y plane was covered by the scan of the 1D MIMO array (x-direction) along the other dimension (y-direction) and the target area is illuminated by a MIMO linear array which is located at a plane z = 0 m. The linear MIMO array scanned along the y-axis forms an equivalent 2D radiation aperture to get the integrated MIMO-SAR scattered wave field.
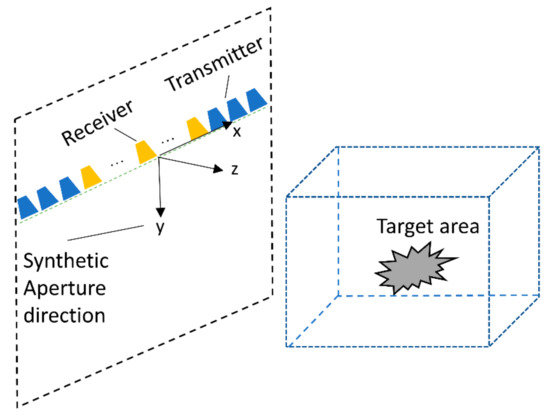
Figure 1.
The scheme of the MIMO-SAR imaging.
2.1. Back-Projection Algorithm with Coherence Factor for MIMO-SAR Imaging
As given in Figure 1, The locations of receivers and transmitters can be denoted as and , respectively. The transmitters transmit step frequency continuous wave (SFCW) signals. Under this 3D imaging geometry, the corresponding scattered field echo can be denoted as:
where denotes the reflectivity distribution function, and are the Green’s functions of transmitting and receiving elements in the free-space,
is the wavenumber in free space, and c represents the propagation speed of electromagnetic waves. denote the distances from target to the transmitters/receivers, which can be expressed as:
As we know, the phase information of the echo plays a key role in the reconstructed image. The amplitude decay factor will have little impact on focusing the image [15,37] and can be ignored. Then, Formula (1) can be simplified as:
The traditional BPA [16] operating in spatial domain for MIMO-SAR 3D imaging can be written as:
CF is defined as the ratio of the coherent power to the incoherent power of the target reflectivity function [31], and can be formulated as:
where
Then, the final reconstructed image can be expressed as:
According to the BPA imaging Formula (6), a quadruple integral operation must be conducted to get the estimated reflectivity of each spatial grid point in the region of interest (ROI) [12]. The incoherent power needs be calculated during the process of BPA, which undoubtedly adds an additional calculation cost. Obviously, the CF-BPA suffers from the huge computational cost.
2.2. PSM Algorithm for MIMO-SAR Imaging
The phase shift migration algorithm which originated from reflection seismology is a non-interpolation imaging algorithm operating in the wavenumber domain. The fundamental theory derives from the exploding reflector model in geophysics [38], which assumed that the targets ‘explode’ at the time and the ‘exploded fields’ propagate toward the receiver with a velocity . In the monostatic scheme, the ‘explosion field’ in 3D space [39] can be expressed as:
where denotes the exploded field at the spatial location . means the spectrum of in the wavenumber domain.
Then, the 3D objective function can be obtained by the integration of angular frequency [39]. Specifically, transform the ‘explosion field’ to the time domain, when ; a form similar to the reflectance function can be obtained and can be expressed as:
The original PSM algorithm applied in the monostatic imaging scheme cannot be directly applied to the bistatic MIMO imaging systems. Hence, in the MIMO-SAR 3D imaging scheme, as long as we can successfully transform the bistatic recorded field to the ‘explode fields’, the 3D object function can be recovered by integral over wavenumber k to get the reconstructed image.
To find out the relationship between the bistatic data and the ‘exploding fields’, 3D FT is firstly performed on (5) over and to obtain the spatial wavenumber spectrum [24].
Then, (14) can be computed as a Fourier transform along the y dimension on the product of the two 1D Fourier transforms over and , respectively, as follows:
It is worth noting that in order to obtain the same spatial wavenumber interval, the transmitting and receiving array needs to apply zero-padding operations, which means , where is the interval of receivers and is the interval of transmitters [22]. Thus, the intervals of spatial wavenumber and can be denoted.
The method of stationary phase (MSP) [40] can be applied to get an analytic solution of the Fourier integral in (15) and (16)
By applying (18) and (19), (14) can be rewritten as:
Similarly, after applying the MSP again, (18) can be further expressed as:
Then, the wavenumber spectrum (13) can be rewritten as:
The wavenumber relations can be defined as:
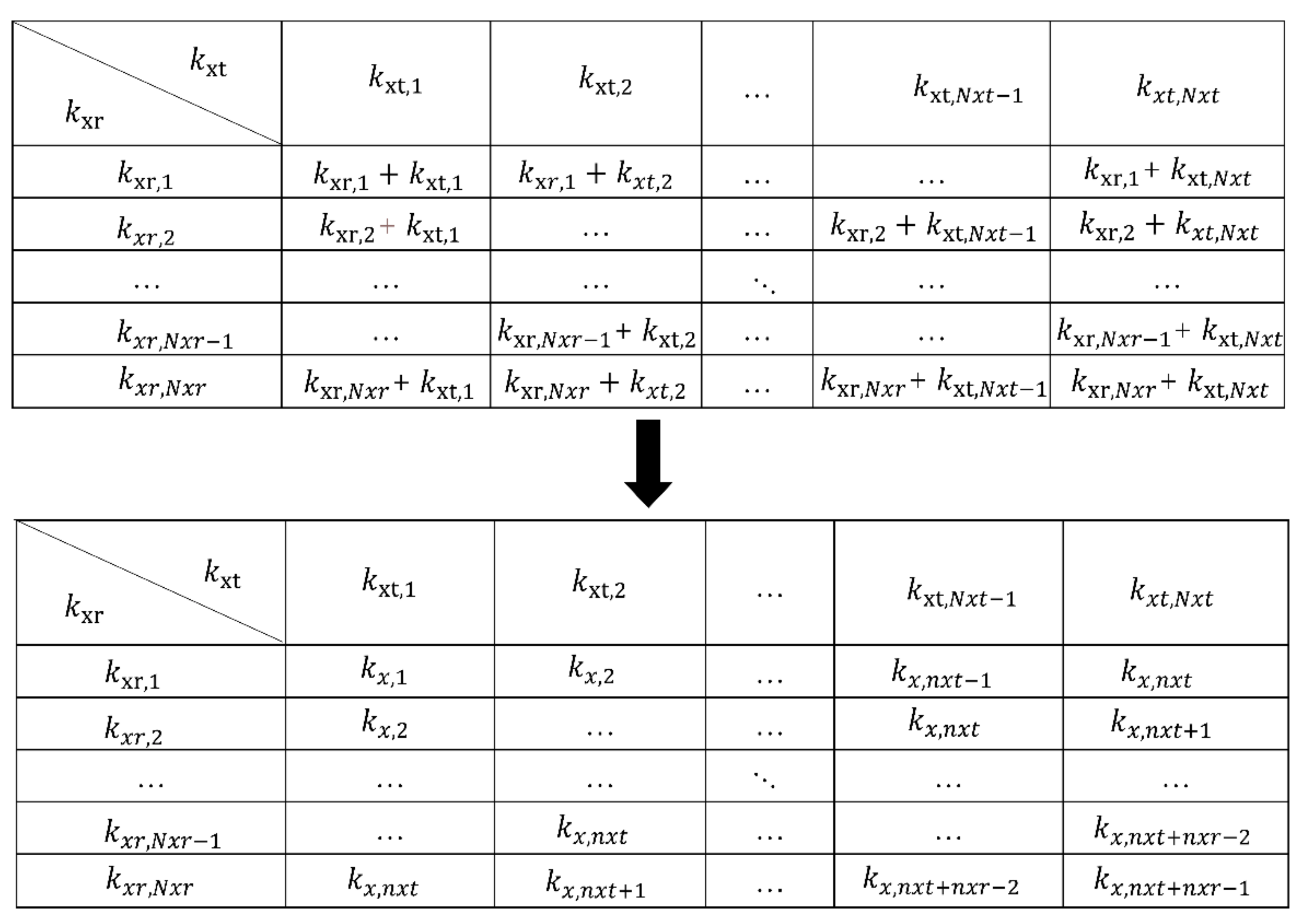
According to (23), can be transformed into monostatic form by data rearrangement operation defined as the windowing method. During the rearrangement operation in the wavenumber domain, it is possible to get the same with two or more different sets of . As shown in Figure 2, under the MIMO-SAR array topology, the sub-diagonal elements contribute the same . The contributions of different sets can be added or averaged. Experiments show that the PSF function obtained by directly accumulating have a lower sidelobe level which is better for imaging application [27]. This conclusion will be applied again in next part when deriving the modified incoherent power calculation formula.
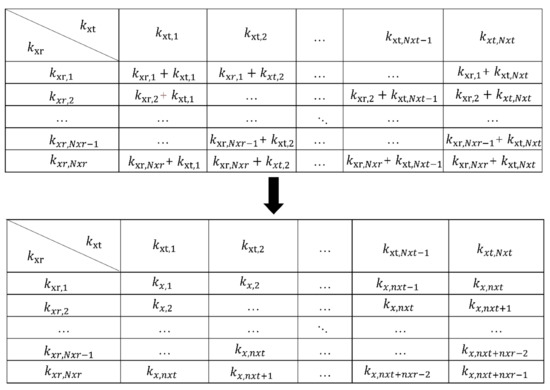
Figure 2.
The spatial wavenumber rearrangement matrix.
Then, the ‘exploding field’ in the frequency-wavenumber domain can be derived with the bistatic MIMO-SAR data as following:
where represent the range planes of ROI. When the array is located at the plane, (25) can be further rewritten as:
By applying the phase shift operator , the integrated PSM imaging formula for MIMO-SAR 3D imaging scheme can be expressed as:
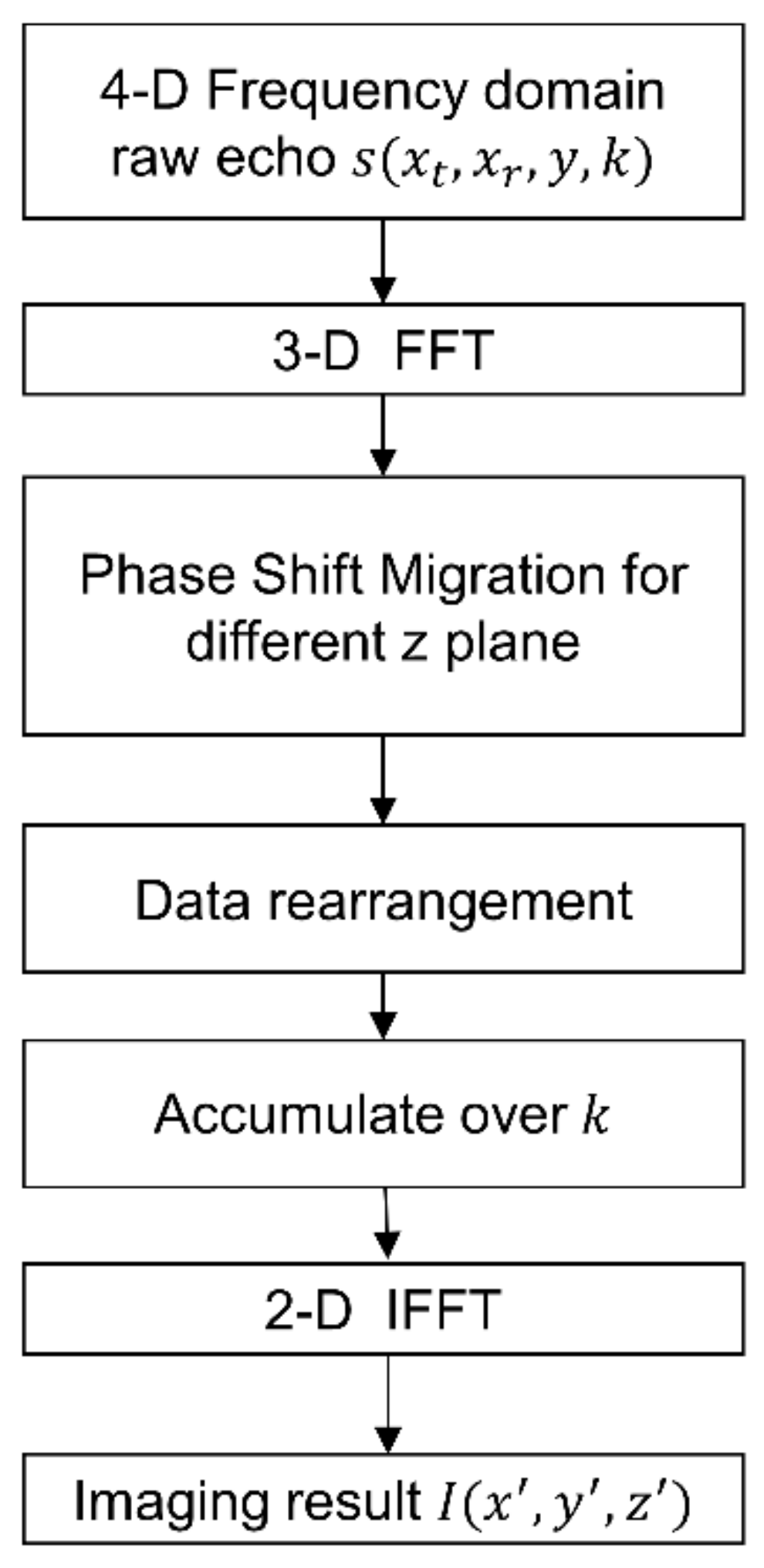
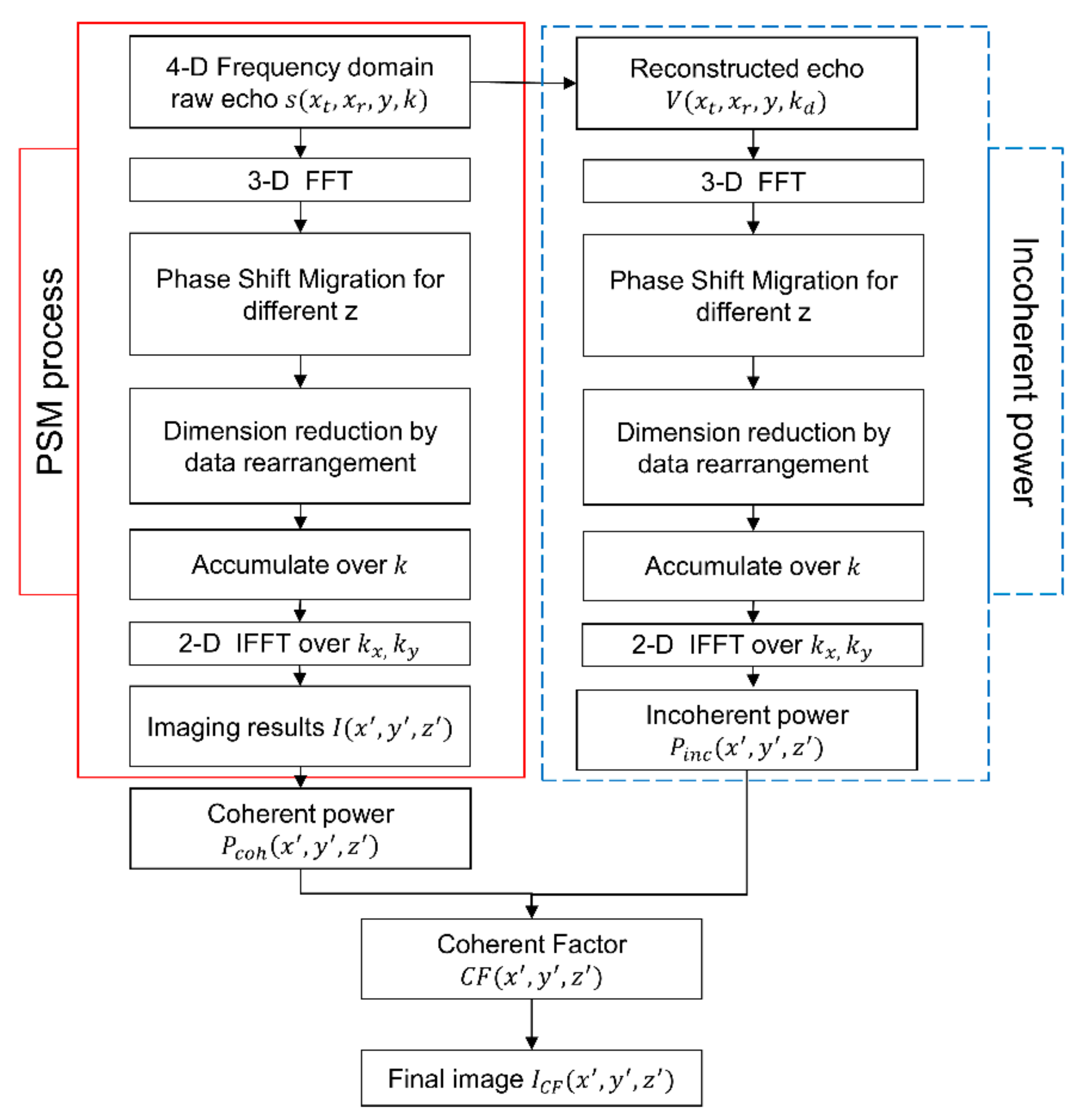
To summarize, Figure 3 presents the whole flowchart of PSM algorithm for the MIMO-SAR imaging procedure, and the practical processing procedures with reference to Figure 2 are presented specifically in Table 1.
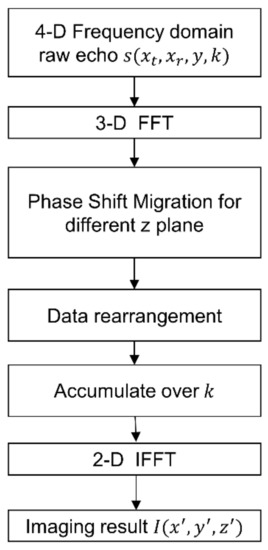
Figure 3.
The flowchart of MIMO-SAR PSM imaging.

Table 1.
Detailed procedures of the PSM imaging.
2.3. Proposed MCF-PSM Algorithm
Now, we reconsider the formula of incoherent power as given in (8). According to the theory of complex signals [41], the square of the modulus of the complex signal is equal to the product of the conjugate of a complex signal and itself, can be expressed as:
where * denotes the conjugate operation. Then, (8) can be rewritten as:
where , and are uniform and independent of each other. Then, we can use to denote the , and it can be seen that is related to .By defining a variable as the difference wavenumber to replace , (29) can be further written as:
It can be seen that (30) has a similar form to (6), which means it is possible to use the procedure of PSM algorithm to calculate the incoherent power as long as the equivalent echo related to can be constructed from the original echo.
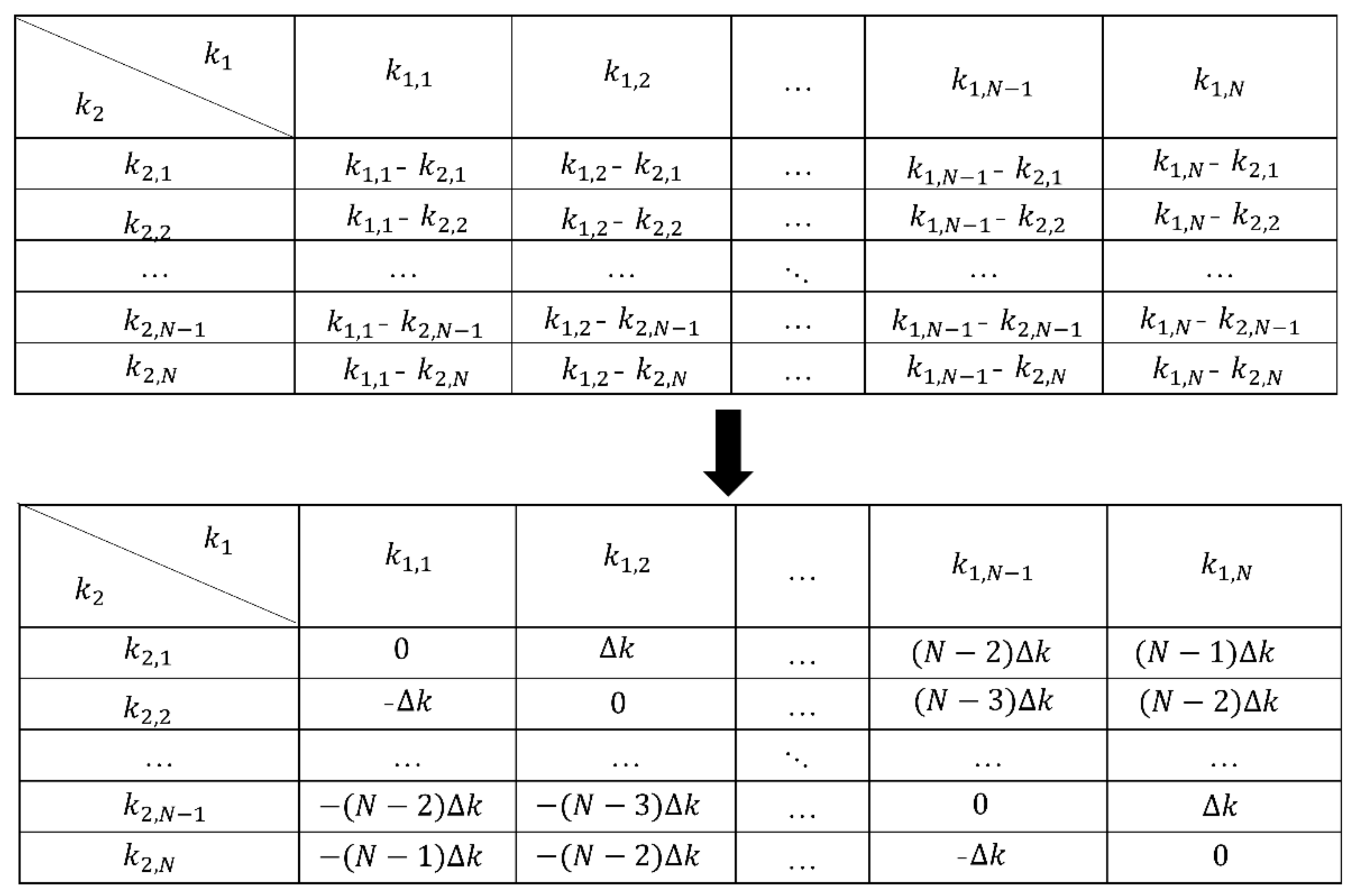
Specifically, the wavenumber k is discretized to N points with uniform interval .
Then, referring to Figure 2, we can get the rearrangement matrix of shown in Figure 4, where and the diagonal elements contribute to a same . Thus, the same as the realization of (23), we can reconstruct the from by data rearrangement.
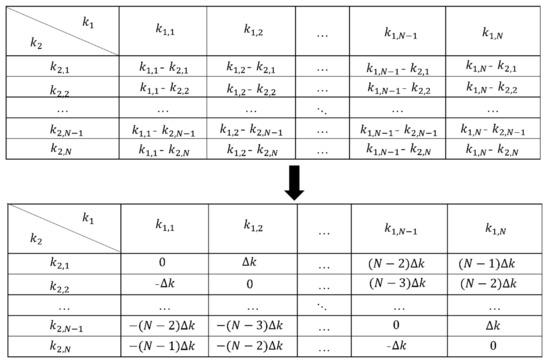
Figure 4.
Difference wavenumber rearrangement matrix.
Then, we can naturally apply the frame of PSM algorithm to calculate by replacing with .It is worth noting that since we have constructed difference wavenumber , we need to define a new range wavenumber .
The corresponding phase shift factor is:
Finally, the proposed MCF-PSM algorithm can be summarized as the process shown in Figure 5, and the practical processing procedures with reference to Figure 5 are presented specifically in Table 2.
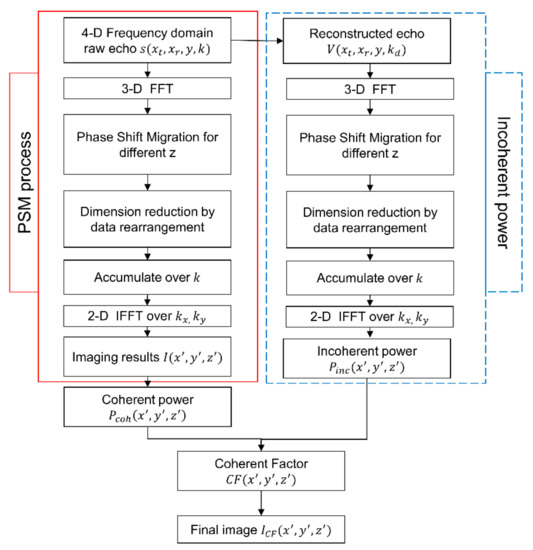
Figure 5.
The flowchart of the proposed MCF-PSM imaging algorithm.

Table 2.
Detailed procedures of the MCF-PSM algorithm imaging.
It should be noted that although the proposed algorithm introduces the process of equivalent echo reconstruction, the calculations of the difference wavenumber and phase shift factor can be calculated in advance and saved in the register for easy recall when the system parameters are determined. Thus, the proposed algorithm can be regarded as two independent PSM imaging processes, so it can be calculated in parallel to improve the computational efficiency. The analysis of computational efficiency will be discussed in the next section.
2.4. Computational Cost
Detailed analysis of the computational cost of the proposed algorithm are discussed in this section. The computation cost can be evaluated by the floating-point operations (FLOPs) index. The independent MIMO-SAR PSM algorithm cost are given in Table 3. According to the processes in Table 2, the integrated calculation cost of the proposed MCF-PSM algorithm and the CF-BP algorithm can be denoted as:
where Nf denotes the frequency steps number of the SFCW signal, are the numbers of transmitters and receivers after zero-padding. refers to the number of the monostatic spatial wave-number after data rearrangement; is the number of samples along the z-direction; Ny refers to the number of scanning positions along the y-axis. denotes the cost of virtual echo reconstruction operation. According to (34), the completed algorithm cost is about twice that of the MIMO-SAR PSM algorithm, which means the echo reconstruction operation just adds a little computation cost. To further simplify the comparison, we can suppose that and . Then, (34) and (35) can be expressed with more intuitive expressions:

Table 3.
Detailed Cost of the MIMO-SAR PSM imaging.
From (36), we can find that the computation complexity of the proposed algorithm has obvious advantage relative to the traditional CF-BPA. In the next section, the simulation results and experimental results will be given to prove the effectiveness of the proposed algorithm.
3. Numerical Simulation Results
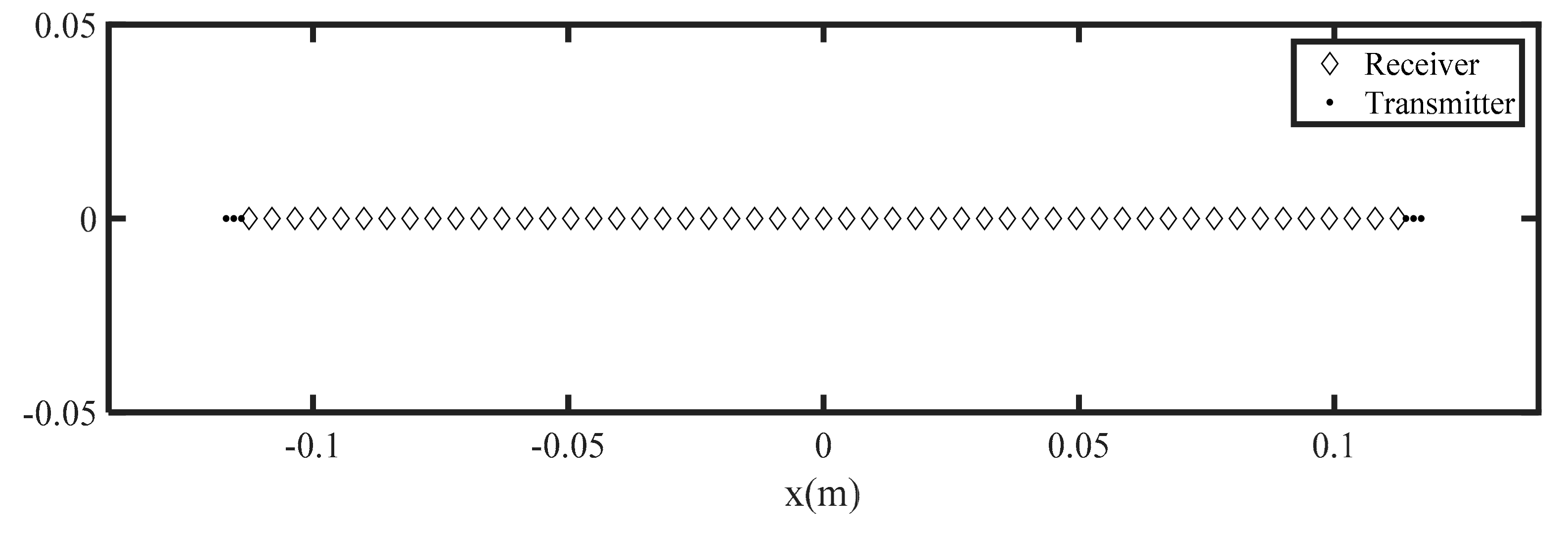
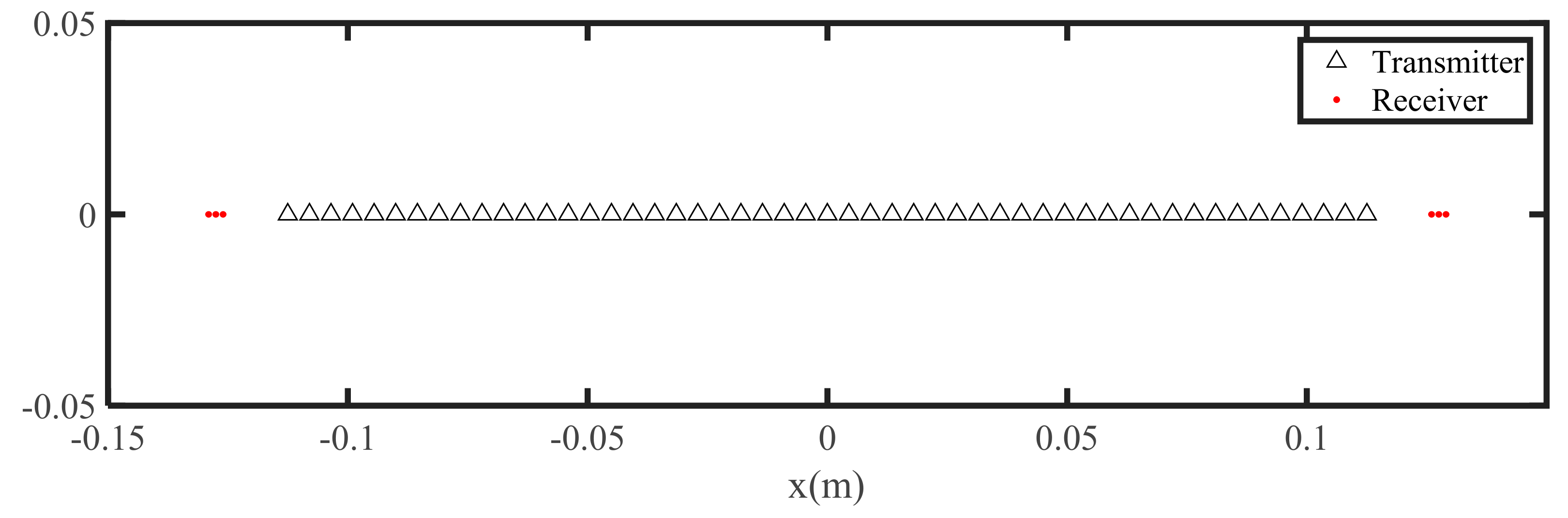
In this section, the simulation results will be given to prove the effectiveness of the proposed MCF-PSM algorithm through the comparison with the CF-BPA. The simulation parameters are given in Table 4. The 1-D MIMO array with 51 receivers and 6 transmitters applied in this simulation are shown in Figure 6. The simulated target is composed of 7-point scatters with 1.03 m away from the array plane.

Table 4.
Simulation Parameters.
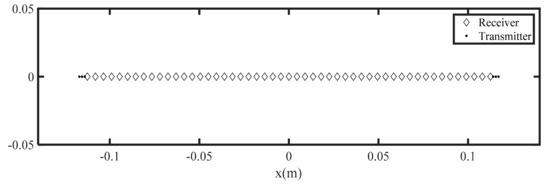
Figure 6.
The MIMO array applied in the simulation.
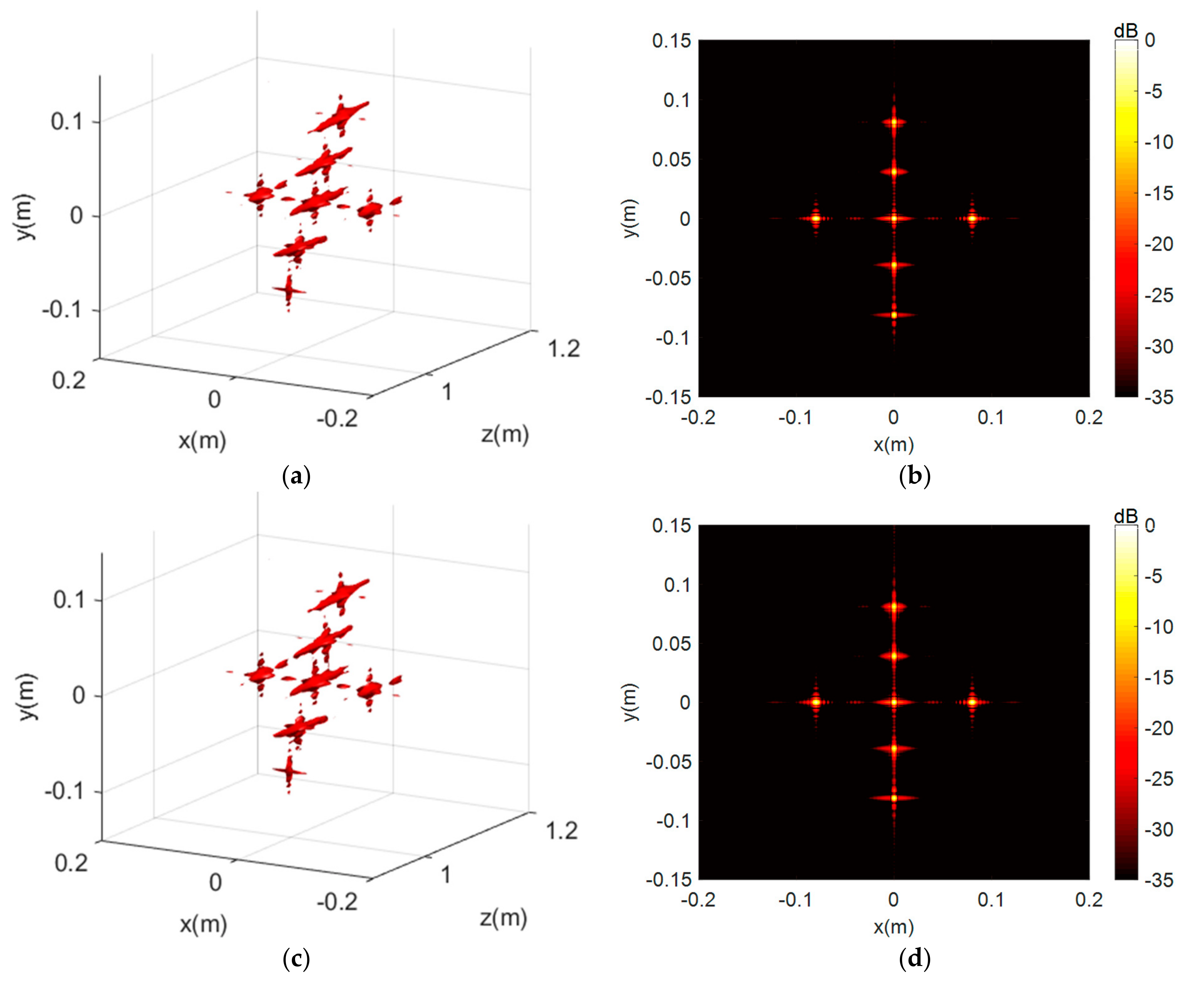
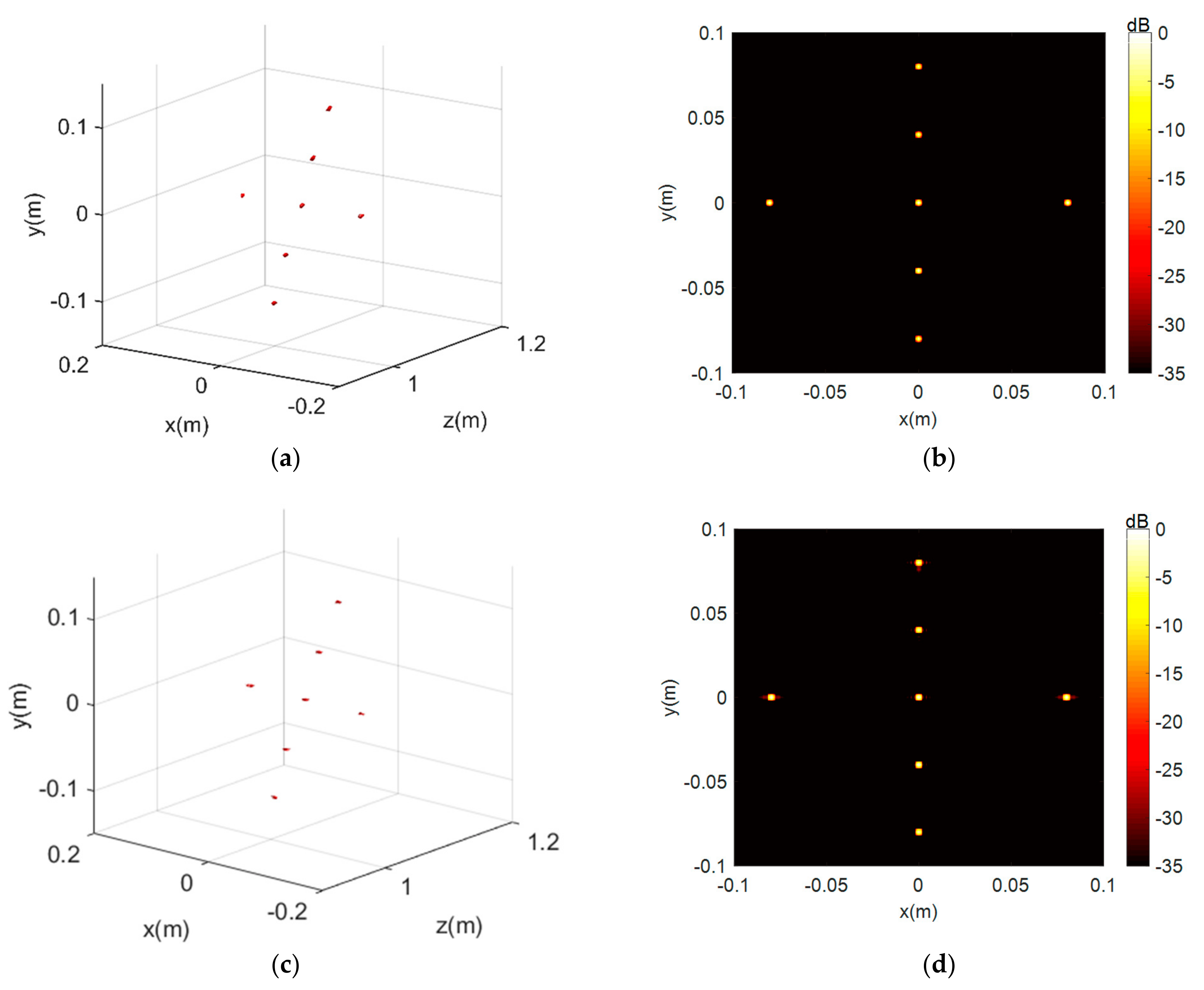
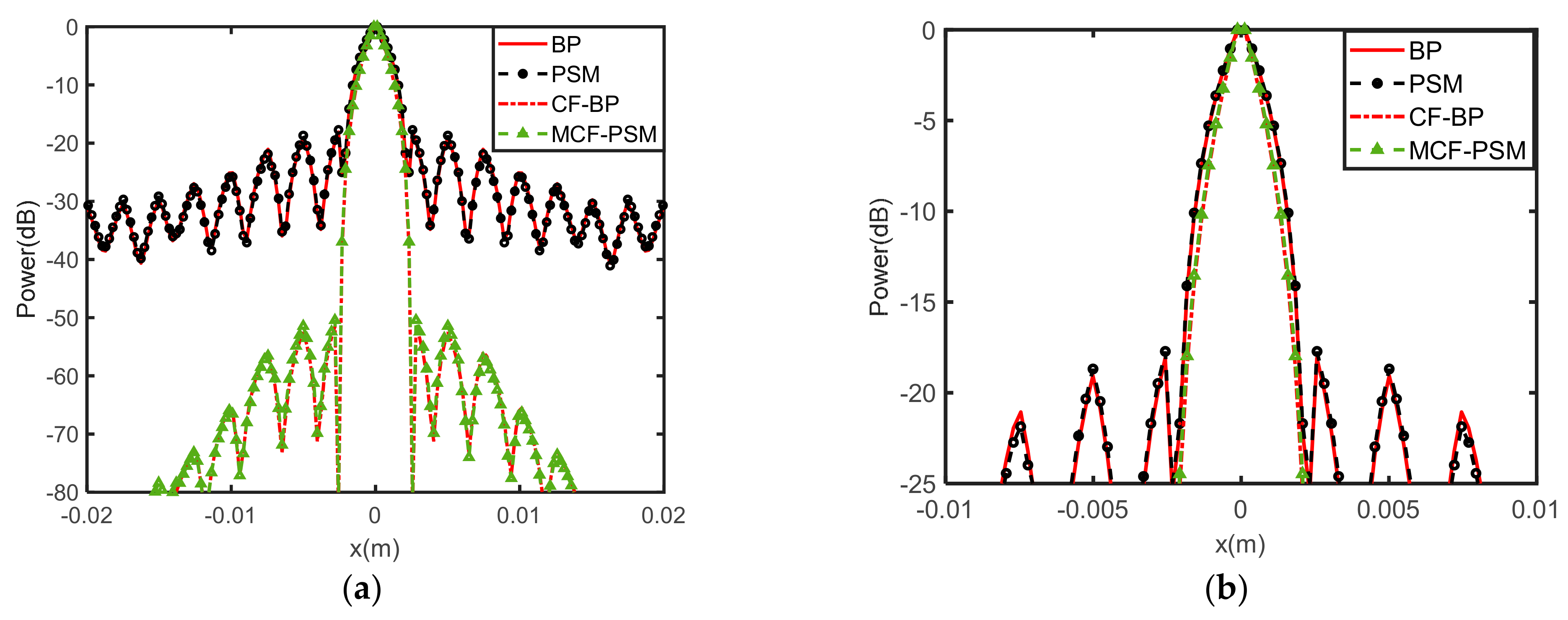
The 3-D imaging results and 2-D projection on the x-y plane results under the 35 dB dynamic are given in Figure 7; it is obvious that the imaging results of the BPA and PSM algorithms are both well-focused but disturbed by the high-energy sidelobes, resulting in blurring of the main lobe. Then, Figure 8 shows the CF-BPA and the proposed MCF-PSM imaging results. The 1-D profiles comparison of the center point along the x-axis are shown in Figure 9. From Figure 8 and Figure 9, it can be found that both the CF-BPA and MCF-PSM algorithms can suppress the sidelobes and get a sharper main lobe.
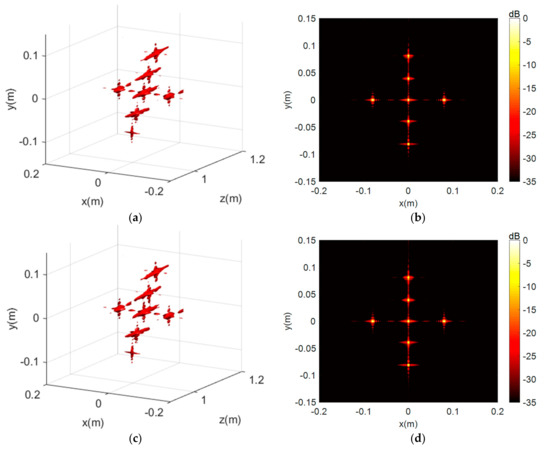
Figure 7.
The simulation results without coherent factor processing. (a,b) are the 3D and 2D projection results of BPA. (c,d) are the 3D and 2D results of PSM.
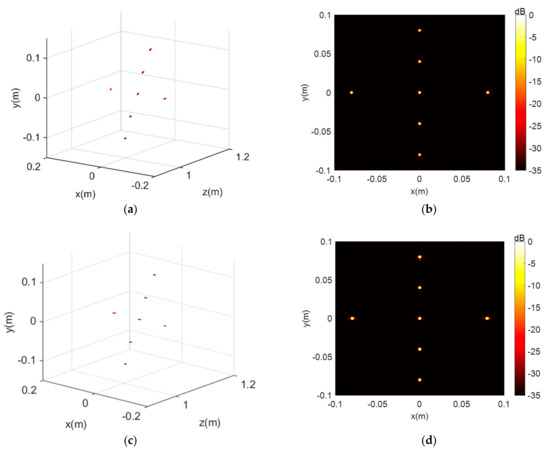
Figure 8.
The simulation results with coherent factor processing. (a,b) are the 3D and 2D projection results of CF-BPA. (c,d) are the 3D and 2D results of the proposed MCF-PSM.
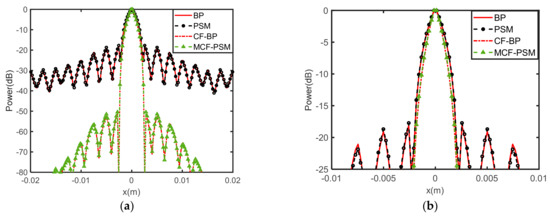
Figure 9.
The 1D profile along x-axis of the center point. (a) 1D Profile under −80 dB dynamic range. (b) Zoomed-in display near the main lobe.
4. Lab Experiments Results
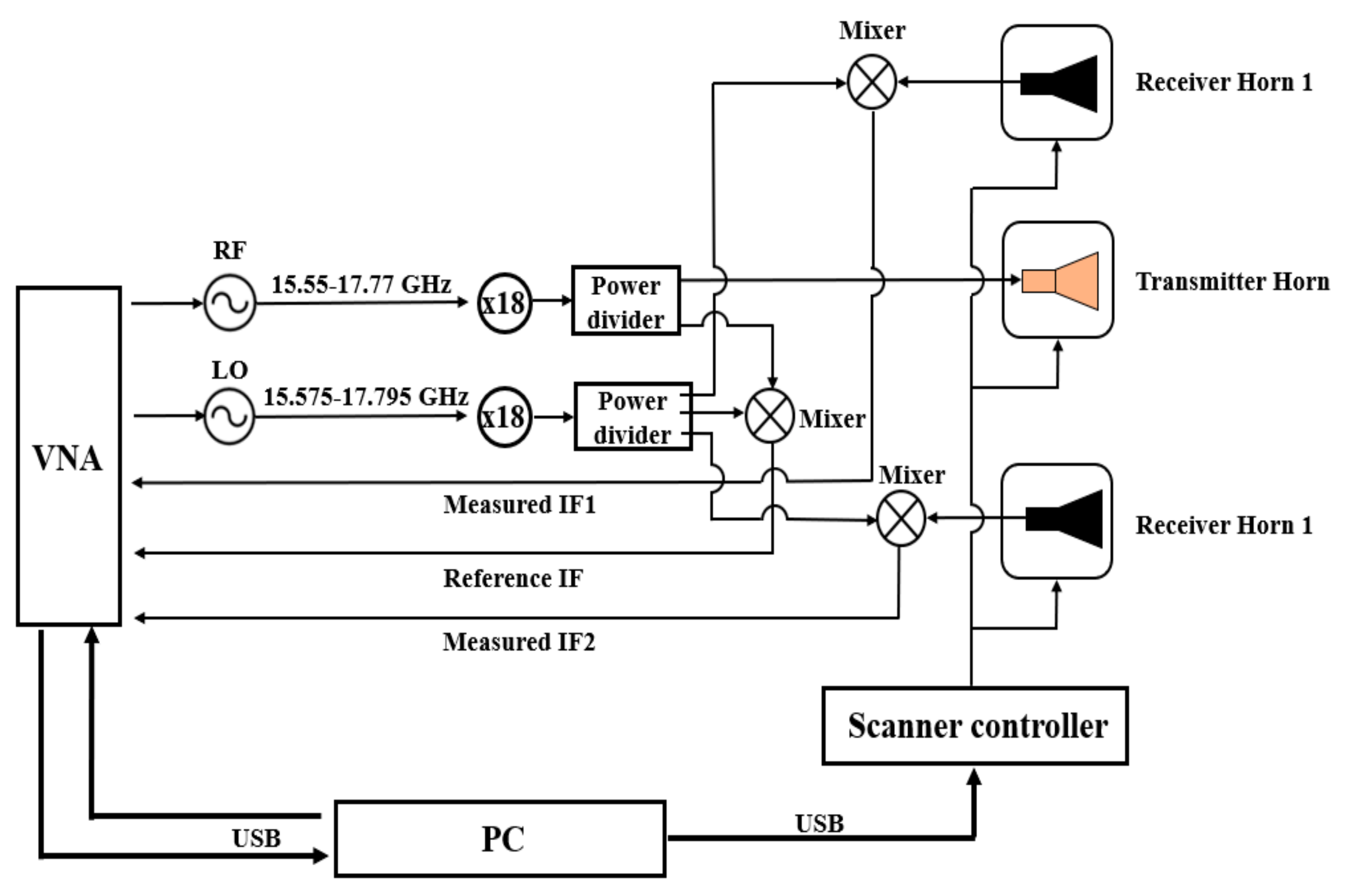
To illustrate the performance of the proposed algorithm in practical applications, a self-designed imaging prototype as shown in Figure 10 was developed. The prototype system adopts a Ku-band Vector Network Analyzer (VNA) with frequency extension modules to generate a 0.3 THz radio frequency signal. The transmitter transmits SFCW in the 280 to 320 GHz frequency band with 200 frequency steps. The receiving channel adopts superheterodyne receiving, and the receivers convert scattered echo to intermediate frequency (IF) to extract the amplitude and phase information of the scattered filed.
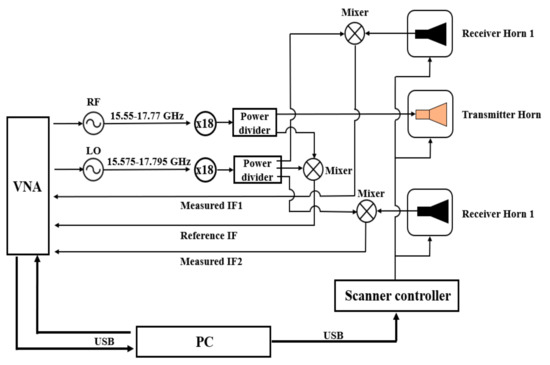
Figure 10.
The schematic of experimental prototype.
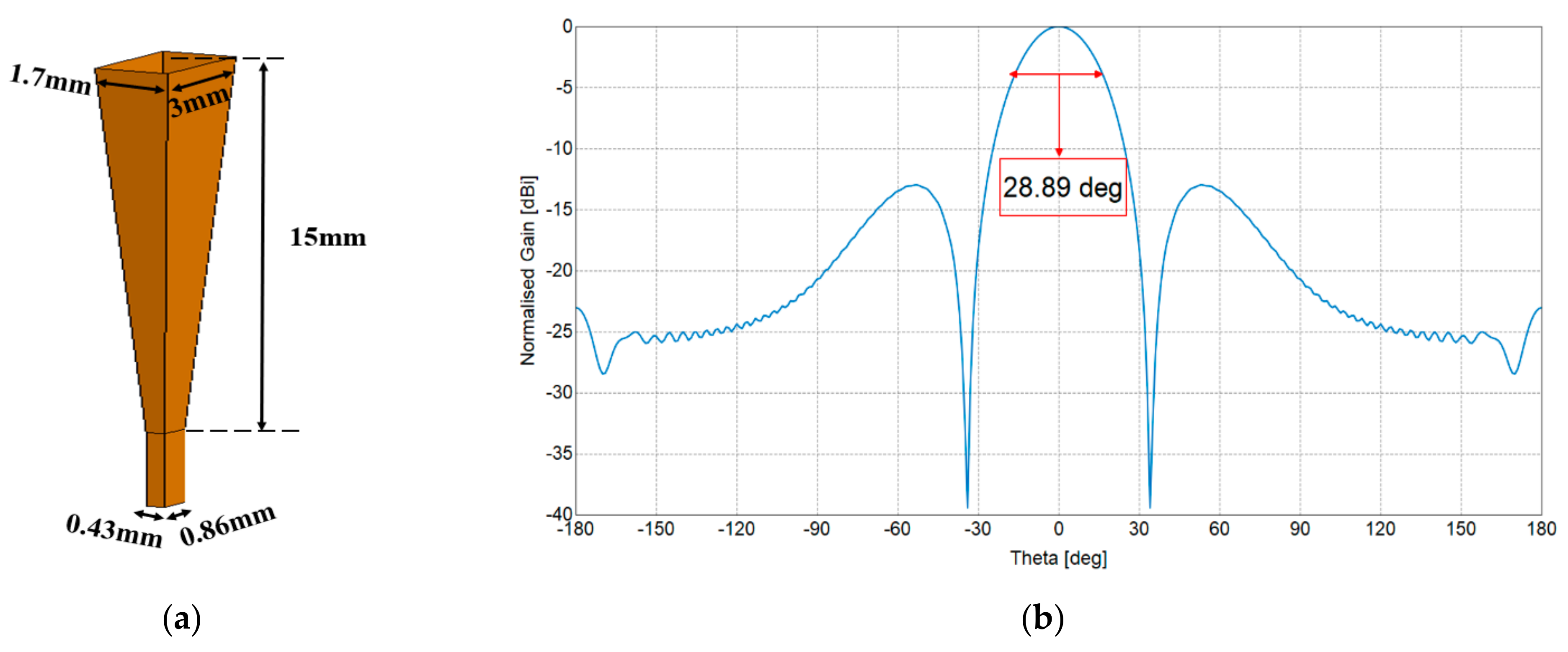
The horn of the transmitter and receivers are the same with an almost 28.89-degree beamwidth. The geometry of the horn and simulation of beamwidth are given in Figure 11. The intervals of transmitters and receivers are consistent with those in simulation. Due to the width limitation of the antenna front-end, the interval between the adjacent transmitter and receiver in the experiment is 12 mm. As denoted in Figure 12, the total length of the array is 255 mm.
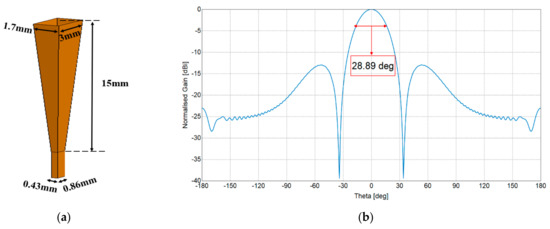
Figure 11.
Horn antenna for experiment with detailed dimensions. (a) The geometry of the horn antenna. (b) The E-plane beamwidth.
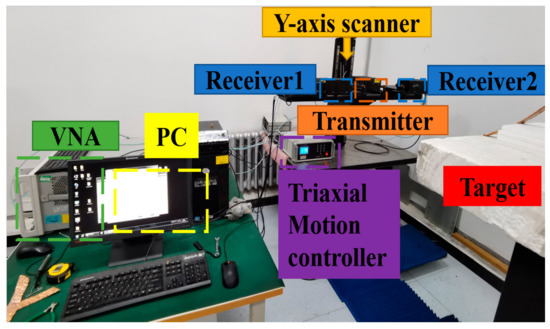
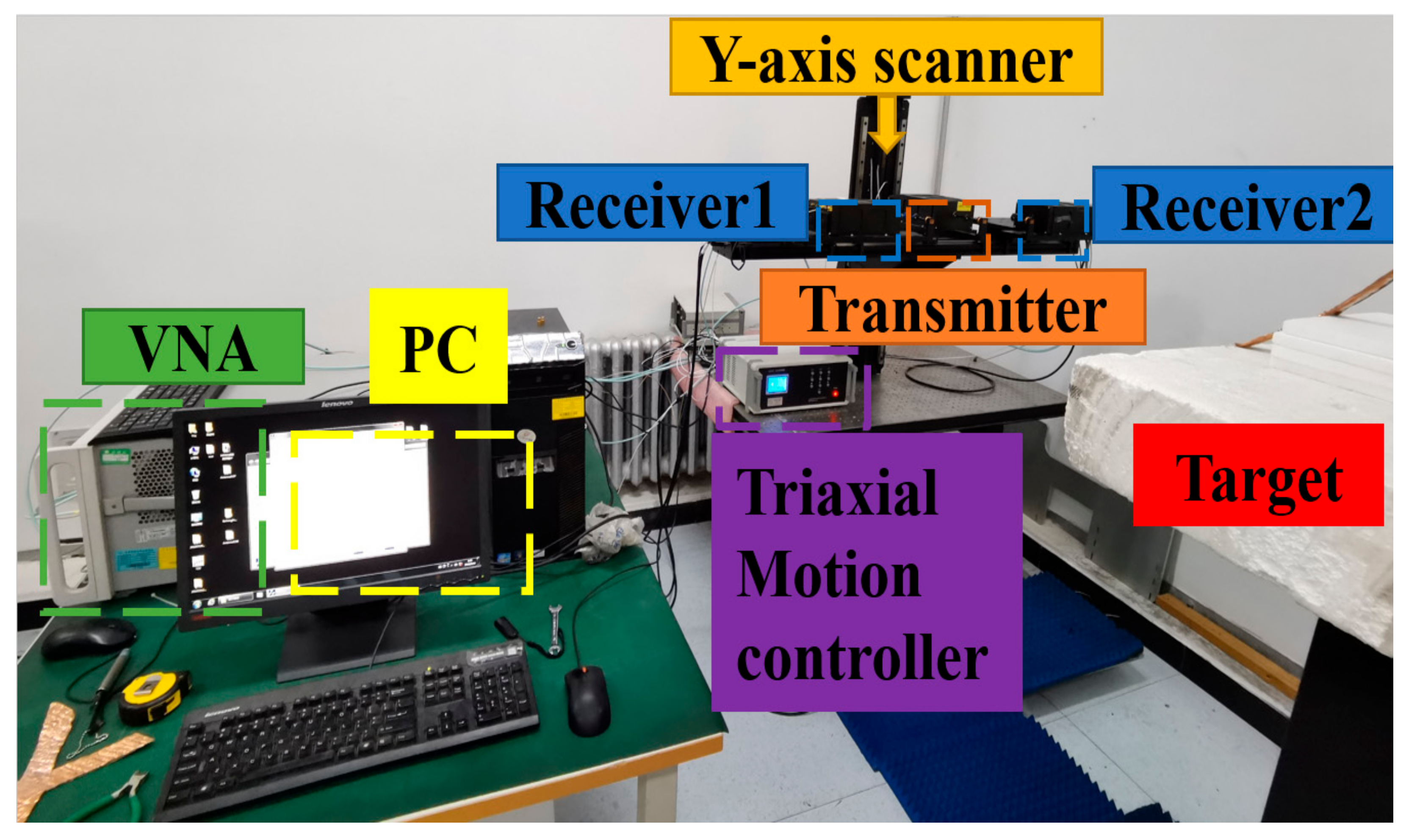
Figure 12.
Laboratory experiment setup.
The equivalent 1-D MIMO array with 51 transmitters and 6 receivers as shown in Figure 13 can be achieved by controlling three motor-driven platforms to scan in a horizontal guide rail. According to the principle of reciprocity, it is equivalent to an array of 6 transmitters and 51 receivers. The fourth motor is used to control the horizontal guide rail to scan in the vertical direction to achieve synthetic aperture. After completing a round of transmitting and receiving in the horizontal direction, the horizontal guide rail moves 2 mm along the vertical y-direction, and the next round of data acquisition starts. In this experiment, the scanning length along y-axis is 240 mm.
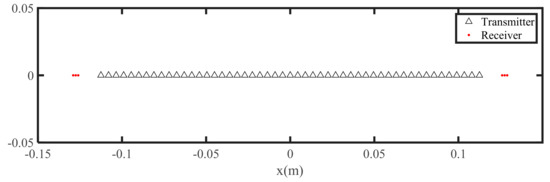
Figure 13.
The equivalent MIMO array in experiment.
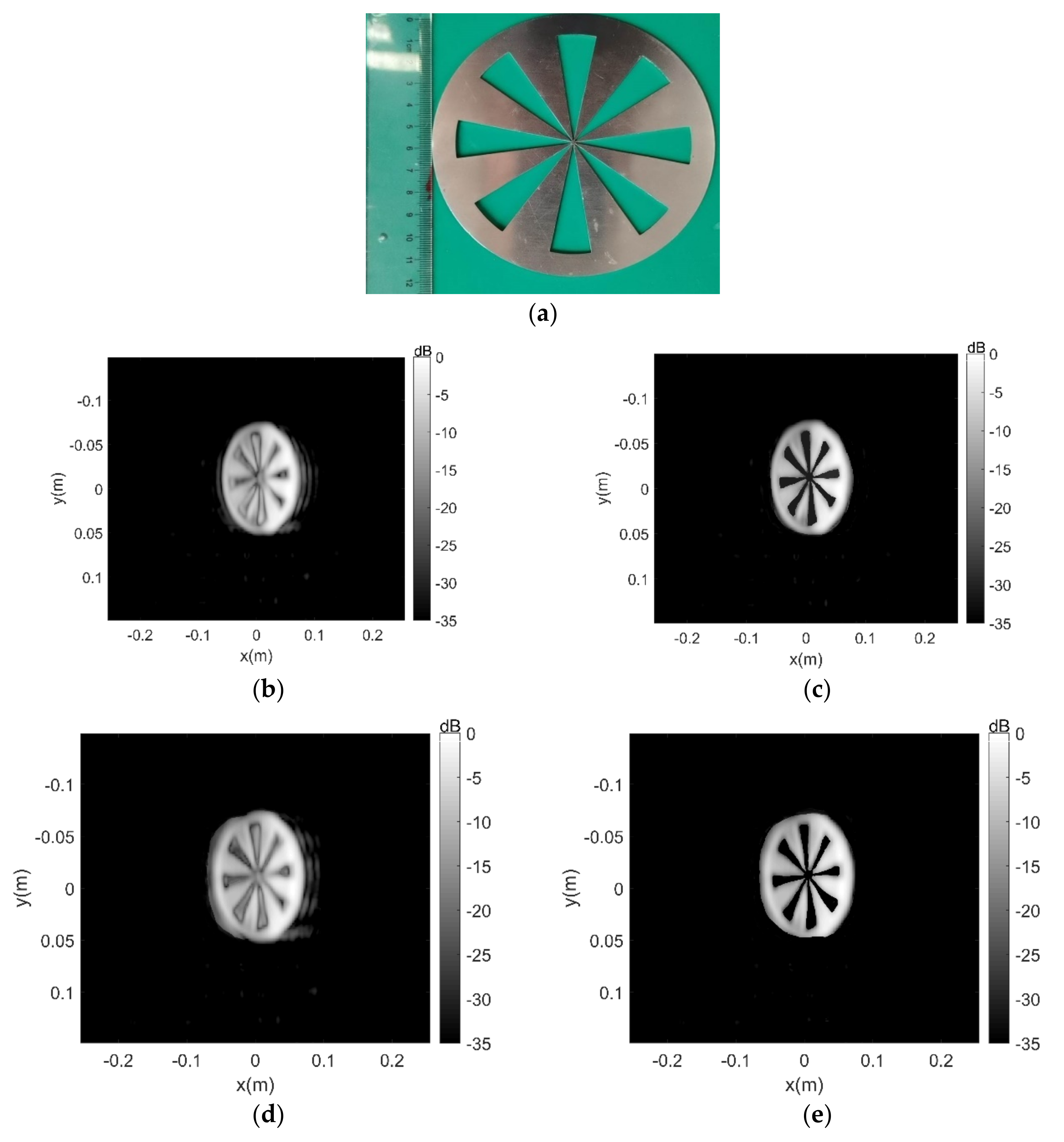
As shown in Figure 14a, a customized Siemens-star target made by steel was used as imaging target. The angle of each fan-shaped incision is 20 degrees and the maximum radius of the incision is 50 mm. The target is placed at a 1.1 m away from the array plane. Then, the BPA and the proposed algorithm are employed to process the raw echo data. The results of BPA and PSM without/with CF processing are shown in Figure 14b–e. Both algorithms successfully reconstruct the target with high quality. Before coherence factor processing, the imaging results are severely interfered by sidelobes, and both algorithms with coherence factor processing achieve sidelobe suppression.
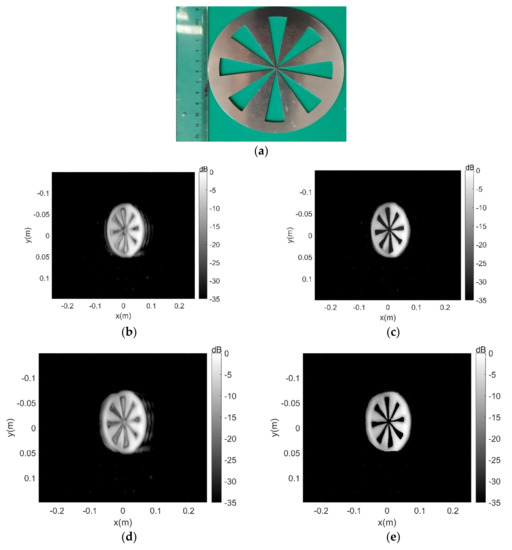
Figure 14.
The experimental results. (a) Optical picture of targets. (b,c) are the results of BPA and CF-BPA. (d,e) are the are the results of the PSM algorithm and the MCF-PSM algorithm.
5. Discussion
For a clear comparison, the structural similarity (SSIM) evaluation index [42] is introduced to quantitatively compare the focusing performance of the 2-D images. The calculation formula of SSIM can be expressed as:
where represents the reference image, denotes the image to be evaluated. , and are the average, variance and cross-covariance of the two images, respectively. C1, C2 are constants to prevent the denominator from being 0 and maintain stability. Usually take ,, where , and . SSIM is a value between 0 and 1. The larger it is, the smaller the gap between the image to be evaluated and the reference image. If the two images are exactly the same, the SSIM is equal to 1.
Then, we use the results of the CF-BPA as the reference image and the results of the MCF-PSM as the image to be evaluated. According to (35), we can get the SSIM value between the two images is 0.948 which means there is a high degree of similarity between the two images. Then, the Table 5 shows the calculation costs and the processing time of the tow algorithms, it can be seen that the proposed algorithm has obvious efficiency advantages.

Table 5.
Computational Costs of Different Algorithms.
6. Conclusions
In this paper, an efficient PSM image reconstruction algorithm with modified coherent factor was proposed for the MIMO-SAR 3-D imaging. By constructing a virtual echo about the difference wavenumber, the PSM algorithm framework can be used to calculate the incoherent power. Therefore, the coherence factor algorithm can be implemented in the wavenumber domain with high computational efficiency. Compared with the golden-standard BPA, the proposed algorithm achieves two orders of magnitude increase in computational efficiency with a 0.948 SSIM value which means the comparable image quality. Proof-of-principle experiments were also carried out in the 0.3 THz band based on a self-designed MIMO-SAR prototype system. The imaging results of the target are given to demonstrate the effectiveness of the proposed image reconstruction algorithm. The main contribution of this paper is to propose a wavenumber domain calculation method for incoherent power, which can theoretically be extended to any wavenumber domain imaging algorithm with considerable flexibility.
Author Contributions
G.Y. performed the theoretical study, conducted the experiments, processed the data and wrote the manuscript. C.L. designed the imaging system and revised the manuscript together with S.W. S.Z. helped in performing the experiments. X.L. and G.F. provided the experiment equipment and funds for the research. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China (2017YFA0701004, 2018YFF01013004); and the National Natural Science Foundation of China (61988102, 61731020, 61671432 and 61971397); and the Project of Equipment Pre-Research (WJ2019G00019); and the Key-Area Research and Development Program of Guangdong Province (2019B010157001, 2020B0101110001); and the Key Program of Scientific and Technological Innovation from Chinese Academy of Sciences (KGFZD-135-18-029).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors would like to thank the editors and reviewers for their efforts to help the publication of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, H.; Li, C.; Wu, S.; Zheng, S.; Fang, G. Adaptive 3D Imaging for Moving Targets Based on a SIMO InISAR Imaging System in 0.2 THz Band. Remote Sens. 2021, 13, 782. [Google Scholar] [CrossRef]
- Cheng, B.; Cui, Z.; Lu, B.; Qin, Y.; Liu, Q.; Chen, P.; He, Y.; Jiang, J.; He, X.; Deng, X.; et al. 340-GHz 3-D Imaging Radar With 4Tx-16Rx MIMO Array. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 509–519. [Google Scholar] [CrossRef]
- Zhong, H.; Xu, J.; Xie, X.; Yuan, T.; Reightler, R.; Madaras, E.; Zhang, X.C. Nondestructive defect identification with terahertz time-of-flight tomography. IEEE Sens. J. 2005, 5, 203–208. [Google Scholar] [CrossRef]
- Meo, S.D.; Espín-López, P.F.; Martellosio, A.; Pasian, M.; Matrone, G.; Bozzi, M.; Magenes, G.; Mazzanti, A.; Perregrini, L.; Svelto, F.; et al. On the feasibility of breast cancer imaging systems at millimeter-waves frequencies. IEEE Trans. Microw. Theory Tech. 2017, 65, 1795–1806. [Google Scholar] [CrossRef]
- Sheen, D.M.; McMakin, D.L.; Hall, T.E.; Severtsen, R.H. Active millimeter-wave standoff and portal imaging techniques for personnel screening. In Proceedings of the 2009 IEEE Conference on Technologies for Homeland Security, Boston, MA, USA, 11–12 May 2009; pp. 440–447. [Google Scholar] [CrossRef]
- Sheen, D.M.; Hall, T.E.; Severtsen, R.H.; McMakin, D.L.; Hatchell, B.K.; Valdez, P.L.J. Standoff concealed weapon detection using a 350 GHz radar imaging system. Proc. SPIE 2010, 7670, 115–118. [Google Scholar] [CrossRef]
- Cooper, K.B.; Dengler, R.J.; Llombart, N.; Bryllert, T.; Chattopadhyay, G.; Siegel, P.H. THz imaging radar for standoff personnel screening. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 169–182. [Google Scholar] [CrossRef]
- Robertson, D.; Macfarlane, D.; Hunter, R.; Cassidy, S.; Llombart, N.; Gandini, E.; Bryllert, T.; Ferndahl, M.; Lindström, H.; Tenhunen, J.; et al. High resolution, wide field view, real time 340GHz 3D imaging radar security screening. Proc. SPIE 2017, 101890, 101890C. [Google Scholar]
- Llombart, N.; Cooper, K.; Dengler, R.; Bryllert, T.; Siegel, P. Confocal ellipsoidal reflector system for a mechanically scanned active terahertz imager. IEEE Trans. Antennas Propag. 2010, 58, 1834–1840. [Google Scholar] [CrossRef] [Green Version]
- Gu, S.; Li, C.; Gao, X.; Sun, Z.; Fang, G. Terahertz aperture synthesized imaging with fan-beam scanning for personnel screening. IEEE Trans. Microw. Theory Technol. 2012, 60, 3877–3885. [Google Scholar] [CrossRef]
- Zhuge, X.; Yarovoy, A. A Sparse Aperture MIMO-SAR Based UWB Imaging System for Concealed Weapon Detection. IEEE Trans. Geosci. Remote Sens. 2011, 49, 509–518. [Google Scholar] [CrossRef]
- Yang, G.; Li, C.; Wu, S.; Liu, X.; Fang, G. MIMO-SAR 3-D Imaging Based on Range Wavenumber Decomposing. IEEE Sens. J. 2021, 21, 24309–24317. [Google Scholar] [CrossRef]
- Zhu, R.; Zhou, J.; Jiang, G.; Fu, Q. Range Migration Algorithm for Near-Field MIMO-SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2280–2284. [Google Scholar] [CrossRef]
- Fan, B.; Gao, J.; Li, H.; Jiang, Z.; He, Y. Near-Field 3D SAR Imaging Using a Scanning Linear MIMO Array With Arbitrary Topologies. IEEE Access 2020, 8, 6782–6791. [Google Scholar] [CrossRef]
- Gao, J.; Qin, Y.; Deng, B.; Wang, H.; Li, X. Novel efficient 3-D shortrange imaging algorithms for a scanning 1D-MIMO array. IEEE Trans. Image Process. 2018, 27, 3631–3643. [Google Scholar] [CrossRef]
- Bleh, D.; Rosch, M.; Kuri, M.; Dyck, A.; Tessmann, A.; Leuther, A.; Wagner, S.; Weismann-Thaden, B.; Stulz, H.P.; Zink, M.; et al. W-Band Time-Domain Multiplexing FMCW MIMO Radar for Far-Field 3-D Imaging. IEEE Trans. Microw. Theory Tech. 2017, 65, 3474–3484. [Google Scholar] [CrossRef]
- Moll, J.; Schops, P.; Krozer, V. Towards Three-Dimensional Millimeter-Wave Radar With the Bistatic Fast-Factorized Back-Projection Algorithm—Potential and Limitations. IEEE Trans. Terahertz Sci. Technol. 2012, 2, 432–440. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, J.; Wang, R.; Deng, Y.; Wang, W.; Li, N. An Accelerated Backprojection Algorithm for Monostatic and Bistatic SAR Processing. Remote Sens. 2018, 10, 140. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Moon, J. Analysis of a Bistatic Ground-Based Synthetic Aperture Radar System and Indoor Experiments. Remote Sens. 2021, 13, 63. [Google Scholar] [CrossRef]
- Wu, J.; Sun, Z.; Li, Z.; Huang, Y.; Yang, J.; Liu, Z. Focusing Translational Variant Bistatic Forward-Looking SAR Using Keystone Transform and Extended Nonlinear Chirp Scaling. Remote Sens. 2016, 8, 840. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Li, Z.; Huang, Y.; Yang, J.; Liu, Q.H. An Omega-K Algorithm for Translational Invariant Bistatic SAR Based on Generalized Loffeld’s Bistatic Formula. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6699–6714. [Google Scholar] [CrossRef]
- Zhuge, X.; Yarovoy, A. Three-Dimensional Near-Field MIMO Array Imaging Using Range Migration Techniques. IEEE Trans. Image Process. 2012, 21, 3026–3033. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Li, C.; Zheng, S.; Wu, S.; Fang, G. Implementation of the phase shift migration in MIMO-sidelooking imaging at Terahertz band. IEEE Sens. J. 2019, 19, 9384–9393. [Google Scholar] [CrossRef]
- Gao, H.; Li, C.; Wu, S.; Zheng, S.; Li, H.; Fang, G. Image reconstruction algorithm based on frequency-wavenumber decoupling for three-dimensional MIMO-SAR imaging. Opt. Express. 2020, 28, 2411–2426. [Google Scholar] [CrossRef] [PubMed]
- Yanik, M.E.; Torlak, M. Near-Field MIMO-SAR Millimeter-Wave Imaging With Sparsely Sampled Aperture Data. IEEE Access. 2019, 7, 31801–31819. [Google Scholar] [CrossRef]
- Alibakhshikenari, M.; Babaeianet, F.; Virdee, B.S.; Aïssa, S.; Azpilicueta, L.; See, C.H.; Althuwayb, A.A.; Huynen, I.; Abd-Alhameed, R.A.; Falcone, F.; et al. A Comprehensive Survey on “Various Decoupling Mechanisms with Focus on Metamaterial and Metasurface Principles Applicable to SAR and MIMO Antenna Systems”. IEEE Access 2020, 8, 192965–193004. [Google Scholar] [CrossRef]
- Althuwayb, A.A. Low-Interacted Multiple Antenna Systems Based on Metasurface-Inspired Isolation Approach for MIMO Applications. Arab. J. Sci. Eng. 2021, 1–10. [Google Scholar] [CrossRef]
- Maleki, A.; Oskouei, H.D.; Shirkolaei, M.M. Miniaturized microstrip patch antenna with high inter-port isolation for full duplex communication system. Int. J. RF Microw. Comput.-Aided Eng. 2021, 31, e22760. [Google Scholar] [CrossRef]
- Tu, X.; Zhu, G.; Hu, X.; Huang, X. Grating Lobe Suppression in Sparse Array-Based Ultrawideband through-Wall Imaging Radar. IEEE Antenn. Wirel. Prop. Lett. 2016, 15, 1020–1023. [Google Scholar] [CrossRef]
- Zhu, R.Q.; Zhou, J.; Fu, Q.; Jiang, G. Spatially Variant Apodization for Grating and Sidelobe Suppression in Near-Range MIMO Array Imaging. IEEE Trans. Microw. Theory Technol. 2020, 68, 4662–4671. [Google Scholar] [CrossRef]
- Zhang, Z.; Buma, T. Terahertz impulses imaging with sparse arrays and adaptive reconstruction. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 169–176. [Google Scholar] [CrossRef]
- Anwar, N.; Abdullah, M. Sidelobe Suppression Featuring the Phase Coherence Factor in 3-D Through-the-Wall Radar Imaging. Radioengineering 2016, 25, 730–740. [Google Scholar] [CrossRef]
- Hu, J.; Zhu, G.; Jin, T.; Lu, B.; Zhou, Z. Grating lobe mitigation based on extended coherence factor in sparse MIMO UWB array. In Proceedings of the 2014 12th International Conference on Signal Processing (ICSP), Hangzhou, China, 19–23 October 2015; pp. 2098–2101. [Google Scholar] [CrossRef]
- Glentis, G.; Jakobsson, A. Efficient implementation of iterative adaptive approach spectral estimation techniques. IEEE Trans. Signal Process. 2011, 59, 4154–4167. [Google Scholar] [CrossRef]
- Sun, W.; So, H.; Chen, Y.; Huang, L.; Huang, L. Approximate subspace-based iterative adaptive approach for fast two-dimensional spectral estimation. IEEE Trans. Signal Process. 2014, 62, 3220–3231. [Google Scholar] [CrossRef]
- Shkvarko, Y.; Yañez, J.; Amao, J.; Martín del Campo, G. Radar/SAR image resolution enhancement via unifying descriptive experiment design regularization and wavelet-domain processing. IEEE Geosci. Remote Sens. Lett. 2016, 13, 152–156. [Google Scholar] [CrossRef]
- Sheen, D.M.; McMakin, D.L.; Hall, T.E. Three-dimensional millimeter-wave imaging for concealed weapon detection. IEEE Trans. Microw. Theory Tech. 2001, 49, 1581–1592. [Google Scholar] [CrossRef]
- Loewenthal, D.; Lu, L.; Roberson, R.; Sherwood, J. The wave equation applied to migration. Geophys. Prospect. 1976, 24, 380–399. [Google Scholar] [CrossRef]
- Gu, S.; Li, C.; Gao, X.; Sun, Z.; Fang, G. Three-dimensional image reconstruction of targets under the illumination of terahertz Gaussian beam—Theory and experiment. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2241–2249. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data, Algorithms and Implementation; Artech House: Boston, MA, USA, 2005. [Google Scholar]
- Conway, J.B. Functions of One Complex Variable; Springer: Berlin/Heidelberg, Germany, 1973. [Google Scholar]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).