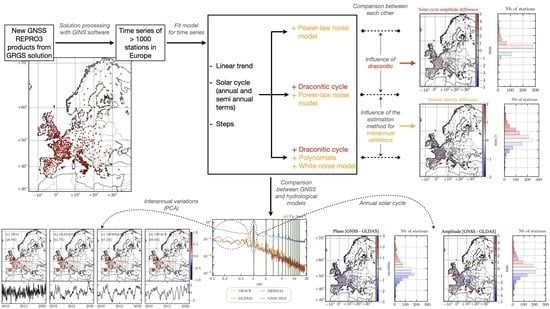
Analysis of GNSS Displacements in Europe and Their Comparison with Hydrological Loading Models
Abstract
:1. Introduction
2. Materials and Methods
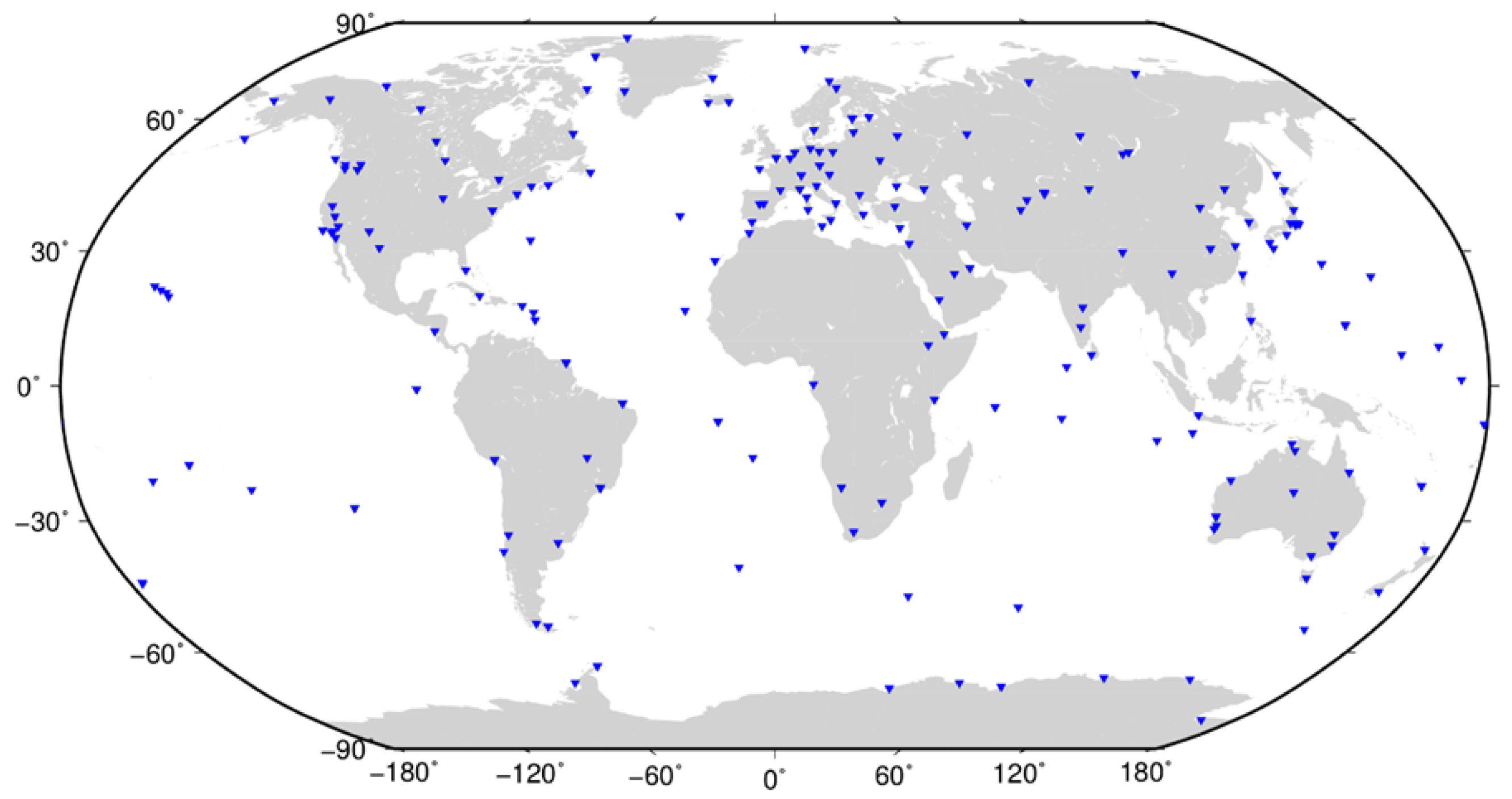
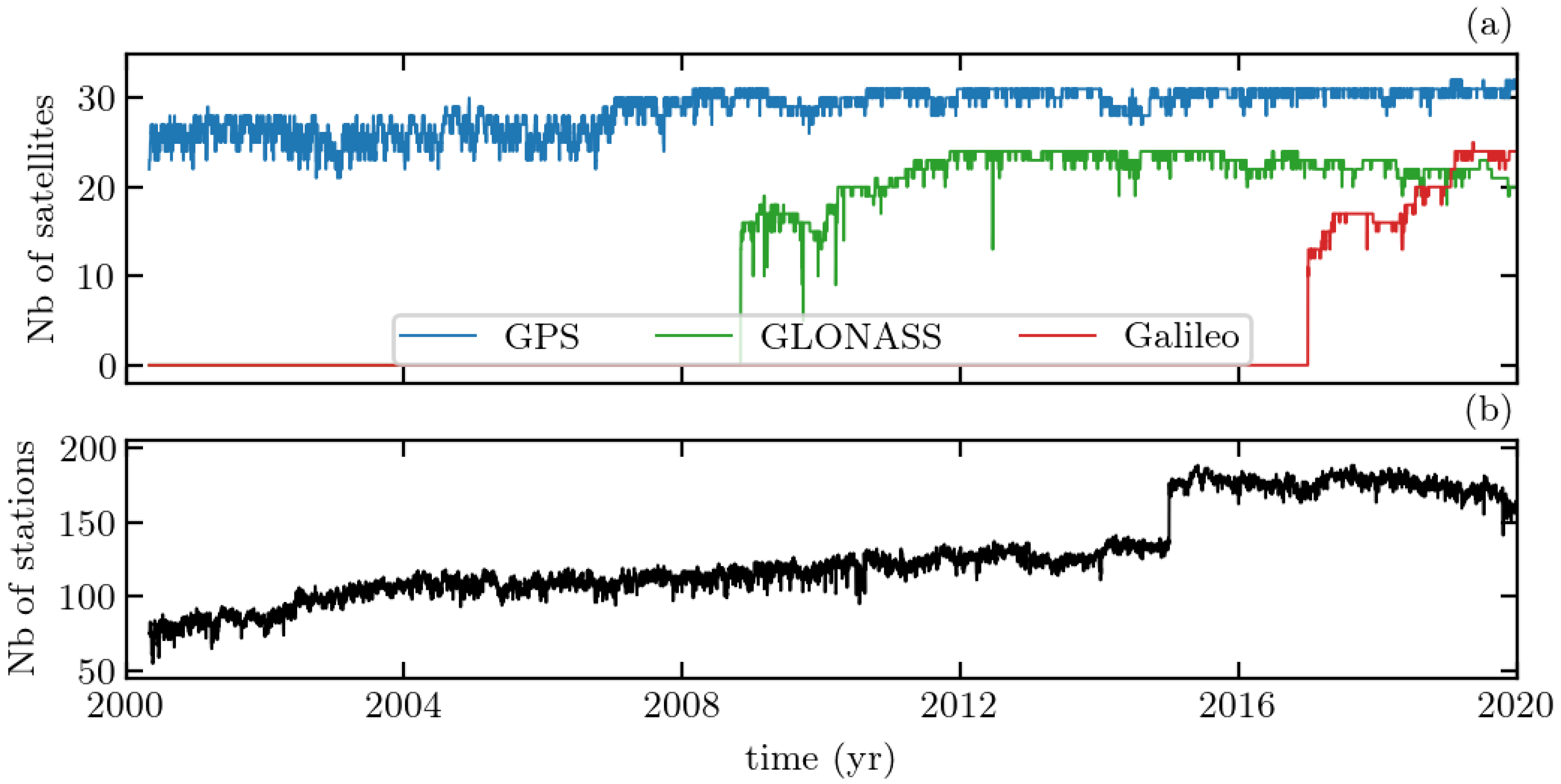
2.1. CNES-CLS Multi-GNSS Orbits and Clock Products
2.2. Time Series Analysis
2.2.1. Selection of Stations
2.2.2. Parameter Estimation
2.2.3. Interannual Polynomial Model
2.3. Hydrological Loading Computations
3. Results
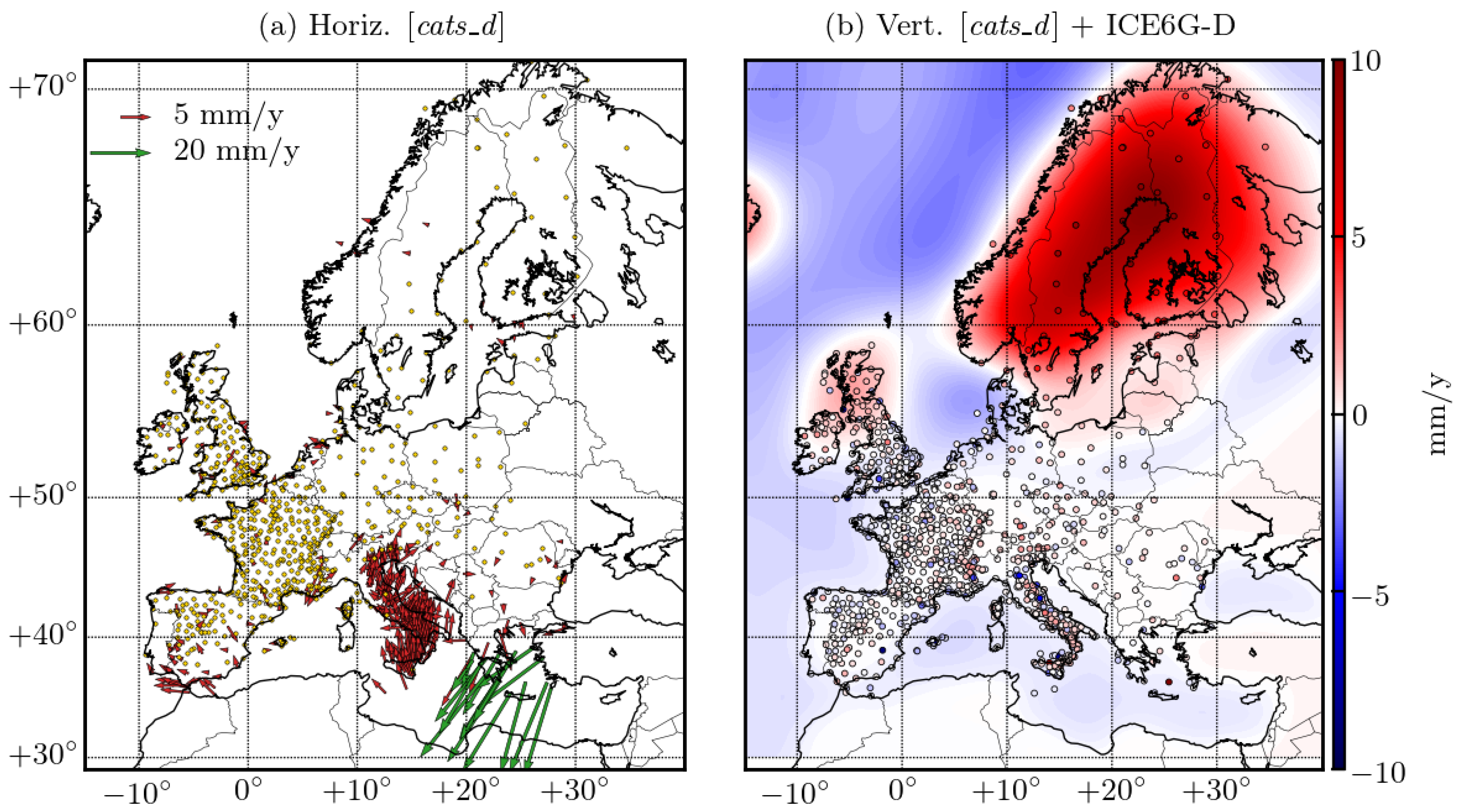
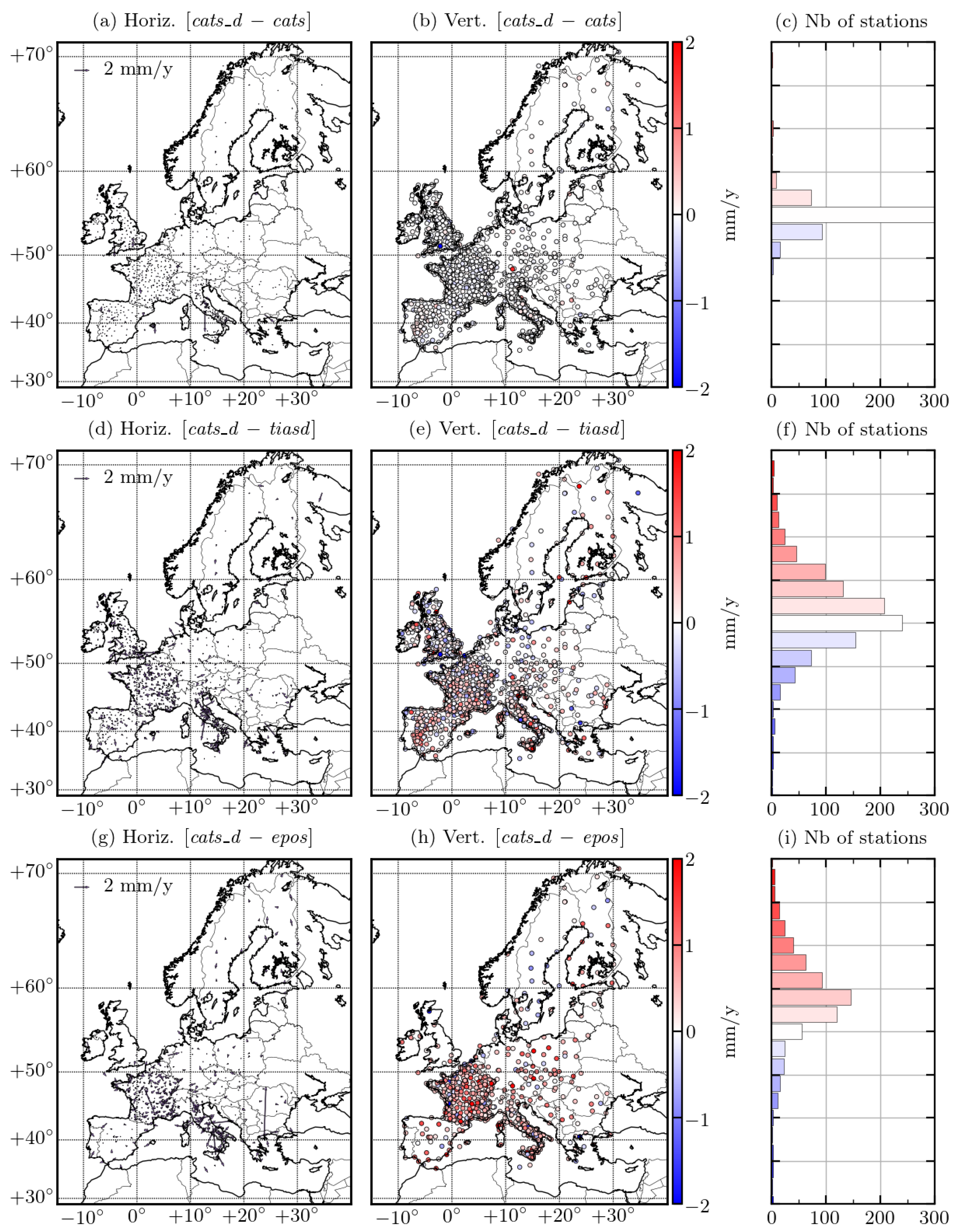
3.1. Tectonic Velocity
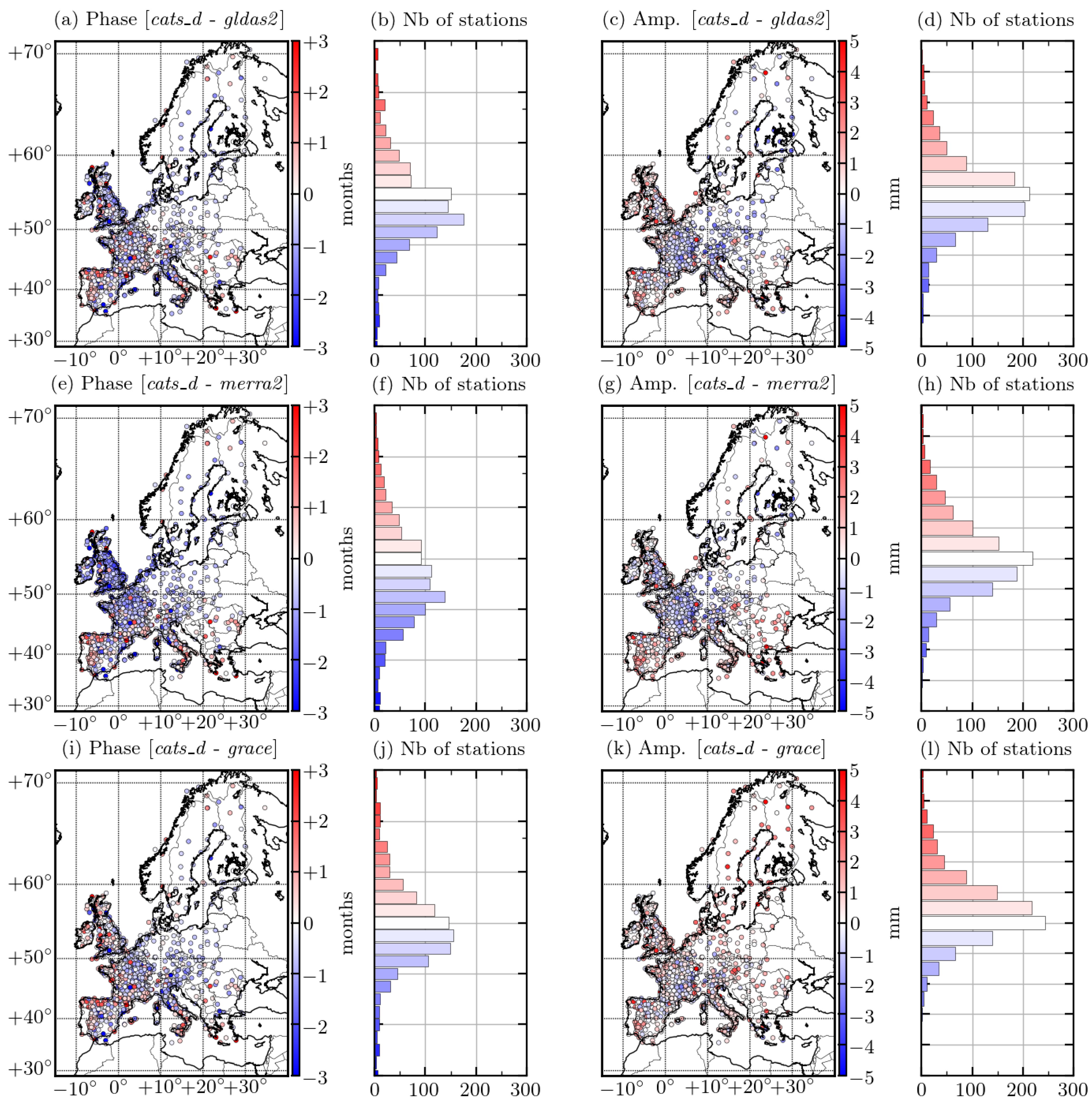
3.2. Annual Signal
3.3. Comparison with Hydrological Models and GRACE
3.4. Principal Component Analysis of the Interannual Signal
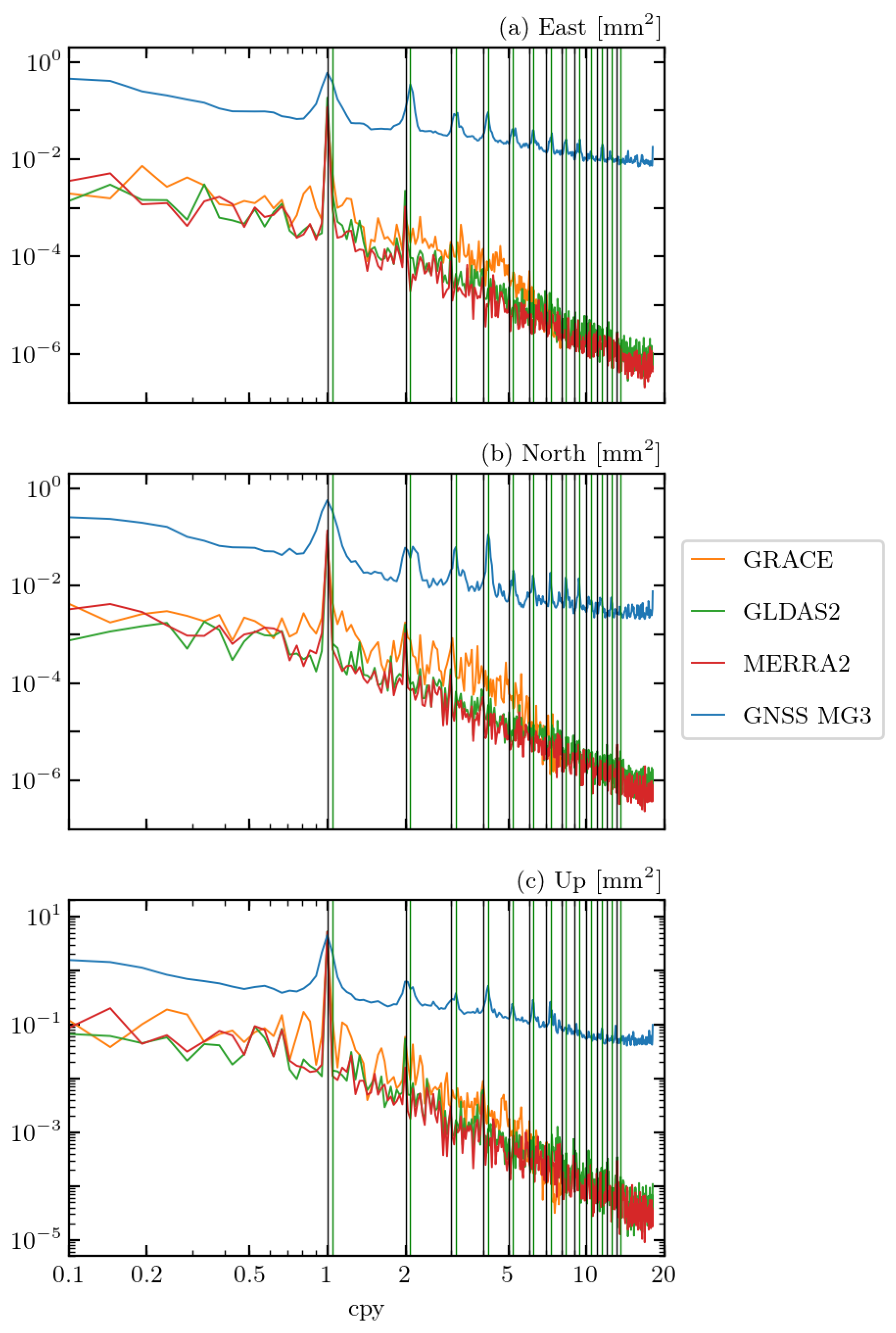
3.5. Frequency Content and Interannual Variations
4. Discussion
4.1. Interannual Signal in GNSS Time Series
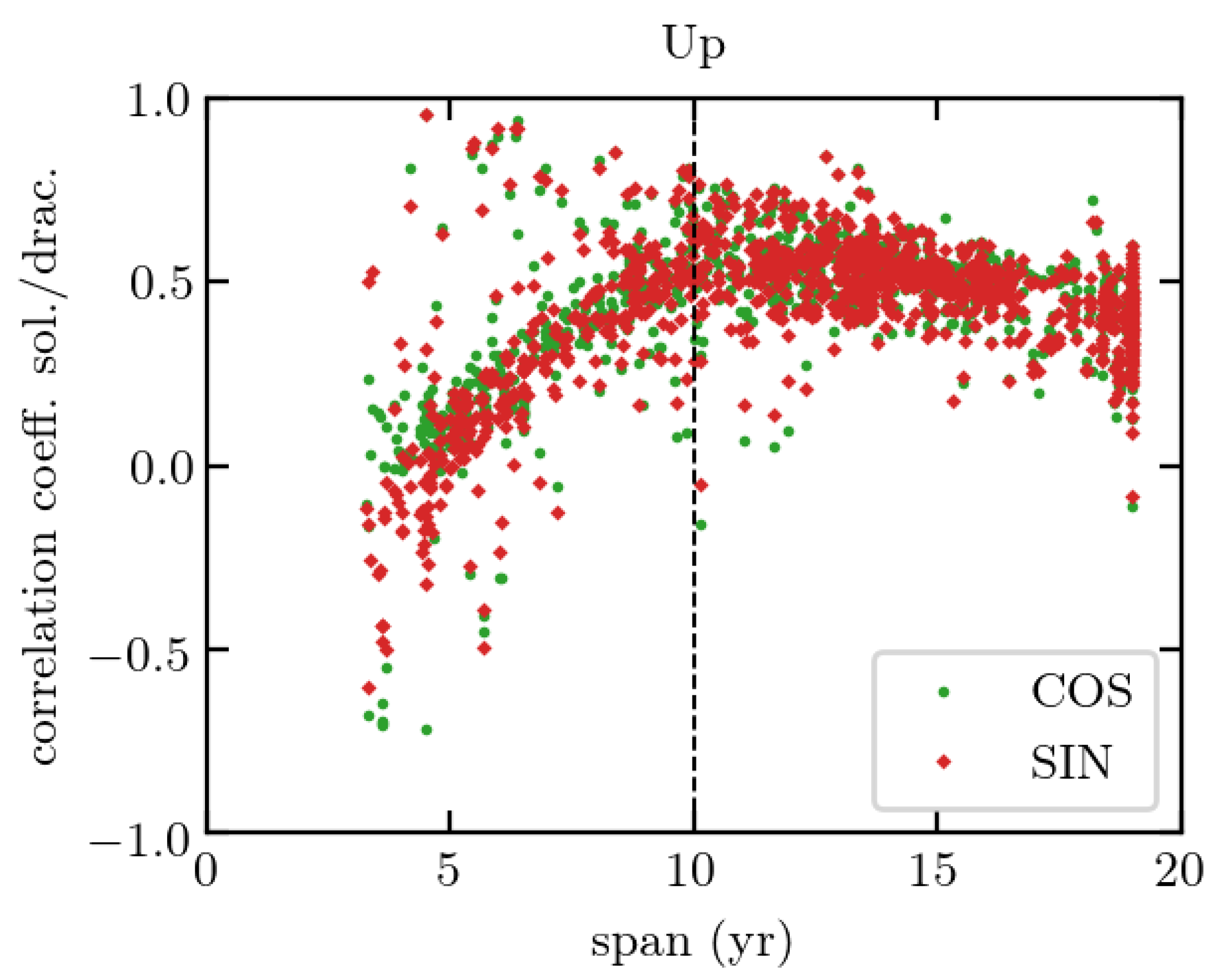
4.2. Importance of Draconitic Adjustment
4.3. Model Phase Advance over GNSS Seasonal Signal
4.4. Common Mode Estimation in GNSS
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nocquet, J.M. Present-day kinematics of the Mediterranean: A comprehensive overview of GPS results. Tectonophysics 2012, 579, 220–242. [Google Scholar] [CrossRef]
- Masson, C.; Mazzotti, S.; Vernant, P.; Doerflinger, E. Extracting small deformation beyond individual station precision from dense Global Navigation Satellite System (GNSS) networks in France and western Europe. Solid Earth 2019, 10, 1905–1920. [Google Scholar] [CrossRef] [Green Version]
- Kouba, J. Measuring seismic waves induced by large earthquakes with GPS. Stud. Geophys. Geod. 2003, 47, 741–755. [Google Scholar] [CrossRef]
- Klein, E.; Fleitout, L.; Vigny, C.; Garaud, J. Afterslip and viscoelastic relaxation model inferred from the large-scale post-seismic deformation following the 2010 M w 8.8 Maule earthquake (Chile). Geophys. J. Int. 2016, 205, 1455–1472. [Google Scholar] [CrossRef] [Green Version]
- van Dam, T.; Wahr, J.; Milly, P.; Shmakin, A.; Blewitt, G.; Lavallée, D.; Larson, K. Crustal displacements due to continental water loading. Geophys. Res. Lett. 2001, 28, 651–654. [Google Scholar] [CrossRef] [Green Version]
- Argus, D.F.; Fu, Y.; Landerer, F.W. Seasonal variation in total water storage in California inferred from GPS observations of vertical land motion. Geophys. Res. Lett. 2014, 41, 1971–1980. [Google Scholar] [CrossRef]
- Chanard, K.; Fleitout, L.; Calais, E.; Rebischung, P.; Avouac, J.P. Toward a global horizontal and vertical elastic load deformation model derived from GRACE and GNSS station position time series. J. Geophys. Res. Solid Earth 2018, 123, 3225–3237. [Google Scholar] [CrossRef]
- Martens, H.R.; Argus, D.F.; Norberg, C.; Blewitt, G.; Herring, T.A.; Moore, A.W.; Hammond, W.C.; Kreemer, C. Atmospheric pressure loading in GPS positions: Dependency on GPS processing methods and effect on assessment of seasonal deformation in the contiguous USA and Alaska. J. Geod. 2020, 94, 1–22. [Google Scholar] [CrossRef]
- Mémin, A.; Boy, J.P.; Santamaria-Gomez, A. Correcting GPS measurements for non-tidal loading. GPS Solut. 2020, 24, 45. [Google Scholar] [CrossRef]
- Johansson, J.M.; Davis, J.L.; Scherneck, H.G.; Milne, G.A.; Vermeer, M.; Mitrovica, J.X.; Bennett, R.A.; Jonsson, B.; Elgered, G.; Elósegui, P.; et al. Continuous GPS measurements of postglacial adjustment in Fennoscandia 1. Geodetic results. J. Geophys. Res. Solid Earth 2002, 107, ETG-3. [Google Scholar] [CrossRef] [Green Version]
- Grapenthin, R.; Sigmundsson, F.; Geirsson, H.; Arnadóttir, T.; Pinel, V. Icelandic rhythmics: Annual modulation of land elevation and plate spreading by snow load. Geophys. Res. Lett. 2006, 33, L24305. [Google Scholar] [CrossRef] [Green Version]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef] [Green Version]
- Mao, A.; Harrison, C.G.; Dixon, T.H. Noise in GPS coordinate time series. J. Geophys. Res. Solid Earth 1999, 104, 2797–2816. [Google Scholar] [CrossRef] [Green Version]
- Williams, S. The effect of coloured noise on the uncertainties of rates estimated from geodetic time series. J. Geod. 2003, 76, 483–494. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Bouin, M.N.; Collilieux, X.; Wöppelmann, G. Correlated errors in GPS position time series: Implications for velocity estimates. J. Geophys. Res. Solid Earth 2011, 116, B01405. [Google Scholar] [CrossRef]
- Klos, A.; Olivares, G.; Teferle, F.N.; Hunegnaw, A.; Bogusz, J. On the combined effect of periodic signals and colored noise on velocity uncertainties. GPS Solut. 2018, 22, 1. [Google Scholar] [CrossRef] [Green Version]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.; Miyazaki, S. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. Solid Earth 2002, 107, ETG-9. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, J.; Ray, J.R. On the precision and accuracy of IGS orbits. J. Geod. 2009, 83, 277–287. [Google Scholar] [CrossRef]
- Tregoning, P.; Watson, C. Atmospheric effects and spurious signals in GPS analyses. J. Geophys. Res. Solid Earth 2009, 114, B09403. [Google Scholar] [CrossRef] [Green Version]
- Johnson, H.O.; Agnew, D.C. Monument motion and measurements of crustal velocities. Geophys. Res. Lett. 1995, 22, 2905–2908. [Google Scholar] [CrossRef]
- King, M.A.; Williams, S.D. Apparent stability of GPS monumentation from short-baseline time series. J. Geophys. Res. Solid Earth 2009, 114, B10403. [Google Scholar] [CrossRef]
- King, M.A.; Watson, C.S. Long GPS coordinate time series: Multipath and geometry effects. J. Geophys. Res. Solid Earth 2010, 115, B04403. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Ray, J. Chameleonic noise in GPS position time series. J. Geophys. Res. Solid Earth 2021, 126, e2020JB019541. [Google Scholar] [CrossRef]
- Williams, S.D.; Bock, Y.; Fang, P.; Jamason, P.; Nikolaidis, R.M.; Prawirodirdjo, L.; Miller, M.; Johnson, D.J. Error analysis of continuous GPS position time series. J. Geophys. Res. Solid Earth 2004, 109, B03412. [Google Scholar] [CrossRef] [Green Version]
- Amiri-Simkooei, A. On the nature of GPS draconitic year periodic pattern in multivariate position time series. J. Geophys. Res. Solid Earth 2013, 118, 2500–2511. [Google Scholar] [CrossRef] [Green Version]
- Silverii, F.; d’Agostino, N.; Métois, M.; Fiorillo, F.; Ventafridda, G. Transient deformation of karst aquifers due to seasonal and multiyear groundwater variations observed by GPS in southern Apennines (Italy). J. Geophys. Res. Solid Earth 2016, 121, 8315–8337. [Google Scholar] [CrossRef]
- Fang, M.; Dong, D.; Hager, B.H. Displacements due to surface temperature variation on a uniform elastic sphere with its centre of mass stationary. Geophys. J. Int. 2014, 196, 194–203. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Dong, D.; Fang, M.; Zhou, Y.; Wei, N.; Zhou, F. Contributions of thermoelastic deformation to seasonal variations in GPS station position. GPS Solut. 2017, 21, 1265–1274. [Google Scholar] [CrossRef]
- Argus, D.F.; Landerer, F.W.; Wiese, D.N.; Martens, H.R.; Fu, Y.; Famiglietti, J.S.; Thomas, B.F.; Farr, T.G.; Moore, A.W.; Watkins, M.M. Sustained water loss in California’s mountain ranges during severe drought from 2012 to 2015 inferred from GPS. J. Geophys. Res. Solid Earth 2017, 122, 10–559. [Google Scholar] [CrossRef] [Green Version]
- Gourmelen, N.; Amelung, F.; Casu, F.; Manzo, M.; Lanari, R. Mining-related ground deformation in Crescent Valley, Nevada: Implications for sparse GPS networks. Geophys. Res. Lett. 2007, 34, L09309. [Google Scholar] [CrossRef] [Green Version]
- Muntean, A.; Mocanu, V.; Ambrosius, B. A GPS study of land subsidence in the Petrosani (Romania) coal mining area. Nat. Hazards 2016, 80, 797–810. [Google Scholar] [CrossRef]
- Ray, J.; Altamimi, Z.; Collilieux, X.; van Dam, T. Anomalous harmonics in the spectra of GPS position estimates. GPS Solut. 2008, 12, 55–64. [Google Scholar] [CrossRef]
- Guo, S.; Shi, C.; Wei, N.; Li, M.; Fan, L.; Zhang, D. Effect of ambiguity resolution on the draconitic errors in sub-daily GPS position estimates. GPS Solut. 2021, 25, 101. [Google Scholar] [CrossRef]
- Loyer, S.; Perosanz, F.; Mercier, F.; Capdeville, H.; Marty, J.C. Zero-difference GPS ambiguity resolution at CNES–CLS IGS Analysis Center. J. Geod. 2012, 86, 991–1003. [Google Scholar] [CrossRef]
- Klos, A.; Bogusz, J.; Bos, M.S.; Gruszczynska, M. Modelling the GNSS Time Series: Different Approaches to Extract Seasonal. In Geodetic Time Series Analysis in Earth Sciences; Springer: Cham, Switzerland, 2019; p. 211. [Google Scholar]
- Williams, S.D. CATS: GPS coordinate time series analysis software. GPS Solut. 2008, 12, 147–153. [Google Scholar] [CrossRef]
- He, X.; Montillet, J.P.; Fernandes, R.; Bos, M.; Yu, K.; Hua, X.; Jiang, W. Review of current GPS methodologies for producing accurate time series and their error sources. J. Geodyn. 2017, 106, 12–29. [Google Scholar] [CrossRef]
- Serpelloni, E.; Faccenna, C.; Spada, G.; Dong, D.; Williams, S.D. Vertical GPS ground motion rates in the Euro-Mediterranean region: New evidence of velocity gradients at different spatial scales along the Nubia-Eurasia plate boundary. J. Geophys. Res. Solid Earth 2013, 118, 6003–6024. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Li, W.; Xu, G.; Li, B. Spatiotemporal filtering of regional GNSS network’s position time series with missing data using principle component analysis. J. Geod. 2014, 88, 1–12. [Google Scholar] [CrossRef]
- Wu, S.; Nie, G.; Liu, J.; Wang, K.; Xue, C.; Wang, J.; Li, H.; Peng, F.; Ren, X. A sub-regional extraction method of common mode components from IGS and CMONOC stations in China. Remote Sens. 2019, 11, 1389. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Dai, W.; Peng, W.; Meng, X. Spatiotemporal analysis of GPS time series in vertical direction using independent component analysis. Earth Planets Space 2015, 67, 189. [Google Scholar] [CrossRef] [Green Version]
- Kreemer, C.; Blewitt, G. Robust estimation of spatially varying common-mode components in GPS time-series. J. Geod. 2021, 95, 13. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Elia, L.; Zerbini, S.; Raicich, F. Interannual Variability of GPS Heights and Environmental Parameters over Europe and the Mediterranean Area. Remote Sens. 2021, 13, 1554. [Google Scholar] [CrossRef]
- Katsigianni, G.; Perosanz, F.; Loyer, S.; Gupta, M. Galileo millimeter-level kinematic precise point positioning with ambiguity resolution. Earth Planets Space 2019, 71, 76. [Google Scholar] [CrossRef] [Green Version]
- Rebischung, P. Terrestrial Frame Solutions from the IGS Third Reprocessing. In Proceedings of the EGU General Assembly Conference Abstracts, online, 19–30 April 2021; p. EGU21-2144. [Google Scholar]
- Lemoine, J.M.; Biancale, R.; Reinquin, F.; Bourgogne, S.; Gégout, P. CNES/GRGS RL04 Earth Gravity Field Models, from GRACE and SLR Data; GFZ Data Services. 2019. Available online: https://doi.org/10.5880/ICGEM.2019.010 (accessed on 1 October 2021).
- Lyard, F.H.; Allain, D.J.; Cancet, M.; Carrère, L.; Picot, N. FES2014 global ocean tide atlas: Design and performance. Ocean Sci. 2021, 17, 615–649. [Google Scholar] [CrossRef]
- Folkner, W.M.; Williams, J.G.; Boggs, D.H. The planetary and lunar ephemeris DE 421. IPN Prog. Rep. 2009, 42, 1–34. [Google Scholar]
- Villiger, A.; Dach, R. International GNSS Service: Technical Report 2019; Technical Report; IGS Central Bureau and University of Bern: Bern, Switzerland, 2020. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions (2010); Technical Report; Bureau International des Poids et Mesures: Sèvres, France, 2010. [Google Scholar]
- Desai, S.D.; Sibois, A.E. Evaluating predicted diurnal and semidiurnal tidal variations in polar motion with GPS-based observations. J. Geophys. Res. Solid Earth 2016, 121, 5237–5256. [Google Scholar] [CrossRef] [Green Version]
- Ray, R.D.; Ponte, R.M. Barometric tides from ECMWF operational analyses. Ann. Geophys. 2003, 21, 1897–1910. [Google Scholar] [CrossRef] [Green Version]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef] [Green Version]
- Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef] [Green Version]
- Williams, S.D. Offsets in global positioning system time series. J. Geophys. Res. Solid Earth 2003, 108, 2310. [Google Scholar] [CrossRef]
- Bruni, S.; Zerbini, S.; Raicich, F.; Errico, M.; Santi, E. Detecting discontinuities in GNSS coordinate time series with STARS: Case study, the Bologna and Medicina GPS sites. J. Geod. 2014, 88, 1203–1214. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Mémin, A. Geodetic secular velocity errors due to interannual surface loading deformation. Geophys. J. Int. 2015, 202, 763–767. [Google Scholar] [CrossRef] [Green Version]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar]
- Collectif Jolidon. Physique Éxpérimentale; EDP Sciences: Les Ulis, France, 2021. [Google Scholar]
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Loomis, B.; Luthcke, S.; Sabaka, T. Regularization and error characterization of GRACE mascons. J. Geod. 2019, 93, 1381–1398. [Google Scholar] [CrossRef]
- Farrell, W. Deformation of the Earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Petrov, L.; Boy, J.P. Study of the atmospheric pressure loading signal in very long baseline interferometry observations. J. Geophys. Res. Solid Earth 2004, 109, B03405. [Google Scholar] [CrossRef] [Green Version]
- Altamimi, Z.; Métivier, L.; Rebischung, P.; Rouby, H.; Collilieux, X. ITRF2014 plate motion model. Geophys. J. Int. 2017, 209, 1906–1912. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, D.; Drummond, R. Space geodesy constrains ice age terminal deglaciation: The global ICE-6G_C (VM5a) model. J. Geophys. Res. Solid Earth 2015, 120, 450–487. [Google Scholar] [CrossRef] [Green Version]
- Peltier, R.W.; Argus, D.F.; Drummond, R. Comment on “An assessment of the ICE-6G_C (VM5a) glacial isostatic adjustment model” by Purcell et al. J. Geophys. Res. Solid Earth 2018, 123, 2019–2028. [Google Scholar] [CrossRef]
- van Dam, T.; Wahr, J.; Lavallée, D. A comparison of annual vertical crustal displacements from GPS and Gravity Recovery and Climate Experiment (GRACE) over Europe. J. Geophys. Res. Solid Earth 2007, 112, B03404. [Google Scholar] [CrossRef] [Green Version]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II-Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. 1982, 263, 835–853. [Google Scholar] [CrossRef]
- Townsend, R. Fast calculation of the Lomb-Scargle periodogram using graphics processing units. Astrophys. J. Suppl. Ser. 2010, 191, 247. [Google Scholar] [CrossRef] [Green Version]
- Laxon, S.; Peacock, N.; Smith, D. High interannual variability of sea ice thickness in the Arctic region. Nature 2003, 425, 947–950. [Google Scholar] [CrossRef]
- Klein, E.; Duputel, Z.; Zigone, D.; Vigny, C.; Boy, J.P.; Doubre, C.; Meneses, G. Deep transient slow slip detected by survey GPS in the region of Atacama, Chile. Geophys. Res. Lett. 2018, 45, 12–263. [Google Scholar] [CrossRef] [Green Version]
- Tobita, M. Combined logarithmic and exponential function model for fitting postseismic GNSS time series after 2011 Tohoku-Oki earthquake. Earth Planets Space 2016, 68, 41. [Google Scholar] [CrossRef] [Green Version]
- Rosat, S.; Gillet, N.; Boy, J.P.; Couhert, A.; Dumberry, M. Interannual variations of degree 2 from geodetic observations and surface processes. Geophys. J. Int. 2021, 225, 200–221. [Google Scholar]
- Nicolas, J.; Verdun, J.; Boy, J.P.; Bonhomme, L.; Asri, A.; Corbeau, A.; Berthier, A.; Durand, F.; Clarke, P. Improved Hydrological Loading Models in South America: Analysis of GPS Displacements Using M-SSA. Remote Sens. 2021, 13, 1605. [Google Scholar] [CrossRef]
- Nahmani, S.; Bock, O.; Bouin, M.N.; Santamaría-Gómez, A.; Boy, J.P.; Collilieux, X.; Métivier, L.; Panet, I.; Genthon, P.; de Linage, C.; et al. Hydrological deformation induced by the West African Monsoon: Comparison of GPS, GRACE and loading models. J. Geophys. Res. Solid Earth 2012, 117, B05409. [Google Scholar] [CrossRef] [Green Version]
- Williams, S.; Penna, N. Non-tidal ocean loading effects on geodetic GPS heights. Geophys. Res. Lett. 2011, 38, L09314. [Google Scholar] [CrossRef] [Green Version]
- van Dam, T.; Collilieux, X.; Wuite, J.; Altamimi, Z.; Ray, J. Nontidal ocean loading: Amplitudes and potential effects in GPS height time series. J. Geod. 2012, 86, 1043–1057. [Google Scholar] [CrossRef] [Green Version]
- Blewitt, G.; Hammond, W.C.; Kreemer, C. Harnessing the GPS data explosion for interdisciplinary science. EOS 2018, 99, 485. [Google Scholar] [CrossRef]





| MG3 Products | |
|---|---|
| Gravity field | EIGEN-GRGS.RL04.MEAN-FIELD [47] |
| Ocean tides (gravity) | FES2014b (Finite Element Solution) [48] |
| Planet ephemerides | de421bdlf.ad [49] |
| Relativistic acceleration | Schwarzschild and geodetic precession and Lense–Thirring |
| Antex | IGSR3.atx [50] |
| Mean pole (C21/S21) | IERS conventions (from geopotential model) [51] |
| Subdaily EOP model | [52] |
| Atmospheric tides (S1/S2) | [53] |
| Ocean tide loading | FES2014b [48] |
| Centre of mass correction | FES2014b [48] |
| Solid tides (station) | IERS conventions [51] |
| Reference frame | IGS_R3 [IGSMAIL-8026] |
| Galileo ponderation | cm/ 1 m |
| GPS ponderation | mm/ 60 cm |
| GLONASS ponderation | cm/ 2 m |
| cats_d | cats | tiasd | |
|---|---|---|---|
| Draconitic frequencies adjustment | Yes | No | Yes |
| Interannual variation | – | – | polynomials |
| Stochastic model | WH + PL noise | WH + PL noise | WH noise |
| East | North | Up | |
|---|---|---|---|
| cats_d (WH + PL) | |||
| cats_d (PL) | |||
| cats (PL) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michel, A.; Santamaría-Gómez, A.; Boy, J.-P.; Perosanz, F.; Loyer, S. Analysis of GNSS Displacements in Europe and Their Comparison with Hydrological Loading Models. Remote Sens. 2021, 13, 4523. https://doi.org/10.3390/rs13224523
Michel A, Santamaría-Gómez A, Boy J-P, Perosanz F, Loyer S. Analysis of GNSS Displacements in Europe and Their Comparison with Hydrological Loading Models. Remote Sensing. 2021; 13(22):4523. https://doi.org/10.3390/rs13224523
Chicago/Turabian StyleMichel, Alexandre, Alvaro Santamaría-Gómez, Jean-Paul Boy, Félix Perosanz, and Sylvain Loyer. 2021. "Analysis of GNSS Displacements in Europe and Their Comparison with Hydrological Loading Models" Remote Sensing 13, no. 22: 4523. https://doi.org/10.3390/rs13224523
APA StyleMichel, A., Santamaría-Gómez, A., Boy, J.-P., Perosanz, F., & Loyer, S. (2021). Analysis of GNSS Displacements in Europe and Their Comparison with Hydrological Loading Models. Remote Sensing, 13(22), 4523. https://doi.org/10.3390/rs13224523