A SINS/SAR/GPS Fusion Positioning System Based on Sensor Credibility Evaluations
Abstract
:1. Introduction
2. Problem Statement
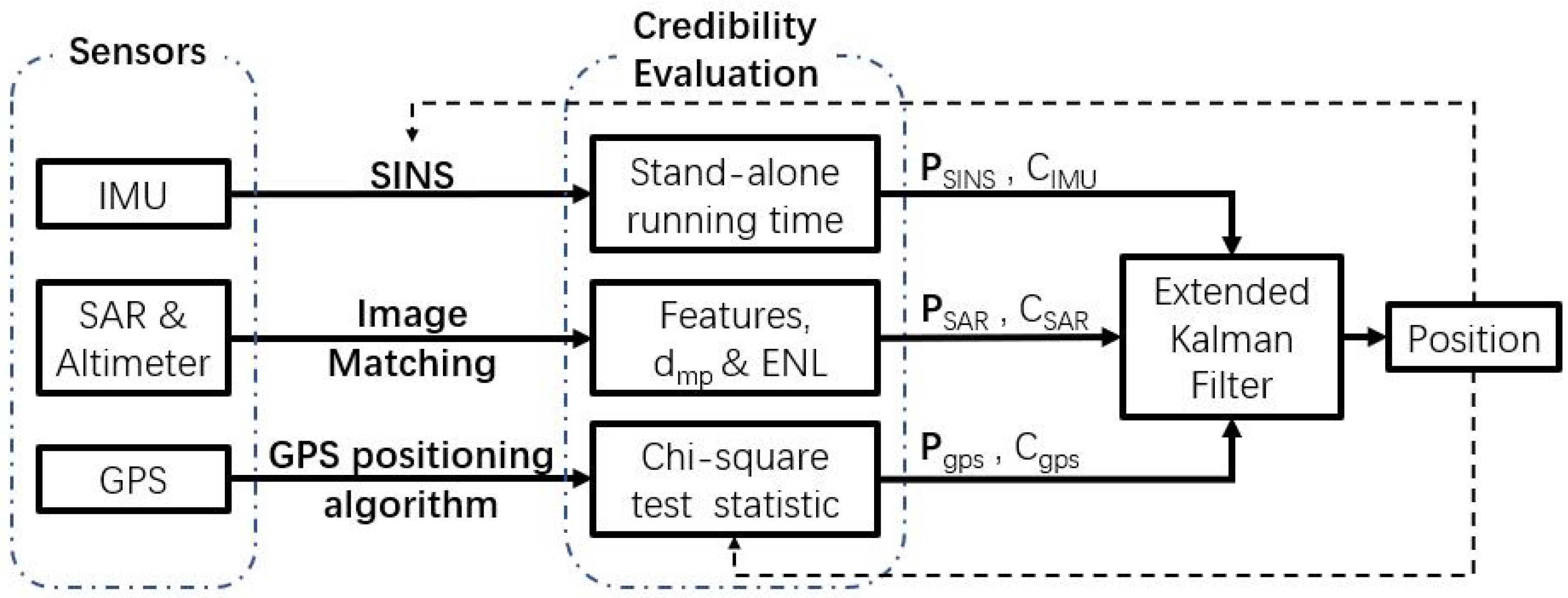
2.1. System Model
2.2. Models of Sensors
2.2.1. IMU
2.2.2. GPS
2.2.3. SAR
2.3. Objective
3. Materials and Methods
3.1. Extended Kalman Filter Estimator
3.1.1. Time Update
3.1.2. Measurement Update
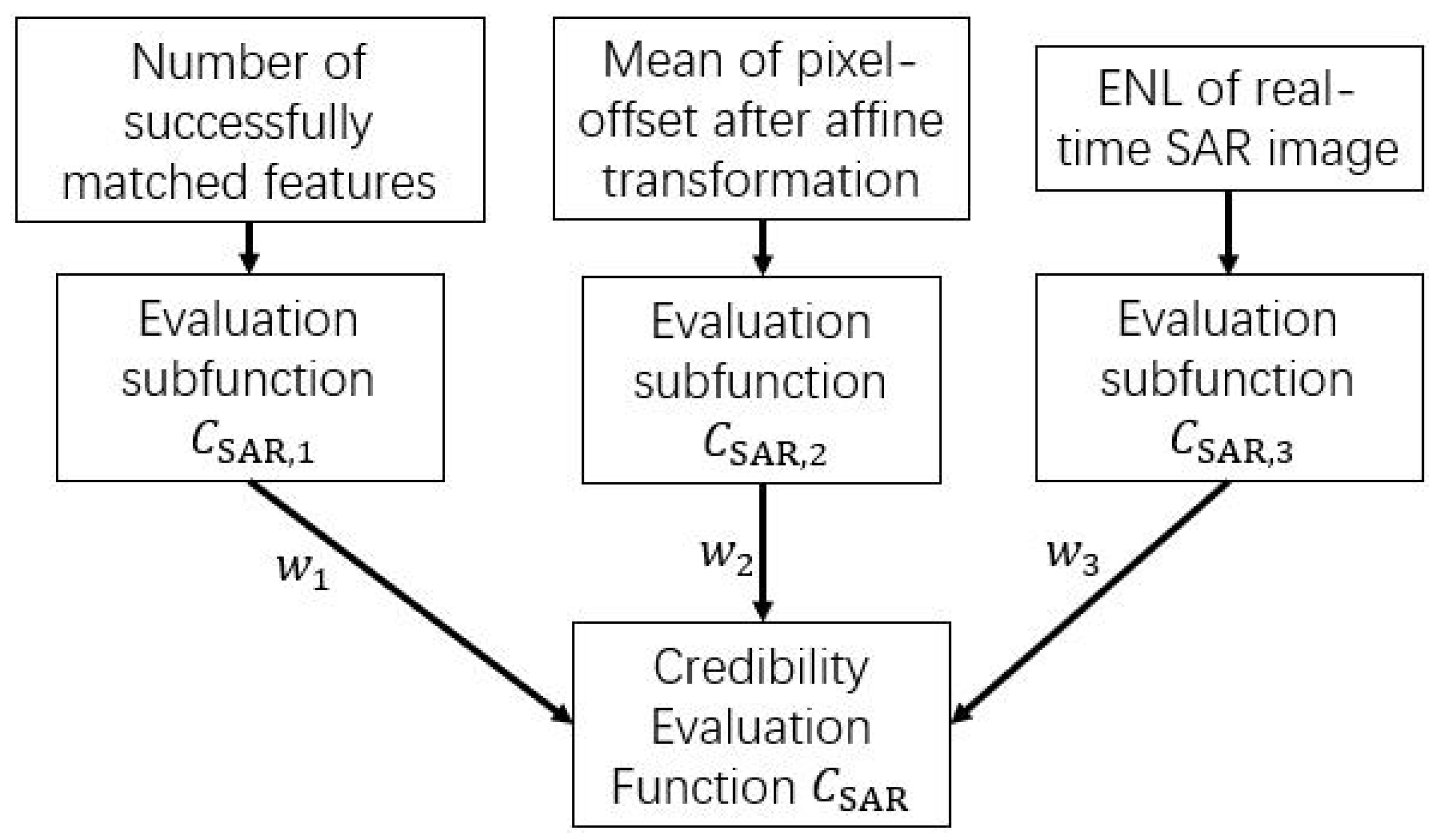
3.2. Sensors’ Credibility Evaluation
3.2.1. IMU
3.2.2. SAR
3.2.3. GPS
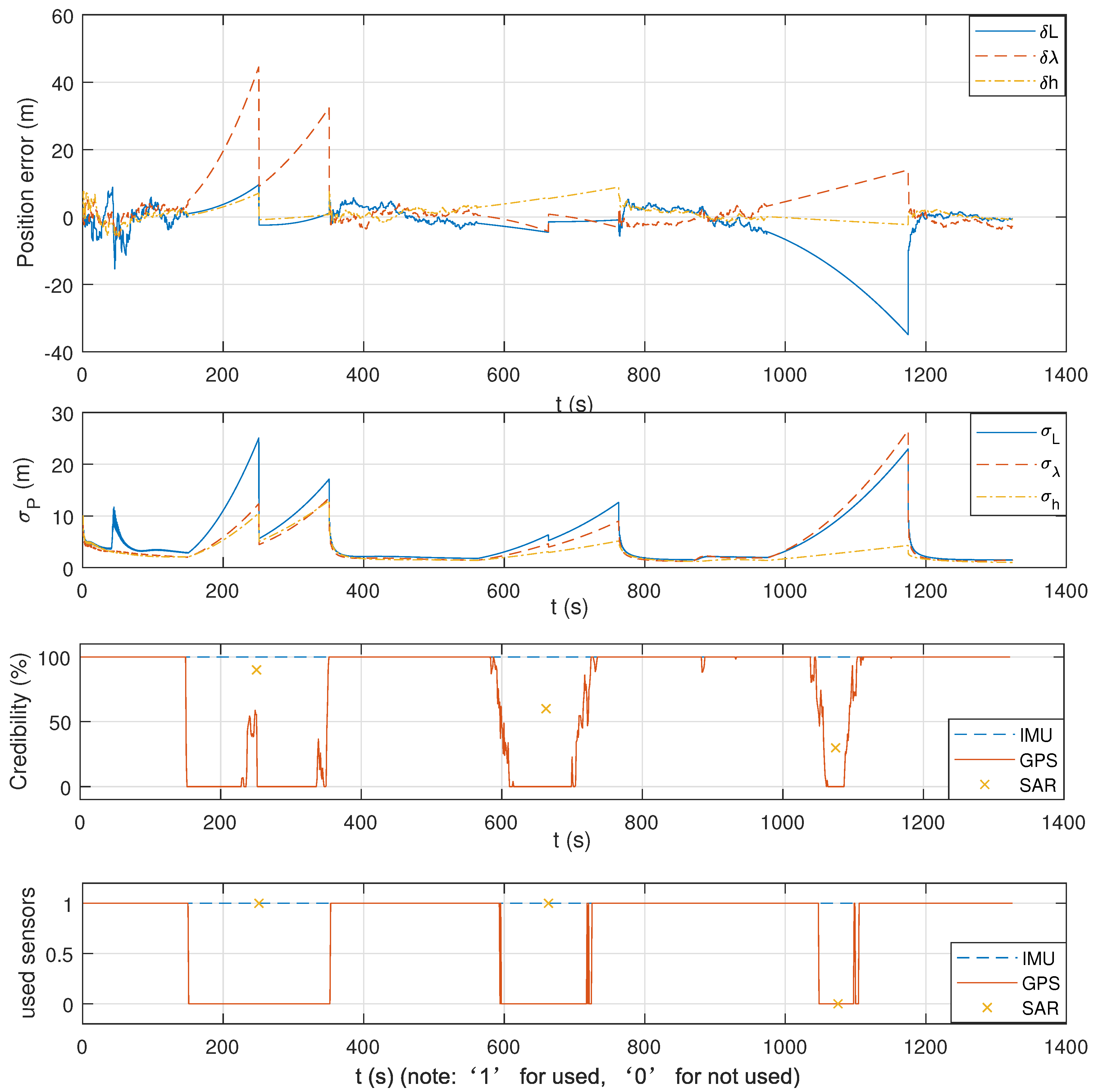
4. Results
4.1. Simulation Verification
4.1.1. Credibility Evaluation for IMU
4.1.2. Credibility Evaluation for SAR Image Matching
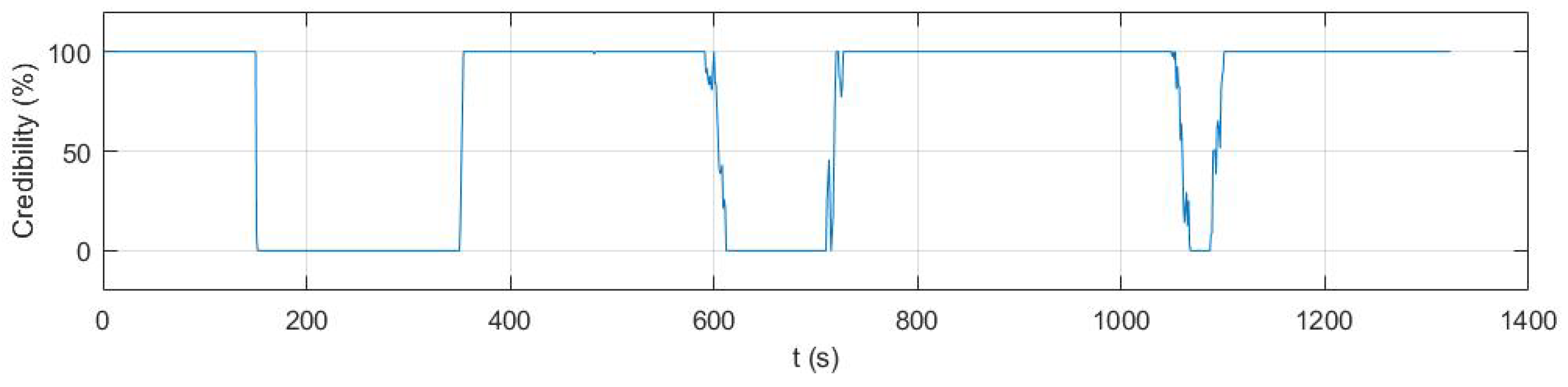
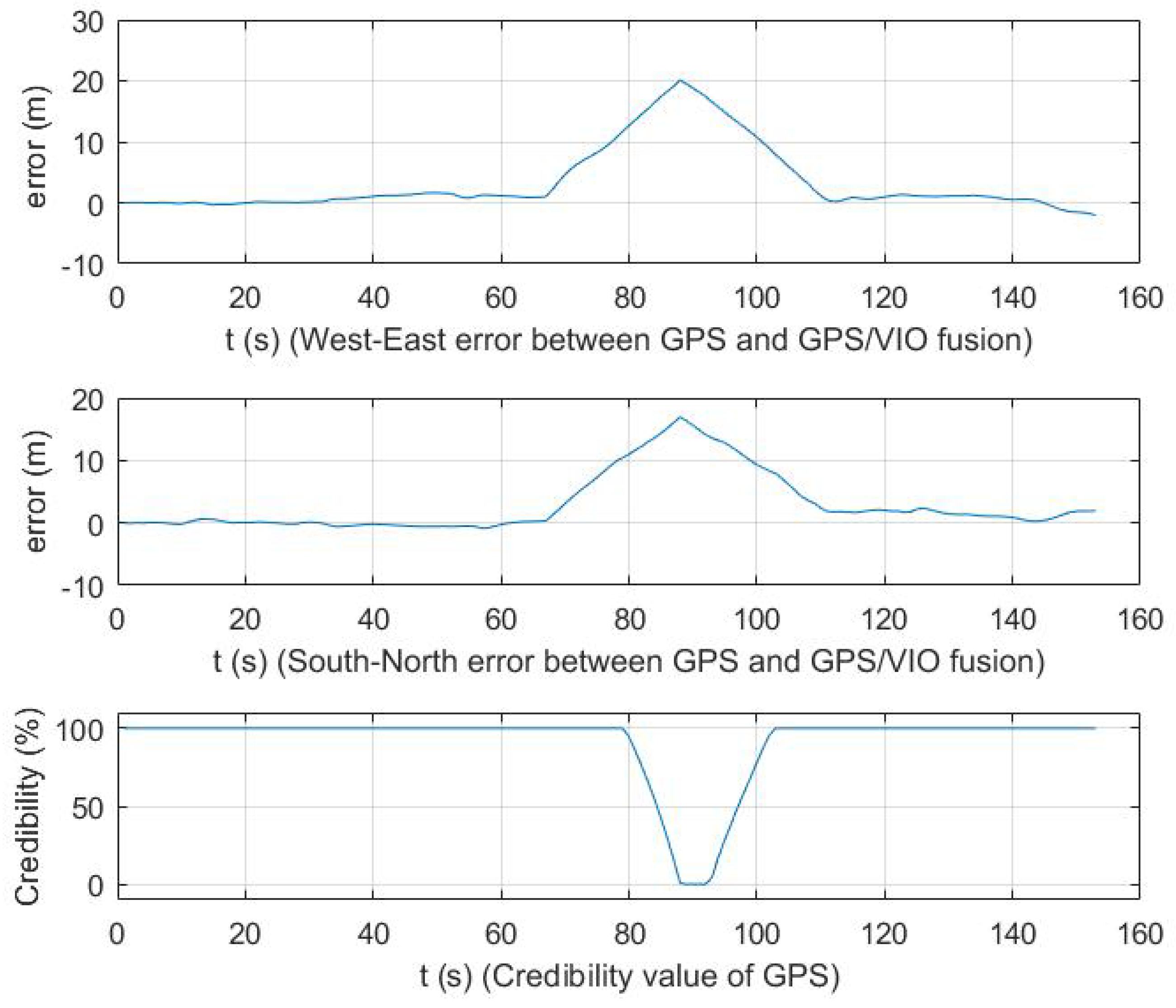
4.1.3. Credibility Evaluation of GPS Measurements
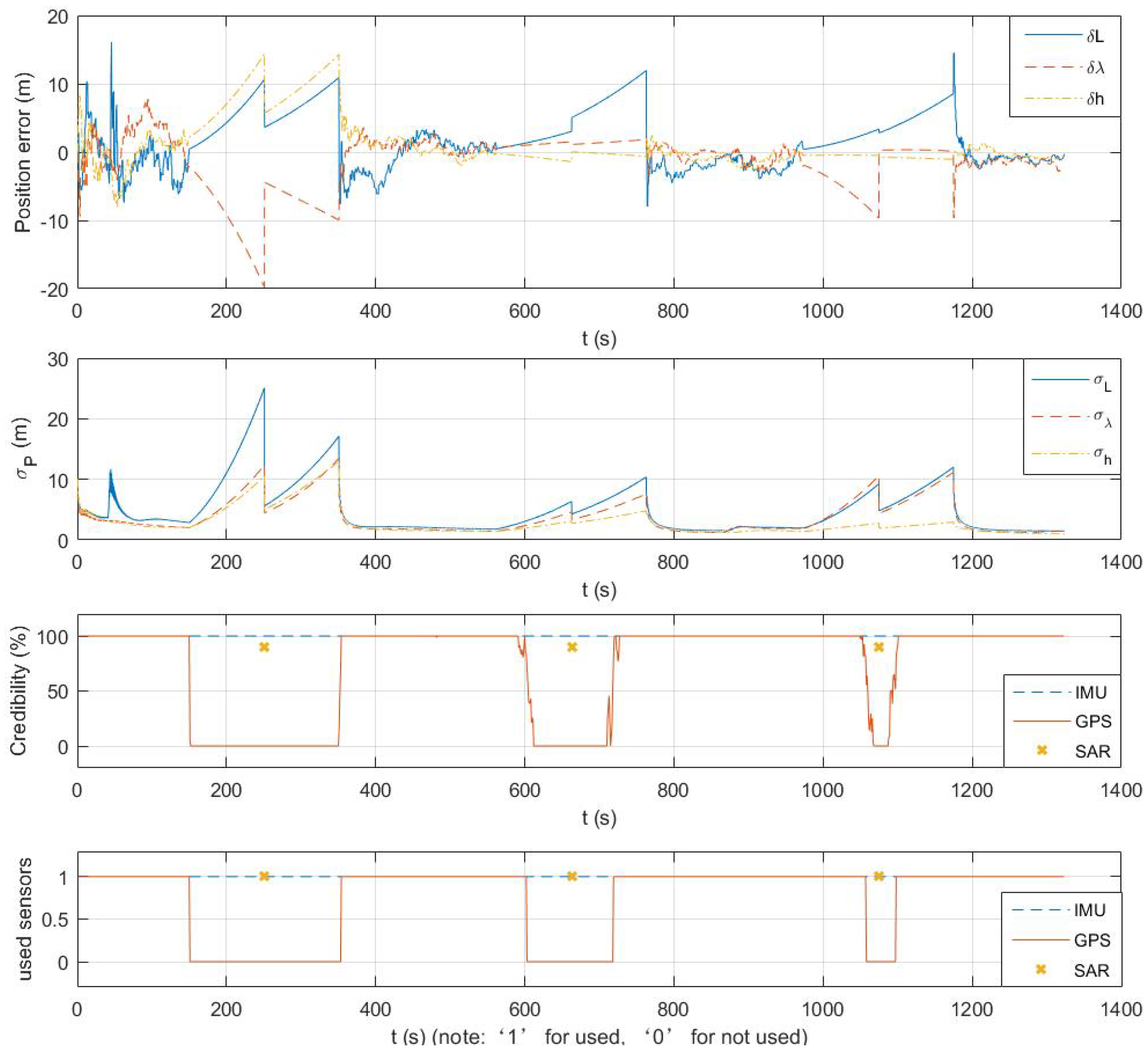
4.1.4. Proposed Estimator Based on Sensors’ Credibility Evaluations
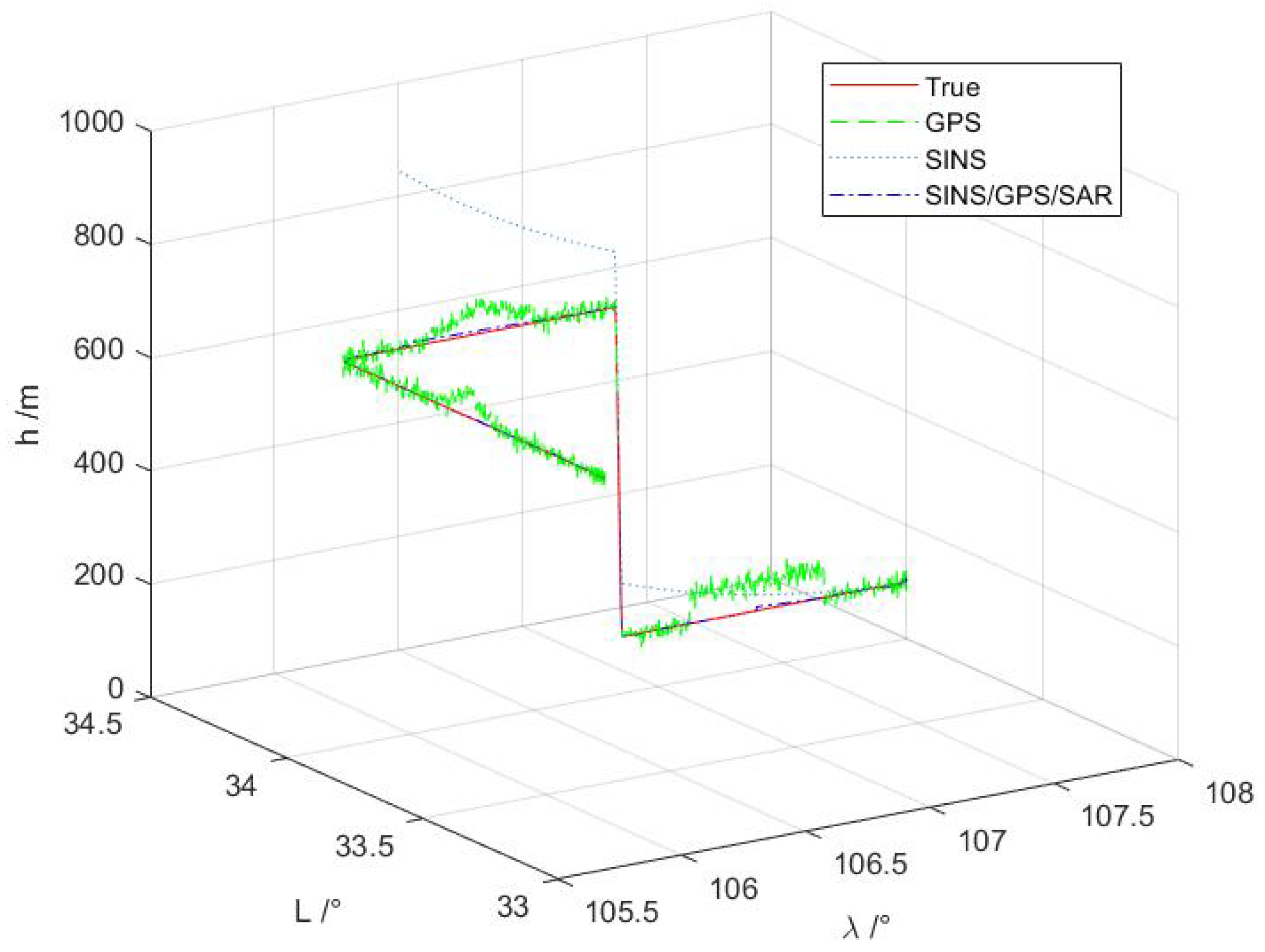
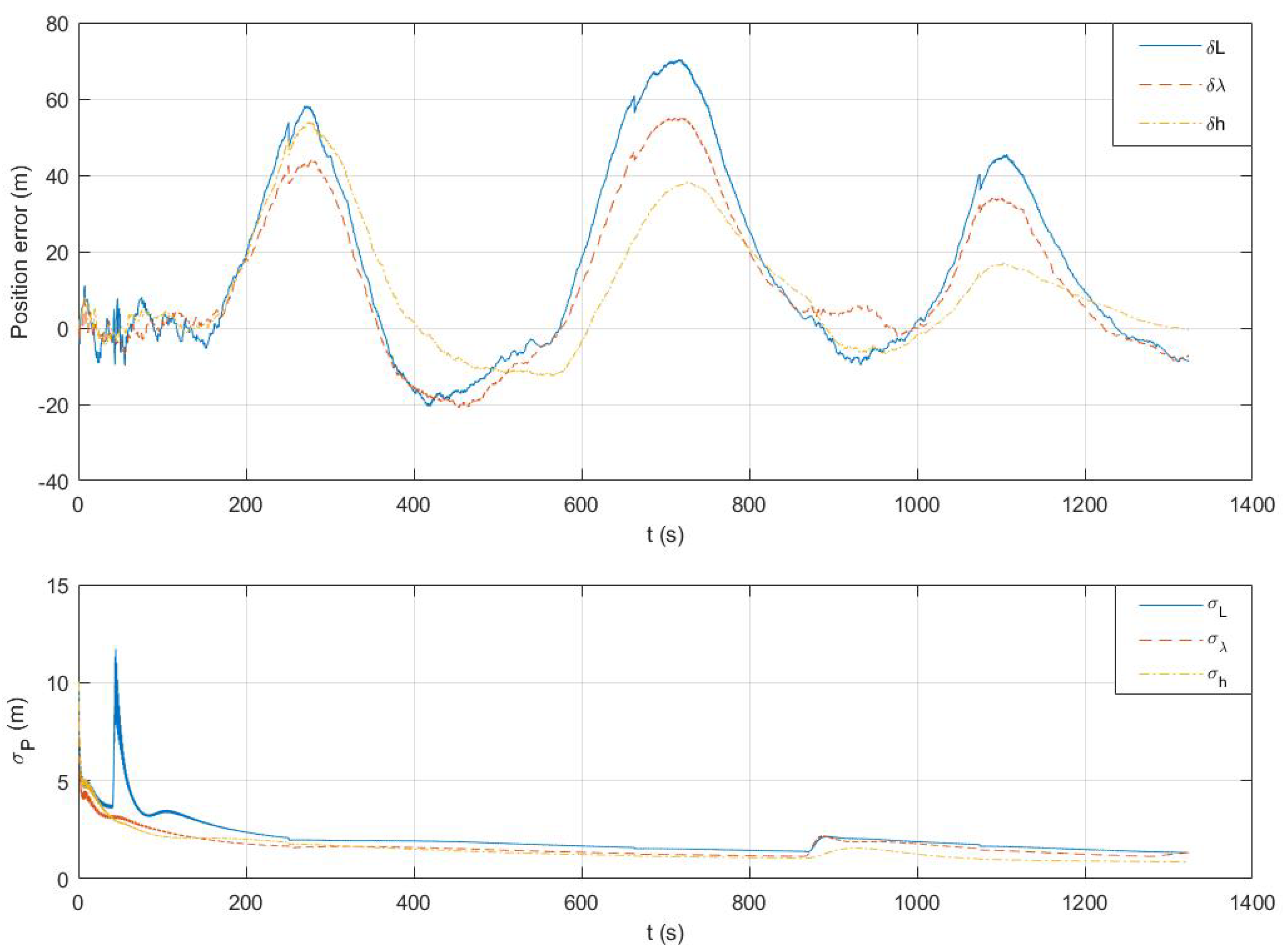
4.2. Experiments
5. Discussion
5.1. Simulations Discussion
5.2. Experiment Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Groves, P.D. Principles of GNSS, inertial, and multisensor integrated navigation systems. IEEE Aerosp. Electron. Syst. Mag. 2015, 30, 26–27. [Google Scholar] [CrossRef]
- Savage, P.G. Strapdown inertial navigation integration algorithm design part 1: Attitude algorithms. J. Guid. Control Dyn. 1998, 21, 19–28. [Google Scholar] [CrossRef]
- Savage, P.G. Strapdown inertial navigation integration algorithm design part 2: Velocity and position algorithms. J. Guid. Control Dyn. 1998, 21, 208–221. [Google Scholar] [CrossRef]
- Gul, F.; Fang, J.; Gaho, A.A. GPS/SINS navigation data fusion using quaternion model and unscented kalman filter. In Proceedings of the 2006 International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 1854–1859. [Google Scholar]
- Wang, D.; Dong, Y.; Li, Z.; Li, Q.; Wu, J. Constrained MEMS-based GNSS/INS tightly-coupled system with robust Kalman filter for accurate land vehicular navigation. IEEE Trans. Instrum. Meas. 2020, 69, 5138–5148. [Google Scholar] [CrossRef]
- Li, D.; Jia, X.; Zhao, J. A novel hybrid fusion algorithm for low-cost GPS/INS integrated navigation system during GPS outages. IEEE Access 2020, 8, 53984–53996. [Google Scholar] [CrossRef]
- Fang, J.; Gong, X. Predictive iterated Kalman filter for INS/GPS integration and its application to SAR motion compensation. IEEE Trans. Instrum. Meas. 2009, 59, 909–915. [Google Scholar] [CrossRef]
- Suri, S.; Schwind, P.; Uhl, J.; Reinartz, P. Modifications in the SIFT operator for effective SAR image matching. Int. J. Image Data Fusion 2010, 1, 243–256. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.; Zhong, Y.; Li, W. Robust adaptive filtering method for SINS/SAR integrated navigation system. Aerosp. Sci. Technol. 2011, 15, 425–430. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.; Zhong, Y.; Zhang, X.; Shirinzadeh, B. Multi-sensor optimal data fusion for INS/GPS/SAR integrated navigation system. Aerosp. Sci. Technol. 2009, 13, 232–237. [Google Scholar] [CrossRef] [Green Version]
- Maier, A.; Kiesel, S.; Trommer, G. Performance analysis of federated filter for SAR/TRN/GPS/INS integration. Gyroscopy Navig. 2011, 2, 293. [Google Scholar] [CrossRef]
- Tanıl, Ç.; Khanafseh, S.; Joerger, M.; Pervan, B. An INS monitor to detect GNSS spoofers capable of tracking vehicle position. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 131–143. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, M.; Tang, K.; Tie, J.; Li, X. Covert spoofing algorithm of UAV based on GPS/INS-integrated navigation. IEEE Trans. Veh. Technol. 2019, 68, 6557–6564. [Google Scholar] [CrossRef]
- Narain, S.; Ranganathan, A.; Noubir, G. Security of GPS/INS based on-road location tracking systems. In Proceedings of the 2019 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2019; pp. 587–601. [Google Scholar]
- Anfinsen, S.N.; Doulgeris, A.P.; Eltoft, T. Estimation of the equivalent number of looks in polarimetric synthetic aperture radar imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3795–3809. [Google Scholar] [CrossRef]
- Sjanic, Z.; Gustafsson, F. Navigation and SAR focusing with map aiding. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1652–1663. [Google Scholar] [CrossRef]
- Yu, Q.; Zhou, S.; Jiang, Y.; Wu, P.; Xu, Y. High-performance SAR image matching using improved sift framework based on rolling guidance filter and ROEWA-Powered feature. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 920–933. [Google Scholar] [CrossRef]
- Rai, A.; Bhateja, V.; Bishnu, A. Speckle suppression and enhancement approaches for processing of SAR images: A technical review. In Smart Intelligent Computing and Applications; Springer: Singapore, 2020; pp. 695–703. [Google Scholar]
- Papazoglou, M.; Tsioras, C. Integrated SAR/GPS/INS for target geolocation improvement. J. Comput. Model 2014, 4, 267–298. [Google Scholar]
- Gao, S.; Xue, L.; Zhong, Y.; Gu, C. Random weighting method for estimation of error characteristics in SINS/GPS/SAR integrated navigation system. Aerosp. Sci. Technol. 2015, 46, 22–29. [Google Scholar] [CrossRef]
- Zhao, Y.; Xiong, Z.; Tian, S.; Liu, J.; Cui, Y. INS/SAR adaptive kalman filtering algorithm based on credibility evaluation of SAR image matching results. Acta Aeronaut. Astronaut. Sin. 2019, 40, 211–222. [Google Scholar]
- Reza, A.M. Realization of the contrast limited adaptive histogram equalization (CLAHE) for real-time image enhancement. J. VLSI Signal Process. Syst. Signal Image Video Technol. 2004, 38, 35–44. [Google Scholar] [CrossRef]
- Derpanis, K.G. Overview of the RANSAC Algorithm. Image Rochester NY 2010, 4, 2–3. [Google Scholar]
- Hughes, L.H.; Schmitt, M. A semi-supervised approach to sar-optical image matching. In Proceedings of the ISPRS Annals of Photogrammetry, Remote Sensing & Spatial Information Sciences, Munich, Germany, 18–20 September 2019; Volume 4. [Google Scholar]
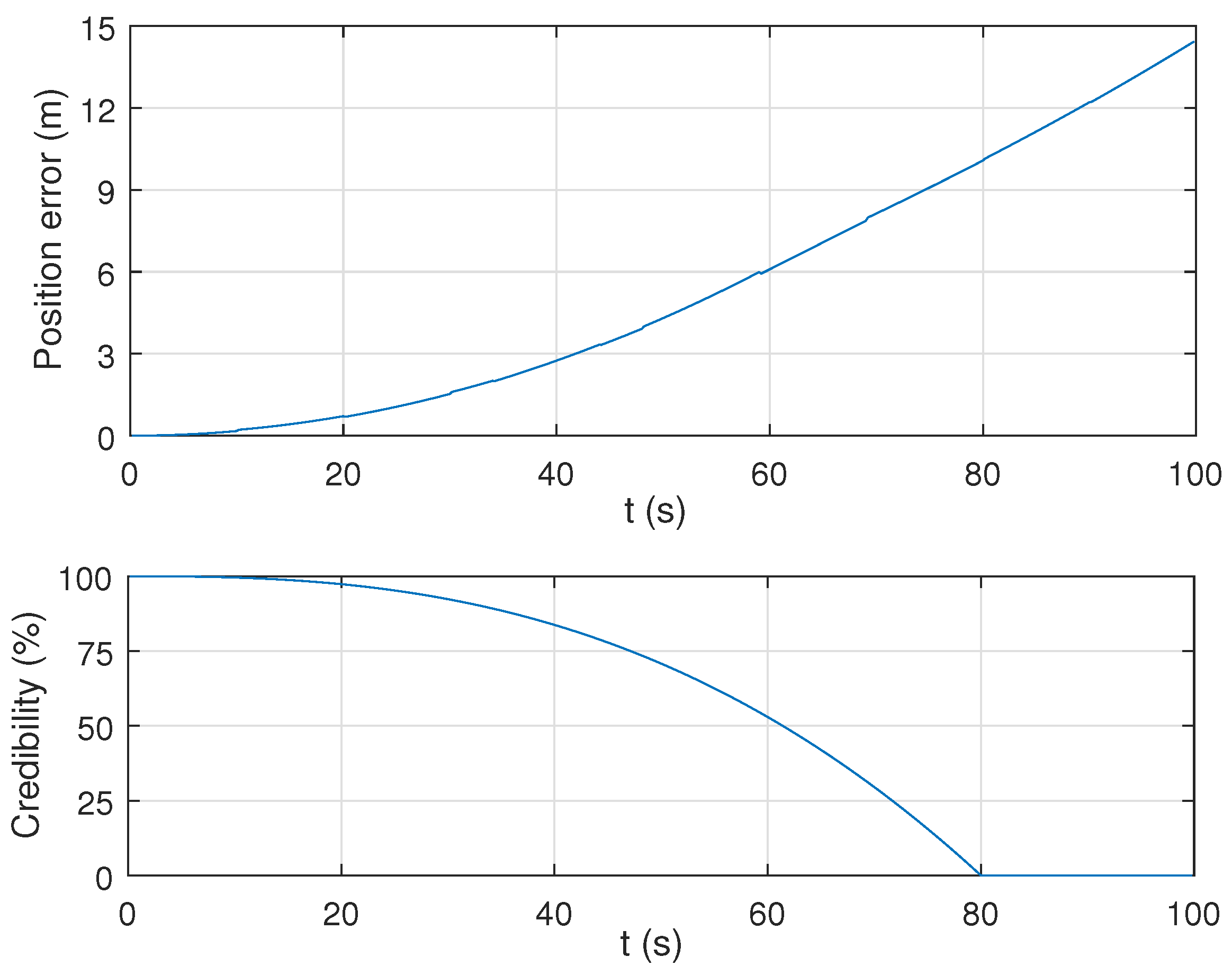






| Algorithm | Mean of Pixel-Offset | ENL | Number of Features | Credibility |
|---|---|---|---|---|
| SIFT | 2.28 | 4.17 | 10 | 89.6% |
| SURF | 2.93 | 4.17 | 9 | 81.3% |
| Algorithm | Mean of Pixel-Offset | ENL | Number of Features | Credibility |
|---|---|---|---|---|
| SIFT | 3.37 | 4.02 | 9 | 80.3% |
| SURF | 4.16 | 4.02 | 8 | 71.7% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, M.; Liu, J.; Meng, Z.; You, Z. A SINS/SAR/GPS Fusion Positioning System Based on Sensor Credibility Evaluations. Remote Sens. 2021, 13, 4463. https://doi.org/10.3390/rs13214463
Liao M, Liu J, Meng Z, You Z. A SINS/SAR/GPS Fusion Positioning System Based on Sensor Credibility Evaluations. Remote Sensing. 2021; 13(21):4463. https://doi.org/10.3390/rs13214463
Chicago/Turabian StyleLiao, Maoyou, Jiacheng Liu, Ziyang Meng, and Zheng You. 2021. "A SINS/SAR/GPS Fusion Positioning System Based on Sensor Credibility Evaluations" Remote Sensing 13, no. 21: 4463. https://doi.org/10.3390/rs13214463
APA StyleLiao, M., Liu, J., Meng, Z., & You, Z. (2021). A SINS/SAR/GPS Fusion Positioning System Based on Sensor Credibility Evaluations. Remote Sensing, 13(21), 4463. https://doi.org/10.3390/rs13214463







