Deep/Transfer Learning with Feature Space Ensemble Networks (FeatSpaceEnsNets) and Average Ensemble Networks (AvgEnsNets) for Change Detection Using DInSAR Sentinel-1 and Optical Sentinel-2 Satellite Data Fusion
Abstract
:1. Introduction
1.1. Deep Learning
1.2. Transfer Learning
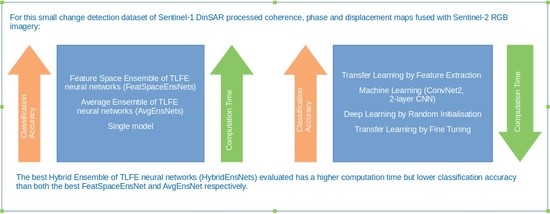
1.3. Aim and Contribution
2. Materials and Methods
2.1. Baseline Machine Learning Methods
2.1.1. Linear SVM and Radial Basis Function (RBF) SVM
2.1.2. Random Forest (RF) and Multi-Layer Perceptron (MLP) Neural Network
2.1.3. ConvNet2: Two Layer Convolutional Neural Network
2.2. Deep and Transfer Learning Methods
2.2.1. Deep Learning and Transfer Learning using Fine-Tuning (TLFT)
2.2.2. Transfer Learning by Feature Extraction (TLFE)
2.3. Ensemble Methods
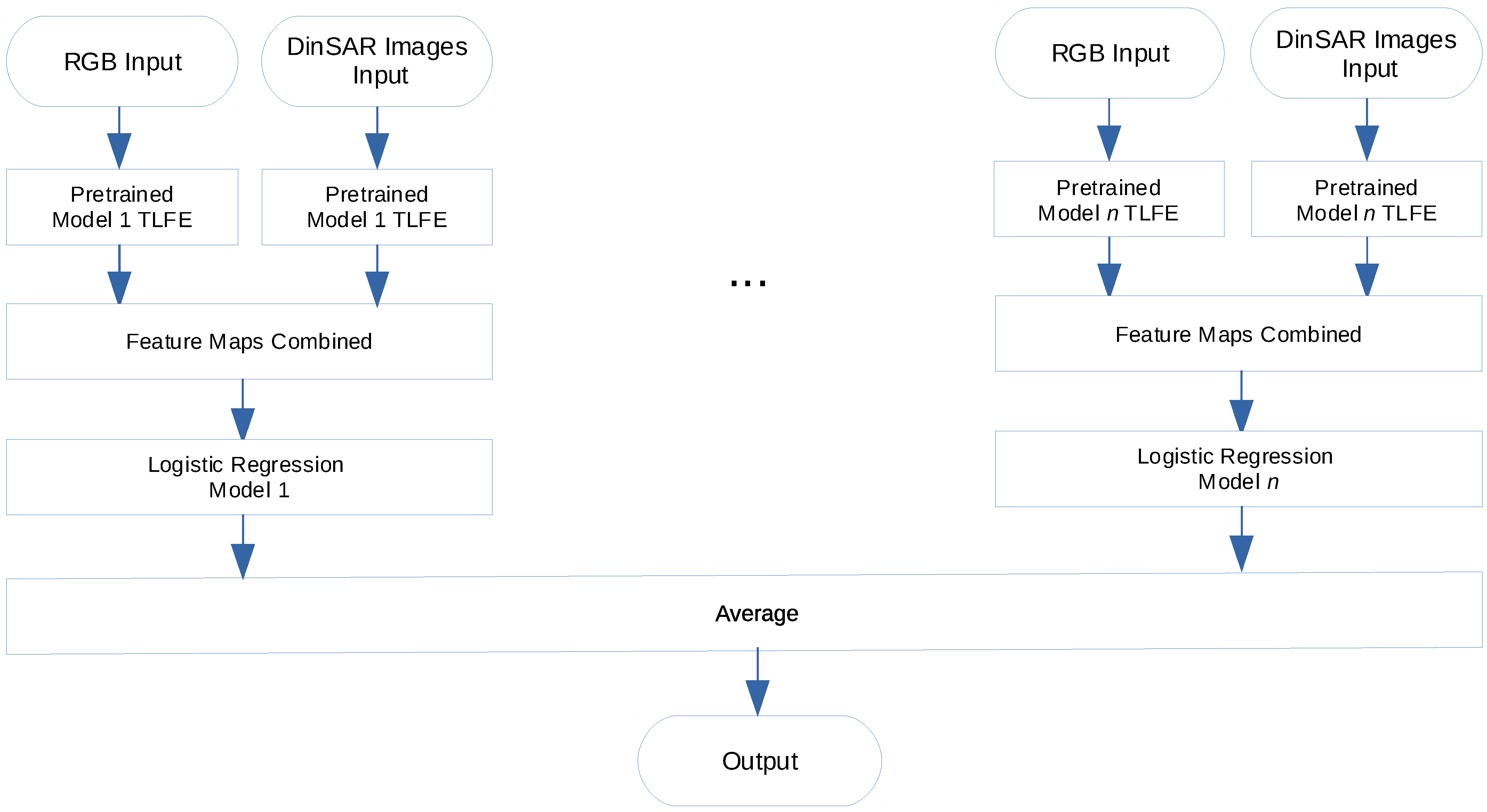
2.3.1. Feature Space Ensemble Networks (FeatSpaceEnsNets)
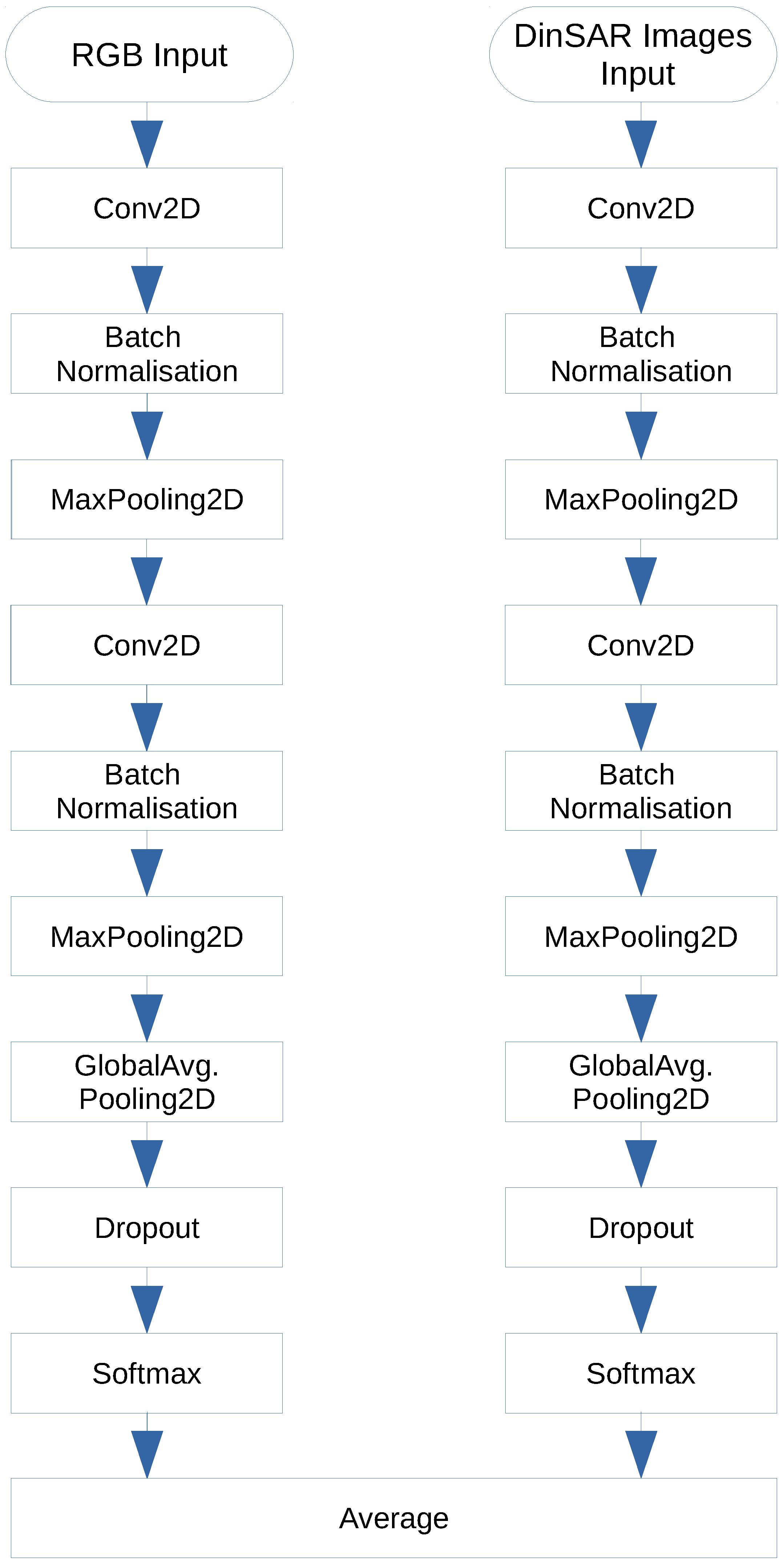
2.3.2. Average Ensemble Networks (AvgEnsNets)
2.3.3. Hybrid Ensemble Networks (HybridEnsNets)
2.4. Analysis of Methods
2.5. Data
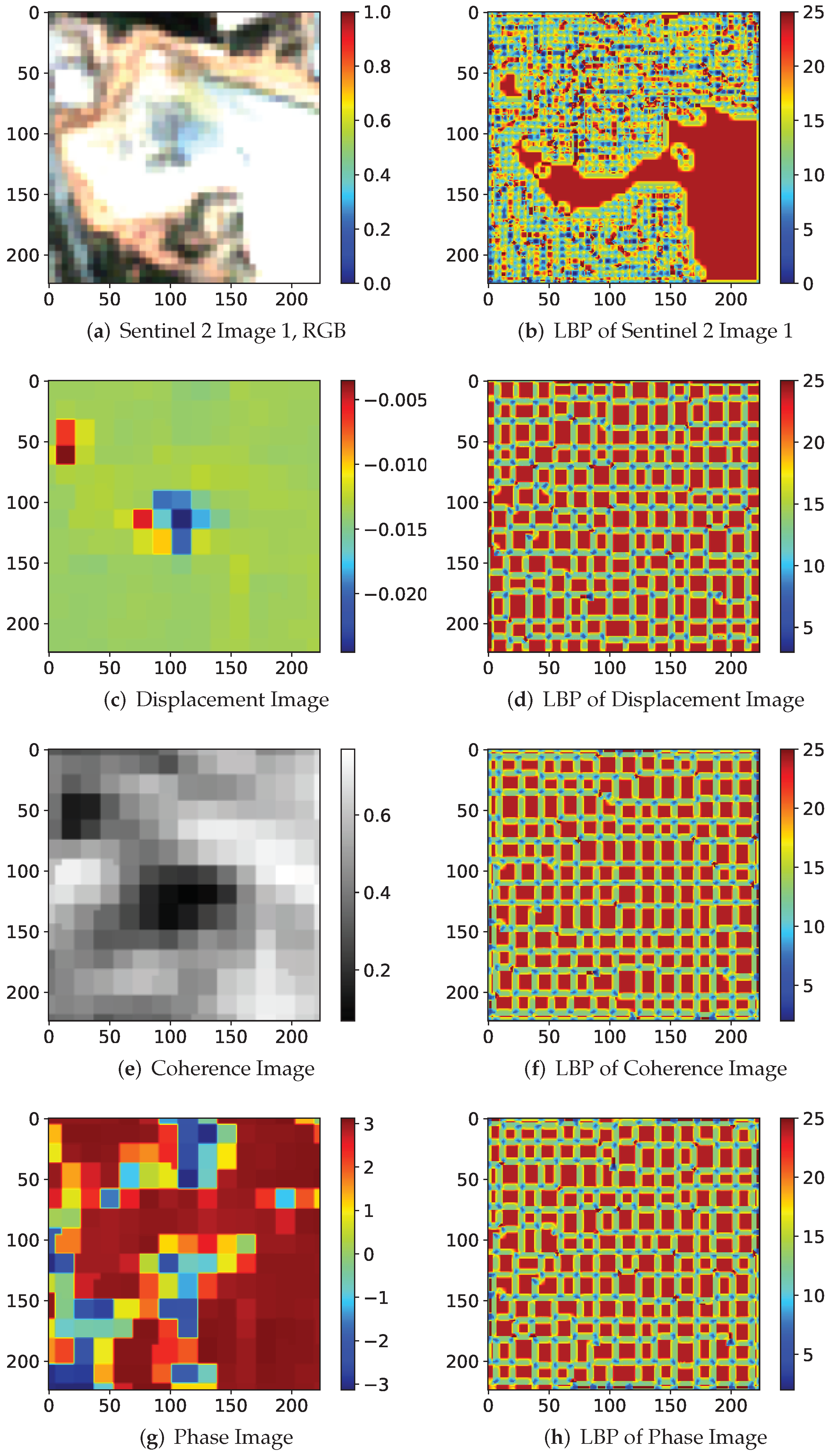
2.6. Data Preprocessing
LBP and HOG Feature Descriptors
2.7. Experimental Design
3. Results
3.1. Candidate Selection
3.1.1. True-Positive Blobs
3.1.2. False-Positive Blobs
3.2. Binary Classification
3.3. Effect of Varying Cross-Validation Folds
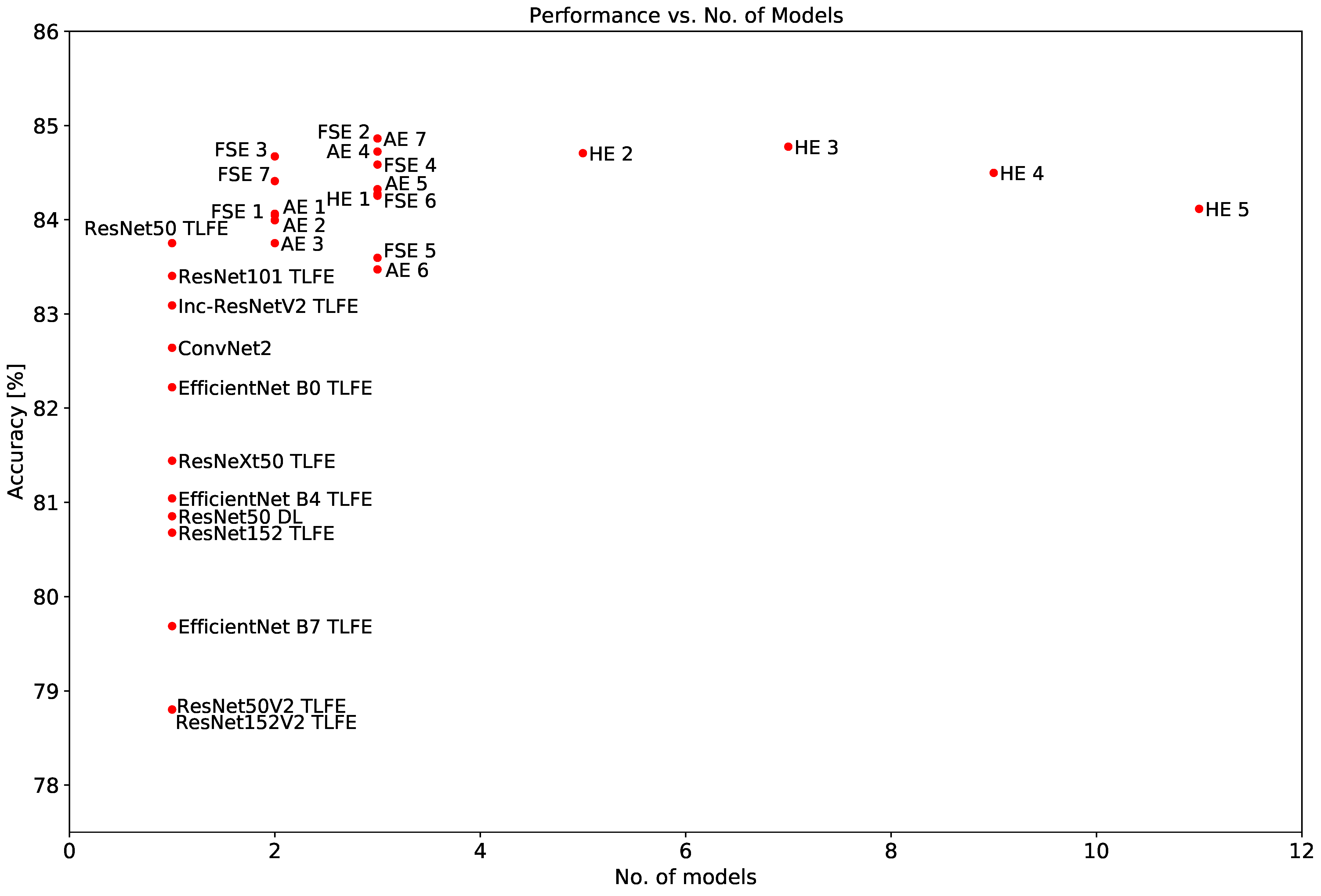
3.4. Visualization of Results
4. Discussion
4.1. Non-Deep Machine Learning: LBP and HOG with Linear SVM, Radial Basis Function (RBF) SVM, Random Forest (RF), and Multi-Layer Perceptron (MLP) Neural Network
4.2. ConvNet2
4.3. Transfer Learning by Feature Extraction
4.4. Transfer Learning by Fine-Tuning and Deep Learning from Random Initialization
4.5. Limitations
4.6. Complexity of the Different Approaches
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DLRI | deep learning random initialization |
| TL | transfer learning |
| FE | feature extraction |
| FT | fine-tuning |
| CNN | convolutional neural network |
| DNN | deep neural network |
| TLFE | transfer learning by feature extraction |
| TLFT | transfer learning by fine-tuning |
| ResNet | Deep Residual Network |
| ResNet50 | 50-layer Deep Residual Network Version 1 |
| ResNet101 | 101-layer Deep Residual Network Version 1 |
| ResNet152 | 152-layer Deep Residual Network Version 1 |
| ResNet50V2 | 50-layer Deep Residual Network Version 2 |
| ResNet152V2 | 152-layer Deep Residual Network Version 2 |
| EfficientNet | efficient network |
| FeatSpaceEnsNet | Feature Space Ensemble of transfer learning by feature extraction neural networks |
| FSE | feature space ensemble of transfer learning by feature extraction neural networks |
| AvgEnsNet | average ensemble of transfer learning by feature extraction neural networks |
| AE | average ensemble of transfer learning by feature extraction neural networks |
| HybridEnsNet | hybrid ensemble of transfer learning by feature extraction neural networks |
| HE | hybrid ensemble of transfer learning by feature extraction neural networks |
| HOG | histogram of oriented gradients |
| LBP | local binary pattern |
| SVM | linear support vector machine |
| RBF-SVM | radial basis function support vector machine |
| RF | random forest |
| MLP | multi-layer perceptron |
References
- Karim, Z.; van Zyl, T. Deep Learning and Transfer Learning applied to Sentinel-1 DInSAR and Sentinel-2 optical satellite imagery for change detection. In Proceedings of the 2020 International SAUPEC/RobMech/PRASA Conference, Cape Town, South Africa, 29–31 January 2020; pp. 579–585. [Google Scholar] [CrossRef]
- Sentinel-1 Team. Sentinel-1 User Handbook; ESA Publications: Noordwijk, The Netherlands, 2013. [Google Scholar]
- Ferretti, A.; Monti-Guarnieri, A.; Prati, C.; Rocca, F. InSAR Principles: Guidelines for SAR Interferometry Processing and Interpretation, TM–19; ESA Publications: Noordwijk, The Netherlands, 2007. [Google Scholar]
- Karim, Z.; van Zyl, T. Research Report: Industrial Change Detection Using Deep Learning Applied to DInSAR and Optical Satellite Imagery; University of the Witwatersrand: Johannesburg, South Africa, 2020. [Google Scholar]
- Van Zyl, T.L.; Celik, T. Did We Produce More Waste During the COVID-19 Lockdowns? A Remote Sensing Approach to Landfill Change Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7349–7358. [Google Scholar] [CrossRef]
- Khalil, R.Z.; ul Haque, S. InSAR coherence-based land cover classification of Okara, Pakistan. EJRS Special Issue: Microwave Remote Sensing in honor of Professor Adel Yehia. Egypt. J. Remote Sens. Space Sci. 2018, 21, S23–S28. [Google Scholar] [CrossRef]
- Corradino, C.; Ganci, G.; Cappello, A.; Bilotta, G.; Hérault, A.; Del Negro, C. Mapping Recent Lava Flows at Mount Etna Using Multispectral Sentinel-2 Images and Machine Learning Techniques. Remote Sens. 2019, 11, 1916. [Google Scholar] [CrossRef] [Green Version]
- Van Tricht, K.; Gobin, A.; Gilliams, S.; Piccard, I. Synergistic Use of Radar Sentinel-1 and Optical Sentinel-2 Imagery for Crop Mapping: A Case Study for Belgium. Remote Sens. 2018, 10, 1642. [Google Scholar] [CrossRef] [Green Version]
- Gašparović, M.; Klobučar, D. Mapping Floods in Lowland Forest Using Sentinel-1 and Sentinel-2 Data and an Object-Based Approach. Forests 2021, 12, 553. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; ISBN 9780262035613. [Google Scholar]
- Papadomanolaki, M.; Verma, S.; Vakalopoulou, M.; Gupta, S.; Karantzalos, K. Detecting Urban Changes with Recurrent Neural Networks from Multitemporal Sentinel-2 Data. arXiv 2019, arXiv:1910.07778. [Google Scholar]
- Saha, S.; Solano-Correa, Y.T.; Bovolo, F.; Bruzzone, L. Unsupervised deep learning based change detection in Sentinel-2 images. In Proceedings of the 2019 10th International Workshop on the Analysis of Multitemporal Remote Sensing Images (MultiTemp), Shanghai, China, 5–7 August 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Ienco, D.; Interdonato, R.; Gaetano, R.; Ho Tong Minh, D. Combining Sentinel-1 and Sentinel-2 Satellite Image Time Series for land cover mapping via a multi-source deep learning architecture. ISPRS J. Photogramm. Remote Sens. 2019, 158, 11–22. [Google Scholar] [CrossRef]
- Gargiulo, M.; Dell’Aglio, D.A.G.; Iodice, A.; Riccio, D.; Ruello, G. Integration of Sentinel-1 and Sentinel-2 Data for Land Cover Mapping Using W-Net. Sensors 2020, 20, 2969. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Wauthier, C.; Stephens, K.; Gervais, M.; Cervone, G.; La Femina, P.; Higgins, M. Automatic Detection of Volcanic Surface Deformation Using Deep Learning. J. Geophys. Res. 2020, 125, e2020JB019840. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Kornblith, S.; Shlens, J.; Le, Q.V. Do Better ImageNet Models Transfer Better? arXiv 2018, arXiv:1805.08974. [Google Scholar]
- Pomente, A.; Picchiani, M.; Del Frate, F. Sentinel-2 Change Detection Based on Deep Features. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Vannes, France, 22–24 May 2018; pp. 6859–6862. [Google Scholar] [CrossRef]
- Qiu, C.; Schmitt, M.; Taubenböck, H.; Zhu, X.X. Mapping Human Settlements with Multi-seasonal Sentinel-2 Imagery and Attention-based ResNeXt. In Proceedings of the 2019 Joint Urban Remote Sensing Event (JURSE), Vannes, France, 22–24 May 2019; pp. 1–4. [Google Scholar] [CrossRef] [Green Version]
- Helber, P.; Bischke, B.; Dengel, A.; Borth, D. EuroSAT: A Novel Dataset and Deep Learning Benchmark for Land Use and Land Cover Classification. arXiv 2017, arXiv:1709.00029. [Google Scholar]
- Wang, C.; Mouche, A.; Tandeo, P.; Stopa, J.; Chapron, B.; Foster, R.; Vandemark, D. Automated Geophysical Classification of Sentinel-1 Wave Mode SAR Images Through Deep-Learning. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Vannes, France, 22–24 May 2018; pp. 1776–1779. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Zhang, H. Combining single shot multibox detector with transfer learning for ship detection using Sentinel-1 images. In Proceedings of the 2017 SAR in Big Data Era: Models, Methods and Applications (BIGSARDATA), Beijing, China, 13–14 November 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Anantrasirichai, N.; Biggs, J.; Albino, F.; Hill, P.; Bull, D. Application of Machine Learning to Classification of Volcanic Deformation in Routinely Generated InSAR Data. J. Geophys. Res. Solid Earth 2018, 123. [Google Scholar] [CrossRef] [Green Version]
- Anantrasirichai, N.; Biggs, J.; Kelevitz, K.; Sadeghi, Z.; Wright, T.; Thompson, J.; Achim, A.; Bull, D. Detecting Ground Deformation in the Built Environment Using Sparse Satellite InSAR Data With a Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2940–2950. [Google Scholar] [CrossRef]
- Brengman, C.M.J.; Barnhart, W.D. Identification of Surface Deformation in InSAR Using Machine Learning. J. Geochem. Geophys. Geosystems 2021, 123. [Google Scholar] [CrossRef]
- Opitz, D.; Maclin, R. Popular ensemble methods: An empirical study. J. Artif. Intell. Res. 1999, 11, 169–198. [Google Scholar] [CrossRef]
- Van Zyl, T.L. Machine Learning on Geospatial Big Data. In Big Data: Techniques and Technologies in Geoinformatics; CRC Press: Boca Raton, FL, USA, 2014; p. 133. [Google Scholar]
- Python Software Foundation. Python. Available online: https://www.python.org/ (accessed on 7 September 2021).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. scikit-image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Ho, T.K. Random Decision Forests. In Proceedings of the Third International Conference on Document Analysis and Recognition, ICDAR ’95, Montreal, QC, Canada, 14–16 August 1995; p. 278. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, T.M. Machine Learning; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network In Network. arXiv 2014, arXiv:1312.4400. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Keras. Available online: https://keras.io/ (accessed on 7 September 2021).
- Chollet, F. Deep Learning with Python; Manning Publications: Shelter Island, NY, USA, 2017. [Google Scholar]
- Razavian, A.S.; Azizpour, H.; Sullivan, J.; Carlsson, S. CNN Features off-the-shelf: An Astounding Baseline for Recognition. arXiv 2014, arXiv:1403.6382. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Chu, B.; Madhavan, V.; Beijbom, O.; Hoffman, J.; Darrell, T. Best Practices for Fine-Tuning Visual Classifiers to New Domains. Computer Vision—ECCV 2016 Workshops; Hua, G., Jégou, H., Eds.; Springer: Cham, Switzerland, 2016; pp. 435–442. [Google Scholar]
- Clemen, R.T. Combining forecasts: A review and annotated bibliography. Int. J. Forecast. 1989, 5, 559–583. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Oni, O.O.; van Zyl, T.L. A Comparative Study of Ensemble Approaches to Fact-Checking for the FEVER Shared Task. In Proceedings of the 2020 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE), Gold Coast, Australia, 16–18 December 2020; pp. 1–8. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity Mappings in Deep Residual Networks. arXiv 2016, arXiv:1603.05027. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–15 June 2015; pp. 1–9. [Google Scholar] [CrossRef] [Green Version]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. arXiv 2016, arXiv:1602.07261. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated Residual Transformations for Deep Neural Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5987–5995. [Google Scholar] [CrossRef] [Green Version]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. arXiv 2016, arXiv:1905.11946. [Google Scholar]
- European Space Agency. Copernicus Open Access Hub. Available online: https://scihub.copernicus.eu/dhus/#/home (accessed on 30 November 2018).
- European Space Agency Sentinel Online. Sentinel-2. Available online: https://sentinel.esa.int/web/sentinel/missions/sentinel-2 (accessed on 30 November 2018).
- Veci, L. Sentinel-1 Toolbox TOPS Interferometry Tutorial; Array Systems Computing Inc.: Toronto, ON, Canada, 2015. [Google Scholar]
- RUS Copernicus Training. RUS Webinar: Land Subsidence mapping with Sentinel-1—HAZA03, Video. Available online: https://www.youtube.com/watch?v=w6ilV74r2RQ (accessed on 30 November 2018).
- RUSCopernicus Training. RUS Webinar: Land Subsidence mapping with Sentinel-1—HAZA03. Available online: https://rus-copernicus.eu/portal/wp-content/uploads/library/education/training/HAZA03_LandSubsidence_MexicoCity_Tutorial.pdf (accessed on 30 November 2018).
- European Space Agency Science Toolbox Exploitation Platform. SNAP. Available online: http://step.esa.int/main/toolboxes/snap/ (accessed on 30 November 2018).
- Stanford Radar Interferometry Research Group. SNAPHU: Statistical-Cost, Network-Flow Algorithm for Phase Unwrapping. Available online: https://web.stanford.edu/group/radar/softwareandlinks/sw/snaphu/ (accessed on 7 December 2020).
- European Space Agency. Sen2Cor. Available online: https://step.esa.int/main/third-party-plugins-2/sen2cor/ (accessed on 7 December 2020).
- Scikit-Image Development Team. Blob Detection. Available online: http://scikit-image.org/docs/dev/auto_examples/features_detection/plot_blob.html (accessed on 30 November 2018).
- OSGeo Project. Geospatial Data Abstraction Library. Available online: https://www.gdal.org (accessed on 7 December 2020).
- Google. Google Earth. Available online: https://earth.google.com (accessed on 7 December 2020).
- Price, S. Computer Vision, Models, Learning and Inference; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of Oriented Gradients for Human Detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; pp. 886–893. [Google Scholar] [CrossRef] [Green Version]
- Scikit-Image Development Team. Histogram of Oriented Gradients. Available online: https://scikit-image.org/docs/dev/autoexamples/featuresdetection/plothog.html (accessed on 31 October 2020).
- Flach, P.; Kull, M. Precision-Recall-Gain Curves: PR Analysis Done Right. In Advances in Neural Information Processing Systems 28; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2015; pp. 838–846. [Google Scholar]
- Drzewiecki, W. Thorough statistical comparison of machine learning regression models and their ensembles for sub-pixel imperviousness and imperviousness change mapping. Geod. Cartogr. 2017, 66, 171–209. [Google Scholar] [CrossRef]

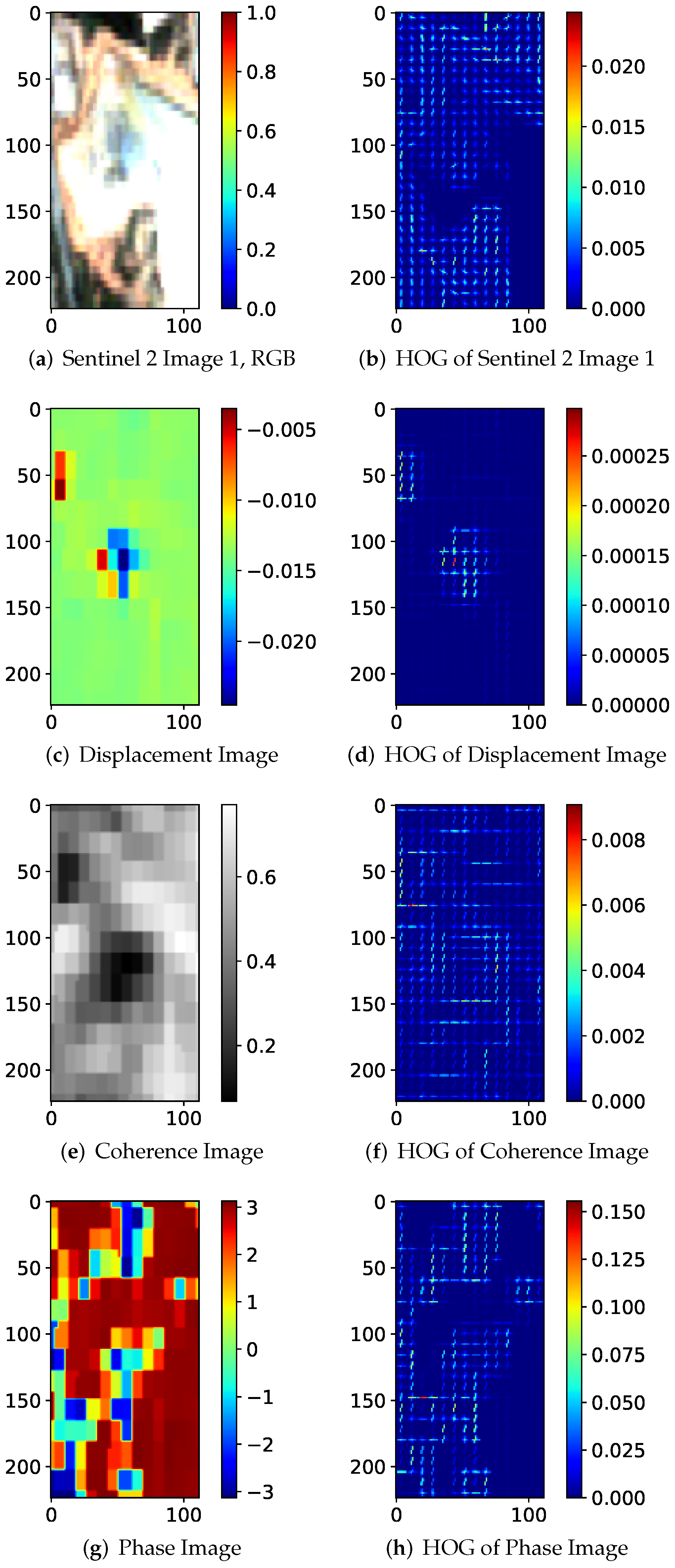
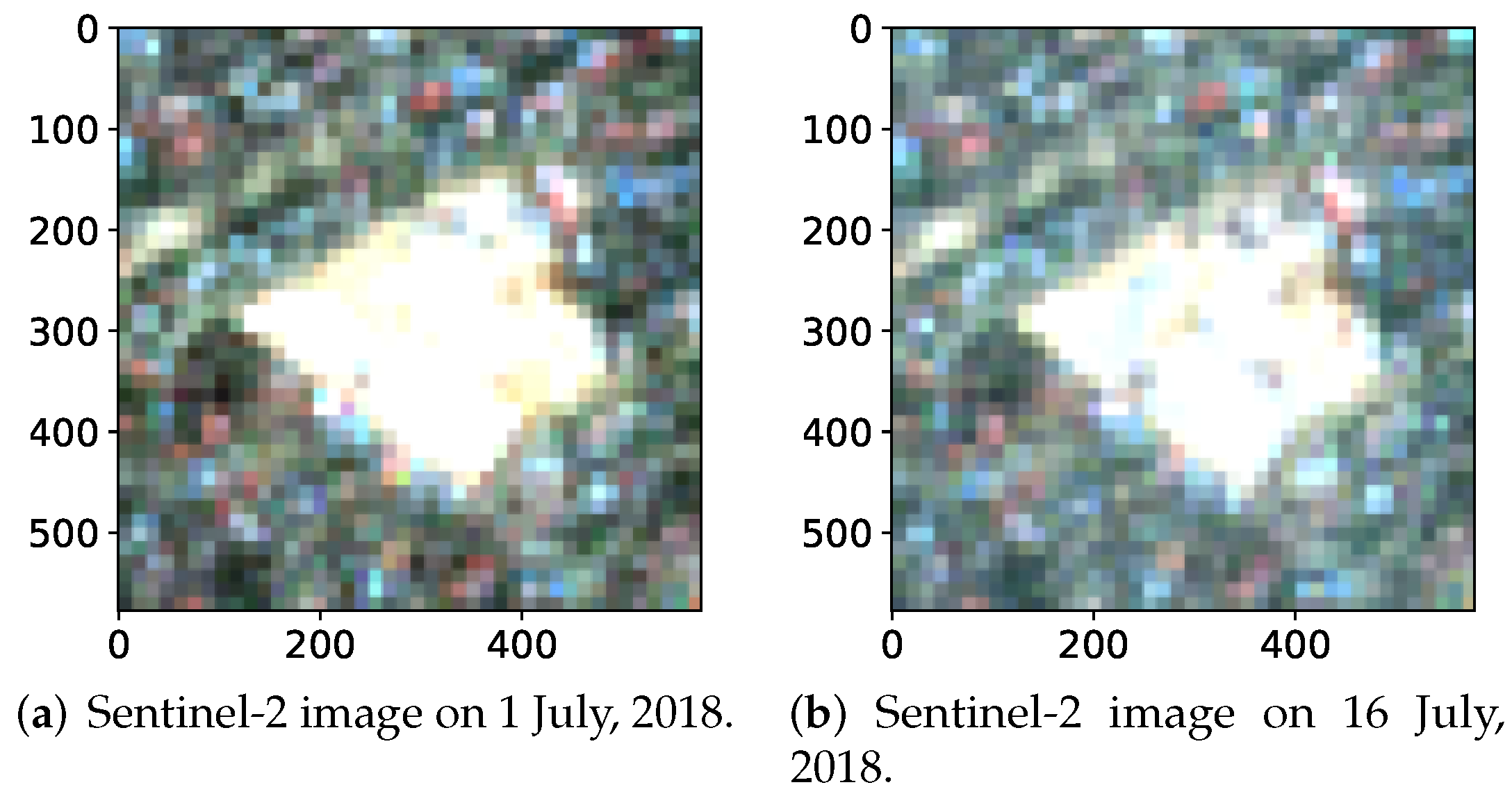

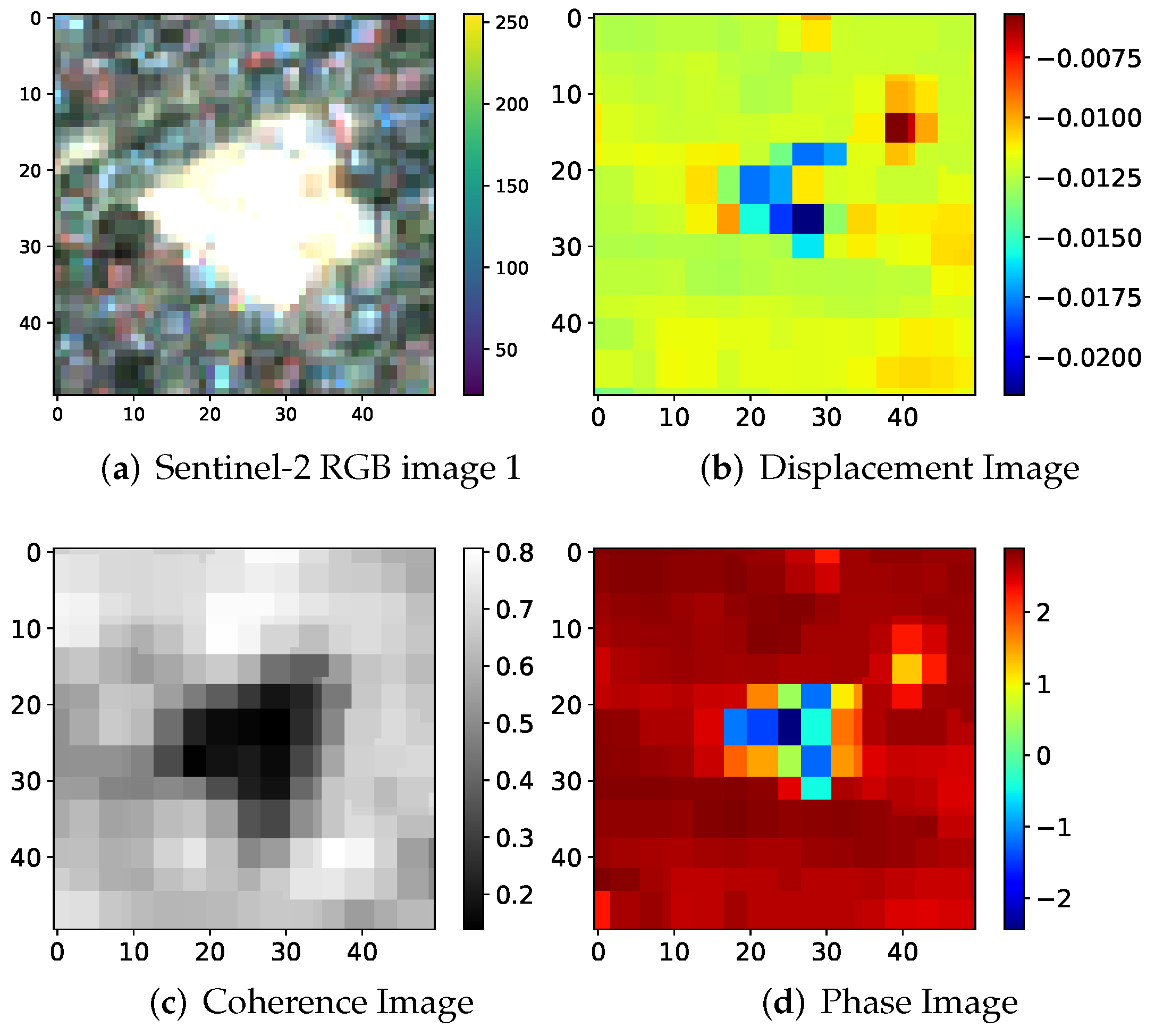
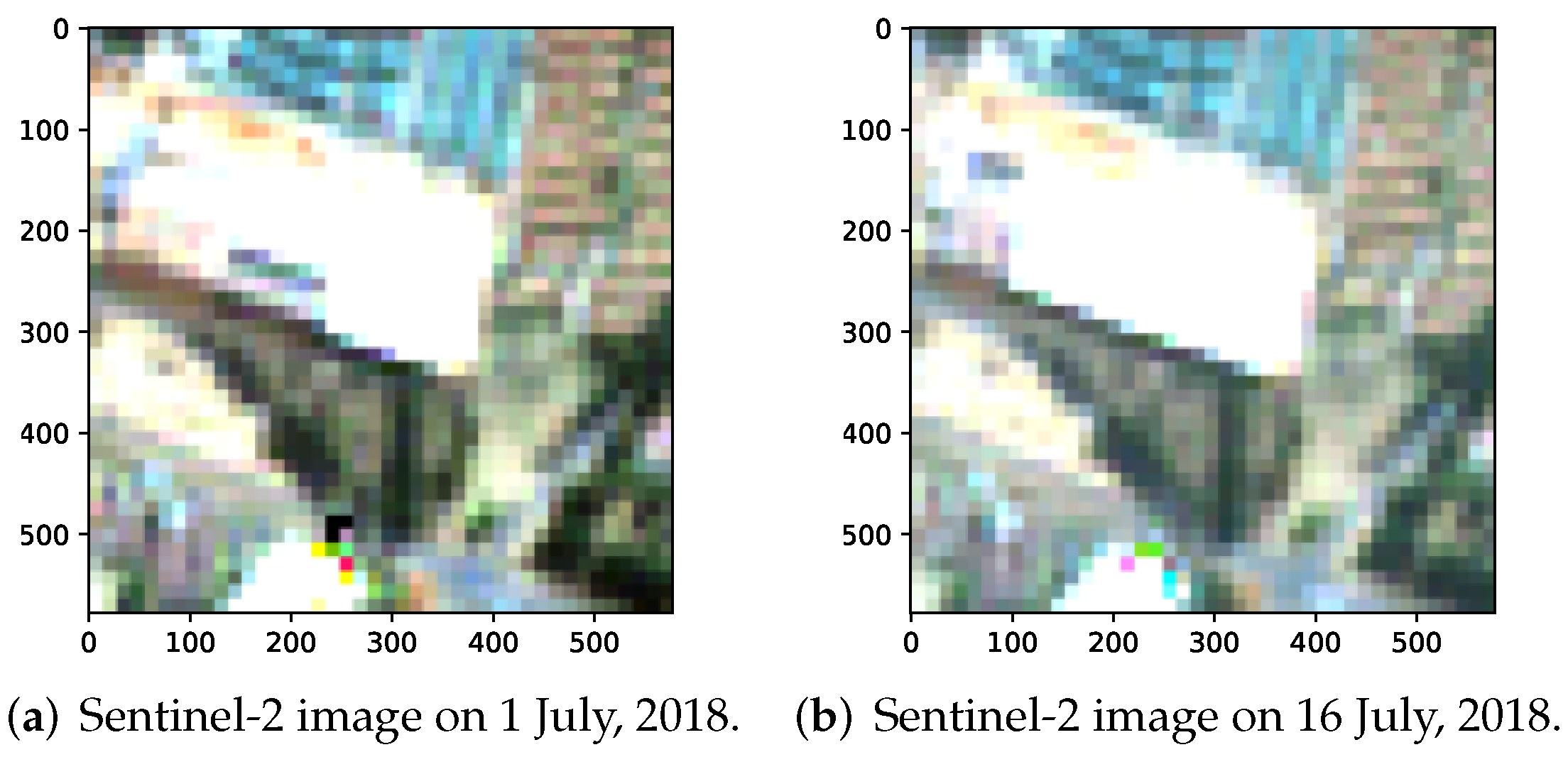

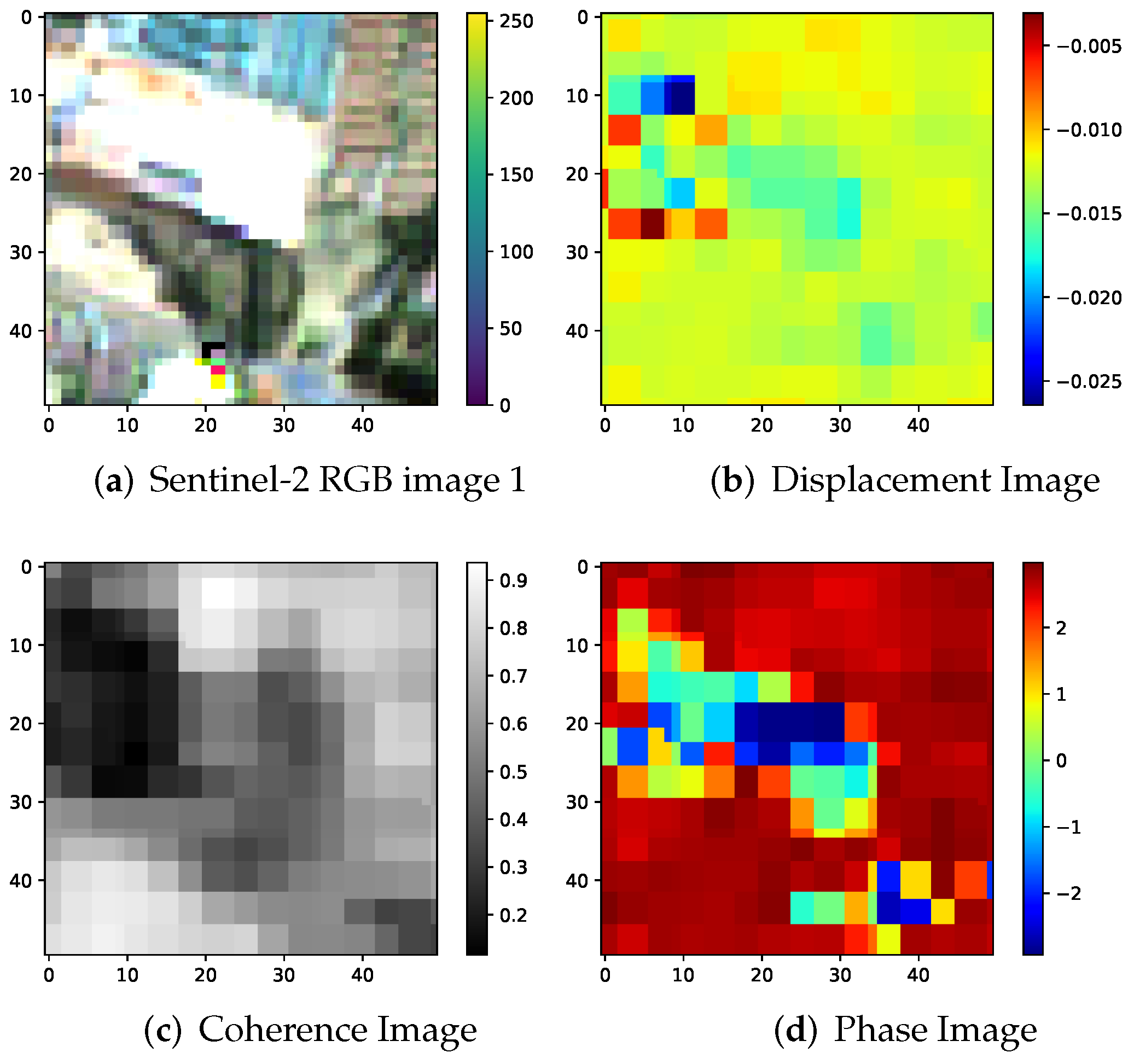
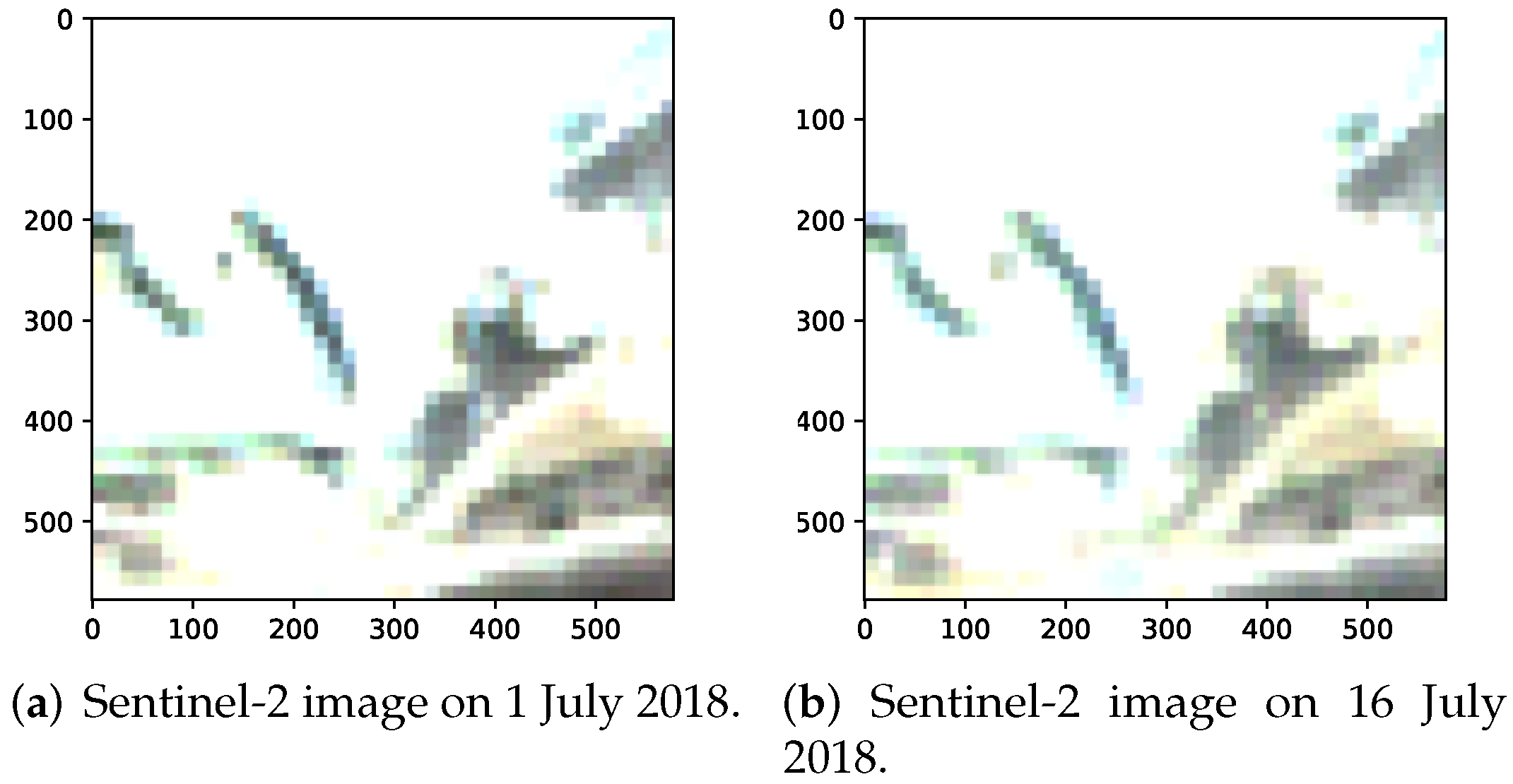

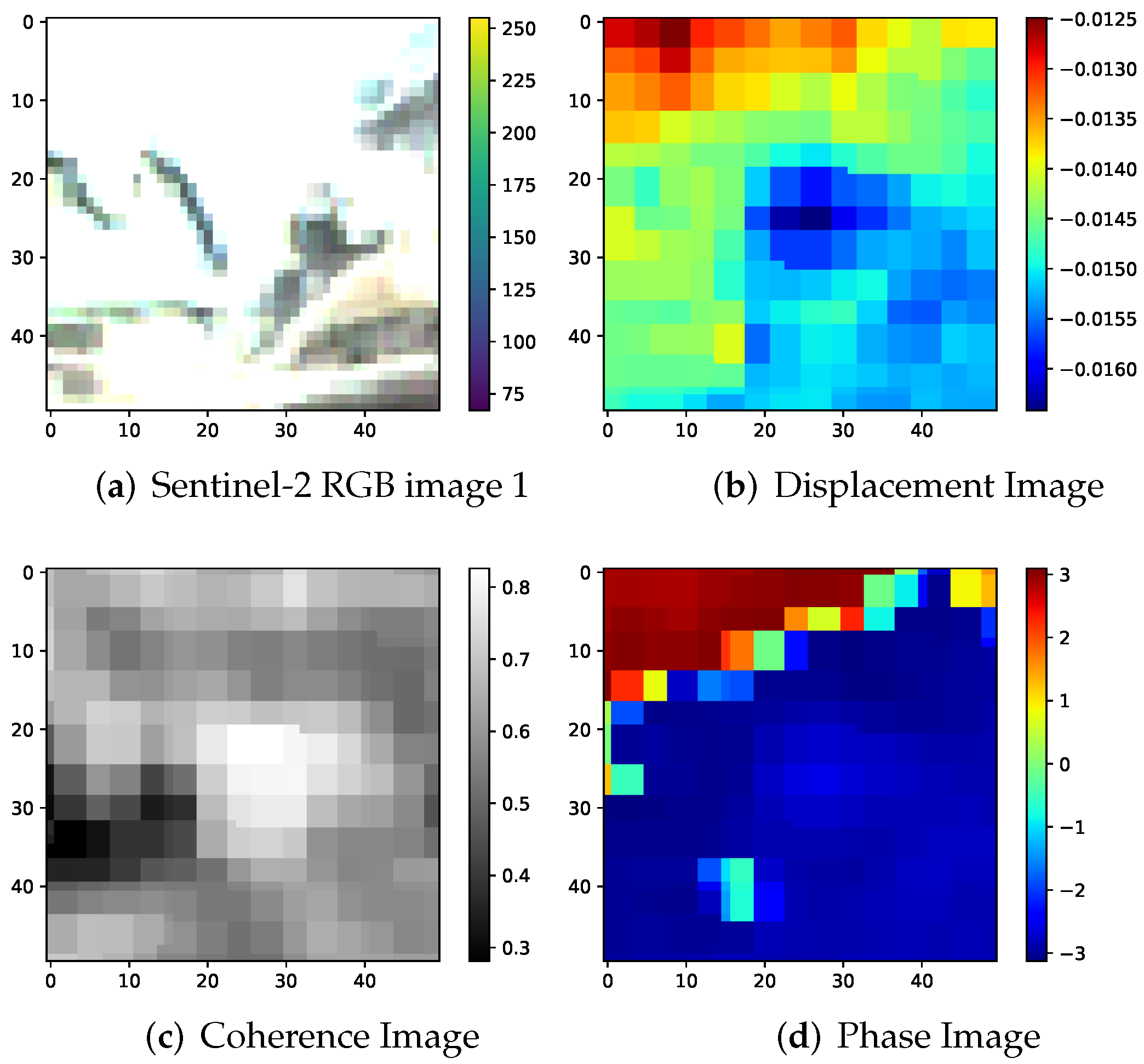


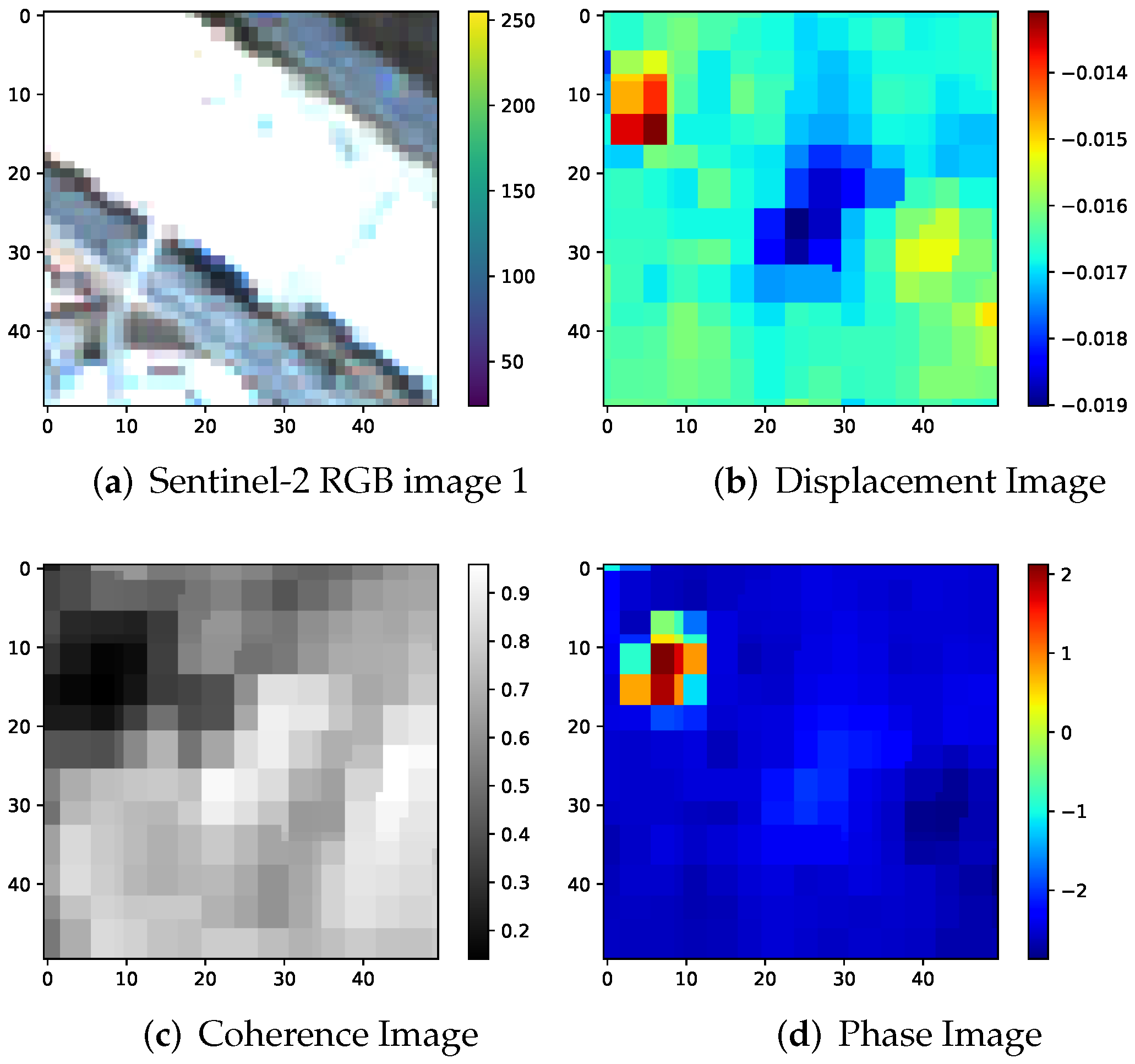

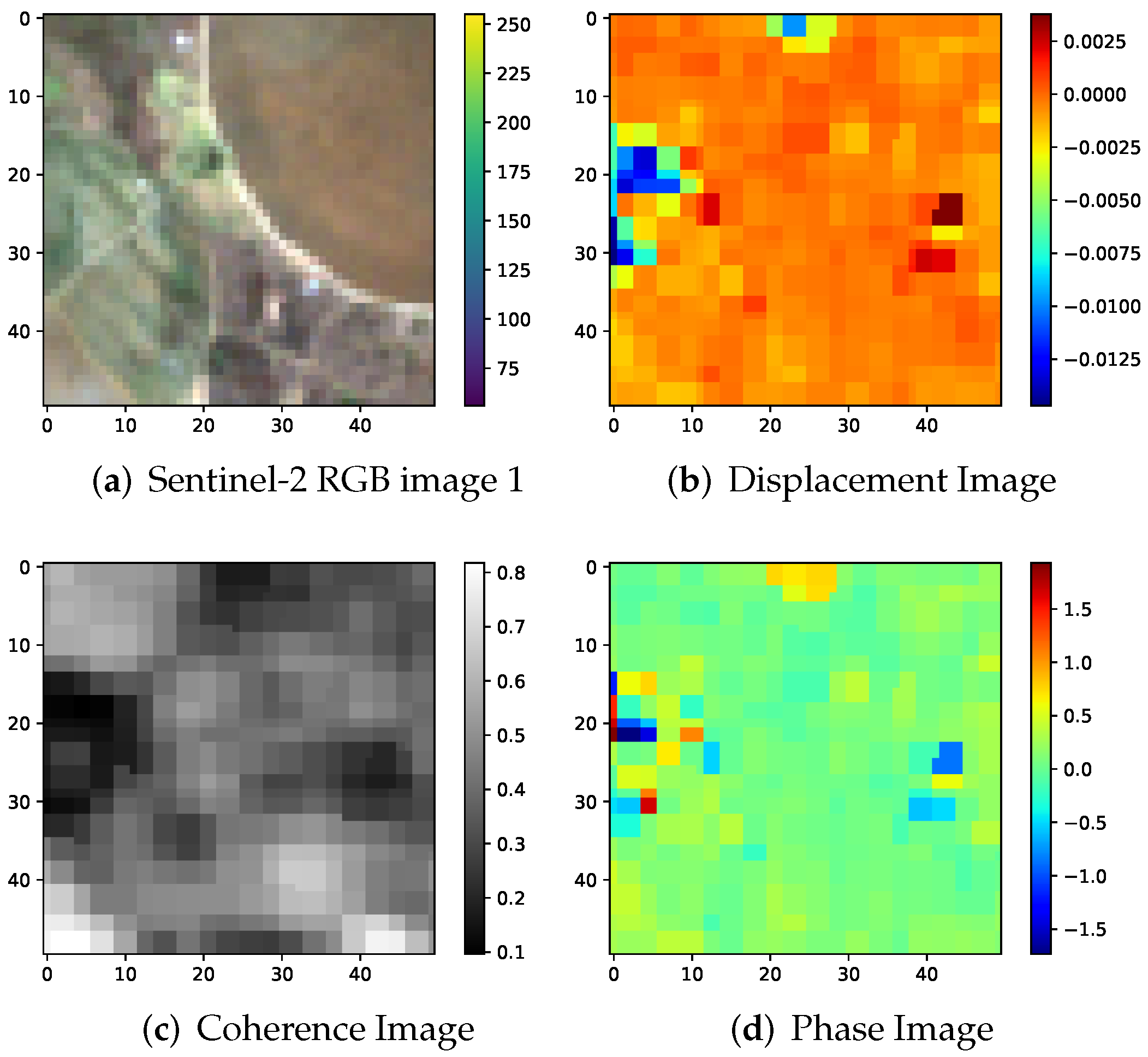
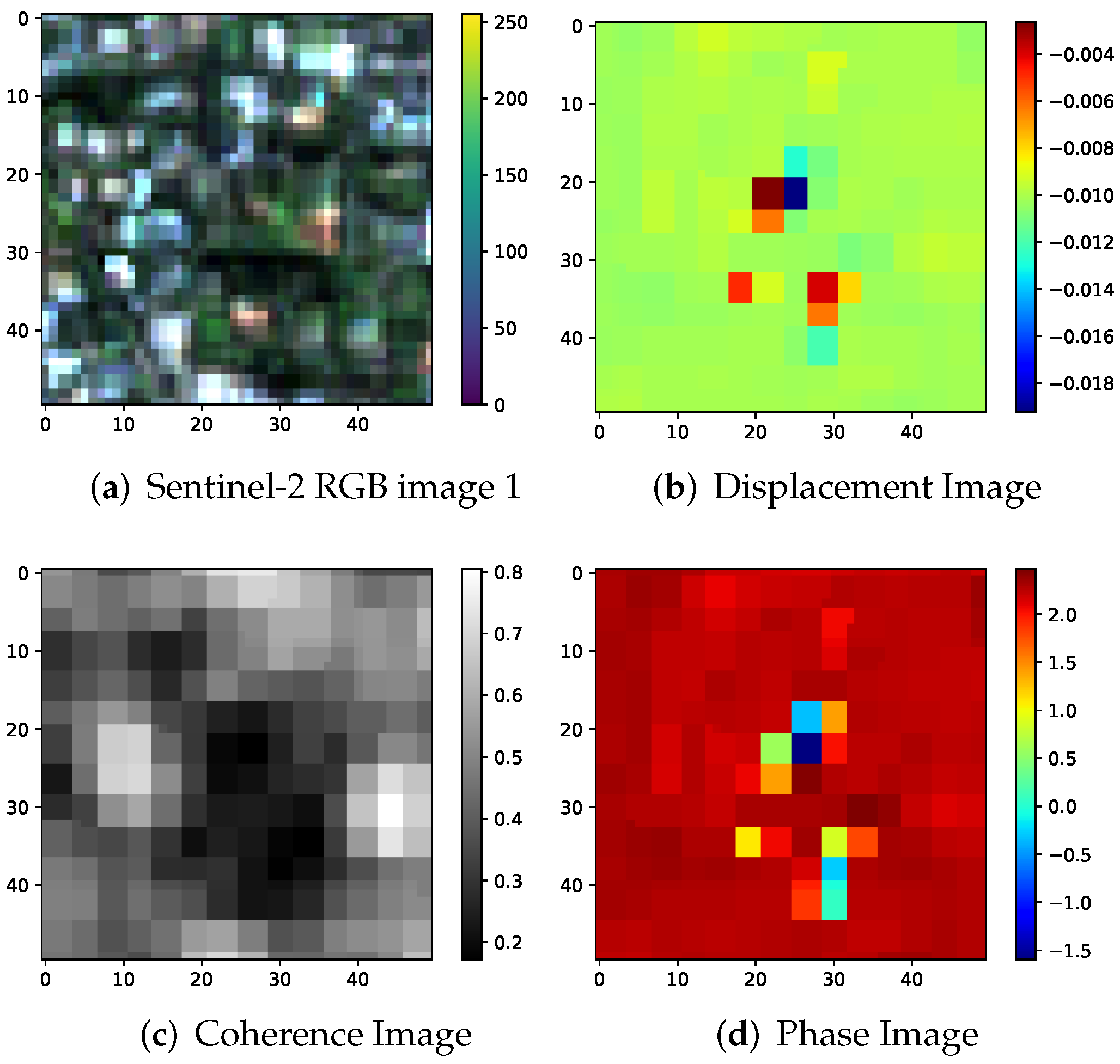



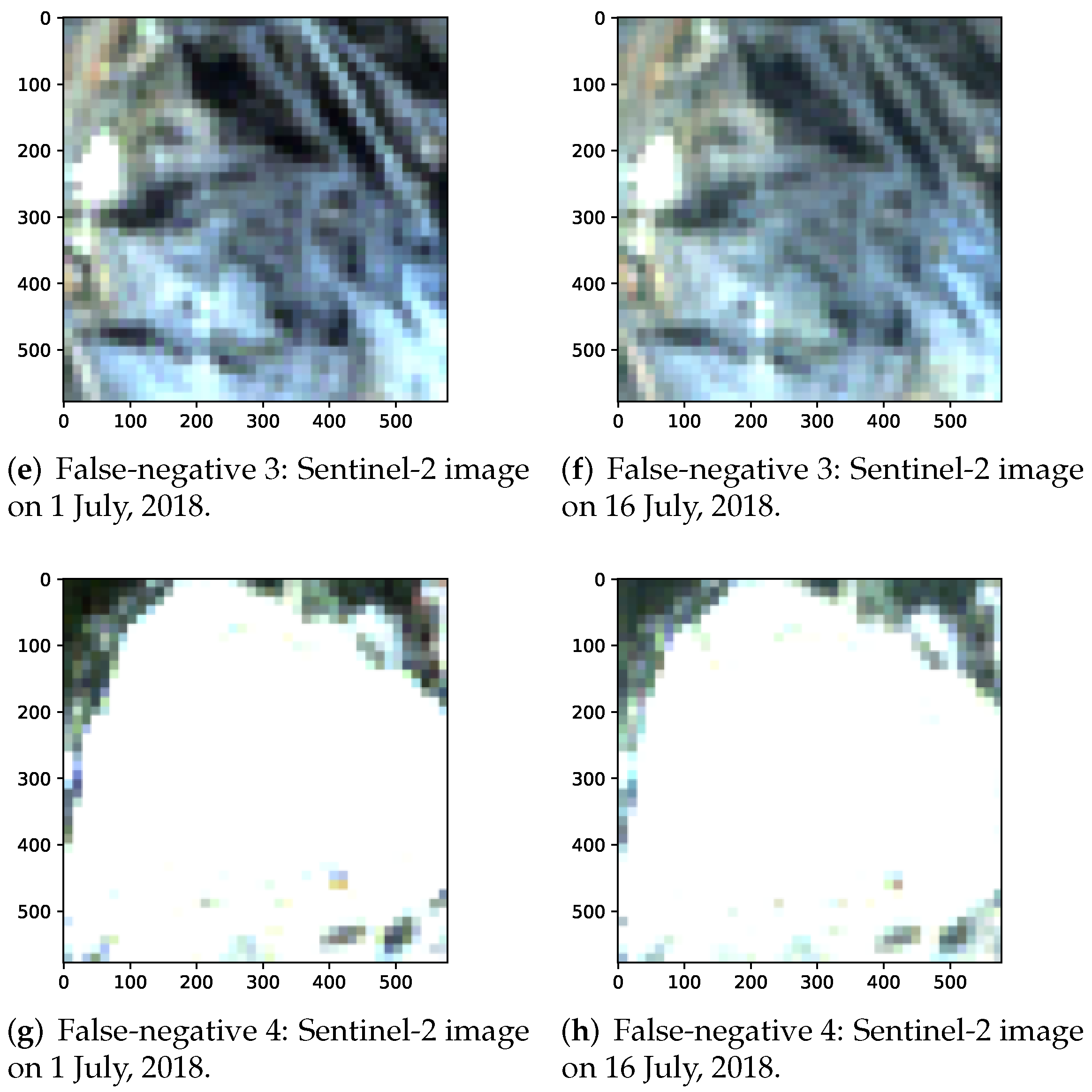
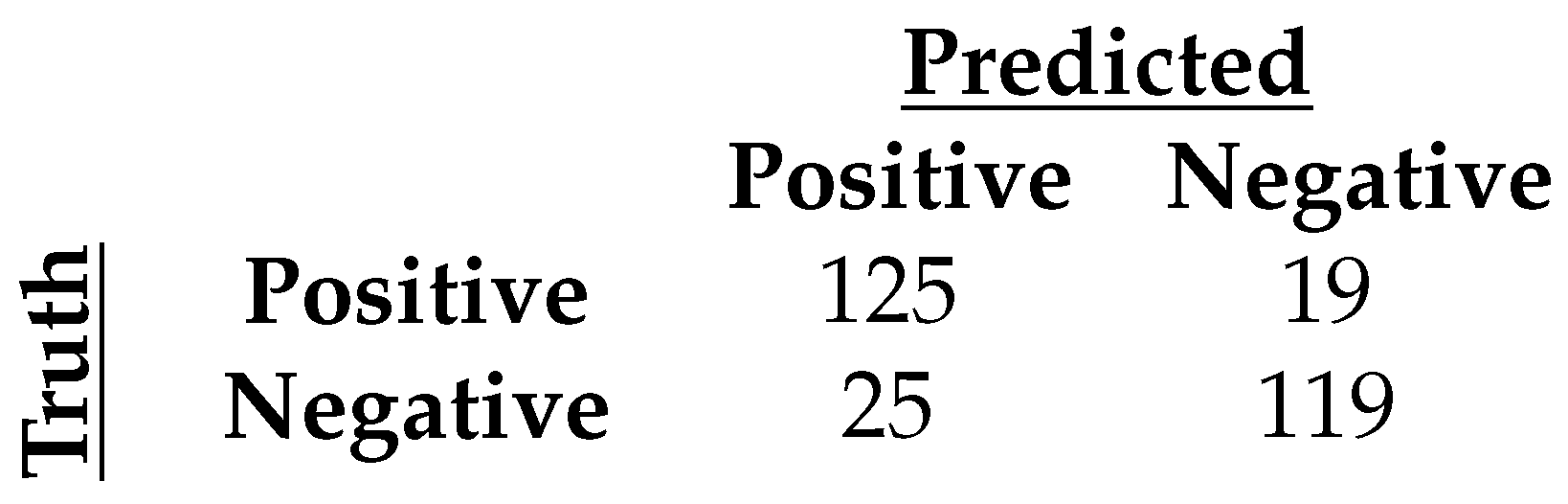
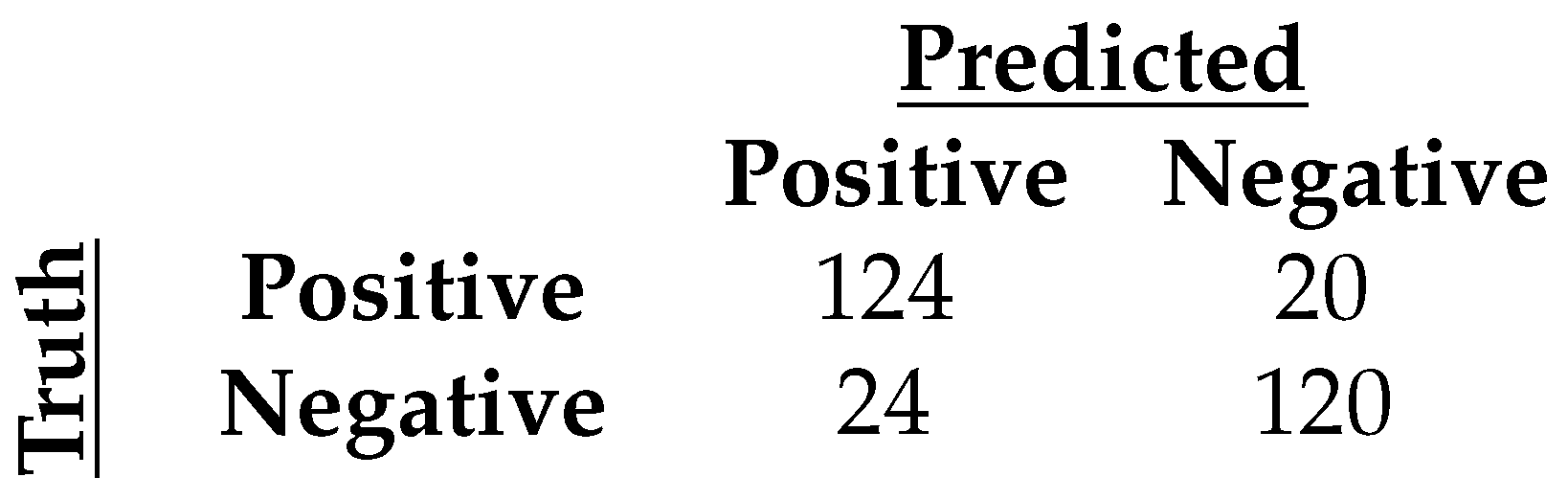
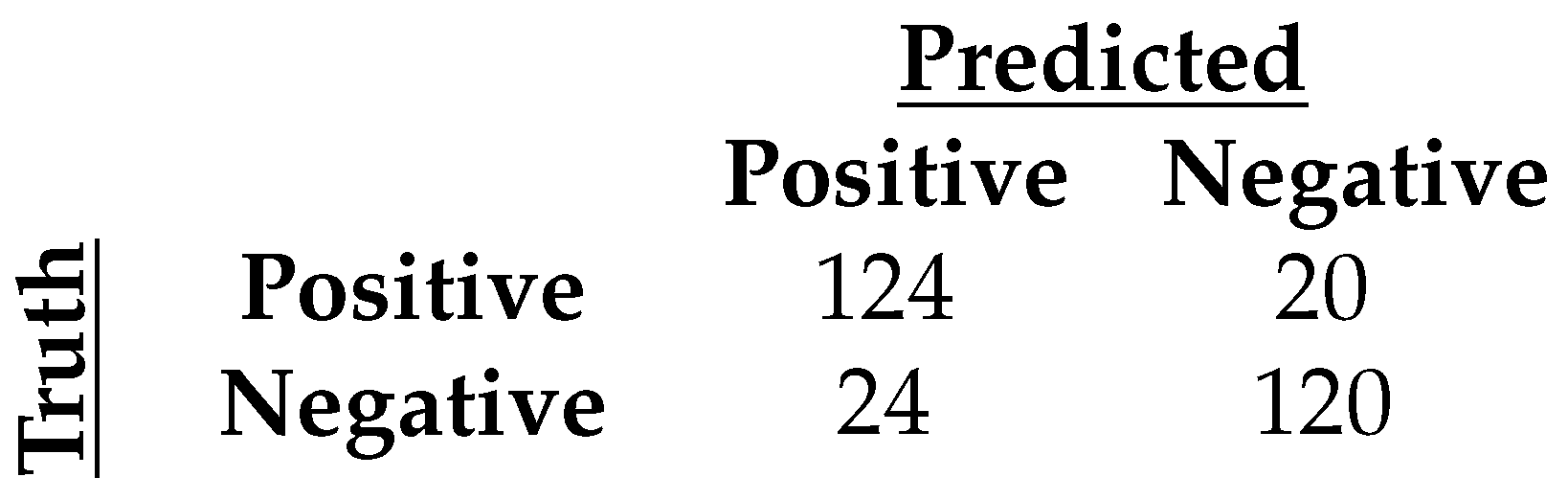
| Ensemble | Models |
|---|---|
| FeatSpaceEnsNet 1 | ResNet50 + ResNeXt50 |
| FeatSpaceEnsNet 2 | ResNet50 + ResNeXt50 + EfficientNetB4 |
| FeatSpaceEnsNet 3 | ResNet50 + ResNet101 |
| FeatSpaceEnsNet 4 | ResNet50 + ResNet101 + ResNeXt50 |
| FeatSpaceEnsNet 5 | ResNet50 + ResNet101 + ResNet152 |
| FeatSpaceEnsNet 6 | ResNet50 + ResNet101 + Inception-ResnetV2 |
| FeatSpaceEnsNet 7 | ResNet50 + Inception-ResnetV2 |
| AvgEnsNet 1 | ResNet50 + Inception-ResnetV2 |
| AvgEnsNet 2 | ResNet50 + ResNet101 |
| AvgEnsNet 3 | ResNet50 + ResNeXt50 |
| AvgEnsNet 4 | ResNet50 + ResNet101 + ResNeXt50 |
| AvgEnsNet 5 | ResNet50 + ResNet101 + Inception-ResnetV2 |
| AvgEnsNet 6 | ResNet50 + ResNet101 + ResNet152 |
| AvgEnsNet 7 | ResNet50 + ResNeXt50 + EfficientNetB4 |
| HybridEnsNet 1 | FeatSpaceEnsNet 3 + AvgEnsNet 2 |
| HybridEnsNet 2 | FeatSpaceEnsNet 3 + AvgEnsNet 2 + IncResNetV2 + EffNetB0 |
| HybridEnsNet 3 | FeatSpaceEnsNet 3 + AvgEnsNet 4 + IncResNetV2 + EffNetB0 + EffNetB4 |
| HybridEnsNet 4 | FeatSpaceEnsNet 3 + AvgEnsNet 4 + IncResNetV2 + EffNetB0 + EffNetB4 |
| + ResNet152 + EffNetB7 | |
| HybridEnsNet 5 | FeatSpaceEnsNet 3 + AvgEnsNet 4 + IncResNetV2 + EffNetB0 + EffNetB4 |
| + ResNet152 + EffNetB7 + ResNet50V2 + ResNet152V2 |
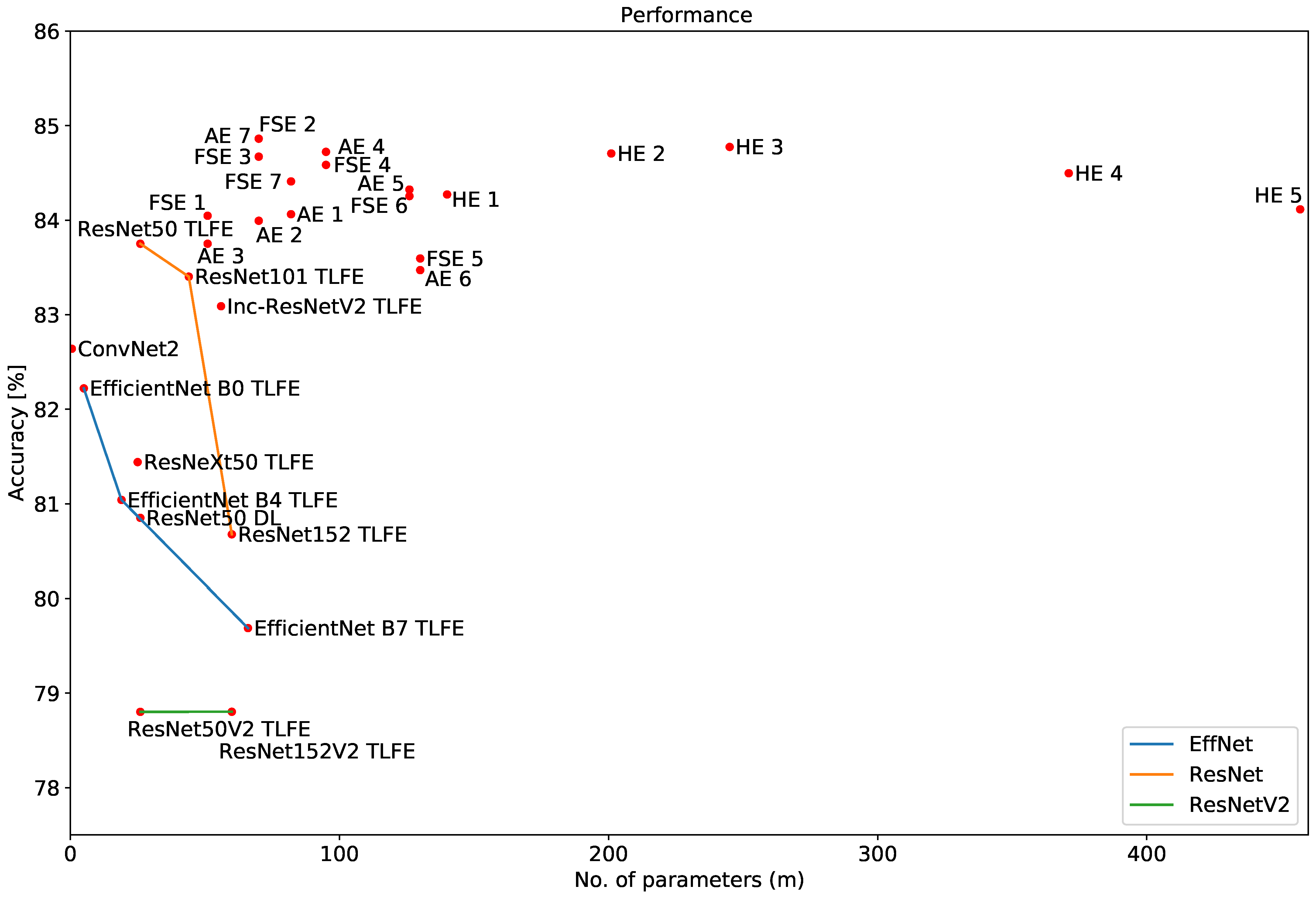
| Model | Method | Acc. [%] | Acc. | F1 Score | Precision | Recall | # Params |
|---|---|---|---|---|---|---|---|
| ResNet50 | TLFE | 83.751 | 1.503 | 0.838 | 0.838 | 0.838 | 26 m |
| ResNet101 | TLFE | 83.403 | 1.341 | 0.834 | 0.834 | 0.834 | 44 m |
| Inception-ResNetV2 | TLFE | 83.090 | 1.271 | 0.831 | 0.831 | 0.831 | 56 m |
| EfficientNet B0 | TLFE | 82.221 | 0.846 | 0.824 | 0.825 | 0.824 | 5 m |
| ResNeXt50 | TLFE | 81.441 | 1.285 | 0.814 | 0.815 | 0.815 | 25 m |
| EfficientNet B4 | TLFE | 81.041 | 1.310 | 0.811 | 0.812 | 0.811 | 19 m |
| ResNet50 | DLRI | 80.851 | 5.161 | 0.808 | 0.810 | 0.809 | 26 m |
| ResNet152 | TLFE | 80.677 | 2.355 | 0.807 | 0.807 | 0.807 | 60 m |
| EfficientNet B7 | TLFE | 79.688 | 2.954 | 0.796 | 0.796 | 0.796 | 66 m |
| ResNet152V2 | TLFE | 78.803 | 1.403 | 0.788 | 0.790 | 0.788 | 60 m |
| ResNet50V2 | TLFE | 78.802 | 1.579 | 0.786 | 0.791 | 0.789 | 26 m |
| ResNet50 | TLFT | 71.078 | 30.288 | 0.702 | 0.732 | 0.710 | 26 m |
| EfficientNet B4 | TLFT | 67.881 | 24.456 | 0.662 | 0.719 | 0.679 | 19 m |
| EfficientNet B4 | DLRI | 65.608 | 41.338 | 0.614 | 0.753 | 0.656 | 19 m |
| Model | Acc. [%] | Acc. | F1 Score | Precision | Recall | # Params |
|---|---|---|---|---|---|---|
| FeatSpaceEnsNet 2 | 84.862 | 1.108 | 0.849 | 0.850 | 0.849 | 70 m |
| FeatSpaceEnsNet 3 | 84.672 | 1.350 | 0.846 | 0.847 | 0.846 | 70 m |
| FeatSpaceEnsNet 4 | 84.585 | 0.501 | 0.845 | 0.845 | 0.845 | 95 m |
| FeatSpaceEnsNet 7 | 84.410 | 0.848 | 0.844 | 0.844 | 0.844 | 82 m |
| FeatSpaceEnsNet 6 | 84.255 | 0.802 | 0.842 | 0.842 | 0.842 | 126 m |
| FeatSpaceEnsNet 1 | 84.047 | 0.908 | 0.840 | 0.840 | 0.840 | 51 m |
| ResNet50 | 83.751 | 1.503 | 0.838 | 0.838 | 0.838 | 26 m |
| FeatSpaceEnsNet 5 | 83.595 | 0.811 | 0.836 | 0.836 | 0.836 | 130 m |
| Model | Acc. [%] | Acc. | F1 Score | Precision | Recall | # Params |
|---|---|---|---|---|---|---|
| AvgEnsNet 7 | 84.862 | 1.374 | 0.850 | 0.850 | 0.850 | 70 m |
| AvgEnsNet 4 | 84.723 | 1.690 | 0.846 | 0.847 | 0.846 | 95 m |
| AvgEnsNet 5 | 84.324 | 1.872 | 0.842 | 0.843 | 0.842 | 126 m |
| AvgEnsNet 1 | 84.063 | 1.739 | 0.841 | 0.842 | 0.841 | 82 m |
| AvgEnsNet 2 | 83.994 | 1.421 | 0.839 | 0.839 | 0.839 | 70 m |
| ResNet50 | 83.751 | 1.503 | 0.838 | 0.838 | 0.838 | 26 m |
| AvgEnsNet 3 | 83.751 | 1.667 | 0.838 | 0.839 | 0.838 | 51 m |
| AvgEnsNet 6 | 83.472 | 1.224 | 0.836 | 0.836 | 0.836 | 130 m |
| Model | Acc. [%] | Acc. | F1 Score | Precision | Recall | # Params |
|---|---|---|---|---|---|---|
| HybridEnsNet 3 | 84.775 | 1.464 | 0.848 | 0.849 | 0.848 | 245 m |
| HybridEnsNet 2 | 84.706 | 0.794 | 0.847 | 0.847 | 0.847 | 201 m |
| HybridEnsNet 4 | 84.497 | 0.829 | 0.845 | 0.845 | 0.845 | 371 m |
| HybridEnsNet 1 | 84.272 | 1.219 | 0.843 | 0.843 | 0.843 | 140 m |
| HybridEnsNet 5 | 84.115 | 1.254 | 0.841 | 0.842 | 0.842 | 457 m |
| ResNet50 | 83.751 | 1.503 | 0.838 | 0.838 | 0.838 | 26 m |
| Model | Method | Acc. [%] | Acc. | F1 Score | Precision | Recall |
|---|---|---|---|---|---|---|
| AvgEnsNet 7 | TLFE | 84.862 | 1.374 | 0.850 | 0.850 | 0.850 |
| FeatSpaceEnsNet 2 | TLFE | 84.862 | 1.108 | 0.849 | 0.850 | 0.849 |
| HybridEnsNet 3 | TLFE | 84.775 | 1.464 | 0.848 | 0.849 | 0.848 |
| ResNet50 | TLFE | 83.751 | 1.503 | 0.838 | 0.838 | 0.838 |
| ConvNet2 | ML | 82.640 | 1.700 | 0.828 | 0.831 | 0.828 |
| LBP + RBF-SVM | ML | 70.522 | 4.619 | 0.705 | 0.707 | 0.705 |
| LBP + RF | ML | 69.896 | 2.885 | 0.699 | 0.701 | 0.699 |
| LBP + SVM | ML | 67.760 | 0.891 | 0.678 | 0.678 | 0.678 |
| LBP + MLP | ML | 66.754 | 4.758 | 0.666 | 0.671 | 0.667 |
| (HOG, LBP) + SVM | ML | 62.639 | 6.251 | 0.626 | 0.627 | 0.627 |
| HOG + SVM | ML | 62.257 | 5.854 | 0.623 | 0.624 | 0.623 |
| (HOG, LBP) + RF | ML | 62.241 | 5.768 | 0.621 | 0.625 | 0.623 |
| (HOG, LBP) + MLP | ML | 61.928 | 8.143 | 0.615 | 0.622 | 0.619 |
| HOG + MLP | ML | 61.563 | 7.716 | 0.611 | 0.622 | 0.614 |
| HOG + RF | ML | 61.007 | 4.404 | 0.608 | 0.611 | 0.609 |
| HOG + RBF-SVM | ML | 50.000 | 0.000 | 0.330 | 0.250 | 0.500 |
| (HOG, LBP) + RBF-SVM | ML | 50.000 | 0.000 | 0.330 | 0.250 | 0.500 |
| Model | Method | Folds | Acc. [%] | Acc. | F1 Score | Precision | Recall |
|---|---|---|---|---|---|---|---|
| AvgEnsNet 7 | TLFE | 84.862 | 1.374 | 0.850 | 0.850 | 0.850 | |
| FeatSpaceEnsNet 2 | TLFE | 10 | 84.862 | 1.108 | 0.849 | 0.850 | 0.850 |
| ResNet50 | TLFE | 83.751 | 1.503 | 0.838 | 0.838 | 0.838 | |
| LBP + RBF-SVM | ML | 70.522 | 4.619 | 0.705 | 0.707 | 0.705 | |
| LBP + RF | ML | 69.896 | 2.885 | 0.699 | 0.701 | 0.699 | |
| LBP + SVM | ML | 67.760 | 0.891 | 0.678 | 0.678 | 0.678 | |
| AvgEnsNet 7 | TLFE | 5 | 85.139 | 1.012 | 0.851 | 0.852 | 0.851 |
| FeatSpaceEnsNet 2 | TLFE | 84.932 | 1.049 | 0.849 | 0.849 | 0.849 | |
| ResNet50 | TLFE | 83.507 | 1.774 | 0.835 | 0.835 | 0.835 | |
| LBP + RF | ML | 69.514 | 3.506 | 0.694 | 0.695 | 0.694 | |
| LBP + RBF-SVM | ML | 69.237 | 5.901 | 0.693 | 0.694 | 0.693 | |
| LBP + SVM | ML | 67.640 | 1.122 | 0.678 | 0.678 | 0.678 | |
| AvgEnsNet 7 | TLFE | 2 | 85.330 | 0.427 | 0.853 | 0.855 | 0.853 |
| FeatSpaceEnsNet 2 | TLFE | 85.245 | 1.411 | 0.853 | 0.853 | 0.853 | |
| ResNet50 | TLFE | 83.423 | 2.764 | 0.835 | 0.835 | 0.835 | |
| LBP + RF | ML | 70.833 | 7.798 | 0.708 | 0.708 | 0.708 | |
| LBP + RBF-SVM | ML | 70.228 | 6.147 | 0.703 | 0.705 | 0.703 | |
| LBP + SVM | ML | 68.228 | 0.362 | 0.680 | 0.683 | 0.680 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karim, Z.; van Zyl, T.L. Deep/Transfer Learning with Feature Space Ensemble Networks (FeatSpaceEnsNets) and Average Ensemble Networks (AvgEnsNets) for Change Detection Using DInSAR Sentinel-1 and Optical Sentinel-2 Satellite Data Fusion. Remote Sens. 2021, 13, 4394. https://doi.org/10.3390/rs13214394
Karim Z, van Zyl TL. Deep/Transfer Learning with Feature Space Ensemble Networks (FeatSpaceEnsNets) and Average Ensemble Networks (AvgEnsNets) for Change Detection Using DInSAR Sentinel-1 and Optical Sentinel-2 Satellite Data Fusion. Remote Sensing. 2021; 13(21):4394. https://doi.org/10.3390/rs13214394
Chicago/Turabian StyleKarim, Zainoolabadien, and Terence L. van Zyl. 2021. "Deep/Transfer Learning with Feature Space Ensemble Networks (FeatSpaceEnsNets) and Average Ensemble Networks (AvgEnsNets) for Change Detection Using DInSAR Sentinel-1 and Optical Sentinel-2 Satellite Data Fusion" Remote Sensing 13, no. 21: 4394. https://doi.org/10.3390/rs13214394
APA StyleKarim, Z., & van Zyl, T. L. (2021). Deep/Transfer Learning with Feature Space Ensemble Networks (FeatSpaceEnsNets) and Average Ensemble Networks (AvgEnsNets) for Change Detection Using DInSAR Sentinel-1 and Optical Sentinel-2 Satellite Data Fusion. Remote Sensing, 13(21), 4394. https://doi.org/10.3390/rs13214394