Vertical Structure of Ice Clouds and Vertical Air Motion from Vertically Pointing Cloud Radar Measurements
Abstract
1. Introduction
2. Data
3. Methods
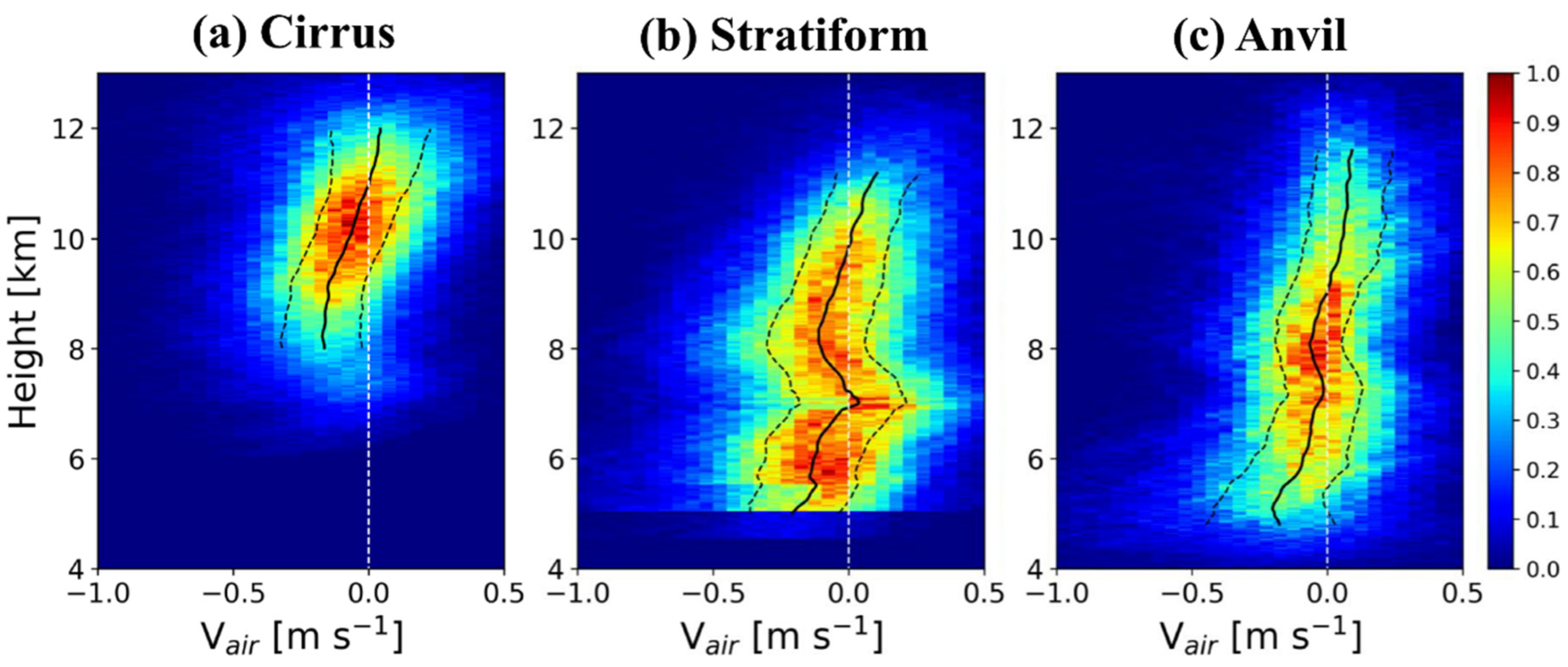
3.1. Classification of Ice Clouds
3.2. Estimation of Terminal Velocity and Vertical Air Motion
4. Results
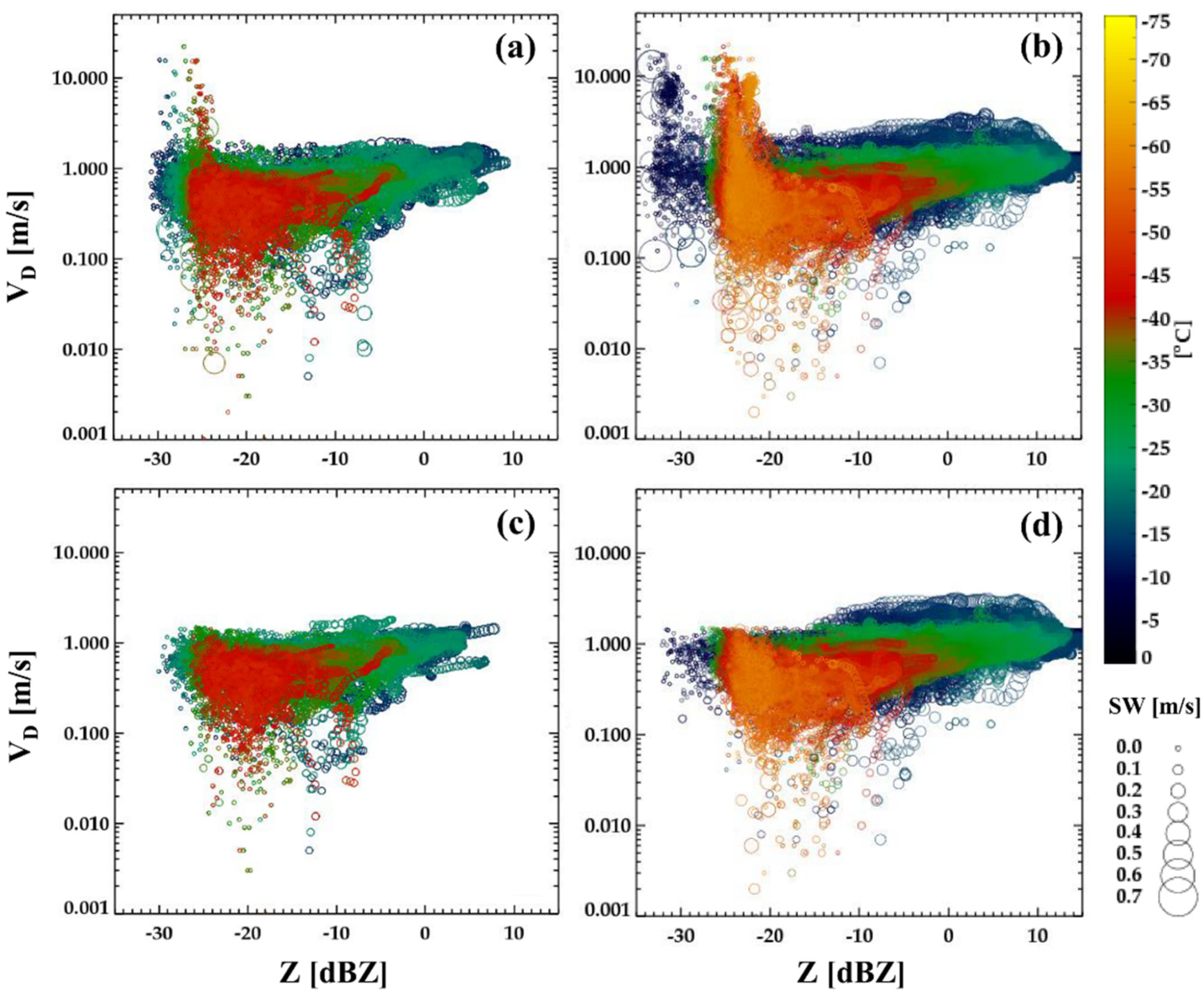
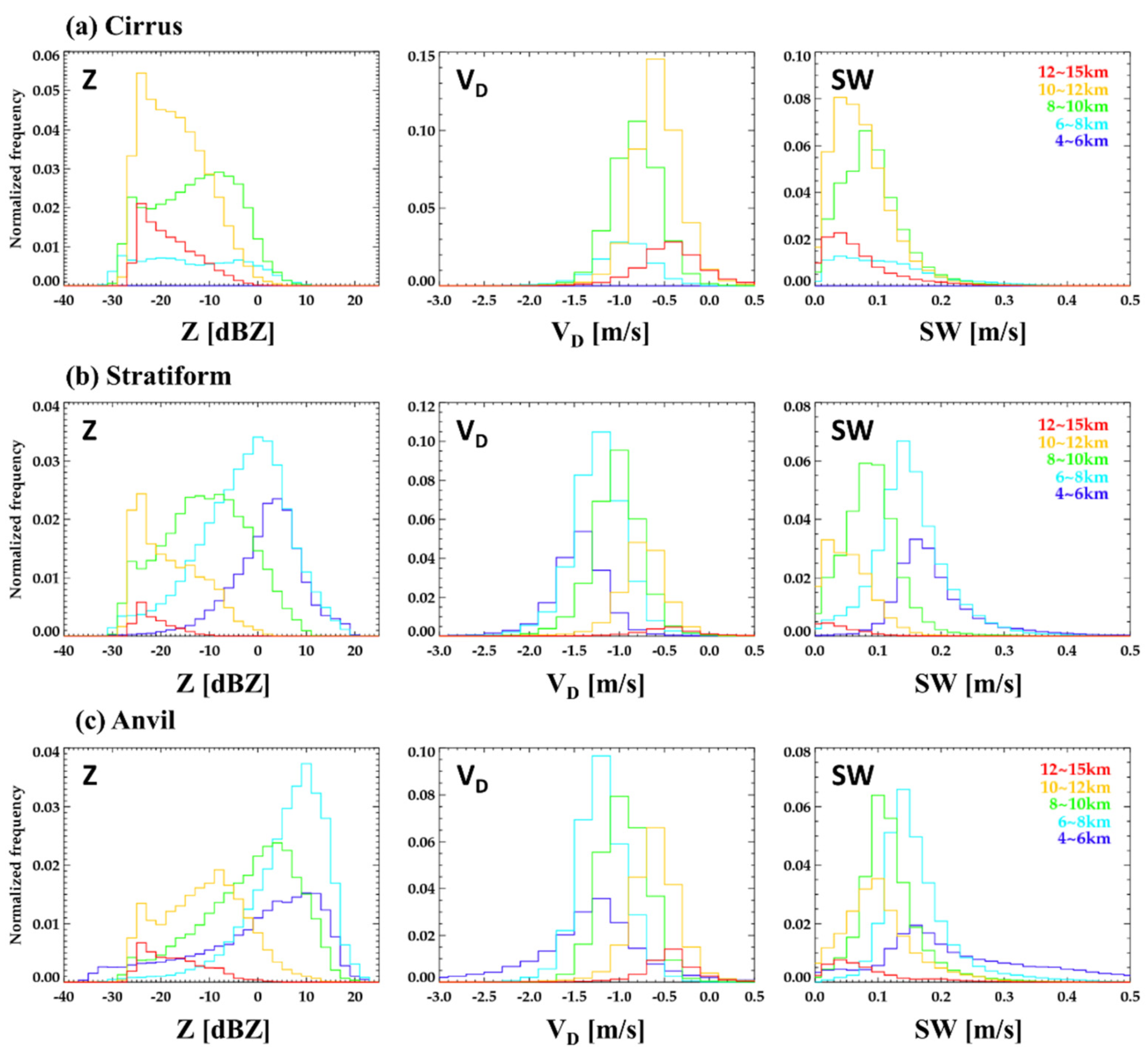
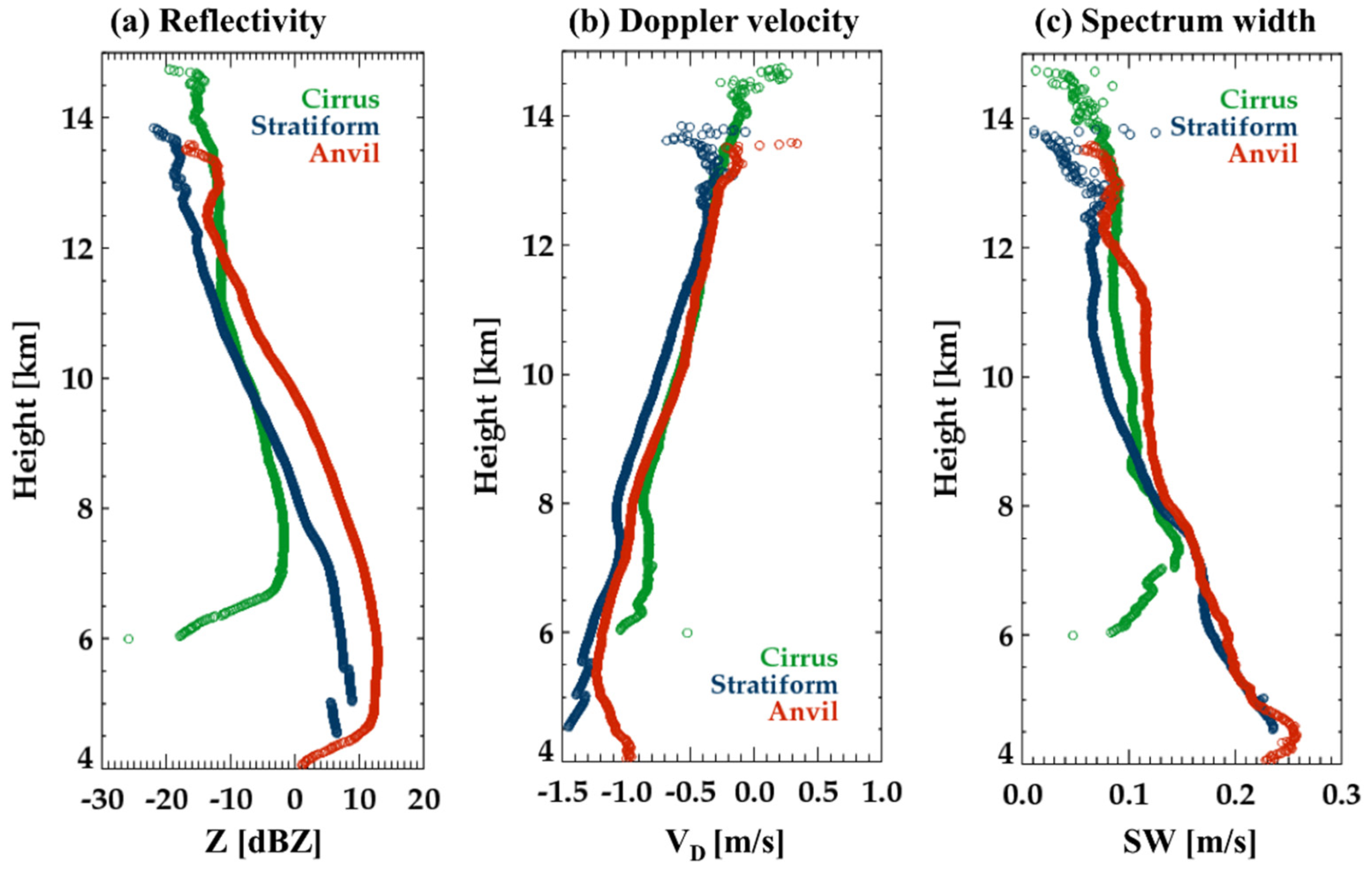
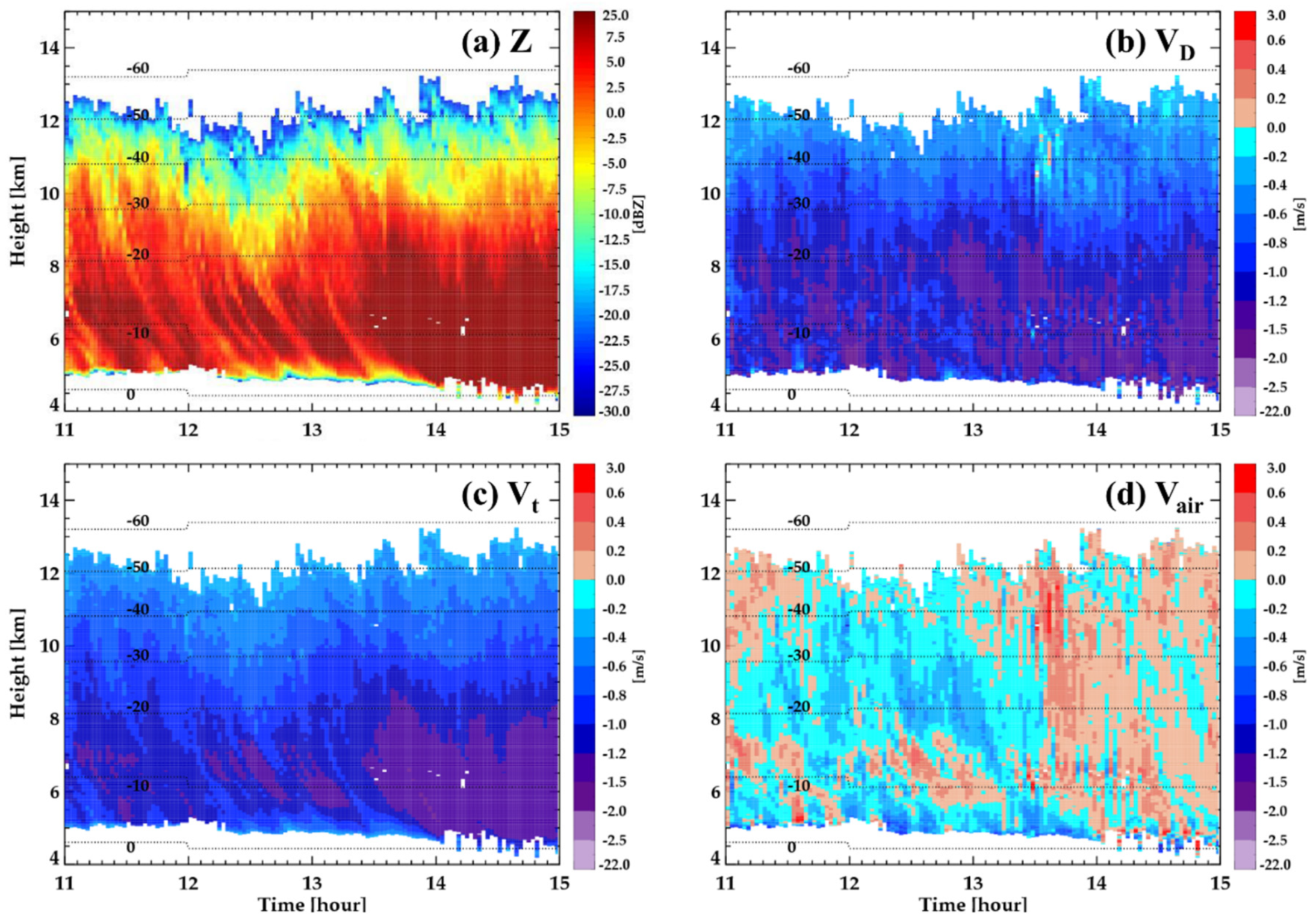
4.1. Properties of Radar Parameters
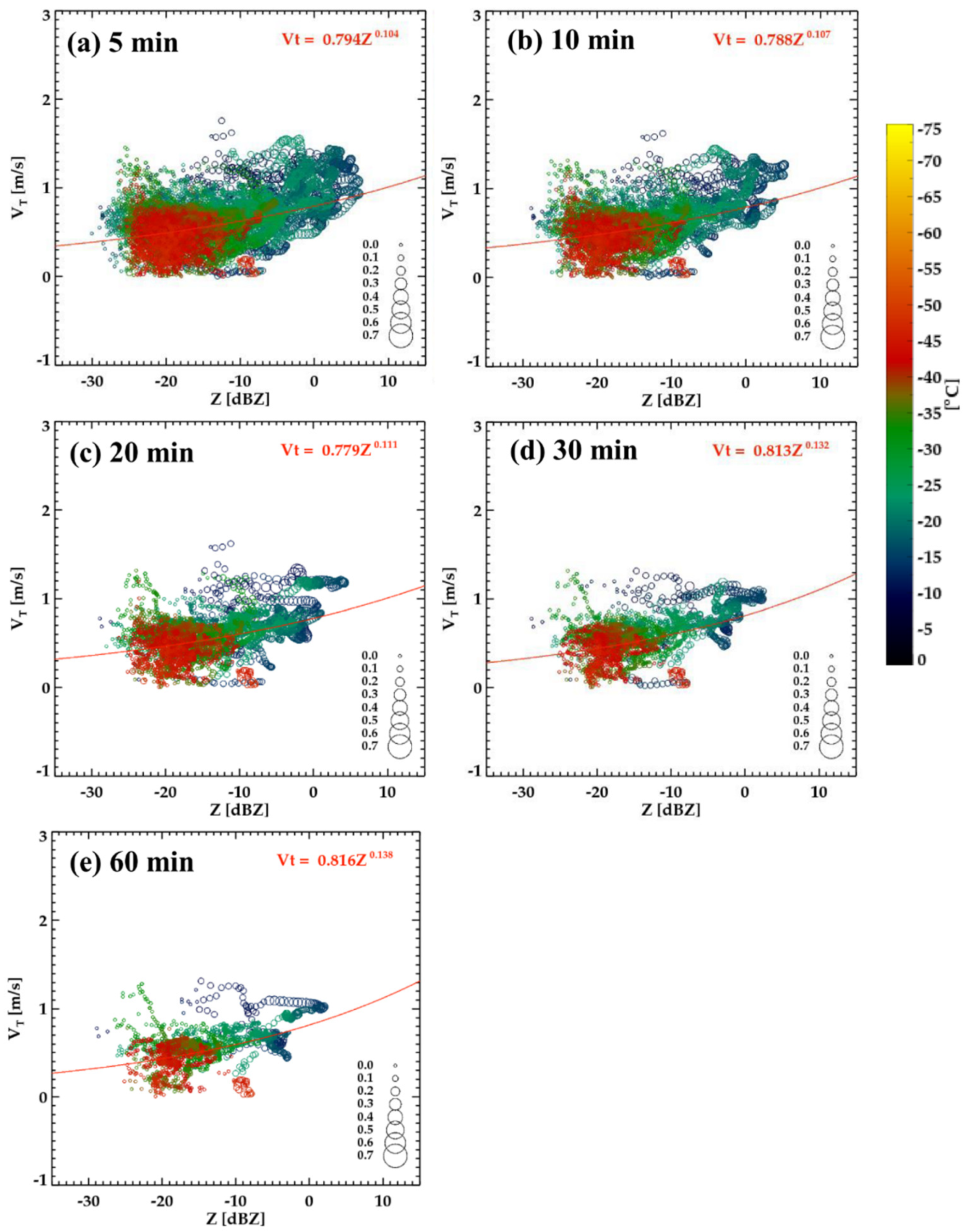
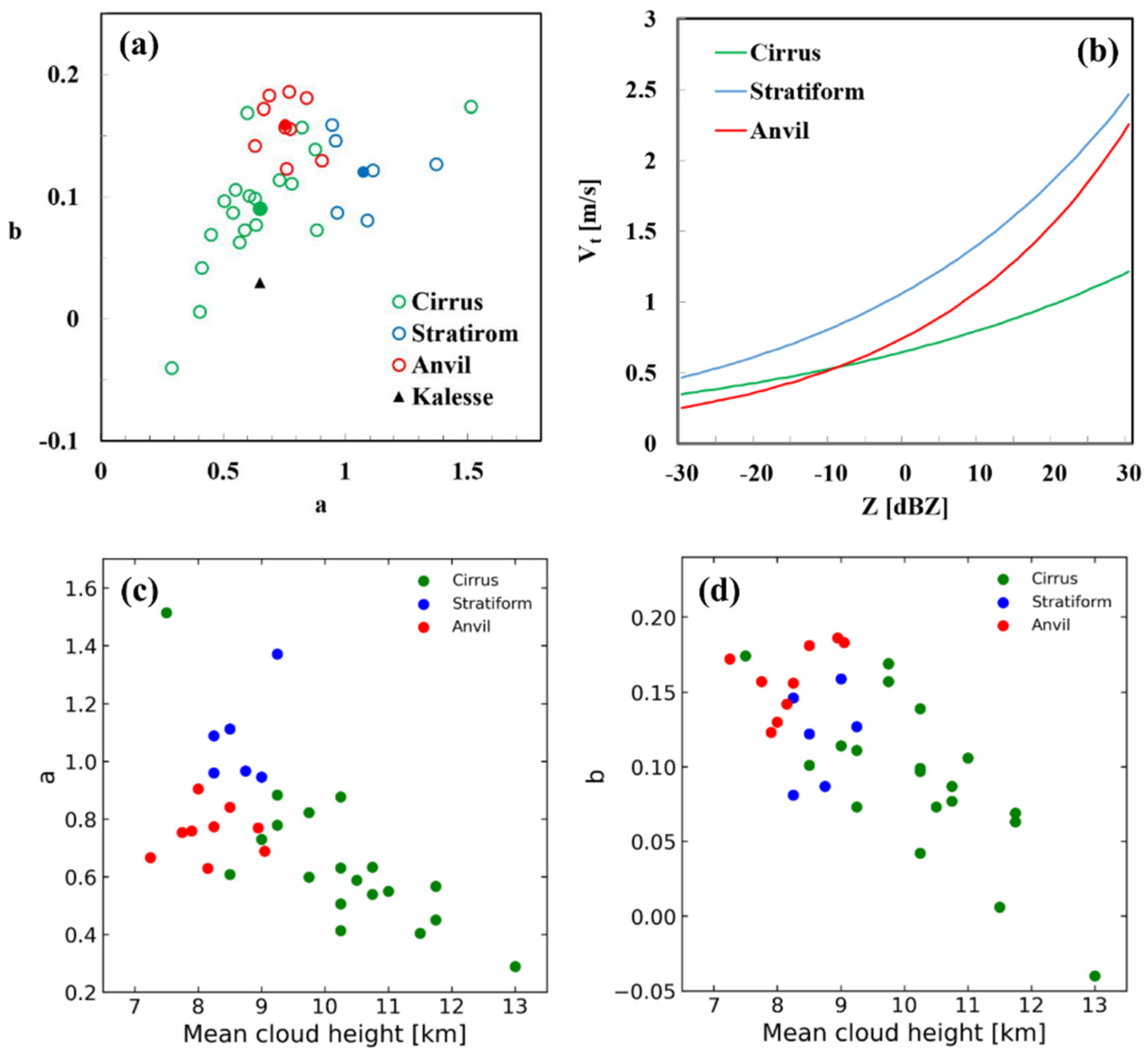
4.2. Estimation of Terminal Velocity and Vertical Air Motion
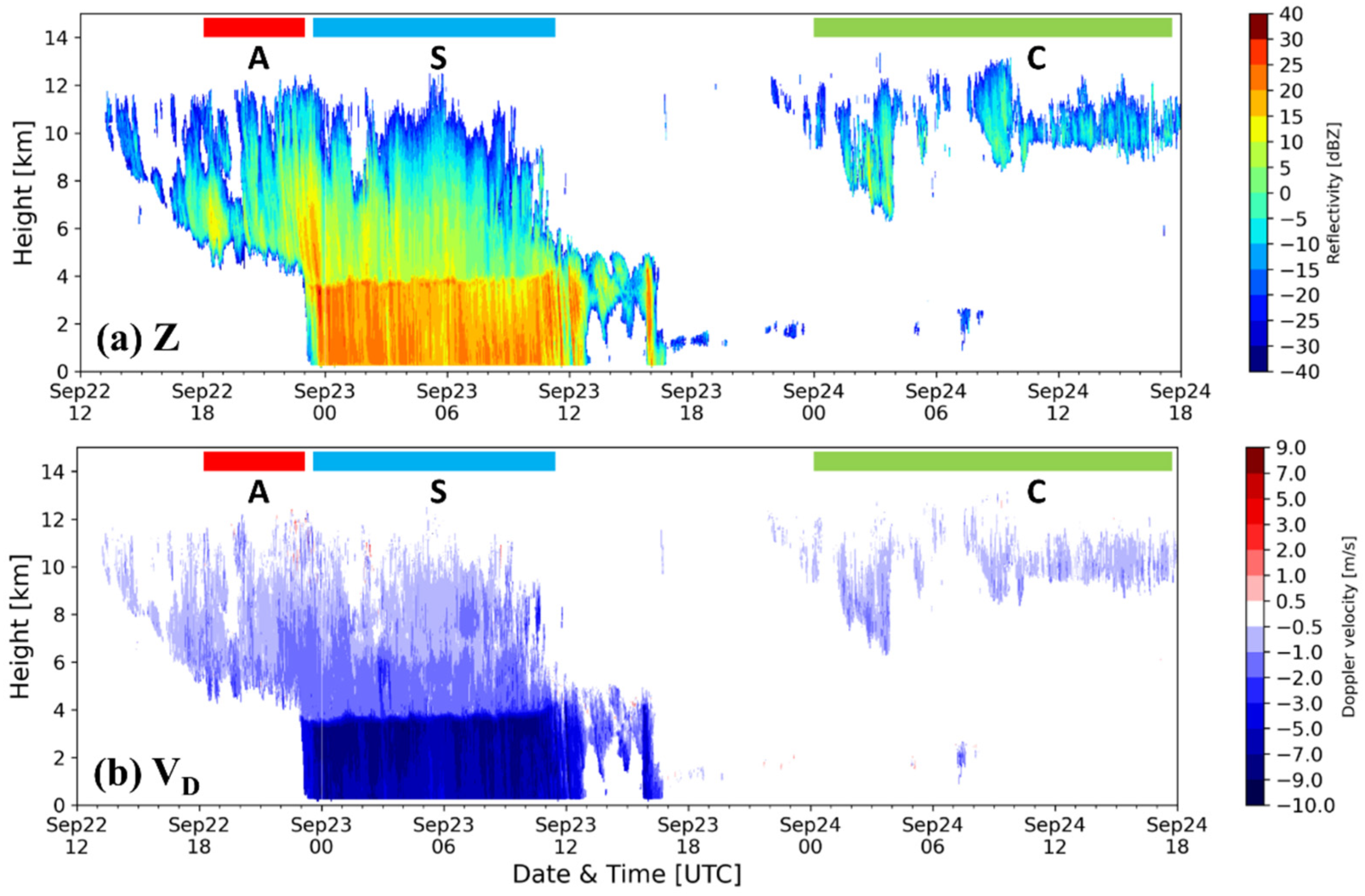
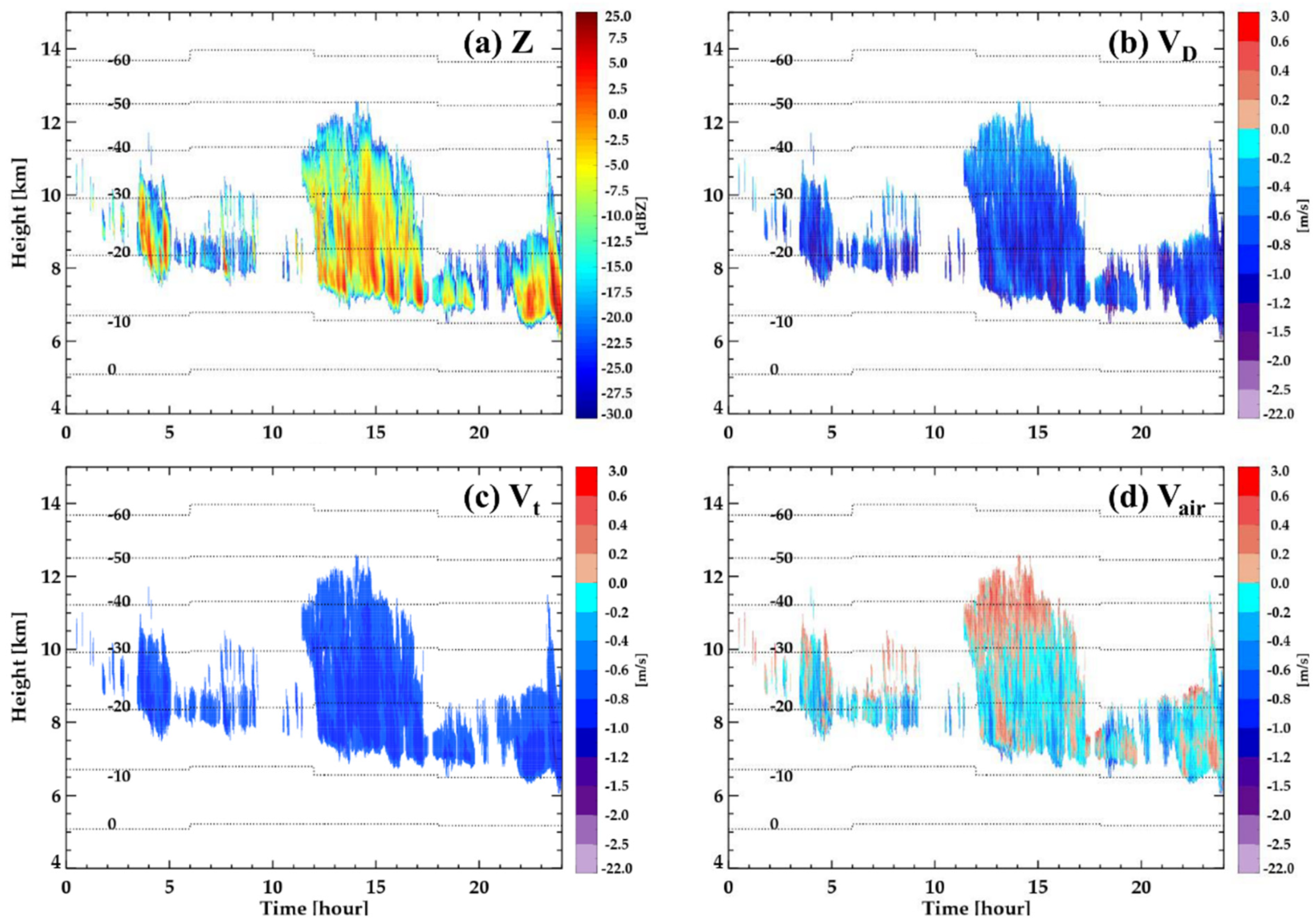
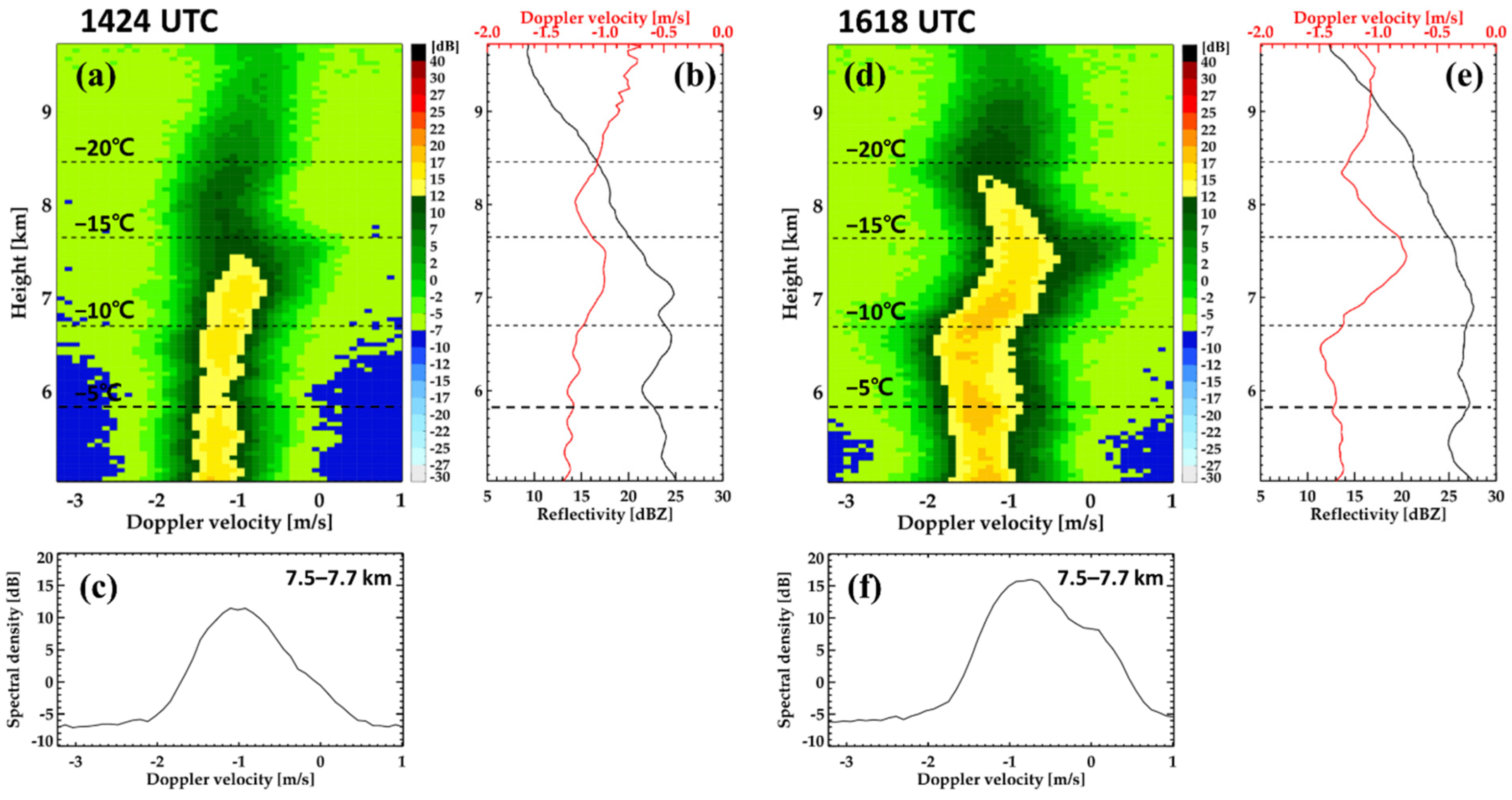
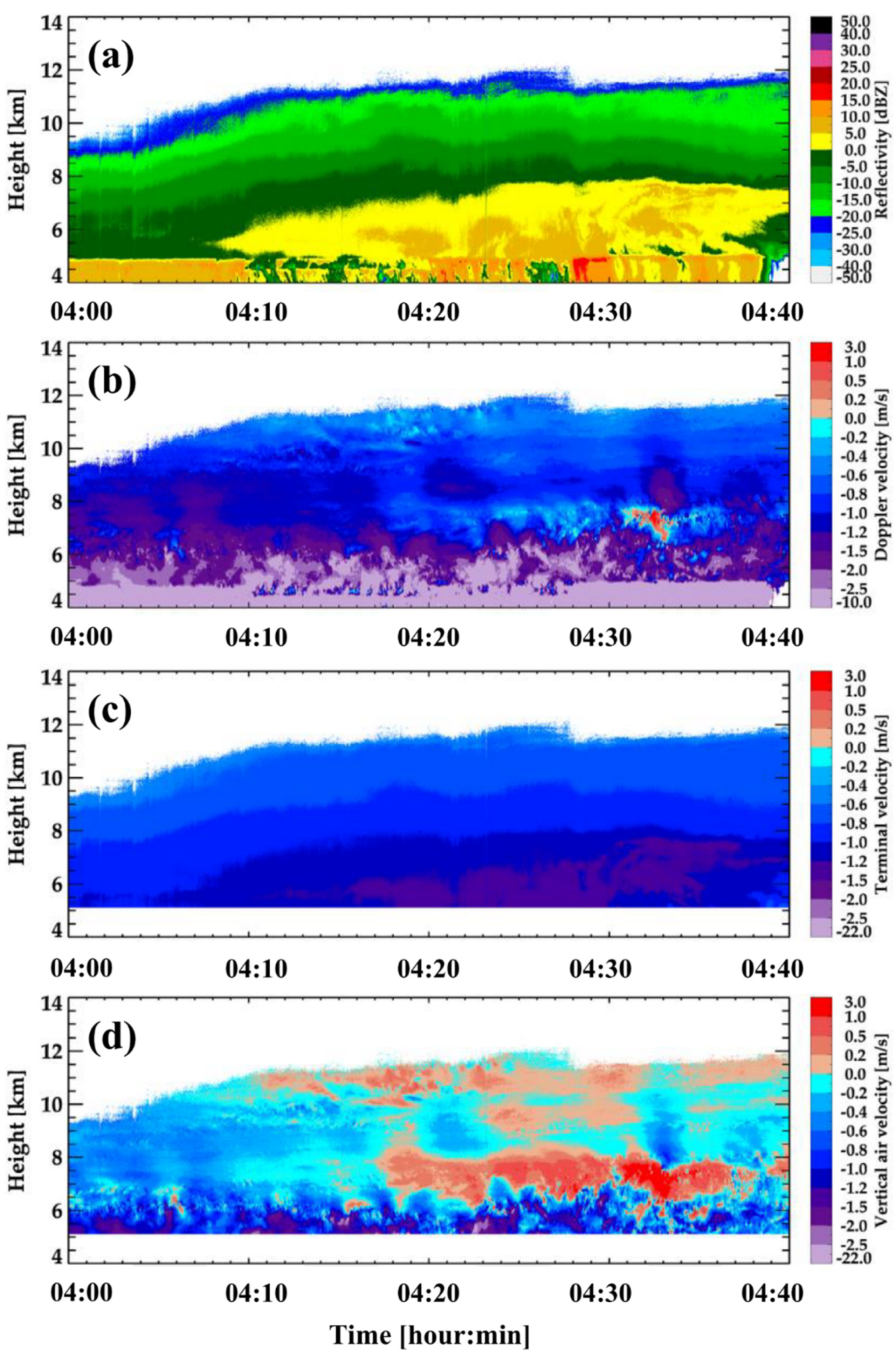
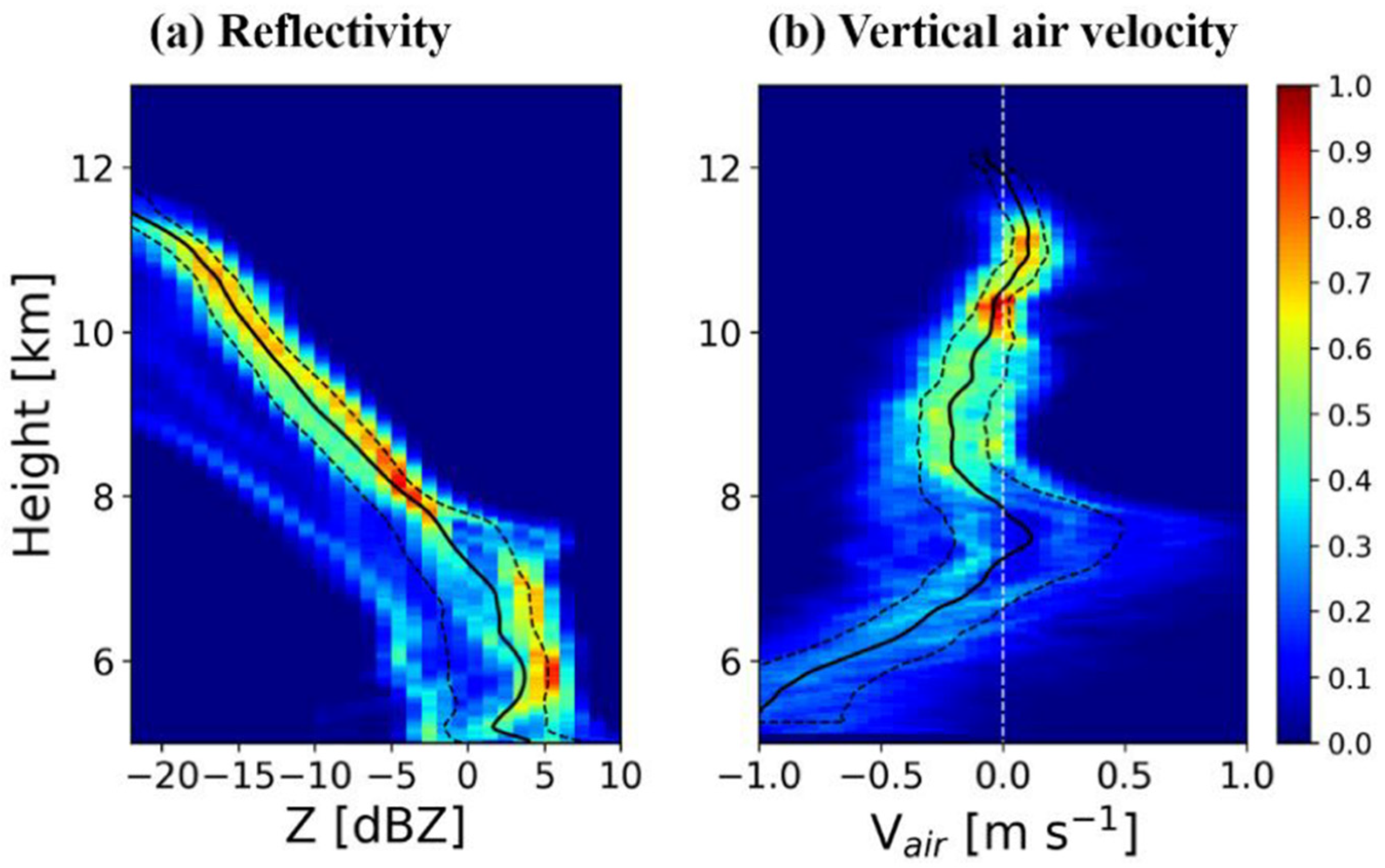
4.3. Variability of Vertical Air Motion in a Case of Kelvin–Helmholtz (K–H) Wave on 18 June 2013
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liou, K.-N. Influence of Cirrus Clouds on Weather and Climate Processes: A Global Perspective. Mon. Weather Rev. 1986, 114, 1167–1199. [Google Scholar] [CrossRef]
- Parry, M.L.; Canziani, O.F.; Palutikof, J.P.; van der Linden, P.J.; Hanson, C.E. Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the IPCC; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Jakob, C. Ice clouds in numerical weather prediction models: Progress, problems, and prospects. In Cirrus; Lynch, D.K., Sassen, K., Starr, D.O., Stephens, G., Eds.; Oxford University Press: Oxford, UK, 2002; pp. 327–345. ISBN 0-19-513072-3. [Google Scholar]
- Heymsfield, A.J.; Donner, L.J. A Scheme for Parameterizing Ice-Cloud Water Content in General Circulation Models. J. Atmos. Sci. 1990, 47, 1865–1877. [Google Scholar] [CrossRef][Green Version]
- Hong, S.-Y.; Lim, K.-S.S.; Kim, J.-H.; Lim, J.-O.J.; Dudhia, J. Sensitivity Study of Cloud-Resolving Convective Simulations with WRF Using Two Bulk Microphysical Parameterizations: Ice-Phase Microphysics versus Sedimentation Effects. J. Appl. Meteorol. Clim. 2009, 48, 61–76. [Google Scholar] [CrossRef]
- Jang, S.; Lim, K.-S.S.; Ko, J.; Kim, K.; Lee, G.; Cho, S.-J.; Ahn, K.-D.; Lee, Y.-H. Revision of WDM7 Microphysics Scheme and Evaluation for Precipitating Convection over the Korean Peninsula. Remote Sens. 2021, 13, 3860. [Google Scholar] [CrossRef]
- Morrison, H.; Gettelman, A. A New Two-Moment Bulk Stratiform Cloud Microphysics Scheme in the Community Atmosphere Model, Version 3 (CAM3). Part I: Description and Numerical Tests. J. Clim. 2008, 21, 3642–3659. [Google Scholar] [CrossRef]
- Hong, S.Y.; Dudhia, J.; Chen, S.H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Bouniol, D.; Delanoë, J.; Duroure, C.; Protat, A.; Giraud, V.; Penide, G. Microphysical characterisation of West African MCS anvils. Q. J. R. Meteorol. Soc. 2010, 136, 323–344. [Google Scholar] [CrossRef]
- Delanoë, J.; Protat, A.; Bouniol, D.; Heymsfield, A.J.; Bansemer, A.; Brown, P. The Characterization of Ice Cloud Properties from Doppler Radar Measurements. J. Appl. Meteorol. Clim. 2007, 46, 1682–1698. [Google Scholar] [CrossRef][Green Version]
- Heymsfield, A.J.; Wang, Z.; Matrosov, S. Improved Radar Ice Water Content Retrieval Algorithms Using Coincident Microphysical and Radar Measurements. J. Appl. Meteorol. 2005, 44, 1391–1412. [Google Scholar] [CrossRef]
- Mace, G.G.; Benson, S.; Vernon, E. Cirrus Clouds and the Large-Scale Atmospheric State: Relationships Revealed by Six Years of Ground-Based Data. J. Clim. 2006, 19, 3257–3278. [Google Scholar] [CrossRef]
- Matrosov, S.Y.; Korolev, A.V.; Heymsfield, A.J. Profiling Cloud Ice Mass and Particle Characteristic Size from Doppler Radar Measurements. J. Atmos. Ocean. Technol. 2002, 19, 1003–1018. [Google Scholar] [CrossRef]
- Protat, A.; Bouniol, D.; Delanoë, J.; O’Connor, E.; May, P.T.; Plana-Fattori, A.; Hasson, A.; Görsdorf, U.; Heymsfield, A.J. Assessment of Cloudsat Reflectivity Measurements and Ice Cloud Properties Using Ground-Based and Airborne Cloud Radar Observations. J. Atmos. Ocean. Technol. 2009, 26, 1717–1741. [Google Scholar] [CrossRef]
- Sassen, K.; Campbell, J.R. A Midlatitude Cirrus Cloud Climatology from the Facility for Atmospheric Remote Sensing. Part I: Macrophysical and Synoptic Properties. J. Atmos. Sci. 2001, 58, 481–496. [Google Scholar] [CrossRef]
- Wang, J.; Dong, X.; Xi, B. Investigation of ice cloud microphysical properties of DCSs using aircraft in situ measurements during MC3E over the ARM SGP site. J. Geophys. Res. Atmos. 2015, 120, 3533–3552. [Google Scholar] [CrossRef]
- Yan, Y.; Liu, Y.; Liu, X.; Wang, X. Effects of Cloud Microphysics on the Vertical Structures of Cloud Radiative Effects over the Tibetan Plateau and the Arctic. Remote Sens. 2021, 13, 2651. [Google Scholar] [CrossRef]
- Ye, B.-Y.; Jung, E.; Shin, S.; Lee, G. Statistical Characteristics of Cloud Occurrence and Vertical Structure Observed by a Ground-Based Ka-Band Cloud Radar in South Korea. Remote Sens. 2020, 12, 2242. [Google Scholar] [CrossRef]
- Kärcher, B.; Ström, J. The roles of dynamical variability and aerosols in cirrus cloud formation. Atmos. Chem. Phys. Discuss. 2003, 3, 823–838. [Google Scholar] [CrossRef]
- Protat, A.; Williams, C. The Accuracy of Radar Estimates of Ice Terminal Fall Speed from Vertically Pointing Doppler Radar Measurements. J. Appl. Meteorol. Clim. 2011, 50, 2120–2138. [Google Scholar] [CrossRef]
- Heymsfield, A.J.; Westbrook, C. Advances in the Estimation of Ice Particle Fall Speeds Using Laboratory and Field Measurements. J. Atmos. Sci. 2010, 67, 2469–2482. [Google Scholar] [CrossRef]
- Kollias, P.; Tselioudis, G.; Albrecht, B.A. Cloud climatology at the Southern Great Plains and the layer structure, drizzle, and atmospheric modes of continental stratus. J. Geophys. Res. Space Phys. 2007, 112, D09116. [Google Scholar] [CrossRef]
- Kollias, P.; Clothiaux, E.E.; Miller, M.A.; Albrecht, B.A.; Stephens, G.L.; Ackerman, T.P. Millimeter-Wavelength Radars: New Frontier in Atmospheric Cloud and Precipitation Research. Bull. Am. Meteorol. Soc. 2007, 88, 1608–1624. [Google Scholar] [CrossRef]
- Kalesse, H.; Kollias, P. Climatology of High Cloud Dynamics Using Profiling ARM Doppler Radar Observations. J. Clim. 2013, 26, 6340–6359. [Google Scholar] [CrossRef]
- Deng, M.; Mace, G.G. Cirrus Microphysical Properties and Air Motion Statistics Using Cloud Radar Doppler Moments. Part I: Algorithm Description. J. Appl. Meteorol. Clim. 2006, 45, 1690–1709. [Google Scholar] [CrossRef]
- Kalesse, H.; Kollias, P.; Szyrmer, W. On using the relationship between Doppler velocity and radar reflectivity to identify microphysical processes in midlatitudinal ice clouds. J. Geophys. Res. Atmos. 2013, 118, 12168–12179. [Google Scholar] [CrossRef]
- Orr, B.W.; Kropfli, R.A. A Method for Estimating Particle Fall Velocities from Vertically Pointing Doppler Radar. J. Atmos. Ocean. Technol. 1999, 16, 29–37. [Google Scholar] [CrossRef]
- Plana-Fattori, A.; Protat, A.; Delanoë, J. Observing ice clouds with a Doppler cloud radar. Comptes Rendus Phys. 2010, 11, 96–103. [Google Scholar] [CrossRef]
- Szyrmer, W.; Tatarevic, A.; Kollias, P. Ice clouds microphysical retrieval using 94-GHz Doppler radar observations: Basic relations within the retrieval framework. J. Geophys. Res. Space Phys. 2012, 117, D14203. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, S.-W.; Kim, M.-H.; Yoon, S.-C. Geometric and optical properties of cirrus clouds inferred from three-year ground-based lidar and CALIOP measurements over Seoul, Korea. Atmos. Res. 2014, 139, 27–35. [Google Scholar] [CrossRef]
- Heymsfield, A.J.; Iaquinta, J. Cirrus Crystal Terminal Velocities. J. Atmos. Sci. 2000, 57, 916–938. [Google Scholar] [CrossRef]
- Matrosov, S.; Heymsfield, A.J. Use of Doppler radar to assess ice cloud particle fall velocity-size relations for remote sensing and climate studies. J. Geophys. Res. Space Phys. 2000, 105, 22427–22436. [Google Scholar] [CrossRef]
- Bailey, M.P.; Hallett, J. A Comprehensive Habit Diagram for Atmospheric Ice Crystals: Confirmation from the Laboratory, AIRS II, and Other Field Studies. J. Atmos. Sci. 2009, 66, 2888–2899. [Google Scholar] [CrossRef]
- Magono, C. Meteorological Classification of Snow Crystals. J. Jpn. Soc. Snow Ice 1962, 24, 33–37. [Google Scholar] [CrossRef]
- Matrosov, S.Y.; Ryzhkov, A.V.; Maahn, M.; de Boer, G. Hydrometeor Shape Variability in Snowfall as Retrieved from Polarimetric Radar Measurements. J. Appl. Meteorol. Clim. 2020, 59, 1503–1517. [Google Scholar] [CrossRef]
- Westbrook, C.D.; Illingworth, A.J.; O’Connor, E.J.; Hogan, R.J. Doppler lidar measurements of oriented planar ice crystals falling from supercooled and glaciated layer clouds. Q. J. R. Meteorol. Soc. 2010, 136, 260–276. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Frequency (wavelength) | 33.44 GHz (8.9 mm) |
| Transmitter | Magnetron |
| Peak power | ≥15 kW |
| Antenna diameter | 1.5 m |
| Beamwidth | 0.42° |
| Gate spacing/maximum range | 15 m/15 km |
| Polarization mode | Single transmitting, dual receiving |
| Product | Linear depolarization ratio (LDR), radar reflectivity (Z), Doppler velocity (VD), spectrum width (SW) |
| Case No. | Period | Height (km) | Case No. | Period | Height (km) |
|---|---|---|---|---|---|
| C1 | 13/06/2014, 10–23 UTC | 8–14 | C18 | 18/09/2015, 06–23 UTC | 7–11 |
| C2 | 14/06/2014, 00–23 UTC | 7–13 | C19 | 24/09/2015, 00–18 UTC | 6–14 |
| C3 | 26/06/2014, 00–09 UTC | 8–13 | S1 | 05/07/2014, 10–21 UTC | 5–14 |
| C4 | 27/06/2014, 05–23 UTC | 6–12 | S2 | 16/07/2014, 08–17 UTC | 5–13 |
| C5 | 08/07/2014, 07–13 UTC | 10–14 | S3 | 12/10/2014, 05–23 UTC | 5–13 |
| C6 | 16/08/2014, 00–11 UTC | 10–13 | S4 | 11/07/2015, 04–23 UTC | 5.5–14 |
| C7 | 30/08/2014, 01–12 UTC | 8–13 | S5 | 23/09/2015, 00–09 UTC | 4.5–13 |
| C8 | 22/09/2014, 10–21 UTC | 11–15 | S6 | 30/09/2015, 00–18 UTC | 5–14 |
| C9 | 25/09/2014, 07–23 UTC | 6–12 | A1 | 16/06/2014, 11–14 UTC | 4–13 |
| C10 | 15/10/2014, 15–21 UTC | 8–12 | A2 | 12/09/2014, 00–02 UTC | 4–12 |
| C11 | 15/03/2015, 05–11 UTC | 6–10 | A3 | 12/10/2014, 00–02UTC | 4–13 |
| C12 | 03/04/2015, 03–10 UTC | 8–13 | A4 | 22/05/2015, 10–14 UTC | 4–13 |
| C13 | 14/06/2015, 07–21 UTC | 8–13 | A5 | 04/06/2015, 14–15 UTC | 4–13 |
| C14 | 23/06/2015, 01–21 UTC | 7–14 | A6 | 17/06/2015, 03–04 UTC | 4–14 |
| C15 | 02/07/2015, 00–09 UTC | 10–14 | A7 | 06/07/2015, 04–10 UTC | 4–14 |
| C16 | 09/07/2015, 00–23 UTC | 8–13 | A8 | 16/09/2015, 02–06 UTC | 4–12 |
| C17 | 09/08/2015, 00–23 UTC | 6–13 | A9 | 22/09/2015, 17–22 UTC | 4–13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, B.-Y.; Lee, G. Vertical Structure of Ice Clouds and Vertical Air Motion from Vertically Pointing Cloud Radar Measurements. Remote Sens. 2021, 13, 4349. https://doi.org/10.3390/rs13214349
Ye B-Y, Lee G. Vertical Structure of Ice Clouds and Vertical Air Motion from Vertically Pointing Cloud Radar Measurements. Remote Sensing. 2021; 13(21):4349. https://doi.org/10.3390/rs13214349
Chicago/Turabian StyleYe, Bo-Young, and GyuWon Lee. 2021. "Vertical Structure of Ice Clouds and Vertical Air Motion from Vertically Pointing Cloud Radar Measurements" Remote Sensing 13, no. 21: 4349. https://doi.org/10.3390/rs13214349
APA StyleYe, B.-Y., & Lee, G. (2021). Vertical Structure of Ice Clouds and Vertical Air Motion from Vertically Pointing Cloud Radar Measurements. Remote Sensing, 13(21), 4349. https://doi.org/10.3390/rs13214349






