Improving Ship Detection in Clutter-Edge and Multi-Target Scenarios for High-Frequency Radar
Abstract
:1. Introduction
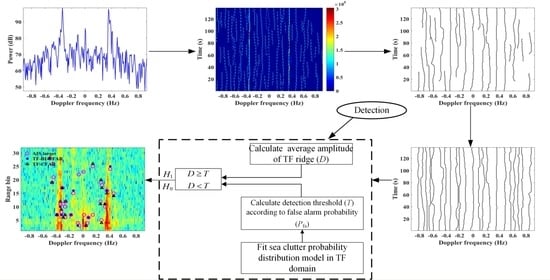
2. Method
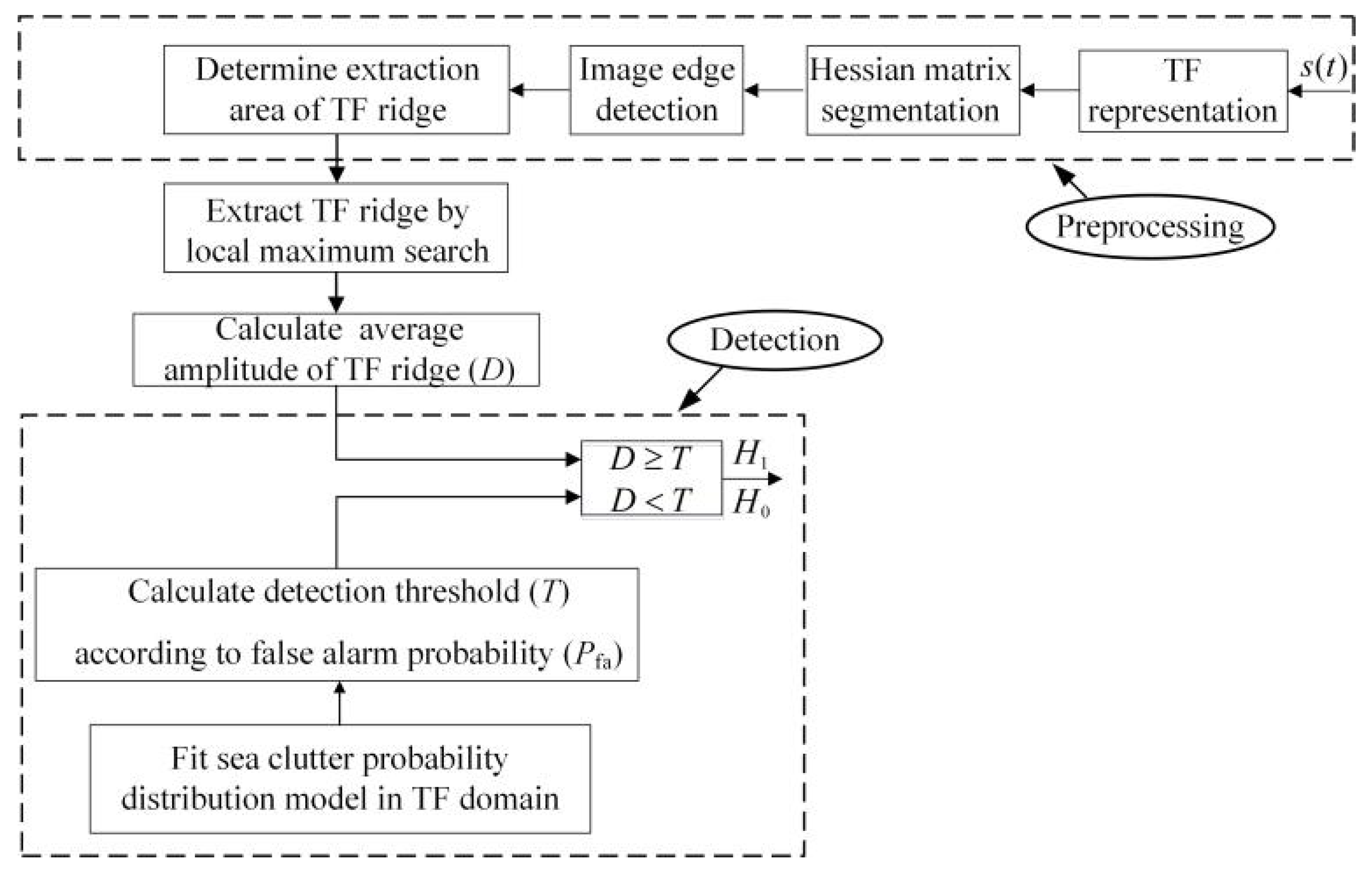
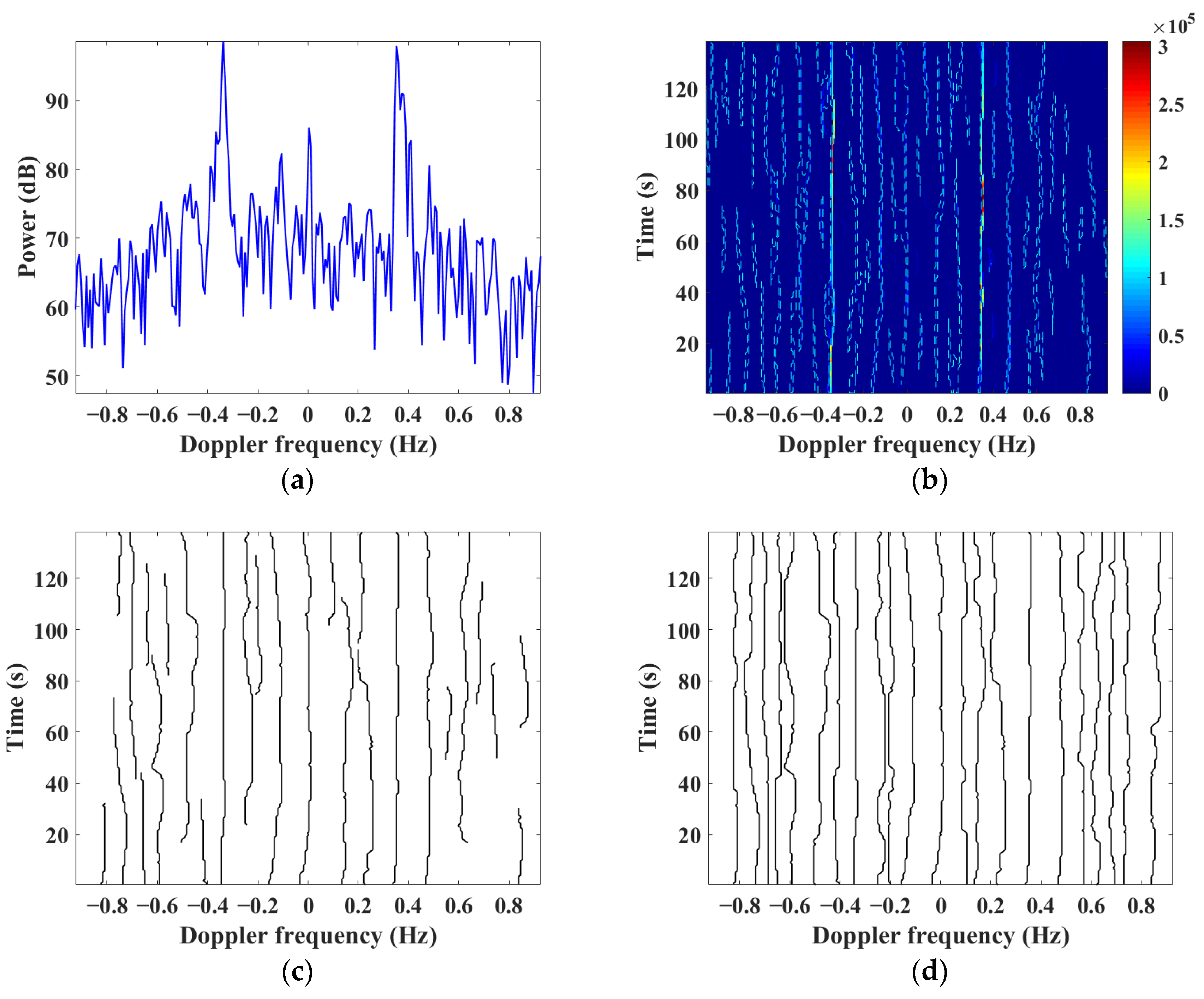
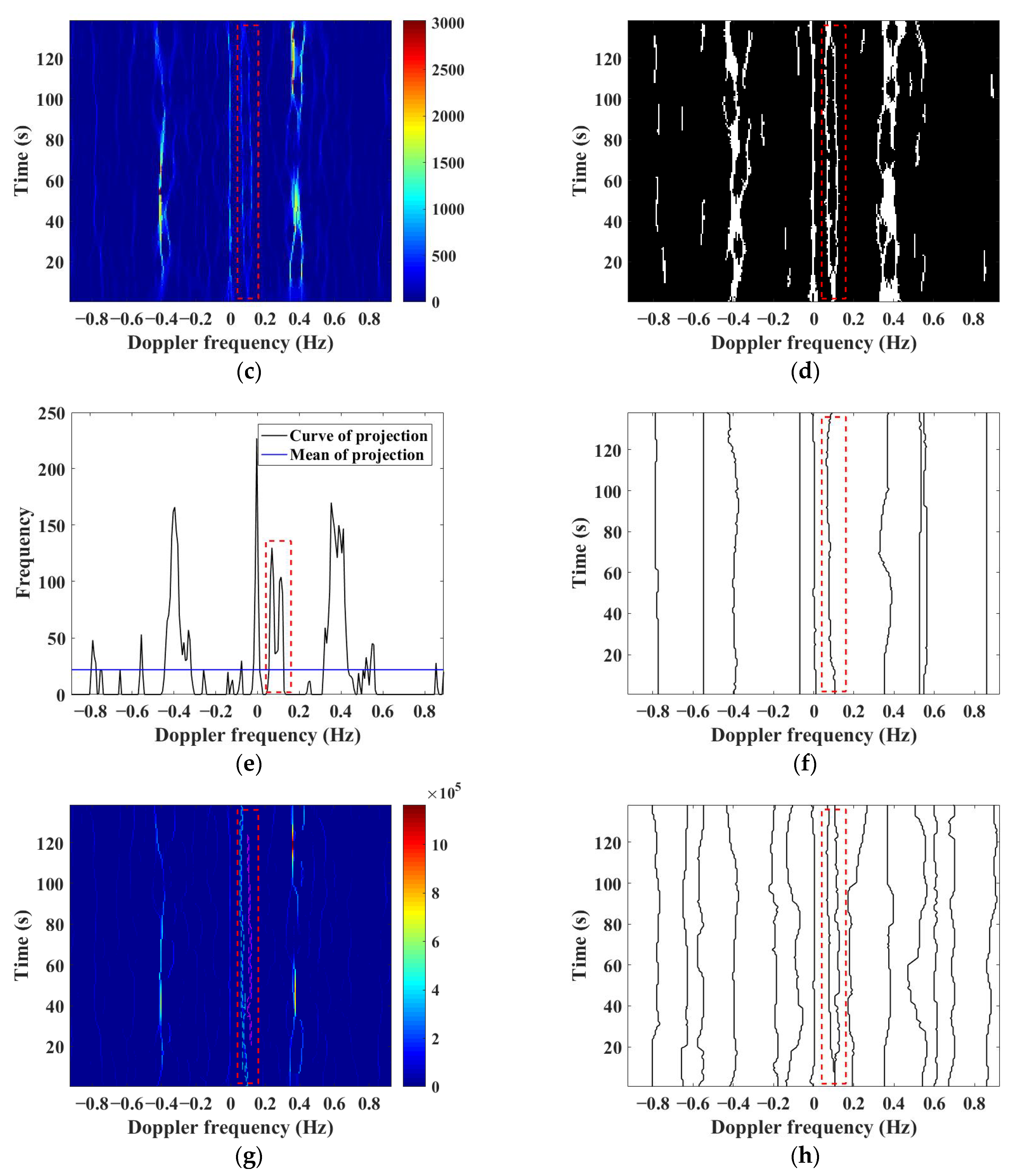
2.1. Signal Representation and Extraction
- The marked area where the TF ridge spans more than 20% of coherent integration time (CIT) is kept and the other areas in the TF plane are removed and set to zero;
- Each marked TF ridge area with a length greater than 80% of CIT is selected as a complete TF ridge region and the Doppler frequency ranges of them are recorded;
- For the broken TF ridge regions, the summation is performed in order in the time direction along the Doppler axis, and the Doppler region where the summation value from non-zero to zero is treated as a complete TF ridge region, and the Doppler range of the region is recorded;
- The complete TF ridge is extracted from the recorded Doppler frequency range based on local maximum search.
2.2. Target Detection
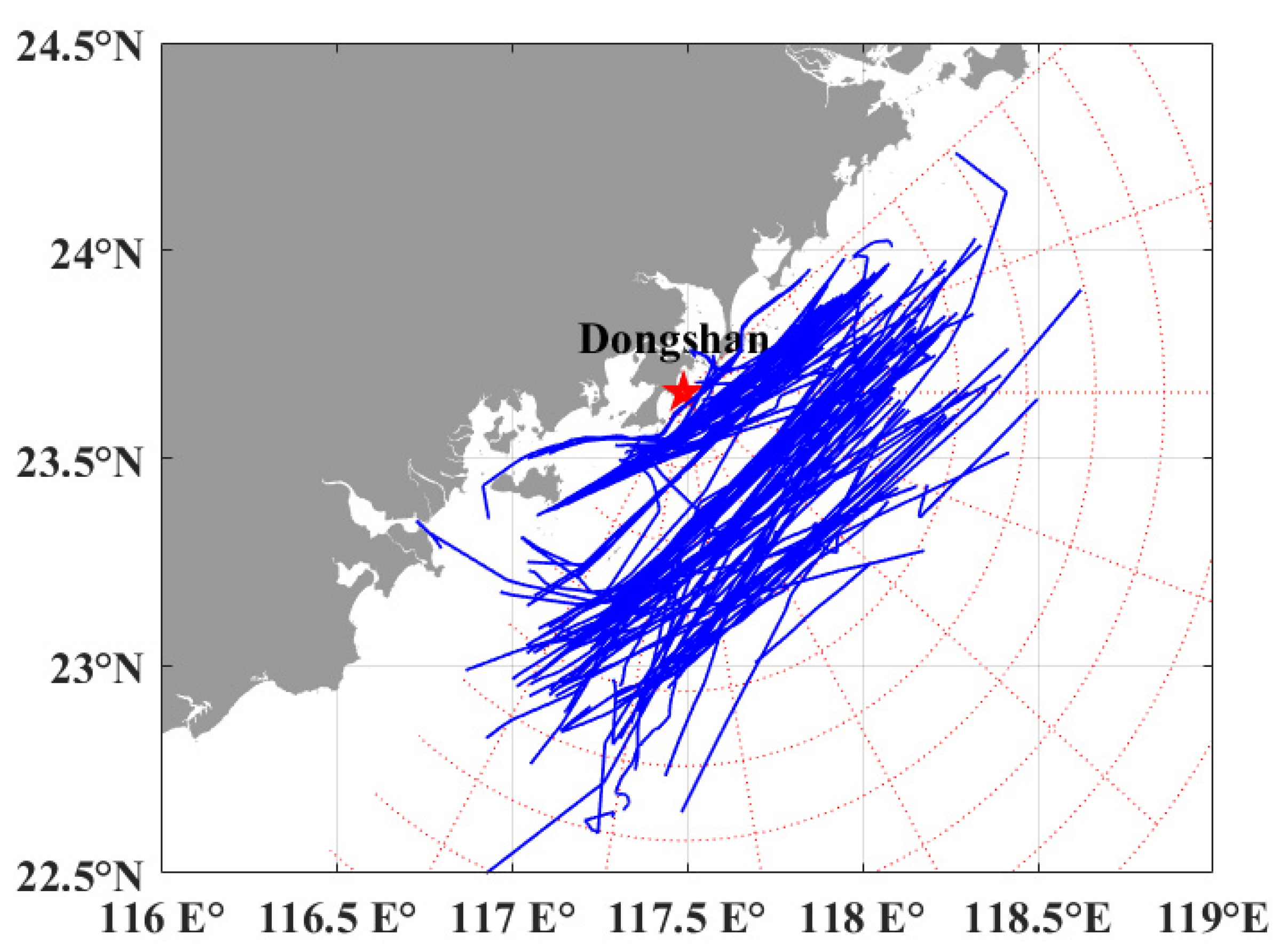
3. Results
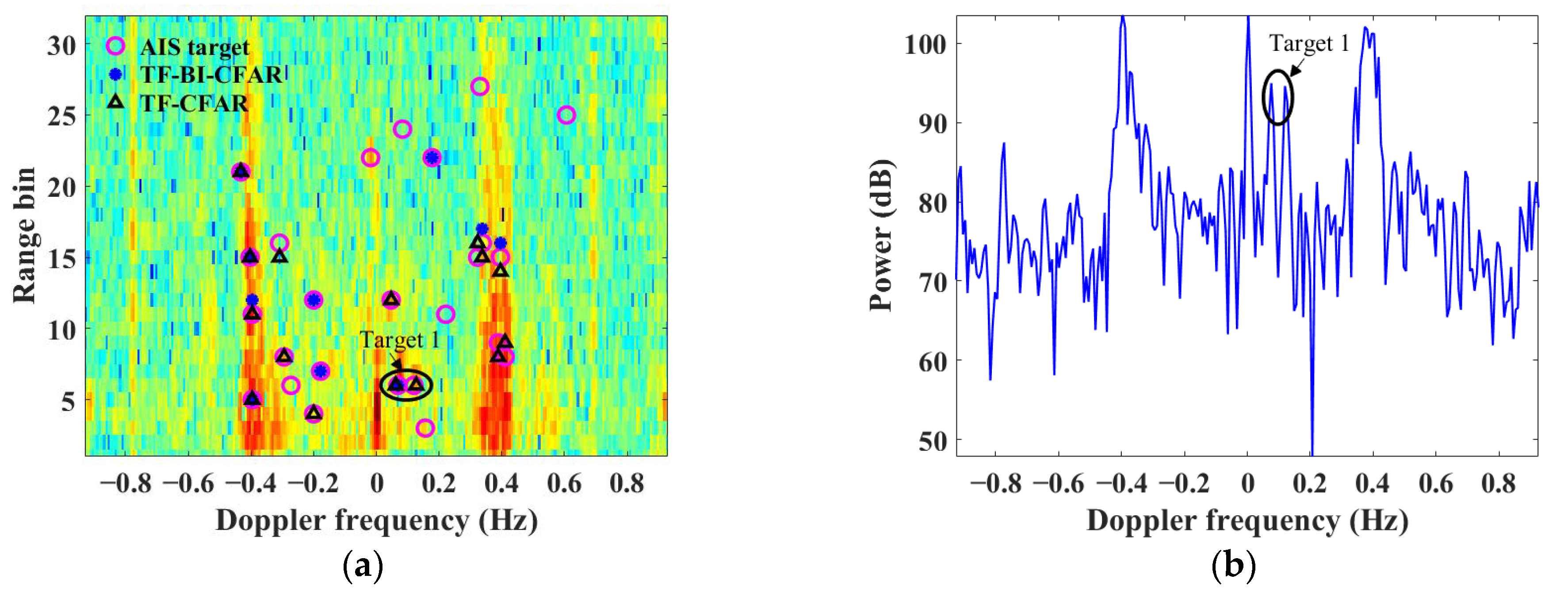
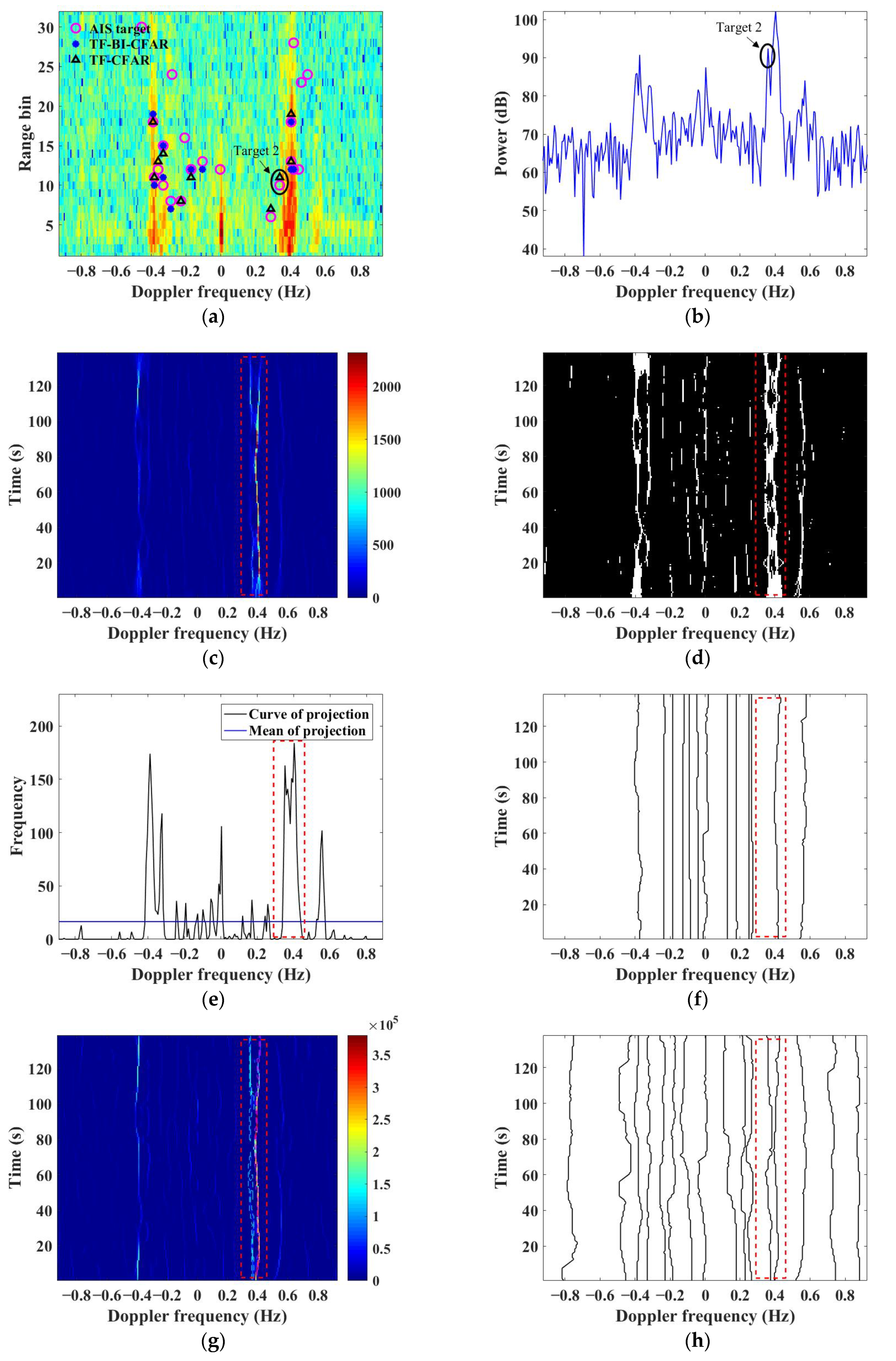
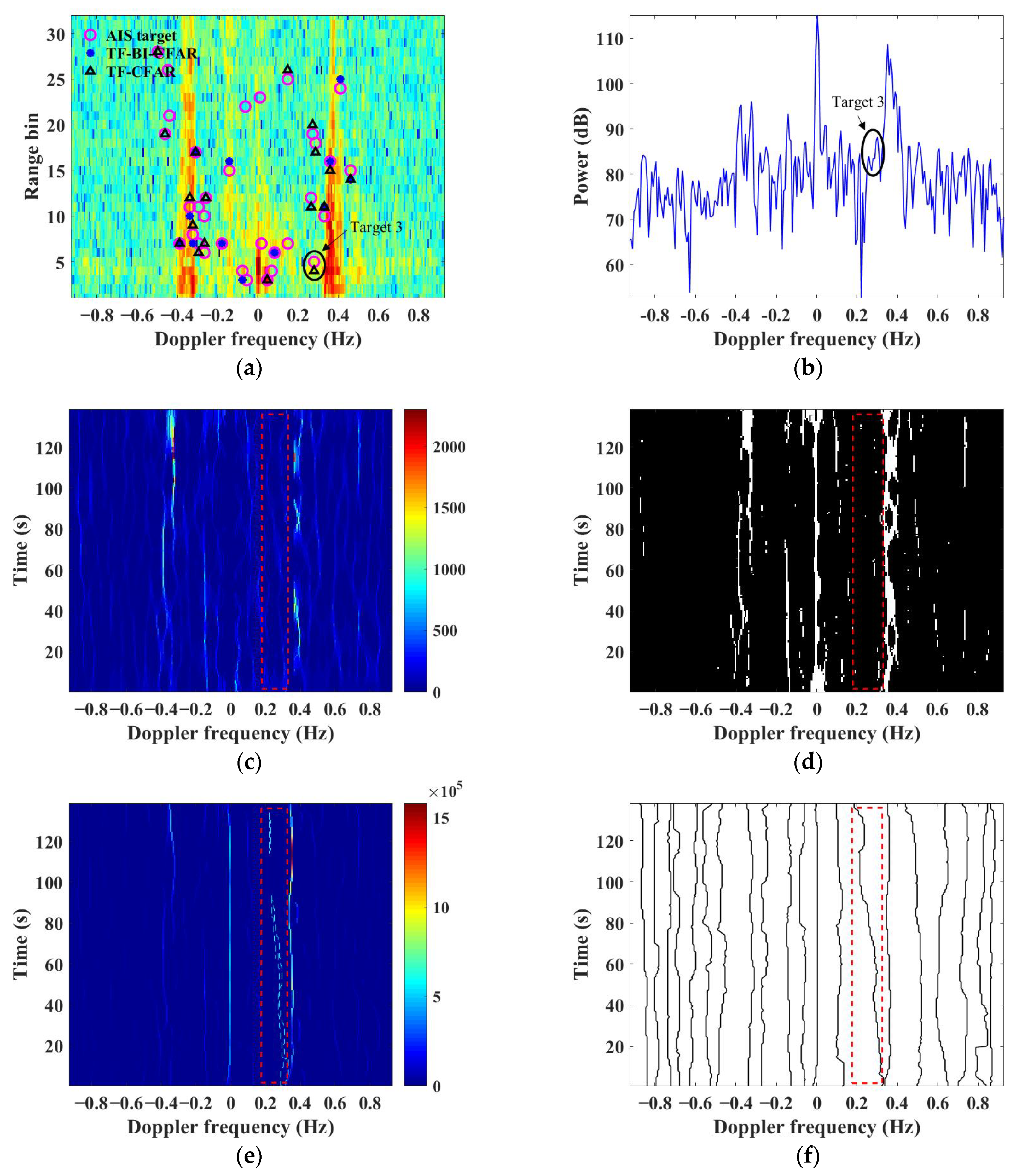
3.1. Comparison of TF-BI-CFAR and TF-CFAR
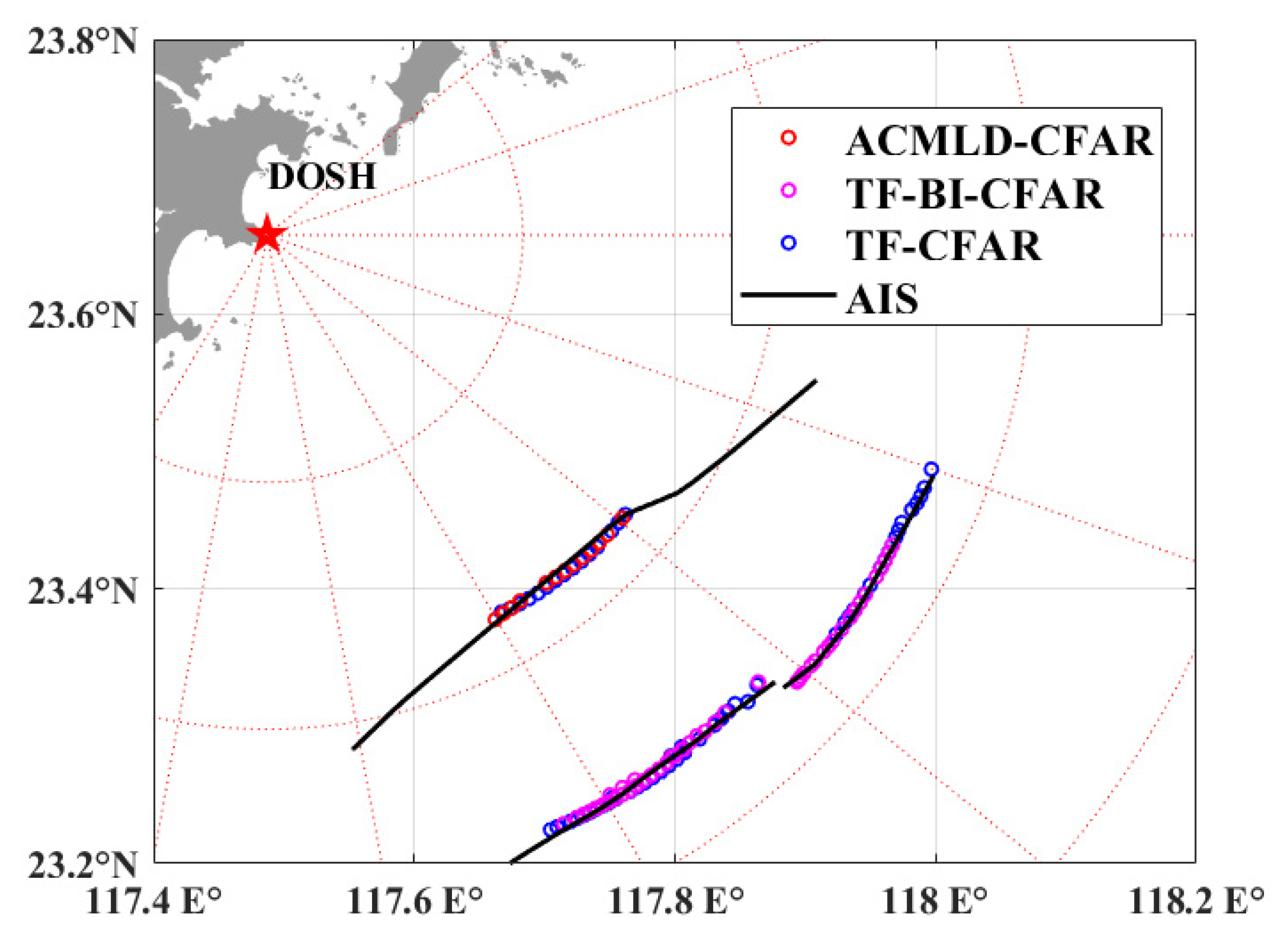
3.2. Target Matching
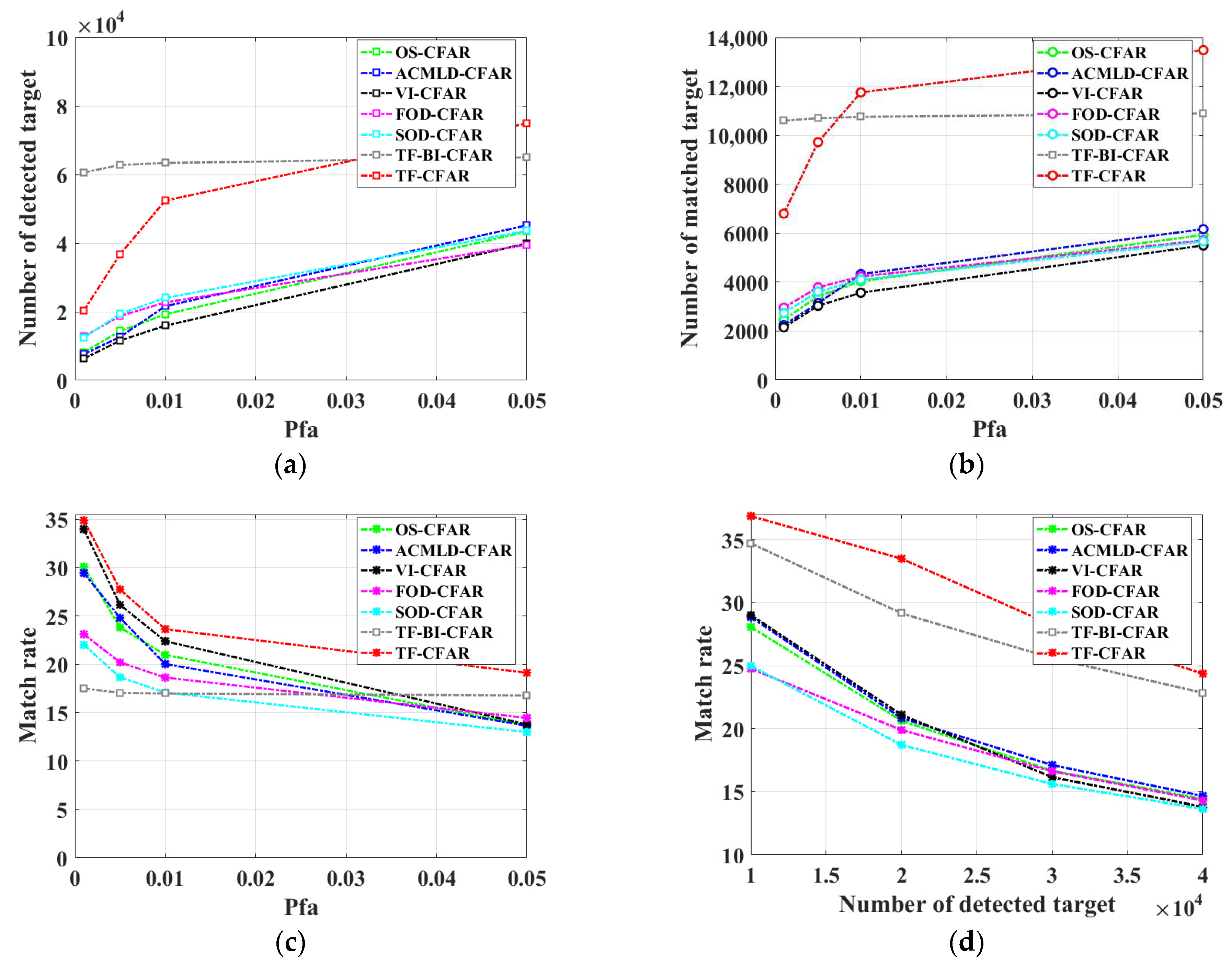
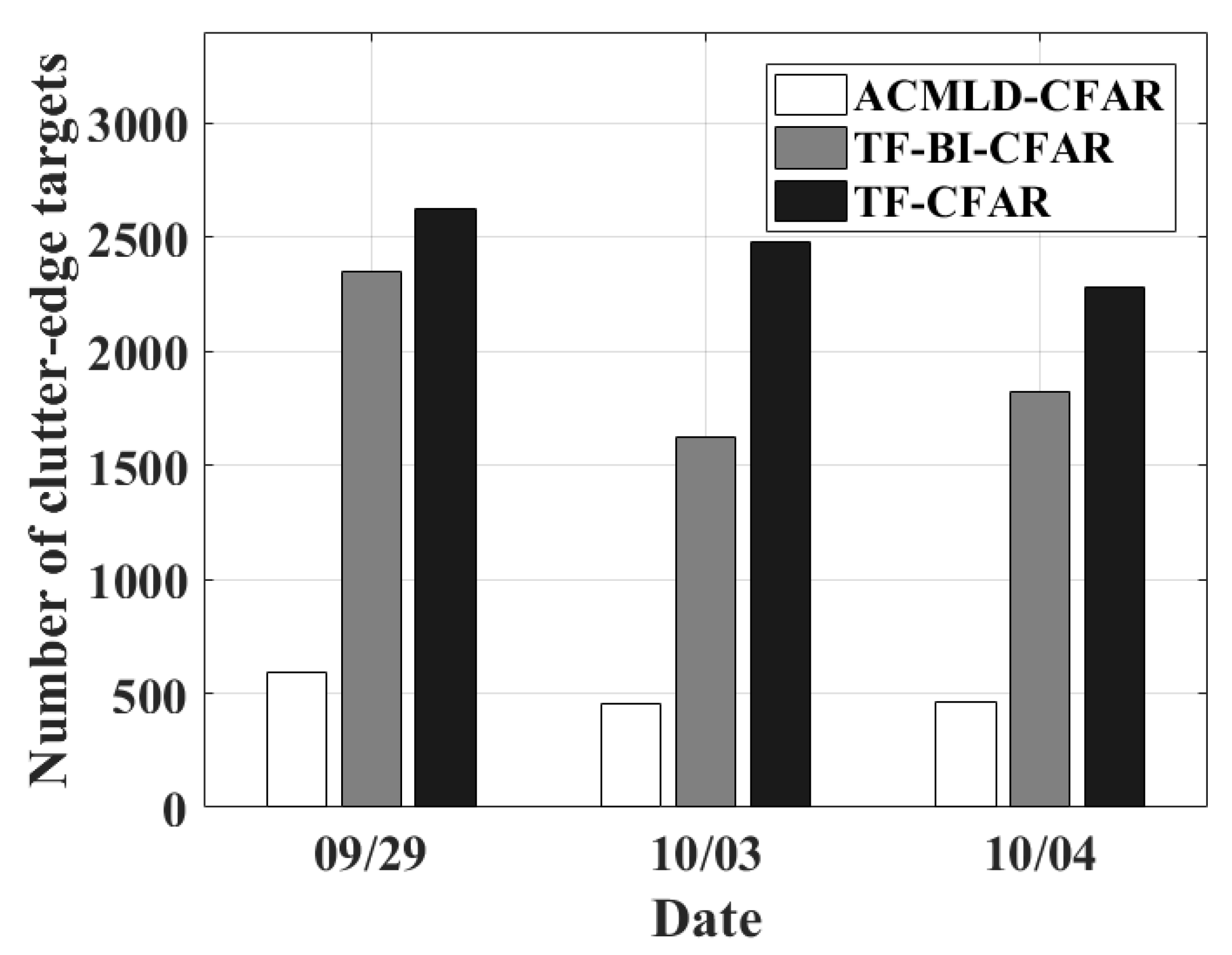
3.3. Comparison of Conventional CFAR and TF-CFAR
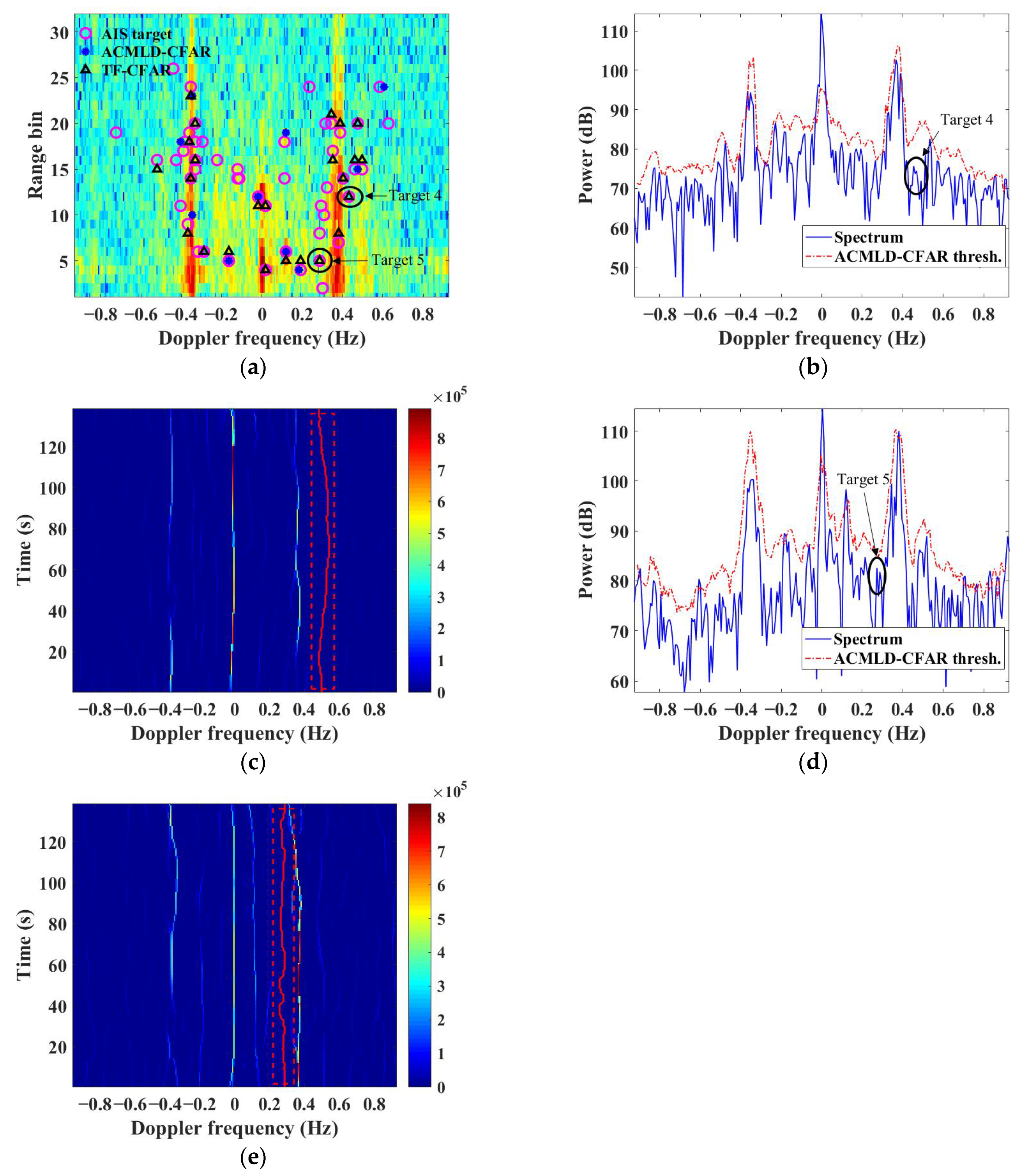
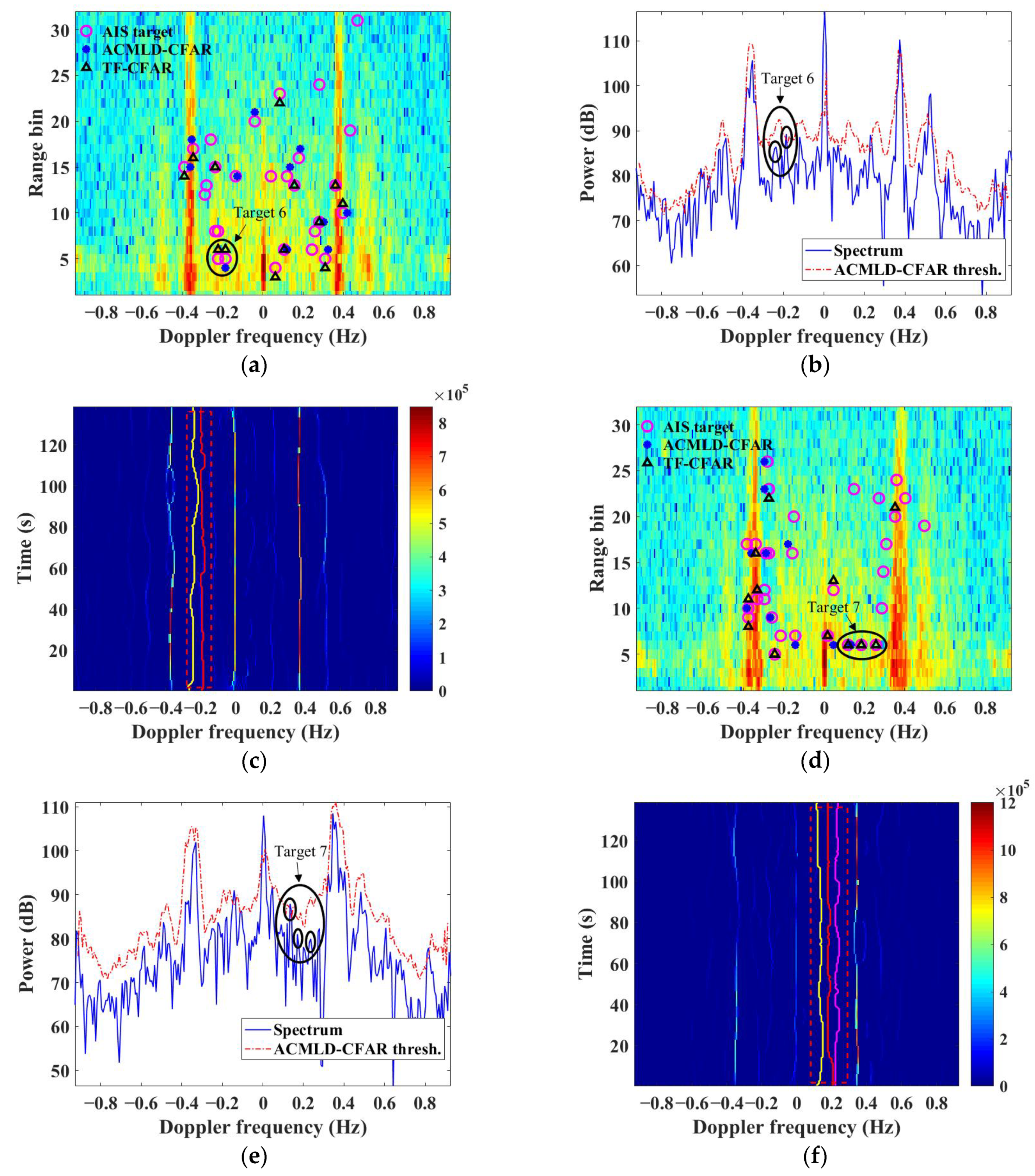
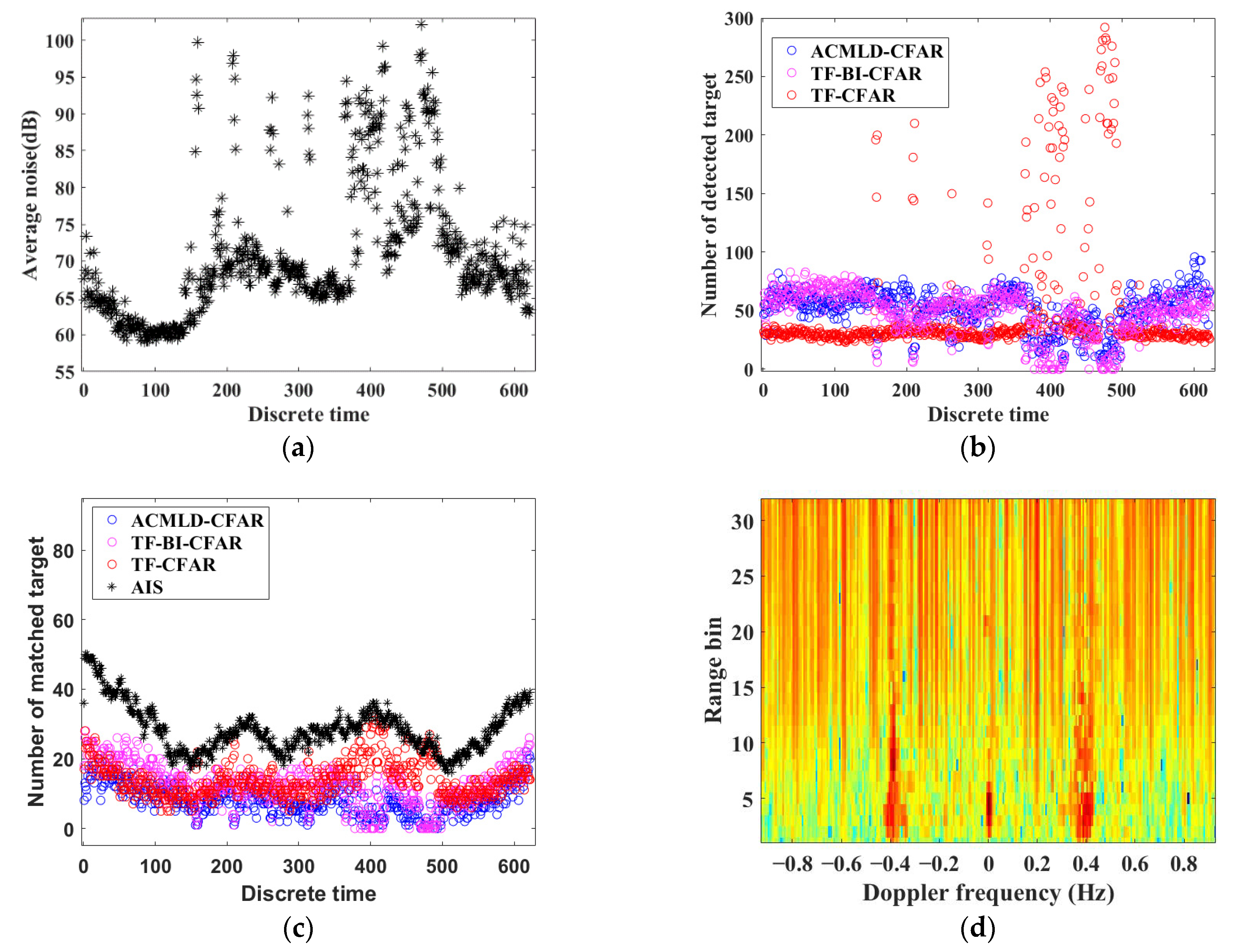
3.4. Impact of Strong Interference
3.5. Statistical Analysis of Matched Targets
4. Discussion
4.1. Length of TF Ridges
4.2. Number of SST
4.3. Strong Interference
4.4. Target Detection Strategies
4.5. The Pros and Cons of Different Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Mao, X.; Zhang, J.; Ji, Y. Detection of Vessel Targets in Sea Clutter Using in Situ Sea State Measurements with HFSWR. IEEE Geosci. Remote Sens. Lett. 2018, 15, 302–306. [Google Scholar] [CrossRef]
- Sun, W.; Huang, W.; Ji, Y.; Dai, Y.; Ren, P.; Hao, X. A Vessel Azimuth and Course Joint Re-Estimation Method for Compact HFSWR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1041–1051. [Google Scholar] [CrossRef]
- Fujii, S.; Heron, M.; Kim, K.; Lai, J.; Lee, S.; Wu, X.; Wu, X.; Wyatt, L.; Yang, W. An Overview of Developments and Applications of Oceanographic Radar Networks in Asia and Oceania Countries. Ocean Sci. J. 2013, 48, 69–97. [Google Scholar] [CrossRef]
- Barrick, D. After 40 years, how are HF radar currents now being used? In Proceedings of the 2011 IEEE/OES 10th Current, Waves and Turbulence Measurements (CWTM), Monterey, CA, USA, 20–23 March 2011; p. 3. [Google Scholar] [CrossRef]
- Lai, Y.; Zhou, H.; Zeng, Y.; Wen, B. Quantifying and Reducing the DOA Estimation Error Resulting from Antenna Pattern Deviation for Direction-Finding HF Radar. Remote Sens. 2017, 9, 1285. [Google Scholar] [CrossRef] [Green Version]
- Abascal, A.J.; Sanchez, J.; Chiri, H.; Ferrer, M.I.; Cárdenas, M.; Gallego, A.; Castanedo, S.; Medina, R.; Alonso-Martirena, A.; Berx, B.; et al. Operational oil spill trajectory modelling using HF radar currents: A northwest European continental shelf case study. Mar. Pollut. Bull. 2017, 119, 336–350. [Google Scholar] [CrossRef]
- Lipa, B.; Barrick, D.; Diposaptono, S.; Isaacson, J.; Jena, B.K.; Nyden, B.; Rajesh, K.; Kumar, T.S. High Frequency (HF) Radar Detection of the Weak 2012 Indonesian Tsunamis. Remote Sens. 2012, 4, 2944–2956. [Google Scholar] [CrossRef] [Green Version]
- Lipa, B.; Barrick, D.; Saitoh, S.-I.; Ishikawa, Y.; Awaji, T.; Largier, J.; Garfield, N. Japan Tsunami Current Flows Observed by HF Radars on Two Continents. Remote Sens. 2011, 3, 1663–1679. [Google Scholar] [CrossRef] [Green Version]
- Dzvonkovskaya, A.; Rohling, H. Cargo ship RCS estimation based on HF radar measurements. In Proceedings of the 11th International Radar Symposium, Vilnius, Lithuania, 16–18 June 2010; pp. 1–4. [Google Scholar]
- Roarty, H.; Barrick, D.; Kohut, J.; Glenn, S. Dual-use of compact HF radars for the detection of mid- and large-size vessels. Turk. J. Electr. Eng. Comput. Sci. 2014, 18, 373–388. [Google Scholar]
- Barrick, D. History, present status, and future directions of HF surfacewave radars in the U.S. In Proceedings of the International Conference on Radar, Adelaide, SA, Australia, 3–5 September 2003; pp. 652–655. [Google Scholar] [CrossRef]
- Gurgel, K.; Antonischki, G. Remote sensing of surface currents and waves by the HF radar WERA. In Proceedings of the 7th International Conference Electronic Engineer in Oceanography, Southampton, UK, 23–25 June 1997; pp. 211–217. [Google Scholar] [CrossRef]
- Dzvonkovskaya, A.; Gurgel, K.; Rohling, H.; Schlick, T. Low power High Frequency Surface Wave Radar application for ship detection and tracking. In Proceedings of the 2008 International Conference on Radar, Adelaide, SA, Australia, 2–5 September 2008; pp. 627–632. [Google Scholar] [CrossRef]
- Dzvonkovskaya, A.; Rohling, H. HF radar performance analysis based on AIS ship information. In Proceedings of the 2010 IEEE Radar Conference, Arlington, VA, USA, 10–14 May 2010; pp. 1239–1244. [Google Scholar] [CrossRef]
- Gurgel, K.; Schlick, T.; Horstmann, J.; Maresca, S. Evaluation of an HF-radar ship detection and tracking algorithm by comparison to AIS and SAR data. In Proceedings of the 2010 International WaterSide Security Conference, Carrara, Italy, 3–5 November 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Martin, R.J.; Kearney, M.J. Remote sea current sensing using HF radar: An autoregressive approach. IEEE J. Ocean. Eng. 1997, 22, 151–155. [Google Scholar] [CrossRef]
- Gurgel, K.W.; Schlick, T. HF radar wave measurements in the presence of ship echoes–Problems and solutions. In Proceedings of the Europe Oceans, Brest, France, 20–23 June 2005; pp. 937–941. [Google Scholar] [CrossRef]
- Dobson, C.; Holenstein, K.; Smith, M.; Roarty, H.; Glenn, S.; Welan, C.; Barrick, D.; Isaacson, J. Monostatic vessel detection statistics from the CODAR SeaSonde. In Proceedings of the 2013 OCEANS, San Diego, CA, USA, 23–27 September 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Holenstein, K.; Dobson, C.; Smith, M.; Roarty, H.; Glenn, S.; Barrick, D.E. Bistatic vessel detection from the CODAR SeaSonde. In Proceedings of the 2013 OCEANS, San Diego, CA, USA, 23–27 September 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Smith, M.; Roarty, H.; Glenn, S.; Whelan, C.; Barrick, D.; Isaacson, J. Methods of associating CODAR seasonde vessel detection data into unique tracks. In Proceedings of the 2013 OCEANS, San Diego, CA, USA, 23–27 September 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Huang, X.J.; Wen, B.Y.; Ding, F. Ship detection and tracking using multi-frequency HFSWR. IEICE Electron. Express 2010, 7, 410–415. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Roarty, H.; Wen, B. Wave extraction with portable high-frequency surface wave radar OSMAR-S. J. Ocean Univ. China 2014, 13, 957–963. [Google Scholar] [CrossRef]
- Barrick, D.; Lipa, B. Using antenna patterns to improve the quality of SeaSonde HF radar surface current maps. In Proceedings of the IEEE Sixth Working Conference on Current Measurement, San Diego, CA, USA, 13 March 1999; pp. 5–8. [Google Scholar] [CrossRef]
- Evans, C.; Roarty, H.; Handel, E.; Glenn, S. Evaluation of three antenna pattern measurements for a 25 MHz seasonde. In Proceedings of the 2015 IEEE/OES Eleveth Current, Waves and Turbulence Measurement (CWTM), St. Petersburg, FL, USA, 2–6 March 2015; pp. 1–5. [Google Scholar] [CrossRef] [Green Version]
- Emery, B.; Washburn, L.; Whelan, C.; Barrick, D.; Harlan, J. Measuring Antenna Patterns for Ocean Surface Current HF Radars with Ships of Opportunity. J. Atmos. Ocean. Technol. 2014, 31, 1564–1582. [Google Scholar] [CrossRef]
- Wilson, H.; Leong, H. An estimation and verification of vessel radar-cross-sections for HF surface wave radar. In Proceedings of the 2003 International Conference on Radar, Adelaide, SA, Australia, 3–5 September 2003; pp. 711–716. [Google Scholar] [CrossRef]
- Leong, H.; Wilson, H. An estimation and verification of vessel radar cross sections for high-frequency surface-wave radar. IEEE Antennas Propag. Mag. 2006, 48, 11–16. [Google Scholar] [CrossRef]
- Emery, B.; Whelan, C.; Barrick, D.; Washbum, L. Ocean Current Radar Calibration with Ships of Opportunity and the Automatic Identification System Phase I Final Report. Available online: https://www.researchgate.net/publication/268256027 (accessed on 21 October 2021).
- Leong, H. An estimation of radar cross sections of small vessels at HF. In Proceedings of the 2007 IET International Conference on Radar Systems, Edinburgh, UK, 15–18 October 2007; pp. 1–4. [Google Scholar] [CrossRef]
- Chen, Z.; He, C.; Zhao, C.; Xie, F. Using SVD-FRFT Filtering to Suppress First-Order Sea Clutter in HFSWR. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1076–1080. [Google Scholar] [CrossRef]
- Chen, S.; Gill, E.W.; Huang, W. A High-Frequency Surface Wave Radar Ionospheric Clutter Model for Mixed-Path Propagation with the Second-Order Sea Scattering. IEEE Trans. Antennas Propag. 2016, 64, 5373–5381. [Google Scholar] [CrossRef]
- Guinvarc’h, R.; Lesturgie, M.; Durand, R.; Cheraly, A. On the Use of HF Surface Wave Radar in Congested Waters: Influence of Masking Effect on Detection of Small Ships. IEEE J. Ocean. Eng. 2006, 31, 894–903. [Google Scholar] [CrossRef]
- Frazer, G.; Williams, C. HF RCS of Small Boat Displacement in the Ocean. In Proceedings of the 2020 IEEE Radar Conference, Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Roarty, H.; Rivera Lemus, E.; Handel, E.; Glenn, S.; Barrick, D.; Isaacson, J. Performance Evaluation of SeaSonde High-Frequency Radar for Vessel Detection. Mar. Technol. Soc. J. 2011, 45, 14–24. [Google Scholar] [CrossRef]
- Blake, S. OS-CFAR theory for multiple targets and nonuniform clutter. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 785–790. [Google Scholar] [CrossRef]
- Kuang, C.; Wang, C.; Wen, B.; Hou, Y.; Lai, Y. An Improved CA-CFAR Method for Ship Target Detection in Strong Clutter Using UHF Radar. IEEE Signal Process. Lett. 2020, 27, 1445–1449. [Google Scholar] [CrossRef]
- Finn, H.M.; Johnson, R.S. Adaptive detection mode with threshold control as a function of spatially sampled clutter level estimates. RCA Rev. 1968, 29, 414–464. [Google Scholar]
- Trunk, G.V. Range Resolution of Targets Using Automatic Detectors. IEEE Trans. Aerosp. Electron. Syst. 1978, 14, 750–755. [Google Scholar] [CrossRef]
- Hansen, V.G.; Sawyers, J.H. Detectability Loss Due to “Greatest Of” Selection in a Cell-Averaging CFAR. IEEE Trans. Aerosp. Electron. Syst. 1980, 16, 115–118. [Google Scholar] [CrossRef]
- Rohling, H. Radar CFAR Thresholding in Clutter and Multiple Target Situations. IEEE Trans. Aerosp. Electron. Syst. 1983, 19, 608–621. [Google Scholar] [CrossRef]
- Himonas, S.D.; Barkat, M. Automatic censored CFAR detection for non-homogeneous environments. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 286–304. [Google Scholar] [CrossRef]
- Kim, C.J.; Han, D.S.; Lee, H.S. Generalized OS CFAR detector with noncoherent integration. Signal Process. 1993, 31, 43–56. [Google Scholar] [CrossRef]
- Gandhi, P.P.; Kassam, S.A. Analysis of CFAR processors in nonhomogeneous background. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 427–445. [Google Scholar] [CrossRef]
- Ozgunes, I.; Gandhi, P.P.; Kassam, S.A. A variably trimmed mean CFAR radar detector. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 1002–1014. [Google Scholar] [CrossRef]
- Gandhi, P.P.; Kassam, S.A. An adaptive order statistic constant false alarm rate detector. In Proceedings of the International Conference on Systems Engineering, Fairborn, OH, USA, 24–26 August 1989; pp. 85–88. [Google Scholar] [CrossRef]
- Viswanathan, R.; Eftekhari, A. A selection and estimation test for multiple target detection. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 509–519. [Google Scholar] [CrossRef]
- Smith, M.E.; Varshney, P.K. Intelligent CFAR processor based on data variability. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 837–847. [Google Scholar] [CrossRef]
- Kim, J.H.; Bell, M.R. A computationally efficient CFAR algorithm based on a goodness-of-fit test for piecewise homogeneous environments. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1519–1535. [Google Scholar] [CrossRef]
- Jiang, W.; Huang, Y.; Yang, J. Automatic censoring CFAR detector based on ordered data difference for low-flying helicopter safety. Sensors 2016, 16, 1055. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abbadi, A.; Abbane, A.; Bencheikh, M.L.; Soltani, F. A new adaptive CFAR processor in multiple target situations. In Proceedings of the 2017 Seminar on Detection Systems Architectures and Technologies (DAT), Algiers, Algeria, 20–22 February 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Abbadi, A.; Bouhedjeur, H.; Bellabas, A.; Menni, T.; Soltani, F. Generalized Closed-Form Expressions for CFAR Detection in Heterogeneous Environment. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1011–1015. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Ascher, S. A survey of tests for exponentiality. Commun. Stat.-Theory Methods 1990, 19, 1811–1825. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Suo, J.; Zhang, J.; Yao, T. Research on a New Comprehensive CFAR (Comp-CFAR) Processing Method. IEEE Access 2019, 7, 19401–19413. [Google Scholar] [CrossRef]
- Beklaouz, H.L.; Hamadouch, M.; Mimi, M.; Ahmed, A.T. Study and analysis of a new detector of radar targets using CFAR with Gabor transform. In Proceedings of the 2008 15th International Conference on Systems, Signals and Image Processing, Bratislava, Slovakia, 25–28 June 2008; pp. 437–440. [Google Scholar] [CrossRef]
- Lei, Z.; Huang, Y. Time-frequency analysis based image processing for maneuvering target detection in HF OTH radar. In Proceedings of the 2009 IET International Radar Conference, Guilin, China, 20–22 April 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Boashash, B. Time–Frequency Signal Analysis and Processing, 2nd ed.; Elsevier: New York, NY, USA, 2015; pp. 256–280. [Google Scholar]
- Chen, V.C.; Ling, H. Joint time-frequency analysis for radar signal and image processing. IEEE Signal Process. Mag. 1999, 16, 81–93. [Google Scholar] [CrossRef]
- Greco, M.; Bordoni, F.; Gini, F. X-band sea-clutter nonstationarity: Influence of long waves. IEEE J. Ocean. Eng. 2004, 29, 269–283. [Google Scholar] [CrossRef]
- Herselman, P.L.; Baker, C.J. Analysis of calibrated sea clutter and boat reflectivity data at C- and X-band in South African coastal waters. In Proceedings of the 2007 IET International Conference on Radar Systems, Edinburgh, UK, 15–18 October 2007; pp. 1–5. [Google Scholar] [CrossRef] [Green Version]
- Herselman, P.L.; Baker, C.J.; Wind, H.J.D. An analysis of X-band calibrated sea clutter and small boat reflectivity at medium-to-low grazing angles. Int. J. Navig. Observ. 2008, 2, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Panagopoulos, S.; Soraghan, J.J. Small-target detection in sea clutter. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1355–1361. [Google Scholar] [CrossRef]
- Grosdidier, S.; Baussard, A.; Khenchaf, A. HFSW radar model simulation and measurement. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3539–3549. [Google Scholar] [CrossRef]
- Stankovic, L.J.; Thayaparan, T.; Dakovic, M. Signal decomposition by using the S-method with application to the analysis of HF radar signals in sea-clutter. IEEE Trans. Signal Process. 2006, 54, 4332–4342. [Google Scholar] [CrossRef]
- Stankovic, L.J.; Bohme, J.F. Time-frequency analysis of multiple resonances in combustion engine signals. Signal Process. 1999, 9, 15–28. [Google Scholar] [CrossRef]
- Zuo, L.; Li, M.; Zhang, X.; Wang, Y.; Wu, Y. An Efficient Method for Detecting Slow-Moving Weak Targets in Sea Clutter Based on Time–Frequency Iteration Decomposition. IEEE Trans Geosci. Remote Sens. 2013, 51, 3659–3672. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, W.; Li, M.; Niu, J.; Jonathan Wu, Q.M. Automatic Detection of Ship Targets Based on Wavelet Transform for HF Surface Wavelet Radar. IEEE Geosci. Remote Sens. Lett. 2017, 14, 714–718. [Google Scholar] [CrossRef]
- Jiao, S.; Li, X.; Lu, X. An improved Ostu method for image segmentation. In Proceedings of the 2006 8th International Conference on Signal Processing, Guilin, China, 16–20 November 2006; pp. 164–166. [Google Scholar] [CrossRef]
- Cai, J.; Zhou, H.; Huang, W.; Wen, B. Ship Detection and Direction Finding Based on Time-Frequency Analysis for Compact HF Radar. IEEE Geosci. Remote Sens. Lett. 2021, 18, 72–76. [Google Scholar] [CrossRef]
- Yang, Z.; Tang, J.; Zhou, H.; Xu, X.; Tian, Y.; Wen, B. Joint Ship Detection Based on Time-Frequency Domain and CFAR Methods with HF Radar. Remote Sens. 2021, 13, 1548. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, H.; Tian, Y.; Zhao, J. Improved CFAR Detection and Direction Finding on Time-Frequency Plane With High-Frequency Radar. IEEE Geosci. Remote Sens. Lett. 2021. [Google Scholar] [CrossRef]
- Yu, G.; Wang, Z.; Zhao, P. Multisynchrosqueezing Transform. IEEE Trans. Ind. Electron. 2019, 66, 5441–5455. [Google Scholar] [CrossRef]
- Meignen, S.; Pham, D.; McLaughlin, S. On Demodulation, Ridge Detection, and Synchrosqueezing for Multicomponent Signals. IEEE Trans. Signal Process. 2017, 65, 2093–2103. [Google Scholar] [CrossRef] [Green Version]
- Xiao, B.; Ou, G.; Tang, H.; Bi, X.; Li, W. Multi-Focus Image Fusion by Hessian Matrix Based Decomposition. IEEE Trans. Multimedia 2020, 22, 285–297. [Google Scholar] [CrossRef]
- Chahine, C.; Vachier-Lagorre, C.; Chenoune, Y.; Berbari, R.E.; Fawal, Z.E.; Petit, E. Information fusion for unsupervised image segmentation using stochastic watershed and Hessian matrix. IET Image Process. 2018, 12, 525–531. [Google Scholar] [CrossRef]
- Anupama, P.; Nandyal, S. Blood vessel segmentation using Hessian matrix for diabetic retinopathy detection. In Proceedings of the 2017 Second International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 22–24 February 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Li, Y.; Gong, H.; Wu, W.; Liu, G.; Chen, G. An automated method using Hessian matrix and random walks for retinal blood vessel segmentation. In Proceedings of the 2015 8th International Congress on Image and Signal Processing (CISP), Shenyang, China, 14–16 October 2015; pp. 423–427. [Google Scholar] [CrossRef]
- Xia, S.; Zhu, H.; Liu, X.; Gong, M.; Huang, X.; Xu, L.; Zhang, H.; Guo, J. Vessel Segmentation of X-ray Coronary Angiographic Image Sequence. IEEE Trans. Biomed. Eng. 2020, 67, 1338–1348. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.H.; Gao, J.B.; White, K.D.; Merk, I.; Yao, K. Perceptual dominance time distributions in multistable visual perception. Biol. Cybern. 2004, 90, 256–263. [Google Scholar] [CrossRef]
- Liu, J.; Han, J.; Zhang, Z.; Li, J. Bayesian Detection for MIMO Radar in Gaussian Clutter. IEEE Trans. Signal Process. 2018, 66, 6549–6559. [Google Scholar] [CrossRef]
- Tian, Y.; Wen, B.; Tan, J.; Li, K.; Yan, Z.; Yang, J. A new fully-digital HF radar system for oceanographical remote sensing. IEICE Electron. Express 2013, 14, 1–6. [Google Scholar] [CrossRef] [Green Version]
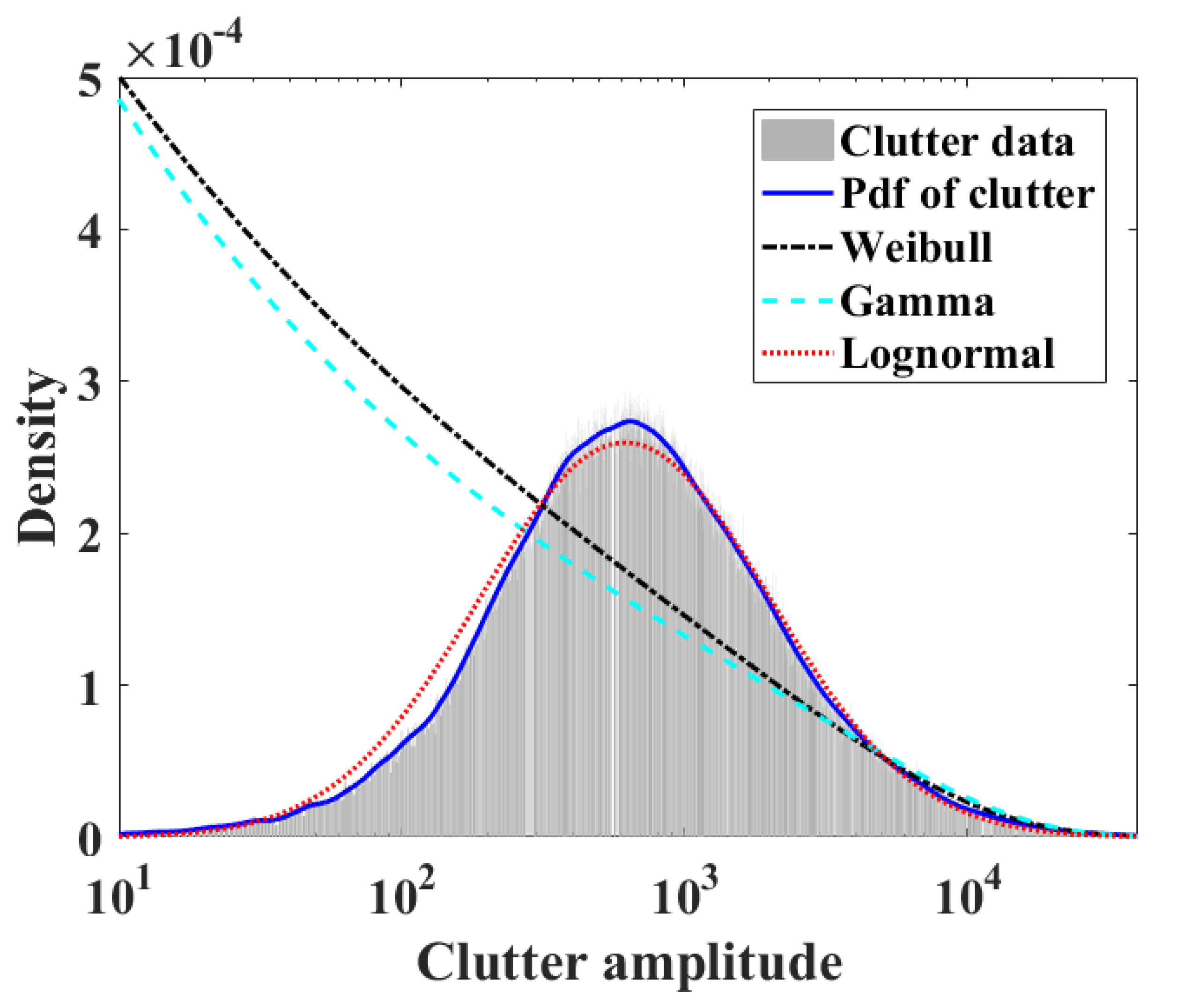

| Clutter Data | Weibull | Gamma | Log-Normal |
|---|---|---|---|
| Test value | 0.0679 | 0.1006 | 0.0165 |
| Parameter | Value |
|---|---|
| Carrier frequency (MHz) | 13.15 |
| Sweep band (kHz) | 60 |
| Range resolution (km) | 2.5 |
| Velocity resolution (m/s) | 0.0825 |
| Receive antenna | Cross-Loop/Monopole |
| Sweep cycle (s) | 0.54 |
| Coherent integration time (CIT) (s) | 138.24 |
| CFAR Method | Detected Number | Matched Number | Match Rate (%) |
|---|---|---|---|
| OS-CFAR | 30,000 | 5031 | 16.77 |
| ACMLD-CFAR | 5133 | 17.11 | |
| VI-CFAR | 4841 | 16.13 | |
| FOD-CFAR | 4984 | 16.61 | |
| SOD-CFAR | 4679 | 15.59 | |
| TF-BI-CFAR | 7737 | 25.79 | |
| TF-CFAR | 8463 | 28.21 |
| Time (Month/Day) | 09/29 | 10/04 | 10/05 | |
|---|---|---|---|---|
| CFAR Method | Detected Number | Match Rate (%) | ||
| OS-CFAR | 30,000 | 22.39 | 18.07 | 16.77 |
| ACMLD-CFAR | 22.71 | 18.21 | 17.11 | |
| VI-CFAR | 21.28 | 17.68 | 16.13 | |
| FOD-CFAR | 21.95 | 17.40 | 16.61 | |
| SOD-CFAR | 20.88 | 16.67 | 15.59 | |
| TF-BI-CFAR | 33.67 | 29.55 | 25.79 | |
| TF-CFAR | 35.55 | 32.47 | 28.21 | |
| Time (Month/Day) | 09/29 | 10/04 | 10/05 |
|---|---|---|---|
| AIS total | 26,861 | 24,483 | 24,435 |
| AIS (clutter edge) | 5877 | 4989 | 4216 |
| OS-CFAR | 574 | 464 | 468 |
| ACMLD-CFAR | 595 | 458 | 465 |
| VI-CFAR | 515 | 425 | 441 |
| FOD-CFAR | 625 | 503 | 496 |
| SOD-CFAR | 542 | 425 | 440 |
| TF-BI-CFAR | 2350 | 1923 | 1824 |
| TF-CFAR | 2628 | 2481 | 2279 |
| Time (Month/Day) | 09/29 | 10/04 | 10/05 |
|---|---|---|---|
| AIS (multi-target) | 2085 | 2341 | 1593 |
| OS-CFAR | 311 | 204 | 201 |
| ACMLD-CFAR | 308 | 206 | 199 |
| VI-CFAR | 271 | 189 | 188 |
| FOD-CFAR | 294 | 216 | 205 |
| SOD-CFAR | 202 | 186 | 140 |
| TF-BI-CFAR | 677 | 559 | 333 |
| TF-CFAR | 884 | 701 | 469 |
| SNR | <0 dB | 0–10 dB | ≥10 dB | Total | |
|---|---|---|---|---|---|
| Number of AIS Targets | 2169 | 5364 | 6964 | 14,497 | |
| OS-CFAR | Matched number | 44 | 912 | 6037 | 6993 |
| Percentage (%) | 0.63 | 13.04 | 86.33 | 100 | |
| VI-CFAR | Matched number | 34 | 729 | 5330 | 6093 |
| Percentage (%) | 0.56 | 11.97 | 87.47 | 100 | |
| FOD-CFAR | Matched number | 25 | 664 | 5875 | 6564 |
| Percentage (%) | 0.38 | 10.12 | 89.50 | 100 | |
| TF-BI-CFAR | Matched number | 66 | 1427 | 6939 | 8432 |
| Percentage (%) | 0.78 | 16.92 | 82.30 | 100 | |
| TF-CFAR (proposed) | Matched number | 335 | 2928 | 6853 | 10,116 |
| Percentage (%) | 3.31 | 28.94 | 67.75 | 100 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Zhou, H.; Tian, Y.; Huang, W.; Shen, W. Improving Ship Detection in Clutter-Edge and Multi-Target Scenarios for High-Frequency Radar. Remote Sens. 2021, 13, 4305. https://doi.org/10.3390/rs13214305
Yang Z, Zhou H, Tian Y, Huang W, Shen W. Improving Ship Detection in Clutter-Edge and Multi-Target Scenarios for High-Frequency Radar. Remote Sensing. 2021; 13(21):4305. https://doi.org/10.3390/rs13214305
Chicago/Turabian StyleYang, Zhiqing, Hao Zhou, Yingwei Tian, Weimin Huang, and Wei Shen. 2021. "Improving Ship Detection in Clutter-Edge and Multi-Target Scenarios for High-Frequency Radar" Remote Sensing 13, no. 21: 4305. https://doi.org/10.3390/rs13214305
APA StyleYang, Z., Zhou, H., Tian, Y., Huang, W., & Shen, W. (2021). Improving Ship Detection in Clutter-Edge and Multi-Target Scenarios for High-Frequency Radar. Remote Sensing, 13(21), 4305. https://doi.org/10.3390/rs13214305