Abstract
This study is focused on concentric rings, which are regularly observed by remote sensing of small river plumes located in different regions worldwide. We report new aerial observations of these features obtained by quadcopters and supported by synchronous in situ measurements, which were collected during the recent field survey at the Bzyb river plume in the eastern part of the Black Sea. Joint analysis of remote sensing imagery and in situ data suggest that the observed concentric rings are surface manifestations of high-frequency internal waves generated in the vicinity of the river mouth. The obtained results demonstrate that the propagation of these waves does not induce offshore material transport within the plume induced by shear instability, which was hypothesized in a recent numerical modeling study of this process. We provide an explanation for the appearance of misleading material features in the numerical simulations discussed above. Finally, we discuss directions for future research of high-frequency internal waves generated in small river plumes.
Keywords:
river plume; internal waves; hydraulic jump; stratification; mixing; aerial drone; aerial imagery 1. Introduction
A river plume is a freshened water mass that is formed in the sea because of the mixing of river discharge and saline seawater. River plumes generally occupy wide but shallow sea surface layers bounded by sharp density gradients. The area of a river plume (in square meters) is several orders of magnitude greater than its depth (in meters). Therefore, even small and narrow rivers form stable river plumes that can be distinctly observed by high-resolution satellite imagery []. The formation and spreading of river plumes are complex hydraulic processes, and many aspects of these processes remain unstudied. Many features of these processes are highlighted in small river plumes due to their small spatial scales that provide the opportunity for effective in situ measurement and aerial observation of said features [,,,,]. One of these features is the formation of concentric rings within small river plumes, which are generated near river mouths and propagate offshore toward the plume’s outer border. These features are observed in satellite imagery of many small river plumes worldwide. They were first reported and described in [] regarding the Mzymta river plume, located in the Black Sea. Based on in situ measurements, it was shown that concentric rings are surface manifestations of internal waves, which are generated by deceleration of the inflowing river jet and the formation of a stationary hydraulic jump near the river mouth.
In a recent paper, Marmorino and Evans used numerical modeling to study these concentric rings []. They used an idealized model based on the OpenFOAM toolbox [] to simulate the inflow of the Mzymta River to the sea. In their simulation, the hydraulic jump and internal waves did not form within the plume; however, the model reproduced ring-like features somewhat similar to those observed in the Mzymta River. The modeled ring-like features were material features, which were deeper, less saline, and faster-moving than the bulk-plume water. Based on the numerical results, they hypothesized that the concentric rings observed within real small river plumes are formed by shear instability and are not induced by high-frequency internal waves. In the present study, we clearly demonstrate that this alternative viewpoint is a product of the artifact of the idealized numerical model. Based on the newly collected in situ data and the continuous aerial observations of these features at the Bzyb river plume (located nearby and similar to the Mzymta plume) [,], we confirm that the observed concentric rings are surface manifestations of internal waves and are not material features. Additionally, we provide an explanation for the appearance of misleading material features in the numerical simulations discussed above.
2. Data
Field measurements analyzed in this study were performed on 16 and 18 April 2021 in the area adjacent to the Bzyb river mouth in the eastern part of the Black Sea (Figure 1). Aerial observations of the Bzyb plume were performed by a DJI Mavik 2 Zoom quadcopter equipped with a 12 MP/4K video camera. The remote sensing data processing included georeferencing of the aerial imagery by direct projection into an earth-based Cartesian coordinate system using GPS and altimetry data from the quadcopter. The obtained projection was validated and corrected according to the location of ground control points registered in the imagery, namely, river mouth capes, lakes near the river mouth, and buildings. The lens distortion did not significantly affect the processed imagery because we used only the central part of the aerial images to calculate velocities of ring-like features.
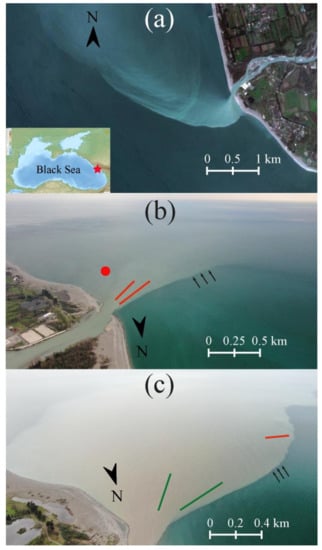
Figure 1.
Study area: (a) satellite image (Sentinel-2) of the Bzyb plume acquired on 15 April 2021; (b,c) aerial images of the Bzyb plume acquired during the field survey on (b) 16 April 2021 at 15:30 and (c) 18 April 2021 at 11:45. The red star at the inset in the panel (a) indicates location of the Bzyb plume in the eastern part of the Black Sea. The black arrows in panels (b,c) indicate ring-like features within the Bzyb plume. The red lines in panels (b,c) indicate trajectories of free-drifting boat on 16 and 18 April. The green lines in panel (c) indicate trajectories of free-drifting buoy on 18 April. The red circle in panel (b) indicates the location of the mooring station on 16 April.
The vertical and horizontal accuracy of the quadcopter positioning were 0.1 and 0.3 m, respectively. Once the remote sensing was performed from the altitudes of 300–500 m at a distance of 1 km from the study area, the accuracy of the direct projection was <1 m. The average velocities of the ring-like features and drifting objects were reconstructed from aerial imagery using the ratio between the distance of the observed motion and the duration of the motion. Once the observed motion durations of these objects were >500 s and the resulting motion distances were >100 m, the accuracy of the reconstructed velocities was <0.01 m/s.
Thermohaline measurements within the Bzyb plume were performed first, from a flat-bottomed boat with a shallow draft to minimize any boat-induced mixing of the sea surface layer. Measurements included surface-to-bottom profiles by the CastAway CTD instrument continuously performed from a free-drifting boat, starting at the river mouth and finishing 200–300 m far from the starting point. Second, we used a free-drifting buoy equipped with Star-Oddi CTD loggers, which measured temperature and salinity along similar tracks within the plume. The loggers were mounted at depths of 0.5, 1.5, and 2.5 m below the buoy and performed measurements at 5 s time intervals. The drifting of the boat and the buoy were recorded by the quadcopter to continuously reconstruct their drift velocity and position within the plume. Finally, we performed measurements using the same CTD loggers at the anchored mooring station within the plume. The loggers were also mounted at the depths of 0.5 and 1.5 m below sea level. The in situ measurements were supported by synchronous wind measurements taken every 1 min by a Gill GMX200 sensor, which was located at an altitude of 8 m on the seashore 1 km north of the Bzyb river mouth.
3. Results
During the period of the field survey, the Bzyb plume was distinctly visible in aerial and satellite imagery (due to increased turbidity). It occupied an area of ~10 km2 (Figure 1). The river velocity at the river mouth was ~1.5 m/s. Concentric ring-like features were registered during the whole observation period; however, their clarity strongly depended on cloud conditions. In particular, they were more pronounced on 18 April under a cloud-free sky (Figure 1c), as compared to overcast conditions on 16 April (Figure 1b). These ring-like features were distinctly visible in satellite imagery 1–3 weeks before and after the field survey (Figure 2); moreover, they are visible every year in multiple rivers of the study area during spring freshet and short-term rain-induced flooding events [].

Figure 2.
Satellite images (Sentinel-2) of the Bzyb plume with distinct ring-like features acquired on (a) 7 April 2021, (b) 30 April 2021, (c) 12 May 2021.
Analysis of aerial images and video records elucidated characteristics of the observed concentric rings. Distances between the neighboring rings decrease from 20 m near the river mouth to 10 m at a distance of 1 km from the mouth. The rings are periodically formed at a distance of 100–150 m from the river mouth and constantly propagate away from the river mouth towards the plume boundary. The periods of formation of the concentric rings reconstructed from aerial observations last ~60 s. The motion velocity of these rings is ~0.3 m/s near the mouth and decelerate to ~0.15 m/s at a distance of 1 km from the mouth. The mooring station equipped with CTD loggers located within the Bzyb plume (indicated by the red circle in Figure 1b) also registered salinity oscillation for a period of ~60 s, which is associated with the propagation of these rings (Figure 3).
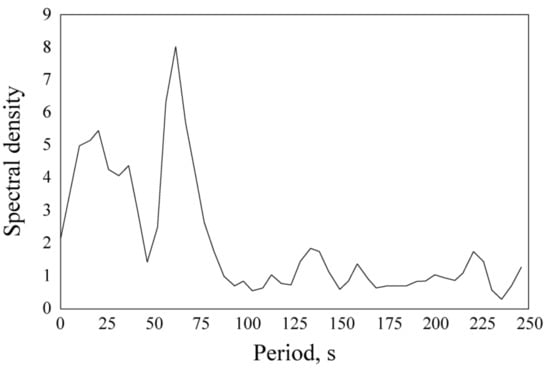
Figure 3.
Spectral density of salinity at a depth of 1.5 m at the mooring station located within the Bzyb plume.
In order to answer the question, “Are the observed ring-like features manifestations of internal waves, or are they material features moving in the plume?”, we performed a video recording of the free-drifting boat within the plume from the quadcopter (indicated by red lines in Figure 1b,c). Three examples with indications of positions of the boat and several nearby propagating concentric rings are presented in Figure 4, Figure 5 and Figure 6. In order to sharpen the images of the concentric rings, the initial aerial imagery was transformed to grayscale and zoomed in to the boat’s drifting area. The initial full-size colored video records of the Bzyb plume and the processed images are included in the Supplementary Material. Two of the drifting experiments, namely at 15:32–15:40 (Figure 4 and Video S1 in the Supplementary Material) and at 16:28–16:36 (Figure 5 and Video S2 in the Supplementary Material) on 16 April, were performed in the near-field part of the plume, while another drift (at 12:04–12:25 on 18 April) (Figure 6 and Video S3 in the Supplementary Material) was performed in the outer part of the plume. The general schematic of the free-drifting experiments is presented in Figure 7.

Figure 4.
Processed aerial images of the Bzyb plume on 16 April at 15:37–15:40 during the first drifting boat experiment. Top images show the near-field part of the Bzyb plume; bottom images show the zoomed-in areas (indicated by the related blue squares in the top images). Red lines indicate ring-like features; black arrows indicate location of the free-drifting boat. Note that the frame of the bottom images is moving.

Figure 5.
Processed aerial images of the Byzb plume on 16 April at 16:33–16:36 during the second drifting boat experiment. Top images show the near-field part of the Bzyb plume; bottom images show the zoomed-in areas (indicated by the related blue squares in the top images). Red lines indicate ring-like features; black arrows indicate location of the free-drifting boat. Note that the frame of the bottom images is moving.

Figure 6.
Processed aerial images of the Byzb plume on 18 April at 12:04–12:25 during the third drifting boat experiment. Top image shows the far-field part of the Bzyb plume; bottom images show the zoomed-in area (indicated by the blue square in the top image). Red lines indicate ring-like features; black arrows indicate location of the free-drifting boat. Note that the frame of the bottom images is not moving.
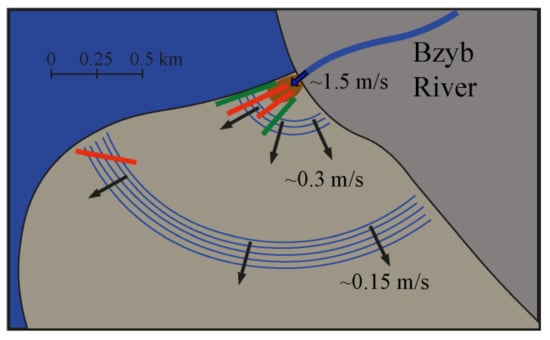
Figure 7.
Generalized schematic of the free-drifting experiments within the Bzyb plume (shown by brown color). The black arrows indicate motion direction (with velocity values) of ring-like features within the Bzyb plume. The red lines indicate trajectories of the free-drifting boat. The green lines indicate trajectories of the free-drifting buoy. The blue arrow indicates the inflow river jet to the sea (with velocity value).
The wind speed during the boat-drifting experiments was low: ~1.5 m/s during 15:32–15:40 on 16 April, ~2.0 m/s during 16:28–16:36 on 16 April, ~1.0 m/s during 12:04–12:25 on 18 April. Wind direction was variable during all three periods. We can parameterize the speed of the free-drifting boat by the following equation: , where ρa and ρs are the air and sea densities equal to 1.2 kg/m3 and 1010 kg/m3, respectively; CDa and CDs are the aerodynamic and hydrodynamic drag coefficients for the boat equal to 0.1 and 0.05, respectively; Sa and Ss are the areas of the above-water and in-water parts of the boat equal to 1 m2 and 0.5 m2, respectively; V is the wind speed. In this case, v ~ 0.07 V, which is equal to ~0.1 m/s of boat drift speed in the case of the observed wind speed. However, due to the variable direction of wind forcing and low wind speed, this equation overestimates the real drifting velocity of the boat, which was much less. As a result, we presume that wind forcing played a negligible role in boat motion.
We clearly observe that the free-drifting boat and the concentric rings have different velocities, i.e., the drifting boat crosses several concentric rings during aerial observations. Moreover, the trajectories of the boat are not perpendicular to the respective ring segments. In particular, the third boat drift in the outer part of the plume was directed northwestward towards the plume border (which is typical for convergence at the plume border []), while the ring-like features propagated southward towards the far-field plume. As a result, the boat trajectory crossed concentric rings at an angle ~30° (Figure 6). The obtained result demonstrates that the observed ring-like features are not material features because in this case, they moved with similar velocity and trajectory as the free-drifting boat.
We want to highlight the methodological complexity of organizing free-drifting experiments in river plumes, even small ones. On the one hand, the drift trajectory has to be long enough (order of hundreds of meters) to detect the relative velocities of the drifter and the surrounding concentric rings. This fact requires aerial remote sensing from an altitude of at least twice the observed drift trajectory. In the field survey, we performed observations from an altitude of 500 m. On the other hand, the drifter observed by the quadcopter has to be large enough to be visible in the aerial imagery and shallow enough not to influence the vertical structure of the plume with its movement and the associated mixing. As a result, the 5 m long flat-bottom boat (served as a drifter) is the only option for the proposed free-drifting experiment. The use of a smaller boat or fluorescent water-tracing dye seems not to be applicable for this purpose.
Continuous surface-to-bottom CTD measurements performed from the free-drifting boat also supported the assumption that the observed ring-like features are induced by internal waves. Once the boat and the internal waves had different velocities, vertical profiles showed variability of vertical structure below the boat caused by the penetration of internal waves (Figure 8). A similar effect was observed by the free-drifting buoy equipped with CTD loggers at depths of 0.5, 1.5, and 2.5 m. Salinity was registered by the loggers at the fixed layers while the buoy was drifting in the central part of the inflowing river jet within the plume (its trajectory is indicated by the left green line in Figure 1c). These measurements showed great variability (Figure 9). We presume that the stationary hydraulic jump and internal waves are the main sources of the observed heterogeneity within this energetic part of the plume.
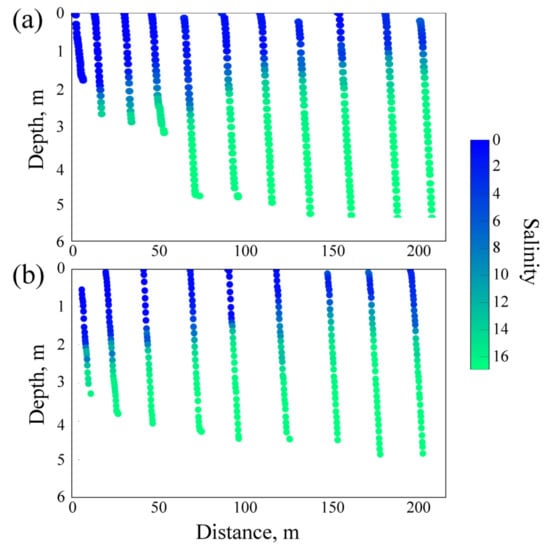
Figure 8.
Vertical salinity profiles performed from the free-drifting boat on 16 April at (a) 15:37–15:40 and (b) 16:33–16:36. Deeper plume areas in panel (a) were registered by crossing the area with bright stripes of IW visible in the respective aerial images on 15:37–15:38 in Figure 4.
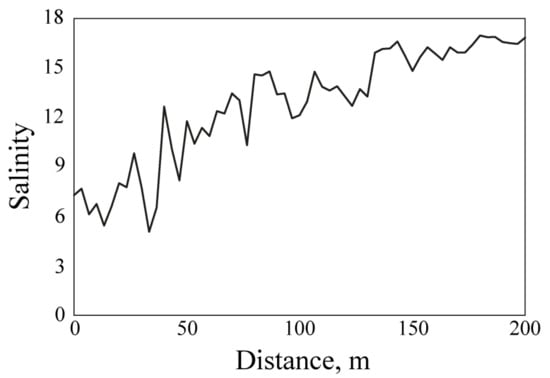
Figure 9.
Salinity at a depth of 1.5 m measured from the free-drifting buoy on 18 April at 10:44–10:49 in the central part of the jet. The trajectory of the buoy is indicated by the left green line in Figure 1c.
The velocity of the drifting buoy (reconstructed from aerial observations) was different within the central part of the jet formed by the inflowing river (0.5–0.6 m/s) and at its northern periphery (0.2 m/s), i.e., along the sharp northern border of the Bzyb plume (green lines at Figure 1c). However, the concentric formation of the ring-like features in the near-field part of the plume shows that their propagation velocity was similar in these plume zones. This result also supports the finding that the ring-like features are not material features but are generated by internal waves.
Another piece of evidence of the internal-wave origin of the concentric rings is their refraction at the plume border. The ring-like features propagate offshore within the plume and occupy the whole plume area in its near-field part. As a result, lateral parts of the waves propagate along the plume boundaries or along the shoreline. Aerial remote sensing displays refraction of internal waves in the vicinity of the plume border, i.e., a modification of their trajectories, which become parallel to the border (Figure 10 and Video S4 in the Supplementary Material). At the same time, the border of the plume does not move in response to the propagation of concentric rings towards the border and their dissipation at the border. If these concentric rings were material features, their propagation in the vicinity of the border would induce an accumulation of freshened water and offshore movement of the border. This process is not observed by aerial remote sensing. Refraction of internal waves near the coast within the Bzyb plume is also clearly visible in Figure 11a in []. The same process in the Mzymta plume is shown in Figure 3b in [] (also appears in Figure 1 in []).

Figure 10.
Aerial images of the Bzyb plume on 18 April at 11:46–11:49 illustrating refraction of internal waves (indicated by red lines) at the plume border. The blue rectangle in the top image indicates location of the zoomed-in area in the bottom images.
Finally, we calculated the velocity of the internal waves, which can be generated within the Bzyb plume, using the following equation for the first-mode waves in a two-layered density-stratified fluid system []:
where and are the densities of the river plume and the subjacent saline sea, g is the gravitational acceleration, d is the depth of the river plume, D is the sea depth, is the wave number, and λ is the wave length. In the case of the internal waves generated near the Bzyb river mouth, k ~ 6.28/20 ~ 0.3 and ~ 0.3 m/s, which is consistent with the propagation velocity of the concentric rings reconstructed from aerial remote sensing.
4. Discussion and Conclusions
This study is focused on patterns of concentric rings occurring within small river plumes in many coastal areas worldwide (Figure 11). We analyzed new aerial observations and in situ measurements of these features in the Bzyb river plume in the eastern part of the Black Sea collected in April 2021. These data provide a clearer understanding of these features, which were previously described in [,]. The main result is that the observed concentric rings are surface manifestations of high-frequency internal waves generated in the vicinity of the river mouth and are not material features, as was hypothesized in []. This is proven by different independent measurements of the structure and dynamics of these concentric rings. First, we demonstrated that the free-drifting objects (the boat and the buoy) in the river plume and the surface manifestations of internal waves have different velocities and trajectories. Second, we showed that the vertical salinity structure and depth of the plume significantly varies below these free-drifting objects. Third, we observed refraction of internal waves near the plume border and near the coast. Finally, we demonstrated that the observed propagation velocity of these internal waves is consistent with the theoretical estimation of the internal wave-phase speed theoretically predicted in a two-layered density-stratified fluid system applied to the Bzyb plume [].
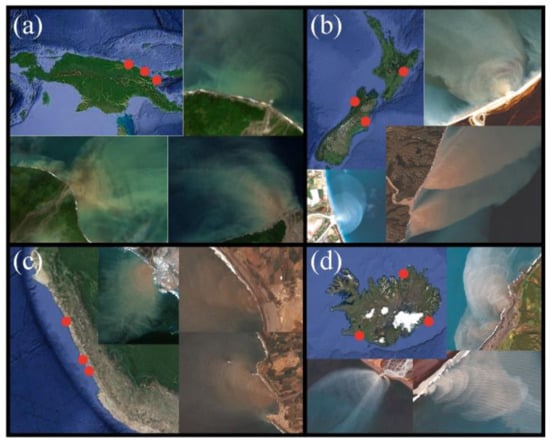
Figure 11.
Satellite images (Sentinel-2) of concentric rings—surface manifestations of high-frequency internal waves in river plumes—in (a) New Guinea, (b) New Zealand, (c) Peru, (d) Iceland. The red dots indicate locations of the presented river plumes. Note that the images are given in different spatial scales.
The numerical model described in [] simulated material features, which have somewhat similar surface manifestations as the internal waves observed in real river plumes. These material features are described as stable rings of deeper water within the plume. However, the existence of these material features seems to be unrealistic due to the following reasons. First, deeper plume areas tend to flatten under buoyancy force and the related horizontal pressure gradient. As a result, the general physical background of the strongly stratified river plume contradicts the existence of stable rings of deeper water within the plume (which is not the case with oscillating internal waves).
Second, the simulated motion velocities of deeper rings equal to 0.6–1 m/s within the whole river plume area (including the areas near the outer border) (Figure 3b in []) are completely unrealistic for a real river plume. Such a high velocity is reproduced in the numerical simulation because of the constant expansion of the simulated river plume (which is clearly visible in Figures 4 and 7 in []). On the other hand, satellite and aerial remote sensing observe concentric ring-like features in stable river plumes, which are not constantly expanding. Note that the propagation of internal waves does not result in intense radial advection of the freshened water within the plume, its accumulation at the plume border, or the resulting constant plume expansion.
Third, the simulated plume in [] has a lobe–cleft structure at the whole length of its outer border, which is also unrealistic. Satellite and aerial remote sensing of these features described in several studies demonstrate that the lobe–cleft structure is formed only at the distinct plume border near the river mouth, while it is absent in the far-field part of the plume [,]. To the extent of our knowledge, the lobe–cleft structure along the whole plume border was never registered and reported. Finally, we can conclude that the numerical modeling of river plumes, especially focused on small-scale hydraulic processes, can produce misleading results if it is not properly validated.
High-frequency internal waves, which are described and discussed in this study, are very energetic features in small river plumes. A hydraulic jump in the vicinity of a river mouth and the transformation of internal waves at the plume border can be important mechanisms in the mixing of a river plume with the subjacent sea. Internal waves are among the most important sources of mixing in many sea areas [,,]. Analogously, they can affect the considered river plumes due to the intense and regular vertical motion of freshened water. Indeed, salinity in the surface layer of the inflowing river jet abruptly increases at a distance of ~50–100 m (Figure 8 and Figure 9).
The processed aerial imagery shows that the distances between the neighboring internal waves change over time. First, they are not homogenous along the individual waves and vary on short-temporal time scales (~1 min). Second, they steadily decrease from ~20 m near the river mouth to ~10 m in the far-field part of the plume. The latter process is accompanied by a deceleration of phase speeds of the internal waves from ~0.3 to ~0.15 m/s. We assume that these changes are not artifacts of the quadcopter positioning and image processing because they are verified by the boat size, which is visible in the related aerial images. High-resolution satellite imagery also proves that distances between the adjacent internal waves are not homogenous within the river plumes, and the wavelengths decrease away from the river mouths [,]. We presume that these processes are caused by the attenuation of high-frequency internal waves as they propagate away from the river mouth due to the decrease in stratification between river plumes and the subjacent sea. Changes of velocity shear at the interface between the plume and the subjacent sea can also affect this process. However, these issues require additional and specific studies.
Previous research has shown the important role of shear stress in the mixing of river plumes []. The improvement of our understanding of different plume-mixing mechanisms, as well as the comparison of mixing estimates in different plume zones, hold promise to be some of the most important issues in future plume studies. These issues require specific in situ measurements and remote sensing of the respective plume zones and can be supported by accurate numerical modeling. It is important to highlight that surface manifestations of internal waves may not be visible in the case of cloudy weather and low illumination, as well as in river plumes with very low or very high turbidity. The significant dependence of the clarity of these surface manifestations on cloud conditions was revealed during our field survey. Therefore, the presence and frequency of the formation of these internal waves in river plumes worldwide can be strongly underestimated.
Supplementary Materials
The following are available online at https://doi.org/10.5281/zenodo.5340929. Video S1: free-drifting boat and propagation of internal waves in the near-field part of the Bzyb plume on 16 April at 15:37–15:40, as in Figure 4; Video S2: free-drifting boat and propagation of internal waves in the near-field part of the Bzyb plume on 16 April at 16:33–16:36, as in Figure 5; Video S3: free-drifting boat and propagation of internal waves in the far-field part of the Bzyb plume on 18 April at 12:04–12:25, as in Figure 6; Video S4: refraction of internal waves in the Bzyb plume border on 18 April at 11:46–11:49, as in Figure 10.
Author Contributions
Conceptualization, A.O.; field measurements, A.O., R.S., A.G. and A.B.; formal analysis, A.O., R.S. and A.G.; writing, A.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Higher Education of the Russian Federation, theme 0128-2021-0001 (collecting of in situ data), the Russian Science Foundation, research project 18-17-00156 (study of river plumes).
Data Availability Statement
The in situ data and aerial imagery are available at https://doi.org/10.5281/zenodo.5340929 (accessed date: 15 October 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Osadchiev, A.A. A method for quantifying freshwater discharge rates from satellite observations and Lagrangian numerical modeling of river plumes. Environ. Res. Lett. 2015, 10, 085009. [Google Scholar] [CrossRef] [Green Version]
- Horner-Devine, A.; Chickadel, C.C.; MacDonald, D. Coherent structures and mixing at a river plume front. In Coherent Flow Structures in Geophysical Flows at the Earth’s Surface; Venditti, J., Best, J.L., Church, M., Hardy, R.J., Eds.; Wiley: Chichester, UK, 2013; pp. 359–369. [Google Scholar]
- Horner-Devine, A.R.; Chickadel, C.C. Lobe-cleft instability in the buoyant gravity current generated by estuarine outflow. Geophys. Res. Lett. 2017, 44, 5001–5007. [Google Scholar] [CrossRef]
- Osadchiev, A.A.; Zavialov, P.O. Structure and Dynamics of Plumes Generated by Small Rivers. In Estuaries and Coastal Zones—Dynamics and Response to Environmental Changes; Pan, J., Devlin, A., Eds.; IntechOpen: London, UK, 2020; Chapter 5; pp. 125–144. [Google Scholar]
- Osadchiev, A.; Barymova, A.; Sedakov, R.; Zhiba, R.; Dbar, R. Spatial structure, short-temporal variability, and dynamical features of small river plumes as observed by aerial drones: Case study of the Kodor and Bzyp river plumes. Remote Sens. 2020, 12, 3079. [Google Scholar] [CrossRef]
- Osadchiev, A.A.; Barymova, A.A.; Sedakov, R.O.; Rybin, A.V.; Tanurkov, A.G.; Krylov, A.A.; Kremenetskiy, V.V.; Mosharov, S.A.; Polukhin, A.A.; Ulyantsev, A.S.; et al. Hydrophysical structure and current dynamics of the Kodor river plume. Oceanology 2021, 61, 1–14. [Google Scholar] [CrossRef]
- Osadchiev, A.A. Small mountainous rivers generate high-frequency internal waves in coastal ocean. Sci. Rep. 2018, 8, 16609. [Google Scholar] [CrossRef] [PubMed]
- Marmorino, G.; Evans, T. Interpreting patterns of concentric rings within small buoyant river plumes. Remote Sens. 2021, 13, 1361. [Google Scholar] [CrossRef]
- OpenFOAM and The OpenFOAM Foundation. Available online: https://openfoam.org/ (accessed on 1 August 2021).
- Jaoshvili, S. The Rivers of the Black Sea; Chomeriki, I., Gigineishvili, G., Kordzadze, A., Eds.; Technical Report No. 71; European Environmental Agency: Copenhagen, Denmark, 2002. [Google Scholar]
- O’Donnell, J.; Marmorino, G.O.; Trump, C.L. Convergence and downwelling at a river plume front. J. Phys. Oceanogr. 1998, 28, 1481–1495. [Google Scholar] [CrossRef]
- Phillips, O.M. The Dynamics of the Upper Ocean, 2nd ed.; Cambridge University Press: Cambridge, UK, 1977. [Google Scholar]
- Morozov, E.G. Semidiurnal internal wave global field. Deep Sea Res. Part I Oceanogr. Res. Pap. 1995, 42, 135–148. [Google Scholar] [CrossRef]
- Kozlov, I.; Romanenkov, D.; Zimin, A.; Chapron, B. SAR observing large-scale nonlinear internal waves in the White Sea. Remote Sens. Environ. 2014, 147, 99–107. [Google Scholar] [CrossRef] [Green Version]
- Fer, I.; Koenig, Z.; Kozlov, I.E.; Ostrowski, M.; Rippeth, T.P.; Padman, L.; Bosse, A.; Kolas, E. Tidally forced lee waves drive turbulent mixing along the Arctic Ocean margins. Geophys. Res. Lett. 2020, 47, e2020GL088083. [Google Scholar] [CrossRef]
- Horner-Devine, A.R.; Hetland, R.D.; MacDonald, D.G. Mixing and transport in coastal river plumes. Ann. Rev. Fluid Mech. 2015, 47, 569–594. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).