Engineering-Geological Analysis of a Subaerial Landslide in Taan Fiord, Alaska
Abstract
1. Introduction
1.1. Landslide in the Context of Natural Multi-Hazard and Recent Climate Change
1.2. The 2015 Taan Fiord Tsunamigenic Landslide Event
2. Data and Materials
2.1. Geological and Structural Setting
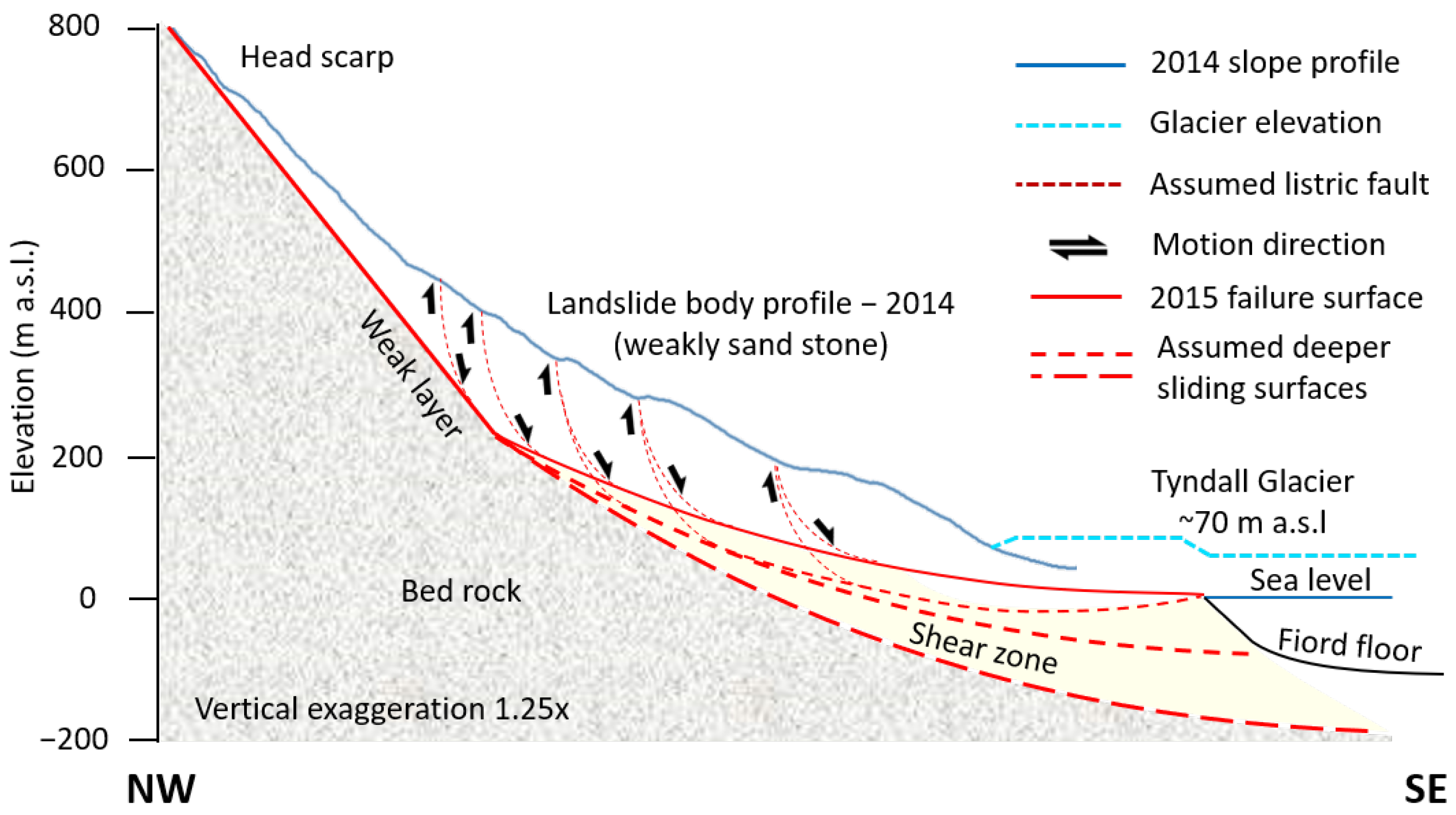
2.2. The Cross Sections
3. Methods
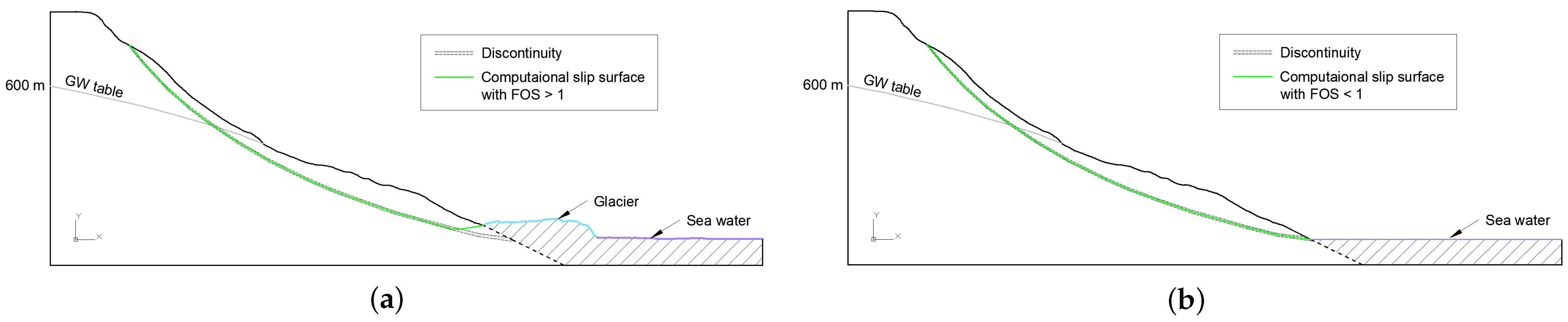
4. Results and Discussion
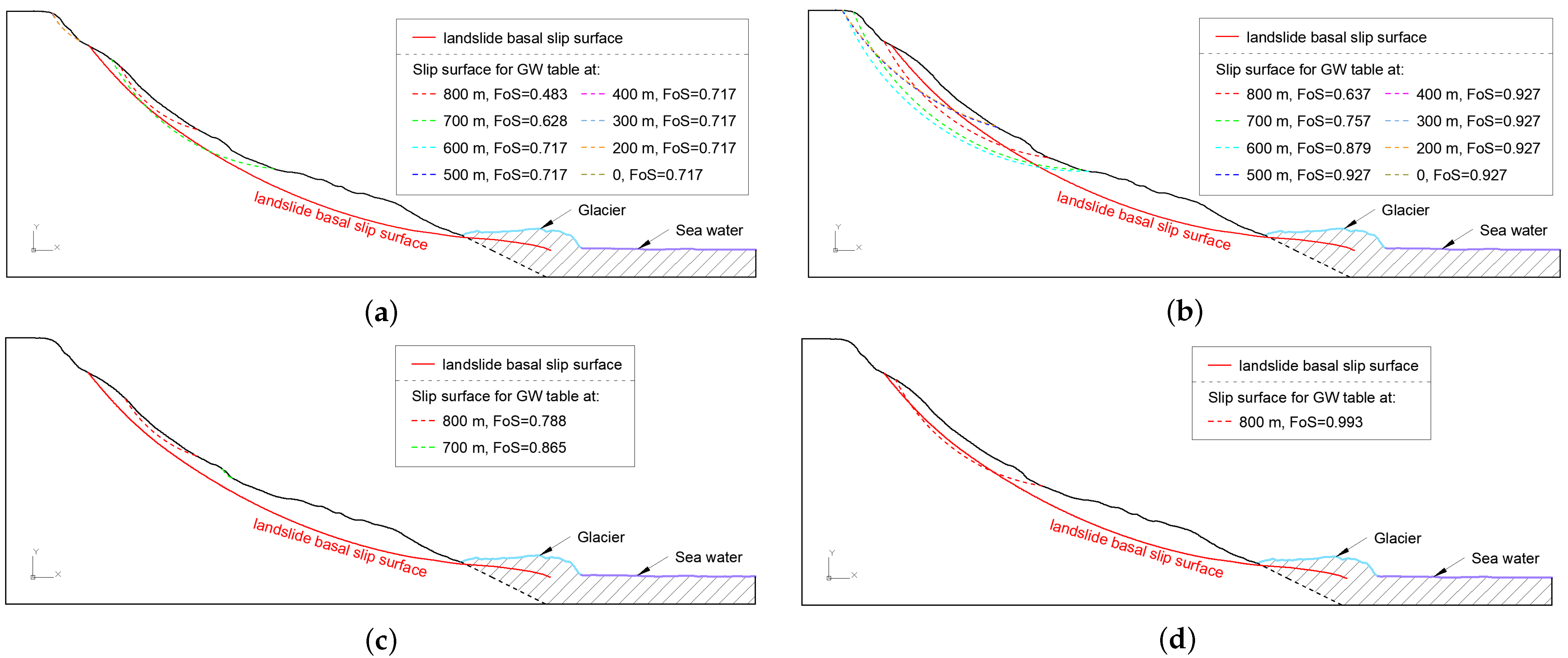
4.1. Preliminary Slope Stability Analysis
4.2. The Formation of a Weak Basal Layer
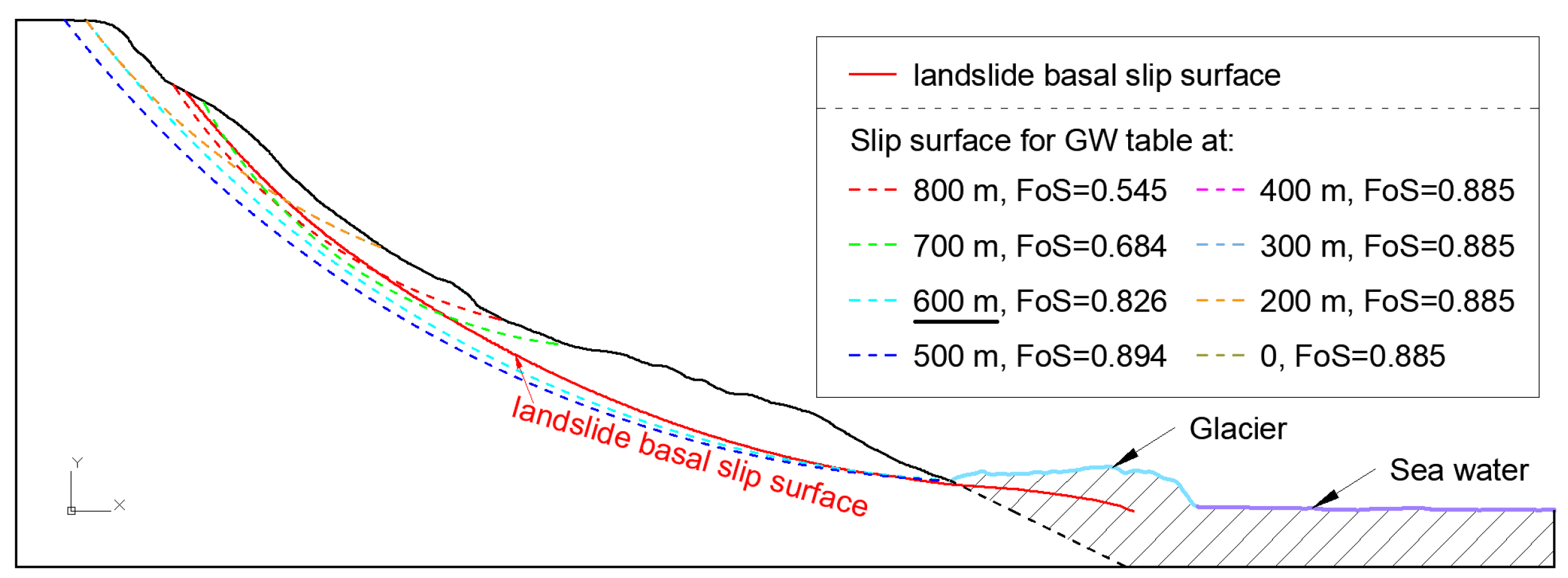
4.2.1. The Influence of Groundwater Level
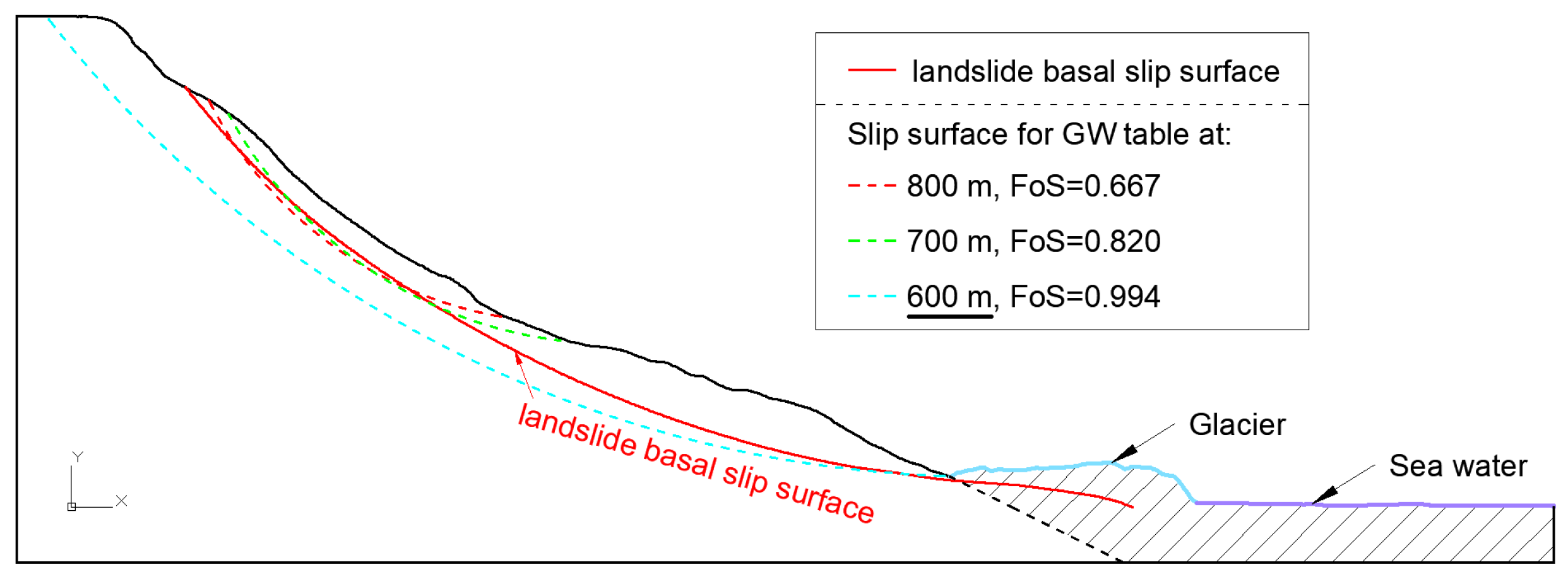
4.2.2. The Influence of Horizontal Seismic Acceleration
4.3. The Final Slope Collapse
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- George, D.; Iverson, R.; Cannon, C. New methodology for computing tsunami generation by subaerial landslides: Application to the 2015 Tyndall Glacier landslide, Alaska. Geophys. Res. Lett. 2017, 44, 7276–7284. [Google Scholar] [CrossRef]
- Higman, B.; Shugar, D.H.; Stark, C.P.; Ekström, G.; Koppes, M.N.; Lynett, P.; Dufresne, A.; Haeussler, P.J.; Geertsema, M.; Gulick, S.; et al. The 2015 landslide and tsunami in Taan Fiord, Alaska. Sci. Rep. 2018, 8, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Dufresne, A.; Geertsema, M.; Shugar, D.; Koppes, M.; Higman, B.; Haeussler, P.; Stark, C.; Venditti, J.; Bonno, D.; Larsen, C.; et al. Sedimentology and geomorphology of a large tsunamigenic landslide, Taan Fiord, Alaska. Sediment. Geol. 2018, 364, 302–318. [Google Scholar] [CrossRef]
- Cruden, D.M.; Varnes, D.J. Landslide Types and Processes. Spec. Rep.-Natl. Res. Counc. Transp. Res. Board 1996, 247, 36–75. [Google Scholar]
- Dai, F.; Lee, C.; Ngai, Y. Landslide risk assessment and management: An overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar] [CrossRef]
- Haque, U.; Blum, P.; Da Silva, P.F.; Andersen, P.; Pilz, J.; Chalov, S.R.; Malet, J.P.; Auflič, M.J.; Andres, N.; Poyiadji, E.; et al. Fatal landslides in Europe. Landslides 2016, 13, 1545–1554. [Google Scholar] [CrossRef]
- McColl, S.T. Landslide causes and triggers. In Landslide Hazards, Risks and Disasters; Elsevier: Amsterdam, The Netherlands, 2015; pp. 17–42. [Google Scholar] [CrossRef]
- Marui, H.; Nadim, F. Landslides and multi-hazards. In Landslides–Disaster Risk Reduction; Springer: Berlin/Heidelberg, Germany, 2009; pp. 435–450. [Google Scholar] [CrossRef]
- Keefer, D.K. Landslides caused by earthquakes. Geol. Soc. Am. Bull. 1984, 95, 406–421. [Google Scholar] [CrossRef]
- Sassa, K.; Fukuoka, H.; Scarascia-Mugnozza, G.; Evans, S. Earthquake-induced-landslides: Distribution, motion and mechanisms. Soils Found. 1996, 36, 53–64. [Google Scholar] [CrossRef]
- Rodríguez, C.; Bommer, J.; Chandler, R. Earthquake-induced landslides: 1980–1997. Soil Dyn. Earthq. Eng. 1999, 18, 325–346. [Google Scholar] [CrossRef]
- Bommer, J.J.; Rodríguez, C.E. Earthquake-induced landslides in Central America. Eng. Geol. 2002, 63, 189–220. [Google Scholar] [CrossRef]
- Stead, D.; Eberhardt, E. Understanding the mechanics of large landslides. Ital. J. Eng. Geol. Environ. 2013, 6, 85–112. [Google Scholar] [CrossRef]
- Kos, A.; Amann, F.; Strozzi, T.; Delaloye, R.; Ruette, J.; Springman, S. Contemporary glacier retreat triggers a rapid landslide response, Great Aletsch Glacier, Switzerland. Geophys. Res. Lett. 2016, 43. [Google Scholar] [CrossRef]
- Hutter, K. Theoretical Glaciology; Springer: Dordrecht, The Netherlands, 1983. [Google Scholar] [CrossRef]
- McColl, S.; Davies, T.; McSaveney, M. Glacier retreat and rock-slope stability: Debunking debuttressing. In Geologically Active; Taylor and Francis: London, UK, 2010; pp. 467–474. [Google Scholar]
- Derbyshire, E.D. Geomorphology and Climate; Wiley Chichester: London, UK, 1976. [Google Scholar]
- Collins, B.D.; Znidarcic, D. Stability analyses of rainfall induced landslides. J. Geotech. Geoenviron. Eng. 2004, 130, 362–372. [Google Scholar] [CrossRef]
- Wu, L.; Huang, R.; Xu, Q.; Zhang, L.; Li, H. Analysis of physical testing of rainfall-induced soil slope failures. Environ. Earth Sci. 2015, 73, 8519–8531. [Google Scholar] [CrossRef]
- Zhu, D.; Lee, C.; Jiang, H. Generalised framework of limit equilibrium methods for slope stability analysis. Geotechnique 2003, 53, 377–395. [Google Scholar] [CrossRef]
- Brideau, M.A.; Stead, D.; Couture, R. Structural and engineering geology of the east gate landslide, Purcell Mountains, British Columbia, Canada. Eng. Geol. 2006, 84, 183–206. [Google Scholar] [CrossRef]
- Bolla, A.; Paronuzzi, P. Numerical investigation of the pre-collapse behavior and internal damage of an unstable rock slope. Rock Mech. Rock Eng. 2019, 53, 2279–2300. [Google Scholar] [CrossRef]
- Sloan, S. Geotechnical stability analysis. Géotechnique 2013, 63, 531–571. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Humpheson, C.; Lewis, R. Associated and non-associated visco-plasticity and plasticity in soil mechanics. Geotechnique 1975, 25, 671–689. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Coggan, J. Numerical analysis of initiation and progressive failure in natural rock slopes—The 1991 Randa rockslide. Int. J. Rock Mech. Min. Sci. 2004, 41, 69–87. [Google Scholar] [CrossRef]
- Tschuchnigg, F.; Schweiger, H.; Sloan, S.W. Slope stability analysis by means of finite element limit analysis and finite element strength reduction techniques. Part I: Numerical studies considering non-associated plasticity. Comput. Geotech. 2015, 70, 169–177. [Google Scholar] [CrossRef]
- Tschuchnigg, F.; Schweiger, H.; Sloan, S.W. Slope stability analysis by means of finite element limit analysis and finite element strength reduction techniques. Part II: Back analyses of a case history. Comput. Geotech. 2015, 70, 178–189. [Google Scholar] [CrossRef]
- Schneider-Muntau, B.; Medicus, G.; Fellin, W. Strength reduction method in Barodesy. Comput. Geotech. 2018, 95, 57–67. [Google Scholar] [CrossRef]
- Dawson, E.; Roth, W.; Drescher, A. Slope stability analysis by strength reduction. Geotechnique 1999, 49, 835–840. [Google Scholar] [CrossRef]
- Choi, S.K.; Park, J.Y.; Lee, D.H.; Lee, S.R.; Kim, Y.T.; Kwon, T.H. Assessment of barrier location effect on debris flow based on smoothed particle hydrodynamics (SPH) simulation on 3D terrains. Landslides 2021, 18, 217–234. [Google Scholar] [CrossRef]
- Conte, E.; Pugliese, L.; Troncone, A. Post-failure analysis of the Maierato landslide using the material point method. Eng. Geol. 2020, 277, 105788. [Google Scholar] [CrossRef]
- Xu, W.J.; Xu, Q.; Liu, G.Y.; Xu, H.Y. A novel parameter inversion method for an improved DEM simulation of a river damming process by a large-scale landslide. Eng. Geol. 2021, 293, 106282. [Google Scholar] [CrossRef]
- Puzrin, A.M.; Germanovich, L. The growth of shear bands in the catastrophic failure of soils. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2005, 461, 1199–1228. [Google Scholar] [CrossRef]
- Meigs, A.; Sauber, J. Southern Alaska as an example of the long-term consequences of mountain building under the influence of glaciers. Quat. Sci. Rev. 2000, 19, 1543–1562. [Google Scholar] [CrossRef]
- Haeussler, P.; Gulick, S.; McCall, N.; Walton, M.; Reece, R.; Larsen, C.; Shugar, D.; Geertsema, M.; Venditti, J.; Labay, K. Submarine deposition of a subaerial landslide in Taan Fiord, Alaska. J. Geophys. Res. Earth Surf. 2018, 123, 2443–2463. [Google Scholar] [CrossRef]
- Bloom, C.K.; MacInnes, B.; Higman, B.; Shugar, D.H.; Venditti, J.G.; Richmond, B.; Bilderback, E.L. Catastrophic landscape modification from a massive landslide tsunami in Taan Fiord, Alaska. Geomorphology 2020, 353, 107029. [Google Scholar] [CrossRef]
- Sturzenegger, M.; Stead, D. The Palliser Rockslide, Canadian Rocky Mountains: Characterization and modeling of a stepped failure surface. Geomorphology 2012, 138, 145–161. [Google Scholar] [CrossRef]
- Francioni, M.; Salvini, R.; Stead, D.; Litrico, S. A case study integrating remote sensing and distinct element analysis to quarry slope stability assessment in the Monte Altissimo area, Italy. Eng. Geol. 2014, 183, 290–302. [Google Scholar] [CrossRef]
- Bonilla-Sierra, V.; Scholtes, L.; Donzé, F.; Elmouttie, M. Rock slope stability analysis using photogrammetric data and DFN–DEM modelling. Acta Geotech. 2015, 10, 497–511. [Google Scholar] [CrossRef]
- Cloutier, C.; Locat, J.; Couture, R.; Jaboyedoff, M. The anatomy of an active slide: The Gascons rockslide, Québec, Canada. Landslides 2016, 13, 241–258. [Google Scholar] [CrossRef]
- Zieher, T.; Schneider-Muntau, B.; Mergili, M. Are real-world shallow landslides reproducible by physically-based models? Four test cases in the Laternser valley, Vorarlberg (Austria). Landslides 2017, 14, 2009–2023. [Google Scholar] [CrossRef]
- Zieher, T.; Rutzinger, M.; Schneider-Muntau, B.; Perzl, F.; Leidinger, D.; Formayer, H.; Geitner, C. Sensitivity analysis and calibration of a dynamic physically based slope stability model. Nat. Hazards Earth Syst. Sci. 2017, 17, 971–992. [Google Scholar] [CrossRef]
- Tordesillas, A.; Kahagalage, S.; Campbell, L.; Bellett, P.; Intrieri, E.; Batterham, R. Spatiotemporal slope stability analytics for failure estimation (SSSAFE): Linking radar data to the fundamental dynamics of granular failure. Sci. Rep. 2021, 11, 1–18. [Google Scholar] [CrossRef]
- Bruhn, R.L.; Pavlis, T.L.; Plafker, G.; Serpa, L. Deformation during terrane accretion in the Saint Elias orogen, Alaska. Geol. Soc. Am. Bull. 2004, 116, 771–787. [Google Scholar] [CrossRef]
- Elliott, J.; Freymueller, J.T.; Larsen, C.F. Active tectonics of the St. Elias orogen, Alaska, observed with GPS measurements. J. Geophys. Res. Solid Earth 2013, 118, 5625–5642. [Google Scholar] [CrossRef]
- Higman, B.; Geertsema, M.; Shugar, D.; Lynett, P.; Dufresne, A. The 2015 Taan Fiord landslide and tsunami. Alsk. Park Sci. 2019, 18, 6–15. [Google Scholar] [CrossRef]
- Franco, A.; Moernaut, J.; Schneider-Muntau, B.; Strasser, M.; Gems, B. Triggers and consequences of landslide-induced impulse waves–3D dynamic reconstruction of the Taan Fiord 2015 tsunami event. Eng. Geol. 2021, 2021, 106384. [Google Scholar] [CrossRef]
- Gualtieri, L.; Ekström, G. Broad-band seismic analysis and modeling of the 2015 Taan Fjord, Alaska landslide using Instaseis. Geophys. J. Int. 2018, 213, 1912–1923. [Google Scholar] [CrossRef]
- Williams, H.B.; Koppes, M.N. A comparison of glacial and paraglacial denudation responses to rapid glacial retreat. Ann. Glaciol. 2019, 60, 151–164. [Google Scholar] [CrossRef]
- Meigs, A.; Krugh, W.C.; Davis, K.; Bank, G. Ultra-rapid landscape response and sediment yield following glacier retreat, Icy Bay, southern Alaska. Geomorphology 2006, 78, 207–221. [Google Scholar] [CrossRef]
- Worthington, L.L.; Van Avendonk, H.J.; Gulick, S.P.; Christeson, G.L.; Pavlis, T.L. Crustal structure of the Yakutat terrane and the evolution of subduction and collision in southern Alaska. J. Geophys. Res. Solid Earth 2012, 117, B01102. [Google Scholar] [CrossRef]
- Franco, A.; Huber, A.; Moernaut, J.; Schneider-Muntau, B.; Aufleger, M.; Strasser, M.; Gems, B. Dynamics and geomorphological analysis of the Taan Fiord 2015 tsunamigenic landslide. In Proceedings of the 14th Congress INTERPRAEVENT 2021, Bergen, Norway, 31 May–2 June 2021. [Google Scholar]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for automated geoscientific analyses (SAGA) v. 2.1. 4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271–290. [Google Scholar] [CrossRef]
- Shean, D.E.; Alexandrov, O.; Moratto, Z.M.; Smith, B.E.; Joughin, I.R.; Porter, C.; Morin, P. An automated, open-source pipeline for mass production of digital elevation models (DEMs) from very-high-resolution commercial stereo satellite imagery. ISPRS J. Photogramm. Remote Sens. 2016, 116, 101–117. [Google Scholar] [CrossRef]
- QGIS Development Team. QGIS Geographic Information System; Open Source Geospatial Foundation: Chicago, IL, USA, 2009. [Google Scholar]
- Williams, R. DEMs of difference, Geomorphological techniques. Br. Soc. Geomorphol. 2012, 1–17. Available online: https://www.geomorphology.org.uk/sites/default/files/geom_tech_chapters/2.3.2_DEMsOfDifference.pdf (accessed on 22 October 2021).
- Miller, D.J. Geology of the Southeastern Part of the Robinson Mountains, Yakataga District, Alaska; Technical report; US Geological Survey: Reston, VA, USA, 1955. [CrossRef]
- Plafker, G.; Moore, J.C.; Winkler, G.R. Geology of the southern Alaska margin. In The Geology of Alaska; Geological Society of America: Boulder, CO, USA, 1994; pp. 389–449. [Google Scholar] [CrossRef]
- Johnston, I.W.; Chiu, H. Strength of weathered Melbourne mudstone. J. Geotech. Eng. 1984, 110, 875–898. [Google Scholar] [CrossRef]
- Rahardjo, H.; Aung, K.; Leong, E.C.; Rezaur, R. Characteristics of residual soils in Singapore as formed by weathering. Eng. Geol. 2004, 73, 157–169. [Google Scholar] [CrossRef]
- Hodgetts, S.J.; O’Kelly, B.C.; Raybould, M.J. Stabilisation of the Stanton Lees landslip using an embedded pile retaining wall. Geotech. Geol. Eng. 2007, 25, 705–715. [Google Scholar] [CrossRef]
- Jibson, R.W.; Michael, J.A. Maps Showing Seismic Landslide Hazards in Anchorage, Alaska; US Geological Survey: Reston, VA, USA, 2009. [CrossRef]
- Sarkar, K.; Singh, T.; Verma, A. A numerical simulation of landslide-prone slope in Himalayan region—A case study. Arab. J. Geosci. 2012, 5, 73–81. [Google Scholar] [CrossRef]
- Wang, P.; Wu, Z.J.; Wang, J.; Zhang, Z.Z.; Wang, Q. Experimental study on mechanical properties of weathered rock covered by loess. J. Shanghai Jiaotong Univ. (Sci.) 2013, 18, 719–723. [Google Scholar] [CrossRef]
- Olkhovatenko, V.E.; Trofimova, G.I. Engineering and geological conditions of an open-cast mining at the urop coal deposits of Kuzbass. World Sci. Discov. Ser. A 2014, 2, 62–81. [Google Scholar]
- Barla, G. Underground powerhouse stability in sandstone and siltstone formations. In Proceedings of the MIR2014-15th Series-Rock Mechanics and Rock Engineering Conferences, Torino, Italy, 19–20 November 2014. [Google Scholar]
- Kim, D.H.; Gratchev, I.; Balasubramaniam, A. A photogrammetric approach for stability analysis of weathered rock slopes. Geotech. Geol. Eng. 2015, 33, 443–454. [Google Scholar] [CrossRef]
- Yang, Y.C.; Zhou, J.W.; Xu, F.G.; Xing, H.G. An experimental study on the water-induced strength reduction in Zigong argillaceous siltstone with different degree of weathering. Adv. Mater. Sci. Eng. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Van Tien, P.; Sassa, K.; Takara, K.; Fukuoka, H.; Dang, K.; Shibasaki, T.; Ha, N.D.; Setiawan, H.; Loi, D.H. Formation process of two massive dams following rainfall-induced deep-seated rapid landslide failures in the Kii Peninsula of Japan. Landslides 2018, 15, 1761–1778. [Google Scholar] [CrossRef]
- Tang, S.C.; Wang, J.J.; Qiu, Z.F.; Tan, Y.M. Effects of Wet–Dry Cycle on the Shear Strength of a Sandstone–Mudstone Particle Mixture. Int. J. Civ. Eng. 2019, 17, 921–933. [Google Scholar] [CrossRef]
- Iyaruk, A.; Phien-wej, N.; Giao, P.H. Landslides and debris flows at Khao Phanom Benja, Krabi, southern Thailand. Int. J. GEOMATE 2019, 16, 127–134. [Google Scholar] [CrossRef]
- Tandon, R.S.; Gupta, V.; Venkateshwarlu, B. Geological, geotechnical, and GPR investigations along the Mansa Devi hill-bypass (MDHB) Road, Uttarakhand, India. Landslides 2021, 18, 849–863. [Google Scholar] [CrossRef]
- Xu, Y.; Liao, X.; Li, J.; Chen, L.; Li, L. The Effects of Water Content and Dry–Wet Cycles of Weak-Interlayer Soil on Stability of Clastic Rock Slope. Geotech. Geol. Eng. 2021, 39, 3753–3760. [Google Scholar] [CrossRef]
- Schmoll, H.R.; Dobrovolny, E. Generalized Geologic Map of Anchorage and Vicinity, Alaska. U.S. Geol. Surv. Misc. Geol. Invest. 1972. [Google Scholar] [CrossRef]
- Sharma, P.V. Environmental and Engineering Geophysics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Koppes, M.; Hallet, B. Erosion rates during rapid deglaciation in Icy Bay, Alaska. J. Geophys. Res. Earth Surf. 2006, 111, F02023. [Google Scholar] [CrossRef]
- Hackett, S.W. Regional Gravity Survey of Beluga Basin and Adjacent Area, Cook Inlet Region, South-Central Alaska; Open-File Report 100; Alaska Division of Geological & Geophysical Surveys: Fairbanks, AK, USA, 1976; 41p. [CrossRef][Green Version]
- Saltus, R.W.; Haeussler, P.J.; Bracken, R.E.; Doucette, J.; Jachens, R.C. Anchorage Urban Region Aeromagnetics (AURA) Project-Preliminary Geophysical Results; U.S. Geological Survey Open-File Report 01-0085; U.S. Geological Survey: Washington, DC, USA, 2001; 21p.
- Fellin, W. Einführung in Eis-, Schnee-und Lawinenmechanik; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Fish, A.M.; Zaretsky, Y.K. Ice Strength as a Function of Hydrostatic Pressure and Temperature; Technical report; Report 97-6; US Army, CRREL: Hanover, NH, USA, 1997. [CrossRef]
- Omori, F. Seismic experiments on the fracturing and overturning of columns. Publ. Earthq. Investig. Comm. Foreign Lang. 1900, 4, 69–141. [Google Scholar]
- Joyner, W.B.; Boore, D.M. Peak horizontal acceleration and velocity from strong-motion records including records from the 1979 Imperial Valley, California, earthquake. Bull. Seismol. Soc. Am. 1981, 71, 2011–2038. [Google Scholar] [CrossRef]
- Campbell, K.W. Near-source attenuation of peak horizontal acceleration. Bull. Seismol. Soc. Am. 1981, 71, 2039–2070. [Google Scholar] [CrossRef]
- Newmark, N.M. Effects of earthquakes on dams and embankments. Geotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
- Strauhal, T.; Zangerl, C.; Fellin, W.; Holzmann, M.; Engl, D.A.; Brandner, R.; Tropper, P.; Tessadri, R. Structure, mineralogy and geomechanical properties of shear zones of deep-seated rockslides in metamorphic rocks (Tyrol, Austria). Rock Mech. Rock Eng. 2017, 50, 419–438. [Google Scholar] [CrossRef]
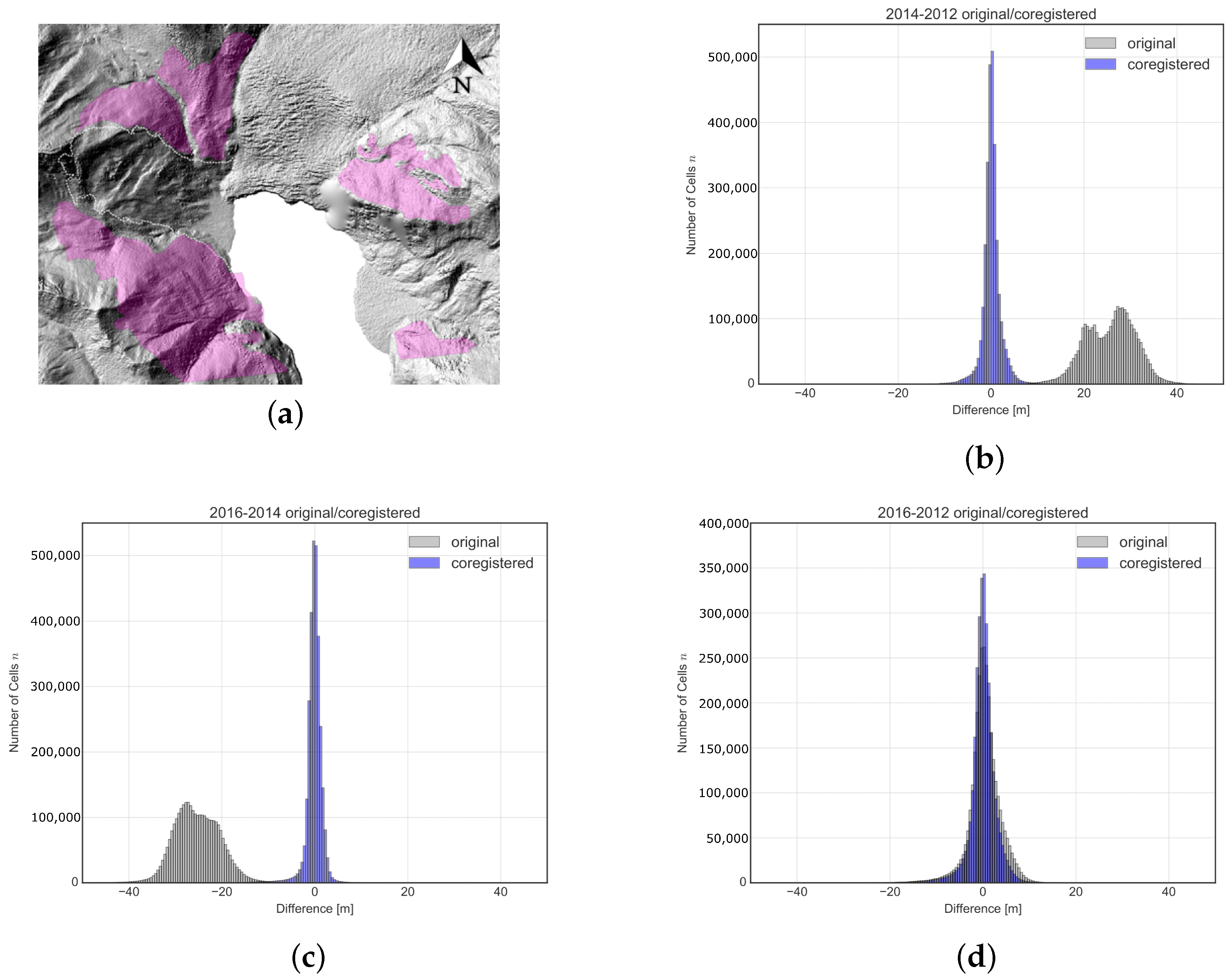
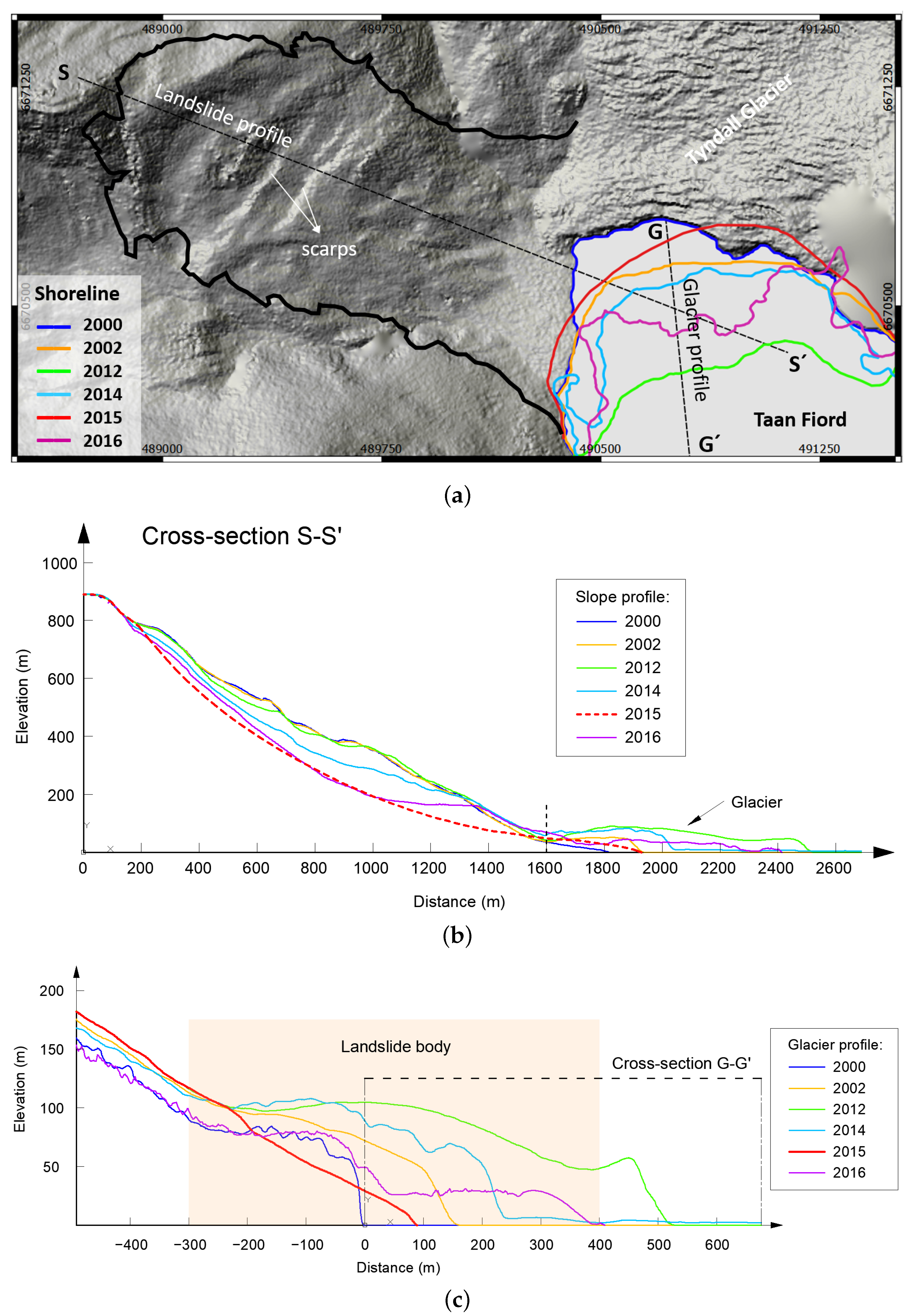

| Name | Acquisition Date | Resolution (m) | Method | EPSG * | Source |
|---|---|---|---|---|---|
| Icy Bay 2000 | 18–26 August 2000 | 5 | Intermap STAR-3i airborne interferometric synthetic aperture radar (InSAR) system mounted in a LearJet 36A aircraft | 32,607 | Discrete Global Grid System (DGGS) Elevation Portal of Alaska |
| Mt Saint Elias 2002 | 3–5 August 2002 | 10 | Intermap Technologies airborne interferometric SAR (InSAR) data acquisition system | 32,607 | DGGS Elevation Portal of Alaska |
| InSAR 2012 | 14 August–8 September 2012 | 5 | InSAR data | 3338 | DGGS Elevation Portal of Alaska—USGS National Map |
| Arctic DEM AK (5 m Mosaic) V2 | 1 March 2014 | 5 | Optical stereo imagery, high-performance computing and open source photogrammetry software | 3413 | DGGS Elevation Portal of Alaska |
| taan_topobathy_ 1m_UTM7_WGS84 | 1 May 2016 | 1 | Light Detection and Ranging (LiDAR) dataset, collected using a system based on a Riegl Laser Measurement Systems (LMS)-Q240i Pulsed Scanning Altimeter | 32,607 | Haeussler et al. [35] |
| Time Interval 2014–2012 | Time Interval 2016–2014 | Time Interval 2016–2012 | ||||
|---|---|---|---|---|---|---|
| Original | After Co-Registration | Original | After Co-Registration | Original | After Co-Registration | |
| Mean difference (MD) | 25.70 | 0.15 | −25.32 | −0.16 | 0.38 | 0.00 |
| Mean abs. difference (MAD) | 25.70 | 1.31 | 25.32 | 1.11 | 2.40 | 1.85 |
| Root mean squared difference (RMSD) | 26.25 | 2.03 | 25.80 | 1.85 | 3.41 | 2.78 |
| No. | Rock type | Cohesion (kPa) | Friction Angle (°) | Reference |
|---|---|---|---|---|
| 1 | Weak rocks | / | 30–40 | Johnston and Chiu, 1984 [60] |
| 2 | Highly to moderately weathered sandstone, siltstone and mudstone | 125 (3–4 m/depth) 55 (4.5–5.5 m/depth) 35 (9–10 m/depth) 225 (22–24 m/depth) | 42 (3–4 m/depth) 51 (4.5–5.5 m/depth) 45 (9–10 m/depth) 50 (22–24 m/depth) | Rahardjo et al., 2004 [61] |
| 3 | Moderately weathered mudstone/siltstone | 50 | 45 | Hodgetts et al., 2007 [62] |
| 4 | Metamorphic rocks comprising weakly siltstone, sandstone, etc. | ≈192 | 40 | Jibson and Michael, 2009 [63,75] |
| 5 | Mainly sandstones and quartzites (weakened) | 120 | 37 | Sarkar et al., 2012 [64] |
| 6 | Weathered sandstone Weathered mudstone | 507 202 | 33 32 | Wang et al., 2013 [65] |
| 7 | Weathered sandstone Weathered mudstone | 130 30 | 45 37 | Olkhovatenko and Trofimova, 2014 [66] |
| 8 | Mainly sandstone/siltstone (weakened) | 410–700 | 32–48 | Barla, 2014 [67] |
| 9 | Weathered sandstone | 70 | 47 | Kim et al., 2015 [68] |
| 10 | Moderately weathered silty mudstone | 268 | 45.34 | Yang et al., 2016 [69] |
| 11 | Mainly sandstone/mudstone (possibly weak) | / | 38.5–40.5 | Van Tien et al., 2018 [70] |
| 12 | A sandstone-mudstone particle mixture | 86.53 | 35.4 | Tang et al., 2019 [71] |
| 13 | Weathered siltstone | 50.2 | 42.8 | Iyaruk et al., 2019 [72] |
| 14 | Sandstone Mudstone | 3800 15 | 50 30 | Tandon et al., 2021 [73] |
| 15 | Weathering sandstone | 845.2 | 33.7 | Xu et al., 2021 [74] |
| Range of Values | |
|---|---|
| Initial groundwater table [m] | 800, 700, 600, 500, 400, 300, 200, 0 |
| c (kPa) | (°) | |
|---|---|---|
| p1 | 20 | 30 |
| p2 | 100 | 30 |
| p3 | 20 | 45 |
| p4 | 100 | 45 |
| 800 m | 700 m | 600 m | 500 m | 400 m | 300 m | 200 m | No GWT | |
|---|---|---|---|---|---|---|---|---|
| p1 | 0.483 | 0.628 | 0.717 | 0.717 | 0.717 | 0.717 | 0.717 | 0.717 |
| p2 | 0.637 | 0.757 | 0.879 | 0.927 | 0.927 | 0.927 | 0.927 | 0.927 |
| p3 | 0.788 | 0.865 | 1.148 | 1.148 | 1.148 | 1.148 | 1.148 | 1.148 |
| p4 | 0.993 | 1.221 | 1.452 | 1.491 | 1.491 | 1.491 | 1.491 | 1.491 |
| Range of Values | |
|---|---|
| Horizontal seismic load coefficient | 0, 0.1, 0.2, 0.3, 0.4, 0.5 |
| (kN/m) | Strength Parameter | ||||
|---|---|---|---|---|---|
| Set 1 | Set 2 | ||||
| Slope body | 24 | Mohr-Coulomb: c = 100 kPa = 45° | Mohr-Coulomb: c = 120 kPa = 50° | ||
| Weak layer | / | a1: c = 100 kPa = 28° | a2: c = 90 kPa = 28° | b1: c = 80 kPa = 30° | b2: c = 60 kPa = 30° |
| Glacier | 9 | c = 4500 kPa, = 6° | |||
| 800 m | 700 m | 600 m | 500 m | 400 m | 300 m | 200 m | No GWT | |
|---|---|---|---|---|---|---|---|---|
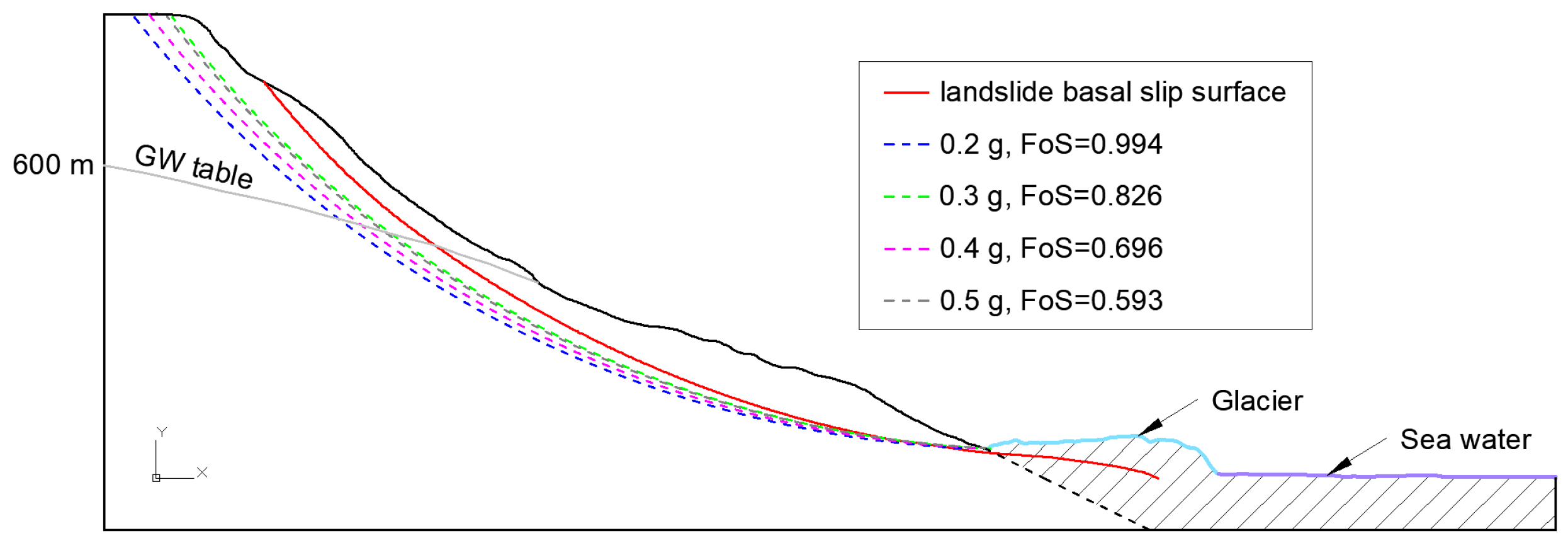
| 0.2 g | 0.667 | 0.820 | 0.994 | 1.044 | 1.044 | 1.044 | 1.044 | 1.044 |
| 0.3 g | 0.545 | 0.684 | 0.826 | 0.894 | 0.885 | 0.885 | 0.885 | 0.885 |
| No Seismic Loading | 0.1 g | 0.2 g | 0.3 g | 0.4 g | 0.5 g | |
|---|---|---|---|---|---|---|
| Set 1 | 1.452 | 1.204 | 0.994 | 0.826 | 0.696 | 0.593 |
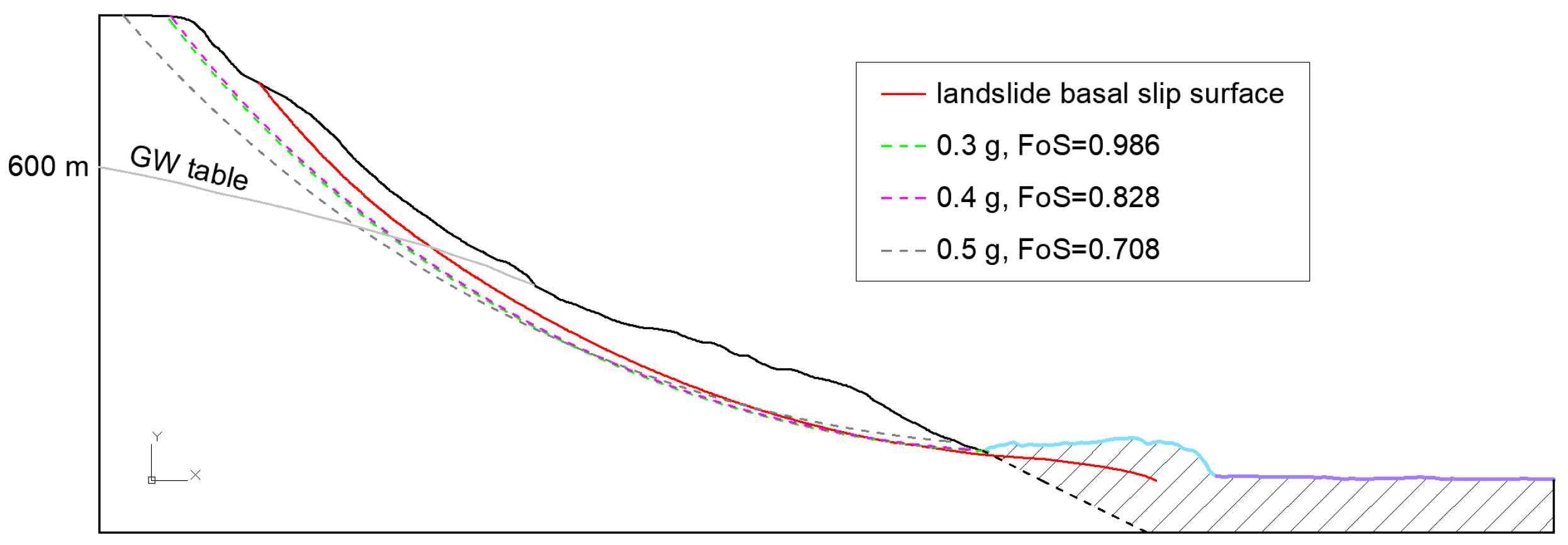
| Set 2 | 1.735 | 1.429 | 1.185 | 0.986 | 0.828 | 0.708 |
| a1 | a2 | b1 | b2 | |
|---|---|---|---|---|
| With glacier | 1.022 | 1.006 | 1.078 | 1.047 |
| Without glacier | 0.952 | 0.934 | 0.985 | 0.945 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, X.; Schneider-Muntau, B.; Fellin, W.; Franco, A.; Gems, B. Engineering-Geological Analysis of a Subaerial Landslide in Taan Fiord, Alaska. Remote Sens. 2021, 13, 4258. https://doi.org/10.3390/rs13214258
Dai X, Schneider-Muntau B, Fellin W, Franco A, Gems B. Engineering-Geological Analysis of a Subaerial Landslide in Taan Fiord, Alaska. Remote Sensing. 2021; 13(21):4258. https://doi.org/10.3390/rs13214258
Chicago/Turabian StyleDai, Xiaoru, Barbara Schneider-Muntau, Wolfgang Fellin, Andrea Franco, and Bernhard Gems. 2021. "Engineering-Geological Analysis of a Subaerial Landslide in Taan Fiord, Alaska" Remote Sensing 13, no. 21: 4258. https://doi.org/10.3390/rs13214258
APA StyleDai, X., Schneider-Muntau, B., Fellin, W., Franco, A., & Gems, B. (2021). Engineering-Geological Analysis of a Subaerial Landslide in Taan Fiord, Alaska. Remote Sensing, 13(21), 4258. https://doi.org/10.3390/rs13214258








