Next Article in Journal
Ship Detection in Sentinel 2 Multi-Spectral Images with Self-Supervised Learning
Previous Article in Journal
Textured Mesh Generation Using Multi-View and Multi-Source Supervision and Generative Adversarial Networks
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 21
10.3390/rs13214251
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Optimal Estimate of Global Biome—Specific Parameter Settings to Reconstruct NDVI Time Series with the Harmonic ANalysis of Time Series (HANTS) Method

by
Jie Zhou
1,2,*,
Li Jia
3,
Massimo Menenti
2,3 and
Xuan Liu
1
1
School of Urban and Environment Sciences, Central China Normal University, Wuhan 430079, China
2
Department of Geoscience & Remote Sensing, Delft University of Technology, 2628 CN Delft, The Netherlands
3
Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(21), 4251; https://doi.org/10.3390/rs13214251
Submission received: 10 August 2021 / Revised: 15 October 2021 / Accepted: 18 October 2021 / Published: 22 October 2021
(This article belongs to the Section Remote Sensing Image Processing)
Browse Figures
Review Reports Versions Notes

Abstract

:
Terrestrial remote sensing data products retrieved from radiometric measurements in the optical and thermal infrared spectrum such as vegetation spectral indices can be heavily contaminated by atmospheric conditions, including cloud and aerosol layers. This contamination results in gaps or noisy observations. The harmonic analysis of time series (HANTS) has been widely used for time series reconstruction of remote sensing imagery in recent decades. To use HANTS model, a series of parameters, such as number of frequencies (NF), fitting error tolerance (FET), degree of over-determinedness (DoD), and regularization factor (Delta), need to be defined by users. These parameters provide flexibilities, but also make it difficult for non-expert users to determine appropriate settings for specific applications. This study systematically evaluated the reconstruction performance of the model under different parameter setting scenarios by simulating pixel-wise reference and noisy NDVI time series. The results of these numerical experiments were further used to identify optimal settings and improve global NDVI reconstruction performance. The results suggested optimal settings for different areas (local optimization). If a user opts to use unique settings for global reconstruction, the setting NF = 4, FET = 0.05, DoD = 5, and Delta = 0.5 can produce the best performance across all setting scenarios (global optimization). In addition, several internal improvements, such as dynamic weighting scheme, polynomial and inter-annual harmonic components, and ancillary attributes of input data can be used to further improve the performance of reconstruction. With these results, future non-expert users can easily determine appropriate settings of HANTS for specific applications in different regions.

Graphical Abstract

1. Introduction

A wealth of terrestrial satellite data products has been accumulated since the Earth Resources Technology Satellite (ERTS-1) was launched into space in 1972 [1,2]. Vegetation spectral indices such as the Normalized Difference Vegetation Index (NDVI) are widely applied to monitor and to evaluate regional and continental vegetation dynamics [3,4]. The medium to coarse spatial resolution sensors, such as Advanced Very High Resolution Radiometer (AVHRR), Moderate Resolution Imaging Spectroradiometer (MODIS), Satellite Pour l’Observation de la Terre Vegetation (SPOT-VEGETATION), and Visible Infrared Imaging Radiometer Suite (VIIRS), onboard sun-synchronous polar orbiting satellites provide daily global coverage observations [5,6]. Moreover, satellites carrying sensors with higher spatial resolution, such as Landsat Thematic Mapper (TM) series and Sentinal-2A/B Multispectral Instrument (MSI), have a re-revisit time ranging from four to more than 15 days [7,8]. The instruments onboard geo-synchronous orbit satellites (such as the Spinning Enhanced Visible and InfraRed Imager (SEVIRI) onboard Meteosat Second Generation (MSG) spacecraft and Advanced Geosynchronous Radiation Imager (AGRI) onboard FengYun-4) can even capture regional vegetation variability at the sub-daily scale [9]. In other words, the temporal coverage of NDVI observations is limited by the combination of platforms and sensors [10]. Moreover, the measurements of spectral radiance by a space-borne imaging radiometer are heavily affected by clouds, aerosols, and atmospheric water vapor [11]. Clouds cover more than 50% of the earth surface at any given time and this is the main constraint on retrieving reliable time series of at-surface NDVI observations [12]. In general, cloud cover causes a large decrease in NDVI compared with clear sky conditions and changes more quickly than vegetation phenology as captured by NDVI [10,13].
To suppress the impact of less-than-ideal atmospheric conditions, especially the cloud cover, daily NDVI observations by moderate spatial resolution sensors are temporally composited to a 10- or 16-day time window using maximum value compositing (MVC) to generate NDVI data products [11]. The maximum NDVI value in each pixel and time window is retained and assumed to capture vegetation conditions in the entire time window [14,15,16]. This procedure may not remove cloud-contaminated observations completely and create gaps in the time series of NDVI, e.g., because there might be no cloud-free observation in a number of pixels and time windows, particularly in some super-humid regions [14,15,16]. Longer compositing window lengths (e.g., one month) can reduce cloud-affected observations further but might also remove meaningful phenological information in terrestrial vegetation [17]. Accordingly, time windows shorter than one month are applied in temporal compositing of NDVI retrievals [18]. To further reduce residual noise in the MVC-produced NDVI time series, other time series reconstruction (TSR) methods have been proposed, such as asymmetric Gaussian (AG) [19], double logistic (DL) [19], Savitzky–Golay (SG) [20], iterative interpolation for data reconstruction (IDR) [21], and Whitaker [22,23]. Some of these methods use temporally close clear-sky observations to estimate NDVI in a given pixel for time windows with no cloud-free observations [20,21]. Comprehensive reviews on TSR methods can be found in [12,24,25,26]. Each TSR method is based on different theories and assumptions about the properties of time series and applies different user-defined parameters, with the consequence that each method performs differently in different regions when applied to global reconstruction of observations [10,12]. For example, the AG and DL methods are more suitable to reconstruct NDVI time series at high latitudes, especially in the boreal and tropical forest areas, where the large faction of noisy observations over tropical humid areas may yield large errors and/or unstable fittings [12]. For continental and global studies on terrestrial vegetation, a TSR method providing stable and accurate reconstruction without excessive local tune-up is necessary [27,28].
Fourier-based harmonic analysis techniques have been extensively applied in modeling time series of remote sensing data especially vegetation index by mimicking surface dynamic with several harmonic components at different frequencies [29,30,31,32,33]. As a Fourier-based model, the harmonic analysis of time series (HANTS) is one of the most popular algorithms for the reconstruction of extended time-series of satellite data and originally conceived for NDVI observations [16,18,30,34]. The main advantages of HANTS include [34] (1) inherent coherence of harmonic components with periodical phenology rhythms; (2) low-pass filtering to preserve the slower phenological signals while excluding the high frequency noise induced by adverse atmospheric conditions; (3) simple (via iteratively linear least square fitting) implementation of the method; (4) impressive compression power for raw time series. Since it was coded by Verheof [35], the algorithm has been implemented with different programming languages, including Fortran, IDL, C, Matlab, R, and Python as well as the Google Earth Engine (GEE) platform [36] (Table 1) to meet the requirements of different users.
Notwithstanding its popularity in the field of time series analysis of satellite data, the reconstruction performance is heterogeneous when applied for global reconstruction [18]. The global reconstruction performance of HANTS was systematically evaluated by Zhou et al. [18], who presented a replicable measure of reconstruction accuracy for different regions on Earth. The same HANTS parameter setting was applied globally, however, while at the same time showing that performance varied with parameter setting, as expected [18]. For instance, HANTS gave rather high reconstruction errors in the boreal forest region as well as in part of cropland area, because of long gaps in time series or an inadequate choice of the number of harmonic components to capture higher frequency features in the NDVI signal [18]. Zhou et al. [12] carried out a comparative evaluation of the global reconstruction performance of several popular time series reconstruction methods, including HANTS, asymmetric Gaussian (AG), double logistic (DL), Savitzky–Golay (SG), and Whitaker smoother (WS). This evaluation suggested that HANTS performance was comparable with and in some cases better than the other methods included in the study. The results confirmed the potential relevance of a site (biome)-specific parameter setting towards better performance. The HANTS implemented by Verheof [35] designs several user-defined control parameters including the length of base period (BP), number of frequencies (NF), fitting error tolerance (FET), degree of over-determinedness (DoD), and regularization factor (i.e., Delta). These parameters all determine the reconstruction performance to a large extent. These parameters offer users a useful flexibility in the analysis of complex time series. On the other hand, effective parameter setting is a challenge for non-expert users and no other choice was available so far but to set these parameters based on a combination of literature and trial-and-error [18]. For the global reconstruction of complex signals affected by heterogeneous gaps, the reconstruction performance may be more sensitive to parameter setting than in regional applications [27,28]. For example, Zhou et al. [27] investigated the sensitivity of the reconstruction error to the selection of harmonic components, fitting error tolerance, as well as weighting schemes in HANTS and concluded that the overall performance can be improved with optimized parameter settings instead of applying a widely accepted setting scheme. Following the initial work in Zhou et al. [27], the optimal setting of other user-defined parameters still needs to be further explored and identified.
Besides the above-mentioned parameters to prescribe the operation of the HANTS algorithm, the impact of several characteristics of the input datasets on the performance of global reconstruction need to be taken into account. These characteristics include but are not limited to:
(1)
Time window applied in compositing the input data. Most freely available NDVI data apply a 10- or 16- or 30-day time window in compositing daily observations by applying maximum value composition (MVC) [37,38,39]. This procedure was believed to be sufficient to eliminate most cloudy observations [11,15]. Most applications were based on such composite data products [16,18,34], although, to our knowledge, no study evaluated the performance of HANTS in processing raw daily NDVI data or products with different composition time windows.
(2)
Quality control (QC) information. Pixel-based QC information, which indicates the retrieving reliability (e.g., good, marginal, snow/ice or cloudy), is an indispensable attribute of quantitative remote sensing data products [40]. Previous studies suggested this information could help to exclude low quality observations and improve reconstruction performance [20,37]. The accuracy of QC information, however, may also degrade its reliability [10,12], and the degree to which the QC information may impact the global reconstruction performance of HANTS needs to be investigated.
(3)
Actual acquisition date of each observation. For each pixel and time window the MVC procedure selects the maximum NDVI value but does not retain the actual date of acquisition [15,41]. This implies that, e.g., in a 7-day composite, there might be a difference in acquisition time of up to 14 days between the NDVI observations retained in adjacent pixels. This inconsistency can be mitigated by assigning an approximate time stamp, e.g., start, middle or end of the time window, to each selected maximum NDVI observation. However, this solution may still yield large differences between this approximate time stamp and the actual date of acquisition for the retained maximum NDVI value. When applying longer time windows, e.g., 30 days, or when observing critical or shorter phenological stages, the vegetation signal can change significantly during the time window [41,42]. It still needs to be evaluated, therefore, whether the global reconstruction performance might be improved by applying the actual date acquisition of each retained NDVI observation in the reconstruction of the time series.
As a summary, the successful worldwide applications of HANTS during the past three decades [24,34] has suggested that the model can be a robust and promising algorithm for global NDVI reconstruction, although the performance requires improvements in some regions [12,18].
The objective of this study is to describe and evaluate an improved HANTS method by systematically optimizing parameter settings and taking into account key-characteristics of input time series data. If successful, the study is likely to trigger further and wider use of HANTS for global and regional reconstruction of NDVI time-series.

2. Materials and Methods

2.1. Materials

Daily NDVI data were generated by using daily land surface reflectance retrieved from Terra/MODIS measurements, i.e., the data product MOD09GA-MODIS/Terra Surface Reflectance Daily L2G Global 1 km and 500 m, for the period 2001–2020 [37]. The Terra/MODIS measurements alone provide more than 6900 independent NDVI estimations for each pixel, which is enough for the statistical analysis of this study (see methods section). Thus, Aqua/MODIS measurements, which provide similar NDVI estimation as Terra/MODIS, were ignored [12]. The “QC_500 m” layer of the MOD09GA product provides an indication of the accuracy of each observation [40]. In order to speed up the evaluation procedure, only the NDVI observations of 445 BELMANIP2 (Benchmark Land Multisite Analysis and Inter-comparison of Products) sites [43] were downloaded from Google Earth Engine (GEE) and used in the evaluation. The BELMANIP2 sites were carefully selected by Baret et al. [43] to represent the global terrestrial vegetation types and their phenology (Figure 1), where the percentage of sites for each biome closely match the global fractional abundance of each biome. The number of sites sampling each biome is given in Figure 1, in which vegetation sites are dominated by grasses/cereal crops (GCC) (97 sites), savanna (SAV) (62 sites), evergreen broadleaf forest (EBF) (61 sites), and shrubs (SHR) (60 sites).

2.2. Methods

2.2.1. Overview of the Evaluation and Optimization Procedures

The procedure to optimize the HANTS configuration for global NDVI time series reconstruction includes an evaluation and an optimization step (Figure 2). For each site, an annual reference NDVI time series and a set of annual noisy series based on raw MODIS daily NDVI time series and QC information was generated using a time series simulator. The simulated noisy series are further processed by applying HANTS for different configurations considering internal parameter settings, improvement schemes, and several external influence factors. The HANTS algorithm coded by Verhoef [35] with predefined parameters was referred as “classical HANTS” to differentiate it from later HANTS versions with several improvements; see Section 2.2.3 for details. The difference between the reconstructed noisy series and reference series was used to quantify the reconstruction performance in terms of overall reconstruction error (ORE) [12] (Section 2.2.4 for details). By comparing the ORE obtained for a set of sites and for different configurations, the configurations providing better reconstruction global performance, i.e., lower ORE, can be identified.

2.2.2. Simulation of Reference and Noisy NDVI Time Series

To measure the reconstruction performance of HANTS quantitatively, the immediate method is to evaluate how close a reconstructed noisy series get to clear-sky NDVI series (or “ground truth”). One cannot expect to find ideal clear-sky NDVI series, however, as few vegetated pixels on Earth can be completely free from cloud cover during the vegetation growth season. We assumed that vegetation phenology and seasonal cloud cover at a specific location (pixel) remain roughly similar across the years. Likewise, in earlier studies [10,12,18], long-term historical NDVI observations were applied to simulate reference annual NDVI series, representing cloud-free vegetation phenology, and noisy NDVI series including cloud contaminated observations. Zhou et al. [12] proposed a robust scheme to synthesize pixel-based annual reference series and simulate noisy conditions (e.g., caused by cloud cover) using long-term historical NDVI observations. The annual reference time series were constructed by targeting the 445 BELMANIP2 (Benchmark Land Multisite Analysis and Intercomparison of Products) sites [43]. The method used daily NDVI retrievals for 14 years and the Quality Assessment (QA) flags indirectly, i.e., to separate the daily observations into high and low quality (HQ, LQ). Temporal composites of the daily HQ observations were generated and further treated as being clear-sky to construct the reference time series for each site, while noise is added to mimic the effect of clouds and snow, generating the noisy time series. The noise is generated by taking into account the probability of LQ observations estimated from the daily time series of each site. In this study, the method of Zhou [12] was applied to construct an annual time series of reference and noisy NDVI observations. A detailed description of the method can be found in [16]. Specifically, for each site, the procedure uses daily MODIS reflectance time series (from MOD09GA) and QC information (“QC_500 m” layer) as input and generates one annual daily reference NDVI series (365 samples) and 100 annual daily noisy NDVI series. The daily NDVI observations were labeled as “high” and “low” quality respectively using the QC flags, with “high” quality NDVI assumed to be less affected by cloud conditions, observation geometry and instrumental errors. In particular, a NDVI observation is assessed “high quality” when the QC flags are “0000” in both bits 2–5 (band 1 quality) and bits 6–9 (band 2 quality) and “00” in bits 0–1 (cloud state). All other NDVI observations are assessed as “low quality”. The “high quality” and “low quality” NDVI observations were used to simulate reference and noisy NDVI time series. In this way, the QC flags are not applied to select specific outliers in the gap-filling stage, but are only applied to extract a large sample of HQ observations. Moreover, we used 20 years (2001~2020) of daily high-quality observations, which we deemed sufficient to construct a robust annual reference series to capture pixel seasonal NDVI dynamic.

2.2.3. Configurations for Evaluation and Optimization

In this study, three kinds of Configurations were developed to evaluate the reconstruction performance (Table 2). Firstly, the classical settings of the NF, FET, DOD, and Delta parameters were evaluated for all possible values. Next step, the candidate improvements were evaluated separately and finally a new functionality was added to the current algorithm to optimize parameter settings. Finally, configurations on external data attributes, e.g., temporal windows applied in compositing, QC flag for initial weights setting, and the actual acquisition date of the retained observations in each pixel, were evaluated to identify procedures for the further improvement of reconstruction performance.
(1)
Configurations of classical HANTS parameters
The performance of HANTS is mainly controlled by multiple critical internal parameters. Except the length of the base period (BP), HiLO flag, and valid range (VR) that can be easily determined based on the physical meaning of the input signal, the other four parameters, i.e., NF, FET, DoD, and Delta, must be selected within a range of possible values by users and the selection procedure needs to be evaluated systematically. A set of configurations needs to be evaluated in order to understand better the impact of each parameter on the model in global NDVI reconstruction and can be briefly described as follows:
(a)
Length of base period (BP): This parameter corresponds to the period of the dominant component of the signal to be reconstructed, while the periods of all other harmonics are derived from the base period (see the description of NF below). Remote sensing-based NDVI data are provided at a daily to monthly sampling interval, with the signal dominated by the seasonal and yearly variations in vegetation greenness. Thus, the BP is normally set to 12-month (i.e., one year or 365 days).
(b)
Number of frequencies (NF): This parameter determines the total number of harmonics (excluding the zero-frequency component) to be used in the time series modeling and reconstruction. The period of the i-th harmonic is given by P(i) = BP/i (i = 1, 2, …, NF). In turn, the frequency is the reciprocal of P(i). Since atmospheric contamination mainly introduces high frequency noise, a few low frequency components (i.e., NF < 4) were used in previous studies (e.g., [18,30,35]). In this study, NF in the range from 2 (12-month and 6-month components) to 6 was applied, i.e., 2 months was the shortest period/highest frequency component, in the global evaluation of time series reconstruction by HANTS.
(c)
Fitting error tolerance (FET): The acceptable maximum deviation between raw observations and the result of the reconstruction. In the case of NDVI(t), at each iteration, a negative deviation from the modeled time series larger than FET will be excluded from further iterative processing. The iteration is terminated when all deviations between the remaining valid observations and the fitted model are smaller than the pre-defined FET value. A small FET may erroneously remove some valid observations as outliers while some real outliers cannot be correctly identified with a too large FET. FET is frequently set between 0.05 and 0.1 in the reconstruction of NDVI time series by HANTS [16,18,44,45]. In this study, a FET range from 0.01 to 0.12 with a 0.01 step was applied.
(d)
Degree of over-determinedness (DoD): A Fourier series including the harmonic components determined by BP and NF is used to model the time series of observations. The coefficients of the modeled series are obtained by solving a linear system of equations, which requires at least 2NF + 1 independent observation, since amplitude and phase value need to be determined for each harmonic component of the series. The observations are inherently accompanied with errors, solutions of the system of equations by using > 2NF + 1 observations may improve the accuracy of estimated amplitude and phase. Such an overdetermined system of equations is best solved using least square method, where more observations give a smaller error of estimate. HANTS is designed to identify and remove outliers iteratively. The DoD is defined as the minimum number of required additional observations, i.e., the minimum difference between the remaining valid observation size and 2NF + 1 [35]. In other words, if the total input observation size is N0, then the removed outliers should not exceed (N0 − (DoD + 2NF + 1)). Therefore, the DoD can be set between 0 and (N0 − (2NF + 1)) and it is a second termination criterion of iterations beside FET. A too large DoD tends, however, to prevent the iteration procedure from detecting possible outliers [16]. The minimum number of valid observations needed to solve a system of equations is 13 when NF = 6. So, the maximum possible DoD for 16-day composited yearly NDVI (N0 = 23) is 10. In this study, we varied DoD between 0 and 12 in steps of 1 to analyze the impact of DoD on model performance.
(e)
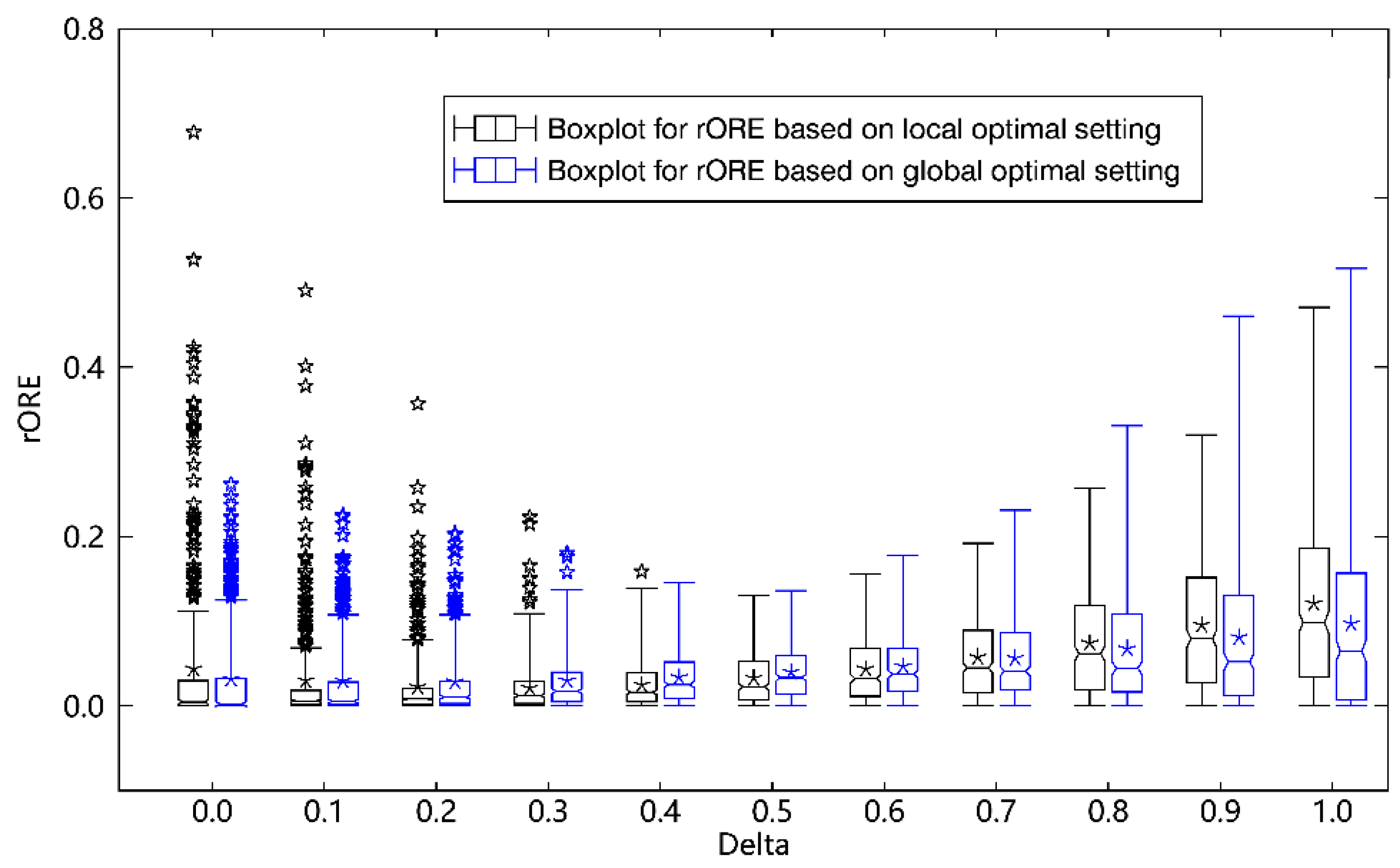
Delta (regularization factor): Although the solution is obtained by solving an overdetermined linear system of equations in HANTS, the solutions may be non-unique because of possible singular matrixes, i.e., ill-conditioned systems. These non-unique solutions may yield large fluctuations in the fitted results, especially in subsequent iterations. The ridge regression method was applied to solve the linear system in the classical HANTS and a regularization factor (i.e., Delta) was used to damp the randomness of the solutions [20]. The Delta is generally set as a small positive value (e.g., 0.1). The impact on model performance was evaluated by varying Delta between 0 and 1 in step of 0.1.
(f)
HiLo flag: This parameter indicates whether outliers are expected either above or below the fitted model, which depends on the nature of observations [16]. For instance, cloud covered or contaminated targets yield lower NDVI values compared to clear-sky conditions, thus outliers are below the fitted model and are rejected (i.e., HiLo = “Low”). Given the type of observations, HiLo parameter is unambiguously defined and there is no need to evaluate the impact on HANTS performance.
(g)
Valid range (VR): The valid range of input signals is determined by the nature of the observations and is defined for each data product [16]. For instance, the land surface NDVI generally ranges between 0 (or −0.2 if including water or snow) and 1.0. Observations outside this range can be rejected as outliers directly.
In summary, the NF, FET, DoD, and Delta are the four most critical parameters of classical HANTS controlling the reconstruction performance. The NF, FET, and DoD jointly determine profile fitting and outlier detection of the model, and thus their settings are evaluated jointly. Here the “joint” evaluation means calculating performance metrics over all sites under each possible combination of NF, FET, and DoD settings. For each site, there will be 5 (NF settings) × 12 (FET settings) × 13 (DoD settings) = 780 combinations. Based on the joint evaluation result, the Delta scenarios are further evaluated, after which the optimized parameter settings for global reconstruction using classical HANTS can be derived.
(2)
Model improvements
In addition to the procedure to optimize parameter settings of the classical HANTS, several ways to improve global reconstruction performance by adapting the design of HANTS were proposed.
Specifically, the proposed improvements and the procedures to evaluate them are described below:
(a)
Dynamic update of weights. Initially, all input observations are assigned a weight = 1 by HANTS. The algorithm was originally designed to apply varying weights, but it was first implemented with binary weights, i.e., = 1 for valid observations and = 0 for outliers. As explained above, at each iteration, any observation negatively deviating from the current Fourier series by more than the FET are assigned a weight = 0 and excluded in further iterations. The FET setting is set on the basis of user experience and erroneous detection of outlier is unavoidable. The dynamic update of weights was proposed to improve the performance. In practice, the weight w k i of the i-th observation is updated at each k-th iteration taking into account the deviation from the current Fourier series as:
w k i = w k − 1 i + y r k i − y r i ( m a x ( y r k ) − m i n ( y r k ) )
where yrk is the vector of estimates by the Fourier series at the k-th iteration. In this case, if the k-th estimates are larger than estimates in the previous iteration, weights are increased. This leads to the estimates in later iterations to approach the upper envelope of NDVI time-series.
(b)
Polynomial or inter-annual harmonic components: If HANTS is applied to annual NDVI time series, the estimated Fourier components can only explain variations over periods shorter than a year while real signals may contain trends or inter-annual variations [12]. Earlier studies on Fourier analysis of NDVI time series were focused on investigate inter-annual variation of vegetation regulated by climate using multi-annual data records [30,46,47,48]. Multi-annual components in the Fourier series or alternatively 3-order polynomial components can be used to capture inter-annual variability.
(3)
Impact of input data attributes
The impact on reconstruction performance of key—characteristics of input data was evaluated, specifically the time window applied in the compositing, QC information, and the actual date of acquisition of the observation retained in the temporal composite for each time window and each pixel:
(a)
Composite time window. MVC-s were generated applying a time window of 1, 5, 8, and 16 days and used to simulate daily noisy series for each site. The overall reconstruction error (ORE) was calculated to evaluate the impact of the MVC time window on reconstruction performance.
(b)
QC-based weighting. The QC flag of each observation was used in the reconstruction. The weights are set initially as 0 or 1 for low quality observations (QC = 0) or high-quality observations (QC = 1) respectively.
(c)
Actual date of acquisition. The actual date of acquisition of the observation retained in the temporal composite for each time window and each pixel was used in the reconstruction instead of the average or central date within each time window.

2.2.4. Performance Metrics

The ORE was defined as the RMSE between the reconstructed noisy series and reference series [12] and was used as the main matric in this study to quantify the performance of HANTS under different scenarios:
ORE i , j = ∑ k = 1 k = N ( y r n o i s e , k i ,   j − y r r e f , k i ) 2 N
where:
  • i = 1, 2, …, 445 sites;
  • j = 1, 2, …, 100 noisy series;
  • y r n o i s e , k i ,   j is the k-th estimate of j-th reconstructed noisy NDVI series for the i-th site;
  • y r r e f , k i is the k-th estimate of simulated reference NDVI series for i-th site;
  • N (=365) is the number of samples in each reconstructed time series.
For each site, there were 100 simulated noisy NDVI series, resulting in 100 noisy-reference series pairs.
Zhou et al. [12] applied the mean ORE over 100 replications as a measure of reconstruction performance at each site under specific scenarios. The standard deviation of ORE over the 100 replications, i.e., Std-OREi, reflects the stability of model performance under different noise conditions [12]. Smaller mean OREi and Std-OREi indicate better performance. The two metrics can be used to rank model configurations independently or can be combined. The configuration yielding the smallest OREi, however, may not yield the smallest Std-OREi, i.e., the optimal configuration was identified via a trade-off between OREi and Std-OREi [12].
The configurations defined by the settings of NF, FET and DoD were ranked separately in the order of increasing OREi and Std-OREi, giving two rankings for each configuration. Then the configuration with the lowest sum of the two rankings was selected as the best setting of NF, FET and DoD for each site. The best setting of NF, FET, and DoD may vary with sites, which leads to “local optimization” [27]. Contrariwise, the global reconstruction of a NDVI dataset would require a unique setting of NF, FET, and DoD. The configuration ranked first at most sites was taken as the “global optimization” [10,27]. For example, if the combination of (NF = 3, FET = 0.05, DoD = 5) gave the smallest OREi for 200 sites and none other configuration gave this performance for more than 200 sites, the configuration (NF = 3, FET = 0.05, DoD = 5) was applied as global optimization to all sites. The global optimal configuration was the same as the local optimal configuration for some sites, while it was different for other sites, i.e., the overall performance achieved by applying the local optimal configuration settings was higher than that with the global optimal configuration.
Different settings of Delta scenarios were evaluated for cases obtained with the best local and global settings of NF, FET and DoD. Zero or small Delta may result in non-unique solutions of the linear system of equations, giving an extremely large ORE for some sites. The normalized ORE, i.e., rORE, was applied to evaluate the impact of Delta settings on reconstruction performance:
rORE = ORE d e l t a − ORE m i n ORE m e a n
where OREmin and OREmean are the minimum and mean ORE values of all Delta settings for a site. OREdelta is the ORE value for a specific Delta setting.

3. Results

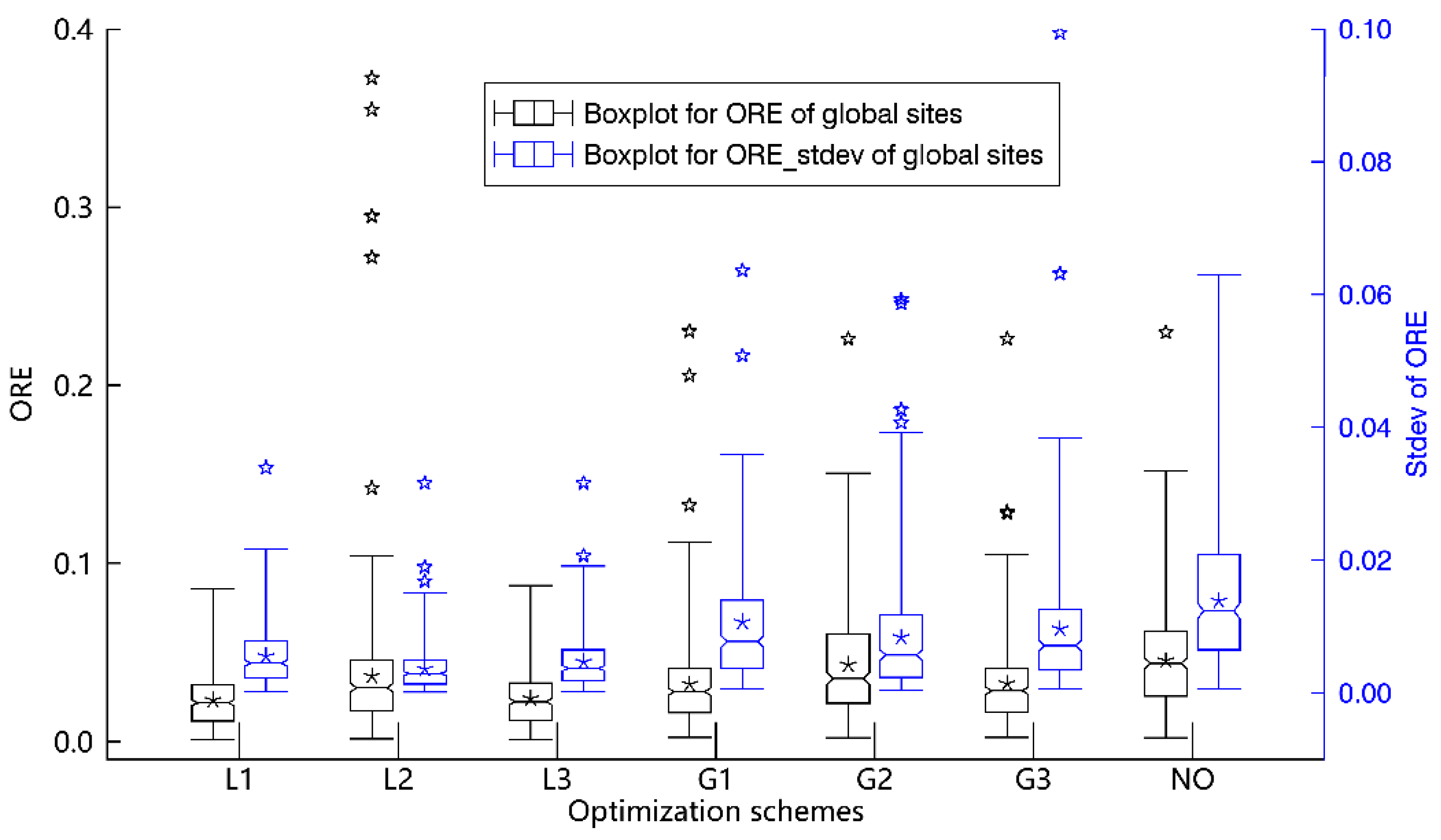
3.1. Optimization of Parameter Setting

Optimal settings for NF, FET, and DOD: There are 780 combinations of settings for NF, FET and DoD for each site, from which the optimal setting was identified by applying ORE and Std-ORE criteria (see Section 2.2.4). The local optimization, i.e., in principle with a different best setting for each site, achieved a better reconstruction performance than the global optimal setting in terms of both ORE and Std-ORE (Figure 3). The best setting based on ORE (L1, G1) gave the smallest ORE but a sub-optimal Std-ORE, and the other way around when applying the best ranking based on Std-ORE. The setting based on the trade-off of ORE and Std-ORE, i.e., L3 (G3), gave a performance in between L1 and L2 (G1 and G2).
The local optimal settings (L3) for global sites were shown in Figure 4. To achieve the best reconstruction performance requires 4–5 or even six harmonic components at high latitudes (e.g., >50 °N) (Figure 4A). In the humid areas at low latitudes, such as the rainforest area, it is better to use two harmonic components (Figure 4A). Cloud contamination of the NDVI observations is more frequent in humid areas due to higher cloud cover, which may result in multiple and adjacent “bad” observations. High frequency harmonic components can capture rapid variations in time series, as the ones due to clouds, and may prevent HANTS from identifying these occurrences as outliers [18]. This results in larger reconstruction errors compared with settings involving only low frequency harmonic components. As regards the FET, the results suggested that a higher value, say 0.05 to 0.09, should be set at higher latitudes in the Northern hemisphere (Figure 4B). Contrariwise, at lower latitudes, it is better to use a lower FET, i.e., 0.01–0.03. The best DoD setting is rather variable across sites, except in the tropical rainforest areas where DoD should be less than 3 (Figure 4C).
Interested readers should in a first instance query the optimal parameter settings for the sites sampling a specific area of interest. To present of an overview of the site-specific results, the optimal parameter settings have been stratified by biome (Figure 4) using the land cover classes applied in the MODIS data product described earlier. The aggregated results suggested that four harmonics can result in better reconstruction performance in the DNF, ENF, DBF, SHR, and GCC classes, while two and three harmonics would be sufficient in EBF, SAV, and BCR respectively (Figure 4A). The optimal FET for DNF, ENF, DBF, and SAV was 0.05 on average, while smaller values were suggested for other biomes (Figure 4B). The mean DoD across different biomes was ranging from 2 to 7, i.e., with a limited dependence on the biome (Figure 4C).
The global best setting G3 corresponds to NF = 4, FET = 0.05, and DoD = 5, which gave a much higher ORE and Std-ORE than the L3 setting (Figure 5). Particularly, the ORE and Std-ORE given by L3 and G3 in the boreal forest area and in the equatorial rainforest area at low latitudes can reach 0.06 and 0.018 respectively, which are much higher than in other areas (Figure 5).
Optimal settings for Delta: The boxplots of ORE with different Delta settings were similar (not shown). The mean rORE was smaller with zero or small Delta value (<0.4), compared to larger Delta values (Figure 6). The former settings, however, produced a severely skewed distribution of rORE across global sites, i.e., with more outliers and averages much higher than the upper quantiles (Figure 6), which suggested an unstable reconstruction. In contrast, less skewed distribution of rORE can be expected with higher Delta values, although a too large Delta may degrade reconstruction performance, i.e., increasing mean ORE globally (Figure 6). As a trade-off, setting Delta between 0.4 and 0.6 seems the best option that can avoid both outliers at some sites caused by small Delta and lower performance caused by a large Delta. As regards the best settings for different regions, a Delta >0.8 is needed for humid areas such as tropical rainforest regions, since the small seasonality of NDVI can aggravate collinearity of the observations and the solutions of the system of equations. For most of the other sites, a Delta < 0.5 is preferred, which presents a slight biome-dependent pattern (Figure 7).

3.2. Impact of Proposed Improvements

The three proposed improvements, i.e., dynamic weighting, three-order polynomial component, and inter-annual harmonic components, gave ORE values comparable to classical HANTS with global optimized settings (G3) for most sites. Moreover, smaller ORE, i.e., significantly better reconstruction performance was obtained for part of the sites as shown in Figure 8. Overall, dynamic weighting had a limited effect at sites where the reconstruction error was low to medium with the global optimal settings of NF, FET, and DoD, while more sites saw a significant improvement with dynamic weighting observed when local optimal settings of NF, FET, and DoD were applied (Figure 8A).

3.3. Impact of Input Data Attributes

The global performance of reconstruction by HANTS with global optimized settings (G3) but different composite lengths of five, eight, and 16 days produced similar ORE statistics (Figure 9). This suggested that composite length does not have a significant effect on reconstruction performance. Contrariwise, the direct use of daily NDVI series without MVC composition gave a higher reconstruction error. Including QC information in the initial weighting (QC + HANTS) in the reconstruction can improve global performance, especially when using daily NDVI time series. Some studies filtered out low quality NDVI observations using QC information [13,49], while our result suggested that the “QC only” reconstruction gave a much larger ORE than all other configurations when detecting and removing outliers. Applying the actual acquisition date (AAD) resulted in a slight improvement in reconstruction performance only for longer composite windows (i.e., 16-day composition). The limited improvement in reconstruction performance by the AAD treatment over short composite windows may be explained by the insufficiently low frequency harmonics used in HANTS to capture the detail of variation in NDVI caused by different time stamps within composite windows.

4. Discussion

4.1. The Improved Harmonic ANalysis of Time Series (iHANTS)

The improved harmonic analysis of time series (iHANTS) proposed in this study can reconstruct global NDVI datasets with improved performance on the basis of the systematic evaluation of the impacts of a broad set of parameters. Specifically, the systematic evaluation of configurations led to the following suggestions:
(1)
The critical internal parameters, i.e., NF, FET, DoD and Delta can be set on the basis of either a “local” or “global” ranking for global reconstruction. For regional applications, users can refer to Figure 3 and Figure 6 for best local settings. The best global settings, based on the trade-off between ORE and Std-ORE, are: NF = 4, FET = 0.05, DOD = 5, and Delta = 0.5, which is the default setting scheme used by [18] to evaluate the performance of global NDVI reconstruction.
(2)
Reconstruction performance can be significantly improved in specific regions of the Earth by using dynamic weighting instead of the classical rigid weighting scheme and by adding 3-order polynomial or inter-annual harmonic components to account for inter-annual variability. Dynamic weighting and 3-order polynomial components require a revised implementation of HANTS.
(3)
Global reconstruction performance can be improved by using QC information of the dataset to set initial weight and applying the actual date of acquisition for each input observation. Most freely accessible implementations of HANTS do not support custom setting of initial weights and input timestamps. Thus, a revised implementation of the model is needed again.
Several freely available NDVI products are generated using the radiometric data acquired by different sensors, such as AVHRR, MODIS, and SPOT-VEGETATION, and may be provided with different composition lengths [38]. The results of this study suggest that the composition length has a limited impact on global reconstruction performance. This may be due to two opposite impacts. On the one hand, a shorter composition length captures rapid variations in NDVI, and on the other hand, it also collects more low-quality observations, which impacts reconstruction performance in opposite directions [14,15]. In other words, no improvement can be achieved by using a different composition length. Of course, if observations are acquired at higher frequency, e.g., by combining radiometric data acquired by both Terra/MODIS and Aqua/MODIS, performance can be improved, since a higher frequency in data acquisition can increase the probability of high-quality observations [17].
Although the gap-filling performance of HANTS is improved by the optimized parameter settings, there remain limitations that should be highlighted. Firstly, parameter settings were optimized using the annual reference NDVI series constructed by Zhou et al. [12]. This implies that the study assumed that the intra-annual variability captured by the annual reference series dominate pixel NDVI dynamics. For pixels with large inter-annual variability or land-cover change developing over even longer periods of time, the real NDVI dynamics may be poorly represented by the annual reference series. In these cases, the optimized parameter settings should be interpreted with caution [12]. Secondly, the optimization procedure applied to synthetic noisy time series constructed using the daily observations acquired by both Terra and Aqua MODIS sensors. This characterization of noisy conditions is not directly applicable to data acquired by satellites with a lower revisit frequency, such as Landsat-8 and Sentinel-2A/B. Lastly, we used the absolute deviation between reference and reconstructed series (i.e., ORE) as a performance metric, which may not be the most appropriate to characterize the accuracy if capturing phenological features. The latter should be addressed in a follow-up study.

4.2. Applying Optimaized HANTS to Other Terrestrial Remote Sensing Variables

Our evaluation of HANTS configurations has been based on NDVI time series, but some findings are applicable to time series of other observables, such as leaf area index (LAI) [50] and land surface temperature (LST) [24,51]. The LAI signal is similar to NDVI in terms of phenology curve, as well as the direction of outliers by clouds effect. It is thus reasonable to assume that the best settings of NF, DoD, and Delta would also improve the performance in the reconstruction of LAI time-series. With regard to the FET, the best global setting is 0.05 for NDVI, i.e., 5% of the valid dynamic range of NDVI (0–1). Taking into account that the valid dynamic range of LAI is from 0 to 10, the FET can be set at about 0.5 (10 × 5%) for the reconstruction of LAI time-series. For LST products, most previous studies [24,45,51] applied small NF (NF = 2 or 3) in HANTS processing, while the Xu et al. [52] reported the optimal NF should be set from 7 to 9 to reconstruct LST over Yangtze River Delta. The appropriate NF settings for global reconstruction still need to be carefully evaluated in future. The FET should also be adapted on the basis of the dynamic range of LST.
Fourier-based gap-filling methods fit time series of available observations with predefined harmonic components but differ in the way potentially contaminated observations are identified and replaced to generate time series of cloud-free images. Besides HANTS, another example is the method proposed by Zhu et al. [29]. Both methods require a threshold to detect outliers. Zhu et al. [29] also use QC flags on clouds, cloud cover, and snow, while other settings were described less precisely and may need to be adjusted depending on the area (biome) observed. We may safely assume, therefore, that optimization towards biome-specific parameter settings is likely to benefit the performance of Fourier-based gap-filling methods.

4.3. Other Application Topics for the HANTS

HANTS has been widely applied to analyze long time series of terrestrial remote sensing observables for almost 30 years, either for gap-filling or extracting accurate harmonic components for further analysis [34,44,46,47]. The algorithm has been implemented using different programming languages and platforms, such as Fortran, ENVI/IDL, Matlab, Python, R, etc. (see Table 1). In 2014, the new release of IDL (8.4 version) included HANTS as an official function (Table 1). Most of these implementations only implement the core of HANTS for single series processing and are commonly used for small scale processing by researchers [18,51]. When applying the method to long time series of images for a large region or at high temporal and spatial resolution, the computational constraints of personal computers (PC) may limit its usage. One needs to consider parallelizing computer processing to make full use of computational resources, such as a multiple-core CPU of the PC or even implementing the method on super computers or clusters [12]. Moreover, cloud-based geo-computation platforms such as the Google Earth Engine (GEE) platform provide a data warehouse of popularly and freely available remote sensing datasets and rich cloud computing resources for earth observation users [2]. Users can design and implement applications without spending a lot of time to download and process large volumes of data on local PCs [5]. We have implemented HANTS on the GEE platform, which can process various remote sensing datasets on request and very efficiently. For instance, to reconstruct one year global 16-day NDVI product with 0.05-degree spatial resolution (MOD13C1), HANTS on the GEE platform only takes 10 min on average, while it may take more than two hours on a local PC without parallelization, not to speak of the time spent on downloading data. The Javascript code for the HANTS implementation on GEE is available by personal request to the senior author of this paper. The full GEE version of HANTS will be published soon.
The amplitudes and phases of the periodic components of NDVI signals are quantitative phenological metrics of vegetation vigor across timescales and have been frequently applied in land cover change detection or vegetation-climate interaction analysis [34,46,47,48]. The main purpose of HANTS is the quantitative analysis of observable signals in the frequency domain. To this end, efficient and accurate reconstruction and gap-filling are necessary and that is the service that globally improved HANTS can provide. The performance of any time series reconstruction method is fundamentally dependent on the quality of raw observations, which means that one cannot expect to perfectly recover clear-sky NDVI signals for pixels where most observations are contaminated by clouds.

5. Conclusions

HANTS has been one of the most widely used time series reconstruction methods in the remote sensing community. Sant attention, however, has been paid to investigating the optimal parameter settings under different conditions and non-expert users have to identify suitable settings by a lengthy, subjective trial and error process, which impedes the method from being applied in a larger community. This study systematically evaluated and quantified the impacts of HANTS configurations on global NDVI reconstruction performance and proposed best settings for each configuration. The evaluation was performed by generating pixel-wise reference and noisy NDVI time series using long-term historical observations from MODIS. The results suggested both local and global optimal settings of critical parameters of the model, i.e., NF, FET, DoD, and Delta. To facilitate the non-expert users of the model, the local optimal settings for global sites have been listed in Supplementary Materials, Table S1. The dynamic weighting scheme, inter-annual harmonic and 3-order polynomial components can be used to improve global reconstruction performance by updating the implementation of classical HANTS. In addition, by including attributes of input NDVI data, such as data quality flag (QC) and the actual acquisition date of each observation retained in the temporal composites, the performance of global reconstruction can be further improved. Future users can refer to the settings described in this study towards the better performance of HANTS for the regional or global reconstruction of time-series of bio-geophysical remote sensing observables.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/rs13214251/s1, Table S1: A CSV file listing the local optimal settings for all BELMANIP2 sites was provided as a supplementary document.

Author Contributions

Conceptualization, J.Z., L.J. and M.M.; formal analysis, J.Z.; methodology, J.Z.; visualization, J.Z.; writing—original draft, J.Z.; writing—review & editing, L.J., M.M. and X.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA19030203), National Natural Science Foundation of China (Grant No. 41701492), and Fundamental Research Funds for the Central Universities (CCNU19TD002). Massimo Menenti acknowledges the support of the Chinese Academy of Sciences President’s International Fellowship Initiative (Grant No. 2020VTA0001), and of the MOST High-Level Foreign Expert Program (Grant No. GL20200161002).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All the data used in this research are public available. The locations of BELMANIP2 (BEnchmark Land Multisite ANalysis and Intercomparison of Products) sites can be found at http://calvalportal.ceos.org/web/olive/site-description (accessed on 9 August 2021). The daily MODIS reflectance dataset (MOD09GA) can be found at https://lpdaac.usgs.gov/tools/data-pool/ (accessed on 9 August 2021). And the site-based long-term daily reflectance time series can be quickly retrieved from Google Earth Engine (GEE).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zeng, L.; Wardlow, B.D.; Xiang, D.; Hu, S.; Li, D. A review of vegetation phenological metrics extraction using time-series, multispectral satellite data. Remote Sens. Environ. 2020, 237, 111511. [Google Scholar] [CrossRef]
  2. Yao, X.; Li, G.; Xia, J.; Ben, J.; Cao, Q.; Zhao, L.; Ma, Y.; Zhang, L.; Zhu, D. Enabling the big earth observation data via cloud computing and DGGS: Opportunities and challenges. Remote Sens. 2020, 12, 62. [Google Scholar] [CrossRef] [Green Version]
  3. Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1–17. [Google Scholar] [CrossRef] [Green Version]
  4. Huang, S.; Tang, L.; Hupy, J.P.; Wang, Y.; Shao, G. A commentary review on the use of normalized difference vegetation index (NDVI) in the era of popular remote sensing. J. For. Res. 2021, 32, 1–6. [Google Scholar] [CrossRef]
  5. Sudmanns, M.; Tiede, D.; Lang, S.; Bergstedt, H.; Trost, G.; Augustin, H.; Baraldi, A.; Blaschke, T. Big earth data: Disruptive changes in earth observation data management and analysis? Int. J. Digit. Earth 2020, 13, 832–850. [Google Scholar] [CrossRef]
  6. Guo, H.; Nativi, S.; Liang, D.; Craglia, M.; Wang, L.; Schade, S.; Corban, C.; He, G.; Pesaresi, M.; Li, J.; et al. Big earth data science: An information framework for a sustainable planet. Int. J. Digit. Earth 2020, 13, 743–767. [Google Scholar] [CrossRef] [Green Version]
  7. Zhu, Z.; Wulder, M.A.; Roy, D.P.; Woodcock, C.E.; Hansen, M.C.; Radeloff, V.C.; Healey, S.P.; Schaaf, C.; Hostert, P.; Strobl, P.; et al. Benefits of the free and open landsat data policy. Remote Sens. Environ. 2019, 224, 382–385. [Google Scholar] [CrossRef]
  8. Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current status of landsat program, science, and applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
  9. Fensholt, R.; Sandholt, I.; Stisen, S.; Tucker, C. Analysing NDVI for the African continent using the geostationary meteosat second generation seviri sensor. Remote Sens. Environ. 2006, 101, 212–229. [Google Scholar] [CrossRef]
  10. Julien, Y.; Sobrino, J.A. Optimizing and comparing gap-filling techniques using simulated NDVI time series from remotely sensed global data. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 93–111. [Google Scholar] [CrossRef]
  11. Holben, B.N. Characteristics of maximum-value composite images from temporal avhrr data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
  12. Zhou, J.; Jia, L.; Menenti, M.; Gorte, B. On the performance of remote sensing time series reconstruction methods–A spatial comparison. Remote Sens. Environ. 2016, 187, 367–384. [Google Scholar] [CrossRef]
  13. Sarmah, S.; Jia, G.; Zhang, A.; Singha, M. Assessing seasonal trends and variability of vegetation growth from NDVI3g, MODIS NDVI and EVI over South Asia. Remote Sens. Lett. 2018, 9, 1195–1204. [Google Scholar] [CrossRef]
  14. Ql, J.; Kerr, Y. On current compositing algorithms. Remote Sens. Rev. 1997, 15, 235–256. [Google Scholar] [CrossRef]
  15. van Leeuwen, W.J.D.; Huete, A.R.; Laing, T.W. MODIS vegetation index compositing approach: A prototype with AVHRR data. Remote Sens. Environ. 1999, 69, 264–280. [Google Scholar] [CrossRef]
  16. Roerink, G.J.; Menenti, M.; Verhoef, W. Reconstructing cloudfree NDVI composites using fourier analysis of time series. Int. J. Remote Sens. 2000, 21, 1911–1917. [Google Scholar] [CrossRef]
  17. Nagai, S.; Saitoh, T.M.; Suzuki, R.; Nasahara, K.N.; Lee, W.-K.; Son, Y.; Muraoka, H. The necessity and availability of noise-free daily satellite-observed NDVI during rapid phenological changes in terrestrial ecosystems in East Asia. For. Sci. Technol. 2011, 7, 174–183. [Google Scholar] [CrossRef]
  18. Zhou, J.; Jia, L.; Menenti, M. Reconstruction of global MODIS NDVI time series: Performance of harmonic analysis of time series (HANTS). Remote Sens. Environ. 2015, 163, 217–228. [Google Scholar] [CrossRef]
  19. Jonsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE T Geosci. Remote 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
  20. Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A Simple method for reconstructing a high-quality NDVI time-series data set based on the savitzky–golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
  21. Julien, Y.; Sobrino, J.A. Comparison of cloud-reconstruction methods for time series of composite NDVI data. Remote Sens. Environ. 2010, 114, 618–625. [Google Scholar] [CrossRef]
  22. Atzberger, C.; Eilers, P.H.C. A time series for monitoring vegetation activity and phenology at 10-daily time steps covering large parts of South America. Int. J. Digit. Earth 2011, 4, 365–386. [Google Scholar] [CrossRef]
  23. Vuolo, F.; Ng, W.-T.; Atzberger, C. Smoothing and gap-filling of high resolution multi-spectral time series: Example of landsat data. Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 202–213. [Google Scholar] [CrossRef]
  24. Menenti, M.; Malamiri, H.R.G.; Shang, H.; Alfieri, S.M.; Maffei, C.; Jia, L. Observing the response of terrestrial vegetation to climate variability across a range of time scales by time series analysis of land surface temperature. In Multitemporal Remote Sensing: Methods and Applications; Ban, Y., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 277–315. ISBN 978-3-319-47037-5. [Google Scholar]
  25. Geng, L.; Ma, M.; Wang, X.; Yu, W.; Jia, S.; Wang, H. Comparison of eight techniques for reconstructing multi-satellite sensor time-series NDVI data sets in the Heihe River Basin, China. Remote Sens. 2014, 6, 2024–2049. [Google Scholar] [CrossRef] [Green Version]
  26. Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing information reconstruction of remote sensing data: A technical review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
  27. Zhou, J.; Jia, L.; van Hoek, M.; Menenti, M.; Lu, J.; Hu, G. An optimization of parameter settings in HANTS for global NDVI time series reconstruction. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3422–3425. [Google Scholar]
  28. Julien, Y.; Sobrino, J.A. TISSBERT: A benchmark for the validation and comparison of ndvi time series reconstruction methods. Rev. De Teledetección 2018, 51, 19–31. [Google Scholar] [CrossRef]
  29. Zhu, Z.; Woodcock, C.E.; Holden, C.; Yang, Z. Generating synthetic landsat images based on all available landsat data: Predicting landsat surface reflectance at any given time. Remote Sens. Environ. 2015, 162, 67–83. [Google Scholar] [CrossRef]
  30. Menenti, M.; Azzali, S.; Verhoef, W.; van Swol, R. Mapping agroecological zones and time lag in vegetation growth by means of fourier analysis of time series of NDVI images. Adv. Space Res. 1993, 13, 233–237. [Google Scholar] [CrossRef]
  31. Sellers, P.J.; Tucker, C.J.; Collatz, G.J.; Los, S.O.; Justice, C.O.; Dazlich, D.A.; Randall, D.A. A Global 1-degrees-by-1-degrees Ndvi data set for climate studies. 2. the generation of global fields of terrestrial biophysical parameters from the Ndvi. Int. J. Remote Sens. 1994, 15, 3519–3545. [Google Scholar] [CrossRef]
  32. Jakubauskas, M.E.; Legates, D.R.; Kastens, J.H. Harmonic analysis of time-series AVHRR NDVI data. Photogramm. Eng. Remote Sens. 2001, 67, 461–470. [Google Scholar]
  33. Xie, F.; Fan, H. Deriving drought indices from MODIS vegetation indices (NDVI/EVI) and land surface temperature (LST): Is data reconstruction necessary? Int. J. Appl. Earth Obs. Geoinf. 2021, 101, 102352. [Google Scholar] [CrossRef]
  34. Menenti, M.; Jia, L.; Roerink, G.J.; Gonzalez-Loyarte, M.; Leguizamon, S.; Verhoef, W. Analysis of vegetation response to climate variability using extended time series of multispectral satellite images. In Remote Sensing Optical Observations of Vegetation Properties; Maselli, F., Massimo, M., Brivio, P.A., Eds.; Research Signpost: Kerala, India, 2010; pp. 131–163. ISBN 978-81-308-0421-7. [Google Scholar]
  35. Verhoef, W. Application of Harmonic Analysis of NDVI Time Series (HANTS); Fourier Analysis of Temporal NDVI in the Southern African and American Continents; DLO Winand Staring Centre: Wageningen, The Netherlands, 1996; pp. 19–24. [Google Scholar]
  36. Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google earth engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
  37. Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
  38. Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; El Saleous, N. An extended AVHRR 8-Km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
  39. Amri, R.; Zribi, M.; Lili-Chabaane, Z.; Duchemin, B.; Gruhier, C.; Chehbouni, A. Analysis of vegetation behavior in a north african semi-arid region, Using SPOT-VEGETATION NDVI data. Remote Sens. 2011, 3, 2568–2590. [Google Scholar] [CrossRef] [Green Version]
  40. Roy, D.P.; Borak, J.S.; Devadiga, S.; Wolfe, R.E.; Zheng, M.; Descloitres, J. The MODIS land product quality assessment approach. Remote Sens. Environ. 2002, 83, 62–76. [Google Scholar] [CrossRef]
  41. Testa, S.; Mondino, E.C.B.; Pedroli, C. Correcting MODIS 16-day composite NDVI time-series with actual acquisition dates. Eur. J. Remote Sens. 2014, 47, 285–305. [Google Scholar] [CrossRef]
  42. Testa, S.; Soudani, K.; Boschetti, L.; Borgogno Mondino, E. MODIS-derived EVI, NDVI and WDRVI time series to estimate phenological metrics in french deciduous forests. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 132–144. [Google Scholar] [CrossRef]
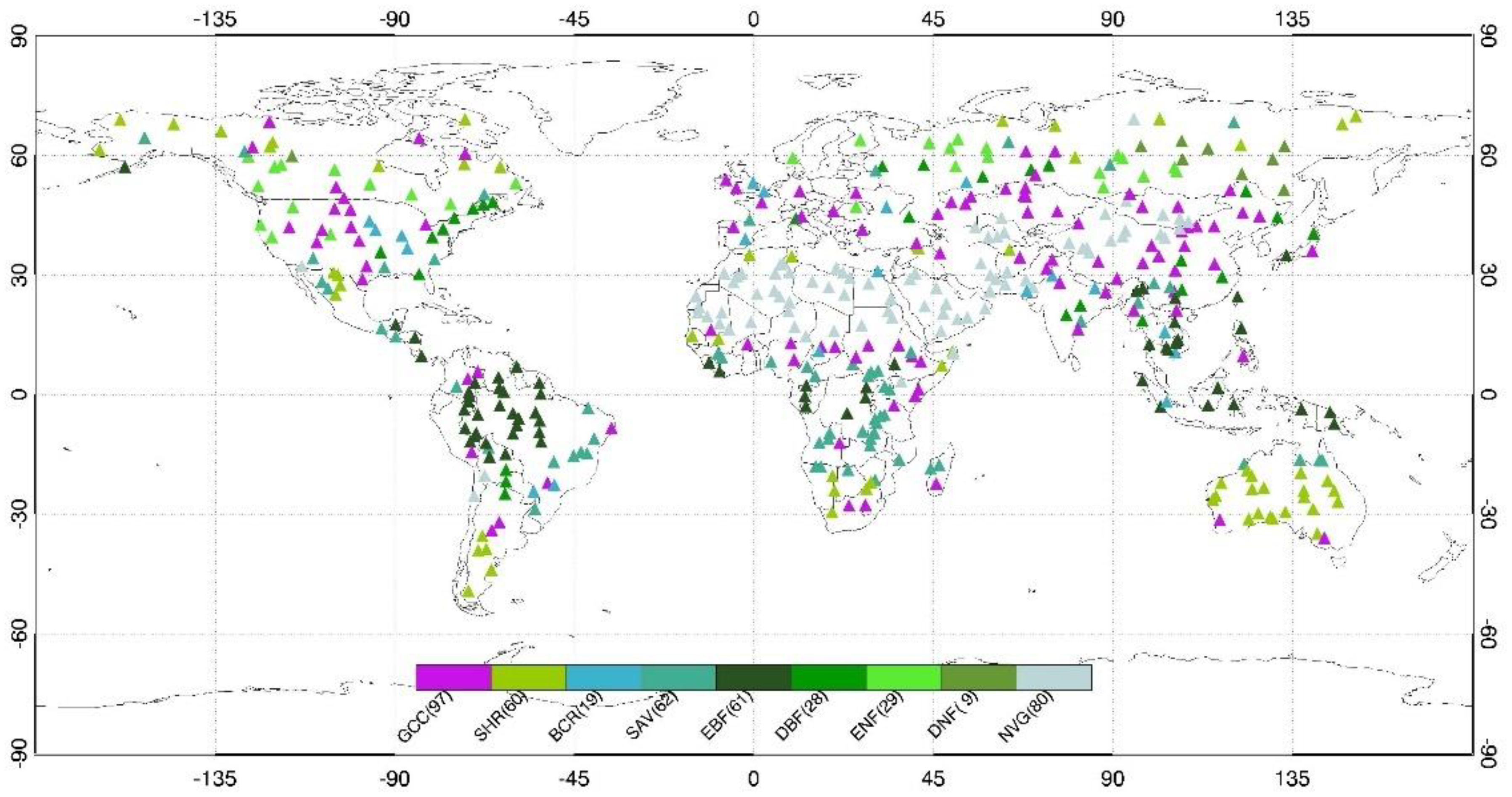
  43. Baret, F.; Morissette, J.T.; Fernandes, R.A.; Champeaux, J.L.; Myneni, R.B.; Chen, J.; Plummer, S.; Weiss, M.; Bacour, C.; Garrigues, S.; et al. Evaluation of the representativeness of networks of sites for the global validation and intercomparison of land biophysical products: Proposition of the CEOS-BELMANIP. IEEE T Geosci. Remote 2006, 44, 1794–1803. [Google Scholar] [CrossRef]
  44. de Jong, R.; de Bruin, S.; de Wit, A.; Schaepman, M.E.; Dent, D.L. Analysis of monotonic greening and browning trends from global NDVI time-series. Remote Sens. Environ. 2011, 115, 692–702. [Google Scholar] [CrossRef] [Green Version]
  45. Julien, Y.; Sobrino, J.A.; Verhoef, W. Changes in land surface temperatures and NDVI values over Europe between 1982 and 1999. Remote Sens. Environ. 2006, 103, 43–55. [Google Scholar] [CrossRef]
  46. Azzali, S.; Menenti, M. Mapping vegetation-soil-climate complexes in southern Africa using temporal fourier analysis of NOAA-AVHRR NDVI data. Int. J. Remote Sens. 2000, 21, 973–996. [Google Scholar] [CrossRef]
  47. Loyarte, M.M.G.; Menenti, M.; Diblasi, A.M. Modelling bioclimate by means of fourier analysis of NOAA-AVHRR NDVI time series in western Argentina. Int. J. Climatol. 2008, 28, 1175–1188. [Google Scholar] [CrossRef]
  48. Roerink, G.J.; Menenti, M.; Soepboer, W.; Su, Z. Assessment of climate impact on vegetation dynamics by using remote sensing. Phys. Chem. Earth Parts A/B/C 2003, 28, 103–109. [Google Scholar] [CrossRef]
  49. Lu, X.; Liu, R.; Liu, J.; Liang, S. Removal of noise by wavelet method to generate high quality temporal data of terrestrial MODIS products. Photogramm Eng. Rem S 2007, 73, 1129. [Google Scholar] [CrossRef] [Green Version]
  50. Jiang, C.; Ryu, Y.; Fang, H.; Myneni, R.; Claverie, M.; Zhu, Z. Inconsistencies of interannual variability and trends in long-term satellite leaf area index products. Glob. Chang. Biol. 2017, 23, 4133–4146. [Google Scholar] [CrossRef] [PubMed]
  51. Alfieri, S.M.; De Lorenzi, F.; Menenti, M. Mapping air temperature using time series analysis of LST: The SINTESI approach. Nonlin. Process. Geophys. 2013, 20, 513–527. [Google Scholar] [CrossRef] [Green Version]
  52. Xu, Y.; Shen, Y. Reconstruction of the land surface temperature time series using harmonic analysis. Comput. Geosci. 2013, 61, 126–132. [Google Scholar] [CrossRef]
Remotesensing 13 04251 g001 550
Figure 1. Spatial distribution and biomes sampled by the BELMANIP2 sites. The number of sites sampling each biome is given in brackets. The land cover information was extracted from the MODIS 500 m global land cover product (MCD12Q1) for 2010. The global land surface except for water and urban area is classified into 9 classes according to the LAI/FPAR classification scheme. The nine classes are: grasses/cereal crops (GCC), shrubs (SHR), broadleaf crops (BCR), savanna (SAV), evergreen broadleaf forest (EBF), deciduous broadleaf forest (DBF), evergreen needleleaf forest (ENF), deciduous needle-leaf forest (DNF), and non-vegetated (NVG).
Figure 1. Spatial distribution and biomes sampled by the BELMANIP2 sites. The number of sites sampling each biome is given in brackets. The land cover information was extracted from the MODIS 500 m global land cover product (MCD12Q1) for 2010. The global land surface except for water and urban area is classified into 9 classes according to the LAI/FPAR classification scheme. The nine classes are: grasses/cereal crops (GCC), shrubs (SHR), broadleaf crops (BCR), savanna (SAV), evergreen broadleaf forest (EBF), deciduous broadleaf forest (DBF), evergreen needleleaf forest (ENF), deciduous needle-leaf forest (DNF), and non-vegetated (NVG).
Remotesensing 13 04251 g001
Remotesensing 13 04251 g002 550
Figure 2. Flowchart to evaluate and optimize HANTS for NDVI time series reconstruction at 445 BELMANIP2 sites.
Figure 2. Flowchart to evaluate and optimize HANTS for NDVI time series reconstruction at 445 BELMANIP2 sites.
Remotesensing 13 04251 g002
Remotesensing 13 04251 g003 550
Figure 3. Boxplot of global ORE and Std-ORE across sites vs. different best settings of NF, FET and DOD (see Section 2.2 for details): L1, smallest ORE for each site; L2, smallest Std-ORE for each site, L3: highest ranking score combining the ORE and Std-ORE rankings for each site; G1, setting with lowest ORE applied to all sites; G2: setting with lowest Std-ORE applied to all sites; G3, setting with the highest combined ranking based on the combination of ORE and Std-ORE rankings; NO: average of all replications. The lower whiskers, lower side of boxes, horizontal line inside boxes, upper side of boxes, and upper whiskers correspond to minimum, lower quartile, median, upper quartile, and maximum values of the samples. The asterisk (“*”) and star (“☆”) indicate the mean values and outliers for each boxplot.
Figure 3. Boxplot of global ORE and Std-ORE across sites vs. different best settings of NF, FET and DOD (see Section 2.2 for details): L1, smallest ORE for each site; L2, smallest Std-ORE for each site, L3: highest ranking score combining the ORE and Std-ORE rankings for each site; G1, setting with lowest ORE applied to all sites; G2: setting with lowest Std-ORE applied to all sites; G3, setting with the highest combined ranking based on the combination of ORE and Std-ORE rankings; NO: average of all replications. The lower whiskers, lower side of boxes, horizontal line inside boxes, upper side of boxes, and upper whiskers correspond to minimum, lower quartile, median, upper quartile, and maximum values of the samples. The asterisk (“*”) and star (“☆”) indicate the mean values and outliers for each boxplot.
Remotesensing 13 04251 g003
Remotesensing 13 04251 g004 550
Figure 4. The best settings of NF (A), FET (B) and DOD (C) across global sites according to the L3 ranking. Sites with historical maximum NDVI less than 0.2 were excluded for evaluation (gray filled cycles). The inset barplots presented the average value of the parameters for specific biome.
Figure 4. The best settings of NF (A), FET (B) and DOD (C) across global sites according to the L3 ranking. Sites with historical maximum NDVI less than 0.2 were excluded for evaluation (gray filled cycles). The inset barplots presented the average value of the parameters for specific biome.
Remotesensing 13 04251 g004
Remotesensing 13 04251 g005 550
Figure 5. ORE and Stdev of ORE for each site according to the L3 (A,B) and G3 ranking (C,D). Sites with historical maximum NDVI less than 0.2 were excluded for evaluation (gray filled cycles).
Figure 5. ORE and Stdev of ORE for each site according to the L3 (A,B) and G3 ranking (C,D). Sites with historical maximum NDVI less than 0.2 were excluded for evaluation (gray filled cycles).
Remotesensing 13 04251 g005
Remotesensing 13 04251 g006 550
Figure 6. Normalized ORE, i.e., rORE, obtained for the L3 and G3 settings vs. Delta values. The lower whiskers, lower side of boxes, horizontal line inside boxes, upper side of boxes, and upper whiskers correspond to minimum, lower quartile, median, upper quartile, and maximum values of the samples. The asterisk (“*”) and star (“☆”) indicate the mean values and outliers for each boxplot.
Figure 6. Normalized ORE, i.e., rORE, obtained for the L3 and G3 settings vs. Delta values. The lower whiskers, lower side of boxes, horizontal line inside boxes, upper side of boxes, and upper whiskers correspond to minimum, lower quartile, median, upper quartile, and maximum values of the samples. The asterisk (“*”) and star (“☆”) indicate the mean values and outliers for each boxplot.
Remotesensing 13 04251 g006
Remotesensing 13 04251 g007 550
Figure 7. Best Delta setting for all sites. The NF, FET, and DoD are according to the G3 setting, i.e., NF = 4, FET = 0.05, and DoD = 6. Sites with historical maximum NDVI less than 0.2 were excluded for evaluation (gray filled cycles).
Figure 7. Best Delta setting for all sites. The NF, FET, and DoD are according to the G3 setting, i.e., NF = 4, FET = 0.05, and DoD = 6. Sites with historical maximum NDVI less than 0.2 were excluded for evaluation (gray filled cycles).
Remotesensing 13 04251 g007
Remotesensing 13 04251 g008 550
Figure 8. ORE achieved with improved schemes: (A) Dynamic weighting, DW; (B) Polynomial components, POLY; and (C) Inter-annual harmonic components, Inter_HA (C) vs. ORE with classical HANTS. Two settings of NF, FET, DOD were compared: (red) L3, and (blue) G3, Delta = 0.5.
Figure 8. ORE achieved with improved schemes: (A) Dynamic weighting, DW; (B) Polynomial components, POLY; and (C) Inter-annual harmonic components, Inter_HA (C) vs. ORE with classical HANTS. Two settings of NF, FET, DOD were compared: (red) L3, and (blue) G3, Delta = 0.5.
Remotesensing 13 04251 g008
Remotesensing 13 04251 g009 550
Figure 9. Boxplot of ORE vs. composite length for different attributes of input data; reference setting: HANTS without QC weighting and actual acquisition date of observations; QC+HANTS” using QC of input data to assign the initial weights, i.e., weight = 1 for QC = 1 and weight = 0 for QC = 0; QC Only: filtering outliers with only QC and no iteration in HANTS; AAD: using the actual date of acquisition in the reconstruction. The asterisk (“*”) and star (“☆”) indicate the mean values and outliers for each boxplot.
Figure 9. Boxplot of ORE vs. composite length for different attributes of input data; reference setting: HANTS without QC weighting and actual acquisition date of observations; QC+HANTS” using QC of input data to assign the initial weights, i.e., weight = 1 for QC = 1 and weight = 0 for QC = 0; QC Only: filtering outliers with only QC and no iteration in HANTS; AAD: using the actual date of acquisition in the reconstruction. The asterisk (“*”) and star (“☆”) indicate the mean values and outliers for each boxplot.
Remotesensing 13 04251 g009
Table
Table 1. A list of available implementations of HANTS algorithm.
Table 1. A list of available implementations of HANTS algorithm.
Implementation of HANTS Version Programing Language Main FeaturesAuthor (First Release Year)
HANTS_Fortran_Verhoef [*1]Fortran With graphic user interface (GUI); Batch processing in command lineVerhoef (1996)
HANTS_IDL_Wit [*2]IDL/ENVI (2004)Implemented with IDL/ENVI APIs; Support parallel processing (Make full usage of the multiple processors of CPU)Wit (2004)
TS_HANTS [*3]IDLIntroduced as an official API in IDL 8.4 in 2014; Only support single series processingN/A (2014)
HANTS_Matlab [*4]Matlab Exactly translated from the Fortran version of Verhoef; No tiling scheme, so the PC memory may pose a limitation on the processing Mohammad Abouali (2011)
HANTS_C_Metz [*5]CAn addon function of GRASS software; Only one function for image set processingMarkus Metz (2013)
HANTS_Python_Mattijn [*6]PythonDemo python implementation of HANTS that can process single series; First publicly available python version.van Hoek (2015)
HANTS_Python_ED [*7]PythonComplete implementation of HANTS in python support image set processingEspinoza-Dávalos et al., (2017)
HANTS_GEE_Zhou [*8]Javascript
/Python		Implemented on the Google earth engine (GEE) platform; Quick processing because of large volume earth observation dataset and powerful computation capacity provided by GEEZhou (2019)
HANTS-GeoTS [*9]RFull processing flow for remote sensing time series gap-filling considering both pre-processing and reconstruction.Tecuapetla-Gómez (2020)
[*1] Previously accessible at http://gdsc.nlr.nl/gdsc/en/tools/hants_, not available now (18 February 2021); [*2] https://github.com/ajwdewit/idl_adewit (Last retrieved 18 February 2021); [*3] https://www.harrisgeospatial.com/docs/TS_HANTS.html(Last retrieved 18 February 2021); [*4] https://www.mathworks.com/matlabcentral/fileexchange/38841-matlab-implementation-of-harmonic-analysis-of-time-series-hants (Last retrieved 18 February 2021). https://mabouali.wordpress.com/ projects/harmonic-analysis-of-time-series-hants/_ (Last retrieved 18 February 2021); [*5] https://grass.osgeo.org/grass78manuals/addons/r.hants.html (Last retrieved 18 February 2021); [*6] https://codereview.stackexchange.com/questions/71489/harmonic-analysis-of-time-series-applied-to-arrays (Last retrieved 18 February 2021); [*7] https://github.com/gespinoza/hants (Last retrieved 18 February 2021); [*8] Currently available on personal request by email to [email protected]. The full version will be public released soon; [*9] https://cran.r-project.org/web/packages/geoTS/ (Last retrieved 18 February 2021).
Table
Table 2. Configurations for performance evaluation & improvement.
Table 2. Configurations for performance evaluation & improvement.
Parameter NameConfiguration SettingThe Number of Configurations
Classical model parameter settings Length of Base Period (BP)365 days *1
Number of Frequencies (NF)2 to 6 in steps of 16
Fitting error tolerance (FET) 0.01 to 0.12 in steps of 0.0112
Degree of Overdeterminess (DoD)0 to 12 in steps of 113
Delta 0 to 1 in steps of 0.111
HiLo flagLow *1
Valid Range (VR)[0, 1] *1
Proposed Improvements Dynamic weights (DW)Non-DW; DW2
Polynomial components (PC)Non-PC; PC2
Interannual Harmonics (Inter-Ha)Non-Inter-Ha, Inter-Ha2
Data attributes Compositing lengths (CL)Daily, 5-day, 8-day, 16-day4
Quality Control information (QC)With-QC, QC-only, Without-QC3
Actual acquisition date (AAD)With-AAD, Without-AAD2
* Fixed parameter setting for NDVI time series.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Zhou, J.; Jia, L.; Menenti, M.; Liu, X. Optimal Estimate of Global Biome—Specific Parameter Settings to Reconstruct NDVI Time Series with the Harmonic ANalysis of Time Series (HANTS) Method. Remote Sens. 2021, 13, 4251. https://doi.org/10.3390/rs13214251

AMA Style

Zhou J, Jia L, Menenti M, Liu X. Optimal Estimate of Global Biome—Specific Parameter Settings to Reconstruct NDVI Time Series with the Harmonic ANalysis of Time Series (HANTS) Method. Remote Sensing. 2021; 13(21):4251. https://doi.org/10.3390/rs13214251

Chicago/Turabian Style

Zhou, Jie, Li Jia, Massimo Menenti, and Xuan Liu. 2021. "Optimal Estimate of Global Biome—Specific Parameter Settings to Reconstruct NDVI Time Series with the Harmonic ANalysis of Time Series (HANTS) Method" Remote Sensing 13, no. 21: 4251. https://doi.org/10.3390/rs13214251

APA Style

Zhou, J., Jia, L., Menenti, M., & Liu, X. (2021). Optimal Estimate of Global Biome—Specific Parameter Settings to Reconstruct NDVI Time Series with the Harmonic ANalysis of Time Series (HANTS) Method. Remote Sensing, 13(21), 4251. https://doi.org/10.3390/rs13214251

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop