Blind Fusion of Hyperspectral Multispectral Images Based on Matrix Factorization
Abstract
:1. Introduction
- An accurate SRF estimation method is proposed based on a quadratic programming model and matrix multiplication iterative solutions to achieve blind hyperspectral, multispectral image fusion.
- The estimated SRF is applied to our proposed semi-blind fusion, and the proposed blind fusion method is used to fuse real remote sensing images obtained by two satellite-based spectral cameras, sentinel 2 and Hyperion. The subjective results of the fusion demonstrate the superiority of our proposed method.
- An automatic parameter optimization method is proposed to automatically adjust the parameters during the fusion process, thus reducing the dependence of the fusion quality on the parameters.
2. Related Works
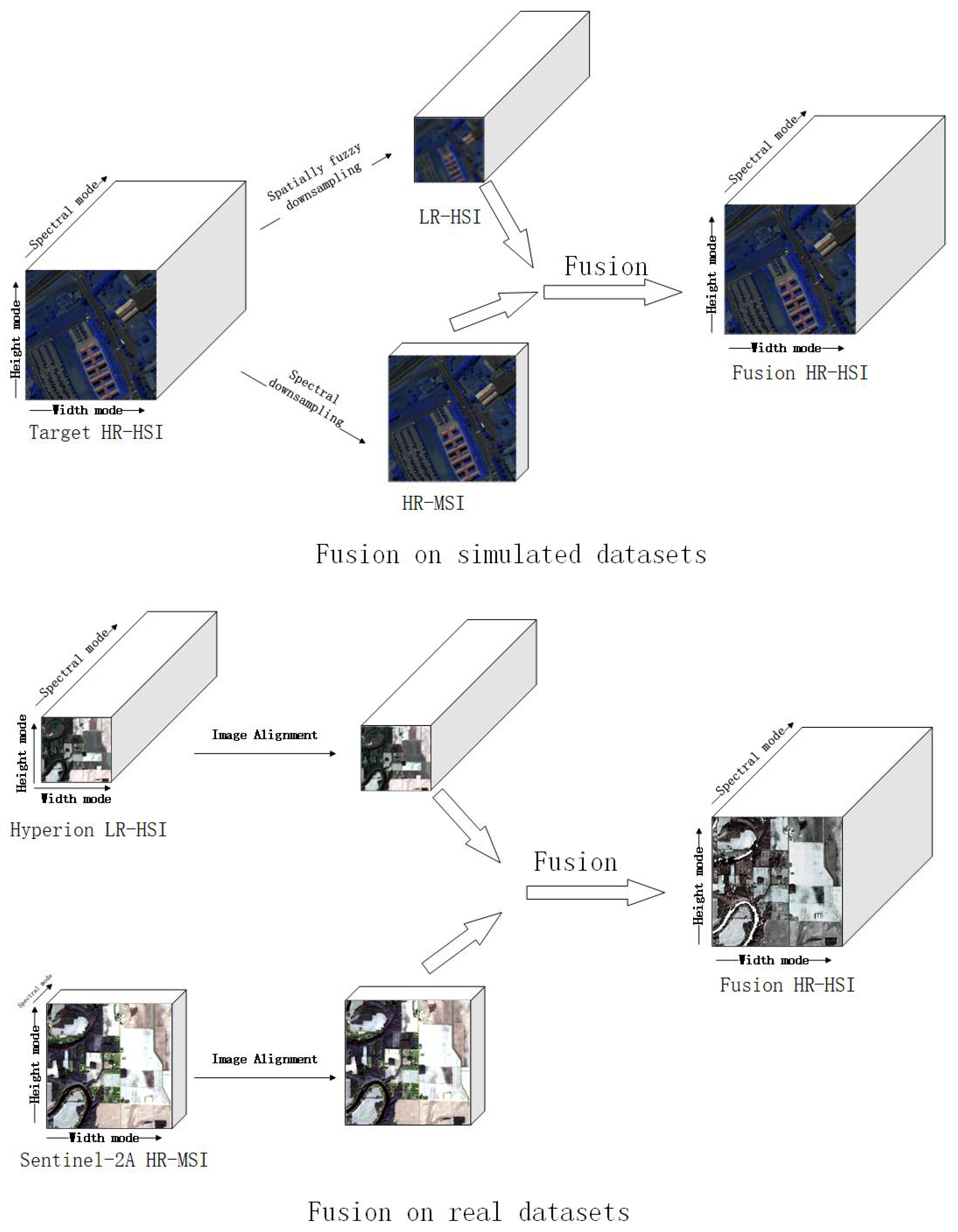
3. Fusion Model
4. Proposed Method
4.1. Estimation of SRF
| Algorithm 1 Estimated SRF |
| Require: |
| Perform spatial downsampling of the MSI matrix . |
| Using the strong fuzzy matrix fuzzy matrix , . |
| for k=1:size(,1) do |
| solution of Equation (9) |
| end for |
| for k=1:K do |
| Update by Equation (13) |
| end for |
| return |
4.2. Blind Fusion Method
| Algorithm 2 Blind Fusion |
| Require: |
| Get by Algorithm 1 |
| Get by Equation (14) |
| Set the and to an initial value |
| for q = 1:6 do |
| if then |
| end if |
| end for |
| for k=1:K do |
| Update by Equation (23) |
| end for |
| return |
5. Experiments
5.1. Dateset
5.2. Compare Method and Parameter Setting
5.3. Quantitative Metrics
6. Results and Analysis
- We will examine the superior performance of our proposed SRF estimation using two state-of-the-art semi-blind fusion methods.
- We will compare our proposed method with five blind fusion methods to demonstrate the advanced performance of our proposed blind fusion.
- We will visually compare the effect of our proposed blind fusion method with the five blind fusion methods on the real dataset to highlight the practicality of our proposed method.
6.1. Advancement of the Proposed Srf Estimation Algorithm
6.2. Advancement of the Proposed Blind Fusion Algorithm
6.3. Practicality of the Proposed Method
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Sample Availability
References
- Samiappan, S. Spectral Band Selection for Ensemble Classification of Hyperspectral Images with Applications to Agriculture and Food Safety. Ph.D. Thesis, Gradworks, Mississippi State University, Starkwell, MS, USA, 2014. [Google Scholar]
- Liu, Z.; Yan, J.Q.; Zhang, D.; Li, Q.L. Automated tongue segmentation in hyperspectral images for medicine. Appl. Opt. 2007, 46, 8328–8334. [Google Scholar] [CrossRef] [Green Version]
- Pechanec, V.; Mráz, A.; Rozkošný, L.; Vyvlečka, P. Usage of Airborne Hyperspectral Imaging Data for Identifying Spatial Variability of Soil Nitrogen Content. ISPRS Int. J. Geo-Inf. 2021, 10, 355. [Google Scholar] [CrossRef]
- Meer, F.D.V.D.; Werff, H.M.A.V.D.; Ruitenbeek, F.J.A.V.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; Meijde, M.V.D.; Carranza, E.J.M.; Smeth, J.B.D.; Woldai, T. Multi- and hyperspectral geologic remote sensing: A review. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- Cui, Y.; Zhang, B.; Yang, W.; Yi, X.; Tang, Y. Deep CNN-based Visual Target Tracking System Relying on Monocular Image Sensing. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar]
- Cui, Y.; Zhang, B.; Yang, W.; Wang, Z.; Li, Y.; Yi, X.; Tang, Y. End-to-End Visual Target Tracking in Multi-Robot Systems Based on Deep Convolutional Neural Network. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 1113–1121. [Google Scholar]
- Li, S.; Dian, R.; Fang, L.; Bioucas-Dias, J.M. Fusing Hyperspectral and Multispectral Images via Coupled Sparse Tensor Factorization. IEEE Trans. Image Process. 2018, 27, 4118–4130. [Google Scholar] [CrossRef] [PubMed]
- Dian, R.; Li, S. Hyperspectral Image Super-Resolution via Subspace-Based Low Tensor Multi-Rank Regularization. IEEE Trans. Image Process. 2019, 28, 5135–5146. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Peng, Y.; Li, J.; Zhang, L.; Xu, Y. Hyperspectral Image Super-resolution via Subspace-based Fast Low Tensor Multi-Rank Regularization. Infrared Phys. Technol. 2021, 116, 103631. [Google Scholar] [CrossRef]
- Long, J.; Peng, Y.; Zhou, T.; Zhao, L.; Li, J. Fast and Stable Hyperspectral Multispectral Image Fusion Technique Using Moore—Penrose Inverse Solver. Appl. Sci. 2021, 11, 7365. [Google Scholar] [CrossRef]
- Kanatsoulis, C.I.; Fu, X.; Sidiropoulos, N.D.; Ma, W. Hyperspectral Super-Resolution: A Coupled Tensor Factorization Approach. IEEE Trans. Signal Process. 2018, 66, 6503–6517. [Google Scholar] [CrossRef] [Green Version]
- Dian, R.; Li, S.; Fang, L.; Lu, T.; Bioucas-Dias, J.M. Nonlocal Sparse Tensor Factorization for Semiblind Hyperspectral and Multispectral Image Fusion. IEEE Trans. Cybern. 2019, 50, 4469–4480. [Google Scholar] [CrossRef]
- Simoes, M.; Bioucas-Dias, J.; Almeida, L.B.; Chanussot, J. A Convex Formulation for Hyperspectral Image Superresolution via Subspace-Based Regularization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3373–3388. [Google Scholar] [CrossRef] [Green Version]
- Yokoya, N.; Mayumi, N.; Iwasaki, A. Cross-Calibration for Data Fusion of EO-1/Hyperion and Terra/ASTER. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 419–426. [Google Scholar] [CrossRef]
- Carper, W.J.; Lillesand, T.M.; Kiefer, P.W. The use of intensity-hue-saturation transformations for merging SPOT panchromatic and multispectral image data. Photogramm. Eng. Remote Sens. 1990, 56, 459–467. [Google Scholar]
- Tu, T.M.; Huang, P.S.; Hung, C.L.; Chang, C.P. A Fast Intensity–Hue–Saturation Fusion Technique With Spectral Adjustment for IKONOS Imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 309–312. [Google Scholar] [CrossRef]
- Gonzalez-Audicana, M.; Otazu, X.; Fors, O.; Alvarez-Mozos, J. A low computational-cost method to fuse IKONOS images using the spectral response function of its sensors. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1683–1691. [Google Scholar] [CrossRef]
- Zhang, Y. Understanding image fusion. Photogramm. Eng. Remote Sens. 2004, 70, 657–661. [Google Scholar]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent No. 6,011,875, 4 January 2000. [Google Scholar]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving Component Substitution Pansharpening Through Multivariate Regression of MS +Pan Data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Smoothing Filter-based Intensity Modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [CrossRef]
- Eismann, M.T. Resolution Enhancement of Hyperspectral Imagery Using Maximum a Posteriori Estimation with a Stochastic Mixing Model. Ph.D. Thesis, University of Dayton, Dayton, OH, USA, 2004. [Google Scholar]
- Yokoya, N.; Member, S.; Yairi, T.; Iwasaki, A. Coupled Nonnegative Matrix Factorization Unmixing for Hyperspectral and Multispectral Data Fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Frederic, P.M.; Dufaux, F.; Winkler, S.; Ebrahimi, T.; Sa, G. A No-Reference Perceptual Blur Metric. In Proceedings of the International Conference on Image Processing, Rochester, NY, USA, 22–25 September 2002; Volume 3, pp. III–57–III–60. [Google Scholar]
- Dell’Acqua, F.; Gamba, P.; Ferrari, A.; Palmason, J.A.; Benediktsson, J.A.; Arnason, K. Exploiting spectral and spatial information in hyperspectral urban data with high resolution. IEEE Geosci. Remote Sens. Lett. 2004, 1, 322–326. [Google Scholar] [CrossRef]
- Yasuma, F.; Mitsunaga, T.; Iso, D.; Nayar, S.K. Generalized Assorted Pixel Camera: Postcapture Control of Resolution, Dynamic Range, and Spectrum. IEEE Trans. Image Process. 2010, 19, 2241–2253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, Q.; Bioucas-Dias, J.; Dobigeon, N.; Tourneret, J.Y. Hyperspectral and Multispectral Image Fusion based on a Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3658–3668. [Google Scholar] [CrossRef] [Green Version]
- Wald, L. Quality of high resolution synthesised images: Is there a simple criterion? In Third Conference Fusion of Earth Data: Merging Point Measurements, Raster Maps and Remotely Sensed Images; SEE/URISCA: Nice, France, 2000; pp. 99–103. [Google Scholar]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and multispectral data fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]


| Method | Strengths | Weaknesses/Improvement |
|---|---|---|
| Component substitution based methods: IHS [15], PCA [18], GIHS [20], GSA [20] | Less time-consuming | Spectral distortion, lower fusion quality |
| Smoothed filter-based intensity modulation method: SFIMHS [21] | Least time consuming | Spectral distortion, lower fusion quality |
| Statistical estimation-based fusion method: MAPSMM [22] | Robust fusion quality on different datasets | The longest fusion time-consuming and the worst fusion quality |
| Matrix factorization-based fusion methods: Hysure [13], CNMF [14,23] | Included SRF and PSF estimation can be extended to non-blind fusion algorithms | More time-consuming, constrained fusion quality |
| The proposed method | Higher fusion quality, faster fusion speed, better SRF estimation | Add a priori information to further improve fusion quality |
| Pavia University | |||||||
|---|---|---|---|---|---|---|---|
| SRF & PSF | Method | SRF | PSNR | RMSE | ERGAS | SAM | SSIM |
| SRF1 PSF1 | NLSTF-SMBF [12] | R1 [13] | 41.566 | 2.25 | 1.285 | 2.271 | 0.987 |
| R2 [14] | 32.29 | 6.991 | 3.62 | 5.827 | 0.969 | ||
| Ours | 41.836 | 2.175 | 1.262 | 2.176 | 0.987 | ||
| SRF1 | 42.8 | 1.995 | 1.145 | 2.051 | 0.988 | ||
| STEREO [11] | R1 [13] | 37.31 | 3.578 | 2.093 | 3.56 | 0.958 | |
| R2 [14] | 32.166 | 6.757 | 3.644 | 5.562 | 0.929 | ||
| Ours | 37.223 | 3.622 | 2.129 | 3.643 | 0.956 | ||
| SRF1 | 37.564 | 3.482 | 2.035 | 3.534 | 0.958 | ||
| SRF2 PSF1 | NLSTF-SMBF [12] | R1 [13] | 40.605 | 2.646 | 1.598 | 2.479 | 0.985 |
| R2 [14] | 34.791 | 5.293 | 2.716 | 3.746 | 0.981 | ||
| Ours | 41.522 | 2.342 | 1.423 | 2.289 | 0.987 | ||
| SRF2 | 42.44 | 2.196 | 1.336 | 2.214 | 0.987 | ||
| STEREO [11] | R1 [13] | 36.813 | 3.932 | 2.304 | 3.79 | 0.954 | |
| R2 [14] | 32.882 | 6.405 | 3.433 | 5.222 | 0.941 | ||
| Ours | 37.225 | 3.734 | 2.265 | 3.797 | 0.955 | ||
| SRF2 | 37.501 | 3.636 | 2.187 | 3.733 | 0.956 | ||
| SRF2 PSF2 | NLSTF-SMBF [12] | R1 [13] | 40.991 | 2.537 | 1.516 | 2.416 | 0.986 |
| R2 [14] | 26.767 | 15.166 | 6.882 | 6.033 | 0.949 | ||
| Ours | 41.311 | 2.396 | 1.478 | 2.268 | 0.987 | ||
| SRF2 | 42.721 | 2.147 | 1.299 | 2.197 | 0.988 | ||
| STEREO [11] | R1 [13] | 36.884 | 3.91 | 2.304 | 3.78 | 0.954 | |
| R2 [14] | 25.716 | 16.688 | 7.699 | 7.793 | 0.892 | ||
| Ours | 37.109 | 3.759 | 2.3 | 3.823 | 0.955 | ||
| SRF2 | 37.517 | 3.62 | 2.18 | 3.707 | 0.957 | ||
| CAVE | |||||||
|---|---|---|---|---|---|---|---|
| SRF & PSF | Method | SRF | PSNR | RMSE | ERGAS | SAM | SSIM |
| SRF1 PSF1 | NLSTF-SMBF [12] | R1 [13] | 25.061 | 15.307 | 5.588 | 29.181 | 0.813 |
| R2 [14] | 33.202 | 5.897 | 2.358 | 8.061 | 0.944 | ||
| Ours | 39.526 | 3.160 | 1.299 | 6.171 | 0.963 | ||
| SRF1 | 40.644 | 2.638 | 1.069 | 5.569 | 0.972 | ||
| STEREO [11] | R1 [13] | 26.122 | 13.515 | 4.903 | 27.559 | 0.807 | |
| R2 [14] | 32.687 | 6.092 | 2.395 | 9.433 | 0.907 | ||
| Ours | 36.692 | 3.966 | 1.596 | 7.900 | 0.934 | ||
| SRF1 | 37.213 | 3.664 | 1.456 | 7.557 | 0.943 | ||
| SRF2 PSF1 | NLSTF-SMBF [12] | R1 [13] | 27.123 | 11.73 | 4.382 | 21.584 | 0.824 |
| R2 [14] | 33.233 | 5.681 | 2.18 | 10.397 | 0.94 | ||
| Ours | 38.578 | 3.618 | 1.469 | 8.257 | 0.957 | ||
| SRF2 | 39.45 | 3.202 | 1.281 | 7.954 | 0.965 | ||
| STEREO [11] | R1 [13] | 24.93 | 16.854 | 5.941 | 24.748 | 0.707 | |
| R2 [14] | 32.471 | 6.26 | 2.457 | 11.122 | 0.913 | ||
| Ours | 36.166 | 4.386 | 1.769 | 9.482 | 0.923 | ||
| SRF2 | 36.604 | 4.066 | 1.616 | 9.134 | 0.935 | ||
| SRF2 PSF2 | NLSTF-SMBF [12] | R1 [13] | 26.864 | 12.027 | 4.491 | 21.869 | 0.82 |
| R2 [14] | 31.486 | 7.139 | 2.786 | 13.62 | 0.912 | ||
| Ours | 38.479 | 3.702 | 1.507 | 8.326 | 0.961 | ||
| SRF2 | 38.818 | 3.54 | 1.425 | 7.936 | 0.965 | ||
| STEREO [11] | R1 [13] | 24.372 | 18.354 | 6.418 | 25.999 | 0.682 | |
| R2 [14] | 30.361 | 7.926 | 3.105 | 14.658 | 0.821 | ||
| Ours | 36.384 | 4.226 | 1.696 | 9.235 | 0.928 | ||
| SRF2 | 36.629 | 4.047 | 1.608 | 9.008 | 0.935 | ||
| Pavia University | |||||||
|---|---|---|---|---|---|---|---|
| SRF & PSF | Method | PSNR | RMSE | ERGAS | SAM | SSIM | Time |
| SRF1 PSF1 | Hysure [13] | 35.581 | 4.501 | 2.637 | 3.852 | 0.972 | 64.431 |
| CNMF [14,23] | 31.307 | 7.019 | 4.181 | 3.855 | 0.934 | 25.953 | |
| GSA [20] | 34.671 | 4.966 | 3.049 | 4.087 | 0.962 | 0.839 | |
| MAPSMM [22] | 27.508 | 10.855 | 6.381 | 4.91 | 0.854 | 92.327 | |
| SFIMHS [21] | 28.461 | 9.736 | 5.771 | 4.129 | 0.892 | 0.234 | |
| Ours | 38.632 | 3.593 | 1.847 | 2.94 | 0.982 | 7.649 | |
| SRF2 PSF1 | Hysure [13] | 33.53 | 6.585 | 3.522 | 4.983 | 0.956 | 69.896 |
| CNMF [14,23] | 32.411 | 6.236 | 3.465 | 3.304 | 0.947 | 25.823 | |
| GSA [20] | 34.98 | 4.813 | 2.931 | 4.004 | 0.966 | 0.865 | |
| MAPSMM [22] | 27.714 | 10.631 | 6.215 | 4.824 | 0.861 | 87.706 | |
| SFIMHS [21] | 28.494 | 9.711 | 5.762 | 4.183 | 0.893 | 0.234 | |
| Ours | 40.032 | 3.34 | 1.72 | 2.89 | 0.985 | 7.639 | |
| SRF2 PSF2 | Hysure [13] | 31.579 | 8.033 | 4.268 | 5.603 | 0.921 | 68.318 |
| CNMF [14,23] | 31.556 | 7.281 | 3.786 | 4.077 | 0.92 | 25.434 | |
| GSA [20] | 32.474 | 6.286 | 3.537 | 4.967 | 0.955 | 0.847 | |
| MAPSMM [22] | 26.182 | 12.735 | 7.329 | 5.649 | 0.81 | 91.43 | |
| SFIMHS [21] | 26.394 | 12.365 | 7.256 | 5.001 | 0.84 | 0.235 | |
| Ours | 40.872 | 2.665 | 1.555 | 2.59 | 0.987 | 9.601 | |
| CAVE | |||||||
|---|---|---|---|---|---|---|---|
| SRF & PSF | Method | PSNR | RMSE | ERGAS | SAM | SSIM | Time |
| SRF1 PSF1 | Hysure [13] | 28.873 | 9.859 | 3.591 | 19.348 | 0.852 | 271.399 |
| CNMF [14,23] | 30.151 | 8.347 | 3.311 | 7.279 | 0.861 | 60.043 | |
| GSA [20] | 33.646 | 5.646 | 2.262 | 10.21 | 0.91 | 1.305 | |
| MAPSMM [22] | 27.069 | 11.638 | 4.563 | 7.949 | 0.849 | 200.775 | |
| SFIMHS [21] | 26.309 | 12.951 | 5.136 | 6.834 | 0.88 | 0.434 | |
| Ours | 37.889 | 3.925 | 1.644 | 11.791 | 0.943 | 10.98 | |
| SRF2 PSF1 | Hysure [13] | 30.872 | 7.856 | 3.072 | 17.963 | 0.879 | 280.453 |
| CNMF [14,23] | 28.487 | 10.201 | 4.09 | 7.662 | 0.831 | 53.476 | |
| GSA [20] | 33.503 | 5.774 | 2.336 | 10.498 | 0.899 | 1.083 | |
| MAPSMM [22] | 27.218 | 11.368 | 4.439 | 7.836 | 0.869 | 154.387 | |
| SFIMHS [21] | 26.762 | 12.06 | 4.727 | 6.787 | 0.883 | 0.276 | |
| Ours | 38.079 | 3.829 | 1.527 | 12.174 | 0.955 | 13.835 | |
| SRF2 PSF2 | Hysure [13] | 29.335 | 9.033 | 3.441 | 18.692 | 0.856 | 279.973 |
| CNMF [14,23] | 28.049 | 10.708 | 4.306 | 7.914 | 0.835 | 52.585 | |
| GSA [20] | 32.609 | 6.346 | 2.559 | 12.127 | 0.868 | 1.400 | |
| MAPSMM [22] | 26.273 | 12.679 | 4.946 | 8.377 | 0.847 | 158.632 | |
| SFIMHS [21] | 25.75 | 13.566 | 5.312 | 7.485 | 0.864 | 0.391 | |
| Ours | 36.224 | 4.705 | 1.900 | 12.475 | 0.947 | 13.384 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, J.; Peng, Y. Blind Fusion of Hyperspectral Multispectral Images Based on Matrix Factorization. Remote Sens. 2021, 13, 4219. https://doi.org/10.3390/rs13214219
Long J, Peng Y. Blind Fusion of Hyperspectral Multispectral Images Based on Matrix Factorization. Remote Sensing. 2021; 13(21):4219. https://doi.org/10.3390/rs13214219
Chicago/Turabian StyleLong, Jian, and Yuanxi Peng. 2021. "Blind Fusion of Hyperspectral Multispectral Images Based on Matrix Factorization" Remote Sensing 13, no. 21: 4219. https://doi.org/10.3390/rs13214219
APA StyleLong, J., & Peng, Y. (2021). Blind Fusion of Hyperspectral Multispectral Images Based on Matrix Factorization. Remote Sensing, 13(21), 4219. https://doi.org/10.3390/rs13214219







