Multi-Resolution STAP for Enhanced Ultra-Low-Altitude Target Detection
Abstract
:1. Introduction
- i
- We not only circumvent the target attenuation induced by the multipath signal, but also exploit the multipath signal power to enhance the ULAT detection performance. In specific, the mechanism of the MTC effect is derived for the fast searching of SCNR-enhanced sub-band distribution. Furthermore, the consistent CCM estimation scheme is proposed in the sub-band STAP to reduce computational burden, and the clutter training sample selection scheme is also proposed to satisfy the sample demand.
- ii
- By dividing the whole base band into multiple independent sub-bands, it is feasible to improve the target detection performance with the joint complementary detection among multiple sub-band STAP outputs.
- iii
- On the basis of the SCNR-enhanced sub-band STAP detection results, the dynamic TG-induced target attenuation is further alleviated by multipath-target decoupling with the full-band STAP, which constrains the target Doppler history and provides the foundation for further SCNR improvement within the long-CPI.
2. Signal Model
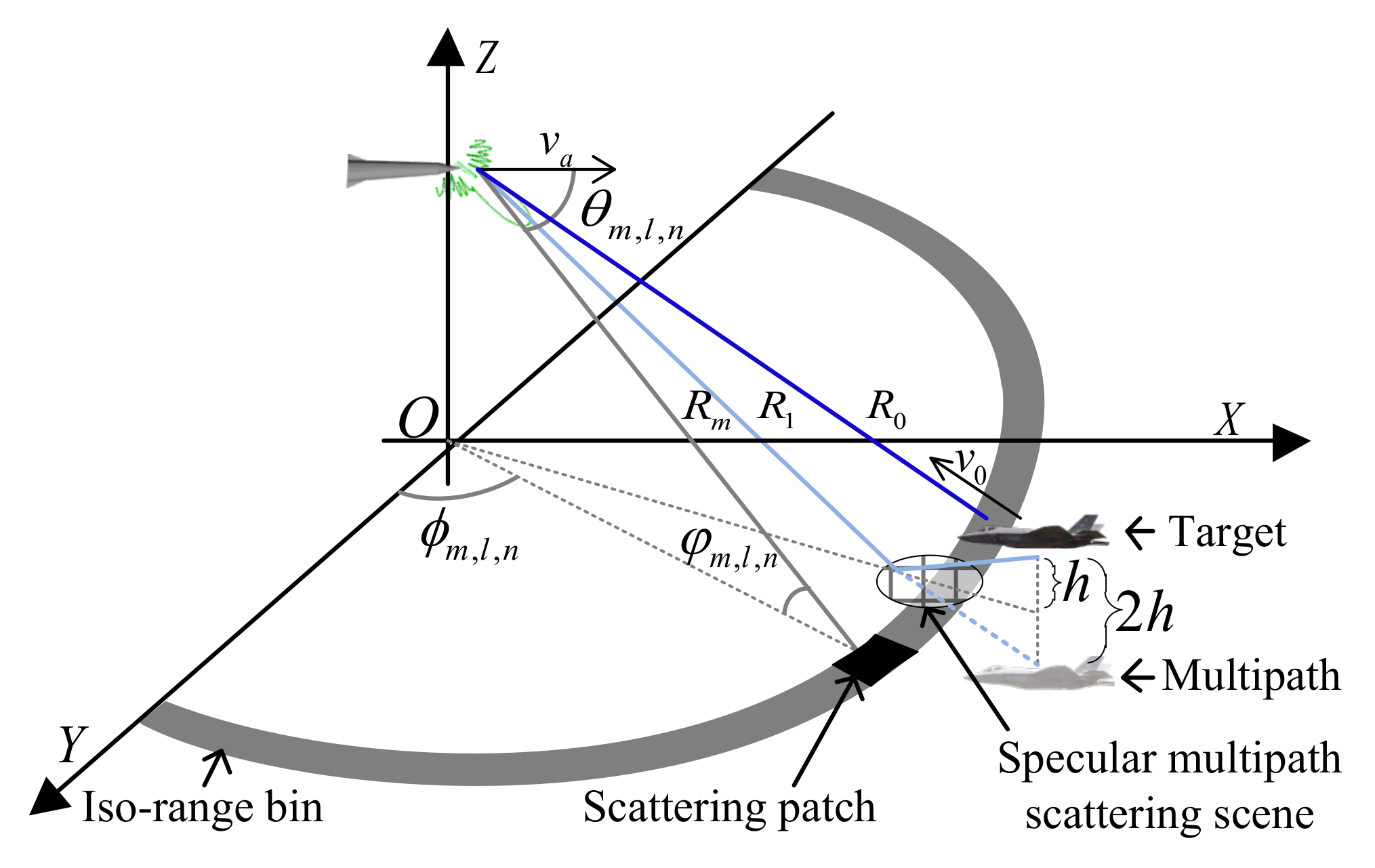
2.1. Geometric Configuration and Multipath-Target Signal Model
2.2. Space-Time Signal Model
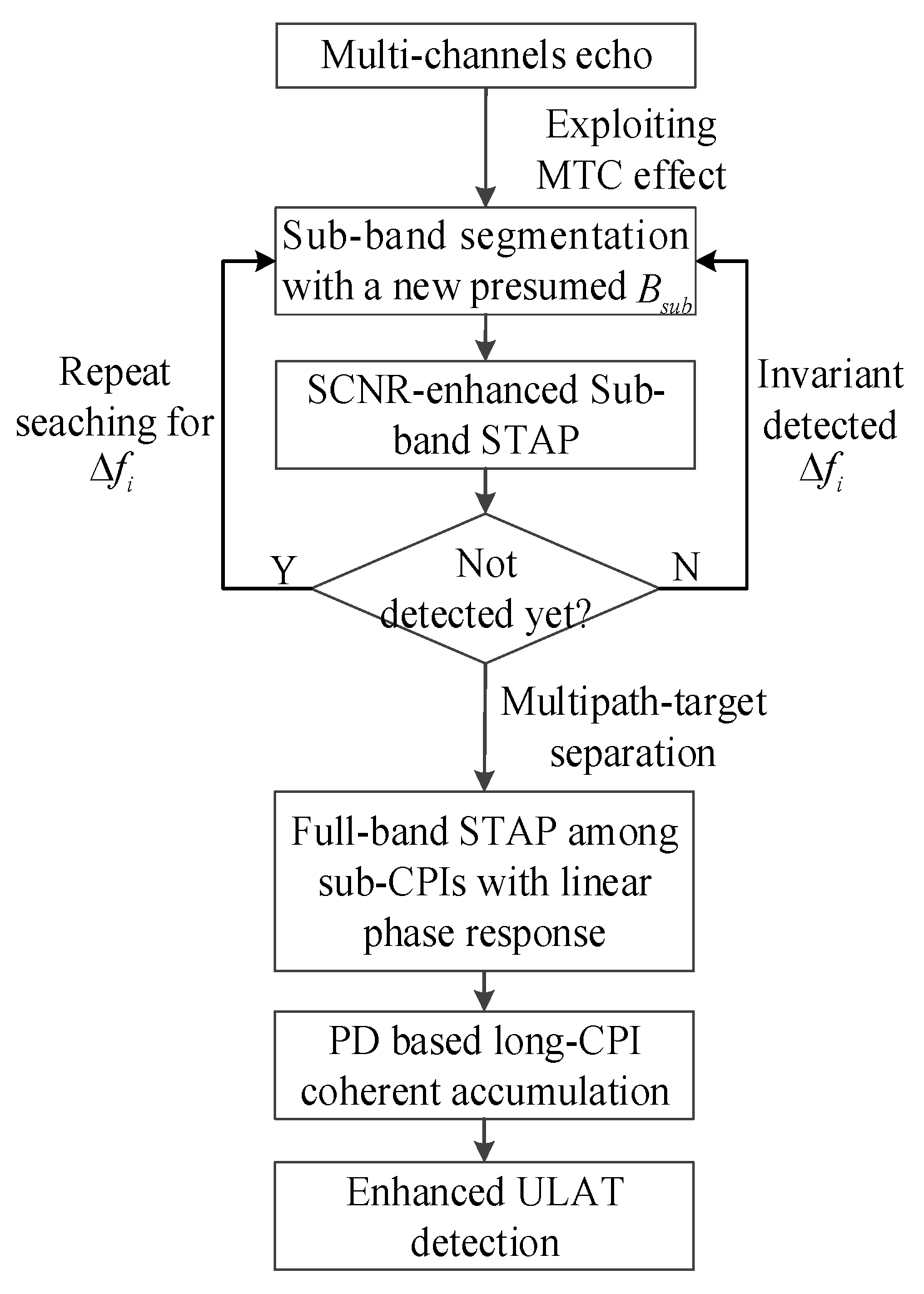
3. Multi-Resolution STAP Based ULAT Detection
3.1. SCNR-Enhanced Sub-Band STAP
3.1.1. Mechanism Analysis of MTC Effect
- i
- The of the SCNR-enhanced sub-band distribution keeps constant with different , because the maximum possible output power is produced under the in-phase envelope superposition condition, which corresponds to a specific .
- ii
- The SCNR performance trend of the sub-band STAP is stable and periodic with respect to the of the sub-band distribution, because of the periodicity of the -dependent phase coupling in the envelope superposition.
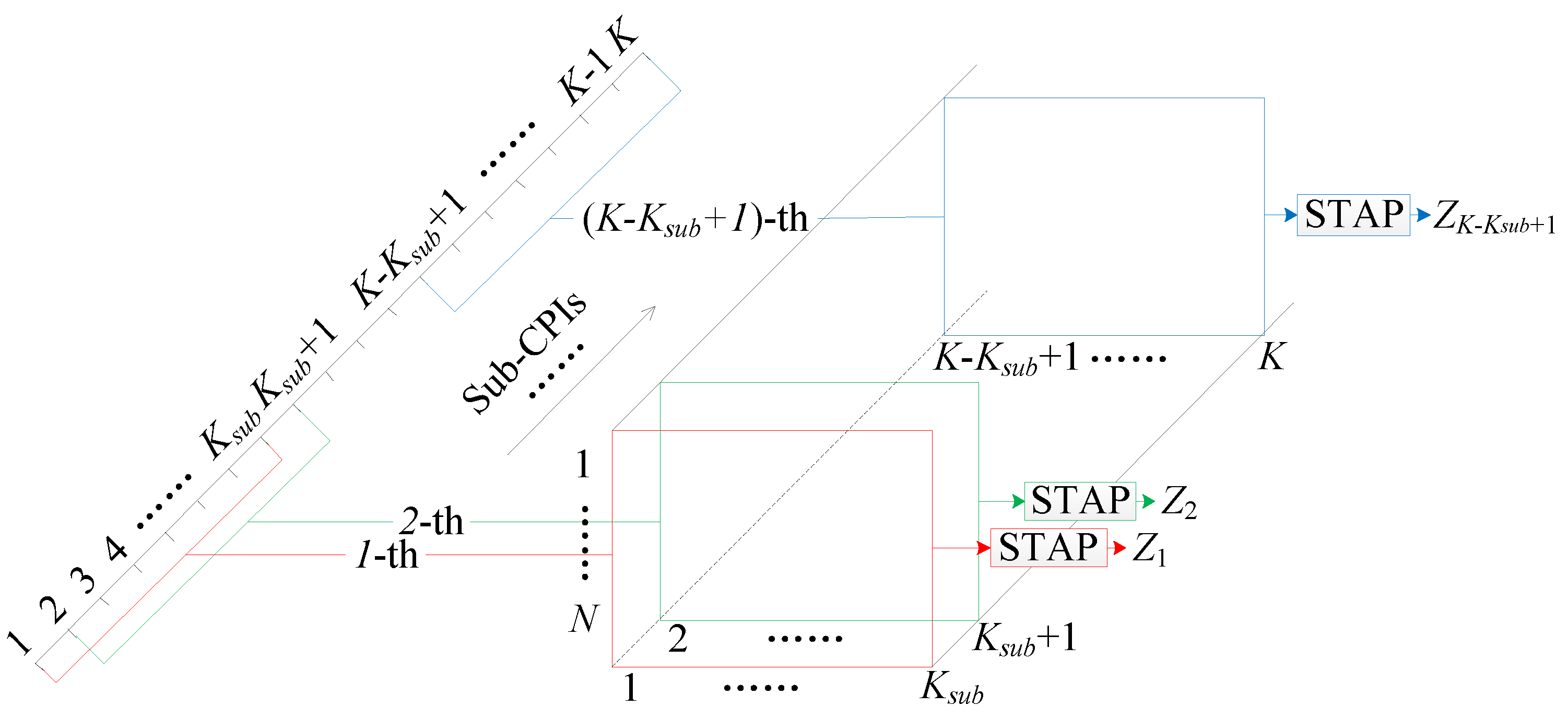
3.1.2. Joint Multiple Sub-Bands ΣΔ-STAP
3.2. Full-Band STAP Based Multipath-Target Separation
4. Performance Analysis
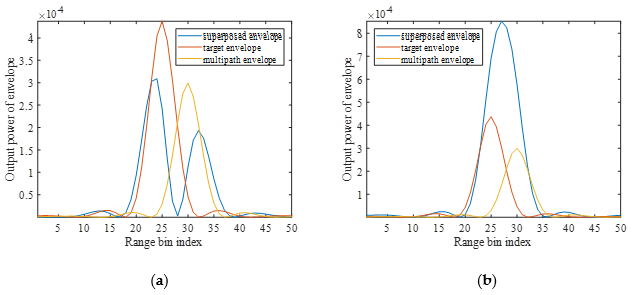
4.1. Mechanism Validation of MTC Effect
4.1.1. Numerical Analysis
4.1.2. Experimental Analysis
4.2. Experiment Results of Joint Multi-Resolution STAP
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Derivations of Sub-Band Range-Compressed Envelope for Target
References
- Liu, Y.; Jiu, B.; Xia, X.-G.; Liu, H.; Zhang, L. Height Measurement of Low-Angle Target Using MIMO Radar Under Multipath Interference. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 808–818. [Google Scholar] [CrossRef]
- Trizna, D. A model for Brewster angle damping and multipath effects on the microwave radar sea echo at low grazing angles. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1232–1244. [Google Scholar] [CrossRef]
- Hu, J.; Tung, W.-W.; Gao, J. A New Way to Model Nonstationary Sea Clutter. IEEE Signal Process. Lett. 2009, 16, 129–132. [Google Scholar] [CrossRef] [Green Version]
- Melvin, W.L. A STAP overview. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 19–35. [Google Scholar] [CrossRef]
- Guerci, J.R. Space-Time Adaptive Processing for Radar; Artech House: Norwood, MA, USA, 2003. [Google Scholar]
- Xu, J.; Zhu, S.; Liao, G.; Huang, L. Joint magnitude and phase constrained STAP approach. Digit. Signal Process. 2015, 46, 32–40. [Google Scholar] [CrossRef]
- Ward, J. Space-Time Adaptive Processing for Airborne Radar; Lincoln Lab, MIT: Lexington, MA, USA, 1994. [Google Scholar]
- Wu, R.; Jia, Q.; Li, H. A novel STAP method for the detection of fast dim air moving targets. In Proceedings of the IEEE 10th International Conference on Signal Processing Proceedings, Beijing, China, 24–28 October 2010; pp. 2160–2163. [Google Scholar]
- Wang, G.; Xin, J.; Zheng, N.; Sano, A. Computationally Efficient Subspace-Based Method for Two-Dimensional Direction Estimation With L-Shaped Array. IEEE Trans. Signal Process. 2011, 59, 3197–3212. [Google Scholar] [CrossRef]
- Yan, H.; Fan, H. On source association of DOA estimation under multipath propagation. IEEE Signal Process. Lett. 2005, 12, 717–720. [Google Scholar]
- Zhang, R.; Wang, S.; Lu, X.; Duan, W.; Cai, L. Two-Dimensional DoA Estimation for Multipath Propagation Characterization Using the Array Response of PN-Sequences. IEEE Trans. Wirel. Commun. 2015, 15, 341–356. [Google Scholar] [CrossRef]
- Kirsteins, I. Blind separation of signal and multipath interference for synthetic aperture sonar. In Proceedings of the Oceans 2003. Celebrating the Past... Teaming Toward the Future (IEEE Cat. No.03CH37492), San Diego, CA, USA, 22–26 September 2003; Volume 5, pp. 2641–2648. [Google Scholar]
- Shi, J.; Hu, G.; Zong, B.; Chen, M. DOA Estimation Using Multipath Echo Power for MIMO Radar in Low-Grazing Angle. IEEE Sens. J. 2016, 16, 6087–6094. [Google Scholar] [CrossRef]
- Lan, L.; Liao, G.; Xu, J.; Zhang, Y.; Liao, B. Transceive Beamforming with Accurate Nulling in FDA-MIMO Radar for Imaging. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4145–4159. [Google Scholar] [CrossRef]
- Lan, L.; Xu, J.; Liao, G.; Zhang, Y.; Fioranelli, F.; So, H.C. Suppression of Mainbeam Deceptive Jammer With FDA-MIMO Radar. IEEE Trans. Veh. Technol. 2020, 69, 11584–11598. [Google Scholar] [CrossRef]
- Xu, J.; Liao, G.; So, H.C. Space-Time Adaptive Processing with Vertical Frequency Diverse Array for Range-Ambiguous Clutter Suppression. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5352–5364. [Google Scholar] [CrossRef]
- Kreyenkamp, O.; Klemm, R. Doppler compensation in forward-looking STAP radar. IEE Proc. Radar Sonar Navig. 2001, 148, 253–258. [Google Scholar] [CrossRef]
- Zych, C.; Wrońska-Zych, A.; Dudczyk, J.; Kawalec, A. A correction in feedback loop applied to two-axis gimbal stabilization. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 217–219. [Google Scholar] [CrossRef]
- Wang, H.; Cai, L. On adaptive multiband signal detection with the SMI algorithm. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 768–773. [Google Scholar] [CrossRef]
- Reed, I.; Mallett, J.; Brennan, L. Rapid Convergence Rate in Adaptive Arrays. IEEE Trans. Aerosp. Electron. Syst. 1974, AES-10, 853–863. [Google Scholar] [CrossRef]
- Xu, J.; Wang, C.; Liao, G.; Zhang, Y. Sum and difference beamforming for angle-doppler estimation with STAP-based radars. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2825–2837. [Google Scholar] [CrossRef]
- Brown, R.; Schneible, R.; Wicks, M.; Wang, H.; Zhang, Y. STAP for clutter suppression with sum and difference beams. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 634–646. [Google Scholar] [CrossRef]
- Brown, R.D.; Wicks, M.C.; Zhang, Y.; Zhang, Q.; Wang, H. A space-time adaptive processing approach for improved performance and affordability. Proc. IEEE Natl. Radar Conf. 1996, 13, 321–326. [Google Scholar]
- Sarkar, T.K.; Wang, H.; Park, S.; Adve, R.; Koh, J.; Kim, K.; Zhang, Y.; Wicks, M.; Brown, R. A deterministic least-squares approach to space-time adaptive processing (STAP). IEEE Trans. Antennas Propag. 2001, 49, 91–103. [Google Scholar] [CrossRef] [Green Version]
- Cristallini, D.; Burger, W. A Robust Direct Data Domain Approach for STAP. IEEE Trans. Signal Process. 2011, 60, 1283–1294. [Google Scholar] [CrossRef]
- Himed, B.; Zhang, Y.; Hajjari, A. STAP with angle-Doppler compensation for bistatic airborne radars. In Proceedings of the 2002 IEEE Radar Conference, Long Beach, CA, USA, 22–25 April 2002. [Google Scholar]
- Stoica, P.; Li, J.; Zhu, X.; Guerci, J.R. On using a priori knowledge in space-time adaptive processing. IEEE Trans. Signal Process. 2008, 56, 2598–2602. [Google Scholar] [CrossRef]
- Ślesicka, A.; Kawalec, A. An application of the orthogonal matching pursuit algorithm in space-time adaptive processing. Sensors 2020, 20, 3468. [Google Scholar] [CrossRef]
- Perry, R.; DiPietro, R.; Fante, R. SAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–200. [Google Scholar] [CrossRef]
- Yuan, H.; Xu, H.; Duan, K.; Xie, W.; Wang, Y. Cross-Spectral metric smoothing-based GIP for space-time adaptive processing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1388–1392. [Google Scholar] [CrossRef]
- Fante, R.; Barile, E.; Guella, T. Clutter covariance smoothing by subaperture averaging. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 941–945. [Google Scholar] [CrossRef]
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: System and Signal Processing; Jone Wiley & Sons, Inc.: Hoboken, NJ, USA, 1991. [Google Scholar]

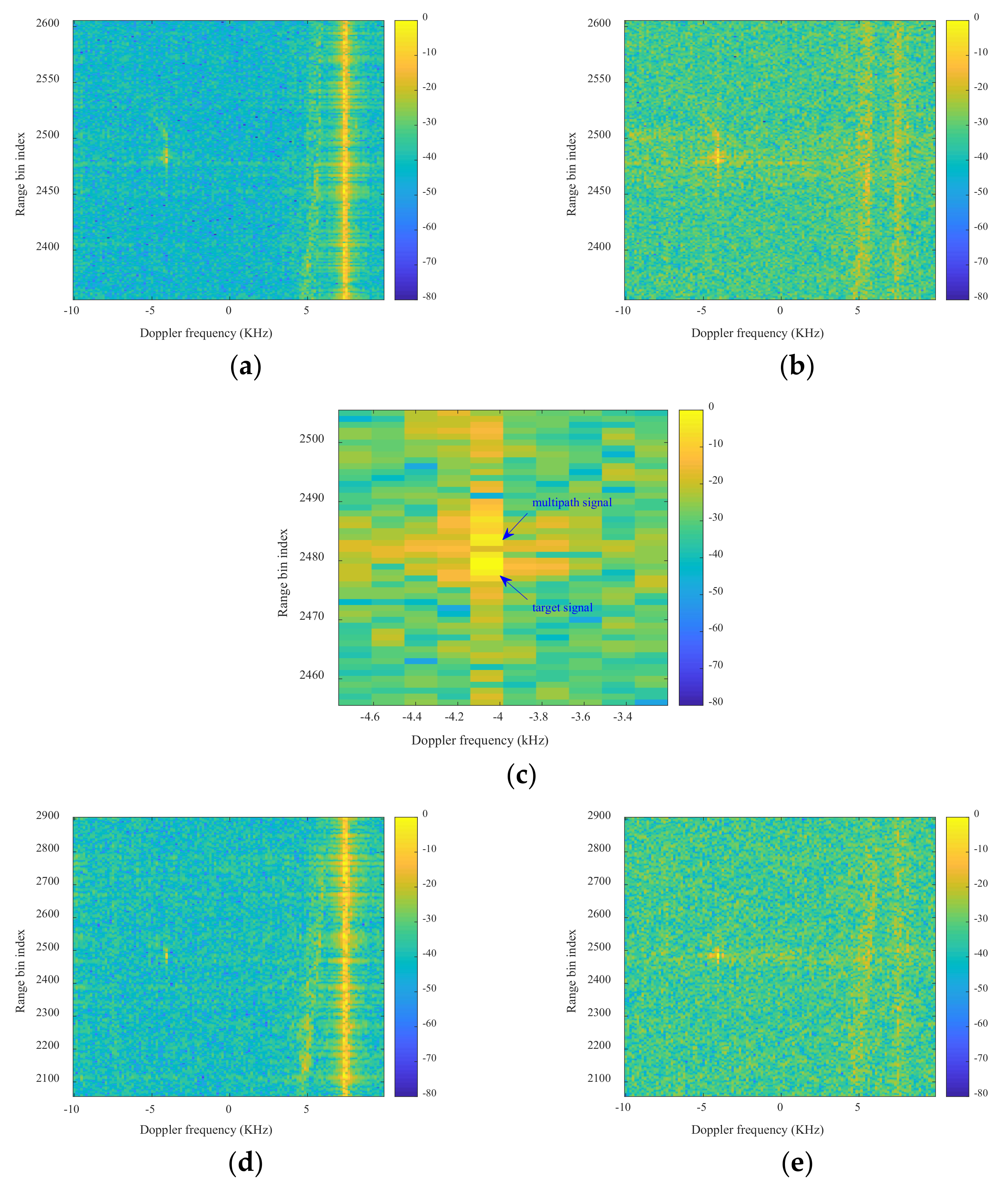
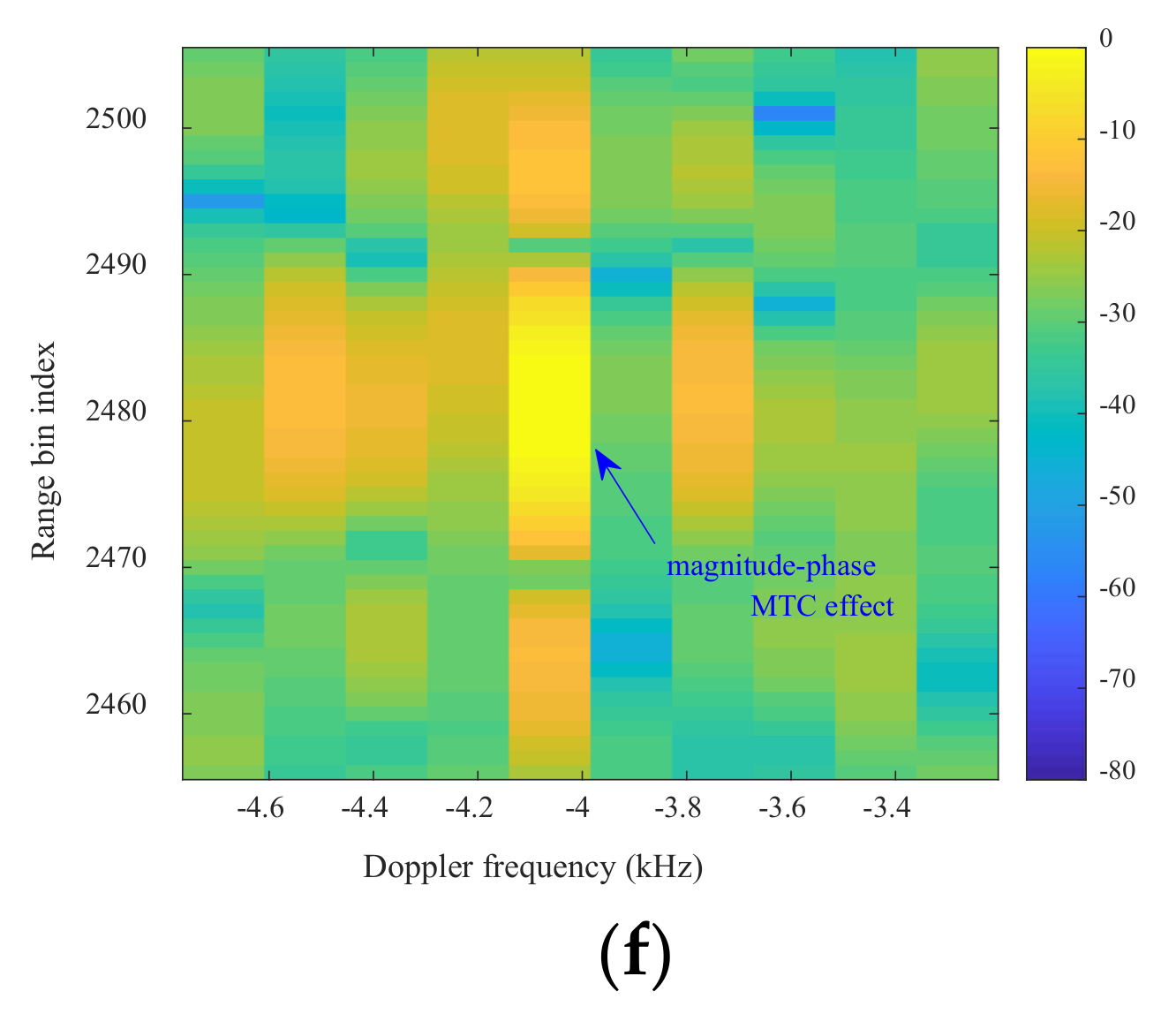

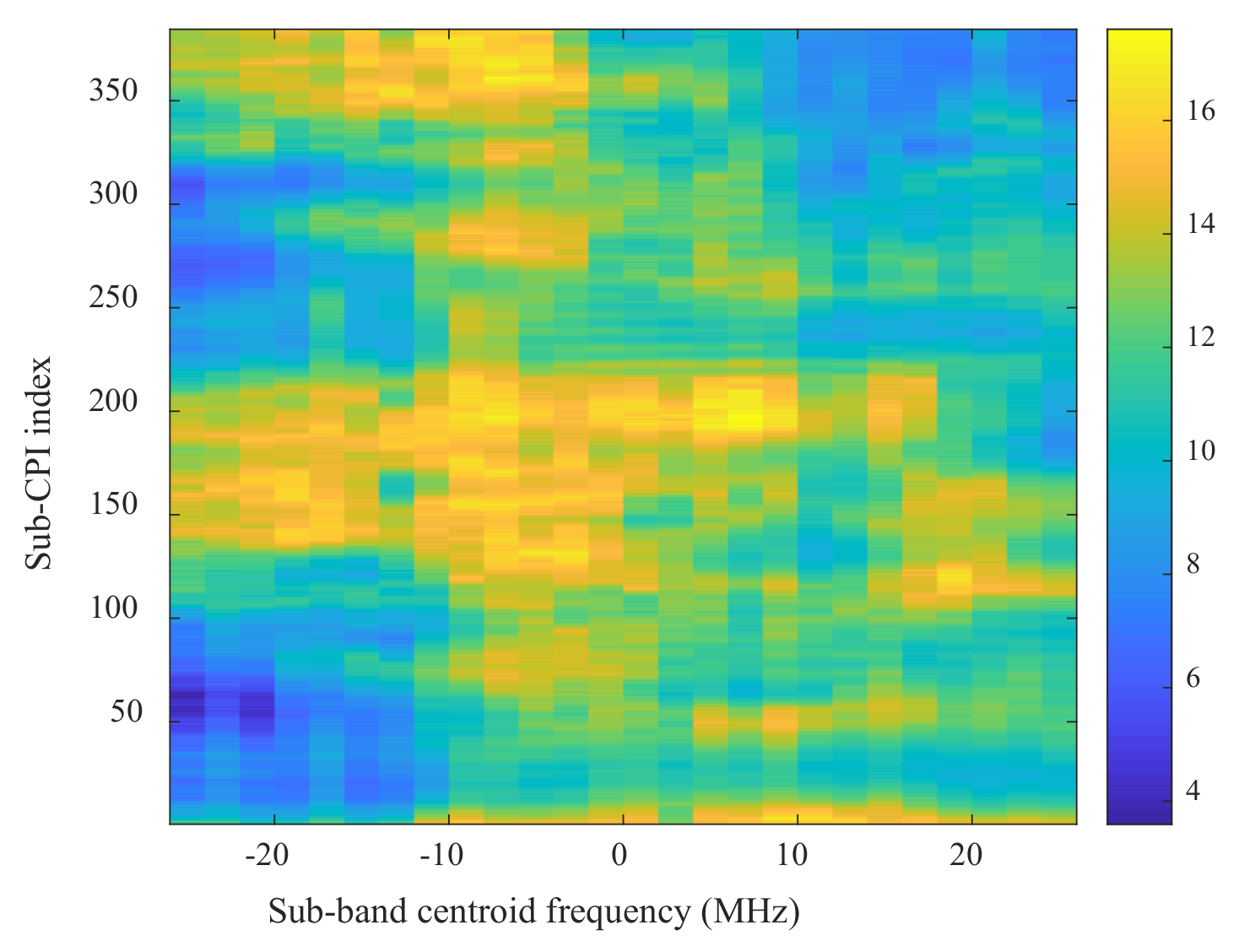
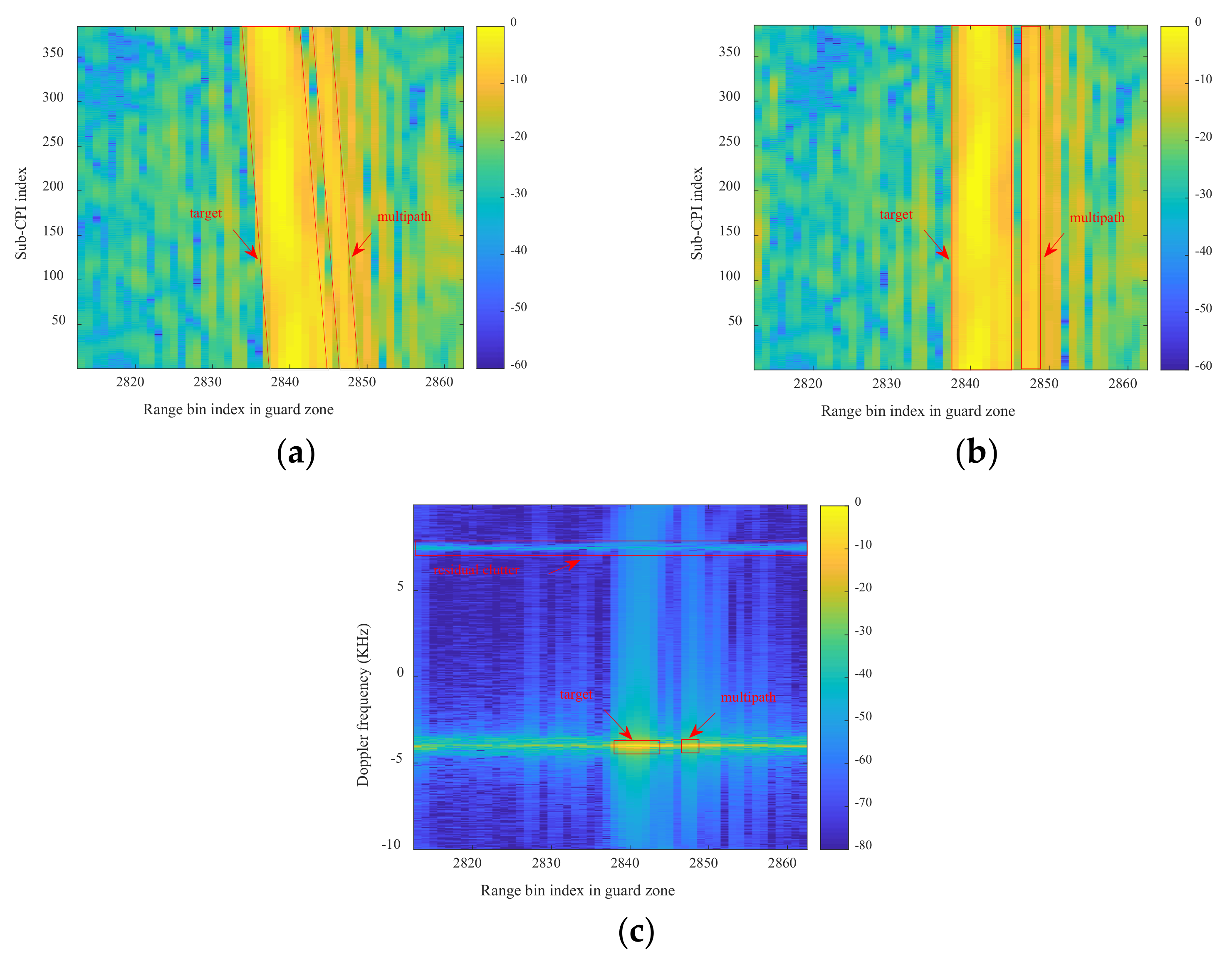
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Carrier frequency | 14.5 GHz | Waveform type | LFM |
| Full-band width | 80 MHz | Sub-band width | 20 MHz |
| Sampling frequency | 192 MHz | Pulse width | 1 µs |
| Center Frequency of Sub-Band | Target | Multipath |
|---|---|---|
| −3 MHz | −7.50 deg | 165.08 deg |
| 15 MHz | −7.50 deg | −3.67 deg |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Platform height | 1.247 km | Platform velocity | 80 m/s |
| PRF | 20 KHz | Beam elevation direction | 9.96 deg |
| CPI | 6.4 ms | Beam azimuth direction | 84.5 deg |
| Guard cells | 50 | Full-band training samples | 200 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| CPI | 25.6 ms | Beam azimuth direction | 84.5 deg |
| Guard cells | 50 | Full-band training samples | 200 |
| Method | STAP Output SCNR | Output SCNR of Further Coherent Accumulation | Computational Consuming Time |
|---|---|---|---|
| Proposed multi-resolution STAP | 8.25 dB | 40.04 dB | 4.34 s |
| Mono-resolution STAP | 20.35 dB | 35.77 dB | Null |
| Conventional full-band STAP | 4.75 dB | Null | 3.37 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Liao, G.; Xu, J.; Zeng, C.; He, X.; Gao, P. Multi-Resolution STAP for Enhanced Ultra-Low-Altitude Target Detection. Remote Sens. 2021, 13, 4212. https://doi.org/10.3390/rs13214212
Li H, Liao G, Xu J, Zeng C, He X, Gao P. Multi-Resolution STAP for Enhanced Ultra-Low-Altitude Target Detection. Remote Sensing. 2021; 13(21):4212. https://doi.org/10.3390/rs13214212
Chicago/Turabian StyleLi, Haodong, Guisheng Liao, Jingwei Xu, Cao Zeng, Xiongpeng He, and Pengfei Gao. 2021. "Multi-Resolution STAP for Enhanced Ultra-Low-Altitude Target Detection" Remote Sensing 13, no. 21: 4212. https://doi.org/10.3390/rs13214212
APA StyleLi, H., Liao, G., Xu, J., Zeng, C., He, X., & Gao, P. (2021). Multi-Resolution STAP for Enhanced Ultra-Low-Altitude Target Detection. Remote Sensing, 13(21), 4212. https://doi.org/10.3390/rs13214212









