Within-Field Yield Prediction in Cereal Crops Using LiDAR-Derived Topographic Attributes with Geographically Weighted Regression Models
Abstract
:1. Introduction
2. Study Area and Methods
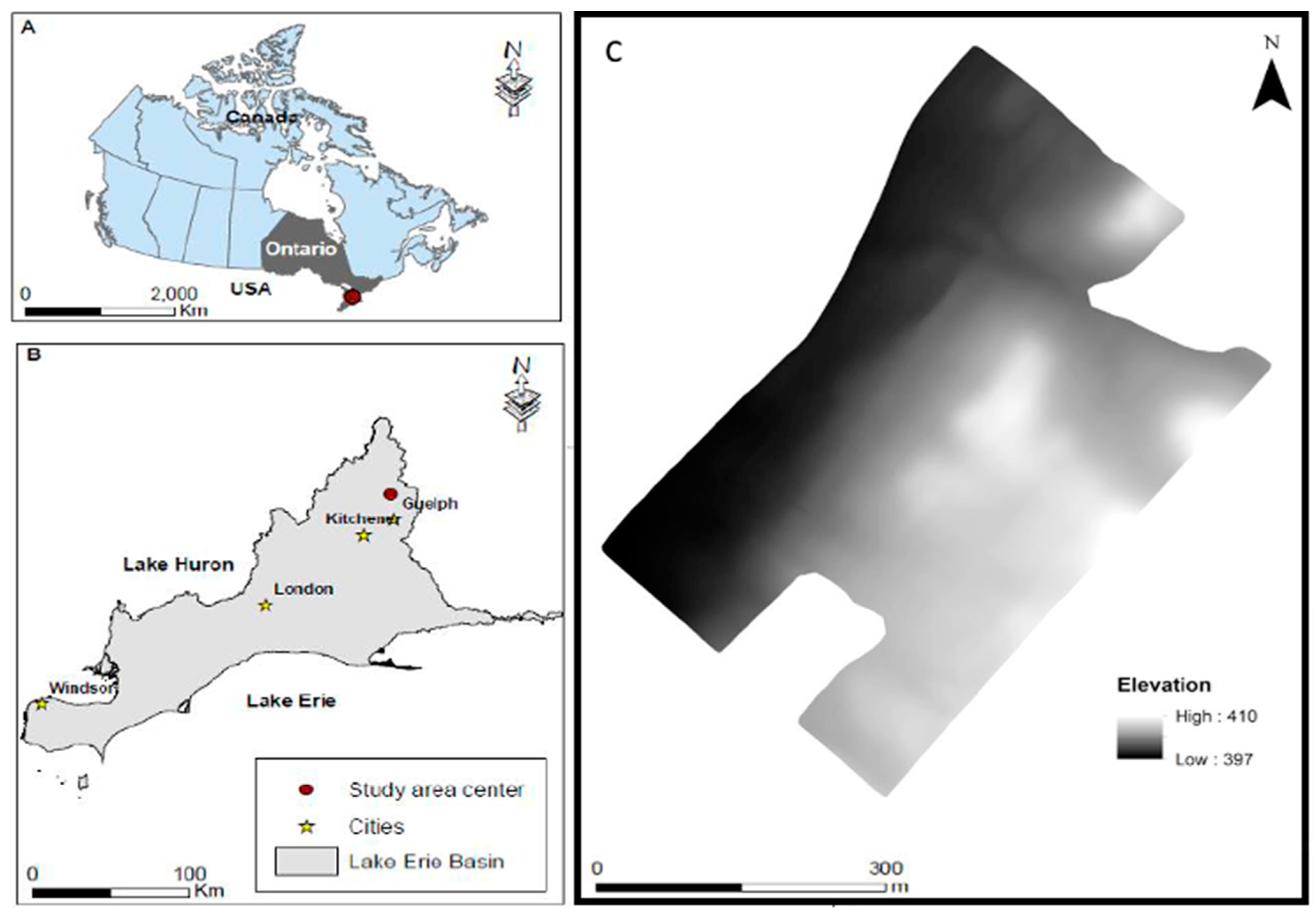
2.1. Site Description
2.2. Processing Crop Yield Data
2.3. LiDAR Dataset Acquisition and Processing
2.4. Statistical Analysis
2.4.1. Field-Wide Statistical Analysis
2.4.2. Local Statistical Analysis
2.4.3. Geographic Weighted Regression
3. Results
3.1. Field Scale Assessment
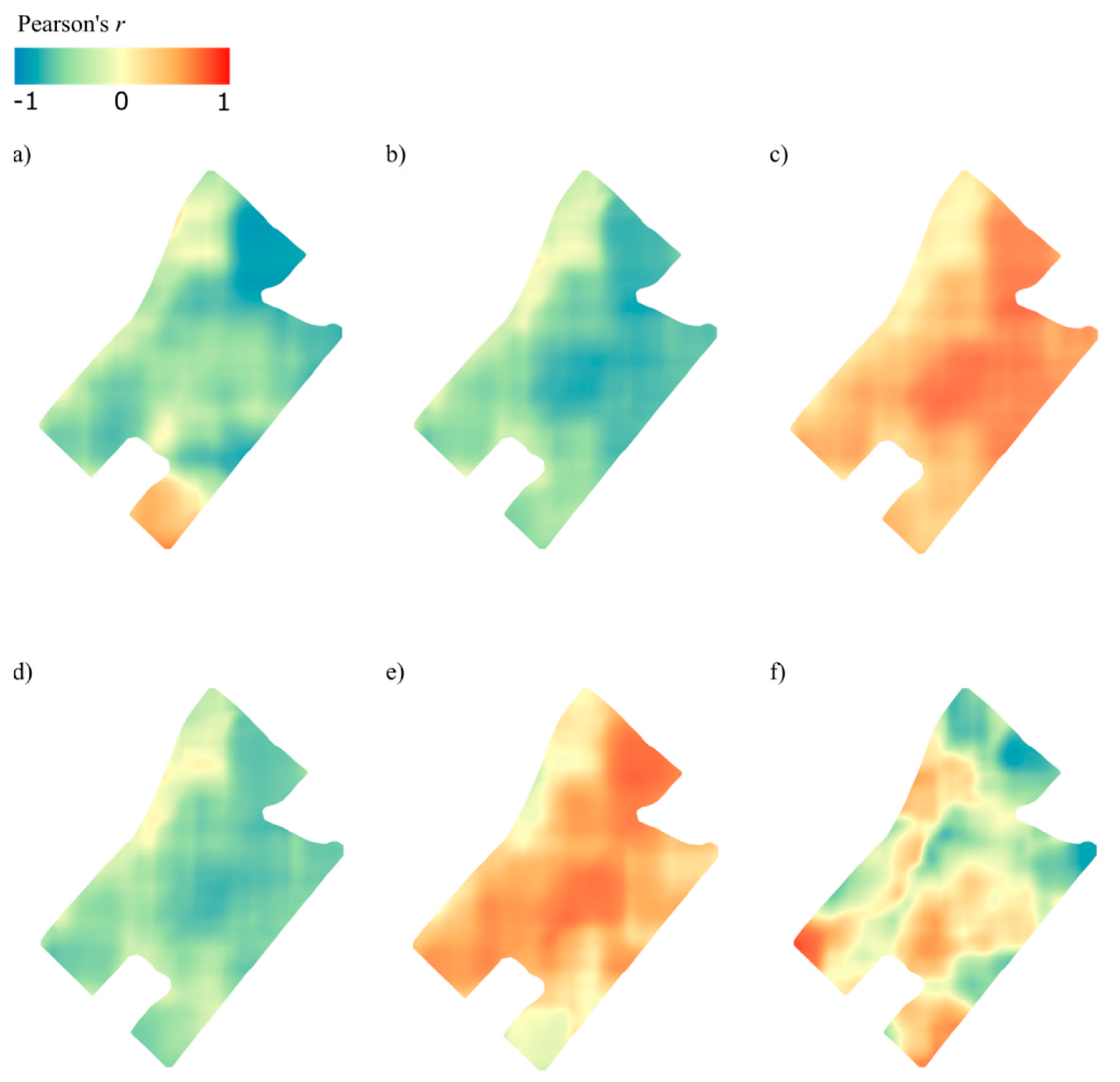
3.2. Localized Correlation Analysis
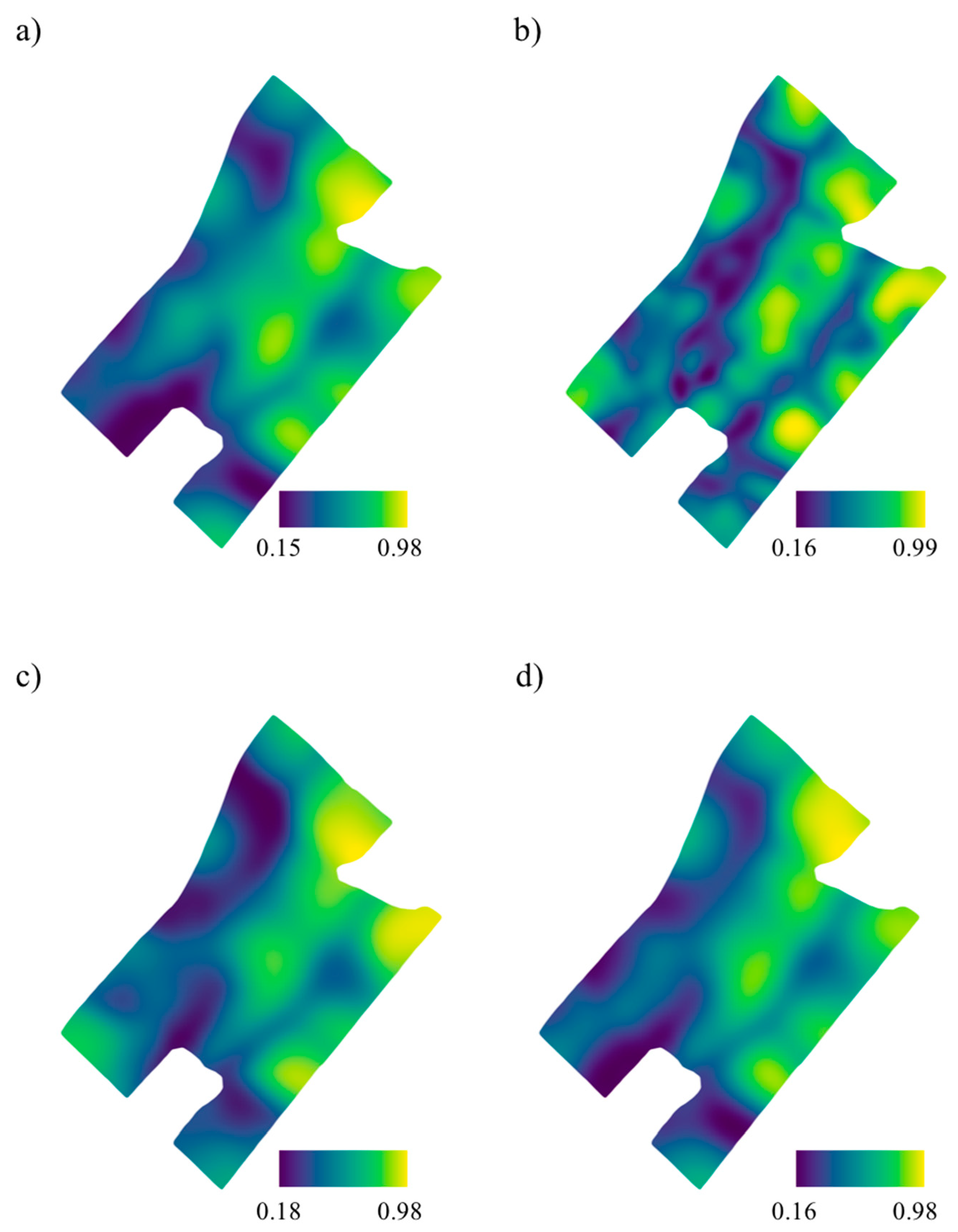
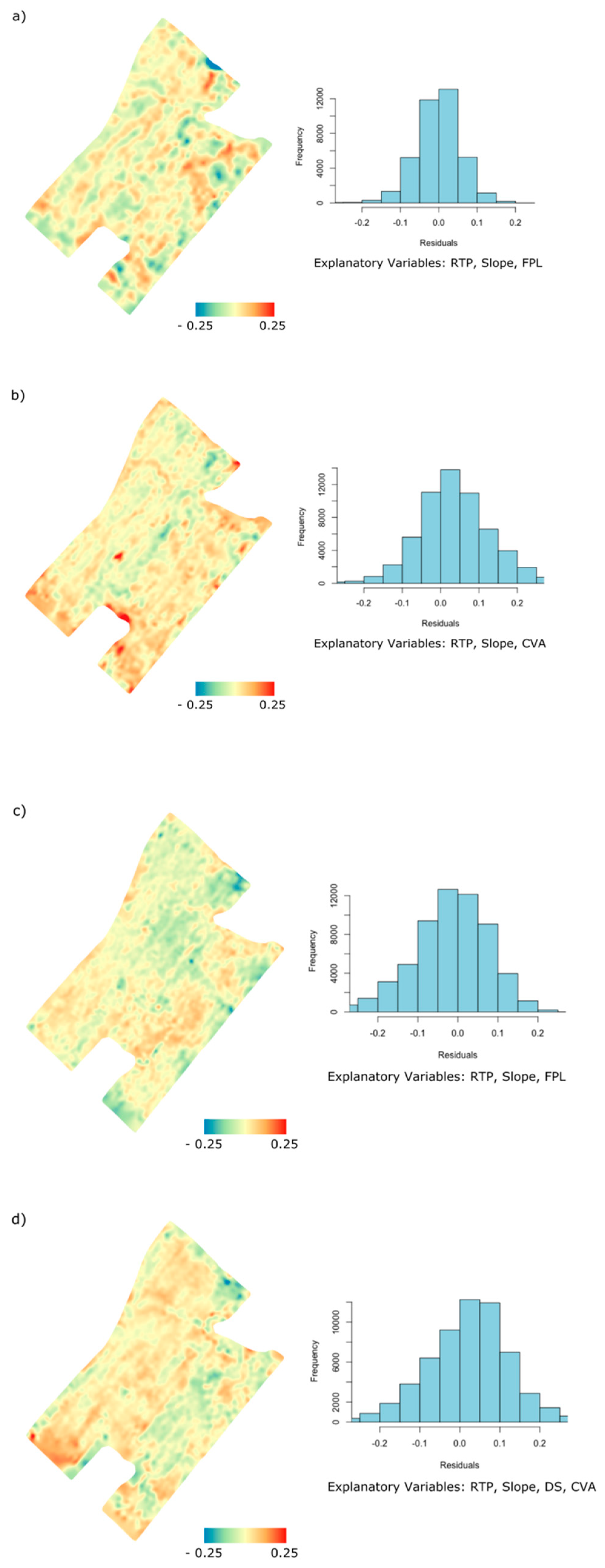
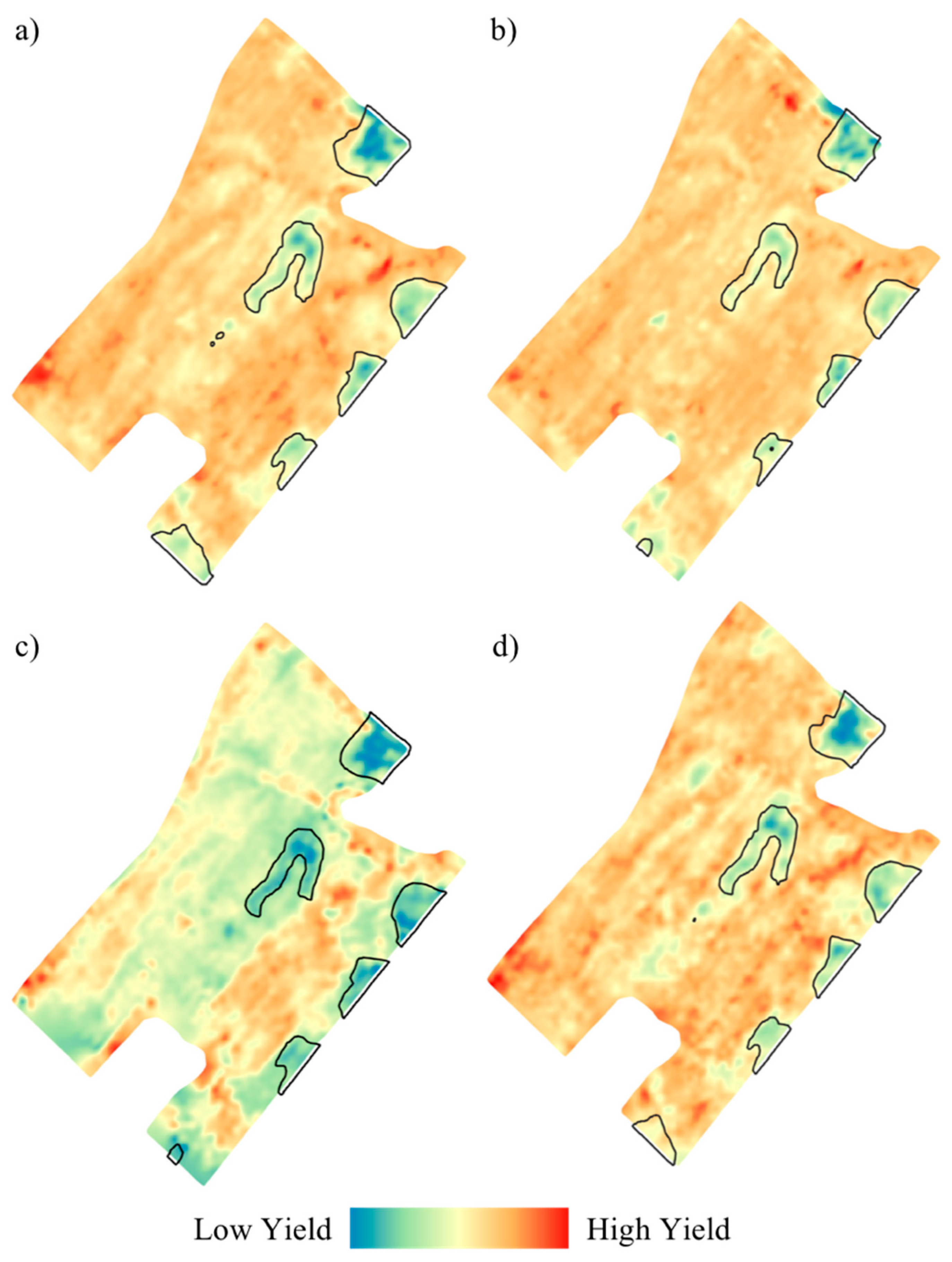
3.3. Crop Yield Predictions
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ferris, J.L. Data privacy and protection in the agriculture industry: Is federal regulation necessary. Minn. JL Sci. Tech. 2017, 18, 309. [Google Scholar]
- Green, T.R.; Salas, J.D.; Martinez, A.; Erskine, R.H. Relating crop yield to topographic attributes using Spatial Analysis Neural Networks and regression. Geoderma 2007, 139, 23–37. [Google Scholar] [CrossRef]
- Jiang, P.; Thelen, K.D. Effect of Soil and Topographic Properties on Crop Yield in a North-Central Corn-Soybean Cropping System. Agronomy J. 2004, 96, 252–258. [Google Scholar] [CrossRef]
- Kumhálová, J.; Kumhála, F.; Kroulík, M.; Matějková, Š. The impact of topography on soil properties and yield and the effects of weather conditions. Precis. Agric. 2011, 12, 813–830. [Google Scholar] [CrossRef]
- Heil, K.; Heinemann, P.; Schmidhalter, U. Modeling the Effects of Soil Variability, Topography, and Management on the Yield of Barley. Front. Environ. Sci. 2018, 6, 146. [Google Scholar] [CrossRef]
- Si, B.C.; Farrell, R.E. Scale-Dependent Relationship between Wheat Yield and Topographic Indices: A Wavelet Approach. Soil Sci. Soc. Am. J. 2004, 68, 577–587. [Google Scholar] [CrossRef]
- Kaspar, T.C.; Colvin, T.S.; Jaynes, D.B.; Karlen, D.L.; James, D.E.; Meek, D.W.; Pulido, D.; Butler, H. Relationship between six years of corn yields and terrain attributes. Precis. Agric. 2003, 1, 87–101. [Google Scholar] [CrossRef]
- Wei, T.; Cherry, T.L.; Glomrød, S.; Zhang, T. Climate change impacts on crop yield: Evidence from China. Sci. Total Environ. 2014, 499, 133–140. [Google Scholar] [CrossRef] [Green Version]
- Whitcomb, J.; Clewley, D.; Colliander, A.; Cosh, M.H.; Powers, J.; Friesen, M.; McNairn, H.; Berg, A.A.; Bosch, D.D.; Coffin, A.; et al. Evaluation of SMAP Core Validation Site Representativeness Errors using Dense Networks of in situ Sensors and Random Forests. IEEE J. Select. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 6457–6472. [Google Scholar] [CrossRef]
- Capmourteres, V.; Adams, J.; Berg, A.; Fraser, E.; Swanton, C.; Anand, M. Precision conservation meets precision agriculture: A case study from southern Ontario. Agric. Syst. 2018, 167, 176–185. [Google Scholar] [CrossRef]
- Lanni, C.; McDonnell, J.J.; Rigon, R. On the relative role of upslope and downslope topography for describing water flow path and storage dynamics: A theoretical analysis. Hydrol Proc. 2011, 25, 3909–3923. [Google Scholar] [CrossRef]
- Moeslund, J.E.; Arge, L.; Bøcher, P.K.; Dalgaard, T.; Ejrnæs, R.; Odgaard, M.V.; Svenning, J.-C. Topographically controlled soil moisture drives plant diversity patterns within grasslands. Biodivers. Conserv. 2013, 22, 2151–2166. [Google Scholar] [CrossRef]
- Wolock, D.M.; Hornberger, G.M.; Musgrove, T.J. Topographic effects on flow path and surface water chemistry of the Llyn Brianne catchments in Wales. J. Hydrol. 1990, 115, 243–259. [Google Scholar] [CrossRef]
- Ghandehari, M.; Buttenfield, B.P.; Farmer, C.J.Q. Comparing the accuracy of estimated terrain elevations across spatial resolution. Int. J. Remote Sens. 2019, 40, 5025–5049. [Google Scholar] [CrossRef]
- McKinion, J.M.; Willers, J.L.; Jenkins, J.N. Spatial analyses to evaluate multi-crop yield stability for a field. Comput. Electron. Agric. 2010, 70, 187–198. [Google Scholar] [CrossRef]
- Statistics Canada. 2016 Census of Agriculture. Available online: https://www150.statcan.gc.ca/n1/daily-quotidien/170510/dq170510a-eng.htm (accessed on 4 May 2020).
- Laamrani, A.; Voroney, P.R.; Berg, A.A.; Gillespie, A.W.; March, M.; Deen, B.; Martin, R.C. Temporal Change of Soil Carbon on a Long-Term Experimental Site with Variable Crop Rotations and Tillage Systems. Agronomy 2020, 10, 840. [Google Scholar] [CrossRef]
- Hoffman, D.W.; Matthews, B.C.; Wicklund, R.E. Soil Associations of Southern Ontario; Report No. 30 of the Ontario Soil Survey; Canada Department of Agriculture: Ottawa, ON, Canada, 1964. [Google Scholar]
- Laamrani, A.; Berg, A.A.; Voroney, P.; Feilhauer, H.; Blackburn, L.; March, M.; Dao, P.D.; He, Y.; Martin, R.C. Ensemble Identification of Spectral Bands Related to Soil Organic Carbon Levels over an Agricultural Field in Southern Ontario, Canada. Remote Sens. 2019, 11, 1298. [Google Scholar] [CrossRef] [Green Version]
- Kharel, T.P.; Maresma, A.; Czymmek, K.J.; Oware, E.K.; Ketterings, Q.M. Combining spatial and temporal corn silage yield variability for management zone development. Agron. J. 2019, 111, 2703–2711. [Google Scholar] [CrossRef]
- Meng, Q.; Liu, Z.; Borders, B.E. Assessment of regression kriging for spatial interpolation-comparisons of seven GIS interpolation methods. Cartogr. Geogr. Inf. Sci. 2013, 40, 28–39. [Google Scholar] [CrossRef]
- Hutchinson, M.F.; Gessler, P.E. Splines-more than just a smooth interpolator. Geoderma 1994, 62, 45–67. [Google Scholar] [CrossRef]
- Lauzon, J.D.; Fallow, D.J.; O’Halloran, I.P.; Gregory, S.D.L.; von Bertoldi, A.P. Assessing the temporal stability of spatial patterns in crop yields using combine yield monitor data. Can. J. Soil Sci. 2005, 85, 439–451. [Google Scholar] [CrossRef]
- Varvel, G.E. Crop rotation and nitrogen effects on normalized grain yields in a long-term study. Agron. J. 2000, 92, 938–941. [Google Scholar] [CrossRef] [Green Version]
- Al-Gaadi, K.A.; Hassaballa, A.A.; Tola, E.; Kayad, A.G.; Madugundu, R.; Assiri, F.; Alblewi, B. Characterization of the spatial variability of surface topography and moisture content and its influence on potato crop yield. Int. J. Remote Sens. 2018, 39, 8572–8590. [Google Scholar] [CrossRef]
- Kravchenko, A.N.; Bullock, D.G. Correlation of Corn and Soybean Grain Yield with Topography and Soil Properties. Agron. J. 2000, 92, 75–83. [Google Scholar] [CrossRef]
- Maestrini, B.; Basso, B. Predicting spatial patterns of within-field crop yield variability. Field Crop. Res. 2018, 219, 106–112. [Google Scholar] [CrossRef]
- Wilson, J.P.; Gallant, J.C. (Eds.) Terrain Analysis: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Schmidt, J.P.; Hong, N.; Dellinger, A.; Beegle, D.B.; Lin, H.S. Hillslope variability in corn response to nitrogen linked to in-season soil moisture redistribution. Agron. J. 2007, 99, 229–237. [Google Scholar] [CrossRef] [Green Version]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Lindsay, J.B. Whitebox GAT: A case study in geomorphometric analysis. Comput. Geosci. 2016, 95, 75–84. [Google Scholar] [CrossRef]
- Grohmann, C.H.; Smith, M.J.; Riccomini, C. Multiscale analysis of topographic surface roughness in the Midland Valley, Scotland. IEEE Trans. Geosci. Remote Sens. 2010, 49, 1200–1213. [Google Scholar] [CrossRef] [Green Version]
- Oleg, A.; Hatic, D.; Pernar, R. DEM-based depth in sink as an environmental estimator. Ecol. Model. 2001, 138, 247–254. [Google Scholar]
- Hjerdt, K.N.; McDonnell, J.J.; Seibert, J.; Rodhe, A. A new topographic index to quantify downslope controls on local drainage. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef] [Green Version]
- Freeman, T.G. Calculating catchment area with divergent flow based on a regular grid. Comput. Geosci. 1991, 17, 413–422. [Google Scholar] [CrossRef]
- Gudim, S. Impoundment Size Index (ISI): The use of potential impoundment size for the characterization of topographic incision in DEMs. MSc Thesis, Presented to the University of Guelph, Guelph, ON, Canada, 2019. [Google Scholar]
- Gallant, J.C. Primary topographic attributes. In Terrain Analysis-Principles and Application; Wilson, J.P., Gallant, J.C., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2000; pp. 51–86. [Google Scholar]
- Newman, D.R.; Lindsay, J.B.; Cockburn, J.M.H. Evaluating metrics of local topographic position for multiscale geomorphometric analysis. Geomorphology 2018, 312, 40–50. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
- Team, R. Core. R: A Language and Environment for Statistical Computing; R foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Robertson, C.; Long, J.A.; Nathoo, F.S.; Nelson, T.A.; Plouffe, C.C.F. Assessing Quality of Spatial Models Using the Structural Similarity Index and Posterior Predictive Checks: Assessing Quality of Spatial Models. Geogr. Anal. 2014, 46, 53–74. [Google Scholar] [CrossRef] [Green Version]
- Tsutsumida, N.; Rodríguez-Veiga, P.; Harris, P.; Balzter, H.; Comber, A. Investigating spatial error structures in continuous raster data. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 259–268. [Google Scholar] [CrossRef]
- Matthews, S.A.; Yang, T.-C. Mapping the results of local statistics: Using geographically weighted regression. Demogr. Res. 2012, 26, 151–166. [Google Scholar] [CrossRef] [Green Version]
- Tu, J.; Xia, Z. Examining spatially varying relationships between land use and water quality using geographically weighted regression I: Model design and evaluation. Sci. Total Environ. 2008, 407, 358–378. [Google Scholar] [CrossRef]
- Foody, G.M. Geographical weighting as a further refinement to regression modelling: An example focused on the NDVI–rainfall relationship. Remote Sens. Environ. 2003, 88, 283–293. [Google Scholar] [CrossRef]
- Musick, J.T.; Jones, O.R.; Stewart, B.A.; Dusek, D.A. Water-Yield Relationships for Irrigated and Dryland Wheat in the U.S. Southern Plains. Agron. J. 1994, 86, 980–986. [Google Scholar] [CrossRef]
- Thompson, R.B.; Gallardo, M.; Valdez, L.C.; Fernández, M.D. Using plant water status to define threshold values for irrigation management of vegetable crops using soil moisture sensors. Agric. Water Manag. 2007, 88, 147–158. [Google Scholar] [CrossRef]
- Paustian, M.; Theuvsen, L. Adoption of precision agriculture technologies by German crop farmers. Precis. Agric. 2017, 18, 701–716. [Google Scholar] [CrossRef]
- Schilling, B.J.; Attavanich, W.; Sullivan, K.P.; Marxen, L.J. Measuring the effect of farmland preservation on farm profitability. Land Use Policy 2014, 41, 84–96. [Google Scholar] [CrossRef]
- Mottaleb, K.A.; Mohanty, S. Farm size and profitability of rice farming under rising input costs. J. Land Use Sci. 2015, 10, 243–255. [Google Scholar] [CrossRef]
- Bullock, D.S.; Boerngen, M.; Tao, H.; Maxwell, B.; Luck, J.D.; Shiratsuchi, L.; Puntel, L.; Martin, N.F. The Data-Intensive Farm Management Project: Changing Agronomic Research Through On-Farm Precision Experimentation. Agron. J. 2019, 111, 2736–2746. [Google Scholar] [CrossRef] [Green Version]
- Buttafuoco, G.; Castrignanò, A.; Cucci, G.; Lacolla, G.; Lucà, F. Geostatistical modelling of within-field soil and yield variability for management zones delineation: A case study in a durum wheat field. Precis. Agric. 2017, 18, 37–58. [Google Scholar] [CrossRef]
- Mzuku, M.; Khosla, R.; Reich, R.; Inman, D.; Smith, F.; MacDonald, L. Spatial Variability of Measured Soil Properties across Site-Specific Management Zones. Soil Sci. Soc. Am. J. 2005, 69, 1572–1579. [Google Scholar] [CrossRef] [Green Version]
- Mittal, S.; Mehar, M. Socio-economic Factors Affecting Adoption of Modern Information and Communication Technology by Farmers in India: Analysis Using Multivariate Probit Model. J. Agric. Educ. Ext. 2016, 22, 199–212. [Google Scholar] [CrossRef]
- Wang, H. The Spatial Structure of Farmland Values: A Semiparametric Approach. Agric. Resour. Econ. Rev. 2018, 47, 568–591. [Google Scholar] [CrossRef] [Green Version]
- Gollini, I.; Lu, B.; Charlton, M.; Brunsdon, C.; Harris, P. GWmodel: An R package for exploring spatial heterogeneity using geographically weighted models. arXiv 2013, arXiv:1306.0413. [Google Scholar] [CrossRef] [Green Version]
- Lu, B.; Charlton, M.; Harris, P.; Fotheringham, A.S. Geographically weighted regression with a non-Euclidean distance metric: A case study using hedonic house price data. Int. J. Geogr. Inf. Sci. 2014, 28, 660–681. [Google Scholar] [CrossRef]
- Harris, P.; Fotheringham, A.S.; Crespo, R.; Charlton, M. The use of geographically weighted regression for spatial prediction: An evaluation of models using simulated data sets. Math. Geosci. 2010, 42, 657–680. [Google Scholar] [CrossRef]

| Year | Crop |
|---|---|
| 2011 | Soybeans |
| 2013 | Soybeans |
| 2014 | Corn |
| 2015 | Soybeans |
| 2016 | Winter Wheat |
| 2017 | Soybeans |
| 2018 | Corn |
| Topographic Attribute | Description | Source |
|---|---|---|
| Circular variance of aspect | Local slope aspect variance | [32] |
| Depression depth | Vertical depth of depressions | [33] |
| Downslope Index | Slope gradient between a cell and downslope cell | [34] |
| Catchment area with divergent flow (upslope area) | Multi-directional flow algorithm | [35] |
| Impoundment size index | Resulting upslope impoundment from placement of dam | [36] |
| Plan curvature | Curvature perpendicular to dominant slope angle | [37] |
| Profile curvature | Curvature parallel to dominant slope angle | [37] |
| Relative topographic position | Cell elevation relative to surrounding cells | [38] |
| Slope | Surface gradient | [37] |
| Tangential curvature | Plan curvature related to slope | [37] |
| Topographic wetness index | Steady state soil moisture index based slope contributing area | [39] |
| Total curvature | Curvature across a surface | [37] |
| Upslope flow path length | Average length of each cell’s upslope flow paths | [31] |
| Topographic Parameter | R2 |
|---|---|
| Circular Variance of Aspect | 0.08 |
| Depression Depth | 0.00 |
| Downslope Index | 0.18 |
| Upslope Area | 0.08 |
| Impound Size Index | 0.03 |
| Plan Curvature | 0.00 |
| Profile Curvature | 0.01 |
| Relative Topographic Index | 0.27 |
| Slope | 0.32 |
| Tangential Curvature | 0.02 |
| Topographic Wetness Index | 0.24 |
| Total Curvature | 0.03 |
| Upslope Flow Path Length | 0.21 |
| Topographic Attribute | GWR Frequency | Models Used |
|---|---|---|
| Relative Topographic Position | 4 | All Models |
| Slope | 4 | All Models |
| Circular variance of aspect | 2 | Corn, Soybeans |
| Upslope Flow Path Length | 2 | Wheat, Average |
| Downslope Index | 1 | Soybeans |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eyre, R.; Lindsay, J.; Laamrani, A.; Berg, A. Within-Field Yield Prediction in Cereal Crops Using LiDAR-Derived Topographic Attributes with Geographically Weighted Regression Models. Remote Sens. 2021, 13, 4152. https://doi.org/10.3390/rs13204152
Eyre R, Lindsay J, Laamrani A, Berg A. Within-Field Yield Prediction in Cereal Crops Using LiDAR-Derived Topographic Attributes with Geographically Weighted Regression Models. Remote Sensing. 2021; 13(20):4152. https://doi.org/10.3390/rs13204152
Chicago/Turabian StyleEyre, Riley, John Lindsay, Ahmed Laamrani, and Aaron Berg. 2021. "Within-Field Yield Prediction in Cereal Crops Using LiDAR-Derived Topographic Attributes with Geographically Weighted Regression Models" Remote Sensing 13, no. 20: 4152. https://doi.org/10.3390/rs13204152
APA StyleEyre, R., Lindsay, J., Laamrani, A., & Berg, A. (2021). Within-Field Yield Prediction in Cereal Crops Using LiDAR-Derived Topographic Attributes with Geographically Weighted Regression Models. Remote Sensing, 13(20), 4152. https://doi.org/10.3390/rs13204152







