Abstract
Before and after earthquakes, abnormal physical and chemical phenomena can be observed by gathering ground-based and satellite data and interpreted by the lithosphere–atmosphere–ionosphere coupling (LAIC) mechanism. In this study, we focused on the mechanism of LAIC electromagnetic radiation and investigated the seismic electromagnetic (EM) wave generated in the lithosphere by earthquakes and its global propagation process from the lithosphere through the atmosphere and into the bottom of ionosphere, in order to analyze the abnormal disturbance of ground-based and space-based observation results. First, analytic formulas of the electrokinetic effect were used to simulate the generation and propagation process of the seismic EM wave in the lithosphere, interpreted as the conversion process of the seismic wave and EM wave in porous media. Second, we constructed a three-dimensional Earth–ionosphere waveguide by applying the finite-difference time-domain (FDTD) algorithm to model the global propagation process of the seismic EM wave into the atmosphere and cavity between the bottom of the ionosphere and the surface of the Earth. By combining the model of the electrokinetic effect in the lithosphere with the numerical model of the Earth–ionosphere waveguide in the atmosphere and ionosphere, we numerically simulated the global transmission process of extremely low-frequency (ELF: 3 Hz–3000 Hz) EM waves which are related to earthquakes. The propagation parameters of coseismic ELF EM waves with different duration times and center frequencies were analyzed and summarized. The simulation results demonstrate that the distribution characteristics of an electric field along longitude, latitude and altitude with time are periodic and the time interval during which an EM wave travels around the whole Earth is approximately 0.155 s when adopting the conductivity of the knee profile. We also compared the observation data with the simulation results and found that the attenuating trends of the ELF electric field are consistent. This proposed ELF EM wave propagation model of lithosphere–atmosphere–ionosphere coupling is very promising for the explanation of abnormal disturbances of ground-based and space-based observation results of ELF EM fields which are associated with earthquakes.
1. Introduction
Seismo-ionospheric effects have become a topic of intensive research in recent years since researchers observed a large number of abnormal ionospheric disturbance events before and after earthquakes which may be related to earthquakes. Since ref. [1] first analyzed ionosphere observation data to determine the seismo-ionospheric signature before the Alaska earthquake, research into pre-earthquake ionospheric anomalies have been continuously intensified [2]. The occurrence of seismic anomalies is related to certain physical or chemical mechanisms, and the lithosphere–atmosphere–ionosphere coupling mechanism has been suggested as a theoretical basis to explain the formation process behind these phenomena. At present, the scientific interpretation of the LAIC mechanism mainly focuses on three aspects: first, that anomalies in the lithosphere, atmosphere and ionosphere are caused by the penetration of the electric field or current induced by earthquakes, namely the LAIC direct current (DC) electric field mechanism; second, that anomalies are caused by the upward propagation of acoustic gravity waves generated by earthquakes, namely the LAIC acoustic gravity wave (AGW) mechanism; third, that anomalies are caused by abnormal EM radiation, namely the LAIC electromagnetic radiation mechanism. These three physical mechanisms have been verified by corresponding observational results [3,4,5]. The anomalies of electric field, acoustic gravity wave and electromagnetic radiation are the direct sources of the disturbance events affecting the ionosphere which are caused by underlying mechanisms. Scholars have put forward lots of physical hypotheses attempting to interpret these abnormal phenomena, such as the propagation of positive holes [6,7] and radon (or other gas) emanation to explain the LAIC DC electric field mechanism preceding earthquakes; internal gravity wave theory [8] to explain the LAIC AGW mechanism after earthquakes; and the electrokinetic effect [9,10] to explain the LAIC electromagnetic radiation mechanism after earthquakes. Various models have been proposed to simulate the corresponding physical mechanisms, including the electric field penetration model in ref. [11] and the acoustic and gravity wave propagation model in ref. [12].
In this paper, we focused on the mechanism of LAIC electromagnetic radiation, and investigated the propagation process and physical mechanism of earthquake-induced ELF electromagnetic waves in the lithosphere, atmosphere and ionosphere. According to the LAIC electromagnetic radiation mechanism, earthquakes lead to the abnormal radiation of EM waves and the radiated seismic energy is a small portion of the entire released energy. In the process of propagating from the underground to the air, seismic abnormal EM waves will cause ELF electric field perturbations in the lithosphere and atmosphere and directly interact with various particles in the ionosphere, affecting various ionosphere parameters, which is called lithosphere–atmosphere–ionosphere coupling. Many researchers have utilized ground-based and satellite data to observe ultra-low frequency/extremely low-frequency/very-low-frequency (ULF/ELF/VLF) electromagnetic emissions that may be associated with earthquakes. Using four stations with magnetotelluric (MT) measurement, ref. [13] observed large variations in the MT fields which are associated with seismic waves. Ref. [14] performed statistical methods to study the relationship among 20 earthquakes (M ≥ 5.0) which occurred from 26 August 2003, to 13 July 2004, with ELF-whistlers/emissions below 100 Hz. Their ELF observation system consisted of magnetic and electric antennas which can measure magnetic fields and electric fields. They summarized that the occurrence ratios of ELF emissions increased significantly 5~7 days before the earthquakes and were proportional to the magnitude of the earthquakes. Analyzing the three magnetic field components (Bx, By and Bz) in the ULF/ELF range which are measured by means of three orthogonal induction coil magnetometers, ref. [15] found that the Schumann resonance (~26.4 Hz) observed in Japan was related to the Chi-chi earthquake in Taiwan. Ref. [16] observed and analyzed the Intercosmos-24 satellite data from 16 November 1989, to 31 December 1989, during which 28 strong earthquakes (5.2 < MS < 6.1) occurred worldwide, and found an enhancement in the emission occurrence probability of ELF, ULF and VLF in the region over the epicenter before the earthquakes. The DEMETER satellite data were processed by [5], and more than 2/3 of the chosen Chilean earthquakes of magnitudes larger than 6.0 were accompanied by significant ULF/ELF electric field perturbations before and after the earthquakes. Observing ULF/ELF data within the frequency range of 0.1 Hz–24 Hz, ref. [17] pinpointed that the precursor of the Japanese earthquake on 11 March 2011 was ULF/ELF radio emission.
Observation results have proved that earthquakes are accompanied by EM fields in the lithosphere [13,18,19]. Some scholars believe that the EM field is induced by seismic waves when earthquakes occur. Refs. [20,21] detected seismoelectric signals related to underground seismic waves. The electrokinetic effect is a physics theory proposed to demonstrate the coseismic and post-seismic electromagnetic radiation mechanism in the lithosphere, which can reasonably interpret the coupling between seismic energy and electromagnetic energy. Ref. [9] set up the governing equations of acoustic-electromagnetic coupling in porous media as the fundamental equations of the electrokinetic effect, which combined the Biot’s poroelastodynamic equations (mechanical equation of an elastic field) and Maxwell’s equations (electromagnetic equation of an EM field) together through the electrokinetic coupling coefficient. Since the coupling coefficient can be measured by experiment, it is feasible to properly model the EM fields generated by seismic waves. Ref. [22] derived the Green functions of solid displacement u, relative fluid–solid displacement w and electric field E in the frequency space domain under single point force. In addition, they calculated the plane wave solutions to Pride equation, and summarized that the electrokinetic effect produced two types of EM field. The first one is an accompanying EM field which propagates with the seismic wave at the same speed and does not exist outside of the seismic disturbance region. The other is an independently propagating EM field which propagates outside the seismic wave with a much higher speed and is generated only when seismic waves pass through the interfaces of different media and accomplish wave type conversion. This phenomenon has corresponding observational evidence: ref. [20] detected it at the surface of the ground with electrode pairs, and the results clearly distinguished the accompanying EM field from the independently propagating EM field. The EM wave induced at the interface and the electric field accompanying the P-wave were also observed near the Earth’s surface by [23]. Furthermore, ref. [24] extended the electrokinetic effect and derived the analytical expression of the EM field induced by a double-couple source in infinite space. In this paper, we mainly investigated the transmission process of the independently propagating EM wave generated by the seismic wave between the lithosphere, atmosphere and ionosphere. Such a wave propagates at a high speed, and can probably be used as an early earthquake warning.
After introducing the physical mechanism of earthquake-induced EM radiation in the lithosphere, it is necessary to investigate the propagation process of EM waves in the atmosphere and the cavity between the bottom of the ionosphere and the surface of the Earth. Compared with the EM wave of higher frequency, there is very little loss in the height range from the Earth’s surface to the ionosphere for the ELF-band wave; therefore, the propagation process of the ELF wave in the atmosphere and the ionosphere can be simulated by utilizing analytical methods. FDTD is a proper method to model Maxwell’s equations and provides a novel idea for the numerical calculation of an EM field—which was first proposed by [25] who derived the difference expression of Maxwell’s equations in the three-dimensional Cartesian coordinate system. Ref. [26] extended the FDTD method with spherical coordinates and derived the difference expression of Maxwell’s equations in the three-dimensional spherical coordinates. Based on the FDTD method and Maxwell’s equations on the neutral medium, ref. [27,28] numerically simulated the propagation process of an ELF wave in a two-dimensional spherical coordinate system and three-dimensional spherical coordinate system, respectively, and presented the results of ELF wave propagation in the Earth space by assuming a current source on the surface.
Before and after earthquakes, abnormal disturbances of an ELF EM wave can be observed at stations on the Earth’s surface and in the air. According to the observations reported in previous research, ELF EM signals related to EQs can be observed both locally and remotely [13,14,15]. On the one hand, stations close to the epicenter can directly receive the abnormal signal caused by earthquakes. On the other hand, the abnormal signal is received by stations after propagating in the Earth–ionosphere waveguide. Since the simulation sources of other researchers are ideal, we further investigated the simulation of physical sources based on electrokinetic effects in this study. Therefore, this paper mainly focused on the simulation of ELF EM waves generated by the underground electrokinetic coseismic effect and its global propagation characteristics in the Earth–ionosphere waveguide model which extends 100 km radially from sea level. The electrokinetic effect model was adopted to simulate the generation process of the underground ELF EM wave more physically and the Earth–ionosphere cavity model is adopted to simulate the propagation of the ELF EM wave in the atmosphere and cavity between the bottom of the ionosphere and the surface of the Earth. The outline of this paper is as follows. In the next section, we briefly introduce the basic process of electrokinetic effect and simulate the equations of EM radiation caused by seismic waves in the lithosphere which were proposed by [24]. Section 3 introduces the three-dimensional spherical FDTD model of the Earth atmosphere and ionosphere, and provides the initial conditions, boundary conditions and stability conditions of the model. Section 4 simulates the global propagation process of the earthquake-induced EM wave in three-dimensional space and analyzes the simulation results. Section 5 and Section 6 presents a discussion and summary of the research.
2. Electrokinetic Effect
When earthquakes occur, a seismic wave (a kind of elastic wave) is produced whose propagation medium is mainly rock. Rock is a natural porous medium due to the existence of pores that allow fluid (usually electrolyte solutions) to pass through, and the porous crust can be divided into solid grain frame and pore fluid. When the fluid flows in the pores, an electric double layer is formed on the solid–fluid interface in a porous medium [29] (174–188). The electric double layer is formed as follows. Anions and cations exist in the electrolyte solution. When the fluid flows in the porosity of the rock, some ions (such as anions) will be selectively adsorbed by the solid grain framework of the rock and form an adsorbed layer, while other ions (cations) remain in the pore fluid will thus form a diffusion layer. The adsorption layer and diffusion layer constitute the electric double layer. When seismic waves propagate in rock, the solid grain framework remains stationary and the pore fluid moves relative to the solid grain framework, thus causing the charged ions in the pore fluid to move so that the mechanical energy is converted into electromagnetic energy and finally, the EM field is generated [22,24]. These processes are called seismoelectric and seismomagnetic conversions, respectively. Seismic waves generated at the earthquake source propagate in the lithosphere and meanwhile stimulate EM waves. When arriving at the Earth’s surface, EM waves penetrate the interface and propagate in the atmosphere and ionosphere. Figure 1 is the schematic diagram.
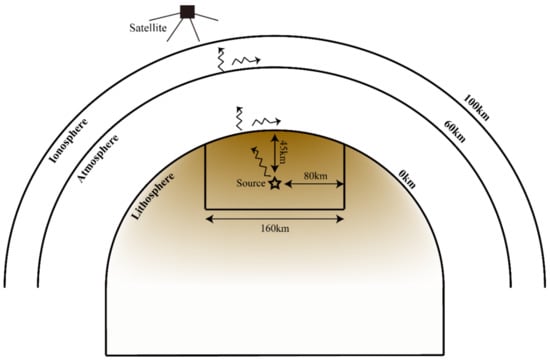
Figure 1.
Schematic diagram of the LAIC electromagnetic radiation mechanism.
In view of the above physical process, ref. [9] set up the governing equations of acoustic-electromagnetic coupling in porous media, which coupled the Biot equations and Maxwell equations. Additionally, in the special case of homogeneous and isotropic wholespace, the homogeneous equations with the average solid displacement u, the average relative fluid–solid displacement w and the electric field E as the basic field quantities are obtained. There are four plane wave solutions calculated, namely fast P wave (Pf), slow P wave (Ps), shear wave (S) and electromagnetic wave (EM) [22]. The first three waves are accompanying EM fields that exist only with seismic waves, and the last wave is an independently propagating EM field with a higher speed. These two types of EM fields have been experimentally confirmed [30].
Furthermore, using the Pride equations, ref. [24] derived the Green function of the electric and magnetic fields in order to calculate the wavefields induced by the double-couple source in infinite space. The analytical expressions of the electric field and magnetic field in the frequency domain are thus obtained [24]:
where ω is the angular frequency; r is the distance between the source and the observation point; s is the complex slowness, which is essentially a complex variable with ω as its independent variable; and are the complex amplitudes of the transverse and longitudinal components, respectively; and are the unit vectors; M0 is the earthquake moment tensor, which is the absolute mechanical quantity defined to describe the magnitude of an earthquake where M0 = 4.37 × 1017 N·m; and μ is the magnetic permeability coefficient where μ = 4π × 10−7 H/m. Thus, the EM radiation propagation process in the lithosphere can be simulated. Ref. [24] proposed that the time-domain waveforms of electric and magnetic fields could be obtained via the discrete Fourier transform. Firstly, a cosine pulse function was set up as the acoustic source function of the seismic source:
where Tc is the pulse duration; f0 is center frequency; and t is the time series. Tc and f0 were chosen to be 2.2 s and 1 Hz, respectively, and can be set to different values depending on the actual situation. Time series t is set here as 0 s~40.96 s, and the time interval is 0.02 s. Therefore, the time series has 2048 points and the sampling frequency is fs = 50 Hz. The waveform of s0(t) in the time domain is shown in Figure 2a and the frequency spectrum of s0(t) can be obtained by fast Fourier transform, which is shown in Figure 2b. The cosine pulse function is mainly distributed between 0 Hz and 2 Hz. Secondly, the physical schematic diagram of the lithosphere is presented. The lithosphere in Figure 1 is a three-dimensional space and the specific parameters in the model are plotted in Figure 3. The electrokinetic effect model can simulate the propagation of the EM wave at any position in the lithosphere. The width (X and Y axes) of the three-dimensional space is 160 km (−80 km ≤ X ≤ 80 km, 0 km ≤ Y ≤ 160 km), and the depth (Z axis) is 60 km (0 km ≤ Z ≤ 60 km). Figure 3 is a simplified model where the seismic fault consists of two layers of porous media with different parameters. The porous medium in the range of 0 km–30 km below the surface is Sandstone 1, and the porous medium in the range of 30 km–60 km below the surface is Sandstone 2. The parameters of Sandstone 1 and Sandstone 2 are shown in Table 1 [24,31]. The seismic source is located 45 km below the surface, and we use Equation (8) as the acoustic source function. Apparently, in real earthquakes, seismic faults are filled with spatially distributed heterogeneous irregular media with different contributions—which can be achieved in simulations by adjusting the model parameters.
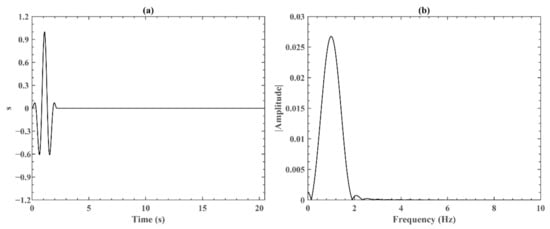
Figure 2.
The acoustic source function of the seismic source: (a) the waveform of s0(t) in the time domain; and (b) the frequency spectrum of s0(t).
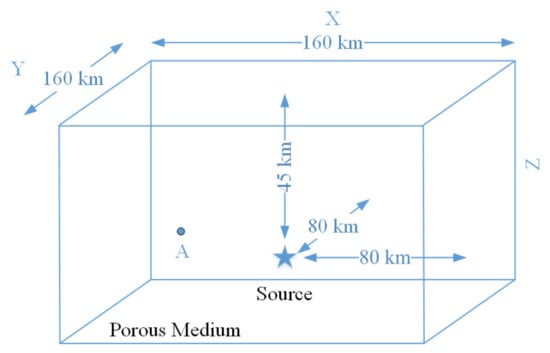
Figure 3.
Schematic diagram of the lithosphere in the electrokinetic effect model. The distance between observation point A and the seismic source is ΔX = 60 km, ΔY = 1.8 km, and the depth of point A is 30 km.

Table 1.
Parameters of Sandstone 1 and Sandstone 2.
Observation point A is selected, and the distance between point A and the seismic source is ΔX = 60 km, ΔY = 1.8 km and ΔZ = 15 km. Finally, by performing the 2048-point Fast Fourier transforming, the frequency response of s0(t) can be calculated, which is S(ω). We multiply S(ω) with Equations (1) and (5) and then apply the inverse Fast Fourier transform method to obtain the time domain waveform of the electric field and magnetic field induced by the seismic source. Point A was selected to intuitively examine the underground results simulated by the electrokinetic effect model.
Figure 4 presents the horizontal component and vertical component of the electric field in the time domain, in which the first 2.2 s of the wave is multiplied by a factor of 10,000 to emphasize the EM wave. Figure 4 demonstrates that the simulated electric fields have multiple disturbances in time-waveforms. It is known that an EM wave propagates faster than a body wave. Meanwhile, the fast P wave propagates faster, followed by the shear wave and slow P wave. Therefore, it can be determined that the first disturbance of the electric field is induced by the EM wave and appears in 0~2.2 s; the second disturbance is induced by the fast P wave and appears in 13~18 s; the third disturbance is induced by shear wave and appears in 22~26 s, and only exists in a vertical component of the electric field. These results are consistent with those of [22,24]. In this paper, we focused on the EM wave because it is the only independently propagating electromagnetic wave which is one of the probable explanations of the LAIC electromagnetic radiation mechanism. Therefore, the EM wave generated by electrokinetic effect can be employed as a source to simulate the propagation process of an abnormal ELF electromagnetic wave in the atmosphere and ionosphere.
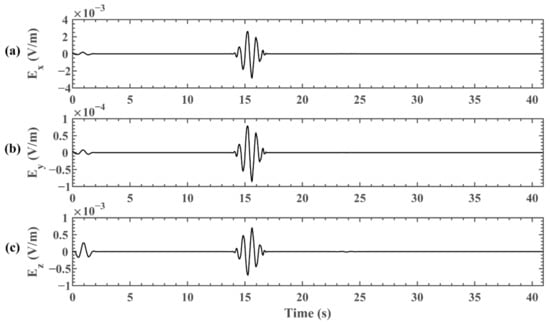
Figure 4.
The abnormal horizontal and vertical ELF electric fields induced by earthquake, calculated by the electrokinetic effect model: (a) the electric field in the x direction; (b) the electric field in the y direction; (c) the electric field in the z direction.
3. Earth–Ionosphere Waveguide
In Section 3, we establish the Earth–ionosphere waveguide model. Compared with the EM wave of higher frequency, the attenuation of the ELF-band wave is very low when transmitting from the Earth’s surface to the ionosphere. Therefore, the propagation process of the ELF wave in the atmosphere and ionosphere can be simulated by utilizing analytical methods. The space between the Earth’s surface and the ionosphere is conceptualized and defined as a waveguide, which is called the Earth–ionosphere waveguide system [32,33,34].
We adopted the finite difference time domain method to set up the difference scheme of Maxwell equations and established the propagation mechanism of EM waves in three-dimensional spherical coordinates. The expressions of the Maxwell equations in differential form are as follows:
where E is the electric field intensity vector; B is the magnetic induction vector; H is the magnetic field intensity vector; D is the electric displacement vector; and J is the current-density vector.
Firstly, the definition of a coordinate in the Earth–ionosphere waveguide model is introduced. Since the Earth is almost spherically symmetrical, the spherical coordinate system is especially suitable for its modeling. We mapped the complete spherical space of the Earth–ionosphere waveguide geometry onto a logically 3-D FDTD grid where r denotes the radial direction, and the grid-cell position index in this direction is i; θ denotes the meridional direction, and the grid-cell position index in this direction is j; φ denotes the zonal direction, and the grid-cell position index in this direction is k. In the radial, meridional and zonal directions, the grids are divided into Nr, Nθ and Nφ segments, respectively. Therefore, in the Earth–ionosphere cavity, i = 1 is the coordinate of the Earth’s surface and i = Nr is the coordinate of the model’s topped layer; j = 1 is the coordinate of the North Pole and j = Nθ is the coordinate of the South Pole; k = 1 is the coordinate of the meridian and k = Nφ is the coordinate of the meridian after traveling along an entire great circle. When modeling the Earth–ionosphere waveguide, we chose equal increments along the radial, meridional and zonal directions, respectively. After dividing the FDTD grids, at all heights, the ordinary cells are trapezoidal, while the cells at the north and south poles are triangular. We chose the value of Nr as 20, therefore, the distance of 100 km from the Earth’s surface to the ionosphere is evenly divided into 20 segments, each of which is 5 km. The value of Nθ is 128, and the south–north span of the model from the South Pole to the North Pole is evenly divided into 128 segments, each of which is π/128. The value of Nφ is 256, and the west–east span of the model is evenly divided into 256 segments, each of which is 2π/256. Thus, the resolutions are Δr = 5, Δθ = π/128 and Δφ = 2π/256.
Secondly, Maxwell equations in differential form can be applied to develop the difference expression of the electric field and magnetic field in the grids:
where Re denotes the Earth’s radius; ε denotes the dielectric constant; σ denotes the conductivity; μ denotes the permeability coefficient; Δt denotes the time interval; and denotes the radial electric field of position (i, j, k) at time step n. When the computational space is filled with lossy medium, due to the high conductivity at the top of the Earth–ionosphere cavity, the ELF EM wave will rapidly decay with the propagation of radial distance. Compared with its amplitude below 60 km, it will be almost exhausted before reaching the surface of the outer spherical shell, which is the bottom of the ionosphere. Therefore, it is not necessary to especially consider the ionospheric reflection, which cannot be significantly helpful for this paper in the study of the propagation characteristics of the ELF EM wave in the Earth–ionosphere cavity [35]. The boundary conditions at the surface of the waveguide were set to match the perfect electric conductor (PEC) boundary conditions in the three-dimensional Earth–ionosphere waveguide model. Where longitude lines of 0° and 360° coincide, the periodic boundary condition in Equation (17) is set:
The conditions of cells at the south and north poles require special processing because the iterative formula in the spherical Earth–ionosphere waveguide model induces instability at the south and north poles. Equation (18) is the iterative equation of the radial component of the electric field in the Arctic region:
Equation (19) is the iterative equation of the radial component of the electric field in the Antarctic region:
Furthermore, we consider the numerical stability of the three-dimensional Earth–ionosphere waveguide model. In the meshing process, the length of the cell is an important factor that decides whether the iterative process will be of convergence. In general, the finer the mesh, the smaller the probability of occurrence of numerical dispersion effect. However, considering the computing power of computers, the model can meet the condition if the grid is less than one-twelfth of the wavelength of the EM wave propagating through it. In this paper, the numerical dispersion constraint was satisfied. In addition, the stability condition of the finite-difference time-domain equation was the Courant stability limit, which is the relationship between the space step and time step. The Courant stability condition of the time step in the spherical coordinate system is Equation (20), and we generally adopt Equation (21) in the actual simulation experiment:
where c is speed of the light; and δmin is the minimum mesh length. It is obvious that the smallest space–cell distance in the waveguide model is the radial length Δr, which is 5 km in this paper. The numerical stability condition can be satisfied and so far, the three-dimensional Earth–ionosphere waveguide model in spherical coordinates is complete.
The next step is to set the relevant parameters of the electromagnetic characteristics of the atmosphere and the ionosphere, and two types of model can be selected: the lossless model and the lossy model. In the lossless model, no parameters of the waveguide environment are set. Thus, the whole waveguide model is in vacuum, which is an ideal state. In the lossy model, the parameters are set as horizontal uniformity. The permeability σm is 0, the dielectric constant ε is 8.85 × 10−12 F/m and the permeability coefficient μ is 4π × 10−7 H/m. Altitude profiles of conductivity can be chosen as the knee model and two-exponential model. Equation (22) is the formula of the conductivity models:
where A = B = 5.6 × 10−10, hkn1 = hkn2 = 45 km, a = 2.9 km and b = 8.3 km for the knee model [36]; A = 4.4 × 10−10, B = 1.6 × 10−4, hkn1 = 50 km, hkn2 = 10 km and a = b = 5 km for the two-exponential model [33,37]; and h is the height in kilometers. The knee profile and the two-exponential profile are plotted in Figure 5 where the blue curve indicates the knee model and the red curve indicates the two-exponential model. Figure 5 illustrates the fact that the knee model is larger than the two-exponential model at the same height below 40 km and they intersect between 40 km and 90 km. Above 90 km, the knee model is less than the two-exponential model at the same height. The Earth’s surface is chosen to be that of rock.
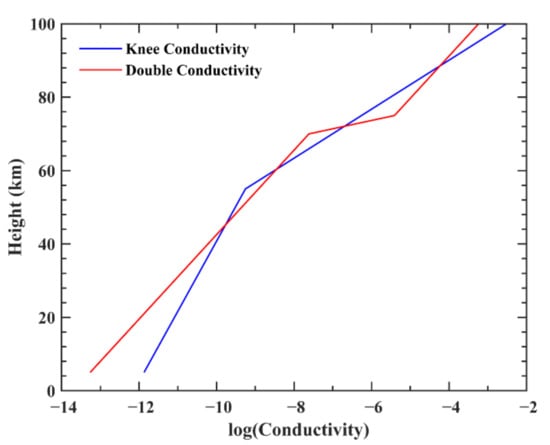
Figure 5.
The conductivity of the knee profile and the two-exponential profile. The blue line corresponds to knee profile and the red line corresponds to the two-exponential profile.
4. Results
In Section 2 and Section 3, the simulation of the lithospheric EM radiation model and the Earth–ionosphere waveguide model were established, respectively. Furthermore, we simulated the wave coupling and alternating electric field coupling in multiple circles of the lithosphere, atmosphere and ionosphere in Section 4. The schematic diagram of the whole process is presented in Figure 1. By combining the lithosphere electrokinetic coseismic effect model and the Earth–ionosphere waveguide model, the global propagation process of the EM wave in the atmosphere and ionosphere could be simulated after calculating the distribution of the EM wave on the Earth’s surface as the initial input waveform. Therefore, a multi-layer coupling simulation was realized, which is a feasible and convenient method of studying the LAIC electromagnetic radiation mechanism.
In Section 2, we obtained the electric field components of an EM wave in the rock medium near the Earth’s surface simulated by the lithosphere electrokinetic coseismic effect model. Before we assume the results, as a source of input into the Earth–ionosphere waveguide system, it is necessary to consider the specific situation in which the EM wave crosses the surface. In the lithosphere, the EM wave simulated by the electrokinetic coseismic effect model propagates in all directions, thus generating electric and magnetic fields in all directions, and finally forming horizontal electric field components Ex, Ey and vertical electric field components Ez in the Cartesian coordinate system, which was clearly demonstrated in Section 2. For continental earthquakes, the boundary of the medium is the surface of the Earth (take rock and air as an example); therefore, the EM wave must satisfy certain boundary conditions when crossing the surface.
After penetrating the boundary of the medium, EM waves either propagate as ground waves along the surface of the Earth, or radiate to high altitudes at certain elevation angles. In both cases, electric field components of the waves exist in all directions. Since this paper is mainly focused on the electric field component of EM waves propagating to the bottom of ionosphere, the vertical electric field component was selected as the initial input for the Earth–ionosphere waveguide model. It is known that when the electric wave propagates from the ground across the boundary to the air, the normal components of the magnetic flux densities and the tangential components of the electric field intensities in two media are continuous at the interface (z = 0 km):
while the normal components are discontinuous and ignore the current:
where k denotes the propagation wave number ; k0 denotes the propagation wave number in air; kg denotes the propagation wave number in rock; ω denotes the angular frequency ; μ denotes the permeability; denotes the complex dielectric constant, which is an important parameter to characterize the electrical characteristics of geology, where ; εr denotes the relative permittivity, where for the air and for the rock; ε0 denotes the vacuum permittivity; σ denotes electrical conductivity, where S/m for the air near the Earth’s surface and S/m for the rock; and λ denotes the wavelength of the radio wave, where λ = 6 × 106 m for the EM wave of 50 Hz. The air occupies the upper half of the space characterized by the permittivity ε0 and permeability μ0 while the ground occupies the lower half space characterized by the permittivity ε1 = εr·ε0, permeability μ0, and conductivity σ1, as presented in Figure 1. Therefore, according to Equation (24), the electric field in the atmosphere near the ground surface is approximately 36 times that in the rock. In order to be more practical and credible, the electric field amplitude on the Earth’s surface can be modified according to the observation values. In Section 4, when modeling the Earth–ionosphere cavity, the results of the electrokinetic coseismic effect model at the surface are normalized to facilitate the comparison with the actual observation results. The waveform of the coseismic simulation result is adopted as the initial electric field imported into the Earth–ionosphere waveguide model, while the amplitude is determined by the observation results in the atmosphere. Additionally, if the wave normal vector is not vertical, the horizontal electric field components can also be chosen as the source by changing the boundary conditions of Earth’s surface.
Refs. [38,39,40] pointed out that the duration and frequency of natural earthquakes and blasting earthquakes are different. Whilst the duration of a blasting earthquake is short, generally less than 1 s, and the frequency is high, ranging from 10 Hz to 100 Hz, the duration of a natural earthquake is long with a main frequency ranging from 1.25 Hz to 10 Hz. By adjusting the parameters of the acoustic source function at the earthquake source, we can obtain the EM waves at the ground with the forms of a one-dimensional point or a two-dimensional surface. Section 4 contains the simulation results of the Earth–ionosphere waveguide model in the following four cases.
4.1. Case 1
The Earth conductivity model is in knee profile, and the EM wave on the Earth’s surface is located in one cell whose initial center frequency is 50 Hz and whose duration time is 0.04 s. The reason for choosing 50 Hz was that the frequency of the blasting earthquake ranges from 10 Hz to 100 Hz, and in order to prevent the influence of Schumann resonance on the simulation, a frequency below 50 Hz was not selected. Based on the electrokinetic coseismic effect model, the normalized waveform of the EM wave at the surface (setting x = 3.5 km; y = 0 km; z = 0 km) was calculated, as shown in Figure 6a. By Fourier transforming the waveform, Figure 6b presents the corresponding frequency which varies from 0 Hz to 100 Hz. Referring to other researchers’ single-point source simulation method, the EM wave in Figure 6a was input into the Earth–ionosphere waveguide model at an altitude of 0 km, a longitude of 176°E and a latitude of 21°N to simulate the propagation process of the EM wave in the atmosphere and ionosphere. Thus, we obtained the simulation result of 20 (0 ≤ r ≤ 95 km) ×128 (−π/2 ≤ θ ≤ π/2) ×256 (−π ≤ φ ≤ π) cells on the three-dimensional sphere of the Earth with time varying from 0 to 0.4 s. The resolutions were Δr = 5, Δθ = π/128 and Δφ = 2π/256, and the time interval was 8.34 × 10−6 s.
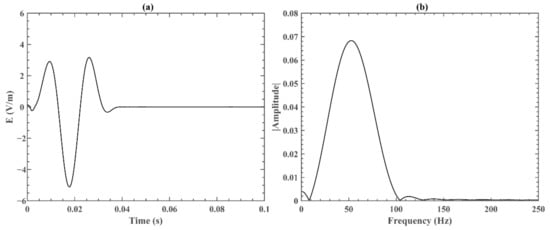
Figure 6.
The abnormal vertical ELF electric field induced by earthquake, as calculated by the electrokinetic effect model and then normalized: (a) the waveform of Ez in the time domain; and (b) the frequency spectrum of Ez.
Figure 7 demonstrates the three components of the electric field and the total electric field received at six positions of the FDTD grid on the Earth–ionosphere waveguide system, in which (a) corresponds to a longitude of 176°E, a latitude of 21°N and a height of 0 km; (b) corresponds to a longitude of 141°E, a latitude of 30°S and a height of 0 km; (c) corresponds to a longitude of 80°W, a latitude of 30°N and a height of 0 km; (d) corresponds to a longitude of 150°W, a latitude of 51°S and a height of 0 km; (e) corresponds to a longitude of 80°W, a latitude of 30°N and a height of 10 km; and (f) corresponds to a longitude of 80°W, a latitude of 30°N and a height of 50 km. Figure 7a–d present the variation of the electric field in four different positions at the height of 0 km and the results are contrastively analyzed. Figure 7a is the source position from which the earthquake-induced EM wave simulated by the electrokinetic effect model was imported into the Earth–ionosphere waveguide model. Figure 7c shows that the waveform is blank before 0.04 s, which is the same as the time required for the EM wave transmitting from the epicenter to the destination at the speed of light in the medium. The first and second waves appear between 0.04 s and 0.08 s and between 0.12 s and 0.16 s, which are spread from the shorter path and longer path between the two positions on the Earth’s surface, respectively. Furthermore, Figure 7 shows the 180 phase reversals of the electric field at the second wave, which is because the phase of the EM wave will jump by 90° When it propagates through the antipode, as proven by ref. [27,41]. Furthermore, after the wave propagates through the observation point and travels along an entire great circle, the third disturbance appears between 0.20 s and 0.23 s, which presents the bounce of the EM wave in the Earth–ionosphere waveguide. The time difference between the first wave and the third wave is approximately 0.155 s, which is uniform with the circumnavigation period of the EM wave. The results in Figure 7b,d are roughly the same as that in Figure 7c, while the second waves appear between 0.08 s and 0.11 s. The distinction is that a new wave appears between 0.13 s and 0.16 s, and the interpretation will be analyzed in detail below.
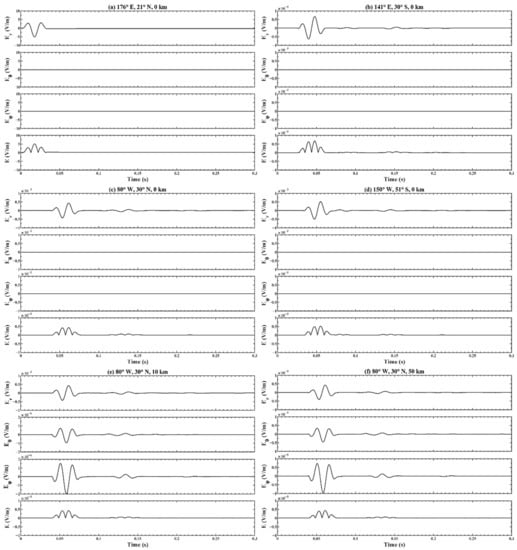
Figure 7.
Horizontal and vertical electric fields and total electric field received at six positions of the FDTD grid on the Earth–ionosphere waveguide model. The longitude, latitude and height were (a) (176°E, 21°N, 0 km); (b) (141°E, 30°S, 0 km); (c) (80°W, 30°N, 0 km); (d) (150°W, 51°S, 0 km); (e) (80°W, 30°N, 10 km); and (f) (80°W, 30°N, 50 km).
Figure 7c,e,f present the variation of the electric field in same position at heights of 0, 10 km and 50 km and the results are contrastively analyzed. The three subfigures all have three disturbances and compare the radial component of electric fields, and the waveforms and amplitudes at heights of 10 km and 50 km are analogous to those at the surface. The meridional and zonal electric fields at heights of 10 km and 50 km have similar waveforms and different amplitudes. Since the amplitude at the height of 50 km is greater than that at 10 km, this illustrates the process of the radial electric field being partially converted into the meridional and zonal electric fields.
As shown in Figure 8, the variation of the total electric field at different heights with time after fixing the longitude and latitude positions are plotted, where (a) corresponds to a longitude of 114°E and a latitude of 21°N; (b) corresponds to a longitude of 141°E and a latitude of 30°S; (c) corresponds to a longitude of 80°W and a latitude of 30°N; and (d) corresponds to a longitude of 150°W and a latitude of 51°S. Figure 8a–d present the variation of the electric field in four different positions with the height from 0 km to 95 km and the results were contrastively analyzed. The emergence time of the EM waves in subfigures c,d is slightly lagging behind because the distances between the positions (c) and (d) and the epicenter are farther than those of positions (a) and (b). Figure 8a,c show three waves which are consistent with the analysis in Figure 7c. As was the case for Figure 7b,d, the interpretation of Figure 8b,d will be analyzed in detail below. Figure 8 indicates that the electric fields significantly attenuate near the height of 60 km, which is influenced by the inflection point of the conductivity knee model and is coherent with the simulation results of [42].
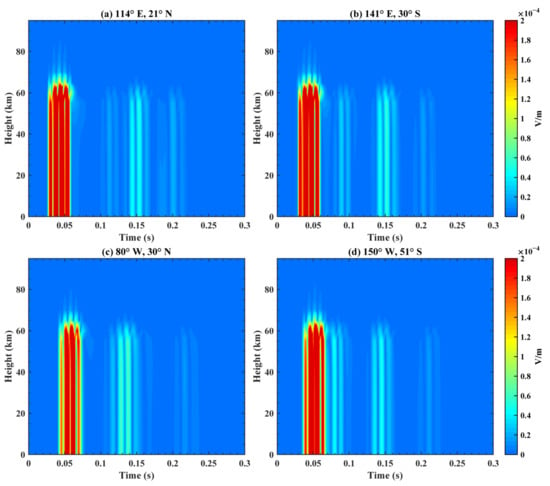
Figure 8.
Total electric field received at different heights with time on the Earth–ionosphere waveguide model. The longitude and latitude are (a) (114°E, 21°N); (b) (141°E, 30°S); (c) (80°W, 30°N); and (d) (150°W, 51°S).
Figure 9 presents the variation of the electric field at different longitudes with time after fixing heights and the latitude position, where (a) corresponds to a height of 30 km and a latitude of 20°S; and (b) corresponds to a height of 90 km and a latitude of 20°S. The EM wave firstly appears near a longitude of 176°E at 0.02 s and then diffuses and propagates towards the west and east, as shown in Figure 9. Then, it converges for the second time near a longitude of 176°E at 0.18 s and continues its propagation process. By comparative analysis of the subfigures in Figure 9, at different heights, the diffusion and propagation processes of the electric field are approximately the same, while the amplitudes at 30 km and 90 km have approximately three orders of magnitude in difference, which is coherent with the conclusion of rapid attenuation above 60 km in Figure 8. At 0.1 s, the amplitude of the EM wave has a slight rise that covers the entire longitude and the interpretation will be analyzed in detail below.
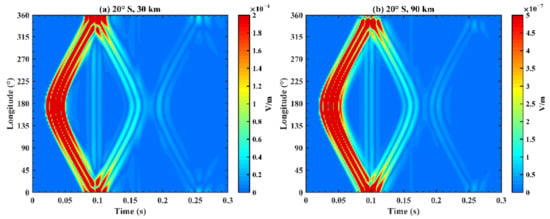
Figure 9.
Total electric field received at different longitudes with time on the Earth–ionosphere waveguide model. The latitude and height are (a) (20°S, 30 km) and (b) (20°S, 90 km).
Figure 10 illustrates the variation of the electric field at different latitudes with time after fixing heights and the longitude position, where (a) corresponds to a height of 20 km and a longitude of 155°E; and (b) corresponds to a height of 60 km and a longitude of 155°E. The EM wave first appears near a latitude of 21°N at 0.01 s, then arrives in the north and south poles at 0.03 s and 0.05 s, respectively. After reaching the north and south poles, the EM wave crosses the poles and appears at a longitude of 25°W (not shown in Figure 10). Meanwhile, waves from a longitude of 25°W appear at 0.05 s and 0.13 s in the north and south poles and converge near a latitude of 21°N at 0.18 s. After comparatively analyzing the subfigures in Figure 10, we found that the diffusion and propagation processes of the electric field are roughly similar at different heights, while the amplitude at 20 km and 60 km is approximately equal, which is coherent with the conclusion that the electric field does not attenuate below a height of 60 km in Figure 8.
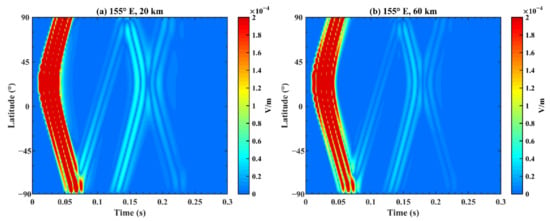
Figure 10.
Total electric field received at different latitudes with time on the Earth–ionosphere waveguide model. The longitude and height are (a) (155°E, 20 km) and (b) (155°E, 60 km).
Combining the distributions of the electric field at different longitudes and latitudes after fixing height and time in Figure 11, Figure 12 and Figure 13—where subfigures a–f correspond to different times and Figure 11, Figure 12 and Figure 13 correspond to different heights—we analyzed the transmission regularity of EM waves. As mentioned above, at the initial time, the simulation result of the electrokinetic coseismic effect model was imported into the Earth–ionosphere model as the source. Subgraphs a, b, c and d demonstrate that the EM waves diffuse around the epicenter and temporally gather at the antipode of the source (longitude 4°W, latitude 21°S) at 0.08 s, which agrees well with the simulation conclusions of other researchers [27,43]. There are circles with increasing and decreasing intensities because of the initial wave pattern. Subfigure e is analyzed in detail to explain Figure 7b,d and Figure 8b,d. At the time of 0.16 s, the EM wave finishes a great circle around the Earth at the speed of light. However, in contrast with the initial moment, the distribution of the EM wave is not only at the epicenter but also around its region, which elucidates the reason for which the additional disturbances exist between 0.13 s and 0.16 s, as shown in Figure 7b,d and Figure 8b,d. At the time of 0.1 s, the EM wave is propagating back to the epicenter from the antipode. Therefore, it leads to the slight increase in the EM wave’s amplitude that covers the entire longitude at the latitude of 20°S in Figure 9. In addition, subgraph f presents the simulation results of 0.32 s and that the distribution shape of EM waves changes after transmitting around the Earth twice. By investigating the subfigures in Figure 11 at different heights, the diffusion and propagation processes of the electric field are roughly analogous, while the amplitude decreases as height increases—which is coherent with the conclusion of Figure 8.
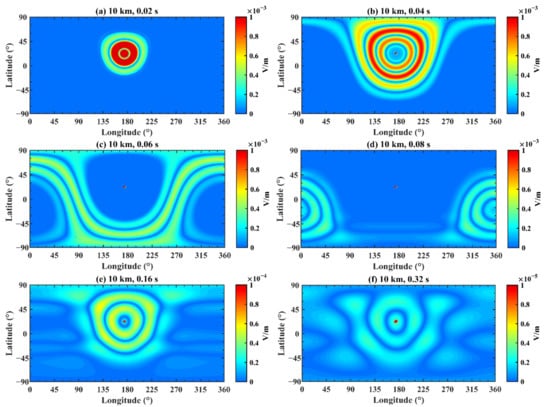
Figure 11.
The electric field distribution on the Earth–ionosphere waveguide model at 10 km. The time is (a) 0.02 s; (b) 0.04 s; (c) 0.06 s; (d) 0.08 s; (e) 0.16 s; and (f) 0.32 s.
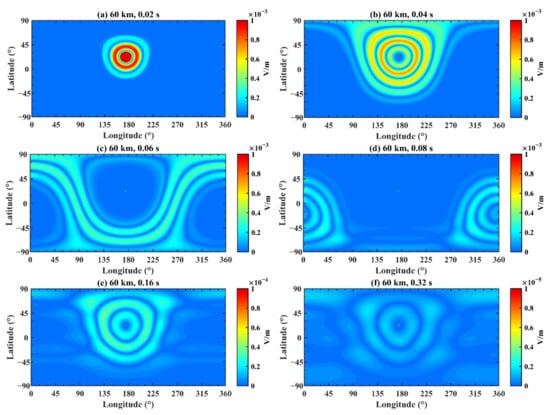
Figure 12.
Same as Figure 11, but for a height of 60 km.
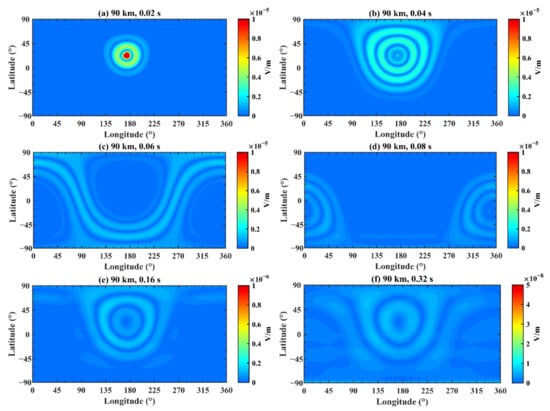
Figure 13.
Same as Figure 11, but for a height of 90 km.
Figure 14 illustrates the variation of the electric field at different latitudes and heights after fixing the time and longitude position, where (a) corresponds to a time of 0.02 s and a longitude of 176°E; (b) corresponds to a time of 0.04 s and a longitude of 176°E; and (c) corresponds to a time of 0.20 s and a longitude of 176°E. At 0.02 s, the disturbance appears near 21°N, and then the EM wave propagates towards the north and south poles. In terms of height, Figure 14 presents an obvious attenuation of the electric field at 60 km, and the propagation range increases at 0.04 s. After transmitting around the Earth, the EM wave converges at the epicenter region again, as shown in Figure 14c.
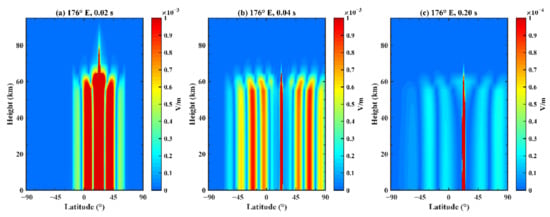
Figure 14.
Total electric field received at different latitudes and heights on the Earth–ionosphere waveguide model. The longitude and time are (a) (176°E, 0.02 s); (b) (176°E, 0.04 s); and (c) (176°E, 0.20 s).
Figure 15 demonstrates the variation of the electric field at different longitudes and heights after fixing the time and latitude position, where (a) corresponds to a time of 0.02 s and a latitude of 21°N; (b) corresponds to a time of 0.04 s and a latitude of 21°N; (c) corresponds to a time of 0.06 s and a latitude of 21°N; and (d) corresponds to a time of 0.20 s and a latitude of 21°N. At 0.02 s near the initial time, the disturbance appears at approximately 176°E, and the EM wave propagates towards the west and east. In terms of height, Figure 15 shows an obvious attenuation of the electric field at 60 km and the propagation range increases at 0.04 s and 0.06 s. At 0.20 s, the EM wave transmits back to the epicenter region, therefore amplitudes around the epicenter region have large values.
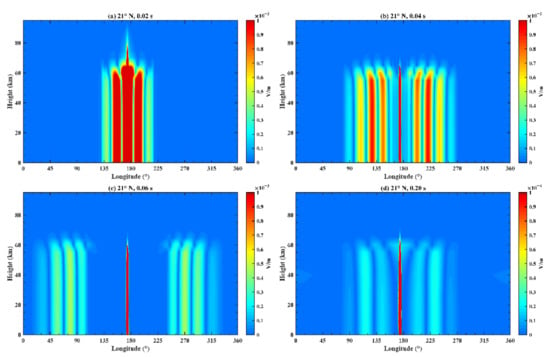
Figure 15.
The total electric field received at different longitudes and heights on the Earth–ionosphere waveguide model. The latitude and time are (a) (21°N, 0.02 s); (b) (21°N, 0.04 s); (c) (21°N, 0.06 s); and (d) (21°N, 0.20 s).
4.2. Case 2
The Earth conductivity model has a two-exponential profile, and the EM wave is located in one cell, whose initial center frequency is 50 Hz and whose duration time is 0.04 s. The EM wave in Figure 6a is input to the Earth–ionosphere waveguide model at the altitude of 0 km, longitude of 176°E and latitude of 21°N.
Figure 16 demonstrates the variation of the electric field at different longitudes and latitudes after fixing the times and altitude, where (a) corresponds to a time of 0.02 s and an altitude of 60 km; (b) corresponds to a time of 0.04 s and an altitude of 60 km; (c) corresponds to a time of 0.06 s and an altitude of 60 km; (d) corresponds to a time of 0.08 s and an altitude of 60 km; (e) corresponds to a time of 0.16 s and an altitude of 60 km; and (f) corresponds to a time of 0.32 s and an altitude of 60 km. Combining Figure 12 and Figure 16, it is obvious that the propagation results are similar while the amplitudes vary by several times because of the discrepancy of the conductivity profiles.
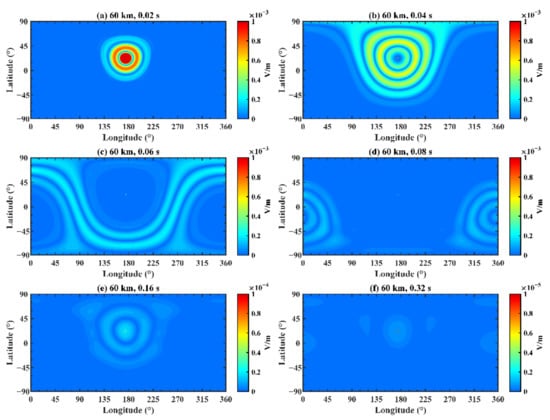
Figure 16.
The electric field distribution on the Earth–ionosphere waveguide model at 60 km. The time is (a) 0.02 s; (b) 0.04 s; (c) 0.06 s; (d) 0.08 s; (e) 0.16 s; and (f) 0.32 s.
4.3. Case 3
The Earth conductivity model is in knee profile, and the EM wave is located in several cells whose initial center frequency is 50 Hz and whose duration time is 0.04 s. We modified the Earth–ionosphere waveguide model in Section 3, including by dividing the radial grid into 5, the meridional grid into 1280, the zonal grid into 640 and selecting an appropriate time step to meet the stability conditions of the model. The EM wave was input into the Earth–ionosphere waveguide model at the altitude of 0 km, longitude of 174.3–177.1°E and latitude of 19.3–22.1°N. Since the range of the electrokinetic effect model on the surface is 160 km × 160 km and the resolution of the Earth–ionosphere model is approximately 30 km × 30 km, the simulation result of electrokinetic effect is constituted of 5 × 5 grids. At every grid, the ELF electric field results are similar to those in Figure 6a. Based on the electrokinetic coseismic effect model, the EM wave at the surface (x = −80 km–80 km, y = −80 km–80 km, z = 0 km) is calculated and the result at initial time is shown in Figure 17. Thus, we obtain the simulation result of 5 (0 ≤ r ≤ 80 km) × 640 (−π/2 ≤ θ ≤ π/2) × 1280 (−π ≤ φ ≤ π) cells on the three-dimensional sphere of the Earth with time varying from 0 s to 0.4 s. The resolutions are Δr = 20, Δθ = π/640 and Δφ = 2π/1280.
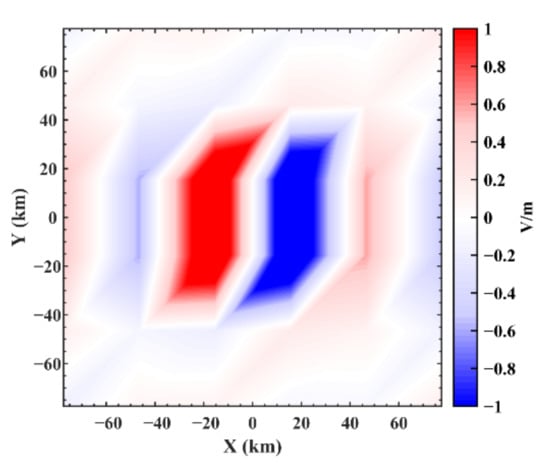
Figure 17.
The seismic electric field distribution on the Earth’s surface at the initial time which is calculated by the electrokinetic coseismic effect model and then normalized.
Figure 18 demonstrates the variation of the electric field at different longitudes and latitudes after fixing the times and altitude. Comparing Figure 12 and Figure 18, in terms of overall morphology, the global distributions of EM waves in two cases are roughly analogous. Nevertheless, it is conspicuous that the details in Figure 18 are more abundant and can reveal the propagation approach of EM waves, although the corresponding calculations are also greatly increased. Furthermore, in some local areas, EM waves have different distribution shapes in two cases because of the increase in data around the epicenter region at the initial time.
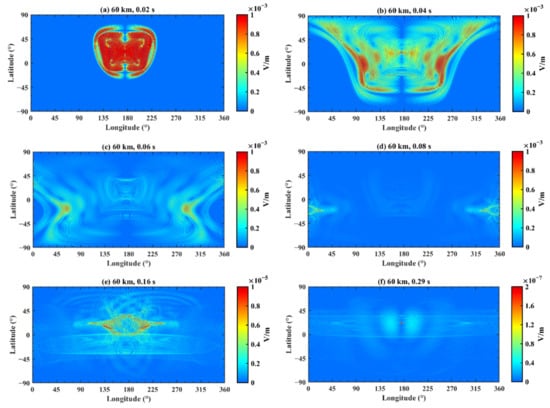
Figure 18.
The electric field distribution on the Earth–ionosphere waveguide model at 60 km. The time is (a) 0.02 s; (b) 0.04 s; (c) 0.06 s; (d) 0.08 s; (e) 0.16 s; and (f) 0.29 s.
4.4. Case 4
The Earth conductivity model is in knee profile, and the EM wave is located in one cell, whose initial center frequency is 3 Hz and whose duration time is 1 s. The reason for choosing 3 Hz is that the frequency of a natural earthquake ranges from 1.25 Hz to 10 Hz. As mentioned above, it takes an EM wave 0.155 s to circle the Earth in the model. Therefore, it is difficult to discern the periodic propagation regulation of the EM wave from the simulation results due to a natural earthquake’s long duration. As shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, the periodic propagation regulation of the EM wave is obvious because its focal duration is far less than 0.16 s. Figure 19 is the same as Figure 6 but for a new EM wave result after altering the center frequency and pulse duration of the acoustic source function at the seismic source. The EM wave in Figure 19a was input into the Earth–ionosphere waveguide model at the altitude of 0 km, longitude of 176°E and latitude of 21°N. The variation of the electric field at different altitudes with time after fixing the longitude and latitude positions is plotted in Figure 20. In the first second, the imported electric field from the epicenter propagates to the whole Earth. Additionally, the electric field’s amplitude gradually attenuates. In accordance with Figure 8, the amplitude rapidly decreases above 60 km, and its maximum height gradually decreases with time. Figure 21 illustrates the variation of the electric field at different longitudes and latitudes after fixing the times and altitude, in which the altitude is 60 km, and subgraphs a, b, c and d correspond to the times of 0.2 s, 0.4 s, 0.6 s and 1.2 s, respectively. In the first second, the distribution regularities of EM waves of Figure 20a–c resemble those in the previous figures because of the input electric field from the epicenter. Afterwards, Figure 20d shows that the eventual global distribution of the EM field will gradually become uniform.
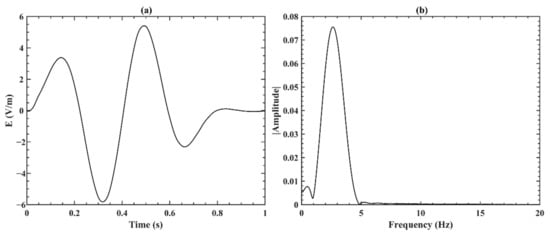
Figure 19.
Same as Figure 6, but for the EM wave with new parameters of center frequency and duration time.
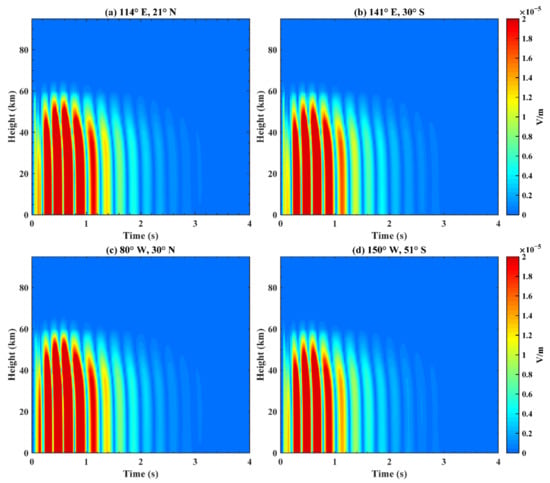
Figure 20.
Total electric field received at different heights with time on the Earth–ionosphere waveguide model. The longitude and latitude are (a) (114°E, 21°N); (b) (141°E, 30°S); (c) (80°W, 30°N); and (d) (150°W, 51°S).
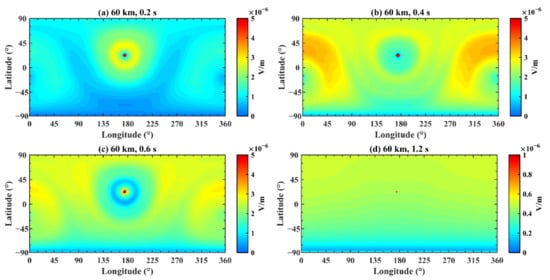
Figure 21.
The electric field distribution on the Earth–ionosphere waveguide model at 60 km. The time is (a) 0.2 s; (b) 0.4 s; (c) 0.6 s; and (d) 1.2 s.
5. Discussions
By means of theoretical analysis and numerical simulation, the global propagation process of ELF electromagnetic waves generated by electromagnetic radiation in the lithosphere, atmosphere and ionosphere during the coseismic period was systematically investigated in this paper. By establishing the model of EM wave propagation across multiple circles, the qualitative and quantitative simulation of coseismic ELF electromagnetic radiation was preliminarily realized. The numerical model adopted in the lithosphere is based on the electrokinetic coseismic effect, and the numerical model applied in the atmosphere and the bottom of ionosphere is based on the Earth–ionosphere waveguide system. Meanwhile, the two models were coupled at the surface by boundary conditions. The results present that it takes the EM wave 0.155 s to circle the Earth in our model, and that this time and the spatial distribution of the EM wave vary in different simulation models. For example, when changing the conductivity, porous media and considering the existence of ocean and plasma, the time distribution and spatial distribution of simulation results will be different, which can be addressed in future works.
We can further update the numerical model by combining the ground-based and space-based observation results of ELF electromagnetic fields in the lithosphere, atmosphere and ionosphere, so as to make the simulation results more consistent with real situations and provide a reliable reference for related research. Considerable observations of the ELF electric field were reported which can be utilized to confirm the amplitude of ELF electric fields in the lithosphere, atmosphere and ionosphere. Ref. [44] mentioned that solar activity, galactic cosmic ray modulation and modulated short-wavelength radiation are accompanied with ELF Ez disturbances of 10−3–1 V/m. They developed a fluxmeter to monitor the weak Ez oscillation in the ELF range at heights of 1 m and 3 m and observations showed that the amplitude of the ELF atmospheric vertical electric field is approximately tens of mV/m under normal conditions. ELF data recorded by two observatory stations in Israel and Hungary during thunderstorms were investigated, and using vertical electric ball antennas for receiving Er, ref. [45] detected the ELF vertical electric field results with amplitudes of tens of mV/m. The vertical DC atmospheric electric field is approximately 102 V/m under fair weather conditions, but will increase to 104 V/m during thunderstorms, and increase to 103 V/m before and after earthquakes [46]. Therefore, it is reasonably speculated that the amplitude of an atmospheric ELF vertical electric field will also significantly increase before and after an earthquake. However, observational evidence to confirm the increase in ELF atmospheric electric field caused by earthquake is still lacking, let alone its specific amplitude. In addition, ref. [5,47,48] investigated different physical phenomena by analyzing Demeter satellite data, respectively, and their results imply that the amplitude of an ELF electric field at an altitude of 660 km is approximately 10μV/m under normal conditions.
In this paper, we simulated the global propagation characteristics of the coseismic ELF electromagnetic wave in the Earth–ionosphere cavity by virtue of the waveform of the lithosphere electrokinetic coseismic effect model on the Earth’s surface. As presented in Figure 11, Figure 12 and Figure 13, the amplitude of the electric field simulated by the Earth–ionosphere waveguide model attenuates by approximately 2–3 orders of magnitude when the ELF wave at the surface propagates to the bottom of the ionosphere, and by approximately 4–5 orders of magnitude when it propagates to a height of 90 km. ELF observation data in the low ionosphere are relatively scarce and cannot be quantitatively compared with the model simulation results, but the decreasing trend of the ELF electric field is consistent with the model results.
Other researchers have also contributed to the numerical simulation of electromagnetic radiation. Utilizing topographic and bathymetric data from the NOAA-NGDC “Global Relief CD-ROM”, a conceptual model of the lithosphere conductivity profile, atmosphere day- and nighttime exponential conductivity profiles, ref. [49] proposed a rigorous 3-D computational solution to the full-vector Maxwell equations for hypothesized pre-seismic EM phenomena propagated within the entire Earth–ionosphere cavity. Furthermore, they simulated electrokinetic currents near the hypocenter of the Loma Prieta earthquake and presented the calculated surface H-field. Furthermore, ref. [50] extended the model in the lithosphere, atmosphere and ionosphere and analyzed ionospheric anomalies during or prior to the earthquakes. Our model and the model in ref. [49] both employ an electrokinetic model as the source of the ELF EM wave. The difference is that they utilized a Biot–Savart model to calculate the EM wave while we adopted Pride’s governing equations of acoustic-electromagnetic coupling in porous media. Additionally, ref. [49] did not present simulation results for the atmosphere. In addition, ref. [49] and [50] did not analyze the global distribution of EM fields because they mainly focused on the frequency distribution of the modeling results. Ref. [42] simulated the Earth–ionosphere system model utilizing a three-dimensional FDTD algorithm and Maxwell equations on the neutral medium, whose excitation sources are Gaussian pulse current sources on the Earth’s surface. They analyzed the distribution of ELF EM fields in a local area and their simulation results of the propagation process in atmosphere and ionosphere were consistent with ours. Moreover, ref. [51] did theoretical calculations on EM fields in the frequency range of 10−2 Hz–102 Hz induced by stochastic micro-current activity inside the seismic sources in the lithosphere, atmosphere and ionosphere. They presented the dependence of radial distance on the ground for the radial and azimuthal current source and their attenuation trends of electric field and magnetic field components with distance were consistent with our simulation results.
However, the simulation of electromagnetic radiation in the lithosphere, atmosphere and ionosphere is complicated work. The multi-layer coupling model in this paper was not sufficiently established, and the current research results are only preliminary. On the one hand, the formation principle of seismic electromagnetic radiation in the lithosphere is still not comprehensive and thorough. In this paper, we adopted the electrokinetic coseismic effect as the formation mechanism of earthquake-induced EM waves in the lithosphere; however, it is only one of the credible theories attempting to elucidate the EM radiation. Other possible theories include the piezoelectric effect, motion of charged edge dislocations (MCD) [52] and stress-induced electromagnetic emissions. In addition, the electrokinetic effect is insufficient to explain the abnormal phenomena of ULF, ELF and VLF observed by researchers before earthquakes and the pre-earthquake seismic EM radiation mechanism has not yet formed a convincing simulation model. The physical mechanism of seismic electromagnetic radiation in the lithosphere still requires further research. Therefore, the electrokinetic coseismic effect model in the lithosphere can be substituted when a reliable numerical model of pre-earthquake seismic electromagnetic radiation is implemented. On the other hand, although the Earth–ionosphere waveguide model established in this paper fulfills the basic requirements of EM wave simulation, it does not embody the realistic characteristics of the ionosphere. We expect that further optimizations can be realized, including by adopting a realistic ionosphere conductivity tensor and introducing interaction between EM waves and plasma.
6. Conclusions
In our study, we aimed to combine the underground electrokinetic coseismic effect model and the Earth–ionosphere waveguide model to investigate the global propagation characteristics of ELF EM waves generated by earthquakes. This proposed ELF EM wave propagation model of lithosphere–atmosphere–ionosphere coupling is very promising for the explanation of abnormal disturbances of ground-based and space-based observation results of ELF EM fields which are associated with earthquakes.
Our principal conclusions are as follows:
- The coseismic EM wave with a frequency of 50 Hz and a duration of 0.04 s is simulated in multiple layers, and the modeling results indicate that it takes approximately 0.155 s to circle the Earth under the influence of the phase delay of the conductivity profiles. When the electromagnetic wave reaches heights of 60 km and 90 km, its amplitude rapidly decreases by approximately 2–3 and 4–5 orders of magnitude, respectively. The electromagnetic field distributions are roughly similar across all altitudes and initially are uncomplicated but later on become irregular.
- The Earth’s conductivity parameter dramatically influences the simulation and leads to several times of difference in the amplitude of the EM wave. Therefore, we can update the model by applying a more sophisticated and realistic conductivity model.
- The simulation results of the blasting earthquake with a short duration (0.04 s) present the periodic propagation regulation of the EM wave, which provides references for the propagation regulation of a natural earthquake of long duration (1 s).
- The electrokinetic coseismic effect model generates a one-dimensional or two-dimensional distribution of EM waves on the surface of the Earth and is coupled with the Earth–ionosphere waveguide model through boundary conditions. Although the computation is larger if the initial source on the Earth’s surface is two-dimensional, the simulation results present more details.
Author Contributions
Conceptualization, C.Z. and S.Z.; methodology, Z.W. and C.Z.; investigation, Z.W.; validation, S.Z., X.X., M.L. and L.L.; formal analysis, Y.L.; resources, C.Z.; visualization, Z.W. and Y.L.; funding acquisition, X.S. and C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (No. 41574146, 41774162, 42074187), the National Key R&D Program of China (No. 2018YFC1503506), Excellent Youth Foundation of Hubei Provincial Natural Science Foundation (No. 2019CFA054), the foundation of National Key Laboratory of Electromagnetic Environment (No. 6142403180204, 20200101), National Institute of Natural Hazards, Ministry of Emergency Management of China (Grant No. ZDJ2020-06) and the China Research Institute of Radiowave Propagation (research on low ionosphere satellite detection and research on the coupling mechanism of lithosphere-atmosphere-ionosphere alternating electric fields).
Data Availability Statement
The data underlying this article will be shared on reasonable request to the corresponding author.
Acknowledgments
We appreciate the editors and the anonymous reviewers for their insightful comments and suggestions to improve this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Leonard, R.S.; Barnes, R.A. Observation of ionospheric disturbances following the Alaska earthquake. J. Geophys. Res. 1965, 70, 1250–1253. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chuo, Y.J.; Shan, S.J.; Tsai, Y.B.; Chen, Y.I.; Pulinets, S.A.; Yu, S.B. Pre-earthquake ionospheric anomalies registered by continuous GPS TEC measurements. Ann. Geophys. 2004, 22, 1585–1593. [Google Scholar] [CrossRef]
- Zhao, B.Q.; Wang, M.; Yu, T.; Wan, W.X.; Lei, J.H.; Liu, L.B.; Ning, B.Q. Is an unusual large enhancement of ionospheric electron density linked with the 2008 great Wenchuan earthquake. J. Geophys. Res. Space Phys. 2008, 113, A11304. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, C.H.; Sun, Y.Y.; Chen, C.H.; Tsai, H.F.; Yen, H.Y.; Chun, J.; Lastovicka, J.; Yang, Q.S.; Chen, W.S.; et al. The vertical propagation of disturbances triggered by seismic waves of the 11 March 2011 M9.0 Tohoku earthquake over Taiwan. Geophys. Res. Lett. 2016, 43, 1759–1765. [Google Scholar] [CrossRef]
- Zhang, X.; Zeren, Z.; Parrot, M.; Battiston, R.; Qian, J.; Shen, X. ULF/ELF ionospheric electric field and plasma perturbations related to Chile earthquakes. Adv. Space Res. 2011, 47, 991–1000. [Google Scholar] [CrossRef]
- Freund, F. Time-resolved study of charge generation and propagation in igneous rocks. J. Geophys. Res. Solid Earth. 2000, 105, 11001–11019. [Google Scholar] [CrossRef]
- Scoville, J.; Sornette, J.; Freund, F. Paradox of peroxy defects and positive holes in rocks Part II: Outflow of electric currents from stressed rocks. J. Asian Earth Sci. 2015, 114, 338–351. [Google Scholar] [CrossRef]
- Shalimov, S.L. Lithosphere-ionosphere relationship—A new way to predict earthquakes. Episodes 1992, 15, 252–254. [Google Scholar] [CrossRef]
- Pride, S. Governing equations for the coupled electromagnetics and acoustics of porous media. Phys. Rev. B. 1994, 50, 15678–15696. [Google Scholar] [CrossRef]
- Gao, Y.X.; Wang, D.D.; Yao, C.; Guan, W.; Hu, H.S.; Wen, J.; Zhang, W.; Tong, P.; Yang, Q.J. Simulation of seismoelectric waves using finite-difference frequency-domain method: 2-D SHTE mode. Geophys. J. Int. 2019, 216, 414–438. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, Y.; Zhao, S.F.; Liu, J.; Zhang, X.M.; Huang, J.P.; Shen, X.H.; Ni, B.B.; Zhao, Z.Y. An electric field penetration model for seismo-ionospheric research. Adv. Space Res. 2017, 60, 2217–2232. [Google Scholar] [CrossRef]
- Inchin, P.A.; Snively, J.B.; Zettergren, M.D.; Komjathy, A.; Verkhoglyadova, O.P.; Ram, S.T. Modeling of Ionospheric Responses to Atmospheric Acoustic and Gravity Waves Driven by the 2015 Nepal 7.8 Gorkha Earthquake. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027200. [Google Scholar] [CrossRef]
- Matsushima, M. Seismo-electromagnetic effect associated with the Izmit earthquake and its aftershocks. Bull. Seismol. Soc. Am. 2002, 92, 350–360. [Google Scholar] [CrossRef]
- Liu, J.Y.; Wang, K.; Chen, C.H.; Yang, W.H.; Yen, Y.H.; Chen, Y.I.; Hatorri, K.; Su, H.T.; Hsu, R.R.; Chang, C.H. A statistical study on ELF-whistlers/emissions and M≥5.0 earthquakes in Taiwan. J. Geophys. Res. Atmos. 2013, 118, 3760–3768. [Google Scholar] [CrossRef]
- Hayakawa, M.; Ohta, K.; Nickolaenko, A.P.; Ando, Y. Anomalous effect in Schumann resonance phenomena observed in Japan, possibly associated with the Chi-chi earthquake in Taiwan. Ann. Geophys. 2005, 23, 1335–1346. [Google Scholar] [CrossRef]
- Molchanov, O.A. Observation by the Intercosmos-24 satellite of ELF-VLF electromagnetic emissions associated with earthquakes. Ann. Geophys. 1993, 11, 431–440. [Google Scholar]
- Ohta, K.; Izutsu, J.; Schekotov, A.; Hayakawa, M. The ULF/ELF electromagnetic radiation before the 11 March 2011 Japanese earthquake. Radio Sci. 2013, 48, 589–596. [Google Scholar] [CrossRef]
- Thompson, A.H.; Gist, G.A. Geophysical applications of electrokinetic conversion. Lead. Edge. 1993, 12, 1169–1173. [Google Scholar] [CrossRef]
- Fan, Y.; Tang, J.; Han, B.; Cui, T.F.; Xu, Q. The background variation of natural source ELF and its EM abnormal phenomena in Yunnan earthquakes. Earthq. Res. China. 2018, 32, 135–145. [Google Scholar]
- Martner, S.T.; Sparks, N.R. The electroseismic effect. Geophysics 1959, 24, 297–308. [Google Scholar] [CrossRef]
- Nagao, T.; Orihara, Y.; Yamaguchi, T.; Takahashi, I.; Hattori, K.; Noda, Y.; Sayanagi, K.; Uyeda, S. Co-seismic geoelectric potential changes observed in Japan. Geophys. Res. Lett. 2000, 27, 1535–1538. [Google Scholar] [CrossRef]
- Pride, S.R.; Haartsen, M.W. Electroseismic wave properties. J. Acoust. Soc. Am. 1996, 100, 1301–1315. [Google Scholar] [CrossRef]
- Haines, S.S.; Pride, S.R.; Klemperer, S.L.; Biondi, B. Seismoelectric imaging of shallow targets. Geophysics 2007, 72, G9–G20. [Google Scholar] [CrossRef]
- Gao, Y.X.; Hu, H.S. Seismoelectromagnetic waves radiated by a double couple source in a saturated porous medium. Geophys. J. Int. 2010, 181, 873–896. [Google Scholar] [CrossRef]
- Yee, K.S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, AP-14, 302–307. [Google Scholar]
- Holland, R. THREDS: A finite-difference time-domain EMP code in 3D spherical coordinates. IEEE Trans. Nucl. Sci. 1983, 30, 4592–4595. [Google Scholar] [CrossRef]
- Simpson, J.J.; Taflove, A. Two-dimensional FDTD model of antipodal ELF propagation and Schumann resonance of the Earth. IEEE Antennas Wirel. Propag. Lett. 2002, 1, 53–56. [Google Scholar] [CrossRef]
- Simpson, J.J.; Taflove, A. Three-dimensional FDTD modeling of impulsive ELF propagation about the Earth-sphere. IEEE Trans. Antennas Propag. 2004, 52, 443–451. [Google Scholar] [CrossRef]
- Shaw, D.J. Introduction to Colloid and Surface Chemistry, 4th ed.; Butterworth-Heinemann: London, UK, 1992; pp. 174–188. [Google Scholar]
- Zhu, Z.; Toksoz, M.N.; Burns, D.R. Electroseismic and seismoelectric measurements of rock samples in a water tank. Geophysics 2008, 73, E153–E164. [Google Scholar] [CrossRef]
- Gao, Y.X.; Wang, M.Q.; Hu, H.S.; Chen, X.F. Seismoelectric responses to an explosive source in a fluid above a fluid-saturated porous medium. J. Geophys. Res. Solid Earth 2017, 122, 7190–7218. [Google Scholar] [CrossRef]
- Wait, J.R. Distortion of an ELF pulse after propagation through an antipode. J. Geophys. Res. Space Phys. 1969, 74, 2982–2986. [Google Scholar] [CrossRef]
- Greifinger, C.; Greifinger, P. Approximate method for determining ELF eigenvalues in the Earth-ionosphere waveguide. Radio Sci. 1978, 13, 831–837. [Google Scholar] [CrossRef]
- Barr, R. ELF radiation from the New Zealand power system. Planet. Space Sci. 1979, 27, 537–540. [Google Scholar] [CrossRef]
- Simpson, J.J. Global FDTD Maxwell’s Equations Modeling of Electromagnetic Propagation from Currents in the Lithosphere. IEEE Trans. Antennas Propag. 2008, 56, 199–203. [Google Scholar] [CrossRef]
- Cole, R.K. The Schumann resonances. J. Res. Natl. Bur. Stand. Sect. D. 1965, 69, 1345–1349. [Google Scholar] [CrossRef]
- Mushtak, V.C.; Williams, E.R. ELF propagation parameters for uniform models of the Earth–ionosphere waveguide. J. Atmos. Sol.-Terr. Phys. 2002, 64, 1989–2001. [Google Scholar] [CrossRef]
- Qian, Q.H.; Chen, S.H. Blasting Vibration Effect. Blasting 2004, 21, 1–5. (In Chinese) [Google Scholar]
- Bohnhoff, M.; Dresen, G.; Ellsworth, W.L.; Ito, H. Passive seismic monitoring of natural and induced earthquakes: Case studies, future directions and socio-economic relevance. In New Frontiers in Integrated Solid Earth Sciences, 1st ed.; Sierd, C., Jörg, N., Eds.; Springer: Amsterdam, The Netherlands, 2009; Volume 1, pp. 261–285. [Google Scholar]
- Zhang, Z.C.; Chen, Y.M.; Liu, H.L. Numerical analysis and evaluation of simulation of nature earthquake by millisecond blasting technique. Rock Soil Mech. 2013, 34, 265–274. (In Chinese) [Google Scholar]
- Simpson, J.J.; Taflove, A. Efficient modeling of impulsive ELF antipodal propagation about the Earth sphere using an optimized two-dimensional geodesic FDTD grid. IEEE Antennas Wirel. Propag. Lett. 2004, 3, 215–218. [Google Scholar] [CrossRef][Green Version]
- Qu, X.; Xue, B.; Fang, G. The propagation model and characteristics for extremely low frequency electromagnetic wave in Earth-ionosphere system and its application in geophysics prospecting. J. Electromagn. Waves Appl. 2018, 32, 319–331. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, H.; Cao, Q. Analysis of ELF propagation along the Earth surface using the FDTD model based on the spherical triangle meshing. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 1017–1020. [Google Scholar] [CrossRef]
- Boldyrev, A.I.; Vyazilov, A.E.; Ivanov, V.N.; Kemaev, R.V.; Korovin, V.Y.; Melyashinskii, A.V.; Pamukhin, K.V.; Panov, V.N.; Shvyrev, Y.N. Registration of weak ULF/ELF oscillations of the surface electric field strength. Geomagn. Aeron. 2016, 56, 503–512. [Google Scholar] [CrossRef]
- Greenberg, E.; Price, C.; Yair, Y.; Ganot, M.; Bór, J.; Sátori, G. ELF transients associated with sprites and elves in eastern Mediterranean winter thunderstorms. J. Atmos. Sol.-Terr. Phys. 2007, 69, 1569–1586. [Google Scholar] [CrossRef]
- Choudhury, A.; Guha, A.; De, B.K.; Roy, R. A statistical study on precursory effects of earthquakes observed through the atmospheric vertical electric field in northeast India. Ann. Geophys. 2013, 56, 1861–1867. [Google Scholar]
- Blecki, J.; Parrot, M.; Wronowski, R. ELF and VLF signatures of sprites registered onboard the low altitude satellite DEMETER. Ann. Geophys. 2009, 27, 2599–2605. [Google Scholar] [CrossRef][Green Version]
- Nemec, F.; Santolik, O.; Hospodarsky, G.; Hajos, M.; Demekhov, A.; Kurth, W.; Parrot, M.; Hartley, D. Whistler mode quasiperiodic emissions: Contrasting Van Allen Probes and DEMETER occurrence rates. J. Geophys. Res. Space Phys. 2020, 125. [Google Scholar] [CrossRef]
- Simpson, J.J.; Taflove, A. Electrokinetic effect of the Loma Prieta earthquake calculated by an entire-Earth FDTD solution of Maxwell’s equations. Geophys. Res. Lett. 2005, 32, L09302. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Q. Analysis of seismic electromagnetic phenomena using the FDTD method. IEEE Trans. Antennas Propag. 2011, 59, 4171–4180. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Hayakawa, M.; Rafalsky, V.A. Penetration characteristics of electromagnetic emissions from an underground seismic source into the atmosphere, ionosphere, and magnetosphere. J. Geophys. Res. 1995, 100, 1691–1712. [Google Scholar] [CrossRef]
- Venegas-Aravena, P.; Cordaro, E.G.; Laroze, D. A review and upgrade of the Lithospheric dynamics in context of the Seismo-electromagnetic Theory. Nat. Hazards Earth Syst. Sci. 2019, 19, 1639–1651. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).