Prediction Potential of Remote Sensing-Related Variables in the Topsoil Organic Carbon Density of Liaohekou Coastal Wetlands, Northeast China
Abstract
:1. Introduction
- (1)
- To construct the best model for predicting topsoil SOC density of coastal wetlands based on 193 sample data and 9 environmental variables;
- (2)
- To discuss the importance of using remote sensing data in predicting topsoil SOC density of coastal wetlands;
- (3)
- To analyze the uncertainty of our method and results.
2. Materials and Methods
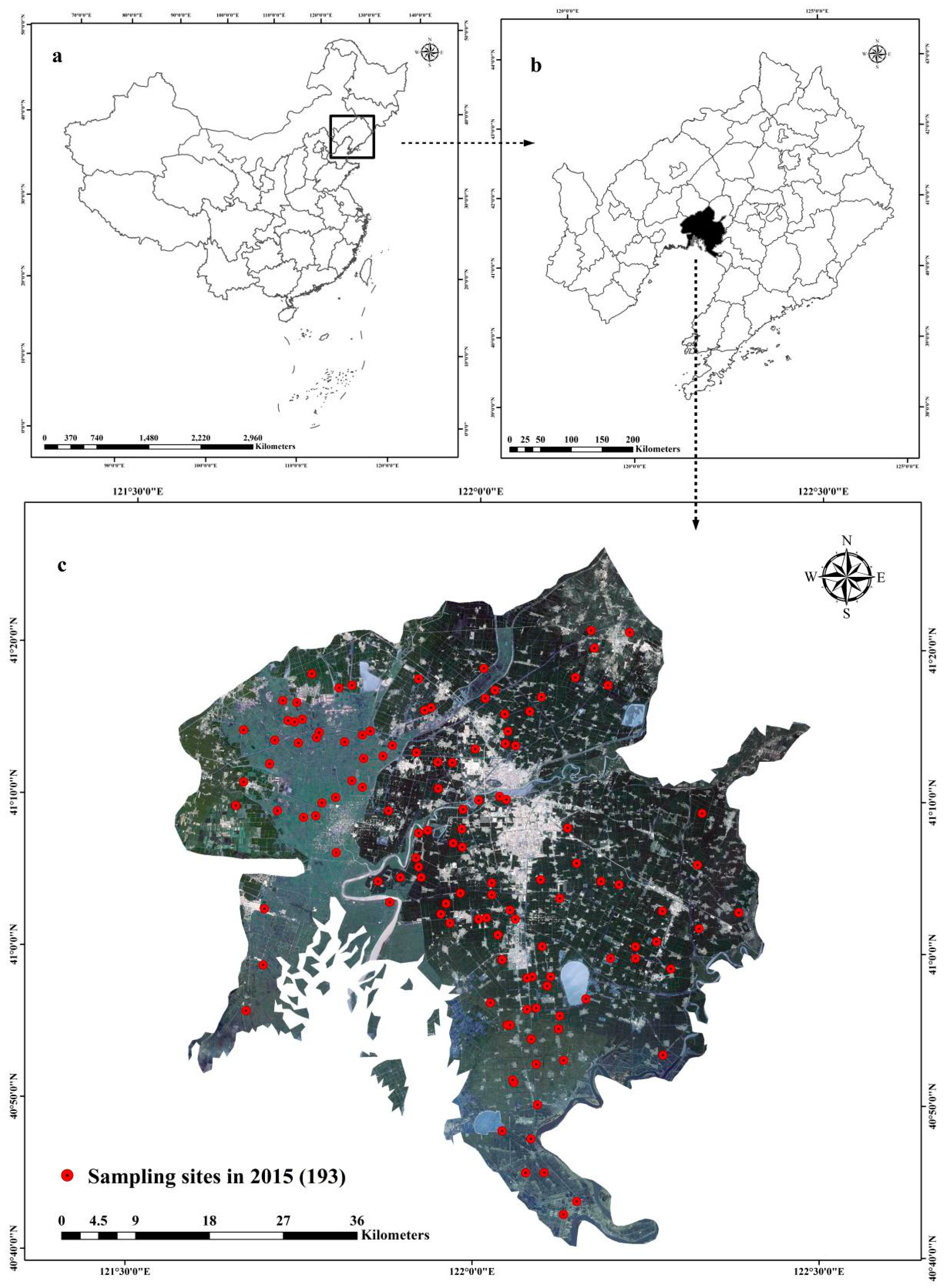
2.1. Description of the Study Area
2.2. Soil Sampling and Laboratory Analysis
2.3. Calculation of SOC Density
2.4. Environmental Variables
2.4.1. Remote Sensing Related Variables
2.4.2. Topographic Variables
2.4.3. Climatic Variables
2.5. Prediction Model
2.6. Model Validation
3. Results
3.1. Descriptive Statistics
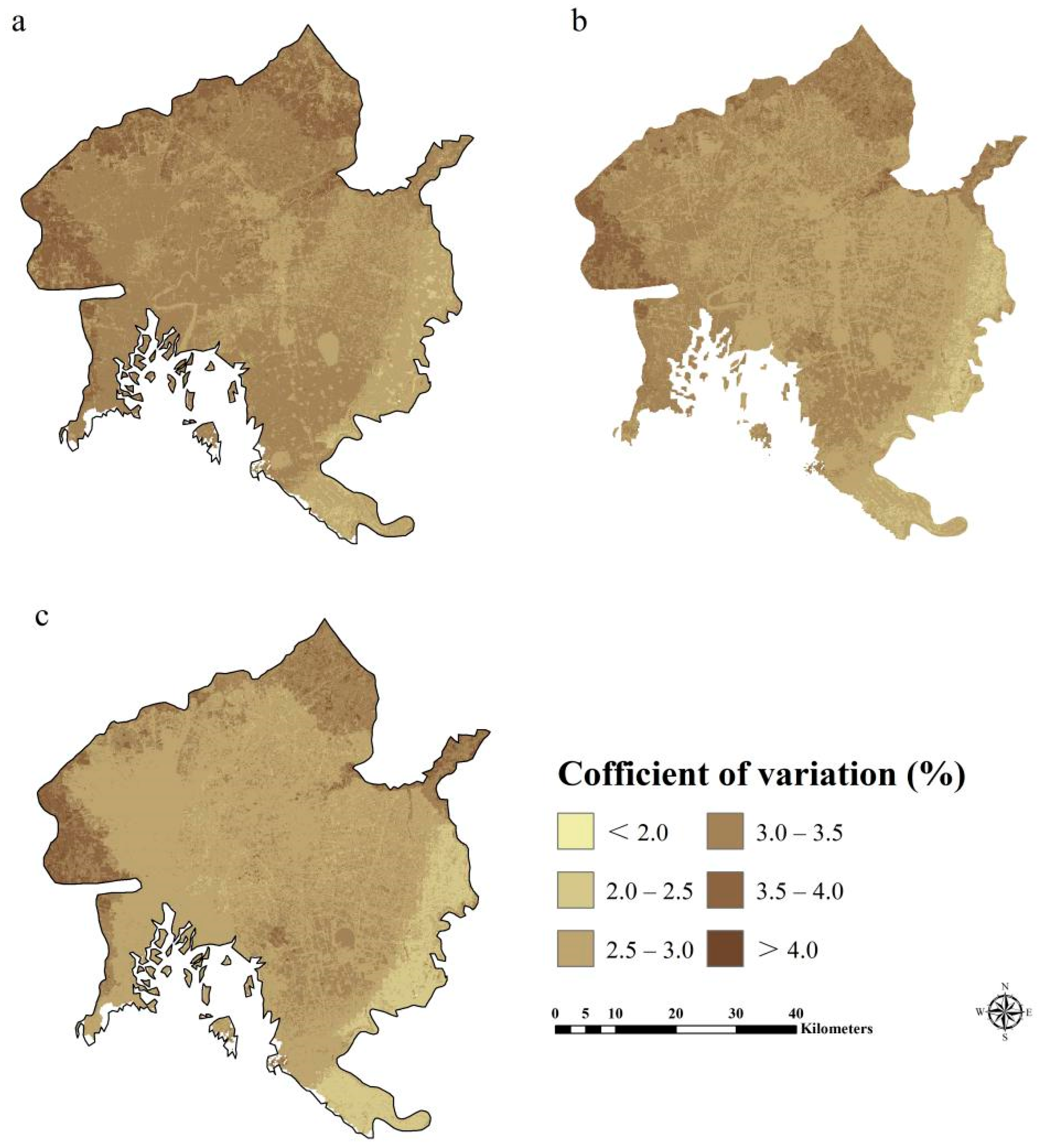
3.2. Model Performance and Uncertainty
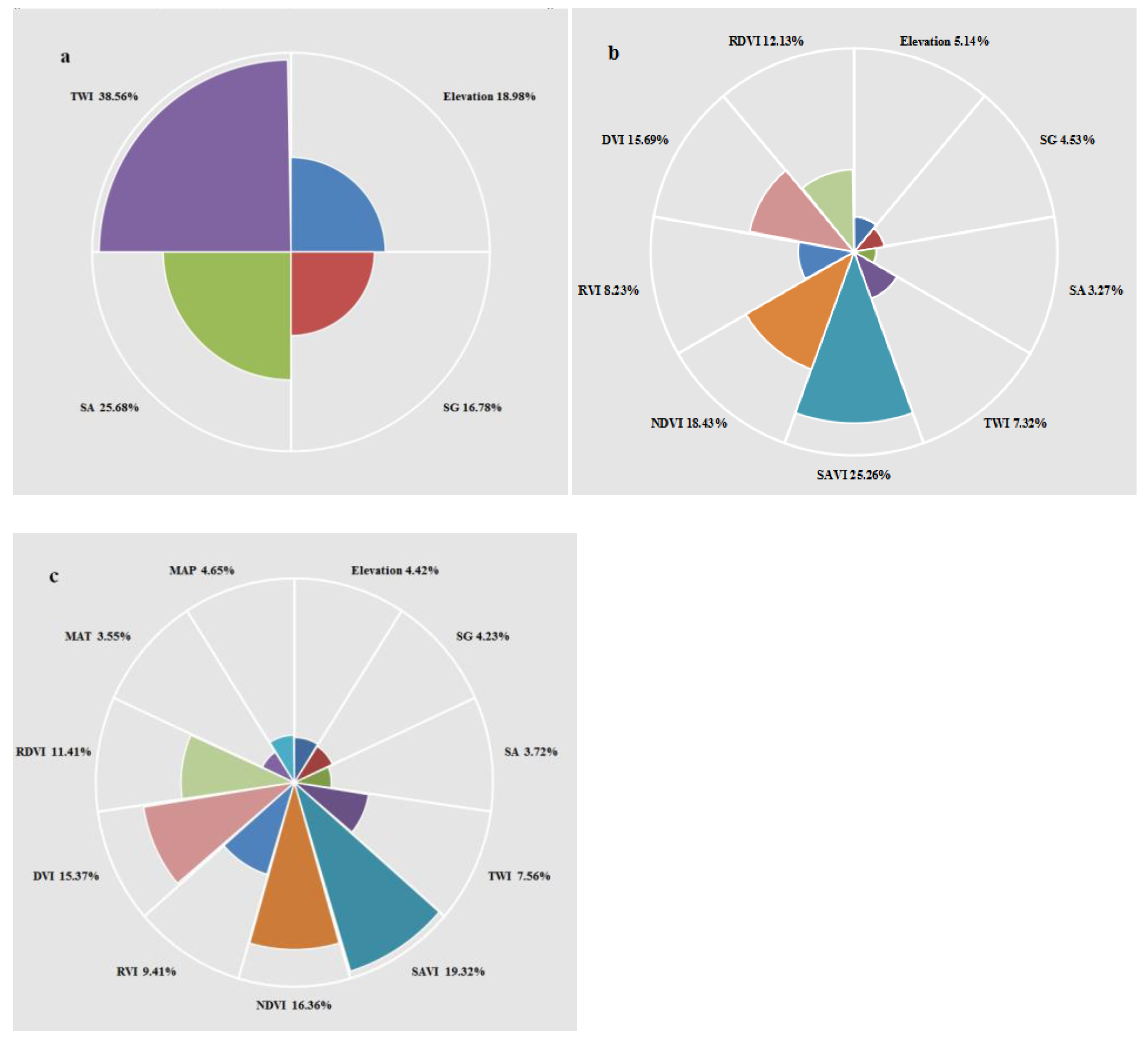
3.3. Importance of Environmental Variables
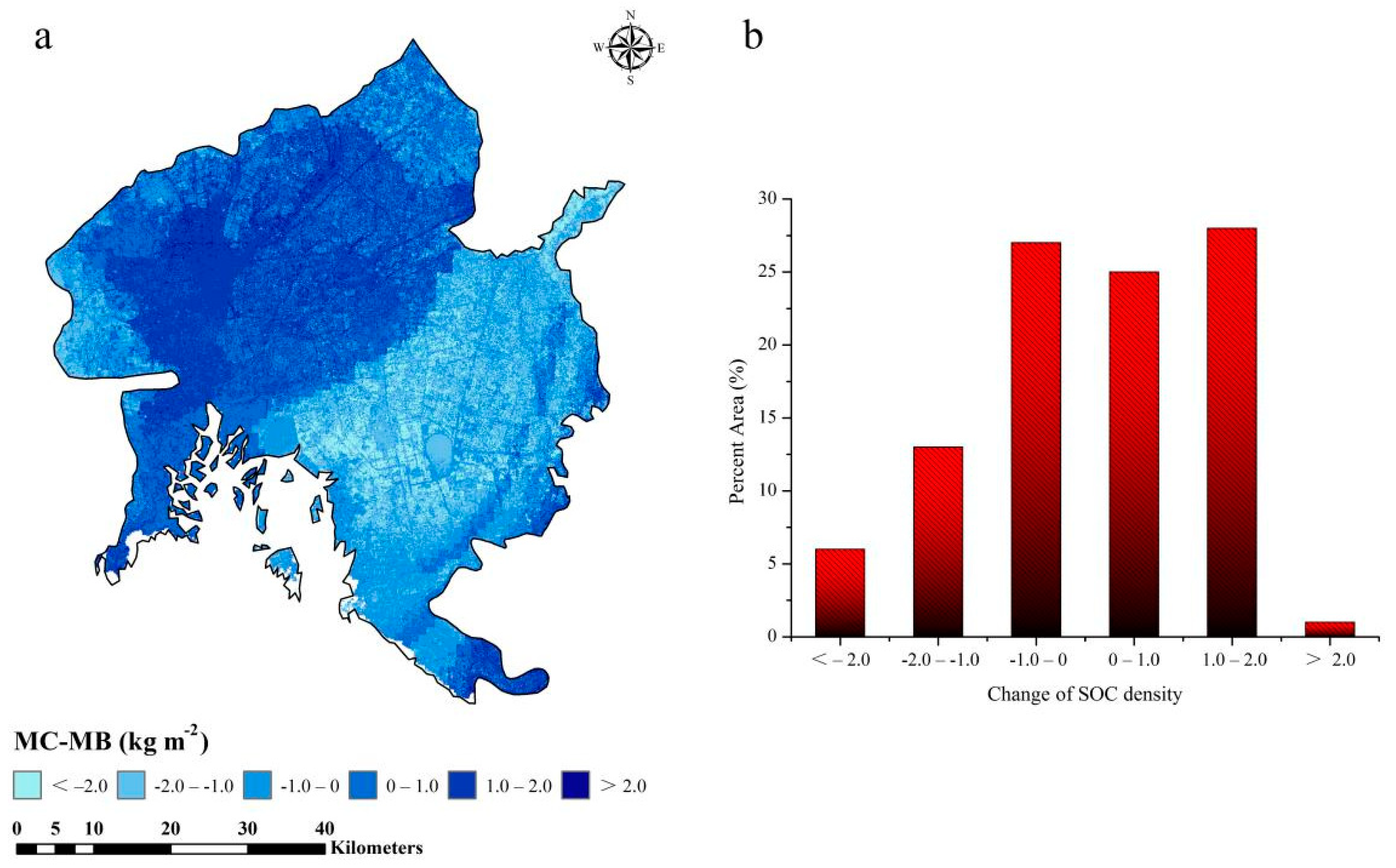
3.4. Spatial Prediction of SOC Density
4. Discussion
4.1. Importance of Remote Sensing-Related Variables in Predicting SOC Density
4.2. SOC Distribution and Associated Predictors
4.3. Uncertainty in Current Research
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bastviken, D.; Tranvik, L.J.; Downing, J.A.; Crill, P.M.; Enrich-Prast, A. Freshwater methane emissions offset the continental carbon sink. Science 2011, 331, 50. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, J.; Wang, Y.; Li, Y.; Dong, H.; Zhou, D.; Han, G.; Wu, H.; Wang, G.; Mao, P.; Gao, Y. Soil organic carbon storage changes in coastal wetlands of the modern yellow river delta from 2000 to 2009. Biogeosciences 2012, 9, 2325–2331. [Google Scholar] [CrossRef] [Green Version]
- Ricker, M.C.; Lockaby, B.G. Soil organic carbon stocks in a large eutrophic floodplain forest of the southeastern atlantic coastal plain, USA. Wetlands 2015, 35, 291–301. [Google Scholar] [CrossRef]
- Twilley, R.R.; Chen, R.H.; Hargis, T. Carbon sinks in mangroves and their implications to carbon budget of tropical coastal ecosystems. Water Air Soil Poll. 1992, 64, 265–288. [Google Scholar] [CrossRef]
- Steinmuller, H.E.; Chambers, L.G. Characterization of coastal wetland soil organic matter: Implications for wetland submergence. Sci. Total Environ. 2019, 677, 648–659. [Google Scholar] [CrossRef]
- Yang, R. Interacting effects of plant invasion, climate, and soils on soil organic carbon storage in coastal wetlands. J. Geophys. Res-Biogeo. 2019, 124, 2554–2564. [Google Scholar] [CrossRef]
- Rogers, K.; Kelleway, J.J.; Saintilan, N.; Megonigal, J.P.; Adams, J.B.; Holmquist, J.R. Wetland carbon storage controlled by millennial-scale variation in relative sea-level rise. Nature 2019, 567, 91–95. [Google Scholar] [CrossRef]
- McBratney, A.B.; Santos, M.L.M.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B.; Malone, B.P.; Wheeler, I. Digital mapping of soil carbon. Adv. Agron. 2013, 118, 4. [Google Scholar]
- Wang, S.; Zhuang, Q.; Wang, Q.; Jin, X.; Han, C. Mapping stocks of soil organic carbon and soil total nitrogen in Liaoning Province of China. Geoderma 2017, 305, 250–263. [Google Scholar] [CrossRef]
- Malone, B.P.; McBratney, A.B.; Minasny, B.; Laslett, G.M. Mapping continuous depth functions of soil carbon storage and available water capacity. Geoderma 2009, 154, 138–152. [Google Scholar] [CrossRef]
- Martin, M.P.; Wattenbach, M.; Smith, P.; Meersmans, J.; Jolivet, C.; Boulonne, L.; Arrouays, D. Spatial distribution of soil organic carbon stocks in France. Biogeosciences 2011, 8, 1053–1065. [Google Scholar] [CrossRef] [Green Version]
- Mulder, V.L.; De Bruin, S.; Schaepman, M.E. The use of remote sensing in soil and terrain mapping—A review. Geoderma 2011, 162, 1–19. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Digital soil mapping: A brief history and some lessons. Geoderma 2016, 264, 301–311. [Google Scholar] [CrossRef]
- Mirzaee, S.; Ghorbani-Dashtaki, S.; Mohammadi, J. Spatial variability of soil organic matter using remote sensing data. Catena 2016, 145, 118–127. [Google Scholar] [CrossRef]
- Xu, L.; Yu, G.R.; He, N.P. Increased soil organic carbon storage in Chinese terrestrial ecosystems from the 1980s to the 2010s. J. Geogr. Sci. 2019, 29, 49–66. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Biswas, A.; Jiang, Q. Estimating soil salinity from remote sensing and terrain data in southern Xinjiang Province, China. Geoderma 2019, 337, 1309–1319. [Google Scholar] [CrossRef]
- Coleman, T.L.; Agbu, P.A.; Montgomery, O.L. Spectral differentiation of surface soils and soil properties-is it possible from space platforms. Soil Sci. 1993, 155, 283–293. [Google Scholar] [CrossRef]
- Vaudour, E.; Bel, L.; Gilliot, J.M. Potential of SPOT multispectral satellite images for mapping topsoil organic carbon content over Peri-Urban Croplands. Soil Sci. Soc. Am. J. 2013, 77, 2122–2139. [Google Scholar] [CrossRef]
- Sullivan, D.G.; Shaw, J.N.; Rickman, D. IKONOS imagery to estimate surface soil property variability in two Alabama physiographies. Soil Sci. Soc. Am. J. 2005, 69, 1789–1798. [Google Scholar] [CrossRef] [Green Version]
- Gomez, C.; Rossel, R.A.V.; McBratney, A.B. Soil organic carbon prediction by hyperspectral remote sensing and field vis-NIR spectroscopy: An Australian case study. Geoderma 2008, 146, 403–411. [Google Scholar] [CrossRef]
- Farifteh, J. Interference of salt and moisture on soil reflectance spectra. Int. J. Remote Sens. 2011, 32, 8711–8724. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Gao, J.; Zhuang, Q.; Lu, Y.; Gu, H.; Jin, X. Multispectral Remote Sensing Data Are Effective and Robust in Mapping Regional Forest Soil Organic Carbon Stocks in a Northeast Forest Region in China. Remote Sens. 2020, 12, 393. [Google Scholar] [CrossRef] [Green Version]
- Qi, L.; Wang, S.; Zhuang, Q.; Yang, Z.; Bai, S.; Jin, X.; Lei, G. Spatial-temporal changes in soil organic carbon and pH in the Liaoning Province of China: A modeling analysis based on observational data. Sustainability 2019, 11, 3569. [Google Scholar] [CrossRef] [Green Version]
- Yoon, L.C.; Pedro, J.; Leitão, T.L. Assessment of land use factors associated with dengue cases in Malaysia using Boosted Regression Trees. Spat. Spatio Tempor. Epidemiol. 2014, 10, 75–84. [Google Scholar]
- IUSS Working Group. World Reference Base for Soil Resources 2014 International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; FAO: Rome, Italy, 2014. [Google Scholar]
- Zhu, A.X.; Yang, L.; Li, B.; Qin, C.; English, E.; Burt, J.E.; Zhou, C. Purposive sampling for digital soil mapping for areas with limited data. In Digital Soil Mapping with Limited Data; Hartemink, A.E., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 33–245. [Google Scholar]
- Yang, L.; Zhu, A.; Qin, C.; Li, B.; Pei, T.; Liu, B. Soil property mapping using fuzzy membership-a case study of a study area in Heshan Farm of Heilongjiang Province. Acta Pedol. Sin. 2009, 46, 9–15. [Google Scholar]
- Yang, L.; Zhu, A.; Qin, C.; Li, B.; Pei, T. A soil sampling method based on representativeness grade of sampling points. Acta Pedol. Sin. 2011, 48, 938–946. [Google Scholar]
- Nelson, D.W.; Sommers, L.E. Total carbon, organic carbon, and organic matter. In Methods of Soil Analysis, Part 2. Chemical and Microbiological Properties; ASA-SSSA: Madison, WI, USA, 1982; pp. 539–594. [Google Scholar]
- Batjes, N.H. Total carbon and nitrogen in the soils of the world. Eur. J. Soil Sci. 1996, 47, 151–163. [Google Scholar] [CrossRef]
- Liu, Z.K.; Hunt, B.R. A new approach to removing cloud cover from satellite imagery. Comput. Vis. Graph. Image Process. 1984, 25, 252–256. [Google Scholar] [CrossRef]
- Perkins, T.; Adlergolden, S.; Matthew, M.; Berk, A.; Anderson, G.; Gardner, J. Retrieval of atmospheric properties from hyper and multispectral imagery with the FLAASH atmospheric correction algorithm. In Remote Sensing of Clouds & the Atmosphere X; International Society for Optics and Photonics: Orlando, FL, USA, 2005. [Google Scholar]
- Odebiri, O.; Mutanga, O.; Odindi, J.; Peerbhay, K.; Dovey, S. Predicting soil organic carbon stocks under commercial forest plantations in KwaZulu-Natal province, South Africa using remotely sensed data. GIScience Remote Sens. 2020, 57, 450–463. [Google Scholar] [CrossRef]
- Richardson, A.J.; Wiegand, C.L. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Major, D.J.; Baret, F.; Guyot, G. A ratio vegetation index adjusted for soil brightness. Int. J. Remote Sens. 1990, 11, 727–740. [Google Scholar] [CrossRef]
- Gilabert, M.A.; González-Piqueras, J.; Garcıa-Haro, F.J.; Meliá, J. A generalized soil-adjusted vegetation index. Remote Sens. Environ. 2002, 82, 303–310. [Google Scholar] [CrossRef]
- Moore, I.D.; Gessler, P.E.; Nielsen, G.A.; Peterson, G.A. Soil attributes prediction using terrain analysis. Soil Sci. Soc. Am. J. 1993, 57, 443–452. [Google Scholar] [CrossRef]
- Olaya, V.F. A Gentle Introduction to Saga GIS; The SAGA User Group eV: Göttingen, Germany, 2004. [Google Scholar]
- Hutchinson, M.F. Interpolation of rainfall data with thin plate smoothing splines—Part i: Two dimensional smoothing of data with short range correlation. J. Geogr. Inf. Decis. Anal. 1998, 2, 139–151. [Google Scholar]
- Friedman, J.H.; Meulman, J.J. Multiple additive regression trees with application in epidemiology. Stat. Med. 2003, 22, 1365–1381. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Phillips, S.; Leathwick, J.; Elith, J. Dismo: Species Distribution Modeling. R Package Version 0. 8–17. 2013. Available online: http://www.idg.pl/mirrors/CRAN/web/packages/dismo/vignettes/sdm.pdf (accessed on 18 July 2020).
- R Development Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; R Development Core Team: Vienna, Austria, 2013; Available online: https://www.rproject.org/ (accessed on 18 July 2020).
- Ishii, Y.; Murakami, J.; Sasaki, K.; Tsukahara, M.; Wakamatsu, K. Efficient folding/assembly in Chinese hamster ovary cells is critical for high quality (low aggregate content) of secreted trastuzumab as well as for high production: Stepwise multivariate regression analyses. J. Biosci. Bioeng. 2014, 118, 223–230. [Google Scholar] [CrossRef]
- Lin, L. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef]
- Goward, S.N.; Markham, B.; Dye, D.G.; Dulaney, W.; Yang, J. Normalized difference vegetation index measurements from the Advanced Very High Resolution Radiometer. Remote Sens. Environ. 1991, 35, 257–277. [Google Scholar] [CrossRef]
- Kim, J.; Grunwald, S. Assessment of carbon stocks in the topsoil using random forest and remote sensing images. J. Environ. Qual. 2016, 45, 1910–1918. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhang, F.; Kung, H.T.; Johnson, V.C. New methods for improving the remote sensing estimation of soil organic matter content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, L.; Chen, Y.; Shi, T.; Luo, M.; Ju, Q.; Wang, S. Prediction of Soil Organic Carbon based on Landsat 8 Monthly NDVI Data for the Jianghan Plain in Hubei Province, China. Remote Sens. 2019, 11, 1683. [Google Scholar] [CrossRef] [Green Version]
- Payero, J.O.; Neale, C.M.U.; Wright, J.L. Comparison of eleven vegetation indices for estimating plant height of alfalfa and grass. Appl. Eng. Agric. 2004, 20, 385. [Google Scholar] [CrossRef] [Green Version]
- Jobbágy, E.G.; Jackson, R.B. The vertical distribution of soil organic carbon and its relation to climate and vegetation. Ecol. Appl. 2000, 10, 423–436. [Google Scholar] [CrossRef]
- Grimm, R.; Behrens, T.; Märker, M.; Elsenbeer, H. Soil organic carbon concentrations and on Barro Colorado Island-Digital soil mapping using Random Forests analysis. Geoderma 2008, 146, 102–113. [Google Scholar] [CrossRef]

| Property | Unit | Min. | Mean | Max. | SD | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| SOC density | kg m−2 | 0.33 | 11.14 | 28.31 | 0.47 | 0.56 | 2.43 |
| SAVI | 0.07 | 0.14 | 0.35 | 0.27 | −0.47 | 1.61 | |
| NDVI | 0.02 | 0.08 | 0.33 | 0.04 | −0.31 | 1.73 | |
| RVI | 0.36 | 0.76 | 1.12 | 0.34 | −1.24 | 1.22 | |
| DVI | 12.76 | 39.43 | 57.23 | 7.72 | 0.39 | 2.33 | |
| RDVI | 21.17 | 42.05 | 60.09 | 8.10 | 0.53 | 3.27 | |
| Elevation | m | 1 | 2.87 | 12 | 1.12 | 1.13 | 3.24 |
| SG | degree | 0 | 0.05 | 2.16 | 0.11 | 0.93 | 0.32 |
| SA | degree | 0 | 174.62 | 360 | 92.65 | −0.42 | −0.89 |
| TWI | 7.30 | 10.70 | 10.95 | 0.54 | 0.96 | 1.12 | |
| MAT | degree Celsius | 9.33 | 9.53 | 9.67 | 0.38 | −1.21 | 2.16 |
| MAP | mm | 648.7 | 650.6 | 652.3 | 1.31 | 0.84 | 0.93 |
| Property | SOC Density | Elevation | SG | SA | TWI | SAVI | NDVI | RVI | DVI | MAT |
|---|---|---|---|---|---|---|---|---|---|---|
| Elevation | 0.19 * | |||||||||
| SG | 0.13 | 0.33 ** | ||||||||
| SA | 0.15 | 0.15 | 0.27 ** | |||||||
| TWI | −0.23 ** | −0.23 ** | −0.40 ** | −0.22 ** | ||||||
| SAVI | 0.31 ** | 0.19 * | 0.07 | 0.13 | −0.07 | |||||
| NDVI | 0.43 ** | 0.21 * | 0.08 | 0.09 | −0.05 | 0.42 ** | ||||
| RVI | −0.16 * | −0.16 * | −0.11 | −0.14 | 0.15 | −0.17 ** | −0.28 ** | |||
| DVI | 0.21 * | 0.28 ** | 0.17 | 0.17 | −0.08 | 0.17 * | 0.26 ** | −0.32 ** | ||
| RDVI | −0.29 ** | −0.25 * | −0.09 | −0.13 | 0.06 | 0.33 ** | 0.37 ** | −0.05 | 0.36 ** | |
| MAT | 0.09 | 0.12 | −0.06 | −0.07 | 0.13 * | −0.15 * | −0.10 | 0.06 | 0.13 | |
| MAP | 0.11 | −0.13 * | 0.08 | 0.06 | −0.12 * | 0.17 * | 0.19 * | −0.09 | 0.16 | 0.22 ** |
| Model | Index | Min. | Median | Mean | Max. |
|---|---|---|---|---|---|
| MA | MAE | 1.38 | 1.39 | 1.40 | 1.41 |
| RMSE | 1.51 | 1.52 | 1.52 | 1.54 | |
| R2 | 0.24 | 0.26 | 0.27 | 0.31 | |
| LCCC | 0.33 | 0.34 | 0.34 | 0.35 | |
| MB | MAE | 1.27 | 1.31 | 1.32 | 1.33 |
| RMSE | 1.47 | 1.48 | 1.49 | 1.50 | |
| R2 | 0.31 | 0.33 | 0.34 | 0.36 | |
| LCCC | 0.37 | 0.38 | 0.39 | 0.40 | |
| MC | MAE | 0.87 | 0.88 | 0.89 | 0.91 |
| RMSE | 0.96 | 0.97 | 0.97 | 0.98 | |
| R2 | 0.53 | 0.55 | 0.57 | 0.59 | |
| LCCC | 0.53 | 0.54 | 0.55 | 0.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhou, M.; Zhuang, Q.; Guo, L. Prediction Potential of Remote Sensing-Related Variables in the Topsoil Organic Carbon Density of Liaohekou Coastal Wetlands, Northeast China. Remote Sens. 2021, 13, 4106. https://doi.org/10.3390/rs13204106
Wang S, Zhou M, Zhuang Q, Guo L. Prediction Potential of Remote Sensing-Related Variables in the Topsoil Organic Carbon Density of Liaohekou Coastal Wetlands, Northeast China. Remote Sensing. 2021; 13(20):4106. https://doi.org/10.3390/rs13204106
Chicago/Turabian StyleWang, Shuai, Mingyi Zhou, Qianlai Zhuang, and Liping Guo. 2021. "Prediction Potential of Remote Sensing-Related Variables in the Topsoil Organic Carbon Density of Liaohekou Coastal Wetlands, Northeast China" Remote Sensing 13, no. 20: 4106. https://doi.org/10.3390/rs13204106
APA StyleWang, S., Zhou, M., Zhuang, Q., & Guo, L. (2021). Prediction Potential of Remote Sensing-Related Variables in the Topsoil Organic Carbon Density of Liaohekou Coastal Wetlands, Northeast China. Remote Sensing, 13(20), 4106. https://doi.org/10.3390/rs13204106









