Global Wave Height Slowdown Trend during a Recent Global Warming Slowdown
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Calculation of Global Time Series
2.3. Mann–Kendall test for Monotonic Trend
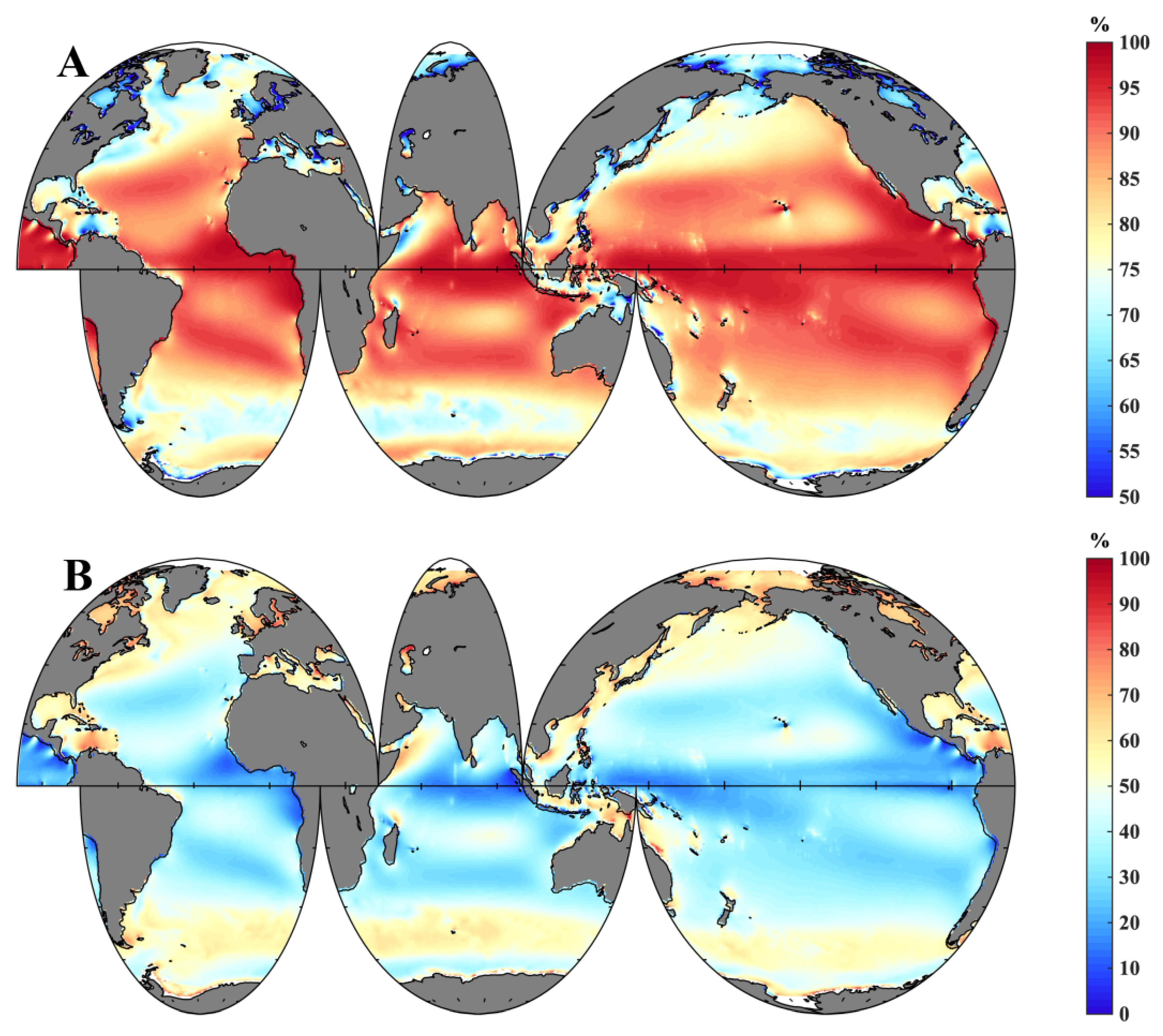
2.4. Swell Index
3. Results
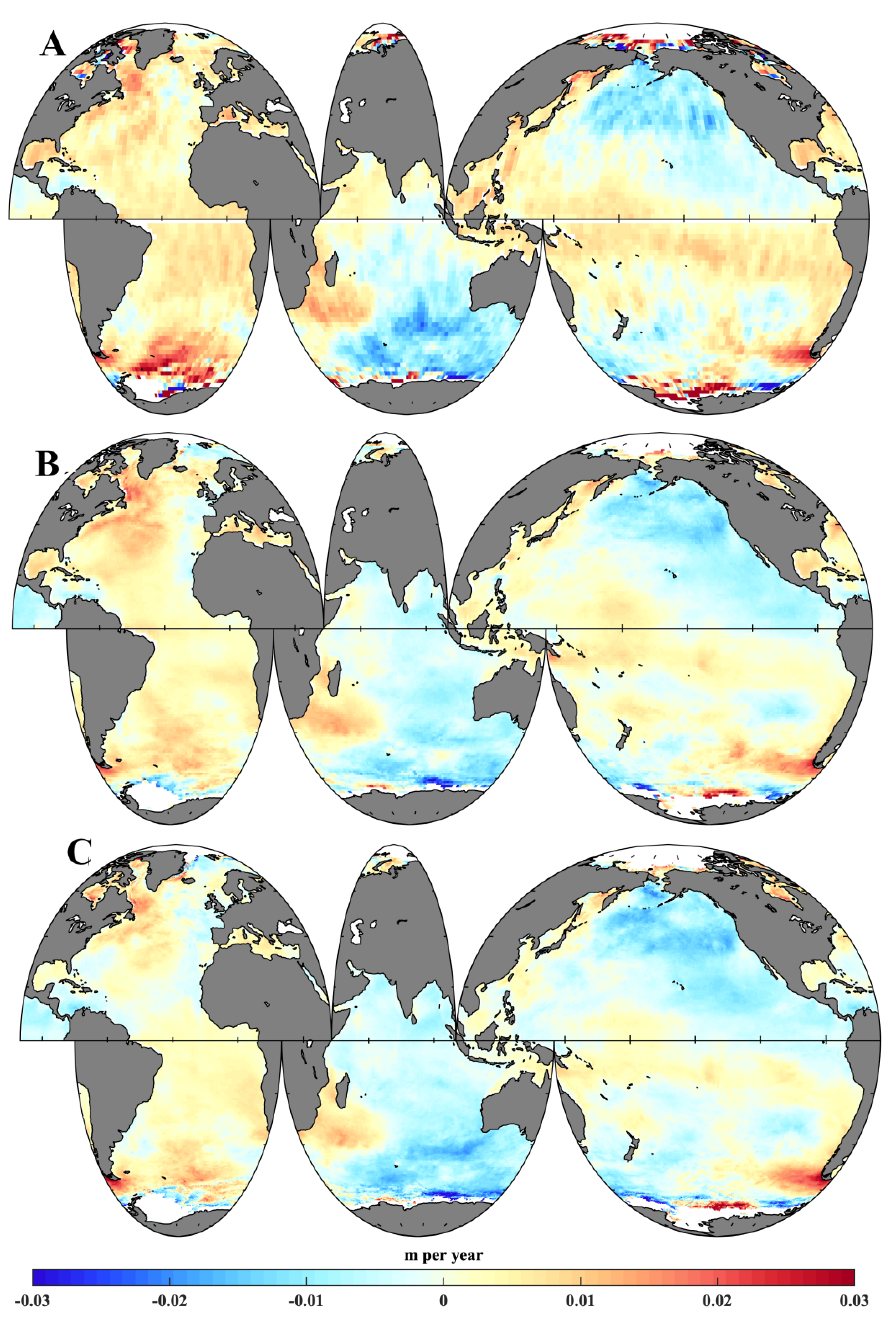
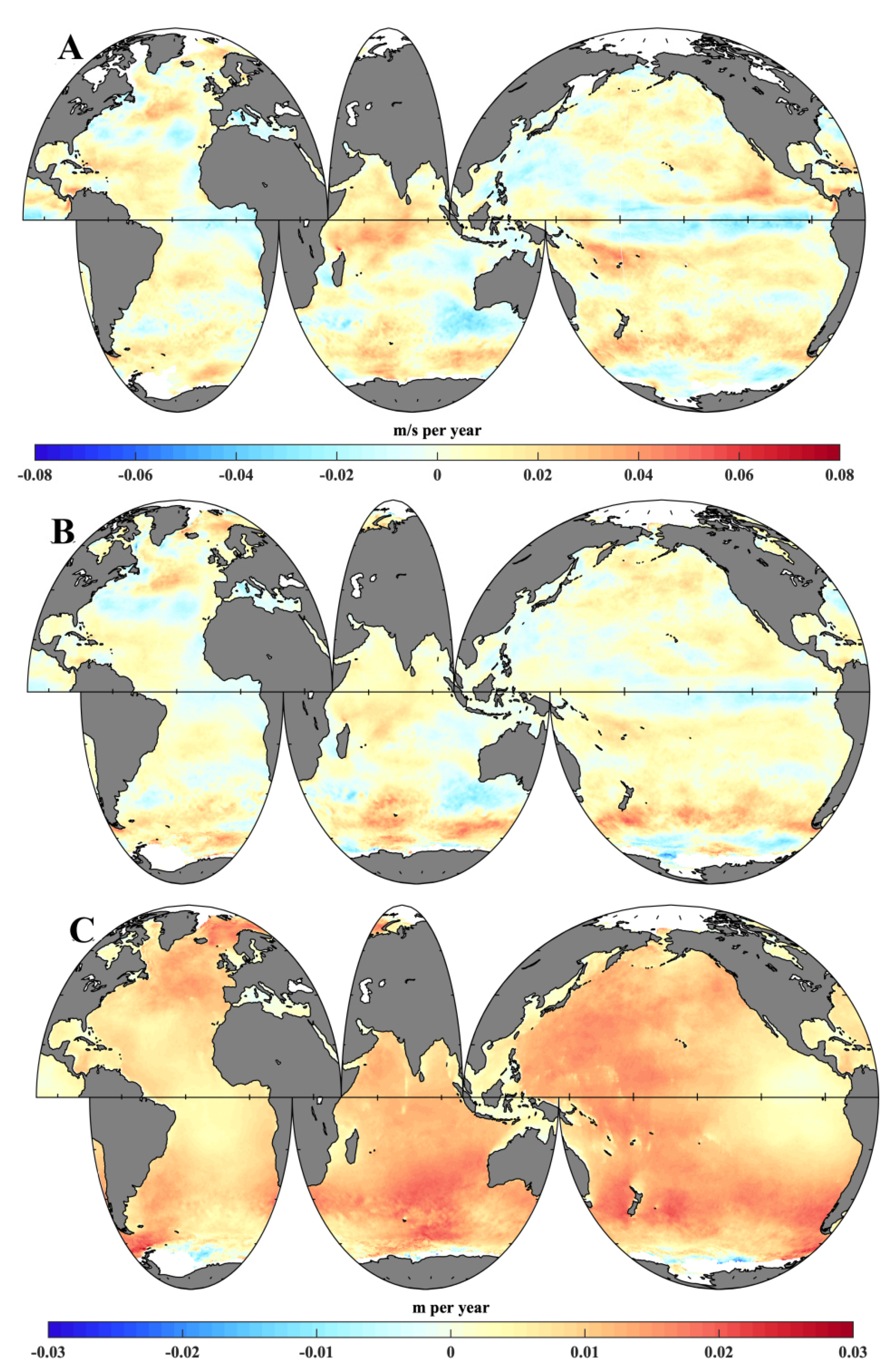
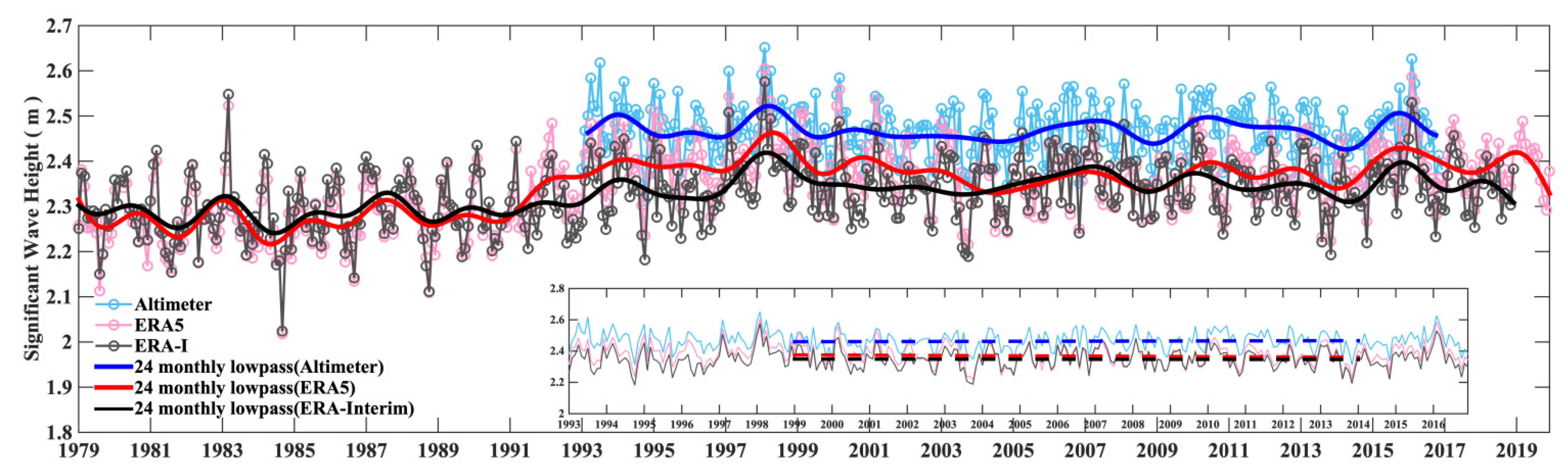
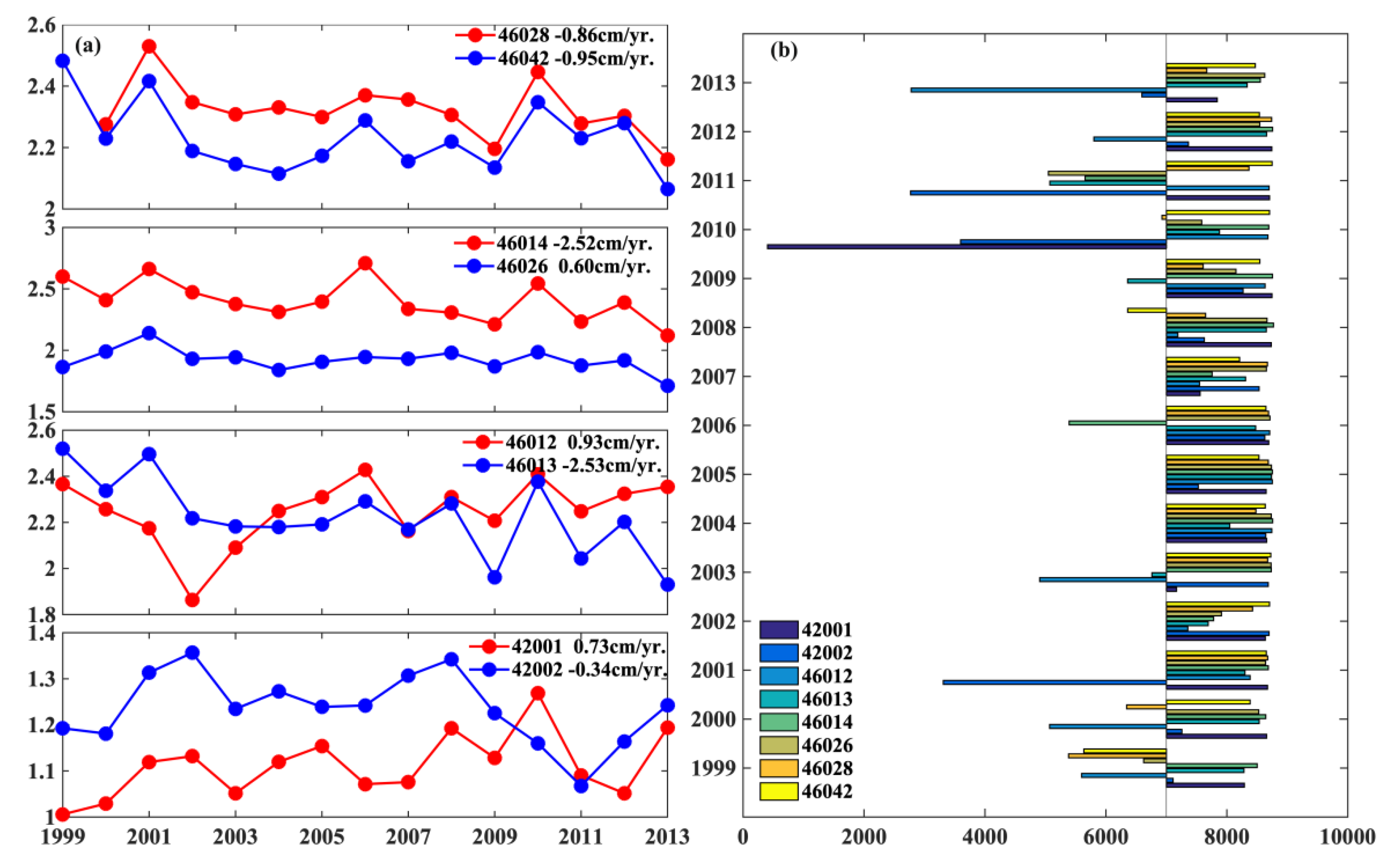
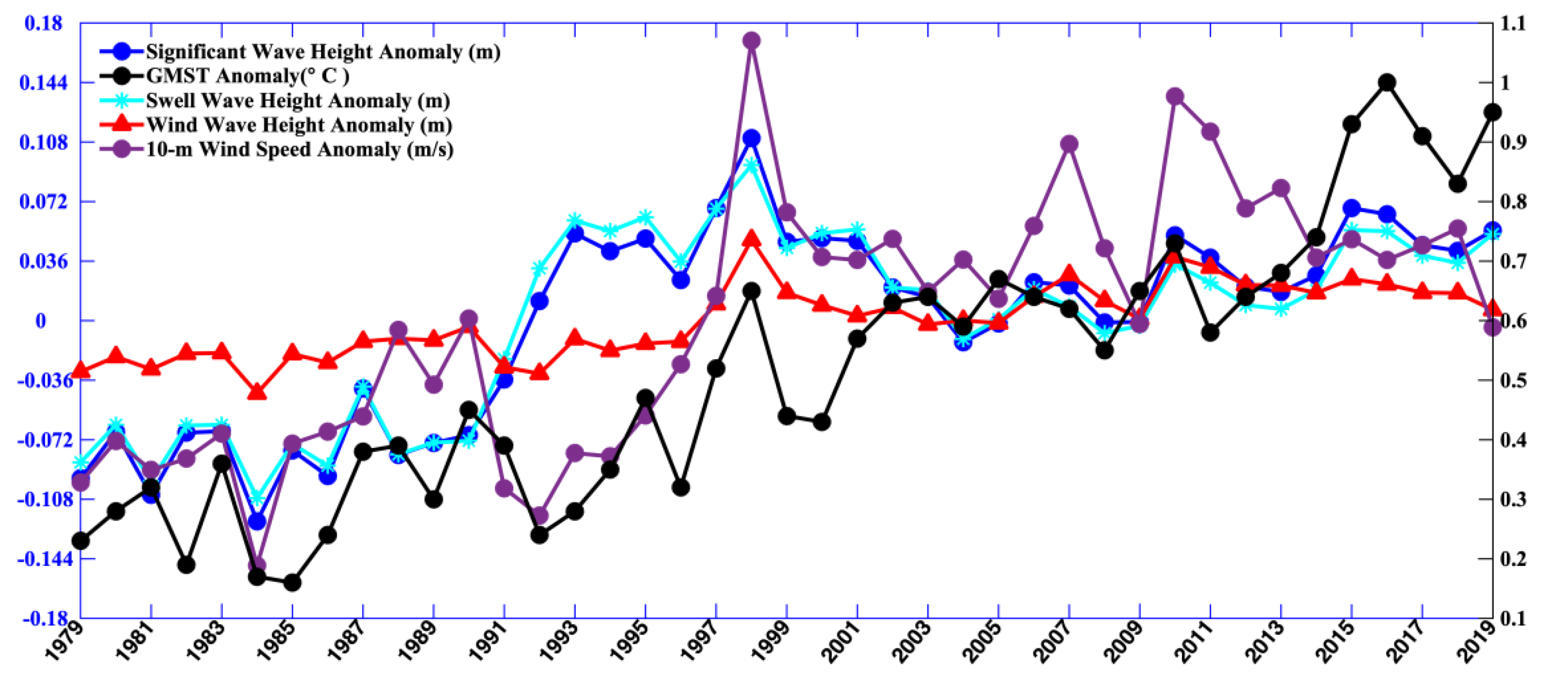
3.1. Slowdown in Trend of Global Average SWH from 1999 to 2013
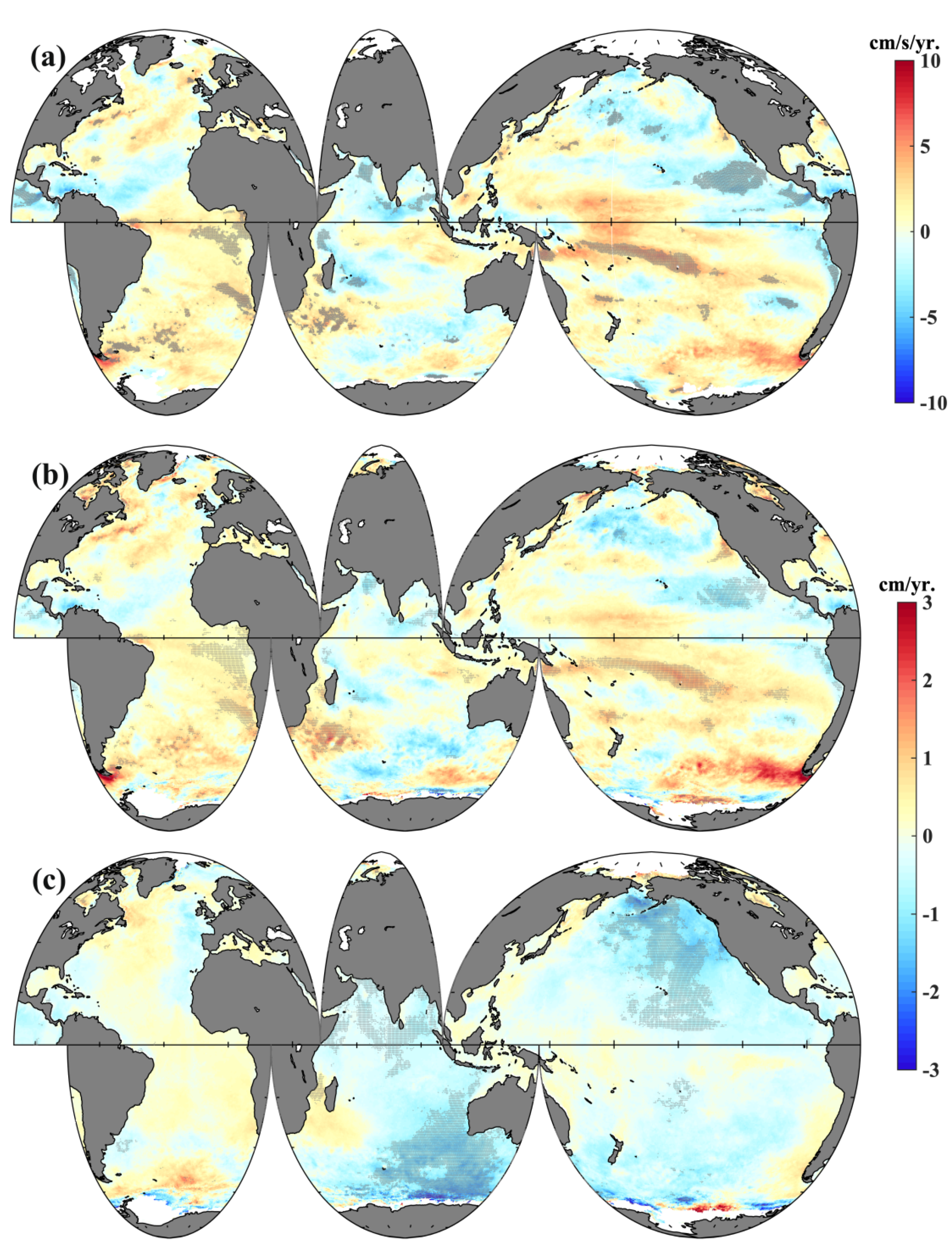
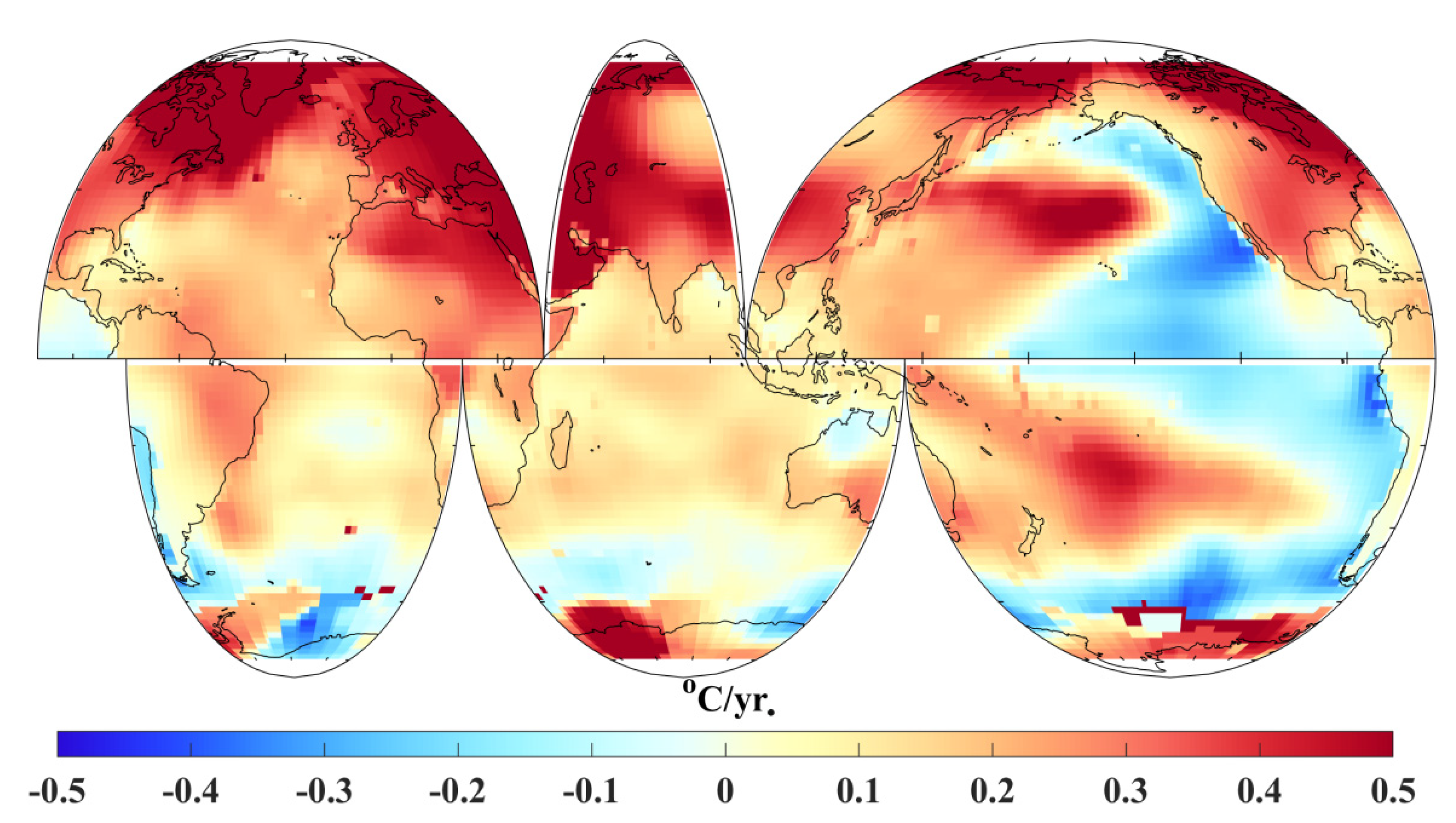
3.2. Uneven Geographical Distribution in SWH Trends from 1999 to 2013
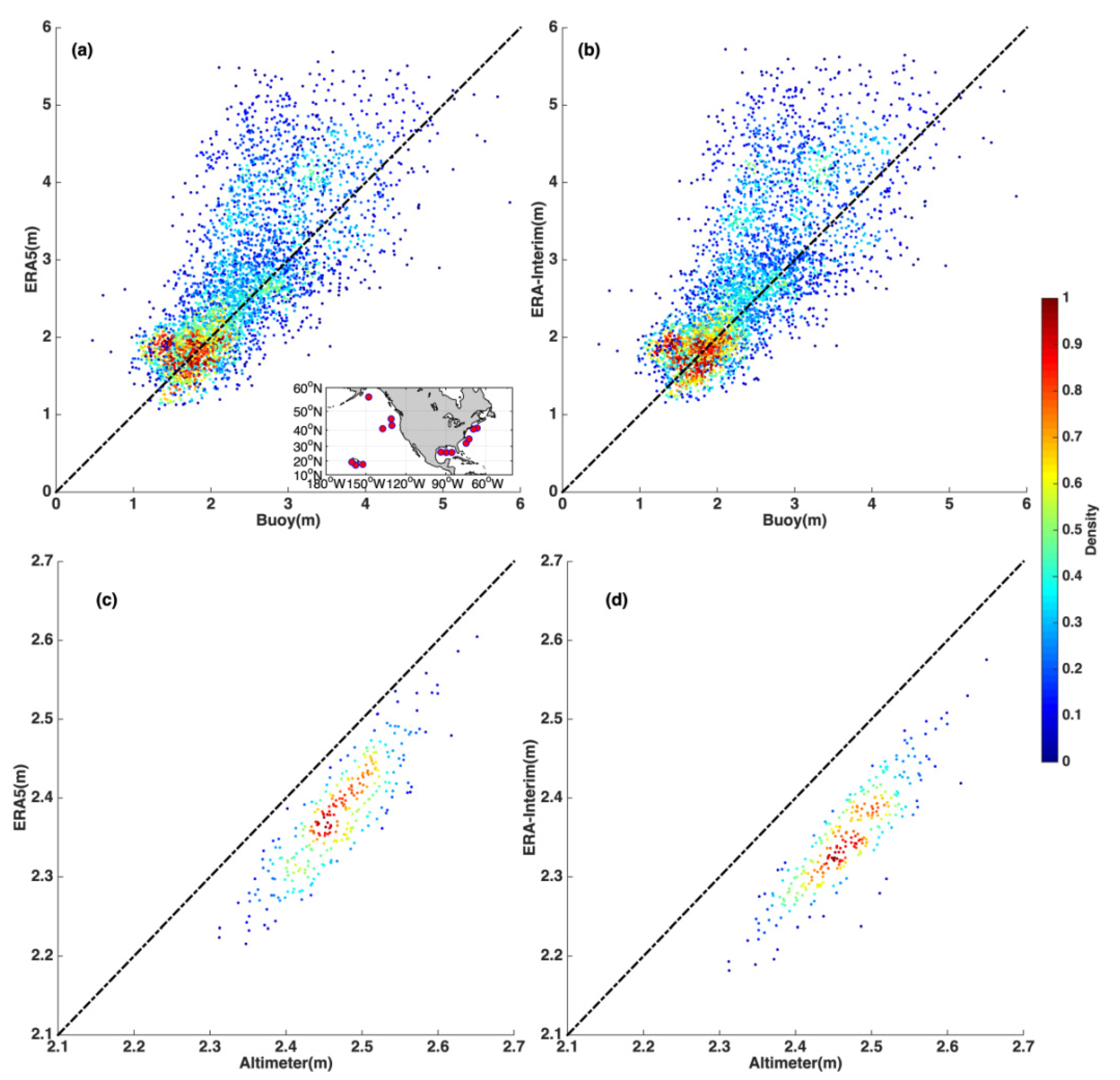
3.3. Reliability of Reanalysis Data for Estimating SWH Trends
3.4. Different Trends in Wind-Generated Waves and Swell
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Young, I.R.; Zieger, S.; Babanin, A.V. Global trends in wind speed and wave height. Science 2011, 332, 451–455. [Google Scholar] [CrossRef]
- Kumar, P.; Min, S.K.; Weller, E.; Lee, H.; Wang, X.L. Influence of climate variability on extreme ocean surface wave heights assessed from ERA-Interim and ERA-20C. J. Clim. 2016, 29, 4031–4046. [Google Scholar] [CrossRef]
- Morim, J.; Hemer, M.; Wang, X.L.; Cartwright, N.; Trenham, C.; Semedo, A.; Young, I.; Bricheno, L.; Camus, P.; Casas-Prat, M.; et al. Robustness and uncertainties in global multivariate wind-wave climate projections. Nat. Clim. Chang. 2019, 9, 711–718. [Google Scholar] [CrossRef]
- Knight, J.; Kenneby, J.; Folland, C.; Harris, G.; Jones, G.S.; Palmer, M.; Stott, P. Do global temperature trends over the last decade falsify climate predictions? Bull. Am. Meteorol. Soc. 2009, 90, 22–23. [Google Scholar]
- Kerr, R.A. What happened to global warming? Scientists say just wait a bit. Science 2009, 326, 28–29. [Google Scholar] [CrossRef][Green Version]
- Kosaka, Y.; Xie, S.-P. Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature 2013, 501, 403–407. [Google Scholar] [CrossRef]
- Yan, X.H.; Boyer, T.; Trenberth, K.; Karl, T.R.; Xie, S.; Nieves, V.; Tung, K.; Roemmich, D. The global warming hiatus: Slowdown or redistribution? Earths Future 2016, 4, 472–482. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.P.; Kosaka, Y. What caused the global surface warming hiatus of 1998–2013? Curr. Clim. Chang. Rep. 2017, 3, 128–140. [Google Scholar] [CrossRef]
- Roberts, C.; Palmer, M.; McNeall, D.; Collins, M. Quantifying the likelihood of a continued hiatus in global warming. Nat. Clim. Chang. 2015, 5, 337–342. [Google Scholar] [CrossRef]
- Fyfe, J.C.; Gillett, N.P.; Zwiers, F.W. Overestimated global warming over the past 20 years. Nat. Clim. Chang. 2013, 3, 767–769. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Alexander, L.V.; Allen, S.K.; Bindoff, N.L.; Bréon, F.M.; Church, J.A.; Cubasch, U.; Emori, S.; et al. Technical summary. In Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Cowtan, K.; Way, R.G. Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends. Q. J. R. Meteorol. Soc. 2014, 140, 1935–1944. [Google Scholar] [CrossRef]
- Karl, T.R.; Arguez, A.; Huang, B.; Lawrimore, J.H.; McMahon, J.R.; Menne, M.J.; Peterson, T.C.; Vose, R.S.; Zhang, H.-M. Possible artifacts of data biases in the recent global surface warming hiatus. Science 2015, 348, 1469–1472. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, X.; Zhang, Q.; Lin, Y.; Hao, M.; Luo, Y.; Zhao, Z.; Yao, Y.; Chen, X.; Wang, L.; et al. Recently amplified arctic warming has contributed to a continual global warming trend. Nat. Clim. Chang. 2017, 7, 875–879. [Google Scholar] [CrossRef]
- Sasaki, W. Changes in the North Pacific wave climate since the mid-1990s. Geophys. Res. Lett. 2014, 41, 7854–7860. [Google Scholar] [CrossRef]
- Wu, L.; Qin, J.; Wu, T.; Li, X. Trends in global ocean surface wave characteristics as represented in the ERA-Interim wave reanalysis for 1979–2010. J. Mar. Sci. Technol. 2018, 23, 2–9. [Google Scholar] [CrossRef]
- Young, I.R.; Ribal, A. Multiplatform evaluation of global trends in wind speed and wave height. Science 2019, 364, 548–552. [Google Scholar] [CrossRef]
- Reguero, B.G.; Losada, I.J.; Méndez, F.J. A recent increase in global wave power as a consequence of oceanic warming. Nat. Commun. 2019, 10, 1–14. [Google Scholar] [CrossRef]
- Hemer, M.A.; Church, J.A.; Hunter, J.R. Variability and trends in the directional wave climate of the Southern Hemisphere. Int. J. Climatol. J. R. Meteorol. Soc. 2010, 30, 475–491. [Google Scholar] [CrossRef]
- Alvarez-Ellacuria, A.; Orfila, A.; Gómez-Pujol, L.; Simarro, G.; Obregon, N. Decoupling spatial and temporal patterns in short-term beach shoreline response to wave climate. Geomorphology 2011, 128, 199–208. [Google Scholar] [CrossRef]
- Semedo, A.; Weisse, R.; Behrens, A.; Sterl, A.; Bengtsson, L.; Gunther, H. Projection of global wave climate change toward the end of the twenty-first century. J. Clim. 2012, 26, 8269–8288. [Google Scholar] [CrossRef]
- Zieger, S.; Vinoth, J.; Young, I.R. Joint calibration of multiplatform altimeter measurements of wind speed and wave height over the past 20 years. J. Atmos. Ocean. Technol. 2009, 26, 2549–2564. [Google Scholar] [CrossRef]
- Timmermans, B.W.; Gommenginger, C.P.; Dodet, G.; Bidlot, J.R. Global Wave Height Trends and Variability from New Multimission Satellite Altimeter Products, Reanalyses, and Wave Buoys. Geophys. Res. Lett. 2020, 47, e2019GL086880. [Google Scholar] [CrossRef]
- Feng, X.; Tsimplis, M.N.; Yelland, M.J.; Quartly, G. Changes in significant and maximum wave heights in the Norwegian Sea. Glob. Planet. Chang. 2014, 113, 68–76. [Google Scholar] [CrossRef]
- Aarnes, O.J.; Abdalla, S.; Bidlot, J.R.; Breivik, O. Marine wind and wave height trends at different ERA-Interim forecast ranges. J. Clim. 2015, 28, 819–837. [Google Scholar] [CrossRef]
- Zheng, C.; Pan, J.; Tan, Y.; Gap, Z.; Rui, Z.; Chen, C. The seasonal variations in the significant wave height and sea surface wind speed of the China’s seas. Acta Oceanol. Sin. 2015, 34, 58–64. [Google Scholar] [CrossRef]
- Zheng, C.; Zhou, L.; Huang, C.; Shi, T.; Li, J. The long-termtrend of the sea surface wind speed and the wave height (wind wave, swell, mixed wave) in global ocean during the last 44 a. Acta Oceanol. Sin. 2013, 32, 1–4. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Munoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balsmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Meindl, E.A. Hamilton G D. Programs of the national data buoy center. Bull. Am. Meteorol. Soc. 1992, 73, 985–994. [Google Scholar] [CrossRef]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 13, 163–171. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
- Chen, G.; Chapron, B.; Ezraty, R.; Vandemark, D. A global view of swell and wind sea climate in the ocean by satellite altimeter and scatterometer. J. Atmos. Ocean. Technol. 2002, 19, 1849–1859. [Google Scholar] [CrossRef]
- Deng, Z.; Wu, K.; Yu, T. The wave transport of the eastern area of the Pacific. Acta Oceanol. Sin. 2007, 29, 1–9. [Google Scholar]
- NOAA National Centers for Environmental Information. Climate at a Glance: Global Time Series. July 2020. Available online: https://www.ncdc.noaa.gov/cag/ (accessed on 18 July 2020).
- Gemmrich, J.; Thomas, B.; Bouchard, R. Observational changes and trends in northeast Pacific wave records. Geophys. Res. Lett. 2011, 38, L22601. [Google Scholar] [CrossRef]
- Ma, J.; Foltz, G.R.; Soden, B.J.; Huang, G.; He, J.; Dong, C. Will surface winds weaken in response to global warming? Environ. Res. Lett. 2016, 11, 124012. [Google Scholar] [CrossRef]
- Thomson, J.; Rogers, W.E. Swell and sea in the emerging Arctic Ocean. Geophys. Res. Lett. 2014, 41, 3136–3140. [Google Scholar] [CrossRef]
- Semedo, A.; Sušelj, K.; Rutgersson, A.; Sterl, A. A global view on the wind sea and swell climate and variability from ERA-40. J. Clim. 2011, 24, 1461–1479. [Google Scholar] [CrossRef]
- Zheng, K.; Sun, J.; Guan, C.; Shao, W. Analysis of the global swell and wind sea energy distribution using WAVEWATCH III. Adv. Meteorol. 2016, 2016, 8419580. [Google Scholar] [CrossRef]
- Zheng, C.W.; Li, C.Y. Analysis of temporal and spatial characteristics of waves in the Indian Ocean based on ERA-40 wave reanalysis. Appl. Ocean Res. 2017, 63, 217–228. [Google Scholar] [CrossRef]
- Meucci, A.; Young, I.R.; Hemer, M.; Kirezci, E.; Ranasinghe, R. Projected 21st Century changes in extreme wind-wave events. Sci. Adv. 2020, 6, eaaz7295. [Google Scholar] [CrossRef]
- Menne, M.J.; Williams, C.N.; Gleason, B.E.; Rennie, J.J.; Lawrimore, J.H. The global historical climatology network monthly temperature dataset, version 4. J. Clim. 2018, 31, 9835–9854. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.-M. Extended reconstructed sea surface temperature, version 5 (ERSSTv5): Upgrades, validations, and intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]


| Region | Station | SWH 1979–1998 cm/yr. | SWH 1999–2013 cm/yr. | SSW 1979–1998 cm/s/yr. | SSW 1999–2013 cm/s/yr. |
|---|---|---|---|---|---|
| Atlantic (West) | 41001 | –0.39 | 0.03 | –4.85 | –0.12 |
| 41002 | |||||
| Gulf of Mexico | 42001 | 0.07 | 0.73 | 1.48 | –1.42 |
| 42002 | 0.02 | –0.34 | 1.86 | –1.30 | |
| 42003 | –0.15 | 0.02 | 1.86 | –2.93 | |
| USA-Northeast 1 | 44008 | 0.85 | 0.46 | 3.09 | –2.29 |
| 44011 | |||||
| Gulf of Alaska | 46001 | 0.05 | –1.78 | 0.14 | –2.16 |
| USA-Northwest | 46002 | 1.63 | –2.70 | –2.04 | –5.69 |
| 46005 | |||||
| 46006 | |||||
| Hawaii 2 | 51002 | 0.55 | –1.73 | 3.48 | –3.13 |
| 51003 | |||||
| 51004 |
| Station | Longitude (°E) | Latitude (°N) | Missing Data (%) |
|---|---|---|---|
| 42001 | −89.7 | 25.9 | 10 |
| 42002 | −93.8 | 26.1 | 20 |
| 46012 | −122.9 | 37.4 | 18 |
| 46013 | −123.3 | 38.2 | 10 |
| 46014 | −124.0 | 39.2 | 7 |
| 46026 | −122.9 | 37.8 | 7 |
| 46028 | −121.9 | 35.8 | 9 |
| 46042 | −122.5 | 36.8 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Dong, C.; Young, I.R.; Yang, J. Global Wave Height Slowdown Trend during a Recent Global Warming Slowdown. Remote Sens. 2021, 13, 4096. https://doi.org/10.3390/rs13204096
Cao Y, Dong C, Young IR, Yang J. Global Wave Height Slowdown Trend during a Recent Global Warming Slowdown. Remote Sensing. 2021; 13(20):4096. https://doi.org/10.3390/rs13204096
Chicago/Turabian StyleCao, Yuhan, Changming Dong, Ian R. Young, and Jingsong Yang. 2021. "Global Wave Height Slowdown Trend during a Recent Global Warming Slowdown" Remote Sensing 13, no. 20: 4096. https://doi.org/10.3390/rs13204096
APA StyleCao, Y., Dong, C., Young, I. R., & Yang, J. (2021). Global Wave Height Slowdown Trend during a Recent Global Warming Slowdown. Remote Sensing, 13(20), 4096. https://doi.org/10.3390/rs13204096







