Abstract
The global statistical median behavior of the electron temperature (Te) in the topside ionosphere was investigated through in-situ data collected by Langmuir Probes on-board the European Space Agency Swarm satellites constellation from the beginning of 2014 to the end of 2020. This is the first time that such an analysis, based on such a large time window, has been carried out globally, encompassing more than half a solar cycle, from the activity peak of 2014 to the minimum of 2020. The results show that Swarm data can help in understanding the main features of Te in the topside ionosphere in a way never achieved before. Te data measured by Swarm satellites were also compared to data modeled by the empirical climatological International Reference Ionosphere (IRI) model and data measured by Jicamarca (12.0°S, 76.8°W), Arecibo (18.2°N, 66.4°W), and Millstone Hill (42.6°N, 71.5°W) Incoherent Scatter Radars (ISRs). Moreover, the correction of Swarm Te data recently proposed by Lomidze was applied and evaluated. These analyses were performed for two main reasons: (1) to understand how the IRI model deviates from the measurements; and (2) to test the reliability of the Swarm dataset as a new possible dataset to be included in the underlying empirical dataset layer of the IRI model. The results show that the application of the Lomidze correction improved the agreement with ISR data above all at mid latitudes and during daytime, and it was effective in reducing the mismatch between Swarm and IRI Te values. This suggests that future developments of the IRI Te model should include the Swarm dataset with the Lomidze correction. However, the existence of a quasi-linear relation between measured and modeled Te values was well verified only below about 2200 K, while for higher values it was completely lost. This is an important result that IRI Te model developers should properly consider when using the Swarm dataset.
1. Introduction
The ionosphere is a plasma medium consisting of ions and electrons with also a neutral component that, for most of the cases, are not in thermal equilibrium. In fact, since the early satellites and rockets missions in the 1950s and 1960s [], a bulk of evidence has been accumulated demonstrating the non-thermal equilibrium between ions, electrons, and neutrals in the ionosphere. Plasma temperature (ions plus electrons) usually exceeds the neutral one by a factor strongly dependent on altitude, time, and location; moreover, large differences among ion and electron temperatures are also observed. As a consequence, when talking about the temperature of the ionosphere, we need to differentiate between ion (Ti), electron (Te), and neutral (Tn) temperature.
The non-thermal equilibrium of the ionosphere has a number of physical and chemical implications for the ionospheric dynamics and composition. For example, the temperature of charged particles deeply influences the distribution of electron density by driving the recombination rate in the bottomside ionosphere, and affects the diffusive equilibrium state in the topside ionosphere [,]. The main source of energy heating the ionosphere is the Sun: either directly, through the EUV and X-ray radiations illuminating the Earth, or indirectly, at high latitudes, through the precipitation of charged particles induced by the interactions between the solar wind and the magnetosphere-ionosphere system and the consequent Joule heating [,,,]. In the ionization processes occurring in the ionosphere, a certain amount of energy is released as an excess of kinetic energy of photoelectrons. Such photoelectrons dissipate their energy through collisions with charged and neutral particles in a cascade process that first raises the temperature of the electrons (because the transfer of energy via elastic collisions is more efficient between particles of similar mass). In a second stage, the established temperature difference drives the transfer of energy between electrons and the surrounding medium. Above the F2 region, most of the energy transfer is from electrons to ions because ion-electron Coulomb collisions are more efficient than neutral-electron ones; then, the temperature of the ions also increases above the neutrals one. As a further step, the ions lose their excess energy through collisions with neutrals and other ions, thereby raising the temperature of neutrals. As a result of these complex interactions, the entire photoelectron energy dissipates in the neutrals and it is finally transferred down in the lower layers of the atmosphere by conduction and radiation.
Among the three mentioned temperatures, Te is the most variable because of the very low heat capacity of electrons []; moreover, electrons are the most affected by the solar radiation energy input and by the interaction with charged particles entering the Earth’s ionosphere following the geomagnetic field lines at auroral latitudes. The close coupling with the geomagnetic field lines and the plasmasphere produces very distinct spatial patterns in the Te distribution []. As a consequence, Te exhibits very distinctive diurnal, seasonal, spatial, and solar activity trends. This large variability makes it difficult to obtain a precise and reliable description of Te through in-situ or remote sensing measurements. In fact, in-situ measurements taken by Langmuir Probes (LPs) and Retarding Potential Analyzers (RPAs) [,] on-board Low-Earth-Orbit (LEO) satellites provide a global spatial description for different local times, but they are highly dependent on the satellite orbital configuration and altitude and are limited to the satellite mission lifetime. Conversely, ground-based remote sensing techniques such as Incoherent Scatter Radars (ISRs) [,] can better describe the altitudinal, diurnal, and seasonal variability but for a fixed geographic location and for the very few existing ISR facilities. Moreover, the solar activity variability can be described when long time series become available. Furthermore, the cost of this measurement technique strongly limits the number and distribution of ISRs worldwide. As a consequence, for modeling purposes, both in-situ satellites and remote sensing ISRs observations are very important and complement each other.
An outstanding example is represented by the International Reference Ionosphere (IRI) model [], which is the empirical climatological model of the ionosphere used as reference by the ionospheric community, and recently recognized as the official ISO (International Organization for Standardization) standard for the ionosphere []. Through the exploitation of different measurement datasets of ionospheric parameters collected by ionosondes, ISRs, LEO satellites, Global Positioning System (GPS) radio occultation, and rockets, IRI describes the hourly monthly median behavior of the electron density, electron and ion temperature, and ion composition in the ionospheric altitude range, on a global basis, for different levels of solar and magnetic activity. Due to its empirical nature, IRI evolves and improves when new datasets become available and are used to derive the empirical coefficients of its analytical formulations. In this framework, the ability to model the changes of the ionospheric ground state as a function of the different climatological conditions of both the interplanetary medium and the Earth’s seasons is also fundamental in relation to space weather science.
Despite a long series of measurements acquired by both satellites and ISRs, the major current gap in modeling and studying ionospheric Te consists in the lack of an accurate description of its dependence on the most important geographic and geophysical parameters. There is still insufficient knowledge of the global distribution and relevant description of Te longitudinal variations as well as of its seasonal and hemispheric asymmetries, despite some attempts [,,]. A difference between long-term and short-term Te variations with F10.7 has also been noted [], which further complicates the modeling of Te. Empirical models still struggle to describe small-scale structures such as the morning overshoot [,,] and its dependence on solar and magnetic activity or the mid-latitude Te enhancement [,]. The dependence on the magnetic activity and the choice of an appropriate magnetic activity proxy for Te modeling is still an open problem; for example, Brace and Theis [] found no clear dependence of Te on the ap index, with exception of perhaps a slight systematic increase of Te with ap at polar latitudes. Apart from modeling, there are still gaps in the fundamental theory. For instance, Pavlov et al. [] introduced an anomalous conductivity to obtain an agreement between theory and EXOS-D data in the plasmasphere. Even very advanced physics-based models still encounter problems with reproducing observational data (e.g., the post-sunset Te enhancement) and must be driven by measured data []. Another tricky point concerns the existing problems associated with the frequent Te differences among satellite data from different missions, and between in-situ data and ground-based ISR measurements [,], which require in many cases a cross calibration and/or a correction of these data. Because of this, studying and global modeling of Te has become a very challenging problem.
From this point of view, Te observations collected by LPs on-board the European Space Agency (ESA) Swarm satellites [] are very promising for a future inclusion in the IRI Te model []. In fact, the three Swarm satellites launched at the end of 2013 and still operating provide Te data in the topside ionosphere region on a global basis, for different local times, at a 2-Hz rate. As a consequence, the present dataset of Swarm LP Te measurements is that large to cover different latitudes, local times, seasons, and also solar activity levels. Contrary to the electron density, Te data have not been extensively exploited so far; only a few and rather narrowly focused studies have been published, such as [,]. In this context, we aimed to investigate the main climatological trends of Te in the topside ionosphere by taking advantage of seven full years (from the beginning of 2014 to the end of 2020) of Swarm Te observations by comparing the corresponding spatial, diurnal, and seasonal trends with those modeled by IRI. Recently, to improve the accuracy of Swarm Te data, Lomidze et al. [] proposed a correction to observations, based on the comparison with three ISRs located at different latitudes. In this study, we applied the Lomidze correction to Swarm data to verify its performance when compared against IRI-modeled Te data and Te data observed by Jicamarca (12.0°S, 76.8°W), Arecibo (18.2°N, 66.4°W), and Millstone Hill (42.6°N, 71.5°W) ISRs over the last decades.
The paper is organized as follows. In Section 2, the Swarm and ISRs Te datasets, along with the IRI Te model and the Lomidze correction, are discussed. In Section 3, an overall comparison between Swarm-measured (original and after applying the Lomidze correction) and IRI-modeled Te values is first given based on the entire dataset composed by the three Swarm satellites; in addition, Swarm B and IRI Te data are climatologically compared with the corresponding values recorded by the Jicamarca, Arecibo, and Millstone Hill ISRs. In the same section, we also describe and discuss the geographic, diurnal, and seasonal trends shown by both Swarm B and IRI data. Section 4 is devoted to the final discussion of our results and is supported by the conditioned probability density function analysis of Swarm-measured and IRI-modeled data. The conclusions and the future developments are the subject of Section 5.
2. Materials and Methods
2.1. ESA Swarm In-Situ Electron Temperature Data and Application of the Lomidze Correction
The ESA Swarm mission is a constellation of three LEO satellites launched at the end of 2013, and still operating, with the aim of studying the geomagnetic field, the electric currents in the magnetosphere and ionosphere, and the impact of the solar wind on the dynamics of the upper atmosphere []. The three Swarm satellites are labeled A, B, and C, and share the same design and on-board instrumentation. All three satellites were put in a circular near-polar orbit. Swarm A and C have the same orbit configuration (inclination of 87.35°, initial altitude of about 460 km, east-west separation of about 1–1.5° in longitude), while Swarm B has a different one (inclination of 87.75°, initial altitude of about 510 km). As a consequence, Swarm A and C fly in tandem, while Swarm B moves away from the couple A and C by covering different local times. Each satellite takes about 130–140 days to cover all the local times.
Among the instruments carried by Swarm satellites, we focused on LPs data []. LPs provide measurements of in-situ electron density (Ne) and Te along the satellite orbit with an original sampling frequency of 2 Hz in the harmonic mode [,]. Moreover, 1-Hz data are also provided by interpolation of the 2-Hz dataset; it is this dataset containing time series of in-situ Ne and Te data at 1-Hz rate that is used in this work. Specifically, LP data collected by Swarm A, B, and C from 1 January 2014 to 31 December 2020 (seven full years) are taken into account. Swarm’s data are freely downloadable at ftp://swarm-diss.eo.esa.int (accessed on 24 September 2021).
Swarm’s LP data are provided with three flags []: Flags_LP contains information on the source of LP measurements, and Flags_Ne and Flags_Te characterize Ne and Te measurements, respectively. Detailed information about Swarm data quality is available at https://earth.esa.int/web/guest/swarm/data-access/quality-of-swarm-l1b-l2cat2-products (accessed on 24 September 2021). In this study, only the most reliable data were considered; specifically, those recorded by LPs in High-Gain mode. LP data were then selected with the following choice of the flags: Flags_LP = 1, Flags_Ne ≤ 29, and Flags_Te = 10 or 20.
Lomidze et al. [] developed a correction of both Ne and Te Swarm LP data based on the analysis of Swarm measurements matching coincident values retrieved by ISRs, COSMIC/FORMOSAT-3 GPS radio occultation, and ionosondes. For what concerns the Swarm’s Te data correction, Lomidze et al. [] separately considered the measurements collected when the LPs are in High-Gain mode (HG in the following) from those collected with the LPs in Low-Gain mode. Since only HG data were considered in this study, we applied only the HG Lomidze correction to Te data. As a consequence, the Equations (4)–(6) in Lomidze et al. [] were applied on the Swarm A, B, and C Te datasets, namely:
In Equations (1)–(3) Te,Lom is the Lomidze-corrected Te, Te,LP is the original Swarm-measured value, Ne,LP is the corresponding Ne value measured by Swarm LP (i.e., unadjusted). In Equations (1)–(3), and throughout the paper, Te values are in K and Ne values are in cm−3. Equation (1) is valid for the dataset of HG Swarm A LP Te dataset, Equations (2) and (3) for the corresponding Swarm B and C datasets, respectively.
As outlined by Equations (1)–(3), the Lomidze correction is based on a regression analysis of Swarm-measured Te,LP with data retrieved by the three ISRs located at Jicamarca, Millstone Hill, and Arecibo from December 2013 to June 2016 (for more information on the dataset selection on which Equations (1)–(3) are based see []). The shortness of the dataset did not allow a characterization of possible diurnal, seasonal, geographic, and solar activity dependences of the corrections introduced in Equations (1)–(3). As a consequence, Equations (1)–(3) were applied on the entire Swarm datasets although some residual diurnal, seasonal, geographic, and solar activity dependences were somewhat expected. The application of these ISRs-based corrections allowed greatly improving the accuracy of Swarm Te data when compared to ISRs ones (stepping from median differences between 300 and 400 K to near zero) without affecting the corresponding precision and correlation []. As outlined by Lomidze et al. [], the inclusion of the term Ne,LP in Equations (1)–(3) produced a worsening in the precision of the correction (less than 60 K) but with the advantage of removing some certain non-physical patterns from Swarm Te data.
In this work, both Swarm Te,LP original data and Lomidze-corrected Te,Lom data were employed. In Section 3, a statistical comparison between Te data measured by Swarm, calibrated after applying the Lomidze correction, and the corresponding ones modeled by IRI is presented. In the same section, a statistical comparison with Te data recorded by Jicamarca, Arecibo, and Millstone Hill ISRs is also performed.
2.2. Electron Temperature Observations by Incoherent Scatter Radars
ISRs exploit the Thomson backscatter from ionospheric electrons to retrieve the value of several ionospheric parameters including Te []. Specifically, Te profiles are recorded by ISRs in the ionospheric altitude range from about 100 to 1000 km.
Te observations collected by Jicamarca, Arecibo, and Millstone Hill ISRs were used in this work for validation purposes. Jicamarca ISR is located right above the magnetic equator at a Quasi-Dipole (QD, []) latitude of 0.2°N, Arecibo (QD latitude 27.0° N) is a low-latitude station, while Millstone Hill (QD latitude 51.8°N) is a mid-latitude/sub-auroral station. Jicamarca data are from 1996 to 2020, Arecibo ones from 1974 to 2015, and Millstone Hill ones from 1976 to 2020. ISRs data are not continuous in time but the length of the datasets here used allow for a quite uniform representation of the different diurnal and seasonal trends.
The ISRs Te data (including corresponding Te error) were downloaded from the http://cedar.openmadrigal.org website (accessed on 24 September 2021). The altitudes of Swarm satellites fall into standard remote sensing altitude ranges of all three ISRs, which provide reliable data for decades. A similar dataset referring to Ti, for Millstone Hill was recently employed in Pignalberi et al. [].
To perform a comparison with Swarm B-measured and IRI-modeled values, we selected Te values recorded by ISRs in the range 510 ± 20 km. Only the most reliable ISRs’ data were selected, i.e., those with a percentage error lower than 10%. This filtering mostly affected data recorded during the night and early-morning, which are those characterized by the largest dispersion.
2.3. Electron Temperature Description by the IRI Model
In the last version of IRI (IRI-2016, []), two different models for Te are implemented; they are conventionally named BIL-1995, and TBT-2012 (http://irimodel.org/, accessed on 24 September 2021). The BIL-1995 is the oldest option and is based on the works by Bilitza [,,] who, through the application of the Booker approach [] to the Brace and Theis [] and Spenner and Pluge [] models, describes the Te vertical profile for the ionospheric altitude range between 60 and 2000 km. Since the IRI-2001 version [], IRI has included an additional option based on Intercosmos data [], that since the IRI-2012 version [] was updated with the most recent TBT-2012 model [] which incorporates all available satellite Te data. The solar activity dependence, also described in Truhlik et al. [], is mainly based on results from Truhlik et al. []. In the current IRI version, this additional option is called TBT-2012+SA and represents the option related to the TBT-2012 model with the solar activity term switched on. Since the TBT-2012+SA is the current default option for the Te modeling in IRI, it has been applied in this work to perform a comparison with Swarm and ISRs measured data and will be briefly described here.
In the TBT-2012 model [], Te values at five fixed anchor points at 350, 550, 850, 1400, and 2000 km of altitude are modeled through a spherical harmonic expansion in a system of associated Legendre polynomials (up to the 8th order) in terms of the magnetic local time and a latitudinal coordinate based on a combination of invariant and dip latitude (invdip, []). Through the use of Te measurements from LPs on-board several satellite missions (for a detailed description of the dataset see Bilitza et al. [] and Truhlik et al. []), the coefficients of the spherical harmonic expansions were calculated for summer and winter solstices, and for the combined equinoxes (independently of the hemisphere); then, interhemispheric differences in magnetic coordinates were not considered in the model. The solar activity dependence was then included by selecting three solar activity ranges and describing the corresponding variability as a function of the PF10.7 solar index [].
The complete vertical Te profile was obtained by applying the Booker profile function formalism [,]. First, a piece-wise function was built making a linear interpolation of modeled Te values between anchor points, which produced a vertical profile divided in regions with a constant Te gradient. Second, Epstein-step functions were applied to realize the transition from regions with different gradients and obtain the skeleton profile, which produced a continuous analytical representation of the Te vertical profile. Finally, the skeleton profile was integrated to obtain the Booker profile function of Te, which output a continuous and smooth description of the entire modeled Te vertical profile. For a detailed mathematical description of the Booker profile function formalism, refer to the Appendix section of Pignalberi et al. [].
In IRI, Te is constrained to be equal to Tn described by the NRLMSISE-00 model [] for altitudes lower than 120 km. An example of IRI (TBT-2012+SA default option) modeled vertical Te profile is given in Figure 1 (green curve) where the anchor points that IRI uses to describe the entire profile are highlighted. An anchor point at a non-fixed altitude around 270 km (Te,m in Figure 1) was introduced on the basis of Jicamarca and Arecibo ISRs data to describe a local daytime maximum in Te characterizing mostly the low latitudes [].
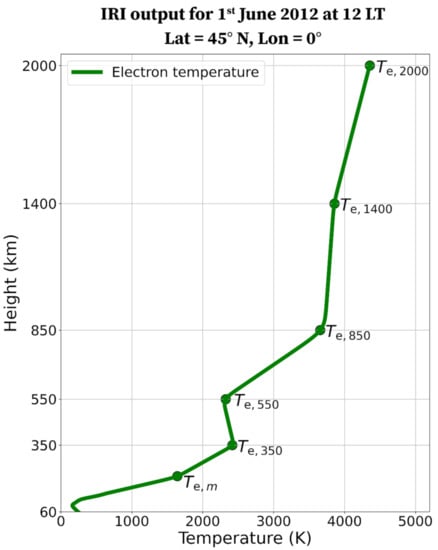
Figure 1.
IRI modeled (TBT-2012+SA default option) vertical profile of Te (green curve) at 45° N of latitude and 0° of longitude for 1 June 2012 at 12 local time (LT). The five fixed anchor points at 350, 550, 850, 1400, and 2000 km of altitude are highlighted along with the additional anchor point Te,m.
In this work, the IRI model (TBT-2012+SA option) was run on the entire Swarm satellites dataset as if it were collocated and synchronized with LPs on-board Swarm satellites. As a consequence, 1-Hz time series of IRI-modeled Te values were produced for the time and locations probed by Swarm satellites. In this way, a one-to-one comparison between Swarm-measured and IRI-modeled Te values was guaranteed.
3. Results
3.1. Overall Statistical Comparison between Measured and Modeled Electron Temperature Values
First of all, we aimed to investigate the effect of the application of the Lomidze correction on Swarm Te measurements through a comparison with IRI-modeled values for the period 2014–2020 for all the three Swarm satellites.
An overall comparison between Swarm-measured (original and Lomidze-corrected) and IRI-modeled Te values is given in Figure 2 and Figure 3 as joint histograms and distributions of residuals between measured and modeled data. From the residuals between measured and modeled values, the following statistical metrics were calculated: mean and standard deviation of the residuals, Root Mean Square Error (RMSE, Equation (4)), and Relative Root Mean Square Error (RRMSE, Equation (5)).
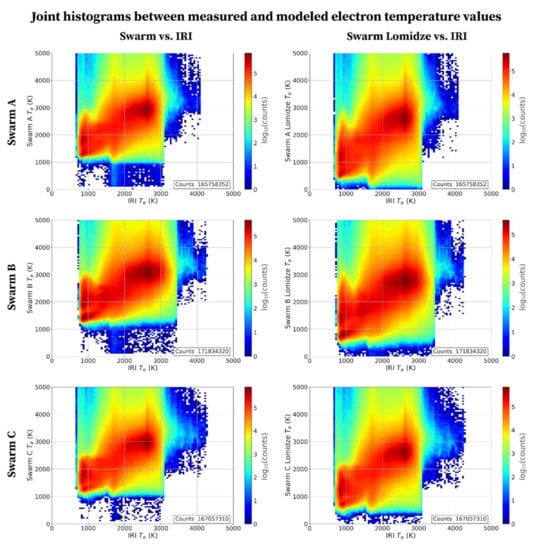
Figure 2.
Joint histograms between Te values measured by Swarm and modeled by IRI (TBT-2012+SA default option): (left panels) original Swarm-recorded values, (right panels) Swarm values corrected with Lomidze et al. []. From top to bottom, the analysis refers to Swarm A, B, and C. In each panel, the number of total counts is reported in the lower right corner.
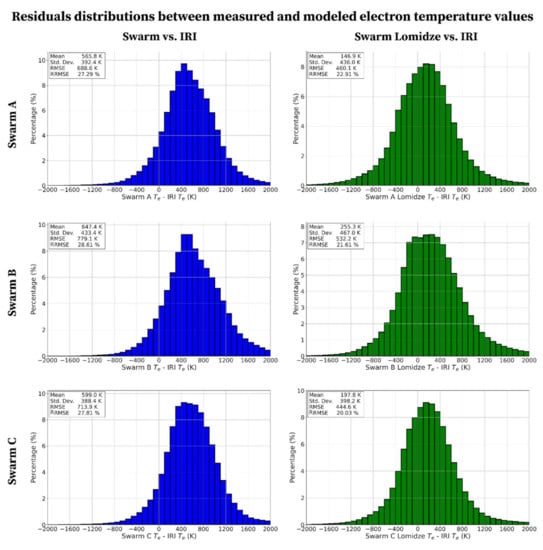
Figure 3.
Statistical distributions of the residuals between Te values measured by Swarm and modeled by IRI (TBT-2012+SA default option): (left panels, in blue) original Swarm-recorded values, (right panels, in green) Swarm values corrected with Lomidze et al. []. From top to bottom, the analysis refers to Swarm A, B, and C. In each panel, some statistical metrics are reported in the upper left corner.
In Equations (4) and (5), Te,measured is the Te measured by Swarm (i.e., Te,LP) or corrected according to Lomidze et al. [] (i.e., Te,Lom), while Te,modeled is the corresponding value modeled by IRI. Temperatures are in K. N is the number of values on which the statistics are calculated.
Figure 2 represents the joint histograms between Te values measured by Swarm and modeled by IRI and gives information on the distribution of measured and modeled data as a function of the corresponding magnitude. Most of the values cluster in the reddish region, i.e., where more than 104 values are counted inside each bin (the scale is logarithmic). It is interesting to note that IRI-modeled data never go beyond about 4300 K, while Swarm data (both original and Lomidze-corrected ones) show a long tail well beyond 5000 K (not shown in the figure), even though the application of the Lomidze correction reduces their magnitude. To characterize the accordance between modeled and measured values and the global effect of the application of the Lomidze correction, corresponding residuals were studied.
Figure 3 represents the statistical distributions of the residuals between values measured by Swarm and modeled by IRI. By looking at the statistical metrics reported in the upper left corner of each panel, it emerges how the application of the Lomidze correction to Swarm data improved the accuracy when compared to IRI-modeled data. In fact, the mean of the residuals decreased from about 560–650 K to about 150–250 K, with a 400 K average improvement. Conversely, the application of the Lomidze correction did not affect the precision of Swarm data, as highlighted by the standard deviation values that remained in the range 380–470 K. Nevertheless, the application of the Lomidze correction generally improved the agreement with IRI data, as demonstrated by the RMSE and RRMSE values that decreased, respectively, from about 690–780 K to about 440–530 K, and from about 27–29% to about 20–23%.
To sum up, the results shown in Figure 3 demonstrate how the application of the Lomidze correction to Swarm Te data can improve the agreement with IRI-modeled values, without impacting the corresponding precision. However, we are aware that the comparison with a model, IRI, cannot guarantee the reliability and efficacy of the Lomidze correction; the only comparison that can truly tell whether this correction improves real Te observations is that with other independent measurements. This is why we performed a comparison against Te data observed by ISRs.
3.2. Statistical Comparison against ISRs Data
We implemented a statistical comparison among Swarm (original and corrected values), IRI, and ISRs Te data for the Jicamarca, Arecibo, and Millstone Hill locations to verify the ability of Swarm and IRI to describe the diurnal and seasonal trends of Te shown by ISRs data, and their accuracy.
Unlike Lomidze et al. [], we did not look for correspondences (in both time and space) between ISRs and Swarm data because of the limited number of correspondences achievable (of the order of some hundreds from 2014 to 2020, for each satellite). Instead, we applied a statistical approach by comparing the diurnal and seasonal trends exhibited by both Te values collected by ISRs and by Swarm B for the ISRs locations. In this way, we could investigate how much Swarm, and also the IRI model, can describe the diurnal and seasonal Te trends at equatorial, low, and mid latitudes by making a comparison with Jicamarca, Arecibo, and Millstone Hill data, respectively. This comparison and those of the following section were limited to the Swarm B satellite because it is the nearest to the IRI vertical profile anchor point at 550 km of altitude. Moreover, as follows from Figure 2 and Figure 3, the statistical analysis for all three satellites was very similar, with slightly larger differences for Swarm B.
Specifically, Te values collected at Jicamarca, Arecibo, and Millstone Hill in the range (510 ± 20) km were binned as a function of the magnetic local time (MLT, in QD coordinates) and season, and corresponding boxplots were generated. The binning in 15-minutes wide (in MLT) bins allowed describing the diurnal trend of Te at ISRs location. The seasonal trend was studied by binning data in four periods (expressed in day of the year, doy) around solstices and equinoxes and covering the entire year:
- March Equinox: 35 ≤ doy ≤ 125;
- June Solstice: 126 ≤ doy ≤ 217;
- September Equinox: 218 ≤ doy ≤ 309;
- December Solstice: doy ≤ 34 OR doy ≥ 310.
No solar activity data selection was performed because the quantity of both ISRs and Swarm data does not allow further split, and because the investigation of Te dependence on solar activity is outside of the scope of this study. As a consequence, the results in Figure 4, Figure 5 and Figure 6 are representative of average solar activity conditions of the years covered by ISRs datasets (see Section 2.2), and of the years 2014–2020 for Swarm and IRI.
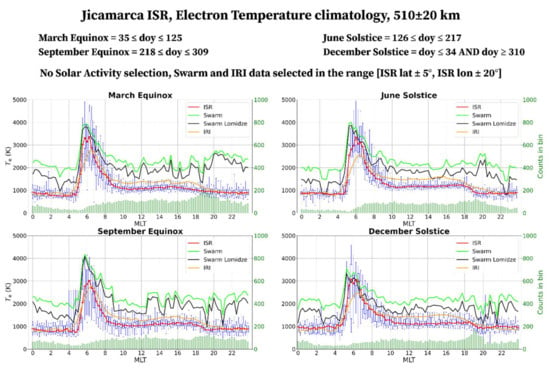
Figure 4.
Comparison between Te data observed by Jicamarca ISR (12.0°S, 76.8°W, QD latitude 0.2°N) at around 510 km of altitude (boxplots), Swarm B satellite (green line), Swarm B corrected with Lomidze (black line), and those modeled by IRI (TBT-2012+SA default option) (orange line). Both measured and modeled data are binned as a function of MLT (x-axis) in bins 15-minutes wide, and of the season by selecting data around the equinoxes and solstices (each panel represents a different season). ISR data are represented as boxplots in which the red horizontal line is the median; the 25th and 75th percentiles are represented as the lower and upper limits of each box; the 5th and 95th percentiles are shown as lines extending below and above each box (whiskers). Green shaded bars at the bottom of each panel represent the number of ISR data falling in that bin. Conversely, for Swarm and IRI, only the median values are represented as solid curves.
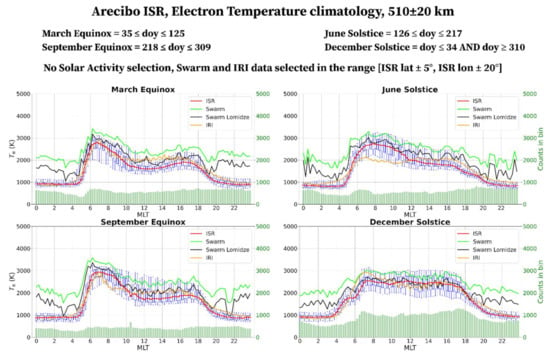
Figure 5.
Same as Figure 4 but for Arecibo ISR (18.2°N, 66.4°W, QD latitude 27.0°N).
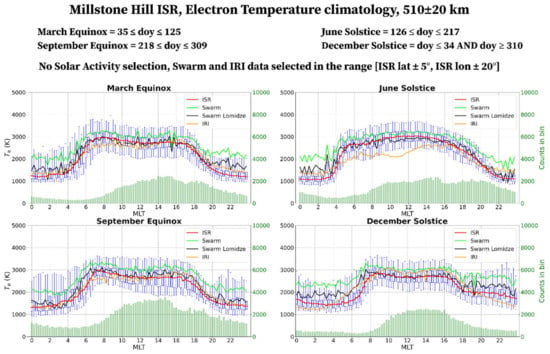
Figure 6.
Same as Figure 4 but for Millstone Hill ISR (42.6°N, 71.5°W, QD latitude 51.8°N).
In summary, every ISR dataset was split in 384 (96 diurnal x 4 seasonal) bins and the following statistical metrics were calculated for the boxplot representation:
- 5th percentile, i.e., the lower whisker;
- 25th percentile, i.e., the first quartile;
- 50th percentile, i.e., the second quartile, representative of the median;
- 75th percentile i.e., the third quartile;
- 95th percentile, i.e., the upper whisker.
For this kind of comparison, the median is the more appropriate statistical metric because it cuts off the outliers of the distribution. The difference between 75th and 25th percentiles defines the inter-quartile range (IQR), which provides a measure of the data dispersion around the median value, while the whiskers highlight the tails of the distribution.
Figure 4, Figure 5 and Figure 6 show the boxplots for the Jicamarca (Figure 4), Arecibo (Figure 5), and Millstone Hill (Figure 6) sites. For the comparison with ISRs results, both Swarm B-measured (original and corrected with Lomidze) and IRI-modeled Te data were selected and binned as done for ISRs data. Specifically, from the Swarm B dataset, we selected those measurements falling inside a region centered at ISRs’ geographic coordinates and extending ±5° in latitude and ±20° in longitude. We tested regions of different extension in both latitude and longitude around the ISRs’ location. The choice we made is the one balancing the amount of data needed for the statistical comparison and the preservation of the characteristic trends at the ISRs locations. Then, the selected Swarm B (original and corrected with Lomidze) and IRI data were binned as ISRs data and the corresponding median values are superposed to ISRs’ boxplots in Figure 4, Figure 5 and Figure 6.
Figure 4 shows how equatorial values at Jicamarca are characterized by the presence of a remarkable morning peak between 5 and 8 MLT, with median values from ISR exceeding 3000 K; this phenomenon is often referred as morning overshoot [,,,]. Overall, daytime values stand at about 1000–1300 K, while nighttime ones at about 700–1000 K, in a quite steady fashion. Differently from the dawn solar terminator hours, the ones related to the dusk solar terminator do not exhibit a peak but only a small ramp with Te smoothly stepping from the daytime to the nighttime behavior. Of course, the MLTs of both the morning overshoot and the dusk ramp slightly change according to the season. The MLTs characterized by the morning overshoot exhibit the highest dispersion of data as described by the IQRs and whiskers values. The seasonal variability is really weak at Jicamarca due to the illumination conditions that do not change significantly over the year. Both Swarm and IRI can catch the main diurnal features of Te for each season but with remarkable differences in the absolute values. IRI represents reliably nighttime values, while it slightly overestimates daytime values and underestimates values in the morning sector when the overshoot occurs. Differently, Swarm (both original and corrected with Lomidze) performs a general overestimation independently of the hour. Moreover, Swarm values do not exhibit differences between day and night, with the exception of the morning peak. The application of the Lomidze correction reduces the original overestimation of Swarm measurements, but not enough to make them match with ISR data. When comparing with ISRs data, we have to take into account that the IRI TBT-2012+SA option is based on data recorded from satellites [], that are often limited in both space and time. In fact, the differences between IRI and Jicamarca ISR values might be related to the limited spatial and temporal resolution of the model (20 degrees in latitude and 80 minutes in MLT), resulting in the inability of the model to accurately describe the equatorial daytime dip in Te and thus resulting in an overestimation of daytime Te at the magnetic equator by IRI. At MLTs of the narrow and high morning peak, this limited resolution is most likely at the base of both the underestimation and some mismatches of the position of the morning peak maximum made by the IRI model. Another reason that could explain the observed differences is the fact that in-situ probes can produce higher Te values in a non-equilibrium plasma [] or if some sort of probe contamination occurs []. A possible combination of both effects thus could result in both an overestimation of about 30% during daytime and an underestimation of about 20% of the peak maximum made by the IRI model (as evidenced by Figure 4). During nighttime, when plasma is in thermal equilibrium and the limited spatial and temporal resolution of the model is not so important, the agreement between IRI and ISR is very good.
Figure 5 shows the results for Arecibo. Compared to Jicamarca, at Arecibo the seasonal variability is more marked above all for MLT hours from noon to dusk. Like Jicamarca, Arecibo values also show a remarkable morning increase with temperatures abruptly increasing from about 1000 to 2500–3000 K. However, Arecibo daytime values do not decrease as for Jicamarca but remain at around 2000 K (except for the December solstice) with significant differences in the sector 14–19 MLT, depending on the season. In fact, March and September equinoxes show a very similar trend where the first hump corresponding to the morning increase is followed by a small second hump before sunset, while for the June solstice (summer), the second hump does not appear and values steadily decrease from daytime to nighttime. The December solstice (winter) is instead characterized by quite constant values (at about 2500 K like the morning peak one) during daytime and a very distinct decrease at sunset. IRI can reliably represent the nighttime Te at Arecibo, while some departures are evident during daytime, above all in the morning for the June solstice (underestimation) and in the central hours of the day at equinoxes (overestimation). Compared to Jicamarca, at Arecibo, the accordance between Swarm and ISR data is better, especially in the daytime sector, while nighttime values are still affected by a remarkable overestimation (even after applying the Lomidze correction). A very good accordance is found for the winter season (December solstice) during daytime. Swarm and IRI can describe both the diurnal and seasonal trends of Te at Arecibo.
Figure 6 summarizes the results for Millstone Hill, where Te manifests a very distinct diurnal behavior characterized by a sharp division between nighttime and daytime values. Nighttime values are of the order of 1100–1500 K, while the daytime values range between 2500 and 3000 K. Differently from Arecibo, in this case, daytime values are always quite constant with a slight tendency to maximize at noon during summer (June solstice). Winter (December solstice) nighttime values are remarkably higher than summer ones due to conjugate heating [,]. Except for June solstice, IRI can reliably describe the diurnal behavior of Te at Millstone Hill. It is the same for Swarm after applying the Lomidze correction; in this case the agreement with ISR’s data is remarkable for both the representation of the diurnal and seasonal trends and the accuracy of the absolute values; only a slight overestimation is visible during nighttime particularly at December solstice.
It has to be considered that the Lomidze correction, aside from being based on the same three ISRs here studied, is heavily biased toward Millstone Hill ISR data that were more represented in the Lomidze et al. [] dataset than Arecibo data and above all Jicamarca. As a consequence, since Lomidze et al. [] cumulated the data of the three ISRs to derive a single calibration curve, it should be expected that the correction is more effective at Millstone Hill than at Arecibo and Jicamarca. This agrees very well with the results shown in Figure 4, Figure 5 and Figure 6. Moreover, the Lomidze correction does not discriminate between daytime and nighttime or between different seasons. Our results show that the Lomidze correction has the best performance for daytime hours and the worst for nighttime hours, with no distinct seasonal difference. This suggests that a latitudinal and day/night dependence should be included in the Lomidze correction when enough data become available in the future.
As we can see from Figure 4, Figure 5 and Figure 6, the daily Te profile varies with the ISR geographic location. For example, at Jicamarca, which is at the magnetic equator, Te shows a single sharp maximum around dawn that can be associated with the well-known morning overshoot. This feature is characteristic of low latitudes, and in fact is present also in the daily profiles acquired at Arecibo. Here, and at Millstone Hill (middle and sub-auroral latitudes), the increase of Te in the dayside is due to the increased sunlight and a second hump at dusk marks the decrease of Te in passing from day to night. At Millstone Hill, an increased Te during nighttime is recorded at the December solstice, mainly due to the decrease of plasma density in the F layer and the following reduction of the collisional cooling effect, and also to the conjugate heating. To better highlight and describe all of these different spatial features exhibited by the topside Te, in the next section, the main spatial trends of Te will also be investigated, in both geographic and magnetic coordinates.
3.3. Statistical Trends of Swarm-Measured Electron Temperature Values and Comparison with IRI-Modeled Ones
The results of Section 3.1 and 3.2 demonstrate that the application of the Lomidze correction improves the agreement between Swarm data and those modeled by IRI and measured by different ISRs. This is why, in the following analyses, we focus only on Swarm B data corrected according to Lomidze et al. [].
Swarm B data from 2014 to 2020, and corresponding IRI-modeled values, were binned as a function of the geographic coordinates with bins 2.5°-wide in latitude and 5°-wide in longitude. For each bin, the median value was considered, as representative of the main statistical trend, after discarding the outliers through the Median Absolute Deviation statistical procedure (see Section 3.3 by Pignalberi et al. [] for a detailed description). The binning was first performed on the entire dataset and then by selecting MLT (in QD coordinates) sectors representative of the dawn (5–7 MLT), daytime (12–15 MLT), and nighttime (0–3 MLT) conditions. This was done because at a fixed altitude, the Te diurnal variations are known to be the most important along with the latitudinal ones [,,].
Figure 7 shows the corresponding results considering all the MLTs and the different MLT sectors, for both Swarm-measured and IRI-modeled data, and the corresponding percentage of the normalized residuals between them. The figure highlights how the Te spatial distribution follows the configuration of the Earth’s magnetic field lines. In fact, the characteristic shape of the magnetic equator and of the auroral regions stand out, and this is somewhat expected because the plasma in the topside ionosphere is generally constrained by the geomagnetic field []. This behavior has also been recently confirmed by Giannattasio et al. [,] that, by using Swarm data, identified patterns in the parallel electrical conductivity (which is crucially affected by Te) related to features of the geomagnetic field such as regions R1 and R2 [] or the magnetic cusp []. They also identified variations in the parallel electrical conductivity due to MLT, QD latitude, season, solar, and geomagnetic activity. The MLTs around dawn highlight the fact that the morning peak is a phenomenon affecting only the low latitudes, which follows the magnetic equator shape and reinforces in the longitudinal sector between 80°W and 80°E (including South America and Africa) where the departure between the magnetic equator and the geographic one is the largest. At the morning peak, Swarm B values exceed 3000 K in many longitudinal sectors, well above those recorded at mid latitudes and even higher than high latitude ones. In contrast, during daytime and nighttime, the high latitudes experience the highest values; in both cases, the increase of Te from mid to high latitudes is limited to a quite narrow latitudinal range where the spatial gradient is concentrated: at mid latitudes during daytime and at the sub-auroral and auroral boundaries during nighttime. When compared to IRI-modeled values, the largest differences emerge at magnetic equator latitudes at dawn, and at low and mid latitudes during daytime and nighttime, respectively. Overall, Swarm measurements exceed IRI values for most cases and this is in line with the results of Figure 2 and Figure 3. The excess is particularly clear at the morning peak and at low and mid latitudes at nighttime. If we recall the analysis shown in the previous section, based on the comparison with ISRs data (Figure 4, Figure 5 and Figure 6), we can say that Swarm overestimates the nighttime values; at the morning peak, Jicamarca ISR results (Figure 4) point out that the difference between Swarm and IRI is mainly due to a joint action of both the Swarm overestimation and the IRI underestimation.
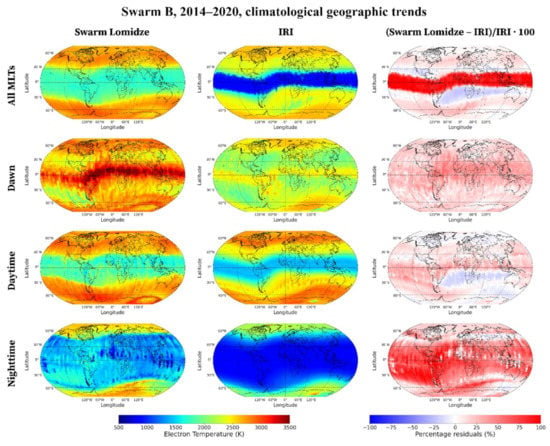
Figure 7.
Statistical geographic trends of Te measured by Swarm B after applying the Lomidze et al. [] correction (first column), of the corresponding values modeled by IRI (second column), and of the percentage of normalized residuals between measured and modeled values (third column). Those represented are median values binned in geographic coordinates; 2.5° in latitude, 5° in longitude. The first row pertains to all MLTs (i.e., to the entire Swarm B dataset), second row to MLTs around dawn, third row to daytime MLTs, and fourth row to nighttime MLTs.
As highlighted by Figure 7, the Earth’s magnetic field has a strong influence on the diurnal trend of Swarm and IRI values. Therefore, we binned Te data also as a function of QD latitude and MLT with bins 2.5°-wide and 15 minutes-wide, respectively. The binning was first performed on the entire dataset and then by selecting different days of the year representative of the March equinox, June solstice, September equinox, and December solstice conditions, as done in Section 3.2. for ISRs data.
Figure 8 shows that the overall diurnal trend of Te is characterized by different well-defined features at different latitudes. At low latitudes, the morning peak is the main feature and small day–night differences are visible, which confirms the results from Jicamarca ISR (Figure 4). At mid latitudes (30–60° QD latitude), no distinct morning peak is present and the main feature is the remarkable difference of absolute values between daytime and nighttime, which confirms the results from Millstone Hill ISR (Figure 6). At high latitudes, the diurnal trend is less pronounced with high values throughout the day that intensify during daytime at the auroral boundaries. The agreement between Swarm and IRI is very good for what concerns the overall diurnal pattern. The main differences characterize the morning peak hours and the nighttime hours for low and mid latitudes. It should be noted that IRI cannot describe the very well-located morning peak maximum just over the magnetic equator, and the Te increase at the auroral boundaries during daytime. For both cases the reason has to be found in the limited spatial resolution of the model. As expected, no remarkable differences characterize the equinoxes, while the comparison between the solstices highlights seasonal differences and a different description of these by Swarm and IRI. In fact, while IRI shows a clear seasonal dependence for daytime hours, with higher Te values in the winter hemisphere than in the summer one, Swarm data show a less marked seasonal difference.
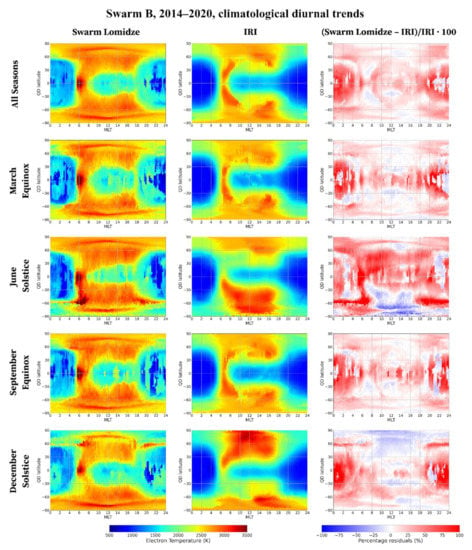
Figure 8.
Statistical diurnal trends of Te measured by Swarm B after applying the Lomidze et al. [] correction (first column), of the corresponding values modeled by IRI (second column), and of the percentage residuals between measured and modeled values (third column). Those represented are median values binned in QD magnetic coordinates; (x-axis) 15 minutes in MLT, (y-axis) 2.5° in QD latitude. First row independently of the season (i.e., for the entire Swarm B dataset), second row for the March equinox, third row for the June solstice, fourth row for the September equinox, and fifth row for the December solstice.
The diurnal behavior of Te shown in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 is also consistent with previous results in the literature, where the observed trend was recognized to be mainly due to solar UV radiation (in the dayside) and the precipitation of particles (both in the dayside and nightside) caused by magnetosphere-ionosphere coupling []. Apart from the obvious contribution due to the excess of energy of photoelectrons in the dayside especially at mid latitudes, electrons, protons and alpha particles of solar origin may be injected into the ionosphere during open magnetosphere conditions, i.e., when reconnection at the magnetopause occurs, at QD latitudes of about 80° and around 12:00 MLT [,]. The precipitation of such particles is expected to enhance Te in the cusp regions [] and at lower latitudes in the pre-noon sector []. Te also increases on the nightside due to particle precipitation. In more detail, plasma acceleration occurs in response to reconnection phenomena in the far-away geomagnetic tail regions, generating a three-dimensional current system modeled by the current wedge paradigm [] that connects the tail to the nightside ionosphere in correspondence of the R2 region []. Interestingly, the peak of such enhancement is observed in correspondence with the boundary between R2 and the main ionospheric trough in the pre-dawn sector due to the joint action of particle precipitation and the decrease of Ne [,].
The diurnal variation of Te also shows a clear dependence on the local season, which emerges from Figure 8 when considering the six-months shift of local seasons in Northern and Southern hemispheres in correspondence with solstices and equinoxes. Specifically, the increase of Te is remarkable above all in the nightside winter, from about 20 MLT to pre-dawn at QD latitudes of about 60° and especially in the Southern hemisphere, and in the dayside summer. Such a behavior can be easily interpreted in light of the previous literature. In fact, previous studies concluded that field-aligned currents density changes from winter to summer by about a factor of 2 in the dayside due to the increase of photoelectron flux and the following increase of Te [,,,,]. In this case, the increase of Te is driven by both the increase of EUV photoionization and, at very high latitudes (~80°), by precipitations in the cusp region around noon. In the nightside, particle precipitation is the dominant process at auroral and sub-auroral latitudes and becomes more and more important when proceeding from summer to winter. In particular, during winter the enhancement of Te reaches the maximum expansion from dusk to about 08:00 MLT, especially in the Southern hemisphere. The explanation of this behavior is the simultaneous collapse of both electron and ion density in the ionospheric F layer, and the following collapse of the contribution of collisional cooling to Te. Therefore, in the absence of mechanisms that reduce the energy of precipitating particles Te is free to increase due, e.g., to energy exchanges with the nightside magnetosphere. Not surprisingly, there is an anticorrelation between Ne and Te, and Te is significantly enhanced in regions of depleted Ne, such as between region R2 and the main trough in the nightside winter; while, in contrast, it decreases in regions of enhanced Ne due to energy loss to the ions [,,,,]. Some studies in the past tried to establish a link between Ne and Te, since Ne is a major factor in electron energy loss due to the ionospheric plasma quasi-neutrality (density of ions is nearly equal to Ne). Generally, an anti-correlation was found. Brace and Theis [] established an interrelationship between Ne and Te using Atmosphere Explorer C data. Kakinami et al. [] found a U shape in the Te–Ne dependence using Hinotori satellite data. Their results suggest that an additional heat source has to be considered, even though the mechanism is unknown. Su et al. [] dealt with the investigation of Te–Ne correlation using data from the DEMETER satellite, by highlighting the variability of this correlation depending on the latitude, local time, and season. Hu et al. [] used Ne measured from COSMIC as a driver for Te in their neural network Te model. Generally, they found a better agreement between their model and ISR data than between ISR data and IRI values. Thus, it is evident that the Te–Ne relationship could help in the investigation of Te behavior in the ionosphere but it is a complex problem itself. This is why, in this study, we did not investigate the Te–Ne correlation using the Swarm data and we focus only on Te.
Compared to the spatial and diurnal trends, the interpretation of the seasonal trends exhibited by Swarm data is more difficult and the differences with IRI are significant. Overall, the main seasonal differences concern the summer and winter seasons for specific MLT sectors. Nighttime Te values at high latitudes have been found to be deeply influenced by the solar illumination conditions []; in fact, high values are found in the summer hemisphere lit by the Sun. In contrast, low latitudes are not affected by seasonal changes at nighttime. Te at mid latitudes during local winter can be affected by strong heating due to conjugate photoelectrons if the opposite hemisphere is already sunlit.
4. Discussion
The results of Section 3.1. highlighted how the application of the Lomidze correction to Swarm-measured data reduces the mismatch with IRI-modeled data but, as pointed out by Section 3.3. results and the comparison with ISRs data (Section 3.2), several differences between measured and modeled data are still present for what concerns both Te magnitude and the corresponding spatial, diurnal, and seasonal variations.
To better highlight the relation between measured and modeled data, the conditioned probability density function between them has been calculated. Specifically, we calculated the probability density of measured Te values, both original and Lomidze-corrected, conditioned by IRI-modeled ones in 50 K-wide range around a given value T0 (ranging from 25 to 4975 K in steps of 50 K):
In Equation (6), Te,measured is the Te measured by Swarm (i.e., Te,LP) or corrected according to Lomidze et al. [] (i.e., Te,Lom), while Te,modeled is the corresponding one modeled by IRI and p is the conditioned probability density. Equation (6) was calculated for each T0 equal to the Te,modeled values used to define the ranges for the conditioned probability density calculation. Conditioned probability density values are represented in Figure 9 as colored bins, while bins with p < 10−6 are in white. For each [T0 − 25; T0 + 25) K range, the median is calculated and represented as a black circle, and corresponding error bars are the median absolute deviation values [].
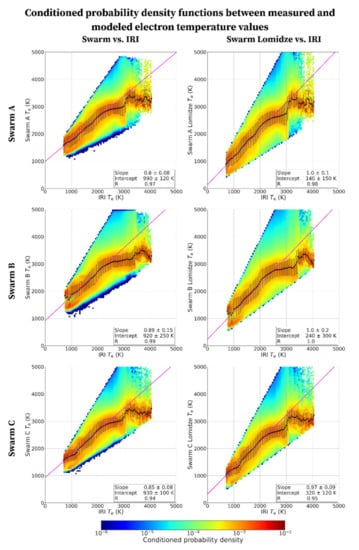
Figure 9.
Conditioned probability density function of Te values measured by Swarm satellites (left panels), and after applying the Lomidze et al. [] correction (right panels), at fixed IRI-modeled Te values. From top to bottom, the analysis refers to Swarm A, B, and C. The black circles refer to the median values of measured and corrected Swarm Te at fixed IRI-modeled Te values. Error bars are the median absolute deviation. The magenta lines are linear regression fits for IRI Te below 2200 K, with corresponding parameters shown in the lower right boxes.
Median values of Figure 9 were used to perform a linear regression analysis and to obtain the corresponding slope, intercept, and Pearson correlation coefficient, namely:
where cov is the covariance matrix and σ the variance.
Linear regression best fit lines are represented in Figure 9 in magenta, with corresponding slope, intercept, and R values reported in each panel. The analysis was restricted to Te,modeled ≤ 2200 K because the linear relation between measured and modeled data fully breaks above this threshold, as clearly highlighted by the median values of Figure 9.
The results of Figure 9 confirm and complement those shown by Figure 2 and Figure 3. Specifically, the slopes of the linear best fit, which range between 0.80 and 0.89 for the original Swarm data, after applying the Lomidze correction range between 0.97 and 1.00, while the intercept values decrease from 920–990 K to 140–320 K. This confirms the accuracy improvement provided by the Lomidze correction. Differently, the correlation coefficient (R) was slightly affected by the Lomidze correction because this correction is substantially linear, apart from the term dependent on Ne,LP (see Equations (1)–(3)); anyway, the correlation is very high in both cases (R > 0.94). However, we have to take into account that these results are valid only in the range Te,modeled ≤ 2200 K, where a linear dependence with a slope near 1 between measured and modeled data is evident. A non-linear dependence is clearly visible for Te,modeled > 2200 K and in principle could be indifferently due to the Swarm LPs instrumentation, possible shortcomings of the Lomidze correction, and the IRI representation of the highest Te values.
Recently, Pignalberi et al. [] studied the occurrence of very high Swarm-measured Te values (Te,measured ≥ 6000 K), and corresponding spatial, diurnal, and seasonal variations. As expected, very high Te values were recorded above all at high latitudes but with well-defined trends. Specifically, the occurrence of very high Te,measured values maximizes in winter and is minimum in summer, with intermediate values at both equinoxes. Moreover, the occurrence is asymmetric between hemispheres, being highest in the Southern hemisphere, where it can reach 40% of the total observations in winter. These extremely high Te values are not represented at all by IRI, which is limited to values below about 4300 K (see Figure 2 and Figure 9). As a consequence, the departure from the linear dependence between Te,measured and Te,modeled for the highest values cannot be related to the application of the Lomidze correction. The fact that the occurrence of Te,measured ≥ 6000 K values is quite remarkable at high latitudes and that it usually happens at small spatial and temporal scales [] drives us to the conclusion that the median climatological representation given by the IRI model cannot properly represent such very fast and steep Te variations. This is mainly due to the limited spatial (20 degrees in invdip latitude) and temporal (80 minutes in MLT) resolution of its current spherical harmonic expansion approach []. Nevertheless, we point out that the Lomidze correction is based on a dataset of Te measurements from Arecibo, Jicamarca, and Millstone Hill ISRs, which are all low- and mid-latitude stations. This means that no high-latitude measurement was considered and, most importantly, only values in the range Te,measured < 3500 K (in HG mode) were used to derive the calibration curves (see Figure 7 in []). With regard to this, it would be of great benefit to include high-latitude ISR stations (e.g., Resolute Bay (74.7°N, 94.9°W), Poker Flat (65.1°N, 147.5°W,), Irkutsk (52.9°N, 103.3°E), EISCAT Tromsø (69.3°N, 19.1°E), EISCAT Kiruna (67.5°N, 20.3°E), EISCAT Sodankylä (67.2°N, 26.4°E), EISCAT Longyearbyen (78.1°N, 16.0°E)) in the Lomidze dataset to also characterize the high Te values usually recorded at auroral latitudes. Finally, the possible overestimation of Te values measured by Swarm LPs due to instrumental/environmental effects cannot be completely ignored. This is why, a more in-depth analysis, based on different datasets and measurement techniques, is needed to clarify the origin and reliability of the very high Te values recorded by Swarm satellites.
5. Conclusions
In this study, the main statistical median features of the topside ionosphere Te were investigated on a global basis through data collected by LPs on-board Swarm satellites from the beginning of 2014 to the end of 2020. Swarm Te measured data were compared with corresponding values modeled by IRI, and with data measured by Jicamarca, Arecibo, and Millstone Hill ISRs, to evaluate the reliability of both Swarm data and IRI model in the description of the spatial, diurnal, and seasonal trends of Te in the topside ionosphere.
We also investigated the effectiveness of the correction to Swarm Te values proposed by Lomidze et al. [] through comparison with IRI-modeled data and ISRs-measured ones. Specifically, we found that the application of the Lomidze correction:
- improves the agreement between Swarm data and corresponding ones modeled by IRI when the entire dataset is considered, for every Swarm satellite. This is attested by the average 400 K improvement in the mean residuals between Swarm and IRI after the Lomidze correction application;
- does not alter either the dispersion of Swarm data around the mean and the correlation between Swarm and IRI, due to the linear character of the correction;
- reduces the Swarm data RMSE from about 690–780 K to about 440–530 K, and RRMSE from about 27–29% to about 20–23%, when compared to IRI data;
- generally improves the agreement between Swarm and ISR data. The improvement is particularly evident at Millstone Hill while it is lower at Arecibo and even lower at Jicamarca. Moreover, the correction is more effective during daytime than nighttime;
- does not alter the linear relation trend between measured and modeled Te values in the range below 2200 K, but it improves the corresponding slope (closer to 1) and intercept (closer to 0) values.
The results obtained with ISRs data suggest that the calibration of Swarm Te data made by Lomidze et al. [] is heavily biased towards mid latitudes and daytime hours due to the ISRs dataset they used, and to the fact that they cumulated the data of the three ISRs to derive a single calibration curve. As a consequence, the accuracy of Swarm Te data would benefit from the inclusion of the latitudinal and diurnal dependence in the calibration procedure. Swarm Te data are very valuable to study the relative changes of Te, but a more detailed correction is needed to obtain more reliable absolute values of Te especially at low and equatorial latitudes. Moreover, to better describe the high Te values, the inclusion of data recorded by high-latitude ISRs in the Lomidze dataset is advisable.
The orbital configuration of Swarm satellites and the extension of the dataset are very tailored for the study of the global features of Te with a spatial and time resolution hardly accessible in the past. Because of this, we were able to study the median spatial, diurnal, and seasonal trends of Te in the topside ionosphere in a very accurate fashion. Moreover, this allowed implementing an important statistical comparison between measured data and corresponding ones modeled by IRI. This comparison is beneficial both to validate the IRI model and to unveil the most important departures between measured and modeled data for a future inclusion of the Swarm Te dataset in the IRI model. The statistical comparison between Swarm and IRI evidenced that:
- the largest differences emerge at magnetic equator latitudes at dawn, and at low and mid latitudes during daytime and nighttime, respectively;
- IRI needs to be improved in the description of the morning peak at low latitudes. This can be achieved by increasing the order of spherical harmonics underlying the IRI Te description;
- IRI needs to be improved in summer daytime for both hemispheres, and in the description of the high Te values characteristic of daytime auroral oval latitudes;
- IRI data never go beyond about 4300 K, while Swarm data show values well beyond 5000 K, and in general Swarm values are higher than IRI ones.
The main statistical features of Te in the topside ionosphere have been pointed out and discussed in the paper and linked to the physical phenomena affecting the Te behavior at these altitudes, and to the existing literature on the topic. One of the most relevant results of this study is the characterization of the high Te values recorded by Swarm LPs, which are customary above all at high latitudes. These high Te values are not represented by the climatological description given by the IRI model. However, IRI has been developed to represent the median behavior of Te at climatological scales, and extreme (off-median) values or very fast and steep Te variations are out of the scope of the model. Nevertheless, a careful characterization of the high Te values recorded by Swarm LPs deserves particular attention for both modeling and scientific purposes.
In this paper, we did not deal with Te variations with the solar and magnetic activity. Since Swarm satellites are still in orbit and the mission will be supported for the next years, the continuous growth of the dataset will allow also studying the effects of the solar and magnetic activity variations on Te in the years to come. Moreover, we focused on the large-scale spatial and temporal variations of Te in order to make a fair comparison with the IRI model that describes the climatological behavior of the ionosphere. However, the very-high resolution of Swarm LPs data also allows the study of small-scale Te features [,] which complement the results of this study and can be of help in the comprehension of the Te behavior in the topside ionosphere.
Author Contributions
Conceptualization, A.P.; methodology, A.P., F.G., and V.T.; software, A.P.; data curation, A.P. and V.T.; investigation, A.P., F.G., V.T., I.C., M.P., G.C., P.D.M. and R.T.; validation, A.P., F.G., V.T., I.C., M.P., G.C., P.D.M. and R.T.; formal analysis, A.P.; writing—original draft preparation, A.P.; writing—review and editing, A.P., F.G., V.T., I.C., M.P., G.C., P.D.M. and R.T.; funding acquisition, F.G. and P.D.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research is partially supported by the Italian MIUR-PRIN grant 2017APKP7T on Circumterrestrial Environment: Impact of Sun–Earth Interaction, and by European Space Agency (ESA contract N. 4000125663/18/I-NB-“EO Science for Society Permanently Open Call for Proposals EOEP-5 BLOCK4” INTENS). V. Truhlik was supported by grant LTAUSA17100 of the Ministry of Education, Youth and Sports of the Czech Republic.
Data Availability Statement
ESA Swarm data are publicly available at ftp://swarmdiss.eo.esa.int (accessed on 24 September 2021). Jicamarca, Arecibo, and Millstone Hill ISR data are available via the public access portal at http://cedar.openmadrigal.org (accessed on 24 September 2021).
Acknowledgments
The IRI team is acknowledged for developing and maintaining the IRI model and for giving access to the corresponding Fortran code via the IRI website (http://irimodel.org/, accessed on 24 September 2021). Thanks to the European Space Agency for making Swarm data publicly available via ftp://swarmdiss.eo.esa.int (accessed on 24 September 2021), and for the considerable efforts made for the Langmuir probes data calibration and maintenance. This publication uses data from Jicamarca, Arecibo, and Millstone Hill ISR made available via the public access portal at http://cedar.openmadrigal.org (accessed on 24 September 2021). The authors are indebted to the observatory directors and operators for the significant investments of their time, effort, expertise, and funds needed to acquire and provide measurement data to academic research over the years.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are frequently used in this manuscript:
| BIL-1995 | Bilitza—1995 model |
| doy | Day of the year |
| ESA | European Space Agency |
| EUV | Extreme ultra-violet |
| GPS | Global positioning system |
| HG | High gain |
| IQR | Inter-quartile range |
| IRI | International Reference Ionosphere |
| ISR | Incoherent Scatter Radar |
| LEO | Low-Earth-orbit |
| LP | Langmuir Probe |
| LT | Local time |
| MLT | Magnetic local time |
| Ne | Electron density |
| QD | Quasi dipole |
| R | Pearson correlation coefficient |
| RMSE | Root mean square error |
| RRMSE | Relative root mean square error |
| TBT-2012 | Truhlik Bilitza Triskova—2012 model |
| TBT-2012+SA | Truhlik Bilitza Triskova—2012 + Solar Activity model |
| Te | Electron temperature |
| Ti | Ion temperature |
| Tn | Neutral temperature |
References
- Willmore, A.P. Electron and ion temperatures in the ionosphere. Space Sci. Rev. 1970, 11, 607–670. [Google Scholar] [CrossRef][Green Version]
- Rishbeth, H.; Garriott, O. Introduction to Ionospheric Physics; International Geophysics Series v. 14; Academic Press: New York, NY, USA, 1969. [Google Scholar]
- Ratcliffe, J.A. An Introduction to the Ionosphere and Magnetosphere; Cambridge University Press: Cambridge, UK, 1972. [Google Scholar]
- Banks, P.M. Ion temperature in the upper atmosphere. J. Geophys. Res. Space Phys. 1967, 72, 3365–3385. [Google Scholar] [CrossRef]
- Roble, R. The calculated and observed diurnal variation of the ionosphere over Millstone Hill on 23–24 March 1970. Planet. Space Sci. 1975, 23, 1017–1033. [Google Scholar] [CrossRef]
- Schunk, R.W.; Nagy, A.F. Electron temperatures in the region of the ionosphere: Theory and observations. Rev. Geophys. 1978, 16, 355–399. [Google Scholar] [CrossRef]
- Bilitza, D. Electron and ion temperature data for ionospheric modelling. Adv. Space Res. 1991, 11, 139–148. [Google Scholar] [CrossRef]
- Evans, J. Theory and practice of ionosphere study by Thomson scatter radar. Proc. IEEE 1969, 57, 496–530. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International reference ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Bilitza, D. IRI the International Standard for the Ionosphere. Adv. Radio Sci. 2018, 16, 1–11. [Google Scholar] [CrossRef]
- Kakinami, Y.; Lin, C.C.H.; Liu, J.Y.; Kamogawa, M.; Watanabe, S.; Parrot, M. Daytime longitudinal structures of electron density and temperature in the topside ionosphere observed by the Hinotori and DEMETER satellites. J. Geophys. Res. Space Phys. 2011, 116, A05316. [Google Scholar] [CrossRef]
- Ma, H.; Liu, L.; Chen, Y.; Le, H.; Li, Q.; Zhang, H. Longitudinal differences in electron temperature on both sides of zero declination line in the mid-latitude topside ionosphere. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028471. [Google Scholar] [CrossRef]
- Slominska, E.; Rothkaehl, H. Mapping seasonal trends of electron temperature in the topside ionosphere based on DEMETER data. Adv. Space Res. 2013, 52, 192–204. [Google Scholar] [CrossRef]
- Brace, L.; Theis, R.; Hoegy, W. Ionospheric electron temperature at solar maximum. Adv. Space Res. 1987, 7, 99–106. [Google Scholar] [CrossRef]
- Oyama, K.-I.; Balan, N.; Watanabe, S.; Takahashi, T.; Isoda, F.; Bailey, G.J.; Oya, H. Morning overshoot of Te enhanced by downward plasma drift in the equatorial topside ionosphere. J. Geomagn. Geoelectr. 1996, 48, 959–966. [Google Scholar] [CrossRef]
- Stolle, C.; Liu, H.; Truhlík, V.; Luehr, H.; Richards, P.G. Solar flux variation of the electron temperature morning overshoot in the equatorialFregion. J. Geophys. Res. Space Phys. 2011, 116, A04308. [Google Scholar] [CrossRef]
- Yang, T.; Park, J.; Kwak, Y.; Oyama, K.; Minow, J.I.; Lee, J. Morning overshoot of electron temperature as observed by the swarm constellation and the international space station. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027299. [Google Scholar] [CrossRef]
- Brace, L.H. Solar cycle variations in F-region Te in the vicinity of the midlatitude trough based on AE-C measurements at solar minimum and DE-2 measurements at solar maximum. Adv. Space Res. 1990, 10, 83–88. [Google Scholar] [CrossRef]
- Prölss, G.W. Subauroral electron temperature enhancement in the nighttime ionosphere. Ann. Geophys. 2006, 24, 1871–1885. [Google Scholar] [CrossRef]
- Brace, L.; Theis, R. Global empirical models of ionospheric electron temperature in the upper F-region and plasmasphere based on in situ measurements from the atmosphere explorer-c, isis-1 and isis-2 satellites. J. Atmos. Terr. Phys. 1981, 43, 1317–1343. [Google Scholar] [CrossRef]
- Pavlov, A.V.; Abe, T.; Oyama, K.-I. Comparison of the measured and modelled electron densities and temperatures in the ionosphere and plasmasphere during 20-30 January 1993. Ann. Geophys. 2000, 18, 1257–1262. [Google Scholar] [CrossRef][Green Version]
- Richards, P.G.; Buonsanto, M.J.; Reinisch, B.W.; Holt, J.; Fennelly, J.A.; Scali, J.L.; Comfort, R.H.; Germany, G.A.; Spann, J.; Brittnacher, M.; et al. On the relative importance of convection and temperature to the behavior of the ionosphere in North America during 6–12 January 1997. J. Geophys. Res. Space Phys. 2000, 105, 12763–12776. [Google Scholar] [CrossRef]
- Bilitza, D.; Truhlik, V.; Richards, P.; Abe, T.; Triskova, L. Solar cycle variations of mid-latitude electron density and temperature: Satellite measurements and model calculations. Adv. Space Res. 2007, 39, 779–789. [Google Scholar] [CrossRef]
- Lomidze, L.; Knudsen, D.J.; Burchill, J.; Kouznetsov, A.; Buchert, S.C. Calibration and validation of swarm plasma densities and electron temperatures using ground-based radars and satellite radio occultation measurements. Radio Sci. 2018, 53, 15–36. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lühr, H.; Hulot, G. Swarm: A constellation to study the Earth’s magnetic field. Earth Planets Space 2006, 58, 351–358. [Google Scholar] [CrossRef]
- Truhlik, V.; Bilitza, D.; Triskova, L. A new global empirical model of the electron temperature with the inclusion of the solar activity variations for IRI. Earth Planets Space 2012, 64, 531–543. [Google Scholar] [CrossRef]
- Knudsen, D.J.; Burchill, J.K.; Buchert, S.C.; Eriksson, A.I.; Gill, R.; Wahlund, J.; Åhlen, L.; Smith, M.; Moffat, B. Thermal ion imagers and Langmuir probes in the Swarm electric field instruments. J. Geophys. Res. Space Phys. 2017, 122, 2655–2673. [Google Scholar] [CrossRef]
- National Space Institute, Technical University of Denmark. Swarm L1b Product Definition; SW-RS-DSC-SY-0007; National Space Institute, Technical University of Denmark: Kongens Lyngby, Denmark, 2018; Available online: https://earth.esa.int/documents/10174/1514862/Swarm_L1b_Product_Definition (accessed on 10 October 2021).
- Laundal, K.M.; Richmond, A.D. Magnetic coordinate systems. Space Sci. Rev. 2017, 206, 27–59. [Google Scholar] [CrossRef]
- Pignalberi, A.; Aksonova, K.D.; Zhang, S.-R.; Truhlik, V.; Gurram, P.; Pavlou, C. Climatological study of the ion temperature in the ionosphere as recorded by Millstone Hill incoherent scatter radar and comparison with the IRI model. Adv. Space Res. 2021, 68, 2186–2203. [Google Scholar] [CrossRef]
- Bilitza, D. Models for ionospheric electron and ion temperature. In International Reference Ionosphere-IRI 79; Report UAG-82; Rawer, K., Lincoln, J.V., Conkright, R.O., Eds.; World Data Center A for Solar-Terrestrial Physics: Boulder, CO, USA, 1981; p. 245. Available online: http://www.irimodel.org/ (accessed on 10 October 2021).
- Bilitza, D.; Brace, L.; Theis, R. Modelling of ionospheric temperature profiles. Adv. Space Res. 1985, 5, 53–58. [Google Scholar] [CrossRef]
- Bilitza, D. International Reference Ionosphere; Report 90-22; National Space Science Data Center: Greenbelt, MD, USA, 1990; Available online: http://irimodel.org/docs/IRI1990pp0-84.pdf (accessed on 10 October 2021).
- Booker, H.G. Fitting of multi-region ionospheric profiles of electron density by a single analytic function of height. J. Atmos. Terr. Phys. 1977, 39, 619–623. [Google Scholar] [CrossRef]
- Spenner, K.; and Plugge, R. Empirical model of global electron temperature distribution between 300 and 700 Km based on data from Aeros-A. J. Geophys. 1979, 46, 43–56. Available online: https://journalgeophysicsjournalcom/JofG/article/view/286 (accessed on 10 October 2021).
- Bilitza, D. International reference ionosphere 2000. Radio Sci. 2001, 36, 261–275. [Google Scholar] [CrossRef]
- Truhlík, V.; Třísková, L.; Šmilauer, J.; Afonin, V. Global empirical model of electron temperature in the outer ionosphere for period of high solar activity based on data of three Intercosmos satellites. Adv. Space Res. 2000, 25, 163–169. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Zhang, Y.; Mertens, C.J.; Truhlik, V.; Richards, P.; McKinnell, L.-A.; Reinisch, B.W. The international reference ionosphere 2012—A model of international collaboration. J. Space Weather Space Clim. 2014, 4, A07. [Google Scholar] [CrossRef]
- Truhlik, V.; Bilitza, D.; Triskova, L. Latitudinal variation of the topside electron temperature at different levels of solar activity. Adv. Space Res. 2009, 44, 693–700. [Google Scholar] [CrossRef]
- Truhlík, V.; Třísková, L.; Smilauer, J. Improved electron temperature model and comparison with satellite data. Adv. Space Res. 2001, 27, 101–109. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. Space Phys. 2002, 107, 1468. [Google Scholar] [CrossRef]
- Oyama, K.-I.; Watanabe, S.; Su, Y.; Takahashi, T.; Hirao, K. Season, local time, and longitude variations of electron temperature at the height of ∼600 km in the low latitude region. Adv. Space Res. 1996, 18, 269–278. [Google Scholar] [CrossRef]
- Hoegy, W.R. Probe and radar electron temperatures in an isotropic nonequilibrium plasma. J. Geophys. Res. Space Phys. 1971, 76, 8333–8340. [Google Scholar] [CrossRef]
- Oyama, K.-I.; Lee, C.H.; Fang, H.K.; Cheng, C.Z. Means to remove electrode contamination effect of Langmuir probe measurement in space. Rev. Sci. Instrum. 2012, 83, 55113. [Google Scholar] [CrossRef]
- Zhang, S.-R.; Holt, J.M. Ionospheric plasma temperatures during 1976–2001 over Millstone Hill. Adv. Space Res. 2004, 33, 963–969. [Google Scholar] [CrossRef]
- Pignalberi, A.; Habarulema, J.; Pezzopane, M.; Rizzi, R. On the development of a method for updating an empirical climatological ionospheric model by means of assimilated vTEC measurements from a GNSS receiver network. Space Weather 2019, 17, 1131–1164. [Google Scholar] [CrossRef]
- Schunk, R.; Nagy, A.F. Ionospheres: Physics, Plasma Physics, and Chemistry, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Giannattasio, F.; De Michelis, P.; Pignalberi, A.; Coco, I.; Consolini, G.; Pezzopane, M.; Tozzi, R. Parallel electrical conductivity in the topside ionosphere derived from swarm measurements. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028452. [Google Scholar] [CrossRef]
- Giannattasio, F.; Pignalberi, A.; De Michelis, P.; Coco, I.; Consolini, G.; Pezzopane, M.; Tozzi, R. Dependence of parallel electrical conductivity in the topside ionosphere on solar and geomagnetic activity. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029138. [Google Scholar] [CrossRef]
- Iijima, T.; Potemra, T.A. Large-scale characteristics of field-aligned currents associated with substorms. J. Geophys. Res. Space Phys. 1978, 83, 599–615. [Google Scholar] [CrossRef]
- Milan, S.E.; Clausen, L.B.N.; Coxon, J.; Carter, J.; Walach, M.-T.; Laundal, K.M.; Østgaard, N.; Tenfjord, P.; Reistad, J.P.; Snekvik, K.; et al. Overview of solar wind-magnetosphere-ionosphere-atmosphere coupling and the generation of magnetospheric currents. Space Sci. Rev. 2017, 206, 547–573. [Google Scholar] [CrossRef]
- Zmuda, A.J.; Martin, J.H.; Heuring, F.T. Transverse magnetic disturbances at 1100 km in the auroral region. J. Geophys. Res. Space Phys. 1966, 71, 5033–5045. [Google Scholar] [CrossRef]
- Brinton, H.C.; Grebowsky, J.M.; Brace, L.H. The high-latitude winter region at 300 km: Thermal plasma observations from AE-C. J. Geophys. Res. Space Phys. 1978, 83, 4767–4776. [Google Scholar] [CrossRef]
- Foster, J.C. An empirical electric field model derived from Chatanika radar data. J. Geophys. Res. Space Phys. 1983, 88, 981–987. [Google Scholar] [CrossRef]
- Dyson, P.L.; Winningham, J.D. Top side ionospheric spread and particle precipitation in the day side magnetospheric clefts. J. Geophys. Res. Space Phys. 1974, 79, 5219–5230. [Google Scholar] [CrossRef]
- McPherron, R.; Russell, C.T.; Aubry, M.P. Satellite studies of magnetospheric substorms on 15 August 1968: Phenomenological model for substorms. J. Geophys. Res. Space Phys. 1973, 78, 3131–3149. [Google Scholar] [CrossRef]
- Wang, W.; Burns, A.G.; Killeen, T.L. A numerical study of the response of ionospheric electron temperature to geomagnetic activity. J. Geophys. Res. Space Phys. 2006, 111, A11301. [Google Scholar] [CrossRef]
- Fujii, R.; Iijima, T.; Potemra, T.A.; Sugiura, M. Seasonal dependence of large-scale Birkeland currents. Geophys. Res. Lett. 1981, 8, 1103–1106. [Google Scholar] [CrossRef]
- Liou, K.; Newell, P.T.; Meng, C.-I. Seasonal effects on auroral particle acceleration and precipitation. J. Geophys. Res. Space Phys. 2001, 106, 5531–5542. [Google Scholar] [CrossRef]
- Papitashvili, V.; Christiansen, F.; Neubert, T. A new model of field-aligned currents derived from high-precision satellite magnetic field data. Geophys. Res. Lett. 2002, 29, 28-1–28-4. [Google Scholar] [CrossRef]
- Christiansen, F.; Papitashvili, V.; Neubert, T. Seasonal variations of high-latitude field-aligned currents inferred from Ørsted and Magsat observations. J. Geophys. Res. Space Phys. 2002, 107, SMP5-1–SMP5-13. [Google Scholar] [CrossRef]
- Wang, H.; Lühr, H.; Ma, S.Y. Solar zenith angle and merging electric field control of field-aligned currents: A statistical study of the Southern Hemisphere. J. Geophys. Res. Space Phys. 2005, 110, 306. [Google Scholar] [CrossRef]
- McDonald, J.; Williams, P. The relationship between ionospheric temperature, electron density and solar activity. J. Atmos. Terr. Phys. 1980, 42, 41–44. [Google Scholar] [CrossRef]
- Kakinami, Y.; Watanabe, S.; Liu, J.-Y.; Balan, N. Correlation between electron density and temperature in the topside ionosphere. J. Geophys. Res. Space Phys. 2011, 116, A12331. [Google Scholar] [CrossRef]
- Su, F.; Wang, W.; Burns, A.G.; Yue, X.; Zhu, F. The correlation between electron temperature and density in the topside ionosphere during 2006-2009. J. Geophys. Res. Space Phys. 2015, 120, 10724–10739. [Google Scholar] [CrossRef]
- Hu, A.; Carter, B.; Currie, J.; Norman, R.; Wu, S.; Zhang, K. A deep neural network model of global topside electron temperature using incoherent scatter radars and its application to GNSS radio occultation. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027263. [Google Scholar] [CrossRef]
- Kitamura, N.; Ogawa, Y.; Nishimura, Y.; Terada, N.; Ono, T.; Shinbori, A.; Kumamoto, A.; Truhlík, V.; Smilauer, J. Solar zenith angle dependence of plasma density and temperature in the polar cap ionosphere and low-altitude magnetosphere during geomagnetically quiet periods at solar maximum. J. Geophys. Res. Space Phys. 2011, 116, A08227. [Google Scholar] [CrossRef]
- Pignalberi, A.; Coco, I.; Giannattasio, F.; Pezzopane, M.; De Michelis, P.; Consolini, G.; Tozzi, R. A new ionospheric index to investigate electron temperature small-scale variations in the topside ionosphere. Universe 2021, 7, 290. [Google Scholar] [CrossRef]
- Pignalberi, A. TITIPy: A Python tool for the calculation and mapping of topside ionosphere turbulence indices. Comput. Geosci. 2021, 148, 104675. [Google Scholar] [CrossRef]
Publisher’s Note:: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).