Response of Mangrove Carbon Fluxes to Drought Stress Detected by Photochemical Reflectance Index
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Environmental Measurements
2.3. Flux Data and LUE Calculation
2.4. Spectral Measurement and Processing
2.5. Statistical Analyses
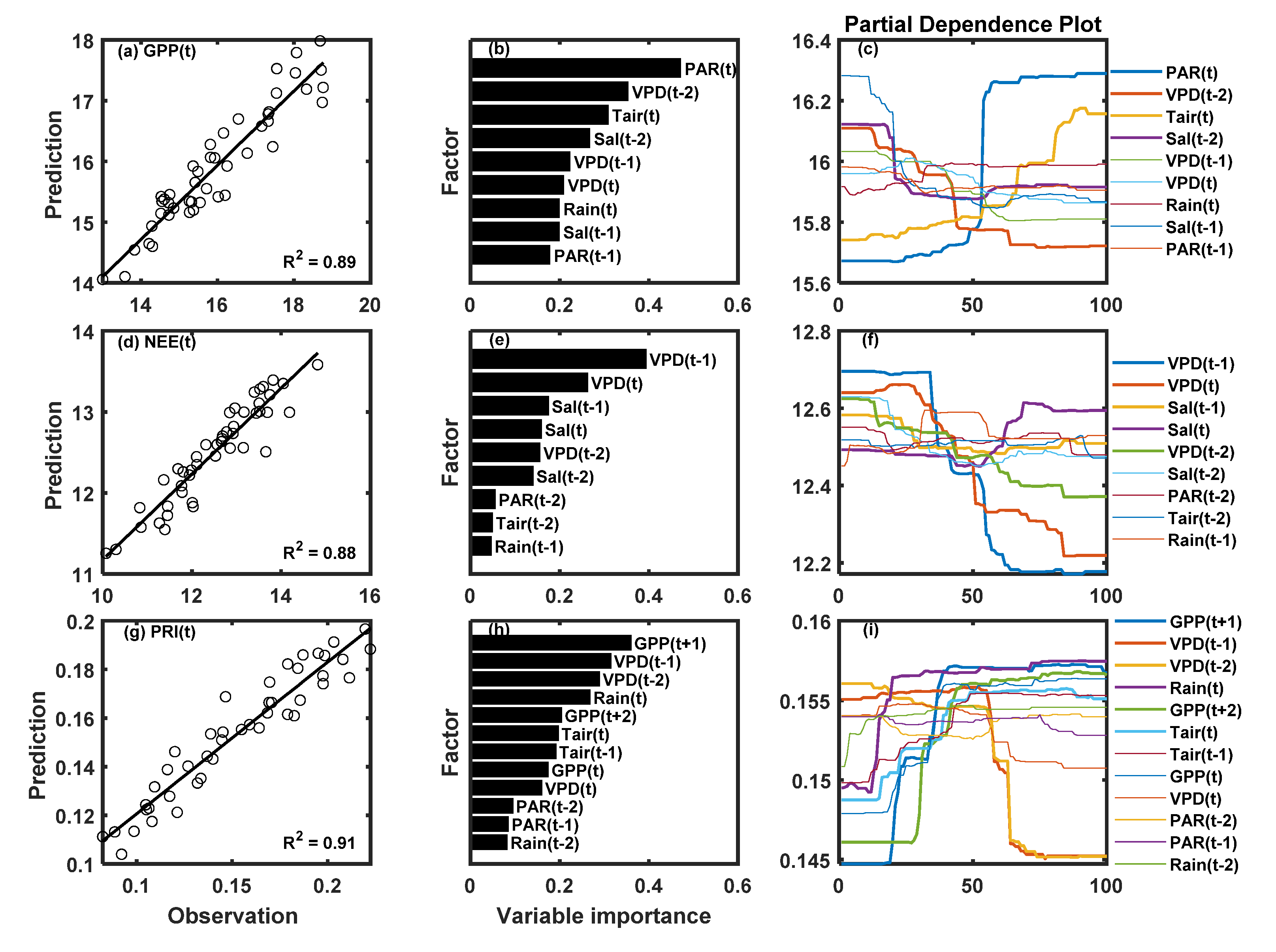
3. Results
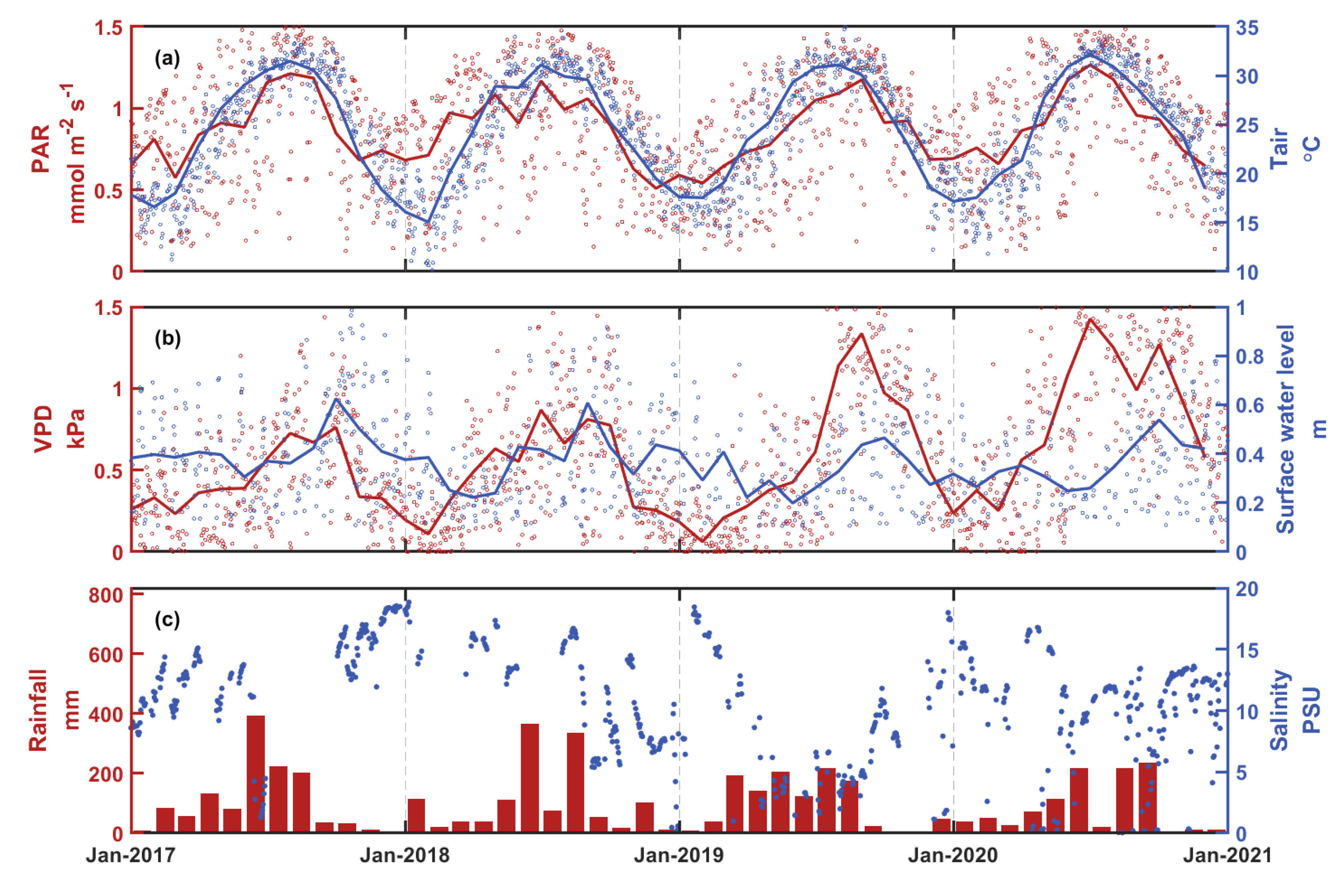
3.1. Temporal Variations of Environmental Factors and Carbon Fluxes
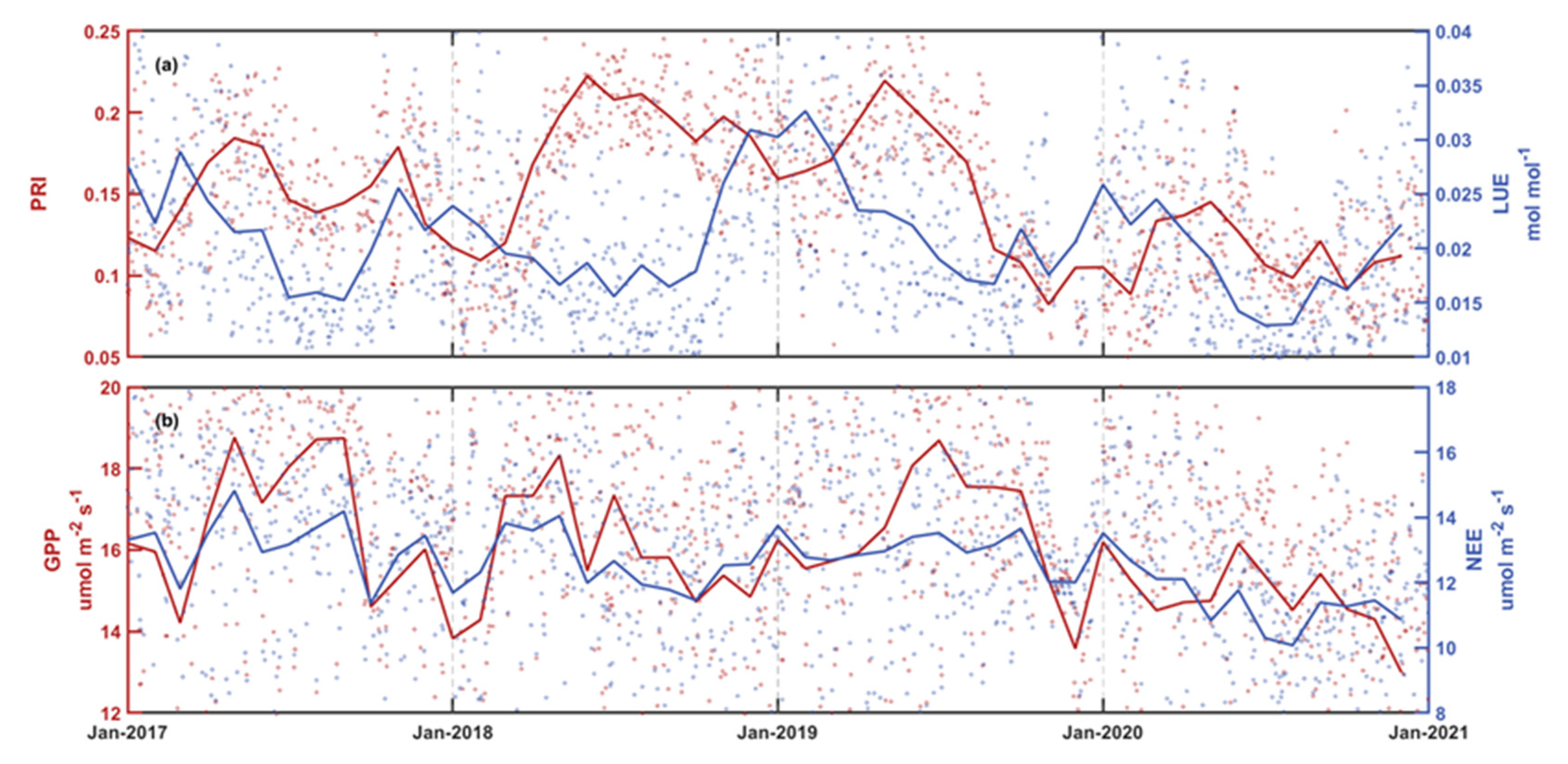
3.2. Temporal Variations of PRI and Its Components
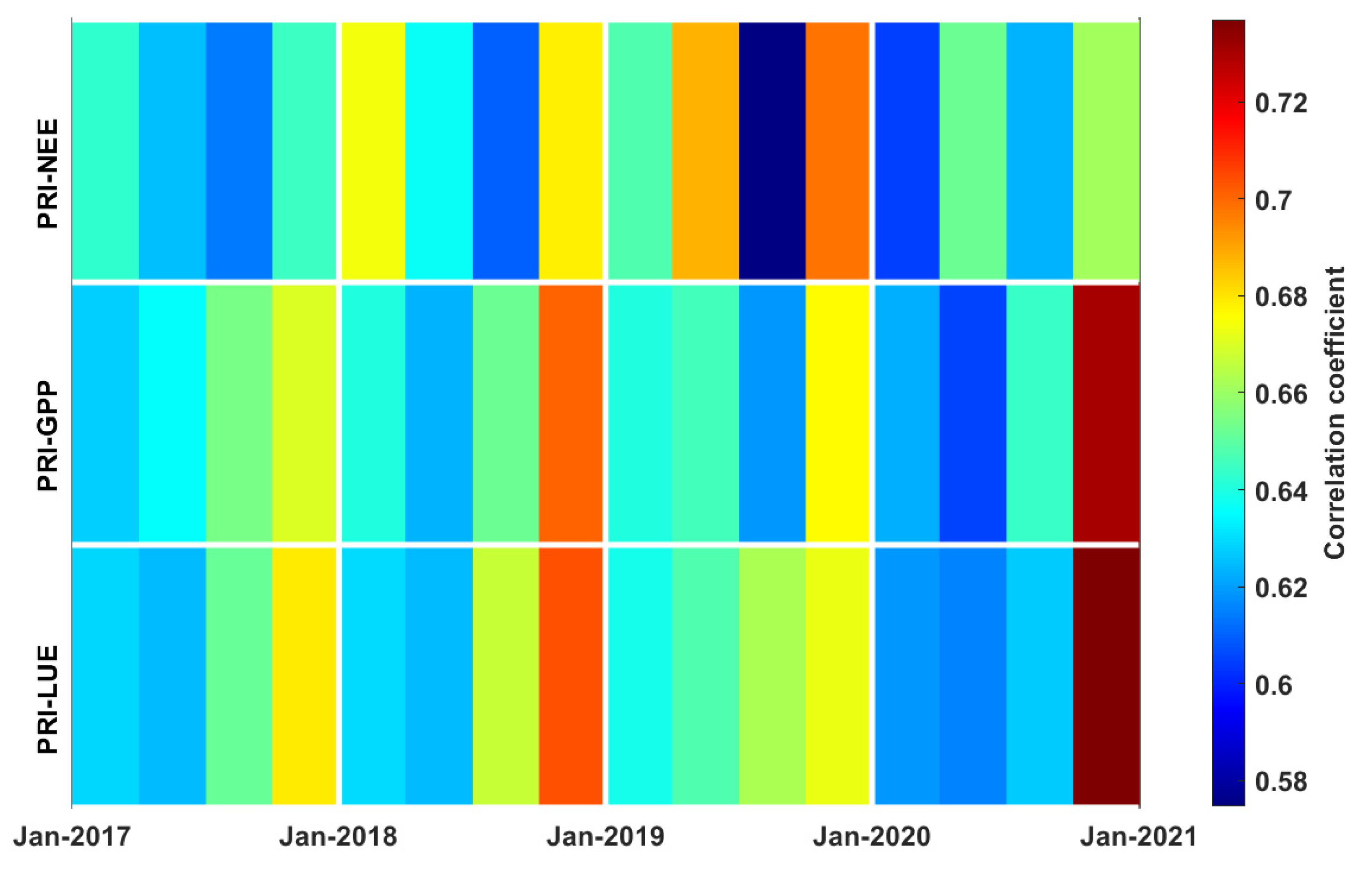
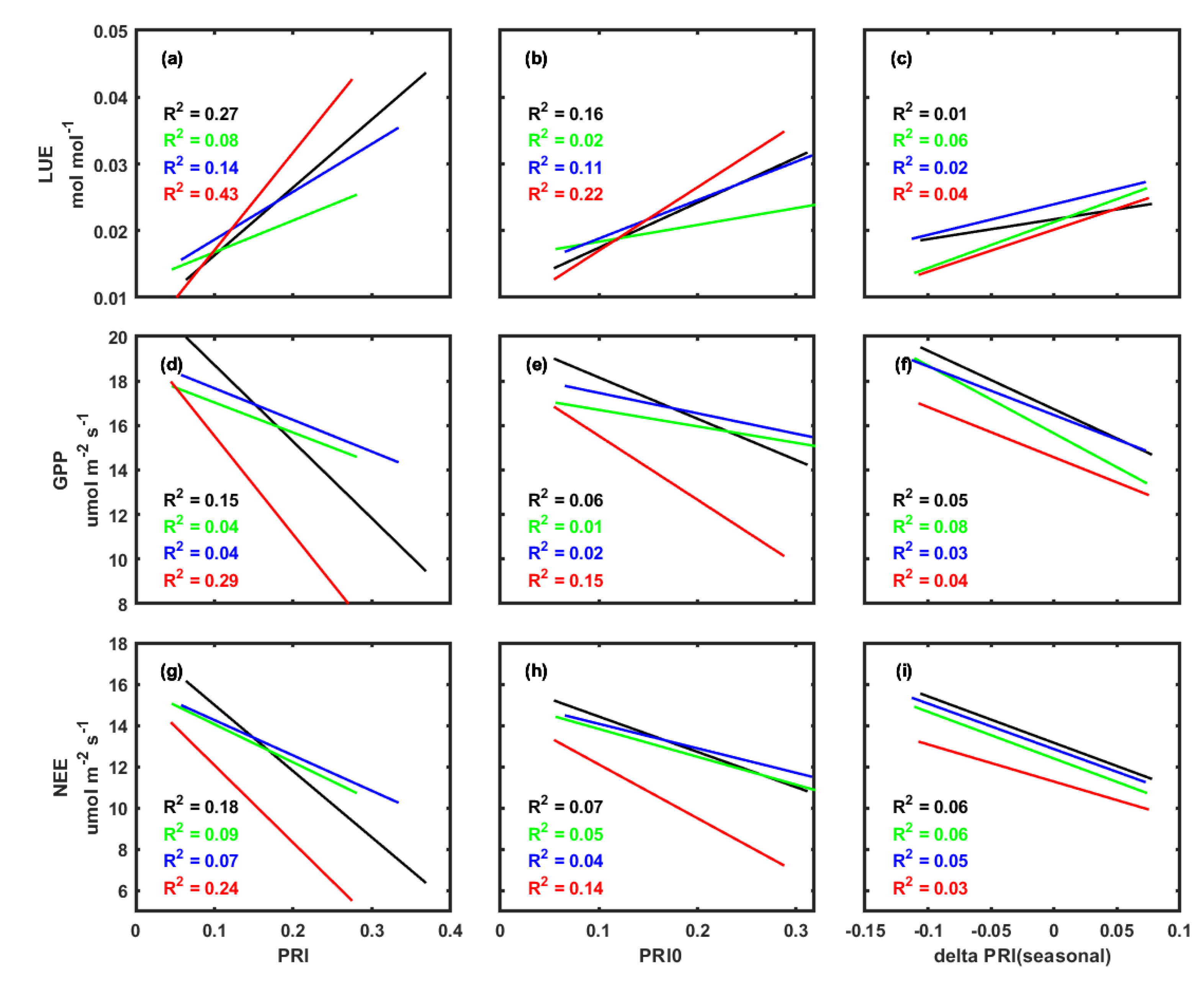
3.3. Correlations between PRI, Environmental Factors, and Carbon Fluxes
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alongi, D.M.; Sasekumar, A.; Chong, V.C.; Pfitzner, J.; Trott, L.A.; Tirendi, F.; Dixon, P.; Brunskill, G.J. Sediment accumulation and organic material flux in a managed mangrove ecosystem: Estimates of land–ocean–atmosphere exchange in peninsular Malaysia. Mar. Geol. 2004, 208, 383–402. [Google Scholar] [CrossRef]
- Bouillon, S.; Borges, A.V.; Castañeda-Moya, E.; Diele, K.; Dittmar, T.; Duke, N.C.; Kristensen, E.; Lee, S.Y.; Marchand, C.; Middelburg, J.J.; et al. Mangrove production and carbon sinks: A revision of global budget estimates. Glob. Biogeochem. Cycles 2008, 22, 22. [Google Scholar] [CrossRef] [Green Version]
- Chmura, G.L.; Anisfeld, S.C.; Cahoon, D.R.; Lynch, J.C. Global carbon sequestration in tidal, saline wetland soils. Glob. Biogeochem. Cycles 2003, 17. [Google Scholar] [CrossRef]
- Crase, B.; Liedloff, A.; Vesk, P.A.; Burgman, M.A.; Wintle, B.A. Hydroperiod is the main driver of the spatial pattern of dominance in mangrove communities. Glob. Ecol. Biogeogr. 2013, 22, 806–817. [Google Scholar] [CrossRef]
- Cui, X.; Liang, J.; Lu, W.; Chen, H.; Liu, F.; Lin, G.; Xu, F.; Luo, Y.; Lin, G. Stronger ecosystem carbon sequestration potential of mangrove wetlands with respect to terrestrial forests in subtropical China. Agric. For. Meteorol. 2018, 249, 71–80. [Google Scholar] [CrossRef]
- Leopold, A.; Marchand, C.; Renchon, A.; Deborde, J.; Quiniou, T.; Allenbach, M. Net ecosystem CO2 exchange in the “Coeur de Voh” mangrove, New Caledonia: Effects of water stress on mangrove productivity in a semi-arid climate. Agric. For. Meteorol. 2016, 223, 217–232. [Google Scholar] [CrossRef]
- Duke, N.C.; Meynecke, J.-O.; Dittmann, S.; Ellison, A.M.; Anger, K.; Berger, U.; Cannicci, S.; Diele, K.; Ewel, K.C.; Field, C.D.; et al. A World Without Mangroves? Science 2007, 317, 41–42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.; Lai, D.Y.F. Subtropical mangrove wetland is a stronger carbon dioxide sink in the dry than wet seasons. Agric. For. Meteorol. 2019, 278, 278. [Google Scholar] [CrossRef]
- Lovelock, C.E.; Krauss, K.W.; Osland, M.J.; Reef, R.; Ball, M.C. The Physiology of Mangrove Trees with Changing Climate. Tree Physiol. 2016, 149–179. [Google Scholar] [CrossRef]
- Mafi-Gholami, D.; Zenner, E.K.; Jaafari, A. Mangrove regional feedback to sea level rise and drought intensity at the end of the 21st century. Ecol. Indic. 2020, 110, 105972. [Google Scholar] [CrossRef]
- Guan, G.-F.; Wang, Y.-S.; Cheng, H.; Jiang, Z.-Y.; Fei, J. Physiological and biochemical response to drought stress in the leaves of Aegiceras corniculatum and Kandelia obovata. Ecotoxicology 2015, 24, 1668–1676. [Google Scholar] [CrossRef]
- Mafi-Gholami, D.; Mahmoudi, B.; Zenner, E.K. An analysis of the relationship between drought events and mangrove changes along the northern coasts of the Pe rsian Gulf and Oman Sea. Estuar. Coast. Shelf Sci. 2017, 199, 141–151. [Google Scholar] [CrossRef]
- Osland, M.J.; Feher, L.C.; Griffith, K.T.; Cavanaugh, K.C.; Enwright, N.M.; Day, R.H.; Stagg, C.L.; Krauss, K.W.; Howard, R.J.; Grace, J.B.; et al. Climatic controls on the global distribution, abundance, and species richness of mangrove forests. Ecol. Monogr. 2017, 87, 341–359. [Google Scholar] [CrossRef] [Green Version]
- Sakho, I.; Mesnage, V.; Deloffre, J.; Lafite, R.; Niang, I.; Faye, G. The influence of natural and anthropogenic factors on mangrove dynamics over 60 years: The Somone Estuary, Senegal. Estuar. Coast. Shelf Sci. 2011, 94, 93–101. [Google Scholar] [CrossRef]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Chang. 2012, 3, 52–58. [Google Scholar] [CrossRef]
- MacKay, F.; Cyrus, D.; Russell, K.-L. Macrobenthic invertebrate responses to prolonged drought in South Africa’s largest estuarine lake complex. Estuar. Coast. Shelf Sci. 2010, 86, 553–567. [Google Scholar] [CrossRef]
- Sobrado, M.A. Drought effects on photosynthesis of the mangrove, Avicennia germinans, under contrasting salinities. Trees 1999, 13, 125–130. [Google Scholar] [CrossRef]
- Duke, N.C.; Ball, M.C.; Ellison, J.C. Factors Influencing Biodiversity and Distributional Gradients in Mangroves. Glob. Ecol. Biogeogr. Lett. 1998, 7, 27. [Google Scholar] [CrossRef] [Green Version]
- Sanders, C.J.; Maher, D.T.; Tait, D.R.; Williams, D.; Holloway, C.; Sippo, J.Z.; Santos, I.R. Are global mangrove carbon stocks driven by rainfall? J. Geophys. Res. Biogeosci. 2016, 121, 2600–2609. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, M.; Xi, Y.; Zhu, J.; Tian, L.; Zhang, X.; Wang, Y.; Li, Y.; Shi, P.; Yu, G.; et al. Lagged climatic effects on carbon fluxes over three grassland ecosystems in China. J. Plant Ecol. 2015, 8, 291–302. [Google Scholar] [CrossRef] [Green Version]
- Flanagan, L.B.; Wever, L.A.; Carlson, P.J. Seasonal and interannual variation in carbon dioxide exchange and carbon balance in a northern temperate grassland. Glob. Chang. Biol. 2002, 8, 599–615. [Google Scholar] [CrossRef]
- Barford, C.C.; Wofsy, S.C.; Goulden, M.L.; Munger, J.W.; Pyle, E.H.; Urbanski, S.P.; Hutyra, L.; Saleska, S.R.; Fitzjarrald, D.; Moore, K. Factors Controlling Long- and Short-Term Sequestration of Atmospheric CO2 in a Mid-latitude Forest. Science 2001, 294, 1688–1691. [Google Scholar] [CrossRef] [Green Version]
- Alongi, D.M. Carbon sequestration in mangrove forests. Carbon Manag. 2012, 3, 313–322. [Google Scholar] [CrossRef]
- Alongi, D.M. Carbon Cycling and Storage in Mangrove Forests. Annu. Rev. Mar. Sci. 2014, 6, 195–219. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Gamon, J.A.; Peñuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Penuelas, J.; Filella, I.; Gamon, J.A. Assessment of photosynthetic radiation-use efficiency with spectral reflectance. New Phytol. 1995, 131, 291–296. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Penuelas, J.; Papale, D.; Filella, I. Remote estimation of carbon dioxide uptake by a Mediterranean forest. Glob. Chang. Biol. 2008, 14, 2860–2867. [Google Scholar] [CrossRef]
- Hall, F.G.; Hilker, T.; Coops, N.C. PHOTOSYNSAT, photosynthesis from space: Theoretical foundations of a satellite concept and validation from tower and spaceborne data. Remote. Sens. Environ. 2011, 115, 1918–1925. [Google Scholar] [CrossRef]
- Soudani, K.; Hmimina, G.; Dufrêne, E.; Berveiller, D.; Delpierre, N.; Ourcival, J.-M.; Rambal, S.; Joffre, R. Relationships between photochemical reflectance index and light-use efficiency in deciduous and evergreen broadleaf forests. Remote. Sens. Environ. 2014, 144, 73–84. [Google Scholar] [CrossRef]
- Zhang, M.; Yu, G.-R.; Zhuang, J.; Gentry, R.; Fu, Y.-L.; Sun, X.-M.; Zhang, L.-M.; Wen, X.-F.; Wang, Q.-F.; Han, S.-J.; et al. Effects of cloudiness change on net ecosystem exchange, light use efficiency, and water use efficiency in typical ecosystems of China. Agric. For. Meteorol. 2011, 151, 803–816. [Google Scholar] [CrossRef]
- Peñuelas, J.; Garbulsky, M.F.; Filella, I. Photochemical reflectance index (PRI) and remote sensing of plant CO2 uptake. New Phytol. 2011, 191, 596–599. [Google Scholar] [CrossRef] [PubMed]
- Suarez, L.; Zarco-Tejada, P.J.; Gonzalez-Dugo, V.; Berni, J.A.J.; Fereres, E. The Photochemical Reflectance Index (PRI) as a Water Stress Indicator in Peach Orchards from Remote Sensing Imagery. Acta Hortic. 2012, 962, 363–369. [Google Scholar] [CrossRef] [Green Version]
- Zinnert, J.C.; Nelson, J.D.; Hoffman, A.M. Effects of salinity on physiological responses and the photochemical reflectance index in two co-occurring coastal shrubs. Plant Soil 2012, 354, 45–55. [Google Scholar] [CrossRef]
- Garrity, S.R.; Eitel, J.U.H.; Vierling, L.A. Disentangling the relationships between plant pigments and the photochemical reflectance index reveals a new approach for remote estimation of carotenoid content. Remote. Sens. Environ. 2011, 115, 628–635. [Google Scholar] [CrossRef]
- Gamon, J.A.; Berry, J.A. Facultative and constitutive pigment effects on the Photochemical Reflectance Index (PRI) in sun and shade conifer needles. Isr. J. Plant Sci. 2012, 60, 85–95. [Google Scholar] [CrossRef]
- Magney, T.S.; Vierling, L.A.; Eitel, J.U.H.; Huggins, D.R.; Garrity, S.R. Response of high frequency Photochemical Reflectance Index (PRI) measurements to environmental conditions in wheat. Remote. Sens. Environ. 2016, 173, 84–97. [Google Scholar] [CrossRef]
- Gamon, J.A. Reviews and Syntheses: Optical sampling of the flux tower footprint. Biogeosciences 2015, 12, 4509–4523. [Google Scholar] [CrossRef] [Green Version]
- Garbulsky, M.F.; Peñuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (PRI) and the remote sensing of leaf, canopy and ecosystem radiation use efficienciesA review and meta-analysis. Remote Sens. Environ. 2011, 115, 281–297. [Google Scholar] [CrossRef]
- Nichol, C.J.; Rascher, U.; Matsubara, S.; Osmond, B. Assessing photosynthetic efficiency in an experimental mangrove canopy using remote sensing and chlorophyll fluorescence. Trees 2005, 20, 9–15. [Google Scholar] [CrossRef]
- Song, C.; White, B.L.; Heumann, B.W. Hyperspectral remote sensing of salinity stress on red (Rhizophora mangle) and white (Laguncularia racemosa) mangroves on Galapagos Islands. Remote. Sens. Lett. 2011, 2, 221–230. [Google Scholar] [CrossRef]
- Zhu, X.; Song, L.; Weng, Q.; Huang, G. Linking In Situ Photochemical Reflectance Index Measurements With Mangrove Carbon Dynamics in a Subtropical Coastal Wetland. J. Geophys. Res. Biogeosci. 2019, 124, 1714–1730. [Google Scholar] [CrossRef]
- Zhu, X.; Hou, Y.; Weng, Q.; Chen, L. Integrating UAV optical imagery and LiDAR data for assessing the spatial relationship between mangrove and inundation across a subtropical estuarine wetland. ISPRS J. Photogramm. Remote. Sens. 2019, 149, 146–156. [Google Scholar] [CrossRef]
- Zhu, X.; Hou, Y.; Zhang, Y.; Lu, X.; Liu, Z.; Weng, Q. Potential of Sun-Induced Chlorophyll Fluorescence for Indicating Mangrove Canopy Photosynthesis. J. Geophys. Res. Biogeosci. 2021, 126. [Google Scholar] [CrossRef]
- Zhu, X.; Qin, Z.; Song, L. How Land-Sea Interaction of Tidal and Sea Breeze Activity Affect Mangrove Net Ecosystem Exchange? J. Geophys. Res. Atmos. 2021, 126. [Google Scholar] [CrossRef]
- Murray, F.W. On the Computation of Saturation Vapor Pressure.pdf. J. Appl. Meteorol. 1966, 6, 203–204. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Zhou, Y.; Valach, A.; Shortt, R.; Kasak, K.; Rey-Sanchez, C.; Hemes, K.S.; Baldocchi, D.; Lai, D.Y.F. Methane emissions reduce the radiative cooling effect of a subtropical estuarine mangrove wetland by half. Glob. Chang. Biol. 2020, 26, 4998–5016. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Wolpert, D.H.; Macready, W.G. An Efficient Method To Estimate Bagging’s Generalization Error. Mach. Learn. 1999, 35, 41–55. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, M.W. Bias of the Random Forest Out-of-Bag (OOB) Error for Certain Input Parameters. Open J. Stat. 2011, 01, 205–211. [Google Scholar] [CrossRef] [Green Version]
- Wong, C.Y.S.; Gamon, J.A. The photochemical reflectance index provides an optical indicator of spring photosynthetic activation in evergreen conifers. New Phytol. 2015, 206, 196–208. [Google Scholar] [CrossRef]
- Novick, K.A.; Ficklin, D.L.; Stoy, P.C.; Williams, C.A.; Bohrer, G.; Oishi, A.C.; Papuga, S.A.; Blanken, P.D.; Noormets, A.; Sulman, B.N.; et al. The increasing importance of atmospheric demand for ecosystem water and carbon fluxes. Nat. Clim. Chang. 2016, 6, 1023–1027. [Google Scholar] [CrossRef] [Green Version]
- Wong, C.Y.S.; Gamon, J.A. Three causes of variation in the photochemical reflectance index (PRI) in evergreen conifers. New Phytol. 2015, 206, 187–195. [Google Scholar] [CrossRef]
- Sims, D.A.; Luo, H.; Hastings, S.J.; Oechel, W.; Rahman, A.F.; Gamon, J. Parallel adjustments in vegetation greenness and ecosystem CO2 exchange in response to drought in a Southern California chaparral ecosystem. Remote. Sens. Environ. 2006, 103, 289–303. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, J.M.; Ju, W.; Wang, H.; Qiu, F.; Yang, F.; Fan, W.; Huang, Q.; Wang, Y.; Feng, Y.; et al. Improving the ability of the photochemical reflectance index to track canopy light use efficiency through differentiating sunlit and shaded leaves. Remote. Sens. Environ. 2017, 194, 1–15. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Barr, J.G.; Engel, V.; Fuentes, J.D.; Zieman, J.C.; O’Halloran, T.L.; Smith, T.J., III; Anderson, G.H. Controls on mangrove forest-atmosphere carbon dioxide exchanges in western Everglades National Park. J. Geophys. Res. Space Phys. 2010, 115, 115. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Lu, W.; Chen, H.; Luo, Y.; Lin, G. Differential Responses of Net Ecosystem Exchange of Carbon Dioxide to Light and Temperature between Spring and Neap Tides in Subtropical Mangrove Forests. Sci. World J. 2014, 2014, 1–11. [Google Scholar] [CrossRef] [Green Version]


| Variables | PAR (mmol m−2 s−1) | Tair (°C) | VPD (kPa) | Surface Water Level (m) | Rainfall (mm) | Salinity (PSU) | PRI | LUE (mol mol−1) | GPP (μmol m−2 s−1) | NEE (μmol m−2 s−1) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2017 | Spring | 0.77 | 22.50 | 0.33 | 0.40 | 265.2 | 12.43 | 0.16 | 0.025 | 16.58 | 13.38 |
| Summer | 1.09 | 30.36 | 0.56 | 0.35 | 814.1 | 5.40 | 0.15 | 0.018 | 17.97 | 13.26 | |
| Autumn | 0.90 | 26.67 | 0.59 | 0.52 | 77.3 | 15.31 | 0.16 | 0.020 | 16.22 | 12.80 | |
| Winter | 0.74 | 17.60 | 0.31 | 0.40 | 94.9 | 13.16 | 0.12 | 0.024 | 16.05 | 13.43 | |
| 2018 | Spring | 1.00 | 24.43 | 0.47 | 0.24 | 186.5 | 14.89 | 0.16 | 0.018 | 17.66 | 13.82 |
| Summer | 1.02 | 29.94 | 0.69 | 0.40 | 774.8 | 14.85 | 0.21 | 0.018 | 16.22 | 12.20 | |
| Autumn | 0.86 | 25.78 | 0.62 | 0.45 | 173.9 | 8.65 | 0.19 | 0.020 | 15.30 | 11.92 | |
| Winter | 0.63 | 16.88 | 0.19 | 0.40 | 146.1 | 11.36 | 0.14 | 0.026 | 14.32 | 12.19 | |
| 2019 | Spring | 0.72 | 22.56 | 0.29 | 0.31 | 536.3 | 6.36 | 0.20 | 0.025 | 16.06 | 12.83 |
| Summer | 1.02 | 30.41 | 0.72 | 0.26 | 511.6 | 3.80 | 0.19 | 0.019 | 18.10 | 13.28 | |
| Autumn | 1.00 | 26.64 | 1.06 | 0.43 | 23.7 | 9.48 | 0.10 | 0.019 | 16.75 | 12.95 | |
| Winter | 0.61 | 17.91 | 0.25 | 0.33 | 92.3 | 13.27 | 0.14 | 0.028 | 15.12 | 12.84 | |
| 2020 | Spring | 0.81 | 23.00 | 0.49 | 0.33 | 209.3 | 10.23 | 0.14 | 0.022 | 14.66 | 11.68 |
| Summer | 1.21 | 31.33 | 1.25 | 0.28 | 453.6 | 9.37 | 0.11 | 0.013 | 15.35 | 10.71 | |
| Autumn | 0.88 | 26.30 | 1.06 | 0.47 | 244.0 | 9.56 | 0.11 | 0.018 | 14.75 | 11.37 | |
| Winter | 0.70 | 17.73 | 0.40 | 0.33 | 99.6 | 11.61 | 0.10 | 0.023 | 14.82 | 12.35 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Zhu, X. Response of Mangrove Carbon Fluxes to Drought Stress Detected by Photochemical Reflectance Index. Remote Sens. 2021, 13, 4053. https://doi.org/10.3390/rs13204053
Lu Y, Zhu X. Response of Mangrove Carbon Fluxes to Drought Stress Detected by Photochemical Reflectance Index. Remote Sensing. 2021; 13(20):4053. https://doi.org/10.3390/rs13204053
Chicago/Turabian StyleLu, Yaqing, and Xudong Zhu. 2021. "Response of Mangrove Carbon Fluxes to Drought Stress Detected by Photochemical Reflectance Index" Remote Sensing 13, no. 20: 4053. https://doi.org/10.3390/rs13204053
APA StyleLu, Y., & Zhu, X. (2021). Response of Mangrove Carbon Fluxes to Drought Stress Detected by Photochemical Reflectance Index. Remote Sensing, 13(20), 4053. https://doi.org/10.3390/rs13204053








