Abstract
The BeiDou Navigation Satellite System (BDS) features a heterogeneous constellation so that it is difficult to mitigate the multipath in the coordinate-domain. Therefore, mitigating the multipath in the observation-domain becomes more important. Sidereal filtering is commonly used for multipath mitigation, which needs to calculate the orbit repeat time of each satellite. However, that poses a computational challenge and damages the integrity at the end of the multipath model. Therefore, this paper proposes a single-difference model based on the multipath hemispherical map (SD-MHM) to mitigate the BDS-2/BDS-3 multipath in a short baseline. The proposed method is converted from double-difference residuals to single-difference residuals, which is not restricted by the pivot satellite transformation. Moreover, it takes the elevation and the azimuth angles of the satellite as the independent variables of the multipath model. The SD-MHM overcomes the unequal observation time of some satellites and does not require specific hardware. The experimental results show that the SD-MHM reduces the root mean square of the positioning errors by 56.4%, 63.9%, and 67.4% in the east, north, and vertical directions; moreover, it contributes to an increase in the baseline accuracy from 1.97 to 0.84 mm. The proposed SD-MHM has significant advantages in multipath mitigation compared with the advanced sidereal filtering method. Besides, the SD-MHM also features an excellent multipath correction capability for observation data with a period of more than seven days. Therefore, the SD-MHM provides a universal strategy for BDS multipath mitigation.
1. Introduction
The BeiDou Navigation Satellite System (BDS) has completed the “three-step” strategy [1]. BDS can provide real-time, convenient, and high-precision services for global users in the positioning [2], navigation [3], and timing [4]. Short-distance relative positioning is a crucial application module of BDS high-precision positioning service. Moreover, the BDS positioning accuracy is equivalent to the GPS in relative positioning [5]. However, the multipath is the primary error source that limits the high-precision application of relative positioning and prevents it from reaching mm or higher level. Since the multipath is challenging to be parameterized, it is difficult to eliminate its influence using the double-differenced technique. BDS has three different orbit types: the geostationary orbit (GEO), the inclined geostationary orbit (IGSO), and the medium Earth orbit (MEO) [6]. Therefore, the multipath processing strategy will be more complicated than the Global Navigation Satellite System (GNSS) of the same orbit type, such as GPS and Galileo (except GLONASS, which is the frequency division multiple access). The existing work for BDS multipath mitigation is mainly based on the time-domain correlation and few studies have focused on the BDS multipath spatial-domain correlation, especially the related studies on BDS-2/BDS-3 multipath mitigation.
The multipath processing methods can be divided into hardware- and software-based methods. The hardware-based methods mainly improve the receiver antenna [7,8,9], which partially mitigate the multipath. However, the cost is high if these devices are widely used. The software-based approaches consist of four categories. The first category is the improved stochastic model [10,11,12]; these methods reduce the influence of multipath based on the statistical significance of the observations. However, the multipath still exists in the positioning results. The second category is the time–frequency analysis, such as wavelet analysis [13], Vondrak filtering [14], and empirical mode decomposition with component analysis [15]. However, these methods are only suitable for post-processing. The third category is based on the multi-antenna solution, such as array antennas [16] and dual-polarized antennas [17]. The hardware equipment is complicated, and it is difficult to fit a complex environment with multipath effects. The last category is based on multipath spatiotemporal correlation, which is also a current hot research topic. The modeling based on multipath spatiotemporal correlation requires the environment and the position of the receiver to be in a relatively stable situation. Therefore, these methods can be used for mitigating the multipath in real-time. Sidereal filtering (SF) is a widely-used method to model the historical multipath [18,19,20,21]. The SF applies the multipath time-domain correlation to mitigate the multipath.
The GPS constellation in space repeats nearly a sidereal day (23 h 56 min 4 s), and the satellite orbit types are the same. Various GPS multipath mitigation studies have been conducted in the coordinate-domain and the observation-domain [22]. However, the BDS features heterogeneous constellation, and the constellation operating periods are complicated. Therefore, the BDS multipath mitigation method in the coordinate-domain will no longer be applicable, and the multipath mitigation can only be performed in the observation-domain. Based on the multipath correlation, the observation-domain multipath mitigation methods can be categorized into two groups: (1) Time-domain correlation-based. Ye et al. [23] converted the double-difference residuals to the single-difference residuals based on the “zero mean” assumption and used the advanced sidereal filtering (ASF) method to effectively mitigate the multipath of the BDS-2 satellites. Zhang et al. [24] proposed the pre-processing single-difference residuals based on Kalman and Rauch–Tung–Striebel Smoother filters and mitigated the multipath by the ASF. However, mitigating the multipath based on time shift has restrictions, such as “end effect” and inconsistent observation time. (2) Spatial-domain correlation-based. Dong et al. [25] applied the dual-antenna receiver with a common clock to establish the single-difference observation equations and constructed a multipath hemispherical map (MHM) using the correlation of GPS satellites spatial-domain multipath. The MHM was not limited by the time shift of each satellite orbit repeat time (ORT) and only needed to calculate the current satellite position to directly mitigate the multipath, which improved the efficiency and the positioning accuracy. Wang et al. [26,27] considered that the satellite tracks were not strictly repeated and proposed a trend surface analysis-based multipath hemispherical map that effectively mitigated the GPS multipath. Moreover, the correlation of satellite spatial-domain multipath has been applied in precision point positioning [28] and dynamic relative positioning [29] to mitigate the multipath. Although the single-difference residuals can conveniently establish a multipath model, the conventional receivers cannot eliminate the receiver clock error, which makes it challenging to make the single-difference observation equations.
Alber et al. [30] proposed the “zero mean” assumption that has been applied to GPS and BDS multipath mitigation based on SF [31,32]. The “zero mean” assumption solved some influencing factors of modeling the double-difference residuals for multipath mitigation. Therefore, the multipath spatial-domain correlation and the “zero mean” assumption are combined in this paper, and the SD-MHM method based on the single-difference residuals and MHM is proposed to mitigate the BDS-2/BDS-3 multipath that is suitable for the conventional receivers. The proposed method reconstructs the double-difference residuals into single-difference residuals and implements multipath mitigation on each BDS satellite. Real field data were used in the experiments and the results suggest that the proposed SD-MHM method outperforms other state-of-the-art methods in mitigating the multipath and improving the positioning accuracy.
This paper is organized as follows. In Section 2, the specific steps of building a single-difference multipath model are described; moreover, the ASF and SD-MHM are introduced. The orbital repeat time of BDS satellite is displayed in Section 3. The experiments and results are analyzed in Section 4. A discussion is made in Section 5. Section 6 gives the conclusions.
2. BDS Multipath
2.1. Multipath Extraction
For short baseline positioning, the double-difference observation equations can be established to eliminate or significantly reduce various errors such as orbit error, receiver and satellite clock errors, tropospheric delay, and ionospheric delay using the double-differenced technique. However, multipath is only related to the geometric relationship of the receiver, reflection, and satellite positions. Since there is no correlation among the stations, the double-differenced technique cannot mitigate the multipath. When two stations receive n + 1 common-view satellites, there are n double-difference observation equations of B1 carrier phase observations that can be expressed as:
where is the wavelength of the B1 carrier phase; is the double-difference operator; , , , , and ∇Δε are the carrier phase, the distance between satellites and stations, the integer ambiguities, the multipath values after double-difference, and the random noise, respectively; i denotes the ith satellite; and p denotes the pivot satellite.
To calculate the baseline vector conveniently, it is necessary to linearize the double-difference observation equation. The linearized observation equation of the carrier phase can be expressed as:
where x is a 3 × 1 order unknown baseline vector; y is the n × 1 order integer ambiguity after double-difference; A and B are the design matrices of order n × 3 and n × n, respectively; L is the n * 1 order the constant term of carrier phase; and V is the double-difference residuals. In short baseline, the double-difference residuals are mainly the multipath and the noise.
As shown in Equation (2), the multipath with noise can be obtained by determining the baseline vector and the ambiguities of the linear observation equation. Therefore, the fixed integer ambiguities are essential. According to the principle of the least-square ambiguity de-correlation adjustment (LAMBDA) algorithm, fixing all the ambiguities is not necessary for positioning, and it is almost impossible to fix all the ambiguities [33]. Moreover, the increase in the number of ambiguities increases will reduce both the searching space and computational efficiency. Therefore, it is recommended to use the partial ambiguity resolution (PAR) [34] to fix the integer ambiguities. The PAR has the advantages of simplicity and a high success rate for fixing the ambiguities. Meanwhile, the search space is reduced when there are many common-view satellites improving the operational efficiency of ambiguities searching.
The double-difference residuals can be obtained by first calculating the baseline vector values and the integer ambiguities, and then substituting them into Equation (2). Under the least square criterion, the solution of Equation (2) is expressed as:
where Q is the variance-covariance matrix of the baseline vector and integer ambiguity; R is the real value of the baseline vector; and Z is the real value of the double-difference integer ambiguities.
2.2. Single-Difference Multipath Modeling
The satellite with the maximum elevation angle is selected as the pivot satellite, which can reduce the influence of the error term of the pivot satellite. The double-difference observation equation will frequently change the pivot satellite, making the double-difference residuals more complicated. Moreover, the satellite ORT is not a constant, which results in the inconsistent time nodes of the pivot satellite in the two revisit periods. Furthermore, using the double-difference residuals as the multipath models will have many limiting factors. Therefore, the double-difference residuals are converted into the single-difference residuals using the transformation matrix, which follows the “zero mean” assumption (). The reconstructed single-difference residuals can be expressed as:
where are the reconstructed single-difference residuals; are the extracted double-difference residuals; and is the weight factor of the ith satellite observation that obeys the elevation angle stochastic model .
Once the double-difference residuals are converted to the single-difference residuals, multipath modeling is performed on the single-difference residuals using ASF and SD-MHM to mitigate the BDS multipath. Moreover, the multipath mitigation capabilities of the two methods in BDS-2/BDS-3 are analyzed. Figure 1 shows the framework of the two methods for multipath mitigation.

Figure 1.
The framework of the ASF and SD-MHM construction and multipath mitigation.
The multipath modeling process comprises three steps: (1) The average baseline vector is calculated and substituted into the double-difference linear observation equation to obtain the double-difference residual. (2) The double-difference residuals are converted into single-difference residuals based on the “zero mean” assumption. (3) The single-difference residuals are denoised based on a low-pass filter to complete the single-difference modeling. The ASF modeling process first needs to calculate all satellite ORTs of the current satellite constellation, and the single-difference model after denoising is time-aligned by the time shift of ORT. Then, the aligned single-difference residuals are transformed into the double-difference residuals to mitigate the multipath. The SD-MHM method requires only the single-difference residuals of the current constellation into the grid corresponding to the elevation angle and the azimuth angle. In the SD-MHM processing stage, the elevation and the azimuth angles of the satellites are calculated, the nearest grid position is searched based on the k-nearest neighbor (KNN) search [35], and the multipath model of the corresponding position is obtained. Finally, the double-difference residuals are transformed to mitigate the multipath in real-time.
3. Orbital Repeat Time of BDS Satellites
Multipath is related to the geometric relationship among the receiver, reflection source, and satellite positions in a stable environment. It is necessary to consider the operating period of the BDS satellite to calculate the ORT using the ASF method. Moreover, the heterogeneous constellation of BDS has three orbit types, namely GEO, IGSO, and MEO, and the operating periods of various satellites need to be considered separately. Among the three types of orbits, the GEO and IGSO ORTs are approximately a sidereal day, and the MEO ORTs are approximately seven sidereal days. Therefore, it is necessary to calculate the time shift of the ORT for each satellite. As the orbit radius and the angular velocity correction are given by the broadcast ephemeris, the angular velocity of the satellite at that moment can be calculated as follows:
where and Δω are the angular velocity of the satellite and the correction parameter of the angular velocity, respectively; is the square root of the product of the gravitational constant and the mass of the earth, and its value is 1.996498 × 107; and a is the square of the semimajor axis of the satellite orbit ellipse. Then, the operating period of the satellite can be obtained based on the angular velocity of the satellite. The time shifts of the GEO/IGSO and MEO satellite operating periods are:
This experiment was carried out based on the broadcast ephemeris from 3 July 2019, to 21 June 2020 (355 days) broadcast by the IGS Data Center of Wuhan University (ftp://igs.gnsswhu.cn/). Figure 2 and Figure 3 show the calculated time shifts of the GEO, IGSO, and BDS-2/BDS-3 MEO ORTs, respectively.
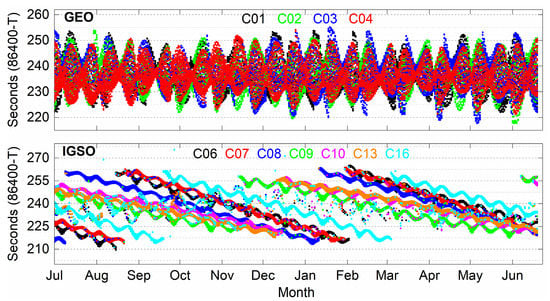
Figure 2.
The time shifts of GEO and IGSO ORTs.
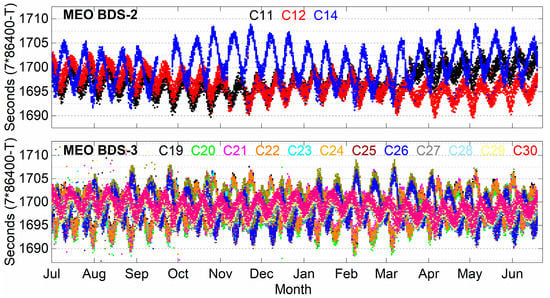
Figure 3.
The time shifts of BDS-2/BDS-3 MEO ORTs.
Figure 2 shows that the calculated time shift at a different time of each day fluctuates significantly, caused by tidal gravity. For IGSO, there is a significant time leap of approximately 50 s in the time shift of each satellite about every six months on average. Figure 3 delineates the time shifts of the MEO ORTs of BDS-2/BDS-3. Among them, the fluctuation of the MEO time shift of BDS-2 is complicated and has a certain trend. The fluctuation of the MEO time shift of BDS-3 is more regular, and it can maintain stable fluctuations around 1700 s.
The BDS satellites of different orbit types have different time shifts. The time shifts of the same orbit type satellites are also different. Moreover, with the satellite operation time, there is a significant change for the time shift. Therefore, it is necessary to calculate the time shift of each satellite ORT while using the ASF in the observation-domain. Obviously, this will limit the application of ASF in real-time.
4. Experiments and Results
4.1. Data Collection
A short baseline experiment was conducted from day of year (DOY) 296 to 311, 2019, on the roof of the School of Spatial Information and Geomatics Engineering, Anhui University of Science and Technology, China. The observation data of the BDS B1 signal were collected using two continuously operating reference stations. The sampling frequency of the observation data was 1 Hz, and the satellite cut-off elevation angle was 15°. Figure 4 shows the observation environment around the stations. The two stations were close and had no elevation difference. It can be considered that the double-differenced technique eliminates atmospheric residuals. Therefore, the stations are only affected by the multipath and the noise.
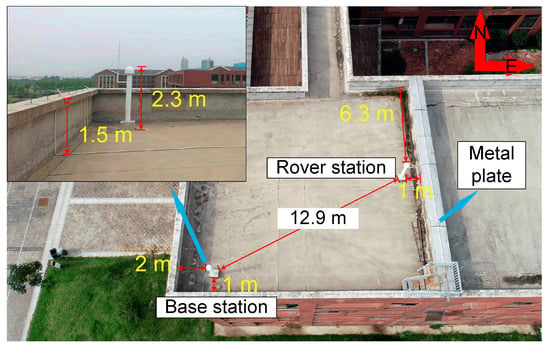
Figure 4.
Observation environment around the stations.
For the ASF method, the ORT time shift of each satellite is used to model the multipath. For the SD-MHM method, the DOY 296~302 residuals are used to model the multipath, the full constellation period. Finally, the coordinates calculated by the long-term observation data of the stations are used to evaluate the accuracy.
4.2. Single-Difference Residual Analysis
To qualitatively compare the multipath characteristics of the three types of satellites, Figure 5 shows the C01/C11/C13/C29 single-difference residuals and the satellite elevation and azimuth angles of DOY 296, 302, and 303. For GEO C01 and IGSO C13 separately, the three-day single-difference residuals have high repeatability, and the elevation and the azimuth series are highly coincident. Although DOY 296 has a longer time interval than DOY 302 towards DOY 303, the single-difference residuals maintain repeatability. It can be observed from MEO C11/C29 that the single-difference residuals of two adjacent days are non-correlated, and the elevation and the azimuth angles are different. Moreover, for satellite types with large changes in IGSO and MEO elevation angles, their single-difference series are correlated with their elevation angles. For C13, as the pivot satellite at a certain time, the single-difference series changes significantly but does not affect its repeatability.
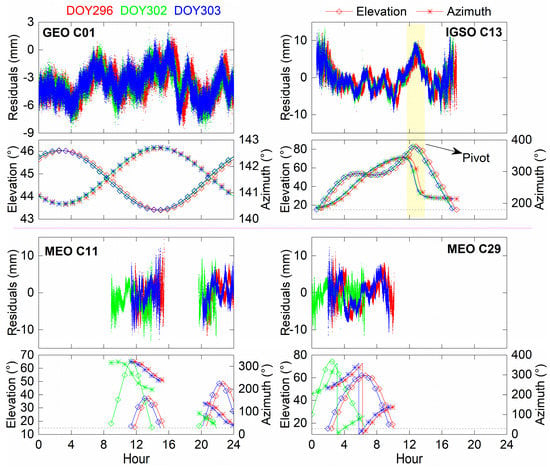
Figure 5.
DOY 296/302/303 single-difference residuals series of C01/C11/C13/C29 and the elevation and azimuth angles.
We first calculate the time shift of the ORT from the broadcast ephemeris to quantitatively analyze the C01/C11/C13/C29 aligned single-difference series and the relevant physical quantities after mitigating the multipath. Moreover, we calculate the correlation coefficient between the multipath model that aligns the time shift and the target DOY single-difference series. Finally, the multipath model is used to mitigate the multipath of the target DOY. The statistical results are listed in Table 1. We observe that the correlation coefficients of GEO C01 and IGSO C13 remain stable with a value greater than 0.92, and the correlation coefficients do not decrease in the case of a long-time span. Moreover, the single-difference series corrected by the multipath model have significant improvement in RMS. The repetition time of the MEO ORT is approximately seven sidereal days. Therefore, there is almost no correlation between the C11/C29 single-difference series of two adjacent days. For DOY 296–303 and DOY 297–304, they have correlation coefficients above 0.848, which are only one day apart. However, there is a difference in correlation coefficients and corrected RMS. To analyze the multipath mitigation degree of each observed satellite single-difference series based on the ASF method, Figure 6 shows the RMS of the original single-difference series and their series with multipath mitigation for the DOY 303 observed satellite by the corresponding multipath model. Most of the observed satellites can significantly mitigate the multipath based on ASF. However, in the background, the multipath of C21 and C24 in the original series has not been effectively mitigated, which is caused by the inconsistent observation time of the corresponding multipath models of C21 and C24. Based on the ASF method, the phenomenon may affect the performance of improving baseline accuracy.

Table 1.
The statistics of multipath mitigation for C01/C11/C13/C29.
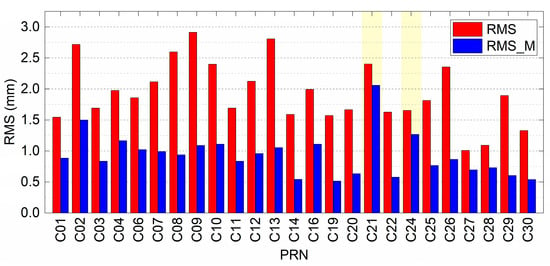
Figure 6.
RMS of the original single-difference series and their series with multipath mitigation for the DOY 303 observed satellite.
In the process of correcting the single-difference series of each satellite based on the multipath model, we find that some satellites still have incomplete multipath correction after determining the time shift because the observation times of the two adjacent ORTs of MEO satellites appearing in the sky are not the same. The SD-MHM method can theoretically avoid the influence of this phenomenon. The SD-MHM model is established using the BDS single-difference denoising residuals from DOY 296 to 302, as shown in Figure 7a. Figure 7b shows the distribution of the single-difference residuals of each satellite dynamically calculated by DOY 303 on the sky map. Although the reconstructed single-difference residual value of the pivot satellite is distorted, the SD-MHM model and the DOY 303 single-difference residuals have a high spatial-domain correlation, which does not affect the accuracy of subsequent multipath mitigation in real-time. The spatial-domain correlation of multipath can be used to model the three-dimensional environment.
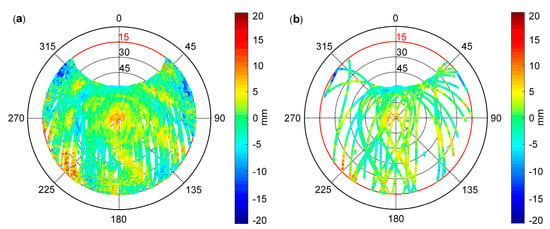
Figure 7.
(a) SD-MHM model established by DOY 296–302; and (b) the distribution of DOY303 single-difference residuals.
To explore and analyze the frequency domain characteristics of the series after mitigating the multipath, the DOY 303 C29 satellite is taken as an example, as shown in Figure 8. Figure 8a shows the original single-difference residuals series, the ASF and SD-MHM multipath models, and their mitigated series. In terms of the multipath model trend, both are almost the same, and the series fluctuates at 0 after the mitigation. In addition, it is necessary to analyze these two methods to mitigate the characteristics of the series after multipath in the frequency domain. For the power spectral density shown in Figure 8b, the low-frequency signal dominates the signal component of the original series. After the mitigation by ASF and SD-MHM, both can effectively mitigate the low-frequency multipath. Moreover, the low-frequency power of the series after SD-MHM correction is lower than that of ASF, and the mitigation effect on low-frequency multipath is better than ASF.
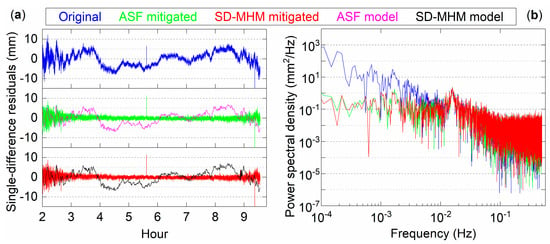
Figure 8.
(a) DOY303 C29 single-difference residuals and ASF and SD-MHM multipath models and their mitigated series; and (b) the power spectral density of the mitigated series and the single-difference residuals.
4.3. Results and Analysis
Figure 9 shows the solution sequence of the original baseline and the corrected baseline series of ASF and SD-MHM. We find that the multipath affects the accuracy of the original baseline, while both ASF and SD-MHM significantly mitigate the multipath. Except for the background period, the ASF corrected result is consistent with SD-MHM. However, in the background period, the series after ASF correction is still affected by the multipath. Therefore, it is necessary to analyze the multipath model and satellite visibility. The observation times of some satellites are different in the two ORTs. For example, the C21 and C24 observation times of DOY 296 and DOY 303 are different. Therefore, the ASF method cannot mitigate the multipath in some satellites, and the corrected series remains multipath. The SD-MHM method can ignore the impact of satellite operations. Based on the multipath spatial correlation, the SD-MHM method can search for the multipath model values of neighboring locations to mitigate the current multipath.
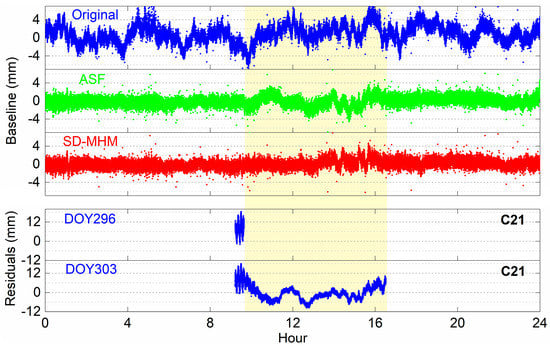
Figure 9.
The original baseline series, ASF, and SD-MHM corrected series and C21 single-difference residuals at the adjacent periods.
Dilution of precision (DOP) reflects the strength of satellite spatial geometry and positioning accuracy. Figure 10a shows the DOP value, elevation angle and number of visible satellites of DOY 303. Figure 10b shows the correction results of the coordinate series in the east, north, and vertical directions obtained by the SD-MHM method. The fluctuation of HDOP has almost no effect on the east and north directions. Moreover, the series after the correction of the east and north directions fluctuates within 2 mm. For the vertical direction, VDOP has a significant correlation with the vertical direction correction series, which is more evident in the VDOP fluctuation, but it still performs well in positioning accuracy. Furthermore, the average number of visible satellites per epoch is 12.5. It provides sufficient observation data for BDS positioning.
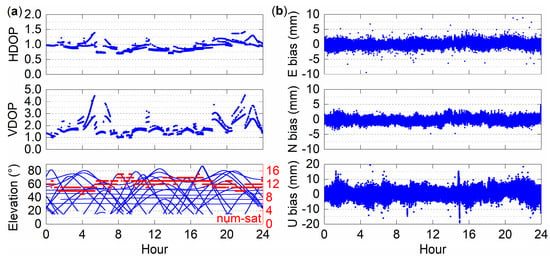
Figure 10.
(a) HDOP, VDOP, and elevation of DOY303; and (b) the corrected series by the SD-MHM in the east, north, and vertical directions.
Figure 11 shows that the proposed SD-MHM method is slightly better than ASF for east, north, and vertical directions and the baseline positioning accuracy. For inconsistent observation time of some satellites, the SD-MHM positioning accuracy is significantly better than the ASF method. Among them, the nine-day average positioning accuracies of the original coordinate series in the east, north, and vertical directions are 1.81, 2.49, and 8.70 mm, respectively. The positioning accuracies of the series corrected by ASF in the east, north, and vertical directions are 0.88, 1.05, and 3.13 mm, and the positioning accuracy improvement rates are 51.4%, 57.8%, and 64.0%, respectively. After correcting by SD-MHM, the positioning accuracies of the series in the east, north, and vertical directions reach 0.79, 0.90, and 2.84 mm, and the positioning accuracy improvement rates reach 56.4%, 63.9%, and 67.4%, respectively. The SD-MHM method is better than the ASF method for BDS multipath mitigation. Moreover, the average accuracy of the original baseline is 1.97 mm. The average accuracy after ASF and SD-MHM corrections are 0.95 and 0.84 mm, and the average improvement rates are 51.8% and 57.4%, respectively. Notice that, for DOY 310 and 311, the BDS constellation has repeated two ORTs compared to the established SD-MHM multipath model, and the SD-MHM method still effectively mitigates the multipath.

Figure 11.
The nine-day positioning accuracy in the east, north, and vertical directions and the baseline accuracy.
5. Discussion
A single-difference multipath hemispherical map is presented in this paper to improve the accuracy of BDS-2/BDS-3 short baseline positioning by mitigating the multipath in real-time. Considering the ORTs of the BDS MEO satellites are approximately seven sidereal days, the consecutive seven-day residuals are established as a multipath model. Moreover, since the spatial geometric structure of GEO is basically unchanged, partial ambiguity resolution is used to improve the fixed ambiguity efficiency. The authors of [25] proposed that multipath is spatially repetitive on the sky map. We use KNN to search for the multipath value on the space position closest to the current satellite to avoid the null value in the current satellite position caused by the slight orbit offset, which improves the computational efficiency and the spatial resolution of multipath.
The sidereal filtering methods are applied in conventional receivers, which can only use double-difference residuals or reconstructed single-difference residuals to mitigate the multipath. These methods need to dynamically update the multipath model, which will occupy a large amount of data memory and reduce the efficiency. Furthermore, when there are hardware problems and data interruptions in the observation data, that will seriously affect the solution results. However, the proposed method avoids all the above-mentioned problems and provides the conventional receivers with a new solution for multipath mitigation.
6. Conclusions
This paper proposes a single-difference residual-based multipath hemispherical map and focuses on dynamically mitigating the multipath errors in the single-frequency carrier phase of BDS-2/BDS-3. The proposed method is not affected by the changeable time shift of each BDS satellite ORT. Moreover, it can effectively and conveniently solve the phenomenon of two inconsistent observation periods of some BDS-3 MEO satellites.
Comparing with the ASF method, the proposed method does not require the specific time shift of each satellite ORT, which significantly improves the computational efficiency. Moreover, with the update of the hardware supporting the BDS-3 signal, the visible satellites of the BDS constellation will reach more than 40, and there will be lot of “end effects” when calculating the timing shift of each satellite. The SD-MHM method reduces the RMS of positioning errors by 56.4%, 63.9%, and 67.4% in the east, north, and vertical directions, respectively. The average positioning accuracy increases from 1.81, 2.49, and 8.70 mm to 0.79, 0.90, and 2.84 mm, and the baseline accuracy increase from 1.97 to 0.84 mm. Moreover, the capability of the SD-MHM multipath mitigation is better than that of ASF. SD-MHM still has excellent multipath mitigation capability for observation data with a period of more than seven days.
It is worth mentioning that the applied BDS-3 satellites are only based on the constellation of 12 MEO satellites (PRN: C19-C30). With the official opening of BDS-3 satellites and the GNSS receiver boards updating, the number of observable satellites will increase significantly. The proposed method has reference significance for the BDS multipath mitigation of conventional hardware receivers.
Author Contributions
Methodology, C.L. (Chao Liu) and Y.T.; software, C.L. (Chao Liu), Y.T., and H.H.; validation, Y.T., C.L. (Chunyang Liu), and X.Z.; formal analysis, C.L. (Chao Liu), C.L. (Chunyang Liu), X.Z., and H.X.; data curation, Y.T., C.L. (Chunyang Liu), and H.H.; writing—original draft preparation, Y.T. and T.Z.; and writing—review and editing, T.Z. and H.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (No. 2016YFC0803109), the Anhui Universities Natural Science Research Project (No. KJ2020A0312), the Hebei Ecological Intelligent Mine Joint Foundation (No. E2020402086), the National Natural Science Foundation of China (No. 41772130), and the Anhui University of Science and Technology Graduate Innovation Foundation (No. 2019CX2077).
Data Availability Statement
Upon a reasonable request, the observation data that support the findings of this study are available from the corresponding author (Y.T.).
Acknowledgments
We would like to thank the anonymous reviewers for their constructive comments and suggestions. Furthermore, we are grateful to the IGS Data Center of Wuhan University for providing the BDS-2/BDS-3 broadcast ephemeris.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef]
- Zhao, X.; Ge, Y.; Ke, F.; Liu, C.; Li, F. Investigation of real-time kinematic multi-GNSS precise point positioning with the CNES products. Measurement 2020, 166, 108231. [Google Scholar] [CrossRef]
- Lv, Y.; Geng, T.; Zhao, Q.; Xie, X.; Zhou, R. Initial assessment of BDS-3 preliminary system signal-in-space range error. GPS Solut. 2020, 24, 16. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, X.; Ge, Y.; Yang, X. Investigation of real-time carrier phase time transfer using current multi-constellations. Measurement 2020, 166, 108237. [Google Scholar] [CrossRef]
- Xi, R.; Jiang, W.; Meng, X.; Chen, H.; Chen, Q. Bridge monitoring using BDS-RTK and GPS-RTK techniques. Measurement 2018, 120, 128–139. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.; Dong, D.; Meng, L.; Chen, J.; Wang, A.; Cui, H. Performance of BDS-3: Satellite visibility and dilution of precision. GPS Solut. 2019, 23, 56. [Google Scholar] [CrossRef]
- Danskin, S.; Bettinger, P.; Jordan, T. Multipath mitigation under forest canopies: A choke ring antenna solution. For. Sci. 2009, 55, 109–116. [Google Scholar]
- Groves, P.D.; Jiang, Z.; Skelton, B.; Cross, P.A.; Lau, L.; Adane, Y.; Kale, I. Novel multipath mitigation methods using a dual-polarization antenna. In Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2010), Portland, OR, USA, 21–24 September 2010; pp. 140–151. [Google Scholar]
- Maqsood, M.; Gao, S.; Brown, T.W.; Unwin, M.; De Vos Van Steenwijk, R.; Xu, J. A compact multipath mitigating ground plane for multiband GNSS antennas. IEEE Trans. Antennas Propag. 2013, 61, 2775–2782. [Google Scholar] [CrossRef]
- Brunner, F.; Hartinger, H.; Troyer, L. GPS signal diffraction modelling: The stochastic SIGMA-Δ model. J. Geod. 1999, 73, 259–267. [Google Scholar] [CrossRef]
- Xi, R.; Meng, X.; Jiang, W.; An, X.; He, Q.; Chen, Q. A refined SNR based stochastic model to reduce site-dependent effects. Remote Sens. 2020, 12, 493. [Google Scholar] [CrossRef]
- Zimmermann, F.; Eling, C.; Kuhlmann, H. Empirical assessment of obstruction adaptive elevation masks to mitigate site-dependent effects. GPS Solut. 2017, 21, 1695–1706. [Google Scholar] [CrossRef]
- Zhong, P.; Ding, X.; Zheng, D.; Chen, W.; Huang, D. Adaptive wavelet transform based on cross-validation method and its application to GPS multipath mitigation. GPS Solut. 2008, 12, 109–117. [Google Scholar] [CrossRef]
- Zheng, D.; Zhong, P.; Ding, X.; Chen, W. Filtering GPS time-series using a Vondrak filter and cross-validation. J. Geod. 2005, 79, 363–369. [Google Scholar] [CrossRef]
- Dai, W.; Huang, D.; Cai, C. Multipath mitigation via component analysis methods for GPS dynamic deformation monitoring. GPS Solut. 2014, 18, 417–428. [Google Scholar] [CrossRef]
- Ray, J.; Cannon, M.; Fenton, P. GPS code and carrier multipath mitigation using a multiantenna system. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 183–195. [Google Scholar] [CrossRef]
- Zhang, K.; Li, B.; Zhu, X.; Chen, H.; Sun, G. Multipath detection based on single orthogonal dual linear polarized GNSS antenna. GPS Solut. 2017, 21, 1203–1211. [Google Scholar] [CrossRef]
- Agnew, D.C.; Larson, K.M. Finding the repeat times of the GPS constellation. GPS Solut. 2007, 11, 71–76. [Google Scholar] [CrossRef]
- Choi, K.; Bilich, A.; Larson, K.M.; Axelrad, P. Modified sidereal filtering: Implications for high-rate GPS positioning. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Genrich, J.F.; Bock, Y. Rapid resolution of crustal motion at short ranges with the global positioning system. J. Geophys. Res. Solid Earth 1992, 97, 3261–3269. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.; Dong, D.; Chen, W.; Li, H.; Wang, Z. Advanced sidereal filtering for mitigating multipath effects in GNSS short baseline positioning. ISPRS Int. J. Geo-Inf. 2018, 7, 228. [Google Scholar] [CrossRef]
- Ragheb, A.E.; Clarke, P.J.; Edwards, S.J. GPS sidereal filtering: Coordinate- and carrier-phase-level strategies. J. Geod. 2007, 81, 325–335. [Google Scholar] [CrossRef]
- Ye, S.; Chen, D.; Liu, Y.; Jiang, P.; Tang, W.; Xia, P. Carrier phase multipath mitigation for BeiDou navigation satellite system. GPS Solut. 2015, 19, 545–557. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, W.; Zhang, S.; Liu, X. Characteristics of BeiDou navigation satellite system multipath and its mitigation method based on Kalman filter and Rauch-Tung-Striebel smoother. Sensors 2018, 18, 198. [Google Scholar] [CrossRef] [PubMed]
- Dong, D.; Wang, M.; Chen, W.; Zeng, Z.; Song, L.; Zhang, Q.; Cai, M.; Cheng, Y.; Lv, J. Mitigation of multipath effect in GNSS short baseline positioning by the multipath hemispherical map. J. Geod. 2016, 90, 255–262. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, W.; Dong, D.; Wang, M.; Cai, M.; Yu, C.; Zheng, Z.; Liu, M. Multipath mitigation based on trend surface analysis applied to dual-antenna receiver with common clock. GPS Solut. 2019, 23, 104. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, W.; Dong, D.; Zhang, C.; Peng, Y.; Zheng, Z. An advanced multipath mitigation method based on trend surface analysis. Remote Sens. 2020, 12, 3601. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, X.; Li, P.; Li, X.; Ge, M.; Guo, F.; Sang, J.; Schuh, H. Multipath extraction and mitigation for high-rate multi-GNSS precise point positioning. J. Geod. 2019, 93, 2037–2051. [Google Scholar] [CrossRef]
- Cai, M.; Chen, W.; Dong, D.; Song, L.; Wang, M.; Wang, Z.; Zhou, F.; Zheng, Z.; Yu, C. Reduction of kinematic short baseline multipath effects based on multipath hemispherical map. Sensors 2016, 16, 1677. [Google Scholar] [CrossRef]
- Alber, C.; Ware, R.; Rocken, C.; Braun, J. Obtaining single path phase delays from GPS double differences. Geophy. Res. Lett. 2000, 27, 2661–2664. [Google Scholar] [CrossRef]
- Chen, D.; Ye, S.; Xia, J.; Liu, Y.; Xia, P. A geometry-free and ionosphere-free multipath mitigation method for BDS three-frequency ambiguity resolution. J. Geod. 2016, 90, 703–714. [Google Scholar] [CrossRef]
- Zhong, P.; Ding, X.; Yuan, L.; Xu, Y.; Kwok, K.; Chen, Y. Sidereal filtering based on single differences for mitigating GPS multipath effects on short baselines. J. Geod. 2010, 84, 145–158. [Google Scholar] [CrossRef]
- Teunissen, P.; Verhagen, S. GNSS carrier phase ambiguity resolution: Challenges and open problems. In Observing Our Changing Earth; Springer: Berlin/Heidelberg, Germany, 2009; pp. 785–792. [Google Scholar]
- Zhao, X.; Wang, Q.; Pan, S.; Deng, J. Partial ambiguity fixing algorithm based on LAMBDA and its performance analysis. J. Chin. Inert. Technol. 2010, 18, 665–669. [Google Scholar]
- Garcia, V.; Debreuve, E.; Nielsen, F.; Barlaud, M. K-nearest neighbor search: Fast GPU-based implementations and application to high-dimensional feature matching. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 3757–3760. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).