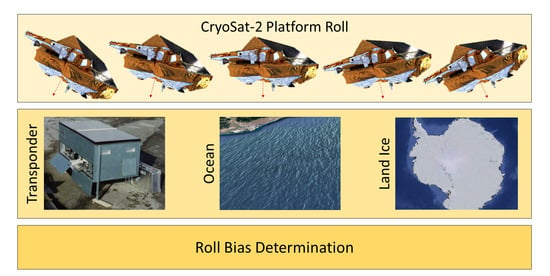
Roll Calibration for CryoSat-2: A Comprehensive Approach
Abstract
1. Introduction
2. Methods
2.1. Transponder Calibration
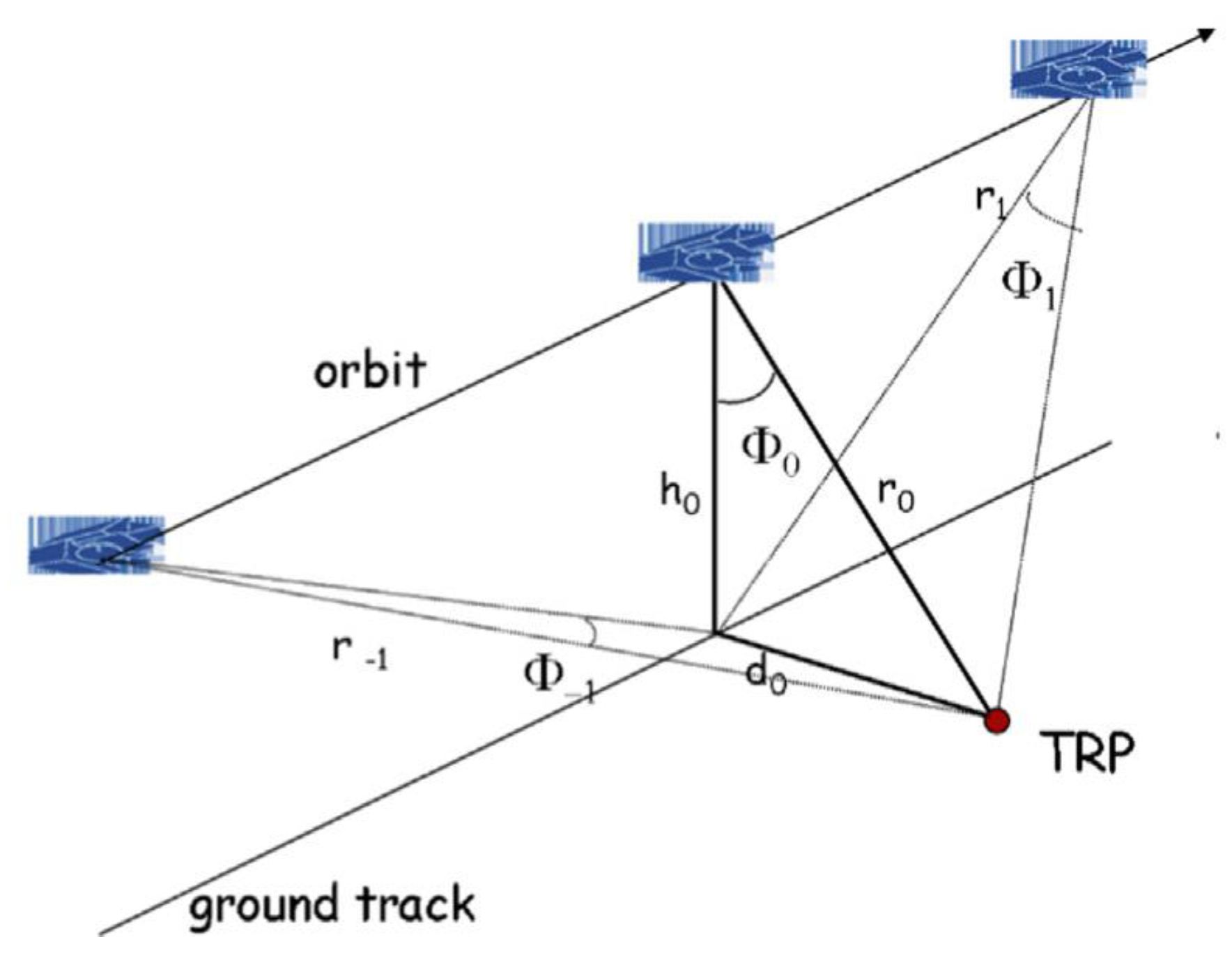
2.2. Roll Campaigns over Ocean
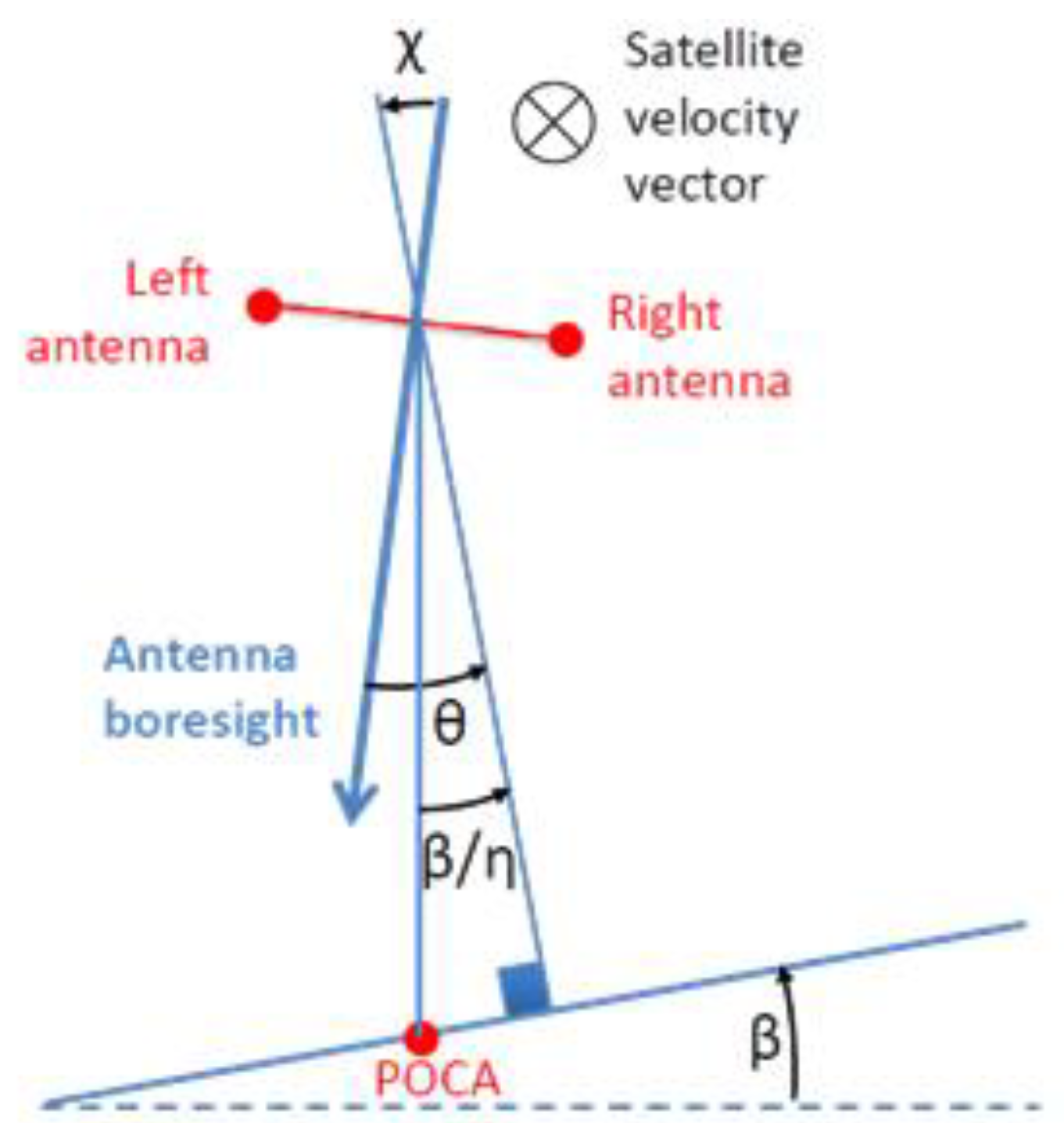
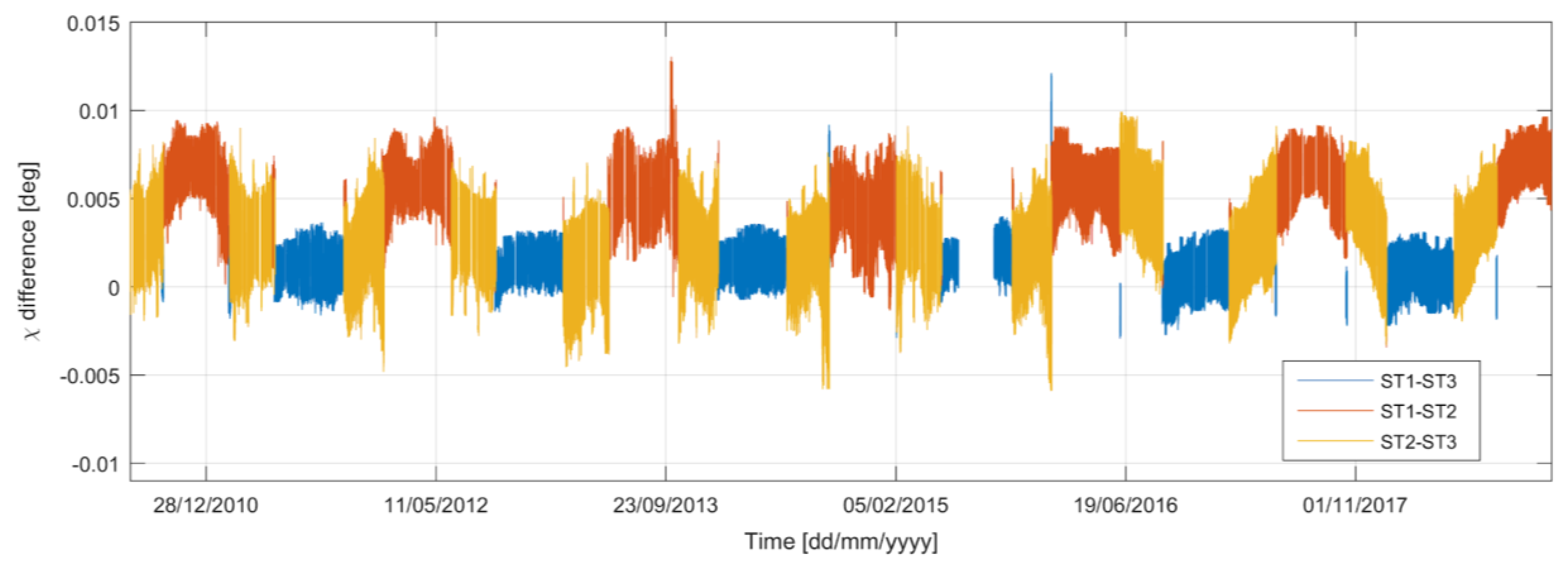
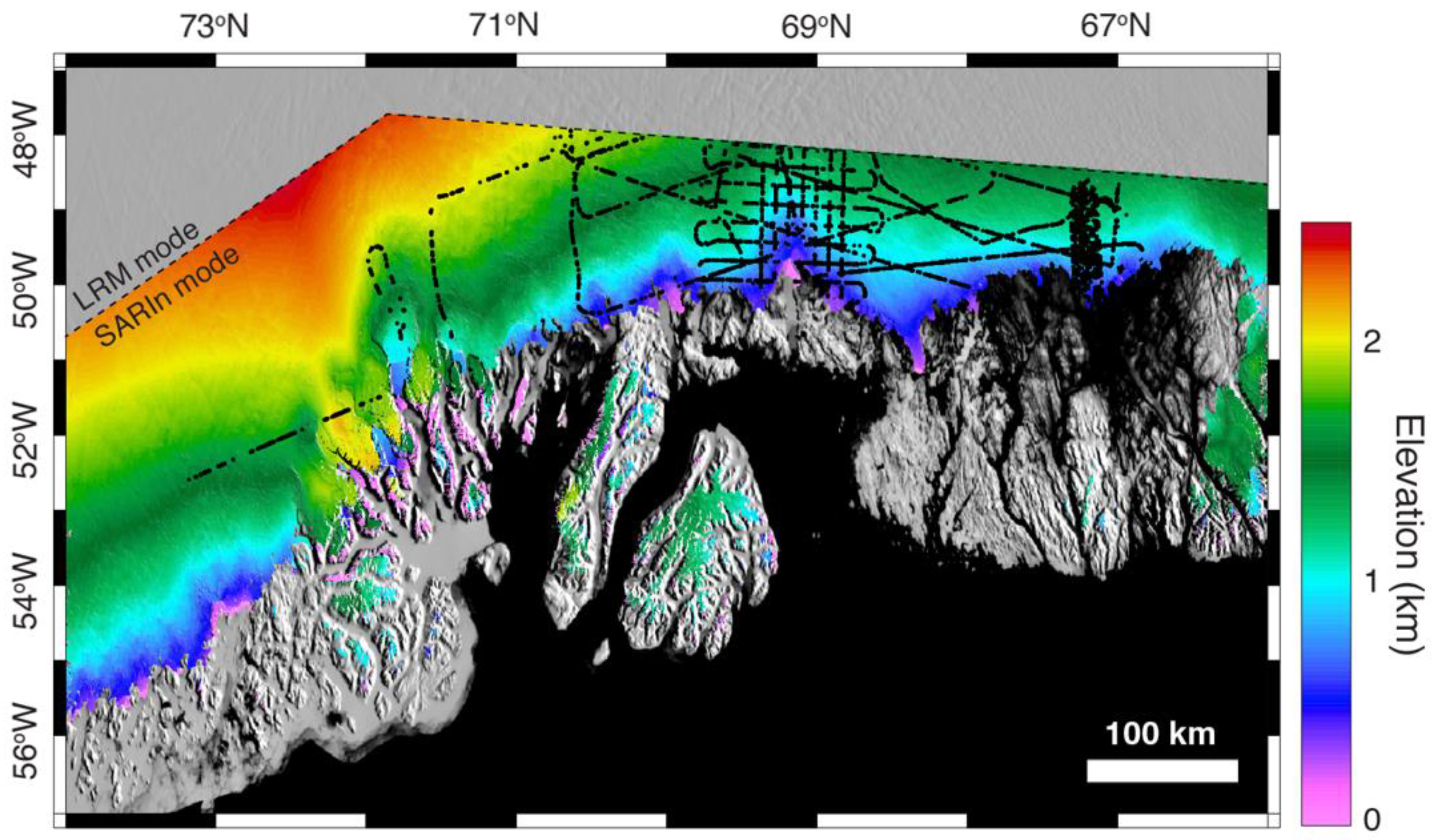
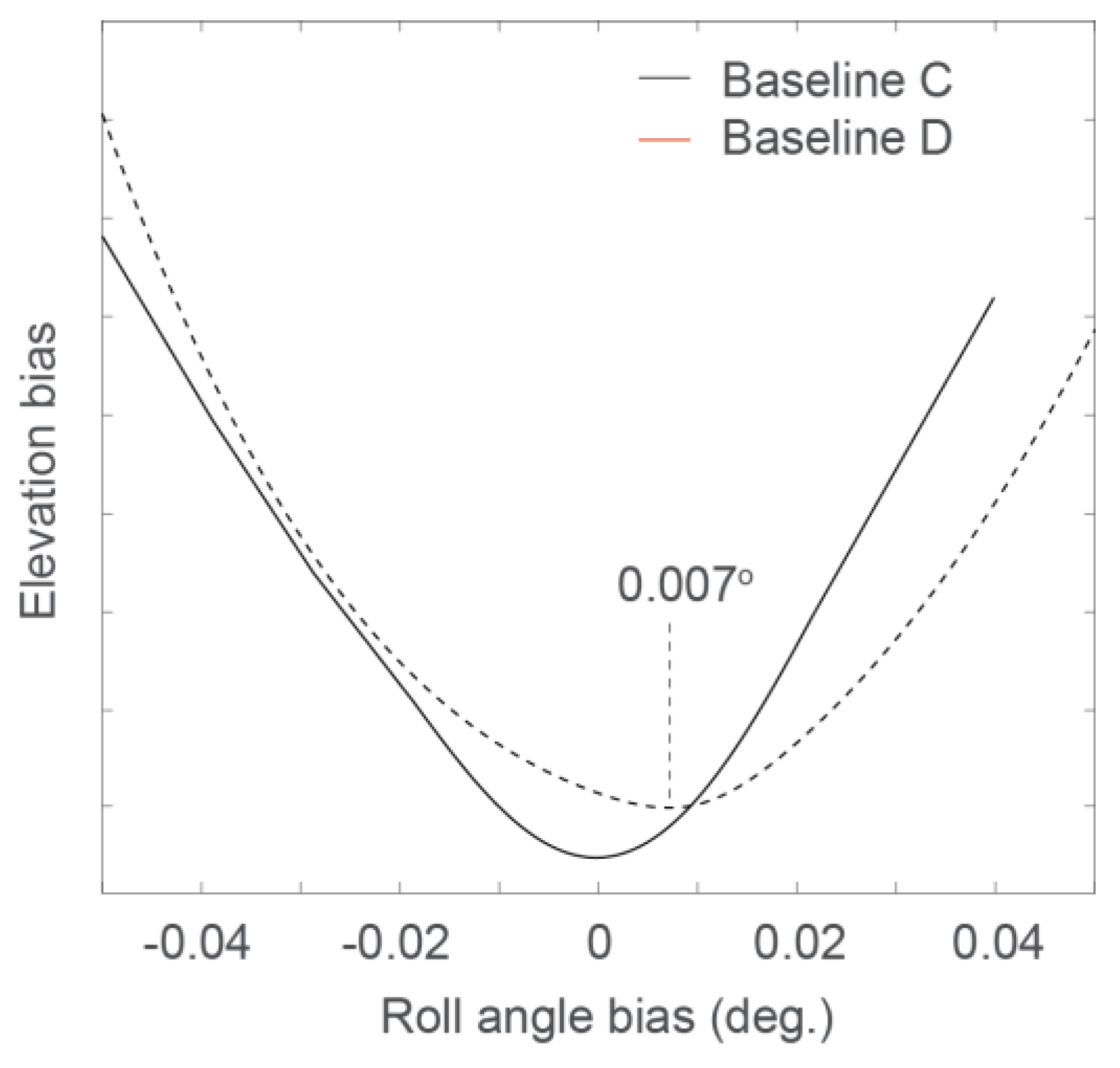
2.3. Swath-Based Roll
3. Results and Discussion
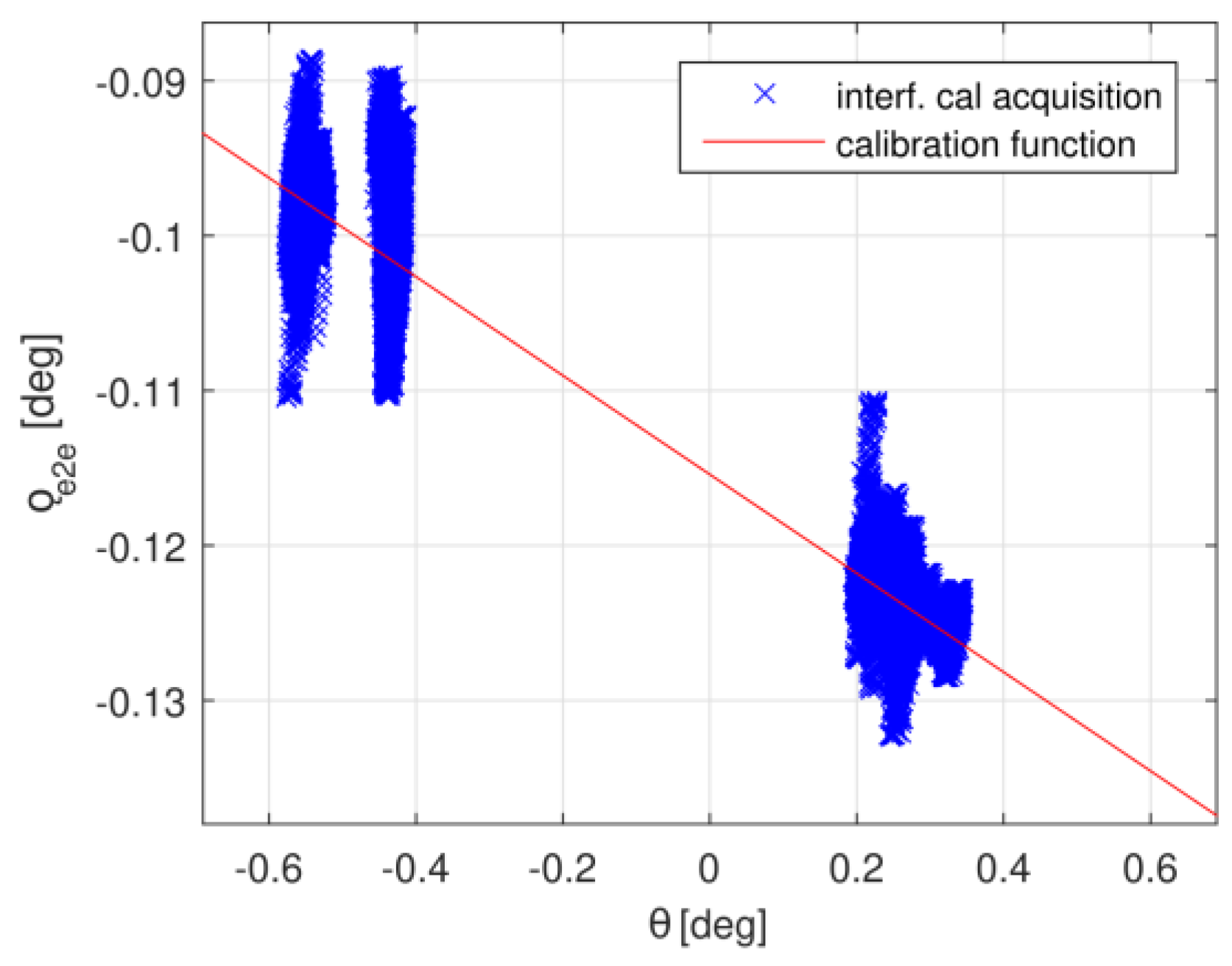
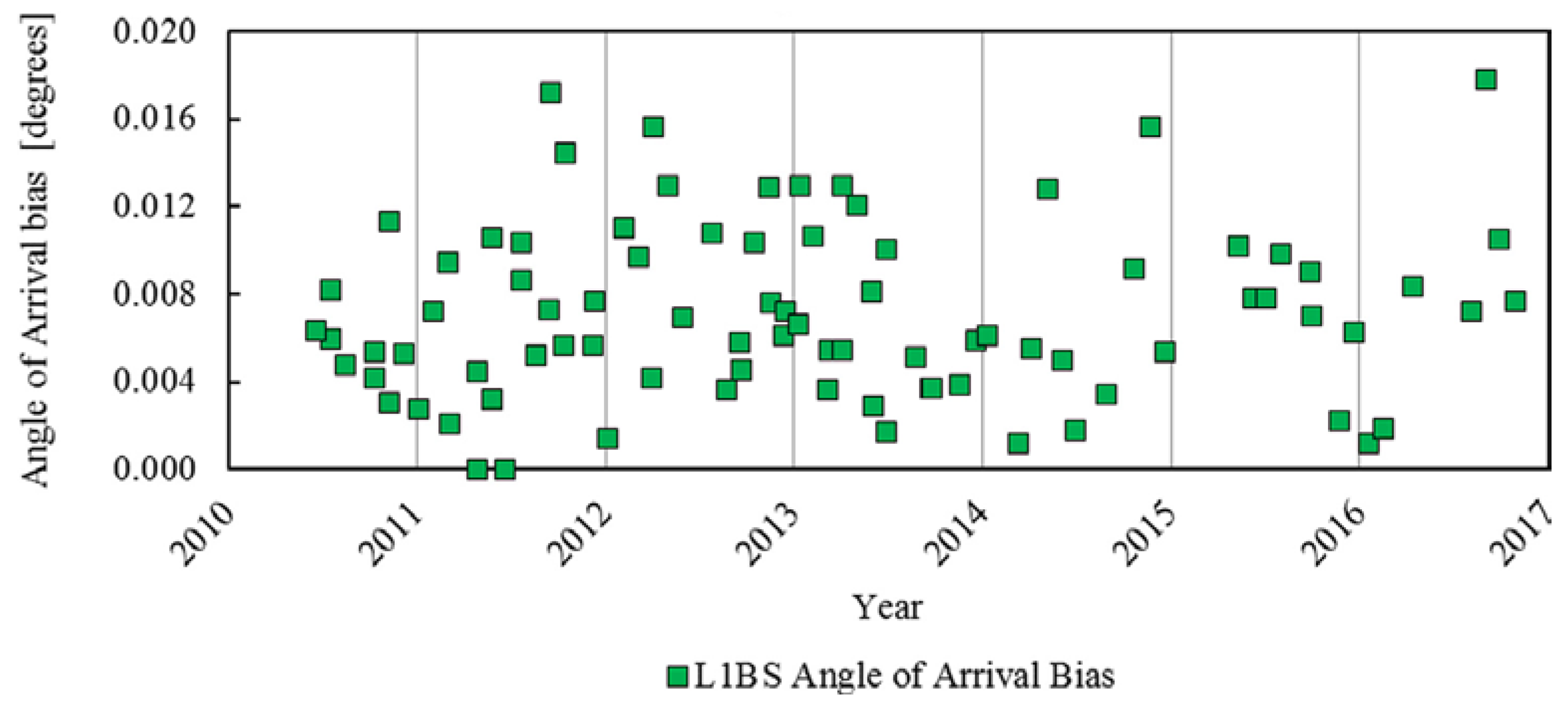
3.1. Transponder Calibration
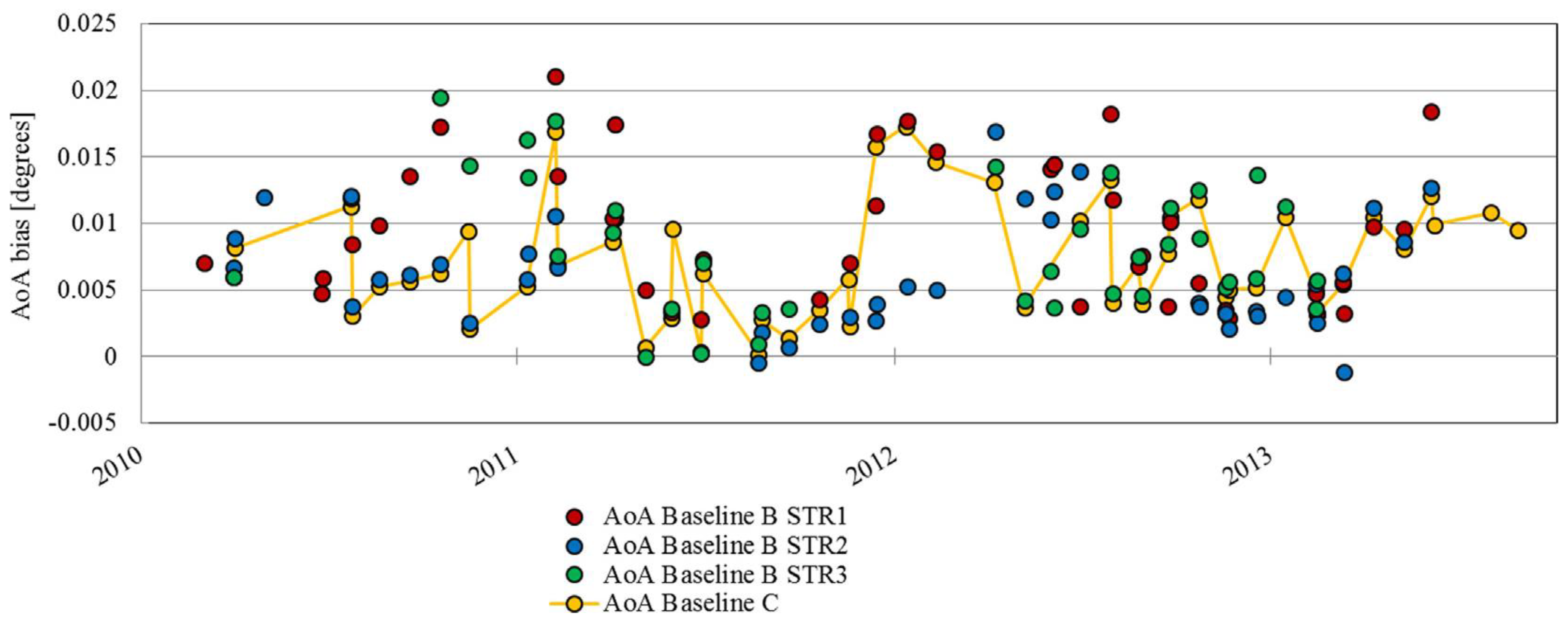
3.2. Roll Campaigns over Ocean
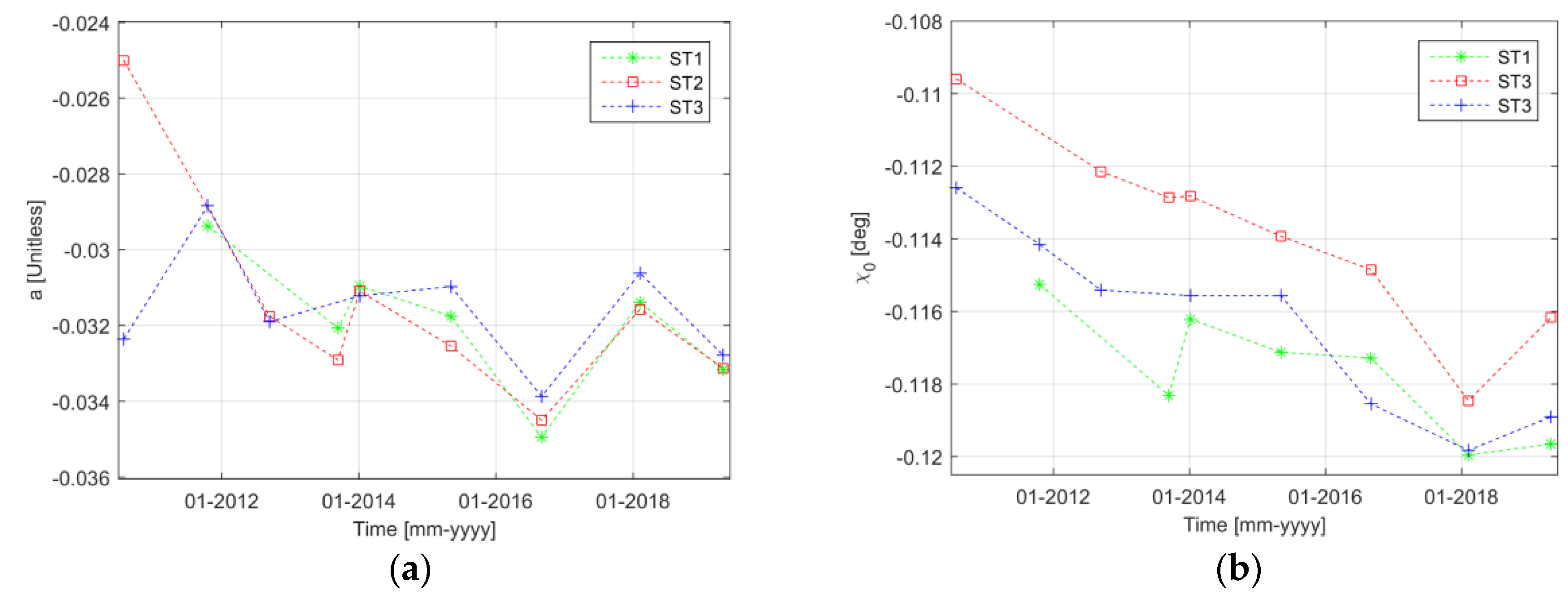
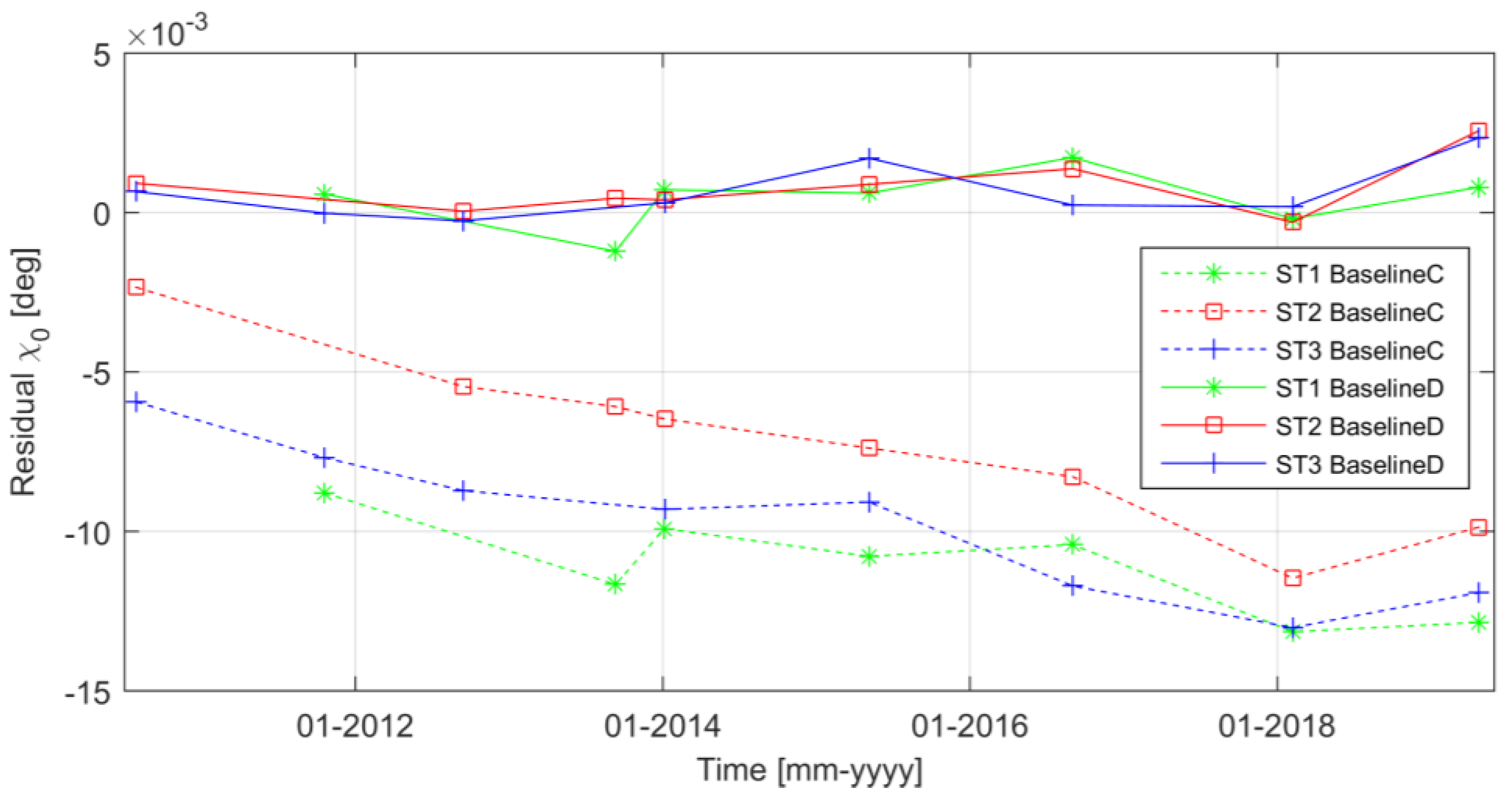
3.3. Swath-Based Roll
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wingham, D.J.; Phalippou, L.; Mavrocordatos, C.; Wallis, D. The mean echo and echo cross product from a beamforming interferometric altimeter and their application to elevation measurement. IEEE Trans. Geosci. Rem. Sens. 2004, 42, 2305–2323. [Google Scholar] [CrossRef]
- ESA Team. CryoSat Mission and Data Description; Report no. CS-RP-ESA-SY-0059; ESTEC: Noordwijk, The Netherlands, 2007; Available online: http://esamultimedia.esa.int/docs/Cryosat/Mission_and_Data_Descrip.pdf (accessed on 15 January 2021).
- Wingham, D.J.; Francis, C.R.; Baker, S.; Bouzinac, C.; Brockley, D.; Cullen, R.; de Chateau-Thierry, P.; Laxon, S.W.; Mallow, U.; Mavrocordatos, C.; et al. CryoSat: A mission to determine the fluctuations in Earth’s land and marine ice fields. Adv. Space Res. 2006, 37, 841–871. [Google Scholar] [CrossRef]
- Galin, N.; Wingham, D.J.; Cullen, R.; Fornari, M.; Smith, W.H.F.; Abdalla, S. Calibration of the CryoSat-2 Interferometer and Measurement of Across-Track Ocean Slope. IEEE Trans. Geosci. Remote Sens. 2012, 51, 57–72. [Google Scholar] [CrossRef]
- Galin, N.; Wingham, D.J.; Cullen, R.; Francis, R.; Lawrence, I. Measuring the Pitch of CryoSat-2 Using the SAR Mode of the SIRAL Altimeter. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1399–1403. [Google Scholar] [CrossRef]
- Scagliola, M.; Fornari, M.; Tagliani, N. Pitch Estimation for CryoSat by Analysis of Stacks of Single-Look Echoes. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1561–1565. [Google Scholar] [CrossRef]
- Meloni, M.; Bouffard, J.; Parrinello, T.; Dawson, G.; Garnier, F.; Helm, V.; Di Bella, A.; Hendricks, S.; Ricker, R.; Webb, E.; et al. CryoSat Ice Baseline-D validation and evolutions. Cryosphere 2020, 14, 1889–1907. [Google Scholar] [CrossRef]
- Garcia-Mondéjar, A.; Fornari, M.; Bouffard, J.; Féménias, P.; Roca, M. CryoSat-2 range, datation and interferometer calibration with Svalbard transponder. Adv. Space Res. 2018, 62, 1589–1609. [Google Scholar] [CrossRef]
- Scagliola, M.; Fornari, M.; Bouffard, J.; Parrinello, T. The CryoSat interferometer: End-to-end calibration and achievable performance. Adv. Space Res. 2018, 62, 1516–1525. [Google Scholar] [CrossRef]
- Hawley, R.L.; Shepherd, A.; Cullen, R.; Helm, V.; Wingham, D.J. Ice-sheet elevations from across-track processing of airborne interferometric radar altimetry. Geophys. Res. Lett. 2009, 36, L22501. [Google Scholar] [CrossRef]
- Gray, L.; Burgess, D.; Copland, L.; Cullen, R.; Galin, N.; Hawley, R.; Helm, V. Interferometric swath processing of Cryosat-2 data for glacial ice topography. Cryosphere Discuss. 2013, 7, 3133–3162. [Google Scholar] [CrossRef]
- Gourmelen, N.; Escorihuela, M.J.; Shepherd, A.; Foresta, L.; Muir, A.; Garcia-Mondejar, A.; Drinkwater, M.R. CryoSat-2 swath interferometric altimetry for mapping ice elevation and elevation change. Adv. Space Res. 2018, 62, 1226–1242. [Google Scholar] [CrossRef]
- Gourmelen, N.; Goldberg, D.; Snow, K.; Henley, S.; Bingham, R.; Kimura, S.; Hogg, A.; Shepherd, A.; Mouginot, J.; Lenearts, J.; et al. Channelized melting drives thinning under a rapidly melting Antarctic ice shelf. Geophys. Res. Lett. 2017, 44, 9796–9804. [Google Scholar] [CrossRef]
- Gray, L.; Burgess, D.; Copland, L.; Langley, K.; Gogineni, P.; Paden, J.; Smith, B. Measuring height change around the periphery of the Greenland Ice Sheet with radar altimetry. Front. Earth Sci. 2019, 7, 146. [Google Scholar] [CrossRef]
- Shepherd, A.; Ivins, E.; Rignot, E.; Smith, B.; van Den Broeke, M.; Velicogna, I.; Whitehouse, P.; Briggs, K.; Joughin, I.; Krinner, G.; et al. Mass balance of the Greenland Ice Sheet from 1992 to 2018. Nature 2020, 579, 233–239. [Google Scholar]
- Gray, L.; Burgess, D.; Copland, L.; Demuth, M.N.; Dunse, T.; Langley, K.; Schuler, T.V. CryoSat-2 delivers monthly and inter-annual surface elevation change for Arctic ice caps. Cryosphere 2015, 9, 1895–1913. [Google Scholar] [CrossRef]
- Foresta, L.; Gourmelen, N.; Pálsson, F.; Nienow, P.; Björnsson, H.; Shepherd, A. Surface elevation change and mass balance of Icelandic ice caps derived from swath mode CryoSat-2 altimetry. Geophys. Res. Lett. 2016, 43, 12138–12145. [Google Scholar] [CrossRef]
- Foresta, L.; Gourmelen, N.; Weissgerber, F.; Nienow, P.; Williams, J.; Shepherd, A.; Drinkwater, M.R.; Plummer, S. Heterogeneous and rapid ice loss over the Patagonian Ice Fields revealed by CryoSat-2 swath radar altimetry. Remote Sens. Environ. 2018, 211, 441–455. [Google Scholar] [CrossRef]
- Jakob, L.; Gourmelen, N.; Ewart, M.; Plummer, S. Ice loss in High Mountain Asia and the Gulf of Alaska observed by CryoSat-2 swath altimetry between 2010 and 2019. Cryosphere 2020. [Google Scholar] [CrossRef]
- Gray, L.; Burgess, D.; Copland, L.; Dunse, T.; Langley, K.; Moholdt, G. A revised calibration of the interferometric mode of the CryoSat-2 radar altimeter improves ice height and height change measurements in western Greenland. Cryosphere 2017, 11, 1041–1058. [Google Scholar] [CrossRef]
- Studinger, M.; Koenig, L.; Martin, S.; Sonntag, J. Operation icebridge: Using instrumented aircraft to bridge the observational gap between Icesat and Icesat-2. IEEE Inter. Geosci. Remote Sens. Symp. 2010. [Google Scholar] [CrossRef]
- Morin, P.; Porter, C.; Cloutier, M.; Howat, I.; Noh, M.J.; Willis, M.; Bates, B.; Williamson, C.; Peterman, K. ArcticDEM; A publically available, high resolution elevation model of the Arctic. In Proceedings of the EGUGA 2016, Vienna, Austria, 17–22 April 2016. EPSC2016-8396. [Google Scholar]
- Haran, T.; Bohlander, J.; Scambos, T.; Fahnestock, M. Modis Mosaic of Greenland (Mog) Image Map; NSIDC—National Snow and Ice Data Center: Boulder, CO, USA, 2013. [Google Scholar]
- Howat, I.M.; Negrete, A.; Smith, B.E. The Greenland Ice Mapping Project (GIMP) land classification and surface elevation data sets. Cryosphere 2014, 8, 1509–1518. [Google Scholar] [CrossRef]
| Campaign | Dates | L1b Products | ST1 | ST2 | ST3 |
|---|---|---|---|---|---|
| #1 | 27–28 July 2010 | 6 | OFF | ON | ON |
| #2 | 17–18 October 2011 | 9 | ON | OFF | ON |
| #3 | 11–12 September 2012 | 8 | OFF | ON | ON |
| #4 | 10–12 October 2013 | 8 | ON | ON | OFF |
| #5 | 4–5 January 2014 | 8 | ON | ON | ON |
| #6 | 6 May 2015 | 8 | ON | ON | ON |
| #7 | 31 August–1 September 2016 | 8 | ON | ON | ON |
| #8 | 6 February 2018 | 8 | ON | ON | ON |
| #9 | 25 April 2019 | 8 | ON | ON | ON |
| Method | Bias | Standard Deviation |
|---|---|---|
| Transponder | 0.0071 degrees | 0.0040 degrees |
| Ocean Roll | 0.0097 degrees | 0.0019 degrees |
| Swath | 0.0070 degrees | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia-Mondéjar, A.; Scagliola, M.; Gourmelen, N.; Bouffard, J.; Roca, M. Roll Calibration for CryoSat-2: A Comprehensive Approach. Remote Sens. 2021, 13, 302. https://doi.org/10.3390/rs13020302
Garcia-Mondéjar A, Scagliola M, Gourmelen N, Bouffard J, Roca M. Roll Calibration for CryoSat-2: A Comprehensive Approach. Remote Sensing. 2021; 13(2):302. https://doi.org/10.3390/rs13020302
Chicago/Turabian StyleGarcia-Mondéjar, Albert, Michele Scagliola, Noel Gourmelen, Jerome Bouffard, and Mònica Roca. 2021. "Roll Calibration for CryoSat-2: A Comprehensive Approach" Remote Sensing 13, no. 2: 302. https://doi.org/10.3390/rs13020302
APA StyleGarcia-Mondéjar, A., Scagliola, M., Gourmelen, N., Bouffard, J., & Roca, M. (2021). Roll Calibration for CryoSat-2: A Comprehensive Approach. Remote Sensing, 13(2), 302. https://doi.org/10.3390/rs13020302