A Proof-of-Concept Algorithm for the Retrieval of Total Column Amount of Trace Gases in a Multi-Dimensional Atmosphere

Abstract

An algorithm for the retrieval of total column amount of trace gases in a multi-dimensional atmosphere is designed. The algorithm uses (i) certain differential radiance models with internal and external closures as inversion models, (ii) the iteratively regularized Gauss–Newton method as a regularization tool, and (iii) the spherical harmonics discrete ordinate method (SHDOM) as linearized radiative transfer model. For efficiency reasons, SHDOM is equipped with a spectral acceleration approach that combines the correlated k-distribution method with the principal component analysis. The algorithm is used to retrieve the total column amount of nitrogen for two- and three-dimensional cloudy scenes. Although for three-dimensional geometries, the computational time is high, the main concepts of the algorithm are correct and the retrieval results are accurate.

1. Introduction

The retrieval of trace gas products from UV/VIS spectrometers is strongly affected by the presence of clouds. In general, there are three different cloud contributions: (i) the albedo effect, associated with the enhancement of reflectivity for cloudy scenes compared to cloud-free scenes; (ii) the shielding effect when a part of the trace gas column below the cloud is hidden; and (iii) the increase in absorption, related to multiple scattering inside clouds. The albedo and in-cloud absorption effects increase the detectability of trace gases at and above the cloud-top (in case of low clouds), while the shielding effect normally results in an underestimation of the trace gas column [1].

The majority of retrieval algorithms are based on one-dimensional radiative transfer modeling and use the so-called independent pixel approximation (IPA). The IPA for an atmosphere containing partial cloudiness means to compute separately the radiances for completely cloudy and clear skies, and then to express the partially cloudy radiance as a weighted sum of the separate radiances; the weighting factor being provided by the intensity weighted cloud fraction. The clouds within each pixel are assumed to be plane-parallel and homogeneous in both horizontal and vertical directions. The main advantage of the IPA is its computational efficiency, as it requires the solution of only two independent one-dimensional radiative transfer problems. The disadvantage is that for cloudy scenes of small horizontal extent, the errors due to the three-dimensional effects may be very significant [2,3,4]. This is the case of the new generation of atmospheric composition UV–VIS–NIR sensors, such as Sentinel-5P, Sentinel-4, and Sentinel-5. In [5] the importance of three-dimensional effects on computations of air mass factors has been shown.

To analyze the impact of cloud inhomogeneity on the retrieval, multi-dimensional radiative transfer models are used. In particular, for a specific cloudy scene, a spectral signal is simulated by a multi-dimensional radiative transfer model and then included in a one-dimensional retrieval algorithm to derive for example, the total column amount of a trace gas. By comparing the retrieved total column with the true value, a bias due to cloud effects can be deduced, and possible correction strategies can be explored.

In this paper, we go one step further and present the main concepts of an algorithm for retrieving the total column amount of trace gases in a multi-dimensional atmosphere. To achieve this goal we combine inverse models and regularization tools from inversion theory with a fast linearized version of the spherical harmonic discrete ordinate method [6]. These theoretical results are summarized in Section 2, while in Section 3, the accuracy and efficiency of the algorithm, used to retrieve the total column amount of nitrogen dioxide ($\mathrm{N}{\mathrm{O}}_2$) for two- and three-dimensional cloudy scenes, are numerically investigated. We conclude our analysis with some recommendations for operational retrievals.

2. Retrieval Algorithm

For a multi-dimensional geometry, the spectral signal of an instrument that measures the radiance at the top of the atmosphere in direction ${\mathsf{\Omega }}_{\mathrm{m}}$ at wavelength $\lambda$ in the spectral interval $[{\lambda }_{\min },{\lambda }_{\max }]$, is given by

$$\begin{array}{cc}\hfill \mathcal{I}\left(\lambda \right)& ={\int }_{{\lambda }_{\min }-s/2}^{{\lambda }_{\max }+s/2}g(\lambda -{\lambda }^{\prime }){\mathcal{I}}_{\mathrm{FOV}}\left({\lambda }^{\prime }\right)\mathrm{d}{\lambda }^{\prime },\hfill \end{array}$$

(1)

where, under the assumption that the distance from the top of the atmosphere to the instrument is large,

$${\mathcal{I}}_{\mathrm{FOV}}\left({\lambda }^{\prime }\right)={\int }_{S_{\mathrm{t}}}h\left({\mathbf{r}}_{\mathrm{t}}\right)I({\lambda }^{\prime },{\mathbf{r}}_{\mathrm{t}},{\mathsf{\Omega }}_{\mathrm{m}})\mathrm{d}{S}_{\mathrm{t}},$$

(2)

is the signal integrated over the field of view (FOV) of the instrument at wavelength ${\lambda }^{\prime }$ (see, e.g., in [7] for a general description), $g\left(\lambda \right)$ the slit function (defined on all $\mathbb{R}$), s the spectral bandwidth, $h\left({\mathbf{r}}_{\mathrm{t}}\right)$ the characteristic function that takes the value $1/A_{\mathrm{tm}}$ for ${\mathbf{r}}_{\mathrm{t}}\in S_{\mathrm{tm}}$ and 0 otherwise, $S_{\mathrm{tm}}$ the footprint of the instrument on the top face $S_{\mathrm{t}}$, and $A_{\mathrm{tm}}$ the area of the instrument footprint. Essentially, Equations (1) and (2) state that the mean radiance across the wavelength and the area $S_{\mathrm{t}}$ at the top of the atmosphere is measured. The top of atmosphere radiance at the exiting point ${\mathbf{r}}_{\mathrm{t}}$ along the characteristic ${\mathsf{\Omega }}_{\mathrm{m}}$, $I(\lambda ,{\mathbf{r}}_{\mathrm{t}},{\mathsf{\Omega }}_{\mathrm{m}})$, is computed by using the integral form of the radiative transfer equation

$$\begin{array}{cc}\hfill I(\lambda ,{\mathbf{r}}_{\mathrm{t}},{\mathsf{\Omega }}_{\mathrm{m}})& =I(\lambda ,{\mathbf{r}}_{\mathrm{b}},{\mathsf{\Omega }}_{\mathrm{m}}){\mathrm{e}}^{-{\int }_0^{s_0}{\sigma }_{\mathrm{ext}}(\lambda ,{\mathbf{r}}_{\mathrm{b}}+s{\mathsf{\Omega }}_{\mathrm{m}})\mathrm{d}s}\hfill \\ \hfill & +{\int }_0^{s_0}{\sigma }_{\mathrm{ext}}(\lambda ,{\mathbf{r}}_{\mathrm{b}}+s{\mathsf{\Omega }}_{\mathrm{m}})J(\lambda ,{\mathbf{r}}_{\mathrm{b}}+s{\mathsf{\Omega }}_{\mathrm{m}},{\mathsf{\Omega }}_{\mathrm{m}})\hfill \\ \hfill & \times \left[{\mathrm{e}}^{-{\int }_s^{s_0}{\sigma }_{\mathrm{ext}}(\lambda ,{\mathbf{r}}_{\mathrm{b}}+s^{\prime }{\mathsf{\Omega }}_{\mathrm{m}})\mathrm{d}{s}^{\prime }}\right]\mathrm{d}s,\hfill \end{array}$$

(3)

where $I(\lambda ,{\mathbf{r}}_{\mathrm{b}},{\mathsf{\Omega }}_{\mathrm{m}})$ is the radiance at the surface point ${\mathbf{r}}_{\mathrm{b}}$, $J(\lambda ,\mathbf{r},{\mathsf{\Omega }}_{\mathrm{m}})$ the source function, and $s_0=|{\mathbf{r}}_{\mathrm{t}}-{\mathbf{r}}_{\mathrm{b}}|$ the distance between the entering and exiting points, respectively. Equation (3) can be derived by integrating the radiative transfer equation [8,9]. The first term corresponds to the upwelling radiance at the bottom of the atmosphere and attenuated exponentially as it propagates through the atmosphere. The second term refers to the gain due to sources. The source function J contains only the solar term and the multiple scattering term [10].

In the case of an atmosphere consisting of gas molecules and a cloud, we assume that (i) the optical coefficients of the gas molecules depend on the altitude level and the wavelength, while (ii) the optical coefficients of the cloud depend on the spatial coordinates but not on the wavelength. The second assumption is justified by the fact that a narrow spectral interval is considered in the retrieval. According to the additivity property of optical cross sections [11], in the case of $N_g$ gases, the extinction coefficient is computed as

$${\sigma }_{\mathrm{ext}}(\lambda ,\mathbf{r})={\sigma }_{\mathrm{ext}}^{\mathrm{cloud}}\left(\mathbf{r}\right)+{\sigma }_{\mathrm{sct}}^{\mathrm{mol}}(\lambda ,z)+\sum _{g=1}^{N_g}{\sigma }_{\mathrm{abs}g}^{\mathrm{gas}}(\lambda ,z),$$

(4)

where ${\sigma }_{\mathrm{ext}}^{\mathrm{cloud}}\left(\mathbf{r}\right)$ is the extinction coefficient in the cloud (methods for computing ${\sigma }_{\mathrm{ext}}^{\mathrm{cloud}}\left(\mathbf{r}\right)$ are summarized in [12]), ${\sigma }_{\mathrm{sct}}^{\mathrm{mol}}(\lambda ,z)$ the molecular scattering coefficient due to Rayleigh scattering [13], ${\sigma }_{\mathrm{abs}g}^{\mathrm{gas}}(\lambda ,z)$ the absorption coefficient of gas g, and $(x,y,z)$ the Cartesian coordinates of point $\mathbf{r}$. Considering a discretization of the atmosphere in $N_{\mathrm{z}}$ levels, i.e., ${\left\{z_j\right\}}_{j=1}^{N_{\mathrm{z}}}$, the absorption coefficient on level $z_j$ is given by

$${\sigma }_{\mathrm{abs}g}^{\mathrm{gas}}(\lambda ,z_j)=C_{\mathrm{abs}g}(\lambda ,z_j)n_g\left(z_j\right),$$

(5)

where $C_{\mathrm{abs}g}(\lambda ,z_j)$ and $n_g\left(z_j\right)$ are the absorption cross section and the number density of gas j on level $z_j$, respectively. Under the assumption that on a layer j bounded below by $z_j$ and above by $z_{j+1}$, the number density $n_g\left(z\right)$ varies linearly with respect to z, the partial and total column of gas g are defined, respectively, by

$$x_{g,j}={\int }_{z_j}^{z_{j+1}}{n}_g\left(z\right)\mathrm{d}z\approx \frac{\Delta z_j}{2}[n_g\left(z_j\right)+n_g\left(z_{j+1}\right)]$$

(6)

and

$$X_g={\int }_{z_1}^{z_{N_{\mathrm{z}}}}{n}_g\left(z\right)\mathrm{d}z=\sum _{j=1}^{N_{\mathrm{z}}-1}{x}_{g,j},$$

(7)

where $\Delta z_j=z_{j+1}-z_j$.

The retrieval algorithm is based on the assumption that cloud information are available from co-located imagers, as, for example, the Moderate Resolution Imaging Spectroradiometer (MODIS) on board the Terra and Aqua satellites and the Visible Infrared Imaging Radiometer Suite (VIIRS) on board the Suomi National Polar-Orbiting Partnership spacecraft. The main cloud products delivered by MODIS/VIIRS are the cloud mask (indicator function of the cloud field), cloud optical thickness, cloud-top height (cloud-top pressure), and effective radius of the size distribution. In the MODIS/VIIRS retrieval algorithm, the cloud geometrical thickness is derived under the assumption that the clouds are homogeneous in the vertical direction, or equivalently, that the liquid water content does not change with the altitude. Therefore, it is appropriate to use stochastic cloud models (in particular statistical cloud generators) which operate with the same assumption. For this reason, we will use stochastic cloud models relying on the vertical homogeneity assumption, and in particular, the two-dimensional broken cloud model of Alexandrov et al. [14].

In general, the design of a retrieval algorithm requires the specification of

• an inverse model,
• a solution method for solving the inverse problem, and
• a linearized multi-dimensional radiative transfer model for computing the forward model and the Jacobian matrix at each iteration step.

2.1. Inverse Models

The retrieval of the total columns $X_g$ of $N_{\mathrm{g}}$ gases can be performed by using two differential radiance models (see details in [15,16,17] and references therein):

• the Differential Radiance Model with Internal closure (DRMI), in which the measured and simulated differential spectral signals are fitted, and
• the Differential Radiance Model with External closure (DRME), in which the measured differential spectral signal and a simulated spectral signal with its smooth component extracted are fitted.

Actually, in DRMI we solve the nonlinear equation

$$\begin{array}{cc}\hfill R_{\mathrm{mes}}^{\delta }\left({\lambda }_k\right)& =R_{\mathrm{sim}}({\lambda }_k,\mathbf{X})+\sum _{j=1}^{N_{\mathrm{s}}}{b}_j{S}_j({\lambda }_k,{\mathbf{X}}_{\mathrm{a}}), k=1,\dots ,N_{\lambda },\hfill \end{array}$$

(8)

where

$$R_{\mathrm{mes}}^{\delta }\left({\lambda }_k\right)=ln{\mathcal{I}}_{\mathrm{mes}}^{\delta }\left({\lambda }_k\right)-P_{\mathrm{mes}}({\lambda }_k,{\mathbf{c}}_{\mathrm{mes}})$$

(9)

and

$$R_{\mathrm{sim}}({\lambda }_k,\mathbf{X})=ln{\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,\mathbf{X})-P_{\mathrm{sim}}({\lambda }_k,{\mathbf{c}}_{\mathrm{sim}}\left(\mathbf{X}\right))$$

(10)

are the measured and simulated differential spectral signals, respectively, while in DRME we solve the nonlinear equation

$$\begin{array}{cc}\hfill R_{\mathrm{mes}}^{\delta }\left({\lambda }_k\right)& =ln{\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,\mathbf{X})+\sum _{j=1}^{N_{\mathrm{s}}}{b}_j{S}_j({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})-P({\lambda }_k,\mathbf{c}), k=1,\dots ,N_{\lambda }.\hfill \end{array}$$

(11)

In Equations (8)–(11), $\mathbf{X}=[X_1,\dots ,X_{N_{\mathrm{g}}}]$ is the vector comprising the total columns of trace gases; ${\mathbf{X}}_{\mathrm{a}}$ an a priori estimate of $\mathbf{X}$; ${\mathcal{I}}_{\mathrm{mes}}^{\delta }\left({\lambda }_k\right)$ the (noisy) spectral signal measured by the instrument at wavelength ${\lambda }_k$, where $k=1,\dots N_{\lambda }$, $N_{\lambda }$ the number of measurement wavelengths; ${\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,\mathbf{X})$ the simulated spectral signal computed by a multi-dimensional radiative transfer model; $S_j({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})$ with $j=1,\dots ,N_{\mathrm{s}}$, the correction spectra including, for example, the polarization correction spectrum and the Ring spectrum, $N_{\mathrm{s}}$ the number of correction spectra; and $b_j$ with $j=1,\dots ,N_{\mathrm{s}}$, the (wavelength independent) amplitudes of the correction spectra. The polynomials $P_{\mathrm{mes}}(\lambda ,{\mathbf{c}}_{\mathrm{mes}})$, $P_{\mathrm{sim}}(\lambda ,{\mathbf{c}}_{\mathrm{sim}}\left(\mathbf{X}\right))$, and $P(\lambda ,\mathbf{c})$ with degree $N_{\mathrm{p}}-1$ account for the low-order spectral structure due to the scattering by clouds and aerosols, while the differential spectral signals $R_{\mathrm{sim}}$ and $R_{\mathrm{mes}}^{\delta }$ are mostly due to the gaseous absorption processes (see Ref. [18] for details). Specifically, in DRMI, the coefficients

$${\mathbf{c}}_{\mathrm{mes}}=[c_{\mathrm{mes}0},\dots ,c_{\mathrm{mes}{N}_{\mathrm{p}}-1}]\mathrm{and}{\mathbf{c}}_{\mathrm{sim}}\left(\mathbf{X}\right)=[c_{\mathrm{sim}0}\left(\mathbf{X}\right),\dots ,c_{\mathrm{sim}{N}_{\mathrm{p}}-1}\left(\mathbf{X}\right)]$$

of the smoothing polynomials $P_{\mathrm{mes}}(\lambda ,{\mathbf{c}}_{\mathrm{mes}})$ and $P_{\mathrm{sim}}(\lambda ,{\mathbf{c}}_{\mathrm{sim}}\left(\mathbf{X}\right))$, respectively, are computed as the solutions of the least-squares problems

$${\mathbf{c}}_{\mathrm{mes}}=arg\underset{\mathbf{c}}{min}\sum _{k=1}^{N_{\lambda }}{\left[ln{\mathcal{I}}_{\mathrm{mes}}^{\delta }\left({\lambda }_k\right)-P_{\mathrm{mes}}({\lambda }_k,\mathbf{c})\right]}^2$$

(12)

and

$${\mathbf{c}}_{\mathrm{sim}}\left(\mathbf{X}\right)=arg\underset{\mathbf{c}}{min}\sum _{k=1}^{N_{\lambda }}{\left[ln{\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,\mathbf{X})-P_{\mathrm{sim}}({\lambda }_k,\mathbf{c})\right]}^2,$$

(13)

respectively. Thus, these coefficients, which are uniquely determined by $ln{\mathcal{I}}_{\mathrm{mes}}^{\delta }\left({\lambda }_k\right)$ and $ln{\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,\mathbf{X})$, are not a part of the retrieval, while in DRMI, the coefficients $\mathbf{c}=[c_0,\dots ,c_{N_{\mathrm{p}}-1}]$ of the smoothing polynomial $P(\lambda ,\mathbf{c})$ are included in the retrieval.

Similar inversion models can be used for tropospheric column retrieval. These models together with the underlying retrieval algorithms are described in Appendix A.

To speed up the calculation, two approximate inverse models can be designed.

• In DRME, we assume the linearized model [19]

  $$\begin{array}{cc}\hfill ln{\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,\mathbf{X})& =ln{\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})+\sum _{g=1}^{N_{\mathrm{g}}}(X_g-X_{\mathrm{a}g})\frac{\partial ln{\mathcal{I}}_{\mathrm{sim}}}{\partial X_g}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})+\delta R_{\mathrm{p}}\left({\lambda }_k\right),\hfill \end{array}$$

  (14)

  where the second term in the right-hand side of the equation describes the variations of $ln{\mathcal{I}}_{\mathrm{sim}}$ with respect to the total column amounts of trace gases $X_g$ with $g=1,\dots ,N_g$, and the third term $\delta R_{\mathrm{p}}\left({\lambda }_k\right)$ comprises the contributions of all other atmospheric parameters. Approximating $\delta R_{\mathrm{p}}\left({\lambda }_k\right)$ by a smoothing polynomial, i.e., $\delta R_{\mathrm{p}}\left({\lambda }_k\right)\approx P_{\mathrm{p}}({\lambda }_k,{\mathbf{c}}_{\mathrm{p}})$, and putting $P({\lambda }_k,\mathbf{c})-P_{\mathrm{p}}({\lambda }_k,{\mathbf{c}}_{\mathrm{p}})\to P({\lambda }_k,\mathbf{c})$, we are led to the linear equation

  $$\begin{array}{cc}\hfill R_{\mathrm{mes}}^{\delta }\left({\lambda }_k\right)& =ln{\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})+\sum _{g=1}^{N_{\mathrm{g}}}(X_g-X_{\mathrm{a}g})\frac{\partial ln{\mathcal{I}}_{\mathrm{sim}}}{\partial X_g}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})\hfill \\ \hfill & +\sum _{j=1}^{N_{\mathrm{s}}}{b}_j{S}_j({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})-P({\lambda }_k,\mathbf{c}), k=1,\dots ,N_{\lambda },\hfill \end{array}$$

  (15)

  which is equivalent with the Differential Optical Absorption Spectroscopy (DOAS) equation [18]. This equivalence is proved in Appendix B.
• We adopt an approximate inverse model in which we compute the spectral signal by an one-dimensional radiative transfer model, and (similar to the Ring and polarization correction spectra) introduce a correction spectrum $S_{3\mathrm{D}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})$ that accounts on three-dimensional effects. To define the correction spectrum, we take into account that, for example, in DRME, we can write

  $$\begin{array}{cc}\hfill & ln{\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}}({\lambda }_k,\mathbf{X})-P({\lambda }_k,\mathbf{c})\hfill \\ \hfill & =ln{\mathcal{I}}_{\mathrm{sim}}^{1\mathrm{D}}({\lambda }_k,\mathbf{X})+ln[1+\delta {\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}}({\lambda }_k,\mathbf{X})]-P({\lambda }_k,\mathbf{c})\hfill \\ \hfill & \approx ln{\mathcal{I}}_{\mathrm{sim}}^{1\mathrm{D}}({\lambda }_k,\mathbf{X})+\delta {\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}}({\lambda }_k,\mathbf{X})-P({\lambda }_k,\mathbf{c})\hfill \\ \hfill & =ln{\mathcal{I}}_{\mathrm{sim}}^{1\mathrm{D}}({\lambda }_k,\mathbf{X})+[\delta {\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}}({\lambda }_k,\mathbf{X})-P_{3\mathrm{D}}({\lambda }_k,{\mathbf{c}}_{3\mathrm{D}}\left(\mathbf{X}\right))]-P_{1\mathrm{D}}({\lambda }_k,{\mathbf{c}}_{1\mathrm{D}}),\hfill \end{array}$$

  (16)

  where ${\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}}({\lambda }_k,\mathbf{X})$ and ${\mathcal{I}}_{\mathrm{sim}}^{1\mathrm{D}}({\lambda }_k,\mathbf{X})$, are the spectral signals computed by a three- and an one-dimensional radiative transfer model, respectively, and

  $$\delta {\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}}({\lambda }_k,\mathbf{X})=\frac{{\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}}({\lambda }_k,\mathbf{X})-{\mathcal{I}}_{\mathrm{sim}}^{1\mathrm{D}}({\lambda }_k,\mathbf{X})}{{\mathcal{I}}_{\mathrm{sim}}^{1\mathrm{D}}({\lambda }_k,\mathbf{X})},$$

  (17)

  is a relative correction spectrum. In deriving Equation (16), we used the first-order Taylor approximation $ln(1+\delta {\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}})\approx \delta {\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}}$ for $\delta {\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}}\ll 1$, and the decomposition $P({\lambda }_k,\mathbf{c})=P_{3\mathrm{D}}({\lambda }_k,{\mathbf{c}}_{3\mathrm{D}}\left(\mathbf{X}\right)+P_{1\mathrm{D}}({\lambda }_k,{\mathbf{c}}_{1\mathrm{D}})$, in which, the coefficients ${\mathbf{c}}_{3\mathrm{D}}\left(\mathbf{X}\right)$ are uniquely determined by $\delta {\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}}({\lambda }_k,\mathbf{X})$ (see below), while the coefficients ${\mathbf{c}}_{1\mathrm{D}}$ are unknown (as the coefficients $\mathbf{c}$ are). In view of Equation (16), we assume that in the retrieval, the differential spectral term

  $$\delta {\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}}({\lambda }_k,\mathbf{X})-P_{3\mathrm{D}}({\lambda }_k,{\mathbf{c}}_{3\mathrm{D}}\left(\mathbf{X}\right))$$

  can be described by $b_{3\mathrm{D}}{S}_{3\mathrm{D}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})$, where

  $$S_{3\mathrm{D}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})=\delta {\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})-P_{3\mathrm{D}}({\lambda }_k,{\mathbf{c}}_{3\mathrm{D}}\left({\mathbf{X}}_{\mathrm{a}}\right))$$

  (18)

  is the (differential) correction spectrum due to three-dimensional effects, $P_{3\mathrm{D}}({\lambda }_k,{\mathbf{c}}_{3\mathrm{D}}\left({\mathbf{X}}_{\mathrm{a}}\right))$ the associated smoothing polynomial, and $b_{3\mathrm{D}}$ the amplitude of the correction spectrum (to be included in the retrieval). From Equation (18), we see that the correction spectrum $S_{3\mathrm{D}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})$ reproduces the differential structure of the relative correction spectrum $\delta {\mathcal{I}}_{\mathrm{sim}}^{3\mathrm{D}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})$.

2.2. Solution Method

The nonlinear Equations (8) and (11) can be written in compact form as

$${\mathbf{y}}^{\delta }=\mathbf{F}\left(\mathbf{x}\right),$$

(19)

where $\mathbf{F}:{\mathbb{R}}^n\to {\mathbb{R}}^m$ is the forward model, $\mathbf{x}\in {\mathbb{R}}^n$ the state vector, and ${\mathbf{y}}^{\delta }\in {\mathbb{R}}^m$ the noisy data vector. In DRMI and DRME, the state vectors are $\mathbf{x}={[\mathbf{X},\mathbf{b}]}^T$ and $\mathbf{x}={[\mathbf{X},\mathbf{b},\mathbf{c}]}^T$, respectively, where $\mathbf{b}=[b_1,\dots ,b_{N_{\mathrm{s}}}]$ is the vector comprising the amplitudes of the correction spectra $b_j$, $j=1,\dots ,N_{\mathrm{s}}$. Furthermore, the number of data points is $m=N_{\lambda }$, and the measured differential spectral signals affected by noise $R_{\mathrm{mes}}^{\delta }\left({\lambda }_k\right)$ for $k=1,\dots N_{\lambda }$ are the components of the noisy data vector ${\mathbf{y}}^{\delta }$.

Because the nonlinear Equation (19) is usually ill-posed, a regularization method, as, for example, the iteratively regularized Gauss–Newton method, is used to compute a solution with physical meaning [15,20,21]. In this approach, at the iteration step k, we consider a linearization of $\mathbf{F}\left(\mathbf{x}\right)$ around the current iterate ${\mathbf{x}}_k^{\delta }$ and solve the linearized equation by means of Tikhonov regularization with the penalty term ${\alpha }_k\left|\right|\mathbf{L}(\mathbf{x}-{\mathbf{x}}_{\mathrm{a}}){\left|\right|}^2$, where ${\alpha }_k$ is the regularization parameter at the iteration step k, $\mathbf{L}$ the regularization matrix, and ${\mathbf{x}}_{\mathrm{a}}$ the a priori state vector, the best beforehand estimate of the solution. Thus, the new iterate minimizing the function

$${\mathcal{F}}_{\mathrm{l}k}\left(\mathbf{x}\right)={∥{\mathbf{y}}_k^{\delta }-{\mathbf{K}}_k(\mathbf{x}-{\mathbf{x}}_{\mathrm{a}})∥}^2+{\alpha }_k{∥\mathbf{L}(\mathbf{x}-{\mathbf{x}}_{\mathrm{a}})∥}^2,$$

(20)

is given by

$${\mathbf{x}}_{k+1}^{\delta }={\mathbf{x}}_{\mathrm{a}}+{\mathbf{K}}_k^{†}{\mathbf{y}}_k^{\delta },$$

(21)

where

$${\mathbf{K}}_k^{†}={({\mathbf{K}}_k^T{\mathbf{K}}_k+{\alpha }_k{\mathbf{L}}^T\mathbf{L})}^{-1}{\mathbf{K}}_k^T$$

(22)

is the regularized generalized inverse, ${\mathbf{K}}_k=\mathbf{K}\left({\mathbf{x}}_k^{\delta }\right)=\partial \mathbf{F}\left({\mathbf{x}}_k^{\delta }\right)/\partial \mathbf{x}$ the Jacobian matrix evaluated at ${\mathbf{x}}_k^{\delta }$, and

$${\mathbf{y}}_k^{\delta }={\mathbf{y}}^{\delta }-\mathbf{F}\left({\mathbf{x}}_k^{\delta }\right)+{\mathbf{K}}_k({\mathbf{x}}_k^{\delta }-{\mathbf{x}}_{\mathrm{a}})$$

(23)

the linearized data vector at the iteration step k. The following peculiarities of the iteratively regularized Gauss–Newton method deserve to be mentioned [15].

• In contrast to the method of Tikhonov regularization [22], the regularization parameter is not constant during the iterative process. Instead, the regularization parameters ${\alpha }_k$ are the terms of a decreasing (geometric) sequence, i.e., ${\alpha }_k=q{\alpha }_{k-1}$ with $q<1$. In this way, the amount of regularization is gradually decreased during the iterative process.
• For iterative regularization methods, the number of iteration steps k plays the role of the regularization parameter, and the iterative process is stopped after an appropriate number of steps $k^{☆}$ in order to avoid an uncontrolled expansion of the errors in the data. The stopping rule used in this study is the discrepancy principle [23], according to which, the iterative process is terminated after $k^{☆}$ steps such that

  $$∥{\mathbf{r}}_{k^{☆}}^{\delta }∥\le \tau \Delta <∥{\mathbf{r}}_k^{\delta }∥, 0\le k<k^{☆},$$

  (24)

  where ${\mathbf{r}}_k^{\delta }={\mathbf{y}}^{\delta }-\mathbf{F}\left({\mathbf{x}}_k^{\delta }\right)$ is the residual vector at ${\mathbf{x}}_k^{\delta }$, $\tau >1$ a control parameter, and $\Delta$ the noise level (an upper bound for the noise in the data). Because in practice the noise level cannot be a priori estimated, we adopt a practical approach based on the observation that the residual $\left|\right|{\mathbf{r}}_k^{\delta }\left|\right|$ decreases during the iterative process and attains a plateau at approximately $\Delta$. Thus, if the nonlinear residuals $\left|\right|{\mathbf{r}}_k^{\delta }\left|\right|$ converge to $\left|\right|{\mathbf{r}}_{\infty }^{\delta }\left|\right|$ within a prescribed tolerance, we use the estimate $\Delta =\left|\right|{\mathbf{r}}_{\infty }^{\delta }\left|\right|$.
• The regularization matrix is chosen as a diagonal matrix, that is, the penalty term ${\alpha }_k\left|\right|\mathbf{L}(\mathbf{x}-{\mathbf{x}}_{\mathrm{a}}){\left|\right|}^2$ is taken as

  $${\alpha }_k\left[\sum _{g=1}^{N_{\mathrm{g}}}\frac{w_g}{X_{\mathrm{a}g}}{(X_g-X_{\mathrm{a}g})}^2+\sum _{j=1}^{N_{\mathrm{s}}}\frac{w_{\mathrm{b}j}}{b_{\mathrm{a}j}}{(b_j-b_{\mathrm{a}j})}^2\right]$$

  (25)

  for DRMI and

  $${\alpha }_k\left[\sum _{g=1}^{N_{\mathrm{g}}}\frac{w_g}{X_{\mathrm{a}g}}{(X_g-X_{\mathrm{a}g})}^2+\sum _{j=1}^{N_{\mathrm{s}}}\frac{w_{\mathrm{b}j}}{b_{\mathrm{a}j}}{(b_j-b_{\mathrm{a}j})}^2+\sum _{p=0}^{N_{\mathrm{p}}-1}\frac{w_{\mathrm{c}p}}{c_{\mathrm{a}p}}{(c_p-c_{\mathrm{a}p})}^2\right]$$

  (26)

  for DRME. Here, the scalars ${\left\{w_g\right\}}_{g=1}^{N_{\mathrm{g}}}$, ${\left\{w_{\mathrm{b}j}\right\}}_{j=1}^{N_{\mathrm{s}}}$, and ${\left\{w_{\mathrm{c}p}\right\}}_{p=0}^{N_{\mathrm{p}}-1}$ give the weight of each component of the state vector into the regularization matrix.

As compared to the method of Tikhonov regularization, the iteratively regularized Gauss–Newton method is less sensitive to overestimations of the regularization parameter, but requires more iteration steps to achieve convergence.

We conclude this section by mentioning that in the case of DRME, one iteration step of the iteratively regularized Gauss–Newton method corresponds to the linear problem described by Equations (11) and (14).

2.3. Linearized Radiative Transfer Model

In order to solve the nonlinear Equation (19) by means of the iteratively Gauss–Newton method, the forward model $\mathbf{F}\left(\mathbf{x}\right)$ and the Jacobian matrix $\mathbf{K}\left(\mathbf{x}\right)$ have to be calculated at each iteration step. From Equation (3) we infer that the computation of $\mathbf{F}\left(\mathbf{x}\right)$ requires the computation of the radiance $I(\lambda ,{\mathbf{r}}_{\mathrm{b}},\mathsf{\Omega })$ and the source function $J(\lambda ,\mathbf{r},\mathsf{\Omega })$ at all surface and grid points, respectively, while the computation of $\mathbf{K}\left(\mathbf{x}\right)$ requires the computation of the partial derivatives of the extinction field $\partial {\sigma }_{\mathrm{ext}}(·,\mathbf{r})/\partial X_g$, the surface radiance $\partial I(·,{\mathbf{r}}_{\mathrm{b}},·)/\partial X_g$, and the source function $\partial J(·,\mathbf{r},·)/\partial X_g$.

For derivative calculations, we employ the same assumption as in the standard DOAS model, that is, the (discrete) number density profile ${\left\{n_{g,j}\right\}}_{j=1}^{N_{\mathrm{z}}}$, where $n_{g,j}=n_g\left(z_j\right)$, is assumed to be a scaled version of an a priori profile ${\left\{n_{\mathrm{a}g,j}\right\}}_{j=1}^{N_{\mathrm{z}}}$. Consequently, if $s_g$ is the scale factor of gas g, i.e., $n_{g,j}=s_g{n}_{\mathrm{a}g,j}$, for all $j=1,\dots ,N_{\mathrm{z}}$, the following equalities,

$$s_g=\frac{n_{g,j}}{n_{\mathrm{a}g,j}}=\frac{{\sigma }_{\mathrm{abs}g,j}^{\mathrm{gas}}\left(\lambda \right)}{{\sigma }_{\mathrm{abs}\mathrm{a}g,j}^{\mathrm{gas}}\left(\lambda \right)}=\frac{x_{g,j}}{x_{\mathrm{a}g,j}}=\frac{X_g}{X_{\mathrm{a}g}}$$

(27)

with ${\sigma }_{\mathrm{abs}g,j}^{\mathrm{gas}}\left(\lambda \right)={\sigma }_{\mathrm{abs}g}^{\mathrm{gas}}(\lambda ,z_j)$, are valid. Thus, for any value of the total column $X_g$, the absorption coefficient is updated as

$${\sigma }_{\mathrm{abs}g,j}^{\mathrm{gas}}\left(\lambda \right)=\frac{{\sigma }_{\mathrm{abs}\mathrm{a}g,j}^{\mathrm{gas}}\left(\lambda \right)}{X_{\mathrm{a}g}}{X}_g,$$

(28)

and the corresponding top of atmosphere radiance $I(\lambda ,{\mathbf{r}}_{\mathrm{t}},{\mathsf{\Omega }}_{\mathrm{m}})$ is determined by means of a radiative transfer calculation. In general, for computing the derivative of a spectral quantity $F\left(\lambda \right)$ with respect to the total column $X_g$, we regard $F\left(\lambda \right)$ as a function of ${\sigma }_{\mathrm{abs}g,j}^{\mathrm{gas}}\left(\lambda \right)$, i.e., $F=F({\sigma }_{\mathrm{abs}g,1}^{\mathrm{gas}},\dots ,{\sigma }_{\mathrm{abs}g,N_{\mathrm{z}}}^{\mathrm{gas}})$, and assume that the partial derivatives $\partial F/\partial {\sigma }_{\mathrm{abs}g,j}^{\mathrm{gas}}$, $j=1,\dots ,N_{\mathrm{z}}$, are known. Taking into account the one-to-one correspondence (28), we are led to the computational formula

$$\frac{\partial F}{\partial X_g}\left(\lambda \right)=\sum _{j=1}^{N_{\mathrm{z}}}\frac{\partial F}{\partial {\sigma }_{\mathrm{abs}g,j}^{\mathrm{gas}}}\left(\lambda \right)\frac{\partial {\sigma }_{\mathrm{abs}g,j}^{\mathrm{gas}}}{\partial X_g}\left(\lambda \right)=\sum _{j=1}^{N_{\mathrm{z}}}\frac{{\sigma }_{\mathrm{abs}\mathrm{a}g,j}^{\mathrm{gas}}\left(\lambda \right)}{X_{\mathrm{a}g}}\frac{\partial F}{\partial {\sigma }_{\mathrm{abs}g,j}^{\mathrm{gas}}}\left(\lambda \right).$$

(29)

Thus, the radiative transfer model should be linearized with respect to the absorption coefficient, that is, the linearized radiative transfer model should deliver the partial derivatives $\partial F/\partial {\sigma }_{\mathrm{abs}g,j}^{\mathrm{gas}}$ for $j=1,\dots ,N_{\mathrm{z}}$ and $g=1,\dots ,N_g$.

The multi-dimensional radiative transfer model used in our retrieval algorithm is the spherical harmonic discrete ordinate method (SHDOM) [6,24]. Linearizations of SHDOM by means of a forward and a forward-adjoint approach have been discussed in [25]. These can be summarized as follows.

• The linearized forward approach relies on an analytical computation of the derivatives. The method is accurate and has the advantage that no assumptions rather than those of the forward model have to be made. However, the method is time consuming and memory demanding when the number of parameters to be retrieved is large. The reason is that not only the source function has to be stored as a spherical harmonic series at each grid point, but also its derivatives with respect to the atmospheric parameters of interest.
• The linearized forward-adjoint approach relies on the application of the adjoint radiative transfer theory. The method requires less storage for derivatives calculation, is much faster, but relatively less accurate. The main reason for this lower accuracy is that different interpolation schemes are used for radiance and derivative calculations.

Because in our application the number of retrieved quantities is relatively small, we decided in the favor of the linearized forward approach. Specifically, the partial derivatives are computed in an analytical manner by using the chain rule in a sort of backward procedure starting with the output radiance and following the chain of dependencies back to the inputs to the model.

In [26], a simplified approach, leading to a considerable reduction of the computation time, was proposed. The idea is to neglect in Equation (3) the contributions of the partial derivatives of the surface radiance $\partial I(·,{\mathbf{r}}_{\mathrm{b}},·)/\partial X_g$ and the source function $\partial J(·,\mathbf{r},·)/\partial X_g$. In other words, when computing the partial derivative of the top of atmosphere radiance $\partial I(·,{\mathbf{r}}_{\mathrm{t}},·)/\partial X_g$, only the contributions of the partial derivatives of the extinction field $\partial {\sigma }_{\mathrm{ext}}(·,\mathbf{r})/\partial X_g$ are taken into account.

To speed up the computations, the linearized SHDOM is equipped with a spectral acceleration approach that combines the correlated k-distribution method with dimensionality reduction techniques. This approach was applied for computing the spectral signal in [27], and can be extended to derivative calculations as follows.

• Correlated k-distribution method. Consider a discretization of the spectral interval $[{\lambda }_{\min }-s/2,{\lambda }_{\max }+s/2]$ into a set ${\left\{{\overline{\lambda }}_k\right\}}_{k=1}^{\overline{W}}$ of $\overline{W}$ equally spaced wavelengths with the discretization step $\Delta \lambda$, and assume that the transmission within a spectral interval depends only on the distribution of the gas absorption coefficient ${\sigma }_{\mathrm{abs}}^{\mathrm{gas}}\left(\lambda \right)$ within the spectral interval [28]. Letting $F=F\left({\sigma }_{\mathrm{abs}k}^{\mathrm{gas}}\right)$ be the cumulative density function of ${\sigma }_{\mathrm{abs}}^{\mathrm{gas}}\left(\lambda \right)$ in the spectral interval $[{\overline{\lambda }}_k-\Delta \lambda /2,{\overline{\lambda }}_k+\Delta \lambda /2]$, ${\sigma }_{\mathrm{abs}k}^{\mathrm{gas}}\left(F\right)$ the inverse distribution function, and ${\{F_l,{\varpi }_l\}}_{l=1}^{N_{\mathrm{q}}}$ a set of $N_{\mathrm{q}}$ quadrature points and weights in the interval $[0,1]$, the spectral signal (1) and its partial derivative with respect to the total column are computed as

  $$\begin{array}{cc}\hfill \mathcal{I}\left(\lambda \right)& =\sum _{w=1}^W{\omega }_{w}g(\lambda -{\lambda }_w){\mathcal{I}}_{\mathrm{FOV}}\left({\sigma }_{\mathrm{abs}}^{\mathrm{gas}}\left({\lambda }_w\right)\right),\hfill \end{array}$$

  (30)

  $$\begin{array}{cc}\hfill \frac{\partial \mathcal{I}}{\partial X_g}\left(\lambda \right)& =\sum _{w=1}^W{\omega }_{w}g(\lambda -{\lambda }_w)\frac{\partial {\mathcal{I}}_{\mathrm{FOV}}}{\partial X_g}\left({\sigma }_{\mathrm{abs}}^{\mathrm{gas}}\left({\lambda }_w\right)\right),\hfill \end{array}$$

  (31)

  where ${\lambda }_w={\overline{\lambda }}_k$, ${\omega }_w=\Delta \lambda {\varpi }_l$, and ${\sigma }_{\mathrm{abs}}^{\mathrm{gas}}\left({\lambda }_w\right)={\sigma }_{\mathrm{abs}k}^{\mathrm{gas}}\left(F_l\right)$ for $w=l+(k-1)N_{\mathrm{q}}$, $k=1,\dots ,\overline{W}$, $l=1,\dots ,N_{\mathrm{q}}$, and $W=\overline{W}{N}_{\mathrm{q}}.$ Thus, in the framework of the correlated k-distribution method, W monchromatic radiative transfer calculations are required for computing ${\mathcal{I}}_{\mathrm{FOV}}\left({\lambda }_w\right)$ and $\partial {\mathcal{I}}_{\mathrm{FOV}}\left({\lambda }_w\right)/\partial X_g$, and so, $\mathcal{I}\left(\lambda \right)$ and $\partial \mathcal{I}\left(\lambda \right)/\partial X_g$. A further acceleration can be achieved when ${\mathcal{I}}_{\mathrm{FOV}}\left({\lambda }_w\right)$ and $\partial {\mathcal{I}}_{\mathrm{FOV}}\left({\lambda }_w\right)/\partial X_g$ are computed by using dimensionality reduction techniques, as for example, the principal component analysis.
• Principal component analysis. At wavelength ${\lambda }_w$, the integrated signal ${\mathcal{I}}_{\mathrm{FOV}}\left({\lambda }_w\right)$ is related to the integrated signal calculated by a simplified (approximate) radiative transfer model ${\mathcal{I}}_{\mathrm{FOV}}^{\mathrm{s}}\left({\lambda }_w\right)$ through the relation

  $$ln\frac{{\mathcal{I}}_{\mathrm{FOV}}\left({\lambda }_w\right)}{{\mathcal{I}}_{\mathrm{FOV}}^{\mathrm{s}}\left({\lambda }_w\right)}=f\left({\lambda }_w\right),$$

  (32)

  i.e.,

  $${\mathcal{I}}_{\mathrm{FOV}}\left({\lambda }_w\right)={\mathcal{I}}_{\mathrm{FOV}}^{\mathrm{s}}\left({\lambda }_w\right){\mathrm{e}}^{f\left({\lambda }_w\right)}.$$

  (33)
  The correction factor $f\left({\lambda }_w\right)$ in Equation (32) is actually the quantity that is calculated by means of the principal component analysis. To summarize this approach, we assume that for each wavelength ${\lambda }_w$, the spectral variability of the optical parameters can be described by a vector ${\mathbf{x}}_w\in {\mathbb{R}}^N$, defined by

  $${\mathbf{x}}_w^T=\left[ln{\sigma }_{\mathrm{abs}1}^{\mathrm{gas}}\left({\lambda }_w\right),...,ln{\sigma }_{\mathrm{abs}L}^{\mathrm{gas}}\left({\lambda }_w\right),ln{\sigma }_{\mathrm{sct}1}^{\mathrm{mol}}\left({\lambda }_w\right),...,ln{\sigma }_{\mathrm{sct}L}^{\mathrm{mol}}\left({\lambda }_w\right),ln{F}_0\left({\lambda }_w\right)\right],$$

  (34)

  where ${\sigma }_{\mathrm{abs}k}^{\mathrm{gas}}$ and ${\sigma }_{\mathrm{sct}k}^{\mathrm{mol}}$ are the optical coefficients in the kth level, $N=2N_{\mathrm{z}}+1$, and $N_{\mathrm{z}}$ is the number of altitude levels. Denoting by $\overline{\mathbf{x}}=(1/W){\sum }_{w=1}^W{\mathbf{x}}_w$ the sample mean of the data, the aim is to find an M-dimensional subspace ($M<N$) spanned by a set of linear independent vectors ${\left\{{\mathbf{a}}_k\right\}}_{k=1}^M$, such that the centered data ${\mathbf{x}}_w-\overline{\mathbf{x}}$ belong to this subspace, i.e., ${\mathbf{x}}_w\approx \overline{\mathbf{x}}+{\sum }_{k=1}^M{y}_{wk}{\mathbf{a}}_k=\overline{\mathbf{x}}+\mathbf{A}{\mathbf{y}}_w$ yielding ${\mathbf{y}}_w={\mathbf{A}}^{†}({\mathbf{x}}_w-\overline{\mathbf{x}})$ for $w=1,\dots ,W$, where $\mathbf{A}={\left[{\mathbf{a}}_k\right]}_{k=1}^M\in {\mathbb{R}}^{N\times M}$, ${\mathbf{A}}^{†}={\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\in {\mathbb{R}}^{M\times N}$ is the pseudoinverse of $\mathbf{A}$, and $y_{wk}$ is the kth component of the vector of parameters ${\mathbf{y}}_w\in {\mathbb{R}}^M$. In the principal component analysis, the original N-dimensional data $\mathbf{X}={\left[{\mathbf{x}}_w\right]}_{w=1}^W\in {\mathbb{R}}^{N\times W}$ are projected on the M-dimensional subspace spanned by the dominant singular vectors of the data covariance matrix ${\mathbf{C}}_{\mathbf{x}}=(1/W)\mathbf{X}{\mathbf{X}}^T\in {\mathbb{R}}^{N\times N}$, that is, with ${\sigma }_k$ and ${\mathbf{u}}_k$ being the kth singular value and vector of the matrix ${\mathbf{C}}_{\mathbf{x}}$, we choose $\mathbf{A}={\mathbf{U}}_M{\mathsf{\Sigma }}_M^{1/2}$ and ${\mathbf{A}}^{†}={\mathsf{\Sigma }}_M^{-1/2}{\mathbf{U}}_M^T$, where ${\mathbf{U}}_M={\left[{\mathbf{u}}_k\right]}_{k=1}^M\in {\mathbb{R}}^{N\times M}$ and ${\mathsf{\Sigma }}_M=\mathrm{diag}{\left[{\sigma }_k\right]}_{k=1}^M\in {\mathbb{R}}^{M\times M}$. Furthermore, approximating the correction factor $f\left({\mathbf{x}}_w\right)$ by a second-order Taylor expansion around $\overline{\mathbf{x}}$, and the gradient and the Hessian of f by central differences, we are led to the computational formula

  $$\begin{array}{cc}\hfill f\left({\mathbf{x}}_w\right)& \approx f\left(\overline{\mathbf{x}}\right)+\frac{1}{2}\sum _{k=1}^M[f(\overline{\mathbf{x}}+{\mathbf{a}}_k)-f(\overline{\mathbf{x}}-{\mathbf{a}}_k)]y_{wk}\hfill \\ \hfill & +\frac{1}{2}\sum _{k=1}^M[f(\overline{\mathbf{x}}+{\mathbf{a}}_k)-2f\left(\overline{\mathbf{x}}\right)+f(\overline{\mathbf{x}}-{\mathbf{a}}_k)]y_{wk}^2.\hfill \end{array}$$

  (35)
  To compute the derivative of the integrated signal with respect to the total column $X_g$, we may use the principal component analysis to calculate the derivative correction factor $f_{X_g}\left({\lambda }_w\right)$, defined by [29]

  $$f_{X_g}\left({\lambda }_w\right)=ln\left[\frac{\partial {\mathcal{I}}_{\mathrm{FOV}}}{\partial X_g}\left({\lambda }_w\right)/\frac{\partial {\mathcal{I}}_{\mathrm{FOV}}^{\mathrm{s}}}{\partial X_g}\left({\lambda }_w\right)\right],$$

  (36)

  in which case, we have

  $$\frac{\partial {\mathcal{I}}_{\mathrm{FOV}}}{\partial X_g}\left({\lambda }_w\right)=\frac{\partial {\mathcal{I}}_{\mathrm{FOV}}^{\mathrm{s}}}{\partial X_g}\left({\lambda }_w\right){\mathrm{e}}^{f_{X_g}\left({\lambda }_w\right)}.$$

  (37)
  Alternatively, taking the derivative of Equation (33) with respect to $X_g$, i.e.,

  $$\frac{\partial {\mathcal{I}}_{\mathrm{FOV}}}{\partial X_g}\left({\lambda }_w\right)=\frac{\partial {\mathcal{I}}_{\mathrm{FOV}}^{\mathrm{s}}}{\partial X_g}\left({\lambda }_w\right){\mathrm{e}}^{f\left({\lambda }_w\right)}+{\mathcal{I}}_{\mathrm{FOV}}\left({\lambda }_w\right)\frac{\mathrm{d}f}{\mathrm{d}{X}_g}\left({\lambda }_w\right),$$

  (38)

  we may use the principal component analysis to calculate the derivative correction factor $f_{X_g}\left({\lambda }_w\right)$, defined by

  $$f_{X_g}\left({\lambda }_w\right)=\frac{\mathrm{d}f}{\mathrm{d}{X}_g}\left({\lambda }_w\right)=\frac{1}{{\mathcal{I}}_{\mathrm{FOV}}\left({\lambda }_w\right)}\frac{\partial {\mathcal{I}}_{\mathrm{FOV}}}{\partial X_g}\left({\lambda }_w\right)-\frac{1}{{\mathcal{I}}_{\mathrm{FOV}}^{\mathrm{s}}\left({\lambda }_w\right)}\frac{\partial {\mathcal{I}}_{\mathrm{FOV}}^{\mathrm{s}}}{\partial X_g}\left({\lambda }_w\right).$$

  (39)

3. Numerical Simulations

In this section, we analyze the accuracy and efficiency of the algorithms for retrieving total column amount of ${\mathrm{NO}}_2$ under cloudy conditions. The cloudy scenes considered in our simulations are similar to those described in [27]. Specifically, the geometrical and optical parameters are chosen as follows.

• The domain of analysis is a rectangular prism of lengths $L_{\mathrm{x}}=L_{\mathrm{y}}=15$ km and $L_{\mathrm{z}}=50$ km. The discretization steps along the horizontal directions are $\Delta x=\Delta y=0.5$ km. Along the vertical direction, the atmosphere between 0 and 50 km is discretized with a step of 0.5 km between 0 and 3 km, 0.1 km between 3 and 4 km, 0.5 km between 4 and 10 km, 1.0 km between 10 and 14 km, 2 km between 14 and 30 km, and 5 km between 30 and 50 km.
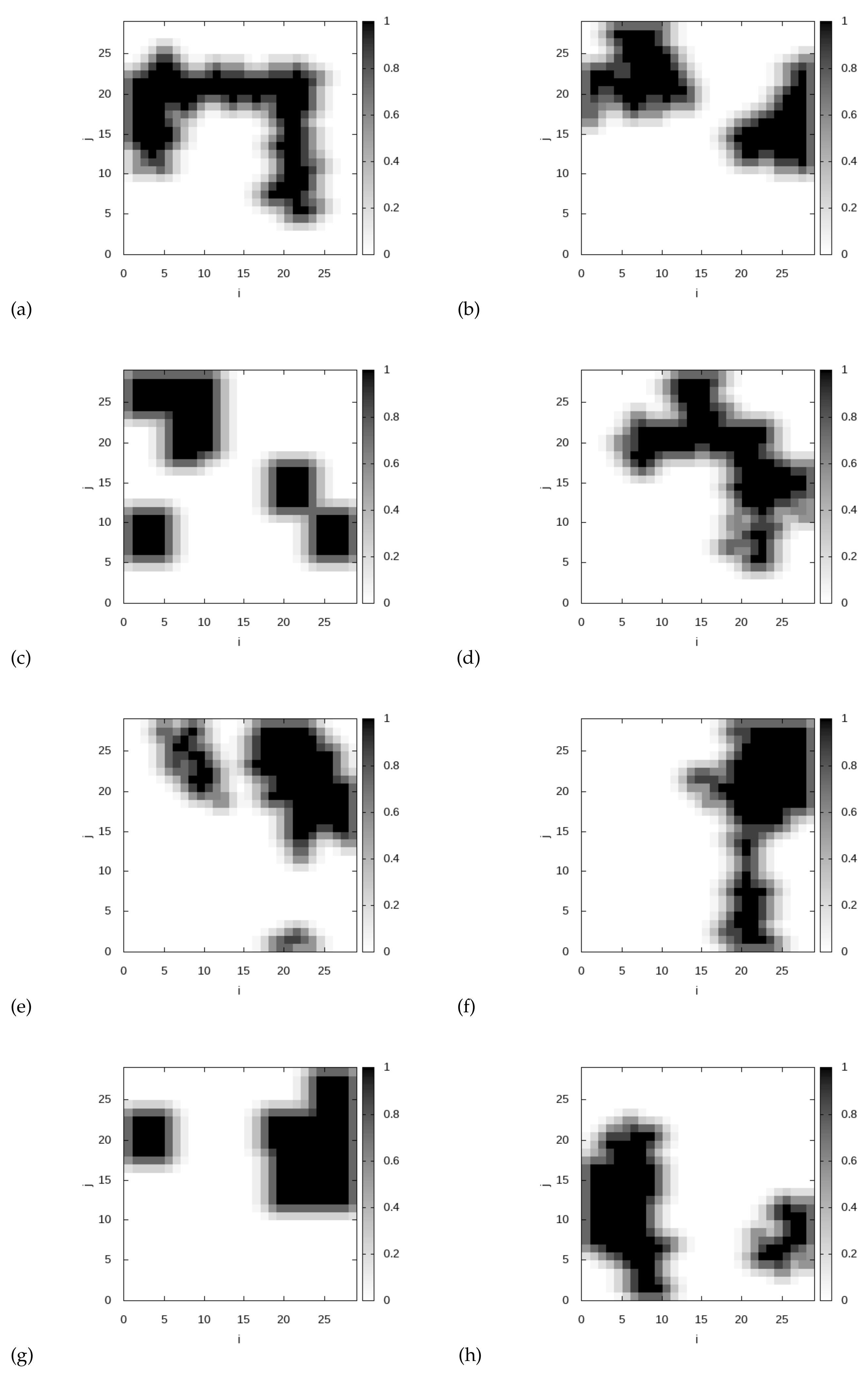
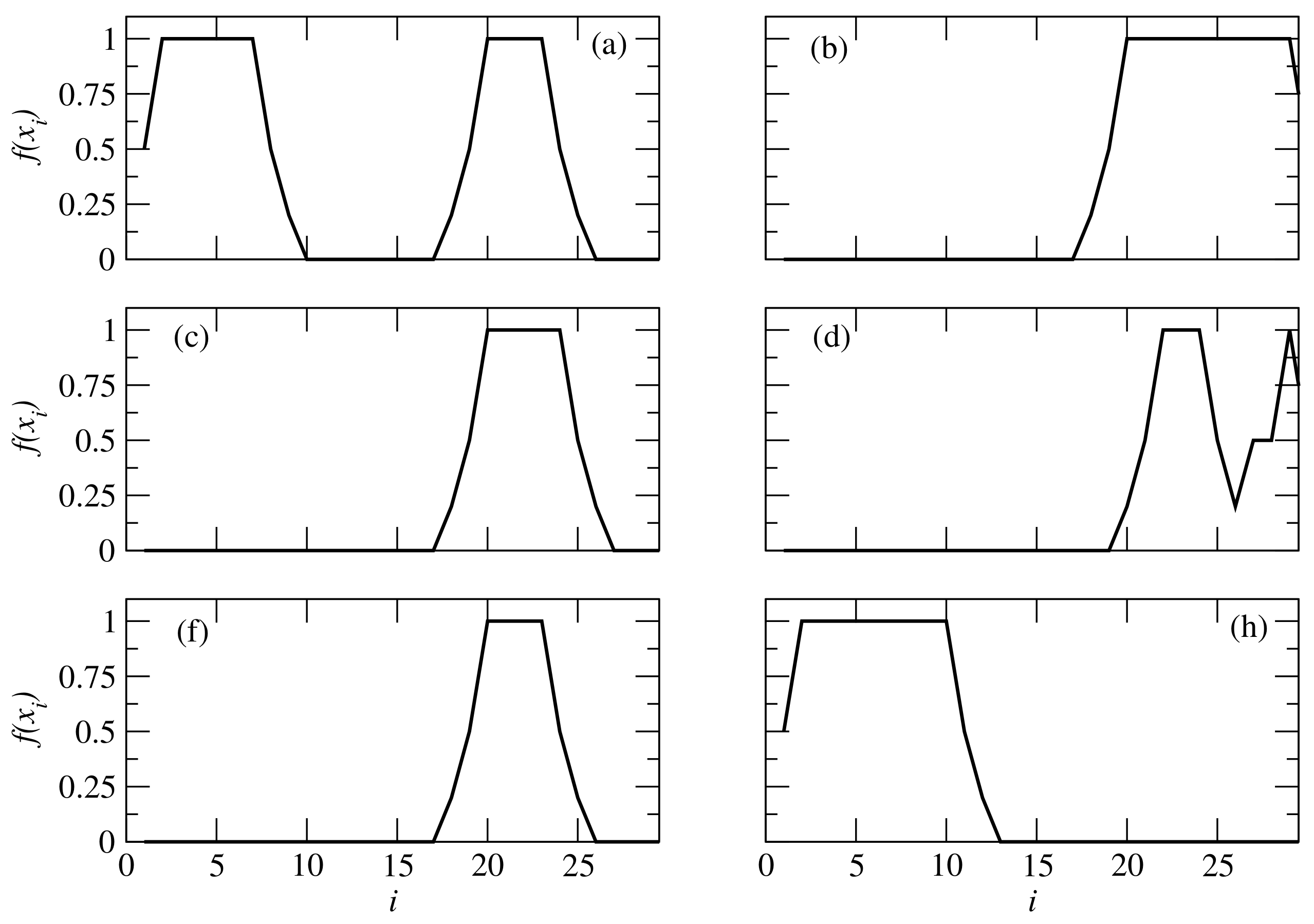
• A homogeneous cloud is placed between 3 and 4 km. The cloud extinction field is given by ${\sigma }_{\mathrm{ext}}^{\mathrm{cloud}}(x,y)={\sigma }_{0}f(x,y)$, where ${\sigma }_0=6 {\mathrm{km}}^{-1}$ and $f(x,y)$ is the indicator function (note that $f(x,y)$ takes the values 1 and 0 inside and outside the cloud, respectively). The cloud phase function is a Henyey–Greenstein phase function [30] with the asymmetry parameter $g=0.8$, and the cloud single-scattering albedo is ${\omega }_{\mathrm{cloud}}=$ 0.99. Eight cloudy scenes are generated by a two-dimensional broken cloud model [14] with a cloud fraction of about $0.4.$ The extinction field ${\sigma }_{\mathrm{ext}}^{\mathrm{cloud}}(x,y)$ is smoothed at the boundary of a cloudy region in order to avoid abrupt changes in the horizontal plane. The indicator functions corresponding to the eight cloudy scenes are illustrated in Figure 1a–h. For two-dimensional geometries, slices at $y=7$ km are selected from the cloud fields 1, 2, 3, 5, 6, and 8. The corresponding indicator functions are shown in Figure 2. Note that the slices corresponding to the cloudy scenes 4 and 7 are similar to the slice corresponding to the cloudy scene 2, and are therefore omitted.
• The number of discrete zenith and azimuth angles are $N_{\mu }=16$ and $N_{\phi }=2N_{\mu }$, respectively, the solar and instrument zenith angles are ${\theta }_0={30}^{\circ }$ and ${\theta }_{\mathrm{m}}^0={45}^{\circ }$, respectively, and the relative azimuth angle is $\Delta \phi =0$.
• A Lambertian reflecting surface with the surface albedo $A=0.2$ is considered.
• The footprint of the detector is a square of length $2a=10\Delta x$ centered at $x_0=y_0=L_{\mathrm{x}}/2$, and $z_0=L_{\mathrm{z}}$, and a wavelength-dependent slit function corresponding to the TROPOMI instrument is assumed.
• In addition to the scattering and absorption by the cloud, molecular Rayleigh scattering and the absorption by ${\mathrm{NO}}_2$, ozone (${\mathrm{O}}_3$), oxygen dimer (${\mathrm{O}}_4$), and water vapor (${\mathrm{H}}_2\mathrm{O}$) are considered. The measurement spectral grid roughly resembles the TROPOMI’s spectral resolution and consists of 119 spectral points between 425 nm and 450 nm.

The process of generating synthetic measurement spectra is organized as follows.

• For a clean scenario, we use the a priori partial column profile of ${\mathrm{NO}}_2$ [17] illustrated in Figure 3 to generate the true (exact) partial column profile. In this regard, denoting the a priori partial columns of gas g by $x_{\mathrm{a}g,j}$, we choose the true partial columns as $x_{g,j}^{†}=s_g{x}_{\mathrm{a}g,j}$, $j=1,\dots ,N_{\mathrm{z}}$ with $s_{{\mathrm{NO}}_2}=2.0$ and $s_{{\mathrm{O}}_3}=s_{{\mathrm{O}}_4}=s_{{\mathrm{H}}_2\mathrm{O}}=1.2$. The true total column $X_g^{†}$ of gas g is then computed as $X_g^{†}={\sum }_{j=1}^{N_{\mathrm{z}}}{x}_{g,j}^{†}=s_g{X}_{\mathrm{a}g}$; thus, $X_{{\mathrm{NO}}_2}^{†}=2X_{\mathrm{a}{\mathrm{NO}}_2}$.
• For ${\mathbf{X}}^{†}=[X_{{\mathrm{NO}}_2}^{†},X_{{\mathrm{O}}_3}^{†},X_{{\mathrm{O}}_4}^{†},X_{{\mathrm{H}}_2\mathrm{O}}^{†}]$, we generate the simulated spectral signal ${\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,{\mathbf{X}}^{†})$ by means of SHDOM.
• For cubic smoothing polynomials, i.e., $N_{\mathrm{p}}=4$, we determine the coefficients ${\mathbf{c}}_{\mathrm{sim}}\left({\mathbf{X}}^{†}\right)$ of the polynomial $P_{\mathrm{sim}}(\lambda ,{\mathbf{c}}_{\mathrm{sim}}\left({\mathbf{X}}^{†}\right))$ as the solutions of the least-squares problem (13).
• We compute the noisy spectral signal as ${\mathcal{I}}_{\mathrm{sim}}^{\delta }({\lambda }_k,{\mathbf{X}}^{†})={\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,{\mathbf{X}}^{†})+{\delta }_k$, where the measurement errors ${\delta }_k$ are assumed to be independent Gaussian random variables with zero mean and standard deviation ${\sigma }_k={\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,{\mathbf{X}}^{†})/\mathrm{SNR}$, where SNR is the signal-to-noise ratio. It should be pointed out that in view of the approximation

  $$\begin{array}{cc}\hfill & ln{\mathcal{I}}_{\mathrm{sim}}^{\delta }({\lambda }_k,{\mathbf{X}}^{†})\approx ln{\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,{\mathbf{X}}^{†})+\frac{{\delta }_k}{{\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,{\mathbf{X}}^{†})},\hfill \end{array}$$

  the error in $ln{\mathcal{I}}_{\mathrm{sim}}^{\delta }({\lambda }_k,{\mathbf{X}}^{†})$ is ${\delta }_{lnk}={\delta }_k/{\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,{\mathbf{X}}^{†})$ yielding ${\sigma }_{lnk}=1/\mathrm{SNR}$ for all k. In other words, the measurement error vector is white noise with the covariance matrix $(1/{\mathrm{SNR}}^2){\mathbf{I}}_m$, where ${\mathbf{I}}_m$ is the identity matrix. Because in our simulations we are mainly interested in multi-dimensional effects, we take $\mathrm{SNR}={10}^4$, that is, we assume an almost perfect instrument and neglect the forward model errors.
• We include the Ring correction spectrum $S_{\mathrm{R}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})$ illustrated in Figure 4 in the retrieval, and choose the a priori and true Ring amplitudes as $b_{\mathrm{aR}}=5\times {10}^{-2}$ and $b_{\mathrm{R}}^{†}=2b_{\mathrm{aR}}$, respectively. Note that the inelastic scattering is described by a first-order Rayleigh scattering model, i.e., by applying a first-order iteration scheme to the one-dimensional radiative transfer equation for inelastic scattering [31].
• For DRMI, we compute the measured differential spectral signal as

  $$R_{\mathrm{mes}}^{\delta }\left({\lambda }_k\right)=[ln{\mathcal{I}}_{\mathrm{sim}}^{\delta }({\lambda }_k,{\mathbf{X}}^{†})-P_{\mathrm{sim}}(\lambda ,{\mathbf{c}}_{\mathrm{sim}}\left({\mathbf{X}}^{†}\right))]+b_{\mathrm{R}}^{†}{S}_{\mathrm{R}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}}),$$

  while for DRME, we choose ${\mathbf{c}}^{†}=0.5 {\mathbf{c}}_{\mathrm{sim}}\left({\mathbf{X}}^{†}\right)$ and compute the measured differential spectral signal as

  $$R_{\mathrm{mes}}^{\delta }\left({\lambda }_k\right)=ln{\mathcal{I}}_{\mathrm{sim}}^{\delta }({\lambda }_k,{\mathbf{X}}^{†})+b_{\mathrm{R}}^{†}{S}_{\mathrm{R}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})-P({\lambda }_k,{\mathbf{c}}^{†}).$$

SHDOM is run with a solution accuracy of ${10}^{-4}$ and by using

• an adaptive grid with a splitting accuracy of ${10}^{-4}$,
• the principal component analysis with $M=4$, and the derivative correction factor $f_{X_g}\left({\lambda }_w\right)$ as in Equation (39),
• periodic boundary conditions,
• the delta-M approximation [32], and the untruncated phase function single-scattering solution (TMS correction of Nakajima and Tanaka [33].

Some parameters characterizing the iteratively regularized Gauss–Newton algorithm are chosen as follows.

• The regularization parameters ${\alpha }_k$ are the terms of a geometric sequence with ratio $q=0.1$ and initial value ${\alpha }_0={10}^{-3}$. Thus, at the first iteration step, the regularization parameter is ${\alpha }_1={10}^{-4}$.
• The weighting factors specifying the contribution of each component of the state vector into the regularization matrix are $w_{{\mathrm{NO}}_2}=1.0$, $w_{{\mathrm{O}}_3}=w_{{\mathrm{O}}_4}=w_{{\mathrm{H}}_2\mathrm{O}}={10}^2$, $w_{\mathrm{R}}={10}^{-3}$, and $w_{\mathrm{c}p}=1.0$ for all $p=0,\dots ,N_{\mathrm{p}}-1$. By this choice, the total columns of the auxiliary gases are stronger constrained to the a priori than the total column of ${\mathrm{NO}}_2$ and the Ring correction spectrum.
• The control parameter $\tau$ in the discrepancy principle Equation (24) is $\tau =1.2$.

The simulations were performed on a computer Intel(R) Core(TM) i5-3340M CPU @ 2.70 GHz with 7858 MB RAM.

3.1. Test Example 1

In the first test example we consider a two-dimensional geometry and perform the retrieval by using the DRMI and DRME inverse models. It may in general be noted that

• the inverse problem is severely ill-posed (for the DRMI model, the condition number of the Jacobian matrix at the initial guess is ${\kappa }_{\mathrm{DRMI}}=2.92\times {10}^7$) and
• there is a strong correlation between the ${\mathrm{NO}}_2$ and Ring effect signatures (when the Ring correction spectrum is not included in the retrieval, the condition number is ${\kappa }_{\mathrm{DRMI}}=2.16\times {10}^4$; thus, ${\kappa }_{\mathrm{DRMI}}$ decreases by three order of magnitude).

The histories of the residuals with respect to the iteration index are shown in Figure 5. The following conclusions can be drawn.

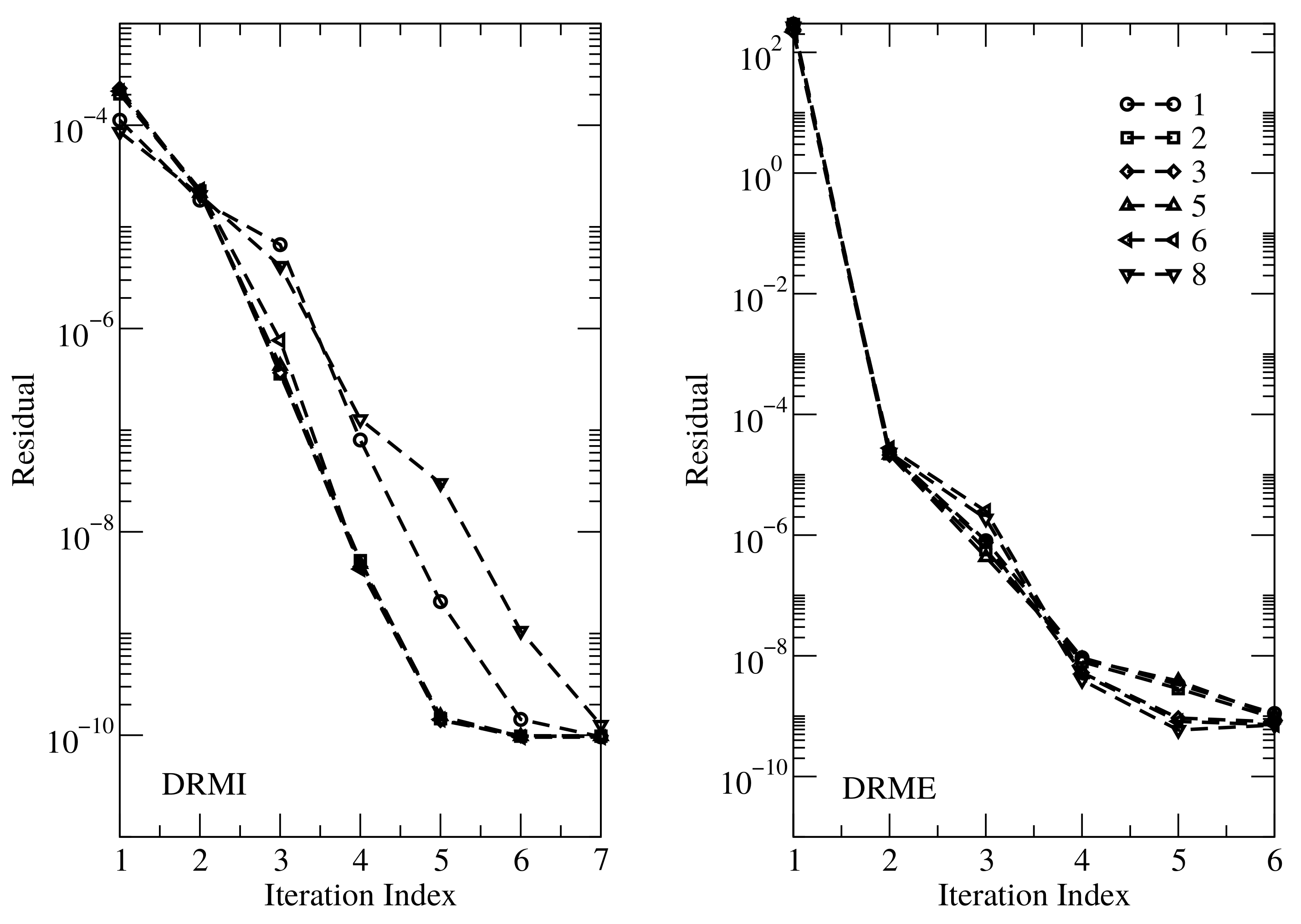
• At the initial guess, the residual corresponding to DRMI is much smaller than that corresponding to DRME. This occurs because the discrepancies between the differential spectra are usually small.
• In DRMI, the residual decreases very fast at the first iteration step and then more steadily, while in DRME, the residual gradually decreases.

The relative errors and the computation times for DRMI and DRME are given in the first two columns of

Table 1. Relative errors and the computation times (CPU) in minutes: seconds for DRMI. The results correspond to a two-dimensional geometry.

Cloudy Scene	DRMI		DRMI Approx. Derivatives
	Rel. Errors	CPU	Rel. Errors	CPU
1	$1.66\times {10}^{-5}$	39:51	$1.18\times {10}^{-1}$	32:24
2	$1.10\times {10}^{-5}$	40:12	$1.50\times {10}^{-1}$	32:48
3	$9.22\times {10}^{-6}$	39:14	$9.79\times {10}^{-2}$	31:06
5	$1.08\times {10}^{-5}$	38:54	$1.37\times {10}^{-1}$	30:44
6	$1.03\times {10}^{-5}$	39:32	$8.77\times {10}^{-2}$	31:16
8	$1.94\times {10}^{-5}$	40:06	$1.51\times {10}^{-1}$	32:33

and

Table 2. Relative errors and the computation times (CPU) in minutes:seconds for DRME. The numbers in parenthesis are the values of the regularization parameter $\alpha$. The results correspond to a two-dimensional geometry.

Cloudy Scene	DRME		DRME (One Iteration)
	Rel. Errors	CPU	Rel. Errors	CPU
1	$6.94\times {10}^{-5}$	35:10	$2.84\times {10}^{-2} (3.0\times {10}^{-6})$	5:33
2	$3.23\times {10}^{-5}$	36:47	$3.74\times {10}^{-3} (1.0\times {10}^{-6})$	5:54
3	$1.23\times {10}^{-5}$	34:57	$7.74\times {10}^{-3} (1.0\times {10}^{-6})$	5:12
5	$4.84\times {10}^{-5}$	34:23	$6.73\times {10}^{-3} (1.0\times {10}^{-6})$	5:01
6	$1.08\times {10}^{-5}$	35:06	$2.60\times {10}^{-2} (5.0\times {10}^{-6})$	5:28
8	$2.31\times {10}^{-5}$	36:23	$1.87\times {10}^{-2} (2.0\times {10}^{-5})$	5:48

, respectively. Because the SNR is high, in both cases, the relative errors are smaller than $0.01\%$. On average, the computation times for DRMI and DRME are of about 40 and 35 CPU minutes, respectively. The higher computation time for DRMI is due to the fact that, according to Equation (13), the partial derivative of ${\mathbf{c}}_{\mathrm{sim}}\left(\mathbf{X}\right)$ with respect to $\mathbf{X}$ needs also to be computed.

In the second two columns of Table 1, we list the relative errors and the computation times for DRMI when the partial derivative of the top of atmosphere radiance $\partial I(·,{\mathbf{r}}_{\mathrm{t}},·)/\partial X_g$ is computed by taking into account only the contributions of the partial derivatives of the extinction field $\partial {\sigma }_{\mathrm{ext}}(·,\mathbf{r})/\partial X_g$. The reduction of the computation time by about 25% does not justify the large relative errors. Thus, the simplified approach suggested in [26] for the retrieval of cloud extinction field, seems not to work in the case of total column trace gas retrieval.

In the second two columns of Table 2, we list the relative errors and the computation times for DRME when the iterative process is stopped after one iteration, that is, when the linear model (14) is considered. A reasonable accuracy can be obtained when the regularization parameter $\alpha$ is optimally chosen. Some hints regarding the selection of the optimal value of the regularization parameter ${\alpha }_{\mathrm{opt}}$ can be found by analyzing the history of the residual curve in Figure 5. From this curve, we infer that for $\alpha ={10}^{-4}$ the residual is of about ${10}^{-5}$, for $\alpha ={10}^{-5}$ of about ${10}^{-6}$, and for $\alpha ={10}^{-6}$ of about ${10}^{-8}$. Therefore, by choosing $\alpha$ in the range ${10}^{-6},\dots ,{10}^{-5}$ we expect good reconstruction errors. However, as it can be seen in Table 2, ${\alpha }_{\mathrm{opt}}$ depends on the cloud field. Moreover, for some cloudy scenes, ${\alpha }_{\mathrm{opt}}$ should be precisely determined (for example, in the case of the cloudy scene 8, the relative errors are $8.30\times {10}^{-2}$, $1.87\times {10}^{-2}$, and $9.02\times {10}^{-2}$ when $\alpha$ takes the values $1\times {10}^{-5}$, $2\times {10}^{-5}$, and $3\times {10}^{-5}$, respectively). In this regard, it should be mentioned that although less inefficient, the iteratively regularized Gauss–Newton method is the best option, i.e., when the initial value of regularization parameter ${\alpha }_0$ is chosen sufficiently large, accurate results will always be found in comparatively small number of iteration steps (which depends on the initial value ${\alpha }_0$ and the ratio q).

3.2. Test Example 2

For the cloudy scenes considered in Figure 1, we illustrate, in

Table 3. The same as in Table 2 but for a three-dimensional geometry.

Cloudy Scene	DRME		DRME (One Iteration)
	Rel. Errors	CPU	Rel. Errors	CPU
1	$4.74\times {10}^{-4}$	14:15:31	$4.05\times {10}^{-2} (4.0\times {10}^{-5})$	2:34:03
2	$3.04\times {10}^{-4}$	14:21:43	$1.04\times {10}^{-2} (1.0\times {10}^{-6})$	2:36:42
3	$1.35\times {10}^{-4}$	14:15:57	$3.01\times {10}^{-2} (2.0\times {10}^{-6})$	2:32:26
5	$3.63\times {10}^{-4}$	14:15:23	$2.38\times {10}^{-2} (1.0\times {10}^{-6})$	2:32:11
6	$1.46\times {10}^{-4}$	14:14:36	$3.56\times {10}^{-2} (5.0\times {10}^{-6})$	2:33:38
8	$1.88\times {10}^{-4}$	14:20:13	$3.18\times {10}^{-2} (4.0\times {10}^{-5})$	2:34:16

, the relative errors and the computation times for DRME with several and one iteration steps. The solution accuracies are comparable to those corresponding to two-dimensional geometries. However, the computation time is extremely high; on average, it is of about 14 h and 15 min for DRME with several iteration steps, and 2 h and 30 min for DRME with one iteration step.

By taking a closer look at the cloudy scenes depicted in Figure 1, we see that the footprint of the detector is almost cloud-free. In this regard, we may try to retrieve the total column amount by using an one-dimensional radiative transfer model for a cloud-free atmosphere. The results given in the first two columns of

Table 4. Relative errors and the computation times (CPU) in minutes:seconds for DRMI. The measured and simulated spectral signals are computed by a three- and an one-dimensional radiative transfer model, respectively.

Cloudy Scene	DRMI		DRMI (Correction. Spectrum)
	Rel. Errors	CPU	Rel. Errors	CPU
1	$1.21\times {10}^{-1}$	2:21	$7.59\times {10}^{-2}$	2:42
2	$5.18\times {10}^{-2}$	2:32	$2.76\times {10}^{-2}$	2:58
3	$7.03\times {10}^{-2}$	2:14	$3.74\times {10}^{-2}$	2:36
4	$1.51\times {10}^{-1}$	2:04	$8.40\times {10}^{-2}$	2:24
5	$6.08\times {10}^{-2}$	2:27	$3.76\times {10}^{-2}$	2:47
6	$9.82\times {10}^{-2}$	2:25	$5.50\times {10}^{-2}$	2:45
7	$5.41\times {10}^{-2}$	2:25	$3.26\times {10}^{-2}$	2:46
8	$7.15\times {10}^{-2}$	2:30	$4.16\times {10}^{-2}$	2:50

and

Table 5. The same as in Table 4 but for DRME.

Cloudy Scene	DRME		DRME (Correction. Spectrum)
	Rel. Errors	CPU	Rel. Errors	CPU
1	$1.21\times {10}^{-1}$	2:10	$8.60\times {10}^{-2}$	2:16
2	$5.19\times {10}^{-2}$	2:12	$2.70\times {10}^{-2}$	2:18
3	$6.99\times {10}^{-2}$	2:05	$3.70\times {10}^{-2}$	2:11
4	$1.53\times {10}^{-1}$	1:52	$8.45\times {10}^{-2}$	2:01
5	$6.12\times {10}^{-2}$	2:16	$3.82\times {10}^{-2}$	2:22
6	$8.82\times {10}^{-2}$	2:14	$5.53\times {10}^{-2}$	2:18
7	$5.37\times {10}^{-2}$	2:13	$3.21\times {10}^{-2}$	2:19
8	$7.11\times {10}^{-2}$	2:21	$4.03\times {10}^{-2}$	2:17

show that in this case, the relative error is about 15%. In these simulations, the spectral signal measured by the instrument is computed by a three-dimensional radiative transfer model, while in the retrieval, the simulated spectral signal is computed by an one-dimensional radiative transfer model. The relative errors can be approximately halved when the differential correction spectrum due to three-dimensional effects (18) is included in the inverse model and its amplitude is retrieved. This is shown in the second two columns of Table 4 and Table 5. Note that the computation time given in these tables does not take into account the time for computing the correction spectrum by a three-dimensional radiative transfer model. As shown in [27], this computation time is of about 1 h and 20 min, so that roughly speaking, this is the time for retrieving the total column amount by an one-dimensional inverse model that accounts on three-dimensional effects. The correction spectra included in the inverse model are shown in Figure 6, and it is apparent that they depend on the cloud field (some similitude can be observed for the cloudy scenes 2 and 7).

4. Discussion

The main concepts of an algorithm for the retrieval of the total column amount of trace gases in a multi-dimensional atmosphere have been presented. The algorithm uses (i) as inverse models, certain differential radiance models with internal and external closures; (ii) as regularization tool, the iteratively regularized Gauss-Newton method; and (iii) as linearized radiative transfer model, the spherical harmonics discrete ordinate method with a spectral acceleration approach that combines the correlated k-distribution method with the principal component analysis.

The algorithm has been applied to the retrieval of the total column amount of ${\mathrm{NO}}_2$ under cloudy conditions. For two-dimensional geometries, we come to the following findings.

• The differential radiance models with internal and external closures yield accurate results with reasonable computation times (of about 35–40 min).
• An inverse model based on an approximate computation of the partial derivative leads to a reduction of the computation time by about 25%, but to large relative errors.
• Provided that the regularization parameter is optimally chosen, reasonable accurate results with a computation time of about 6 min can be obtained when the iterative process, corresponding to the differential radiance model with external closure, is stopped after one iteration step. The fact that the optimal value of the regularization parameter depends on the cloudy scene, makes it more difficult to apply this one-step retrieval algorithm, or equivalently, DOAS-type models.

For three-dimensional geometries, we come to the following results.

• Although accurate, the retrievals based on the differential radiance model with external closures are inefficient; the computation time is of about 14 h and 15 min for a full-step retrieval algorithm, and 2 h and 30 min for an one-step retrieval algorithm. The one-step retrieval algorithm is less accurate than in the case of two-dimensional geometries, but the results are still acceptable.
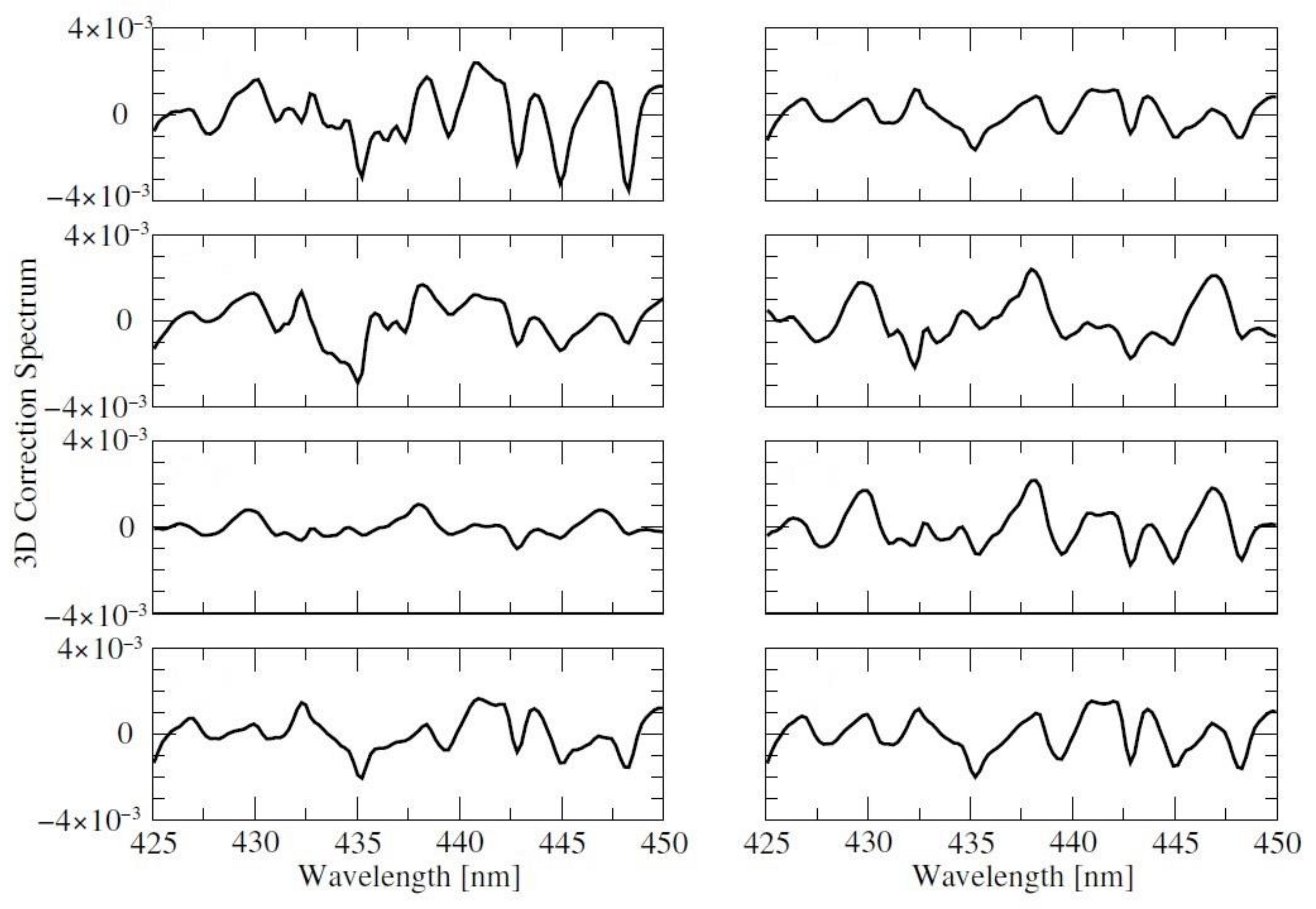
• The application of a fast one-dimensional radiative transfer model to retrieve the ${\mathrm{NO}}_2$ column amount for a three-dimensional cloudy scene leads to relative errors up to 15%. These errors can be reduced when a differential correction spectrum due to three-dimensional effects is included in the retrieval.

The main conclusion of our analysis is that although for three-dimensional geometries the computational time is high, the main concepts of the algorithm are correct and the retrieval results are accurate.

For operational retrievals, we recommend

• to construct a database for the spectral signal ${\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})$ and its derivatives $\partial ln{\mathcal{I}}_{\mathrm{sim}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})/\partial X_g$, and to use these spectra in an one-step, three-dimensional retrieval algorithm, or
• to construct a database for the differential correction spectra accounting on three-dimensional effects $S_{3\mathrm{D}}({\lambda }_k,{\mathbf{X}}_{\mathrm{a}})$, and to use these spectra in a full-step, one-dimensional retrieval algorithm.

The databases should be built up for different cloud scenarios, surface albedo, and solar and satellite geometries. The main problem which has to be solved is the design of a classification algorithm for broken clouds. One option is to use a nearest neighbor classifier based on the two-dimensional principal component analysis. Another option is to use a classification algorithm in which only the distributions of the cloud fields in the two-dimensional domains around the azimuth planes of the solar and viewing directions are of interest. The width of these domains corresponds to the instrument footprint. Note that these domains are also relevant in the tilted independent pixel approximation [34]: the direct solar beam is computed at all grid points which belong to the vertical columns inside the instrument footprint and for all characteristics within the entrance (solar direction) domain, while the measured radiance is computed by integrating the source function along all characteristics within the exit (viewing direction) domain. This will be the topic of a forthcoming paper.