An Accurate GEO SAR Range Model for Ultralong Integration Time Based on mth-Order Taylor Expansion
Abstract
1. Introduction
- (1)
- As the azimuth resolution increases, the low-order Taylor expansion range model shows insufficient accuracy in ultralong integration time.
- (2)
- The iterative approximation range model has a high accuracy but cannot be expressed by an analytical expression.
- (3)
- The range models lack the flexibility of precision adjustment for different exposure times.
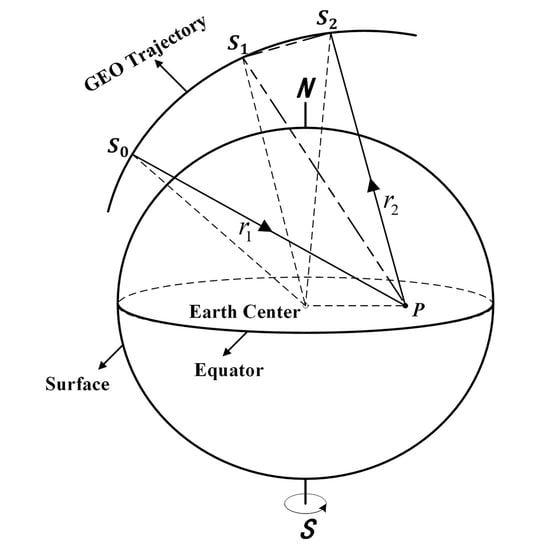
2. Characteristics of GEO SAR
2.1. Invalidation of “Stop-and-Go” Assumption
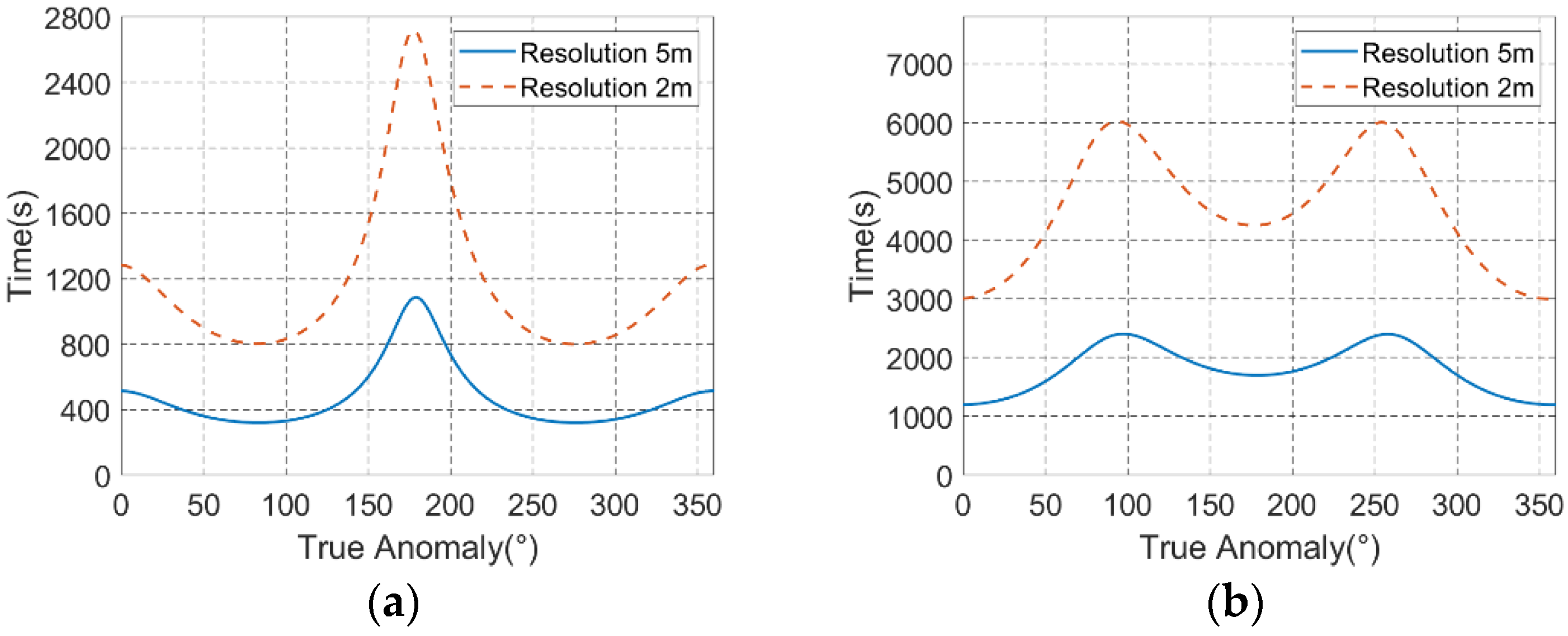
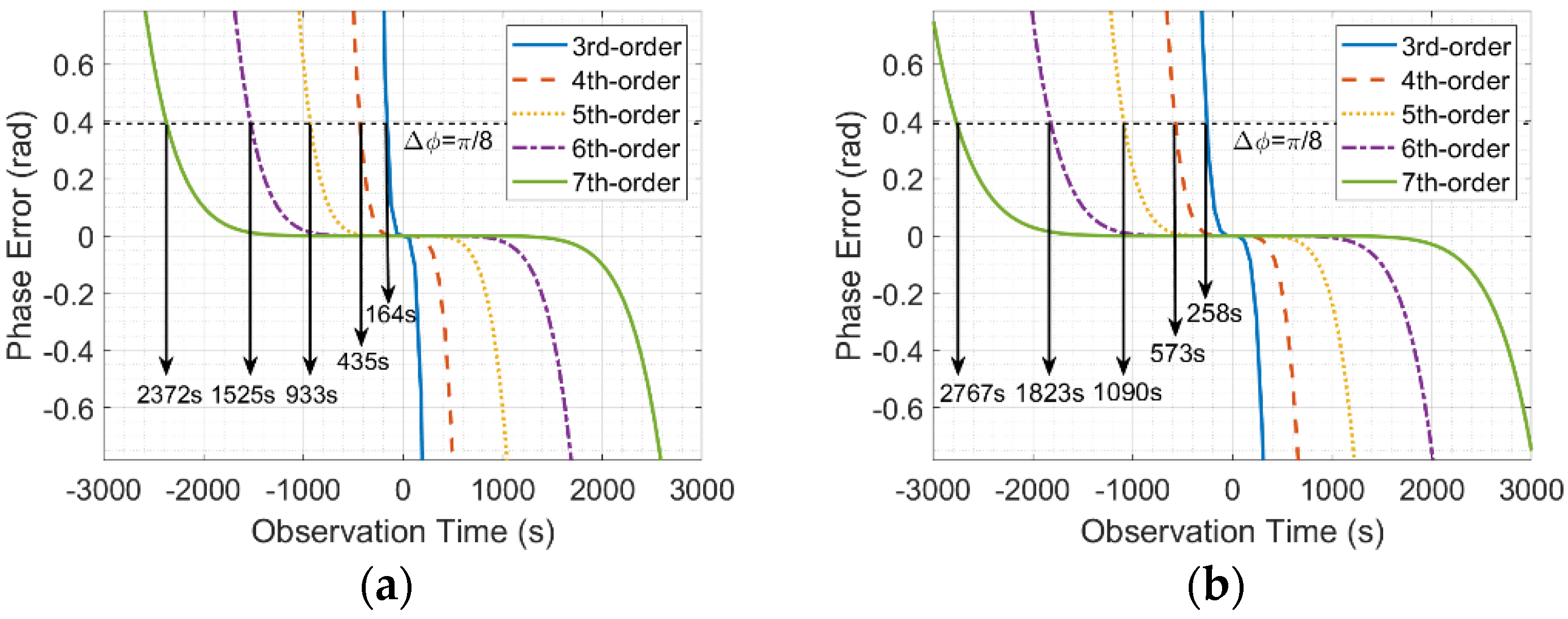
2.2. Ultralong Integration Time
- Set an initial search region [Tmin, Tmax] according to the estimated integration time by (1), and this region is required to include the real integration time.
- Define Tmid = (Tmin + Tmax)/2. If Tmax − Tmin is smaller than the threshold, then return the Treal = Tmid and stop the iteration.
- Calculate the synthetic aperture angle of different exposure time Tmin, Tmax, and Tmid, denoted as θmin, θmax, and θmid.
- Define the new search region: if θmid > θsyn, then Tmax = Tmid, else let Tmin = Tmid. Return to step 2.
2.3. “Non-Stop-and-Go” Range Models
- (1)
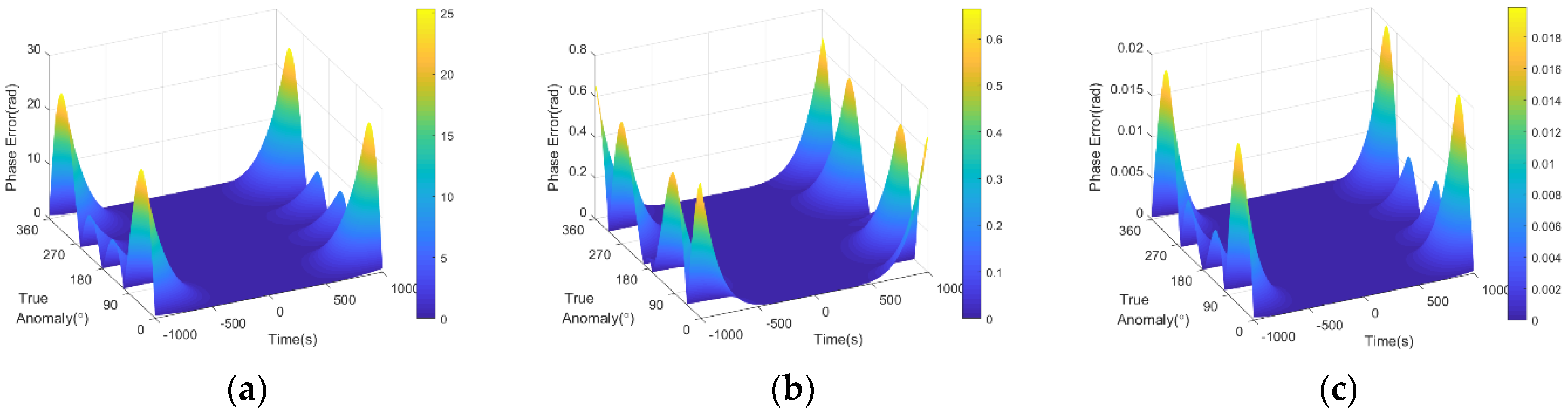
- Fourth-order Taylor expansion model considering the invalidation of “stop-and-go” assumption. This model can be expressed in the form of a power series, which can obtain the 2-D spectrum to form an efficient frequency domain imaging algorithm. However, limited by the order of expansion, this model only has a satisfactory fitting effect in a short observation time. As the exposure time increases, the fitting error accumulates rapidly at both edges of the aperture.
- (2)
- Iterative approximation range model. The main idea of this range model is to use twice the transmitting delay to approximately calculate the satellite position in the orbit, then an iteration can be formed to calculate a relatively accurate result. The calculation of this model is simple, and only one iteration already has a high accuracy, which can be used in echo generation and time-domain imaging algorithms. However, this range model cannot be expressed by an analytical expression, so its usage for frequency domain imaging algorithms is limited.
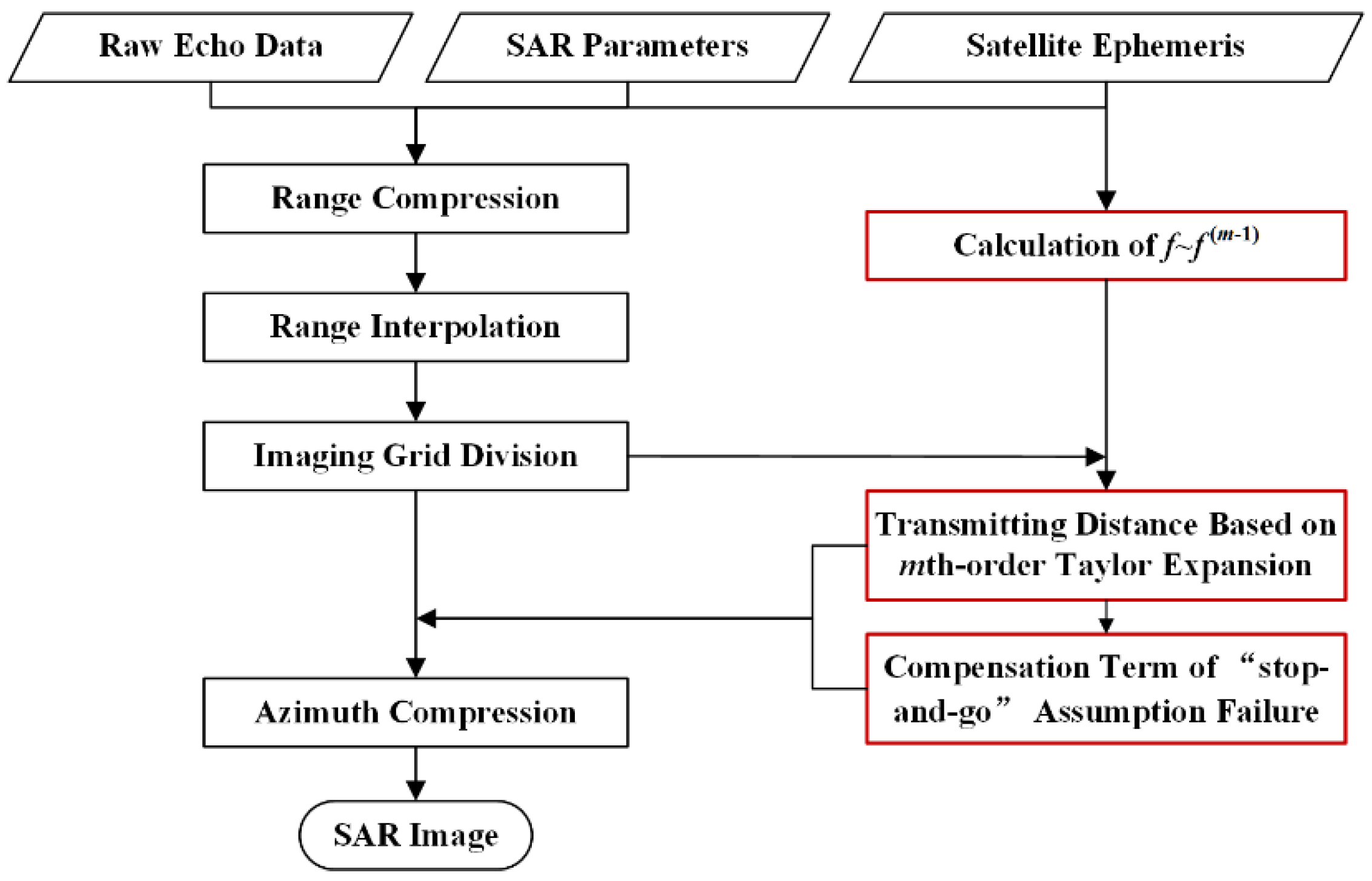
3. Proposed Range Model and Imaging Algorithm
3.1. Proposed Range Model
- (1)
- A general calculation method for mth-order expansion of pulse transmitting distance is given, and the expansion order can be adjusted according to the integration time and error accuracy requirement.
- (2)
- An accurate pulse receiving distance is obtained by using the thought of iterative approximation, and the analytical expression is obtained by Taylor expansion in the ECEF coordinate system.
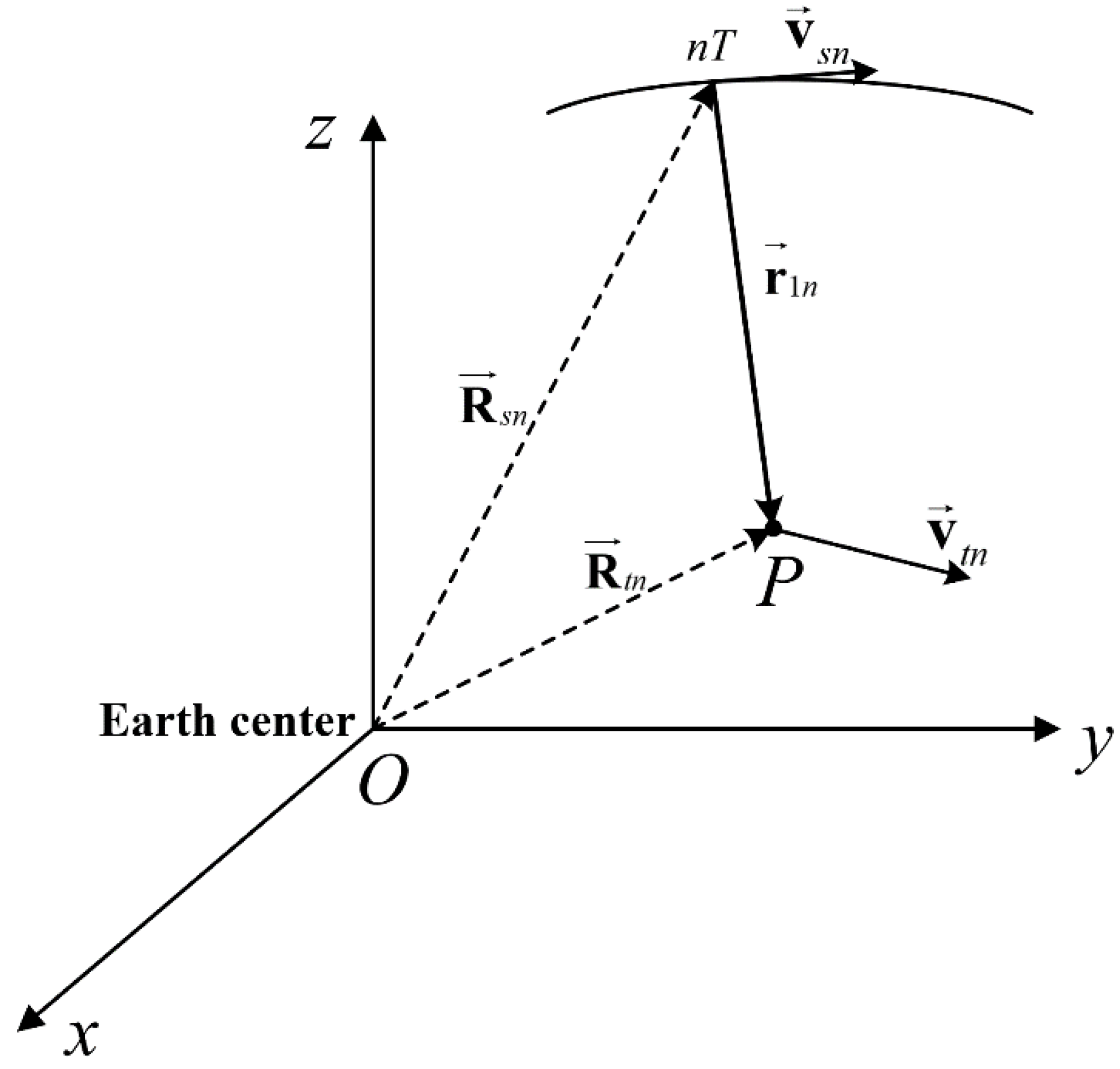
3.1.1. Pulse Transmitting Distance
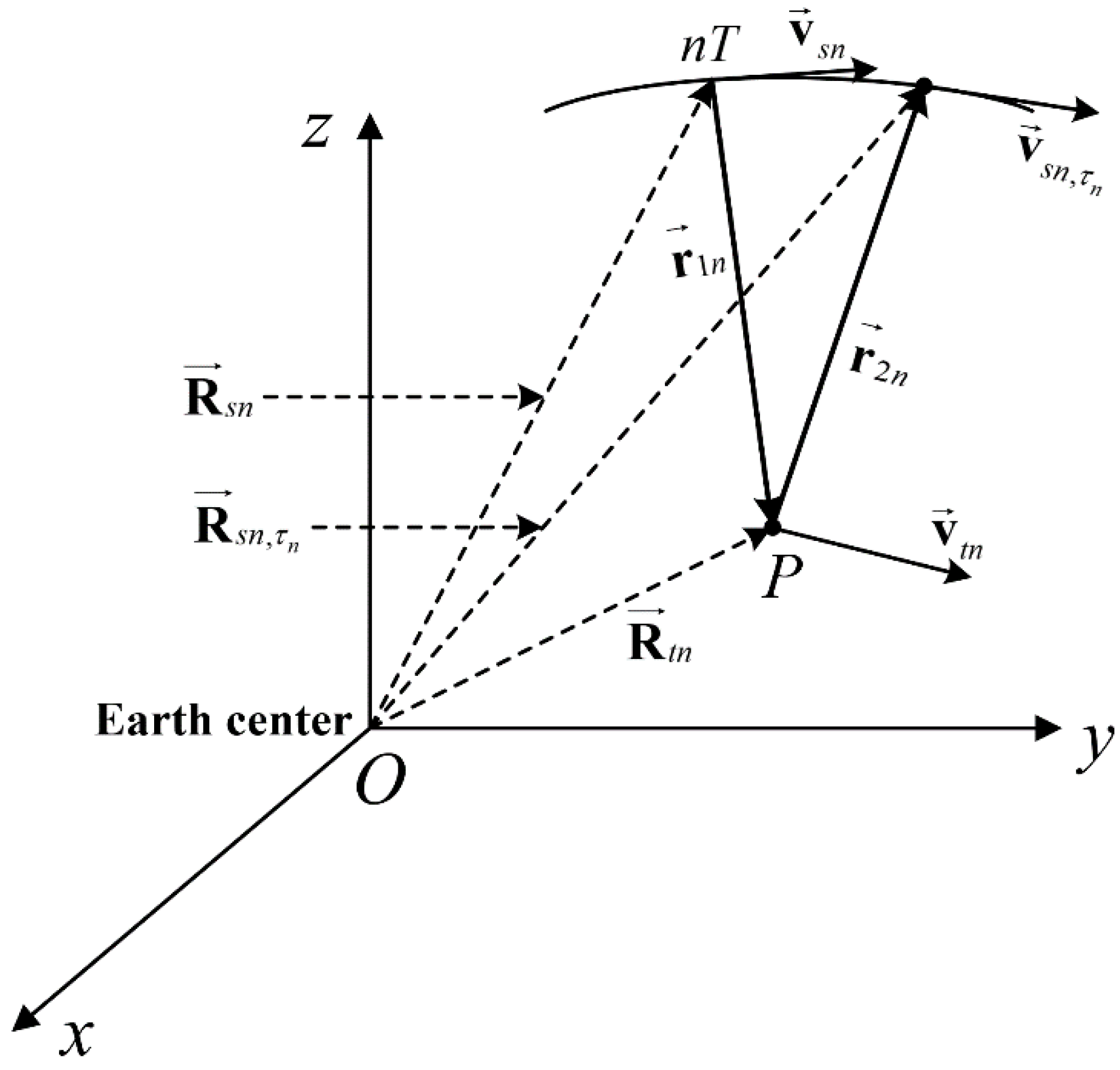
3.1.2. Pulse Receiving Distance
3.1.3. Total Pulse Propagation Distance
3.2. Imaging Method
- (1)
- Calculating the true anomaly and its derivatives from 1st to (m − 1)-th order based on the satellite ephemeris data and orbit configuration;
- (2)
- Determining the Taylor expansion order m by the SAR system parameters and error accuracy, and then performing the mth-order Taylor expansion to obtain the transmitting distance for each grid point.
- (3)
- Calculating the compensation term of the “stop-and-go” assumption failure, and then bringing the complete pulse propagation distance into the azimuth compression.
4. Simulation Results and Discussion
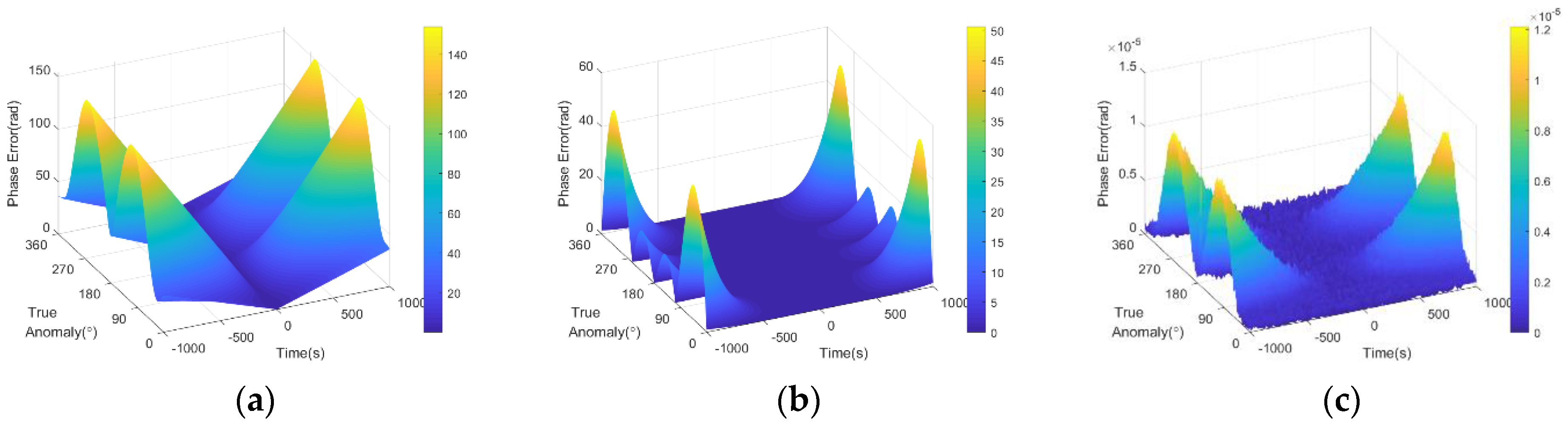
4.1. Fitting Error of the Pulse Transmitting Distance
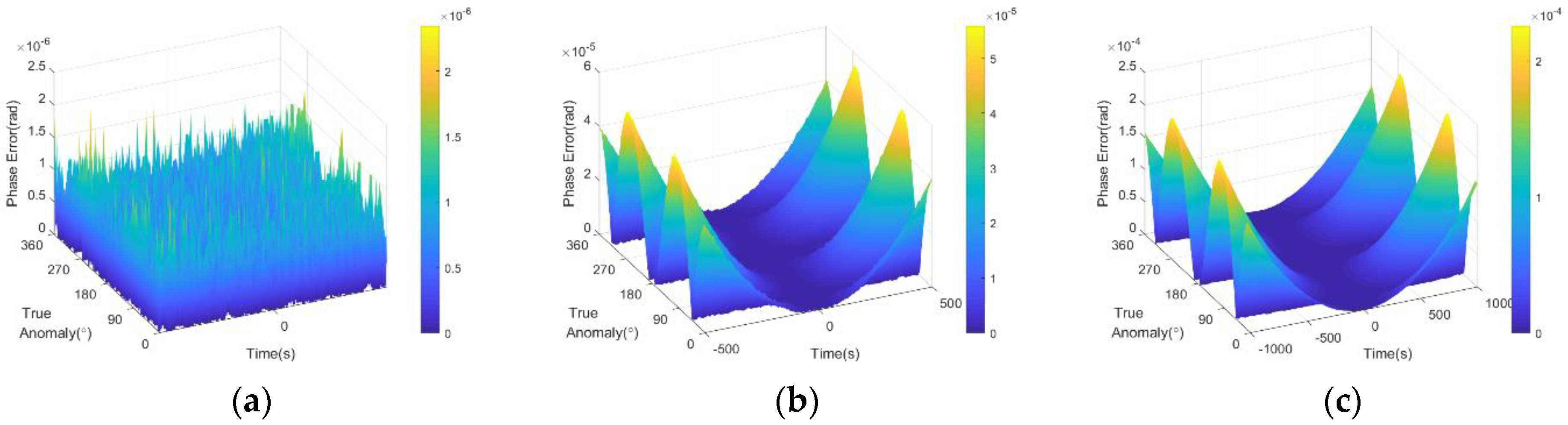
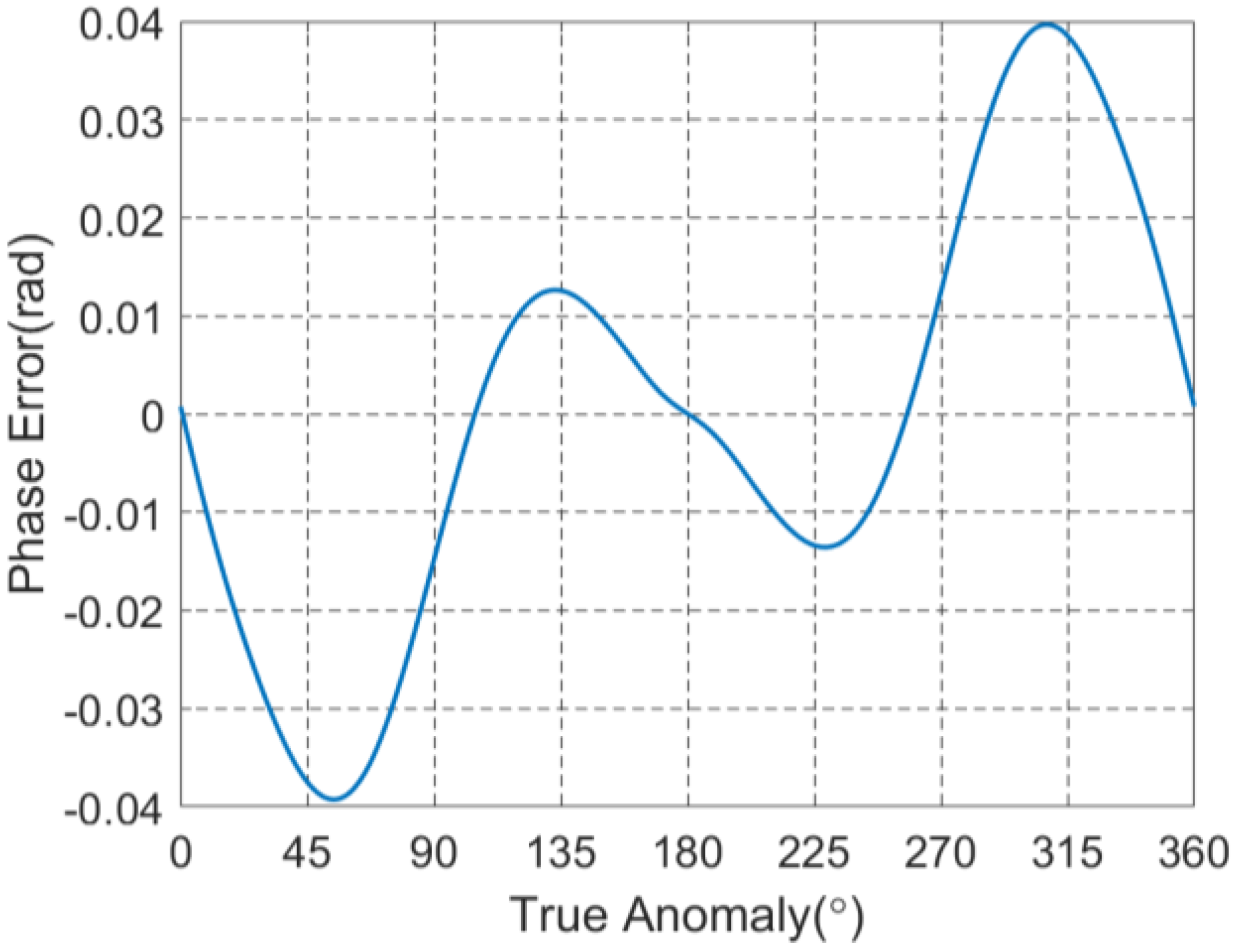
4.2. Fitting Error of Compensation Term
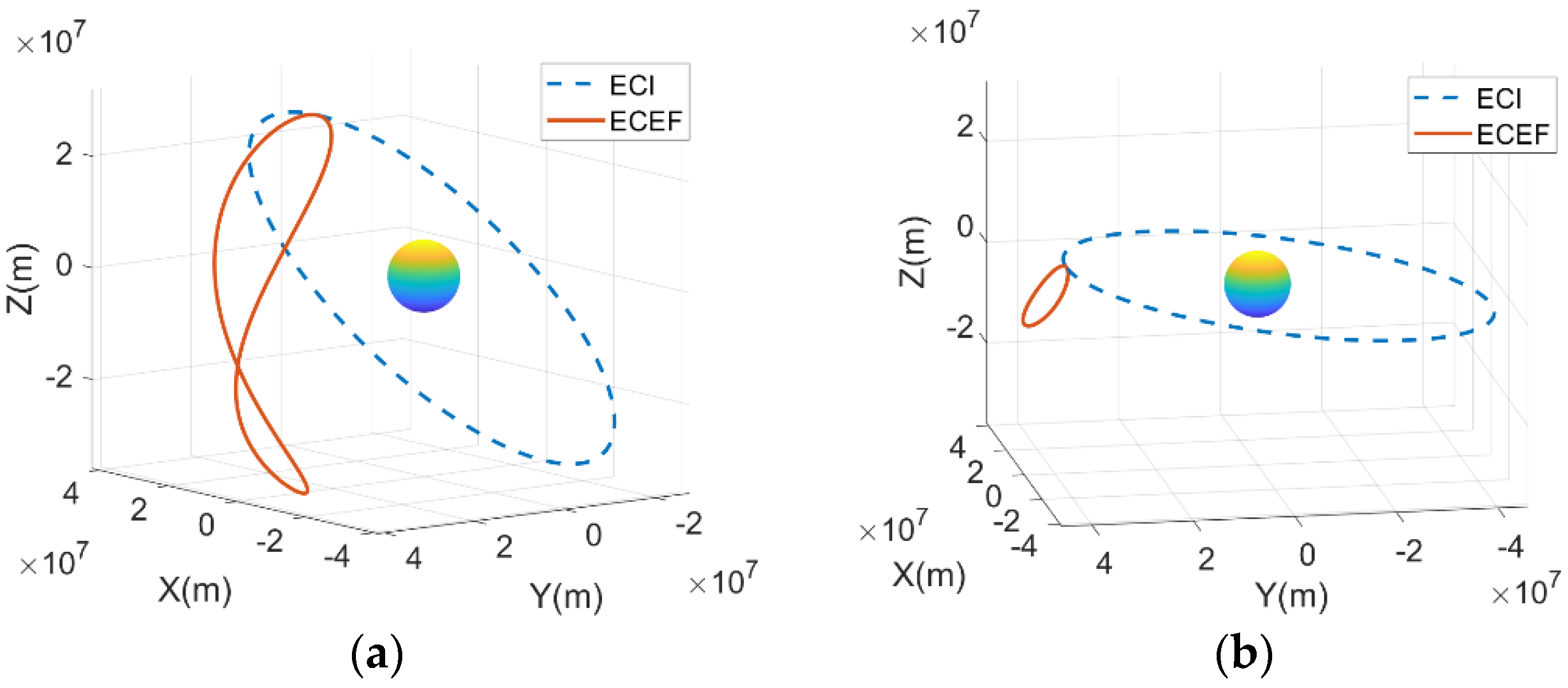
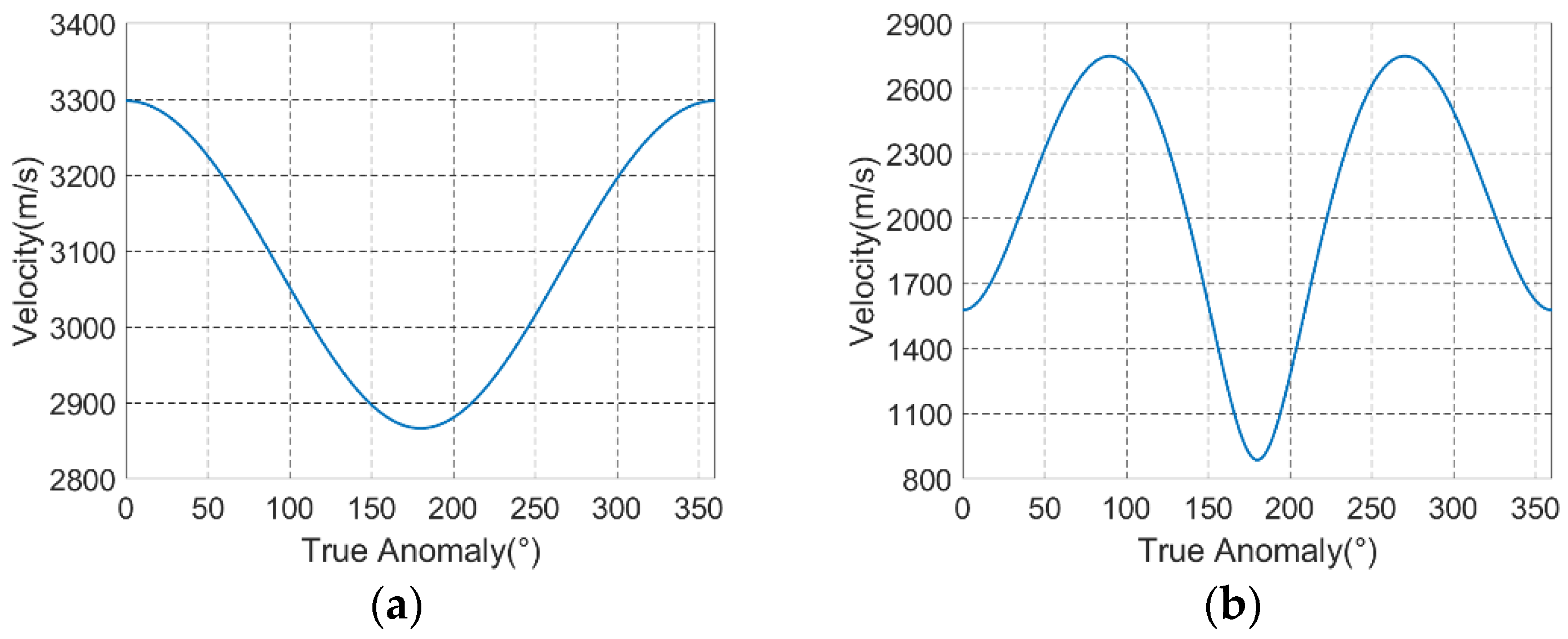
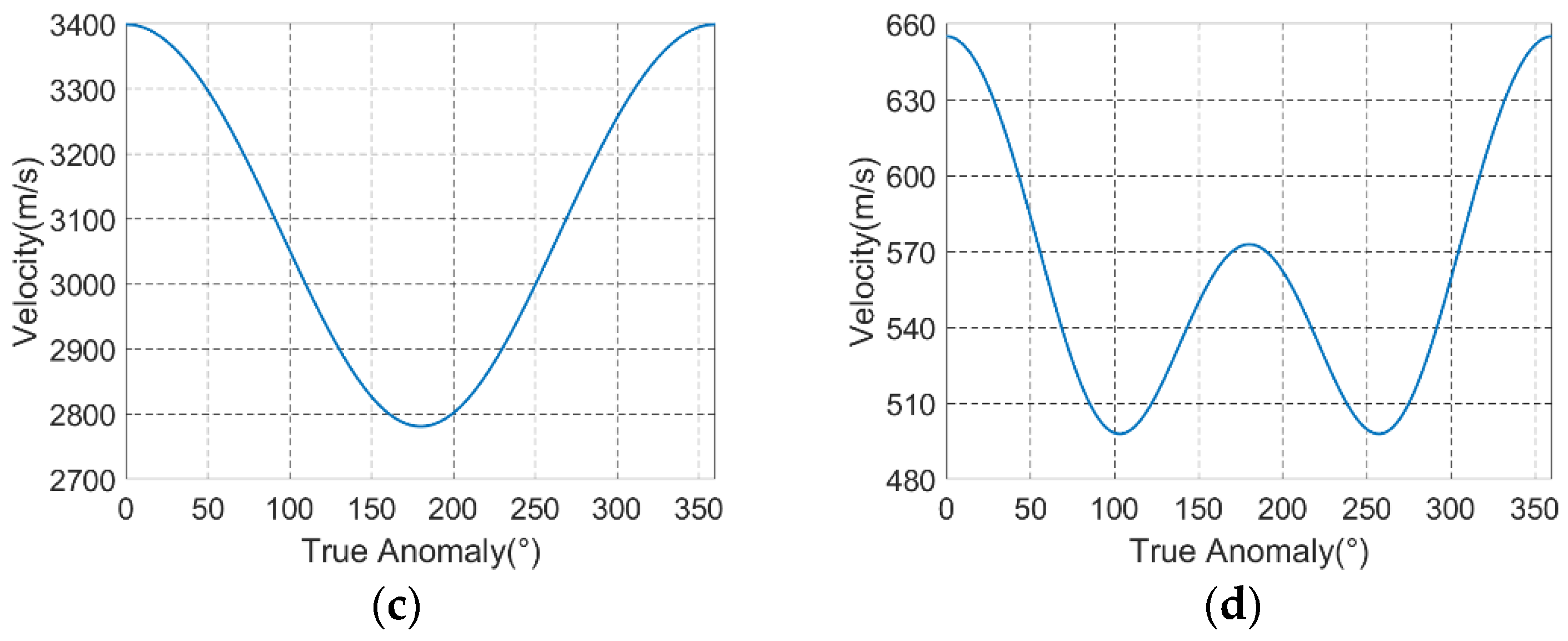
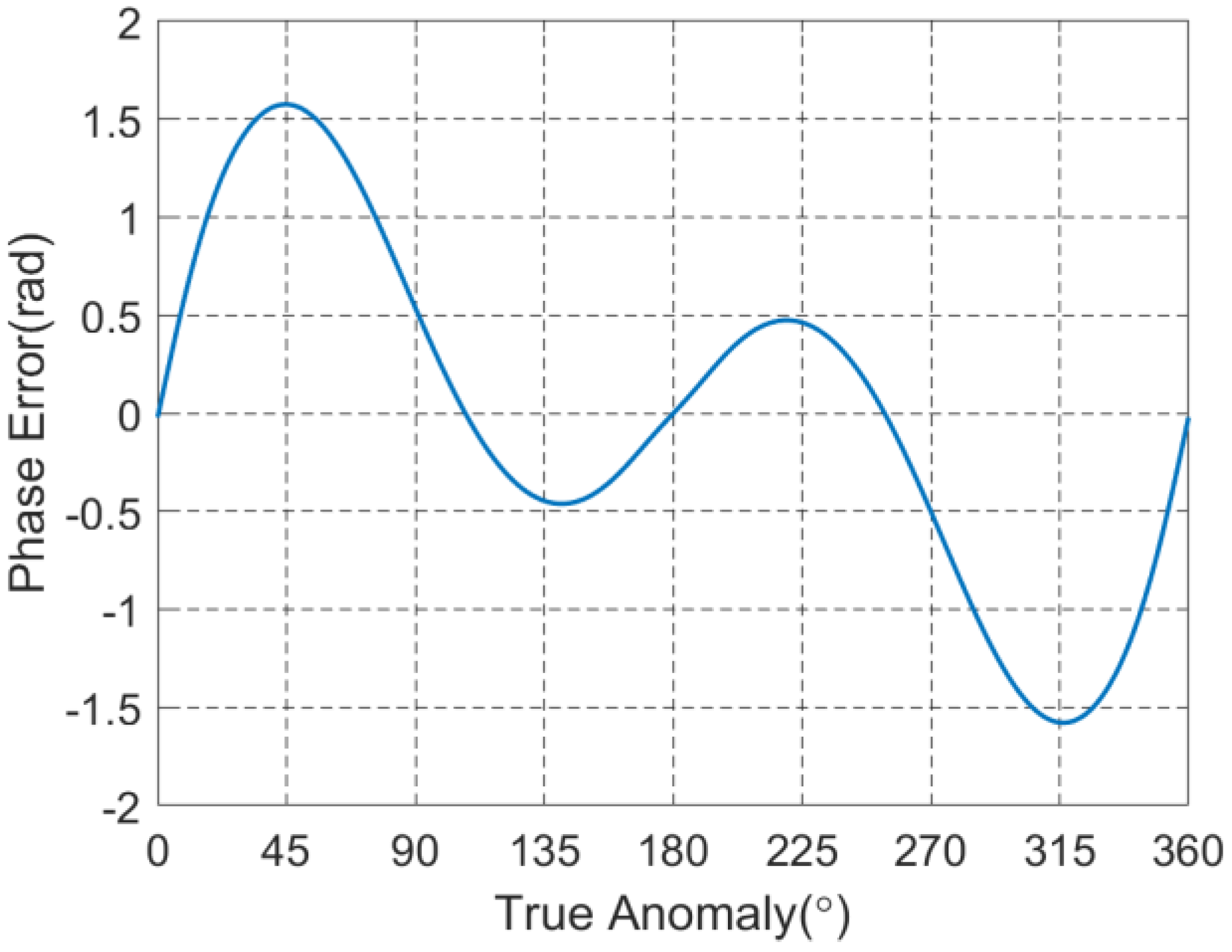
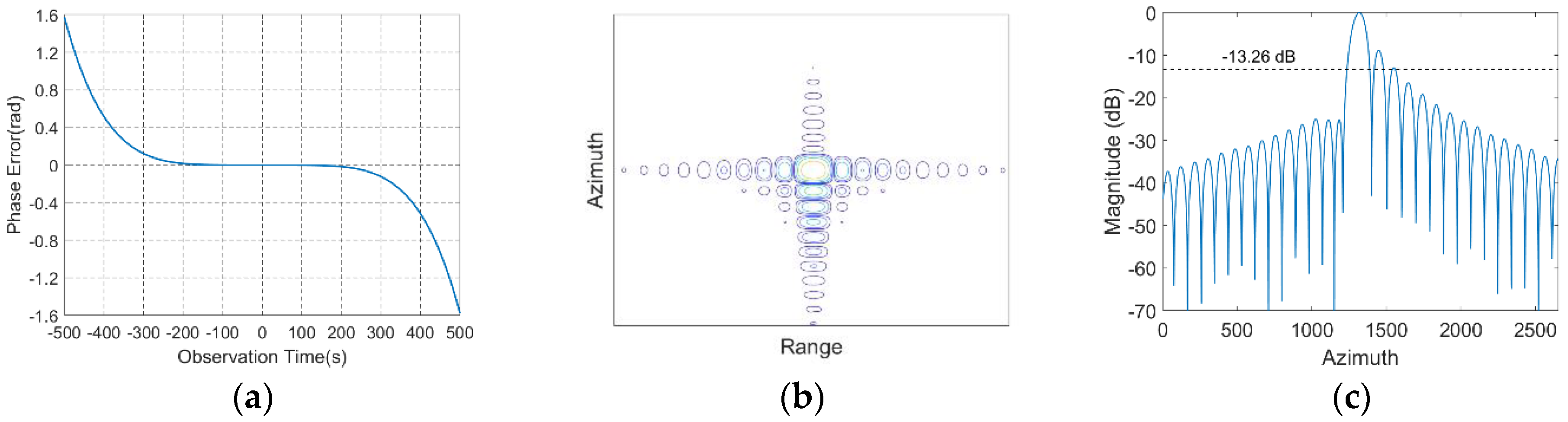
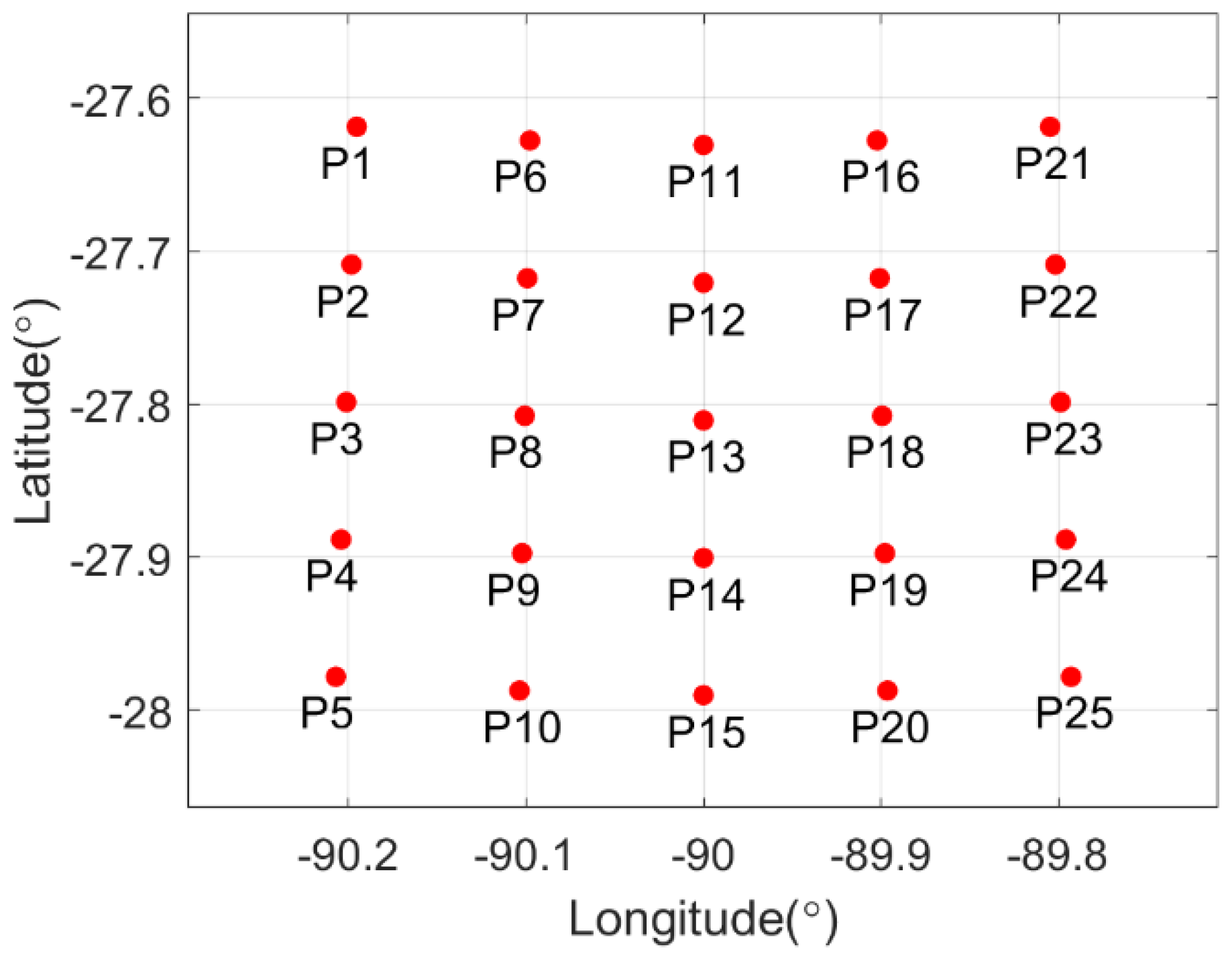
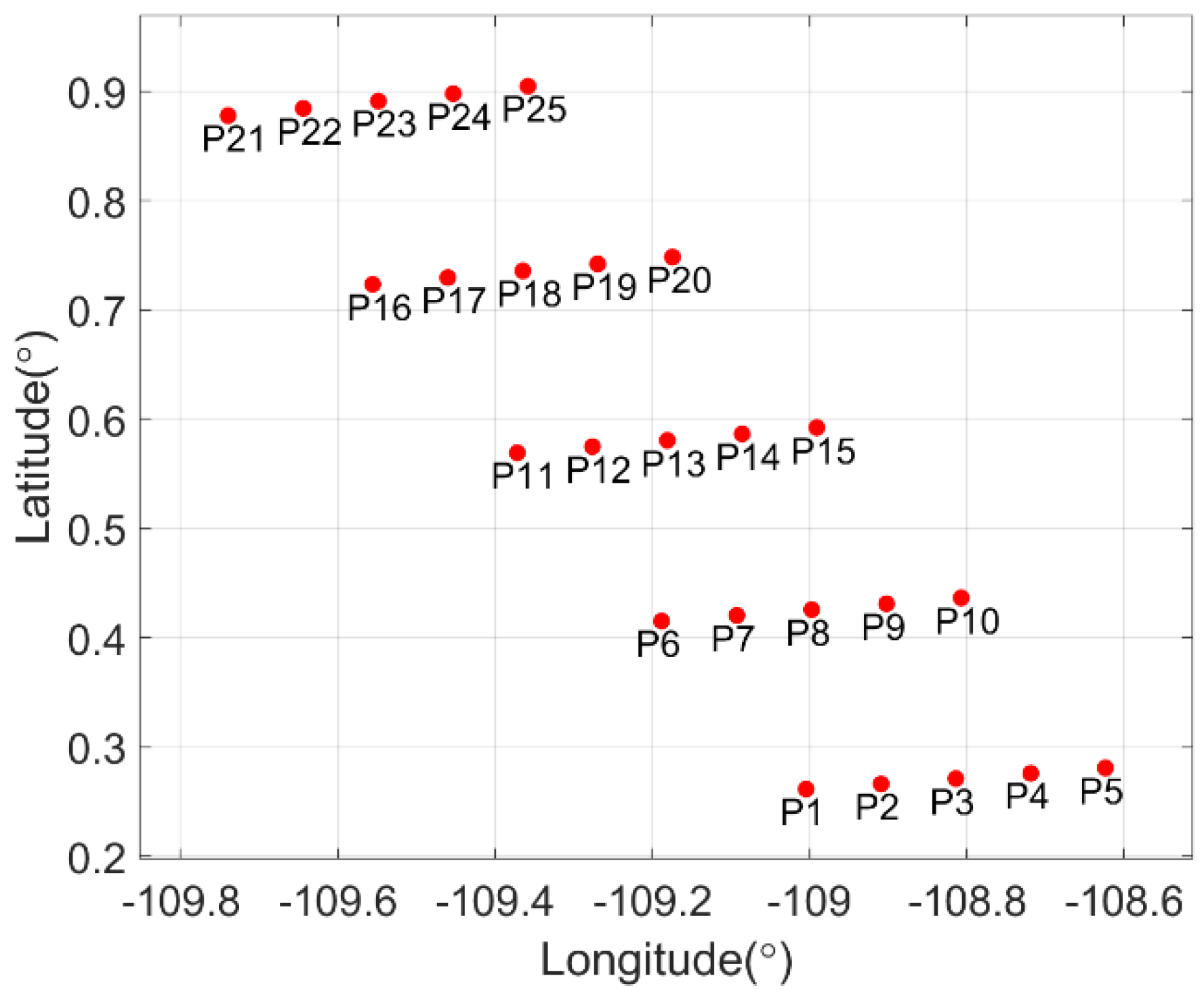
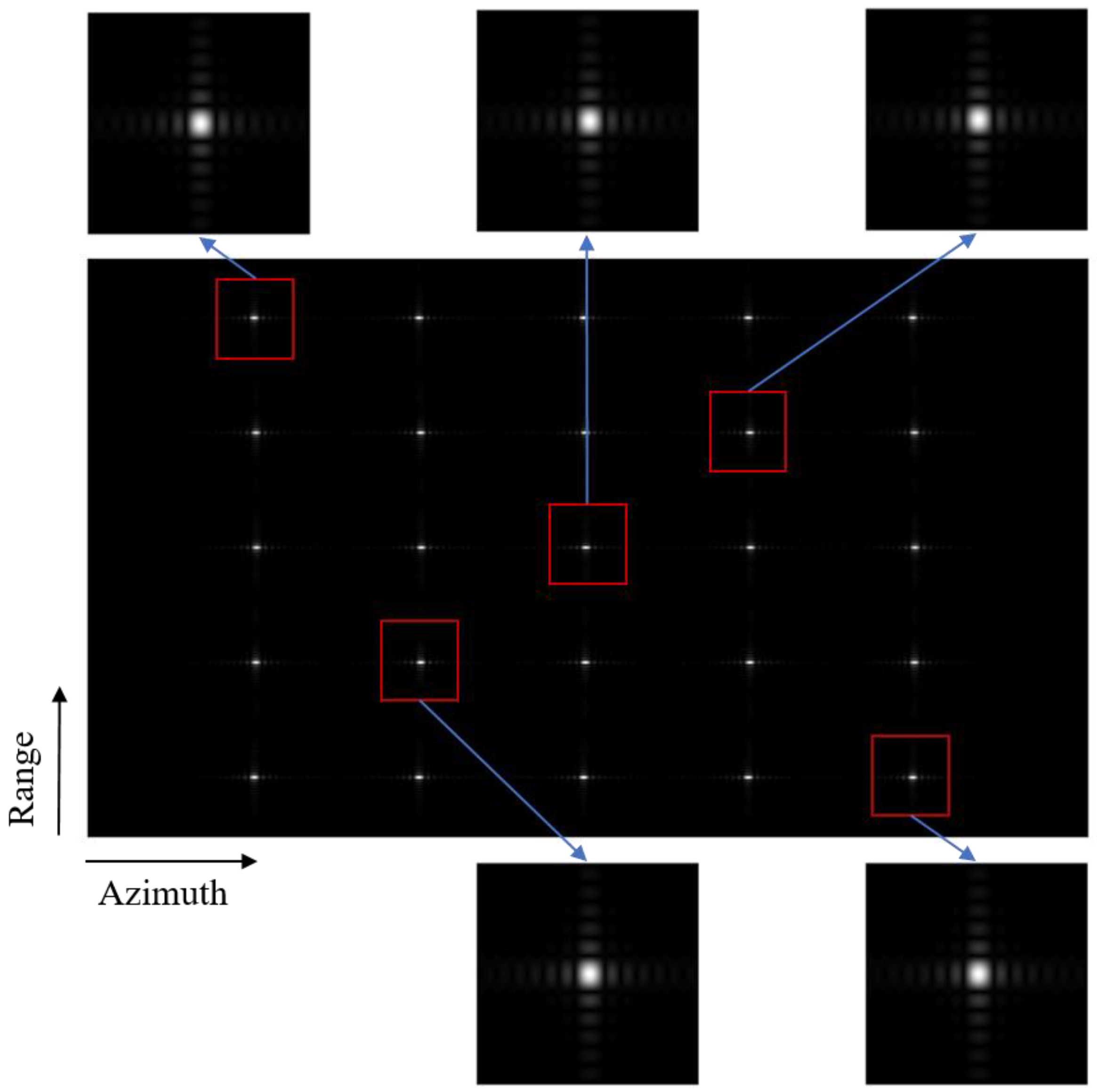
4.3. Focusing Results at Different Orbit Position
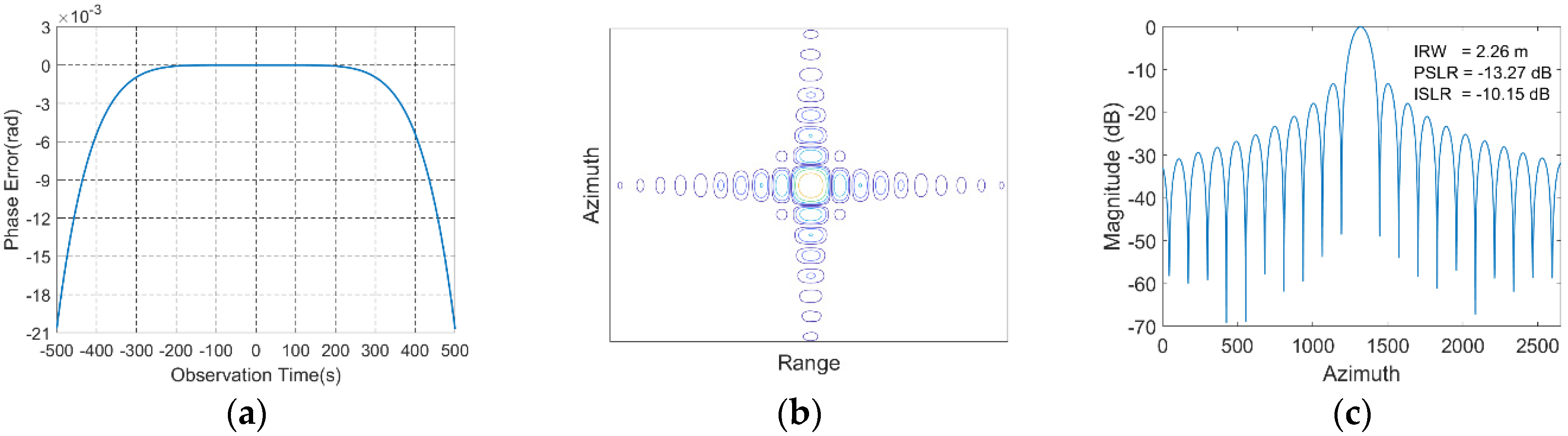
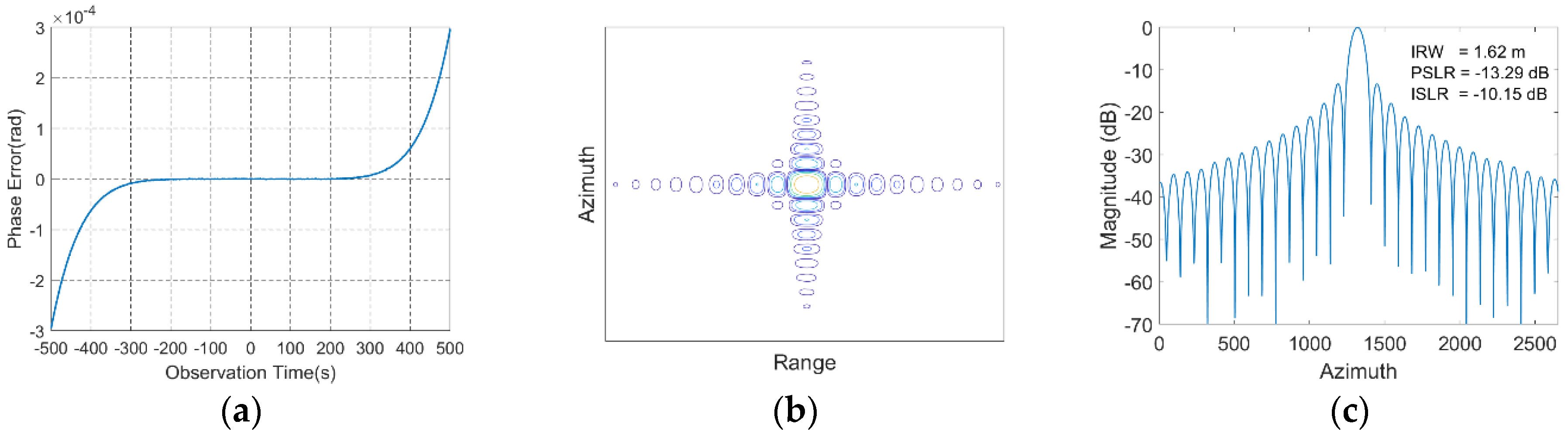
4.4. Focusing Results with Ultralong Integration Time
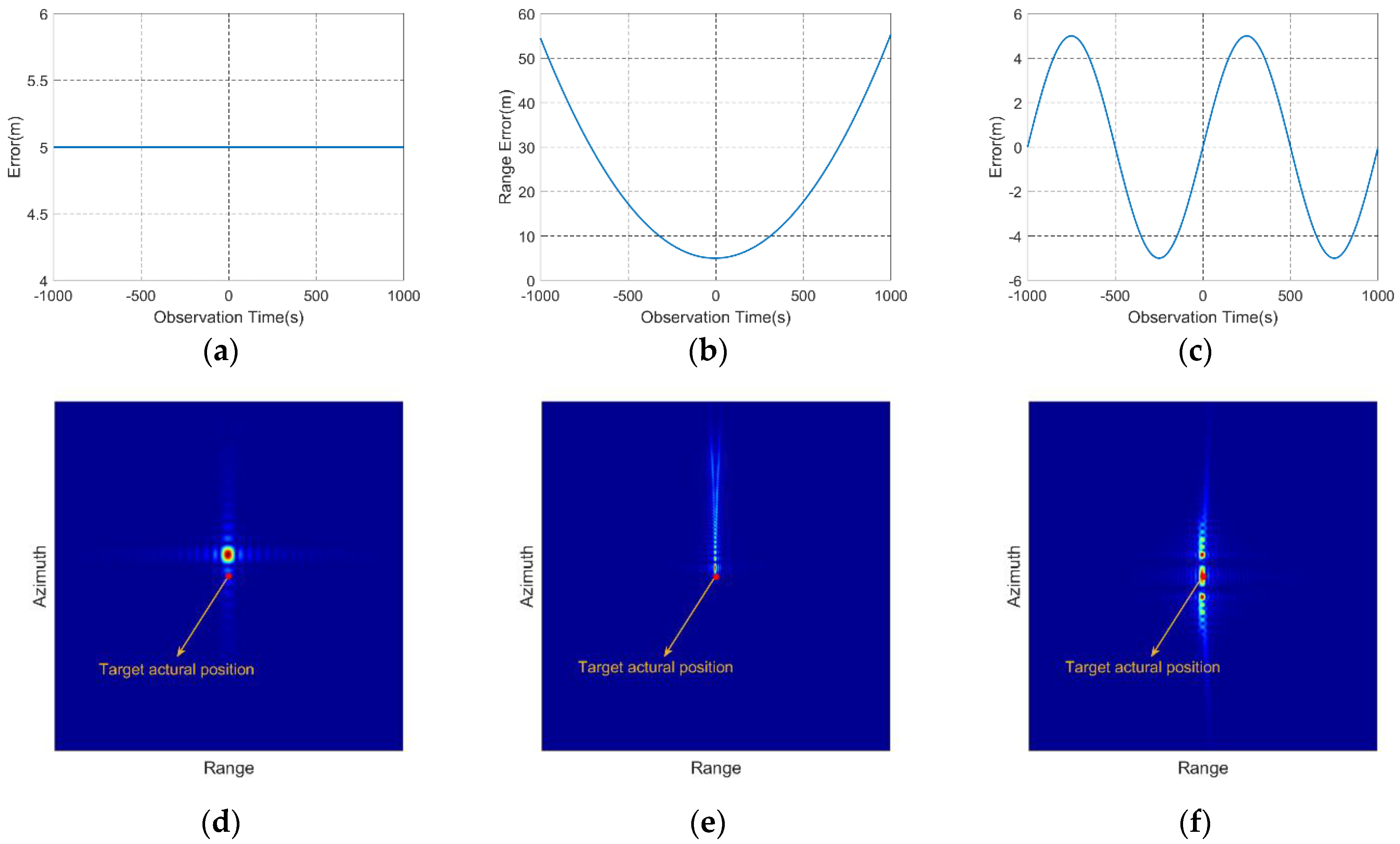
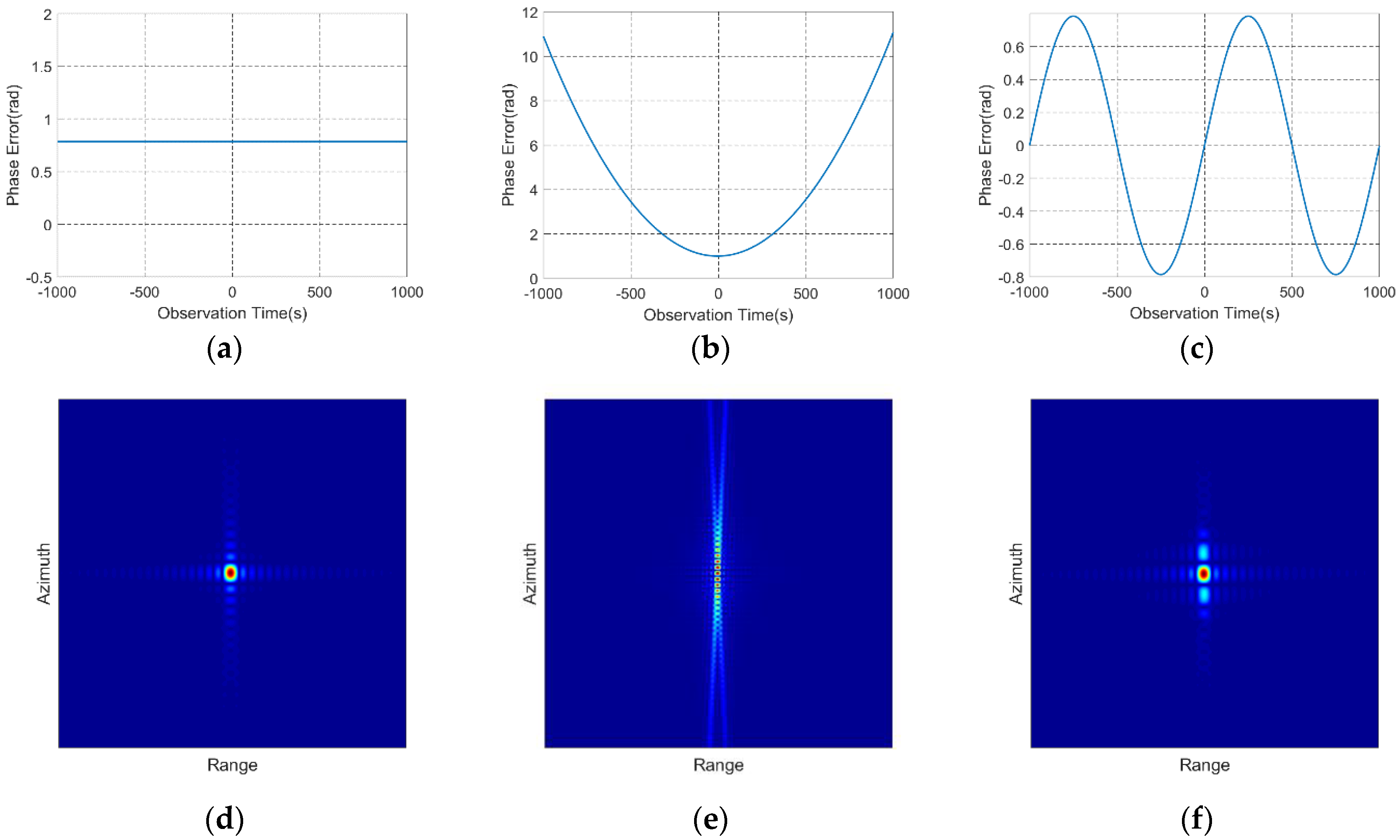
4.5. The Influence of Different Sources of Distortion on Imaging
- (1)
- Trajectory distortions caused by errors in measuring the parameters of the spacecraft motion.
- (2)
- Hardware distortions and instabilities during the formation and reception of probing signals (in particular, phase instability, instability of the microwave path parameters).
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Cumming, I.; Wong, F. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Boston, MA, USA, 2005; pp. 113–168. [Google Scholar]
- Tomiyasu, K. Synthetic aperture radar in geosynchronous orbit. In Proceedings of the 1978 Antennas and Propagation Society International Symposium, Washington, DC, USA, 15–19 March 1978; pp. 42–45. [Google Scholar]
- Tomiyasu, K.; Pacelli, J. Synthetic aperture radar imaging from an inclined geosynchronous orbit. IEEE Trans. Geosci. Remote Sens. 1983, 21, 324–329. [Google Scholar]
- Hensley, S.; Chapin, E.; Freedman, A.; Le, C.; Madsen, S.; Michel, T.; Rodriguez, E.; Siqueira, P.; Wheeler, K. First P-band results using the GeoSAR mapping system. In Proceedings of the IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, NSW, Australia, 9–13 July 2001; pp. 126–128. [Google Scholar]
- Madsen, S.; Edelstein, W.; DiDomenico, L.; LaBrecque, J. A geosynchronous synthetic aperture radar; for tectonic mapping, disaster management and measurements of vegetation and soil moisture. In Proceedings of the IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, NSW, Australia, 9–13 July 2001; pp. 447–449. [Google Scholar]
- Madsen, S.; Chen, C.; Edelstein, W. Radar options for global earthquake monitoring. In Proceedings of the IEEE 2002 International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 1483–1485. [Google Scholar]
- Chen, C.; Raymond, C.; Madsen, S. Observational architectures for enabling earthquake forecasting. In Proceedings of the IEEE 2003 International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 618–620. [Google Scholar]
- NASA JPL. Global Earthquake Satellite System: A 20-Year Plan to Enable Earthquake Prediction; California Institute of Technology: Pasadena, CA, USA, 2003.
- Hobbs, S. GeoSAR: Summary of the Group Design Project, MSc in Astronautics and Space Engineering 2005/06; College of Aeronautics Rep 509; Cranfield University: Bedford, UK, 2006. [Google Scholar]
- Hobbs, S.; Bruno, D. Radar imaging from geo: Challenges and applications. In Proceedings of the 2007 Remote Sensing and Photogrammetry Society Annual Conference, Newcastle, UK, 12–14 September 2007; pp. 1–6. [Google Scholar]
- Bruno, D.; Hobbs, S. Radar Imaging from Geosynchronous Orbit: Temporal Decorrelation Aspects. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2924–2929. [Google Scholar]
- Hobbs, S.; Sanchez, J.; Kingston, J. Extended lifetime Laplace plane GEO SAR mission design. In Proceedings of the IET International Radar Conference 2015, Hangzhou, China, 14–16 October 2015; pp. 1–4. [Google Scholar]
- Guarnieri, A.; Rocca, F.; Ibars, A. Impact of atmospheric water vapor on the design of a Ku band geosynchronous SAR system. In Proceedings of the IEEE 2009 International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; pp. II-945–II-948. [Google Scholar]
- Guarnieri, A.; Tebaldini, S.; Rocca, F.; Broquetas, A. GEMINI: Geosynchronous SAR for Earth Monitoring by Interferometry and Imaging. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 210–213. [Google Scholar]
- Hu, C.; Chen, Z.; Dong, X.; Cui, C. Multistatic Geosynchronous SAR Resolution Analysis and Grating Lobe Suppression Based on Array Spatial Ambiguity Function. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6020–6038. [Google Scholar]
- Dong, X.; Cui, C.; Li, Y.; Hu, C. Geosynchronous Spaceborne-Airborne Bistatic Moving Target Indication System: Performance Analysis and Configuration Design. Remote Sens. 2020, 12, 1810. [Google Scholar]
- Xu, W.; Wei, Z.; Huang, P.; Tan, W.; Liu, B.; Gao, Z.; Dong, Y. Azimuth Multichannel Reconstruction for Moving Targets in Geosynchronous Spaceborne–Airborne Bistatic SAR. Remote Sens. 2020, 12, 1703. [Google Scholar]
- Zhang, Y.; Xiong, W.; Dong, X.; Hu, C. A Novel Azimuth Spectrum Reconstruction and Imaging Method for Moving Targets in Geosynchronous Spaceborne–Airborne Bistatic Multichannel SAR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5976–5991. [Google Scholar]
- Li, Y.; Monti Guarnieri, A.; Hu, C.; Rocca, F. Performance and Requirements of GEO SAR Systems in the Presence of Radio Frequency Interferences. Remote Sens. 2018, 10, 82. [Google Scholar]
- Jiang, M.; Hu, W.; Ding, C.; Liu, G. The Effects of Orbital Perturbation on Geosynchronous Synthetic Aperture Radar Imaging. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1106–1110. [Google Scholar]
- Li, D.; Zhu, X.; Dong, Z.; Yu, A.; Zhang, Y. Background Tropospheric Delay in Geosynchronous Synthetic Aperture Radar. Remote Sens. 2020, 12, 3081. [Google Scholar]
- Dong, X.; Hu, J.; Hu, C.; Long, T.; Li, Y.; Tian, Y. Modeling and Quantitative Analysis of Tropospheric Impact on Inclined Geosynchronous SAR Imaging. Remote Sens. 2019, 11, 803. [Google Scholar]
- Zhang, Y.; Xiong, W.; Dong, X.; Hu, C.; Sun, Y. GRFT-Based Moving Ship Target Detection and Imaging in Geosynchronous SAR. Remote Sens. 2018, 10, 2002. [Google Scholar]
- Xiong, W.; Zhang, Y.; Dong, X.; Cui, C.; Liu, Z.; Xiong, M. A Novel Ship Imaging Method with Multiple Sinusoidal Functions to Match Rotation Effects in Geosynchronous SAR. Remote Sens. 2020, 12, 2249. [Google Scholar]
- Zhang, T.; Ding, Z.; Zhang, Q.; Zhao, B.; Zhu, K.; Li, L.; Gao, Y.; Dai, C.; Tang, Z.; Long, T. The First Helicopter Platform-Based Equivalent GEO SAR Experiment with Long Integration Time. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8518–8530. [Google Scholar]
- Hu, C.; Long, T.; Zeng, T. The accurate focusing and resolution analysis method in geosynchronous SAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3548–3563. [Google Scholar]
- Yu, Z.; Chen, J.; Li, C.; Li, Z.; Zhang, Y. Concepts, properties, and imaging technologies for GEO SAR. In Proceedings of the Sixth International Symposium on Multispectral Image Processing and Pattern Recognition, Yichang, China, 30 October–1 November 2009; Volume 7494, p. 749407. [Google Scholar]
- Hu, C.; Liu, Z.; Long, T. An improved CS algorithm based on the curved trajectory in geosynchronous SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 795–808. [Google Scholar]
- Sun, G.; Xing, M.; Wang, Y.; Yang, J.; Bao, Z. A 2-D Space-Variant Chirp Scaling Algorithm Based on the RCM Equalization and Subband Synthesis to Process Geosynchronous SAR Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4868–4880. [Google Scholar]
- Ding, Z.; Shu, B.; Yin, W. A modified frequency domain algorithm based on optimal azimuth quadratic factor compensation for geosynchronous SAR imaging. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1119–1131. [Google Scholar]
- Hu, C.; Long, T.; Liu, Z.; Zeng, T.; Tian, Y. An Improved Frequency Domain Focusing Method in Geosynchronous SAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5514–5528. [Google Scholar]
- Zhao, B.; Han, Y.; Gao, W.; Luo, Y.; Han, X. A new imaging algorithm for geosynchronous SAR based on the fifth-order Doppler parameters. Prog. Electromagn. Res. B 2013, 55, 195–215. [Google Scholar]
- Zhao, B.; Qi, X.; Song, H.; Wang, R.; Mo, Y.; Zheng, S. An Accurate Range Model Based on the Fourth-Order Doppler Parameters for Geosynchronous SAR. IEEE Geosci. Remote Sens. Lett. 2014, 11, 205–209. [Google Scholar]
- Tian, Y.; Yu, W. Accurate slant range model analysis of geosynchronous SAR. J. Electron. Inf. Technol. 2014, 36, 1960–1965. [Google Scholar]
- Liu, J.; Li, C.; Tan, X.; Shi, P. Characteristics Analysis of “Stop Go Stop” Hypothesis of GEO SAR. Mod. Radar 2014, 36, 38–42. [Google Scholar]
- Zhang, X.; Huang, P.; Wang, W. Equivalent slant range model for geosynchronous SAR. Electron. Lett. 2015, 51, 783–785. [Google Scholar] [CrossRef]
- Liu, Q.; Hong, W.; Tan, W. An improved polar format algorithm with performance analysis for geosynchronous circular SAR 2D imaging. Prog. Electromagn. Res. 2011, 119, 155–170. [Google Scholar] [CrossRef][Green Version]
- Li, Z.; Li, C.; Yu, Z. Back projection algorithm for high resolution GEO-SAR image formation. In Proceedings of the IEEE 2011 International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011. [Google Scholar]
- Yu, Z.; Zhou, Y.; Chen, J.; Li, C. A new satellite attitude steering approach for zero Doppler centroid. In Proceedings of the IET International Radar Conference, Guilin, China, 20–22 April 2009; pp. 1–4. [Google Scholar]
- Long, T.; Dong, X.; Hu, C.; Zeng, T. A New Method of Zero-Doppler Centroid Control in GEO SAR. IEEE Geosci. Remote Sens. Lett. 2011, 8, 512–516. [Google Scholar] [CrossRef]




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Semi-major Axis | 42,164 km | RAAN 1 | 0° |
| Inclination | 53°/7.4° | Argument of Perigee | 270° |
| Eccentricity | 0.07/0.1 | Down Angle | 4.65° |
| PRF | 70 Hz/140 Hz | Wave Length | 0.24 m |
| Bandwidth | 75 MHz /150 MHz | Pulsewidth | 20 μs |
| Range Model | Mean Error (rad) | Max Error (rad) | Standard Deviation (rad) |
|---|---|---|---|
| “Stop-and-go” assumption | 47.29 | 153.72 | 12.79 |
| Fourth-order Taylor expansion | 3.95 | 50.56 | 4.41 |
| Iterative approximation | 1.84 × 10−6 | 1.21 × 10−5 | 1.16 × 10−6 |
| Expansion Order | Mean Error (rad) | Max Error (rad) | Standard Deviation (rad) |
|---|---|---|---|
| Fourth-order | 1.97 | 25.28 | 2.20 |
| Fifth-order | 0.05 | 0.66 | 0.05 |
| Sixth-order | 1.16 × 10−3 | 0.02 | 1.55 × 10−3 |
| Positions (km) | PSLR(dB) | ISLR(dB) | IRW(m) | |||
|---|---|---|---|---|---|---|
| Range | Azimuth | Range | Azimuth | Range | Azimuth | |
| (−20, 20) | −13.29 | −13.29 | −9.97 | −10.54 | 0.88 | 1.13 |
| (−10, −10) | −13.29 | −13.30 | −9.98 | −10.54 | 0.88 | 1.13 |
| (0, 0) | −13.28 | −13.31 | −9.97 | −10.55 | 0.88 | 1.13 |
| (10, 10) | −13.28 | −13.32 | −9.97 | −10.55 | 0.88 | 1.13 |
| (20, −20) | −13.30 | −13.33 | −9.97 | −10.56 | 0.88 | 1.13 |
| Positions (km) | PSLR(dB) | ISLR(dB) | IRW(m) | |||
|---|---|---|---|---|---|---|
| Range | Azimuth | Range | Azimuth | Range | Azimuth | |
| (−20, 20) | −13.30 | −13.19 | −10.07 | −10.55 | 0.88 | 0.76 |
| (−10, −10) | −13.29 | −13.19 | −10.07 | −10.57 | 0.88 | 0.76 |
| (0, 0) | −13.32 | −13.21 | −10.07 | −10.55 | 0.88 | 0.76 |
| (10, 10) | −13.31 | −13.20 | −10.07 | −10.57 | 0.88 | 0.76 |
| (20, −20) | −13.31 | −13.19 | −10.07 | −10.56 | 0.88 | 0.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, B.; Qi, X.; Zhang, H. An Accurate GEO SAR Range Model for Ultralong Integration Time Based on mth-Order Taylor Expansion. Remote Sens. 2021, 13, 255. https://doi.org/10.3390/rs13020255
Zhou B, Qi X, Zhang H. An Accurate GEO SAR Range Model for Ultralong Integration Time Based on mth-Order Taylor Expansion. Remote Sensing. 2021; 13(2):255. https://doi.org/10.3390/rs13020255
Chicago/Turabian StyleZhou, Binbin, Xiangyang Qi, and Heng Zhang. 2021. "An Accurate GEO SAR Range Model for Ultralong Integration Time Based on mth-Order Taylor Expansion" Remote Sensing 13, no. 2: 255. https://doi.org/10.3390/rs13020255
APA StyleZhou, B., Qi, X., & Zhang, H. (2021). An Accurate GEO SAR Range Model for Ultralong Integration Time Based on mth-Order Taylor Expansion. Remote Sensing, 13(2), 255. https://doi.org/10.3390/rs13020255