Abstract
Soil moisture is one of the vital environmental variables in the land–atmosphere cycle. A study of the sensitivity analysis of bistatic scattering coefficients from bare soil at the Ku-band is presented, with the aim of deepening our understanding of the bistatic scattering features and exploring its potential in soil moisture retrieval. First, a well-established advanced integral method was adopted for simulating the bistatic scattering response of bare soil. Secondly, a sensitivity index and a normalized weight quality index were proposed to evaluate the effect of soil moisture on the bistatic scattering coefficient in terms of polarization and angular diversity, and the combinations thereof. The results of single-polarized VV data show that the regions with the maximum sensitivity and high quality index, simultaneously, to soil moisture are in the forward off-specular direction. However, due to the effect of surface roughness and surface autocorrelation function (ACF), the single-polarized data have some limitations for soil moisture inversion. By contrast, the results of two different polarization combinations, as well as a dual-angular simulation of one transmitter and two receivers, show significant estimation benefits. It can be seen that they all provide better ACF suppression capabilities, larger high-sensitivity area, and higher quality indices compared to single-polarized estimation. In addition, dual polarization or dual angular combined measurement provides the possibility of retrieving soil moisture in backward regions. These results are expected to contribute to the design of future bistatic observation systems.
1. Introduction
Soil moisture is a determining variable in earth climate dynamics [1] and plays a necessary essential role in maintaining soil–atmosphere surface energy balance [2], crop yields forecasting [3], hydrology, floods and droughts monitoring [4], and other agricultural and hydrological applications [5,6]. As one of the most important tools for retrieving soil moisture, microwave remote sensing is able to measure the electromagnetic properties of bare soil over large areas under long-term all-weather conditions. Up to now, bistatic radar measurements in soil moisture estimation have mainly been performed in the specular region using the global navigation satellite system (GNSS-R) [7]. For bistatic off-specular regions, the studies mainly oriented on the simulations at the L- or C- band based on different scattering models [8,9]. Zeng [9] illustrated a preliminary understanding of the radar response of bistatic scattering to soil moisture at the L band. However, the sensitivity index used may need further improvement, as it does not consider the effect of small soil moisture and roughness variation. On the other hand, when the changes in absolute values of the scattering coefficients, caused by changes in soil moisture and surface roughness, are extremely small, a sensitivity analysis is not needed. Recently studies show a strong interest to use higher frequencies for surface parameter estimation for example, several microwave emissions have significant soil moisture sensitivity at the C-band, X band, and higher frequencies such as the Advanced Microwave Scanning Radiometer, launched in 2002 [10], and the WindSat radiometer, operating since 2006 [11]. Some researchers proved that the backscattering coefficient at the Ku-band is also effective in soil moisture retrieval. Sano [12] showed that the correlation of backscattering coefficients with volumetric soil moisture is as high as 0.81 at an incidence angle of 35° in the Ku-band (14.85 GHz) (r2 = 0.81, slope = 0.24). Oveisgharan [13] proposed a backscattering format and retrieved soil moisture using HH and VV QuikSCAT (13.4 GHz) backscattered power. The results show that there is almost no correlation between retrieved soil moisture for forested areas because of the big attenuation of the vegetation cover and the less direct backscattering of the ground in the Ku-band. However, as the bare surface fraction increases, the correlation between soil moisture QuikSCAT and WindSat significantly increases and the correlation is up to 0.62 when the bare surface fraction is in the range of 80–90%. According to Ku-band (13.58 GHz) ENVISAT RA-2 data, soil moisture changes from 0.02 to 0.4, resulting in an increase of 5 dB in the backscattering coefficient [14]. Although both simulations and measurements have shown the potential of soil moisture detection at Ku-band monostatic cases, Moran [15] pointed out that the Ku-band backscattering power is more sensitive to ground roughness than soil moisture, which may make it difficult to estimate soil moisture. Thus, more attention should be paid to the bistatic radar simulations and measurements to fully understand the possibility of soil moisture inversion at the Ku-band.
Ku-band (17.2 GHz) KAPRI ground-based radar [16] was originally proposed for operation in differential radar interferometry; however, in addition, it is possible to measure the bistatic scattering response of bare soil. The main objective of this study is to investigate the potential of the bistatic Ku-band ground-based radar for soil moisture retrieval. It should be pointed out that the chosen high frequency of the Ku-band leads to a shallow penetration depth, so the main research focus of this paper is the bare soil surface with low vegetation coverage. The bistatic radar responses of soil moisture in the whole scattering zone were simulated using the advanced integral equation model (AIEM), combined with the local sensitivity analysis, to find the most promising bistatic configurations for soil moisture retrieval. This study is expected to provide a theoretical basis for the subsequent configuration selection of the optimal design of a Ku-band ground-based bistatic instrument.
2. Simulation of Bistatic Scattering Using AIEM
Figure 1 shows the bistatic scattering geometry. An incident plane wave from the incident angle and azimuth angle impinges upon a rough dielectric surface. The upper-medium is assumed to be a free space and the lower medium represents the bare soil with a complex dielectric permittivity ε. The scattered wave is received at a scattering angle and azimuth angle . We set in this paper so the incidence plane is the x-z plane with or and the cross-plane is the y-z plane with or . and are wave vectors of transmitting (incident component) and receiving (scattering component), respectively.
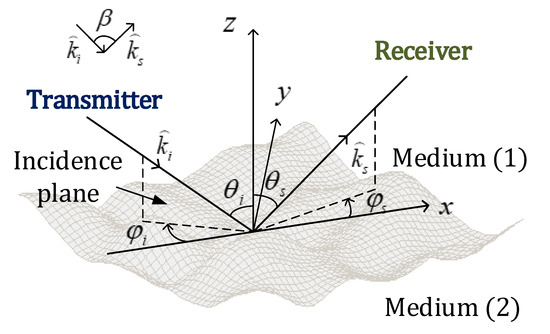
Figure 1.
Bistatic scattering geometry.
Bistatic angle is the angle between two wave vectors derived from the geometric relationship:
The validation and effectiveness of AIEM [17] to simulate the scattering coefficient of the bare soil surface were studied in many previous papers. The surface single-normalized scattering coefficient has three components, namely the Kirchhoff term (k), the cross-term (kc), and the complementary term (c). It can be written as follows:
where q and p denote the transmitting and receiving polarization, respectively. is the wavenumber, are the components of the wave vector along the , , and axes, respectively, in which the subscripts and represent the incident and scattering, respectively. is related to soil dielectric permittivity; W(n) is the Fourier transform of the nth power of the normalized surface correlation function of root-mean-square height and correlation length . Three commonly used autocorrelation functions are Gaussian, exponential, and 1.5 power. Besides, a semiempirical and theoretical dielectric mixing model for 1.4 to 18 GHz was adopted in this paper to link the permittivity to soil moisture [18]. It should be mentioned, except for the region near the null, that for most combinations, the differences of normalized radar cross sections (NRCS) values between the second-order small-slope approximation and the single-scattering AIEM are within ±1 dB [19]. In addition, the good agreement of emissivity between AIEM and numerical Maxwell model of 3-D NMM3D for co-polarization in [20] also verified the model performance with the whole hemisphere. In cross-polarization scattering, the multiple scattering is dominant and the single scattering disappears in the incident plane. Thus, the higher-order solution mainly affects the cross-polarization of the incident surface. In this paper, we just analyze the sensitivity of bistatic co-polarized scattering to soil moisture.
3. Analysis Methodology
3.1. Sensitivity Index
The indices and describe the sensitivity of soil moisture and roughness to the scattering coefficients, respectively:
where and are scattering coefficient changes due to the moisture change and the roughness change , respectively. The higher the values, the stronger the sensitivity, and the more beneficial to high-precision inversion to soil moisture and roughness, respectively. Conversely, it is susceptible to interference from noise background.
3.2. Quality Index
The scattering coefficient of bare soil is mostly affected by two coupling factors at the same time: Moisture and roughness. To invert for soil moisture, eliminating the effect of roughness as much as possible from the scattering coefficient is necessary. The index describes the weight of the effect on the soil moisture-derived scattering coefficient.
The higher the value, the stronger the dependency. and are normalized and are dimensionless. When the index is maximum, soil moisture is the most contributing input variable to the scattering coefficient, and surface roughness () can be considered a noninfluential input. If the surface roughness has a major effect on the output, this value is close to zero. Therefore, for soil moisture retrieval, the optimal estimation is obtained when the sensitivity and the quality index are high.
4. Results and Discussion
In the following results of the unit circle, the x-axis is set to and the y-axis is set to . Thus, the slant angle of each point in the plot is , that is the azimuth angle , and the distance from each point to the origin point is , that is . The left and right semicircles correspond to the backward and the forward scattering space, respectively. The horizontal axis and vertical axis represent the plane of incidence and cross (), respectively. The incident angle is . The specular direction is located on the right side of the horizontal axis, shown as a black solid point, while backscattering is located on the left side and is marked as a white solid point. Let us first review some of the bistatic scattering polarization features. Figure 2 and Figure 3 are bistatic scattering coefficients obtained by changing the soil moisture (5%, 25%, and 45%) for relatively smooth ( and rougher surface conditions, respectively. From the results, it is clearly seen that as soil moisture or roughness increases, the scattering coefficient increases in both the backward and forward directions. The broadening of the lobe under HH polarization is mainly concentrated in the backward direction, while for VV polarization, the broadening of the lobe is mainly concentrated in the forward direction. In addition, the dip moves forward for HH polarization but moves backward for VV polarization, and both become shallower as the soil moisture increases [21]. Then, we conducted a sensitivity analysis with when and (ε = 17.5632 − i9.7983 and ε = 5.8807 − i0.6132, respectively) on a smooth surface () and (ks varies from 0.63 to 2.09) for the dry soil (). We also performed simulations of smaller differences with and . For correlation length , we conducted two sets of the results at different values of correlation length and . From our results, also from [22], has a weaker effect on scattering responses than the ; thus, we fixed it (l = λ) and can simplify the analysis. The qualitative conclusions are similar to those shown here; thus, they are not presented in this paper.
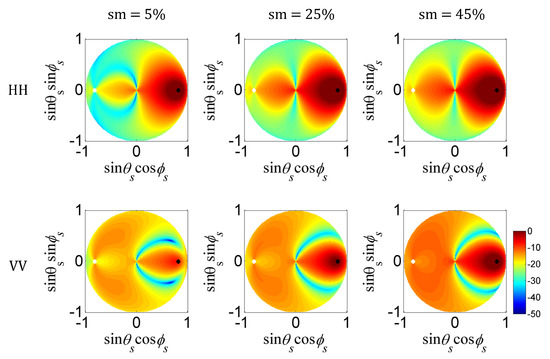
Figure 2.
Patterns of bistatic scattering coefficients for changing the soil moisture (5%, 25%, and 45%) for relatively smooth ( surface.
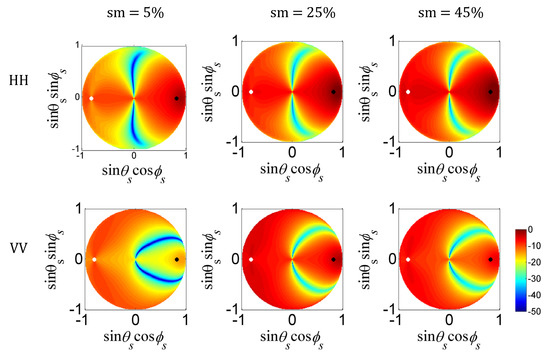
Figure 3.
Patterns of bistatic scattering coefficients for changing the soil moisture (5%, 25%, and 45%) for relatively rough ( surface.
4.1. Single-Polarized Simulation and Choice of Polarization
Figure 4 shows the single-co-polarized (HH or VV) sensitivity to soil moisture obtained at the Ku-band. The sensitivity is strongly dependent on polarizations and bistatic geometry. For HH polarization, the sensitive regions to soil moisture are almost concentrated in the backward direction. For VV polarization, the maximum sensitivity to soil moisture is in the forward off-specular direction, which is higher than that for HH polarization, i.e., . The above results can be explained by the polarization features [23]. Taking the example of VV-polarization, the VV returns vanish along the arc in the forward zone. As soil moisture increases, the pattern gets wider and stronger and the location of VV minima shifts toward the off-specular direction. When observing near the minimum location for dry soil with sm = 10%, the scattering coefficient increases significantly as the soil becomes wetter (sm = 40%) and the minimum region moves. Therefore, we can observe the two off-specular regions with higher sensitivity in the forward zone for the patterns in VV polarization.
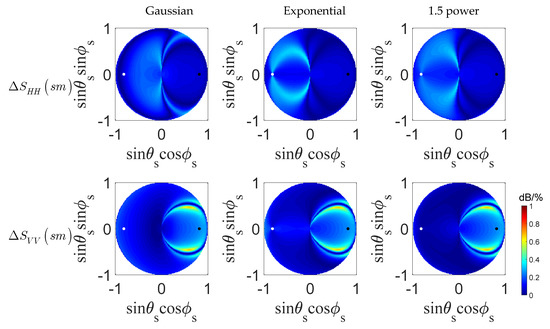
Figure 4.
Patterns of single-co-polarized (HH or VV) sensitivity to soil moisture between 40% and 10%, obtained at Ku band, and .
The feasibility of performing sensitivity analysis on the arcs with the lower power needs to be studied. Figure 5 shows the relationships of bistatic scattering coefficients and (a) soil moisture variations and (b) surface roughness variations, respectively. The geometry is at and , which is near the minimum region for dry soil . To make the results more robust, the average of the bistatic scattering coefficients was calculated based on 100 randomly generated values for surface roughness (ks ~ [0.5, 3]) at a given soil moisture, as seen in Figure 5a, and for soil moisture (sm ~ [0.1, 0.6]) at a given surface roughness, as seen in Figure 5b. From the results, the sensitivity of the HH polarized scattering coefficient to soil moisture is extremely low, and the scattering coefficient is greatly affected by roughness, which is not conducive to the inversion of soil moisture. For VV polarization in Figure 5a, as the soil moisture increases, the scattering coefficients increase. In the case of extremely low signals, and high sensitivity, it is important to be cautions of whether the soil is facing a strong drought. When we detect a strong echo signal and the sensitivity is relatively saturated, we need to be alert to whether the soil is facing the risk of flooding. Except for the above two extreme cases, the change rates of the scattering coefficients corresponding to the medium soil moisture changes are high. In addition, due to the null region changing with the change in soil moisture, as shown in Figure 3, the echo signal from the surface with medium soil moisture also avoids the null regions obtained by sm = 10%, which means configurations in these arcs, as shown in Figure 4, are beneficial to the inversion of soil moisture. From Figure 5b, as the surface roughness increases, the VV-polarized scattering coefficient increases first and then decreases for the exponential autocorrelation function (ACF) or becomes stable for Gaussian and 1.5 power ACFs. This means the effect of roughness is lower than that of soil moisture. Thus, the conclusions of the sensitivity study on the conditions of extremely dry or extremely smooth are versatile, because in most soil conditions, the soil moisture and roughness are at a medium level.
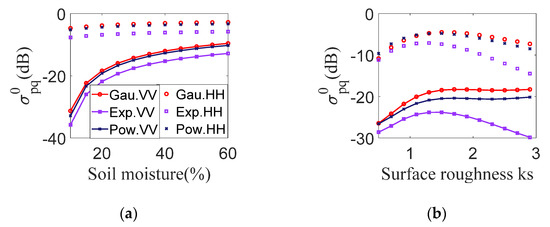
Figure 5.
Variations in bistatic scattering coefficients with (a) soil moisture and (b) surface roughness.
Figure 6 shows the patterns of the single-co-polarized quality index to soil moisture. It can be seen that the high values of the quality index for soil moisture are in the forward zone for both polarizations for Gaussian and 1.5-power ACF, while for exponential ACF, the maximum regions are observed in both the backward and forward scattering zone. For the surface roughness, the quality index is opposite to the distribution of soil moisture, where the regions show the minimum . In this paper, we only describe the situation of soil moisture.
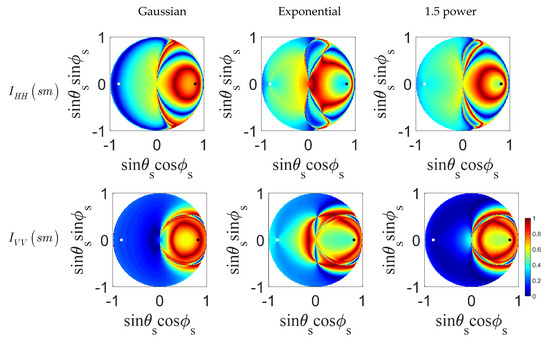
Figure 6.
Patterns of the single-co-polarized (HH or VV) quality index to soil moisture obtained at Ku band, and .
Combining the sensitivity and quality indices, VV polarization is superior to HH polarization in retrieving soil moisture. Therefore, only the results of VV polarization are shown below. For a more intuitive display of the promising configuration, the quality index versus the bistatic angle is shown in Figure 7. The polar axis indicates the quality index and the angle axis represents the bistatic angle. The sensitivity and scattering space of each point are distinguished by different color points. We can see the obvious difference in the distributions under the three ACFs. Before real data are obtained, it is difficult to determine which ACF is closer to the actual surface correlation function. Therefore, the dependence of the results on ACFs should be suppressed as much as possible to reduce errors caused by ACF selection. According to the results in [8], the configurations with the highest sensitivity is chosen using the following parameter set , high quality index , and for all three different ACFs. There are 10 results with and that meet the requirements in the single-polarized case. It can be concluded that single-polarized data are seriously affected by ACF effects, and the number of potential observations obtained is limited.
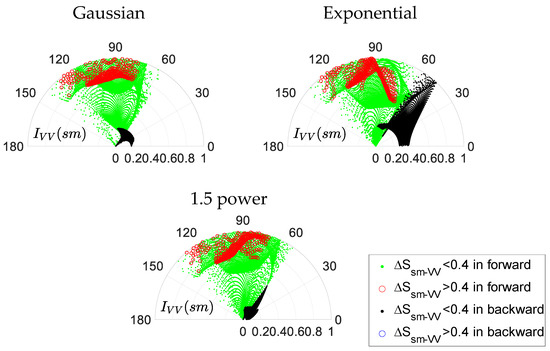
Figure 7.
Distribution of VV-polarized quality index versus bistatic angle with Gaussian, exponential, and 1.5-power autocorrelation functions (ACFs) from left to right, respectively.
4.2. Combination of Dual-Polarized Simulation
In the following, the study with dual polarization is conducted, opening up the observation space to potentially improve the sensitivity to soil moisture estimation.
4.2.1. Dual Polarization Combination Simulation Case 1
Figure 8 shows the dual-polarized sensitivity and quality index. Similar to the results in Figure 6, the maximum sensitivity to soil moisture is obtained in the forward direction. However, we noted a different bistatic responding pattern; the effect of the ACF on the results is effectively suppressed by the combination of dual polarization. It can also be seen that the region with the highest sensitivity and quality at the same time lies in forward off-specular regions. This suggests that these two half-arc regions are beneficial to soil moisture inversion. Besides, compared to the results in the single-polarized case, both indices of sensitivity and quality exhibit increases in the backward region, indicating an improved inversion ability of soil moisture in this area.
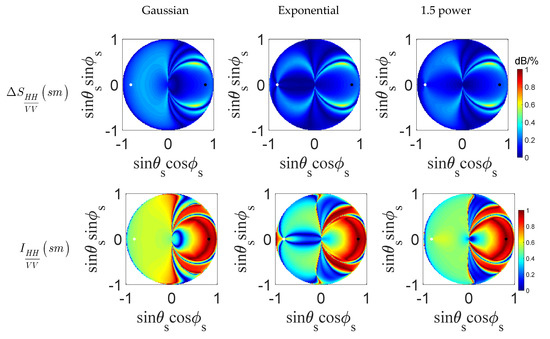
Figure 8.
Patterns of dual-polarized sensitivity to soil moisture between 40% and 10% (first line), and the quality index I (second line).
Figure 9 shows the distributions of the quality index corresponding to the bistatic angle under the dual-polarized case with Gaussian, exponential, and 1.5-power ACFs from left to right. Compared to the results in Figure 5, the differences between the distributions under three ACFs are greatly suppressed. There are 90 result points with and that meet the requirements mentioned in the single-polarized case. Thus, this opens up a range of possible design solutions, and the available angular distribution is more beneficial to the construction of the actual measurement scene than in the single-polarized case.
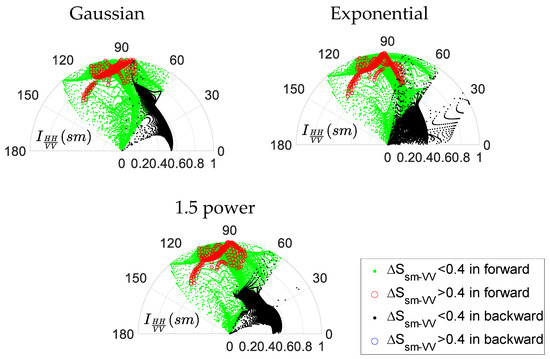
Figure 9.
Distribution of dual-polarized quality index versus bistatic angle with Gaussian, exponential, and 1.5-power ACFs from left to right, respectively.
4.2.2. Dual Polarization Combination Simulation Case 2
To further investigate more favorable combinations of dual-polarized measurements for soil moisture estimation, a sensitivity analysis of was conducted. Figure 10 is identical to Figure 8 except for . From the pattern in Figure 10, the suppression of the ACF effect on the bistatic scattering behavior is further enhanced in the forward region. Compared with case 1, the sensitive region of soil moisture shifts toward the specular area in the forward zone, so its signal level is stronger than that in off-specular regions. Most of the sensitive zones and high-quality zones of soil moisture are overlapped in the forward specular area, which is more conducive to parameter inversion. Again, it is noted that some highly sensitive regions for soil moisture are also observed in the backward direction, which probably enhances the application of the backward configuration in retrieving soil moisture. This can also be confirmed in Figure 11; compared to the results in Figure 9, the regions with high sensitivity and medium quality () can be found in the backward direction shown as the blue circle points, which provides the possibility for soil moisture inversion in the backward regions. Therefore, seems to be a beneficial complement to because of larger sensitive areas, higher ACF effect suppression, and stronger signal level.
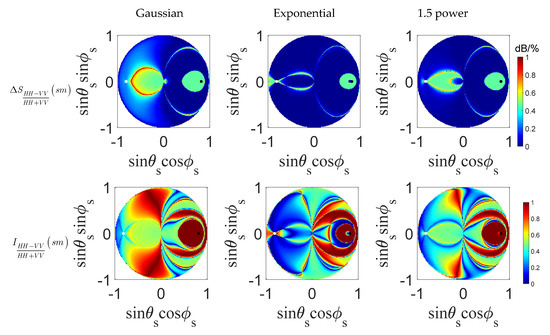
Figure 10.
Patterns of sensitivity to soil moisture between 40% and 10% (first line), and the quality index I (second line).
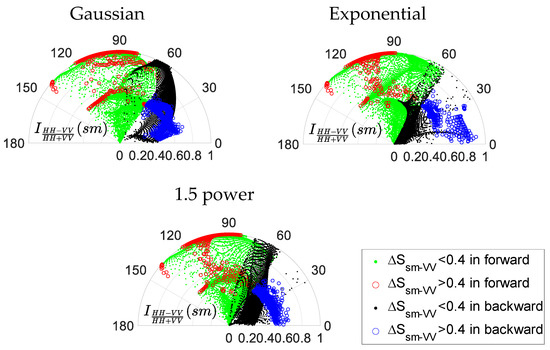
Figure 11.
Distribution of quality index versus bistatic angle.
There are 692 result points with and that meet the requirements mentioned in the single-polarized case. The angular range and the number of options are significantly increased, but it should also be noted that the sensitivity index of most options is at a medium level, i.e., around . Therefore, this combination is more suitable for soil moisture inversion under the requirement of medium sensitivity.
4.3. Combination of Dual-Angular Simulation
Figure 12 shows the dual-angular sensitivity and quality index. The dual-angular configuration consists of a transmitter with and two receivers. Based on the results in the single-polarized case, set the position of one receiver to and , and then find the optimal position of another receiver through simulation. The plots confirm a weak ACF effect on the dual-angle measurement, especially in the forward region, which is consistent with the results of the dual-polarization combination. In addition, the regions with high sensitivity along two off-specular arcs are observed in the forward region. Moreover, medium or even higher quality indices can also be found in the backward zone.
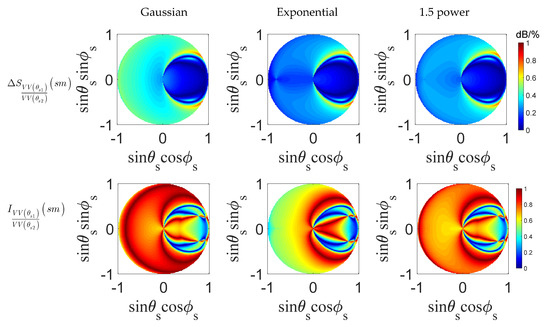
Figure 12.
Patterns of sensitivity to soil moisture between 40% and 10% (first line), and the quality index (second line).
In Figure 13, a large number of red circles lie in the radius range of 0.8–1, which reveals the great advantages of the dual-angle-combined forward scattering coefficient in both, obtaining high sensitivity and high quality index. The distributions of red points are very similar under three ACFs, which suggest a powerful ACF effect suppression ability. Although the sensitivity in the backward zone is medium (around 0.4), the dependence of the combined scattering coefficients on soil moisture is mostly higher than 0.6, which indicates the soil moisture is the main factor affecting combined scattering coefficients. There are 120 satisfying options with and .
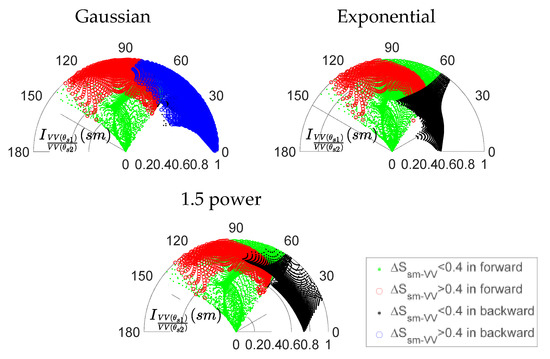
Figure 13.
Distribution of dual-angular quality index versus bistatic angle.
5. Conclusions
Generally, the L- or C- band is more beneficial to soil moisture retrieval. However, L-band bistatic systems have not existed up to now, which brings difficulties to the verification of the theory. Although the Ku-band has a short wavelength and is not ideal for soil moisture retrieval, the moisture content of shallow bare soil can be estimated. In addition, the sensitivity of the soil moisture to the Ku-band can be increased by adjusting the bistatic observation configuration, providing a good theoretical basis for our later ground campaigns. This paper analyzed the sensitivity of the Ku-band scattering coefficient to soil moisture under single-polarized, dual-polarized, and dual-angular combinations. The results show that Ku-band single-polarized data have certain limitations for the retrieval of soil moisture. The influence of ACFs cannot be ignored when using a single-polarized scattering coefficient, but its effects can be suppressed by a combination of dual-polarized or dual-angular measurements. Among the combinations investigated, under medium-sensitivity requirements, is the best choice due to higher ACF effect suppression, stronger signal level, and more options. Dual-angular measurements provide the strongest ACF suppression effect in the forward region. The combinations of or can better meet the requirements of high sensitivity. All three combinations offer the possibility of inversion of soil moisture in the backward direction. Besides, we give a reference range of the receiver angles that can be selected in different combinations when . With only VV polarization, and are suggested. In the case of full polarization, and are suggested, and in the case of two receivers, and are suggested when and . Although we obtain preliminary analysis results to validate the potential bistatic Ku-band KAPRI ground-based radar in bare soil parameter retrieval, the local sensitivity analysis is to identify the soil moisture and roughness for a given set of values. It always ignores the interaction of parameters. Therefore, the global sensitivity analysis should be applied to further explore the promising configuration by varying parameters in a multi-parametric space. In addition, the rough surface we consider is isotropic, and Comite [24] described that the presence of a larger-scale component that produces a backscattering coefficient enhancement greater than 15 dB for the observation direction of tilled rows around 0° and 180° in the case of anisotropic surface. Therefore, the sensitivity analysis of bistatic scattering for soil moisture retrieval under the anisotropic soil condition should be done in the future.
Author Contributions
T.L. conceives methodology, validation, writing manuscript; I.H. reviews, provides scientific inputs, and edits the manuscript, K.-S.C. validates, reviews and edits. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the China Scholarship Council, China and ETH Zurich, Switzerland and in part the Guangxi Natural Science Fund for Innovation Research Team under the grants 2019GXNSFGA245001. And the APC was funded by Guangxi Natural Science Fund for Innovation Research Team under the grants 2019GXNSFGA245001.
Institutional Review Board Statement
Not applicable for studies not involving humans or animals.
Informed Consent Statement
Not applicable for studies not involving humans.
Data Availability Statement
The data presented in this study are generated by the model described in the manuscript. The computer code in Matlab© is available on request from the corresponding author.
Acknowledgments
The authors are indebted to the anonymous reviewers for their valuable comments and suggestions that improve the manuscript. Discussions from Ying Yang has been constructive.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Famiglietti, J.S.; Rudnicki, J.W.; Rodell, M. Variability in surface moisture content along a hillslope transect: Rattlesnake Hill. Texas. J. Hydrol. 1998, 210, 259–281. [Google Scholar] [CrossRef]
- Unninayar, S.; Olsen, L. Monitoring, observations, and remote sensing global dimensions. In Encyclopedia of Ecology; Academic Press: Oxford, UK, 2008; pp. 2425–2446. [Google Scholar] [CrossRef]
- Holzman, M.E.; Rivas, R.; Piccolo, M.C. Estimating soil moisture and the relationship with crop yield using surface temperature and vegetation index. Int. J. Appl. Earth Observ. Geoinf. 2014, 28, 181–192. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil moisture for hydrological applications: Open questions and new opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Sprenger, M.; Leistert, H.; Gimbel, K.; Weiler, M. Illuminating hydrological processes at the soil-vegetation-atmosphere interface with water stable isotopes. Rev. Geophys. 2016, 54, 674–704. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Srivastava, P.K.; Piles, M.; Pearson, S. Earth observation-based operational estimation of soil moisture and evapotranspiration for agricultural crops in support of sustainable water management. Sustainability 2018, 10, 181. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Pablos, M.; Foti, G.; Gommenginger, C.P.; Liu, P.W.; Judge, J. Sensitivity of GNSS-R spaceborne observations to soil moisture and vegetation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 10, 1–13. [Google Scholar] [CrossRef]
- Brigioni, M.; Pettinato, S.; Macelloni, G.; Paloscia, S.; Pampaloni, P.; Pierdicca, N.; Ticconi, F. Sensitivity of bistatic scattering to soil moisture and surface roughness of bare soils. Int. J. Remote Sens. 2010, 31, 4227–4255. [Google Scholar] [CrossRef]
- Zeng, J.Y.; Chen, K.S.; Bi, H.Y.; Chen, Q.; Yang, X.F. Radar response of off-specular bistatic scattering to soil moisture and surface roughness at L-band. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1945–1949. [Google Scholar] [CrossRef]
- Jackson, T.J.; Cosh, M.H.; Bindlish, R.; Stark, P.J.; Bosch, D.D.; Seyfried, M.D.; Goodrich, C.; Moran, M.S.; Du, J. Validation of advanced microwave scanning radiometer soil moisture products. IEEE Trans. Geosci. Remote Sens. 2010, 12, 4256–4272. [Google Scholar] [CrossRef]
- Li, L.; Gaiser, P.W.; Gao, B.C.; Bevilacqua, R.M.; Jackson, T.J.; Njoku, E.G.; Rudiger, C.; Calvet, J.C.; Bindlish, R. WindSat Global Soil Moisture Retrieval and Validation. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2224–2241. [Google Scholar] [CrossRef]
- Sano, E.E.; Moran, M.S.; Huete, A.R.; Miura, T. C and multiangle Ku-band synthetic aperture radar data for bare soil moisture estimation in agricultural areas. Remote Sens. Environ. 1998, 64, 77–90. [Google Scholar] [CrossRef]
- Oveisgharan, S.; Haddad, Z.; Turk, J.; Rodriguez, E.; Li, L. Soil moisture and vegetation water content retrieval using QuikSCAT data. Remote Sens. 2018, 10, 636. [Google Scholar] [CrossRef]
- Fatras, C.; Borderies, P.; Frappart, F.; Mougin, E.; Blumstein, D.; Niño, F. Impact of surface soil moisture variations on radar altimetry echoes at Ku and Ka bands in semi-arid areas. Remote Sens. 2018, 10, 582. [Google Scholar] [CrossRef]
- Moran, M.S.; Vidal, A.; Troufleau, D.; Inoue, Y.; Mitchell, T.A. Ku- and C-Band SAR for Discriminating Agricultural Crop and Soil Conditions. IEEE Trans. Geosci. Remote Sens. 1998, 36, 265–272. [Google Scholar] [CrossRef]
- Baffelli, S.; Frey, O.; Werner, C.; Hajnsek, I. Polarimetric Calibration of the Ku-Band Advanced Polarimetric Radar Interferometer. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2295–2311. [Google Scholar] [CrossRef]
- Chen, K.S.; Wu, T.-D.; Tsang, L.; Li, Q.; Shi, J.; Fung, A.K. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations. I EEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- Peplinski, N.R.; Ulaby, F.T.; Dobson, M.C. Dielectric properties of soils in the 0.3–1.3-GHz range. IEEE Trans. Geosci. Remote Sens. 1995, 33, 803–807. [Google Scholar] [CrossRef]
- Yardim, C.; Johnson, J.T.; Burkholder, R.J.; Teixeira, F.L.; Pierdicca, N. An intercomparison of models for predicting bistatic scattering from rough surfaces. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 2759–2762. [Google Scholar] [CrossRef]
- Zeng, J.Y.; Chen, K.S.; Bi, H.Y.; Zhao, T.J.; Yang, X.F. A comprehensive analysis of rough soil surface scattering and emission predicted by AIEM with comparison to numerical simulations and experimental measurements. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1696–1708. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, K.S.; Liu, Y.; Zeng, J.Y.; Xu, P.; Li, Z.L. On angular features of radar bistatic scattering from rough surface. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3223–3235. [Google Scholar] [CrossRef]
- Pierdicca, N.; Pulvirenti, L.; Ticconi, F.; Brogioni, M. Radar bistatic configurations for soil moisture retrieval: A simulation study. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3252–3264. [Google Scholar] [CrossRef]
- Johnson, J.T.; Ouellette, J. Polarization features in bistatic scattering from rough surfaces. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1616–1626. [Google Scholar] [CrossRef]
- Comite, D.; Pierdicca, N. Monostatic and bistatic scattering modeling of the anisotropic rough soil. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2543–2556. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).