Dynamic Mapping of Subarctic Surface Water by Fusion of Microwave and Optical Satellite Data Using Conditional Adversarial Networks
Abstract
1. Introduction
2. Materials and Methods
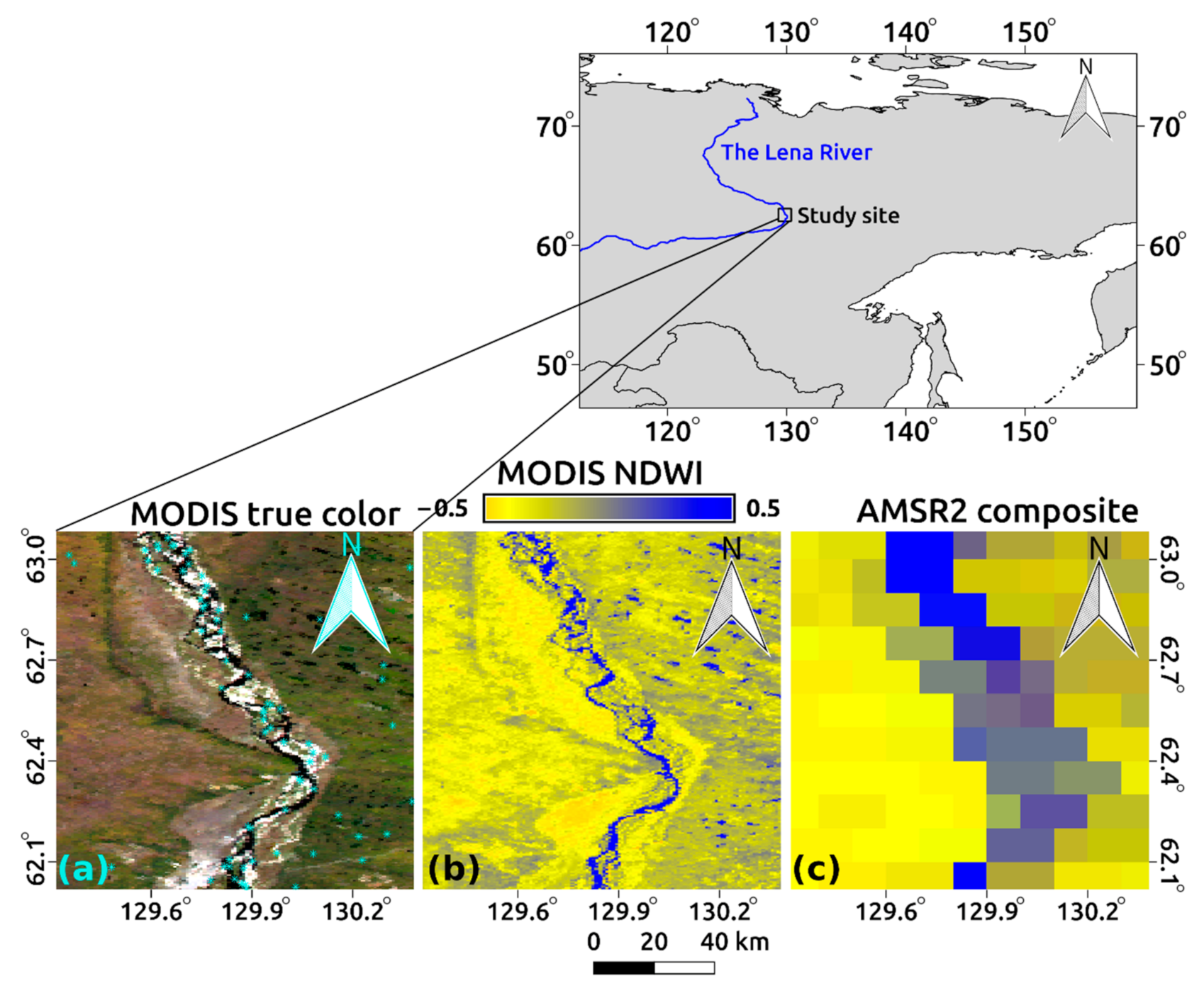
2.1. Study Site and Period
2.2. Data and Preprocessing
2.2.1. Advanced Microwave Scanning Radiometer 2
2.2.2. Moderate Resolution Imaging Spectroradiometer
2.2.3. Ancillary Data
2.2.4. Water Indices
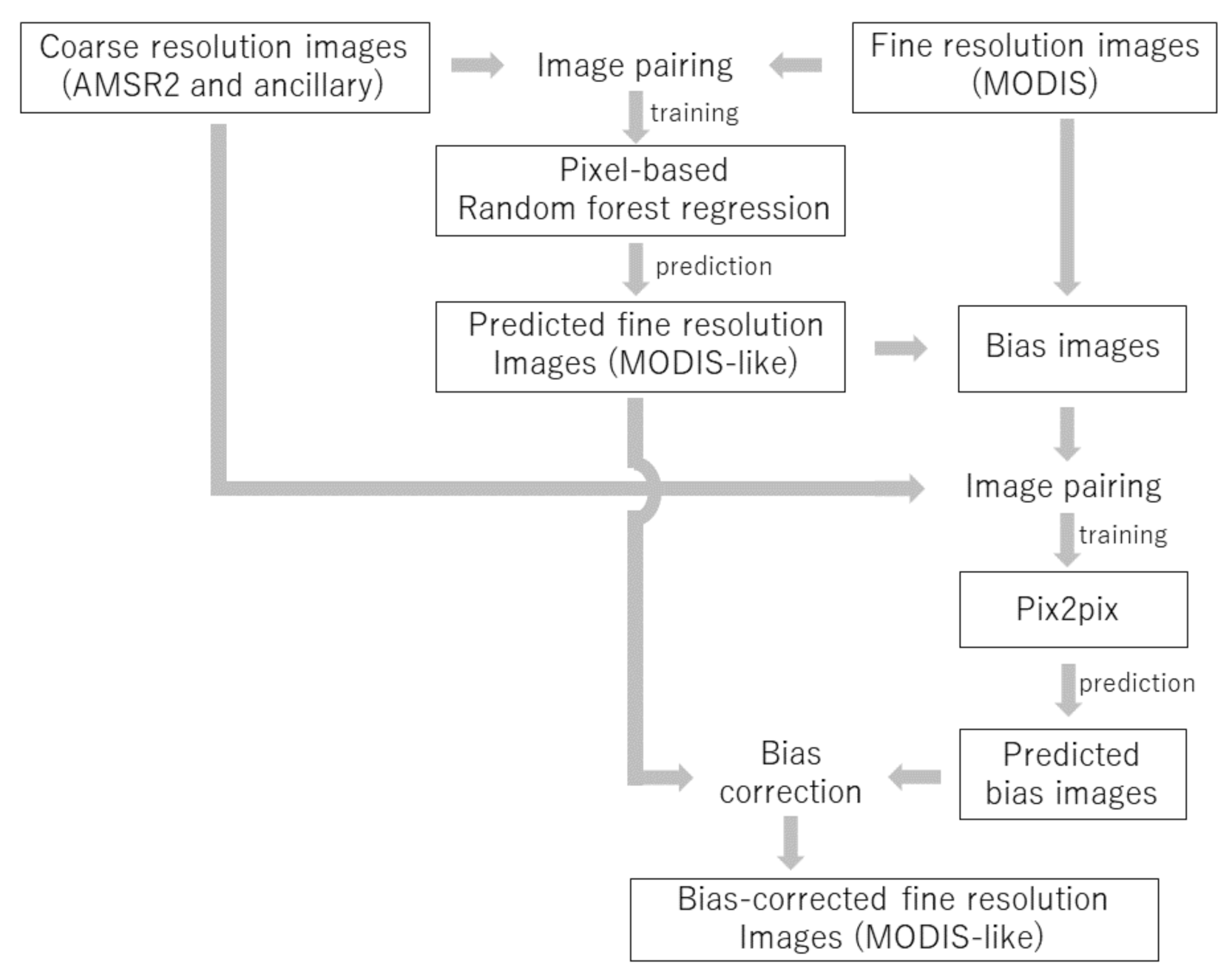
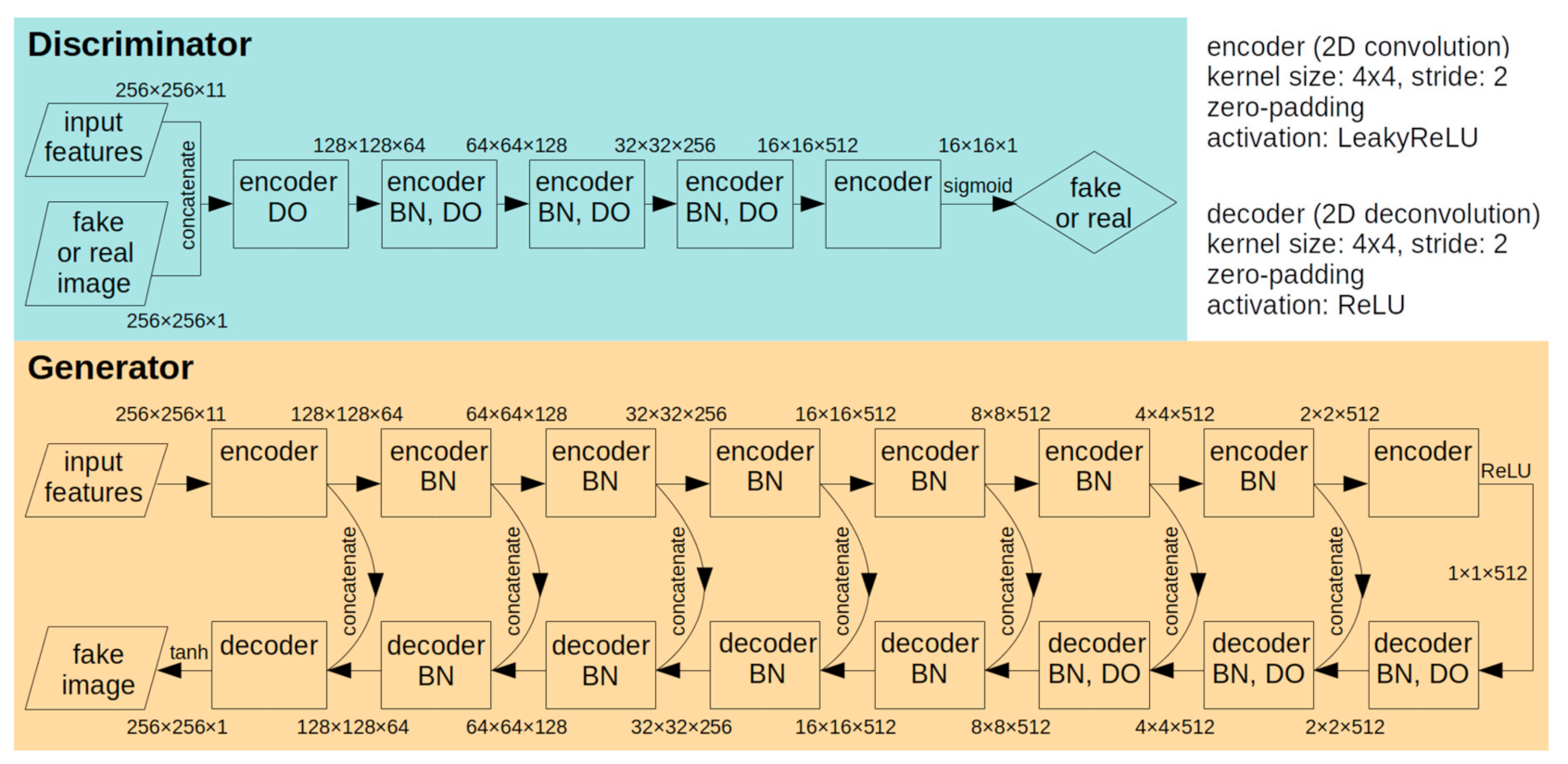
2.3. Machine-Learning Algorithms
2.4. Experiments
2.4.1. Fusion-then-Thresholding vs. Thresholding-then-Fusion
2.4.2. Input-Feature Selection
2.4.3. Validation
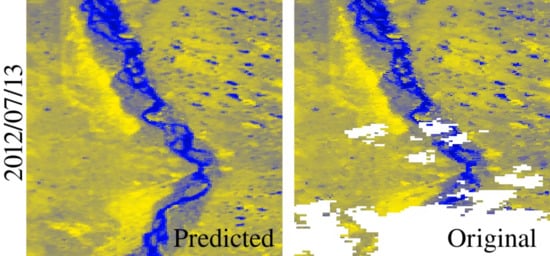
3. Results
3.1. Preliminary Experiments by Random Forest Method
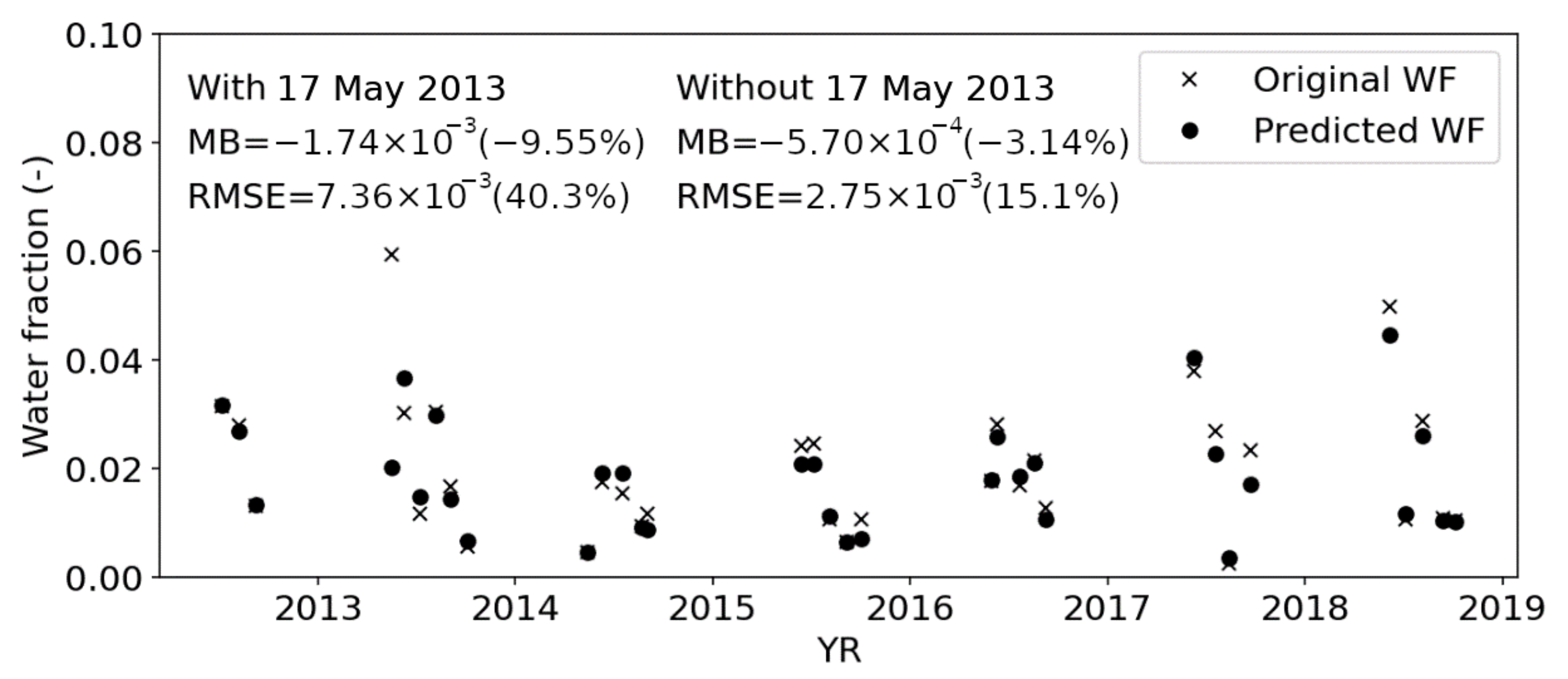
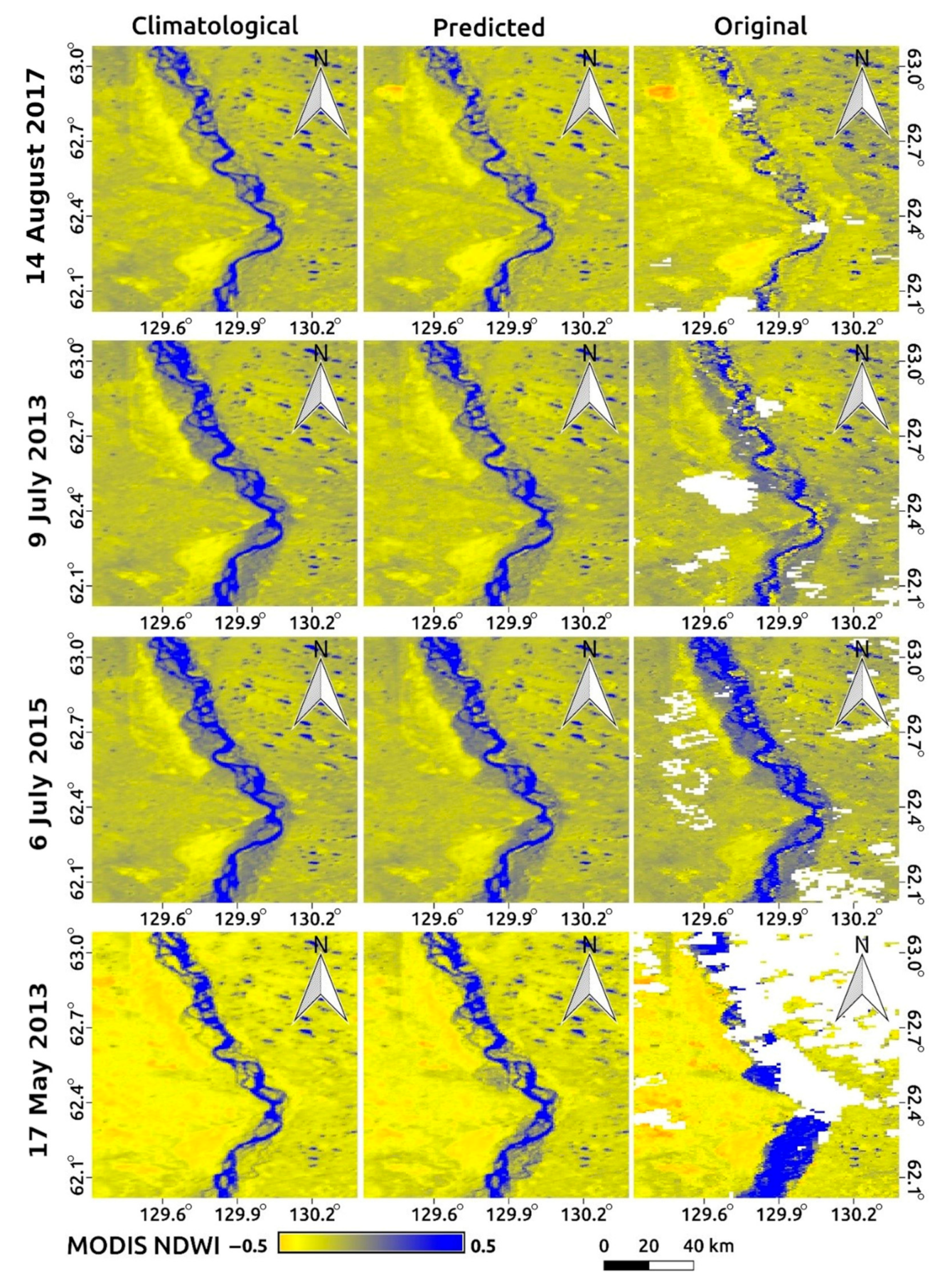
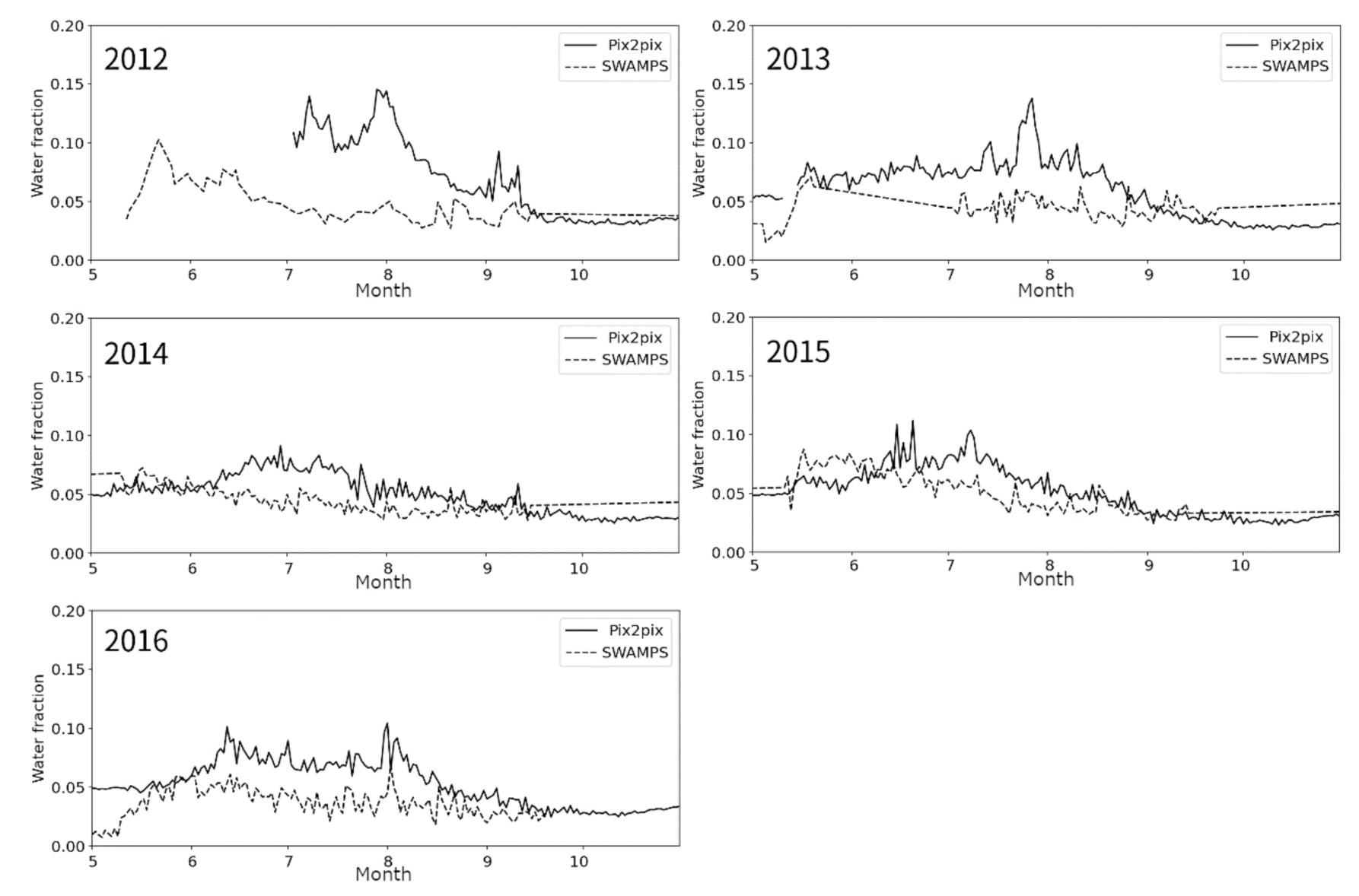
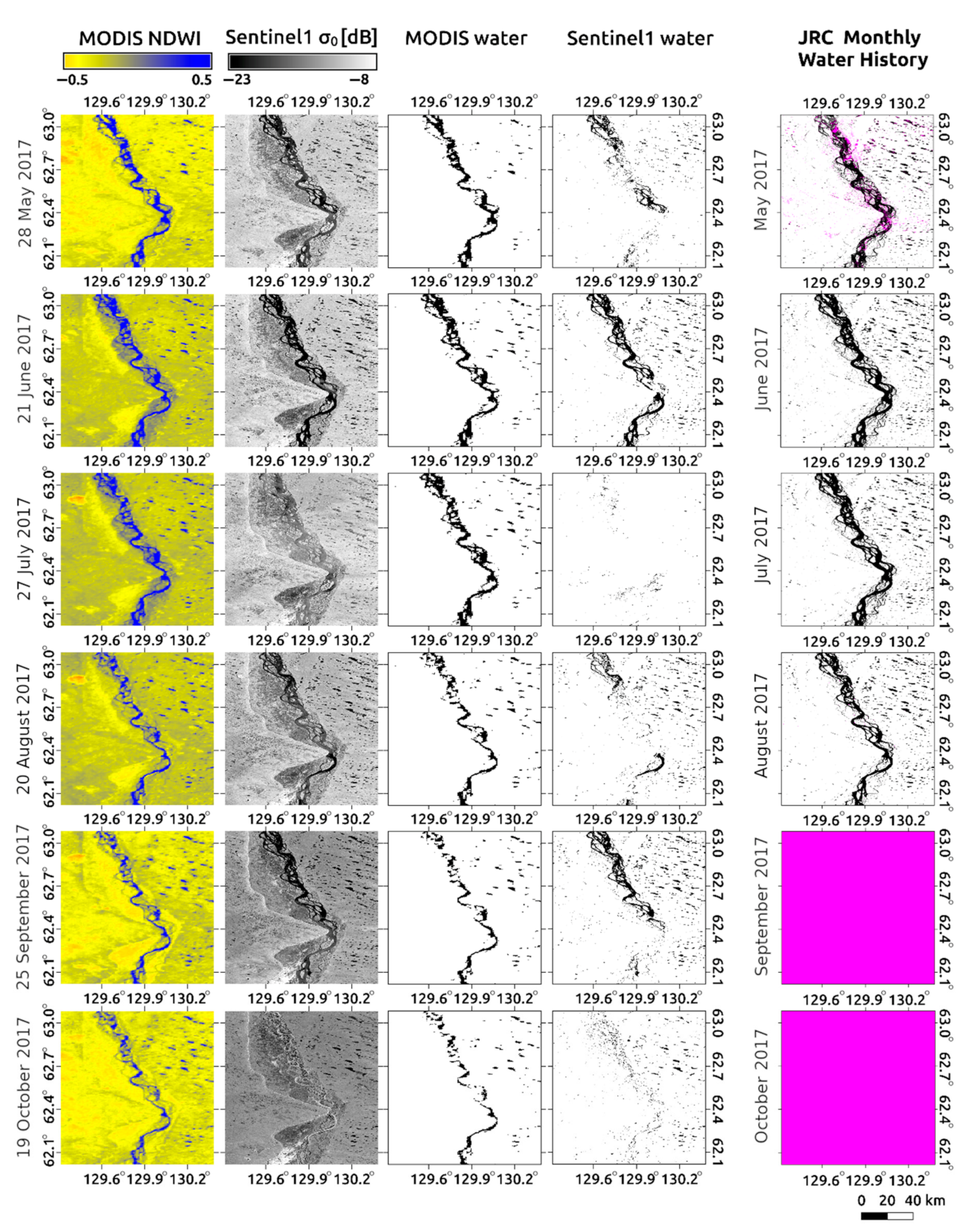
3.2. Overall Performance of the Algorithm
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Snow, Water, Ice and Permafrost in the Arctic (SWIPA) 2017; Arctic Monitoring and Assessment Programme (AMAP): Oslo, Norway, 2017; p. 269. Available online: https://swipa.amap.no/ (accessed on 4 January 2021).
- Suzuki, K.; Matuo, M. Remote sening of Terrestrial Water. In Water-Carbon Dynamics in Eastern Siberia, 1st ed.; Ohta, T., Hiyama, T., Iijima, Y., Kotani, A., Maximov, T.C., Eds.; Springer Nature: Singapore, 2019; pp. 253–277. [Google Scholar]
- Chasmer, L.; Mahoney, C.; Millard, K.; Nelson, K.; Peters, D.L.; Merchant, M.A.; Hopkinson, C.; Brisco, B.; Niemann, K.O.; Montgomery, J.; et al. Remote Sensing of Boreal Wetlands 2: Methods for Evaluating Boreal Wetland Ecosystem State and Drivers of Change. Remote Sens. 2020, 12, 1321. [Google Scholar] [CrossRef]
- Velicogna, I.; Tong, J.; Zhang, T.; Kimball, J.S. Increasing subsurface water storage in discontinuous permafrost areas of the Lena River basin, Eurasia, detected from GRACE. Geophys. Res. Lett. 2012, 39, 09403. [Google Scholar] [CrossRef]
- Suzuki, K.; Hiyama, T.; Matsuo, K.; Ichii, K.; Iijima, Y.; Yamazaki, D. Accelerated continental-scale snowmelt and ecohydrological impacts in the four largest Siberian river basins in response to spring warming. Hydrol. Process. 2020, 34, 3867–3881. [Google Scholar] [CrossRef]
- Yang, D.; Zhao, Y.; Armstrong, R.; Robinson, D.; Brodzik, M.-J. Streamflow response to seasonal snow cover mass changes over large Siberian watersheds. J. Geophys. Res. Space Phys. 2007, 112, F02S22. [Google Scholar] [CrossRef]
- Bartsch, A.; Balzter, H.; George, C. The influence of regional surface soil moisture anomalies on forest fires in Siberia observed from satellites. Environ. Res. Lett. 2009, 4, 045021. [Google Scholar] [CrossRef]
- Watts, J.D.; Kimball, J.S.; Jones, L.A.; Schroeder, R.; McDonald, K.C. Satellite Microwave remote sensing of contrasting surface water inundation changes within the Arctic–Boreal Region. Remote Sens. Environ. 2012, 127, 223–236. [Google Scholar] [CrossRef]
- Guimberteau, M.; Zhu, D.; Maignan, F.; Huang, Y.; Yue, C.; Dantec-Nédélec, S.; Ottlé, C.; Jornet-Puig, A.; Bastos, A.; Laurent, P.; et al. ORCHIDEE-MICT (v8.4.1), a land surface model for the high latitudes: Model description and validation. Geosci. Model Dev. 2018, 11, 121–163. [Google Scholar] [CrossRef]
- Hogstrom, E.; Bartsch, A. Impact of Backscatter Variations Over Water Bodies on Coarse-Scale Radar Retrieved Soil Moisture and the Potential of Correcting With Meteorological Data. IEEE Trans. Geosci. Remote Sens. 2016, 55, 3–13. [Google Scholar] [CrossRef]
- Cherbunina, M.Y.; Shmelev, D.G.; Brouchkov, A.V.; Kazancev, V.S.; Argunov, R.N. Patterns of spatial methane distribution in the upper layers of the permafrost in central Yakutia. Moskow Univ. Geol. Bull. 2018, 73, 100–108. [Google Scholar] [CrossRef]
- Lehner, B.; Döll, P. Development and validation of a global database of lakes, reservoirs and wetlands. J. Hydrol. 2004, 296, 1–22. [Google Scholar] [CrossRef]
- Prigent, C.; Matthews, E.; Aires, F.; Rossow, W.B. Remote sensing of global wetland dynamics with multiple satellite data sets. Geophys. Res. Lett. 2001, 28, 4631–4634. [Google Scholar] [CrossRef]
- Fluet-Chouinard, E.; Lehner, B.; Rebelo, L.-M.; Papa, F.; Hamilton, S.K. Development of a global inundation map at high spatial resolution from topographic downscaling of coarse-scale remote sensing data. Remote Sens. Environ. 2015, 158, 348–361. [Google Scholar] [CrossRef]
- Yamazaki, D.; Trigg, M.A.; Ikeshima, D. Development of a global ~90 m water body map using multi-temporal Landsat images. Remote Sens. Environ. 2015, 171, 337–351. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Curzi, G.; Modenini, D.; Tortora, P. Large constellations of small sateliites: A survey of near future challenges and missions. Aerospace 2020, 7, 133. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F. A cubesat enabled spatio-temporal enhancement method (CESTEM) utilizing Planet, Landsat and MODIS data. Remote Sens. Environ. 2018, 209, 211–226. [Google Scholar] [CrossRef]
- Chen, B.; Huang, B.; Xu, B. Comparison of spatiotemporal fusion models: A review. Remote Sens. 2015, 7, 1798–1835. [Google Scholar] [CrossRef]
- Belgiu, M.; Stein, A. Spatiotemporal image fusion in remote sensing. Remote Sens. 2019, 11, 818. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal MODIS-Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sens. Environ. 2008, 112, 3112–3130. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Gao, F.; Hain, C.R.; Kustas, W.P. Mapping daily evapotranspiration at field scales over rainfed and irrigated agricultural areas using remote sensing data fusion. Agric. For. Meteorol. 2014, 186, 1–11. [Google Scholar] [CrossRef]
- Weng, Q.; Fu, P.; Gao, F. Generating daily land surface temperature at Landsat resolution by fusing Landsat and MODIS data. Remote Sens. Environ. 2014, 145, 55–67. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.S.; Gao, F. A Spatio-Temporal Enhancement Method for medium resolution LAI (STEM-LAI). Int. J. Appl. Earth Obs. Geoinf. 2016, 47, 15–29. [Google Scholar] [CrossRef]
- Li, X.; Long, D. An improvement in accuracy and spatiotemporal continuity of the MODIS precipitable water vapor product based on a data fusion approach. Remote Sens. Environ. 2020, 248, 111966. [Google Scholar] [CrossRef]
- Mizuochi, H.; Nishiyama, C.; Ridwansyah, I.; Nasahara, K.N. Monitoring of an Indonesian tropical wetland by machine learning-based data fusion of passive and active microwave sensors. Remote Sens. 2018, 10, 1235. [Google Scholar] [CrossRef]
- Sahour, H.; Sultan, M.; Vazifedan, M.; Abdelmohsen, K.; Karki, S.; Yellich, J.A.; Gebremichael, E.; Alshehri, F.; Elbayoumi, T.M. Statistical applications to downscale GRACE-derived terrestrial water storage data and to fill temporal gaps. Remote Sens. 2020, 12, 533. [Google Scholar] [CrossRef]
- Mizuochi, H.; Hiyama, T.; Ohta, T.; Nasahara, K.N. Evaluation of the surface water distribution in north-central Namibia based on MODIS and AMSR series. Remote Sens. 2014, 6, 7660–7682. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Isola, P.; Zhu, J.-Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar]
- Wang, X.; Yan, H.; Huo, C.; Yu, J.; Pant, C. Enhancing pix2pix for remote sensing image classification. In Proceedings of the 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 2332–2336. [Google Scholar] [CrossRef]
- Kniaz, V.V. Conditional GANs for semantic segmentation of multispectral satellite images. In Proceedings of the SPIE 10789, Image and Signal Processing for Remote Sensing XXIV, Berlin, Germany, 10–12 September 2018. [Google Scholar]
- Xiong, Y.; Guo, S.; Chen, J.; Deng, X.; Sun, L.; Zheng, X.; Xu, W. Improved SRGAN for remote sensing image super-resolution across locations and sensors. Remote Sens. 2020, 12, 1263. [Google Scholar] [CrossRef]
- Costard, F.; Gautier, E.; Brunstein, D.; Hammadi, J.; Fedorov, A.; Yang, D.; Dupeyrat, L. Impact of the global warming on the fluvial thermal erosion over the Lena River in Central Siberia. Geophys. Res. Lett. 2007, 34, 14501. [Google Scholar] [CrossRef]
- Kirpotin, S.; Polishchuk, Y.; Bryksina, N. Abrupt changes of thermokarst lakes in Western Siberia: Impacts of climatic warming on permafrost melting. Int. J. Environ. Stud. 2009, 66, 423–431. [Google Scholar] [CrossRef]
- Katamura, F.; Fukuda, M.; Bosikov, N.P.; Desyatkin, R.V.; Nakamura, T.; Moriizumi, J. Thermokarst formation and vegetation dynamics inferred from a palynological study in Central Yakutia, Eastern Siberia, Russia. Arct. Antarct. Alp. Res. 2006, 38, 561–570. [Google Scholar] [CrossRef][Green Version]
- Osawa, A.; Zyryanova, O.A.; Matsuura, Y.; Kajimoto, T.; Wein, R.W. (Eds.) Permafrost Ecosystems—Siberian Larch Forests, Ecological Studies; Springer: London, UK, 2010; Volume 2019, pp. 3–15. [Google Scholar]
- Oshima, K.; Tachibana, Y.; Hiyama, T. Climate and year-to-year variability of atmospheric and terrestrial water cycles in the three great Siberian rivers. J. Geophys. Res. Atmos. 2015, 120, 3043–3062. [Google Scholar] [CrossRef]
- GCOM-W1 “SHIZUKU” Data Users Handbook. Japan Aerospace Exploration Agency, January 2013. Available online: https://gportal.jaxa.jp/gpr/assets/mng_upload/GCOM-W/GCOM-W1_SHIZUKU_Data_Users_Handbook_EN.pdf (accessed on 17 December 2020).
- JAXA GPortal. Available online: https://gportal.jaxa.jp (accessed on 3 November 2020).
- LP DAAC Data pool. Available online: https://e4ftl01.cr.usgs.gov/MOLA (accessed on 3 November 2020).
- Petty, G.W. A First Course in Atmospheric Radiation, 2nd ed.; Sundog Publishing: Madison, WI, USA, 2006; p. 100. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalized difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Sippel, S.J.; Hamilton, S.K.; Melack, J.M.; Choudhury, B.J. Determination of inundation area in the Amazon river floodplain using the SMMR 37 GHz polarization difference. Remote Sens. Environ. 1994, 76, 70–76. [Google Scholar] [CrossRef]
- Takeuchi, W.; Gonzalez, L. Blending MODIS and AMSR-E to predict daily land surface water coverage. In Proceedings of the International Remote Sensing Symposium (ISRS), Busan, Korea, 29 October 2009. [Google Scholar]
- Fily, M.; Royer, A.; Goita, K.; Prigent, C. A simple retrieval method for land surface temperature and fraction of water surface determination from satellite microwave brightness temperatures in sub-arctic areas. Remote Sens. Environ. 2003, 85, 328–338. [Google Scholar] [CrossRef]
- Temimi, M.; Leconte, R.; Brissette, F.; Chaouch, N. Flood monitoring over the Mackenzie River Basin using passive microwave data. Remote Sens. Environ. 2005, 98, 344–355. [Google Scholar] [CrossRef]
- Mizuochi, H.; Hiyama, T. Investigation of the ability of a passive microwave sensor to monitor surface water over complex landscape in Eastern Siberia. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, 26 September–2 October 2020; Available online: https://igarss2020.org/ (accessed on 4 January 2021).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Huang, B.; Song, H. Spatiotemporal Reflectance Fusion via Sparse Representation. IEEE Trans. Geosci. Remote. Sens. 2012, 50, 3707–3716. [Google Scholar] [CrossRef]
- Ichii, K.; Ueyama, M.; Kondo, M.; Saigusa, N.; Kim, J.; Alberto, M.C.; Ardö, J.; Euskirchen, E.S.; Kang, M.; Hirano, T.; et al. New data-driven estimation of terrestrial CO2 fluxes in Asia using a standardized database of eddy covariance measurements, remote sensing data, and support vector regression. J. Geophys. Res. Biogeosci. 2017, 122, 767–795. [Google Scholar] [CrossRef]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial- and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Mizuochi, H.; Hiyama, T.; Ohta, T.; Fujioka, Y.; Kambatuku, J.R.; Iijima, M.; Nasahara, K.N. Development and evaluation of a lookup-table-based approach to data fusion for seasonal wetlands monitoring: An integrated use of AMSR series, MODIS, and Landsat. Remote Sens. Environ. 2017, 199, 370–388. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; pp. 33–38. [Google Scholar]
- Schroeder, R.; McDonald, K.C.; Chapman, B.D.; Jensen, K.; Podest, E.; Tessler, Z.D.; Bohn, T.J.; Zimmermann, R. Development and evaluation of a multi-year fractional surface water data set derived from Active/Passive microwave remote sensing data. Remote Sens. 2015, 7, 16688–16732. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Jarihani, A.A.; McVicar, T.R.; Van Niel, T.G.; Emelyanova, I.V.; Callow, J.N.; Johansen, K. Blending Landsat and MODIS data to generate nultispectral indices: A comparison of “index-then-blend” and “blend-then-index” approaches. Remote Sens. 2014, 6, 9213–9238. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of dynamic thresholds for the normalized difference water index. Photogramm. Eng. Rem. S. 2009, 75, 1307–1317. [Google Scholar] [CrossRef]
- Iijima, Y.; Fedorov, A.N. Permafrost-Forest Dynamics. In Water-Carbon Dynamics in Eastern Siberia, 1st ed.; Ohta, T., Hiyama, T., Iijima, Y., Kotani, A., Maximov, T.C., Eds.; Springer: Singapore, 2019; pp. 175–205. [Google Scholar]
- Bosikov, N.P. Evolution of Alases in Central Yakutia; Permafrost Institute, Siverian Division of Russian Academy of Science: Yakutsk, Russia, 1991; p. 127. (In Russian) [Google Scholar]
- Saito, H.; Iijima, Y.; Basharin, N.I.; Fedorov, A.N.; Kunitsky, V.V. Thermokarst development detected from high-definition topographic data in central Yakutia. Remote Sens. 2018, 10, 1579. [Google Scholar] [CrossRef]

| Variables | Abbreviations | Units | Spatial Resolution | Temporal Resolution |
|---|---|---|---|---|
| 2 m temperature | T2M | K | 0.1° × 0.1° | Hourly |
| Skin reservoir content | SRC | m of water equivalent | 0.1° × 0.1° | Hourly |
| Skin temperature | SKT | K | 0.1° × 0.1° | Hourly |
| Snowmelt | SMLT | m of water equivalent | 0.1° × 0.1° | Hourly |
| Soil temperature in layer 1 (0–7 cm) | STL1 | K | 0.1° × 0.1° | Hourly |
| Soil temperature in layer 2 (7–28 cm) | STL2 | K | 0.1° × 0.1° | Hourly |
| Soil temperature in layer 3 (28–100 cm) | STL3 | K | 0.1° × 0.1° | Hourly |
| Soil temperature in layer 4 (100–289 cm) | STL4 | K | 0.1° × 0.1° | Hourly |
| Surface runoff | SRO | m | 0.1° × 0.1° | Hourly |
| Total evaporation | E | m of water equivalent | 0.1° × 0.1° | Hourly |
| Total precipitation | TP | m | 0.1° × 0.1° | Hourly |
| Volumetric soil water in layer 1 (0–7 cm) | SWVL1 | m3/m3 | 0.1° × 0.1° | Hourly |
| Volumetric soil water in layer 2 (7–28 cm) | SWVL2 | m3/m3 | 0.1° × 0.1° | Hourly |
| Volumetric soil water in layer 3 (28–100 cm) | SWVL3 | m3/m3 | 0.1° × 0.1° | Hourly |
| Volumetric soil water in layer 4 (100–289 cm) | SWVL4 | m3/m3 | 0.1° × 0.1° | Hourly |
| Basin aggregated total precipitation | TPAGG | m | Entire basin | Aggregated 1 |
| Basin aggregated snowmelt | SMLTAGG | m of water equivalent | Entire basin | Aggregated 2 |
| Name | Optimizer | Beta 1 | Beta 2 | Learning Rate |
|---|---|---|---|---|
| Generator | Adam | 0.5 | 0.999 | 0.0004 |
| Discriminator | Adam | 0.5 | 0.999 | 0.00002 |
| Case | Input Features |
|---|---|
| 1 | NDPI; FWS18.7, V; FWS36.5, V; BWI |
| 2 | NDPI; FWS18.7, V; FWS36.5, V; BWI; DOYcos and DOYsin |
| 3 | NDPI; FWS18.7, V; FWS36.5, V; BWI; DOYcos and DOYsin; T2M; SRC; SKT; SMLT, STL1, STL2, STL3, STL4; SRO; E; TP; SWVL1, SWVL2, SWVL3, SWVL4; TPAGG; SMLTAGG |
| Case of Input Features | Fusion Target | Relative MB (%) | Relative RMSE (%) | Mean PA (%) | Mean UA (%) | Mean OA (%) |
|---|---|---|---|---|---|---|
| 1 | NDWI map | −10.8 | 41.7 | 82.6 | 83.5 | 99.3 |
| 2 | NDWI map | −9.55 | 41.7 | 83.1 | 85.0 | 99.4 |
| 3 | NDWI map | −9.63 | 40.7 | 83.9 | 85.4 | 99.4 |
| 1 | Water map | −105 | 139 | 43.9 | 85.5 | 98.8 |
| 2 | Water map | −86.7 | 118 | 48.3 | 87.4 | 98.9 |
| 3 | Water map | −87.3 | 119 | 49.2 | 88.3 | 98.9 |
| Rank | Input Features | Variable Importance | Rank | Input Features | Variable Importance | Rank | Input Features | Variable Importance |
|---|---|---|---|---|---|---|---|---|
| 1 | DOYsin | 0.105 | 9 | STL4 | 0.047 | 17 | SKT | 0.033 |
| 2 | DOYcos | 0.096 | 10 | BWI | 0.045 | 18 | TPACC | 0.022 |
| 3 | STL2 | 0.069 | 11 | SWVL3 | 0.044 | 19 | SMLTACC | 0.020 |
| 4 | NDPI | 0.069 | 12 | SWVL2 | 0.043 | 20 | TP | 0.008 |
| 5 | FWS18.7, V | 0.063 | 13 | STL1 | 0.042 | 21 | SRC | 0.007 |
| 6 | SWVL4 | 0.060 | 14 | SWVL1 | 0.041 | 22 | SMLT | 0.003 |
| 7 | E | 0.053 | 15 | STL3 | 0.040 | 23 | SRO | 0.003 |
| 8 | FWS36.5, V | 0.052 | 16 | T2M | 0.036 |
| Rank | Input Features | VIF | Rank | Input Features | VIF | Rank | Input Features | VIF |
|---|---|---|---|---|---|---|---|---|
| 7 | DOYsin | 23.5 | 16 | STL4 | 173.2 | 23 | SKT | 3593.0 |
| 8 | DOYcos | 26.0 | 17 | BWI | 302.1 | 6 | TPACC | 14.4 |
| 20 | STL2 | 1593.1 | 15 | SWVL3 | 153.9 | 5 | SMLTACC | 12.3 |
| 18 | NDPI | 920.5 | 12 | SWVL2 | 127.8 | 4 | TP | 5.7 |
| 10 | FWS18.7, V | 81.8 | 22 | STL1 | 2921.0 | 3 | SRC | 4.5 |
| 11 | SWVL4 | 90.3 | 14 | SWVL1 | 146.2 | 1 | SMLT | 1.4 |
| 9 | E | 51.1 | 13 | STL3 | 135.6 | 2 | SRO | 1.8 |
| 19 | FWS36.5, V | 1202.0 | 21 | T2M | 2172.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mizuochi, H.; Iijima, Y.; Nagano, H.; Kotani, A.; Hiyama, T. Dynamic Mapping of Subarctic Surface Water by Fusion of Microwave and Optical Satellite Data Using Conditional Adversarial Networks. Remote Sens. 2021, 13, 175. https://doi.org/10.3390/rs13020175
Mizuochi H, Iijima Y, Nagano H, Kotani A, Hiyama T. Dynamic Mapping of Subarctic Surface Water by Fusion of Microwave and Optical Satellite Data Using Conditional Adversarial Networks. Remote Sensing. 2021; 13(2):175. https://doi.org/10.3390/rs13020175
Chicago/Turabian StyleMizuochi, Hiroki, Yoshihiro Iijima, Hirohiko Nagano, Ayumi Kotani, and Tetsuya Hiyama. 2021. "Dynamic Mapping of Subarctic Surface Water by Fusion of Microwave and Optical Satellite Data Using Conditional Adversarial Networks" Remote Sensing 13, no. 2: 175. https://doi.org/10.3390/rs13020175
APA StyleMizuochi, H., Iijima, Y., Nagano, H., Kotani, A., & Hiyama, T. (2021). Dynamic Mapping of Subarctic Surface Water by Fusion of Microwave and Optical Satellite Data Using Conditional Adversarial Networks. Remote Sensing, 13(2), 175. https://doi.org/10.3390/rs13020175