Accuracy of Vaisala RS41 and RS92 Upper Tropospheric Humidity Compared to Satellite Hyperspectral Infrared Measurements
Abstract
1. Introduction
2. Data and Methods
2.1. Collocated Radiosonde Launches and Their Collocations with IASI Data
2.2. Methodology
2.2.1. Radiosonde Profile Data Processing
2.2.2. Cloud Screening for IASI Pixels
2.2.3. Consistency of Radiosonde Data with IASI Measurements
2.2.4. Converting the Radiance Difference to RH Difference
3. Results
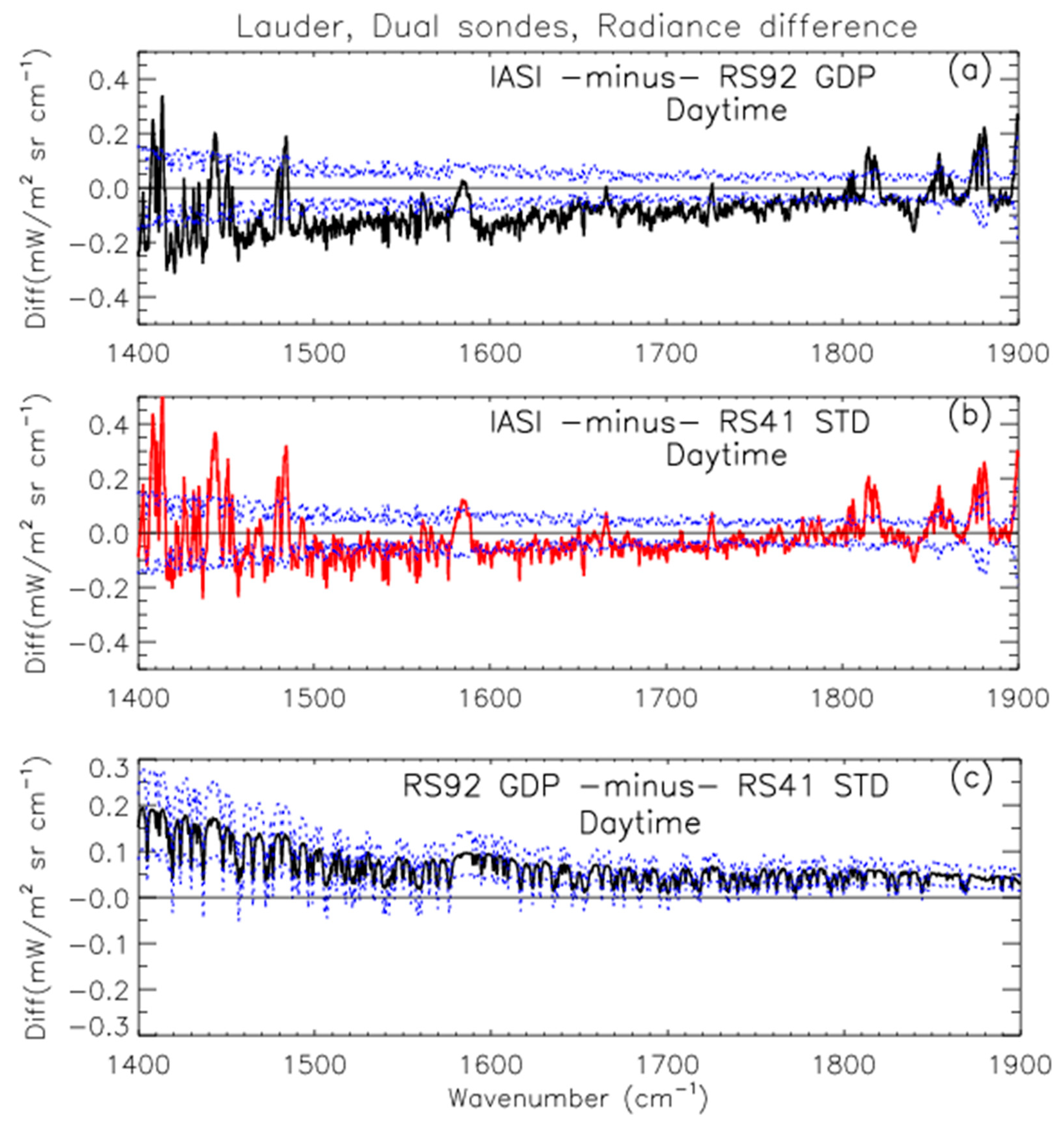
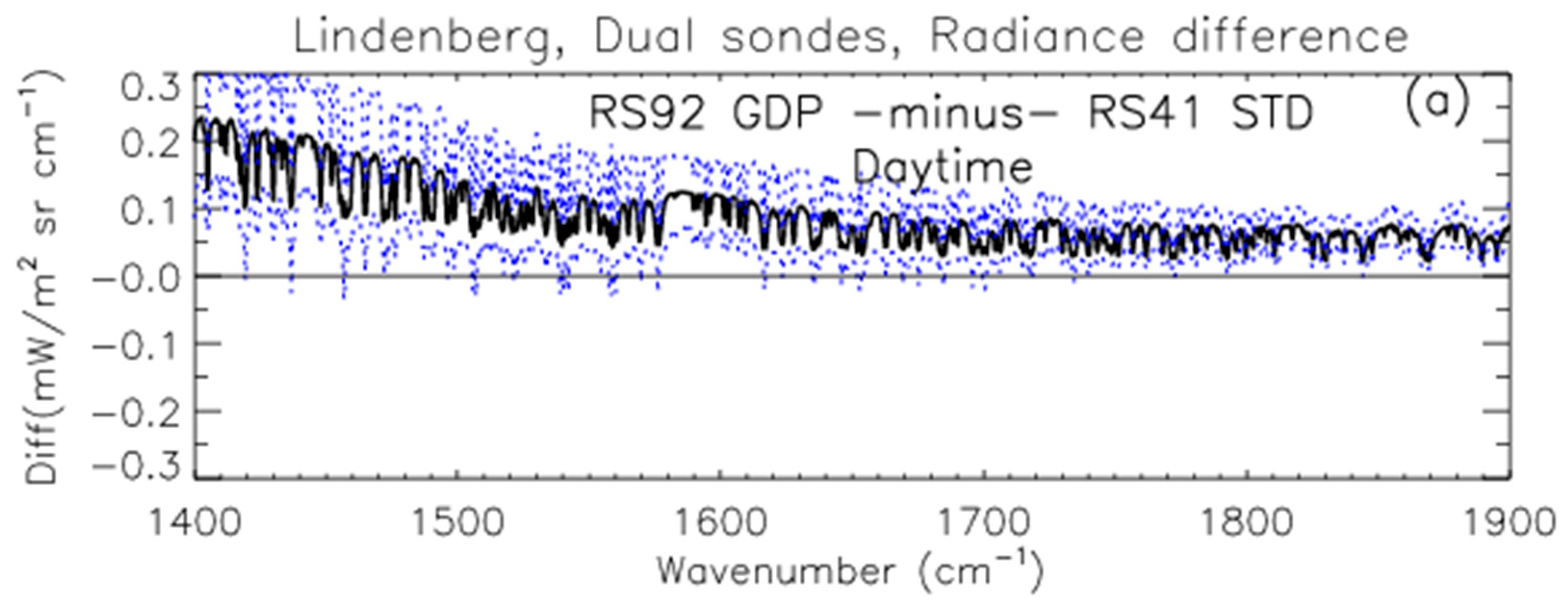
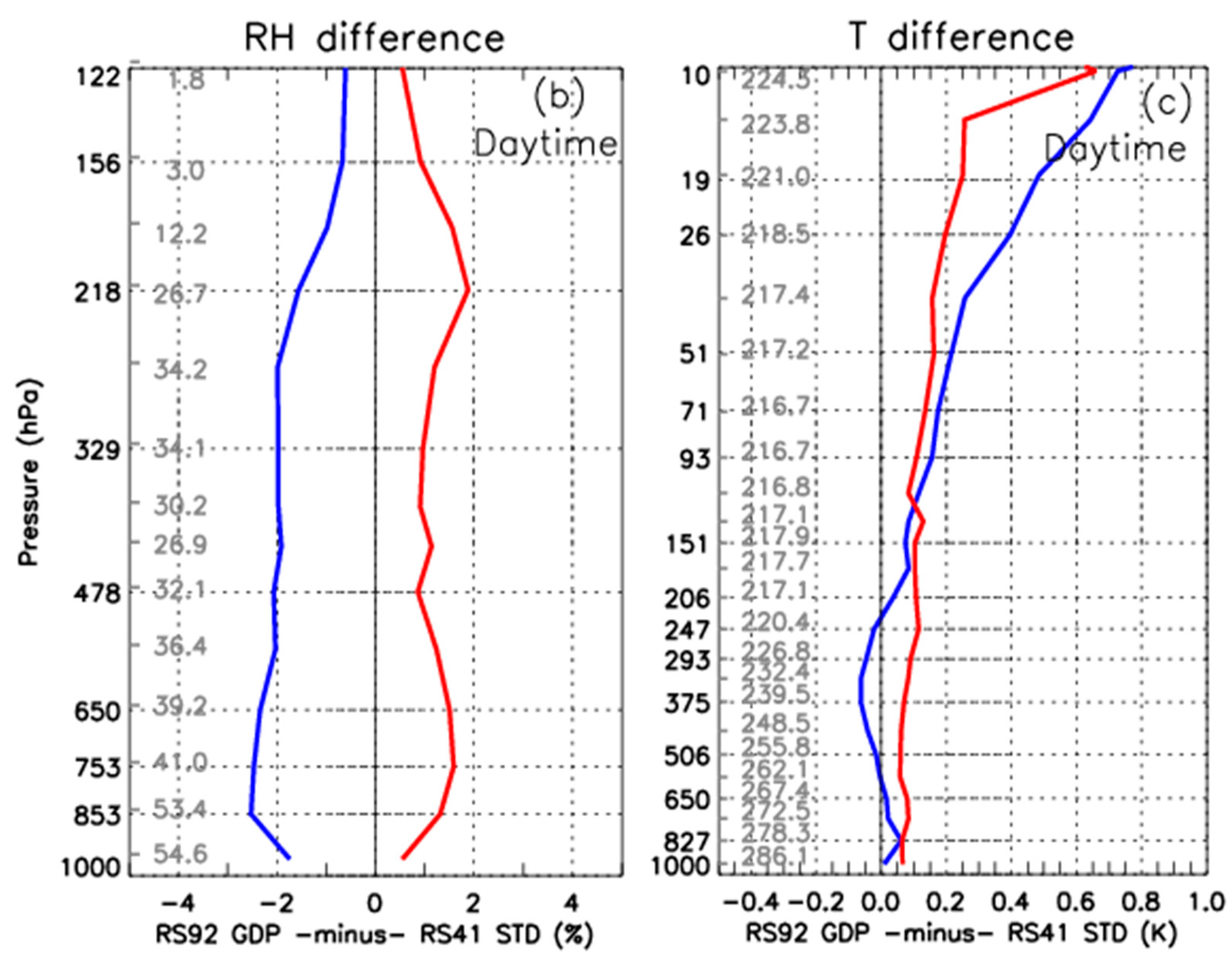
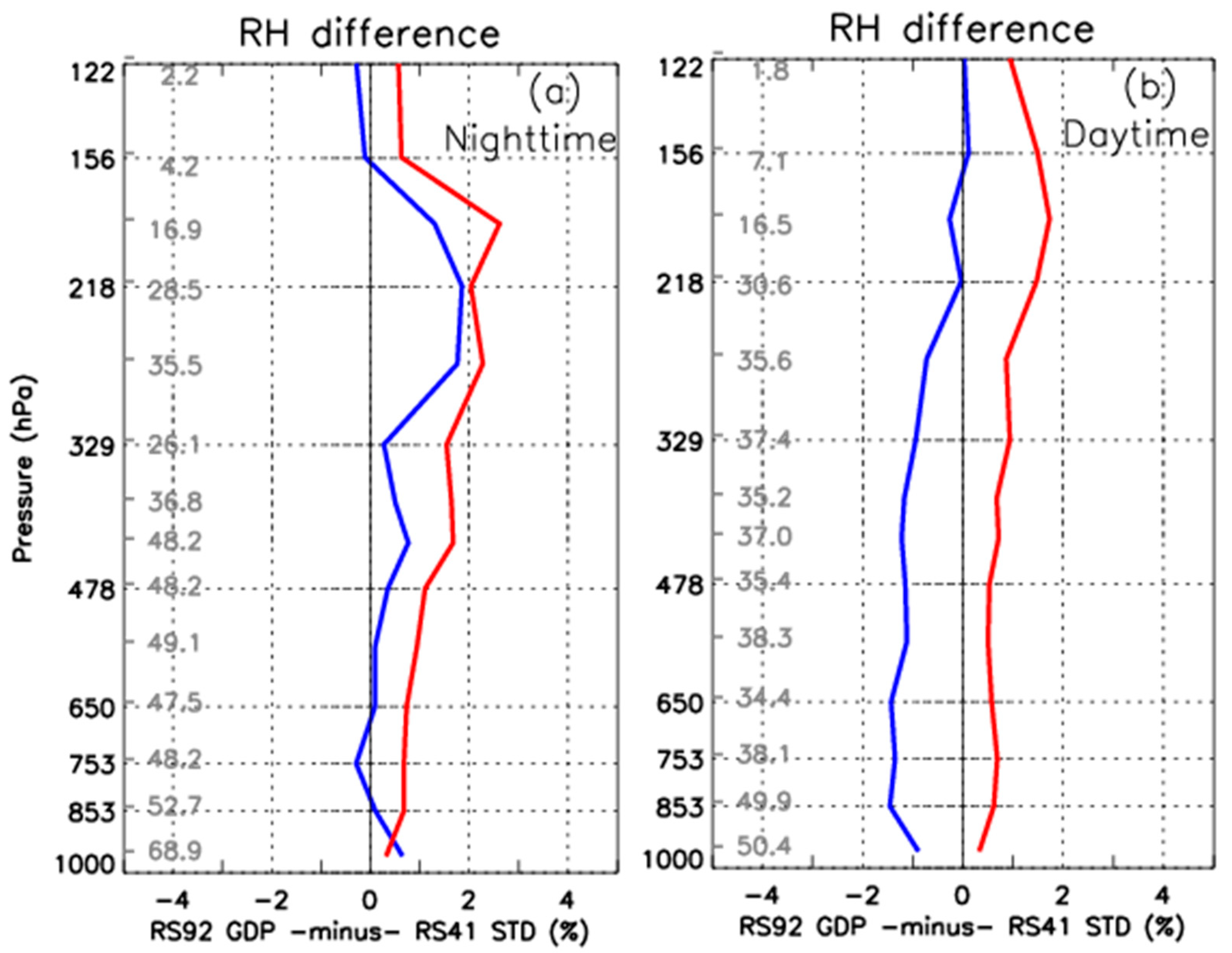
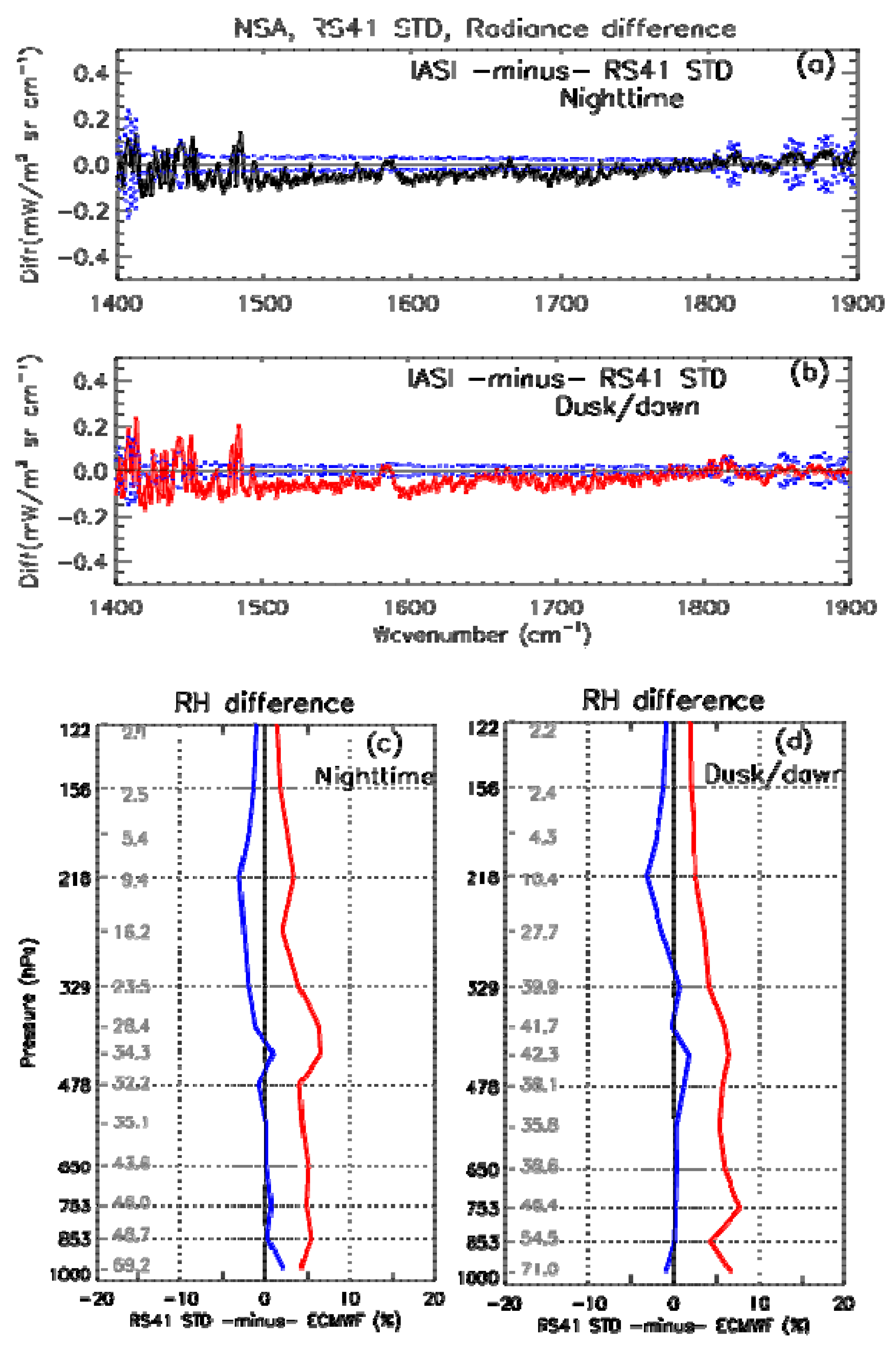
3.1. Dual Launches of RS92 GDP and RS41 STD
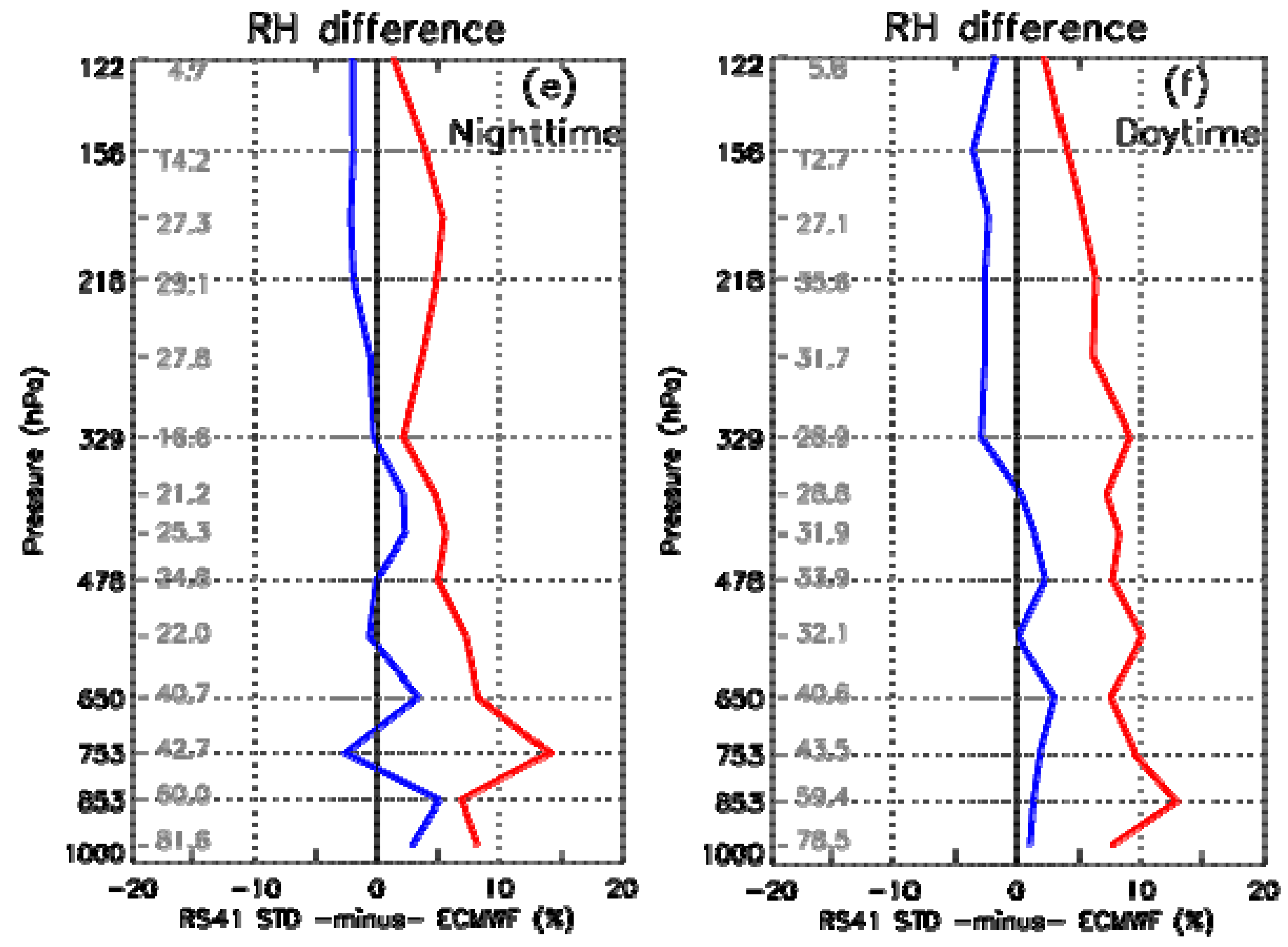
3.2. Single Launches of RS41 STD
3.3. Single Launches of RS92 GDP
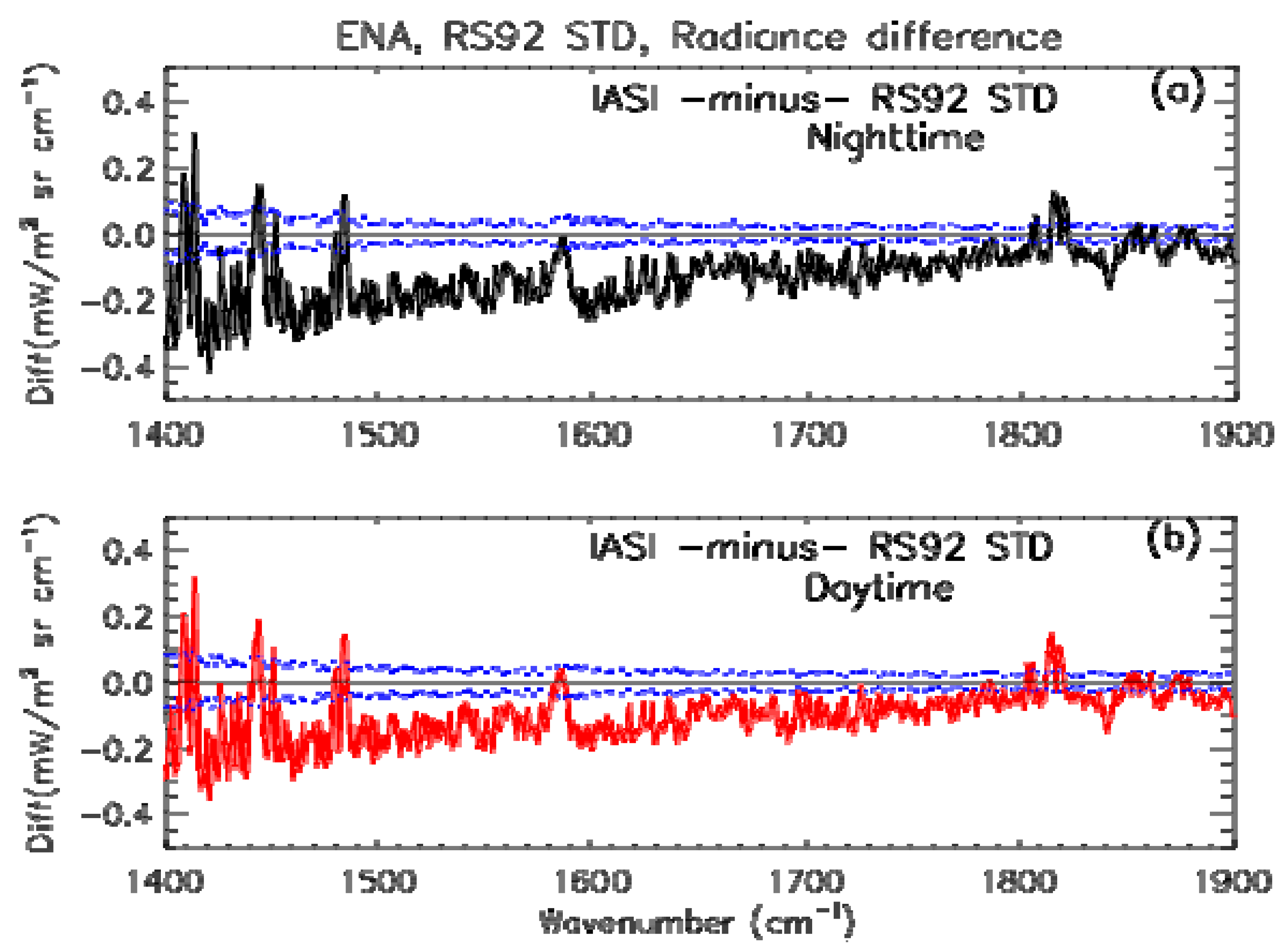
3.4. Single Launches of RS92 STD
4. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Station (RS92 GDP, Single Launches) | OBS-CAL (IASI-RS92 GDP) Radiance Diff 1500–1570 cm−1 | OBS-CAL RH Diff 150–1570 cm−1 | OBS-CAL (IASI-RS92 GDP) Radiance Diff 161–1800 cm−1 | OBS-CAL RH Diff 161–1800 cm−1 |
|---|---|---|---|---|
| ENA (Night) | CLD1 (14) | |||
| −0.0529 (0.057) | 1.17 (1.3) | −0.0301 (0.045) | 1.04 (1.6) | |
| CLD2 (29) | ||||
| −0.0526 (0.099) | 1.17 (2.2) | −0.0323 (0.062) | 1.12 (2.1) | |
| ENA (Day) | CLD1 (21) | |||
| −0.1225 (0.095) | 2.72 (2.1) | −0.0702 (0.074) | 2.43 (2.5) | |
| −0.1174 (0.086) | 2.61 (1.9) | −0.0736 (0.053) | 2.54 (1.8) |
Appendix B


References
- Bodeker, G.E.; Bojinski, S.; Cimini, D.; Dirksen, R.J.; Haeffelin, M.; Hannigan, J.W.; Hurst, D.F.; Leblanc, T.; Madonna, F.; Maturilli, M.; et al. Reference upper-air observations for climate: From concept to reality. Bull. Am. Meteorol. Soc. 2016, 97, 123–135. [Google Scholar] [CrossRef]
- Miloshevich, L.M.; Vömel, H.; Paukkunen, A.; Heymsfield, A.J.; Oltmans, S.J. Characterization and correction of relative humidity measurements from Vaisala RS80-A radiosondes at cold temperatures. J. Atmos. Ocean. Technol. 2001, 18, 135–156. [Google Scholar] [CrossRef]
- Miloshevich, L.M.; Paukkunen, A.; Vömel, H.; Oltmans, S.J. Development and validation of a time-lag correction for Vaisala radiosonde humidity measurements. J. Atmos. Ocean. Technol. 2004, 21, 1305–1327. [Google Scholar] [CrossRef]
- Miloshevich, L.M.; Vömel, H.; Whiteman, D.N.; Lesht, B.M.; Schmidlin, F.J.; Russo, F. Absolute accuracy of water vapor measurements from six operational radiosonde types launched during AWEX-G and implications for AIRS validation. J. Geophys. Res. 2006, 111, D09D10. [Google Scholar] [CrossRef]
- Miloshevich, L.M.; Vömel, H.; Whiteman, D.N.; Leblanc, T. Accuracy assessment and correction of Vaisala RS92 radiosonde water vapor measurements. J. Geophys. Res. 2009, 114, D11305. [Google Scholar] [CrossRef]
- Nash, J.; Oakley, T.; Vömel, H.; Wei, L. WMO Intercomparison of High-Quality Radiosonde Systems, Yangjiang, China, 12 July–3 August 2010. Instruments and Observing Methods Rep. 107 (IOM-107, WMO/TD-No. 1580), 238 pp. World Meteorological Organization: Geneva, 2011. Available online: https://www.wmo.int/pages/prog/www/IMOP/publications/IOM-107_Yangjiang.pdf (accessed on 4 January 2021).
- Vömel, H.; Selkirk, H.; Miloshevich, L.; Valverde-Canossa, J.; Valdés, J.; Kyrö, E.; Kivi, R.; Stolz, W.; Peng, G.; Diaz, J.A. Radiation dry bias of the Vaisala RS92 humidity sensor. J. Atmos. Ocean. Technol. 2007, 24, 953–963. [Google Scholar] [CrossRef]
- Soden, B.J.; Lanzante, J.R. An assessment of satellite and radiosonde climatologies of upper-tropospheric water vapor. J. Clim. 1996, 9, 1235–1250. [Google Scholar] [CrossRef]
- Kottayil, A.; Buehler, S.A.; John, V.O.; Miloshevich, A.M.; Milz, M.; Holl, G. On the importance of Vaisala RS92 radiosonde humidity corrections for a better agreement between measured and modeled satellite radiances. J. Atmos. Ocean. Technol. 2012, 29, 248–259. [Google Scholar] [CrossRef][Green Version]
- Calbet, X.; Kivi, R.; Tjemkes, S.; Montagner, F.; Stuhlmann, R. Matching radiative transfer models and radiosonde data from the EPS/Metop Sodankylä campaign to IASI measurements. Atmos. Meas. Tech. 2011, 4, 1177–1189. [Google Scholar] [CrossRef]
- Moradi, I.; Buehler, S.A.; John, V.O.; Reale, A.; Ferro, R.R. Evaluating instrumental inhomogeneities in global radiosonde upper tropospheric humidity data using microwave satellite data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3615–3624. [Google Scholar] [CrossRef]
- Moradi, I.; Soden, B.; Ferro, R.R.; Arkin, P.; Vömel, H. Assessing the quality of humidity measurements from global operational radiosonde sensors. J. Geophys. Res. Atmos. 2013, 118, 8040–8053. [Google Scholar] [CrossRef]
- Calbet, X.; Peinado-Galan, N.; Ripodas, P.; Trent, T.; Dirksen, R.; Sommer, M. Consistency between GRUAN sondes, LBLRTM and IASI. Atmos. Meas. Tech. 2017, 10, 2323–2335. [Google Scholar] [CrossRef]
- Serio, C.; Masiello, G.; Camy-Peyret, C.; Jacquette, E.; Vandermarcq, O.; Bermudo, F.; Coppens, D.; Tobin, D. PCA determination of the radiometric noise of high spectral resolution infrared observations from spectral residuals: Application to IASI. J. Quant. Spectrosc. Radiat. Transf. 2018, 206, 8–21. [Google Scholar] [CrossRef]
- Clough, S.A.; Shephard, M.W.; Mlawer, E.J.; Delamere, J.S.; Iacono, M.J.; Cady-Pereira, K.; Boukabara, S.; Brown, R.D. Atmospheric radiative transfer modeling: A summary of the AER codes. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 233–244. [Google Scholar] [CrossRef]
- Dirksen, R.J.; Sommer, M.; Immler, F.J.; Hurst, D.F.; Kivi, R.; Vömel, H. Reference quality upper-air measurements, GRUAN data processing for the Vaisala RS92 radiosonde. Atmos. Meas. Tech. 2014, 7, 4463–4490. [Google Scholar] [CrossRef]
- Reale, A.; Sun, B.; Tilley, F.H.; Pettey, M. The NOAA Products Validation System (NPROVS). J. Atmos. Ocean. Tech. 2012, 29, 629–645. [Google Scholar] [CrossRef]
- Sun, B.; Reale, A.; Tilley, F.H.; Pettey, M.; Nalli, N.R.; Barnet, C.D. Assessment of NUCAPS S-NPP CrIS/ATMS sounding products using reference and conventional radiosonde observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1–18. [Google Scholar] [CrossRef]
- Nalli, N.R.; Gambacorta, A.; Liu, Q.; Barnet, C.D.; Tan, C.; Iturbide-Sanchez, F.; Reale, T.; Sun, B.; Wilson, M.; Borg, L.; et al. Validation of atmospheric profile retrievals from the SNPP NOAA-Unique Combined Atmospheric Processing System. Part I: Temperature and moisture. IEEE Trans. Geosci. Remote Sens. 2018, 56, 180–190. [Google Scholar] [CrossRef]
- Nalli, N.R.; Barnet, C.D.; Reale, A.; Tobin, D.; Gambacorta, A.; Maddy, E.S.; Joseph, E.; Sun, B.; Borg, L.; Mollner, A.K.; et al. Validation of satellite sounder environmental data records: Application to the Cross-track Infrared Microwave Sounder Suite. J. Geophys. Res. Atmos. 2013, 118, 13628–13643. [Google Scholar] [CrossRef]
- August, T.; Klaes, D.; Schlüssel, P.; Hultberg, T.; Crapeau, M.; Arriaga, A.; ’Carroll, A.O.; Coppens, D.; Munro, R.; Calbet, X. IASI on Metop-A: Operational level 2 retrievals after five years in orbit. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 1340–1371. [Google Scholar] [CrossRef]
- Sun, B.; Reale, A.; Pettey, M.; Smith, R.; Nalli, N.R.; Zhou, L. Leveraging the strength of dedicated, GRUAN and conventional radiosondes for EUMETSAT IASI atmospheric sounding assessment. In Proceedings of the 2017 EUMETSAT Meteorological Satellite Conference, Rome, Italy, 2–6 October 2017; pp. 1–8. [Google Scholar]
- ECMWF. IFS Documentation CY45r1. ECMWF Rep.; 2018; p. 103. Available online: https://www.ecmwf.int/en/publications/ifs-documentation (accessed on 21 December 2018).
- Eresmaa, R.; McNally, A.P. Diverse Profile Datasets from the ECMWF 137-Level Short-Range Forecasts. NWP Satellite Application Facilities Rep. NWPSAF-EC-TR-017. 2014, p. 12. Available online: https://nwpsaf.eu/oldsite/reports/nwpsaf-ec-tr-017.pdf (accessed on 21 December 2018).
- Hyland, R.; Wexler, A. Formulations for the thermodynamic properties of the saturated phases of H2O from 173.15 K to 473.15 K. ASHRAE Trans. 1983, 89, 500–519. [Google Scholar]
- Tobin, D.C.; Revercomb, H.E.; Knuteson, R.O.; Lesht, B.M.; Strow, L.L.; Hannon, S.E.; Feltz, W.F.; Moy, L.A.; Fetzer, E.J.; Cress, T.S. Atmospheric radiation measurement site atmospheric state best estimates for atmospheric infrared sounder temperature and water vapor retrieval validation. J. Geophys. Res. 2006, 111, D09S14. [Google Scholar] [CrossRef]
- Immler, F.J.; Dykema, J.; Gardiner, T.; Whiteman, D.N.; Thorne, P.W.; Vömel, H. Reference Quality Upper Air Measurements: Guidance for developing GRUAN data products. Atmos. Meas. Tech. 2010, 3, 1217–1231. [Google Scholar] [CrossRef]
- Sun, B.; Reale, A.; Schroeder, S.; Pettey, M.; Smith, R. On the accuracy of Vaisala RS41 versus RS92 upper-air temperature observations. J. Atmos. Ocean. Technol. 2019, 36, 635–653. [Google Scholar] [CrossRef]
- Seidel, D.J.; Sun, B.; Pettey, M.; Reale, A. Global radiosonde balloon drift statistics. J. Geophys. Res. 2011, 116, D07102. [Google Scholar] [CrossRef]
- Sun, B.; Reale, A.; Seidel, D.J.; Hunt, D.C. Comparing radiosonde and COSMIC atmospheric profile data to quantify differences among radiosonde types and the effects of imperfect collocations on comparison statistics. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- EUMETSAT 2014: IASI Level 2: Product Format Specification. Doc. No.: EPS.SYS.SPE.990013, Date: 28 November 2014. Eumetsat-Allee 1, D-64295 Darmstadt, Germany. Available online: https://www.eumetsat.int (accessed on 9 March 2015).



| Launch Types | Station Name (WMO ID) | Radiosonde | Latitude, Longitude (Launch Elevation) | Starting and Ending Date | Number of Soundings [Time Collocation Limits] |
|---|---|---|---|---|---|
| RS92 and RS41 dual launches | Lauder, New Zealand (93817) | RS92 GDP, RS41 STD | 45.0376°S 169.6826°E (370 m) | Nov 2015 to Nov 2016 | 14 (26) [0~+1 h] |
| Lindenberg, Germany (10393) | RS92 GDP, RS41 STD | 52.2094°N 14.1203°E (115 m) | Dec 2014 to Oct 2017 | 29 (152) [+1~+3 h] | |
| Payerne, Switzerland (06610) | RS92 GDP, RS41 STD | 46.8131°N 6.9437°E (490.5 m) | Aug 2014 to Oct 2017 | 19 (86) [+1~+3 h] | |
| RS92 or RS41 single launches | Eastern North Atlantic (ENA), Graciosa, Azores (08507) | RS41 STD RS92 GDP RS92 STD | 39.0912°N 28.0263°W (31 m) | Jan 2015 to May 2020 | 225 (1297) [−30~+15 min] |
| North Slope Alaska (NSA), Barrow (Utqiaġvik) (70027) | RS41 STD RS92 GDP | 71.3226°N 156.6180°W (8 m) | Jan 2015 to May 2020 | 122 (978) [−30~+15 min] | |
| Ny Alesund, Norway (01004) | RS41 STD RS92 GDP | 78.9230°N 11.9225°E (15.5 m) | May 2015 to May 2020 | 45 (900) [−30~+15 min] |
| Station (Dual Launches) | OBS-CAL Radiance Diff 1500–1570 cm−1 | OBS-CAL RH Diff 1500–1570 cm−1 | OBS-CAL Radiance Diff 1615–1800 cm−1 | OBS-CAL RH Diff 1615–1800 cm−1 | Direct Obs RH Diff 200.9–407.4 hPa |
|---|---|---|---|---|---|
| Lauder (day, 14) | IASI-RS92 GDP | ||||
| −0.1291 (0.085) | 2.86 (1.9) | −0.0818 (0.059) | 2.82 (2.0) | ||
| IASI-RS41 STD | |||||
| −0.0705 (0.081) | 1.56 (1.8) | −0.0386 (0.057) | 1.33 (2.0) | ||
| RS92-RS41 | |||||
| 0.0585 (0.029) | −1.30 (0.6) | 0.0431 (0.019) | −1.49 (0.7) | −1.33 (0.8) | |
| Lindenberg (day, 19) | IASI-RS92 GDP | ||||
| −0.2204 (0.107) | 4.89 (2.4) | −0.1447 (0.082) | 5.00 (2.8) | ||
| IASI-RS41 STD | |||||
| −0.1307 (0.103) | 2.90 (2.3) | −0.0841 (0.080) | 2.90 (2.8) | ||
| RS92-RS41 | |||||
| 0.0897 (0.044) | −1.99 (1.0) | 0.0606 (0.031) | −2.09 (1.1) | −1.91 (1.2) | |
| Payerne (night, 10) | IASI-RS92 GDP | ||||
| −0.1160 (0.196) | 2.57 (4.3) | −0.0847 (0.135) | 2.92 (4.7) | ||
| IASI-RS41 STD | |||||
| −0.1318 (0.182) | 2.93 (4.0) | −0.0894 (0.126) | 3.09 (4.4) | ||
| RS92-RS41 | |||||
| −0.0158 (0.055) | 0.35 (1.2) | −0.0047 (0.033) | 0.16 (1.1) | 1.13 (1.9) | |
| Payerne (day, 9) | IASI-RS92 GDP | ||||
| −0.1578 (0.131) | 3.50 (2.9) | −0.0741 (0.108) | 2.56 (3.7) | ||
| IASI-RS41 STD | |||||
| −0.1073 (0.130) | 2.38 (2.9) | −0.0423 (0.108) | 1.46 (3.7) | ||
| RS92-RS41 | |||||
| 0.0505 (0.042) | −1.12 (0.9) | 0.0319 (0.027) | −1.10 (0.9) | −0.73 (1.0) |
| Station (RS41 STD Single Launches) | OBS-CAL Radiance Diff 1500–1570 cm−1 | OBS-CAL RH Diff 1500–1570 cm−1 | OBS-CAL Radiance Diff 1615–1800 cm−1 | OBS-CAL RH Diff 1615–1800 cm−1 | Direct Obs RH Diff 200.9–407.4 hPa |
|---|---|---|---|---|---|
| ENA (night, 12) | IASI-RS41 STD | ||||
| −0.0528 (0.054) | 1.18 (1.2) | −0.0334 (0.039) | 1.15 (1.3) | ||
| IASI-ECMWF | |||||
| 0.0131 (0.057) | −0.29 (1.3) | −0.0081 (0.042) | 0.28 (1.4) | ||
| RS41-ECMWF | −1.46 (1.2) | 0.0253 (0.043) | |||
| 0.0659 (0.053) | −0.87 (1.5) | −0.42 (3.5) | |||
| ENA (day, 27) | IASI-RS41 STD | ||||
| −0.0633 (0.042) | 1.41 (0.9) | −0.0370 (0.028) | 1.28 (1.0) | ||
| IASI-ECMWF | |||||
| 0.0238 (0.063) | −0.53 (1.4) | 0.0070 (0.054) | −0.24 (1.9) | ||
| RS41-ECMWF | |||||
| 0.0871 (0.065) | −1.93 (1.4) | 0.0440 (0.053) | −1.52 (1.8) | −2.38 (7.2) | |
| NSA (night, 29) | IASI-RS41 STD | ||||
| −0.0610 (0.057) | 1.35 (1.3) | −0.0356 (0.032) | 1.23 (1.1) | ||
| IASI-ECMWF | |||||
| −0.0052 (0.065) | 0.11 (1.4) | −0.0117 (0.038) | 0.41 (1.3) | ||
| RS41-ECMWF | |||||
| 0.0558 (0.046) | −1.23 (1.0) | 0.0239 (0.027) | −0.83 (0.9) | −2.34 (3.4) | |
| NSA (dusk/dawn, 36) | IASI-RS41 STD | ||||
| −0.0662 (0.027) | 1.47 (0.6) | −0.0416 (0.022) | 1.44 (0.8) | ||
| IASI-ECMWF | |||||
| −0.0338 (0.037) | 0.75 (0.8) | −0.0261 (0.030) | 0.90 (1.0) | ||
| RS41-ECMWF | |||||
| 0.0324 (0.043) | −0.72 (1.0) | 0.0155 (0.031) | −0.54 (1.1) | −1.00 (3.8) | |
| Ny Alesund (dusk/dawn, 12) | IASI-RS41 STD | ||||
| −0.0593 (0.047) | 1.31 (1.0) | −0.0372 (0.026) | 1.28 (0.9) | ||
| IASI-ECMWF | |||||
| −0.0012 (0.082) | 0.03 (1.9) | −0.0047 (0.066) | 0.16 (2.3) | ||
| RS41-ECMWF | |||||
| 0.0580 (0.096) | −1.29 (2.1) | 0.0324 (0.068) | −1.12 (2.4) | −2.41 (4.0) | |
| Ny Alesund (day, 15) | IASI-RS41 STD | ||||
| −0.0977 (0.061) | 2.17 (1.4) | −0.0422 (0.038) | 1.46 (1.3) | ||
| IASI-ECMWF | |||||
| −0.0065 (0.057) | 0.14 (1.3) | −0.0008 (0.041) | 0.28 (1.4) | ||
| RS41-ECMWF | |||||
| 0.0912 (0.067) | −2.02 (1.5) | 0.0414 (0.045) | −1.43 (1.5) | −0.66 (5.8) |
| Station (RS92 GDP Single Launches) | OBS-CAL Radiance Diff 1500–1570 cm−1 | OBS-CAL RH Diff 1500–1570 cm−1 | OBS-CAL Radiance Diff 1615–1800 cm−1 | OBS-CAL RH Diff 1615–1800 cm−1 | Direct obs RH Diff 200.9–407.4 hPa |
|---|---|---|---|---|---|
| ENA (night, 43) | IASI-RS92 GDP | ||||
| −0.0527 (0.088) | 1.17 (1.9) | −0.0316 (0.057) | 1.09 (2.0) | ||
| IASI-ECMWF | |||||
| 0.0471 (0.115) | −1.04 (2.6) | 0.0208 (0.082) | −0.72 (2.8) | ||
| RS92-ECMWF | |||||
| 0.0998 (0.134) | −2.21 (3.0) | 0.0524 (0.093) | −1.81 (3.2) | −0.43 (8.4) | |
| ENA (day, 50) | IASI-RS92 GDP | ||||
| −0.1196 (0.090) | 2.65 (2.0) | −0.0722 (0.063) | 2.49 (2.2) | ||
| IASI-ECMWF | |||||
| 0.0097 (0.096) | −0.22 (2.2) | −0.011 (0.078) | 0.36 (2.7) | ||
| RS92-ECMWF | |||||
| 0.1293 (0.127) | −2.87 (2.8) | 0.0617 (0.092) | −2.13 (3.2) | −1.90 (6.1) | |
| NSA (night, 10) | IASI-RS92 GDP | ||||
| −0.0596 (0.063) | 1.32 (1.4) | −0.0396 (0.036) | 1.37 (1.2) | ||
| IASI-ECMWF | |||||
| −0.0043 (0.095) | 0.10 (2.1) | −0.0135 (0.055) | 0.47 (1.9) | ||
| RS92-ECMWF | |||||
| 0.0553 (0.086) | −1.23 (1.9) | 0.0260 (0.055) | −0.89 (1.9) | −3.65 (5.4) | |
| NSA (day, 5) | IASI-RS92 GDP | ||||
| −0.0924 (0.039) | 2.05 (0.9) | −0.0554 (0.019) | 1.91 (0.7) | ||
| IASI-ECMWF | |||||
| −0.0521 (0.029) | 1.16 (0.6) | −0.0413 (0.029) | 1.42 (1.0) | ||
| RS92-ECMWF | |||||
| 0.0403 (0.043) | −0.90 (1.0) | 0.0141 (0.037) | −0.49 (1.3) | −1.70 (4.4) | |
| Ny Alesund (day, 6) | IASI-RS92 GDP | ||||
| −0.1190 (0.046) | 2.64 (1.0) | −0.0558 (0.031) | 1.93 (1.1) | ||
| IASI-ECMWF | |||||
| 0.0030 (0.107) | −0.065 (2.4) | 0.0002 (0.086) | −0.01 (3.0) | ||
| RS92-ECMWF | |||||
| 0.1220 (0.084) | −2.71 (1.9) | 0.0643 (0.026) | −1.94 (2.2) | −3.88 (4.5) |
| Station (RS92 STD Single Launches) | OBS-CAL Radiance Diff 1500–1570 cm−1 | OBS-CAL RH Diff 1500–1570 cm−1 | OBS-CAL Radiance Diff 1615–1800 cm−1 | OBS-CAL RH Diff 1615–1800 cm−1 | Direct Obs RH Diff 200.9–407.4 hPa |
|---|---|---|---|---|---|
| ENA (night, 43) | IASI-RS92 STD | ||||
| −0.1758 (0.075) | 3.90 (1.7) | −0.1132 (0.05) | 3.91 (1.7) | ||
| IASI-ECMWF | |||||
| 0.0096 (0.080) | −0.21 (1.8) | −0.0133 (0.056) | 0.46 (1.9) | ||
| RS92-ECMWF | |||||
| 0.1854 (0.112) | −4.11 (2.5) | 0.1000 (0.075) | −3.4 (2.6) | −3.08 (6.0) | |
| ENA (day, 50) | IASI-RS92 STD | ||||
| −0.1448 (0.118) | 3.21 (2.6) | −0.0952 (0.075) | 3.29 (2.6) | ||
| IASI-ECMWF | |||||
| 0.0082 (0.105) | −0.18 (2.3) | −0.0681 (0.078) | 0.24 (2.7) | ||
| RS92-ECMWF | |||||
| 0.1529 (0.144) | −3.39 (3.2) | 0.0088 (0.094) | −3.05 (3.3) | −2.32 (7.8) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Calbet, X.; Reale, A.; Schroeder, S.; Bali, M.; Smith, R.; Pettey, M. Accuracy of Vaisala RS41 and RS92 Upper Tropospheric Humidity Compared to Satellite Hyperspectral Infrared Measurements. Remote Sens. 2021, 13, 173. https://doi.org/10.3390/rs13020173
Sun B, Calbet X, Reale A, Schroeder S, Bali M, Smith R, Pettey M. Accuracy of Vaisala RS41 and RS92 Upper Tropospheric Humidity Compared to Satellite Hyperspectral Infrared Measurements. Remote Sensing. 2021; 13(2):173. https://doi.org/10.3390/rs13020173
Chicago/Turabian StyleSun, Bomin, Xavier Calbet, Anthony Reale, Steven Schroeder, Manik Bali, Ryan Smith, and Michael Pettey. 2021. "Accuracy of Vaisala RS41 and RS92 Upper Tropospheric Humidity Compared to Satellite Hyperspectral Infrared Measurements" Remote Sensing 13, no. 2: 173. https://doi.org/10.3390/rs13020173
APA StyleSun, B., Calbet, X., Reale, A., Schroeder, S., Bali, M., Smith, R., & Pettey, M. (2021). Accuracy of Vaisala RS41 and RS92 Upper Tropospheric Humidity Compared to Satellite Hyperspectral Infrared Measurements. Remote Sensing, 13(2), 173. https://doi.org/10.3390/rs13020173





