Abstract
Soil nutrients, including soil available potassium (SAK), soil available phosphorous (SAP), and soil organic matter (SOM), play an important role in farmland soil productivity, food security, and agricultural management. Spectroscopic analysis has proven to be a rapid, nondestructive, and effective technique for predicting soil properties in general and potassium, phosphorous, and organic matter in particular. However, the successful estimation of soil nutrient content by visible and near-infrared (Vis-NIR) reflectance spectroscopy depends on proper calibration methods (including preprocessing transformation methods and multivariate methods for regression analysis) and the selection of appropriate variable selection techniques. In this study, raw spectrum and 13 preprocessing transformations combined with 2 variable selection methods (competitive adaptive reweighted sampling (CARS) and the successive projections algorithm (SPA)) and 2 regression algorithms (support vector machine (SVM) and partial least squares regression (PLSR)), for a total of 56 calibration methods, were investigated for modeling and predicting the above three soil nutrients using hyperspectral Vis-NIR data (400–2450 nm). The results show that first-order derivatives based on logarithmic and inverse transformations (FD-LGRs) can provide better predictions of soil available potassium and phosphorous, and the best form of soil organic matter transformation is SG+MSC. CARS was superior to the SPA in selecting effective variables, and the PLSR model outperformed the SVM models. The best estimation accuracies (R2, RMSE) for soil available potassium, phosphorous, and organic matter were 0.7532, 32.3090 mg/kg; 0.7440, 6.6910 mg/kg; and 0.9009, 3.2103 g/kg, respectively, and their corresponding calibration methods were (FD-LGR)/SPA/PLSR, (FD-LGR)/SPA/PLSR, and SG+MSC/CARS/SVM, respectively. Overall, for the prediction of the soil nutrient content, organic matter was superior to available phosphorous, followed by available potassium. It was concluded that the application of hyperspectral images (Vis-NIR data) was an efficient method for mapping and monitoring soil nutrients at the regional scale, thus contributing to the development of precision agriculture.
1. Introduction
As the foundation for most terrestrial life, soil has unrivaled complexity and dynamicity [1]. Soil contains minerals, organic matter, uncountable numbers of organisms, and varying amounts of air, water, and essential nutrients which provide life support for the growth of terrestrial plants and other organisms [2]. Meanwhile, as definitive indicators of soil fertility, soil nutrients and properties play a crucial role in agricultural productivity, food security, and the sustainable development of agricultural ecology [3]. Soil organic matter (SOM) accumulates decaying debris—mainly of plant origin [4]—supports many physical, chemical, and biological processes sustaining vital ecosystem functions, and acts as an important source of nutrients and energy for biota. The nitrogen (N), phosphorus (P), and potassium (K) contents in soil are closely related to the nutrient cycle during crop growth and fertilization [5,6,7]. Therefore, the fast and accurate assessment of soil nutrients and properties is vital for monitoring soil fertility and developing sustainable agriculture.
The traditional way to map the spatial distribution of soil nutrients depends on field sampling and chemical analysis, which has the advantages of high precision and accuracy [6], but there are some contradictions between continuous spatial distribution mapping and discrete sampling methods based on limited sample numbers [8]. Moreover, traditional methods are time-consuming, expensive, and inefficient, especially for large-scale sampling and mapping [9,10]. The appearance of imaging spectroscopy in the 1980s brought optical remote sensing into a new stage of hyperspectral remote sensing [11]. Due to its rapidity, reduced labor intensity, cost-effectiveness, and non-destruction compared with conventional chemistry experiments [12,13], since the 1990s, the application of visible-near-infrared (Vis-NIR) (350–2500 nm) spectroscopy in soil science and agricultural management has attracted increasing attention, and the number of papers published in related fields has grown rapidly (e.g., [14]). The variation of the spectral curve is caused by the difference in the absorption and reflection characteristics of electromagnetic waves for different material components, and little sample preparation is required [12]. For example, 3 distinct absorption peaks are affected by free water at approximately 1400, 1900 and 2200 nm. A Vis-NIR spectrum provides comprehensive information on the physical (e.g., color, particle size, texture, and water content) or chemical (e.g., soil pH, the properties affected by soil minerals, and organic matter as the dominant elements) properties of soil [15]. Furthermore, based on chemometrics and modeling methods, Vis-NIR spectroscopy has been used to retrieve the contents of various soil properties, such as NPK [6], pH [16], SOM [17], moisture [18], clay [19], SOC [20], and heavy metals [21]. Specifically, the study involved P and K, mainly including the total phosphorus, total potassium, available phosphorus, and available potassium [5,6,22]. Currently, remote sensing and Vis-NIR data are important data sources in the field of digital soil mapping and play an increasingly important role in assessing soil fertility and soil quality [8,22]. However, there have been some problems for predicting the contents of some soil nutrients (e.g., soil potassium and soil phosphorus). One of these is the need to rely on indirect inversion of other soil component contents because there is no direct response associated with them at the spectral wavelength and the other is usually exists at low concentrations, which increases the difficulty of inversion [23,24].
The steps for using Vis-NIR data for soil properties or nutrient content inversion are usually as follows. First, after completing a pretreatment (e.g., air-drying, grinding, and sieving) of the soil sample, the soil of each sample is divided into two parts, one of which is a soil sample for chemical experiment analysis while the other is for spectral measurement. On this basis, after spectrum pretreatment, the optimal subset of wavelength variables is selected, an inversion model is established, and the best model is selected for prediction. Relevant research has revealed that it is necessary and crucial to preprocess spectral data [25]. Specifically, preprocessing the spectral data can correct the background effect [26,27] to a certain extent, eliminate part of the nonlinearity in the spectrum, and make it more suitable for analysis [27,28]. The Savitzky-Golay filter algorithm [29] is currently one of the most commonly used spectral smoothing methods [5,10,30,31], but some studies have also shown that spectral smoothing does not affect the results of soil property models [32,33]. To obtain the optimal preprocessing method and produce better results, multiple methods are combined with SG (e.g., [34]). Multiplicative scatter correction (MSC) [35] and the standard normal variate (SNV) [28] can effectively reduce the influence of spectral differences caused by different scattering intensities. Derivative transformations represented by the first derivative (FD), second derivative (SD) [13], and logarithmic transformation (LG) [24] have been used to remove the baseline while improving the correlation to the sample concentrations and the linear trend [5]. A continuous wavelet transformation (WT) [36] and a Fourier transform (FT) [37], belonging to the high-frequency noise removal method, have been used to enhance the features in the spectrum [5]. Vis-NIR data are usually characterized by a high spectral resolution with a large data volume and multicollinearity [38]. Currently, some studies using Vis-NIR spectroscopy to predict the soil nutrient content under field and laboratory conditions use full-spectrum wavelengths involved in modeling analysis, and some of these studies have also confirmed the superiority of the predictions using the full-spectrum over the correlation coefficient wavelength selection method [39,40]. However, when using other wavelength selection methods such as a genetic algorithm (GA), this showed the improvements in the accuracy and robustness of the model compared with the full-spectrum approach [41]. To some extent, reducing the spectral dimension is another common method to further optimize the model [20] because it can filter out some noisy, unreliable, and irrelevant variables from the whole spectral data [42]. Thus, several previous studies have demonstrated that calibration models are more accurate when wavelength variable selection methods are applied [22,42,43,44,45]. Among them, the most commonly used method is Pearson correlation analysis [6,30,46,47]. To a certain extent, the correlation coefficient (r) and significance level reflect the correlation relationship between soil elements and wavelength variables [46], and one or more bands with the highest correlation coefficient can be used to build the model. Furthermore, competitive adaptive reweighted sampling (CARS) [48], a genetic algorithm (GA) [49], and the successive projections algorithm (SPA) [50] are also widely used variable selection techniques in spectral modeling. The variables selected by these feature collection algorithms can be used as the input variables for modeling and then predicting soil nutrients or properties. In terms of model analysis methods, there are many methods, such as multiple linear regression (MLR), least squares regression, and partial least squares regression (PLSR), which are easy to use and act as simple model structures. Among them, PLSR is a commonly used method in hyperspectral regression modeling [17,30,44,51,52,53]. However, in reality, correlations between wavelength variables and soil nutrients are rarely linear. Therefore, nonlinear prediction methods have become popular. For example, artificial neural networks (ANNs), support vector machines (SVMs), random forests (RFs), and extreme learning machines (ELMs) can explain complex nonlinear relationships to a certain extent. These methods have been employed in many fields [44,54,55,56,57,58], and the results have shown that nonlinear prediction methods have high accuracy and perform better than linear methods.
However, due to the heterogeneity of the geographical environment, no single (or combination of) preprocessing method is suitable for different geographic soilscapes, and the same is true for wavelength variable selection and modeling methods [13,59]. Additionally, the reflectance of the soil spectrum in Vis-NIR (350–2500 nm) is generally low (compared with any other typical object), and the extension of the inversion model based on measured spectra is limited. There has been some research on the use of logarithmic (log(R)), reciprocal (1/R), and first-order differential (R’) transformation as a preprocessing method [24,26], but this research has been rarely mentioned, especially for the combined transformation of logarithmic or reciprocal derivatives. On the one hand, this study focuses on preprocessing methods that combine logarithmic, reciprocal, and first-order differential transformation, including the first-order differential of the reciprocal logarithm (FD-RLG, log(1/R)’) and the first-order differential of the reciprocal of the logarithm (FD-LGR, (1/log(R))’). We also process the spectral data in five different ways (SNV, MSC, SG, FD, and LG). On the other hand, according to our reviews, only a few studies have focused on the application of three variable selection techniques (CARS, SPA, and GA) and two regression methods (PLSR and SVM) in soil available potassium (SAK), soil available phosphorus (SAP), and soil organic matter (SOM) estimation at the same time, especially with Southwest China as the study area. Thus, the purpose of this study is to (a) compare the existing preprocessing methods and the combined transformation for SAK SAP and SOM estimation; (b) evaluate the differences of the two existing spectral wavelength selection methods (CARS and SPA) and select the best method as the modeling input; (c) compare the performance of the linear (PLSR) and nonlinear (SVM) multivariate methods for three soil nutrient estimations; and (d) evaluate the feasibility of establishing SAK, SAP, and SOM fertility levels using the output optimal model combination and provide scientific theoretical support for the spectral prediction of soil nutrient content and the development of precision agriculture.
2. Materials and Methods
2.1. Description of the Study Area
The study region was in the Xihe River watershed (30°38′28″–30°50′12″ N, 103°26′45″–103°40′52″ E) of Chongzhou (Figure 1c) west of the Chengdu Plain (Figure 1b). The Chengdu Plain is situated in the western Sichuan Basin (Figure 1a) of China, which has been referred to as a land of abundance since ancient times because of its temperate climate and fertile soil [60]. This region is characterized by relatively gentle terrain with elevations ranging from 468 m to 882 m. The elevation and slope both decrease from northwest to southeast, with a total area of approximately 2.81 × 104 ha. The region has a subtropical humid monsoon climate with an annual mean temperature and precipitation of approximately 15.9 °C and 1012.4 mm, respectively. The soil in Chengdu was developed based on Quaternary, tertiary, Jurassic, and Cretaceous parent rocks, according to the classification and codes for Chinese soil (National Standard of China, GB/T 17296–2009), and the representative soil type in this area (Chongzhou) is paddy soil. The region’s soil-forming parent material mainly consists of Minjiang gray alluvium, West River purple alluvium, and purple-gray alluvium mixed with alluvium of the Minjiang River and West River, and the soil’s parent material mainly consists of Minjiang gray alluvium, West River purple alluvium, Minjiang West River alluvium mixed with purple-gray alluvium and redeposited yellow mud. The land use types are primarily cultivated land, mainly including wheat rice and rapeseed rice, two typical water drought rotation modes, rapeseed corn, and horticultural crops, with two dry farming methods.
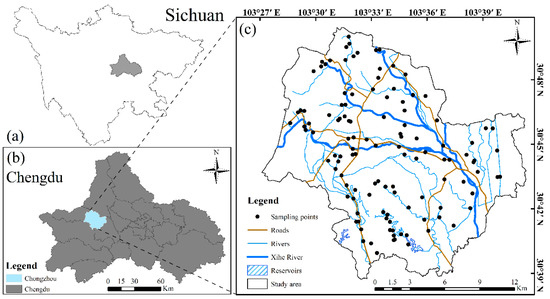
Figure 1.
Location of the study area (c) in the city of Chengdu (b), Sichuan Province (a), China, and the spatial distribution of the sampling points.
2.2. Field Sampling and Soil Analysis
Soil samples were collected at a 0–20 cm depth at 105 sampling points (Figure 1c) in October 2018. Here, we adopted a five-point sampling method. First, a square region (1 m2) was selected, and then each soil sample was collected at five points and mixed as one representative sample (i.e., four corners plus the center point). At the same time, the decaying branches and withered leaves, stones, and other non-soil objects on the soil surface were removed. We used GNSS receivers to record the geographic coordinates and altitude at the center of the plot for each sampling site [21]. In addition, the land use type (i.e., woodland or paddy field) of the sample site was also recorded and used to analyze the spectral differences of the soil nutrients (SAK, SAP, and SOM) of different surface features. The soil samples were brought back to the laboratory for physical and chemical analyses.
Each sample was taken to the laboratory for air drying in a natural indoor environment for one month. After air drying, impurity removal, grinding, and sieving (<2 mm), each sample was divided into two parts. One part was designated for standard chemical laboratory analysis and the other for hyperspectral Vis-NIR acquisition [61]. The chemical analysis for SOM was performed with the potassium bichromate titrimetric method [62], the SAK was measured with the ammonium acetate extraction-flame photometric detection method, the titration of the SAK extracts was performed with 1 mol L−1 NH4-OAc with a 1:5 weight-to-volume ratio, and the SAP was measured with the sodium hydrogen carbonate solution-Mo-Sb anti-spectrophotometric method. Titration of the SAP extracts was performed with 0.5 mol L−1 NaHCO3 [63].
2.3. Laboratory Spectral Measurements and Data Preprocessing
The soil spectral reflectance was measured using an ASD FieldSpec 3 spectrometer (Analytical Spectral Devices Inc., Boulder, CO, USA), which was able to measure the reflectance in the interval from 350 to 2500 nm with a 1-nm spectral resolution. Each sample was placed into a Petri dish (diameter of 9 cm and thickness of 2 cm), and a piece of black light-absorbing cloth was placed under the targeted object as a background [5]. The light source was a halogen lamp with a power of 50 W. The spectrum was measured through the soil sample with a viewing zenith angle of 30° at a 30-cm distance from the light source, and a Spectralon® white reference panel was used as a reference of 100% reflectance (absolute reflectance) for calibration of the spectroradiometer every 20 min to ensure that the instrument was calibrated before the spectral measurements were processed. For each soil sample, spectral reflectance was obtained from four measurements with a 90° turn between measurements, and a total of 40 spectra were averaged into 1 spectrum for each sample.
The wavelengths on the fringe (350–399 nm and 2451–2500 nm) of the spectrometers had a relatively low signal-to-noise ratio. To eliminate the influence of noise, the spectral regions mentioned above were removed [64,65]. To further reduce the influence of the instrument, experimental environment, baseline shifts, overall curvature, and soil samples on the spectral data and intensify the more chemically related peaks in the spectrum, several commonly used preprocessing transformations were applied in this study, including the Savitzky-Golay filter (SG) [29] with a polynomial order of 2 and window size of 11. Along with a first derivative (FD), SNV, MSC, LG, FD-RLG, and FD-LGR, seven different transformation forms were involved in this paper. Among them, different transformation forms had different effects, such as FD and SD, which could reduce the baseline variation and increase spectral peak features. The SG method was used to smooth and remove random noise from the spectra [66]. In this paper, the transformation forms of FD, SNV, MSC, LG, FD-RLG, and FD-LGR were performed on the SG spectra.
2.4. Spectral Variable Selection Methods
2.4.1. Competitive Adaptive Reweighted Sampling
The principle of CARS is derived from the principle of “survival of the fittest” in Darwin’s theory of evolution [48]. The CARS method selects the wavelength with a large absolute regression coefficient in the PLS model through adaptive reweighted sampling (ARS) technology, eliminates the wavelength points with small weights, and selects the subset with the lowest root mean square error of cross validation (RMSECV) value through interactive verification to obtain the optimal variable combination. Further detailed information and steps for the CARS algorithm can be found in [10,48,67].
2.4.2. Successive Projections Algorithm
As a forward feature variable selection algorithm that minimizes the collinearity of vector space, the SPA has been widely used for extracting sensitive variables in recent years [31,44]. In the wavelength selection process, the wavelength with the largest projection vector is added to the wavelength combination, and each newly selected wavelength has the smallest linear relation with the previous wavelength. Therefore, useful information can be optimized to the maximum extent, and the combination of variables can be obtained with the minimum collinearity and the least redundant information of hyperspectral data, which is helpful for improving the model prediction ability.
2.5. Regression Algorithms
As the SAK, SAP, and SOM contents may have linear and nonlinear relationships with the spectral reflectance or transformed spectrum, linear algorithms and nonlinear algorithms are commonly used for modeling, and the proper model is selected to predict the soil nutrient content. In this study, we used a linear regression method (PLSR) and a nonlinear method (SVM). These two regression algorithms were chosen because of their ability and applicability in spectral wavelength selection and robustness when used in parallel [68]. A brief summary of these techniques (PLSR and SVM) is provided below with key references for more detailed information.
As a well-known linear multivariate algorithm, PLSR has been used in chemometric and quantitative spectral analyses and other wide applications. PLSR is particularly appropriate when the number of independent variables is greater than the number of dependent variables [69]; in particular, there is multicollinearity in independent variables. PLSR is related to principal component regression (PCR), but instead of looking for the hyperplane with the maximum variance between the dependent variables and independent variables, PLSR finds a linear regression model by projecting the dependent variables and independent variables into a new space [70], and through integration, compression, and regression steps, continuous orthogonal factors (i.e., LVs, latent variables for PLSR) are selected to maximize the covariance between the predictive variables and the response variables [22,43]. The PLSR method combines the advantages of three components: principal component analysis (PCA), multiple linear regression, and canonical correlation analysis [31,46]. Leave-one-out cross-validation (LOOCV) was used to evaluate the PLSR models for the calibration set and to select the optimal number of LVs for PLSR [71,72].
The support vector machine (SVM) model is a nonlinear and supervised learning method that, based on statistical learning theory [73], can transform the problem of the data from low-dimensional nonlinear to high-dimensional linear [74]. Support vector machine regression (SVR) can be obtained by extending the SVM from the classification field to the regression field. Here, we still followed the SVM representation, which is essentially SVR. At this time, the standard SVM algorithm is also known as support vector classification (SVC), and the hyperplane decision boundary in SVC is the regression model of SVR. SVR is different from the traditional regression method; the loss function is redefined by introducing relaxation variables (ε), and by using boundary samples, training data points fall into or close to the margin defined by ε as much as possible. The sizes of the coefficients and prediction errors are reduced simultaneously by using a loss function to obtain the best model [75]. In this paper, we selected the radial basis function as the kernel function.
2.6. Accuracy Comparison
This paper used determination coefficients (R2), the root mean square error (RMSE), and the ratio of performance to deviation (RPD) to evaluate the accuracy of model inversion. These three statistical indicators have been widely used for regression models of the Vis-NIR spectrum [22,53,76,77]. Regarding the stability and fitness of the R2 reaction model, the closer R2 approached 1, the higher the model fit and the more stable it was. The RMSE of prediction measures the spread of prediction errors through the arithmetic mean of errors, and RPD, which is the standard deviation divided by the RMSE, indicates the predictive capacities of the calibration models. Low RMSE and high RPD values indicate good model prediction performance. In this study, according to [78], three categories of the prediction ability were performed: category A (RPD < 1.4) with poor accuracy, making it generally difficult to predict the content effectively; category B (1.4 ≤ RPD ≤ 2) with moderate accuracy, indicating that the prediction ability of the model was moderate and could be roughly estimated; and category C (RPD > 2) with good accuracy, indicating that the model had excellent prediction ability. Detailed information about the formulas can be found in the literature [5]. MATLAB 2020 R2019a was used to select the spectral variables and establish the models. The main method process is shown in Figure 2.
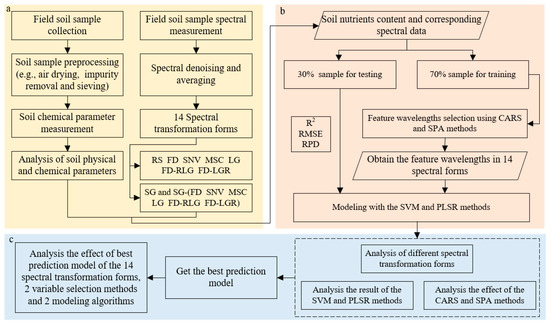
Figure 2.
Method flow chart. (a) Data preprocessing; (b) variable selection and modeling; and (c) analysis of the results.
3. Results
3.1. Descriptive Statistics of the Soil Nutrients
The total number of soil samples was 105, which were split into a calibration set and a validation set by the Kennard-Stone (KS) method at a proportion of 7:3 [53]. In reality, the levels of the soil properties were affected not only by the natural environment but also by human behaviors (i.e., before sample collection, there were fertilization activities in the field). Here, we detected outliers by using the Monte Carlo cross validation (MCCV) method. The total number of SOM samples was determined to be 97, while for SAK it was 103, and for SAP it was 101.
Summary statistics for the entire calibration and validation datasets for the soil nutrients measured in the laboratory are provided in Table 1. The SAP (2.23–49.91 mg/kg) had wider ranges than SOM (4.90–39.90 g/kg) and SAK (100.18–342.52 mg/kg), with mean values of 14.86 mg/kg, 17.32 g/kg, and 222.72 mg/kg, respectively. Furthermore, [79] categorized the coefficient of variation (CV) values into 3 classes: CV > 35% is considered highly variable, 15% < CV < 35% is moderate, and CV < 15% is low variability. The coefficients of variation (CVs) of the SAP, SOM, and SAK in the calibration dataset were 65.06%, 43.62%, and 24.08%, and these values in the validation dataset were higher than those in the calibration dataset at 80.28%, 50.76%, and 26.73%, respectively. The skewness of the SAP, SOM, and SAK were 1.33, 0.73, and 0.31, respectively, and all were greater than zero; the distribution of SAP, SOM, and SAK could be considered offset to the right. The kurtosis of the SAP was 2.05. Hence, the distribution of the SAP could be considered a steep distribution, but the SOM and SAK were flat distributions and smoother-than-normal distributions, respectively.

Table 1.
Descriptive statistics of soil nutrients in the study areas.
3.2. Spectral Characteristic Analysis
The average spectral reflectance and its degree of distribution of the different soil nutrients are illustrated in Figure 3 and Figure 4. In the entire band range (400–2450 nm), with an increase in the SOM, SAK, and SAP content, the spectral reflectance decreased gradually, but the exhibited spectral shapes were similar. This trend was significant at wavelengths of 400–1000 nm, which were mainly associated with minerals that contained iron, as well as the presence of SOM, SAK, and SAP [38,72,80]. In the Vis region, the reflectance spectrum affected by the soil chromophore and the black color of the SOM showed different spectral intensities. However, the NIR region (1000–2500 nm) was dominated by absorptions related to water, clay minerals, organic matter, and carbonates, and the spectral intensity variation was linked to the double-frequency and combined-frequency absorption of chemical bonds such as N-H, C-H, and C-O. In addition, water had strong absorption bands at approximately 1200 nm, 1400 nm, 1780 nm, and 2200 nm and weak absorption bands at approximately 1900 nm. The wavelengths of strong or weak water absorption were different from some existing studies [38,59,81,82], and the relevant reasons require further study.
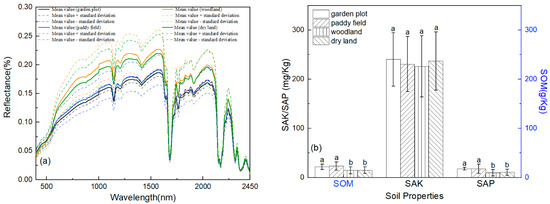
Figure 3.
Soil nutrients, mean value, and standard deviation of the spectrum relative to land use (a). Letters on top of each box indicate statistical similarity (boxes with similar letters) or dissimilarity (boxes with dissimilar letters) between land use systems (p < 0.05) (b).
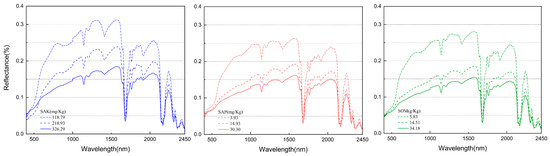
Figure 4.
Spectral signatures of three soil nutrients’ contents under different classes.
The SOM, SAK, and SAP contents in garden plots, paddy fields, woodlands, and dry land showed a certain gradient distribution. The SOM, SAK, and SAP contents were lowest in the woodlands, and the land use types with the highest SAK or SAP and SOM contents were garden plots and paddy fields, respectively. The content of SAK in the dry land was higher than that in the paddy fields, but the content of SAP was the opposite. For the SOM, the dry land SOM was behind the paddy field and garden field SOM. According to the climate characteristics, paddy field planting in Chongzhou usually occurs 2–3 times, so the lowest SOM, SAK, and SAP in being in the woodlands may partly have been due to more crop residue left in the area with 2–3 plantings a year.
3.3. Feature Wavelength Selection
To reduce the number of wavelengths and obtain a simpler, more reliable model, CARS and SPA were applied to select the feature wavelengths with the main effective information from the whole spectrum. Figure 5 shows the concentrated map of the selected bands of the different spectral variable selection methods. As shown in Figure 5, there were significant differences in the feature wavelengths selected by the CARS and SPA algorithms under 13 spectral transformations. First, the number of feature wavelengths selected was different, and CARS’ were significantly higher than SPA’s. Compared with SPA, the distribution of feature wavelengths was more scattered. Second, due to the differences in the responses of wavelengths to soil nutrients, under the same algorithm, there were significant differences in the selection of feature wavelengths. Except for being selected only once as the feature wavelength, using SPA as the spectral variable selection method, the range of the SAK was mainly concentrated at 400–421 nm, 996 nm, 1350 nm, 1351 nm, 1680 nm, 2372 nm, and 2448 nm, while the SAP was mainly concentrated at 400–436 nm, around 1000 nm, 1325–1417 nm, 1604 nm, 1659 nm, 1835–1946 nm, and 2355–2450 nm. The SOM was mainly concentrated at 405–442 nm, 543–788 nm, around 1000 nm, 1295 nm, 1835–1934 nm, and 2210 nm. The results of CARS showed that the wavelengths selected for the SAK were concentrated at 405–483 nm, around 728 nm, 967–1031 nm, 1271–1409 nm, 1643–1789 nm, 1975–2004 nm, 2109–2174 nm, 2312–2449 nm; those for the SAP were concentrated at 400–450 nm, 1005–1083 nm, 1292–1358 nm, around 1577 nm, 1964–2044 nm, 2113–2216 nm, and 2381–2421 nm; and SOM’s were concentrated at 411–508 nm, 984–1028 nm, around 1233 nm, 1347–1358 nm, 1608–1620 nm, around 836 nm, 1930–2052 nm, and 2309–2448 nm.
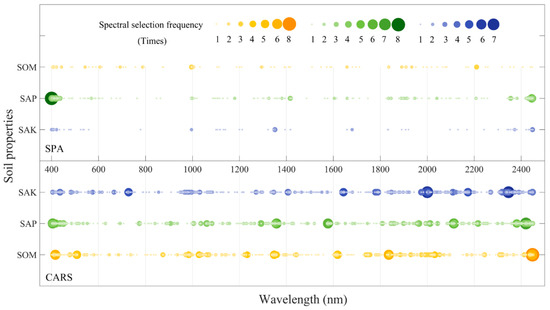
Figure 5.
Concentrated map of selected wavelengths of the different spectral variable selection methods (the horizontal axis represents the wavelength from 400 nm to 2450 nm, the vertical axis represents the three soil nutrients, the different size indicates the numbers of times each wavelength was selected by the 14 spectral forms).
3.4. Model Performances of Different Calibration Methods
The preprocessing transformation methods provided different calibration and prediction accuracies for the SAK, SAP, and SOM regarding the R2, RMSE, and RPD values. Table 2 and Figure 6 and Figure 7 show the R2, RMSE, and RPD performance with different calibration methods for the prediction of the SAK, SAP, and SOM. The standard deviation (SD) between groups through SG transformation (SDSG = 0.1881) was smaller than that of the original transformation (SDraw = 0.2220), and based on the standard deviation of the raw spectral (RS), the difference of the samples in the group was the largest. The calibration accuracy based on SG transformation was not significantly improved compared with the unprocessed method, but the effect obtained for the specific part of the transformation form was better (e.g., RS or SNV). Some of them had differences in R2 that were greater than 0.1 (e.g., RS and FD-LGR). The highest R2 values of the SAK, SAP, and SOM were 0.8931, 0.9518, and 0.9277, respectively, which were obtained with the calibration methods of FD-RLG/PLSR, FD-RLG/PLSR, and FD-LGR/SVM, while the calibration methods with the lowest accuracy were more irregular. The highest R2 value of the SAK was 0.1150 (RS/PLSR), while it was 0.3713 for the SAP (SNV/PLSR), and 0.2379 for the SOM (FD-RLG/PLSR). As shown by the calibration results in Table 2, among the three investigated soil nutrients, the SAP was the most accurate calibration element with an average R2 = 0.7356 followed by the SOM (R2 = 0.7165), and the worst was for the SAK (R2 = 0.5522). Similarly, the dispersion of these three soil nutrients of modeling R2 from large to small was the SAK, SOM, and SAP. Furthermore, for the two regression methods, the modeling accuracy of the SVM was significantly higher than that of PLSR, regardless of the kind of soil nutrients, and the average R2 values of the SVM and PLSR were 0.8054 and 0.5309. Except for the SAK, the discrete degree of modeling accuracy data (R2) of the other two soil nutrients is shown, as PLSR is more discrete than the SVM.

Table 2.
The performance (R2) of the PLSR and SVM models with the feature wavelengths selected by using CARS and the SPA under 14 spectral transformations.
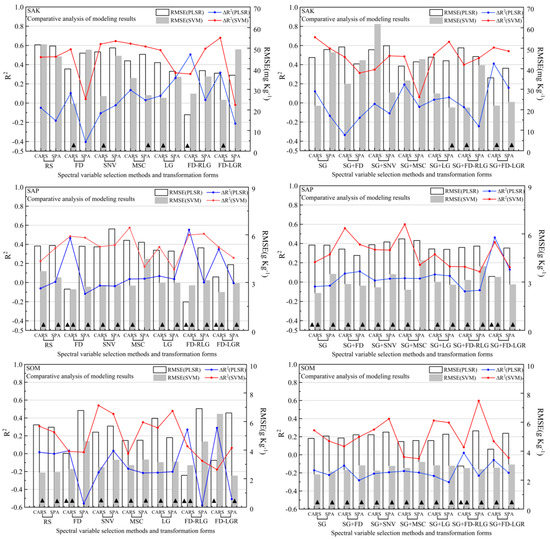
Figure 6.
Independent validation results for three soil nutrient (SAK, SAP, and SOM) estimations under different spectra pre-processing transformation methods and spectral variable selection methods. (∆R2: calibration model R2, prediction result of R2. ▲ represents the model belonging to category C (RPD > 2) with good accuracy.)
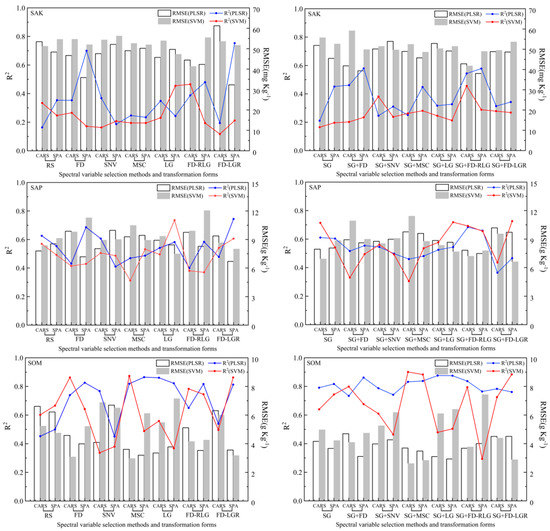
Figure 7.
Independent prediction results for three soil nutrient (SAK, SAP, and SOM) estimations under different spectra pre-processing transformation methods and spectral variable selection methods.
The RMSE explains the difference between the samples and the model predictions, and RPD represents the ratio of the standard error of the prediction to the standard deviation of the sample. The details of the RPD can be found in Section 2.6. Generally, a model that performs well will have a high R2 and RPD value and a low RMSE value. The RMSE value trend of the three soil nutrients was similar to the statistical indicator R2; the lowest R2 values of the SAK, SAP, and SOM were 17.6897 mg/kg, 1.7887 mg/kg, and 2.2046 g/kg, as obtained with the calibration method of FD-RLG/PLSR, FD-RLG/PLSR, and FD-LGR/SVM, respectively, while the calibration methods with the highest RMSEs were irregular as well. For the difference in R2, the highest RMSE value of the SAK was 61.7496 mg/kg (SG-SNV/SVM), while it was 6.3700 mg/kg for the SAP (SNV/PLSR) and 6.7730 g/kg for the SOM (FD/PLSR). Considering that the RMSE value could be affected by different soil nutrient dimensions, we used the coefficient of variation (CV) to evaluate the degree of dispersion between groups. The results show that, except for the SAP, the variation degree of the RMSE values of the other two soil nutrients (SAK and SOM) was shown as the SVM being more discrete than PLSR, which was different from the results for R2. For soil nutrients, the variation degree of the SAK was greater than that of the SOM, followed by the SAP. Here, we also used the difference analysis of significance to evaluate the difference of the accuracy value (R2 and RMSE) based on SG transformation and the difference between the two modeling methods. The results showed that SG transformation had no significant difference, as the p values of the R2 and RMSE were 0.6451 and 0.9904, respectively. Comparing the two modeling methods of different soil nutrients, the accuracy values of PLSR and the SVM had extremely significant differences (p < 0.001). The RPD value indicates the prediction performance of the model, as shown in Figure 6. The model prediction performance of the three soil nutrients shows that the SAP and SOM were better than the SAK. The RPD value of the SVM was generally higher than that of PLSR.
Through the above calibration results, we can conclude that the SVM modeling algorithm was better than PLSR because its comprehensive performance was better than PLSR for the R2, RMSE, and RPD indicators. However, through the prediction results, we calculated the ∆R2, which indicated a numerical difference between the modeling determination coefficient and the predicted determination coefficient. The ∆R2 variation ranges of the SAK, SAP, and SOM were −0.4045–0.6860, −0.1172–0.2070, and −0.5591–0.2704, respectively, and the corresponding standard deviations were 0.2981, 0.2033, and 0.2671, respectively. In addition, the analysis results of significant differences between the groups showed extremely significant differences (p < 0.001). Specifically, SG transformation had little effect on the degree of dispersion of data in the group. Generally, the degree of dispersion in the original form was slightly higher than that processed by SG transformation, and the numerical difference of ∆R2 was not significant. For the two model algorithms, there were significant differences between PLSR and the SVM for ∆R2 (p < 0.001), and the variation ranges and data discreteness of PLSR were slightly higher than those of the SVM.
3.5. Model Performances of Different Variable Selection Methods
The purpose of variable selection methods is to select wavelengths whose information content is minimally redundant. Figure 6 and Figure 7 show the results of the calibration and prediction accuracy under different variable selection methods. The concentrated map of selected bands of CARS and the SPA (Figure 5) also reflects the relationship between the number of bands selected, and during the modeling process, we counted the number of wavelengths that were ultimately involved in the modeling. Under the CARS algorithm, the SAK, SAP, and SOM were all approximately 16. For the SPA algorithm, the number of soil nutrients had a certain difference, and the average numbers of the SAK, SAP, and SOM were 6, 20 and 9, respectively. The R2 average value of the calibration set showed that CARS was higher than the SPA; however, there was no significant difference between the three soil nutrients through significant difference analysis (p > 0.05). Specifically, the SAP performed better than the SOM, and the SAK was the worst for the two variable selection methods.
In the prediction results, the variable selection methods used for the highest R2 values for the SAK, SAP, and SOM were the SPA, SPA, and CARS, respectively. Additionally, through the CV value, except for the SAP, the variation degree of the R2 values of the other two soil nutrients (SAK and SOM) was shown as the SPA being more discrete than CARS, and the SAK was the most discrete no matter which selection method was chosen. The maximum CV was 48.0522%, which appeared in the SPA variable selection method for the SAK, and the lowest CV was 18.1591%, which appeared in the SPA variable selection for the SAP.
4. Discussion
4.1. Preprocessing Transformations
The spectrum contains useful information as well as considerable redundant and useless information. Consequently, the presence of unexpected irrelevant information in the spectra can also significantly affect the performance of the calibrated models used to quantify the SAK, SAP, and SOM. In this paper, the transformation forms of FD, SNV, MSC, LG, DF-RLG, and DF-LGR were utilized on the SG spectra. Thus, together with the raw spectral form (R and SG), there were a total of 14 transformation forms. These preprocessing transformations based on various mathematical functions can be used for eliminating the influence of noise, correcting for nonlinearity, measurement and sample variations, and noisy spectra [64]. The results of the regression with PLSR, the SVM, and the performance of the models during the prediction phase are shown in Table 2 and Figure 6 and Figure 7. In general, the prediction accuracy under some transformation forms was improved after SG processing, but the significant difference analysis of the prediction results with and without SG treatment showed that the results did not differ significantly (p > 0.05). This was different from most of the current studies, where the SG method was used in combination with other methods to obtain an optimal pretreatment method that was proven to produce good results [34,81]. The SG method was used to smooth and remove random noise (physical jitter, external environmental interference, etc.) from the spectra. The effect of SG filtering was not obvious (though the enhancement was obvious compared with the original spectrum), and the prediction accuracy of PLSR with some preprocessing transformations (e.g., LG and FD-RLG) for predicting the SAK, SAP, and SOM even decreased after SG filtering. which may have been related to the process of noise signal reduction. Part of the important corresponding nonlinear information was removed by SG filtering [5]. In addition, the most commonly used preprocessing transformations performed better than raw spectral reflectance, and similar results have been presented in other works (e.g., [5,83]). This means that various transformations of the spectral variables can successfully eliminate the effects of physical phenomena such as the light scattering effects of particles of different sizes and shapes when using hyperspectral Vis-NIR data for prediction [35].
4.2. Feature Wavelengths
The spectrum contains information about the fundamental composition of the soil, which can be used to describe the soil types and their changes in the landscape [84]. Soil’s spectral information is affected by its physical properties, chemical composition, and mineral composition [85]. From the microscopic level, the chemical bonds of different molecules vibrate at a characteristic frequency under the action of electromagnetic energy. In this process, there is a process of absorption, reflection, and scattering of energy, which may have a certain relationship with a specific wavelength [86]. Therefore, under the condition of known reflectivity, we can obtain information on the soil property content through the relationship between reflectivity and the soil’s nutrients [44,80]. Spectroscopy has been widely recognized as an effective tool for analyzing soil nutrients [84]. Some soil properties or nutrients (e.g., soil moisture content or soil organic matter) can establish a direct relationship with the nutrient content at a specific spectral wavelength. O-H stretch vibrations near 1400 nm [87], 2200 nm [88], and 1900 nm correspond to H2O molecules [89]. However, some soil nutrients (e.g., soil potassium and soil phosphorus) need to rely on indirect inversion of other soil component contents, because there is no direct response associated with them at the spectral wavelength and they usually exist at low concentrations [23,24]. This is just as some research teams have revealed the effects of hydrogen bond perturbations in water systems [90]. When these elements (indirect response soil nutrients) are measured, the changes in the spectral profile are due to indirect effects of the association of soil nutrients with other elements (direct response elements). The direct response elements will also be influenced by the environment, and the effects of such changes are dynamic and complex. In this paper, the most common sensitive wavelengths associated with SAK are 400–483 nm, around 728 nm, 967–1031 nm, 1271–1409 nm, 1643–1789 nm, 1975–2004 nm, 2109–2174 nm, and 2312–2449 nm. For SAP, they are 400–450 nm, 1000–1083 nm, 1292–1417 nm, around 1557 nm, 1604 nm, 1659 nm, 1835–2044 nm 2113–2216 nm, and 2355–2450 nm. These feature wavelength selection results are similar to those found in [91,92]. Based on soil absorbance in the visible-near-infrared regions [84], the feature wavelengths of the SAK are mainly related to ferrihydrite, goethite, amine (N-H), organic matter, free water (O-H), cellulose, lignin, starch, the first overtone of O-H stretch, Al-OH or Mg-OH, among others. The components corresponding to the wavelength selection of the SAP are similar to those of the SAK, and the element types are complex and inconsistent. This adds a challenge to the prediction of SAK and SAP concentrations [5]. Due to the overtones and combination absorptions of O-H, C-H, and N-H bonds, the SOM has broad, sensitive bands from the visible to the shortwave infrared range (350–2500 nm) [88]. The range of wavelengths selected for the SOM in this paper were 405–442 nm, 543–788 nm, around 1000 nm, 1295 nm, 1347–1358 nm, 1608–1620 nm, 1835–1934 nm, 2210 nm, and 2309–2448 nm. Some of these wavelengths were consistent with those selected (570–700 nm, 769 nm, 1020 nm, 1340 nm, and 1986 nm) in existing studies [93,94,95].
4.3. The Effect of the Variable Selection Methods
Figure 5 shows the distribution of selected wavelengths in the 400–2450 nm spectral range under different spectral variable selection methods. The number of effective wavelength variables selected by the CARS method was more than that of the SPA for the SAK, SAP, and SOM. Through the significant difference analysis, there was no significant difference in the accuracy of the models corresponding to the two methods (p > 0.05). Moreover, although the SPA method greatly reduced the number of spectral variables, in Table 2 and Figure 6 and Figure 7, it can be seen that the corresponding integrated stability and accuracy of the model was inferior to that of the CARS method. This may be related to the processing mechanism and process of the SPA algorithm. The wavelength selection process adds the wavelength with the largest projection vector to the wavelength combination, and each newly selected wavelength has the smallest linear relationship with the previous wavelength so it can maximize the preferential selection of useful information, reduce the variable covariance, and reduce the amount of hyperspectral redundant information to enhance the model’s computing power. In this process, unstable variables are selected, and some important and relevant variables that contain both confounding and informative variables are removed [44].
4.4. The Availability of the Model
According to Figure 6 and Figure 7 and Table 2, both preprocessing transformations, variable selection methods, and regression algorithms influenced the model’s performance regarding R2, RMSE, and RPD. Similar results have been presented by others (e.g., [5,96]). The results in this paper show that, for the modeling of the SOM, the SVM was better than PLSR, but for the SAK and SAP, PLSR was better than the SVM. It was also shown in [5] that PLSR performed better than the LS-SVM and BPNN. Figure 6 shows the difference between the modeling and prediction results in terms of the metric R2, which enabled us to roughly see the stability of the modeling approach. The results connected by the red line, which deviates more from the horizontal axis 0 and is basically above the horizontal axis 0, indicate an obvious overfitting situation of the SVM compared with the blue line. At the same time, we found that the modeling results using the PLSR algorithm were partially underfitted, but the overall performance was better than that of the SVM algorithm. The modeling prediction accuracy for the SAP and SOM was significantly better than that for the SAK. This also shows that the spectral inversion analysis of trace elements such as potassium (K) is more difficult than that for other elements [24]. Table 3 illustrates the best preprocessing transformation, variable selection methods, and regression methods after combining the modeling and prediction accuracy results for the SAK, SAP, and SOM ((FD-LGR)/SPA/PLSR for the SAK, (FD-LGR)/SPA/PLSR for the SAP, and SG+MSC/CARS/SVM for the SOM. It can also be concluded that the integrated inversion of the SOM was significantly better than that of the SAP and SAK. For the results of the final model, although the study areas had the same soil type, historically different land-use types (garden plot, paddy field, woodland, dry land, and wasteland) and different terrain, treatments (variable fertilization, variable straw returning, and variable planting density) resulted in significant data variation of the available nutrient contents. These effects were manifested in the different spectral curves, making it difficult to have a general model to predict the soil nutrient content at present. Moreover, proper sampling strategy in a more homogeneous area and a large dataset may increase the performance of the model. This conclusion was confirmed in the prediction of soil organic carbon [75], and further in-depth studies are needed for nutrients such as SAK, SAP, and SOM.

Table 3.
Summary statistics of soil nutrients in the calibration and prediction sets.
5. Conclusions
This study measured the spectra of 103 sample sites in the Xihe River watershed of Chongzhou in the western Chengdu Plain and collected corresponding soil samples. To reveal the relationship between the soil spectral information and soil nutrient content, in this study, two regression methods (SVMR and PLSR) combined with two variable selection methods (CARS and SPA) and 13 preprocessing transformations were used to estimate the SAK, SAP, and SOM contents based on Vis-NIR reflectance spectroscopy. The results illustrate that the prediction performance could be significantly improved by applying proper calibration methods, and the details for this are as follows:
1. In addition to RS, the other 13 kinds of spectra showed different changes in the SAK, SAP, and SOM contents to varying degrees, and SG transformation did not significantly improve the results except for RS. First-order derivatives based on logarithmic and inverse transformations (FD-LGR) can provide better predictions of the SAK and SAP nutrient contents, and the best form of SOM transformation is SG+MSC.
2. In terms of selecting effective wavelength variables for modeling, the CARS technique was superior to the SPA techniques, although the number of bands selected by the SPA methods was much smaller.
3. According to our comprehensive statistical comparison, the PLSR models performed better than the SVM model for estimation because of the overfitting problem of the SVM.
4. As a result, hyperspectral Vis-NIR data (400–2450 nm) showed a good ability to predict the SOM, a moderate ability to predict the SAP, and poor ability to predict the SAK.
According to numerical and visual tradeoffs, in this paper, (FD-LGR)/SPA/PLSR, (FD-LGR)/SPA/PLSR, and SG+MSC/CARS/SVM were selected as the most suitable methods for predicting the SAK, SAP, and SOM. Their corresponding predicted R2 and RMSE were 0.7532 and 32.3090 mg/kg, 0.7440 and 6.6910 mg/kg, and 0.9009 and 3.2103 g/kg, respectively.
The current study evaluating calibration and spectral variable selection methods for predicting three soil nutrients using Vis-NIR spectroscopy also provides a framework for predicting various soil nutrients that meet the requirements of modern soil management and high-quality development. Further work should investigate other calibration methods and pay more attention to optimizing these methods to improve the predictive performance. In addition, the number of soil samples and the variation in soil types can affect the shape of the spectral curve, and research should focus on the relationship between soil spectral characteristics and chemical composition-especially for elements without direct correlation wavelengths in the band range—to make the model more stable and robust. Moreover, in-depth research on the prediction mechanism is also important to enhance the generalization of the model.
Author Contributions
Conceptualization, P.G. and T.L.; methodology, P.G. and X.C.; software, P.G.; validation, P.G. and H.G.; formal analysis, P.G. and H.G.; investigation, T.L.; resources, T.L.; data curation, T.L.; writing—original draft preparation, P.G.; writing—review and editing, P.G., Y.C. and Y.H.; visualization, P.G.; supervision, X.C.; project administration, X.C.; funding acquisition, T.L. and X.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by a national key research and development program (Integovernmental cooperation in international science and technology innovation of the Ministry of Science and Technology, 2021YFE0102000), the scientific research project of the National Natural Science Foundation of China (41601311), and the key projects of the Science & Technology Department of Sichuan Province(17ZA0308).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the project requirements.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Du, C.; Zhou, J. Evaluation of Soil Fertility Using Infrared Spectroscopy: A Review. Environ. Chem. Lett. 2009, 7, 97–113. [Google Scholar] [CrossRef]
- Wilding, L.P.; Lin, H. Advancing the frontiers of soil science towards a geoscience. Geoderma 2006, 131, 257–274. [Google Scholar] [CrossRef]
- Nowak, B.; Nesme, T.; David, C.; Pellerin, S. Nutrient recycling in organic farming is related to diversity in farm types at the local level. Agric. Ecosyst. Environ. 2015, 204, 17–26. [Google Scholar] [CrossRef]
- Sokol, N.W.; Kuebbing, S.E.; Karlsen-Ayala, E.; Bradford, M.A. Evidence for the primacy of living root inputs, not root or shoot litter, in forming soil organic carbon. New Phytol. 2018, 221, 233–246. [Google Scholar] [CrossRef] [Green Version]
- Qi, H.; Paz-Kagan, T.; Karnieli, A.; Jin, X.; Li, S. Evaluating calibration methods for predicting soil available nutrients using hyperspectral VNIR data. Soil Tillage Res. 2018, 175, 267–275. [Google Scholar] [CrossRef]
- Song, Y.; Zhao, X.; Su, H.; Li, B.; Hu, Y.; Cui, X. Predicting Spatial Variations in Soil Nutrients with Hyperspectral Remote Sensing at Regional Scale. Sensors 2018, 18, 3086. [Google Scholar] [CrossRef] [Green Version]
- Bedada, W.; Lemenih, M.; Karltun, E. Soil nutrient build-up, input interaction effects and plot level N and P balances under long-term addition of compost and NP fertilizer. Agric. Ecosyst. Environ. 2016, 218, 220–231. [Google Scholar] [CrossRef]
- McBratney, A.; de Gruijter, J.; Bryce, A. Pedometrics timeline. Geoderma 2019, 338, 568–575. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Ayoubi, S.; Jafari, A.; Tajik, S.; Finke, P. Digital mapping of soil properties using multiple machine learning in a semi-arid region, central Iran. Geoderma 2019, 338, 445–452. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Chen, Y.; Linderman, M.; Mouazen, A.M.; Liu, Y.; Guo, L.; Yu, L.; Liu, Y.; Cheng, H.; et al. Comparing laboratory and airborne hyperspectral data for the estimation and mapping of topsoil organic carbon: Feature selection coupled with random forest. Soil Tillage Res. 2020, 199, 104589. [Google Scholar] [CrossRef]
- Lillesand, T.M.; Kiefer, R.W. Remote Sensing and Image Interpretation, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1994; p. 750. [Google Scholar]
- Ji, W.; Adamchuk, V.I.; Chen, S.; Mat Su, A.S.; Ismail, A.; Gan, Q.; Shi, Z.; Biswas, A. Simultaneous measurement of multiple soil properties through proximal sensor data fusion: A case study. Geoderma 2019, 341, 111–128. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, J.; Zhu, C.; Wang, J. Combination of efficient signal pre-processing and optimal band combination algorithm to predict soil organic matter through visible and near-infrared spectra. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 240, 118553. [Google Scholar] [CrossRef]
- Guerrero, C.; Viscarra Rossel, R.A.; Mouazen, A.M. Diffuse reflectance spectroscopy in soil science and land resource assessment. Geoderma 2010, 158, 1–2. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Yang, M.; Mouazen, A.; Zhao, X.; Guo, X. Assessment of a soil fertility index using visible and near-infrared spectroscopy in the rice paddy region of southern China. Eur. J. Soil Sci. 2020, 71, 615–626. [Google Scholar] [CrossRef]
- Ba, Y.; Liu, J.; Han, J.; Zhang, X. Application of Vis-NIR spectroscopy for determination the content of organic matter in saline-alkali soils. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 229, 117863. [Google Scholar] [CrossRef]
- Morellos, A.; Pantazi, X.E.; Moshou, D.; Alexandridis, T.; Whetton, R.; Tziotzios, G.; Wiebensohn, J.; Bill, R.; Mouazen, A.M. Machine learning based prediction of soil total nitrogen, organic carbon and moisture content by using vis-nir spectroscopy. Biosyst. Eng. 2016, 152, 104–116. [Google Scholar] [CrossRef] [Green Version]
- Nawar, S.; Buddenbaum, H.; Hill, J.; Kozak, J.; Mouazen, A.M. Estimating the soil clay content and organic matter by means of different calibration methods of vis-NIR diffuse reflectance spectroscopy. Soil Tillage Res. 2016, 155, 510–522. [Google Scholar] [CrossRef] [Green Version]
- Hong, Y.; Chen, Y.; Yu, L.; Liu, Y.; Liu, Y.; Zhang, Y.; Liu, Y.; Cheng, H. Combining Fractional Order Derivative and Spectral Variable Selection for Organic Matter Estimation of Homogeneous Soil Samples by VIS–NIR Spectroscopy. Remote Sens. 2018, 10, 479. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Liu, Z.; Hu, Y.; Shi, Z.; Pan, Y.; Wang, L.; Wang, G. Integrating a Hybrid Back Propagation Neural Network and Particle Swarm Optimization for Estimating Soil Heavy Metal Contents Using Hyperspectral Data. Sustainability 2019, 11, 419. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Zhao, Y.; Wang, M.; Shi, X. Comparison of multivariate methods for estimating selected soil properties from intact soil cores of paddy fields by Vis–NIR spectroscopy. Geoderma 2018, 310, 29–43. [Google Scholar] [CrossRef]
- Wang, X.; Meng, J. Research Progress and Prospect on Soil Nutrients Monitoring with Remote Sensing. Remote Sens. Technol. Appl. 2015, 30, 1033–1041, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Ji, W.; Shi, Z.; Huang, J.; Li, S. In situ measurement of some soil properties in paddy soil using visible and near-infrared spectroscopy. PLoS ONE 2014, 9, e105708. [Google Scholar] [CrossRef] [Green Version]
- Rinnan, Å.; van den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. Trac-Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Conforti, M.; Matteucci, G.; Buttafuoco, G. Using laboratory Vis-NIR spectroscopy for monitoring some forest soil properties. J. Soils Sediments 2017, 18, 1009–1019. [Google Scholar] [CrossRef]
- Rossel, R.A.V. ParLeS: Software for chemometric analysis of spectroscopic data. Chemom. Intell. Lab. Syst. 2008, 90, 72–83. [Google Scholar] [CrossRef]
- Barnes, R.J.; Dhanoa, M.S.; Lister, S.J. Standard Normal Variate Transformation and De-Trending of Near-Infrared Diffuse Reflectance Spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Lin, L.; Liu, X. Water-based measured-value fuzzification improves the estimation accuracy of soil organic matter by visible and near-infrared spectroscopy. Sci. Total Environ. 2020, 749, 141282. [Google Scholar] [CrossRef]
- Wang, S.; Chen, Y.; Wang, M.; Zhao, Y.; Li, J. SPA-Based Methods for the Quantitative Estimation of the Soil Salt Content in Saline-Alkali Land from Field Spectroscopy Data: A Case Study from the Yellow River Irrigation Regions. Remote Sens. 2019, 11, 967. [Google Scholar] [CrossRef] [Green Version]
- Vasques, G.M.; Grunwald, S.; Sickman, J.O. Comparison of multivariate methods for inferential modeling of soil carbon using visible/near-infrared spectra. Geoderma 2008, 146, 14–25. [Google Scholar] [CrossRef]
- Van de Broek, M.; Govers, G. Quantification of organic carbon concentrations and stocks of tidal marsh sediments via mid-infrared spectroscopy. Geoderma 2019, 337, 555–564. [Google Scholar] [CrossRef]
- Paz-Kagan, T.; Shachak, M.; Zaady, E.; Karnieli, A. A spectral soil quality index (SSQI) for characterizing soil function in areas of changed land use. Geoderma 2014, 230–231, 171–184. [Google Scholar] [CrossRef]
- Helland, I.S.; Næs, T.; Isaksson, T. Related versions of the multiplicative scatter correction method for preprocessing spectroscopic data. Chemom. Intell. Lab. Syst. 1995, 29, 233–241. [Google Scholar] [CrossRef]
- Peng, J.; Shen, H.; He, S.W.; Wu, J.S. Soil moisture retrieving using hyperspectral data with the application of wavelet analysis. Environ. Earth Sci. 2012, 69, 279–288. [Google Scholar] [CrossRef]
- Terra, F.S.; Viscarra Rossel, R.A.; Demattê, J.A.M. Spectral fusion by Outer Product Analysis (OPA) to improve predictions of soil organic C. Geoderma 2019, 335, 35–46. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, Z.; Wang, H.; Wang, J.; Yang, S. Assessing Soil Organic Matter Content in a Coal Mining Area through Spectral Variables of Different Numbers of Dimensions. Sensors 2020, 20, 1795. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Shen, G.; Xiang, Q.; Wu, Y. Spectral Characteristics of Soil Salinity Based on Different Pre-processing Methods. Chin. J. Soil Sci. 2017, 48, 560–568, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Yu, L.; Hong, Y.; Geng, L.; Zhou, Y.; Zhu, Q.; Cao, J.; Nie, Y. Hyperspectral estimation of soil organic matter content based on partial least squares regression. Trans. Chin. Soc. Agric. Eng. 2015, 31, 103–109, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Kawamura, K.; Tsujimoto, Y.; Nishigaki, T.; Andriamananjara, A.; Rabenarivo, M.; Asai, H.; Rakotoson, T.; Razafimbelo, T. Laboratory Visible and Near-Infrared Spectroscopy with Genetic Algorithm-Based Partial Least Squares Regression for Assessing the Soil Phosphorus Content of Upland and Lowland Rice Fields in Madagascar. Remote Sens. 2019, 11, 506. [Google Scholar] [CrossRef] [Green Version]
- Zou, X.; Zhao, J.; Povey, M.J.W.; Holmes, M.; Mao, H.P. Variables selection methods in near-infrared spectroscopy. Anal. Chim. Acta 2010, 667, 14–32. [Google Scholar] [CrossRef]
- Xu, Y.; Smith, S.E.; Grunwald, S.; Abd-Elrahman, A.; Wani, S.P. Effects of image pansharpening on soil total nitrogen prediction models in South India. Geoderma 2018, 320, 52–66. [Google Scholar] [CrossRef]
- Cheng, H.; Wang, J.; Du, Y. Combining multivariate method and spectral variable selection for soil total nitrogen estimation by Vis–NIR spectroscopy. Arch. Agron. Soil Sci. 2020, 67, 1665–1687. [Google Scholar] [CrossRef]
- Ning, J.; Sheng, M.; Yi, X.; Wang, Y.; Hou, Z.; Zhang, Z.; Gu, X. Rapid evaluation of soil fertility in tea plantation based on near-infrared spectroscopy. Spectrosc. Lett. 2019, 51, 1–9. [Google Scholar] [CrossRef]
- Shen, Q.; Xia, K.; Zhang, S.; Kong, C.; Hu, Q.; Yang, S. Hyperspectral indirect inversion of heavy-metal copper in reclaimed soil of iron ore area. Spectroc. Acta Part A Mol. Biomol. Spectosc. 2019, 222, 117191. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, C.; Lu, Y.; Shen, Q.; Zhao, H.; Tao, Y.; Pan, X. Evaluating the characteristics of soil vis-NIR spectra after the removal of moisture effect using external parameter orthogonalization. Geoderma 2020, 376, 114568. [Google Scholar] [CrossRef]
- Li, H.; Liang, Y.; Xu, Q.; Cao, D. Key wavelengths screening using competitive adaptive reweighted sampling method for multivariate calibration. Anal. Chim. Acta. 2009, 648, 77–84. [Google Scholar] [CrossRef]
- Whitley, D. A genetic algorithm tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Araújo, M.C.U.; Saldanha, T.C.B.; Galvão, R.K.H.; Yoneyama, T.; Chame, H.C.; Visani, V. The successive projections algorithm for variable selection in spectroscopic multicomponent analysis. Chemom. Intell. Lab. Syst. 2001, 57, 65–73. [Google Scholar] [CrossRef]
- Farifteh, J.; Van der Meer, F.; Atzberger, C.; Carranza, E.J.M. Quantitative analysis of salt-affected soil reflectance spectra: A comparison of two adaptive methods (PLSR and ANN). Remote Sens. Environ. 2007, 110, 59–78. [Google Scholar] [CrossRef]
- Zhang, T.-T.; Zeng, S.-L.; Gao, Y.; Ouyang, Z.-T.; Li, B.; Fang, C.-M.; Zhao, B. Using hyperspectral vegetation indices as a proxy to monitor soil salinity. Ecol. Indic. 2011, 11, 1552–1562. [Google Scholar] [CrossRef]
- Jin, X.; Li, S.; Zhang, W.; Zhu, J.; Sun, J. Prediction of Soil-Available Potassium Content with Visible Near-Infrared Ray Spectroscopy of Different Pretreatment Transformations by the Boosting Algorithms. Appl. Sci. 2020, 10, 1520. [Google Scholar] [CrossRef] [Green Version]
- Mouazen, A.M.; Kuang, B.; De Baerdemaeker, J.; Ramon, H. Comparison among principal component, partial least squares and back propagation neural network analyses for accuracy of measurement of selected soil properties with visible and near infrared spectroscopy. Geoderma 2010, 158, 23–31. [Google Scholar] [CrossRef]
- Ramoelo, A.; Skidmore, A.K.; Cho, M.A.; Mathieu, R.; Heitkönig, I.M.A.; Dudeni-Tlhone, N.; Schlerf, M.; Prins, H.H.T. Non-linear partial least square regression increases the estimation accuracy of grass nitrogen and phosphorus using in situ hyperspectral and environmental data. ISPRS J. Photogramm. Remote Sens. 2013, 82, 27–40. [Google Scholar] [CrossRef]
- Jia, S.; Li, H.; Wang, Y.; Tong, R.; Li, Q. Hyperspectral Imaging Analysis for the Classification of Soil Types and the Determination of Soil Total Nitrogen. Sensors 2017, 17, 2252. [Google Scholar] [CrossRef]
- Pullanagari, R.R.; Kereszturi, G.; Yule, I.J. Quantification of dead vegetation fraction in mixed pastures using AisaFENIX imaging spectroscopy data. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 26–35. [Google Scholar] [CrossRef]
- Li, H.; Jia, S.; Le, Z. Quantitative Analysis of Soil Total Nitrogen Using Hyperspectral Imaging Technology with Extreme Learning Machine. Sensors 2019, 19, 4355. [Google Scholar] [CrossRef] [Green Version]
- Dotto, A.C.; Dalmolin, R.S.D.; Caten, A.; Grunwald, S. A systematic study on the application of scatter-corrective and spectral-derivative preprocessing for multivariate prediction of soil organic carbon by Vis-NIR spectra. Geoderma 2018, 314, 262–274. [Google Scholar] [CrossRef]
- Huang, M.; Zhu, C.; Ma, C.; Yang, Z.; Liu, Y.; Jia, T. The Hongqiaocun Site: The earliest evidence of ancient flood sedimentation of the water conservancy facilities in the Chengdu Plain, China. Catena 2020, 185, 104296. [Google Scholar] [CrossRef]
- Ward, K.J.; Chabrillat, S.; Neumann, C.; Foerster, S. A remote sensing adapted approach for soil organic carbon prediction based on the spectrally clustered LUCAS soil database. Geoderma 2019, 353, 297–307. [Google Scholar] [CrossRef]
- Walkley, A.; Black, I.A. An examination of Degtjareff method for determining soil organic matter and a proposed modification of the chromic acid titration method. Soil Sci. 1934, 37, 29–37. [Google Scholar] [CrossRef]
- Lu, R.K. Methods of Soil and Agrochemistry Analysis; China Agricultural Science and Technology Press: Beijing, China, 2000. [Google Scholar]
- Stenberg, B.; Viscarra Rossel, R.A.; Mouazen, A.M.; Wetterlind, J. Visible and near infrared spectroscopy in soil science. Adv. Agron. 2010, 107, 163–215. [Google Scholar] [CrossRef] [Green Version]
- Xu, D.; Ma, W.; Chen, S.; Jiang, Q.; He, K.; Shi, Z. Assessment of important soil properties related to Chinese Soil Taxonomy based on vis–NIR reflectance spectroscopy. Comput. Electron. Agric. 2018, 144, 1–8. [Google Scholar] [CrossRef]
- Peng, X.; Shi, T.; Song, A.; Chen, Y.; Gao, W. Estimating Soil Organic Carbon Using VIS/NIR Spectroscopy with SVMR and combining Methods. Remote Sens. 2014, 6, 2699–2717. [Google Scholar] [CrossRef] [Green Version]
- Li, H.-D.; Xu, Q.-S.; Liang, Y.-Z. libPLS: An integrated library for partial least squares regression and linear discriminant analysis. Chemom. Intell. Lab. Syst. 2018, 176, 34–43. [Google Scholar] [CrossRef]
- Feilhauer, H.; Asner, G.P.; Martin, R.E. Multi-method ensemble selection of spectral bands related to leaf biochemistry. Remote Sens. Environ. 2015, 164, 57–65. [Google Scholar] [CrossRef]
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, W.J., III. The collinearity problem in linear regression. The partial least squares (PLS) approach to generalized inverses. SIAM J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef] [Green Version]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Vohland, M.; Besold, J.; Hill, J.; Fründ, H. Comparing different multivariate calibration methods for the determination of soil organic carbon pools with visible to near infrared spectroscopy. Geoderma 2011, 166, 198–205. [Google Scholar] [CrossRef]
- Vasques, G.M.; Grunwald, S.; Sickman, J.O. Modeling of Soil Organic Carbon Fractions Using Visible–Near-Infrared Spectroscopy. Soil Sci. Soc. Am. J. 2009, 73, 176. [Google Scholar] [CrossRef] [Green Version]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Seifi Majdar, R.; Ghassemian, H. A probabilistic SVM approach for hyperspectral image classification using spectral and texture features. Int. J. Remote Sens. 2017, 38, 4265–4284. [Google Scholar] [CrossRef]
- Moura-Bueno, J.M.; Dalmolin, R.S.D.; ten Caten, A.; Dotto, A.C.; Demattê, J.A.M. Stratification of a local VIS-NIR-SWIR spectral library by homogeneity criteria yields more accurate soil organic carbon predictions. Geoderma 2019, 337, 565–581. [Google Scholar] [CrossRef]
- Saeys, W.; Mouazen, A.M.; Ramon, H. Potential for Onsite and Online Analysis of Pig Manure using Visible and Near Infrared Reflectance Spectroscopy. Biosyst. Eng. 2005, 91, 393–402. [Google Scholar] [CrossRef]
- Shao, Y.; He, Y. Nitrogen, phosphorus, and potassium prediction in soils, using infrared spectroscopy. Soil Res. 2011, 49, 166. [Google Scholar] [CrossRef]
- Chang, C.-W.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R. Near-infrared reflectance spectroscopy–principal components regression analyses of soil properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef] [Green Version]
- Wilding, L.P. Spatial variability: It’s documentation, accommodation and implication to soil surveys. In Soil Spatial Variability, Las Vegas NV, 30 November—1 December 1984; Nielsen, D.R., Bouma, J., Eds.; Pudoc: Wageningen, The Netherlands, 1985; pp. 166–194. [Google Scholar]
- Hong, Y.; Chen, Y.; Zhang, Y.; Liu, Y.; Liu, Y.; Yu, L.; Liu, Y.; Cheng, H. Transferability of Vis-NIR models for Soil Organic Carbon Estimation between Two Study Areas by using Spiking. Soil Sci. Soc. Am. J. 2018, 82, 1231–1242. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, J.; Yao, X.; Cao, W.; Zhu, Y. Laboratory assessment of three quantitative methods for estimating the organic matter content of soils in China based on visible/near-infrared reflectance spectra. Geoderma 2013, 202–203, 161–170. [Google Scholar] [CrossRef]
- Wang, G.; Wang, W.; Fang, Q.; Jiang, H.; Xin, Q.; Xue, B. The Application of Discrete Wavelet Transform with Improved Partial Least-Squares Method for the Estimation of Soil Properties with Visible and Near-Infrared Spectral Data. Remote Sens. 2018, 10, 867. [Google Scholar] [CrossRef] [Green Version]
- Gras, J.P.; Barthès, B.G.; Mahaut, B.; Trupin, S. Best practices for obtaining and processing field visible and near infrared (VNIR) spectra of topsoils. Geoderma 2014, 214–215, 126–134. [Google Scholar] [CrossRef]
- Knadel, M.; Viscarra Rossel, R.A.; Deng, F.; Thomsen, A.; Greve, M.H. Visible–Near Infrared Spectra as a Proxy for Topsoil Texture and Glacial Boundaries. Soil Sci. Soc. Am. J. 2013, 77, 568–579. [Google Scholar] [CrossRef]
- Galvdo, L.S.; Vitorello, I.; Formaggio, A.R. Relationships of spectral reflectance and color among surface and subsurface horizons of tropical soil profiles. Remote Sens. Environ. 1997, 61, 24–33. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Banin, A. Near infrared analysis (nira) as a method to simultaneously evaluate spectral featureless constituents in soils. Soil Sci. 1995, 159, 259–270. [Google Scholar] [CrossRef]
- Bishop, J.L.; Pieters, C.M.; Edwards, J.O. Infrared spectroscopic analyses on the nature of water in montmorillonite. Clays Clay Miner. 1994, 42, 707–716. [Google Scholar] [CrossRef]
- Clark, R.N.; King, T.; Klejwa, M.; Swayze, G.A.; Vergo, N. High spectral resolution reflectance spectroscopy of minerals. J. Geophys. Res. 1990, 95, 12653–12680. [Google Scholar] [CrossRef] [Green Version]
- Hunt, G. Spectral signatures of particulate minerals in the visible and near infrared. Geophysics 1977, 42, 501–513. [Google Scholar] [CrossRef] [Green Version]
- Gowen, A.A.; Amigo, J.M.; Tsenkova, R. Characterisation of hydrogen bond perturbations in aqueous systems using aquaphotomics and multivariate curve resolution-alternating least squares. Anal. Chim. Acta 2013, 759, 8–20. [Google Scholar] [CrossRef]
- Chen, H.Y. Hyperspectral Estimation of Major Soil Nutrient Content. Ph.D. Thesis, Shandong Agricultural University, Tai’an, China, 2012. (In Chinese with English Abstract). [Google Scholar]
- Guo, P.; Li, T.; Zhang, S.; Li, Z.; Liang, J. Hyperspectral Estimation of Soil Available Potassium at different Altitudes of the Xihe Watershed. Chin. J. Soil Sci. 2019, 50, 274–281, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Galvao, L.S.; Vitorello, I. Role of organic matter in obliterating the effects of iron on spectral reflectance and colour of Brazilian tropical soils. Int. J. Remote Sens. 1998, 19, 1969–1979. [Google Scholar] [CrossRef]
- Ertlen, D.; Schwartz, D.; Trautmann, M.; Webster, R.; Brunet, D. Discriminating between organic matter in soil from grass and forest by near-infrared spectroscopy. Eur. J. Soil Sci. 2010, 61, 207–216. [Google Scholar] [CrossRef]
- Ye, Q.; Jiang, X.; Li, X.; Lin, Y. Comparison on Inversion Model of Soil Organic Matter Content Based on Hyperspectral Data. Trans. Chin. Soc. Agric. Mach. 2017, 48, 164–172, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Shi, T.; Cui, L.; Wang, J.; Fei, T.; Chen, Y.; Wu, G. Comparison of multivariate methods for estimating soil total nitrogen with visible/near-infrared spectroscopy. Plant Soil 2013, 366, 363–375. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).